Computation-guided optimization of split protein systems

Abstract

Splitting bioactive proteins into conditionally reconstituting fragments is a powerful strategy for building tools to study and control biological systems. However, split proteins often exhibit a high propensity to reconstitute even without the conditional trigger, limiting their utility. Current approaches for tuning reconstitution propensity are laborious, context-specific, or often ineffective. Here, we report a computational design strategy grounded in fundamental protein biophysics to guide experimental evaluation of a sparse set of mutants to identify an optimal functional window. We hypothesized that testing a limited set of mutants would direct subsequent mutagenesis efforts by predicting desirable mutant combinations from a vast mutational landscape. This strategy varies the degree of interfacial destabilization while preserving stability and catalytic activity. We validate our method by solving two distinct split protein design challenges, generating both design and mechanistic insights. This new technology will streamline the generation and use of split protein systems for diverse applications.

INTRODUCTION

Split proteins and conditional reconstitution systems are powerful tools for interrogating biology and controlling cell behavior.^1-4 These systems work by splitting a protein into two fragments to disrupt the protein’s function. Each fragment is then fused to a partner domain such that the split protein is reconstituted, and its function is restored, only when the partner domains interact. This modular strategy may be applied to diverse functional proteins to control bioluminescence^5,6, fluorescence⁷, proteolytic cleavage^8-10 and transcription^11,12. As a result, conditionally reconstituted split proteins have been employed in a variety of applications including probing and discovering new protein-protein interactions^13-16, studying post-translational modifications¹⁷, establishing small molecule-regulated control over enzymatic activity^18,19, and rewiring cellular signaling^9,10.

Despite their utility in certain contexts, broader application of split protein systems is largely limited by the spontaneous reconstitution of fragments, resulting in high background activity (Fig. 1a). Past approaches to optimize split protein systems include the development of computational algorithms to computationally identify split sites that avoid extremes of spontaneous reconstitution or failure to reconstitute²⁰, experimental screens to identify thermostabilizing split fragments as these tend to yield more functional split proteins^21-23, and utilization of other computational methods to enable design-driven stabilization of existing proteins^24-27. However, fundamental molecular rules on optimizing a split protein system remain poorly understood. Splitting a protein tends to expose its hydrophobic core, creating highly unfavorable interactions between the core and solvent. Reconstitution is driven by a strong inherent preference to desolvate by recombining the fragments. Evaluating alternative splitting sites can vary reconstitution propensity, but this approach often only partially ameliorates the problem because changing splitting sites may not substantially affect underlying hydrophobic forces. Therefore, it is necessary to identify variants with a reconstitution propensity that precludes spontaneous reconstitution but enables reconstitution under desired conditions. Variants with a range of reconstitution propensities can be generated by random mutagenesis and screened for the desired property.^6,28 However, high-throughput screening is not readily available for all split protein systems, and low-throughput clonal testing of variants can be laborious and suffer from inefficient exploration of sequence space. Even when screens generate improved variants, it may be difficult to interpret why only certain mutants were successful, and as a result, generalizable rules cannot be transferred to guide the tuning of new split protein systems. Furthermore, split protein systems tuned by mutagenesis exhibit performance characteristics determined by (and limited to) the conditions used in the initial screens, again posing a barrier to general applications. This knowledge and capability deficit can be addressed by employing computational protein design tools.

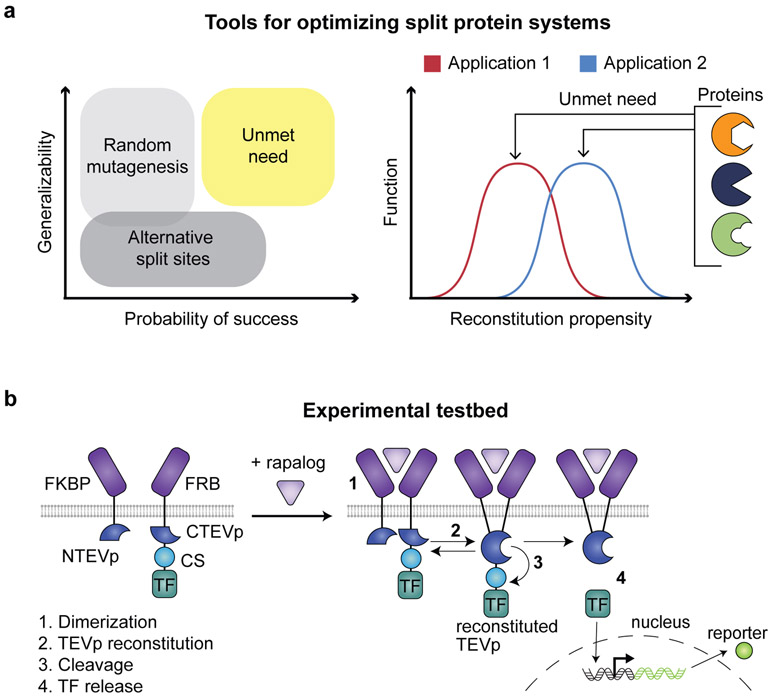
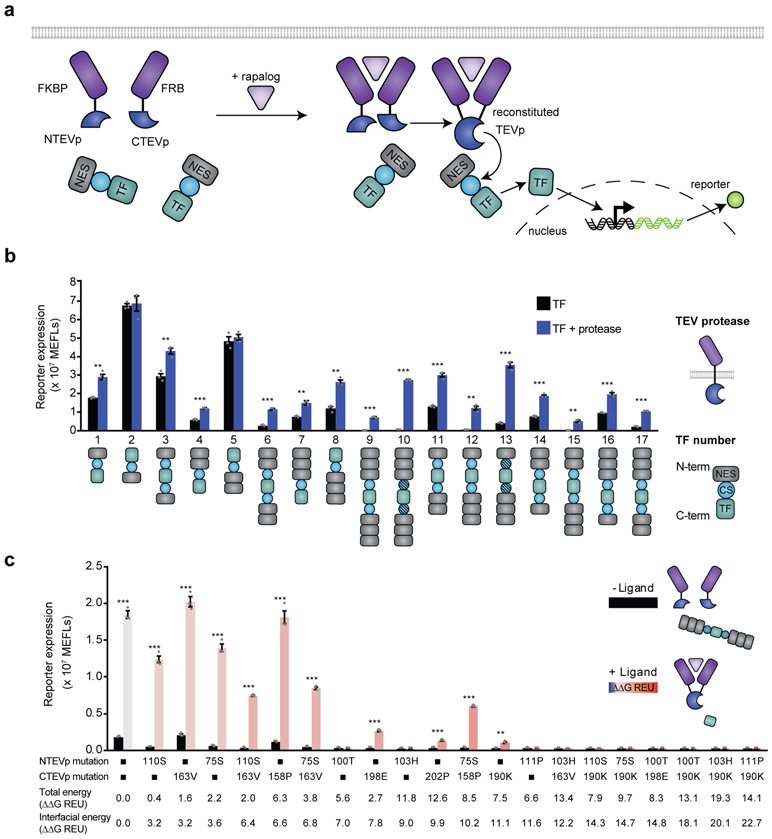
Fig. 1. Design-driven strategy for tuning split protein systems.

a, Current methods for optimizing split proteins are limited (left); an ideal tool would enable adapting split proteins for multiple applications, each of which may require distinct reconstitution propensities (right). b, This cartoon illustrates the experimental testbed used here. Ligand binding-induced chain dimerization results in split TEVp reconstitution, trans-cleavage, and release of a previously sequestered transcription factor to drive reporter expression.

Here, we report a general computational design strategy based on biophysical principles to guide experimental screening for optimizing split protein systems which we term Split Protein Optimization by Reconstitution Tuning, or SPORT. We demonstrate proof-of-concept by optimizing a split protease system for conditional reconstitution in two different contexts, and this exploration yields a straightforward design method that may be extended to tune other split protein systems and can be implemented by most research laboratories. This new method for efficiently engineering split protein systems will streamline the generation and use of split protein systems for diverse applications.

RESULTS

Formulation of the design challenge and strategy

As a first step toward developing a strategy that addresses the challenge of designing split proteins, we selected a model system based on the well-studied Tobacco Etch Virus protease (TEVp) and we sought to tune the reconstitution propensity of split TEVp. For this purpose, we modified a synthetic receptor system that we previously reported (Modular Extracellular Split Architecture, MESA)²⁹ to report upon conditional split TEVp reconstitution. In this testbed, ligand binding-induced dimerization of a membrane receptor reconstitutes an intracellular split TEVp, which autolytically liberates a sequestered transcription factor to drive reporter gene expression (Fig. 1b). Initially, the canonical split TEVp (split between residues 118/119)³⁰ showed high background (ligand-independent) signaling (Supplementary Fig. 1). As the original screens used to identify this split were performed in a soluble rather than membrane-bound context, these data suggest that tethering split TEVp to a membrane may promote reconstitution. This problem was not limited to the canonical split site, as other TEVp partitioning also yielded poor performance (Supplementary Fig. 2). Given these observations, we formulated a design goal: rationally mutate split TEVp to optimize two key MESA performance characteristics, minimal reporter expression in the absence of ligand and a substantial fold increase in reporter expression upon ligand addition.

Biophysical principles underlying SPORT

We developed SPORT, a computation-guided workflow to rationally design split protein interfaces to optimize reconstitution propensity. In this discussion, “reconstitution propensity” is a lumped term that describes the combined effects of the two reversible reactions: (1) fragment association and dissociation, governed by the equilibrium binding constant, and (2) fragment reconstitution, governed by the folding and unfolding equilibrium. SPORT employs Rosetta, a state-of-the-art software package for single-state protein design.³¹ Given a protein with a predetermined split site, we first identified key interfacial residues to target for mutagenesis. Residues with large differences in solvent-accessible surface area (SASA)—when comparing intact protein and split fragments—were classified as buried residues. These buried residues are ideal targets for mutagenesis as they likely contribute substantially to the driving force for spontaneous reconstitution. For each buried residue, we performed a comprehensive, in silico mutational scan to evaluate the energy perturbation of all possible single-point mutations on the interaction energy across the split protein interface (ΔΔG_Interfacial) and total stability of the mutated protein (ΔΔG_Total) relative to the parent. The degree of disruption is a critical design consideration. Insufficient disruption may retain high background activity while excessive disruption may impair catalytic activity due to loss of overall protein stability. Therefore, the interface must be carefully tuned so that the driving force provided by ligand binding-induced dimerization promotes reconstitution. This “Goldilocks zone” likely differs for each individual protein and perhaps depends upon context, and this zone is difficult to define a priori. Therefore, our strategy was to identify the Goldilocks zone for a given protein by choosing mutations that span the range of ΔΔG values. We hypothesized that a limited test set would direct subsequent mutagenesis efforts by predicting desirable mutations from a vast amount of sequence space. Each of these propositions was tested using experimental case studies.

Tuning membrane-tethered split TEV protease

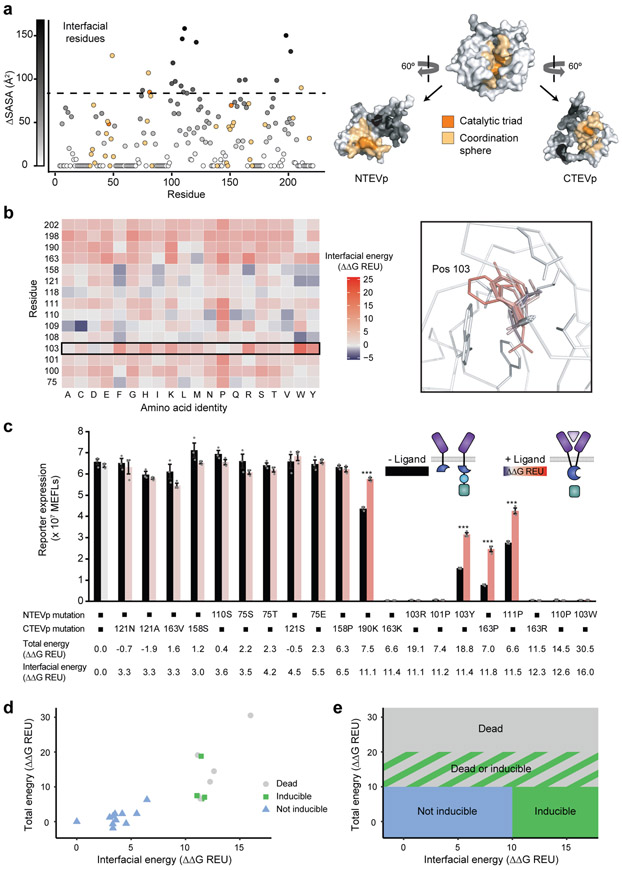
To investigate and validate SPORT, we applied our design workflow to the split TEVp MESA system. We first assessed the per-residue change in solvent accessible surface area (ΔSASA) between the intact form and split fragments (Fig. 2a). In total, 130 of the 218 residues showed increased SASA in the isolated fragments. We excluded from this set the catalytic triad and 27 residues lying within a 6-Å coordination sphere around the catalytic triad to avoid perturbing the catalytic function of reconstituted TEVp. Of the remaining 100 positions, we chose the 15 positions with the largest ΔSASA (9 in the N-terminal half (NTEVp) and 6 in the C-terminal half (CTEVp) of split TEVp) as candidates for mutagenesis. Next, we evaluated the energy perturbation of all possible single-point mutations (285 in total) at these positions using Rosetta. As expected, few mutations were predicted to increase stability, and a vast majority were destabilizing (Fig. 2b, Supplementary Figs. 3, 4). Many positions exhibited a variety of stabilizing, benign, and destabilizing point mutations that were consistent with structure. For instance, bulky sidechain substitutions (Trp, Phe, Tyr, Arg, Lys and His) at position 103 resulted in many steric clashes with neighboring residues (Fig. 2b, right panel) and subsequently conferred large decreases in predicted stability. To validate our selection of the 15 positions with the largest ΔSASA as optimal targets for mutagenesis, we evaluated the energy perturbation of all possible single-point mutations at 18 randomly selected positions not buried at the interface (ΔSASA = 0 Ų) and all positions moderately buried (50 ≤ ΔSASA ≤ 85 Ų) using Rosetta (Supplementary Fig. 4). Although the interface may be perturbed with mutations at moderately buried positions, the greatest diversity of energy perturbations was achieved at positions with the highest ΔSASA. Thus, we concluded that high ΔSASA positions exhibit the greatest potential for tuning reconstitution to various degrees.

Fig. 2. Computation guided method development and experimental analysis.

a, Left, characterization of the change in solvent-accessible surface area (SASA), between fragment and reconstituted forms, of each residue of 118/119 split TEVp. Right, 3D depiction of 118/119 split TEVp, showing the catalytic triad (orange), coordination sphere (yellow), and ΔSASA (greyscale). b, Mutational scanning of high ΔSASA residues (left) and example of all possible mutations of residue 103 (right), with change in interfacial energy indicated by color. Energetic perturbations to total protein stability are shown in Supplementary Fig. 3. c, Experimental analysis of TEVp mutations predicted to span a range of interfacial energies. We hypothesize that modest rapalog-induced toxicity or inhibition of protein expression could explain the slight decrease in signal observed upon rapalog addition for some mutants. Error bars depict S.E.M. Two-tailed Student’s t-test (*p ≤ 0.05, ***p ≤ 0.001). Experiments were performed in biological triplicate. Results are representative of two independent biological experiments. d, Experimental phenotypes observed in c were plotted on an energy landscape and annotated as indicated by color (reporter expression normalized to WT < 0.05 is “dead”, fold induction < 1.2 is “not inducible”, fold induction ≥ 1.2 is “inducible”). e, Proposed model for predicting zones of functional phenotypes based upon total and interfacial energy; the boundaries comprise hypotheses posed based upon observations using the initial 20 mutants tested in c.

Guided by these predictions, we next experimentally characterized 20 single-mutant split TEVp variants that span a wide range of ΔΔG_Interfacial (3.1 to 16.1 Rosetta Energy Units, or REU) and ΔΔG_Total (−1.9 to 30 REU) energies (Fig. 2c). We observed high background signaling (i.e., reporter expression) for disruptions up to ΔΔG_Interfacial ~6.6 REU, suggesting that destabilization was insufficient. However, four out of ten variants with ΔΔG_Interfacial >10 REU exhibited reduced background signaling and substantial ligand-induced activation (Fig. 2c). The remaining six were completely inactive (or “dead”); they induced no signaling under any conditions. Energy-based partitioning across different phenotypes—inducible (fold induction ≥ 1.2), not inducible, and dead—became evident when comparing ΔΔG_Interfacial and ΔΔG_Total of all 20 single mutant split TEVp variants (Fig. 2d). Variants with high background activity due to insufficient destabilization fell in the region where ΔΔG_Interfacial < 10 and ΔΔG_Total < 10 REU. Variants with the dead phenotype had ΔΔG_Interfacial > 10 and ΔΔG_Total > 10 REU; since these mutants were expressed, as confirmed by Western blot (Supplementary Fig. 5), the lack of signaling suggested that these mutations directly preclude reconstitution. Most of the inducible variants (three out of four) were observed in the energy window where ΔΔG_Interfacial > 10 and ΔΔG_Total < 10 REU, which may represent the Goldilocks zone we hypothesized to exist. An additional region contained a mixture of inducible and dead phenotypes. By inspection of these results, we then proposed a model for broadly classifying experimental phenotypes based on energy partitions (Fig. 2e); this hypothesis was used to guide our selection of the subsequent round of mutants for experimental characterization.

SPORT predicts outcomes of combining mutations

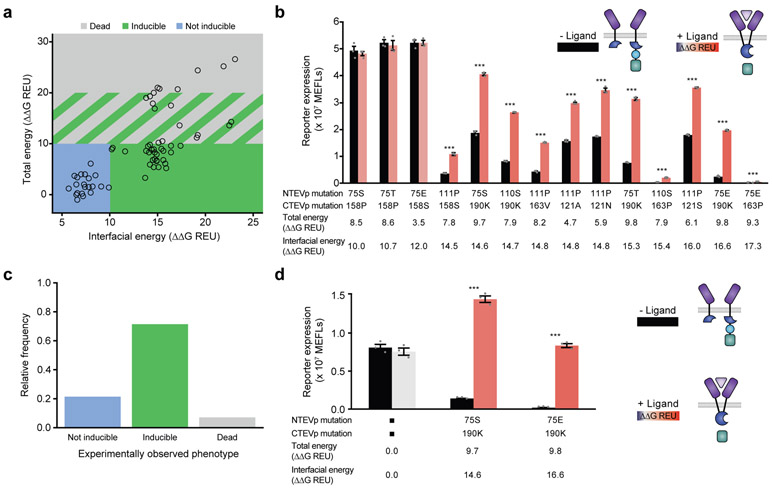
We next evaluated whether our proposed classifier model—a hypothesis proposed based upon observations with single mutants—could predict the phenotypes of combined NTEVp and CTEVp mutations, including both double (two mutations on one chain) and paired (one mutation on each chain) mutants derived by combining the initial 14 single, non-dead mutations tested, yielding 67 possible double and paired mutants. Of these 67 possible double and paired mutants, 28 mutants were predicted to be inducible (Fig. 3a). The region of predicted inducibility encompasses high ΔΔG_Interfacial energy and low ΔΔG_Total energy; mutations that have a large effect on the interface and a small effect on overall folding are desired. We selected 14 mutants that span the interfacial energy range for experimental investigation. Ten mutants exhibited inducible signaling as predicted, one was dead, and three were not inducible (yielding an observed accuracy of 0.71 for inducible predictions) (Fig. 3b,c). Interestingly, three of the prediction failures fell at the low end of the range of predicted changes in interfacial energy, suggesting opportunities for refining our initial classification hypothesis. For the 67 mutants tested, the calculated ΔΔG for the double and paired mutants were nearly identical to the sums of the ΔΔG calculated for the associated single mutants (Supplementary Fig. 6), which is unsurprising given that our analysis focuses primarily on the local effects of each mutation. Thus, for subsequent analyses of combined mutants, we simply added the effects of single mutants in our calculations.

Fig. 3. Evaluation of model-predicted phenotypes for combined mutations.

a, Computed energies and computationally predicted phenotypes (open circle data points) based on the classifier model (shaded boxes)—proposed as a hypothesis in Fig. 2e—of all possible double and paired mutants constructed by combinatorial sampling of the 20 initial single mutants tested (omitting the 6 dead mutations) in Fig. 2c. b, Experimental evaluation of selected mutants predicted to be inducible. c, Experimentally observed phenotypes for the fourteen mutants predicted to be inducible (from b), showing that the model predicts inducibility at a fairly high rate (10/14). d, Normalizing protein expression levels improves performance (fold induction) of selected mutants (from b), whereas WT function is not changed. Fold inductions for 75S/190K and 75E/190K: 2.2 and 7.9 respectively (from b) and 10.3 and 43.3 respectively (from d). The normalization results in a statistically significant improvement of fold induction (between panels b and d) for each of the two mutant pairs analyzed (two-tailed Student’s t-test, p ≤ 0.001). Normalization was achieved using Western blot analysis (Supplementary Fig. 7) to adjust DNA doses transfected (per well, N-terminal chains: 0.4 ng WT, 1 ng 75S, 1.4 ng 75E; C-terminal chains: 5 ng WT, 12 ng 190K). Error bars depict S.E.M. (*p ≤ 0.05, ***p ≤ 0.001). Experiments were performed in biological triplicate. Results are representative of two independent biological experiments.

We next investigated how variations in expression level might impact inducibility. We used Western blot analysis to normalize and vary chain expression levels by adjusting DNA doses (Supplementary Fig. 7). Notably, multiple constructs remained inducible across the entire range of doses tested, suggesting that our SPORT-optimized mechanism is robust to variations in chain expression level and ratio. However, the performance of these constructs (i.e., fold induction of signaling upon ligand addition) could be substantially improved through tuning expression such that protein levels of each fragment are comparable (Fig. 3d, Supplementary Fig. 8). It is possible that some mutations altered both catalytic efficiency of the reconstituted TEVp and reconstitution propensity. For example, for mutants that exhibit decreased “ON” state compared to WT split TEVp, it is difficult to disentangle these effects. However, changes in catalytic efficiency alone cannot explain the behavior of many mutants exhibiting increased fold-induction upon ligand addition (Supplementary Fig. 8), because simply decreasing catalytic efficiency would decrease both background signaling and ligand-induced signaling²⁹. Moreover, there exist several mutants for which the magnitude of the “ON” state is comparable to that of the WT, providing no evidence of altered catalytic efficiency. Taken together, these results suggest that a classifier calibrated with a limited set of experimental observations spanning the full range of ΔΔG can predict function of new mutants with high accuracy in a manner that is independent of expression level of the construct.

Mechanistic insights of SPORT-guided mutations

In order to generate insights into how the high-performing mutants identified above achieve improved function, we investigated overall protein stability, dimerization-induced stabilization, and reconstitution propensity. We investigated each of these phenomena in the cellular context to best enable comparisons with the functional evaluations used to identify these high-performing variants. We previously observed that each individual mutant fragment was expressed in the absence of ligand, many at levels comparable to those of the WT fragments (Supplementary Fig. 5); thus, these mutations did not act by diminishing global stability of the fragments. However, this does not rule out the possibility that some mutants exhibit some dimerization-induced stabilization or dimerization-induced stabilization plus altered reconstitution propensity, so we explored this possibility by quantifying levels of protein expression (accumulation) in cells as a contextually relevant measure of stability³². Chains were expressed in various pairings, and several mutant chain pairs showed some elevated accumulation in the presence of ligand (Supplementary Fig. 9a,b). Interestingly, the magnitude of this effect depended upon which chains were paired. However, no mutants exhibited enough destabilization in the absence of ligand to explain functional consequences such as diminished background protease activity (Supplementary Fig. 9c). Therefore, although some SPORT-guided mutations confer modest ligand-induced stabilization, this effect is insufficient to explain the functional ligand-induced signaling trends observed when comparing mutants to WT versions of split TEVp.

We next investigated how split TEVp domains interact using a single-cell resolution FRET-based flow cytometry assay we recently reported³³. As illustrated in Supplementary Fig. 10a, adding FRET fluorophores mCerulean and mVenus onto the C-termini of the split TEVp chains enables the evaluation of association-dependent FRET signal in the absence and presence of ligand. Interestingly, mutant split TEVp variants did not exhibit substantially reduced FRET, compared to WT, in the absence of ligand (Supplementary Fig. 10b). This could indicate that FRET due to transient diffusive interaction between chains (that does not result in sufficient protease activity to yield reporter induction), is the dominant contributor to FRET in the absence of ligand (compared to FRET due to spontaneous reconstitution). Mutant pairs that were highly inducible in functional assays (e.g., all combinations including CTEVp 190K) generally exhibited an increase in FRET signal upon ligand addition, whereas WT split TEVp exhibited no such increase. There were also exceptions to this rule; for instance, all combinations including NTEVp 111P exhibited enhanced ligand-inducible signaling but no ligand-induced increase in FRET. Overall, these experiments provided additional mechanistic insights and demonstrated that SPORT-guided mutations may identify split protein variants that exhibit enhanced performance through subtly distinct mechanisms.

SPORT predicts phenotypes of novel variants

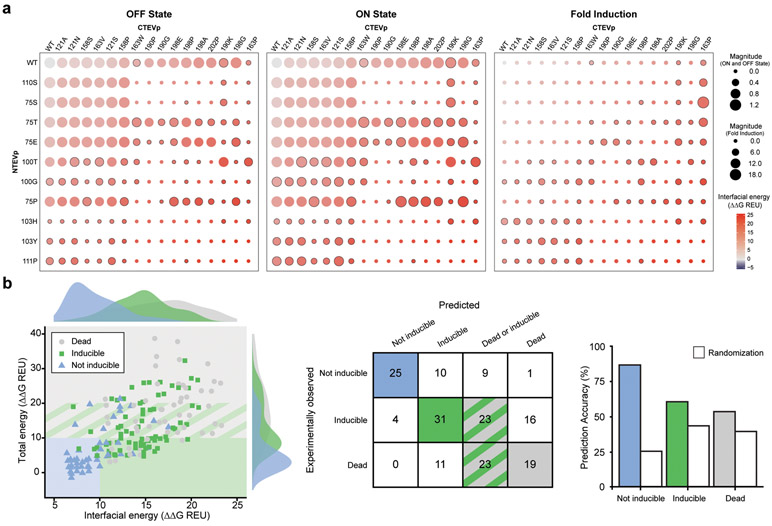
To investigate the accuracy of our classification scheme, we next tested a broad set of mutants (not included in our calibration set) including new single mutants and all combinations of paired mutations derived from both the original and this expanded mutation set (omitting dead constructs). Mutants were selected to explore the boundaries of the energy landscape classifier model and were expected to reflect a wide range of induced and uninduced reporter expression levels and ratios (Figs. 2e, 3a). We also sought to investigate whether the phenotypic partitioning demonstrated for inducibility (Fig. 3b,c) is extensible to the other phenotype classes (i.e., dead and not inducible). This expanded set paired 10 N-terminal mutations with 16 C-terminal mutations. In general, variants with larger ΔΔG_Interfacial energies had lower reporter expression levels in both the background (OFF) and ligand-induced (ON) states (Fig. 4a left and middle panels; Supplementary Fig. 11a; Supplementary Fig.11b left and middle panels). Thus, the cost of lowering the OFF state is to also lower the ON state, but these reductions are not always proportional. This is evident by the diversity of calculated fold inductions (Fig. 4a, right panel, Supplementary Fig. 11b, right panel). Only one variant, 75P/198E, exhibited a substantial decrease in the OFF state and an increase in the ON state relative to wild type (WT). However, the variants with highest fold inductions, such as 75S/163P (17.3 fold induction) and 75T/163P (9.92 fold induction), exhibited substantially lower OFF and ON states than did the WT, reflecting a tradeoff between desirable performance characteristics.

Fig. 4. Evaluation of model-predicted phenotypes for novel mutations and combinations.

a, For each experimentally characterized construct, reporter output was quantified in the absence of ligand (OFF state) and following ligand addition (ON state), and the fold induction was calculated. Calculated interfacial energy for each construct is indicated by circle color, magnitude of reporter expression (or fold-induction) is indicated by circle size, and constructs with a fold induction ≥ 1.2 are denoted with a black border. Single mutants observed to be dead (Fig. 2c) were not carried forward to this analysis. b, Left, experimentally observed phenotypes (data point color) were mapped onto the proposed classifier model (shaded boxes) from Fig. 2e, with observed frequency distributions shown as histograms. Right, evaluation of model prediction accuracy compared to random assignment of phenotypes.

Overall, we observed moderate agreement between the experimental phenotypes (data point color) and predicted phenotypes (classification scheme proposed based upon initial observations—the shaded boxes) for these novel variants and combinations (Fig. 4b). The classifier model was most accurate for predicting the not-inducible phenotype (25 of 29, 86%). Many inducible phenotype predictions were confirmed (31 of 52, 60%). This success rate is impressive given that phenotypic classification boundaries were set roughly based upon the sparse calibration set (Fig. 2e). The distributions of total and interfacial energies indicate natural phenotype boundaries like those drawn from the calibration set (Fig. 4b). The “Goldilocks” zone of this extended data set appears to represent regions of sequence space where one can increase ΔΔG_Interfacial as high as possible without incurring a substantial penalty in ΔΔG_Total. The “dead” zone may represent variants with high ΔΔG_Total and high ΔΔG_Total, which may indicate a disruption of proper protein folding.

In order to gain additional insight into how choice of calibration set and sample size may impact the accuracy of SPORT predictions, we performed retrospective bootstrapping analysis of the data presented in Figure 4 (see Supplementary Software 1 for full details). Experimental data were stratified by the energy landscape and partitioned randomly into calibration and prediction subsets. Linear discriminate analysis was applied to evaluate the accuracy of classification under various conditions (Supplementary Fig. 12). We observed robust prediction accuracy using multiple unique calibration sets and using sample sizes ranging from 4 to 28. This outcome suggests that our ability to generate a general classification model was not dependent upon the specific calibration data we used in our initial characterization experiment (Fig. 2c), and that a relatively small set of calibration data drawn from a distribution like that included in Figure 4 would be sufficient to generate a general classification model.

Extension of SPORT predictions to new design goals

A major limitation to current approaches for employing split proteins is that often a variant selected to perform well in one context fails in a different context. To investigate whether the SPORT design method is generalizable beyond our initial model system, we developed a distinct model system that employs split TEVp in a soluble form, where we hypothesized that a different reconstitution propensity would be required (compared to the membrane-bound model system). In this system (Fig. 5a), ligand binding domains were fused to split TEVp domains, and a separate soluble transcription factor flanked by protease cleavage sites and nuclear export signals (NES) was expressed; TEVp-mediated cleavage removes the NES from the transcription factor to enable nuclear localization and reporter expression. We first built and tested a panel of candidate constructs, varying the number of NES elements, their placement at the N and/or C termini of the transcription factor, and the P1’ residue of the TEVp cleavage sequence which governs cleavage kinetics³⁴ (Fig. 5b). Several soluble transcription factor constructs exhibited the desired phenotype of low signaling in the absence of TEVp and high signaling when co-expressed with full TEVp; construct TF10 was selected for evaluating split TEVp variants.

Fig. 5. Model-guided design of a new split TEVp application in soluble context.

a, This cartoon illustrates the soluble split TEVp testbed. Ligand-binding-induced dimerization mediates reconstitution of split TEVp, which then cleaves one or more nuclear export sequence (NES) elements from a soluble transcription factor, leading to nuclear import and reporter expression. b, The testbed was developed by evaluating engineered transcription factors (TF) for consistency with the mechanism proposed in a; varying the number of NES elements, NES placement at the N and/or C terminus of the transcription factor, and the P1’ residue of the TEVp cleavage sequence, where shaded cleavage sequence (CS) domains indicate a Gly residue in the P1’ position, and unshaded CS domains indicate a Met residue in this position.³⁴ c, Experimental analysis of single and paired mutants sampling a range of interfacial energies (indicated by color and labeled), employing TF10 from b. Error bars depict S.E.M. Two-tailed Student’s t-test (*p ≤ 0.05, ***p ≤ 0.001). Experiments were performed in biological triplicate. Results are representative of two independent biological experiments.

Using our soluble split TEVp test system, we evaluated a subset of mutants comprising 10 single TEVp mutants and 10 paired TEVp mutants that span a range of interfacial energies (Fig. 5c). The construct based upon WT split TEVp exhibited a substantial fold induction, which is consistent with the fact that this split protein was identified by screens performed in the soluble phase³⁰. However, the WT construct also yielded high background signaling, indicating an opportunity to improve performance. For modest increases in ΔΔG_Interfacial (~0–3.6 REU), background signaling persisted. For intermediate increases in ΔΔG_Interfacial (~6-10 REU), a mixture of phenotypes was observed, including dead constructs and those with both substantially reduced background signaling and substantial fold inductions. For large increase in ΔΔG_Interfacial > ~10 REU, constructs were generally weakly-inducible or dead. Thus, a focused evaluation of 20 design variants, guided by SPORT, yielded ~5 variants exhibiting improved performance compared to the WT construct. Altogether, these observations demonstrate that the SPORT method and associated energy landscape concept can be employed to efficiently solve distinct split protein optimization challenges.

DISCUSSION

In this study, we developed and validated what is to our knowledge the first computation-guided strategy for tuning split protein reconstitution propensity. Although the split TEVp MESA used as our first model system would have been deemed infeasible using standard evaluations of split proteins (Supplementary Figs. 1-2), application of SPORT to tune this system yielded multiple high-performing new synthetic receptor scaffolds (Fig. 3d). We show that unlike the classical MESA receptors we have characterized in prior work^29,35,36, split TEVp MESA tuned by SPORT exhibit excellent performance characteristics (i.e., low-background and high fold-induction) in a manner that is robust to variations in both biosensor expression level and the ratio at which biosensor chains are expressed (Supplementary Fig. 8). This property is of great practical utility, as it precludes the need to carefully tune the implementation of each biosensor.

Several important insights emerged from this study. First, our approach demonstrated that testing a sparse set of mutants along the energy landscape is an effective strategy to choose optimal interfacial energies to promote conditional reconstitution. Second, multiple point mutations with similar energies exhibited similar performance, which suggests reconstitution propensity depends on the energy of destabilization but may be agnostic to specific mutations. Third, the concept of a Goldilocks zone is intuitively appealing and likely generalizable to different proteins and application contexts. Fourth, although the optimal energy window may have to be adjusted on a case-by-case basis, SPORT provides a simple design framework for engineering split protein systems. We find that membrane-bound split proteins must be destabilized to a greater degree than soluble split proteins in order to avoid spontaneous reconstitution. Altogether, these results show that split protein systems can be engineered based on fundamental principles of protein biophysics, which obviates the need for exhaustive screening and generates rules applicable to new candidate proteins.

There are several interesting opportunities for extending and improving SPORT in future work. First, it would be valuable to identify general principles as to when SPORT is a useful tool for tuning a given split protein of interest. For example, it could also be interesting to determine how properties such as intrinsic protein thermostability influence the opportunity for tuning reconstitution propensity through this method. In addition, although our analysis showed that SPORT can be used to identify mutations that confer specific energy changes, it does not yet enable a priori prediction of where the Goldilocks zone will fall for new applications. It is possible that subsequent analysis of many case studies could identify trends that enable such predictions and thus harness SPORT to further focus experimental investigations. Another opportunity is pairing SPORT with a multiparameteric optimization framework for exploring pareto-optimal tradeoffs between performance characteristics; for example, in our model system, there seems to be such a tradeoff between low background in the ligand-free state and high signaling in the ligand-induced state. Finally, the SPORT algorithm itself may be refined to better avoid false positives (e.g., dead mutants that share a region of the energy landscape with inducible variants). Altogether, our findings suggest many opportunities for expanding the utility of split proteins for many new applications and highlight the impact of SPORT-guided development of novel biochemical and synthetic biology tools.

METHODS

General DNA assembly

Plasmid cloning was performed using standard molecular biology techniques of PCR and restriction enzyme cloning with Phusion DNA Polymerase (NEB), restriction enzymes (NEB; Thermo Fisher), T4 DNA Ligase (NEB), and Antarctic Phosphatase (NEB). Development of the tTA-responsive YFP reporter plasmid was described previously²⁹. Plasmids were transformed into chemically competent TOP10 E. coli (Thermo Fisher) and grown at 37°C.

Plasmid preparation

Plasmid DNA used for transfection was prepared using the PEG precipitation method, which was previously described in detail.³⁷

Cell culture

HEK293FT cells (Life Technologies/Thermo) were maintained at 37°C incubator and 5% CO₂. Cells were cultured in DMEM (Gibco #31600-091) with 4.5 g/L glucose (1 g/L, Gibco #31600-091; 3.5 g/L additional, Sigma #G7021), 3.7 g/L sodium bicarbonate (Fisher Scientific #S233), 10% FBS (Gibco #16140-071), 6 mM L-glutamine (2 mM from Gibco 31600-091 and 4 mM from additional Gibco 25030-081), penicillin (100 U/μL), and streptomycin (100 μg/mL) (Gibco 15140122). Cells were cultured in a 37°C incubator with 5% CO₂.

Transfection

Transfections were performed in 24-well plates seeded at 1.5 x 10⁵ cells in 0.5 mL of DMEM media (for functional experiments), or 6 well plates seeded at 7 x 10⁵ cells in 2 mL DMEM media (for Western blot experiments). At 6-8 hours post-seeding, cells were transfected using calcium phosphate method with a total DNA content of 1-2 ug DNA per mL of media (see Supplementary Table 1 for plasmid doses used in each experiment), using DNA prepared by PEG precipitation. All experiments included blue fluorescent protein (BFP) as a control to assess transfection efficiency. Plasmid DNA was mixed in H₂O, and 2 M CaCl₂ was added to a final concentration of 0.3 M CaCl₂. This mixture was added dropwise to an equal-volume solution of 2x HEPES-Buffered Saline (280 mM NaCl, 0.5 M HEPES, 1.5 mM Na₂HPO₄) and gently pipetted up and down four times. After 2.5 minutes, the solution was mixed vigorously by pipetting ten times. 100 μL of this mixture was added dropwise to each well of a 24-well plate, or 200 μL was added dropwise to each well of a 12-well plate, and the plates were swirled gently. For functional experiments, 12 hours post-transfection, media containing 0.1 μM rapamycin analog (Takara AP21967) or 0.1% ethanol as a control was added to cells. At 24-30 hours post-media change, cells were harvested for flow cytometry with Trypsin-EDTA (Gibco #25300-054), which was then quenched with medium, and the resulting cell solution was added to at least 2 volumes of FACS buffer (PBS pH 7.4 with 2–5 mM EDTA and 0.1% BSA). Cells were spun at 150 x g for 5 min, FACS buffer was decanted, and fresh FACS buffer was added. All experiments were performed in biological triplicate.

Flow Cytometry

Approximately 10⁴ live cells from each transfected well of the 24-well plate were analyzed using a BD LSR Fortessa Special Order Research Product (Robert H. Lurie Cancer Center Flow Cytometry Core) running FACSDiva software. Flow cytometer lasers and filter sets used for data acquisition are listed in Supplementary Table 2 (for experiments involving reporter expression) and Supplementary Table 3 (for experiments involving FRET). Samples were analyzed using FlowJo v10 software (FlowJo, LLC). Fluorescence data were compensated for spectral bleed-through, and additional spectral bleed-through compensation for FRET experiments was performed to compensate fluorescence of either mCerulean or mVenus out of the AmCyan (FRET) channel. As shown in Supplementary Fig. 13, the HEK293FT cell population was identified by FSC-A vs. SSC-A gating, and singlets were identified by FSC-A vs. FSC-H gating. A control sample of cells—generated by transfecting cells with a mass of pcDNA (empty vector) equivalent to the mass of DNA used in other samples in the experiment—was used to distinguish transfected and non-transfected cells. For the single-cell subpopulation of the pcDNA-only sample, a gate was made to identify cells that were positive for the constitutively driven blue fluorescent protein (BFP) used as a transfection control in other samples such that the gate included no more than 1% of the non-fluorescent cells.

Quantification of reporter output

The mean fluorescence intensity (MFI) of the single-cell transfected population was calculated and exported for further analysis. To calculate reporter expression, the FITC channel MFI was averaged across three biological replicates and cell autofluorescence was subtracted. As shown in Supplementary Fig. 14, to convert MFI to Mean Equivalents of Fluorescein (MEFLs), UltraRainbow Calibration Particles (Spherotech URCP-100-2H) were run in each individual experiment. The bead population was identified by FSC-A vs. SSC-A gating, and 9 bead subpopulations were identified through two fluorescent channels, with MEFL values corresponding to each subpopulation supplied by the manufacturer. For each experiment, a calibration curve was generated for the experimentally determined MFI vs. the manufacturer MEFL values, a linear regression was performed, and the slope of the regression was used as a conversion factor. Standard error was propagated through all calculations.

Quantification of FRET by flow cytometry

The workflow used for quantification of FRET by flow cytometry was previously reported in detail³³. Briefly, the mCerulean+/mVenus+ population was distinguished from samples transfected with the transfection control (miRFP670) and pcDNA only, mCerulean only, and mVenus only, by gating such that less than 1% of the single-color samples were included. The normalized FRET (NFRET) parameter³⁸ was defined in the FlowJo workspace, as described by equation (1):

$$NFRET=\frac{CompAmCyanFI}{\sqrt{CompPacificBlueFI\times CompFITCFI}}$$ (1)

Where Comp AmCyan FI is the compensated fluorescence intensity (FI) of a cell in the AmCyan channel, Comp Pacific Blue FI is the compensated fluorescence intensity of that cell in the Pacific Blue channel, and Comp FITC FI is the compensated fluorescence intensity of that cell in the FITC channel. Average NFRET metrics were calculated for negative (cytosolic mCerulean and mVenus co-transfected) and positive (membrane-tethered mCerulean-mVenus fusion protein) controls included in each experiment. A calibrated NFRET parameter was defined with these controls such that the NFRET of all samples is scaled linearly between these controls, as described by equation (2):

$$NFRE{T}_{Calibrated}=\frac{(NFRET-NFRE{T}_{negativecontrol})}{(NFRE{T}_{positivecontrol}-NFRE{T}_{negativecontrol})}$$ (2)

The calibrated NFRET metrics were exported for further analysis. Standard error was propagated through all calculations.

Western blotting

Western blots were performed to evaluate protein expression and normalize total expression of each TEVp chain. A 3X-FLAG tagged NanoLuciferase was used as a normalization control. A detailed Western blot protocol was previously described.³⁷ Antibodies used are Monoclonal ANTI-FLAG M2 antibody produced in mouse (Sigma Cat F#1804; RRID: AB_262044) ; Anti-mouse IgG, HRP-linked Antibody (Cell Signaling Technology Cat# 7076; RRID: AB_330924).

Quantification and expression normalization of split TEVp chains

Scanned Western blot images were imported into ImageJ and analyzed with the analyze gel feature. The intensity for each NTEVp or CTEVp chain band was quantified and reported as the percent of the total signal from all NTEVp or CTEVp chains on the blot. The intensity of the NanoLuciferase normalization control was quantified in the same way. For the expression normalization experiment, this analysis was repeated for multiple image captures at a range of exposure times. The calculated intensity was averaged across all exposure times, and then the NTEVp or CTEVp chain intensity (expression level) was divided by the NanoLuciferase intensity (expression level). This calculated value was compared to the intensity calculated for the WT CTEVp sample, which was included as an internal control for normalization and quantification experiments.

Solvent-accessible Surface Area

The structure of TEVp was obtained from the Research Crystallography for Structural Bioinformatics (RCSB) PDB (ID code: 1LVM). Per-residue solvent-accessible surface areas (SASA) were computed using GROMACS v2018.1, which utilizes the double cubic lattice method (DCLM) described by Eisenhaber et al.³⁹ The change in solvent accessible area was computed as

$$\Delta SASA=SAS{A}_{fragments}-SAS{A}_{reconstituted}$$

where structures of the N and C-terminal fragments were isolated from the crystal structure.

Computational Interface Scanning

All modeling calculations were performed using the Rosetta molecular modeling suite v3.9. Single-point mutants were generated using the standard Relax application, which enables local conformational sampling to minimize energy (Supplementary Note 1 includes full details). The total energy (ΔG_Total) of each mutant was computed as the average of 100 relaxed models.⁴⁰ The energy perturbation to total energy was computed as

$$\Delta \Delta G_{Total}=\Delta G_{Total}^{Mutant}-\Delta G_{Total}^{WT}$$

The Rosetta Scripts application with the InterfaceAnalyzeMover was applied to each relaxed model to evaluate the average residue-residue interaction energies between the N- and C-terminal fragments (Supplementary Note 1 includes the full details). The interfacial energy was computed as the pair-wise sum of all short-range interaction energies as shown by

$$\Delta G_{Interfacial}=\sum _i\sum _{j}Energ{y}_{i-j}^{SR}$$

where i and j denote the sets of residues within each fragment. The energy perturbation of each mutation to the interfacial energy was then computed as

$$\Delta \Delta G_{Interfacial}=\Delta G_{Interfacial}^{Mutant}-\Delta G_{Interfacial}^{WT}$$

Phenotype Classifier

Experimentally characterized variants were assigned class labels (not-inducible, inducible and dead) based on reporter expression levels in the ligand-absent and ligand-induced states. Variants with ≥1.2 fold higher reporter expression in the ligand-induced state relative to the ligand-absent state were labeled as inducible. For variants with expression levels <5% of wild-type (WT) sequence in the ligand-induced state and <1.2 fold activation were classified as functionally dead. The remaining variants were assigned the not-inducible class label.

STATISTICAL ANALYSIS

Statistical details for each experiment are included in the figure legends. The data shown reflect the mean across these biological replicates of the mean fluorescence intensity (MFI) of approximately 2,000–3,000 single, transfected cells. Error bars represent the SEM (standard error of the mean). For statistical analyses, two-tailed Student’s t-tests were used to evaluate whether a significant difference exists between two groups of samples, and the reported comparisons meet the two requirements of this test: (1) the values compared are expected to be derived from a normal distribution, and (2) the variance of each group is expected to be comparable to that of the comparison group since the same transfection methodologies and data collection methods were used for all samples that were compared. A p value of ≤ 0.05 was considered to be statistically significant.

DATA AVAILABILITY

The datasets generated during and/or analyzed during the current study are available from the corresponding authors on reasonable request. Raw experimental data and computation generated data for main text figures are provided in Source Data. Raw experimental data for supplementary figures are provided in Supplementary Dataset 1. Plasmid maps are provided in Supplementary Dataset 2, and annotated descriptions of all plasmids are in Supplementary Dataset 3. The structure of TEVp was obtained from the Research Crystallography for Structural Bioinformatics (RCSB) PDB (ID code: 1LVM). A subset of plasmids used in this study will be made available on Addgene, including complete and annotated GenBank files, at https://www.addgene.org/Joshua_Leonard/.

CODE AVAILABILITY

Rosetta details and script are provided in Supplementary Note 1. Linear discriminate analysis details and script are provided in Supplementary Software 1. Jupyter notebook code used to make Figure 4a is provided in Supplementary Software 2.

Supplementary Material

1657285_Supp_Data1

Supplementary Data 1 Raw data for supplementary figures

1657285_Supp_Software1

Supplementary Software 1 Linear discriminate analysis script. Note that this is a text file with a file extension indicating that it is for use with R.

1657285_Supp_Software2

Supplementary Software 2 Jupyter notebook code for Figure 4a. Note that this is a text file with a file extension indicating that it is for use with Jupyter.

1657285_Supp_Data2

Supplementary Data 2 Archive of plasmid maps

1657285_Supp_Data3

Supplementary Data 3 List of all plasmids and annotation of key features