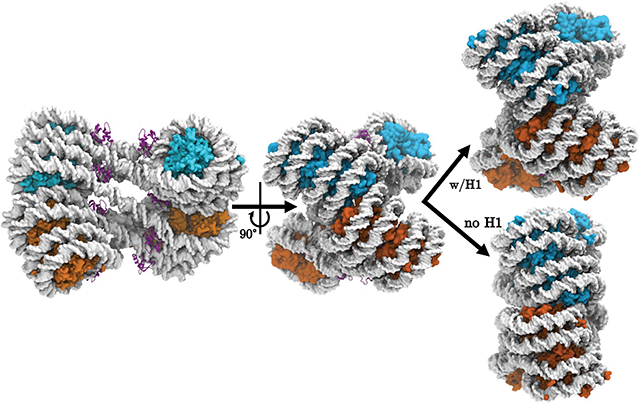
Abstract
Linker histones bind to nucleosomes and modify chromatin structure and dynamics as a means of epigenetic regulation. Biophysical studies have shown that chromatin fibers can adopt a plethora of conformations with varying levels of compaction. Linker histone condensation, and its specific binding disposition, has been associated with directly tuning this ensemble of states. However, the atomistic dynamics and quantification of this mechanism remains poorly understood. Here, we present molecular dynamics simulations of octa-nucleosome arrays, based on a cryo-EM structure of the 30-nm chromatin fiber, with and without the globular domains of the H1 linker histone to determine how they influence fiber structures and dynamics. Results show that when bound, linker histones inhibit DNA flexibility and stabilize repeating tetra-nucleosomal units, giving rise to increased chromatin compaction. Furthermore, upon the removal of H1, there is a significant destabilization of this compact structure as the fiber adopts less strained and untwisted states. Interestingly, linker DNA sampling in the octa-nucleosome is exaggerated compared to its mono-nucleosome counterparts, suggesting that chromatin architecture plays a significant role in DNA strain even in the absence of linker histones. Moreover, H1-bound states are shown to have increased stiffness within tetra-nucleosomes, but not between them. This increased stiffness leads to stronger long-range correlations within the fiber, which may result in the propagation of epigenetic signals over longer spatial ranges. These simulations highlight the effects of linker histone binding on the internal dynamics and global structure of poly-nucleosome arrays, while providing physical insight into a mechanism of chromatin compaction.
Keywords: chromatin fiber dynamics, linker histones, epigenetic mechanisms
Graphical Abstract
Introduction
Serving as the primary storage vessel of genomic information within eukaryotic organisms, chromosomes consist predominantly of organized, long condensed fibers of DNA and structural proteins.1 Known as chromatin, these fibers are made of compacted repeating arrays of distinct DNAprotein complexes called nucleosomes.1–4 Nucleosomes consist of ~147 bp of DNA wrapped around an octamer core of organized histone proteins.5 Within the array, nucleosomes are inter-spaced between varying lengths of linker DNA, which is often quantified by their nucleosome-repeat-length (NRL).6 Computational modeling and topological studies have shown that the NRL regularity can directly affect chromatin compaction via variations in local fiber stiffness.7,8 Furthermore, this value can depend on interactions with a variety of cosolute compounds, nucleosome remodeling factors,6 or DNA sequence9 usually related to a level of charge neutralization and/or structural accommodation. Some examples include cosolute cations (i.e. Mg2+, nuclear polyamines, etc.), basic amino acids found on the terminal tail domains of core histones, proteins found outside of the nucleosome core, and H1 linker histones.10–15
Structural studies have shown chromatin fibers adopt multiple states, including solenoid16,17 or zigzag18–24 like-conformations, with evidence of both forms being present within the same fiber.25 At high ionic strength, nucleosome arrays compact to create fibers with a diameter of about 30-nm in a closed zigzag conformation, 22,23,26–30 similar to what is shown in Figure 1. However, despite the fact that canonical chromatin does form chains with regular and irregular zigzag structures, there is a particular absence of 30-nm fibers from eukaryotic nuclei,31–38 except within terminally differentiated cells.39–42
Figure 1:
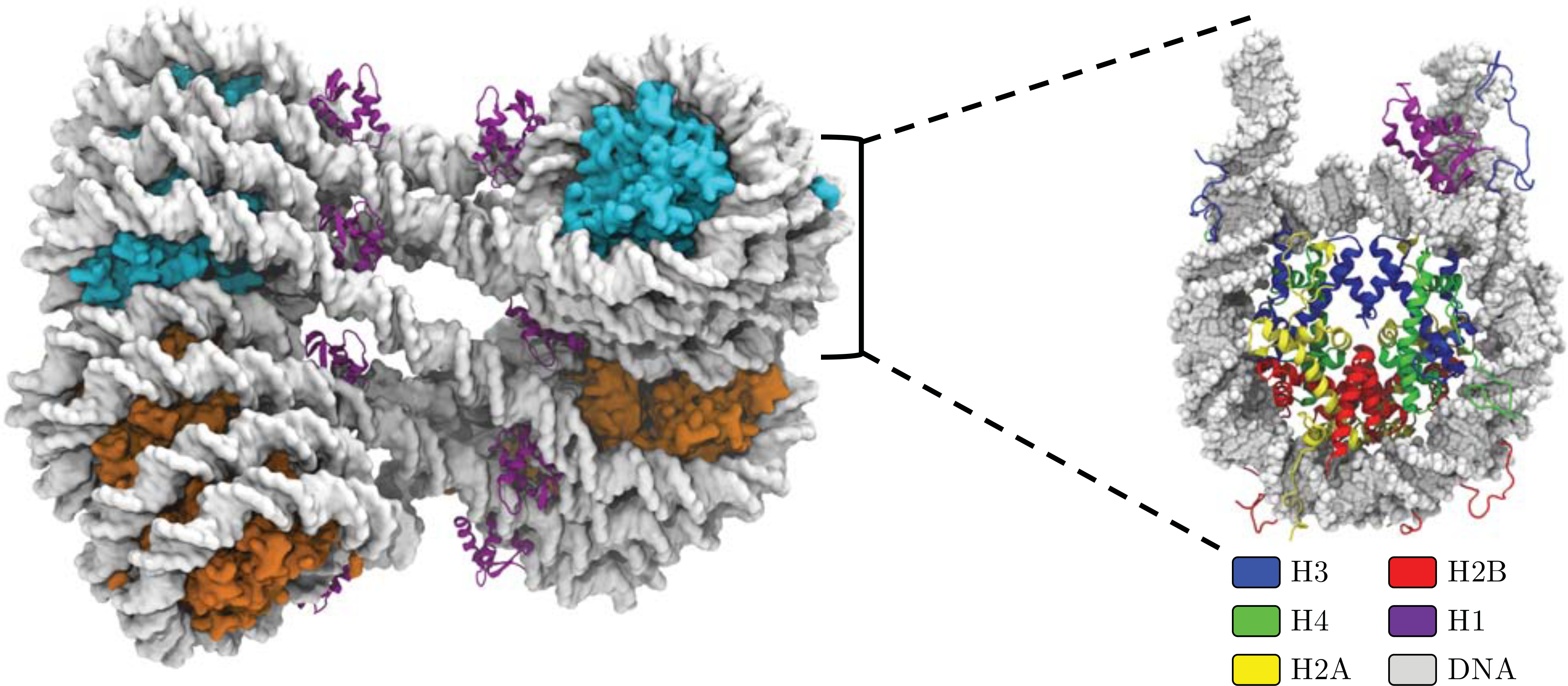
Shown on the left is the octa-nucleosome array constructed using the cryo-EM map of the 30 nm chromatin fiber.23 Each nucleosome is paired with a linker histone (purple) bound asymmetrically off the dyad axis. All core histone tails were included in this study, but are not shown in this figure for visual clarity. On the right is an example of a mono-nucleosome unit from the array with each individual histone shown. The core histones in the poly-nucleosome (left) are colored cyan and orange to distinguish between the upper and lower tetra-nucleosome sub-units.
To date, chromatin structural and mechanistic studies have largely focused on structural regulation at the single-nucleosomal level,43 including such phenomena as nucleosome opening,44–46 the influence of extra-nucleosomal proteins,47–49 and histone variants.50 More recently, studies involving poly-nucleosomal arrays and models of higher order structures have begun to show that chromatin exists in a dynamic equilibrium of states,25,34,38,51–53 suggesting that it exhibits large-scale, concerted dynamics orchestrated by motifs such as remodeling factors and histone variants. Moreover, contemporary coarse-grained modeling of poly-nucleosome arrays with H1 have further emphasized the diversity of chromatin dynamics highlighting structures with irregular NRLs,51 varied cation concentrations,25,52 and higher order structures.38,53 However, there is a severe lack of atomistic resolution studies of poly-nucleosome arrays54,55 which may provide residue-specific information otherwise lost by coarse-grained models.
Interacting with both core and linker DNA,10 the linker histone (H1) plays a crucial role in the condensation of nucleosome chains into higher order architecture,22,49,56–58 like the zig-zag structure,38 along with other cellular functions57 such as gene expression,59–62 heterochromatin genetic activity,63 and cell differentiation,64,65 among many others.66–68 They are found roughly every 200 ± 40 base pairs,69 but may be spaced more intermittently to regulate DNA accessibility for transcription factors. Additionally, linker histones predominantly interact electrostatically with the backbone phosphates of DNA using positively charged residues,70–72 which stabilizes nucleosome arrays hindering linker DNA accessibility and competing with core histone tails for binding space.27,49,73–76 However, this effect has been shown to be completely abrogated upon the addition of nucleosome-free regions within H1-saturated arrays.77 Additionally, Kalashnikova et al. proposed a new model where linker histones serve as regulators of chromatin protein recruitment through interactions with numerous nuclear and nucleolar proteins, suggesting that they provide additional functionality beyond architectural stability.61
In a previous study, we used all-atom molecular dynamics (MD) simulations to demonstrate that the linker histone binding mode on nucleosomes can have substantial effects on linker DNA dynamics.78 Furthermore, we postulated that its presence would have cascading effects on higher order chromatin structures. Indeed, this is highlighted in many of the previously mentioned studies, but none of which provide a mechanism detailing the atomistic molecular dynamics of the chromatin fiber in and out of the presence of H1.79 To extend these ideas to the chromatin fiber, we examined these dynamics via all-atom MD simulations of an octa-nucleosome array with and without the D. melanogaster generic globular domain of H1 (GH1) bound asymmetrically off the dyad. Results suggest that linker histones provide stabilization to the fiber structure at multiple levels. Helical parameters, inspired by similar DNA base-pairing metrics,80–82 quantified a major conformational shift from a twisted condensed state to an untwisted ladder-like state. Stiffness parameters of these metrics show GH1 binding increases torsional stress within tetra-nucleosome sub-units. Furthermore, while an angular analysis of linker DNA motions shows that linker histones limit sampling, it also highlights the stark contrast in mono- versus poly-nucleosome dynamics, especially among in-plane DNA motions. Moreover, generalized correlation analyses shows that linker histone saturation strengthens long-range correlations throughout each system, which can lead to further transfer of epigenetic information across the fiber. This linker histone saturation provides stabilization to the highly strained linker DNA resulting in a highly compact system that is unfavorable for transcription factor binding. Complete abrogation of these extra-nucleosomal proteins allows the fiber to untwist and thus alleviating the aforementioned linker DNA strain.
Results
Linker Histones Stabilize Tetra-Nucleosome Repeats
Models of compact octa-nucleosome structures were generated through a combination of manual placement and flexible fitting of the 1KX5 nucleosome83 and GH1 linker histone crystal structures78 into the cryo-EM map by Song et al. (see Methods), which contains a saturated linker histone stoichiometry.23 To quantify the configurations of these complexes, we took advantage of their double-helical like structures and measured the six canonical parameters of rise, twist, roll, tilt, shift, and slide, which are typically associated with DNA basepairs (see Methods for definitions). For each system there are three sets of tetra-nucleosomal sections, which for clarity we refer to as the top, middle, and bottom segments of the array and that contain nucleosomes one through four, three through six, and five through eight respectively (Figures 2 and 3). Over our simulations, most of these metrics maintained values close to zero, with the exception of the inter-nucleosomal rise and twist which largely describe the observed large-scale conformational changes.
Figure 2:
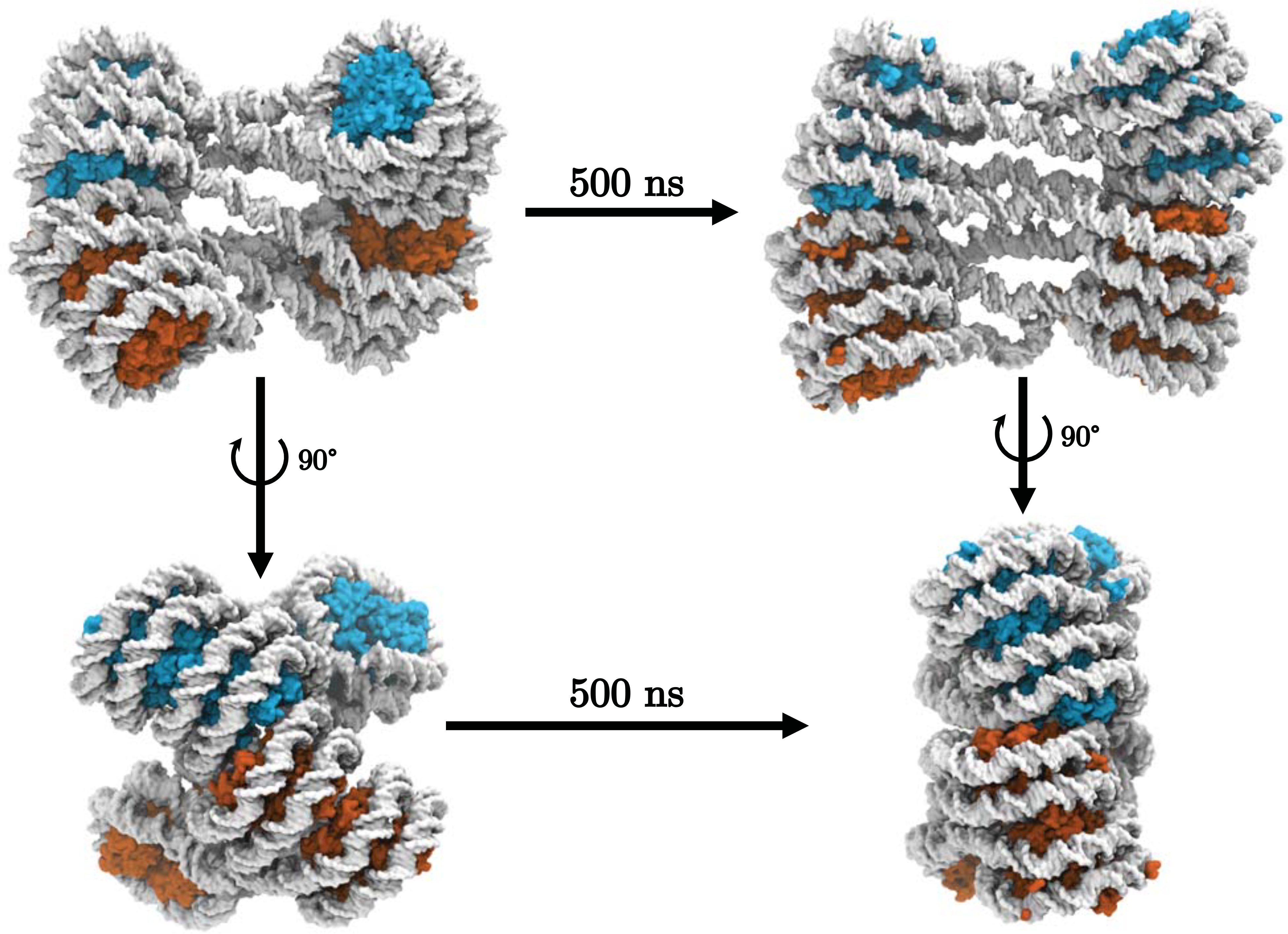
Shown are selected images from a system without the linker histone, at the beginning a simulation (left) and after 500 ns of production (right). The core histones in the poly-nucleosomes are colored to represent the different tetra-nucleosome sub-units as in Figure 1. For analogous images containing GH1, see Figure S6. For additional images at more frequent intervals, see Figures S13 and S14.
Figure 3:
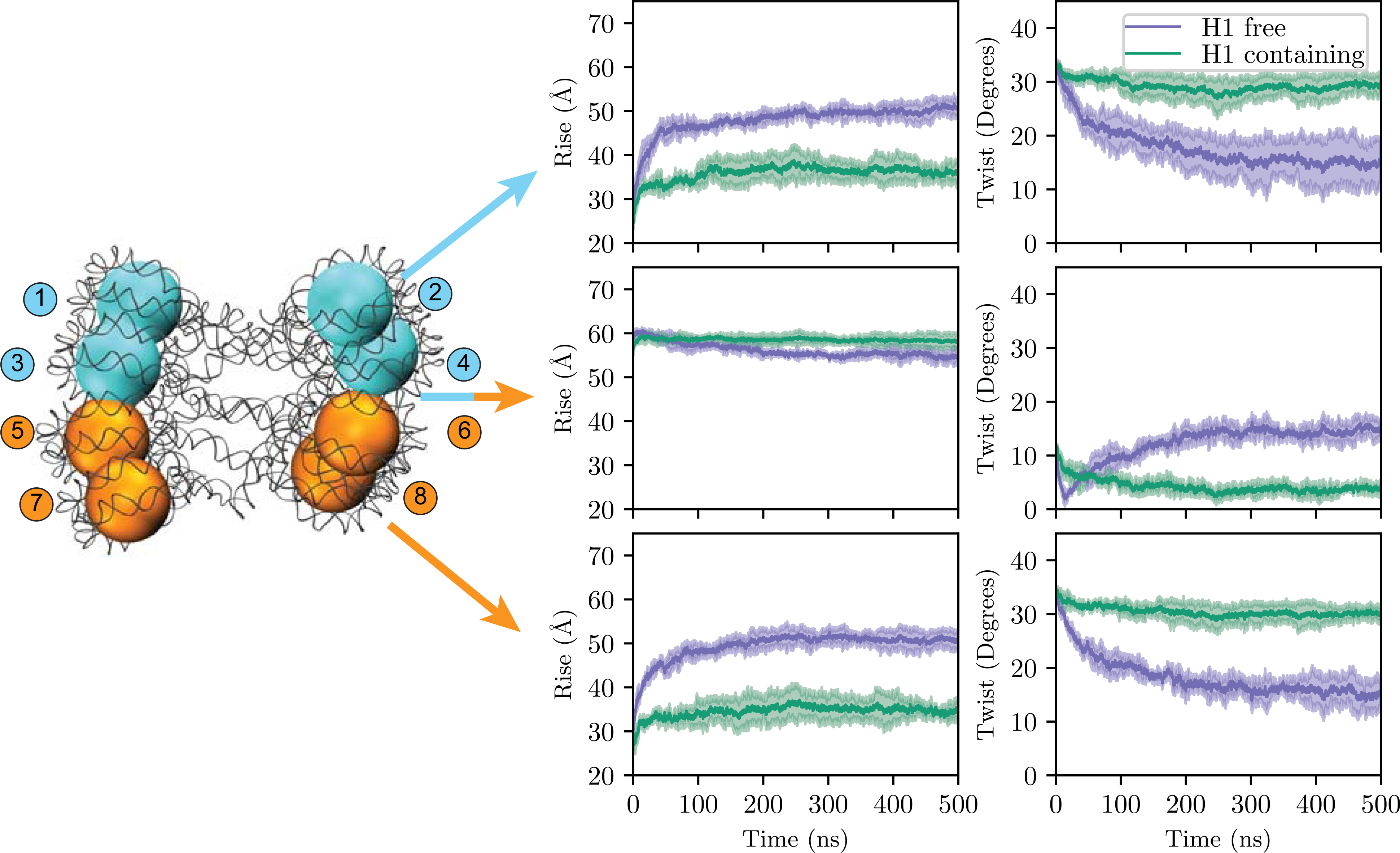
Nucleosomal rise and twist during simulations between the top, middle, and bottom four nucleosomes. Simulations with H1 (orange) maintain the initial stacked tetranucleosome structure, whereas simulations without H1 (blue) adopt a looser stacked conformation. Shown are the average and standard deviations (shaded regions) between the three simulations for each system. Colors of the octa-nucleosome array are to distinguish between tetra-nucleosome sub-units such as in Figures 1 and 2. Each nucleosome is designated with a number from 1 to 8 which is referenced throughout this manuscript.
In each of the three 500 ns simulations we performed with GH1, the rise and twist parameters remained similar to their initial values (middle and right of Figures 2, 3, and S1–S2). In particular, for both the bottom and top tetra-nucleosome segments (tetraNuc), the initial rise and twist of ~27 Å and 33° were largely maintained, equilibrating at ~35 Å and 30°. In contrast, for the middle segment the initial and final rises were higher, with an average value of 58 Å, with a reduced twist that equilibrated from 14° to 4°. This difference in values for the top and bottom array segments relative to the middle highlights the difference in the intra- and inter-tetraNuc structures: in a tetraNuc unit there is relatively little rise between nucleosomes (Nuc), as Nuci forms a tight packing interface with NuCi+2 that creates a twist around the central fiber axis. Meanwhile, between tetraNuc structures the inter-nucleosomal packing is reduced and there is looser interface that has a higher rise and less twist around the helical axis. In addition, the minimal changes in these parameters during each simulation, and their reproducibility between each independent simulation (Figures S1–S2) demonstrates the stability on this stacked tetraNuc structure on the hundreds of nanoseconds timescales.
In contrast, in each of the three 500 ns simulations without GH1, there were dramatic and irreversible changes in all measured rise and twist values which resulted in an elongated and less twisted array (Figures 2, S6, S13, and S14). Despite starting with values identical to GH1 arrays, the stacked tetra-nucleosome structure was lost in the first 150 ns, as is evidenced by the increase in rise of the top and bottom sections to 51 Å and the decrease in twist to 15°. These values approach those of the middle array segment, which equilibrate to 53 Å with an identical twist of 15°. This close agreement between the rise and twist for the middle with the top and bottom array segments demonstrates that the stacked tetraNuc structure is lost, as there is little physical difference between the structures of nucleosomes 1–4 and 5–8 with 3–6. This large conformational change is also demonstrated by the elevated root mean square deviation (RMSD) values for the Cα and phosphate atoms, which ranged between 39 and 47 Å for GH1 lacking arrays, relative to a range of 15–18 Å for GH1 containing arrays (Figure S3).
Greater Poly-Nucleosome Architecture Dictates Linker DNA Sampling
Linker histones have a direct effect on the motions of linker DNA and nucleosomal DNA through favorable energetic interactions driven by electrostatic and Van der Waals forces. In a previous study, we emphasized the significance of these interactions by demonstrating how the linker histone binding pose, along with how their mere presence, can affect experimental results.78 Here, we translated these ideas to the context of poly-nucleosomal arrays by plotting the in- and out-of-nucleosomal-plane motions of both linker DNA arms in Figure 4 and Supplementary Figure S7, respectively. In general, removing linker histones from the array not only results in overall increased DNA sampling, but the development of novel linker DNA states. This is especially evident in the terminal nucleosomes, labelled Nuc 1, Nuc 2, Nuc 7, and Nuc 8 in Figures 4 and S7. Nucleosomes 2 and 7 presented the most structural distortion, which can be attributed to the drastic global change in conformation which occurred in the all simulations lacking linker histones.
Figure 4:
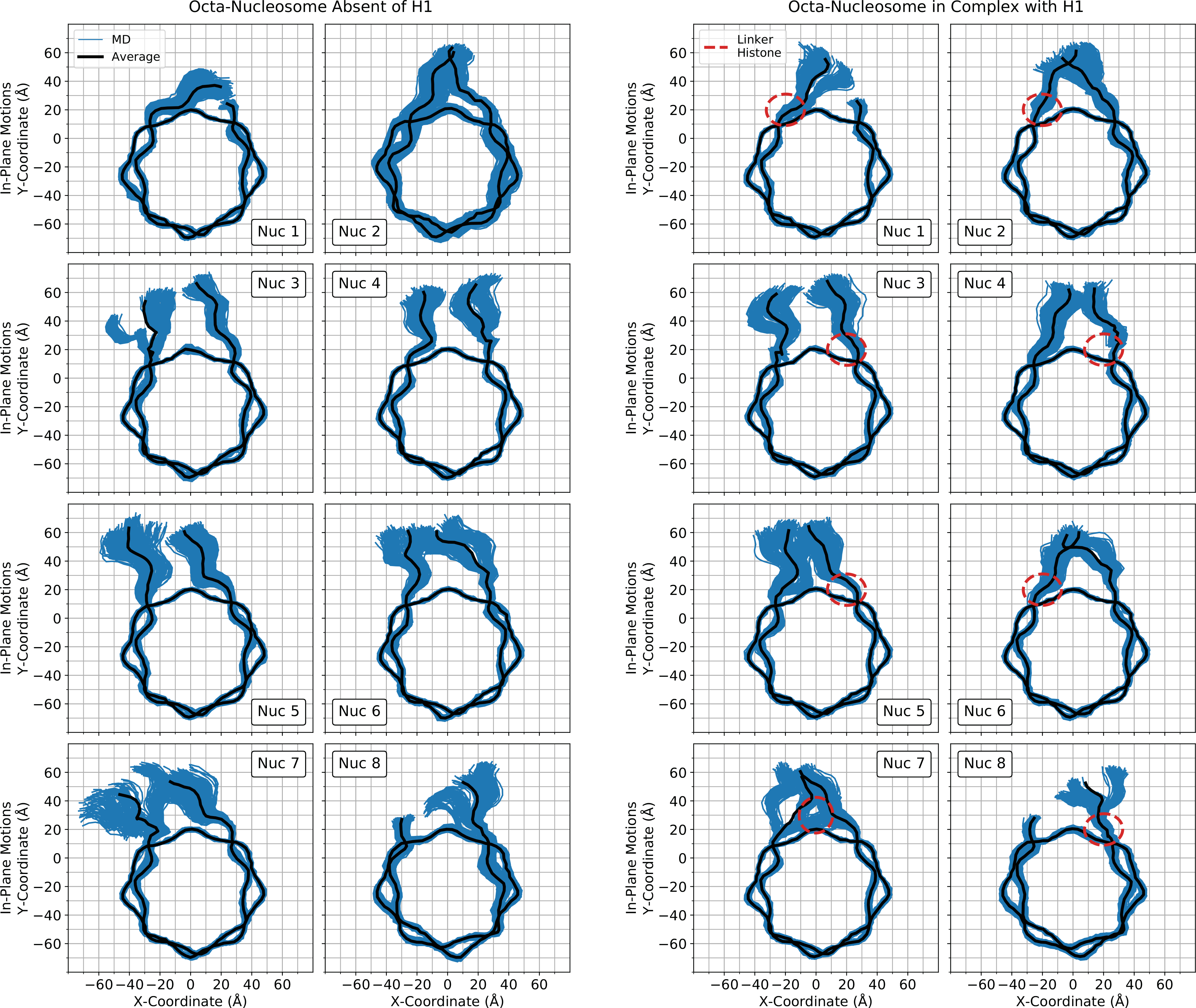
In-plane (top) DNA motions sampled by the octa-nucleosome arrays absent (left) and in complex (right) with the linker histone H1. Shown in blue are configurations sampled throughout the MD simulation (263 representative frames - every 4 ns of simulation time) while the average configuration is shown in black. For reference, the relative position of each nucleosome in its array is labeled in the corner of each graph. This label is consistent with the numbering in Figure 3. Additionally, the approximate position of the linker histone is shown as a dashed-line red ellipse. Figures inspired by work from Shaytan et al 84 and single comparative nucleosome results were published previously.78
To quantify these dynamics, the in- and out-of plane linker DNA motions were calculated and denoted as the α- and β- angles, respectively (as inspired by Bednar et al., see Methods and Supporting Information for detailed definitions, Figures 5 and S4). The α-angles relate predominately to fluctuations in DNA breathing and ranged from −112.2° to 96.9° with an average of 35.4°. Out-of-plane motions, or β-angles, ranged from −56.4° to 62.9° and averaged 1.1°. An additional observation was that the entry and exit DNA arms of GH1-absent nucleosomes had somewhat different probability distributions, which can be attributed to the asymmetric initial conformation within the poly-nucleosome array and the asymmetric nucleic acid sequence of Widom 601. While we previously illustrated that linker histone binding alters linker DNA fluctuations, Figure 5 shows that those effects are more pronounced in poly-nucleosome systems. For example, the α-Entry angle sampling range was reduced by 56.7° when the octa-nucleosome is saturated with GH1. However, this large reduction in sampling space is not present in the α-Exit angles. This occurs because the majority of the structural strain within the compact array is distributed onto the Entry linker DNA. When the linker histone is no loner present, the distorted Entry DNA must endure the bulk of the conformational alleviation. In contrast to the mono-nucleosomes, the octa-nucleosome arrays sample a wider breadth of angles, particularly the α-angle dimension. However, the individual nucleosomes that constitute the array do not readily transition throughout this entire phase space. More often, it is the case that each nucleosome will exist as a single stable, but independent, state unable to sample much outside of its respective potential well. Despite the apparent increased sampling of angles within the array, there is an inherent entropic cost for each individual nucleosome as oppose to existing solitary in solution.
Figure 5:
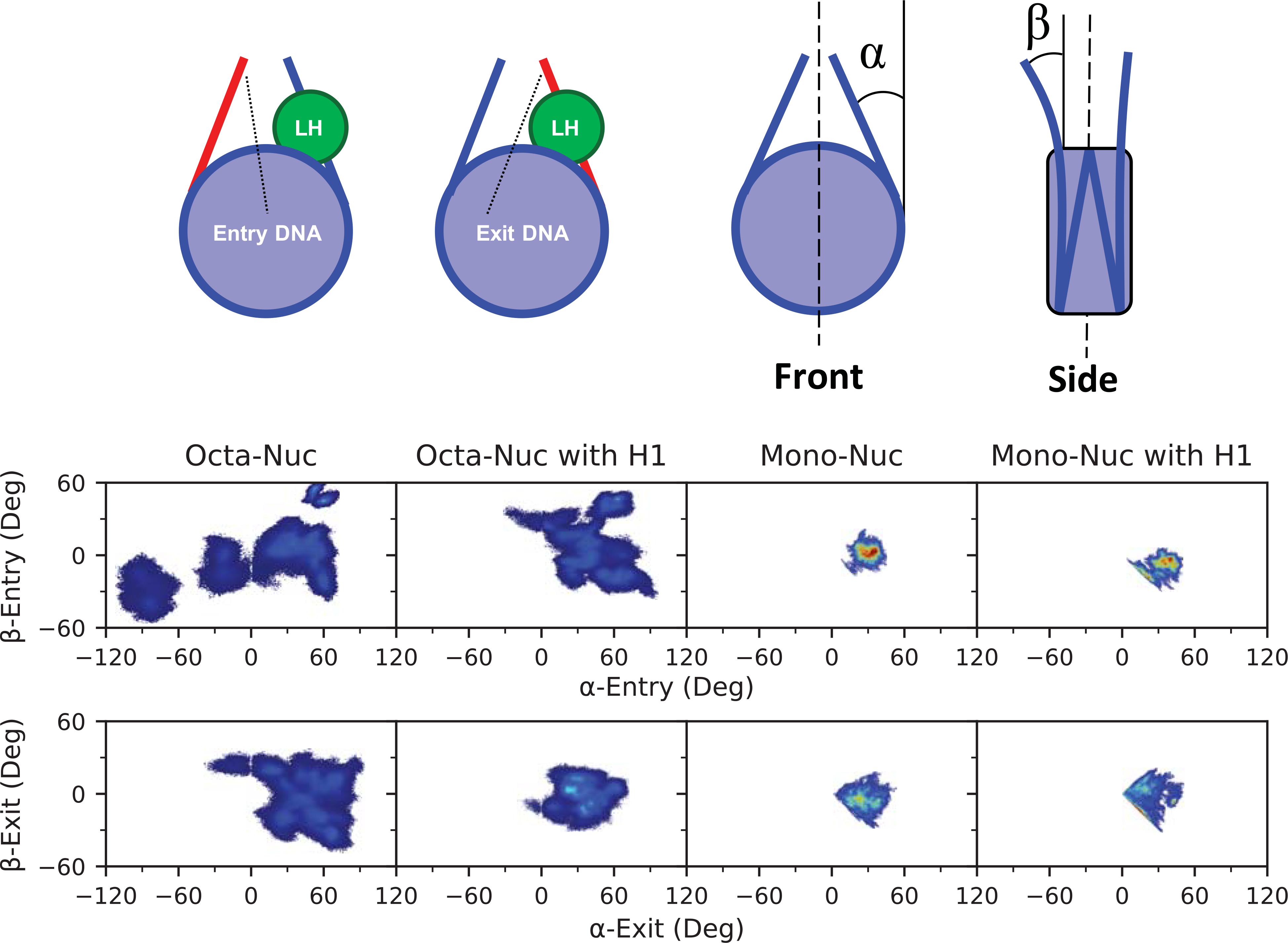
Comparison of DNA sampling for the entry (top plots) and exit (bottom plots) DNA segments for systems with and without H1. The α-angles described in-plane motions, whereas β-angles describe out-of-plane, as depicted in the diagrams on the to of the figure. For clarity, the entry- and exit-DNA segments are depicted in the top left diagram with the linker histone (LH), if present, in green. Density is represented as a gradient from blue (low density) to red (high density). Mono-nucleosome results are from previously published results.78
Although mono-nucleosomes had more available conformational freedom, linker DNA in poly-nucleosomes sample a broader spectrum of states throughout the simulations, which we attribute to the strained nature of nucleosome arrays biasing linker DNA into ordinarily unattainable states, as observed in Figure 4. To further quantify these differences, we calculated Jensen-Shannon distances (JSdist) (Table 1), based on the Jensen-Shannon divergence (JSD), between the one-dimensional probability distributions displayed in Figure S4. Values closer to zero correspond to a greater similarity in probability distributions, whereas values approaching 1.0 correspond to a greater dissimilarity. The JSdist values generally exhibit a stark contrast between mono-nucleosome and octa-nucleosome systems with values often above 0.50, although with some exceptions. In particular, α/β-angles of the Exit DNA (in contact with GH1) sample a much more similar phase space than the Entry DNA angles. Additionally, highlighted by a JSdist of 0.72, binding of the GH1 severely alters sampling of β-Entry angles in mono-nucleosomes and thus presenting an extreme case for which to compare poly-nucleosome systems.
Table 1:
Jensen-Shannon distances (equation (4)) for one dimensional probability distributions (Figure S5) of DNA motions between systems. For clarity, comparisons with low differences (JSdist<0.20) are in blue, increased differences (0.20<JSdist<0.40) are in green, high differences (0.40 <JSdist<0.60) are in orange, and very high differences (0.60<JSdist<1.00) in red. The lower numerical values correspond to a greater similarity in probability distributions, whereas higher numerical values correspond to a greater dissimilarity. Two identical distributions will produce a Jensen-Shannon distance of 0.00, whereas distributions that do no share any phase space commonality will result in 1.00.
| α-Entry | α-Exit | |||||
| MonoNuc with H1 | OctaNuc | OctaNuc with H1 | MonoNuc with H1 | OctaNuc | OctaNuc with H1 | |
| MonoNuc | 0.35 | 0.69 | 0.64 | 0.35 | 0.62 | 0.36 |
| MonoNuc with H1 | 0.63 | 0.54 | 0.67 | 0.54 | ||
| OctaNuc | 0.42 | 0.41 | ||||
| β-Entry | β-Exit | |||||
| MonoNuc with H1 | OctaNuc | OctaNuc with H1 | MonoNuc with H1 | OctaNuc | OctaNuc with H1 | |
| MonoNuc | 0.72 | 0.53 | 0.64 | 0.30 | 0.59 | 0.36 |
| MonoNuc with H1 | 0.69 | 0.58 | 0.44 | 0.15 | ||
| OctaNuc | 0.39 | 0.46 | ||||
Linker Histones Lead to Stiffer Nucleosome Arrays
To characterize the effects of linker histones on the flexibility of compact nucleosomal arrays, the local elastic properties of these systems were computed based on the helical parameter covariance matrices (see Methods for details). For each of the diagonal elements in these matrices, the associated force constants were equal or higher for GH1 containing arrays as compared to GH1 free arrays (Figure 6). However, in many cases the stiffness, and the difference between the GH1-free and containing systems, was dependent on whether inter- or intra-tetra-nucleosome units were considered. For example, in consideration of the rise parameter, in GH1-free arrays all of these elastic constants had values that were approximately equal to one another (within the standard error). In GH1-containing arrays the stiffness parameters were similar, however, given the smaller standard errors we are able to conclude that the inter-nucleosome rise stiffness is sightly higher than the intra-nucleosome stiffness. Other parameters, such as slide shift, tilt, and roll, displayed a similar trend that any difference between the stiffness parameters were small, and close to the standard errors. In contrast, linker histones created a significant increase in the stiffness of the twist within tetra-nucleosome units, but did not influence the force constants between them, suggesting that stacked tetra-nucleosome units impart resistance in poly-nucleosomal arrays via torsional stress.
Figure 6:
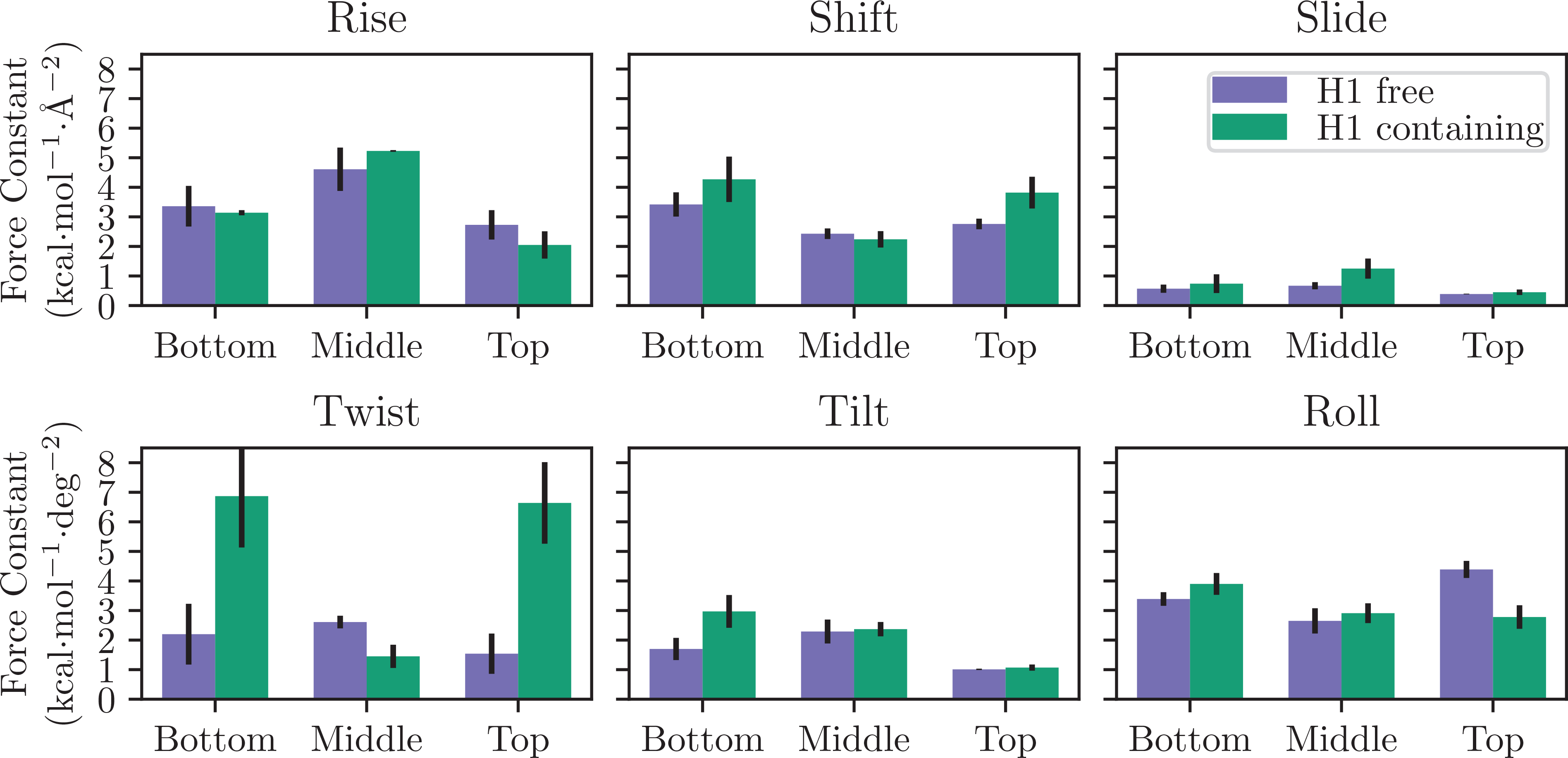
Force constants of helical parameters for the Bottom, Middle, and Top tetra-nucleosomal structures (as defined in Figure S1) and reported in Tables S1 and S2. Error bars represent the standard error of the mean computed from all three simulations.
While the on-diagonal elements of the stiffness matrices are the force constants for the canonical helical parameter, the off-diagonal elements correspond to the coupling between these parameters (Tables S1–S2). The majority of these elements are small and within the standard error of zero, indicating that these degrees of freedom are largely uncorrelated from one another. In contrast, the twist-rise coupling is significant and shows a pattern similar to the twist force constants: without GH1 the coupling constants range from 1.60 ± 0.51 to 2.95 ± 0.24 kcal·mol−1·Å−1·deg−1, with the highest being for the middle segment of the octa-nucleosome array. In contrast, there is a more significant difference with GH1, where the bottom and top tetra-nucleosome segments contain coupling constants of 3.92 ± 0.45 and 3.08 ± 0.69 kcal·mol−1·Å−1·deg−1, and the middle has a significantly reduced value of 1.21 ± 0.24 kcal·mol−1·Å−1·deg−1. This further points to the increased rigidity within linker histone stabilized tetra-nucleosome units, and the relative looseness in these arrays between them. In addition, the positive values observed for all twist-rise coupling constants show that these arrays contract upon overtwisting, which is in line with what one would expect from models of simple helical elastic polymers but is contrary to DNA which elongates when overtwisted.85,86
Linker Histones Create Long Range Correlations
Having established that linker histones create stiffer nucleosomal arrays, we sought to understand the implications for larger scale dynamical properties. We therefore performed a generalized correlation analysis on each system to determine the pairwise correlations between each DNA base and protein residue in the system.87 The average GH1-free correlation matrix shows the expected behavior that within each nucleosome there is a high correlation, as individual nucleosomes are highly rigid on the nanosecond timescale (see red square in Figure 7a). In addition, core histones are highly correlated with the DNA which wraps around it, as evidenced by the red patterns at the top and right side of these figures, and DNA bases are highly correlated with the base they are paired with, as shown by the “X” mark in the upper right hand corner. More interestingly, individual nucleosomes are highly correlated with nucleosomes that stack directly above or below them. That is, Nuci is highly correlated with Nuci+2 and Nuci−2. In contrast, nucleosomes did not have a large correlation with their adjacent nucleosome, as the Nuci and Nuci+1 correlations were relatively low.
Figure 7:
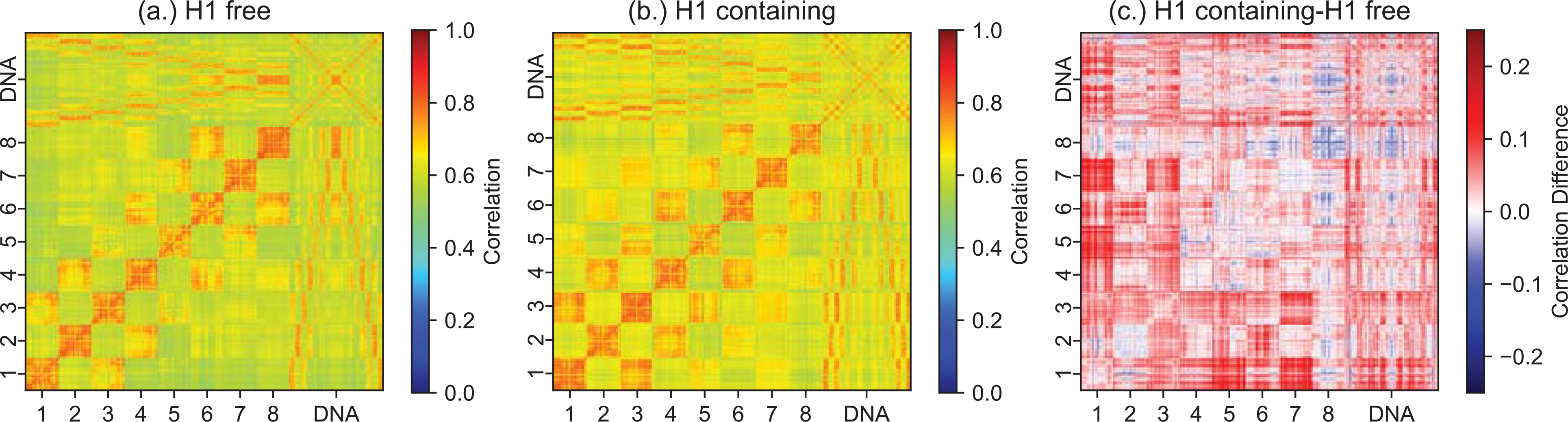
Inter-residue correlations for systems lacking (a.) and containing (b.) H1. H1 increases system correlations, notably through increased correlations in stacked nucleosomes, as shown in the difference between system with and without H1 (c.).
Upon the addition of linker histones, the overall pattern of strong intra-nucleosomal and local nucleosome/DNA correlations remained (Figure 7b). In addition, the majority of correlations were enhanced, as evidenced in the difference map between the correlations in the GH1-containing and free systems (Figure 7c). Of particular interest are the stronger correlations between all of the odd numbered and even numbered nucleosomes, that is between nucleosomes 1,3,5, and 7 and 2,4,6, and 8. This suggests that in the more compact and stiffer arrays induced by linker histones, correlations are able to propagate throughout each side of these two-start zig-zag arrays much further then they can without linker histones.
Discussion
Here, we have used conventional MD simulations to probe the effects of linker histone binding on an octa-nucleosome model of the chromatin fiber. We calculated nucleosomal helical parameters quantifying a global conformational shift that demonstrate the importance of GH1 in the structural stability of chromatin fibers. Moreover, we have captured a physical phenomenon that has been rarely observed experimentally52,88 - the helical untwisting of the poly-nucloeosme array. The most probable explanation for this occurrence is the lack of strong protein-DNA interactions provided by the linker-histone/DNA motif. The chromatin fiber is highly compact and very strained by our observations. The saturated binding of linker histones to the linker DNA stabilizes the system and prevents it from untwisting. We suspect that these LH-DNA interactions, while strong, are likely independent of nucleic acid sequence, similar to LH-protein interactions studied extensively by the Hansen Lab.61,62,89–91 Presumably, the untwisting effect we observed could be mimicked by a decrease in salt concentration. In fact, Garcia-Saez et al. presented an untwisted nucleosome array model based on cryo-EM data of arrays under low-salt conditions. Interestingly, this phenomenon was not hindered by the presence of the linker histone, but occurs readily in saturated arrays. One potential explanation for this discrepancy is that the Garcia-Saez et al. poly-nucleosome array exhibited a low packing density resulting in inherently less inter-nucleosome protein-DNA interactions. This can be attributed to longer linker DNA length between nucleosomes (50 bp versus 30 bp) and the more rigid on-dyad binding mode. As shown in Figures 4 and 5, our more compact model requires more diverse sampling of the linker DNA, which was previously shown to be hindered upon on-dyad binding.78 A compact chromatin fiber with GH1 bound on-dyad would be more strained than its off-dyad bound counterpart and easily perturbed upon a reduction in ionic strength, as observed by Garcia-Saez et al.
By altering linker DNA dynamics, linker histones inherently inhibit transcription and promote the compaction of chromatin fibers. Our simulations have shown how substantial an impact the linker histones have on the global chromatin compaction. This effect is highlighted by the dramatic reduction in sampling space upon GH1 binding. Once bound, the linker histone increases the rigidity of the entire system, as was further emphasized by the increase in correlation throughout the poly-nucleosome array (Figure 7). Similar observations have been associated with the existence of dynamic networks within nucleosomes which may communicate epigentic information throughout chromatin fibers.92 Moreover, these networks may be altered through changes in post-translational modifications (PTMs) via allosteric hotspots.93 Furthermore, the disparity in sampling between mono- and poly-nucleosomes is extensive, which we accredit to the unique chromatin fiber structure. In mono-nucleosomes, linker DNA is generally free to move about in solution, unless bound to a linker histone. However, in poly-nucleosome arrays each nucleosome must adopt a specific conformation to alleviate strain on the entire system. Here, we stress caution when studying mono-nucleosomes and deducing conclusions about their dynamics. The Jensen-Shannon distances in Table 1 highlights the vast dissimilarities between the two systems, specifically with in-plane linker DNA motions, and why results from mono-nucleosome studies, especially related to DNA, may not be transferable when describing the greater chromatin architecture.
An interesting study by Kilic et al. also highlights the variability in chromatin structure and how it can be modulated by extra-nucleosomal proteins.88 First, Kilic et al. used FRET to illustrate that dodeca-nucleosome fibers can transition between multiple dynamic states. Furthermore, they demonstrate how the heterochromatin protein 1α(HP1α) can induce chromatin compaction by transiently stabilizing inter-nucleosome contacts via interactions with DNA, particularly around the nucleosome dyad, and the heterochromatin marker H3K9me3. While not focused on linker histones, this study similarly emphasizes the presence of multiple populated chromatin states in solution and how they can be regulated by proteins such as HP1α, or the GH1, as exhibited here. However, it should be indicated that the dynamic transitions that Kilic et al. observed were on much longer timescales, hundreds of miliseconds to seconds, whereas the poly-nucleosome dynamic adjustments observed here are on the order of hundreds nanoseconds.
The octa-nucleosome system studied here is composed of two distinct, although attached, tetra-nucleosome sub-units, as illustrated throughout this manuscript by light-blue and orange colored core histones (Figures 1, 3, 2, and S6). Using force constants derived from the helical parameters, we found that linker histones impart increased torsional stress within these tetra-nucleosome units while slightly decreasing it between units. Interestingly, linker histones between tetra-nucleosome sub-units are quite close proximity to one another and have been speculated to interact,23,52 giving rise to potential sites for PTMs.94–97 Our calculations show only a few inter-linker histone contacts, specifically between linker histones associated with Nuc4 and Nuc6 (Figures S8, S9, and S10). Unfortunately, the presence of these interactions did not contribute to the overall stiffness of our model. This is evident by the aforementioned force constants which show a decrease in torsional stress between tetra-nucleosome sub-units upon GH1 binding. Therefore, by our observations, inter-linker histone interactions do not significantly contribute to chromatin compaction in the octa-nucleosome model studied here. However, it should be stated that this model included only the globular domain of each linker histone and not the N- and C-terminal tails, known to interact with H3 tails to facilitate binding,98 translating to an examination of localized interactions. The inclusion of these motifs may lead to more interactions with other linker histones, linker DNA, and/or nucleosomes, resulting in increased chromatin fiber compaction and rigidity. Furthermore, in our previous study examining the dynamics of mono-chromatosomes78 we hypothesized that the C-terminal domain was positioned such that it could compete for binding with the long H3 tail along the same DNA arm. In the context of the poly-nucleosome array studied here, this effect would likely be minimal due to the greater availability of linker DNA. However, the C-terminal domain is long enough (~100 residues) that interactions with adjacent nucleosomes might be observed. We also examined inter-nucleosome contacts and did not find any significant interactions, such as contacts between the H4 tails and the H2A/H2B acidic patch of adjacent nucleosomes within the fiber.90
In a recent comprehensive study, Perišić et al. used meso-scale modeling to demonstrate the extent to which linker histone binding modes and variants affect chromatin compaction.99 They were able to connect existing ideas suggesting that combinations of on- and off-dyad binding result in varying levels of compaction on a spectrum between condensed22,23 and uncondensed100 arrays, respectively. Their work provided strong reinforcement that shifts between these two states are directly associated with a shift in linker histone binding mode,52 a sentiment which we share.78 Here, we quantified the effects of linker histones on condensation using various metrics from an atomistic perspective. Furthermore, this work demonstrates that chromatin can experience large conformational transitions in timescales of under a microsecond, which is well under the time it may take to expose nucleosomes for transcription and DNA repair.101–103
Materials and Methods
System Construction
Core histones and the asymmetric Widom 601 DNA were modelled based on the 1KX5 crystal structure83 We chose this crystal structure because it is well resolved compared to other models (1.94 Å) and used in much of our previous simulation work. While this structure contains most of the core histone tails and loops, some residues are not resolved and were added using Modeller via the Chimera graphical user, along with missing nucleotides.104,105 Nucleosomes were manually placed to fit within the 12 Å cryo-EM map,23 followed by 30 bp of linker DNA between them, which was built using the Nucleic Acids Builder (NAB) module within AmberTools18 software package.106 From here, each linker histone was placed in complex with each nucleosome as is shown in the cryo-EM map.23 To do so, rigid docking was performed using the Colores module of Situs,107,108 which was followed by flexible docking using internal coordinates normal mode analysis (iMOD).109 Finally, we built, placed, and validated the linker histone binding mode within the octa-nuclesome array using methods detailed in our previous work.78 When solvated, the resulting system sizes were approximately 290 Å × 310 Å × 320 Å, and composed of approximately 2,757,000 atoms, which includes approximately ~800,000 water molecules and 3,759 Na+ and 2,157 Cl− atoms to neutralize the system and create a bulk 150 mM NaCl environment.
Molecular Dynamics simulations
All systems were prepared and simulated using the GROMACS 2016.4 software package.110 Each system was solvated in a TIP3P water box extending at least 10 Å from the solute,111,112 enough to minimize interactions between periodic images (Figure S11). Using Joung-Cheatham ions,113,114 the solvent contained 150 mM NaCl, sodium cations to neutralize negative charges, and magnesium ions that replaced the manganese ions in the 1KX5 crystal structure. Only magnesium ions in the DNA grooves were included, whereas those located close to the the linker histones binding locations were excluded so as to not interfere with LH-DNA interactions. The AMBER14SB and BSC1 force fields were used for protein and DNA interactions, respectively.115,116 A cutoff distance of 10.0 Å with a switching function beginning at 8.0 Å was used for nonbonded interactions, and long range electrostatics were treated with particle mesh Ewald calculations.117 Systems were minimized for 10,000 steps, and then equilibrated for 100 ps at constant volume and temperature and for 1 ns at constant pressure and temperature. Production simulations were carried out for 500 ns in the NPT ensemble, using a Parrinello-Rahman barostat118 with a time constant of 1.0 ps to control the pressure and a Nosé-Hoover thermostat at 300K with a time constant 0.5 ps. Electrostatic interactions were treated with the Particle-Mesh Ewald (PME) method117 and 10 Å cut-off. Simulations were conducted on two systems: one with the linker histone bound to the DNA of each nucleosome and one without the presence of GH1. Each simulation was run in triplicate for 500 ns with a 2 fs timestep using resources provided by the Extreme Science and Engineering Discovery Environment (XSEDE).119
Analysis
Helical Parameters
The local double helical structure of the chromatin fiber was quantified based upon three translational (rise, shift, and slide) and three rotational (twist, tilt, and roll) parameters.81 In analogy with DNA structure, a “base pair” was defined as two nucleosomes that were in the same z-plane with one another, where the z-axis is defined as the principal fiber axis. For each nucleosome pair, the local x-axis was defined as a vector from the center of mass of the DNA phosphate atoms of NCP i to the center of mass of the DNA phosphate atoms of NCP i + 1. The z-axis was defined as the average of the third principal axis of inertia of NCPs i and i + 1, as computed with gromacs, and the y-axis was computed as the vector perpendicular to these two vectors. Following the definition of these “base-pair” axis, the algorithm outlined by Lu et al. was used to compute the rise, shift, slide, twist, tilt, and roll.80
To compute the elastic force constants, a harmonic approximation was made for each of the basepair parameters, such that the internal energy of the fiber is estimated by:
| (1) |
where w is the vector of inter-base pair parameters, is their mean, and K a stiffness matrix.120 Given small fluctuations, the equipartion theorem can be used to construct K from the inverse of the covariance matrix, C:
| (2) |
where kb is Boltzmann’s constant, and T the system temperature. Terms along the diagonal of K are the individual parameter force constants, and off-digonal terms represent the parameter coupling constants. Error bars were computed by calculating the stiffness matrices for each of the three simulations and taking the standard error of the mean.
Generalized Correlation
Mutual-information based generalized correlation methods were employed to capture non-collinear correlations between residue pairs to describe both linear and non-linear coupled motions. Results were computed using the g_correlation plugin for GROMACS/3.3.87,110,121 The first 150 ns of simulation time was allotted for equilibration while trajectories were analyzed every 50 ps. Analyses were performed only on the protein Cα and the nucleotide C1’ heavy atoms.
Linker DNA Dynamics
The linker DNA in- and out-of nucleosomal plane motions were quantified to describe the linker DNA motions. To define the plane, the nucleosomal DNA was divided into four quadrants and the center of mass of the C1’ atoms within the two quadrants located distal from the linker DNA were used for two points, while the third point was defined as the C1’ center of mass of bases 83 and 250 which are located approximately on the dyad axis (see previous work78 for details). The linker DNA vectors were defined as the C1’ center of mass of the base pairs at the origin of the linker DNA (bases 20–315 and 148–187) and terminal base pairs (bases 1–354 and 177–178), respectively. The α-angles were defined as in-plane and the β-angles were defined as out-of-plane motions of this vector. Positive α-angles were defined as inward motions towards the dyad axis while positive β-angles were defined as outward motions away from the nucleosomal-plane. For reference, the angles shown in Figure 5 are positive.
The change in linker DNA sampling between GH1-bound and -free systems were computed using two metrics, the KullbackLeibler122 (KLD) and Jensen-Shannon divergences (JSD),123,124 respectively:
| (3) |
| (4) |
where,
| (5) |
where, in equation (4), Q(x) is the normalized reference distribution and P(x) is the normalized data set. In equation (4), the JSD gives equal weight to Q(x) and P(x) by calculating their KLD with respect to an average distribution, M in equation (5). With these measures, we are comparing two probability distributions and thus employ a base 2 logarithm as shown in equation (3). Due to its symmetric nature, the square root of the JSD can be used as a true mathematical metric known as the Jensen-Shannon distance125–127 which is how we have reported it in this study.
Supplementary Material
Research Highlights.
Inclusion of linker Histone H1 results in stabilization of the compact chromatin structure, while its removal results in a major conformational change towards an untwisted ladder-like state.
Increased rigidity and correlations within the H1-bound array suggests that H1-saturated chromatin fibers are better suited to transferring long-range epigenetic information.
An analysis of linker DNA motions highlights disparities between studying mono-nucleosome and poly-nucleosome systems.
Acknowledgments
Work in the Wereszczynski group is funded by the National Science Foundation [CAREER-1552743] and the National Institutes of Health [1R35GM119647]. This work used the Extreme Science and Engineering Discovery Environment, which is supported by the National Science Foundation [ACI-1053575].
Footnotes
Declaration of interests
☒ The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Kornberg RD Chromatin structure: a repeating unit of histones and DNA. Science 1974, 184, 868–871. [DOI] [PubMed] [Google Scholar]
- [2].McGinty RK; Tan S Nucleosome structure and function. Chem. Rev. 2015, 115, 2255–2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Olins AL; Olins DE Spheroid chromatin units (v bodies). Science 1974, 183, 330–332. [DOI] [PubMed] [Google Scholar]
- [4].Kaplan N; Moore IK; Fondufe-Mittendorf Y; Gossett AJ; Tillo D; Field Y; LeProust EM; Hughes TR; Lieb JD; Widom J et al. The DNA-encoded nucleosome organization of a eukaryotic genome. Nature 2009, 458, 362–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Luger K; Mader AW; Richmond RK; Sargent DF; Richmond TJ Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature 1997, 389, 251–260. [DOI] [PubMed] [Google Scholar]
- [6].Baldi S; Korber P; Becker PB Beads on a string-nucleosome array arrangements and folding of the chromatin fiber. Nat. Struct. Mol. Biol. 2020, 27, 109–118. [DOI] [PubMed] [Google Scholar]
- [7].Wiese O; Marenduzzo D; Brackley CA Nucleosome positions alone can be used to predict domains in yeast chromosomes. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 17307–17315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bass MV; Nikitina T; Norouzi D; Zhurkin VB; Grigoryev SA Nucleosome spacing periodically modulates nucleosome chain folding and DNA topology in circular nucleosome arrays. J. Biol. Chem. 2019, 294, 4233–4246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Pusarla RH; Vinayachandran V; Bhargava P Nucleosome positioning in relation to nucleosome spacing and DNA sequence-specific binding of a protein. FEBS J. 2007, 274, 2396–2410. [DOI] [PubMed] [Google Scholar]
- [10].Noll M; Kornberg RD Action of micrococcal nuclease on chromatin and the location of histone H1. J. Mol. Biol. 1977, 109, 393–404. [DOI] [PubMed] [Google Scholar]
- [11].Blank TA; Becker PB Electrostatic mechanism of nucleosome spacing. J. Mol. Biol. 1995, 252, 305–313. [DOI] [PubMed] [Google Scholar]
- [12].Zhang T; Zhang W; Jiang J Genome-Wide Nucleosome Occupancy and Positioning and Their Impact on Gene Expression and Evolution in Plants. Plant Physiol. 2015, 168, 1406–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Rodríguez-Campos A; Shimamura A; Worcel A Assembly and properties of chromatin containing histone H1. J. Mol. Biol. 1989, 209, 135–150. [DOI] [PubMed] [Google Scholar]
- [14].Garcia-Ramirez M; Dong F; Ausio J Role of the histone “tails” in the folding of oligonucleosomes depleted of histone H1. J. Biol. Chem. 1992, 267, 19587–19595. [PubMed] [Google Scholar]
- [15].Tremethick DJ; Drew HR High mobility group proteins 14 and 17 can space nucleosomes in vitro. J. Biol. Chem. 1993, 268, 11389–11393. [PubMed] [Google Scholar]
- [16].Robinson PJ; Fairall L; Huynh VA; Rhodes D EM measurements define the dimensions of the “30-nm” chromatin fiber: evidence for a compact, interdigitated structure. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 6506–6511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Finch JT; Klug A Solenoidal model for superstructure in chromatin. Proc. Natl. Acad. Sci. U.S.A. 1976, 73, 1897–1901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Worcel A; Strogatz S; Riley D Structure of chromatin and the linking number of DNA. Proc. Natl. Acad. Sci. U.S.A. 1981, 78, 1461–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Williams SP; Athey BD; Muglia LJ; Schappe RS; Gough AH; Langmore JP Chromatin fibers are left-handed double helices with diameter and mass per unit length that depend on linker length. Biophys. J. 1986, 49, 233–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Dorigo B; Schalch T; Kulangara A; Duda S; Schroeder RR; Richmond TJ Nucleosome arrays reveal the two-start organization of the chromatin fiber. Science 2004, 306, 1571–1573. [DOI] [PubMed] [Google Scholar]
- [21].Schalch T; Duda S; Sargent DF; Richmond TJ X-ray structure of a tetranucleosome and its implications for the chromatin fibre. Nature 2005, 436, 138–141. [DOI] [PubMed] [Google Scholar]
- [22].Routh A; Sandin S; Rhodes D Nucleosome repeat length and linker histone stoichiometry determine chromatin fiber structure. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 8872–8877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Song F; Chen P; Sun D; Wang M; Dong L; Liang D; Xu RM; Zhu P; Li G Cryo-EM study of the chromatin fiber reveals a double helix twisted by tetranucleosomal units. Science 2014, 344, 376–380. [DOI] [PubMed] [Google Scholar]
- [24].Ekundayo B; Richmond TJ; Schalch T Capturing Structural Heterogeneity in Chromatin Fibers. J. Mol. Biol. 2017, 429, 3031–3042. [DOI] [PubMed] [Google Scholar]
- [25].Grigoryev SA; Arya G; Correll S; Woodcock CL; Schlick T Evidence for heteromorphic chromatin fibers from analysis of nucleosome interactions. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 13317–13322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Greulich KO; Wachtel E; Ausio J; Seger D; Eisenberg H Transition of chromatin from the “10 nm” lower order structure, to the “30 nm” higher order structure as followed by small angle X-ray scattering. J. Mol. Biol. 1987, 193, 709–721. [DOI] [PubMed] [Google Scholar]
- [27].Thoma F; Koller T; Klug A Involvement of histone H1 in the organization of the nucleosome and of the salt-dependent superstructures of chromatin. J. Cell Biol. 1979, 83, 403–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Makarov VL; Dimitrov SI; Petrov PT Salt-induced conformational transitions in chromatin. A flow linear dichroism study. Eur. J. Biochem. 1983, 133, 491–497. [DOI] [PubMed] [Google Scholar]
- [29].Gerchman SE; Ramakrishnan V Chromatin higher-order structure studied by neutron scattering and scanning transmission electron microscopy. Proc. Natl. Acad. Sci. U.S.A. 1987, 84, 7802–7806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Ghirlando R; Felsenfeld G Hydrodynamic studies on defined heterochromatin fragments support a 30-nm fiber having six nucleosomes per turn. J. Mol. Biol. 2008, 376, 1417–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Eltsov M; Maclellan KM; Maeshima K; Frangakis AS; Dubochet J Analysis of cryo-electron microscopy images does not support the existence of 30-nm chromatin fibers in mitotic chromosomes in situ. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 19732–19737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Fussner E; Strauss M; Djuric U; Li R; Ahmed K; Hart M; Ellis J; Bazett-Jones DP Open and closed domains in the mouse genome are configured as 10-nm chromatin fibres. EMBO Rep. 2012, 13, 992–996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Gan L; Ladinsky MS; Jensen GJ Chromatin in a marine picoeukaryote is a disordered assemblage of nucleosomes. Chromosoma 2013, 122, 377–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Nishino Y; Eltsov M; Joti Y; Ito K; Takata H; Takahashi Y; Hihara S; Frangakis AS; Imamoto N; Ishikawa T et al. Human mitotic chromosomes consist predominantly of irregularly folded nucleosome fibres without a 30-nm chromatin structure. EMBO J. 2012, 31, 1644–1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Ou HD; Phan S; Deerinck TJ; Thor A; Ellisman MH; O’Shea CC ChromEMT: Visualizing 3D chromatin structure and compaction in interphase and mitotic cells. Science 2017, 357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Cai S; Bock D; Pilhofer M; Gan L The in situ structures of mono-, di-, and trinucleosomes in human heterochromatin. Mol. Biol. Cell 2018, 29, 2450–2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Hsieh TH; Weiner A; Lajoie B; Dekker J; Friedman N; Rando OJ Mapping Nucleosome Resolution Chromosome Folding in Yeast by Micro-C. Cell 2015, 162, 108–119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Grigoryev SA; Bascom G; Buckwalter JM; Schubert MB; Woodcock CL; Schlick T Hierarchical looping of zigzag nucleosome chains in metaphase chromosomes. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 1238–1243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Langmore JP; Schutt C The higher order structure of chicken erythrocyte chromosomes in vivo. Nature 1980, 288, 620–622. [DOI] [PubMed] [Google Scholar]
- [40].Woodcock CL Chromatin fibers observed in situ in frozen hydrated sections. Native fiber diameter is not correlated with nucleosome repeat length. J. Cell Biol. 1994, 125, 11–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Kizilyaprak C; Spehner D; Devys D; Schultz P In vivo chromatin organization of mouse rod photoreceptors correlates with histone modifications. PLoS ONE 2010, 5, e11039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Scheffer MP; Eltsov M; Bednar J; Frangakis AS Nucleosomes stacked with aligned dyad axes are found in native compact chromatin in vitro. J. Struct. Biol. 2012, 178, 207–214. [DOI] [PubMed] [Google Scholar]
- [43].Zhou K; Gaullier G; Luger K Nucleosome structure and dynamics are coming of age. Nat. Struct. Mol. Biol. 2019, 26, 3–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Chen Y; Tokuda JM; Topping T; Meisburger SP; Pabit SA; Gloss LM; Pollack L Asymmetric unwrapping of nucleosomal DNA propagates asymmetric opening and dissociation of the histone core. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 334–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Parsons T; Zhang B Critical role of histone tail entropy in nucleosome unwinding. J Chem Phys 2019, 150, 185103. [DOI] [PubMed] [Google Scholar]
- [46].Schlingman DJ; Mack AH; Kamenetska M; Mochrie SGJ; Regan L Routes to DNA accessibility: alternative pathways for nucleosome unwinding. Biophys. J. 2014, 107, 384–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Alkhatib SG; Landry JW The nucleosome remodeling factor. FEBS Lett. 2011, 585, 3197–3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Pentakota S; Zhou K; Smith C; Maffini S; Petrovic A; Morgan GP; Weir JR; Vetter IR; Musacchio A; Luger K Decoding the centromeric nucleosome through CENP-N. Elife 2017, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Fyodorov DV; Zhou BR; Skoultchi AI; Bai Y Emerging roles of linker histones in regulating chromatin structure and function. Nat. Rev. Mol. Cell Biol. 2018, 19, 192–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Talbert PB; Henikoff S Histone variants on the move: substrates for chromatin dynamics. Nat. Rev. Mol. Cell Biol. 2017, 18, 115–126. [DOI] [PubMed] [Google Scholar]
- [51].Collepardo-Guevara R; Schlick T Chromatin fiber polymorphism triggered by variations of DNA linker lengths. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, 8061–8066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Garcia-Saez I; Menoni H; Boopathi R; Shukla MS; Soueidan L; Noirclerc-Savoye M; Le Roy A; Skoufias DA; Bednar J; Hamiche A et al. Structure of an H1-Bound 6-Nucleosome Array Reveals an Untwisted Two-Start Chromatin Fiber Conformation. Mol. Cell 2018, 72, 902–915. [DOI] [PubMed] [Google Scholar]
- [53].Grigoryev SA; Schubert M Unraveling the multiplex folding of nucleosome chains in higher order chromatin. Essays Biochem. 2019, 63, 109–121. [DOI] [PubMed] [Google Scholar]
- [54].Wong H; Victor JM; Mozziconacci J An all-atom model of the chromatin fiber containing linker histones reveals a versatile structure tuned by the nucleosomal repeat length. PLoS ONE 2007, 2, e877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Ozer G; Luque A; Schlick T The chromatin fiber: multiscale problems and approaches. Curr. Opin. Struct. Biol. 2015, 31, 124–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Maresca TJ; Freedman BS; Heald R Histone H1 is essential for mitotic chromosome architecture and segregation in Xenopus laevis egg extracts. J. Cell Biol. 2005, 169, 859–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Hergeth SP; Schneider R The H1 linker histones: multifunctional proteins beyond the nucleosomal core particle. EMBO Rep. 2015, 16, 1439–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Adhireksan Z; Sharma D; Lee PL; Davey CA Near-atomic resolution structures of interdigitated nucleosome fibres. Nat Commun 2020, 11, 4747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Fan Y; Nikitina T; Zhao J; Fleury TJ; Bhattacharyya R; Bouhassira EE; Stein A; Woodcock CL; Skoultchi AI Histone H1 depletion in mammals alters global chromatin structure but causes specific changes in gene regulation. Cell 2005, 123, 1199–1212. [DOI] [PubMed] [Google Scholar]
- [60].Shen X; Gorovsky MA Linker histone H1 regulates specific gene expression but not global transcription in vivo. Cell 1996, 86, 475–483. [DOI] [PubMed] [Google Scholar]
- [61].Kalashnikova AA; Rogge RA; Hansen JC Linker histone H1 and protein-protein interactions. Biochim Biophys Acta 2016, 1859, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Hansen JC Silencing the genome with linker histones. Proc Natl Acad Sci U S A 2020, 117, 15388–15390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Lu X; Wontakal SN; Kavi H; Kim BJ; Guzzardo PM; Emelyanov AV; Xu N; Hannon GJ; Zavadil J; Fyodorov DV et al. Drosophila H1 regulates the genetic activity of heterochromatin by recruitment of Su(var)3–9. Science 2013, 340, 78–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Lee H; Habas R; Abate-Shen C MSX1 cooperates with histone H1b for inhibition of transcription and myogenesis. Science 2004, 304, 1675–1678. [DOI] [PubMed] [Google Scholar]
- [65].Zhang Y; Khan D; Delling J; Tobiasch E Mechanisms underlying the osteo- and adipo-differentiation of human mesenchymal stem cells. ScientificWorldJournal 2012, 2012, 793823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Christophorou MA; Castelo-Branco G; Halley-Stott RP; Oliveira CS; Loos R; Radzisheuskaya A; Mowen KA; Bertone P; Silva JC; Zernicka-Goetz M et al. Citrullination regulates pluripotency and histone H1 binding to chromatin. Nature 2014, 507, 104–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Thorslund T; Ripplinger A; Hoffmann S; Wild T; Uckelmann M; Villumsen B; Narita T; Sixma TK; Choudhary C; Bekker-Jensen S et al. Histone H1 couples initiation and amplification of ubiquitin signalling after DNA damage. Nature 2015, 527, 389–393. [DOI] [PubMed] [Google Scholar]
- [68].Konishi A; Shimizu S; Hirota J; Takao T; Fan Y; Matsuoka Y; Zhang L; Yoneda Y; Fujii Y; Skoultchi AI et al. Involvement of histone H1.2 in apoptosis induced by DNA double-strand breaks. Cell 2003, 114, 673–688. [DOI] [PubMed] [Google Scholar]
- [69].McGhee JD; Felsenfeld G Nucleosome structure. Annu. Rev. Biochem. 1980, 49, 1115–1156. [DOI] [PubMed] [Google Scholar]
- [70].Lever MA; Th’ng JP; Sun X; Hendzel MJ Rapid exchange of histone H1.1 on chromatin in living human cells. Nature 2000, 408, 873–876. [DOI] [PubMed] [Google Scholar]
- [71].Misteli T; Gunjan A; Hock R; Bustin M; Brown DT Dynamic binding of histone H1 to chromatin in living cells. Nature 2000, 408, 877–881. [DOI] [PubMed] [Google Scholar]
- [72].Catez F; Ueda T; Bustin M Determinants of histone H1 mobility and chromatin binding in living cells. Nat. Struct. Mol. Biol. 2006, 13, 305–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Shimamura A; Sapp M; Rodriguez-Campos A; Worcel A Histone H1 represses transcription from minichromosomes assembled in vitro. Mol. Cell. Biol. 1989, 9, 5573–5584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Laybourn PJ; Kadonaga JT Role of nucleosomal cores and histone H1 in regulation of transcription by RNA polymerase II. Science 1991, 254, 238–245. [DOI] [PubMed] [Google Scholar]
- [75].O’Neill TE; Meersseman G; Pennings S; Bradbury EM Deposition of histone H1 onto reconstituted nucleosome arrays inhibits both initiation and elongation of transcripts by T7 RNA polymerase. Nucleic Acids Res. 1995, 23, 1075–1082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Kale S; Goncearenco A; Markov Y; Landsman D; Panchenko AR Molecular recognition of nucleosomes by binding partners. Curr. Opin. Struct. Biol. 2019, 56, 164–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Mishra LN; Hayes JJ A nucleosome-free region locally abrogates histone H1-dependent restriction of linker DNA accessibility in chromatin. J. Biol. Chem. 2018, 293, 19191–19200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Woods DC; Wereszczynski J Elucidating the influence of linker histone variants on chromatosome dynamics and energetics. Nucleic Acids Res. 2020, 48, 3591–3604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Ötürk MA and De M and Cojocaru V and Wade RC, Chromatosome Structure and Dynamics from Molecular Simulations. Annu Rev Phys Chem 2020, 71, 101–119. [DOI] [PubMed] [Google Scholar]
- [80].Lu XJ; El Hassan MA; Hunter CA Structure and conformation of helical nucleic acids: analysis program (SCHNAaP). J. Mol. Biol. 1997, 273, 668–680. [DOI] [PubMed] [Google Scholar]
- [81].Olson WK; Bansal M; Burley SK; Dickerson RE; Gerstein M; Harvey SC; Heinemann U; Lu XJ; Neidle S; Shakked Z et al. A standard reference frame for the description of nucleic acid base-pair geometry. J. Mol. Biol. 2001, 313, 229–237. [DOI] [PubMed] [Google Scholar]
- [82].Lu XJ; Olson WK 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Res. 2003, 31, 5108–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Davey CA; Sargent DF; Luger K; Maeder AW; Richmond TJ Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 a resolution. J. Mol. Biol. 2002, 319, 1097–1113. [DOI] [PubMed] [Google Scholar]
- [84].Shaytan AK; Armeev GA; Goncearenco A; Zhurkin VB; Landsman D; Panchenko AR Coupling between Histone Conformations and DNA Geometry in Nucleosomes on a Microsecond Timescale: Atomistic Insights into Nucleosome Functions. J. Mol. Biol. 2016, 428, 221–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85].Lionnet T; Joubaud S; Lavery R; Bensimon D; Croquette V Wringing Out DNA. Phys. Rev. Lett. 2006, 96, 178102–1–178102–4. [DOI] [PubMed] [Google Scholar]
- [86].Gore J; Bryant Z; Nöllmann M; Le MU; Cozzarelli NR; Bustamante C DNA overwinds when stretched. Nature 2006, 442, 836–839. [DOI] [PubMed] [Google Scholar]
- [87].Lange OF; Grubmüller H Generalized correlation for biomolecular dynamics. Proteins 2006, 62, 1053–1061. [DOI] [PubMed] [Google Scholar]
- [88].Kilic S; Felekyan S; Doroshenko O; Boichenko I; Dimura M; Vardanyan H; Bryan LC; Arya G; Seidel CAM; Fierz B Single-molecule FRET reveals multiscale chromatin dynamics modulated by HP1. Nat Commun 2018, 9, 235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Kalashnikova AA; Winkler DD; McBryant SJ; Henderson RK; Herman JA; DeLuca JG; Luger K; Prenni JE; Hansen JC Linker histone H1.0 interacts with an extensive network of proteins found in the nucleolus. Nucleic Acids Res 2013, 41, 4026–4035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Kalashnikova AA; Porter-Goff ME; Muthurajan UM; Luger K; Hansen JC The role of the nucleosome acidic patch in modulating higher order chromatin structure. J R Soc Interface 2013, 10, 20121022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Healton SE; Pinto HD; Mishra LN; Hamilton GA; Wheat JC; Swist-Rosowska K; Shukeir N; Dou Y; Steidl U; Jenuwein T et al. H1 linker histones silence repetitive elements by promoting both histone H3K9 methylation and chromatin compaction. Proc Natl Acad Sci U S A 2020, 117, 14251–14258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92].Shi X and Prasanna C and Soman A and Pervushin K and Nordenskiöld L, Dynamic networks observed in the nucleosome core particles couple the histone globular domains with DNA. Commun Biol 2020, 3, 639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93].Bowerman S; Wereszczynski J Effects of MacroH2A and H2A.Z on Nucleosome Dynamics as Elucidated by Molecular Dynamics Simulations. Biophys J 2016, 110, 327–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Wisniewski JR; Zougman A; Krüger S; Mann M Mass spectrometric mapping of linker histone H1 variants reveals multiple acetylations, methylations, and phosphorylation as well as differences between cell culture and tissue. Mol. Cell Proteomics 2007, 6, 72–87. [DOI] [PubMed] [Google Scholar]
- [95].Zhou BR; Feng H; Ghirlando R; Li S; Schwieters CD; Bai Y A Small Number of Residues Can Determine if Linker Histones Are Bound On or Off Dyad in the Chromatosome. J. Mol. Biol. 2016, 428, 3948–3959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Li Y; Li Z; Dong L; Tang M; Zhang P; Zhang C; Cao Z; Zhu Q; Chen Y; Wang H et al. Histone H1 acetylation at lysine 85 regulates chromatin condensation and genome stability upon DNA damage. Nucleic Acids Res. 2018, 46, 7716–7730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Ötürk MA and Cojocaru V and Wade RC, Toward an Ensemble View of Chromatosome Structure: A Paradigm Shift from One to Many. Structure 2018, 26, 1050–1057. [DOI] [PubMed] [Google Scholar]
- [98].Stützer A; Liokatis S; Kiesel A; Schwarzer D; Sprangers R; Söding J; Selenko P; Fischle W Modulations of DNA Contacts by Linker Histones and Post-translational Modifications Determine the Mobility and Modifiability of Nucleosomal H3 Tails. [DOI] [PubMed] [Google Scholar]
- [99].Perišić O; Portillo-Ledesma S; Schlick T Sensitive effect of linker histone binding mode and subtype on chromatin condensation. Nucleic Acids Res. 2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Bednar J; Garcia-Saez I; Boopathi R; Cutter AR; Papai G; Reymer A; Syed SH; Lone IN; Tonchev O; Crucifix C et al. Structure and Dynamics of a 197 bp Nucleosome in Complex with Linker Histone H1. Mol. Cell 2017, 66, 384–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Li G; Levitus M; Bustamante C; J. W Rapid spontaneous accessibility of nucleosomal DNA. Nat. Struct. Mol. Biol. 2005, 12, 46–53. [DOI] [PubMed] [Google Scholar]
- [102].Tims H; Gurunathan K; Levitus M; J. W Dynamics of Nucleosome Invasion by DNA Binding Proteins. J. Mol. Biol. 2011, 411, 430–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [103].North J; Shimko J; Javaid S; Mooney A; Shoffner M; Rose S; Bundschuh R; Fishel R; Ottesen J; Poirier M Regulation of the nucleosome unwrapping rate controls DNA accessibility. Nucleic Acids Res. 2012, 40, 10215–10227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104].Sali A; Blundell TL Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993, 234, 779–815 [DOI] [PubMed] [Google Scholar]
- [105].Pettersen EF; Goddard TD; Huang CC; Couch GS; Greenblatt DM; Meng EC; Ferrin TE UCSF Chimera–a visualization system for exploratory research and analysis. J Comput Chem 2004, 25, 1605–1612. [DOI] [PubMed] [Google Scholar]
- [106].Case DA; Betz RM; Cerutti DS; Cheatham TE; Darden TA; Duke RE; Giese TJ; Gohlke H; Goetz AW; Homeyer N et al. AMBER 2018; University of California, San Francisco, 2018. [Google Scholar]
- 107.Wriggers W, Milligan RA, McCammon JA, (1999). Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. J. Struct. Biol, 125, 185–195. [DOI] [PubMed] [Google Scholar]
- 108.Wriggers W, (2012). Conventions and workflows for using Situs. Acta Crystallogr. D Biol. Crystallogr, 68, 344–351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Lopez-Blanco JR, Garzon JI, Chacon P, (2011). iMod: multipurpose normal mode analysis in internal coordinates. Bioinformatics, 27, 2843–2850. [DOI] [PubMed] [Google Scholar]
- 110.Abraham M, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E, (2015). GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX, 1–2, 19–25. [Google Scholar]
- 111.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML, (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys, 79, 926–935. [Google Scholar]
- 112.Mahoney MW, Jorgensen WL, (1983). A five-site model for liquid water and the reproduction of the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys, 112, 8910–8922. [Google Scholar]
- 113.Joung IS, Cheatham TE, (2008). Determination of alkali and halide monovalent ion parameters for use in explicitly solvated biomolecular simulations. J. Phys. Chem. B, 112, 9020–9041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Joung IS, Cheatham TE, (2009). Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters. J. Phys. Chem. B, 113, 13279–13290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C, (2015). ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Ivani I, Dans PD, Noy A, Perez A, Faustino I, Hospital A, Walther J, Andrio P, et al. , (2016). Parmbsc1: a refined force field for DNA simulations. Nature Methods, 13, 55–58. D.C. Woods, F. Rodríguez-Ropero and J. Wereszczynski Journal of Molecular Biology 433 (2021) 166902 15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Darden T, York D, Pedersen L, (1993). Particle mesh Ewald: An N.log(N) method for Ewald sums in large systems. J. Chem. Phys, 98, 10089–10092. [Google Scholar]
- [118].Parrinello M; Rahman A Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52–12. [Google Scholar]
- [119].Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson G et al. XSEDE: accelerating scientific discovery. Computing in Science & Engineering 2014, 16, 62–74. [Google Scholar]
- [120].Dršata T; Pérez A; Orozco M; Morozov AV; Šponer J; Lankaš F Structure, Stiffness and Substates of the Dickerson-Drew Dodecamer. J Chem Theory Comput 2013, 9, 707–721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [121].Kraskov A; Stögbauer H; Grassberger P Estimating mutual information. Phys Rev E Stat Nonlin Soft Matter Phys 2004, 69, 066138. [DOI] [PubMed] [Google Scholar]
- [122].McClendon CL; Hua L; Barreiro A; Jacobson MP Comparing Conformational Ensembles Using the Kullback-Leibler Divergence Expansion. J Chem Theory Comput 2012, 8, 2115–2126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [123].Roa CR; Nayak TK Cross Entropy, Dissimilarity Measure, and Characterizations of Quadratic Entropy. IEEE Trans. Inf. Theory 1985, 31, 589–593. [Google Scholar]
- [124].Lin J Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–149 [Google Scholar]
- [125].Endres DM; Schindelin JE A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar]
- [126].Österreicher F; Vajda I A new class of metric divergences on probability spaces and its applicability in statistics. Ann. Inst. Stat. Math 2003, 55, 639–653. [Google Scholar]
- [127].Fuglede B; Topsoe F Jensen-Shannon divergence and Hilbert space embedding. International Symposium on Information Theory, 2004. ISIT 2004. Proceedings. 2004; p 31. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


