Abstract
Contemporary individuals are the combination of genetic fragments inherited from ancestors belonging to multiple populations, as the result of migration and admixture. Isolating and characterizing these layers are crucial to the understanding of the genetic history of a given population. Ancestry deconvolution approaches make use of a large amount of source individuals, therefore constraining the performance of Local Ancestry Inferences when only few genomes are available from a given population. Here we present WINC, a local ancestry framework derived from the combination of ChromoPainter and NNLS approaches, as a method to retrieve local genetic assignments when only a few reference individuals are available. The framework is aided by a score assignment based on source differentiation to maximize the amount of sequences retrieved and is capable of retrieving accurate ancestry assignments when only two individuals for source populations are used.
Keywords: admixture, local ancestry, ChromoPainter, NNLS
Significance
As the results of migration and admixture between populations, contemporary genomes can be seen as a mosaic, where each piece is an inherited genomic fragment. Isolating and characterizing these fragments help the understanding of the genetic and evolutionary history of a given population. The key approach to study the admixed fragments is Ancestry Deconvolution, though it is generally limited by both the quality and amount of the genomes of source populations. Here we developed a local ancestry framework derived from the combination of ChromoPainter and NNLS approaches, as a method to perform Ancestry Deconvolution when only a few reference individuals are available.
Introduction
In the last decade, the advent of dense genotyping arrays and high-throughput sequencing technologies has paved the way to the development of methods aimed at reconstructing Local Ancestry patterns along the chromosomes.
A large variety of local ancestry deconvolution methods have been proposed, harnessing different statistical algorithms such as Hidden Markov Models (HMM) (HapMix [Price et al. 2009], LAMP-LD [Baran et al. 2012], ELAI [Guan, 2014], MOSAIC [Salter-Townshend and Myers, 2019]), Principal Component analysis (PCAdmix [Brisbin et al. 2012]) and machine learning classification tools (RF-Mix [Maples et al. 2013]).
Most Local Ancestry Inference (LAI) methods available to date, identify fragments putatively descending from a limited number of reference populations, for which tens of individuals are typically required. Although a reasonable amount of data for most of the contemporary human groups are available (Yelmen et al. 2019), this is not the case for many key populations. Some human groups remain poorly sampled (hindered by social, geographic, or ethical factors), and historical populations are often incompletely captured by ancient DNA, which is reliant on preservation conditions, burial practice, extent of archeological activity, and other biasing factors. Furthermore and beyond the human realm, for contemporary or extinct species, few individuals are usually available to represent source populations due to the limited availability of samples or resources. A limited number of source individuals causes an under-estimation of the genetic diversity within populations, increasing the assignment error of the traditional LAI methods.
In this study, we propose that leveraging a larger panel of populations to genetically characterize both the sources and the admixed population could yield a better performance even when little amounts of source individuals are available for the analyses.
ChromoPainter provides the best approach to overcome the issue of lack of data for the sources of the target admixed population, as it uses the genetic information acquired from a large panel of populations, even unrelated to the admixture event, to describe (or paint) both sources and target individuals. A NNLS (Nonnegative Least Squares) is then used to summarize the painting information.
ChromoPainter/NNLS (Lawson et al. 2012; Hellenthal et al. 2014; Leslie et al. 2015) approach has been successfully employed to reconstruct the global ancestry of modern day and ancient populations, and simulation-based comparisons showed that it yields high accuracy at a genome wide level, even when a limited number of reference samples are available (Montinaro et al. 2015; van Dorp et al. 2015; Busby et al. 2016; Hofmanová et al. 2016; Järve et al. 2019; Ongaro et al. 2019).
We propose to turn the ChromoPainter/NNLS framework into a LAI tool, by applying the NNLS step on genetic windows, instead of the entire genomes. This approach could leverage on a large number of donor populations to characterize not only the admixed targets, but also the source populations, and thus provide a versatile solution when only a few samples are available for source populations.
We tested the performance of the proposed approach through coalescent simulations, validated it on an additional set of simulated individuals and applied it to real case scenarios. All simulated individuals were admixed 100 generations ago, a limit date for which most dating tools can detect an admixture event (Moorjani et al. 2011).
We benchmarked our performance against three Local Ancestry tools: a machine learning-based tool (RFmix, a commonly used LAI software), a Principal Component analysis-based tool (PCAdmix), and a HMM-based tool (ELAI, shown to outperform many of the state-of-the-art methods [Geza et al. 2019] and to perform well even in regions with small ancestral track length [Guan, 2014]).
The results showed that our method is capable of outcompeting all methods and particularly ELAI, which shows higher performances than PCAdmix and RFmix, when harnessing admixed individuals whose sources diverged at least 30 kilo years ago (ka), using as little as two individuals as sources.
Materials and Methods
Simulating Admixed Individuals: Test Set
We simulated 13 populations with changing population sizes and divergence times ranging from 250 to 4,000 generations (7.5–120 ka), to represent current European, East Asian, and African groups. We simulated approximately 250 Mb (for a total of 4,745,025 SNPs) which mimics the length of chromosome 1. We used a constant mutation and recombination rate, both set at 1.25 × 10−8 (Scally and Durbin, 2012). In detail, we assigned 20,000 and 10,000 as effective population size (Ne) for African and Eurasian populations, respectively and followed a similar model as in Van Dorp et al. 2015 (2015).
We then added seven sister groups, characterized by a divergence time from their sister group of 100 generations (3 ka), for a total of 20 simulated populations. These additional sister groups were not present in the model of Van Dorp et al. and were labeled as “Ghost” (GST) (supplementary fig. S1, Supplementary Material online). These populations were later used to create admixed groups, but were not included in any following step, as in a real scenario it would not be possible to perform Ancestry Deconvolution with the actual sources of the admixture.
Simulations were carried out with mspms (Kelleher et al. 2016) software using the following command:
mspms 2000 1 -t 15000 -r 12500 -I 20 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 -p 10 -n 1 20.0 -n 2 20.0 -n 3 20.0 -n 4 20.0 -n 5 20.0 -n 6 20.0 -n 7 20.0 -n 8 10.0 -n 9 10.0 -n 10 10.0 -n 11 10.0 -n 12 10.0 -n 13 10.0 -n 14 20.0 -n 15 10.0 -n 16 10.0 -n 17 10.0 -n 18 10.0 -n 19 10.0 -n 20 10.0 -ej 0.025 14 4 -ej 0.025 15 8 -ej 0.025 16 9 -ej 0.025 17 10 -ej 0.02 5 18 11 -ej 0.025 19 12 -ej 0.025 20 13 -ej 0.0625 13 12 -ej 0.075 12 11 -ej 0.1 9 8 -ej 0.125 3 2 -ej 0.175 6 5 -en 0.175 11 2.0 -ej 0.2 10 8 -ej 0.25 11 8 -ej 0.25 7 5 -ej 0.425 5 4 -ej 0. 45 4 2 -en 0.45 2 10.0 -en 0.45 8 2.0 -ej 0.625 8 2 -ej 1.0 2 1 -en 1.0 1 1
We generated 8 admixed populations (50 individuals each) combining pairs of simulated Ghost demes, with admix-simu (https://github.com/williamslab/admix-simu) with the proportions of 70–30%, constant recombination rate (1.25 × 10−8) and admixture time of 100 generations. We included an additional population obtained from a three-way admixture with the proportion of 40–30–30%, using the same parameters of the two-way admixture runs.
The pairs of admixing Ghosts were selected to cover a broad spectrum of divergence times, allowing us a deeper evaluation of the framework performance. The resulting data were combined with the previously simulated data set, after the removal of Ghosts demes.
Admix-simu records the source for each SNP in a “truth file,” which was harnessed to infer the accuracy of the Local Ancestry methods.
We analyzed the pairwise genetic distances among all pairs of simulated populations and elected populations from the 1000 Genome Project with smartpca (Patterson et al. 2006) (eigensoft-7.2.0), with the option fstonly: YES.
Simulating Admixed Individuals: Empirical Set
We simulated three admixed populations (N = 50 individuals each), from the 1000 Genome Project (1000 Genomes Project Consortium, 2015), using admix-simu (https://github.com/williamslab/admix-simu) and using chromosome 1 (943,790 SNPs) as input; with admixture time of 100 generations ago and 70–30% proportions. We simulated the admixture events between a European (TSI, Toscani in Italy) and African (YRI, Yoruba in Nigeria) population (comparable to approximately 75 ka TMRCA of the Test Set [Pagani et al. 2016]), European (TSI) and Asian (CHB, Han Chinese in Beijing) population (comparable to approximately 30 ka TMRCA of the Test Set [Pagani et al. 2016]), within European populations (TSI and FIN, Finnish in Finland, comparable to approximately 7.5 ka TMRCA of the Test Set [Pagani et al. 2016]) and created a three-way continental admixture between YRI, CHB, and TSI (with the proportion of 40–30–30%, respectively). We used CEU (Utah residents with European ancestry) as a source population to retrieve TSI fragments, ESN (Esan in Nigeria) for YRI and CHS (Han Chinese South) for CHB. To retrieve FIN fragments, we set as source all FIN individuals not used to create the admixed population TSI-FIN. We then run WINC using first 45 individuals from each source then we downsampled to two individuals. As donor panel, we used all populations from the 1000 Genome Project.
Real Case Scenario: ASW and MXL
We applied the developed framework on ASW and MXL (American of African Ancestry in SW and Mexican Ancestry from Los Angeles, USA) from the 1000 Genome Project (1000 Genomes Project Consortium, 2015). We painted 61 ASW individuals using all the non-American populations in the data set. We set as source populations CEU (Utah residents with European ancestry) and ESN (Esan in Nigeria), first performing Local Ancestry analyses using 45 individuals each and then downsampled to 2 individuals per source. We deconvoluted 64 MXL with CEU, ESN, and PEL (Peruvians from Lima in Peru), using first 45 and then only 2 individuals. We applied both WINC and WINC with the addition of the Reference C-AS matrix for several AS. Given that in this case we could not compare our result with a “truth file”, we used ELAI results on ASW and MXL obtained using 45 individuals as sources as benchmark.
ChromoPainter
We estimated the nuisance parameters mu (mutation rate) and Ne (effective population size), through an Expectation-Maximization algorithm for both the Testing Set and Empirical Set. For the Test Set, we set the mu parameter as 0.0011, and Ne as 2,516.3133, whereas for the Empirical Set mu was set as 0.0008281 and Ne as 939.2658. The parameters used for the Empirical Set were also used for MXL and ASW analyses.
Splitting Copying Vector
We splitted both sources and target populations’ copying vectors in windows each containing 500 kb. The expected tile length of the ancestry block in a population is:
with L = expected length, m = mixing proportion, r = recombination rate, t = time (in generations) since the admixture event (Racimo et al. 2015).
The expected length of the ancestry tiles in our data set, in which all populations admixed 100 generations ago, is ∼1 Mb. We thus chose the length of 500 kb genomic windows in order to retrieve ancestry blocks that fall within the expected tile length.
Nonnegative Least Squares
We performed the NNLS on the window-based copying vectors. In this step, for each genomic window, we summarized the copying vector of the target individuals as a combination of the copying vectors of the sources.
We used the NNLS function, as described in Hellenthal et al. (2014), Leslie et al. (2015), Ongaro et al. (2019), which is a modification of the Lawson–Hanson NNLS implementation of nonnegative least squares function (Lawson and Hanson, 1995) available in the statistical software package R 3.5.1 (R Core Team, 2020).
Taken together all steps should take the following running time at the current level of software optimization: ChromoPainter, which can be run upstream, can take up to 3 h per sample, while splitting windows and NNLS steps should take less than 10 min per sample. However, we note that these estimates are highly dependent on the study design (e.g., number of ChromoPainter donor samples and overall number of SNPs: 4,745,025 for the simulated data set and 943,790 SNPs for the empirical data set in our case), hence these running time are to be intended for the current design only.
Evaluating WINC Performance on Different Window Lengths
The expected ancestry tiling length of a population that admixed 100 generations ago is ∼1 Mb long. We chose to show WINC results with genomic window length set at 500 kb, to select a haplotype block that could be contained entirely within a given ancestry tile.
Additionally, we applied our method on the Test Set using a longer window length (1 million base pairs) and a shorter one (100 kb per window) (supplementary fig. S14, Supplementary Material online).
We also took into account the amount of markers ChromoPainter can harness in the analyses and therefore the density of the biological information contained in each window. Thus, we tested our approach by splitting the copying vectors based on the average number of markers per 500 kb window, so that the length of the windows would be dependent on the number of SNPs within. We ran the SNP density analyses only on the Empirical Set, since the Test Set SNP density had low variance, on windows containing 1,892 SNPs (supplementary fig. S15, Supplementary Material online).
Benchmarks
In order to provide a comparative measure of the performance of the newly developed framework, we performed LAI using different Local Ancestry softwares.
ELAI
We performed 10 independent runs and averaged the “estimated ancestral allele dosages for each individual at each SNP” (Guan, 2014). ELAI analyses were performed on phased data using the following parameters: -C 2, for two upper clusters when inferring a two-way admixture, and -C 3 when inferring a three-way admixture. We used -c 10 for 10 lower-layer clusters when harnessing 50 individuals and -c 8 when harnessing 2, -mg 100 for 100 admixture generations, -s 20 for 20 EM iterations, as recommended in ELAI manual. All the ELAI inferences have been obtained by averaging the results of all individuals tested.
PCAdmix
We used PCAdmix (Brisbin et al. 2012) with default parameters with windows size set to 0.5 cM for all analyses.
RFmix
We performed RFmix (Maples et al. 2013) with the following parameters: -w 0.5 for 0.5 cM window size, -G 100 to indicate 100 generation since admixture, -e 2 to perform 2 number of EM iterations, –forward-backward to output the forward-backward probabilities. The parameters not listed here were set as default.
Refining WINC Inference Using Window-Based Affinity among Sources
We evaluated the performance of WINC with respect to the similarity of the copying vectors for each window in the Test Set. For each analyzed window, we estimated the Pearson correlation among the averaged copying vectors from the two sources. In order to increase the number pairs at a given correlation, we performed WINC resampling N source individuals 10 times, with N ∈ (2, 10, 20, 30, 40, 45).
We then binned Assignment Scores (AS) and Pearson’s r in 10 and 20 intervals respectively, and summarized the accuracy of WINC. In doing so, we obtained a Correlation Assignment Score (C-AS) reference matrix.
The C-AS matrix generated is suited for human populations at cross-continental level, or populations with pairwise genetic distances values similar to the groups we simulated (indicated in supplementary fig. S2, Supplementary Material online). We note that the C-AS matrix can be re-calibrated by any user through a new set of simulations believed to be more fitting to the case study. The advised procedure would be simulating a data set as similar as possible to the one the user would like to apply WINC on and recreate a C-AS matrix that is more suited to the data set of interest.
Results
Proposed Window-Based ChromoPainter/NNLS Framework
As the core of our strategy, we used the recently developed approach implemented in the ChromoPainter/NNLS (Lawson et al. 2012; Hellenthal et al. 2014; Leslie et al. 2015) algorithm (the combination of ChromoPainter and NNLS algorithms).
In a given phased data set, ChromoPainter (Lawson et al. 2012) identifies the closest neighbor “donor” for any “recipient” individual haplotype. Along the chromosome, the combination of all the identified closest neighbors summarizes the different ancestry of an individual. Given the high complexity and computational resources needed for computing the whole set of genealogies, ChromoPainter exploits the approximation provided in the HMM developed by Li and Stephens (2003), reconstructing recipient individuals as a combination of genomic segments, or chunks, “donated” by any other individual in the data set. The information is then stored in a copying vector, an array that summarizes the amount of genome copied by a given recipient from each donor sample. However, the coalescent events in natural groups may predate the time of population split, therefore creating only small differences in the amount of genetic fragments copied by closely related populations, adding a confounding factor in the ancestral deconvolution approach. This limitation is solved using a multiple linear regression approach, in which a modification of the NNLS is exploited to reconstruct the painting profile of a given individual as a combination of copying vectors from a set of source individuals or populations. In this approach, the target admixed individuals are usually set as recipients, and the putative sources of the admixture as donors. We propose to set as recipients both the admixed individuals and the unadmixed sources, in order to paint them with a large panel of donor populations not necessarily related with the admixture event.
Here we develop a framework for performing Local Ancestry Decolvolution using ChromoPainter/NNLS onto genomic windows that approximate the expected ancestry tiling in an admixed individual, and named it WINC as short for Window-based NNLS/ChromoPainter.
Unlike the regular pipeline, we applied it on 500 kb genomic windows, rather than the whole genomes. The length of 500 kb genomic windows has been chosen to fall within the expected chunk length of an admixture event that happened 100 generations ago (see Materials and Methods). In doing so, we aim to convey ChromoPainter/NNLS accuracy as a global ancestry estimator onto a genomic localized context, hence turning it into a local ancestry tool.
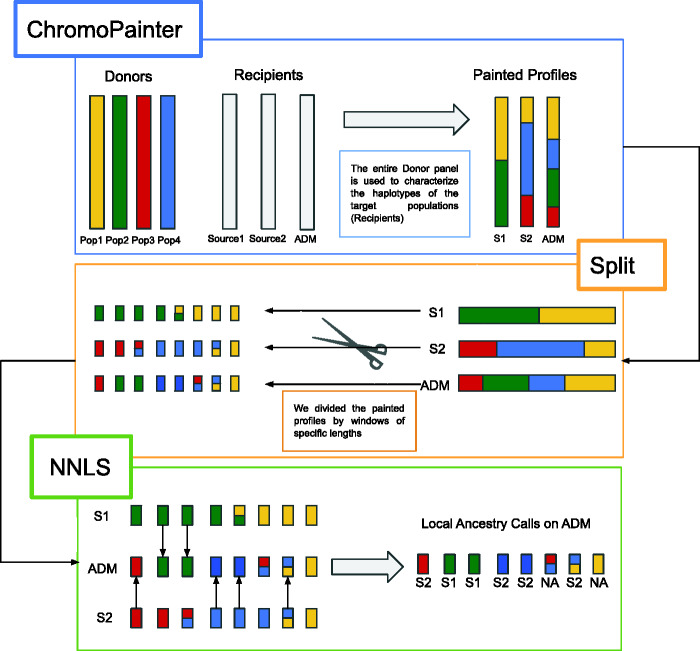
A schematic representation of the process is shown in figure 1. More in detail 1) we performed a ChromoPainter run in which source and target individuals are painted using the entire donor panel. The donor panel is composed of presumably unadmixed groups. The admixed target populations were set as recipients, along with the source populations. Setting as recipients both the target and the source individuals allowed us to obtain the copying vectors for both, which were then used for the following step. 2) For each painted haplotype, we splitted the copying vector into genomic windows of the same length. For any window, we averaged the amount of genome copied from any donor populations and normalized the resulting copying vector to sum 1. 3) We then moved to the NNLS step, in which we described each target individual as a mixture of the selected source populations. The NNLS approach identifies the sources’ copying vector that better match the copying vector of recipient populations as estimated by ChromoPainter. In this way, for each window belonging to admixed individuals, we used NNLS to assign the window to one of the putative sources. The assignment indicates the proportion of the admixed copying vector that matches each source’s copying vector. 4) Each ancestry assignment proportion can be seen as a score (AS), on which we apply several cutoffs. We then averaged the window-based copying vectors through all the individuals.
Fig. 1.
Schematic representation of WINC approach. WINC is based on the ChromoPainter/NNLS framework, with the additional step of splitting the copying vectors resulting from the ChromoPainter (CP) run before analyzing them through the NNLS step. First step: ChromoPainter run. CP identifies the closest neighbor “donor” for any “recipient” individual haplotype. ChromoPainter then reconstructs the recipient individuals as a combination of genomic segments, or chunks, “donated” by any other individual in the data set. The information is then stored in copying vectors, where, for each recipient haplotype, it is indicated which donor individual is the closest neighbour. In this way, we obtain the copying vectors of our target populations: both the sources and the admixed individuals. Second step: splitting copying vectors. We then split the copying vectors in genomic windows of the same length. Window size depends on the ancestry chunks, which in turn depends on the amount of generations since the admixture. Third step: performing NNLS analyses on the copying vector’s genomic windows obtained from the previous step. The NNLS step assigns a window to a specific ancestry, by reconstructing the painting profile of a given individual as a combination (or proportion) of copying vectors from the source individuals.
We tested the performance of the proposed approach through coalescent simulations, validated it on an additional simulated data set and finally on real individuals, and benchmarked our performance against other LAI tools. Each analysis was performed twice, first using 50 individuals as sources and then only 2 (100 and 4 haplotypes, respectively), but maintaining in both cases a large number of donor populations unrelated to the admixture event.
Evaluation Parameters
All LAI tools tested here assign a probability of ancestry to each genomic window. On the other hand, our approach employs the proportion assignment given by the NNLS (see Materials and Methods). In both cases, we refer to the value assignments as AS. The AS values range from 0 to 1 and they are used to evaluate the performance of all tools by applying several cutoffs.
We set different thresholds for each run in order to remove windows with an AS (or ancestry assignment probability/proportion) lower than the threshold. All removed windows are then labeled as “Unassigned.” We set for all LAI tools the following AS thresholds: 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.91, 0.92, 0.93, 0.94, 0.95, 0.96, 0.97, 0.98, 0.99.
Given the presence of unassigned values, we accounted for accuracy and assignation separately. We set Accuracyg as the portion of windows correctly assigned given all genome windows, taking into consideration both the assigned and the unassigned windows. We set Accuracya as the portion of windows correctly assigned given only the windows that passed the threshold, therefore not taking into account the “Unassigned” blocks. We calculated separately “Assigned Genome” as the portion of all the windows that reached the AS threshold.
Simulating Admixed Individuals
We simulated a Test Set of 13 populations with different population sizes and with divergence times ranging from 250 to 4,000 generations (7.5–120 ka), to represent current European, East Asian, and African groups, following a modified Van Dorp et al. model (van Dorp et al. 2015).
We then added seven sister groups, characterized by a divergence time from their sister group of 100 generations (3 ka), for a total of 20 simulated populations. These additional sister groups were not present in the model of Van Dorp et al. and were labeled as “Ghost” (GST) (supplementary fig. S1, Supplementary Material online). These populations were later used to create admixed groups, but were not included in any following step, as in a real scenario it would not be possible to perform Ancestry Deconvolution with the actual sources of the admixture.
We generate eight two-ways admixed populations combining pairs of simulated Ghost demes, and one three-ways admixed population with admix-simu (https://github.com/williamslab/admix-simu) with an admixture time of 100 generations and proportions of 70–30% and 40–30–30%, respectively (see supplementary table S1, Supplementary Material online).
Similarly, we also simulated an Empirical Set of three two-ways admixed populations and one three-ways admixed population from the 1000 Genome project (1000 Genomes Project Consortium 2015) using admixture proportions and generation times as per the Test Set (70–30% for the two ways, 40–30–30% for the three ways, and 100 generations since the admixture in all cases). We simulated the admixture events between a European (TSI, Toscani in Italy) and African (YRI, Yoruba in Nigeria) population, European (TSI) and Asian (CHB, Han Chinese in Beijing) population, and within European populations (TSI and FIN, Finnish in Finland). The three-way continental admixture was created between YRI, CHB, and TSI. We used CEU (Utah residents with European ancestry) as a source population to retrieve TSI fragments, ESN (Esan in Nigeria) for YRI and CHS (Han Chinese South) for CHB. To retrieve FIN fragments, we set as source all FIN individuals not used to create the admixed population TSI-FIN. As donor panel, we used all populations from the 1000 Genomes Project.
Global Ancestry Estimates
First, we analyzed the pairwise genetic distance among all pairs of simulated populations from the Test Set and showed that they are consistent with those observed among modern populations (supplementary figs. S2 and S3, Supplementary Material online). We then applied ChromoPainter/NNLS global ancestry methodology on the entire chromosome and showed that it correctly assigns the two ancestries (supplementary fig. S4, Supplementary Material online), with a discrepancy of 0.01% when the sources diverged 75 ka and 10% when they diverged just 7.5 ka.
WINC Performance on the Testing Set
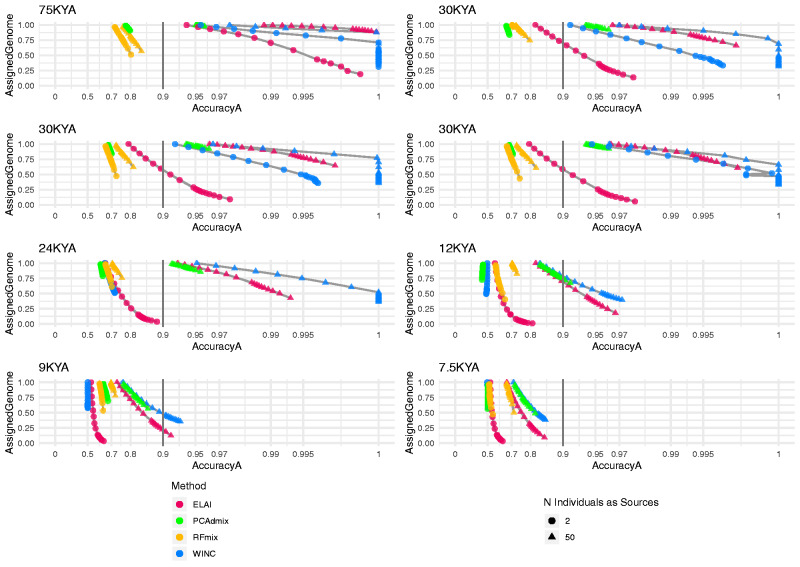
To test our approach, we applied WINC on a set of simulated individuals (Test Set). All populations are characterized by a distant admixture time (100 generation), which causes the ancestral fragments to be relatively small in all target individuals. On the other hand, all admixed populations vary on the similarity of the sources of the admixture, given by the different divergence time between sources. Thus, we expect that the LAI tools more robust in inferring ancestries in small regions will yield high performances. On the other hand, we expect that each tool performance will decrease as the divergence between sources decreases, despite the admixture generations. We compared WINC with RFmix, PCAdmix and ELAI. To compare LAI tools, we considered both Assigned Genome, the portion of the windows that reached the threshold, and accuracya, an accuracy computed only on windows for which ancestry assignment was performed.
Overall, RFmix performance does not exceed the accuracya of 85% in any target population (fig. 2), probably due to the high number of generation elapsed since the admixture (Dias-Alves et al. 2018) (supplementary fig. S5, Supplementary Material online). This is shown when using 50 individuals per source as well as 2. WINC outcompetes RFMix, showing that our framework could detect ancestries in a target population with small ancestry tiles.
Fig. 2.
WINC performance on the Test Set compared with several Local Ancestry tools: ELAI, PCAdmix, and RFmix. The eight panels represent results for different admixed populations with different divergence times. Within each series, different data points linked by a gray line represent experiments run using increasingly stringent AS thresholds, and for which a nonzero amount of genomes was assigned to at least one ancestry by that particular LAI method. x axis shows accuracy(a) values, y axis shows the proportion of genome windows retrieved. Red points indicate the results obtained using ELAI, green dots indicate PCAdmix results, orange dots list RFmix results, whereas blue points list WINC results. Triangles indicate Local Ancestry results using 50 individuals per source, whereas dots list results using two individuals. We note that in the “12 ka” panel, when two individuals are used as reference, both PCAdmix and WINC accuracy values decrease with increasingly stringent AS thresholds. This effect is however minor (PCAdmix accuracy values range from 0.44 to 0.43 and WINC values range from 0.51 to 0.49).
PCAdmix results are comparable with WINC and ELAI when using 50 individuals per source. When two individuals are employed to deconvolute the target population, PCAdmix accuracya is always lower than 0.8, regardless of the divergence between sources (fig. 2).
Of all tested tools, the only one matching WINC’s performance appears to be ELAI (fig. 2). In fact, when using 50 samples for each source population, both ELAI and WINC display a comparable amount of Assigned Genome and accuracy levels for all divergences between the sources (fig. 2 and supplementary tables S2–S7, Supplementary Material online).
Supported by the promising evidence, we moved to test our approach using only two individuals per source, the main focus of our investigation.
ELAI and WINC show comparable levels of accuracya and Assigned Genome when only two individuals are used per source. For populations with highly differentiated sources and older split times, such as 75 ka or 30 ka, WINC assigns up to 99% of the genome with a minimum accuracya of 0.9 (fig. 2, supplementary tables S2–S7, Supplementary Material online). When tested on the 30-ka populations, WINC outperforms ELAI in terms of accuracy levels reached and proportion of Assigned Genome maintained. For more recent split times (up to 24 ka), both WINC and ELAI show a decrease in accuracya and amount of genome retrieved, as expected when the sources of the admixture are genetically similar.
We further provide specific results for both WINC and ELAI considering only one AS threshold (0.8), to provide performance for a standard run under default parameters (supplementary figs. S6–S9, Supplementary Material online).
Given that RFmix is suited for more recent admixture times (supplementary fig. S5, Supplementary Material online) and PCAdmix does not reach high performance levels when only two individuals are used as sources, we performed the subsequent tests using only ELAI as a benchmark.
WINC Calibration Using a Correlation-Assignment Score Matrix
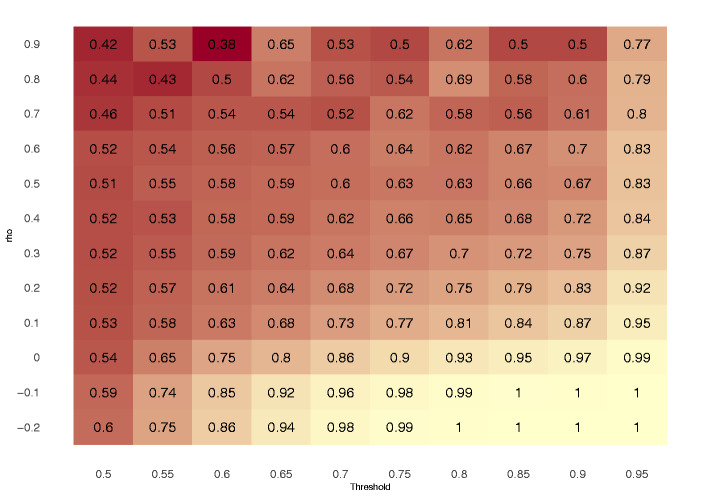
LAI approaches are expected to have a higher accuracy when the admixing sources are genetically distant at the locus of interest. The more two sources are differentiated at a given genomic window, the easier it should be for NNLS to assign a haplotype to one or the other source population. We can leverage the similarity between sources to predict when NNLS has sufficient information to correctly infer the local ancestries, providing a calibration for WINC. To assess the similarity between different sources, we computed a Pearson correlation coefficient (rho) between ChromoPainter copying vectors obtained on the same window for each pair of source populations. We then performed the NNLS analysis applying different cutoffs, therefore removing all windows where the AS was lower than the specified threshold. We calculated the accuracy obtained considering windows in ten equally spaced rho values and AS thresholds. In doing so, we obtained a C-AS matrix (fig. 3) that, given different values of similarity between sources (correlation) and AS, should inform on the expected accuracy values.
Fig. 3.
Reference C-AS matrix on Test Set, a correlation matrix obtained using rho values between sources and ASs. Each slot indicates accuracya values obtained by selecting a given set of ASs (x axis) threshold and rho values of similarity between source populations (y axis). High accuracya values are listed with lighter colors, low accuracya values are indicated by darker colors.
Application of Reference C-AS Matrix and Effects on WINC Performance
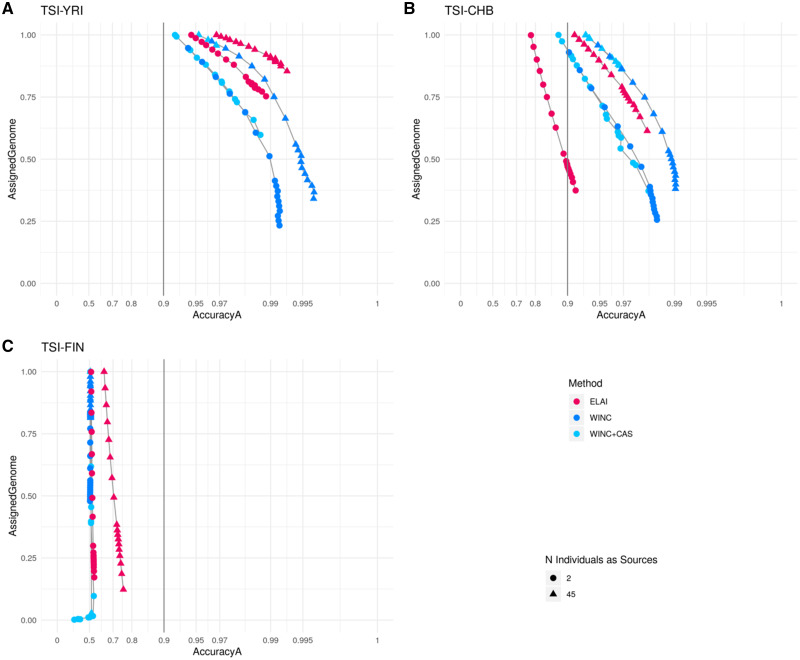
We tested the applicability of the C-AS matrix (estimated on the Test Set) on the Empirical Set (see fig. 3 and supplementary fig. S10, Supplementary Material online for a schematic representation). For a given correlation in a specific window, we used the minimum AS threshold needed to obtain the desired accuracya value. We analyzed the overall performance and transferability of the C-AS matrix on the Empirical Set and compared it with the results obtained by selecting the windows only by AS thresholds.
Our tool operates with high accuracya values (over 0.9) also on the Empirical Set when 50 individuals are available for the LAIs, and the sources are genetically differentiated (see fig. 4A and B and supplementary tables S8 and S9, Supplementary Material online). In fact, similarly with the Test Set results on populations with genetically similar sources, all LAI tools tested do not reach satisfactory accuracya levels on TSI-FIN (fig. 4C and supplementary table S10, Supplementary Material online).
Fig. 4.
WINC and WINC + C-AS performances compared with ELAI on the Empirical Set. Panel A indicates the resuts of TSI-YRI population, panel B shows the results of TSI-CHB population and panel C displays results of TSI-FIN population. Red points indicate the results obtained using ELAI, blue points list WINC results, and light blue points list WINC + C-AS performances. Triangles indicate Local Ancestry results using 45 individuals per source, whereas dots list results using two individuals. On the x axis, we listed accuracya values, computed only on windows for which ancestry assignment was performed, and on the y axis, we listed the proportion of genome windows retrieved.
We thus moved to study its performances when only two individuals per source were set. We observed that, for both TSI-YRI and TSI-CHB populations, WINC calibrated with the C-AS matrix performs equally well to WINC alone in terms of accuracya, but retrieves higher portions of the genome (fig. 4A and B and supplementary tables S8 and S9, Supplementary Material online), with the additional notable difference that WINC + C-AS is predictable in its outcome. By applying the C-AS matrix to WINC, we could in fact assign windows with the desired accuracya, with the only exception being reaching an observed accuracya of ∼0.97 when the expected one was set at 0.99 (see supplementary figs. S11 and S12 and table S8 and S9, Supplementary Material online).
Differently from WINC alone, WINC + C-AS matrix tends to not assign any genomic window of TSI-FIN (maximum 0.1%), when threshold values were set to 0.85 or higher (fig. 4C and supplementary table S10, Supplementary Material online), hence providing an effective way of drastically reducing false positives when true positives cannot be obtained at all.
The C-AS matrix, created from the Test Set and applied to the Empirical Set, returned windows that reached the selected desired accuracya, showing its efficacy when used on a different data set. We also applied the C-AS matrix on the Test set, as a control (supplementary fig. S13, Supplementary Material online).
Additionally we investigated WINC performance of different window lengths: 1,000 kb, 100 kb, and on variable lengths depending on the SNP density (see supplementary figs. S14 and S15, Supplementary Material online) and confirmed 500 kb to be the optimal window size for the current study.
Evaluating WINC Performance on Three-Way Admixtures
As a proof of principle, we show the analyses on the three-ways admixtures simulated in the Test Set and Empirical Set jointly. Results on the Test Set show that ELAI outcompetes both WINC and WINC + C-AS when harnessing the ancestries of a three-ways admixture, even when only a few individuals are used as source. On the other hand, on the Empirical Set, WINC and WINC + C-AS outperformed ELAI when two individuals are set per source (see supplementary figs. S16 and S17 and table S11 and S12, Supplementary Material online).
Evaluating WINC Performance on Real Data
Lastly, we applied the WINC and WINC + C-AS matrix approaches to real genomes from ASW (American of African Ancestry in SW) and from MXL (Mexican Ancestry from Los Angeles, USA) (1000 Genomes Project Consortium, 2015). To analyze ASW, we used CEU and ESN as sources, whereas for MXL we used CEU, PEL, and ESN. Each analysis was composed of either 45 or 2 of source individuals. For comparison, we also performed ELAI analyses on ASW and MXL using two individuals per source. To assess WINC and ELAI accuracies, being a real case not resulting from simulations, we chose to take as “truth” the results with ELAI ancestry assignments using 45 individuals.
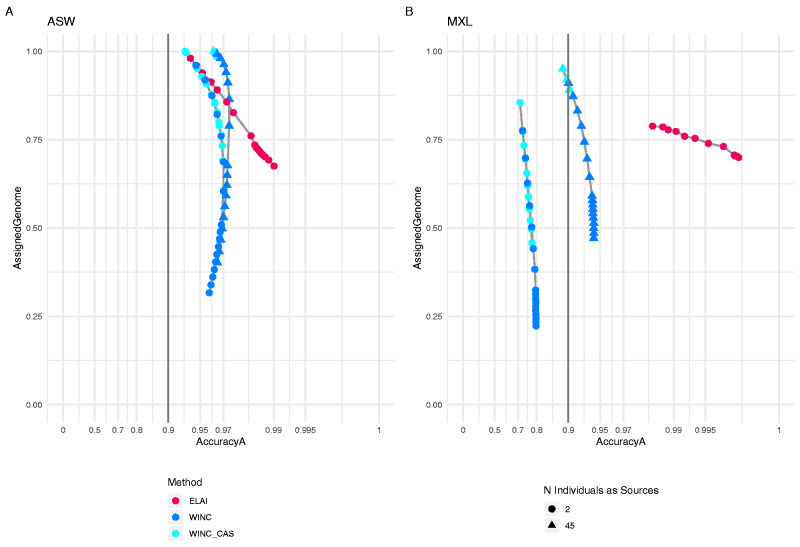
On ASW population, both ELAI (when using 2 individuals) and WINC (when using 50 or 2 individuals as sources) show accuracya levels of 0.9 or higher (see fig. 5A and supplementary table S13, Supplementary Material online). Consistently with the highly divergent simulated populations of the Test Set, WINC and WINC + C-AS matrix both show accuracya levels higher than 0.9. Discrepancies on the portions of the assigned genome could be due to the fact that ELAI assigns windows that WINC set as NA, or vice versa.
Fig. 5.
WINC and WINC + C-AS results compared with ELAI in ASW and MXL populations. Panel A shows results of ASW population, panel B shows results of MXL population. All results were obtained comparing our methods WINC (in blue) and WINC + C-AS matrix (in light blue) with ELAI runs in which we use 45 individuals as sources. Additionally, we show ELAI results using only two individuals as sources and benchmarked them with ELAI runs using 45 individuals as sources. Red points indicate the results obtained using ELAI, blue points list WINC results, and light blue points list WINC + C-AS performances. Triangles indicate Local Ancestry results using 45 individuals per source, whereas dots list results using two individuals. On the x axis we listed accuracya values, on the y axis, we listed the percentage of genome windows retrieved.
On MXL population (fig. 5B and supplementary table S14, Supplementary Material online), WINC reaches accuracya of 0.9 or higher when using 45 individuals per source, but unlike ELAI, it does not reach high accuracya levels when inferring the three MXL ancestries when only two individuals are used per source.
Discussion
In this work, we describe WINC, a local ancestry approach based on chromosome painting through ChromoPainter/NNLS. The approach is aimed at characterizing genomic fragments in admixed populations, with different degrees of relatedness and small sample sizes among source populations and with as many as 100 generations since the admixture.
We applied the method on genomic data obtained through coalescent simulations which also forms the basis for the C-AS matrix, a reference grid to inform a priori on the accuracya to be expected by WINC for a given set of Ancestry Assignments and local diversification between sources.
When applied on a set obtained by admixing real genomes, WINC and the C-AS matrix match ELAI for admixture scenarios involving African and European sources and outperform it for admixtures involving European and East Asian sources when using as little as two individuals as reference. We speculate that the reduced diversity in the source populations is compensated by the large donor panel used by ChromoPainter. This factor allowed our method to reach high accuracy levels when only two individuals were used per source, but only when the sources retained a certain level of genetic differentiation. In fact, in the case of a subcontinental admixture, the donor panel populations used were not able to fully characterize and differentiate the two sources of the admixture.
All the tested methods fail at yielding acceptable performance when applied on admixtures between two European populations, with the notable difference represented by the ability of the C-AS matrix to filter out most of the potentially inaccurate output, hence avoiding spurious ancestry assignments.
Another unique feature of our method is the option to know in advance (based on the ChromoPainter power to discriminate between the source populations) what fraction of the genome will be assigned with satisfactory accuracya. This feature can be exploited in the C-AS matrix, where specific windows of the genome can be selected to obtain the desired accuracya level.
Our method relies on biological information to perform optimally: the user needs to set the window length of the genome on which the local ancestry can be inferred, this information can be estimated from the admixture generation time. Additionally, given that our approach relies on ChromoPainter, it also uses phased data and a recombination map in the ChromoPainter step.
In conclusion, since the majority of ChromoPainter discriminatory power relies on the availability of a sufficiently diverse panel of donors, we envisage that a constant improvement of the donor panel may allow any user to maximize the performances of our approach even for trials where the admixing populations are particularly similar and for which the number of available source individuals is limited, like in the cases of aDNA or of most nonhuman species. Future improvements of the method, including a more flexible definition of the sliding window used to perform the local ancestry, will contribute to increase the fraction of the confidently assigned genome.
Supplementary Material
Supplementary data are available at Genome Biology and Evolution online.
Supplementary Material
Acknowledgments
The authors thank Garrett Hellenthal for fruitful discussion on an early version of this manuscript. This work was supported by the European Union through the European Regional Development Fund (2014-2020.4.01.16-0024, MOBTT53 to D.M., L.M., B.Y., and L.P. and 2014-2020.4.01.16-0030 to F.M., M.M., L.O.).
Author Contributions
L.P., F.M., and L.M. designed the approach, L.M., F.M., D.M., L.O., B.Y, and M.M. performed the analyses, L.P., F.M., and L.M. wrote the manuscript with the help of all the coauthors.
Code Availability
WINC pipeline can be found in: https://github.com/lm-ut/WINC-pipeline (last accessed February 16, 2021).
Data Availability
Human genomic data used in this study were taken from: https://www.internationalgenome.org/ (last accessed February 16, 2021). Software used for this study were downloaded from: https://people.maths.bris.ac.uk/~madjl/finestructure-old/chromopainter_info.html, https://github.com/williamslab/admix-simu, https://haplotype.org/software.html, https://pypi.org/project/msprime/ (all URLs were last accessed February 16, 2021).
Literature Cited
- 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526:68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baran Y, et al. 2012. Fast and accurate inference of local ancestry in Latino populations. Bioinform. Oxf. Engl. 28(10):1359–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisbin A, et al. 2012. PCAdmix: principal components-based assignment of ancestry along each chromosome in individuals with admixed ancestry from two or more populations. Hum. Biol. 84(4):343–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busby GBJ, et al. 2016. Admixture into and within sub-Saharan Africa. eLife 5:1–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dias-Alves T, Mairal J, Blum MGB.. 2018. Loter: a software package to infer local ancestry for a wide range of species. Mol. Biol. Evol. 35(9):2318–2326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geza E, et al. 2019. A comprehensive survey of models for dissecting local ancestry deconvolution in human genome. Brief. Bioinform. 20(5):1709–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan Y. 2014. Detecting structure of haplotypes and local ancestry. Genetics 196(3):625–642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellenthal G, et al. 2014. A genetic atlas of human admixture history. Science 343(6172):747–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofmanová Z, et al. 2016. Early farmers from across Europe directly descended from Neolithic Aegeans. Proc. Natl. Acad. Sci. U.S.A. 113(25) 6886–6891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Järve M, et al. 2019. Shifts in the genetic landscape of the western Eurasian steppe associated with the beginning and end of the Scythian dominance. Curr. Biol. 29(14):2430–2441.e10. [DOI] [PubMed] [Google Scholar]
- Kelleher J, Etheridge AM, McVean G.. 2016. Efficient coalescent simulation and genealogical analysis for large sample sizes. PLoS Comput. Biol. 12:1–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson CL, Hanson R.. 1995. Solving least squares problems. Philadelphia (PA): Reprinted by the Society for Industrial and Applied Mathematics.
- Lawson DJ, Hellenthal G, Myers S, Falush D.. 2012. Inference of population structure using dense haplotype data. PLoS Genet. 8(1):e1002453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leslie S, et al. 2015. The fine-scale genetic structure of the British population. Nature 519(7543):309–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li N, Stephens M.. 2003. Modeling linkage disequilibrium and identifying recombination hotspots using single-nucleotide polymorphism data. Genetics 2233:2213–2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maples BK, Gravel S, Kenny EE, Bustamante CD.. 2013. RFMix: a discriminative modeling approach for rapid and robust local-ancestry inference. Am. J. Hum. Genet. 93(2):278–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montinaro F, et al. 2015. Unravelling the hidden ancestry of American admixed populations. Nat. Commun. 6:6596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moorjani P, et al. 2011. The history of African gene flow into Southern Europeans, Levantines, and Jews. PLoS Genet. 7(4):e1001373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ongaro L, et al. 2019. The genomic impact of European colonization of the Americas. Curr. Biol. 29(23):3974–3986.e4. [DOI] [PubMed] [Google Scholar]
- Pagani L, et al. 2016. Genomic analyses inform on migration events during the peopling of Eurasia. Nature 538(7624):238–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D.. 2006. Population structure and eigenanalysis. PLoS Genet. 2(12):e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, et al. 2009. Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genet. 5(6):e1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2020. R: A language and environment for statistical computing. R Found. Stat. Comput., Vienna, Austria.
- Racimo F, Sankararaman S, Nielsen R, Huerta-Sánchez E.. 2015. Evidence for archaic adaptive introgression in humans. Nat. Rev. Genet. 16(6):359–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salter-Townshend M, Myers S.. 2019. Fine-scale inference of ancestry segments without prior knowledge of admixing groups. Genetics 212(3):869–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scally A, Durbin R.. 2012. Revising the human mutation rate: implications for understanding human evolution. Nat. Rev. Genet. 13(10):745–753. [DOI] [PubMed] [Google Scholar]
- van Dorp L, et al. 2015. Evidence for a common origin of Blacksmiths and cultivators in the Ethiopian Ari within the Last 4500 years: lessons for clustering-based inference. PLOS Genet. 11(8):e1005397–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yelmen B, et al. 2019. Ancestry-specific analyses reveal differential demographic histories and opposite selective pressures in modern South Asian populations. Mol. Biol. Evol. 36(8):1628–1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Human genomic data used in this study were taken from: https://www.internationalgenome.org/ (last accessed February 16, 2021). Software used for this study were downloaded from: https://people.maths.bris.ac.uk/~madjl/finestructure-old/chromopainter_info.html, https://github.com/williamslab/admix-simu, https://haplotype.org/software.html, https://pypi.org/project/msprime/ (all URLs were last accessed February 16, 2021).