Machine learning discovery of high-temperature polymers

Summary

To formulate a machine learning (ML) model to establish the polymer's structure-property correlation for glass transition temperature $T_g$, we collect a diverse set of nearly 13,000 real homopolymers from the largest polymer database, PoLyInfo. We train the deep neural network (DNN) model with 6,923 experimental $T_g$ values using Morgan fingerprint representations of chemical structures for these polymers. Interestingly, the trained DNN model can reasonably predict the unknown $T_g$ values of polymers with distinct molecular structures, in comparison with molecular dynamics simulations and experimental results. With the validated transferability and generalization ability, the ML model is utilized for high-throughput screening of nearly one million hypothetical polymers. We identify more than 65,000 promising candidates with $T_g$ > 200°C, which is 30 times more than existing known high-temperature polymers (∼2,000 from PoLyInfo). The discovery of this large number of promising candidates will be of significant interest in the development and design of high-temperature polymers.

Graphical abstract

Highlights

• •Large datasets for polymer's glass transition temperature are collected
• •Transferability of ML models depends on feature representations
• •Molecular dynamics models and experimental results validate the formulated ML model
• •Extensive promising candidates for high-temperature polymers are screened by ML model

The bigger picture

The design and development of high-temperature polymers has been an experimentally driven and trial-and-error process guided by experience, intuition, and conceptual insights. However, such an Edisonian approach is often costly, slow, biased toward certain chemical space domains, and limited to relatively small-scale studies, which may easily miss promising compounds. To overcome this challenge, we formulate a data-driven machine learning (ML) approach, integrated with high-fidelity molecular dynamics simulations, for quantitatively predicting the glass transition temperature of a polymer from its chemical structure and rapid screening of promising candidates for high-temperature polymers. Our work demonstrates that ML is a powerful method for the prediction and rapid screening of high-temperature polymers, particularly with growing large sets of experimental and computational data for polymeric materials.

Polymers with outstanding high-temperature properties have been identified as promising materials for aerospace, electronics, and automotive applications. However, the current design and development of high-temperature polymers has been an experimentally driven and trial-and-error process guided by experience, intuition, and conceptual insights. Therefore, we formulate a machine learning model that can quantitatively predict the glass transition temperature of a polymer from its chemical structure, such that more promising high-temperature polymers can be efficiently filtered out through high-throughput screening.

Introduction

Lightweight and high-strength polymers with outstanding high-temperature properties have been identified as promising materials for aerospace, electronics, and automotive applications.1, 2, 3 These high-temperature polymers are expected to have long-term durability at high temperatures, high thermal decomposition temperatures, or high glass transition temperature $T_g$. For example, polytetrafluoroethylene is a synthetic fluoropolymer of tetrafluoroethylene with a maximum service temperature >260°C, which has been widely used for non-stick coatings and insulations.⁴ The other successful high-temperature polymers are perfluoroalkoxy alkanes, polyether ether ketone (PEEK), and fluorinated ethylene propylene. The high-temperature properties of these polymers are realized through the heteroatoms in the polymer chain of thermoplastics.5, 6, 7 However, the molecular engineering and design of hydrocarbon polymers and other polymers with high-temperature properties remain to be explored. The current design and development of high-temperature polymers have been an experimentally driven and trial-and-error process guided by experience, intuition, and conceptual insights. For example, different experimental strategies have been developed to synthesize high-temperature hydrocarbon polymers, such as (1) enhancement of the tacticity of the polymer chains,^8,9 (2) introduction of bulky pendant groups into the side chain,10, 11, 12 and (3) incorporation of cyclic structures into the backbone chain.13, 14, 15 Nevertheless, this Edisonian approach is often costly, slow, biased toward certain chemical space domains, and limited to relatively small-scale studies, which may easily miss promising compounds.¹⁶ Thus, a robust and reliable high-throughput screening method is essential for the discovery and design of high-temperature polymers.¹⁷

For high-temperature polymers, a critical property is the $T_g$,^10,13,14 which determines the polymer's phase transition between a rubbery state and a glassy state, yielding orders of magnitude difference in elastic modulus.¹⁸ Until now, $T_g$ is well known to be related to many factors, including molecular weight,¹⁹ chain stiffness,²⁰ side groups,²¹ additives,²² regularity.²³ Considering these aspects, researchers have proposed theoretical correlations between the chemical structure and the $T_g$ of polymers. These empirical methods are built upon the assumption that the chemical groups in the repeating units of the polymer chain contribute to the $T_g$ additively with different weighting factors.24, 25, 26 For example, Van Krevelen and Te Nijenhuis¹⁸ and Hoftyzer and colleagues²⁶ have proposed the “Molar Glass Transition Function,” based on nearly 600 experimental $T_g$ values of polymers, with different group contributions and structural corrections to $T_g$. This approach provides an effective way for molecular interpretation of $T_g$. However, this additive method is only applicable to the polymers containing previously investigated chemical structures.¹⁸ Later, Dudowicz et al.²⁷ formulated an analytic theory to estimate $T_g$ of polymer melts as a function of the relative rigidities of the chain backbone and side groups, monomer structure, polymer mass, and pressure, based on the generalized Lindemann criteria. This analytical theory can explain the general trends in the variation of $T_g$ related to the microstructure of the polymer, e.g., influences of side-chain length, and relative rigidities between side groups and chain's backbone. Nevertheless, it cannot be used to directly predict the $T_g$ of the polymer based on its chemical structure. Very recently, Xie et al.²⁸ established a relationship between $T_g$ and molecular structure of 32 conjugated polymers with a single adjustable parameter $\zeta$. $\zeta$ is an effective mobility value, determined by assigned atomic mobility for the repeating unit of conjugated polymers. The experimental results confirm that $\zeta$ is strongly correlated to the $T_g$ of conjugated polymers, although they differ drastically in aromatic backbone and alkyl side-chain chemistry. Yet, quantitatively predicting a polymer's $T_g$ from its chemical structure remains a significant challenge. We still lack a universal model that connect a polymer's $T_g$ to its repeating unit and molecular structure.

With advancements in molecular simulation and high-performance computing, all-atom molecular dynamics (MD) simulations can reasonably predict a polymer's $T_g$,²⁹ despite the limitations of computational cost, cooling rate, and uncertainty.30, 31, 32, 33 Nevertheless, it is not feasible to use these expensive MD simulations to explore the vast chemical space of polymers, defined by the almost infinite combinations of their chemical elements and molecular structures. With the growing amount of polymer database,^16,30, 31, 32, 33 data-driven methods are emerging to build correlations between chemical structure and the $T_g$ of polymers, including quantitative structure-property relationships (QSPR) method34, 35, 36 and machine learning (ML).37, 38, 39 For the QSPR method, a large array of molecular descriptors are extracted from the polymer's repeating unit, which applies to any chemical structure.⁴⁰ For example, Katritzky et al. have extracted more than 400 constitutional, topological, geometrical, and quantum chemical descriptors for the repeating unit of the polymer.⁴⁰ Subsequently, a multi-step linear regression analysis is adopted to train these descriptors, leading to a good match between predicted and experimental $T_g$values for 88 homopolymers. Wu et al.⁴¹ encoded a descriptor vector of seven different fingerprints, such as standard, extended, hybridization, maccs. And their Bayesian linear model reported an R value of 0.916 for $T_g$ prediction. Liu and Cao⁴² have adopted the artificial neural network to predict the $T_g$ for 113 polyacrylates and polystyrenes, as a function of four molecular descriptors: the molecular average polarizability, the energy of the highest occupied molecular orbital, the total thermal energy, and the total entropy. Later, Cai et al.⁴³ have combined a support vector regression with particle swarm optimization, using six quantum chemical descriptors as inputs, to predict $T_g$ values for 32 methacrylate polymers. However, the QSPR method suffers two major drawbacks: (1) it is expensive to quantify a large array of molecular descriptors, such as quantum chemical descriptors, which require the time-consuming density-functional theory calculations; (2) the QSPR method might generate many parameters that are challenging to physically interpret, such as topological bond connectivity and Kier shape index.⁴⁰

Considering these aspects, several ML models have been established to predict a polymer's $T_g$ directly from its chemical structure. For instance, Ramprasad and co-workers37, 38, 39^,44 utilized three hierarchical levels of descriptors, including atomic level, QSPR, and morphological descriptors, for feature representation of polymers. They fitted their datasets of 451–1,321 polymers with the Gaussian process regression model in the polymer genome platform.^38,45, 46, 47, 48 When using 1,321 polymers for training, their ML model reported a root-mean-square error of 27 K and $R^2$ of 0.92.³⁹ In addition to molecular descriptors as feature representation, ML models, such as convolutional neural networks (CNNs) with image-based input, have also been examined. For example, Miccio et al.^49,50 converted the Simplified Molecular Input Line Entry System (SMILES) notations of 331 polymers into a two-dimensional (2D) matrix (binary images) by the presence or absence of composing characters in the SMILES formulation. This approach can be used to predict the unknown $T_g$ of polymers with average relative errors as low as 6%, particularly without time-consuming calculations of molecular descriptors. Table 1 summarizes the database, feature representation, models, and prediction metrics from these theoretical, QSPR and ML studies.

Table 1.

Summary of theoretical, QSPR, and machine learning (ML) models investigated in the literature

Database	Features	Model	$R^2$	Ref.
600	chemical groups	group contributions approach	N/Aa	18
32	an effective mobility value	single adjustable parameter	N/Ab	28
113	quantum chemical descriptors	artificial neural networks	0.955c	42
37	quantum chemical descriptors	support vector regression	0.97	43
251	Descriptors	computational neural networks	0.96	51
389	descriptors	support vector regression	0.78	52
133	descriptors	random forest	N/Ad	53
88	descriptors	multi-layer perceptron neural network	0.96	54
77	descriptors	support vector machine (SVM)	0.92	55
54	descriptors	artificial neural network	0.91	56
52	descriptors	artificial neural network	0.978e	57
451	hierarchy fingerprint	Gaussian process regression	0.94	38
751	hierarchy fingerprint	Gaussian process regression	0.87	37
1,321	hierarchy fingerprint	Gaussian process regression	0.92	39
5,917	combined fingerprint	Bayesian linear model	0.916f	41
331	SMILES-based binary images	convolutional neural network	N/Ag	49
234	SMILES-based binary images	fully connected neural networks	N/Ah	50
6,923 + 5,690 + 1 million	descriptors Morgan fingerprint SMILES-based binary images	lasso regression deep neural network convolutional neural network	0.80 0.85 0.87	this work

N/A, not applicable.

^aAbout 80% of the calculated T_g values differed less than 20 K from the experimental values.

^bOnly root-mean-square error of 13°C was reported for all 32 alkylated conjugated polymers.

^cR = 0.955 was reported for the prediction set.

^dOnly root-mean-square error of 4.76 K was reported for the test set of the model.

^eR = 0. 978 was reported for the test set.

^fR = 0. 916 was reported for the test set.

^gThe model performance was evaluated by relative error of 3%–8%.

^hThe model performance was evaluated by average relative errors of ∼3%.

Despite these extensive studies, we are still facing several significant challenges in creating ML models to directly predict a polymer's $T_g$ based on its chemical structure.¹⁶ Firstly, most of these data-driven models are built upon a small dataset of polymer $T_g$ values with less than 1,000 data points, focusing on a certain category of polymers, such as polyacrylates and polystyrenes. It is very difficult to generalize these models for other classes of polymers due to the limited range of chemical space. Secondly, it is challenging to choose appropriate feature representations to describe the chemical structures of polymers. Molecular descriptors, fingerprints, and images have been adopted to represent the chemical structures of polymers. It is not clear which feature representation is the most appropriate, leading to a predictive ML model for exploring a large chemical space of polymers. Finally, it is not straightforward to associate ML predictions on a polymer's $T_g$ with physically meaningful quantities. Since most ML models are highly nonlinear with complicated architectures, it is difficult to pinpoint a specific set of physical quantities or chemical groups that are important in the prediction and design of a polymer's $T_g$.

To overcome the above challenges, we manually collected about 13,000 homopolymers structures from the largest polymer database, PoLyInfo.⁵⁸ Copolymers that are formed by two types of monomers are not collected here as the effect of their different components on $T_g$ requires extra consideration,^59,60 and polymer composites are not included either when their $T_g$ is affected by polymers interplaying with nanomaterials.^61,62 Focusing on homopolymers allows us to put our focus mainly on revealing the correlation of a polymer's chemical structure and its $T_g$. Among the around 13,000 homopolymers, 6,923 experimental $T_g$ values are available, which form dataset-1, as shown in Figure 1. The remaining 5,690 polymers without reported $T_g$ values form dataset-2. Also, a benchmark database, named PI1M⁶³, with nearly one million hypothetical polymers generated by a recurrent neural network (RNN) model, is taken as dataset-3, while the corresponding $T_g$ values are unknown. Note that dataset-3 covers a similar chemical space as dataset-1 and dataset-2 because the RNN models are also trained on the PoLyInfo database, but significantly populate regions where PolyInfo data are sparse.⁶³ Such a large and diverse dataset allows us to develop four representative ML models based on dataset-1, namely Lasso_Descriptor, Lasso_Fingerprint, DNN_Fingerprint, and CNN_Image, by using the molecular descriptors, Morgan fingerprints, or images as inputs, and Lasso (least absolute shrinkage and selection operator), DNN (deep neural network) or CNN as the ML models. The predictivity and transferability of these ML models are tested on dataset-2 with distinct chemical substructures (Figure 1), in comparison with MD simulations and experimental results. Interestingly, our study reveals that the DNN_Fingerprint model can reasonably predict the $T_g$ values of polymers from dataset-2, as the Morgan fingerprinting method⁶⁴ can take into account the chemical connectivity and appearance of different substructures of a polymer's repeating unit. More importantly, we use these ML models to identify key molecular descriptors and chemical substructures that can significantly affect the polymer's $T_g$, providing physical insights into the prediction and design of the $T_g$ for polymeric materials. We further examine the chemical functional groups of high-/low-$T_g$ polymers and their common characteristics through Checkmol.⁶⁵ We also identify strong correlations between these common functional groups with the key chemical substructures revealed by our ML models. Eventually, we apply the validated DNN_Fingerprint model for rapid screening of one million hypothetical polymers in PI1M (dataset-3), and identify more than 65,000 promising candidates for high-temperature polymers with $T_g$ > 200°C. We then use MD simulations to validate the predicted $T_g$ values of the top four high-temperature polymers, which are previously unexplored and have not been tested to date. Thus, our study demonstrates that ML is a powerful method for the prediction and rapid screening of high-temperature polymers, particularly with growing large sets of experimental and computational data for polymeric materials. The key molecular descriptors and chemical substructures informed by ML models, combined with identified chemical functional groups, are important design motifs for the molecular engineering of high-temperature polymers.

Figure 1.

Chemical space visualization of dataset-1, dataset-2, and dataset-3

(A) 2D visualization based on descriptors and fingerprints using the t-SNE algorithm. Dataset-1 has reported $T_g$ values, and each data point is colored based on the corresponding $T_g$ value. Dataset-2 and dataset-3 do not have reported $T_g$ values, colored with yellow and red, respectively.

(B) Set diagram showing representative substructures in dataset-1 (green circle), dataset-2 (yellow circle), and dataset-3 (red circle) based on Morgan fingerprint. Some substructures are common for all datasets, while some others are unique to certain datasets.

Results and discussion

Dataset, feature representation, and chemical space

To formulate robust and predictable ML models for diverse polymers, we need to consider a larger dataset in contrast to previous studies (cf. Table 1). Dataset-1 contains 6,923 polymers from the largest polymer database, PoLyInfo,⁵⁸ as listed in Table 2. They are real polymers with experimentally measured $T_g$values reported in literature. Thus, it is ideal to use dataset-1 as a labeled dataset for ML model training. For experimentally measured $T_g$ values, they depend on conditions, such as the cooling or heating rate, or even curing process and moisture content, thus there cannot be an exact value for $T_g$.66, 67, 68, 69 Although there are variations in experimental measurements, the reported $T_g$ with a common experiment practice can be considered characteristic only of the polymer and not of the measuring method.⁷⁰ If measurement conditions are so extreme that the obtained $T_g$ is not a proper representative of the real value, such records will mislead all analysis, including ML model training.

Table 2.

Comparison of three datasets

Dataset	No. of polymers	$T_g$ (oC)	Source
Dataset-1	6,923	−118∼495	real polymers from PoLyInfo58
Dataset-2	5,690	unknown	real polymers from PoLyInfo58
Dataset-3	1 million	unknown	hypothetical polymers from PI1M63

A total of 5,690 real polymers of dataset-2 were collected from the same data source as dataset-1, but their $T_g$ values were not previously reported. Dataset-3 is based on an ML-generated database PI1M⁶³ with approximately one million hypothetical polymers. Note that PI1M is enumerated using a generative ML model, RNN, based on PolyInfo (dataset-1 plus dataset-2). These three datasets are regarded as similar to each other in terms of chemical space.⁶³ The collected three datasets in Table 2 are more than one order of magnitude of most datasets from the kinds of literature in Table 1, making up a broader range of chemical space involving various categories of polymers. The challenge of having ML models that can be generalized to all categories of polymers then becomes straightforward to address with the collected large datasets.

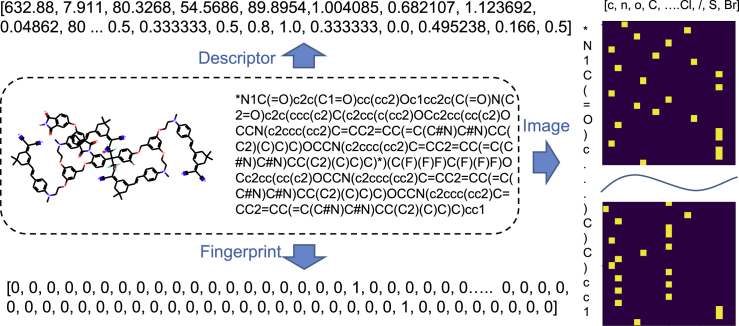
All polymers' chemical formulas and structures are represented by the SMILES notation,⁷¹ which is a line notation for describing the structure of chemical species using short ASCII strings. For example, “∗C(C∗)C” represents the repeating unit for “poly(prop-1-ene).” It is worth noting that a special symbol “∗” is used to indicate the polymerization points for the repeating unit. From the same molecular block, such as “CCC,” the polymerization positions in ∗C(C∗)C take into account the bonding information between repeating units, and determine the spatial structure of the polymer chain. The chemical species contained in these three datasets include C, O, N, Cl, F, Br, I, S, Si, B, P, Sn, Fe, Na, Li, Ge, Se, K, Co, Ni, Ca, Cd, Pb, Zn, and Te.

One challenge when creating ML models for evaluation of a polymer's $T_g$ is choosing appropriate feature representation to describe the chemical structures being studied. Representation options include descriptors, fingerprints, molecular graph, molecular embedding, quantum chemical quantities, images, etc. The effect of using different representations on $T_g$ estimation has been demonstrated through systematic representation evaluation⁷² or separate model development.37, 38, 39^,42,43,50, 51, 52, 53, 54, 55, 56, 57 In addition, the development of new representations remains critical for the development of high-performance ML models. To carry out a thorough study considering different types of representations, we explore three types of feature representation based on the SMILES notation of each polymer: molecular descriptors, Morgan fingerprints, and images, as presented in Figure 2. In terms of molecular descriptors, the feature-generating engine alvaDesc⁷³ supports the calculation of about 5,305 descriptors within 32 categories, ranging from constitutional indices and ring descriptors to chirality descriptors.^73,74 The ensemble of descriptors represents the physical and chemical characteristics of polymers/molecules being studied, which have been widely adopted in the QSPR and ML models (Table 1). Thus, these molecular descriptors can provide physical information regarding charges, topological indices, functional groups, etc., of polymers. Among these 5,305 descriptors, 3,579 descriptors are all available for real polymers in dataset-1 and dataset-2. However, not all 3,579 descriptors are available to the one million hypothetical polymers in dataset-3. Around 5% of hypothetical polymers in dataset-3 cannot be processed using the alvaDesc. But it does not affect too much the chemical space visualization based on molecular descriptors for dataset-3. We should emphasize that the alvaDesc cannot process the ∗ symbol in the SMILES notation and, thus, it misses the chemical connectivity of the repeating units.

Figure 2.

Three types of feature representation calculated based on the polymer's SMILES notation for ML models: molecular descriptor, Morgan fingerprint, and image

In addition to molecular descriptors, we also choose the fingerprinting method (extended connectivity fingerprinting [ECFP])⁶⁴ to numerically represent the chemical connectivity in a repeating unit of the polymer. Specifically, the fingerprinting method has a significant advantage over the traditional group contribution and molecular descriptor methods, where all the possible build blocks and molecule descriptors have to be defined a priori and remain static. However, the fingerprinting method is more dynamic, and it can evolve to include new chemical structures and connectivities.⁶⁴ Essentially, to derive the ECFP of the repeating unit, we need to: (1) assign each atom with an identifier, (2) update each atom's identifiers based on its neighbors, (3) remove duplicates, and (4) fold list of identifiers into a 2,048-bit vector (a Morgan fingerprint). In this case, we transform each polymer's SMILES notation into a binary “fingerprint,” by using the Daylight-like fingerprinting algorithm as implemented in RDKit⁷⁵ with radius 3 and 2,048 bits. Note that radius 3 is large enough to identify/encode large fragments of the chemical structure, with more than 45,000 distinct substructures detected from all datasets. Such a topological-based approach analyzes the various substructures of a molecule within a certain number of chemical bonds (here it is 3), and then hashes each substructure into a 2,048-bit vector, as shown in Figure 2. If the 45,000 distinct substructures are hashed into 2,048 buckets, collisions are inevitable. Then, the 1/0 (on/off) bit of a bucket does not indicate the occurrence of a specific substructure but represents the occurrence of several substructures. Besides, the number of occurrences for a substructure is not recorded through these buckets. To avoid the drawbacks of using buckets, we directly record each substructure and its number of occurrences. This dictionary of substructures is further used for the training of our ML models. We should emphasize that our fingerprinting method is different from previous studies using the ECFP and Morgan fingerprinting,^41,76,77 as we need to consider the number of occurrences for certain substructures in the training of ML models, to be discussed in the following section.

Based on the SMILES notation of polymers, we further define an ordered list of SMILES characters as a dictionary [“c”, “n”, “o”, “C”, “N”, “F”, “ = “, “O”, “(‘, ‘)”, “∗”, “[‘, ‘]”, “1”, “2”, “3”, “#”, “Cl”, “/”, “S”, “Br”]. This dictionary creates a binary column for each character, with which one-hot encoding algorithm⁷⁸ transforms each polymer's SMILES into a sparse matrix (a 2D binary image in Figure 2). The dimensions of all images are 21 (the number of characters in the dictionary) × 310 (the length of the longest SMILES code in the dataset). The key points of the one-hot encoding algorithm are: (1) defining a reasonable dictionary is the premise of a good model; (2) simple polymers (represented by a short SMILES code) return much sparser matrices than complex polymers (represented by a long SMILES code). Obviously, any change of dataset could lead to changes in the dictionary and corresponding images, significantly influencing the performance of a CNN model.

In view of the molecular descriptors and Morgan fingerprints, similarities between different datasets can be compared from their chemical space. To better visualize this space, the high-dimensional chemical spaces are reduced to a low-dimensional representation. By t-distributed stochastic neighbor embedding,⁷⁹ the chemical spaces can be shown in 2D plots as shown in Figure 1A. The top row of Figure 1A is for dataset-1, whose $T_g$ values are marked with a color bar. The middle and bottom rows are for dataset-2 and dataset-3, respectively. We can see that, on both descriptor and fingerprint space, dataset-1 and dataset-2 distribute randomly on similar regions. The random distribution suggests that dataset-1 and dataset-2 are across similar chemical spaces. Dataset-3 is also found filling up a similar chemical space but significantly populate regions where PoLyInfo data (dataset-1 plus dataset-2) are sparse. Although Figure 1A shows similarities between dataset-1, dataset-2, and dataset-3, disparities still exist. For example, using Morgan fingerprints, we show some substructures of these polymers in dataset-1, dataset-2, and dataset-3 (Figure 1B). Besides the shared substructures enclosed in the overlapped area of the circles, all three datasets have their own unique substructures. As ML models are trained based on dataset-1, when they encounter a polymer in other datasets with new substructures, it is difficult to make an accurate prediction. Compared with the performance on dataset-1, whether the ML model can be well transferred to new dataset-2 and dataset-3 is more worthy of concern. ML models with good transferability and generalization ability are of significant importance for the discovery and design of high-temperature polymers.

ML models for the chemistry-$T_g$ relation of polymers

Four ML models trained on dataset-1 (listed in Table 3) involve the Lasso model, the DNN model, and the CNN model. Lasso is a least-squares regression model with a shrinkage penalty, through which it performs variable selection by forcing the coefficients of trivial variables to become zero. Thus, the variables that are strongly associated with the output are identified in a variable selection process. DNN consists of connected units called nodes or neurons. Each node receives signals and triggers a process function to output new signals. Several nodes are grouped into layers and constructed into a complicated network architecture, which is processed between the input and output layers. DNN is capable of learning complex relationships between input and output. CNN is distinguished from DNN by its superior performance on image input. The convolutional layers with filters or kernels are the core building blocks of CNN. The optimized weights and biases in convolutional layers can identify the presence of various features in the input, showing an advanced performance, particularly in image processing. Although the ML algorithms are applicable for various kinds of problems, such as video recognition, image analysis, or natural language processing, their suitability and reliability are actually highly domain dependent. For the task of estimating a polymer's $T_g$ based on structure features, ML models require a proper feature representation that depicts polymer physics and chemistry to the greatest extent.

Table 3.

Four ML models trained on dataset-1

Name	ML model	Features	$R^2$ (train/test)
Lasso_Descriptor	Lasso regression model	3,579 descriptors	0.80/0.71
Lasso_Fingerprint	Lasso regression model	2,048 fingerprints	0.74/0.73
DNN_Fingerprint	deep neural network	2,048 fingerprints	0.85/0.83
CNN_Image	convolutional neural network	310 × 21 binary images	0.87/0.80

Here, descriptors or fingerprints are used as the input features for Lasso regression models or DNN models. They have clear chemical or physical meanings for an organic molecule, but the time-consuming calculation is usually required considering a very large database of polymers. When representing polymers from the perspective of 2D images, the input is much easier to calculate.^49,50 Therefore, a CNN model using images is also investigated for comparison. Through these ML models, we aim to discover critical physical and chemical features affecting $T_g$, and to establish a reliable model for $T_g$ screening of high-temperature polymers. Lasso regression is suitable for feature selection, while DNN and CNN models are more powerful to establish a correlation between chemical structure and $T_g$ of polymers.⁷⁶

The performances of these four ML models are illustrated by parity plots in Figures 3A–3D (see the supplemental experimental procedures Figures S1–S3 for model training details). Based on dataset-1, they all show good performances. The best one is the CNN_Image model, which produces an $R^2$of 0.87/0.80 for training/test sets. It indicates that, although there is no explicit physical meaning in the image representation, the CNN model is still able to establish a correlation between the image input and the physical property $T_g$ of polymers. The DNN and Lasso models also lead to high $R^2$ values of 0.74–0.87. Their performances are satisfactory, considering the large chemical diversity of 6,923 polymers involved in dataset-1.

Figure 3.

Performance of four ML models

(A) The Lasso regression model using descriptors as input features (Lasso_Descriptor model).

(B) The Lasso regression model using fingerprints as input features (Lasso_Fingerprint model).

(C) The DNN model using fingerprints as input features (DNN_Fingerprint model).

(D) The CNN model using images as input features (CNN_Image model).

(E) The comparison between the MD-simulated $T_g$ and the ML-predicted $T_g$ on 20 polymers randomly selected from dataset-2. Three dashed lines are a unity line and lines with a mean absolute error of 40°C. The chemical structure of these 20 polymers is followed by their MD-simulated $T_g$ value.

To examine the transferability of ML models on new polymers, these four ML models are applied to dataset-2 to predict their $T_g$values. The prediction accuracy of ML models is further validated with MD simulations (see Figure S4 and Table S2 for the MD simulation details and results). Twenty polymers are randomly selected from dataset-2. Their MD-simulated $T_g$ and ML-predicted $T_g$ values are compared in Figure 3E. Four ML models show different prediction performances on these polymers of dataset-2 (see Table S3 in the supplemental experimental procedures). The performances of CNN_Image model and Lasso_Descriptor model degrade remarkably to $R^2$ of −0.52 and 0.39, respectively, indicating poor transferability from dataset-1 to dataset-2. These two previously well-trained ML models on dataset-1 are found to be no longer accurate when giving a new and different dataset. Due to their worse generalization capabilities, the CNN_Image model and Lasso_Descriptor model are not considered for high-temperature polymer screening in the following sections.

On the contrary, the Lasso_Fingerprint and the DNN_Fingerprint models demonstrate good performance on these randomly selected polymers, with $R^2$of 0.63 and 0.53, respectively. Their small changes of $R^2$ from dataset-1 to dataset-2 suggest good transferability. Although with a little degradation, the prediction performances are still satisfactory considering: (1) dataset-2 is not exactly the same as dataset-1 in terms of substructures (cf. Figure 1), and (2) uncertainties may exist as the reference $T_g$ values obtained by MD simulations can be higher than the true values due to the high cooling rate.^31,32,80,81 To avoid the uncertainties from MD simulations, validation using experimental results is more preferred. Thus, a newly reported experimental dataset is further utilized to verify the transferability of these two ML models. The experimental dataset contains 32 semiflexible (mostly conjugated) polymers²⁸ that are new to our ML models. These 32 polymers differ drastically in the aromatic backbone and alkyl side-chain chemistry (Table S4 in the supplemental experimental procedures), serving as an ideal experimental dataset to test our ML models. The predictions of the Lasso_Fingerprint model and the DNN_Fingerprint model lead to $R^2$ values of 0.20 and 0.68 (see Figure S5 in the supplemental experimental procedures for detailed results). Thus, the performance of the Lasso_Fingerprint model is found to be degrading on this new experimental dataset. According to these results, we find that the DNN_Fingerprint model has a consistent performance on different datasets with excellent transferability through the validations by MD simulations and experimental results. Also, Morgan fingerprints are identified to be more appropriate as feature representation for the ML model of polymer $T_g$ in comparison with molecular descriptors and images.

As mentioned above, both molecular descriptors and images are representations of all the possible building blocks of a polymer's repeating unit, which must be defined a priori and remain static. However, Morgan fingerprints are an inherent more dynamic representation, as they can evolve to include new chemical substructures once encountered. Also, according to the previous theoretical models on $T_g$ values of polymers,¹⁸ we know that the number of occurrences for these substructures also plays an important role. Therefore, our Morgan fingerprints explicitly consider more than 45,000 distinct substructures and their frequency of occurrence, which allows us to study the effects of various substructures and their linkages on polymer $T_g$ values. Combined with the powerful and transferable DNN model,⁸² the DNN_Fingerprint model trained from dataset-1 demonstrates the best performance on dataset-2 and a new experimental dataset of 32 conjugated polymers. We should emphasize that, if we only derive the Morgan fingerprints by hashing all the substructures into 2,048-bits, without considering their number of occurrences, the trained DNN model cannot reasonably predict the $T_g$ values of these 32 conjugated polymers (see Figure S6 the supplemental experimental procedures for detailed results). Extensive studies using molecular descriptors, fingerprints, or images alone (Table 1) lead to well-trained ML models that are applicable for a certain category of polymers, but how well these models are suitable to predict other polymers is not getting much attention. Here, we demonstrate an appropriate feature representation through large dataset training, MD simulations, and experimental dataset verification, particularly from a perspective of the model's good transferability and generalization. The Morgan fingerprints with their number of occurrences are found most suitable in terms of $T_g$ prediction, due to the encoded information of substructures and polymerization.

Machine learns physical rules for polymer $T_g$ values

One of the challenges in using ML models for property predictions of organic molecules and polymers is correlating these predictions with meaningful physical quantities.^16,83 This is the major driving force of current research activities in interpretable artificial intelligence and ML methods.84, 85, 86 Although our DNN_Fingerprint model demonstrates the best predictivity and transferability, it uses the fingerprinting representation of polymers, leading to the difficulty of pinpointing a specific set of physical quantities that are important in the prediction of a polymer's $T_g$. On the contrary, the performances of Lasso_Descriptor and Lasso_Fingerprint models are not as ideal as DNN_models, but they are still useful to establish reasonable correlations between a polymer's chemical structure and $T_g$ with $R^2$ > 0.7 (cf. Figure 3). Furthermore, the Lasso method has an advantage for feature selection and extraction.^76,87 By applying L1-norm regularization on the weights, unimportant features are shrunk, and only important features are left. The feature importance is directly indicated by the obtained weight for each feature.^87,88

Focusing on molecular descriptors, the Lasso_Descriptor model finds 444 descriptors having non-zero weights. More than 50% of the total absolute weight is contributed by 61 features. These features are considered important in determining $T_g$. The top 10 physical descriptors are listed in Table 4 (see the full list in Table S1 of the supplemental experimental procedures). Descriptors, such as “frequency of C-N at topological distance 2,” “number of heavy atoms,” “number of total quaternary C(sp3),” etc., are revealed to be principle features associated with the $T_g$ of polymers. These structural and chemical parameters are expected to be the essential constituents of polymers in terms of $T_g$.

Table 4.

The top 10 physical descriptors and their absolute weight ratio from the Lasso model

Name	Description	Block	Ratio
AVS_B(i)	average vertex sum from Burden matrix weighted by ionization potential	2D matrix-based descriptors	0.0684
NssCH2	number of atoms of type ssCH2	atom-type E-state indices	0.0272
F02[C-N]	frequency of C–NA topological distance 2	2D atom pairs	0.0181
nHM	number of heavy atoms	constitutional indices	0.0145
BIC2	bond information content index (neighborhood symmetry of 2-order)	information indices	0.0138
NsCH3	number of atoms of type sCH3	atom-type E-state indices	0.0137
B03[F-F]	presence/absence of F–F at topological distance 3	2D atom pairs	0.0120
nCq	number of total quaternary C(sp3)	functional group counts	0.0113
nCrs	number of ring secondary C(sp3)	functional group counts	0.0098
C-006	CH2RX	atom-centered fragments	0.0097

Several topological descriptors, such as F02[C-N] and B03[F-F], appear in the discovered top features as they encode the spatial relationship of the polymer backbone, such as the molecular size and free volume. Using topological descriptors alone is considered to be enough for a $T_g$prediction model when dealing with a very limited dataset of 251 polymers.⁴⁴ However, our Lasso_Descriptor model, dealing with a larger dataset, indicates the same level of importance as other factors, such as the functional group counts. Eleven functional groups (see the full list in Table S1 of the supplemental experimental procedures), such as “number of ring secondary C(sp3),” “number of hydroxyl groups,” and “number of primary amines (aromatic)” are identified key factors affecting the $T_g$ of polymers. They demonstrate no less significance than topological descriptors, and some critical functional groups are found to be good indicators to identify high-$T_g$ or low-$T_g$polymers as shown later.

Focusing on Morgan fingerprints, the Lasso_Fingerprint model examines local substructures in a similar way. Among the 124 most common substructures found in dataset-1, 85 substructures have non-zero weights, and 18 substructures contribute more than 50% of the total absolute weight. These 18 substructures with the highest absolute weight are presented in Figure 4. These substructures also provide us physical insights into the $T_g$ of polymers, including the importance of aromatic compounds⁸⁹ (substructures 16406, 24417, 17135, 17618, 11337, 11881, and 4916) and functional groups containing oxygen and nitrogen atoms (substructures 16406, 17748, 426, 24417, 770, 11337, 23586, 11881, 4916, 7305, and 24993), which indicates the positive influence of hydrogen bonds on $T_g$.⁹⁰ Also, some of these substructures are highly related to the important physical descriptors shown in Table 4, providing cross-validations between these two ML models.

Figure 4.

Substructures with the highest absolute weight based on Morgan fingerprint and Lasso ML model

The central atom of the substructures is highlighted in blue. Aromatic atoms are highlighted in yellow. Connectivity of Atoms is highlighted in light gray.

Besides the physical insights revealed by the Lasso regression models, critical functional groups can also be identified for their contributions to polymer $T_g$ values as a posteriori analysis. Here, we can examine the polymers with high/low $T_g$ values and their common characteristics (functional groups), and thereby gain insights into what physical quantities are important for enhancing/reducing their $T_g$ values. We process all the polymers in dataset-1 through the Checkmol⁶⁰ package, and identify the functional groups only occurring in high-$T_g$ (>200°C) and low-$T_g$ (<50°C) polymers. These functional groups are listed in Table 5, where each functional group's key atom is highlighted in the red circle. For high-$T_g$ polymers, we find that the functional groups, such as oxohetarene, lactam, amine, and enamine, play critical roles in their high-temperature property. In contrast, the functional groups, such as disulfide, phosphoric acid, and acetal, are only shown in the low-$T_g$ polymers. These observations are consistent with the key substructures discovered from the fingerprint (Figure 4). For example, the substructures with oxygen “O” atom are revealed to be highly correlated to a polymer's $T_g$, and the most exclusive functional groups also involve the oxygen O atom in either high-$T_g$ or low-$T_g$ polymers, highlighting its important contribution to the $T_g$. Therefore, it is evident that the ML models indeed capture the critical features affecting a polymer's $T_g$.

Table 5.

Important functional groups recognized using the Checkmol package

Within low-$T_g$ polymers (<50°C)	Within high-$T_g$ polymers (>200°C)
Orthocarboxylic acid derivative	Oxohetarene
Disulfide	Lactam
Phosphoric acid derivative	Tertiary arom_amine
Phosphoric acid ester	Secondary aromatic amine
Phosphoric acid amide	Secondary mixed amine (aryl alkyl)
Acetal	Enamine

These key features not only provide physical insights into understanding how the molecular structures influence a polymer's $T_g$, but also are design motifs that are important in the inverse molecular design of high-temperature polymers. For instance, the generative ML models, such as variational autoencoders (VAE)^91,92 and generative adversarial networks (GAN),^93,94 when integrated with reinforcement learning (RL),^95,96 can take into account the importance of these physical and chemical features. Such a strategy of combining the predictive ML model and generative ML model has been utilized in the inverse molecular design of small-drug-like molecules and organic molecules.^97,98 Successful examples include the chemical VAE,⁹⁹ ReLeaSE (reinforcement learning for structural evolution),¹⁰⁰ and ORGANIC (objective-reinforced generative adversarial network for inverse-design chemistry).¹⁰¹ The generative ML model serves as an agent in generating molecules, while the predictive model acts as an external world to monitor the generation action taken by the agent. According to the feedback, either a reward or penalty can be assigned. Through training, the agent or the generative model learns to make good sequences of decisions in molecular generation toward a maximum reward. Therefore, our predictive ML model demonstrates its potential to be integrated with an inverse molecular design framework for high-temperature polymers or polymers with tailored $T_g$ values.

High-throughput screening of high-temperature polymers

Since the DNN_Fingerprint model demonstrates the best transferability from dataset-1 to dataset-2 and to a new experimental dataset (32 conjugated polymers), we adopt this ML model for high-throughput screening to identify promising candidates for high-temperature polymers. Dataset-1, with 6,923 real polymers, has nearly 2,000 polymers with $T_g$ larger than 200°C, as shown in Figure 5. These polymers have the great potential to be used in a harsh environment with high temperatures, but more candidates are still desired as many of these 2,000 polymers might not be easily synthesized and processed.¹ Dataset-2 and dataset-3, with 5,690 real polymers and one million hypothetical polymers, respectively, form a promising candidate pool for the screening of high-$T_g$ polymers. Here, we aim to identify the polymers with $T_g$ values larger than 200°C, because the $T_g$ for high-temperature PEEK polymer is about 143°C.¹⁰² Almost all predicted $T_g$ values for dataset-2 and dataset-3 remain in the same range of dataset-1 (−118°C to 495°C), as shown in Figure 5. Excitingly, the population of potential promising candidates has been significantly increased. For example, dataset-1 has about 2,000 known polymers with $T_g$≥ 200°C. Through our DNN_Fingerprint model, we find an additional 1,000 and 65,000 new candidates in dataset-2 and dataset-3 with $T_g$ ≥ 200°C, respectively. Thus, through this high-throughput screening, we find 30 times more promising candidates for high-temperature polymers, in comparison with the 2,000 known high-temperature polymers in dataset-1. If we consider a harsher environment with required $T_g$≥ 300°C (comparable with melting temperature of lead, 328°C), dataset-1, dataset-2, and dataset-3 have 309, 249, and 3,567 polymers, respectively, that can potentially satisfy this requirement.¹ Again, our high-throughput screening method identifies 11 times more promising candidates from dataset-2 and dataset-3 compared with dataset-1. The ML high-throughput screening for high-temperature polymers overcomes the challenges from theoretical analysis or MD simulations. Theoretical equations derived using small groups of polymers have difficulties in handling polymers of different categories, and are therefore not applicable to all data points of the vast chemical space. MD simulations, although capable of computing $T_g$ vaues of various kinds of polymers, are restricted by the computational cost considering the vast amount of candidates to be screened. However, our high-throughput screening method processes the one million hypothetical polymers efficiently with proven reliability for $T_g$ estimation.

Figure 5.

High-throughput screening of high $T_g$ polymers with the DNN_Fingerprint model

The $T_g$ distribution of the dataset-1, dataset-2, and dataset-3 are plotted in green, yellow, and red, respectively. The polymer samples on the right are following by their predicated $T_g$ and true $T_g$ values. For the sample in dataset-1 (green box), true $T_g$ is the collected experimental value. For the samples in dataset-2 (yellow box) and dataset-3 (red box), true $T_g$ is the MD-simulated value. More than 1,000 real polymers and 65,000 hypothetical polymers were discovered with $T_g$ > 200°C.

We then focus our attention on the top four high-temperature polymers, with ML-predicted $T_g$ > 400°C. These four polymers are unknown and hypothetical, although they share similar chemical structures as the other known high-temperature polymers, e.g., aromatic rings, sulfone groups, oxygen linkages, and amine groups. Each of these groups is highlighted during our analysis of the ML models as being related to the high-temperature properties of polymers (Figure 4; Table 5). Without making any assumptions or premises for the ML model, it is observed that the structures of the screened top four high-temperature polymers well follow the general rule controlling the $T_g$ of polymers. The backbone structure with rigid benzene rings contributes to the stiffness of the chain, which is known to play a major role in determining the $T_g$ of a polymer.^50,103,104 Also, there are no long alkyl chains that lead to lower glass transition.¹⁰⁵ Although the similar sulfur-containing polyimides, such as poly[(2,8-dimethyl-5,5-dioxodibenzothiophene-3,7-diamine)-alt-(biphenyl-3,3’:4,4′-tetracarboxylic dianhydride)] (polymer ID: P130369 in PoLyInfo), have been tested with $T_g$ values as high as 490°C,¹⁰⁶ the $T_g$ values of these hypothetical polymers have not yet been reported. We take advantage of MD simulations to build all-atom molecular models for these hypothetical polymers and predict their $T_g$ values (more details are given in the supplemental experimental procedures). As shown in Figure 5, our physics-based MD simulations confirm that these hypothetical polymers indeed have ultra-high $T_g$ values. Furthermore, we find that the MD-predicted and ML-predicted $T_g$ values are in relatively good agreement with each other (within the error of the prediction), indicating that the ML model could be used as a predictive tool for screening of previously unexplored chemical spaces for high-temperature polymers.

The key substructures (Figure 4) and functional groups (Table 5) related to the high-$T_g$ polymers are revealed based on dataset-1. Their important roles are further confirmed on the identified high-$T_g$ polymers with ML-predicted $T_g$ > 200°C from dataset-2 and dataset-3. The key substructures of high-$T_g$ polymers in dataset-1 (2,268 polymers), dataset-2 (1,155 polymers), and dataset-3 (65,283 polymers) are compared in Figure 6A (more details are given in Table S5 of the supplemental experimental procedures). For example, the substructure "16406" (a center carbon connected to aromatic compounds and oxygen) is recognized with percentages of 15.04%, 16.54%, and 27.55% of high-$T_g$polymers in dataset-1, dataset-2, and dataset-3, respectively. This indicates that the contributions of this substructure to the high-$T_g$polymers are similar across these different datasets. As mentioned above, one of the most important contributions comes from substructure "23586"—a single oxygen side chain, which consists of 53.40%, 53.16%, and 76.05% high-$T_g$ polymers in dataset-1, dataset-2, and dataset-3, respectively. Overall, most of these 18 key substructures' contributions in different datasets are quite similar. Their comparable influences also explain the good transferability of the ML model based on the Morgan fingerprints. The frequency of occurrence is also an important aspect because of the probability of a substructure emerging during the inverse molecular design of high-$T_g$ polymers. In terms of the functional groups, the six key functional groups exclusive to high-$T_g$ polymers are compared in Figure 6B in a similar manner (also see Table S6 for detailed results). Interestingly, the six recognized functional groups are special ones only found in a few high-$T_g$ polymers. For instance, the secondary aromatic amine functional group is identified in about 0.13% of the high-$T_g$ polymers in dataset-1, while 3.32% of the high-$T_g$ polymers in dataset-3 are found to have this functional group. Although training dataset-1 shows a quite negligible 0.13% of this functional group, its importance is successfully captured by the ML model using Morgan fingerprints and then demonstrated in dataset-3. In addition, we generally observe that polymers containing amine groups, oxygen along the backbone, and/or nitrogen rings, demonstrate high-temperature properties.¹ In short, our ML models for the chemistry-$T_g$ relation of polymers seems to pinpoint meaningful physical-chemistry insights that can be used to enhance high-temperature performance and may be further utilized in the inverse molecular design of high-$T_g$ polymers that have not been experimentally studied.

Figure 6.

Comparison of key substructures and functional groups in high-$T_g$(>200°C) polymers

(A) Comparison of the 18 substructures recognized in Figure 4.

(B) Comparison of the six high-$T_g$-related functional groups recognized in Table 5.

Concluding remarks

Quantitatively predicting a polymer's $T_g$ from its chemical structure is a significant challenge in material science and engineering, chemistry, and polymer science fields. Here, we use an ML-based approach to correlate a polymer's chemical structure with its $T_g$, taking advantage of a large and diverse dataset collected from PoLyInfo. The transferability and generalization ability of ML models are particularly focused and demonstrated by utilizing a large dataset of different categories of polymers. We consider three different feature representations of polymer's repeating unit, such as molecular descriptors, Morgan fingerprints, and images, and three different ML models, e.g., Lasso, DNN, and CNN. All of these ML models demonstrate comparable performances in training and testing on the experimentally available dataset-1. However, only the DNN_Fingerprint model exhibits the best transferability to dataset-2 with distinct substructures from dataset-1. We find that this excellent transferability is attributed to the dynamic representation of Morgan fingerprints, as they can evolve to include new substructures encountered. Furthermore, our Morgan fingerprints take into account the chemical connectivity between neighboring repeating units and the frequency of occurrence of different substructures, which play important roles in determining a polymer's $T_g$. Although Morgan fingerprints ignore all high-order polymer descriptors, e.g., stereoregularity, polarity, and chain length, the DNN_Fingerprint model gives satisfactory predictions on the $T_g$ values of unknown polymers from dataset-2 and dataset-3. As we have discussed, choosing the appropriate feature representation for polymeric materials remains an open question in the ML field, which is also highly dependent on the specific application.^16,17,48,83

Our ML approaches are designed with the specific goal to quickly predict a polymer's $T_g$ from an extremely large set of known (dataset-2) and hypothetical (dataset-3) polymers. Such a high-throughput screening allows us to perform posterior correlations between high-$T_g$ polymers with common functional groups and chemical substructures. These observations allow us to quantify physical quantities that are important in determining a polymer's $T_g$. For instance, our Lasso regression models reveal principal $T_g$-related features, including 61 molecular descriptors and 18 chemical substructures. Also, the functional groups exclusive to high-$T_g$ (>200°C) or low-$T_g$ (<50°C) polymers are further identified, which can cross-validate our Lasso regression models. It allows us to determine which chemical elements and molecular structures are worth experimental studies in molecular engineering and design of high-temperature polymers, leading to a molecular understanding of a polymer's $T_g$. With the DNN_Fingerprint model for high-throughput screening of nearly one million hypothetical polymers, we find more than 65,000 promising candidates with $T_g$ > 200°C, which is 30 times more than existing known high-temperature polymers (∼2,000 from dataset-1). The discovery of this large number of promising candidates will be of significant interest in the development and design of high-temperature polymers. The same task is very difficult to accomplish by screening with either theoretical equations or MD simulation due to their limitations in dealing with such large and diverse datasets. In summary, our study demonstrates that ML is a powerful method for the prediction and rapid screening of high-temperature polymers, particularly with growing large sets of experimental and computational data for polymeric materials. The key molecular descriptors and chemical substructures informed by ML models, combined with identified chemical functional groups, are important design motifs for the molecular engineering of high-temperature or high-performance polymers in an inverse materials design task.

Experimental procedures

Resource availability

Lead contact

Ying Li is the lead contact of this study and can be reached by e-mail: yingli@engr.uconn.edu.

Materials availability

This study did not generate new unique reagents.

Data and code availability

Data and code are available at https://github.com/figotj/Polymer_Tg_.

Published: April 9, 2021