Computational study on the allosteric mechanism of Leishmania major IF4E-1 by 4E-interacting protein-1: Unravelling the determinants of m⁷GTP cap recognition

Graphical abstract

Highlights

• •Atomistic details on perturbations induced by Lm4E-IP1 binding are described.
• •The modulation of LmIF4E-1 affinity for the cap is confirmed by energetic analyses.
• •Signaling paths between the allosteric and othosteric sites of LmIF4E-1 are predicted.
• •Lm4E-IP1 binding increases the side-chain entropy of W83 and R172 of LmIF4E-1.
• •A mechanism of dynamic allostery is proposed for the regulation mediated by Lm4E-IP1.

Abstract

During their life cycle, Leishmania parasites display a fine-tuned regulation of the mRNA translation through the differential expression of isoforms of eukaryotic translation initiation factor 4E (LeishIF4Es). The interaction between allosteric modulators such as 4E-interacting proteins (4E-IPs) and LeishIF4E affects the affinity of this initiation factor for the mRNA cap. Here, several computational approaches were employed to elucidate the molecular bases of the previously-reported allosteric modulation in L. major exerted by 4E-IP1 (Lm4E-IP1) on eukaryotic translation initiation factor 4E 1 (LmIF4E-1). Molecular dynamics (MD) simulations and accurate binding free energy calculations (ΔG_bind) were combined with network-based modeling of residue-residue correlations. We also describe the differences in internal motions of LmIF4E-1 apo form, cap-bound, and Lm4E-IP1-bound systems. Through community network calculations, the differences in the allosteric pathways of allosterically-inhibited and active forms of LmIF4E-1 were revealed. The ΔG_bind values show significant differences between the active and inhibited systems, which are in agreement with the available experimental data. Our study thoroughly describes the dynamical perturbations of LmIF4E-1 cap-binding site triggered by Lm4E-IP1. These findings are not only essential for the understanding of a critical process of trypanosomatids’ gene expression but also for gaining insight into the allostery of eukaryotic IF4Es, which could be useful for structure-based design of drugs against this protein family.

1. Introduction

Leishmaniasis is an endemic disease of tropical and subtropical regions caused by the protozoa from the genus Leishmania [1], [2] and is considered one of the most neglected parasitic diseases in terms of drug discovery [3], [4]. There is a lack of effective vaccines and means or proper control for this infection, and the currently available treatments are based on the administration of toxic drugs [5], [6].

The Leishmania spp organisms have a complex life cycle, which alternates between the promastigote and amastigote stages. The passage through different hosts (vertebrates and insects of Phlebotomus and Lutzomyia genera) leads to several morphological and biochemical changes in these parasites [7]. The previous transformations are a consequence of the modulation of gene expression regulation, in response to environmental signals such as temperature, nutritional resources, and pH shifts [8], [9], [10], [11].

In Leishmania parasites, gene transcription is characterized mainly by the synthesis of a polycistronic transcript, which is usually described as a process lacking a fine-tuned regulation [9], [11], [12], [13]. Subsequently, these transcripts are trans-spliced and polyadenylated, yielding several mature monocistronic mRNAs. However, remarkable differences in the basal levels of proteins derived from a common polycistronic mRNA have been observed in Leishmania spp [9]. Besides, the proteome surveys of representative species of this genus have shown changes in every life cycle stage [14]. Nowadays, it is known that the gene expression in these organisms is ultimately controlled at post-transcriptional level, being the most common ways the regulation of trans-splicing and mRNA transport, turnover, and translation [15], [16].

The essential function of the eukaryotic initiation factor F complex (eIF4F) in the translation of mRNAs has been thoroughly described since the last century [17]. This complex is formed by several subunits, i.e., the RNA helicase eIF4A, the regulatory subunit eIF4G and the cap-binding factor eIF4E. eIF4F is mainly responsible for the recognition of cap structure at the 5′-end of mRNAs and for facilitating the recruitment of 43S pre-initiation complexes to mRNA templates [17]. The eIF4F components of Leishmania parasites and all trypanosomatids are highly divergent from their orthologs in higher eukaryotes, and their potential functions have been previously elucidated and discussed [18]. The existence of multiple eIF4F complexes in trypanosomatids suggests a peculiar way for differential mRNA recognition, which constitutes a distinctive feature of the gene expression regulatory mechanisms at the post-transcriptional level mentioned above [18], [19].

eIF4E is the subunit within the eIF4F complex which recognizes the cap structure of mRNAs [17], [20]. The three-dimensional (3D) structure of this initiation factor is made up of eight anti-parallel β-sheets and three α-helices, which form a pocket with the shape of a “baseball glove” that binds the 7-methyl-guanosine 5'-triphosphate (m⁷GTP). eIF4Es sequences have a high content of Trp residues involved in the binding to the cap and to eIF4G protein [21]. This initiation factor can also interact with other proteins termed 4E-binding proteins (4E-BPs), e.g., eIF4G [22], [23]. This interaction occurs through a conserved motif present in almost all 4E-BPs, including eIF4G, which contains the sequence YX₄LΦ (where Y denotes Tyr, X denotes any amino acid, L denotes Leu, and Φ denotes a hydrophobic residue). Therefore, sometimes, the presence of this shared motif blocks the translation initiation process through the competition of 4E-BPs with eIF4G for binding to the same conserved patch of hydrophobic residues on the dorsal side of eIF4E [24], [25], [26].

In Leishmania spp, eIF4E isoforms range from IF4E-1 to IF4E-6, sharing a moderate degree of conservation between them (40–60% of sequence identity) and a minor degree with the higher eukaryote homologs (30–40%). In addition, proteins belonging to the same family of 4E-BPs have been identified in Leishmania spp, i.e., Lm4E-IP1 and Lm4E-IP2, thus giving new insights and significance to the role of LeishIF4Es/Lm4E-IPs complexes in the process of gene expression regulation in these parasites [27], [28]. Deciphering the distinctive role of eIF4E isoforms in trypanosomatid parasites has been a complex task, especially when there is a high functional divergence with respect to their higher eukaryotic orthologs, which have been the most studied systems. Although the amastigote is the human infective stage, the real components of the eIF4F complex in Leishmania amastigotes remain elusive [29], [30], [31].

The recently-reported crystal structures of two eIF4Es from trypanosomatids has revealed the structural determinants underlying the crucial role of these proteins during the translation initiation process. First, the structure of eukaryotic translation initiation factor 4 1 of L. major (LmIF4E-1) in complex with 4E-interacting protein 1 (Lm4E-IP1) was solved in 2018 (Fig. 1). In that work, NMR experiments were also performed to determine the chemical shift spectrum derived from the interaction of LmIF4E-1 with Lm4E-IP1 [32]. In 2019, Reolon et al. reported the structures of the Trypanosoma cruzi eIF4E5 (TcIF4E5) in complex with several cap variants. The previous study was mainly focused on determining the atomistic details of the TcIF4E5/cap-4 interfaces and on describing the binding mechanism. In addition, a structural alignment between LmIF4E-1 and TcIF4E5 was performed in that work, thus enabling the description of the structural similarities and differences between these two initiation factors [33]. Finally, an NMR assignment of the backbone of LmIF4E-1 bound to m⁷GTP was obtained, which provided additional information about cap-binding mode in this initiation factor [34].

Fig. 1.

Three-dimensional structure of LmIF4E-1/Lm4E-IP1 complex. Representation of 5WB5 structure, where each secondary structure element of LmIF4E-1, i.e., β strands (S), α helices (H) and loops (L), are labeled and numbered from the N- to C-terminus. Tryptophans involved in m⁷G binding are depicted as green sticks and the Lm4E-IP1 fragment is colored in dark gray. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Even though an allosteric inhibition exerted by Lm4E-IP1 was proposed to explain the affinity decrease of this initiation factor for m⁷GTP [32], no 3D structure of the LmIF4E/cap complex has been obtained, thus, the atomistic and dynamical bases of this phenomenon remain elusive. Here, we perform MD simulations in order to provide an ensemble-based understanding of the interactions between LmIF4E-1 and Lm4E-IP1. The experimental evidence of the decrease in affinity of LmIF4E-1 for the cap, triggered by the interaction with Lm4E-IP1, is also supported here by accurate ΔG_bind calculations. The residue-residue correlated motions and community interaction networks reveal the allosteric mechanisms exerted by Lm4E-IP1 on LmIF4E-1. To the best of our knowledge, the key residues involved in the propagation of allosteric signals between the 4E-IPs binding groove and the cap-binding site have not been studied before for this system. All these findings provide the molecular bases and a comprehensive description of the LmIF4E-1 function, as well as the possibility of exploring the remaining LeishIF4Es as potential drug targets for new antileishmanials.

2. Methods

2.1. Building the full-length LmIF4E-1

The crystal structure of LmIF4E-1/Lm4E-IP1_4-43 was accessed in Protein Data Bank (PDBID: 5WB5, 2.7 Å) [32]. The unsolved regions of LmIF4E-1 loops L1, L2, and L3 (residues 101–121, residues 149–155 and residues 198–201, respectively), were modeled with the loopmodel function of Rosetta v3.0, employing the method of Kinematic Closure (KIC) with fragments [35]. The Robetta fragment server [36] was used to generate a fragment library, based on the target protein sequence and Pymol v2.3.0 [37] was employed for placing the missing residues before the calculation. One hundred models were generated for each loop, taking the structures with the lowest value of Rosetta energetic function as the best result for further simulations (see Fig. S1). Subsequently, 20 ns of MD simulations were performed to refine the structure of calculated loops. These simulations were performed in the presence of harmonic restraints in backbone atoms of the rest of the protein and allowing the free movement of these loops.

2.2. Assembly of LmIF4E-1/cap complex

To study the impact of LmIF4E-1/Lm4E-IP1 interactions on the affinity of this initiation factor for the mRNA cap, a complex of LmIF4E-1 with a mimetic structure of 5′-end cap was built. There is solid knowledge about the conservation of the cap-binding site within this protein family [38]. Therefore, by extracting the relative positions of the cap structure from another eIF4E-cap complex, with an appropriated further refinement, one can reliably infer the cap-binding mode upon interacting with LmIF4E-1. In this sense, the superposition of the ternary complex human eIF4E (HsIF4E)/m⁷GpppA/4E-BP1 (PDBID: 1WKW, 2.1 Å) [39] and LmIF4E-1 structure was performed to orient the m⁷GpppA within the cap-binding site. It is worth noting that, despite the availability of a cocrystal structure of TcIF4E5 in complex with the native trypanosomatids’ cap (cap-4) (PDBID: 6O7Y), we decided to perform the simulations using a shorter cap variant, m⁷GpppA, for two main reasons. First, the allosteric modulation of LmIF4E-1 affinity for the cap exerted by Lm4E-IP1 has been experimentally studied with cap analogs even simpler (m⁷GTP) than the one chosen here [32]. Therefore, the complex built in our work contains all the molecular elements essential to probe the allosteric mechanism, thus making the inclusion of additional nucleotides unnecessary for the intended purposes. Second, the native cap-4 is likely to undermine the convergence of the MD simulations of the complexes, especially those conducted during the Adaptive Biasing Force (ABF) free energy calculations, as the large number of freely-rotatable bonds present in this ligand greatly increases the latter’s accessible conformations in the binding site.

2.3. Parametrization of m⁷GpppA

The m⁷GpppA parametrization was performed by fragments, i.e., 7-methyl-guanosine (m⁷G), adenosine, and dimethyl-triphosphate (DMTP). The parameters of m⁷G and adenosine were obtained from an Amber force-field (Amberff) version developed for naturally modified nucleosides of RNA [40], and from the refined version of Amberff for RNA molecules [41], respectively. Finally, the DMTP was parametrized with the Generalized Amber Force-Field 2 (GAFF2) force field [42]. The electrostatic potential (ESP) of this molecule was generated by single-point (SP) calculations using Gaussian 09 package [43] with Hartree-Fock level of theory, 6-31G(d) basis and Merz-Kollman (MK) scheme [44]. Atom-centered partial charges were calculated using the RESP methodology implemented in Antechamber18 [42].

2.4. MD simulation setup

Protonation states of LmIF4E-1 residues were determined at physiological pH (pH = 7.14) using the PDB2PQR server [45]. Systems setup was performed with tleap program from AmberTools18 [42] and the AMBER14SB force field (ff14SB) [46] was employed to derive the protein parameters. All complexes were solvated with explicit TIP3P water molecules [47] in a cubic box extending at least 10 Å from the solute surface, treated with periodic boundary conditions. Systems were neutralized by replacing water molecules with Na + and Cl- counterions, depending of their net charges.

All simulations were conducted with NAMD v.2.13 program [48]. 50,000 energy minimization (EM) steps using conjugate gradient were performed to eliminate the atomic clashes. The equilibration procedure was carried out in the NPT ensemble during 50 ns. In this step, all protein backbone and m⁷GpppA heavy atoms were restrained with a harmonic constraint of 1 kcal∙mol⁻¹∙Å⁻² and the system was slowly heated up from zero to 298 K during 1 ns. Finally, the non-constrained MD simulation was performed at constant pressure (1 atm) employing the Langevin piston [49] and constant temperature (298 K) with a Langevin dynamics [50]. The particle mesh Ewald (PME) method was used to handle long-range electrostatic interactions [51] and a distance cutoff of 9 Å was employed for short-range interactions. The MD integration step was set to 2 fs and one snapshot was saved every 10,000 steps for all simulations. Each system was simulated for 200 ns and five replicas were carried out in all cases by assigning different random velocities to the systems’ atoms during the respective heating steps.

2.5. Trajectory analysis

The cpptraj program of Ambertools18 package [52] was employed to calculate several metrics such as root-mean-square deviation (RMSD), root-mean-square fluctuation (RMSF), dihedral angles, RMSD-clustering analysis, water bridges, and hydrogen bonds. In order to monitor the structural changes of LmIF4E-1, RMSD and RMSF values were calculated for backbone atoms, using as reference the representative structure obtained by clustering analysis of the LmIF4E-1 apo simulations. Hydrogen bonds established between the cap and LmIF4E-1 were calculated with the default geometric definition of cpptraj, i.e., a distance cutoff ≤ 3.0 Å between acceptor and donor heavy atom, and the acceptor-hydrogen-donor angle ≥ 135° [42]. The interaction energy of LmIF4E-1/cap and LmIF4E-1/Lm4E-IP1 interfaces was obtained with NAMD energy plugin v1.4 [48]. Electrostatic potentials were calculated using the Adaptive Poisson-Boltzmann Solver (APBS) with PyMol APBS tools [53]. To characterize the side-chains motions of Trp residues critical to the cap-binding site, the measurement of the dihedral angles χ₁ (angle formed between the planes defined by N-CA-CB-CG) and χ₂ (angle formed between the planes defined by CA-CB-CG-CD1) were performed.

Rotamer Nomenclature. Rotameric conformations are labeled according to the angle values: g+ (gauche positive), 0≤angle≤180°; t (trans), angle ~180°; g- (gauche negative), 0≥angle≥-180°.

2.6. Adaptive Biasing force (ABF) simulations

The ABF method [54], [55], [56] was employed to study the changes in ΔG_bind of m⁷GpppA in two conditions, i.e., LmIF4E-1/m⁷GpppA and LmIF4E-1/Lm4E-IP1/m⁷GpppA. m⁷GpppA was moved away from LmIF4E-1 cap-binding pocket along the Y-axis, the reaction coordinate (RC) being defined as the Y component of the distance between the centers of mass of LmIF4E-1 and m⁷GpppA.

The cap motion along the Y-axis was performed starting from the representative structure obtained for each system (LmIF4E-1/cap and LmIF4E-1/Lm4E-IP1/cap) in the equilibrium MD simulations, and the RC was divided into fifteen non-overlapping windows of 2 Å width. 10 ns NPT equilibration was carried out for each window. Subsequently, three consecutive ABF simulations of 50 ns were performed to combine and refine the bias potentials, having a total simulation time of 150 ns. The bin width was set to 0.1 Å, and the boundary potential was defined by a force constant of 10 kcal∙mol⁻¹∙Å⁻². 1000 unbiased samples were collected for each bin before the estimation of the biasing force. Finally, all simulations of separated windows belonging to the same RC were combined to obtain the Potential Mean Force (PMF). For convenience, the minimal distance between the centers of mass of the LmIF4E-1 and m⁷GpppA was set as the RC origin.

2.7. Principal component analysis

PCA was performed employing Bio3D v2.3 [57]. All trajectory frames were used for this analysis in all studied systems. The overall translational and rotational motions were eliminated by fitting each trajectory to the corresponding representative structure. A covariance matrix was generated using Cartesian coordinates of Cα atoms from the apo trajectory. We further projected the conformers sampled during the holo trajectories onto the subspace defined by the first two eigenvectors (PC1 and PC2) obtained from the apo trajectory. This analysis allows us to investigate how the distributions of the structures change in the selected subset of PCs.

2.8. Per-residue entropy calculations

The concept of entropy-driven allostery was clarified in the past two decades when it was experimentally observed in several biological systems [58], [59], [60], [61], [62], [63]. In the thermodynamic view of allostery, the structural changes of a protein can be directly associated with the enthalpic part of the free energy changes, while the modulation of thermal vibrations represents the entropic component of this state function [62]. Entropic forces arise from stochastic interactions among a large number of elements and their study requires a complete picture of the interactions inside the object of interest. Despite the challenges of studying entropic phenomena, several approaches have emerged to account for the impact of entropy on allosteric regulation. Nowadays, several lines of evidence reveal the entropy perturbation of a distant site induced by a ligand-binding [58], [59], [60], [61], [62], [63].

In this study, CARDS (Correlation of all Rotameric and Dynamical States) program from the Enspara python package was employed to calculate the per-residue entropy [64], [65]. The method implemented in CARDS is based on the concept of dihedral transitions, which can occur between “ordered” and “disordered” regimes [64]. CARDS also applies the concept of Shannon entropy (Eq. (1)) [66], thus providing a quantification of how much any single dihedral of a protein changes across an MD simulation trajectory.

$$H\left(X\right)=-\sum _{x\in X}\rho \left(\chi \right)log\left(\rho \left(\chi \right)\right)$$ (1)

The above equation can measure the disorder in a dataset by looking at the population of each bin, where $x$ ∊ X refers to the set of possible states that dihedral X can adopt and ρ(ᵡ) is the probability for the dihedral to adopt state x. The entropy of a single residue was computed as described by Sun et al. [65].

2.9. Community network analysis and shortest path calculation

We employed a graph-based representation of protein structures, where residues are nodes and the couplings between them are edges [67], [68], [69], [70], [71]. Here, g_correlation program of GROMACS v3.3.4 was employed for the calculation of generalized correlation coefficient (GC) of Cα_i-Cα_j [72]. The GC of each pair of residues (GC_ij) was obtained for every simulated system, which were averaged over independent replicas for both, apo and holo systems. The length of the edge (i.e., weight) that connects nodes i and j was calculated from the corresponding GC coefficient between the nodes applying the following formula: ${\omega }_{\mathit{ij}}=-log\left[C_{\mathit{ij}}\right]$[67]. Network graph calculations were performed using the Bio3D package v2.3 implemented in R program [57]. The GC matrices were then filtered using heavy atom contact maps calculated for the same set of MD trajectories, in order to zero the correlations between non-contacting residues. The distance used for contact maps calculation was 5.0 Å, and an interaction prevalence ≥ 75% was used for contact definition. An edge between two nodes was established when at least one of the following conditions was met: (i) GC_ij ≥ 0.6 in all MD simulation replica, and (ii) GC_ij ≥  0.6 in the contact map-filtered correlation matrix of at least one MD simulation replica [73], [74].

The Girvan-Newman algorithm [75] was used to maximize the modularity and optimize the quality of the community structure, according to the methodology reported by Luthey-Schulten and colleagues [67]. This method utilizes the edge betweenness as a partitioning criterion and splits the network into local communities, where the connections (interactions) within local communities are strong and dense, while the connections between communities are weaker and sparser [75]. However, instead of partitioning according to the maximum modularity score, we selected the partition closest to the maximum score but with a smaller number of communities (i.e., the earliest high scoring partition) [73]. Optimal and suboptimal paths between residues linking the allosteric groove and the cap-binding site were calculated using Dijkstra’s algorithm [76] implemented in the Weighted Implementation of Suboptimal Paths (WISP) program [77]. In this sense, for a given pair of residues termed source and sink, 500 suboptimal pathways were calculated and the path lengths were assigned according to the ω_ij values of the residues forming the paths. The path length distributions were plotted for all systems to display differences in the signal propagation in the apo and holo forms.

3. Results

3.1. The m⁷GpppA binding mode to LmIF4E-1 shows the characteristic m⁷G stacking with W37 and W83

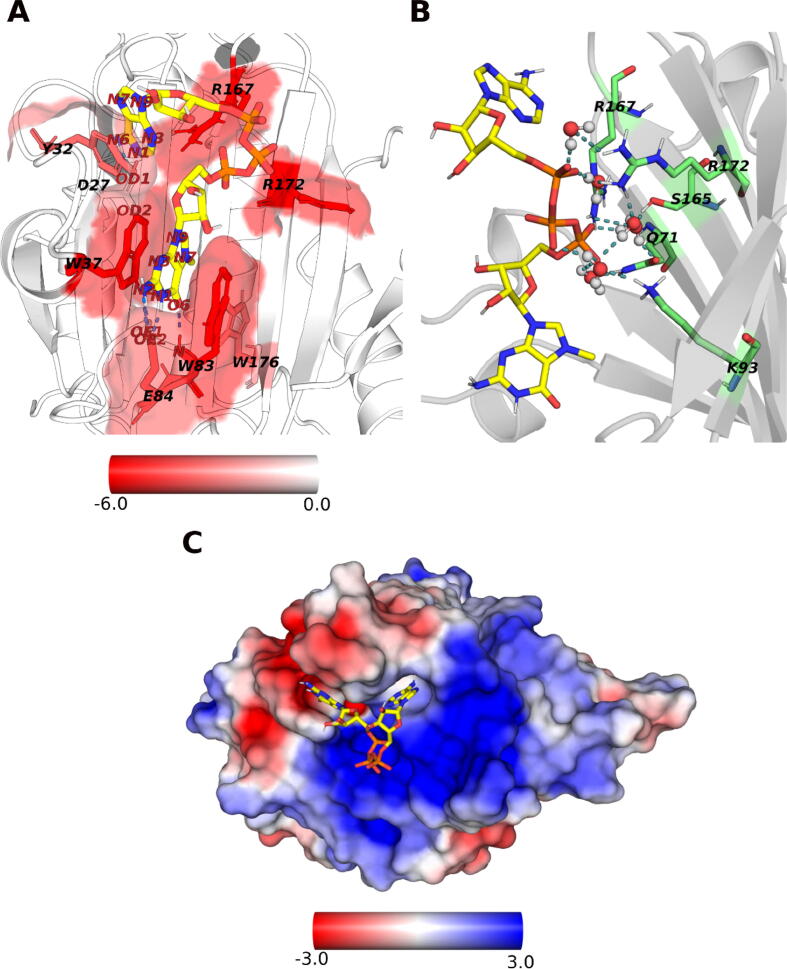
The binding mode of m⁷GpppA into the cap-binding pocket of LmIF4E-1 was studied throughout the MD simulations of LmIF4E-1/cap complex. Here, no significant differences were observed between the conformation of m⁷GTP (7-methylguanosine triphosphate) moiety within LmIF4E-1 (Fig. 2A) and the binding pose of this fragment within the crystal structures of TcEIF4E5 (PDB: 6O80 and 6O7Z) [33] and several eIF4Es complexes of other parasites and mammals (PDB: 3HXI, 1IPB, and 1L8B) [78], [79], [80]. The characteristic conformation resembling a “sandwich” established between W37, the m⁷G, and W83 is well reproduced in all replicas (Fig. 2A). In addition, the RMSF profile of m⁷GpppA confirms the stability of the m⁷G moiety along the simulation time (Fig. S2). Note that W83 not only contributes to the correct stabilization of m⁷G within the LmIF4E-1 binding site by enabling π-π staking interactions but also with the formation of a hydrogen bond between its N atom and the O6 oxygen of m⁷G. Besides, we observe that E84 plays a pivotal role in the m⁷G recognition by forming hydrogen bonds through the carbonyl oxygens of its side-chain and N1 and N2 nitrogen atoms of m⁷G. Unlike the binding modes of cap analogues in complex with HsIF4E, Schistosoma mansoni eIF4E (SmIF4E) and TcEIF4E5, the representative structure of LmIF4E-1/cap complex shows that the second base of m⁷GpppA molecule displays a different conformation within the cap-binding site of LmIF4E-1 (Fig. S3) [33], [39], [80]. In LmIF4E-1 system, the N6 nitrogen of adenine forms a hydrogen bond with the carbonyl oxygen of the D27 side-chain and π-π stacking interactions are observed between the aromatic rings of this nitrogenated base and the phenolic ring of Y32 located at the S1-S2 loop. This stabilization of the adenine mediated by Y32 may mimic the π-π interaction established between the second and the third base of the mRNA. However, the RMSF profile of m⁷GpppA displays a high fluctuation of adenosine moiety (Fig. S2), indicating the lack of interactions that favor a well-defined conformation of this base within the cap-binding site of this initiation factor. Nevertheless, the high flexibility of the second base observed in the studied system cannot be extrapolated for longer cap-analogs such as cap-4, as the stacking with downstream bases are likely to reduce the second base motions. Moreover, the phosphate groups are stabilized within the pocket region displaying a positive electrostatic potential due to the presence of R167, K168, R172, and K93 (Fig. 2C). Note that most of the above-mentioned residues involved in the binding of m⁷GpppA are evolutionarily conserved or, at least, their chemical properties are preserved within this protein family [79].

Fig. 2.

Binding mode of m⁷GpppA within the cap-binding pocket of LmIF4E-1. (A) Representative structure calculated from the MD simulations of the LmIF4E-1/m⁷GpppA complex. The surface of the cap-binding site is colored according to the values of per-residue energy contribution (ΔG_res) and the m⁷GpppA molecule is depicted as sticks. The ΔG_res values are expressed in kcal/mol. Hydrogen bonds are displayed as blue-dashed lines, and the main interacting residues are labeled in each case. (B) Water bridges network established at the interface of m⁷GpppA and LmIF4E-1. Water molecules are represented as spheres and interacting residues are labeled. (C) Electrostatic potential surface representation of LmIF4E-1. Electrostatic potentials are colored using a −3 to + 3 scale, expressed in kbT/e units, where kb, T, and e stand for the Boltzmann’s constant, the temperature (298.15 K), and the electron charge, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The influence of stable water bridges was also evaluated in the cap-binding process. Five water bridges were observed between the phosphate oxygens of m⁷GpppA and several residues of the binding pocket in the same spatial location along the simulation time (Fig. 2B). We noted that the amino acids involved in the water network are mostly those establishing favorable electrostatic interactions with the cap, i.e., K93, R167, and R172. On the other hand, Q71 and S165 also participate in this intricate hydrogen bond network, not only by forming solvent bridges with the cap but also with other residues lying within β-sheet nucleus of LmIF4E-1. The side-chain orientation of these residues towards the surface of the pocket seems to have a critical role in the formation of water-mediated interactions with the cap.

3.2. Calculated binding free energies confirm that Lm4E-IP1 is a cap-binding repressor of LmIF4E-1

Recent advances in computational chemistry and mainly in the improvement of modern computer performance have significantly enhanced the ability to predict the binding free energies (ΔG_bind) of protein–ligand complexes. Ensemble-based methods such as MD simulations have provided the correct statistical–mechanical way to estimate thermodynamic observables such as free energies from microscopic dynamics. Within the wide range of methods for calculating ΔG_bind based on MD simulations, the pathway sampling methods are perhaps the most intuitive approach. This is because in addition to the ΔG_bind values, such calculations can also provide insight in the process of binding, which are often inaccessible experimentally [81], [82].

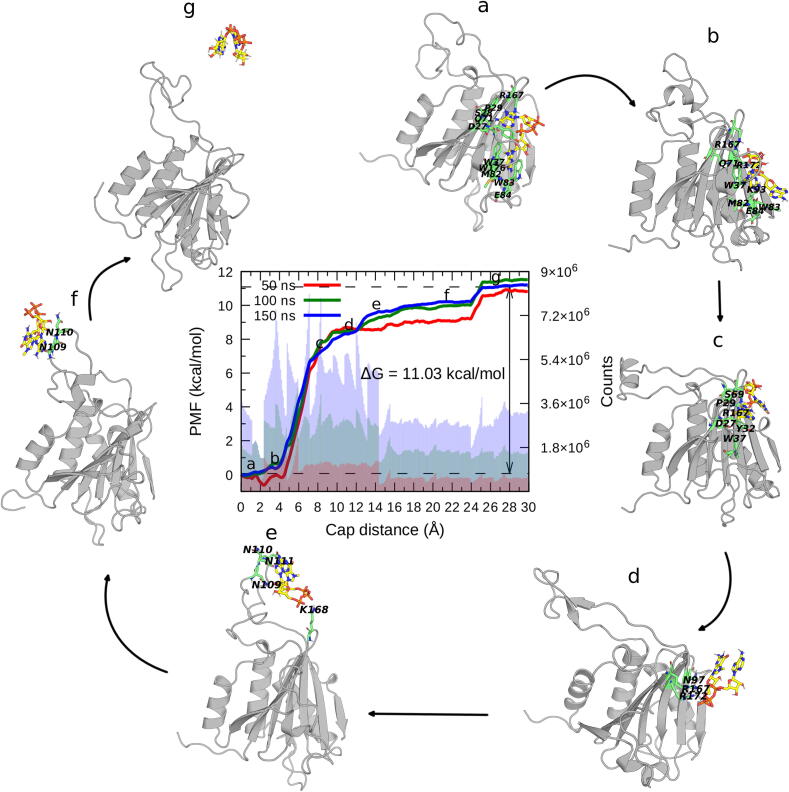
Through ABF free energy calculations, we assessed the impact of Lm4E-IP1 modulation on the cap binding to LmIF4E-1. The ΔG_bind values were derived from the PMF, which was obtained along a reaction coordinate consisting in the distance between the respective centers of mass of the cap molecule and the LmIF4E-1 backbone. For all simulated systems the results revealed that the increase of the simulation time (up to 150 ns) led to more converged results (Fig. 3, Fig. 4). Also, we noticed that the PMFs for the two simulated systems are different. In fact, for the LmIF4E-1/cap complex (Fig. 3), two energy barriers were observed from 4 to 14 Å along the reaction coordinate, which involve the cap exit from the binding site, and a third one, from 23 to 25 Å, related to the interaction with L1. On the other hand, for the PMF in the presence of Lm4E-IP1, two energy barriers are observed in the 4 to 14 Å distance range, corresponding also to the cap dissociation from the binding site, but the third barrier is missing in this case. As shown by the characteristic shape of each PMF (Fig. 4), Lm4E-IP1 precludes L1 from interacting with the cap and, thus, no related energy barrier was sampled for the ternary complex. In addition, the total ΔG_bind values for the two complexes are significantly different, being −11.03 and −8.63 kcal/mol for the LmIF4E-1/cap and LmIF4E-1/Lm4E-IP1/cap complexes, respectively (ΔΔG_bind = −2.36 kcal/mol). Therefore, the cap needs to overcome a higher overall energy barrier in the active complex than in the inhibited one to fully dissociate from the LmIF4E-1. These results are in agreement with the experimental information, which revealed that the allosteric modulation mediated by Lm4E-IP1 favors the dissociation of m⁷GTP from LmIF4E-1 [32].

Fig. 3.

PMF profiles obtained from ABF simulations performed for the LmIF4E-1/cap system. The ΔG value shown in the graph was calculated as the difference between the average of the PMF values in the global minima and the plateau of the 150 ns curve. Representative conformations of the LmIF4E-1 and the cap are displayed as transition states of each local and global minima along the reaction coordinate. The protein is shown in gray cartoon and the cap-interacting residues are displayed as green sticks. The m⁷GpppA molecule is represented in yellow sticks. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 4.

PMF profiles obtained from ABF simulations performed for the LmIF4E-1/Lm4E-IP1/cap system. The ΔG value shown in the graph was calculated as the difference between the average of the PMF values in the global minima and the plateau of the 150 ns curve. Representative conformations of the LmIF4E-1, Lm4E-IP1, and the cap are displayed as transition states of each local and global minima along the reaction coordinate. LmIF4E-1 and Lm4E-IP1 are shown in gray and teal cartoons, respectively. The cap-interacting residues and the m⁷GpppA molecule are displayed as green and yellow sticks, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Structural details on the intermediate states of the unbinding process sampled during the ABF simulations were provided through clustering analysis (Fig. 3, Fig. 4). For the LmIF4E-1/cap system, the cap association to LmIF4E-1 binding site initiates at a distance of approximately 15 Å (Fig. 3, state f). The interaction between the cap and three adjacent asparagine residues (N109, N110, and N111) is crucial for the initial approximation of the binding partners. In Fig. 3, state e, we also observe the occurrence of electrostatic interactions between the phosphate moiety of m⁷GpppA and K168. The formation of all these interactions represents a key step of the binding mechanism because once they are formed, the cap begins the association with residues lying in β-sheets of LmIF4E-1 (Fig. 3, states a-d). At a distance of ~ 4 Å, the cap is completely associated with some residues of the LmIF4E-1 binding site, establishing interactions with W37, Q71, M81, W83, E84, K93, R167, and R172 (Fig. 3, state b). Note that the conformation reached in state a reproduces the orientation of the representative structure obtained in equilibrium MD simulations (compare Fig. 3, state a with Fig. 2A).

On the other hand, the comparison of the ABF trajectories of active and allosterically-inhibited forms of LmIF4E-1 suggests different paths of the cap to finally adopt the equilibrium position in both systems (see the clusters of Fig. 3, Fig. 4). The interactions observed in the second transition state of the active complex (Fig. 3, state e) are missing in the allosterically-inhibited system. Therefore, we suggest that the changes in the dynamical properties of LmIF4E-1 induced by Lm4E-IP1 limit the full insertion of the cap. In the LmIF4E-1/Lm4E-IP1/cap complex, we found a decrease in the flexibility of L1, restricting the protein motions with respect to the active form. Note that N109, N110, and N111 of this loop facilitate the cap entrance to the binding pocket and that pathway was not observed in the inhibited system (Fig. 4).

3.3. Lm4E-IP1 decreases the flexibility of LmIF4E-1, disfavoring the cap accommodation in the initiation factor binding site

The analysis of LmIF4E-1 dynamics provides valuable insights into the allosteric effects induced by Lm4E-IP1. Here, the LmIF4E-1 RMSF and RMSD profiles were computed as a metric for monitoring the structural behavior of this initiation factor in the presence or absence of the cap and Lm4E-IP1 (Fig. 5). The results show that L1 displays the highest flexibility in all simulated systems, which is consistent with the fact that the structure of this loop could not be solved previously [32]. However, in the absence of Lm4E-IP1, the fluctuation of this loop is significantly higher (approximately 6.4 Å versus 9.7 Å with and without Lm4E-IP1, respectively) (Fig. 5A). On the other hand, in the simulation of apo and cap-bound systems, we can observe greater flexibility not only in L1 but also in the loop corresponding to residues 27–42 (S1-S2 loop), which forms a sort of “lid“ for the cap-binding site and contains several hot spot residues, such as W37 and Y32. Conversely, we can notice that in the simulations of Lm4E-IP1-bound complexes the degree of flexibility of S1-S2 loop remains appreciably low. Therefore, there is a direct correlation between the flexibility of L1 and that of S1-S2 loop (Fig. 5A). In addition, the cap presence led to an increase in the fluctuation of H1-S3 loop. Note that β3 also forms the cap-binding site cavity and the interaction of β3 residues with the cap may influence the motions of this loop. Among all the effects caused by Lm4E-IP1 binding, the decrease in the flexibility at LmIF4E-1 N-terminus is one of the most remarkable ones (Fig. 5A), and this change could have a negative impact on the function of this initiation factor.

Fig. 5.

RMSF and RMSD analysis of LmIF4E-1 simulated complexes. (A) RMSF profiles and (B) RMSD distribution calculated for the backbone atoms of LmIF4E-1 in each simulated condition. On the right panel, LmIF4E-1 is drawn in cartoon putty representation; the blue and red colors represent the lowest and the highest values of RMSF assigned to B-factor, respectively. In addition, the size of the tube is proportional to the value of the B-factor, i.e., the larger the B-factor, the thicker the tube. The representative structure obtained from the MD simulations of the apo form was taken as a reference for RMSF and RMSD calculations. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The backbone RMSD values also highlight the stability arisen from Lm4E-IP1 binding to the dorsal groove of LmIF4E-1 (Fig. 5B, Supplementary Fig. S4). This analysis was performed taking as reference the representative structure of the apo form obtained from MD simulations. Based on the RMSD distributions, an overlap in the populations of the analyzed systems can be observed. However, we notice that in the active complexes, the RMSD distributions are shifted toward higher values with respect to those of the inhibited states. Our results also show that the LmIF4E-1/cap complex has the highest RMSD values, thus revealing that the presence of the cap in the binding site increases the overall protein motions, contrary to the effect triggered by the Lm4E-IP1 binding.

On the other hand, the PCA approach showed that the first three eigenvectors or PCs represent the main large-scale functional motions of the LmIF4E-1 apo form (57.37%, see Supplementary Figs. S5 and S6). In the binary complexes, the contribution of the first three PCs was also over 50% (58.9% and 62.62% for LmIF4E-1/cap and LmIF4E-1/Lm4E-IP1, respectively), while the ternary complex shows a lower value (45.94% of the total variance). In both systems (apo and holos), the first and the second PCs (PC1 and PC2) were associated mainly with loop motions. Along the PC1 vector, the Cαs of L1 undergo large motions while the secondary structures remain stable. Interestingly, we observe that, in the apo form, PC2 roughly describes the “opening/closing” movement of S1-S2 loop, which is critical for the configuration of W37 within the cap-binding site (Supplementary Fig. S6). The projection of the holo trajectories onto the two first apo PCs confirms that MD conformers of apo form sampled a broader conformational space compared to the holo ones. Also, the landscape of the inhibited states reveals the collapse of the multiple energy basins to a single one, in stark contrast with the apo results (Fig. 6). These lines of evidence reinforce that the presence of Lm4E-IP1 stabilizes the LmIF4E-1 structure by decreasing the loop flexibility of the latter molecule (as inferred from the RMSF results).

Fig. 6.

Two-dimensional projection of LmIF4E-1 trajectories onto the first two eigenvectors obtained from the PCA. (A) Projection of the structural ensembles of the LmIF4E-1 apo form along PC1 (horizontal axis) and PC2 (vertical axis). The color gradient employed for coloring the histogram was defined according to the population density of each conformational state of LmIF4E, i.e., blue (less populated) to red (more populated). The holo forms (yellow-orange scale) were projected onto the eigenvectors of the apo form (blue scale) for (B) LmIF4E-1/cap, (C) LmIF4E-1/Lm4E-IP1 and (D) LmIF4E-1/Lm4E-IP1/cap complexes. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

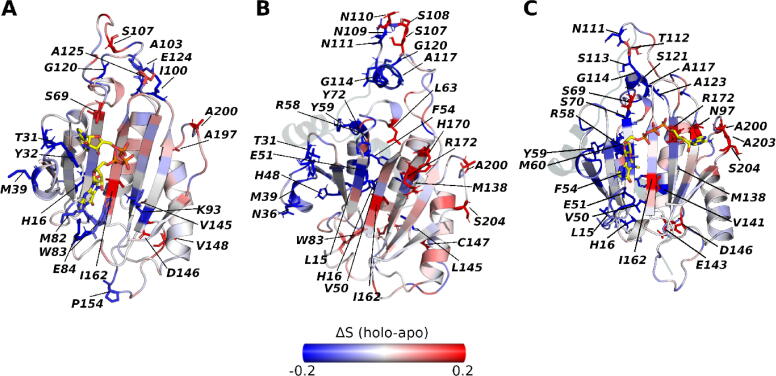
3.4. Lm4E-IP1 binding alters the side-chain entropy of residues W83 and R172 of LmIF4E-1

As far as we know, the allosteric modulation exerted by 4E-BPs does not involve large conformational changes of eIF4E structures [83], [84]. For that reason, we sought to obtain an insight into the local motions of LmIF4E-1 in terms of the dynamic changes within its residue side-chains. Therefore, we measured the entropy associated with the degrees of freedom sampled by all residue dihedrals, i.e., the entropy associated with the stability of any dihedral conformation along the simulation time. In the presence of m⁷GpppA (Fig. 7A), we observed that several residues participating in the cap-binding decrease their conformational disorder (>20% for Y32, M82, W83, E84, and K93). Besides, residues T31 and M39, lying within S1-S2 loop, also significantly decrease their entropy. This is because the interactions with the cap stabilize the position of such residues, thus reducing their flexibility. We also noted that several residues from L1 and L2 undergo variations in their dihedral conformations because of the cap presence. On the other hand, there are some residues from β3 and β5 that increase the disorder in the presence of this molecule, i.e., S69 and I162. Interestingly, the side-chains of these residues face the cap-binding pocket.

Fig. 7.

Changes in conformational disorder (Shannon entropy) of LmIF4E-1 residues. The ΔS values are defined as the difference between the S values of the apo form from those of the holo forms in (A) LmIF4E-1/cap, (B) LmIF4E-1/Lm4E-IP1, and (C) LmIF4E-1/Lm4E-IP1/cap complexes. The scale is colored from blue (decreased disorder relative to the apo form) to red (increased disorder relative to the apo form). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the LmIF4E-1/Lm4E-IP1 complex, most of the residues lying in α1 and L1 reduce their conformational entropy when compared to the apo system (Fig. 7B). Note that mainly α1 and L1 are at the interface of this complex and residues such as R58, Y59 and M138 have been mentioned before as critical hot spots establishing interactions with the consensus binding motif of Lm4E-IP1 [32]. In addition, some residues of S1-S2 loop, such as T31, Y32, N36, and M39, decrease their entropy in the presence of Lm4E-IP1, while, critical residues for the cap-binding, such as W83 and R172, increase the conformational entropy under the same condition.

In the ternary complex, we observed a reduction in the conformational disorder within several regions of LmIF4E-1 (Fig. 7C). Note that most of the residues that decreased their entropy are in contact with the cap and Lm4E-IP1. It is important to highlight that even in the presence of the cap, R172 increases its entropy relative to the apo and LmIF4E-1/cap systems when the regulatory protein is bound (compare Fig. 7A with 7C). This fact confirms that Lm4E-IP1 induces a conformational modification of R172 dihedrals that cannot be reversed by the cap.

The previously-reported NMR experiments performed with LmIF4E-1 in the presence and absence of Lm4E-IP1 highlighted the chemical shift perturbations of tryptophan side-chains of this initiation factor [32]. In order to reveal the atomistic details of this phenomenon, we assessed the heat maps of the χ₁ and χ₂ dihedral angles of W37 and W83, key residues for the cap-binding process. The results for W37 show that the apo simulations sample several populations of these torsion angles (Fig. 8, upper panel). Here, it can be observed that there are two prevalent minima: Min1, with a rotameric state of trans-gauche+ (tg + ) for χ₁ and χ₂ dihedrals, respectively, and Min2, with a rotameric state g + g- (see Text S1 and Fig. S7 for a detailed explanation). On the other hand, the cap-binding to LmIF4E-1 shifts the equilibrium of W37 dihedral populations towards Min3, where the rotameric states switch to tg-. Moreover, note that Min3 is represented by a conformation where the side-chain of W37 adopts a position allowing the stacking interactions between the indole ring and m⁷G of the cap. As we showed in the previous section, the m⁷G sandwich in this system is characterized by a conformation where the condensed phenyl and pyrrole rings of W37 are facing the imidazole and pyrimidine groups of m⁷G, respectively. Conversely, when Lm4E-IP1 is present, the conformation of W37 shifts towards Min1. In this minimum, as a result of 180° rotation of χ₂, the phenyl ring of W37 side-chain is “upside-down” relative to its position in the LmIF4E-1/cap system. Moreover, structural analyses of the recently reported TcIF4E5-cap complexes reveal differences in the rotamers of W33 side-chains (compare rotamers of W33 in structures 6O80 and 6O7Y), even when all of these systems are bound to the cap [33].

Fig. 8.

Free energy as a function of torsion angledistributionsof tryptophan residues establishing sandwich-like interactions with m⁷G. Global and local minima of rotameric states sampled for W37 (top) and W83 (bottom) along the MD simulations in each LmIF4E-1 system. The distribution of the calculated values for χ₁ and χ₂ dihedral angles are shown beside each axis. The representative structure of Trp residue in the highly-populated minima are displayed as sticks, and the χ₁ and χ₂ angles are colored as yellow and red, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Conversely, the analysis of W83 dihedral angles shows that there is one prevailing minimum in the MD simulations of the apo form (Min1), occurring as the g + g + conformer (Fig. 8, lower panel). When the cap is bound, a secondary minimum arises (Min1′), which, like Min1, contains a g + g + conformer. However, the latter is characterized by a different value of χ₂, where W83 adopts the conformation required for establishing aromatic interactions with m⁷G. On the other hand, we observed an increase in the sampling of W83 torsion angles in the presence of Lm4E-IP1 when compared to apo and LmIF4E-1/cap systems. There are two representative minima, i.e., Min1 and Min2, in the inhibited complex, with Min2 being a conformation only sampled for this system. Interestingly, the rotameric shift of the χ₁ dihedral observed in Min2 (from g + to trans) is likely to place W83 in a flipped-out conformation, thus suggesting the rupture of the aromatic stacking interaction between W83 and m⁷G. These findings are consistent with the entropy analysis, where we identified an increase in the W83 entropy.

3.5. Lm4E-IP1 binding reduces the correlated motions between S1-S2 and S3-S4 loops of LmIF4E-1

In proteins, the community analysis method consists in clustering the protein residues into communities, i.e., groups of residues whose motions are tightly intra-correlated and that are loosely correlated with those outside. Therefore, community analysis allows the partitioning of the protein structure into modules of collective motions and constitutes an excellent approach to detect protein dynamic changes in different conditions, such as the presence and absence of allosteric modulators [67], [85].

Here, the MD trajectories of LmIF4E-1 were used to analyze the residues that are closely correlated in both the apo and holo conformational ensembles. The Cα-Cα correlation matrices show remarkable differences between the LmIF4E-1/cap and LmIF4E-1/Lm4E-IP1 systems (Fig. S10). The ΔGC matrix of the LmIF4E-1/Lm4E-IP1 complex reveals the prevalence of negative values (Fig. S10, dark green spots), which reflects a decrease in residue-residue correlation motions along the entire structure of LmIF4E-1. In the case of the LmIF4E-1/cap complex, an appreciable decrease in correlation values is observed within the regions containing S1-S2 loop and residues 156–162 (near the N-extreme of β5) (Fig. S10, pink spots). However, the β4, β5 and β6 strands, and residues 195–199 (linker between α3 and β7) increase their coupled motions. Finally, in the ternary complex, the correlated values significantly decrease in all the LmIF4E-1 structure.

The analysis of cross-correlation weighted networks identified six communities in the apo form of LmIF4E-1, being Com1 and Com6 the largest ones (Fig. 9A). The results show that the community organization captured the functional regions of the LmIF4E-1 structure. In fact, well-known regions of this initiation factor, such as loops S1-S2 and S3-S4, show a high degree of intra-correlations, thus forming Com2 and Com5, respectively. However, the β-sheet core is divided into four functional communities, i.e, the blue region, which is more correlated with α1 (Com1), the red region, which is correlated with S1-S2 loop (Com2), the yellow region, coupled with S3-S4 loop (Com5), and the orange region (Com4), which includes the positively charged residues of the cap-binding site. Com3 comprises the whole L1 fragment whereas Com6 is formed by α2 and α3. Residues forming the cap-binding site of LmIF4E-1 are distributed in four different communities: W176 within Com1; Y32, W37, and Q71 within Com2; R167 and R172 within Com4, and W83, E84, and K93 within Com5. The edge widths indicate that three of these communities display strong couplings between them (Com1-Com2, Com1-Com4, and Com2-Com4), while Com5 establishes weaker connections with the remaining ones.

Fig. 9.

Analysis of community networks in LmIF4E-1. Community organization of (A) LmIF4E-1 apo, (B) LmIF4E-1/cap, (C) LmIF4E-1/Lm4E-IP1, and (D) LmIF4E-1/Lm4E-IP1/cap systems. The circle size is proportional to the number of residues contained within each community and the edge thickness is proportional to the strength of the intercommunity correlations. The right panel shows the community organization within the LmIF4E-1 structure in each case. Correlation values above 0.6 are represented as red lines connecting the initiation factor Cα’s. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The community networks also show significant differences between the apo and holo states. The LmIF4E-1/cap complex displays changes in the size of Com1, Com3, and Com6, and, at the same time, the appearance of a new community (Com7 at the H2-S5 region) is observed (Fig. 9B). Also, the coupling between Com2 and Com3 is enhanced as a consequence of more concerted motions between L1 and S1-S2 loop. Conversely, a thorough community rearrangement was detected in the LmIF4E-1/Lm4E-IP1 complex (Fig. 9C). Here, a decrease of concerted motions within the L1 fragment induces a smaller Com3 size. Additionally, the weaker L1 correlations are not only revealed by Com3 reduced size, but also by the loss of its edges with Com1 and Com2. In this system, an increase of Com5 size is observed because the S3-S4 loop is not only coupled to residues of β4, β5, β6, and β7 but also to several residues of α3. These findings indicate that Lm4E-IP1 induces a perturbation in the communications between the allosteric groove and the cap-binding site of LmIF4E-1. Interestingly, the edge between Com5 and Com2 is missing from this system and both communities contain residues of the cap-binding site, which suggests the occurrence of a perturbation in the correlations within this pocket. On the other hand, a disruption in correlated motions within the LmIF4E-1 structure upon Lm4E-IP1 and cap binding is observed (Fig. 9D). Most communities in the ternary complex shrink and have their residues reorganized. However, residues of S1-S2 loop and the positively-charged residues of β-sheets core lie now within the same community (Com2). Therefore, these findings indicate a loss in protein flexibility when both the cap and Lm4E-IP1 are bound.

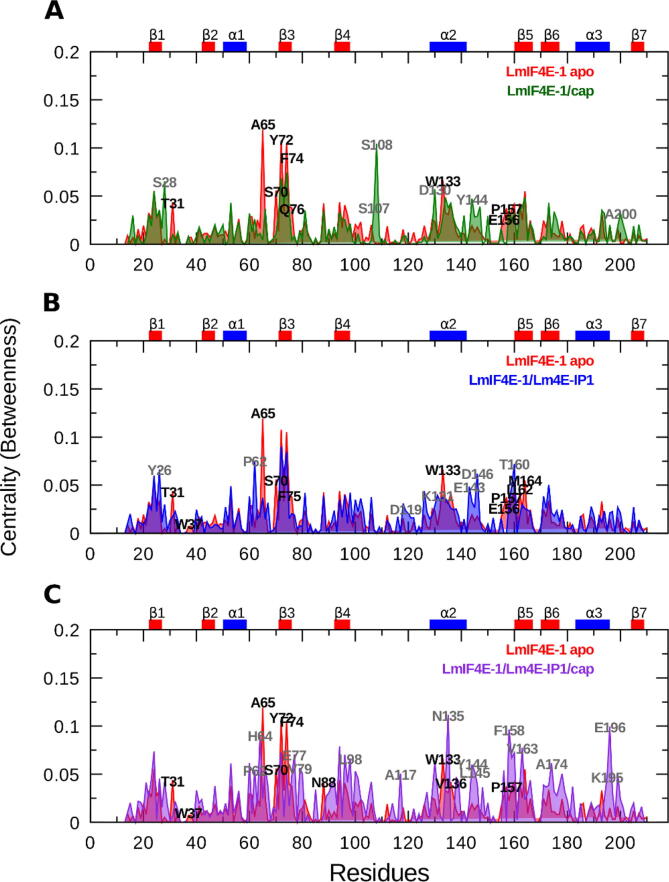
3.6. Lm4E-IP1 disturbs the allosteric signal propagation across the β2 region of LmIF4E-1

To identify the critical residues responsible for the communication throughout the allosteric network of LmIF4E-1, we calculated the node-betweenness centrality for each residue Cα in all simulated systems (Fig. 10). The apo simulations show that residues A65, Y72, F74, and W133, located within the H1-S3 loop, β3, and α2 regions, exhibit high centrality values. On the other hand, hub residues in the LmIF4E-1/cap system differ from those of the apo protein, with S28 (S1-S2 loop), S107, and S108 (L1 loop) being the most outstanding ones. Also, there are other significant differences in centrality values that can be observed for several residues, e.g., Y144 (H2-S5 loop) and A200 (H3-S7 loop). However, in the LmIF4E-1/Lm4E-IP1 complex, residues such as Y26 (β1 region), P62 (H1-S3 loop), E143, D146, and T160 (H2-S5 loop) undergo the largest variations in centrality values. These results point out that there are qualitative changes of the LmIF4E-1 regions where the allosteric signal propagates in both, active and inactive forms of this initiation factor. Conversely, the ternary complex displays a significant change in the LmIF4E-1 network topology. In this case, higher centrality values are observed throughout the protein structure, caused by the overall increase in LmIF4E-1 correlated motions.

Fig. 10.

Residue centralities calculated fortheLmIF4E-1 analyzed systems. Profiles of normalized centrality values represented as a comparison between the apo form (red graph) and (A) LmIF4E-1/cap, (B) LmIF4E-1/Lm4E-IP1, and (C) LmIF4E-1/Lm4E-IP1/cap complexes. Residues with significative changes in centrality values (high ΔCentrality) are labeled in black for the apo system and in gray for the holo ones. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Alternatively, the calculation of the optimal and suboptimal paths between W37 and Y59, one of the major hot spots of the LmIF4E-1 allosteric groove (see Fig. S11A), provided us a deeper understanding about the propagated signal between the two functional sites of this initiation factor. Fig. 11 shows the normalized node degeneracy and the 1000 suboptimal signaling pathways emerging from the source residue Y59 and reaching the sink residue W37. Here, we observe some common residues that are critical for this communication in all simulated systems, which are located mainly in β1, β2, and S1-S2 regions. In the apo system, the signal propagation mainly occurs from α1, traversing β2 and finally reaching the S1-S2 loop, while in the LmIF4E-1/cap complex, the suboptimal pathways spread throughout β1, β2, β3, and β5 regions. Note that in the latter system, there is a decrease in the number of paths traversing the nodes of the S1-S2 loop. Conversely, the LmIF4E-1/Lm4E-IP1 complex shows a decrease in the number of paths crossing β2 and an increase of those involving the β1 and β3 regions. For the ternary complex, we can observe almost the same behavior of the previous system.

Fig. 11.

Node degeneracy derived from calculations of the suboptimal paths connecting Y59 and W37 residues. The apo form (red) was used as a reference system and was compared with (A) LmIF4E-1/cap (green), (B) LmIF4E-1/Lm4E-IP1 (blue), and (C) LmIF4E-1/Lm4E-IP1/cap (purple) complexes. All degeneracy values are normalized. The 1000 suboptimal paths emerging from Y59 (allosteric groove) and reaching the W37 (cap-binding site) are displayed within the representative structure of LmIF4E-1 as splines, and are always compared with those of the apo system. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

By examining the path lengths distribution in Fig. S12A, we found that the shorter or suboptimal paths of the holo forms are significantly different from those of the apo protein (1.36 for apo form; ~2.0 for LmIF4E-1/cap, 2.21 for LmIF4E-1/Lm4E-IP1, and 2.49 for the ternary complex). The distribution of path lengths derived from the LmIF4E-1/cap complex trajectory is appreciably shifted toward larger values (compare the green and red histograms), indicating a weaker correlation between the two functional sites and a possible increase in the entropy along the pathways due to the cap binding. Interestingly, the number of residues involved in these paths in the apo system is greater than in the LmIF4E-1/cap complex (six residues in ~900 of calculated paths for LmIF4E-1/cap complex, Fig. S12B). This shows that an efficient communication between two sites is not only determined by the number of nodes along the pathway but also by the strength of the correlation established between them. Nevertheless, the distribution derived from the LmIF4E-1/Lm4E-IP1 complex and the ternary system is shifted toward larger path lengths with respect to the apo form due to the loosely-correlated motions of resides linking the allosteric groove and the cap-binding site under these conditions. Besides, the number of nodes along the pathways increased in both systems.

Finally, the analysis of the shortest or optimal path connecting the source and sink residues reveals the loss of the allosteric communication involving residues of the β2 region in all holo forms (Fig. 12). The apo form shows the path Y59 → I44 → P43 → L41 → W37, in which positions 43 and 44 corresponds to β2 residues (Fig. 12A). By contrast, when the cap is bound, the optimal path comprises the following residues: Y59 → Y72 → D27 → W37. Fig. 12B also shows that the cap-binding brings β2 closer to the major binding site of LmIF4E-1, which in turn leads to a loss of the main contacts between α1 and β2 residues. On the other hand, the binding of Lm4E-IP1 generates the same shortest path for either binary or tertiary systems, i.e., Y59 → M60 → Y72 → Y26 → S40 → W37 (Fig. 12C and 12D). Here, we can see a larger path in which the direct connection between Y72 and Y59, previously observed in the LmIF4E-1/cap system, is obstructed because of the presence of Lm4E-IP1.

Fig. 12.

Structural representation of the shortest paths calculated for the different LmIF4E-1 systems. Residues forming the shortest path of (A) LmIF4E-1 apo, (B) LmIF4E-1/cap, (C) LmIF4E-1/Lm4E-IP1 and (D) LmIF4E-1/Lm4E-IP1/cap complexes. The surface of source (Y59) and sink (W37) residues is colored in red and the surface of connecting residues is in yellow. Each residue involved in signal transmission is labeled and represented as green sticks. LmIF4E-1 and Lm4E-IP1 are shown in gray and teal cartoons, respectively, and the m⁷GpppA molecule is displayed as yellow sticks. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

The functions of the translation initiation factor eIF4E and its assembly regulator 4E-BPs are central for protein synthesis in eukaryotic organisms. 4E-BPs belong to the large family of intrinsically disordered proteins that perform a wide range of roles in the cell. The most described function of the 4E-BPs in yeast and metazoa has been the competitive binding to eIF4E, preventing eIF4E–eIF4G interactions and inhibiting cap-dependent translation. However, recent studies and the discovery of new 4E-BPs have demonstrated that the function of these proteins is not only restricted to translation inhibition [86], [87], [88], [89], [90], [91], [92]. On the other hand, there is an insufficient knowledge about the basic concepts of 4E-BPs function and the differential expression of eIF4Es isoforms in trypanosomatids [27], [29], [32], [93]. In the LmIF4E-1/Lm4E-IP1 system, we see that the Lm4E-IP1 binding promotes the loss of LmIF4E-1 affinity for the cap. Notwithstanding the existence of the crystallographic structure of LmIF4E-1/Lm4E-IP1 complex, the dynamical insights that explain how this interaction reduces the LmIF4E-1 affinity for the cap remain elusive. Therefore, we performed a thorough comparison between the apo and holo forms of LmIF4E-1 in terms of atomic-level motions, dynamics of dihedral angles, binding free energy calculations and community network analysis.

Through 1 μs concatenated MD simulations, we were able to analyze the interactions between m⁷GpppA and the cap-binding pocket of LmIF4E-1. Our results showed the stability of the sandwich-like classical conformation adopted by the cap m⁷G moiety, which inserts between W37 and W83 indole groups during all the simulation time. Conversely, the adenosine base displays high flexibility in the sampled structures, as monitored through RMSF calculations. In this sense, we observed that adenosine extends towards the solvent and even towards S1-S2 and S3-S4 loops in many LmIF4E-1/cap frames. Structural comparisons of our model with the crystallographic structures of HsIF4E/m⁷GpppA/4E-BP1 (1WKW), SmIF4E/m⁷GpppG/4E-BP (3HXI), and TcIF4E5 in complex with cap-1 and cap-4 (6O7Z and 6O7Y, respectively) showed differences in the accommodation of the second base in all cases (see Fig. S3). Interestingly, the electron density of the second nucleotide in the crystal structures of HsIF4E/m⁷GpppA and TcIF4E5/cap-1 is barely detected, which indicates the flexibility of this fragment within the cap-binding site. However, we believe that this phenomenon is a consequence of the absence of the downstream bases, since it has been observed that in a mRNA chain with three or more polynucleotides the nitrogenous bases establish π-π interactions with each other (see the well-defined electron density of the cap-4 structure in 6O7Y). We also found that residues R167 and R172 have a crucial role in cap stabilization through the interaction with the phosphate groups of m⁷GpppA. Actually, Reolon et al. previously exposed the hypothesis of charge complementarity between the phosphate groups and the basic residues of LmIF4E-1 cap-binding site when they compared the electrostatic potential surface of TcIF4E5 and LmIF4E-1. In addition, we detected six waters molecules forming a stable network of hydrogen bonds involving S165 and the basic residues of this pocket. Interestingly, the role played by the water bridges in the stabilization and recognition of the eIF4E pocket has been described for several eukaryotic orthologs [94]. S165 is conserved in TcIF4E5 (position 135), which also forms a water bridge with the phosphate groups of the cap in the 6O7Z structure (Fig. S13) [33]. This finding suggests that this serine residue constitutes an interesting position for designing more specific inhibitors against some trypanosomatid eIF4Es.

Here, we have conducted energetic analyses to assess the impact of the Lm4E-IP1 on the cap binding. The chosen approach, ABF simulations, allowed the calculation of PMFs along the distance between the centers of mass of LmIF4E-1 and the cap by applying a force (F_ABF) [54], [55], [56] that cancels the force associated with the gradient of the potential energy, thus leading to a diffusive regime and enhanced sampling. It is worth noting that, even though the obtained PMFs do not provide a direct estimate of standard binding free energy, they can be used to determine the relative free energy associated with two different conditions, as the other free energy contributions are expected to cancel. Our results showed that, in the presence of the regulatory protein, the affinity of LmIF4E-1 for the cap dropped by 2.36 kcal/mol, which is agreement with previous experimental findings based on affinity chromatography [32]. Therefore, the structural models generated in our work are consistent with a key property of the analyzed molecules, that is, the allosteric modulation exerted by Lm4E-IP1 on the cap binding. Moreover, the ABF simulations offered insightful information about the dissociation paths of LmIF4E-1 and the cap. In this sense, we concluded that the higher flexibility of L1 loop in the absence of the regulatory protein was a crucial feature leading to the higher affinity for the cap. Interestingly, site-directed mutagenesis experiments have confirmed the role of the HsIF4E equivalent loop (S4-H2 region) in the affinity of this initiation factor for m⁷GTP [95]. Also, Volpon et al revealed that alterations in the S4-H4 loop seem to be the key to modulating the cap and eIF4G binding in HsIF4E. In that work, the impact of the interaction established between S4-H2 and S5-S6 loops on the cap affinity was also suggested [96]. Based on these findings and in the fact L1 loop sampled a wide range of conformations in the space between the alpha-helices and beta-sheets nuclei, we propose that the possible interaction of this loop with α1, H1-S3 and S5-S6 regions may have a critical influence on LmIF4E-1 function and on the dynamical communication between the dorsal groove and the cap-binding site of this initiation factor.

By means RMSD and RMSF profiles and PCA the dynamical signatures of LmIF4E-1 were detected in all simulated systems (LmIF4E-1 with/without cap, with/without Lm4E-IP1). We found that the main influence of Lm4E-IP1 binding is the decrease in LmIF4E-1 flexibility, mostly in L1, S1-S2 loop and the N-terminus. On the other hand, an increase in the LmIF4E-1 conformational flexibility was observed in the presence of the cap. In this sense, our hypothesis suggests that LmIF4E-1 flexibility is critical for the cap accommodation within the main pocket and for the recognition of different variants of the mRNA cap structure. Therefore, despite the core structure of LmIF4E-1 does not display large conformational changes due to Lm4E-IP1 binding, we propose that the induced decrease in LmIF4E-1 motions is sufficient to hinder the cap binding. As it is well known, allostery can happen with the absence of large-scale conformational changes, therefore, we consider that the bases of the dynamic allostery mechanism exerted upon Lm4E-IP1 binding to the LmIF4E-1 dorsal face occur through subtle modifications on the dynamics of the initiation factor.

In the past decades, the chemical shifts and NMR relaxation experiments have been used to study allosteric phenomena, thus enabling the detection of residues undergoing subtle changes in different states of the same protein (e.g., with/without ligands, wild/mutated residues, etc.) [97], [98], [99], [100], [101]. In our study, the prediction of per-residue entropies through the calculation of the side-chain dihedral disorder allowed us to describe dynamic changes in local regions within the structure of the LmIF4E-1 bound states. Our results indicated that the dihedral angles of the residues surrounding LmIF4E-1 binding sites decreased their disorder upon the interaction with the cap and Lm4E-IP1. We observed that there is a decrease in the conformational entropy of α1 and L1 in the inhibited states of LmIF4E-1. Interestingly, Volpon et al. reported that regions on the dorsal surface involved in eIF4G/4E-BP binding exhibit less flexibility upon cap binding, thus suggesting a communication between the dorsal and the cap binding sites of eIF4E [96]. In addition, several experimental studies conducted for eIF4E/4E-BPs complexes have described local changes associated with the binding of 4E-BPs [84], [102]. Siddiqui et al. performed NMR experiments with human apo-eIF4E and cap free eIF4E/4E-BP1 complex where they reported several residues such as W102, G151, R157 and K159 (equivalent positions within LmIF4E-1 structure W83, I162, L166 and H170, respectively) displaying strong and medium chemical shifts induced by 4E-BP1 peptide [83]. Here, we see that despite the existence of structural differences between LmIF4E-1 and HsIF4E, and between 4E-BP1 and Lm4E-IP1, our results match those described by Siddiqui et al. [83]. Moreover, as a remarkable finding, we observed that residues involved in cap binding, such as R172 and W83, increased their entropy upon Lm4E-IP1 binding. This result points out that the interactions established at the dorsal groove of LmIF4E-1 could propagate an effect far from the allosteric site, which eventually ends up affecting the dynamics of residues lying within cap-binding site. The structural determinants and mechanisms driving the side-chain motion of arginine residues such as R172 could be determined by several factors, such as the solvent accessibility, and electrostatic interactions [103]. In this sense, the examination of RMSF profiles calculated for W83 and R172 residues (Figs. S8 and S9) show a higher flexibility in the inhibited system relative to the apo form. In addition, the solvent accessible surface area (SASA) distributions of W83 and R172 are wider in the presence of Lm4E-IP1, reinforcing that these residues are more structurally disordered in such condition than in the apo protein.

Interestingly, our analyses show that the W37 side-chain occurs in multiple minima in apo LmIF4E-1, which collapse to a single minimum upon the cap binding through conformational selection. On the other hand, the presence of the regulatory protein shifts the W37 orientation toward states incompatible with the cap stacking, as the minimum associated with the latter event disappears under this condition. Moreover, the cap binding to the main site of LmIF4E-1 brings the W83 χ₂ dihedral toward smaller values, thus slightly shifting its main orientation (Min1) in the complexed form (compare Min1 and Min1′ relative positions in Fig. 8). The Lm4E-IP1 binding also alters the conformational equilibrium of this Trp residue by promoting a second orientation (Min2) unable to form the stacking interactions with the cap. Overall, our results provide a more elaborate vision of the role of W37 and W83 in the cap-binding process than the two-state model proposed by Meleppattu et al. on the basis of the crystallographic structure and NMR experiments [32].

Finally, the community network analysis performed on the MD simulations of the LmIF4E-1 complexes has provided an evidence of the decrease in the correlations between L1 and the rest of LmIF4E-1 regions because of the Lm4E-IP1 binding. This result reinforces the importance of L1 in the process of cap recognition and binding and, at the same time, indicates that the allosteric inhibition exerted by Lm4E-IP1 could involve the disruption of this loop function. Our study also indicated that Lm4E-IP1 reduces the correlations between two critical communities comprising S1-S2 and S3-S4 loops, which in turn, contain W37 and W83, respectively. Interestingly, the reorganization of communities containing key functional residues has been considered as a signature of allosteric modulation in several systems [104], [105]. Intuitively, we would have expected that the residues of cap-binding site lying closer to the allosteric groove would have been the most affected in terms of coupling motions. Surprisingly, the most reorganized region after the Lm4E-IP1 binding was the S3-S4 one (see Com5 in the LmIF4E-1/Lm4E-IP1 system). Therefore, the correlated motions of W83 are more affected than those of W37 when the Lm4E-IP1 is bound, which is in agreement with the previously-discussed increase of W83 entropy. Other analyses conducted here revealed changes induced by Lm4E-IP1 in residue centralities and in communication pathways connecting the allosteric groove and the cap-binding site, thus suggesting the impact of the LmIF4E-1/Lm4E-IP1 complex formation on the overall process of signal propagation within the LmIF4E-1 structure. In particular, we observed that the signaling pathways emerging from the allosteric groove and heading toward W37 become weaker in terms of correlated motions in the presence of Lm4E-IP1. Also, we observed that the signal propagation through β2 is hampered upon Lm4E-IP1 binding. In 2016, Salvi et al. reported the pairwise Cα cross-correlation coefficients in the HsIF4E-4EGI-1 complex [106], but to our knowledge, there is no previous work reporting the signal communication between the dorsal groove and the cap-binding site in eIF4Es at atomic level. Therefore, this study would be the first to perform this kind of analysis, which provides a microscopic insight about the allosteric mechanism exerted by 4E-BPs in terms of biomolecular dynamics and function.

5. Conclusions

Overall, this computational study contributes to the comprehension at molecular level of the control of mRNA translation exerted by 4E-IPs and LeishIF4Es in Leishmania spp. Moreover, it provides an in-depth view of the cap-binding mode to this initiation factor and reveals the impact of Lm4E-IP1 binding on LmIF4E-1 dynamics and function. The allosteric hotspots involved in the communication between the dorsal groove and the cap binding site identified here can also guide mutagenesis studies useful to dissect the inhibition mechanism. In this sense, our work will foster the structure-based rational design of antileishmanial inhibitors targeting this protein family.

CRediT authorship contribution statement

Lilian Hernández Alvarez: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing - original draft. Antonio B. Oliveira: Methodology, Software, Investigation, Visualization. Jorge Enrique Hernández González: Methodology, Validation. Jorge Chahine: Methodology, Supervision, Visualization. Pedro Geraldo Pascutti: Funding acquisition, Resources, Validation. Alexandre Suman de Araujo: Conceptualization, Methodology, Supervision, Validation. Fátima Pereira de Souza: Project administration, Funding acquisition, Supervision.

Declaration of Competing Interest

The authors declare no competing interests.

Appendix A. Supplementary data

The following are the Supplementary data to this article: