Deciphering the “Art” in Modeling and Simulation of the Knee Joint: Variations in Model Development

Abstract

The use of computational modeling to investigate knee joint biomechanics has increased exponentially over the last few decades. Developing computational models is a creative process where decisions have to be made, subject to the modelers' knowledge and previous experiences, resulting in the “art” of modeling. The long-term goal of the KneeHub project is to understand the influence of subjective decisions on the final outcomes and the reproducibility of computational knee joint models. In this paper, we report on the model development phase of this project, investigating model development decisions and deviations from initial modeling plans. Five teams developed computational knee joint models from the same dataset, and we compared each teams' initial uncalibrated models and their model development workflows. Variations in the software tools and modeling approaches were found, resulting in differences such as the representation of the anatomical knee joint structures in the model. The teams consistently defined the boundary conditions and used the same anatomical coordinate system convention. However, deviations in the anatomical landmarks used to define the coordinate systems were present, resulting in a large spread in the kinematic outputs of the uncalibrated models. The reported differences and similarities in model development and simulation presented here illustrate the importance of the “art” of modeling and how subjective decision-making can lead to variation in model outputs. All teams deviated from their initial modeling plans, indicating that model development is a flexible process and difficult to plan in advance, even for experienced teams.

Introduction

Computational modeling and simulation are frequently used in biomedical engineering and is a growing area of research. Computational knee joint modeling is no exception with the number of publications involving knee models or simulations per year increasing exponentially [1]. Anatomical components of knee models are typically digitized and represented by meshes, whose material behavior is characterized by constitutive equations. These models provide insight into the form-function relationships in the knee, enabling predictions of patient-specific knee mechanics in health, injury, and disease, in a relatively quick and low-cost manner. As such, computational models have a range of applications from scientific exploration to clinical tools such as orthopedic implant design, implant evaluation, surgical planning, and design of treatment strategies.

Computational modeling is a creative process involving subjective decision-making. Although based on scientific principles, decisions rely on the experience, expertise, and preference of the modeler; and form the “art” of modeling [1]. Decisions are influenced by the research question, anticipated engineering labor, computational cost, access to modeling software, and prior modeling successes. Although important, it is not clear how, and to what extent, the art of modeling influences the final outcomes of computational knee joint models.

The art of modeling could also be a fundamental and substantial source of diminished reproducibility, which is a serious concern of the scientific community since repeatable results form the cornerstone of science [2]. In generating consensus in knowledge, scientific studies must provide enough detail in their documentation about the procedures and data, such that studies can be repeated and results can be confirmed by others [3]. Computational modeling is no exception here, and more vigilance is required by the biomechanics community to repurpose our models for further exploration and clinical application, with improved model reproducibility and sharing helping to avoid duplicate efforts and accelerate advancements in the field.

With the pressing concerns on the reproducibility of modeling and simulation, the KneeHub project2 is exploring modelers' decisions in computational knee biomechanics. The project aims to investigate the art in modeling and simulation workflows to understand the influence of the approaches and decisions of the modelers on the computational models and their consequent outcomes [1]. Five independent teams work with the same data to build and use computational knee joint models with prescribed simulation goals. The KneeHub project consists of four phases: model development, model calibration, model benchmarking, and model reuse (Fig. 1). The model development phase is aimed to deliver an initial working model to simulate passive knee flexion of a cadaver specimen (using imaging and data from the literature only). The model calibration phase aims to calibrate the initial model to experimental data obtained from joint mechanics tests. The model benchmarking phase evaluates model performance against experimental data obtained from the specimens that were modeled, which are intentionally separated from data used in previous phases. Finally, in the model reuse phase, individual teams will use their models for in silico investigations that have scientific and clinical relevance. Throughout all phases of the project, the teams prospectively document their decisions and deviations from proposed plans, as foundational knowledge to decipher the art of modeling.

Fig. 1.

Phases of the KneeHub project. Adapted from Erdemir et al. [1].

This paper aims to report the experiences throughout the model development phase of the KneeHub project. We compare the initial, uncalibrated models built by each team, their model development workflows, and corresponding documentation to understand the decisions that modelers make to deliver an initial working model. The documentation is used to exemplify differences and similarities in the researchers' plans, the level of detail provided, deviations from the plans, and rationale for deviations.

Materials and Methods

KneeHub Model Development Phase.

In the model development phase of the KneeHub project, all five teams developed two computational knee models from two independent datasets and documented their efforts. The five teams are based at Cleveland Clinic (CC) (Cleveland), University of Denver (DU) (Denver), Cleveland State University (CSU) (Cleveland), Hospital for Special Surgery (HSS) (New York), and the Auckland Bio-engineering Institute (ABI) (Auckland, New Zealand). The goal of this phase was to develop initial working models capable of simulating passive flexion from 0 deg to 90 deg, without focusing on calibration, that include tibiofemoral and patellofemoral articulations. Together with the working models, teams uploaded detailed documentation of the entire model development process. Before building the models, each team prepared and delivered a detailed model development specification document that described their intended plan. These plans were then executed to build the models during which any deviations to these plans were recorded. After building the model, a model development deviation document was supplied by each team to specify where and why they deviated from their initial plan. At the completion of this phase, each team delivered a modeling and simulation (M&S) “Outputs and Processes” package per dataset which contained the uncalibrated models, individual model components, processes, simulation results, and postprocessed outputs.

Datasets.

Two independent datasets were provided to the teams to investigate how teams handled different data. Of the available data earmarked for model development, teams decided at their discretion which subset of data to use.

Data A are part of the natural knee dataset (specimen DU02)3 [4,5]. These data were obtained from the right knee of a 44-year-old male (1.83 m and 70.31 kg), including imaging data from magnetic resonance imaging (MRI) (sagittal and fat-suppressed) and clinical computed tomography (CT), and digitized probed points on the femur, tibia, and patella.

Data B are part of the open knee(s) dataset (specimen oks003)4 [6–9]. These data were collected from the left knee of a 25-year-old female (1.73 m and 68 kg) and contained imaging data from five different MRI sequences: general-purpose MRI (3D T1-weighted without fat suppression - isotropic voxel size); cartilage imaging MRI (3D T1-weighted with fat suppression—anisotropic voxel size); soft tissue imaging (proton-density, turbospin echo)—axial plane MRI; soft tissue imaging—sagittal plane MRI; soft tissue imaging—coronal plane MRI.

Model Development Phase Outputs.

For each dataset, an M&S outputs and processes package was supplied along with their corresponding specification and deviation documentation. The packages of each team contained the final and intermediate outcomes of the model development phase. The final outcomes included the working uncalibrated models and the simulation results of these models for passive knee flexion from 0 deg to 90 deg. The intermediate outcomes included all model components, consisting of representations of anatomy (segmentations, geometries of the modeled tissues, and meshes) and of tissue behavior (e.g., constitutive models and tissue responses). In addition, intermediate outcomes included the interactions between model components (connectivity representations and contact models), anatomical coordinate systems (ACSs), and loading and boundary conditions. These packages and documentation are publicly available on the KneeHub project SimTK page.2

Specifications and Deviations Documentation.

The specifications and protocol deviations documents were supplied before and after model development, respectively. Minimal guidance was provided for these documents to allow teams to document as they saw fit, with the proviso that sufficient detail is provided to enable a scientist in the field to reproduce the decision-making process, including the justification for modeling decisions. The specifications document aimed to describe the steps taken to obtain the M&S outputs from the data available. The protocol deviations document recorded all deviations from the protocol specifications, providing as much detail as possible to justify the deviations. For each deviation, a description of the deviation, what output would be impacted by the deviation, who implemented the deviation, when the deviation was made, and the justification for the deviation was requested.

Methods for Comparison.

We examined the final and intermediate outputs, and the documents provided by each team and tabulated the differences in the workflow choices of each modeling team for each section. Differences in the bone and cartilage meshes across modeling teams were quantified in detail and described in Rooks et al. [10]. In that study [10], we presented bone mesh-to-mesh distances, differences in subchondral bone boundaries, and cartilage thicknesses. In this study, we compare only gross properties of the meshes, e.g., density and element types and material models used. Differences in mesh elements and material models of the menisci were tabulated and visually compared.

To compare the anterior cruciate ligament (ACL) and posterior cruciate ligament (PCL) attachment sites, the bone meshes were registered to each other using an iterative closest point registration using CloudCompare (version 2.10-alpha) with tolerance set to 1 × 10⁻⁵ mm. The ligament nodes involved in the contact between the bone and the ACL and PCL were extracted and transformed using each teams' bone registration transformation matrix. The ligament attachment nodes were then visualized on a single bone mesh for comparison. The centroids of all ligament attachment sites were calculated and a mean of these centroids was determined for each attachment site. Distances from each centroid to the mean was then determined and used to calculate the variance.

The same registration enabled a comparison of the ACSs between teams. The local coordinate systems were visualized on one bone by registering the bones and visualizing the local coordinate system vectors for both the femur and tibia. The variance in local coordinate system origins was determined by first calculating the mean of all teams' origins. The distance of each teams' origin to this mean was then calculated and used to obtain the variance. Relative internal rotation angles as a function of knee flexion were plotted to illustrate differences in the predicted kinematic outputs across the teams. For the teams who provided absolute angles, the internal rotation angles were shifted by the value at zero degrees flexion.

Methods for Comparing the M&S Documentation.

We examined the specifications and deviations documents for each team to investigate if the teams adhered to their initial plans and if not, where and why they deviated from their initial plan. The following categories were created to group the rationale for the deviations:

• Anatomical agreement. Deviations were made to improve resemblance to the reference knee geometry and its behavior.

• Software or workflow limitation. Deviations were made when the specified software or workflow did not meet the expectations of the modeler.

• Data limitation. Deviations were made due to inadequate data (lacking quality or quantity).

• Model convergence. Deviations were made to improve model stability and convergence.

• Computational cost. Deviations were made to decrease computational time.

• Convenience. Deviations were made based on the comfort of the modeler to manage the M&S workflow.

• Deviation due to another deviation. Deviations change the model or the modeling workflow and therefore might induce other deviations to be made.

• Documentation. Deviations to the specification's documentation, for example adding detail, correcting a mistake, or improving the report in general.

• Unclear or not stated. This category is assigned to a deviation, when in the protocol deviations documentation, no rationale is given or the rationale is unclear.

Assigning a maximum of three categories per deviation was found to be sufficient for all deviations. For a weighted analysis, each deviation was assigned with three categories. If the deviation only belonged to one category, three of the same categories were assigned. If a deviation belonged to two categories, the primary category was assigned twice and the secondary category was assigned once. If a deviation belonged to three categories, each category was assigned once. The percentage of each category to the total number of assignments per team and dataset was calculated.

The resulting data were analyzed to summarize the main reasons for deviations provided by the teams and how closely each team adhered to their original plan. For situations where model specifications were excluded in the specifications document but included in the deviations document, our analysis did not compare where the team differed from what they intended to do.

Results

Comparison of Computational Models.

Differences were identified in almost all aspects of the knee joint models and implemented workflows. Visual inspection illustrated differences in the model components, ligament representations, and smoothness of the geometries (Fig. 2). A summary of the model generation workflow and model parameters is provided in Tables 1 and 2, respectively.

Fig. 2.

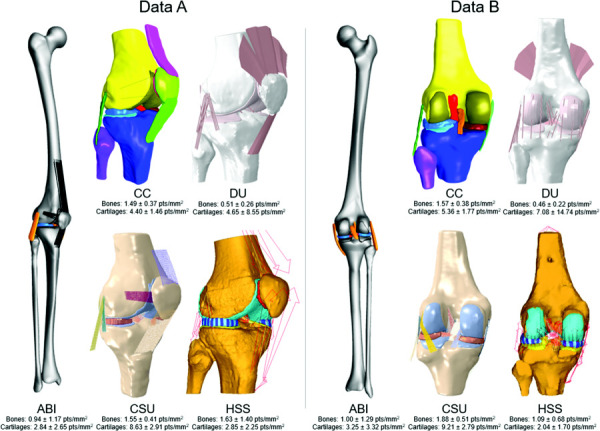
Delivered models of all teams for both datasets, anterior-lateral view (data A) and posterior view (data B). Mean mesh surface density (±SD) given per team per dataset for bones and cartilages separately. Note: Team ABI's segmentations and therefore also their model of data B was mirrored to a right knee to facilitate the ABI mesh generation workflow.

Table 1.

Summary of the model generation workflows of all five teams

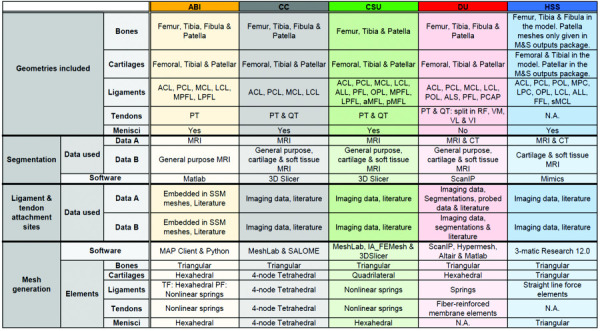Note: Ligament abbreviations: Anterior/posterior cruciate (ACL/PCL), medial/lateral collateral (MCL/LCL), medial/lateral patellofemoral (MPFL/LPFL), anterolateral (ALL), popliteofibular (PFL), oblique popliteal (OPL), anterior/posterior meniscofemoral (aMFL/pMFL), posterior oblique (POL), fabellofibular (FFL) and superficial medial collateral (sMCL). Other abbreviations: anterolateral structure (ALS), posterior capsule (PCAP), medial/lateral posterior capsule (MPC/LPC), patellar tendon (PT), quadriceps tendon (QT), rectus femoris (RF), vastus medialis/lateralis/intermedius (VM/VL/VI), magnetic resonance imaging (MRI), computed tomography (CT), tibiofemoral (TF) and patellofemoral (PF).

Table 2.

Summary of model parameters of all five teams

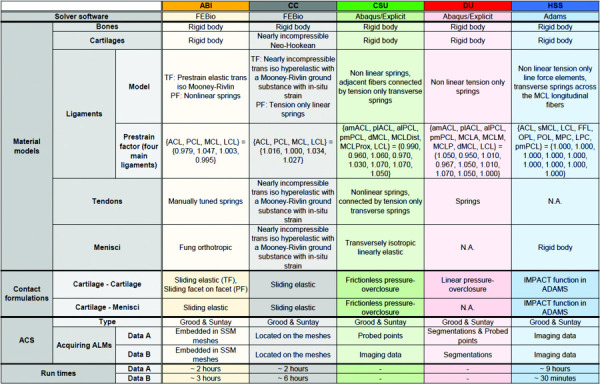Note: Ligament abbreviations: Anterior/posterior cruciate (ACL/PCL), medial/lateral collateral (MCL/LCL), Fabellofibular (FFL), oblique popliteal (OPL), posterior oblique (POL) and medial/lateral posterior capsule (MPC/LPC). Prefixes: anteromedial/anterolateral (am-/al-), posteromedial/posterolateral (pm-/pl-), deep (d-) and superficial (s-). Postfixes: distal (-Dist), proximal (-Prox), anterior (-A), medial (-M) and posterior (-P). Other abbreviations: tibiofemoral (TF) and patellofemoral (PF).

Data Used.

Not all teams used the same data to develop their models (Table 1). For segmentation, most teams used multiple scans and their choice of scans depended on their opinion of which imaging protocol most clearly displayed the structure to segment. In contrast, Team ABI only used one set of MRI scans for their segmentation. Each group also used different data from the datasets provided to obtain the anatomical landmarks (ALMs) for the anatomical coordinate systems and to obtain the ligament and tendon origins and insertions (Tables 1 and 2).

Bone and Cartilage Representations.

Teams used different approaches to generate meshes from imaging data, and a range of software tools were used (Table 1). Different segmentation software was used across teams (Table 1), with varying amounts of smoothing applied to the raw segmentation data. All teams, except for Team ABI, built their bone meshes by meshing their segmentation data directly. In contrast, Team ABI built their bone meshes by fitting a statistical shape model (SSM) to the segmentation data. To generate the cartilage meshes, all teams except for Team ABI and DU, created their cartilage meshes by meshing their segmentations directly. Team ABI generated their cartilage meshes using a custom Python script and Team DU used a custom matlab script to morph a hexahedral template mesh to the cartilage segmentation. The meshes differed in their element types and mesh surface densities (Tables 1 and Fig. 2). All teams used triangular elements for the bone meshes, where either hexahedral, tetrahedral, quadrilateral, or triangular elements were used for the cartilage meshes. The meshes also differed in the degree of smoothing applied (Fig. 2). For example, the meshes of Team HSS appear to have the least amount of smoothing applied. The shape model-fitting method used by Team ABI produced smooth meshes and no additional smoothing was applied. The ABI meshes differed in the amount of bone included in the models. Most teams developed knee models that contained partial femurs and tibias according to the field of view available in the imaging data, whereas Team ABI generated geometries of the entire femur and tibia as part of SSM fit.

Ligament and Tendon Representations.

There were differences in which ligaments were included in the models (Table 1) and their method of representation (Table 2). Three teams used spring or line segment ligament representations (CSU, DU, and HSS) and two teams used a continuum representation (ABI and CC). Team CSU used line segment representations that connected adjacent fibers with tension-only transverse springs (Table 2). Team HSS used this method as well, but only in their medial collateral (MCL) representation. Furthermore, the number of line-segments used to represent ligament bundles and fibers varied across these teams. Among the two teams that used continuum representations for ligaments, differences were present in the geometry (Fig. 2) and material models used (Table 2). Team CC segmented the ligaments from imaging data and generated a mesh from the segmentations, whereas Team ABI used ligament template meshes, which were not model specific.

Differences were also present in the representation of tendons. Three teams (ABI, CSU, and DU) represented their tendons with springs, one team (CC) used a continuum representation, and one team (HSS) did not model any tendons (Table 2).

Ligament Origins and Insertions.

The method to decide the location of the ligament origins and insertions in the models, and the data used for this, differed between teams (Table 1). For example, Team ABI's origin and insertion sites were extracted from previously labeled nodes within a SSM. Figure 3 shows differences in the ACL and PCL ligament attachment sites across teams.

Fig. 3.

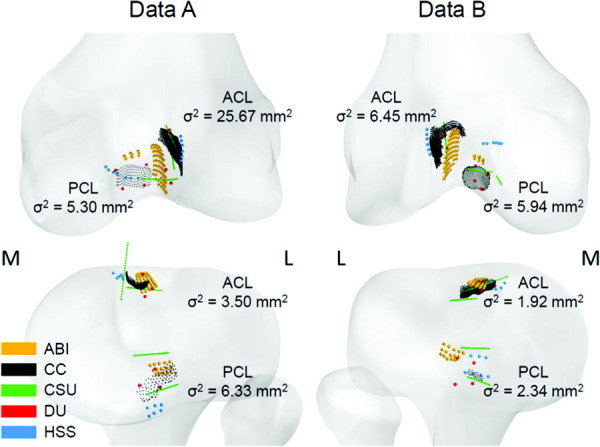
ACL and PCL attachment sites of all teams on the femur (top, posterior view) and tibia (bottom, superior/posterior view) for both data A and data B. The variance (σ²) in distance of each teams' centroid to the mean of the centroids of all teams is stated for each ligament attachment site. The medial and lateral sides are indicated by M and L, respectively.

Menisci Representations.

All teams except for Team DU included the menisci in their models (Table 1 and Fig. 2). The modeled menisci consisted of either triangular, tetrahedral, or hexahedral elements (Table 2).

Simulation Software.

Three software packages were chosen to perform the simulations across the five teams (Table 2). These included an open-source finite element solver, febio (used by ABI and CC); a commercial fe package, abaqus (used by CSU and DU); and a multibody dynamics package, adams (used by HSS).

Material Models.

The material models used to represent the different tissues of the knee joint were typically based on previous literature (Table 2). All teams modeled the bones and cartilages as rigid bodies except for Team CC who modeled their bones as rigid bodies but their cartilages using a nearly incompressible Neo-Hookean material model. The ligament material models used varied between teams, depending on the model representation (i.e., continuum or spring elements). Ligament prestrain values for the uncalibrated models are also listed in Table 2, although they will likely change in the calibration process. The reference state of the knee joint for the prestrain of the ligaments also differed across teams. For example, Team ABI used a reference state in full extension (0 deg of knee flexion according to their ACS), whereas Team CC, CSU, and DU used the imaging state as the reference state. Team HSS did not include prestrain in their models in this phase of the project.The four teams including the menisci in their models, all used a different menisci material model (Table 2).

Contact.

Varying formulations were used by each team to model cartilage-cartilage and cartilage-menisci contact (Table 2). All teams applied some form of ligament or tendon wrapping to prevent penetration into other structures. Team ABI and CC used a frictionless contact (augmented Lagrangian (ABI) or penalty method (CC)) between the ligaments or tendons and the other structures of the model. Team CSU applied a force overclosure constraint and Team DU used a pressure overclosure relationship for ligament or tendon wrapping. Team HSS placed a planar joint between the spheres of the superficial medial collateral ligament, connecting the proximal and distal fiber groups to the proximal tibia.

Anatomical Coordinate System.

All teams used the Grood and Suntay ACS [11]. However, the teams used different data and methods to locate anatomical landmarks used to describe the coordinate system (Table 2). Most notably, there was substantial variance in the origins of the local coordinate systems, particularly the femoral coordinate system. There were also differences in the direction of the ACS vectors, including some vectors pointing in the reverse direction to other groups (Fig. 4). These directions were less consistent in Data B than in Data A.

Fig. 4.

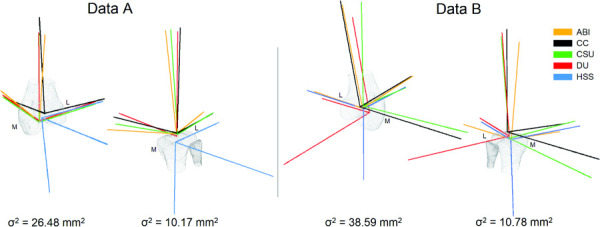
Local anatomical coordinate systems of all teams for both the femur and tibia in both datasets (posterior—medial view). The variance (σ²) of the local anatomical coordinate system origins between teams is presented underneath the corresponding bone. The medial and lateral sides are indicated by M and L, respectively.

Simulation: 0 deg to 90 deg of Knee Joint Flexion.

The goal of the model development phase was to simulate 0 deg to 90 deg of passive knee flexion with both datasets. Not every team stated their interpretation of passive knee flexion, but Team CC defined the motion as “guided by joint contact and connective tissue recruitment.”

Boundary conditions.

All groups fixed the tibia and prescribed flexion rotation to the femur, except for Team HSS, where the femur was fixed in all degrees-of-freedom (DOF) except for about the trans-epicondylar axis where rotation was prescribed, and the flexion DOF of the tibia was fixed. All teams enabled 6 DOF of the patella.

Loads.

Team ABI, CSU, and HSS reported to have included a compressive force or axial load, applied to either the femur or tibia (50 N, 20 N, and 10 N, respectively). Team ABI stated to include this force to “ensure cartilage to cartilage contact and to obtain kinematics resembling the natural knee behavior.” Two teams included muscle forces. Team DU included 10 N to each quadriceps muscle and Team CSU added a 20 N load to the quadriceps muscles along its line of action.

Computational time.

three of five teams reported the computational time taken for the simulations to run. There were large differences in both the intrateam and interteam simulation times (Table 2). There was a significant spread of computational times across teams for both data A and data B, ranging from 2 to 9 h and 0.5 to 6 h, respectively. The largest intrateam computational time difference across datasets was 8.5 h for Team HSS, while the smallest was Team ABI with a difference of 1 h. The stated computational time for Team ABI did not include a completed simulation from 0 deg to 90 deg of knee flexion, as their simulation stopped at ∼80 deg for both datasets.

Kinematic outcomes.

The kinematic predictions of initial, uncalibrated models from both datasets illustrate a large spread in internal rotation as a function of knee flexion across teams (Fig. 5).

Fig. 5.

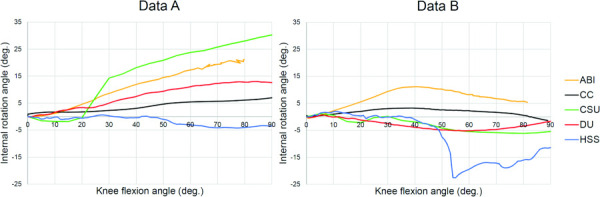
Kinematic outcomes of the initial, uncalibrated working models; Internal rotation plotted over flexion angle for all s and both datasets. The kinematic outcomes are plotted in each teams' individual interpretations of the ACS and passive flexion loading scenario.

Comparison of Documentation.

The extent and level of detail provided in the documentation varied as much as the simulations. For example, CSU and HSS submitted specification documents of 97 and 85 pages in length, whereas CC, ABI, and DU supplied documentation with 40, 27, and 22 pages, respectively. Some teams provided detailed instructions on how to use software (CSU, DU, and HSS), whereas others only stated which software to use (ABI). The documentation from Team DU was written in a slightly different way compared to the other teams. Their protocol specifications included all modeling decisions until the coordinate systems, but provided no information on the material models used, contact formulations, or simulation boundary conditions. Instead, this information was specified in the protocol deviations document. Information on when changes were made was only provided in the documents supplied by teams ABI, CC, and CSU.

Comparison of the Deviations.

The most common categories of deviations across teams included Anatomical agreement, Software or workflow limitation, model convergence, and documentation (Fig. 6, complete summary available at the following link2). Differences in deviations among teams were mainly found in the first part of the model building workflow up to and including mesh generation. Interestingly, the relative proportions of categories remain consistent within teams from one dataset to the next.

Fig. 6.

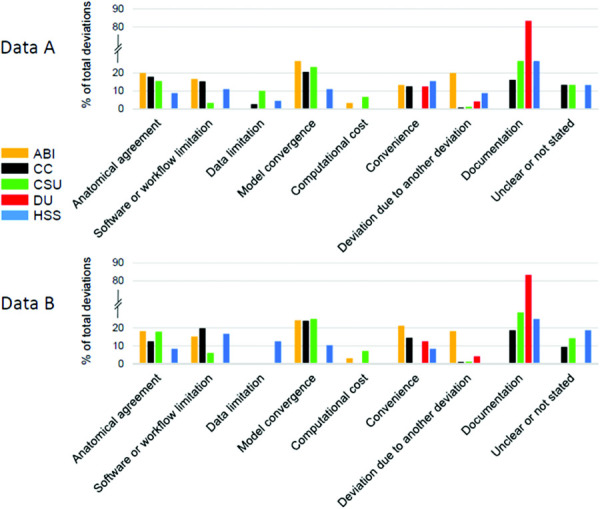
Percentage of deviations in each deviation category per team per dataset

Most teams reported deviations that were categorized as Documentation, except for the team from ABI, which did not report any. For the majority of teams whose deviations were categorized as Documentation deviations, the relative proportion of the documentation deviations was similar (up to a quarter of total deviations). The exception was Team DU, where the majority of deviations were categorized as Documentation deviations.

The team with the minimum number of categories of deviations was Team DU with three categories, followed by Team ABI with six categories, and the remaining teams with eight categories. Only Team ABI and CSU reported deviations related to Computational cost. Some teams, including CC, CSU, and HSS, did not always clearly state the reason for their deviation.

Discussion

This paper aimed to report on the model development phase of the KneeHub project, exemplifying the approaches used by teams in building computational knee models from the same datasets. We compared to initial, uncalibrated models, model development workflows, and documentation of plans and deviations provided by each team in the project. We found evidence of the art of modeling and subjective decision making throughout the modeling and simulation workflow in all teams. Workflows were influenced by the modeling experience of the teams and their modeling approach. For example, Team ABI's choices were influenced by their use of previously developed SSMs and goal to use a minimal amount of data and open-source software tools. In contrast, Team DU used commercial software packages they were familiar with and included a larger amount of data to construct their models, perhaps because they were also familiar with the experimental data collection.

Anatomical Representations.

To obtain the geometries representing the anatomy of the knee joint, subjective decisions have to be made on which geometries to include, and which data, software, and approaches to use. For the geometries included, decisions were made on; tissue boundaries during segmentation, meshing methods, number and type of mesh elements, and smoothing parameters. These decisions are influenced by the knowledge and previous experiences of the modeling team, as well as the software used (which might have its own constraints or limitations). We found differences in the meshed geometry across teams, indicating that modeling decisions here will influence the final model. For example, Team DU did not include a meniscus in their model, making geometric comparisons to other models infeasible. Such modeling decisions will also likely influence the resulting kinematics, making the comparison of model outcomes challenging. As another example, Team ABI used a SSM to obtain meshes of the entire femur and tibia, while other teams meshed their segmentations directly from the imaging data and did not predict bone geometries outside of the imaging field of view. Associated differences in the location of anatomical landmarks led to discrepancies in the anatomical coordinate systems and subsequent simulated kinematics. Team HSS kept the geometries in their model as close as possible to the original segmentations, which influenced their choice of smoothing parameters, and resulted in less smooth meshes compared to the other teams. Depending on the impact these differences in geometry generation have on the final model outputs, there may be a need to develop a unified, openly available protocol for obtaining knee joint bone and cartilage meshes from imaging data to decrease discrepancies between model geometries. Detailed analyses of the bone and cartilage meshes are provided in Rooks et al. [10] and the analysis of the final model outputs will be made in the follow up phases of the KneeHub project.

The art of modeling was most evident in combinations of line segments and continuum representations of ligament and tendon. Teams ABI and CC used continuum representations for the ligaments, while the remaining teams used line segment springs. Team CC used a continuum representation to model tendon, while Team HSS did not model any tendon. These modeling choices were likely based on the preference and experience of the team and the capabilities of the software used, thus constraining the material behavior and constitutive properties of each model. For example, febio version 2.9 does not support ligament wrapping of line-segments or the ability to form cross bundles, which are features available in abaqus. Continuum representations of the ligaments improve the accuracy of the contact outcomes because of their resemblance to the anatomical geometry, more anatomical line of action for the force, and ligament wrapping [12,13]. Line segments have advantages, including decreased computational cost, decreased modeling effort in segmenting and meshing the geometry, and are simple to define and attach between nodes on bone meshes [13]. The constitutive models used to model the ligaments also depend on the representation used. Differences were also found in the number of ligaments represented and the geometry, including the location of the attachment sites, area of the attachment site, and the morphology of the continuum meshes. These differences might arise from the difficulty associated with segmenting ligaments from the imaging data available, the anatomical expertise of the user, and varying interpretations of the anatomy in the literature. We expect that these differences will influence the kinematic outcomes of the models, due to the variance in the lines of action and distribution of force on the bones [13].

The material properties of the joint tissues were another point of difference amongst teams. All teams, except Team HSS, applied a form of prestrain to their ligaments for the simulations of their model. However, prestrain values for the ligaments were inconsistent, due to variation in the number of ligaments represented, the location of the attachment sites, and the type of representation. Furthermore, how the reference state for the ligament prestrain was defined likely had an impact on the prestrain factors. These prestrain factors are important because they will influence the reproduction of the natural kinematics as well as the predictive capabilities of the knee joint model. In the calibration phase, teams will calibrate their models to experimental data, after which a comparison of the calibrated prestrain factors will be performed. All teams modeled the bones as rigid bodies, likely, to reduce the computational cost of the simulation. Similarly, in the cartilage, all teams used rigid bodies, except for Team CC who used a nearly incompressible Neo-Hookean constitutive model. We expect that using a rigid body will not impact the results of the kinematic simulations due to the small, relative deformations of the cartilage compared to the overall kinematics [14]. However, tissue stresses and strains cannot be calculated using rigid body formulations, so deformable material models will need to be implemented if research questions require knowledge of tissue stress. Thus, the choice of material model constrains the research questions that computational knee models can address.

Model Simulation and Outcomes.

The ACSs differed between teams, even though all teams used a Grood and Suntay definition [11]. Some axis directions were reversed compared to the other teams' axes, which indicates an opposite naming convention for which direction is positive. Substantial variance was found in the origins of the local femoral and tibial coordinate systems. These differences were primarily due to the methods of locating anatomical landmarks. For example, since most models did not include the proximal femur, those teams had to decide how to define the anatomical landmark at the femoral head necessary for the ACS. Furthermore, there was more variance in the origins of the femoral ACS than the tibial ACS, suggesting difficulty in accurately prescribing femoral ACS based on landmarks. Differences in the ACSs have a direct influence on the kinematic outputs of the model simulations. Therefore, there is a need for a consistent and openly available method for applying the Grood and Suntay coordinate system to any knee model, to enable reliable comparison of reported kinematics. Fitting spheres or cylinders to the bone model to create anatomical landmarks is one approach that might help here (such as Fernandez et al. [15] and Miranda et al. [16]).

There are fewer modeling choices when it comes to defining the boundary conditions, and these were applied consistently across teams. The majority of teams fixed the tibia in 6DOF and prescribed flexion rotation to the femur with the remaining DOF unconstrained. The exception was Team HSS where the femur was fixed in all DOF except for the flexion axis, and the tibia was fixed in the flexion axis and free in the remaining DOF. Furthermore, the patella was unconstrained in all DOFs in each model. Loads were also applied consistently across teams. In some models, compressive axial loads were applied to either the tibia or femur while in others the quadriceps muscle forces were modeled to contract the joint. Although the amount of force varied, the magnitudes of these forces were low (<50 N). The documentation suggests that these forces were implemented by teams to ensure cartilage contact. The magnitude of force was often determined from literature values but was also determined from experimental protocols of cadaveric studies. Some teams reported no initial intentions for applying a compressive force but found that applying this force produced kinematics that appeared more ‘natural’ and improved the numerical stability of the model. The presence of a compressive force may be a requirement of computational knee models due to their influence on the kinematic and kinetic outcomes of the model.

A number of different software tools were used by the teams for the simulation of knee flexion. Four of the five teams chose to use finite element modeling software with two teams using an open-source package (febio) and two teams using a commercial solver (abaqus explicit). Team HSS used a commercial multibody dynamics modeling software (adams). The choice of software may have been preferential due to the ease of use, availability of customer support, or experience of the team using the software. In some cases, this choice was influenced by the modeling approach. For example, the choice of Team ABI to use febio stemmed from their goal of using open source tools to reduce the number of barriers to use and eventual clinical adoption. However, this choice may have also depended on the availability of that software to teams. Commercial packages such as abaqus and adams have licensing fees that may not be afforded by all teams. Software availability is an important consideration as each software has its own advantages and limitations, which influence the modeling decisions. Its impact was apparent in the deviations documentations, where changes to the planned workflows were made due to limitations in the software used.

Of the five teams, only three reported simulation times. This might suggest a difference amongst the modeling community regarding the importance of computational time as a metric of model performance. However, the computational time is reflective of the complexity and stability of computational models, and differences were found in the intrateam (differences of 1–8.5 h within teams) and interteam computational times (0.5–9 h). These metrics may be useful in indicating the robustness of models during repurposing. Furthermore, the computational time is likely an important factor to minimize when considering the clinical implementation of computational models.

There was a large spread in the kinematic outputs of the uncalibrated models. This exemplifies that using the same dataset to develop computational models does not guarantee the same kinematic outcomes. Many factors in the model development framework may have contributed to these differences. For example, the kinematics of the five teams were not normalized to their corresponding ACS before visualization (i.e., the kinematics were presented in each teams' individual ACSs as opposed to one ACS), which may contribute to the discrepancies between teams. Furthermore, most teams have not yet calibrated the ligaments in their models. As such, we anticipate closer agreement in the kinematic outputs between teams after the models have been calibrated to the same cadaveric data in the calibration phase of the KneeHub project. After this phase, it will be possible to investigate the influence of model calibration on the model outcomes.

Modeling Deviations.

All teams reported deviations from their initial modeling plans, and the number of deviations reported varied across teams. This indicates that it is difficult to plan the entire modeling workflow in advance, even with prior experience. It may also indicate that model development is an agile process. However, it is difficult to quantify the extent of deviation to the initial modeling plans from the number of deviations reported. This is because some deviations had a larger impact on the model outcomes than others. For example, changes to how the ligaments were represented would have had a larger impact on the model and its outcomes than the correction of a typo in the documentation. For this reason, we categorized the deviations to gain insight into the types of changes teams made to their initial plans, and consequently to understand where teams failed to plan ahead.

The four most common deviations across teams included those related to the anatomical agreement, software or workflow limitation, model convergence, and documentation. The art of modeling played a large role in deviations that were categorized as Anatomical agreement. These deviations involved decisions made to improve the likeness of the model to the natural knee and to reproduce what appeared to be its natural behavior. Therefore, these decisions have a great impact on the model outcomes. However, they were subjective to what the modeler interpreted as anatomically correct based on their knowledge and experience. As such, many of these decisions may not necessarily have been repeated by another modeler under the same circumstances.

Many deviations were made to account for Software or workflow limitations. These deviations suggest that decisions were not always made to “best represent” the joint, but also to enable the model to work with the tools and workflow available. A large number of deviations categorized as Model convergence suggest similar decision making. These deviations are considered to have a large impact on the model outcomes, as these models are unable to produce useful outputs unless they converge. The large number of deviations in these two categories exemplifies the difficulty involved in the development of computational knee joint models.

Between the two datasets, a large portion of deviations of many teams consisted of documentation deviations. This is especially the case for Team DU where ∼80% of deviations were categorized as documentation. This is because their specifications documents only partially specified the model development steps, with the remaining steps provided in the protocol deviations documentation. This made it difficult to investigate where Team DU deviated from their initial plan. Despite this, we believe that documentation deviations are unlikely to have a large impact on the model and the kinematic outcomes it produces.

Within teams, different deviations were made between the two datasets and were mainly in the first part of the model development workflow, up to and including mesh generation. These deviations were probably due to the different data and file formats available in both datasets, which required different software and workflows for segmentation and mesh generation. The workflows and deviations made in the steps following mesh generation were similar between datasets for all teams, and the relative proportions of deviation categories within teams were consistent. This similarity suggests that teams had shortcomings common to both of their plans. Since plans were not independent of each other, adapting an existing plan to another dataset may be more time-efficient and easier than preparing a new plan. This approach might also suggest bias in the decisions made by each team, which causes both plans to have similar shortcomings.

Documentation Comparisons.

Although teams were instructed to provide enough detail such that an expert in the field would be able to reproduce the model and their outputs, the level of detail and the amount of documentation provided varied across teams. Our findings suggest that the level of detail required to reproduce the models is not well understood, and not agreed upon in the field. In fact, across the documentation provided, certain details were often excluded perhaps because they were considered to be trivial or obvious. This contributes to one of the biggest issues facing the field of computational biomechanics, which is the reproducibility of models and their results [2,17]. Part of the problem is the lack of model sharing [18,19] but more so is the insufficient documentation provided on the model development workflow in the literature [17]. This might reflect the word limits imposed by scientific journals, which are normally between 3000 and 5000 words, of which the methods section is but a fraction. Considering the shortest specification document provided by teams was 22 pages (∼5500 words), this brings into question whether the methods section of scientific manuscripts is sufficiently long for their intended purpose. Further work could explore the amount of reporting required to rebuild a model and attempt to find consensus on the level of detail to provide in scientific reporting of computational models [20]. A consensus on model reporting, however, might still be viewed as too onerous for the researchers, particularly given the constraints of the journals that publish the findings from these models. An interesting solution to this problem is the newly formed Physiome Journal,5 which publishes reproducible and reusable mathematical models of physiological processes, which have otherwise been published elsewhere in a recognized “primary” peer-reviewed journal. In this instance, the researcher is obliged to be transparent and detailed to improve reproducibility. These publications enable the reuse and reproduction of models by other research groups, saving both time and money, while further bolstering confidence in the results of these models.

Limitations.

Although the analysis was performed by a single member of Team ABI, the analysis processes and outcomes were checked by all teams to minimize any potential bias or misinterpretation of the data. This study is limited to the model development workflow and explores differences in the model, its uncalibrated outputs, and the accompanying documentation. The impact of these variations on resulting mechanical predictions was not reported. Our results represent a sample of only five research teams participating in the KneeHub project, so they might not be representative of the entire knee joint modeling community. Even so, we have established a large variation of outputs from the model development phase. Direct comparison across research teams was not always possible, thus necessitating a qualitative comparison. The subjective categorization of model deviations may not adequately summarize the deviations made, however, we have provided the detailed results of this analysis for completeness on the following link.2 Finally, because minimal guidance was provided to the teams on how to prepare the documentation, the amount of detail varied.

Conclusion

In this study, we have begun to characterize the art of developing computational knee joint models, which is an important first step toward achieving reproducible and credible predictions from computational models of the knee. Differences and similarities found in model development workflows and outputs provide evidence that there is an “art” to modeling and that decision making during the modeling process is subjective. Furthermore, deviations from the initial plans were made by each team, suggesting that the model development process is both flexible as well as difficult to plan in advance.

Differences in the teams' models were found in multiple parts of the model development workflow, from geometries included to material models used, which makes it difficult to interpret the results and to find what the influence of each variable is on the model outcomes found. To answer this, systematic parametric studies might be necessary. The large variability found between the models is an important outcome of this study. It shows that the model development workflow depends on the modeler and the resources available, contributing toward the lack of reproducibility in computational knee joint models.

The next step is to quantify how the differences in these models due to the art of modeling affect the model results and outcomes after calibrating the models to the same cadaveric laxity data. This will be investigated in the remaining phases of the KneeHub project to further unravel the art of knee joint modeling.

Funding Data

• US National Institutes of Health (NIH, NOA_ 1R01EB024573-01; Funder ID: 10.13039/100000002).