Age and Generational Patterns of Overdose Death Risk from Opioids and Other Drugs

Abstract

The ongoing substance misuse epidemic in the United States is complex and dynamic and should be approached as such in the development and evaluation of policy.¹ Drug overdose deaths (largely attributable to opioid misuse) in the USA have grown exponentially for almost four decades, but the mechanisms of this growth are poorly understood.² Analyzing 661,565 overdose deaths from 1999 through 2017, we show that the age-specific drug overdose mortality curve for each birth-year cohort rises and falls according to a Gaussian shaped curve. The ascending portion of each successive birth-year cohort mortality curve is accelerated compared with that of all preceding birth-year cohorts. This acceleration can be attributed to either of two distinct processes: a stable peak age, with an increasing amplitude of mortality rate curves from one birth-year cohort to the next; or a youth-ward shift in the peak age of the mortality rate curves. The overdose epidemic emerged and increased in amplitude among the 1945-1964 cohort (Baby Boomers), shifted youth-ward among the 1965-1980 cohort (Generation X), and then resumed the pattern of increasing amplitude in the 1981-1990 Millennials. These shifting age and generational patterns are likely driven by socioeconomic factors and drug availability, the understanding of which is important for development of effective overdose prevention measures.

The mortality rate for overdose deaths has been growing exponentially since at least 1979²; overdose deaths are now a leading cause of premature deaths in the United States.³ In 2017 there were 192 deaths per day due to drug overdoses. We apply the term “epidemic” to describe this growing overall pattern. By analyzing overdose mortality patterns according to age at death (age), calendar year (period), and year of birth (cohort) of the decedents⁴, and using novel data visualization techniques, we reveal predictable patterns that describe the drug overdose epidemic from opioids and other drugs in the USA.

Results

Mortality rate by age, period and cohort reveals a wedge-shaped epidemic pattern

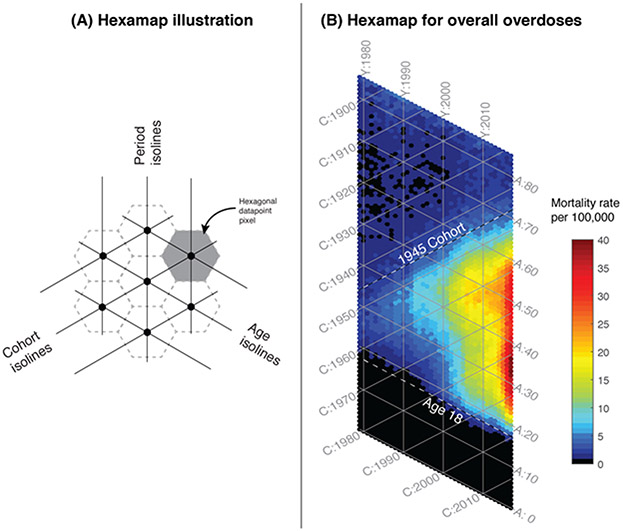
Accidental drug poisoning deaths in the USA were identified with ICD-9 and ICD-10 codes and extracted from the Mortality Multiple Cause Microdata Files from 1979 through 2017.⁵ Statistical analyses used to reveal the relationships between age, period and cohort (APC) are provided in the online methods. We implemented our newly developed hexagonal heatmap (hexamap) ⁶ to visualize death records for 661,565 accidental drug poisoning deaths between 1979 through 2017 (Figure 1). The hexamap consists of a display of hexagonal datapoint pixels that are aligned by age, period and cohort (Figure 1A). Coloring the pixels reveals patterns of overdose mortality rate by age, period, or birth-year (Figure 1B). Overall, the epidemic has a wedge-shaped pattern with an upper boundary approximately aligned along the 1945 birth-year cohort isoline, and the lower boundary aligned along the 18 year old age isoline as shown by the dashed lines. The vast majority of overdose deaths are constrained within these boundaries.

Figure 1.

Hexamaps illustrating the age and generational structure of overdose deaths from 1979 through 2017. (A) Schematic of the components of the hexamap, showing hexagonal data points as defined by age, period and cohort, arrayed along axes at 60 degree angles, and (B) Hexamap of the overall epidemic of overdose deaths where the colors indicate the mortality rates as shown in the legend. The top dashed line is drawn along the isoline of cohort = 1945, and the bottom dashed line is drawn along the isoline of age = 18. These dashed lines represent the boundaries of the wedge-shaped epidemic. [A = age, Y = calendar year, C = cohort].

This wedge shape of overdose mortality pattern illustrates the changing involvement of age groups and birth-year cohorts over time. The upper boundary of this wedge pattern, approximately along the post World War II 1945 birth-year cohort isoline, reveals a relatively abrupt emergence of the epidemic among the Baby Boomer generation⁷. Generations born earlier than 1945 had very low rates of overdose deaths. By tracing along any given birth-year cohort isoline upward from left to right across calendar years, it can be seen that the annual mortality rate for that birth-year cohort increases as each cohort has aged. This general pattern of increasing overdose mortality with increasing age holds true for all birth-year cohorts from 1945 to the present. Early signs of slowing in overdose mortality rates is apparent after 2015 especially among the Baby Boomer with the earliest birth-years (1945-1955 cohorts), as individuals in these cohorts exceed the age of peak overdose mortality.

The lower overdose epidemic boundary runs approximately along the 18-year-old age isoline, consistent with the increase in risk taking behaviors that occurs in adolescence. Prior to 2000, this lower epidemic boundary was closer to age 30 years, but this age boundary has since shifted to age 18 years.

Bands of high mortality are arrayed vertically along period (year) isolines. These vertical bands of high mortality do not conform to specific birth-year cohorts nor age groups, rather they are constrained to specific time periods. One example is the strong vertical band in deaths in the most recent years 2014-2017; this recent period effect of high mortality cuts across all affected birth-year cohort and age group isolines, coinciding with the surge of fentanyl-associated deaths.⁸

Mortality rates by birth-year cohorts

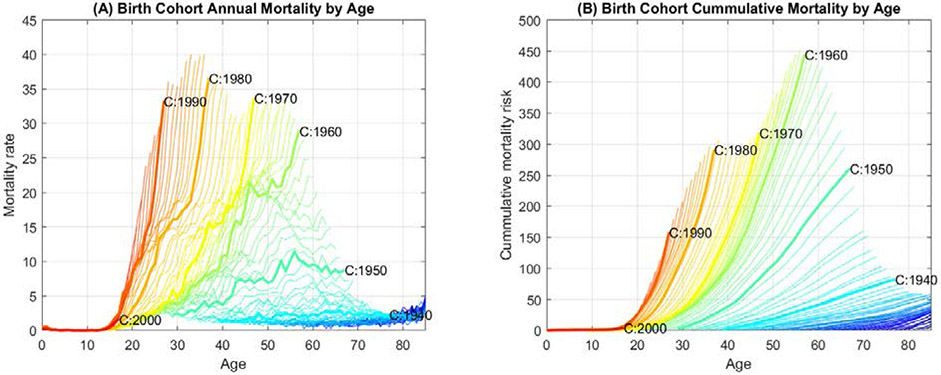
To examine the successive increases in mortality rates with each birth-year cohort, we graphically compared the mortality rate trajectories for all birth-year cohorts across their respective lifespans (Figure 2). In this analysis, all birth-year cohorts are aligned on the same age axis, showing age specific mortality rates for ages 0 to 85 for that birth-year cohort. These comparative mortality trajectories are plotted in Figures 2A and 2B.

Figure 2.

Rapid rise in age-specific overdose mortality curves by birth-year cohort. (A) and (B) show the annual and the cumulative overdose mortality rates per 100,000 persons by birth-year cohorts, respectively. Each line represents a specific birth-year cohort, with the order of birth-year cohorts shown as a color spectrum, earlier cohorts to more recent cohorts represented by blue to red. Overdose mortality data from 1979-2017 are displayed. Decennial birth-year cohorts are highlighted and labeled. See Supplementary Movie 1 for the mortality rate curves for each successive cohort.

These graphs of annual overdose mortality by age (Figure 2A; Supplementary Movie 1) comparing every birth-year cohort to the cohorts before and after, show that the mortality rate has increased for every birth-year cohorts to the next, at every age. Among the birth-year cohorts prior to 1945, the pattern was mostly flat. Successive birth-year cohorts have invariably reached higher mortality rates faster than the cohort born the year before. Figure 2B shows the cumulative overdose mortality by age for birth-year cohorts from 1940 through 2000, where the age-specific cumulative mortality increases more rapidly for every successive birth-year cohort. Similar rising trends can be observed by tracing the cumulative mortality at most ages.

Although the epidemic growth trajectories for each successive birth-year cohort are consistently faster than those preceding it, the magnitude of this year-to-year increase in mortality rate is variable. For example, there appears to have been a relative slowing of the pace of the increase in annual cohort-to-cohort mortality rate among persons born between 1965 and 1980. This transient relative slowing gives rise to a waxing and waning pattern of peak values in the composite graph of birth-year cohort mortality curves (Figure 2A).

Statistical age, period and cohort analysis reveals age and generational structure

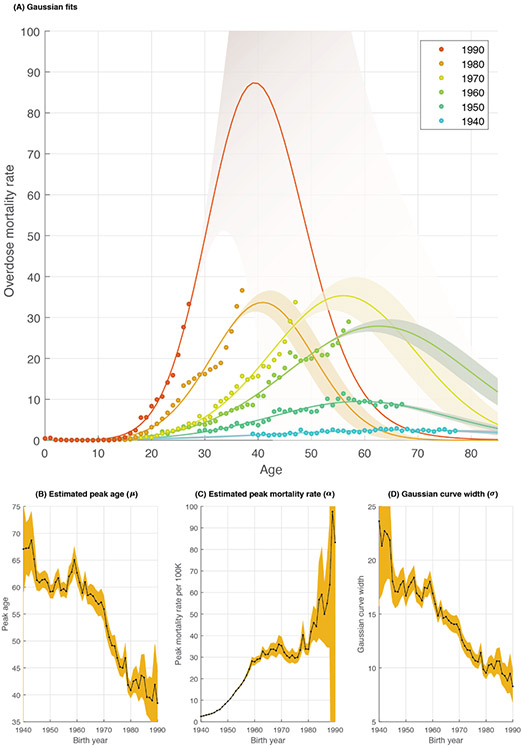
To reveal the relation between age, period and cohort, we started by fitting a Poisson log-linear age-period-cohort model (Extended Data 1). The main finding from this analysis is a net drift of 8.23% per year [CI = (8.17, 8.30)] indicating that on average, the expected age-specific overdose mortality rate has significantly increased by 8.23% every year. This analysis revealed statistically significant deviations of mortality by age and cohort. To account for the Gaussian shape of the mortality curves in Figure 2A, and to further examine these age and cohort deviations, we fit a set of Gaussian curves of mortality rates, one for each birth-year cohort. Figure 3A shows the Gaussian curves for the six decennial birth-year cohorts 1940-1990. An animation of the fitted Gaussian curves for all 51 birth-year cohorts between 1940-1990 is provided in Supplementary Movie 1. These Gaussian curves closely reconstruct the wedge-shape pattern in Figure 1B (Extended Data 2). Among the Millennial birth-year cohorts, the estimated Gaussian curve extends beyond the available 2017 data into future years, with confidence intervals widening for these curves.

Figure 3.

Birth-year specific overdose mortality follows Gaussian curves. (A) Observed and projected age-specific overdose mortality rate curves, showing six representative (decennial, 1940-1990) birth-year cohorts. Shown are the observed data (points) and the fitted/projected Gaussian curve approximations (solid lines with 95% confidence bounds). The order of birth-year cohorts is shown as a color spectrum, from earlier cohorts to more recent cohorts represented by blue to red. The bottom panels show the parameter estimates (black line) and 95% confidence intervals (orange colored area) for: (B) The peak age of overdose mortality (μ), (C) the peak mortality rate amplitude (α), and (D) the Gaussian curve width (σ).

From these curves, we computed the peak age for overdose mortality (μ), the peak overdose mortality rate (α), and the Gaussian curve width (σ) for each birth-year cohort. The peak age (μ) of the overdose mortality rate curves is expected to decline from 61 years in the 1945 birth-year cohort to 39 years in the 1990 birth-year cohort (Figure 3B). Across this same span of birth-year cohorts the approximated peak mortality rate (α) increases from 3 to 83 deaths per 100,000 persons per year (Figure 3C). These patterns indicate long-term general trends toward younger ages and rising mortality rates by age. The Gaussian curve width σ (Figure 3D) of the approximated mortality rate curves was also narrowed by about half from 1940 to 1990. This may in part reflect recent encroachment of the curves on the lower boundary of the onset of age-specific overdose mortality at approximately 18 years old shown in Figure 1B.

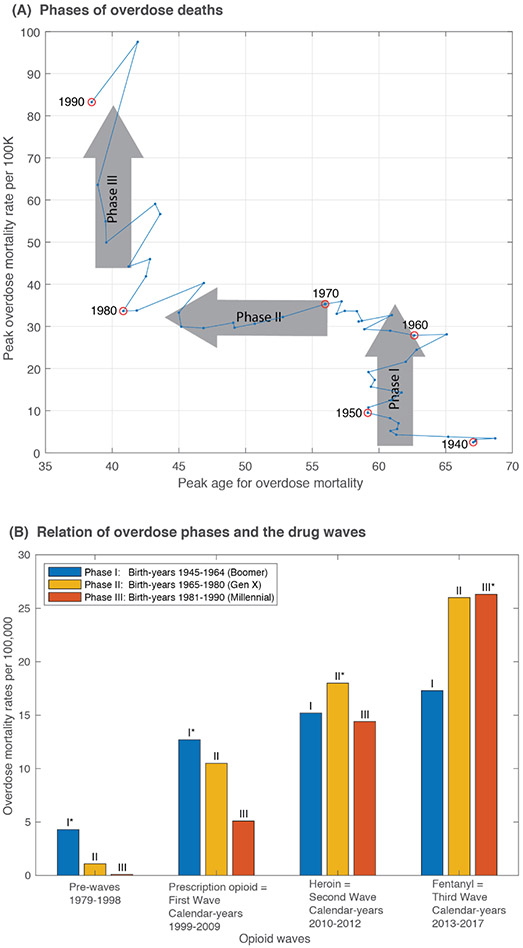
Close examination of the relationships between birth-year cohort to birth-year cohort changes in peak mortality age (μ) and peak mortality amplitude (α) reveals three distinct phases (Figure 4). We observed that these phases correspond with conventional generational birth cohort groupings (Figure 4A). In phase I (1945-1964 birth-year cohorts; Baby Boomers), the peak mortality rate increased while the peak mortality age remained steady. Phase II (1965-1980 birth-year cohorts; Generation X) is characterized by a youth-ward shift where the peak mortality rate is expected to remain largely unchanged, while the peak mortality age consistently shifted to younger ages. This youth-ward shift is almost at a rate of one year of age reduction per newer birth-year cohort. In phase III (1981-1990 birth-year cohorts; Millennials) as in phase I, the peak age remained unchanged while the mortality rate increased. Estimates of the mortality rate curve shape for birth-year cohorts later than 1990 were too uncertain to include in the current analysis. [Extended Data 3 shows the confidence intervals for the peak mortality rate and peak age of mortality].

Figure 4.

Three phases of overdose deaths revealed by plotting of the estimated peak age of overdose mortality versus the estimated peak amplitude of the overdose mortality rate, for all fifty-one birth-year cohorts 1940-1990 (A). Phase I – increasing peak mortality rates among Baby Boomer birth-year cohorts (1945-1964), Phase II – youth-ward shift among Generation X birth-year cohorts (1965-1980), and Phase III – increasing mortality rates among Millennial birth-year cohorts (1981-1990). Confidence bounds are provided in the supplemental materials Extended Data 3. These three generational phases correspond to the previously recognized three opioid drug waves of prescription opioids, heroin, and fentanyl (B). For each drug wave, the phase with the highest mortality rate in that drug wave is marked with an asterisk (*).

The epidemic generational phases, defined by birth-year cohort to birth-year cohort changes in the peak age and peak mortality rates are without regard to specific drugs, but are nonetheless closely related to the previously described drug waves of the opioid epidemic attributed to prescription opioids, heroin and fentanyl.⁹ Figure 4B shows the mortality rates at the intersection of the phases (birth-year cohort generational patterns) and waves (drug period patterns). Mortality from the phase I birth-year cohorts (Baby Boomers) predominates the pre-prescription opioid and prescription opioid phases, while mortality from phase II (Generation X) and phase III (Millennial) birth-year cohorts dominate in the heroin and fentanyl waves, respectively.

Discussion

In our analysis, the epidemic of drug overdose deaths from opioids and other drugs appears to have emerged among birth-year cohorts of the late 1940’s. To better visualize and understand the inter-dependent time measures of year of birth, calendar year, and age at death we devised a novel hexagonal age-period-cohort graphical display method. We then found that the risk of overdose death for any given individual is strongly a function of both their year of birth and age. For each new birth-year cohort, overdose mortality rates by year of age grew more rapidly than in preceding birth-year cohorts.

These mortality patterns can be mathematically represented as a coherent family of Gaussian-shaped age-specific mortality curves, one for each birth-year cohort. Given this regular epidemic structure, it is apparent that for any given individual, knowledge of the birth-year alone is sufficient to predict a pattern of overdose death risk over the life course, as they move along their cohort-specific Gaussian-shaped risk curves. We hypothesize that this consistent Gaussian shape of the risk curves across all birth-year cohorts reflect human age-specific susceptibility to substance use and risk of overdose death, with low rates in childhood, higher rates in adolescence and adulthood, and a return to lower risk in older age.¹⁰ By contrast to the consistent shape of the mortality curves across birth-year cohorts, we determined that there were major changes in the peak age and peak amplitude of mortality across birth-year cohorts. We suggest that these changing patterns of epidemic severity could reflect external or societal drivers, possibly analogous to the concept of “force of infection” from infectious disease epidemiology.^11-13

After the epidemic emerged among the 1945-1960 (Baby Boomers), the peak amplitude of the age specific mortality curve grew rapidly among this generation, from 5 deaths per 100,000 in the 1946 birth-year cohort, to 28 deaths per 100,000 in the 1960 birth-year cohort. The Boomer generation reached adolescence in the 1960’s, a decade of social turbulence. Factors that might contribute to the emergence of epidemic drug overdoses could be generational factors commonly associated with the Baby Boomers, such as a culture of drug experimentation, increased cigarette smoking, and disaffection with the Vietnam War. These new social attitudes could have become sustained for a lifetime.¹⁴

After its emergence and intensification among the Boomer generation, the overdose epidemic entered a phase in which the peak mortality rate did not change dramatically from birth-year cohort to cohort. However, the peak amplitude of the age-specific mortality curve did change, shifting younger by almost a full year with every new birth-year cohort. This change gave rise to a rapid youthward shift of the epidemic among the Generation X birth-year cohorts, with the estimated peak age dropping from approximately 60 years old to 40 years old. The pattern of younger peak mortality with each new birth-year cohort suggests the possibility of birth-year cohort to birth-year cohort propagation of substance use behaviors, from older to younger cohorts. Drug sharing behaviors show strong age homophily¹⁵, and among persons with substance use disorder, the risk of subsequent substance use is greater among their younger than older siblings^16-18.

After the 1965-1980 Generation X’s youthward shift, the epidemic age structure changed again. Among birth-year cohorts in the 1981-1990 Millennial generation, the projected peak age remained at age 40, but in each successive birth-year cohort the estimated peak amplitude of the mortality curve tripled from 32 per 100,000 among the 1980 birth-year cohort to near 90 per 100,000 among the 1990 birth-year cohort. Heroin use increased among Millennials, and since 2013, overdose deaths have surged across all major sex, race, and geographic groups, almost certainly due to the introduction of fentanyl^19,20.

The three overdose epidemic phases we describe here can be readily identified when the analytic focus is on birth-year cohorts. However, when observed in calendar time, the Baby Boomer increase in peak amplitude, the Generation X youthward shift, and the following Millennial increase in peak amplitude all overlap in calendar time. Indeed, it is this overlap of birth-year cohort and generational curves that collectively gives rise to the smooth and continuous exponential growth pattern of the overall overdose mortality epidemic.

One consequence of the consistent Gaussian shape of the age-specific mortality curve for every birth-year cohort is that, by definition, the mortality rate declines at ages beyond the peak age. For more recent birth-year cohorts, the peak mortality amplitude and subsequent decline are not actual observed values, but are calculated projections. Nonetheless it appears possible that as the Baby Boomers reach older ages their competing risk of dying from causes other than drugs increases. Given the large number of the Baby Boomers, a reduction in overdose deaths among this generation may contribute to a slowing of the overall epidemic. Early signs of this slowdown can be seen in the decline of mortality rates among the Baby Boomers with the earliest birth years. Another possible rate limiting factor of future epidemic growth is the lower age boundary of approximately 18 years. The youthward propagation of the epidemic could be constrained as the lower age limit of 18 years is being approached. Unless this lower age barrier is breached, the future involvement of younger new susceptibles could be limited. These two epidemic rate-limiting processes, one among the elderly and one among the youth, might already be contributing to the slowing of overdose deaths in the USA, as has been reported by the CDC based on analysis of provisional numbers of overdose deaths in 2018.²¹

Other factors not directly studied here could contribute to the future changes in the growth of the epidemic. One factor might be the permanence, or not, of the hyper-exponential surge in deaths due to fentanyl since 2013², during which time the annual increases in overdose mortality rates exceeded the 39 year trajectory. Other potential factors relate to the effectiveness of current control efforts to bend the epidemic curve ^22-24. Many interventions to lower overdose deaths have been aimed at reducing opioid prescribing ^25,26, using alternatives to opioids for pain relief ^27,28, harm reduction via expanding naloxone distribution^29,30 and syringe services^31-33, and increased access to medication assisted therapies. Conversely, the generational, birth-year cohort, and age-specific epidemic growth processes we describe here could, in part, determine the effectiveness of these current epidemic control measures.

The generational phases that we identified by studying changes in the peak amplitude and peak age of mortality rate among birth-year cohorts, are closely related to the changing patterns of opioid use (Table 1). The opioid epidemic is understood as having three successive major waves, each dominated by different opioids: prescription opioids, heroin, and synthetic opioids.^8,9 The prescription opioid wave was due largely to physician prescriber patterns.³⁴ When access and cost of prescription opioids became prohibitive, users switched to cheaper, more readily available heroin.^35,36 The rise of heroin-related overdose deaths has been attributed to an increase in users, but also an increase in supply^8,37,38 and especially to adulteration with fentanyl beginning around 2013^38-40.

Our study has some limitations. First, the transition from ICD-9 to ICD-10 presented some diagnostic ambiguities, as the definition of the diseases change from one classification to the next. Second, intent of the overdose death is not always clearly determined. In this analysis, we focused on accidental drug overdose deaths as they represent the majority of the overdose deaths. Third, our analyses were done at a national level, and it is likely that the national trends and patterns we report here will not be consistent across different states, counties, and cities. Fourth, our Gaussian curve fits to the data for the more recent birth-year cohorts are confined to the ascending portion (younger ages) of the mortality curve and consequently the confidence bounds for the future morality curve peak and beyond are very wide. Finally, understanding of the dynamics of the substance use epidemic cannot be fully captured by analysis of overdose deaths alone. Such an understanding requires integration of data analyses of other key dimensions of substance use, including but not limited to initiation, progression, treatment, and recovery.

There are some important implications of this study. First, it is likely that there are many more discoverable patterns underlying the epidemiological mechanisms and drivers of the substance misuse crisis. By analyzing the Mortality Multiple Cause Micro-Data Files, a widely used national level dataset, we were able to discover considerable epidemic structure and predictability. Every effort should be made to make other large datasets - on all aspects of the substance misuse crisis, not just mortality - available for similar analyses. Second, policy makers should use computational analyses of the epidemic structure in the formulation and evaluation of intervention strategies. Here, we showed that the well-recognized drug waves of the epidemic have been accompanied by a major youth-ward shift in mortality, with younger birth-year cohorts adopting drug use patterns that differ from earlier birth-year cohorts. Understanding these epidemiological clusters may help guide treatment and prevention resources. Lastly, age, generational, and drug use patterns, along with other geographic and demographic features of the drug use epidemic, will continue to evolve into the future. Computational analysis and forecasting of these complex dynamics may prove valuable in planning, and then evaluating, epidemic control efforts.

Online Methods

Mortality data were obtained from the Mortality Multiple Cause Micro-data Files form 1979 through 2017.⁵ Accidental drug poisoning deaths were identified (1979-1998) using ICD-9 E850-E858, and ICD-10 codes X40-X44 for the period (1999-2017). To compute mortality rates, we used USA census population estimates from 1979 through 2017.⁴¹

Hexagonal Age-Period-Cohort (APC) heatmaps

In this paper, we use both graphical and statistical APC analyses of the overdose data. The graphical method consists of hexamaps that display the overdose data on all A-P-C axes. We describe the details of the hexamaps and provide open-source implementation in R elsewhere⁶. Briefly, the hexamaps consist of colored hexagonal data points a long three sets of isolines – one for each axes of the APC. For example, examining the colors along the 1960 birth-year cohort reveals the increasing mortality when that cohort was 20 years of age (the intersection of age 20 isoline and 1980 period isoline), 30 years of age (the intersection of age 30 and 1990 isoline), and so forth. We developed the hexamaps to clearly display the “wedge-shaped” overdose mortality rate that is bounded by cohort:1945, age:18 and the right edge period:2017 of the data.

Statistical Analysis

To reveal the relation between age, period and cohort (APC), we start by fitting a previously developed age-period-cohort model⁴². This model fits a Poisson (or quasi-Poisson) log-linear model for the log mortality rates, such that

$$\log \left(\frac{\text{deaths}}{\text{pop}}\right)={\lambda }_0+{\lambda }_1(\text{age}-{\text{age}}_0)+{\lambda }_2(\text{cohort}-{\text{cohort}}_0)+{\tilde{\alpha }}_{\text{age}}+{\tilde{\pi }}_{\text{period}}+{\tilde{\gamma }}_{\text{cohort}}$$ (1)

where age₀ = 40 and cohort₀ = 1960 are arbitrary set reference age and cohort, respectively; ${\tilde{\alpha }}_{\text{age}}$, ${\tilde{\pi }}_{\text{period}}$ and ${\tilde{\gamma }}_{\text{cohort}}$ are the age, period and cohort deviations, respectively; λ₀ is the overall mean mortality rate, λ₁ is the longitudinal age trend, and λ₂ is the net drift which measures the overall change in the age-specific overdose mortality rate over time. In this specification, both age and cohort are treated as continuous. The main finding from this analysis is the net drift of 8.23% per year [CI = (8.17, 8.30)] indicating that on average, the expected age-specific overdose mortality rate has significantly increased by 8.23% every year. Importantly, this analysis revealed significant deviations of mortality by age and cohort (Extended Data 1). To account for the Gaussian shape of the mortality curves in Figure 2A, and further examine these age and cohort deviations, we fit a second Poisson log-linear model (Equation 2). This model fits a set of Gaussian curves of mortality rates, one for each birth-year cohort, such that

$$\log (\text{deaths})=\beta \times {\text{age}}^2\times \text{cohort}+\gamma \times \text{age}\times \text{cohort}+\theta \times \text{cohort}+1\times \log (\text{pop})$$ (2)

where age is continuous, cohort is a categorical variable indicating the birth year, and β, γ and θ are three vectors of regression coefficients for the interaction of age-squared and birth year, interaction of age and birth year, and birth year, respectively. The age-squared term allows for mortality rates to decline at older ages as we observe in Figure 2. In addition, we specify the equation without a global intercept since each birth-year cohort will have its own intercept specified by the value of θ for that cohort.

Details transformation of the quadratic model to the individual Gaussian curves:

Equation 2 is equivalent to fitting a set of cohort-specific Gaussian curves that describe the change in mortality rates by age. The parameters of each birth-year cohort’s Gaussian curve can be estimated from the regression coefficients (β, γ and θ). These Gaussian parameters consist of the peak age of mortality rate (μ), the peak mortality rate (α), and the Gaussian width (σ). The Gaussian width and the peak mortality rate determine how fast mortality rate increases by age for each birth-year cohort (c), such that

$$\frac{\text{deaths}}{\text{pop}}\times 100,000={\alpha }_c{e}^{-\frac{(\text{age}-{\mu }_c{)}^2}{2{\sigma }_c^2}}$$ (3)

which can also be expressed as a quadratic equation, such as

$$\log (\text{deaths})=-\frac{1}{2{\sigma }_c^2}{\text{age}}^2+\frac{{\mu }_c}{{\sigma }_c^2}\text{age}+\log \left(\frac{{\alpha }_c}{100,000}\right)-\frac{{\mu }_c^2}{2{\sigma }_c^2}+\log (\text{pop})$$ (4)

From Equations (2) and (4), one can determine the values for μ, σ and α for each birth cohort c, given β_c < 0 (i.e., the mortality curve is concave), such that

$${\sigma }_c^2=-\frac{1}{2{\beta }_c}$$ (5)

$${\mu }_c={\gamma }_c{\sigma }_c^2$$ (6)

$${\alpha }_c=e^{{\theta }_c+\frac{{\mu }_c^2}{2{\sigma }_c^2}}\times 100,000$$ (7)

This expression is similar to previously described quadratic age-period-cohort models^43,44, which include linear and quadratic terms for age, period and cohort. However, our specification only includes age and cohort as they appear to be the most important patterns from our first statistical model. In addition, we include interaction terms of age and age-squared with birth-year cohort which allow for cohort-specific Gaussian curve fits. From these Gaussian curves we estimate the peak age and peak mortality rates. We believe that the Gaussian curves can be useful alternatives to spline-based methods that can fit the data smoothly but lack interpretable parameters.

To compute the 95% confidence bounds for μ_c, σ_c and α_c, we took 10,000 samples from a multivariate normal distribution with means equal to the regression coefficients, (β, γ and θ), and the covariance equal to the covariance matrix from the regression. We computed μ_c, σ_c and α_c for each sample using Equations 5-7 and then calculated the 95% confidence intervals by computing the 1.96 × standard error below and above the mean estimates.