Abstract
The COVID-19 pandemic is viewed as the most basic worldwide disaster that humankind has observed since the second World War. There is no report of any clinically endorsed antiviral medications or antibodies that are successful against COVID-19. It has quickly spread everywhere, presenting tremendous well-being, financial, ecological, and social difficulties to the whole human populace. The COVID flare-up is seriously disturbing the worldwide economy. Practically all the countries are battling to hinder the transmission of the malady by testing and treating patients, isolating speculated people through contact following, confining huge social affairs, keeping up total or incomplete lockdown, etc. Proper scheduling of nursing workers and optimal designation of nurses may significantly affect the quality of clinical facilities. It is delivered by eliminating unbalanced workloads or undue stress, which could lead to decreased nurse performance and potential human errors., Nurses are frequently asked to leave while caring for all sick patients. However, regular scheduling formulas are not thought to consider this possibility because they are out of scheduling control in typical scenarios. In this paper, a novel model of the Hybrid Salp Swarm Algorithm and Genetic Algorithm (HSSAGA) is proposed to solve nurses’ scheduling and designation. The findings of the suggested test function algorithm demonstrate that this algorithm has outperformed state-of-the-art approaches.
Keywords: COVID-19, Nurse, Designation, Scheduling, Salp swarm, Genetic algorithm
1. Introduction
COVID-19 outbreak has changed from epidemics to pandemics in the first months of 2020 [1]. The coronavirus COVID-19 affects 212 countries and territories around the world and two international conveyances [2]. Effective monitoring of an infectious disease outbreak requires immediate intervention and emergency management, supply chain, and personnel sequencing. During the monitoring operation, large volumes of medical equipment and personnel schedules are transported from regional stores to dispensing sites. While infectious diseases endanger the public, Decision-makers must decide whether distributing and planning scarce resources to populations and preventing infectious disease transmission is a complicated public health challenge. As the COVID-19 pandemic expands globally, physicians, healthcare administrators, states, politicians, and experts in the intensive care unit (ICU) must brace for a rise in seriously sick patients [3]. Statistics of infected and dead cases of COVID-19 are possibly underestimated due to limitations of surveillance and testing [4]. Resources are scarce, and hospitals cannot cope with a similar pandemic. Additionally, characteristics linked to disease spread can differ across sub-populations. Consequently, the complexity and extreme impact of the problem require complex, real-time, and efficient solutions, making the subject very suitable for OR/MS research in disaster operations [5].
2. Research problem statement and contributions
In reaction to the COVID-19 outbreak, management of the epidemic was complicated. The nursing scheduling quickly established a COVID-19 management unit with the nursing department head as the team member responsible for delivering and implementing care facilities. The leadership team changed the priorities of nursing work according to the actual state of the hospital. It established outpatient clinics and lockdown ward nursing work systems and the related employee standards to ensure that nursing work complies with requirements and objectives. The Nursing Department formulated standard screening guidelines for staff and patients based on the characteristics of this epidemic. When selecting the head nurse for outpatient fever clinics, technical assistance experience and good physical fitness were given priority [6]. When choosing the quarantine unit’s lead nurse, experience in disinfection and quarantine management is the priority. Some of the nurse selection criteria are two or more years of work experience, good physical fitness, and expertise in necessary nursing procedures (infusion, ventilation of air, and observation of condition) [7].
The concept of a statistical model for nurse scheduling shifts is where nurses can work more hours to accommodate additional shifts. It would provide healthcare facilities with a smart-automated framework capable of eliminating exposed shiftswhile mitigating nursing staff’s commitment and tension and ensuring the compliance of working conditions legislation as far as possible. Nurses find justice and equal workload essential to their well-being [4]. Proper scheduling of nursing workers may significantly affect the quality of clinical facilities delivered by eliminating unbalanced workloads or undue stress, leading to decreased nurse performance and potential human errors. Nurses are asked to work overtime, but regular scheduling formulas are not thought to consider this possibility because they are out of scheduling control in typical scenarios. The findings of the proposed test function algorithm show that this algorithm benefits from elevated convergence and coverage.
3. Literature review
At present, COVID-19 reverse transcription-polymerase chain reaction (RT-PCR) has been developed and used in clinics. For the conclusive diagnosis of COVID-19 infection, RT-PCR is the standard reference [5], [6]. However, due to the RT-PCR’s inactivity, rapid diagnosis of infectious patients is limited to radiological exams. CT often. In fighting this contagious disease, a chest scan plays a vital function. Chest CT detected primary pulmonary infection [7], [8] and accelerated monitoring and response programs for public health [9]. The results of researches are proposed CT findings as crucial evidence for confirmed clinical diagnosis. COVID-19 diagnosis depends on radiological and laboratory observations. In the early diagnosis and treatment of COVID-19, radiological exams are of utmost importance. In patients with severe coronavirus pneumonia, radiological imaging requires ground-glass opacity and pulmonary consolidation to affect both lungs [10]. Primary findings have found that individuals with underlying disorders are at increased risk due to COVID-19 for developing morbidity and mortality. Around 50% of reported new coronavirus patients have chronic background diseases. Moreover, about 40 percent of confirmed new SARS-COV-2 coronavirus patients have cardiovascular or cerebrovascular disorders. The researchers have observed a significant difference in age group mortality. It is essential to consider the clinical signs of COVID-19 since the clinical symptoms are nonspecific. COVID-19 severe symptoms include fever (above 38 degrees), cough, and discomfort or muscle weakness. Sputum, headache, coughing, diarrhea, indigestion, and lymph glands are symptoms [11], [12], [13]. A few days before the fever, patients may initially feel diarrhea and nausea, suggesting that the fever is prevalent but not the leading symptom of infection. There are few cases with a headache or hemoptysis [14] and comparatively asymptomatic conditions [6]. Due to extreme alveolar in-jury, older men with comorbidity are more likely to suffer respiratory failure [15]. In severe cases, the disease’s onset progress quickly to organ failure (e.g., trauma, Acute respiratory distress syndrome (ARDS), acute heart damage, and acute kidney injury) and even lead to death [12], [16].
Many studies have been done during the Coronavirus outbreak, some of which have focused on hospital strategies and scheduling. Eichberg et al. (2020) focused on maximizing healthcare services while minimizing healthcare providers’ risk [17]. To reduce the risk of nursing infection in encounters with COVID-19 patients, it is critical to know hospital protocols [18]. Health care priorities are being changed after the pandemic, but emergency surgery is also a concern [19]. As key members of health systems, nurses have heavy responsibilities during this time. They are asked to work overtime to guarantee enough assistance to patients in critical conditions [20]. Mascha et al. (2020) hypothesized that staff shortage could be diminished when staff scheduling takes the disease’s epidemiology into account [21]. Front-line clinicians need to protect themselves and healthcare staff’s health and safety to avoid adverse outcomes adverse effects on the quality of patient care [22]. Mathematical models have also been one of the most robust ways to manage and schedule hospitals [23], [24], [25], [26], [27], [28], [29]. There are several methods in the literature for disease prediction using machine learning-based approaches. For example, a knowledge-based method for disease prediction using clustering, noise reduction, and prediction techniques was proposed by Nilashi et al. [30]. The findings revealed that the combination of noise reduction and clustering strategies based on fuzzy rules could help detect diseases from real-world medical datasets. In another study, the study results accepted the feasibility of applying various blurry approaches in the illness’s diagnostic process, providing researchers with new perspectives into what kind of diseases were most focused on it. It can help to evaluate the diagnostic dimensions that are being ignored in medical fields [31]. A method of remote control of Parkinson’s Disease progression was also proposed by Nilashi et al. [32]. The mechanism is focused on approaches to deep learning and clustering. To predict the sub-epidemic waves of the COVID-19 outbreak, Ahmadi et al. [33] introduced the generalized logistic growth model. The model simulated event scenarios of two, three, and four waves. Based on the lung x-ray image, Hassantabar et al. used a machine learning system to diagnose contaminated COVID-19 patient tissue. This result can also track and manage patients’ development in contaminated regions [34], [35].
4. Methods and materials
4.1. Generation of primary response chromosome
The chromosome in the numerical example is the result of three variables , , and . It means that first, we have zero and one as many as the matrix X, which must be a combination of j (the size of the number of provinces), b (the size of the number of beds), and i (the size of the number of patients). The same procedure applies to and . These matrices are connected horizontally, and algorithm operators are used to them. In the objective function, this sizeable horizontal matrix is first divided into three parts (depending on the number of members of the three matrices , , and ), and then each of the three parts is reshaped. For example, if there are two provinces. The number of patients in the first province is two, and the number of patients in the second province is 3, the number of beds in the first province is three, and the number of beds in the second province is 2. The number of nurses in the first province is five and the number of nurses in the second province is 4; there are three shifts and 30 days, so the chromosome is as follows:
: It becomes a cell (a cell that has two parts. The first part is proportional to the number of beds in the first province multiplied by the number of patients in the first province. The second part is similar to the second province).
| An matrix for province 1 | Two matrices for province 2 | |||
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | |||
Now the matrix is connected by the loop first to j, then to b, and then to i:
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Now it is time for the matrix. This matrix has two sections as many as the number of provinces. Each province has a three-dimensional matrix of the number of nurses * the number of services * the number of patients. Similarly, the matrix is connected to the matrix, and when it becomes a horizontal matrix, a matrix is obtained from the flat connection of two to three three-dimensional matrices.
4.2. Grasshopper Optimization Algorithm (GOA)
This algorithm, like other optimization algorithms, tries to find the optimal answer among several answers. This algorithm is derived from natural grasshopper movements. The GOA is one of the most novel and robust algorithms of optimization. The GOA uses mathematical models and imitates locust behavior in nature to solve optimization problems. The GOA algorithm was first tested in a set of issues, including CEC2005, and its quantitative and qualitative performance was evaluated and analyzed. It was then used to find the desired shape for a truss 52 times, three times truss. To indicate its use. The results also demonstrate the practicality and strength of GOA to solve real-world problems with unknown search spaces [36].
4.3. Gray Wolf Optimization algorithm (GWO)
The GWO algorithm mimics the leadership hierarchy and the gray wolf hunting system in nature. Four kinds of gray wolves, alpha, beta, delta, and omega, are used to mimic the leadership hierarchy. Often, there are three significant hunting phases: the quest for prey, siege, and attack on the target. The results show that the GWO algorithm can provide highly competitive products compared to these meta-processing processes. The GWO can be used for challenging issues with unknown search spaces [37].
4.4. Cuckoo Optimization Algorithm (COA)
The COA is one of the newest and most potent evolutionary optimization approaches, which has a more remarkable ability to find global optimal points. This algorithm simulates the behavior of cuckoo birds in nesting and spawning to solve optimization problems. The results of reviewing and reviewing various articles indicate the high efficiency of the cuckoo algorithm for solving multiple issues. The life of a family of birds called cuckoos is inspired by this algorithm. The characteristics of the bird in spawning and reproduction have motivated the emergence of this algorithm. This algorithm begins with an initial population, much as other evolutionary algorithms. The location of cuckoos is of two types: first, adult cuckoos, and second, eggs, which are the functional basis of this algorithm based on trying to survive. In this process, some are destroyed, and the best remain and migrate to a better place and start laying eggs [38].
4.5. Whale Optimization Algorithm (WOA)
WOA is a meta-optimization algorithm inspired by nature that mimics stray whales’ social behaviors and focuses on the population. The pure bubble hunting strategy boosts this algorithm. Favorite prey is whales, krill, and small fish groups. Her way of hunting is the most entertaining thing about humpback whales. This exploratory activity is referred to as the process of bubble-net eating. Near the sea’s surface, humpback whales tend to hunt a group of krill or small fish. This discovery and hunting are achieved by generating essential bubbles along a circle or paths [39].
4.6. Hybrid Salp Swarm Algorithm and Genetic Algorithm (HSSAGA)
In this article, a novel hybrid method is proposed for solving the mathematical optimization problem for the allocation of nurses to COVID-19 patients. The process is constructed by combining a salp swarm algorithm (SSA) with a Genetic algorithm (GA). In this method, firstly, the initial population of the GA algorithm is generated randomly. For selecting proper individuals or chromosomes from the people in each generation, the SSA method used its searching techniques to find the best individual to go forward generation. The pseudo-code of the presented method is given in Algorithm V.
4.7. Mathematical problem statement
Model assumptions:
-
Every province must receive all the essential expert services
-
There is a limit to the maximum leave
-
Maximum working days for nurses are limited
-
It is only planned for one ICU. (We have two wards: 1- ICU and 2- Normal hospitalization of COVID-19 patients)
| Sets: | |
| Provinces | |
| Set of patients in the province j, | |
| Set of services | |
| Set of nurses in the province j, | |
| Set of days | |
| Set of shifts | |
| Model Parameters: | |
| Total leave time for patients | |
| Waiting time of province for services | |
| Duration of activity performed by the nurse | |
| Total nursing day per month | |
| Shift length | |
| Number of provinces that receive service of | |
| Number of all patients in each province | |
| Number of Nursers type in each province | |
| Decision variables: | |
| If the patient i is assigned to bed is 1, otherwise zero. | |
| If service s is provided to the patient i by nurse is 1, otherwise zero. | |
| If nurse n is used on day in shift is 1, otherwise zero. | |
| , | The auxiliary variable of goal programming for nurses’ working days per month |
| , | The auxiliary variable of goal programming for allocating expert nurses to the provinces |
| , | The auxiliary variable of goal programming for nurse’s allocation to the ICU section |
| , | The auxiliary variable of goal programming for nurses’ working hours in each shift |
Mathematical modeling
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
The objective function of this model minimizes deviation from the desired constraints. Constraint (2) means that every nurse must have working days per month. In fact, in this constraint, we minimize overtime or unemployment in the objective function. Constraint (3) indicates the allocation of beds to patients. Constraint (4) shows the maximum waiting time for the province for services, which in the objective function, we are looking for minimizing the waiting time of each region to receive services. Constraint (5) indicates the number of hours nurses work per shift, which in the objective function, we seek to minimize the amount of unemployment in each shift. Constraints (6), (7) also indicate the type of variables.
5. Results and discussion
5.1. Data collection
In this paper, data is collected from the dataset provided by the World Health Organization and the Ministry of Health and Medical Education of Iran data center from the starting time of COVID-19 until early April 2021. Data consists of the number of COVID-19 patients for each province of Iran until experiment time consists of ICU and ordinary hospitalization patients. To allocate nurses to patients and beds number of designated hospitals, beds, and personnel for COVID-19 by the Iranian government are collected. In the experiment time, some of the nurses also are infected or died. In the presented model, this gap also is evaluated and studied the hospital needs of extra personnel. Moreover, with involved patients, the nurses working shift is scheduled to increase work performance and decrement nurse’s tiredness.
5.2. Results of nurse scheduling and allocation
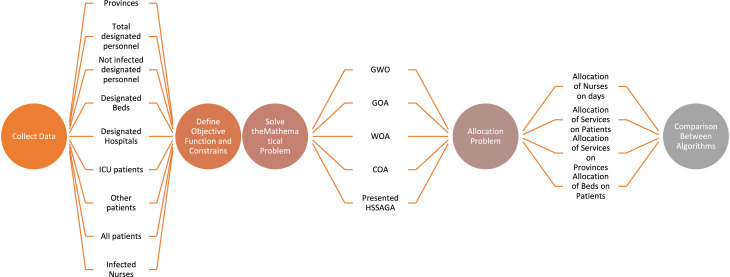
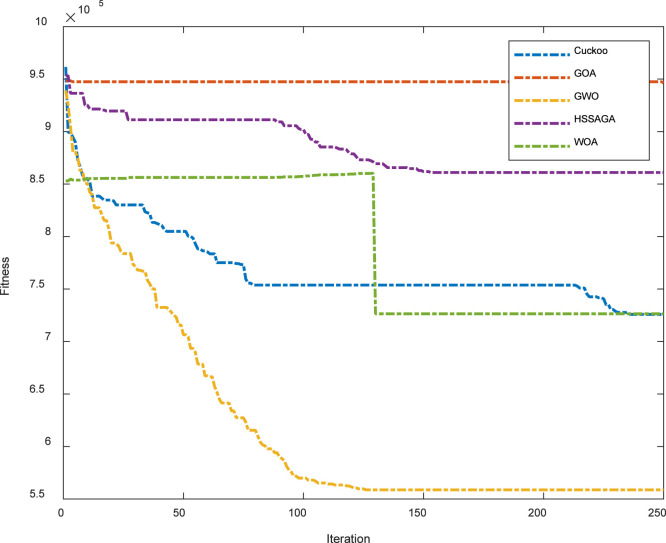
The findings of implementing the suggested model with the algorithm HSSAGA are discussed in this section. One of these models aims to assign specific nurses to a shift on a particular day. The following diagrams are related to nurses’ assignment as if nurse n is used on day d in shift k. Due to many nurses, a chart associated with the first eight nurses for each province is given (31 regions of Iran are studied). The objective function termination criterion is 10−3. The conceptual diagram is presented in Fig. 1. As seen in Fig. 2, all the algorithms’ behavior has been shown in a graphing form in 250 iterations. The GOA has shown consistent behavior for almost 250 iterations and only a small initial response to the overall movement. In the hybrid algorithm HSSAGA, the objective function has practically the same behavior and a downtrend as the COA. Each one has its optimal value if the COA response is more optimal than the hybrid algorithm HSSAGA. The WOA, after about 130 iterations, has been fixed.
Fig. 1.
The conceptual diagram of the model.
Fig. 2.
Comparison between algorithms convergences.
In the GWO, the objective function in 125 iterations is the first iteration of good descending order. It has achieved the best possible response and then continued until the end of its path has been fixed.
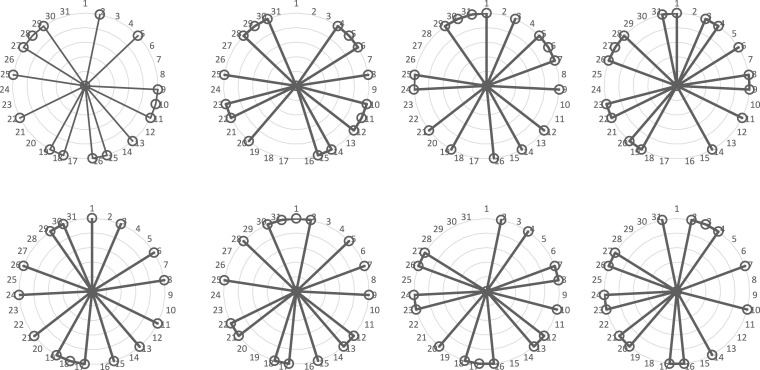
The outcomes of meta-heuristic algorithms are adaptive to their corresponding parameters. The Taguchi approach is based on the average S/N ratio for each degree of variables used to handle this sensitivity and set the initial conditions for accessing more successful solutions. Table 1 includes the optimum values of the parameters. Regarding Table 2 and the radar plot of Fig. 3, the eight selected nurses are allocated three days each month to decrease the personnel tiredness.
Table 1.
The optimum parameter levels of the algorithms.
| Algorithm | Parameter | Level 1 | Level 2 | Level 3 | Optimal value |
|---|---|---|---|---|---|
| GWO | Number of Initial populations | 30 | 40 | 50 | 40 |
| Max number of iterations | 100 | 250 | 500 | 250 | |
| GOA | Number of Initial populations | 30 | 40 | 50 | 65 |
| Max number of iterations | 100 | 250 | 500 | 250 | |
| Intensification Factor | 1 | 2 | 3 | 1 | |
| WOA | Number of Initial populations | 30 | 40 | 50 | 30 |
| Max number of iterations | 100 | 250 | 500 | 250 | |
| r1 | Random | Random | Random | Random | |
| r1 | Random | Random | Random | Random | |
| COA | Number of Initial populations | 30 | 40 | 50 | 50 |
| Max number of iterations | 100 | 250 | 500 | 250 | |
| Max number of Cuckoos at the same time | 50 | 70 | 100 | 100 | |
| Min number of eggs | 1 | 2 | 3 | 2 | |
| Max number of eggs | 2 | 4 | 6 | 4 | |
| Number of KNN cluster | 1 | 2 | 3 | 3 | |
| Lambda | 3 | 5 | 9 | 9 | |
| Control parameter of egg laying | 2 | 5 | 7 | 5 | |
| HSSAGA | Number of Initial populations | 30 | 40 | 50 | 30 |
| Max number of iterations | 100 | 250 | 500 | 100 | |
| Crossover rate | 0.3 | 0.5 | 0.7 | 0.5 | |
| Mutation rate | 0.1 | 0.2 | 0.3 | 0.3 | |
Table 2.
Allocation of first eight nurses if a nurse is used on a specific day of a month.
| Day of month | Nurse 1 | Nurse 2 | Nurse 3 | Nurse 4 | Nurse 5 | Nurse 6 | Nurse 7 | Nurse 8 | All |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 4 |
| 2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 4 |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 4 |
| 4 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 4 |
| 5 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 4 |
| 6 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 4 |
| 7 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 4 |
| 8 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 4 |
| 9 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 4 |
| 10 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 4 |
| 11 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 4 |
| 12 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 4 |
| 13 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 4 |
| 14 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 4 |
| 15 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 4 |
| 16 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 4 |
| 17 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 4 |
| 18 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 4 |
| 19 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 4 |
| 20 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 4 |
| 21 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 4 |
| 22 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 4 |
| 23 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 4 |
| 24 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 4 |
| 25 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 4 |
| 26 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 4 |
| 27 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 4 |
| 28 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 4 |
| 29 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 4 |
| 30 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 4 |
| 31 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 4 |
| Sum | 15 | 16 | 16 | 16 | 15 | 16 | 15 | 15 | |
Fig. 3.
Assign nurses if a nurse is used on a specific day of a month.
In the presented condition, each nurse only works 15 or 16 days of the month. However, each day four nurses are allocated a day. With this given condition number of nurses should be doubled to increase the performance of the personnel. The main goal is to increase the leave period for each of the nurses. It increases the leave period to 5 days in someone like a nurse of 7. Also, another goal of the proposed research model is to allocate the services provided by the nurse to the patient, whether the service s is provided by the nurse to patient or not. In other words, we should allocate expert personnel to travel each province on any day (see Table 2 for first-eighth nurses).
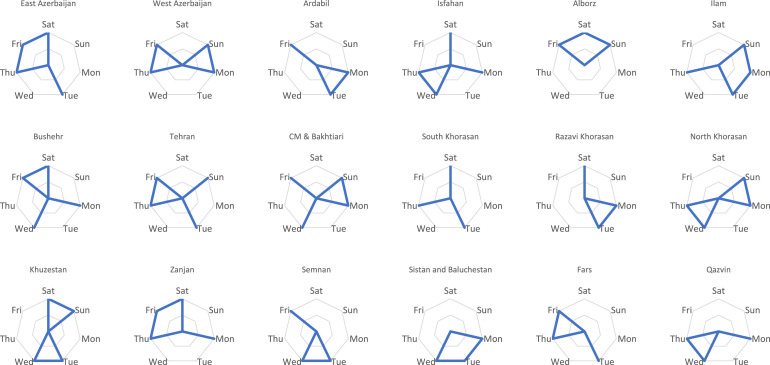
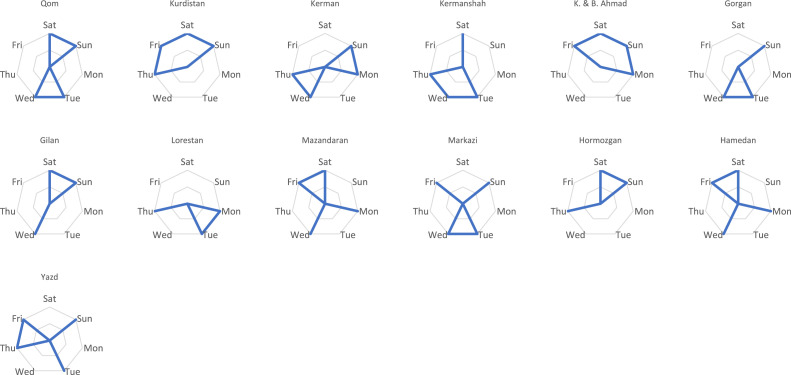
The following charts of Fig. 4 show the allocation of service s by nurse n to province i. Regarding Table 3 and Fig. 3, a total of 16 expert nurses travels to each region to provide services or supply health care requirements. In each province totally, 3 or 4 experts are existing. In this problem, each expert can be a particular service. Therefore, we tried to minimize the days’ interval that service is in a province. Another aim that the proposed model seeks to answer is to allocate nurses to the hospital ICU section if nurse i is assigned to bed b in the ICU section. Regrading overwhelming conditions of work in the ICU section in conjunction with spaces with a high rate of infection possibility, in this model, we try to minimize nurse participation in the ICU section with maximum interval shift day. Based on the result, each nurse should be two days a week in the ICU section. Moreover, the difference between their shift is maximum (two or three days) (see Table 4).
Fig. 4.
Allocation of services provided by the traveler nurse to the patients in each province.
Table 3.
Allocation of the first service provided by a specific nurse to a particular patient.
| Provinces | Saturday | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday | Sum |
|---|---|---|---|---|---|---|---|---|
| East Azerbaijan | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 4 |
| West Azerbaijan | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 4 |
| Ardabil | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 3 |
| Isfahan | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 4 |
| Alborz | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 3 |
| Ilam | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 4 |
| Bushehr | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 |
| Tehran | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 4 |
| CM & Bakhtiari | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 4 |
| South Khorasan | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 3 |
| Razavi Khorasan | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 3 |
| North Khorasan | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 4 |
| Khuzestan | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 4 |
| Zanjan | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 4 |
| Semnan | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 3 |
| S.& Baluchestan | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 3 |
| Fars | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 3 |
| Qazvin | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 3 |
| Qom | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 4 |
| Kurdistan | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 4 |
| Kerman | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 4 |
| Kermanshah | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 4 |
| K. & B. Ahmad | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 4 |
| Gorgan | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 3 |
| Gilan | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 3 |
| Lorestan | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 3 |
| Mazandaran | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 |
| Markazi | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 4 |
| Hormozgan | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 3 |
| Hamedan | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 |
| Yazd | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 4 |
| 16 | 16 | 16 | 16 | 16 | 16 | 16 | ||
Table 4.
Allocation of the first service provided by a specific bed to a particular patient.
| Nurses | Saturday | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday | Sum |
|---|---|---|---|---|---|---|---|---|
| Nurse1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 2 |
| Nurse2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse3 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 2 |
| Nurse4 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| Nurse5 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse6 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 2 |
| Nurse7 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| Nurse8 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 2 |
| Nurse9 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse10 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 2 |
| Nurse11 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| Nurse12 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse13 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 2 |
| Nurse14 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| Nurse15 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 2 |
| Nurse16 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse17 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 2 |
| Nurse18 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 2 |
| Nurse19 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 2 |
| Nurse20 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 2 |
| Nurse21 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 2 |
| Sum | 6 | 6 | 6 | 6 | 6 | 6 | 6 | – |
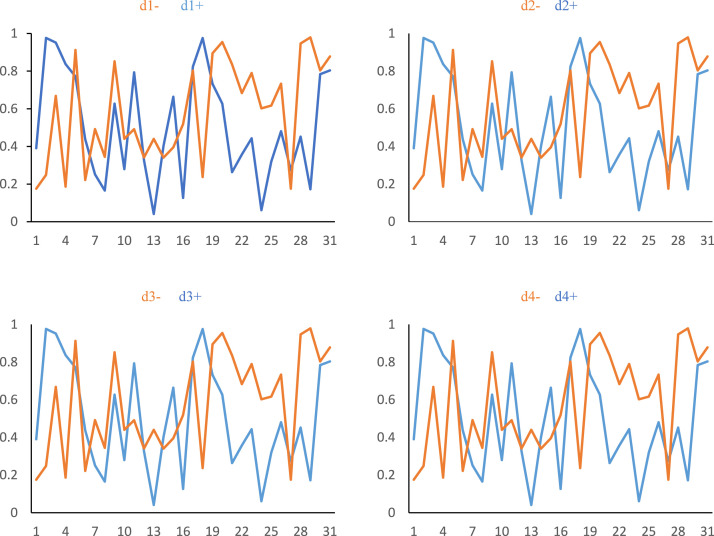
The values of auxiliary variables are illustrated in Fig. 5 for all the provinces. d1 and d1 are related to nurses scheduling a time that the results were shown in Table 2 and Fig. 3. Also, d2 and d2 are related to expert nurses’ allocation in each province, illustrated in Table 3 and Fig. 4. Finally, d3 and d4 are related to a nurse’s allocation and scheduling in the ICU section. Regarding Fig. 5, the value of the auxiliary variable has fluctuated from 0 to 1.
Fig. 5.
The auxiliary variable’s value for the process of mathematical problem solution.
This paper solved the scheduling problem using GWO, GOA, WOA, COA and presented the HSSAGA method. Now we compared the results obtained from these methods. Table 5 shows the best objective function from the five algorithms is the hybrid algorithm HSSAGA. After that, the COA and the GWO in ranks 2 and 3 are considered improved. As visible in the table, algorithms in terms of the number of function evaluations have almost the same result. The value of d1 to d4 in both algorithms has fluctuated from 0 to 1, with an average of 0.5 and a standard deviation of 0.0231.
Table 5.
Comparison between algorithms.
| Algorithm | Best objective function | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| GWO | 858742 | 0.578 | 0.504 | 0.602 | 0.521 | 0.538 | 0.588 | 0.592 | 0.578 |
| GOA | 946511 | 0.611 | 0.568 | 0.506 | 0.592 | 0.503 | 0.527 | 0.573 | 0.611 |
| WOA | 949964 | 0.539 | 0.547 | 0.503 | 0.543 | 0.581 | 0.541 | 0.616 | 0.539 |
| COA | 725864 | 0.514 | 0.546 | 0.505 | 0.538 | 0.550 | 0.561 | 0.619 | 0.514 |
| HSSAGA | 561020 | 0.586 | 0.548 | 0.597 | 0.622 | 0.601 | 0.533 | 0.592 | 0.586 |
6. Discussion
The prevalence of the COVID-19 pandemic has made the emergency departments of hospitals more crowded. However, the number of emergency departments has not increased significantly in recent years, especially in the pandemic period. The quality of services provided in the emergency department is also essential in the formal evaluation of hospitals, and the assessment of other hospital departments depends on the quorum. One of the most important indicators for evaluating the emergency department’s quality of services is nurses’ schedule to provide services (clinical, paraclinical). Scheduling refers to the number of times nurses have to work in a hospital setting. On the other hand, the high density of patients causes fatigue and disability of nurses. In other words, nurses need more time off and rest than usual. Therefore, the speed of providing services in medical centers to increase the efficiency of nurses and reduce fatigue is of particular importance.
Moreover, some of the provinces need special expert services. Therefore, optimization and scheduling of service are essential. The mathematical optimization model is a tool to predict the impact of changes in existing systems and a design tool to predict new systems’ performance. In recent years, the application of optimization in the healthcare sector has become increasingly widespread. The main reasons for this are the increasing complexity of healthcare systems, the general ability of simulation in modeling complex and uncertain systems, and the significant advancement of simulation software. However, the use of this technique in the health sector is much less than in industrial areas. An optimization is a valuable tool for accurate and evidence-based decisions. It provides remarkable results for studying and planning complex and uncertain systems that are prominent health systems’ features.
7. Conclusion
In this article, a novel model of the HSSAGA is proposed to solve nurses’ scheduling and designation. We provide three primary goals for this paper:(1) Scheduling healthcare personnel each month for increasing time offs and rising work efficiency, (2) allocating and scheduling particular expert services to each province by traveling experts to the target area, and (3) scheduling nurses to participate in the ICU overwhelming sector. This model’s objective function minimizes divergence from the optimal constraints. The constraints include working days of nurses in a month to reduce overtime or unemployment in the objective function. The allocation of beds to patients, the overall waiting time for care, the number of hours nurses work per shift are other restrictions. Any of the nurses are also infected or died during the experiment phase. This void is also assessed in the model presented, and the hospital needs of additional employees are analyzed. One of this model’s goals is to delegate a change on a given day to individual nurses. Each nurse only works 15 to 16 days a month in the proposed situation. However, each day 4 of them are assigned on a day. For this provided situation, the number of nurses should be doubled to improve the staff’s efficiency. For any of the nurses who extend the leave time to 5 days, the key aim is to increase the leave period. A total of 16 specialist nurses rotate to each province to offer services or provide health care standards depending on outcomes. In general, 3 or 4 experts are present in each region. Each specialist can be a particular service in this issue, so we tried to reduce the days the service is in a province. In this model, we aim to minimize nurse involvement in the ICU section by minimizing exhausting working environments in the ICU section combined with spaces with a high rate of probability of infection. Based on the outcome, each nurse should be in the ICU section two days a week. In comparison, the maximum difference between their changes is (two or three days). The observations on the test functions of the proposed algorithm reveal that this algorithm outperformed the state-of-the-art approaches. We suggested applying artificial intelligence and machine learning methods for scheduling problems with training ability and development for future research.
CRediT authorship contribution statement
Moein Qaisari Hasan Abadi: Writing - review & editing. Sara Rahmati: Responsible for gathering information. Abbas Sharifi: Writing - original draft. Mohsen Ahmadi: Writing - original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Funding
The funding sources was not involved in the study design, collection, analysis, or interpretation of data, writing of themanuscript, or in the decision to submit the manuscript for publication.
References
- 1.Remuzzi A., Remuzzi G. COVID-19 and Italy: what next? Lancet. 2020 doi: 10.1016/S0140-6736(20)30627-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.https://www.worldometers.info/coronavirus/ (access date 5/12/2020).
- 3.Phua J., Weng L., Ling L., Egi M., Lim C.M., Divatia … J.V., Nishimura M. Intensive care management of coronavirus disease 2019 (COVID-19): challenges and recommendations. Lancet Respir. Med. 2020 doi: 10.1016/S2213-2600(20)30161-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Singhal T. A review of coronavirus disease-2019 (COVID-19) Indian J. Pediatr. 2020:1–6. doi: 10.1007/s12098-020-03263-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. Coronavirus disease 2019 (covid-19): A perspective from china. Radiology. 2020 doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chan J.F.-W., Yuan S., Kok K.-H., To K.K.-W., Chu H., Yang J., Xing F., Liu J., Yip C.C.-Y., Poon R.W.-S., et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395:514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kanne J.P. Chest ct findings in 2019 novel coronavirus (2019-ncov) infections from wuhan, china: key points for the radiologist. Radiology. 2020 doi: 10.1148/radiol.2020200241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pan Y., Guan H. 2020. Imaging changes in patients with 2019-ncov. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ng M.-Y., Lee E.Y., Yang J., Yang F., Li X., Wang H., M.-s. Lui M., Lo C.S.-Y., Leung B., Khong P.-L., et al. Imaging profile of the covid-19 infection: radiologic findings and literature review. Radiol.: Cardiothorac. Imaging. 2020;2 doi: 10.1148/ryct.2020200034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Song F., Shi N., Shan F., Zhang Z., Shen J., Lu H., Ling Y., Jiang Y., Shi Y. Emerging 2019 novel coronavirus (2019-ncov) pneumonia. Radiology. 2020 doi: 10.1148/radiol.2020209021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang W., Tang J., Wei F. Updated understanding of the outbreak of 2019 novel coronavirus (2019-ncov) in wuhan, china. J. Med. Virol. 2020;92:441–447. doi: 10.1002/jmv.25689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X., et al. Clinical features of patients infected with 2019 novel coronavirus in wuhan, china. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carlos W.G., Dela Cruz C.S., Cao B., Pasnick S., Jamil S. Novel wuhan (2019-ncov) coronavirus. Am. J. Respir. Crit. Care Med. 2020;201:P7–P8. doi: 10.1164/rccm.2014P7. [DOI] [PubMed] [Google Scholar]
- 14.W.-j. Guan, Z.-y. Ni, Y. Hu, W.-h. Liang, C.-q. Ou, J.-x. He, L. Liu, H. Shan, C.-l. Lei, D.S. Hui, et al. Clinical characteristics of 2019.
- 15.Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y., Qiu Y., Wang J., Liu Y., Wei Y., et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in wuhan, china: a descriptive study. Lancet. 2020;395:507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang D., Hu B., Hu C., Zhu F., Liu X., Zhang J., Wang B., Xiang H., Cheng Z., Xiong Y., Zhao Y., Li Y., Wang X., Peng Z. Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus–infected pneumonia in wuhan, china. JAMA. 2020;323:1061. doi: 10.1001/jama.2020.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen X., Tian J., Li G., Li G. Initiation of a new infection control system for the COVID-19 outbreak. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30110-9. PMID: 32085850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Guan W.-J., Ni Z.-Y., Hu Y., et al. 2. Clinical characteristics of coronavirus disease 2019 in China. New Engl. J. Med. 2020 doi: 10.1056/NEJMoa2002032. Published Online First: February 28 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Han H.-R., Gleason K.T., Sun C.-A., et al. Using patient portals to improve patient outcomes: Systematic review. JMIR Hum. Fact. 2019;6 doi: 10.2196/15038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Oldenkamp J.H., 4. University of Groningen; 1996. Quality in Fives: On the Analysis, Operationalization and Application of Nursing Schedule Quality. (Ph.D. thesis) [Google Scholar]
- 21.Eichberg D.G., Shah A.H., Luther E.M., Menendez I., Jimenez A., Perez-Dickens … M., Levi A.D. Academic neurosurgery department response to COVID-19 pandemic: the University of Miami/Jackson Memorial Hospital model. Neurosurgery. 2020 doi: 10.1093/neuros/nyaa118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huang L., Lin G., Tang L., Yu L., Zhou Z. 2020. Special attention to nurses’ protection during the COVID-19 epidemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tuech J.J., Gangloff A., Fiore F.Di., Michel P., Brigand C., Slim … K., Schwarz L. Strategy for the practice of digestive and oncological surgery during the Covid-19 epidemic. J. Visceral Surg. 2020 doi: 10.1016/j.jviscsurg.2020.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Seccia R. 2020. The Nurse Rostering Problem in COVID-19 Emergency Scenario: Tech. rep. url: http://www.optimization-online.org/DB_FILE/2020/03/7712.pdf. [Google Scholar]
- 25.Mascha E.J., Schober P., Schefold J.C., Stueber F., Luedi M.M. Staffing with disease-based epidemiologic indices may reduce shortage of intensive care unit staff during the COVID-19 pandemic. Anesth. Anal. 2020 doi: 10.1213/ANE.0000000000004849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dewey C., Hingle S., Goelz E., Linzer M. 2020. Supporting clinicians during the COVID-19 pandemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Azaiez M.N., Al Sharif S.S. A 0-1 goal programming model for nurse scheduling. Comput. Oper. Res. 2005;32(3):491–507. [Google Scholar]
- 28.Bagheri M., Devin A.G., Izanloo A. An application of stochastic programming method for nurse scheduling problem in real word hospital. Comput. Ind. Eng. 2016;96:192–200. [Google Scholar]
- 29.Dodaro C., Maratea M. International Conference on Logic Programming and Nonmonotonic Reasoning. Springer; Cham: 2017. Nurse scheduling via answer set programming; pp. 301–307. [Google Scholar]
- 30.Nilashi M., bin Ibrahim O., Ahmadi H., Shahmoradi L. An analytical method for diseases prediction using machine learning techniques. Comput. Chem. Eng. 2017;106:212–223. [Google Scholar]
- 31.Ahmadi H., Gholamzadeh M., Shahmoradi L., Nilashi M., Rashvand P. Diseases diagnosis using fuzzy logic methods: A systematic and meta-analysis review. Comput. Methods Programs Biomed. 2018;161:145–172. doi: 10.1016/j.cmpb.2018.04.013. [DOI] [PubMed] [Google Scholar]
- 32.Nilashi M., Ahmadi H., Sheikhtaheri A., Naemi R., Alotaibi R., Alarood … A.A., Zhao J. Remote tracking of Parkinson’s disease progression using ensembles of deep belief network and self-organizing map. Expert Syst. Appl. 2020;159 [Google Scholar]
- 33.Ahmadi M., Sharifi A., Khalili S. Presentation of a developed sub-epidemic model for estimation of the COVID-19 pandemic and assessment of travel-related risks in Iran. Environ. Sci. Pollut. Res. 2020:1–9. doi: 10.1007/s11356-020-11644-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hassantabar S., Ahmadi M., Sharifi A. Diagnosis and detection of infected tissue of COVID-19 patients based on lung X-ray image using convolutional neural network approaches. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nasirpour M.H., Sharifi A., Ahmadi M., Ghoushchi S.J. Revealing the relationship between solar activity and COVID-19 and forecasting of possible future viruses using multi-step autoregression (MSAR) Environ. Sci. Pollut. Res. 2021:1–11. doi: 10.1007/s11356-021-13249-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Saremi S., Mirjalili S., Lewis A. Grasshopper optimisation algorithm: theory and application. Adv. Eng. Softw. 2017;105:30–47. [Google Scholar]
- 37.Mirjalili S., Mirjalili S.M., Lewis A. Grey wolf optimizer. Adv. Eng. Softw. 2014;69:46–61. [Google Scholar]
- 38.Rajabioun R. Cuckoo optimization algorithm. Appl. Soft Comput. 2011;11(8):5508–5518. [Google Scholar]
- 39.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]