Skip to main content
PMC home page
Biomedical Optics Express logoLink to Biomedical Optics Express
. 2021 Mar 2;12(4):1834–1845. doi: 10.1364/BOE.419564

Axial accuracy and signal enhancement in acoustic-resolution photoacoustic microscopy by laser jitter effect correction and pulse energy compensation

Amir Asadollahi 1, Hamid Latifi 1,2,*, Manojit Pramanik 3, Hamed Qazvini 1, Ali Rezaei 1,4, Hamed Nikbakht 1,5, Abolfazl Abedi 6
PMCID: PMC8086458  PMID: 33996201

Abstract

In recent years, photoacoustic imaging has found vast applications in biomedical imaging. Photoacoustic imaging has high optical contrast and high ultrasound resolution allowing deep tissue non-invasive imaging beyond the optical diffusion limit. Q-switched lasers are extensively used in photoacoustic imaging due to the availability of high energy and short laser pulses, which are essential for high-resolution photoacoustic imaging. In most cases, this type of light source suffers from pulse peak-power energy variations and timing jitter noise, resulting in uncertainty in the output power and arrival time of the laser pulses. These problems cause intensity degradation and temporal displacement of generated photoacoustic signals which in turn deteriorate the quality of the acquired photoacoustic images. In this study, we used a high-speed data acquisition system in combination with a fast photodetector and a software-based approach to capture laser pulses precisely in order to reduce the effect of timing jitter and normalization of the photoacoustic signals based on pulse peak-powers simultaneously. In the experiments, maximum axial accuracy enhancement of 14 µm was achieved in maximum-amplitude projected images on XZ and YZ planes with ±13.5 ns laser timing jitter. Furthermore, photoacoustic signal enhancement of 77% was obtained for 75% laser pulses peak-power stability.

1. Introduction

The photoacoustic (PA) effect was first discovered by Alexander Graham Bell over a century ago; however, this effect has attracted more attention and had applications in recent decades due to the availability of advanced short pulsed lasers, fast data acquisition (DAQ) devices, and computing capabilities. One of the major applications of using the PA effect is photoacoustic imaging (PAI), in which a light absorbing specimen is illuminated by the short laser pulse. The light absorption results in a rise in temperature leading to rapid thermoelastic expansion and consequently generation of PA waves. The detection of generated waves provides the possibility of locating initial PA wave sources, i.e., the spatial distribution of light absorbers. These absorbers could be microvasculature in tissue. This imaging method enjoys the advantages of high optical contrast as well as low acoustic scattering in soft tissue simultaneously and can be used for deep tissue imaging beyond the optical diffusion limit [1–4]. PAI can be utilized for structural imaging of vascular networks, functional imaging of the brain, and blood flow hemodynamics of the soft tissue in vivo [5,6]. PAI is divided into a number of categories, such as photoacoustic tomography (PAT), photoacoustic microscopy (PAM), and photoacoustic endoscopy (PAE) systems [7]. In PAM, the 3D images of absorbers can be directly captured by scanning the sample in confined optical illumination and acoustic detection conditions [8] without further reconstruction algorithms as used in PAT systems [9–13]. Based on the type of optical and/or acoustic focusing used, PAM systems are divided into two categories: 1) optical-resolution (OR-PAM) and 2) acoustic-resolution (AR-PAM) systems. In OR-PAM, tightly focused laser light is utilized to generate acoustic waves detected by a focused or unfocused high-frequency, broadband ultrasound transducer (UT). Alternatively, in AR-PAM, weakly focused laser pulses induce acoustic waves detected by a focused UT. Lateral and axial resolutions of both systems depend on the degree of optical or acoustic focus and the bandwidth of UT [14–16]. AR-PAM has been also used for many biomedical imaging applications [17–20].

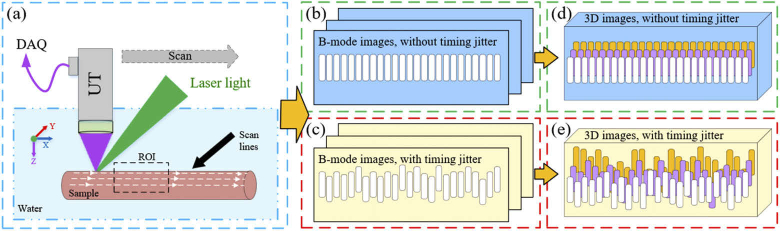
In PAI systems, light sources are often Q-switched lasers with the pulse-width of several nanoseconds. Since the lasing process initially starts by spontaneous emission, Q-switched lasers have an inevitable so-called timing jitter (TJ) noise. TJ is the variation in the output time of laser pulses after the external triggering. It can be caused by several phenomena such as the temperature fluctuations of the gain medium, response time of the electronic devices, and pump power/spectrum [21,22]. This jitter causes temporal displacement of PA signals, thereby degrading the axial accuracy of images and not allowing signals temporal averaging to increase SNR [23]. A TJ of 10 ns axially shifts the signals by approximately 15 µm (in water or soft tissue) and thus a random pattern is obtained from a smooth sample [24]. When constructing the images of maximum-amplitude projection on XZ or YZ planes (MAPxz, MAPyz), the integration of these random uneven patterns increases the sample image thickness (as illustrated in Fig. 1). In Fig. 1, (a) is an example of imaging set-up for a tube-like sample. Dashed lines on the sample indicate the direction of the scan lines to capture B-mode images which are comprised of A-mode signals. (b) and (d) are 2D B-mode and 3D images of the sample in the absence of TJ, while (c) and (e) refer to the same images with TJ. Since the sample is opaque, measured thickness is the envelope width of the generated A-mode signals and not the sample thickness.

Fig. 1.

Fig. 1.

Open in a new tab

Effect of timing jitter on photoacoustic signals, B-mode, and MAP images. The system scans the sample according to the scan lines marked on the sample. Signals affected by TJ undergo a temporal displacement and thus the constructed B-mode images will have an uneven pattern. The combination of these uneven B-mode images results in a thicker 3D or MAP images.

Although the axial resolution of PAM systems utilizing UTs with the bandwidth of 70-80% is around 30 µm, in case of imaging fine structures such as microvasculature networks, the axial accuracy and visibility of the images are degraded due to the TJ of the lasers, since the diameter and axial distance of the structures are comparable to the axial resolution of the system. Moreover, in very fast scanning OR-PAM systems for imaging fine structures where TJ is in the order of microseconds, TJ could also reduce the accuracy of MAP images on the XY plane (MAPxy) and lateral resolution due to the mismatch between the scanning and laser excitation positions at the XY coordinate. This is only observable in the fast scanning axis [25]. Proposed solutions for TJ problem are discussed later in this section.

Another problem with the Q-switched light sources is the laser pulses peak-power (PP) variations. Since the amplitude of generated PA signals is related to the pulse energies based on the equation p0=ΓμaF where p0 is the initial induced pressure (pa), Γ the dimensionless Grüneisen coefficient, μa the absorption coefficient (cm−1), and F the local light fluence(J/cm2). PP variations can randomly change the amplitude of acquired signals. In the case of quantitative and functional imaging, where multiple wavelengths are used to measure oxygen saturation (SO2), PP variations can have a major effect on the precision of images [26]. Therefore, accurate measurement of pulse PP is vital for normalization of the captured signals and thus improving PA signals strength. Two solutions could be used to reduce the effect of PP variations: 1) utilizing highly stable lasers and 2) measuring PP variations and normalization of signals. The first solution requires expensive lasers while the second one needs fast photodetectors (PD) and data acquisition (DAQ) systems.

As regards the TJ problem, two main solutions have been offered: 1) reducing TJ in the lasers and 2) compensating for the TJ effect in PA signals. Khurgin et al. reduced the TJ of a passively Q-switched laser by composite pumping. Two main limitations with this method were low repetition-rate and a high TJ of about 500 ns [21,27]. Using a combined active and passive Q-switched laser, Wang et al. reduced the TJ of a passively Q-switched laser from 58 µs to less than 400 ns. As for an actively Q-switched laser, they could reduce the TJ to below 200 ns at a repetition-rate of 5 kHz [28,29]. In another study, Cole et al. reduced the TJ of a passively Q-switched laser by direct bleaching of saturable absorber from 241 ns to 20 ns at the repetition-rate of 10 Hz [22]. In comparison to other works, they could reduce TJ to a greater extent, yet the repetition-rate was far beyond what is needed in scanning PAM systems. With regard to reducing the effect of laser TJ on PA signals, several methods have been used. One method was to use an external trigger source to synchronize DAQ and an actively Q-switched laser [30–32]. This, however, merely compensates for the delay between laser triggering and pulse generation, and thus there still will be TJ noise due to uncertainty about pulse generation after triggering the laser. In some studies, laser pulses were captured by a PD whose output was used to trigger DAQ and in some studies to estimate PP variation [33–35]. In this technique, the clock and sampling frequencies of most DAQ systems were not high enough and reduced the timing accuracy of triggering as well as the accuracy with which PP variation is measured for short pulses [36]. In a super-resolution photoacoustic microscopy, Kim et al. used PD and DAQ with an increased sampling-rate of 500 MS/s to further enhance the timing accuracy of triggering and capturing pulse-to-pulse energy variations [37]. Using PA signals generated from transducer surface for temporal alignment of PA signals was another proposed technique to compensate for the laser TJ effect. In an acoustic radiation force impulse (ARFI) imaging technique for measuring cell mechanics, Kang et al. used the PA signals arrival time generated by the ultrasonic transducer surface to align displacement signals of the sample [38]. Despite its strengths in PAM systems, this method is only applicable to thin and transparent samples in the transmission mode and cannot be used in bulky samples or in vivo experiments. In another study, Zhang et al. used a similar technique in a super-resolution photoacoustic tomography system [39]. They utilized DAQ with the sampling-rate of 40 MS/s in the set-up. Since the low sampling-rate of the DAQ does not allow for accurate measurement of TJ and PP variation, this method cannot be applied to high-resolution PAM systems.

In this study, we proposed and experimentally demonstrated direct and simultaneous measurement of laser pulses’ PP variation and their temporal location using a fast PD and custom-built high sampling-rate DAQ in an AR-PAM system. By applying timing jitter effect correction (TJEC) and peak-power compensation (PPC) for all signals prior to constructing 3D PA images, a significant improvement was achieved regarding the axial accuracy and intensity of B-mode images as well as MAPxz and MAPyz images. This method is not limited to AR-PAM and can be applied to other PAI systems, including OR-PAM, PAT, and PAE.

2. Methods

2.1. Experimental set-up

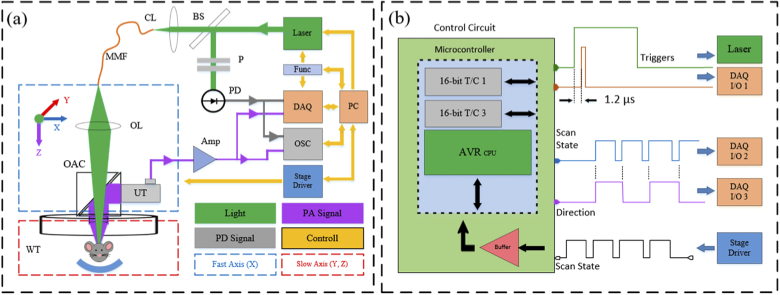
The block diagram of the AR-PAM system is shown in Fig. 2(a). An actively Q-switched laser (MSL-AO-532-500μJ, CNI Lasers) with the wavelength of 532 nm, pulse-width of 8 ns, and repetition rate of 1-5 kHz was used as the light source. The laser output was coupled to a multi-mode fiber (M29L05 - Ø600 µm, 0.39 NA, Thorlabs) using a coupling lens (focal length = 50 mm). A small portion of laser light was directed toward a fast PD (Silicon PIN Detector, 818-BB-22, Newport) by a beam splitter in order to achieve TJEC and PPC. In addition, we placed a pair of polarizers in front of the PD to control the energy of the incident light and prevent saturation or damage. PD can be placed before or after coupling lens. The output of multi-mode fiber was focused on the sample by an objective lens (focal length = 50 mm) after passing through an opto-acoustic-combiner comprised of two right angle prisms filled with silicon oil [40]. Silicon oil serves as the index matching material for the laser light and as the reflective interface for the PA waves. Generated PA waves are detected by a UT (V214-BB-RM, 50 MHz, Olympus) attached to the right-angle prisms by epoxy resin (G14250, General Purpose, Thorlabs). An acoustic lens (LC4573, f = -10.0 mm, Ø6 mm, UV Fused Silica, Plano-Concave, Thorlabs) was also glued on the bottom of opto-acoustic-combiner using UV-curing adhesive (UV 30-24, LOXEAL Engineering Adhesives) to collect acoustic signals from a focused area. We employed a water tank as the acoustic coupling media with a thin transparent and flexible membrane at its center between the sample and system. Furthermore, a motorized XYZ stage comprised of fast (X direction) and slow-scanning-stages (Y and Z direction) was utilized for XY scanning of the system in a triangular pattern [41]. The fast-scanning-stage scans the imaging head along the X direction whereas the slow-scanning-stages scan both the water tank and the sample along the Y and Z directions. Acquired PA signals along with the laser pulse signals coming from PD are visualized by an oscilloscope (GDS-2304A, 2GS/s, 4Channel, GWINSTEK) and captured by the DAQ.

Fig. 2.

Fig. 2.

Open in a new tab

Block diagram of the imaging system and the control circuit. (a) Imaging System and (b) Control Circuit. Abbreviations: personal computer (PC), control circuit (Func), data acquisition card (DAQ), oscilloscope (OSC), fast photodetector (PD), polarizers (P), beam splitter (BS), coupling lens (CL), multi-mode fiber (MMF), objective lens (OL), opto-acoustic combiner (OAC), ultrasonic transducer (UT), water tank (WT), amplifiers (Amp), DAQ general-purpose input/output (DAQ I/O)

2.2. Data acquisition

A home-made control circuit includes an 8-bit microcontroller (Atmega2560, microchip) with 16-bit timer/counters (T/C) generating two PWM pulses at 1 kHz is used to simultaneously control the laser and DAQ. The duty-cycle of PWM pulses was 20% and 0.1%, respectively. Figure 2(b) illustrates the control circuit and both PWM pulses. The delay of about 1.2 µs was merely used to compensate for the delay between the laser triggering and pulse generation and not for correcting the TJ effect. A signal from the stage is read by the microcontroller to determine the scan state of the stage (High/Low) and is then converted to two signals one of which still indicating the scan state of the stage and the other indicating the scan direction. The DAQ was a 2-channel, 12-bit resolution, and 1.8 GS/s simultaneous-sampling custom-built card (Xilinx Kintex-7 FPGA). The output of UT was amplified by two cascade amplifiers (ZFL-500-LN, 0.1-500MHz, 24dB, Mini-Circuits) along with laser pulse signals from PD were captured with desired durations and digitized by DAQ. Amplifiers were supplied with batteries to eliminate electronic noises from switching power supplies. Also, it was assured that impedance mismatching and external noises in electronic signal transmission lines did not occur. The signals were saved as a single binary file for the entire scan of the sample on a personal computer (CPU: Intel corei9-9900k, Ram: 32 GB). This binary file contains information about the direction of the scan provided by the microcontroller, as well as PD and PA signals for any XY scan location/pixel. PD signals are used for TJEC and PPC of PA signals at the processing stage. Further, the directional information is utilized for rearranging 1D signals to 3D PA data.

2.3. Data processing

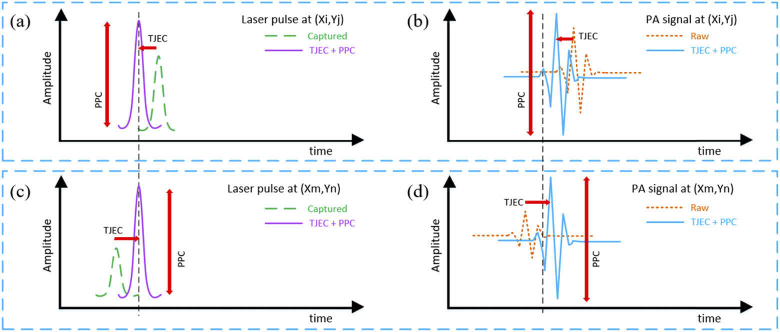
A C-Sharp (C#) analysis platform was prepared in the Visual Studio (Microsoft Visual Studio 2015) environment. Parallel and multi-thread processing were utilized in the platform to have good performance in loading and processing the large raw data. At first, the raw data is loaded and the PPC is applied to the data based on the PP of laser pulses. Next, TJEC is executed on PA signals by shifting/aligning signals based on the temporal location of laser pulses. Methods of PPC and TJEC are illustrated in Fig. 3 schematically. Figure 3(a, b) and (c, d) are laser pulses and PA signals for two specific locations/pixels, respectively. Based on the temporal location of the laser pulses and their PP, TJEC by realigning signals and PPC by correcting signals amplitudes were executed on signals. In Fig. 3, dashed lines refer to acquired laser pulses and PA signals, and solid lines illustrate corrected signals. Bandpass filtering to eliminate out-of-range frequencies (noise reduction), Hilbert transformation to calculate PA signals envelope, down-sampling to reduce the size of final images, preparation of 2D B-mode images/slices and MAPs on different planes, as well as color-coding were performed in the main processing stage. Further, 16-bit grayscale images were used in the analysis instead of 8-bit mapped images to maintain vertical voltage resolution of the captured PA and PD signals. For a 25-square mm area with a depth of 3 mm and step size of 10 µm, the size of each binary file was approximately 2.6 GB. The whole processing procedure took 30 to 50 seconds depending on the setting.

Fig. 3.

Fig. 3.

Open in a new tab

Method of timing jitter effect correction and peak-power compensation. (a, b) and (c, d) are the laser pulse and the PA signal in location (Xi,Yj) and (Xm,Yn). Dashed signals and solid lines indicate captured signals and corrected signals, respectively.

3. Results and discussion

3.1. System performance

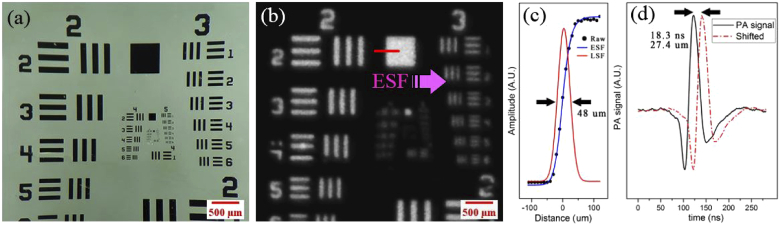
In order to examine the system performance and analysis platform, the PA image of a USAF 1951 resolution test target was captured. Figure 4(a, b) illustrates the photograph of the target taken by a stereo microscope and the constructed MAPxy image, respectively. Figure 4(c) shows the intensity profile, edge-spread-function (ESF), and line-spread-function (LSF) for the edge of the square indicated by the red line in Fig. 4(b). The width of LSF, which is the lateral resolution of the system, was measured to be 48 µm. Figure 4(d) shows the simulated photoacoustic shifted signals and indicates the possibility of distinguishing two separate absorbers within an axial distance of 27.4 µm. By using very small samples such as gold nanoparticles, the measured axial resolution of the system can even be better. The obtained results is deemed satisfactory considering the lateral resolution of such imaging systems [8].

Fig. 4.

Fig. 4.

Open in a new tab

Photoacoustic imaging results of USAF 1951 resolution test target. (a) shows the photograph of the resolution target taken by a stereo microscope, (b) the photoacoustic MAPxy image of the sample captured by the AR-PAM system, (c) the ESF and LSF graphs of the edge of the square on the test target, and (d) the simulated photoacoustic shifted signals.

3.2. Effect of laser timing jitter and peak-power variation on system resolution

The lateral resolution of an AR-PAM system can be calculated theoretically using the equation RL=0.72λ/NA, where λ is the acoustic wavelength and NA the numerical aperture of the acoustic lens [14]. Empirically, the lateral resolution of the system can be measured by imaging a small sample or a sharp edge in the system’s focus and calculating ESF as well as LSF. The width of the LSF will be the lateral resolution of the system. Based on the equation and also the fact that temporal displacement of the signals doesn’t affect the lateral distribution of the signals due to TJ, the lateral resolution will not be disturbed by TJ of the laser pulses. PP variations could make the profile of ESF and LSF noisy but smoothing or fitting ESF by a Sigmoid-like function and LSF by a Gaussian-like function eliminates the effect of PP variations on lateral resolution measurement.

The axial resolution of the AR-PAM system is calculated by the equation RA=0.88c/BW, where c stands for the speed of acoustic waves in the medium and BW for the frequency bandwidth of the transducer [14]. In practice, axial resolution is measured by axial FWHM of the B-mode image of a fine sample, such as a nanoparticle which is the FWHM of its PA signal. Based on the axial resolution equation and due to the fact that the temporal/axial displacement of the signals has no effect on the FWHM of the signals or B-mode images, the axial resolution of the system is the same regardless of TJ. PP variations (similar to the case of lateral resolution) could only decrease PA signals amplitude. Since the amplitude of the signal envelope (as a Gaussian-like function) has no considerable effect on the FWHM of the envelope, the axial resolution is not degraded due to PP variations.

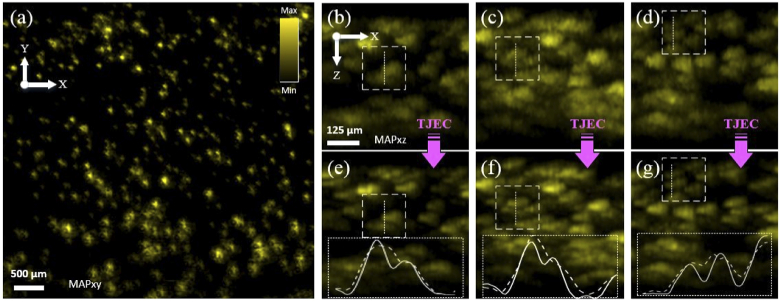
TJ affects the PA image axial accuracy when constructing 3D or MAPxz/MAPyz images from B-mode images. First, for small samples such as microvascular networks, structures with a small distance in depth are combined in the images. Second, as a result of this combination and also the axial displacement of signals in B-mode images, the thickness of samples in the images increases. To show this in practice, tiny laser-jet printer toner particles immobilized on a glass slide were imaged. To immobilize particles on the glass slide, a small amount of toner was solved in 70% (v/v) isopropyl alcohol and distilled water solution and then sprayed on the glass slide. It was left to dry at the room temperature and then airflow of approximately 300 °C was applied on the surface of the glass slide using a heat gun. After the preparation process was completed, the sample was submerged in the water tank and imaged at an inclined angle to have particles in different positions close to the focus of the system. Figure 5 illustrates the results. Figure 5(a) shows the MAPxy image of the toner sample, in which the presence of particles in different system focus positions is clear. TJ had no effect on the MAPxy image since it was responsible only for the temporal/axial displacement of the signals. Figure 5(b-d) are the MAPxz images of the sample with TJ. Figure 5(e-g) are the corresponding images following TJEC. In these images, the graphs inside dotted boxes show the intensity profiles of raw and corrected images over dotted lines. Dashed graphs correspond to raw images and solid graphs to corrected images. The analogy of the images and graphs with TJ and corrected ones indicates two points. First, mixing is eliminated and the visibility of images is enhanced. Second, the thickness of particles is decreased due to TJEC

Fig. 5.

Fig. 5.

Open in a new tab

Effect of Laser Timing Jitter and Peak-Power Variation on System Axial Accuracy. (a) is the MAPxy image of the toner sample immobilized on a glass slide and imaged at an inclined angle. (b-d) are MAPxz images of the sample with TJ and (e-g) are the corresponding TJ corrected images. Dashed boxes in two image groups show the same locations before and after TJEC.

3.3. Quantitative investigation of impact of laser TJEC and PPC

For a better and quantitative evaluation of the impact of TJEC and PPC, three sets of experiments with different samples including surgical blade, human black hair, and floppy disk were conducted. In all the experiments, an area of approximately 25 square mm with 3 mm in depth was imaged with the laser repetition-rate of 1 kHz. The fast scanning stage speed was 10 mm/s and the scanning and data acquisition lasted 4.2 minutes for the 10 µm step size. Since the validation of the aforementioned corrections in different system conditions is crucial, three experiments in random laser states (warm-up times and energies) were carried out; thus, TJs and laser stability/PP variations were different. Additionally, samples were imaged in different positions of the system focus. Figure 6–8 illustrate the obtained results.

Fig. 6.

Fig. 6.

Open in a new tab

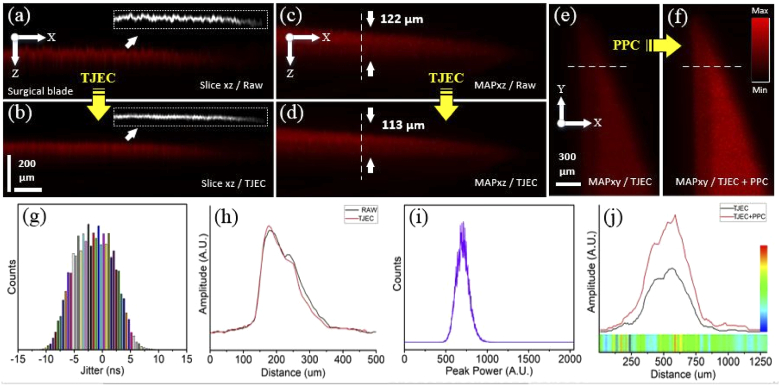
Results of timing jitter effect correction and pulse peak-power compensation for the PA images of the surgical blade sample. (a, b) are the B-mode images of raw and TJ effect corrected signals and their corresponding surface edges, (c, d) the MAPxz images of raw and TJ effect corrected signals, and (e, f) the MAPxy images of TJ effect corrected and TJ effect corrected plus PP compensated signals. (g, i) illustrate the laser TJ and PP histograms and (h, j) are intensity profiles on the dashed lines in (c, d) and (e, f). The horizontal colored ribbon in (j) indicates the PP enhancement factor for any pixel and the vertical color-bar is the scale-bar of the PP enhancement factor.

Fig. 8.

Fig. 8.

Open in a new tab

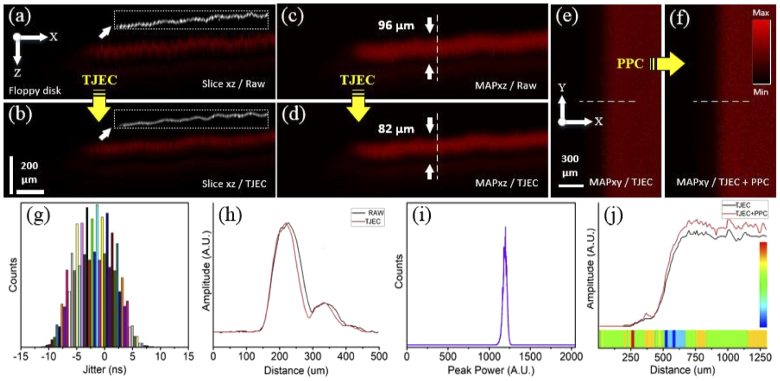
Results of timing jitter effect correction and pulse peak-power compensation for the PA images of the floppy disk sample. (a, b) are the B-mode images of raw and TJ effect corrected signals and their corresponding surface edges, (c, d) the MAPxz images of raw and TJ effect corrected signals, and (e, f) the MAPxy images of TJ effect corrected and TJ effect corrected plus PP compensated signals. (g, i) illustrate the laser TJ and PP histograms and (h, j) are intensity profiles on the dashed lines in (c, d) and (e, f). The horizontal colored ribbon in (j) indicates the PP enhancement factor for any pixel and the vertical color-bar is the scale-bar of the PP enhancement factor.

Figure 6 shows the PA imaging results for the surgical blade in different views and modes. In this experiment, the imaging system was slightly out of focus, and maximum TJ and peak-power stability (PPS) of the laser were ±12.3 ns and 75%, respectively. Histograms of the laser TJ and PP are illustrated in Fig. 6(g) and (i). Laser PPS was described using the equation PPS= (100 - ΔI/Ic* 100), where ΔI is the FWHM of the laser PP histogram and Ic its center intensity in Fig. 6(h). Figure 6(a) and (b) are the B-mode images of raw and TJ effect corrected signals. The conversion of random and uneven pattern to a smooth one is clear in these images after TJEC. In Fig. 6(a, b), images in dotted boxes are the edge of corresponding image surfaces extracted by ImageJ and LabVIEW. Surface profiles were generated from edge images and the deviation from mean profiles was calculated. The standard deviations of the profiles were 0.56 and 0.3 for raw and corrected images, respectively. There was an enhancement of 46% in the smoothness of surfaces. Figure 6(c) and (d) show the MAPxz images of raw and TJ effect corrected signals. By plotting the intensity profile for Fig. 6(c) and (d) on the dashed lines, the width of the MAPxz for the surgical blade sample was measured 122 and 113 µm (Fig. 6(h)). Axial accuracy enhancement of 9 µm in the MAPxz image was obtained after TJEC. Figure 6(e) and (f) are the MAPxy images of the TJ effect corrected and the TJ effect corrected plus PP compensated signals. As indicated in Fig. 6(j), plotting the intensity profile on the dashed lines in (e) and (f) results in an increase of 45-113% in the intensity of the image. The horizontal colored ribbon in (j) indicates the PP enhancement factor for any pixel on the dashed lines and the vertical color-bar is its scale-bar. This ribbon indicates that the intensity enhancement is not the same for all signals/pixels and that it depends on the PP of the laser pulse in that specific pixel. One-by-one comparisons of the whole pixels of both MAPxy images in Fig. 6(e) and (f) indicated that the mean and maximum enhancement after PPC were 77% and 180%, respectively. The detailed enhancement factors statistics are summarized in Table 1.

Table 1. Different intensity enhancement factors statistics for the blade sample.

Enhancement Mean Minimum Maximum Standard deviation
Over the dashed lines 74% 45% 113% 14
Whole MAP images 77% 0% 180% 20
Open in a new tab

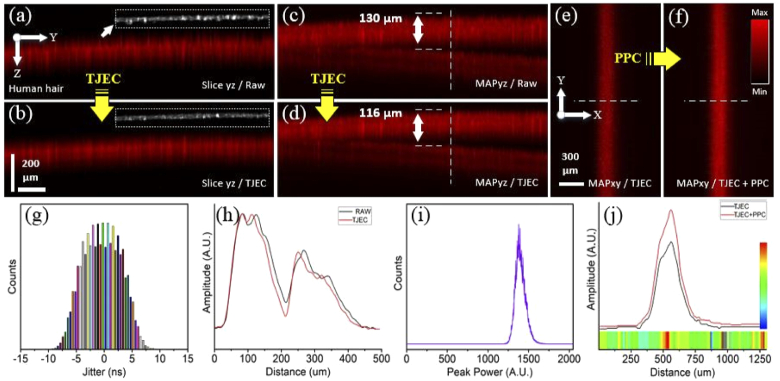
The results obtained for the human black hair sample are demonstrated Fig. 7. The hairs were fixed on a heavy metal ring prior to imaging in order to be mechanically stable during scanning. Also, imaging was performed in an out-of-focus system configuration; that is, the out-of-focus state of the system in this experiment was adjusted to a greater extent compared to the previous one. Here, the TJ and PPS of the laser were ±11.4 ns and 90%. The standard deviations of surface profiles were 2.56 and 1.81 for raw and corrected images, respectively, and an enhancement of 29% in the smoothness of B-mode images was obtained. Axial accuracy enhancement of 14 µm in the MAPyz image after TJEC and an increase of 10-48% in the intensity of the pixels following PPC on the dashed lines were obtained. For the whole pixels of the MAPxy images, a mean and maximum enhancement of 30% and 64% were yielded. Further information on the enhancement factors after PPC can be found in Table 2.

Fig. 7.

Fig. 7.

Open in a new tab

Results of timing jitter effect correction and pulse peak-power compensation for the PA images of the human hair sample. (a, b) are the B-mode images of raw and TJ effect corrected signals and their corresponding surface edges, (c, d) the MAPxz images of raw and TJ effect corrected signals, and (e, f) the MAPxy images of TJ effect corrected and TJ effect corrected plus PP compensated signals. (g, i) illustrate the laser TJ and PP histograms and (h, j) are intensity profiles on the dashed lines in (c, d) and (e, f). The horizontal colored ribbon in (j) indicates the PP enhancement factor for any pixel and the vertical color-bar is the scale-bar of the PP enhancement factor.

Table 2. Different intensity enhancement factors statistics for the hair sample.

Enhancement Average Minimum Maximum Standard deviation
Over the dashed lines 29% 10% 48% 6
Whole MAP images 30% 0% 64% 6
Open in a new tab

Figure 8 shows the results of the experiment using the floppy disk sample. Here, imaging was performed in the system focus, and the TJ and PPS of the laser were ±13.5 ns and 95%, respectively. The standard deviation of surface profiles were 0.53 and 0.26 for raw and corrected images, respectively, and an enhancement of 50% in the smoothness of B-mode images was obtained. Axial accuracy enhancement of 14 µm in the MAPxz image and intensity enhancement of 6-14% were obtained. The mean and maximum intensity enhancement for the whole area of MAPxy images were measured 11% and 23%. In this experiment, signal intensity enhancement was smaller than previous ones due to better stability of the laser. Table 3 summarizes additional information about the intensity enhancement due to PPC.

Table 3. Different intensity enhancement factors statistics for the floppy disk sample.

Enhancement Average Minimum Maximum Standard deviation
Over the dashed lines 10% 6% 14% 1.4
Whole MAP images 11% 0% 23% 2.6
Open in a new tab

4. Conclusion

In this study, the influence of laser timing jitter effect correction (TJEC) and pulse peak-power compensation (PPC) in an acoustic-resolution photoacoustic microscopy (AR-PAM) system were investigated. The effect of TJEC and PPC was verified by imaging different samples in different conditions in terms of timing jitters, peak-powers, and systems focus. It was found that our proposed method improved the axial accuracy and mean intensity of acquired photoacoustic B-mode and MAP images by 14 µm and 77%, respectively. Capturing laser pulses with a high temporal resolution, applying TJEC and PPC, and obtaining high processing performance were among the main challenges. To capture laser pulses precisely, a high-speed custom-build DAQ system and photodetector were employed. To have more effective processing performance and to handle big captured data more efficiently, an analysis platform was prepared using C#, which is a fast, fully object-oriented, and statically-typed compiled language. Moreover, parallel and multi-thread processing was used to accelerate processing procedures. Further efforts could be using CUDA supported graphic cards to have an enhanced parallel GPU computing power as well as using processing power capabilities of FPGAs of DAQs which seems to be vital for the clinical application of the photoacoustic imaging systems. The proposed method can be used in multi-wavelength functional and quantitative imaging of living samples where the laser pulse intensities need to be measured accurately. There are no limitations in the application of the method in OR-PAM, PAT, and PAE imaging systems.

Acknowledgments

The authors would like to thank Dr. Mohammad Sadegh Feiz from Shahid Beheshti University, Tehran, Iran for his helpful comments during conducting experiments related to the toner test.

Disclosures

The authors declare that there are no conflicts of interest related to this article.

Data availability

The data that support the findings of this study are available from the corresponding author on request.

References

  • 1.Omar M., Aguirre J., Ntziachristos V., “Optoacoustic mesoscopy for biomedicine,” Nat. Biomed. Eng. 3(5), 354–370 (2019). 10.1038/s41551-019-0377-4 [DOI] [PubMed] [Google Scholar]
  • 2.Upputuri P. K., Pramanik M., “Recent advances toward preclinical and clinical translation of photoacoustic tomography: a review,” J. Biomed. Opt. 22(4), 041006 (2016). 10.1117/1.JBO.22.4.041006 [DOI] [PubMed] [Google Scholar]
  • 3.Wang L. V., Yao J., “A practical guide to photoacoustic tomography in the life sciences,” Nat. Methods 13(8), 627–638 (2016). 10.1038/nmeth.3925 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Das D., Sharma A., Rajendran P., Pramanik M., “Another decade of photoacoustic imaging,” Phys. Med. Biol. 66, 05TR01 (2021). 10.1088/1361-6560/abd669 [DOI] [PubMed] [Google Scholar]
  • 5.Li L., Zhu L., Ma C., Lin L., Yao J., Wang L., Maslov K., Zhang R., Chen W., Shi J., Wang L. V., “Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution,” Nat. Biomed. Eng. 1(1), 0001–11 (2017). 10.1038/s41551-016-0001 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Wang L. V., “Multiscale photoacoustic microscopy and computed tomography,” Nat. Photonics 3(9), 503–509 (2009). 10.1038/nphoton.2009.157 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Hu S., Wang L. V., “Photoacoustic imaging and characterization of the microvasculature,” J. Biomed. Opt. 15(1), 011101 (2010). 10.1117/1.3281673 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Moothanchery M., Pramanik M., “Performance characterization of a switchable acoustic resolution and optical resolution photoacoustic microscopy system,” Sensors 17(2), 357 (2017). 10.3390/s17020357 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Deán-Ben X. L., Razansky D., “Optoacoustic image formation approaches—a clinical perspective,” Phys. Med. Biol. 64(18), 18TR01 (2019). 10.1088/1361-6560/ab3522 [DOI] [PubMed] [Google Scholar]
  • 10.Poudel J., Lou Y., Anastasio M. A., “A survey of computational frameworks for solving the acoustic inverse problem in three-dimensional photoacoustic computed tomography,” Phys. Med. Biol. 64(14), 14TR01 (2019). 10.1088/1361-6560/ab2017 [DOI] [PubMed] [Google Scholar]
  • 11.Pramanik M., “Improving tangential resolution with a modified delay-and-sum reconstruction algorithm in photoacoustic and thermoacoustic tomography,” J. Opt. Soc. Am. A 31(3), 621 (2014). 10.1364/JOSAA.31.000621 [DOI] [PubMed] [Google Scholar]
  • 12.Huang C., Wang K., Nie L., Wang L. V., Anastasio M. A., “Full-wave iterative image reconstruction in photoacoustic tomography with acoustically inhomogeneous media,” IEEE Trans. Med. Imaging 32(6), 1097–1110 (2013). 10.1109/TMI.2013.2254496 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Gutta S., Kalva S. K., Pramanik M., Yalavarthy P. K., “Accelerated image reconstruction using extrapolated Tikhonov filtering for photoacoustic tomography,” Med. Phys. 45(8), 3749–3767 (2018). 10.1002/mp.13023 [DOI] [PubMed] [Google Scholar]
  • 14.Jeon S., Kim J., Lee D., Baik J. W., Kim C., “Review on practical photoacoustic microscopy,” Photoacoustics 15, 100141 (2019). 10.1016/j.pacs.2019.100141 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Yao J., Wang L. V., “Photoacoustic microscopy,” Laser Photon. Rev. 7(5), 758–778 (2013). 10.1002/lpor.201200060 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Moothanchery M., Pramanik M., “Combined optical and acoustic resolution photoacoustic microscopy,” Photons Plus Ultrasound Imaging Sens. 2017 10064, 100644P (2017). 10.1117/12.2251258 [DOI] [Google Scholar]
  • 17.Moothanchery M., Seeni R. Z., Xu C., Pramanik M., “In vivo studies of transdermal nanoparticle delivery with microneedles using photoacoustic microscopy,” Biomed. Opt. Express 8(12), 5483 (2017). 10.1364/BOE.8.005483 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Park K., Kim J. Y., Lee C., Jeon S., Lim G., Kim C., “Handheld photoacoustic microscopy probe,” Sci. Rep. 7(1), 13359 (2017). 10.1038/s41598-017-13224-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Chuangsuwanich T., Moothanchery M., Yan A. T. C., Schmetterer L., Girard M. J. A., Pramanik M., “Photoacoustic imaging of lamina cribrosa microcapillaries in porcine eyes,” Appl. Opt. 57(17), 4865 (2018). 10.1364/AO.57.004865 [DOI] [PubMed] [Google Scholar]
  • 20.Estrada H., Turner J., Kneipp M., Razansky D., “Real-time optoacoustic brain microscopy with hybrid optical and acoustic resolution,” Laser Phys. Lett. 11(4), 045601 (2014). 10.1088/1612-2011/11/4/045601 [DOI] [Google Scholar]
  • 21.Khurgin J. B., Jin Feng, Solyar G., Wmg Chen-Chia, Trivedi S., “Timing jitter reduction in diode pumped passively Q-switched laser with composite pumping pulses,” in IEEE Cat. No.01CH37170 (IEEE, 2001), pp. 532–533. [Google Scholar]
  • 22.Cole B., Goldberg L., Trussell C. W., Hays A., Schilling B. W., McIntosh C., “Reduction of timing jitter in a Q-Switched Nd:YAG laser by direct bleaching of a Cr4+:YAG saturable absorber,” Opt. Express 17(3), 1766 (2009). 10.1364/OE.17.001766 [DOI] [PubMed] [Google Scholar]
  • 23.Kruizinga P., “Contrast enhancement in photoacoustic imaging: a multi-dimensional approach,” Delf University of Technology; (2010). [Google Scholar]
  • 24.Li M., Chen J., Wang L., “High acoustic numerical aperture photoacoustic microscopy with improved sensitivity,” Opt. Lett. 45(3), 628 (2020). 10.1364/OL.384691 [DOI] [PubMed] [Google Scholar]
  • 25.Hajireza P., Forbrich A., Zemp R., “In-Vivo functional optical-resolution photoacoustic microscopy with stimulated Raman scattering fiber-laser source,” Biomed. Opt. Express 5(2), 539 (2014). 10.1364/BOE.5.000539 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Bi R., Dinish U. S., Goh C. C., Imai T., Moothanchery M., Li X., Kim J. Y., Jeon S., Pu Y., Kim C., Ng L. G., Wang L. V., Olivo M., “In vivo label-free functional photoacoustic monitoring of ischemic reperfusion,” J. Biophotonics 12(7), e201800454 (2019). 10.1002/jbio.201800454 [DOI] [PubMed] [Google Scholar]
  • 27.Khurgin J. B., Jin F., Solyar G., Wang C.-C., Trivedi S., “Cost-effective low timing jitter passively Q-switched diode-pumped solid-state laser with composite pumping pulses,” Appl. Opt. 41(6), 1095 (2002). 10.1364/AO.41.001095 [DOI] [PubMed] [Google Scholar]
  • 28.Wang X., Xu Z., “Timing jitter reduction and single-frequency operation in an acousto-optic Q-switched Cr,Nd:YAG laser,” Appl. Opt. 45(33), 8477–8483 (2006). 10.1364/AO.45.008477 [DOI] [PubMed] [Google Scholar]
  • 29.Xue-Jun W., Zu-Yan X., “Timing jitter and pulse width reduction in a hybrid q -switched Cr,Nd:YAG laser,” Chinese Phys. Lett. 23(7), 1800–1802 (2006). 10.1088/0256-307X/23/7/040 [DOI] [Google Scholar]
  • 30.Zemp R. J., Song L., Bitton R., Shung K. K., Wang L. V., “Realtime photoacoustic microscopy in vivo with a 30-MHz ultrasound array transducer,” Opt. Express 16(11), 7915 (2008). 10.1364/OE.16.007915 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Harrison T., Ranasinghesagara J. C., Lu H., Mathewson K., Walsh A., Zemp R. J., “Combined photoacoustic and ultrasound biomicroscopy,” Opt. Express 17(24), 22041 (2009). 10.1364/OE.17.022041 [DOI] [PubMed] [Google Scholar]
  • 32.Song L., “High-Speed Photoacoustic Microscopy In Vivo,” Washington University in St. Louis; (2010). [Google Scholar]
  • 33.Mahmud M. S., Forbrich A., Shao P., Shi W., Zemp R. J., “A tunable MOPA for optical resolution photoacoustic microscopy,” Proc. SPIE 9323, 93233V (2015). 10.1117/12.2077300 [DOI] [Google Scholar]
  • 34.Subochev P., Orlova A., Shirmanova M., Postnikova A., Turchin I., “Simultaneous photoacoustic and optically mediated ultrasound microscopy: an in vivo study,” Biomed. Opt. Express 6(2), 631 (2015). 10.1364/BOE.6.000631 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Horstmann J., Spahr H., Buj C., Münter M., Brinkmann R., “Full-field speckle interferometry for non-contact photoacoustic tomography,” Phys. Med. Biol. 60(10), 4045–4058 (2015). 10.1088/0031-9155/60/10/4045 [DOI] [PubMed] [Google Scholar]
  • 36.Ma R., Söntges S., Shoham S., Ntziachristos V., Razansky D., “Fast scanning coaxial optoacoustic microscopy,” Biomed. Opt. Express 3(7), 1724 (2012). 10.1364/BOE.3.001724 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Kim J., Kim J. Y., Jeon S., Baik J. W., Cho S. H., Kim C., “Super-resolution localization photoacoustic microscopy using intrinsic red blood cells as contrast absorbers,” Light: Sci. Appl. 8(1), 103 (2019). 10.1038/s41377-019-0220-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Kang B. J., Yoon C., Man Park J., Hwang J. Y., Shung K. K., “Jitter reduction technique for acoustic radiation force impulse microscopy via photoacoustic detection,” Opt. Express 23(15), 19166 (2015). 10.1364/OE.23.019166 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Zhang P., Li L., Lin L., Shi J., Wang L. V., “In vivo superresolution photoacoustic computed tomography by localization of single dyed droplets,” Light: Sci. Appl. 8(1), 36 (2019). 10.1038/s41377-019-0147-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Wang L., Maslov K. I., Xing W., Garcia-Uribe A., Wang L. V., “Video-rate functional photoacoustic microscopy at depths,” J. Biomed. Opt. 17(10), 106007 (2012). 10.1117/1.JBO.17.10.106007 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Abolhasani D., Seyedkashi S. M. H., Kim Y. T., Gollo M. H., Moon Y. H., “A double raster laser scanning strategy for rapid die-less bending of 3D shape,” J. Mater. Res. Technol. 8(5), 4741–4756 (2019). 10.1016/j.jmrt.2019.08.021 [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author on request.

Articles from Biomedical Optics Express are provided here courtesy of Optica Publishing Group

RESOURCES