Limited-angle tomographic phase microscopy utilizing confocal scanning fluorescence microscopy

Abstract

We present a multimodal imaging technique, combining tomographic phase microscopy with limited angular projection range and number, and two-channel spinning-disk confocal scanning fluorescence microscopy. This technique allows high-accuracy 3D refractive index (RI) profiling of live cells in spite of the missing projections. The cellular outer shape and its interior organelles measured by the confocal fluorescence imaging not only specify the cell in molecular levels, but also provide the 3D distributions of the whole cell as well as its organelles. We take these additional 3D morphological details as constraints in Gerchberg-Papoulis-based optical diffraction tomography algorithm. We then obtain an accurate 3D RI tomogram, even with a sparse angular range having a small number of perspective projections, otherwise providing low-accuracy RI reconstruction. Then, we obtain both cellular molecular specificity and inner RI values of the cell and its organelles. We compare the reconstructed 3D RI profiles of various samples, demonstrating the superiority of the proposed technique.

1. Introduction

The 3D refractive-index (RI) distribution of biological cells in vitro provides valuable information about their intracellular contents and position-dependent structure [1]. Digital holographic microscopy can provide the quantitative phase profile of the cell, defined, per each spatial point on the image, as the integral of the RI differences across the cell thickness. With such knowledge, various cellular measurements in biological research and medical diagnosis can be carried out [2–4]. These include a 3D morphometric characterization of red blood cells [5,6], dry mass and density analysis of lymphocytes [7], pathogen infection evaluation [8,9], identifying a cell growing state [10,11], bacterial microbiology [12], evaluation of sperm cells for fertilization studies [13–16] and some other biophysical applications [17,18]. Digital holographic microscopy, however, provides the topographic cell map containing the integral RI values without sectioning capability [3].

Tomographic phase microscopy (TPM), on the other hand, can yield the 3D RI of the cell [1,19–29]. The technique is based on recording perspective interferometric projections of the cell from various angles using digital holographic microscopy. The 3D RI distribution can then be reconstructed by the diffraction-based tomography procedure [30]. The angular projections can be obtained by rotating the sample [19–23] or rotating the illumination beam [25–29]. Although rotating the sample allows full angular coverage, it necessitates micro-mechanical elements, such as optical tweezers [19], dielectrophoresis [20], an optical capillary [21], or a microfluidic chip [22,23], increasing the overall complexity of the apparatus. Another problem is the difficulty in obtaining accurate assignment of the angular projection to the rotation angle, which is required for high accuracy reconstruction. Alternatively, if rotating the illumination beam, the sample is kept stationary while the illumination beam scans the sample along a line, a circle, or another trajectory. In this case, the angular coverage is limited to typically up to 140 degree. In some cases, when mapping the angular spectrum in the 3D Fourier space, the centered low-frequency along optics axis cannot be recovered, which is called the missing cone problem [30]. This effect leads to a lower resolution as well as a prolongation of the 3D RI profile along its axial direction. Several numerical algorithms have been proposed to partially overcome these artefacts in the reconstruction [31–35], at the cost of heavy computing complexity. One of these methods uses of prior knowledge on the sample shape in the RI reconstruction procedure to reduce the artefacts effectively [34]. However, in order to generate the 3D mask of the sample, over one hundred projections need to be taken, which requires specialized tomographic microscopes. More importantly, the physical mask of interior organelles in the cell could not be obtained, and the axial distortion may still occur inside the cell due to the different intracellular organelles.

Confocal fluorescence microscopy enables high-resolution 3D imaging of biological cells with aid of chemical fluorescence staining procedure [36,37]. Specifically, spinning-disk confocal microscopy (SDCM) rapidly measures the sample with minimal photo-bleaching [36,38]. Although the measurement results are qualitative, confocal fluorescence microscopy provides molecular specificity, which is capable of distinguishing the 3D distribution of the organelles inside the cell, where TPM lacks this advantage since it base on RI imaging that does not necessarily discriminate between the different organelles. Attempts to combine fluorescence imaging with tomographic RI imaging have been developed for both gaining molecular specificity with quantitative imaging capabilities [39–42]. By co-localizing both images, the RI values of the cell organelle, such as the nucleus and the cytoplasm regions, can be determined. In these previous studies, the RI tomogram and the 3D fluorescence image were reconstructed independently. The fluorescence image was just used for identifying the native locations of the cell and its organelles. The artefacts in the RI reconstruction, inherited from limited angle TPM, still exist, which, in turn, lead to an inaccurate evaluation of the RI values.

In the present study, we suggest a new 3D RI measurement technique for evaluation the RI values of the cytoplasm and the nucleus inside a biological cell, although only a small number of perspective projections is available. By integrating TPM and rapid two-channel SDCM, we can use the knowledge from the SDCM image to improve the TPM image. Sections of fluorescently labeled cells were first captured by SDCM. On the same setup combining both modalities, off-axis interferograms, capturing the complex wave fronts of the cells, were also recorded, using a low-coherence self-interference module. In the reconstruction process, from the confocal sections, either the whole cell contour mask alone or both the cell and nucleus contour masks can be constructed, due to the molecular specificity obtained by using the suitable fluorescence labels. By taking these masks as the object support in the Gerchberg-Papoulis (GP) based iterative algorithm [32,33], accurate RI reconstruction can be achieved with a smaller number of angular projections. The proposed reconstruction method was first assessed by measuring a fluorescent bead under different numbers of projections. The application of the method was then showcased by measuring a red blood cell. Finally, we used the proposed method to image a human monocyte and a HT-29 human cancer cell, with segmentation of the cytoplasm and the nucleus structures and evaluation of their RI values.

2. Setup and methods

2.1. Optical setup

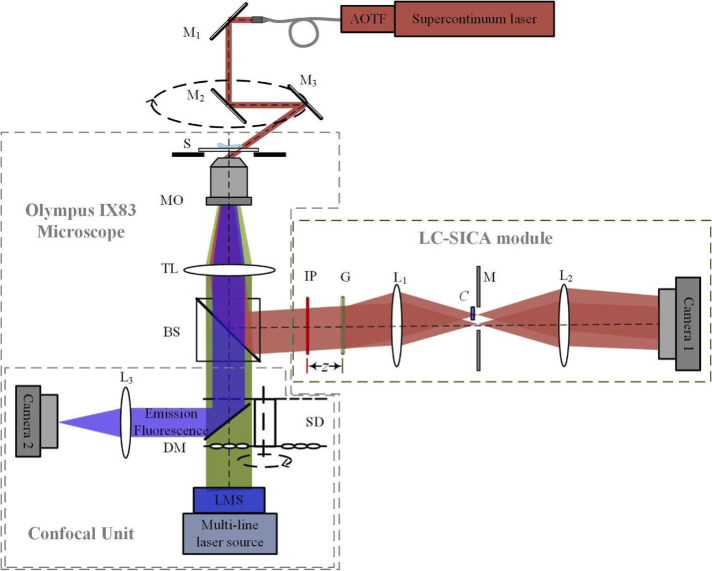
The dual-mode imaging system is built by integrating a custom-built TPM setup with an external interferometric module into a commercial inverted microscope (IX83, Olympus, Tokyo, Japan) with SDCM, as shown in Fig. 1. For capturing the complex wave front of the sample, an external custom-made interferometric module is connected to the output port of the microscope. This module is based on our low-coherence shearing-interferometry with constant angle (LC-SICA) [43].

Fig. 1.

Simplified schematic diagram of the combined TPM-SDCM system. The TPM beams appear in dark red; the fluorescent excitation beams appear in green and the fluorescent emission beams appear in blue. The LC-SICA module is placed at the output of an IX83 microscope for low-coherence phase imaging. The scanning confocal unit is for 3D fluorescent imaging. AOTF, acousto-optic tunable filter; M₁, M₂, M₃, mirrors; S, sample; MO, microscope objective; TL, tube lens; BS, beam splitter; IP, image plane; G, grating; L₁, L₂, lenses with focal lengths f₁=150 mm and f₂=300 mm. z, distance of G from IP; M, mask that selects only two diffraction orders; C, compensating plate; SD, spinning disk; DM, dichroic mirror; L₃, relay lens; LMS, laser merging module.

For interferometric imaging, a supercontinuum laser source SC (S422-205-000, SuperK Extreme, NKT, Birkerød, Denmark), coupled with a computer-controlled acousto-optical tunable filter, AOTF (A901-100-000, SuperK SELECT, NKT, Birkerød, Denmark), is used. The AOTF output is set to a central wavelength of 633 ± 3 nm, inducing a low-coherence beam. After being reflected by mirror M1, the beam enters into the microscope. Mirror pair, M2 and M3, mechanically rotated along the optical axis, are used to generate oblique illuminations from various azimuth angles. The scattered beam passing through the sample S is magnified by microscope objective MO (60×, NA 1.3, oil-immersion, UPlanSApo, Olympus, Tokyo, Japan), and then collimated by tube lens TL. Afterwards, it is reflected out the microscope by beam splitter BS, and an intermediate image is formed on the image plane IP, where the LC-SICA module in positioned. In this module, the image is further magnified by a factor of 2 as f₂ / f₁= 2. A grating G (100 lines/mm, Holo-or, Israel) is placed at a distance z = 43 mm behind IP to generate multiple diffraction orders, where just the zero and the first orders are selected by mask M, placed at the Fourier plane of L₁. A vacant area containing no samples in the first order beam is used as reference beam. To compensate for the optical path delay between the two beams and enable interference between them despite the low-coherence beam, a 0.17-mm thickness glass slide is inserted in the first order beam [43,44]. The traces of the focal spots of the zeroth and first diffraction beams are two identical and separated small circles in the spectra plane when the illumination beam scans along a circle. The two focal spots move in the same way, and they have a constant distance 9.45 mm (150 × 0.63/10). The glass plate is placed to cover the trace of the first beam while not covering the trace of the zeroth beam. Then, an off-axis interferogram with high fringe visibility is created over the field of view (FOV) of CMOS camera 1 (DCC1545M, 1280 × 1024 resolution, with square pixels of 5.2 μm, Thorlabs, Newton, New Jersey). This scheme is different from the one presented in Ref. [45], where an additional galvanometric mirror is used to compensate for the lateral shift of the two focal spots, as a fixed pinhole is used for filtering the referencing beam. For tomographic reconstruction, multiple interferograms were sequentially recorded at equidistant azimuth angles by rotating the mirror pair. There are two obvious advantages in this TPM scheme. First, the mirror pair M2 and M3, which control the illumination beam angle, is located 55-mm up to the objective; thus allowing adequate working space above the sample stage. Then, biological cells in a culture dish can be measured, while it cannot be done in other schemes, as they have very limited working space above the sample when a high NA objective is used as the condenser [40–42]. Second, the low-coherence illumination used here improves the phase imaging sensitivity dramatically in comparison to highly coherent illumination [43].

For fluorescence imaging, a multi-line laser source (VSLaser control, Visitron Systems, Puchheim, Germany) is placed at the back of MO to generate the fluorescence excitation beams, where a central wavelength of 488 nm is used for GFP excitation and a central wavelength of 408 nm is used for Hoechst excitation. Spinning disk SD consists of two layers of disks, in which the bottom layer disk contains a micro-lens array producing multifocal excitations from collimated excitation beams, whereas the top layer disk consists coinciding pinholes. As the micro-lens array is placed concentrically with the pinhole array, multiple excitation spots focus on the sample on parallel. After interacting with the sample, the emitted fluorescence light is collected by MO and focused on the pinhole array after transmitted through TL and BS. These emitted light spots are then reflected by dichroic mirror DM to relay lens L3. By rotating the SD, a fluorescence section is rapidly imaged on CMOS camera 2 (acA2440-75-μm, 2448 × 2048 resolution with pixels of 3.45 μm, Basler, Ahrensburg, Germany). Due to the rapid acquisition, the photobleaching rate is decreased. During this process, the pinhole array enables confocal sectioning by rejecting out-of-focus emissions, as well as increases the spatial resolution.

For 3D fluorescence imaging, a z-scan of the sample is collected by moving MO with a pizeo actuator, in order to obtain a series of section images. In the experiments, the z steps were 0.15 μm for the red blood cell, and 0.2 μm for the other samples. To obtain high contrast images, the exposure time was set to 0.2 s per each section for both channels. On average, it took 30 s to image all 75 sections per cell. This measurement time could be shortened by setting a reduced exposure time, possible by increasing the fluorescence signal. For two-channel imaging, the two excitation lasers alter between each other at each axial section to get two different fluorescent emissions. As the MO used was oil objective with immersion oil of RI 1.518, there was the RI mismatch between immersion oil and the surrounding medium. As a result, the movement of the focal plane in the sample was not in concert with the movement of objective, which leaded to a slightly prolongation along z axis in the 3D confocal image. To correct the fluorescent image, an empirical scaling method was used [37]. A fluorescent bead with known dimensions, immersed in the same medium of the imaged sample, was measured by SDCM. The scaling factor was found by dividing the actual diameter by the calculated depth diameter. The final confocal image of measured sample was then scaled by this factor.

2.2. Reconstruction method

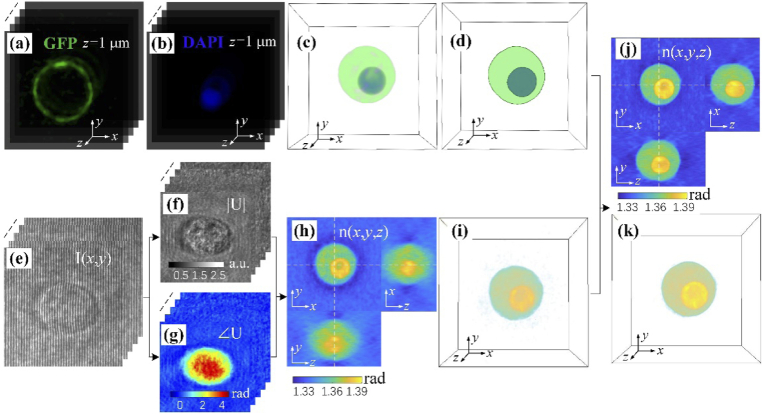
 Figure 2 schematically demonstrates the presented RI tomographic reconstruction procedure. The reconstructed confocal image is not used only for identifying specific features in the sample, but also for providing precise object support in the tomographic RI reconstruction. Hence, 3D masks containing the whole cell and the selected subcellular organelles need to be calculated first. To obtain this, for both fluorescence channels, each section images were binarized, where pixels containing samples were set to 1 and background pixels were set to 0. Then, all the binarized images were collected to generate 3D masks. Figures 2(a)–2(d) show the 3D masks generation procedure for a monocyte. The membrane of the cell was labeled. This gives the contour of the whole cell, and a part of sections captured in GFP channel is shown in Fig. 2(a). The nucleus of the monocyte was stained by Hoechst 33342. Part of the sections captured in DAPI channel is shown in Fig. 2 (b). Figure 2(c) shows the merged 3D fluorescence image and Fig. 2(d) shows the masks created from the two-channel 3D confocal image, where the green mask represents cytoplasm and inner blue mask represents the nucleus.

Fig. 2.

Schematic diagram of the reconstruction procedure. (a,b) Stacks of fluorescent images of the cell along the axial direction obtained for the cell membrane from the GFP channel (a), and for the cell nucleus from the DAPI channel (b). (c) The fluorescence 3D distributions of the cell, as merged from (a) and (b). (d) Two distinct 3D masks generated from (c), in which green color indicates the cytoplasm of the cell and blue color indicates the nucleus. Using these generated masks as constraints in the FM-GP reconstruction, the new rendered higher accuracy reconstruction can be obtained. (e) Raw off-axis holograms of a cell obtained from different illumination angles. Stacks of (f) amplitude images and (g) phase images of the complex wave fields. (h) The reconstructed three orthogonal cross-sectional slices, showing low-accuracy reconstruction due to lack of angular projections. (i) 3D distribution of the reconstructed RI. (j) The improved three orthogonal cross-sectional slices of the reconstructed RI (compared to (h)). (k) The improved 3D map of the reconstructed RI (compared to (i)).

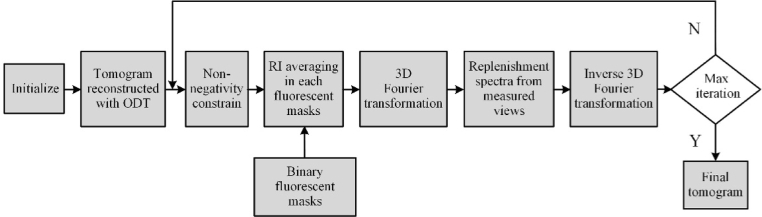
For the RI tomogram reconstruction, the complex wave front of the cell needs to be retrieved. Figure 2(e) demonstrates a stack of nine off-axis interferograms at various illumination angles. The corresponding amplitudes and phase images were extracted using a Fourier filtering method [43]. They are shown in Figs. 2(f) and 2(g), respectively. For comparison, a 3D RI map was also reconstructed from these 2D complex amplitudes by the optical diffraction tomography (ODT) algorithm, in which Rytov approximation was applied [32]. However, obvious blurring and prolongation effect along z direction is observed in Figs. 2(h), which is induced by the missing coverage of projections in the 3D Fourier spectrum due to using only nine projections. Figure 2(i) presents the 3D distribution of the reconstructed RI. To solve this problem, we suggest fluorescent-mask-assistant GP (FM-GP)-based iterative reconstruction method [32,33], in which the measured 3D masks are used as additional regularization terms. A flowchart of the iterative reconstruction algorithm is shown in Fig. 3. Besides the two operations in each iteration in the standard GP approach: nonnegativity in the object domain and replenishment of known data in the spectrum domain [34], an operation that averages the RI values in each individual mask is implemented. In addition, we take the region outside the outer mask as an additional mask, and replace its value with the RI value of surrounding medium in each iteration. We also assume that each sub-organelle should have a close RI distribution as in the others [17,46]. The operation can eliminate the overestimation effect in the central layers of the tomogram [32,35]. In principle, the method can be considered as a constrained minimization problem [32]:

$$\text{min}E(x)\mathit{\text{s.t.}}Ax=B,$$ (1)

where x denotes the reconstruction, A is a forward operation characterized by the illumination scheme, A x represents the computational field, B is the measured field, and E(x) denotes averaging operation in each mask and the nonnegativity constraint. This new method improves the reconstruction quality, since the blurring and prolongation effects are overcome as shown in Figs. 2(j) and 2(k). Before implementing the iterative reconstruction method, an iterative registration procedure [38] is applied between the 3D fluorescence masks and the 3D RI map, directly obtained from the ODT algorithm. The procedure, including cropping, resizing, and rotating operations in x-y plane, enables co-localization between the two images. Therefore, in the final RI map, the cytoplasm and the nucleus can be clearly identified.

Fig. 3.

Flowchart of the iterative FM-GP reconstruction algorithm.

2.3. Sample preparation

Three types of human biological cells were measured: red blood cells, white blood cells, and HT-29 (human colorectal adenocarcinoma) cells. For red blood cells (RBCs), only the membrane was stained by wheat germ lectin (WGA) conjugated to FITC (15 µg/ml, Sigma #L4895-5MG), and imaged in the microscope GFP channel. Blood was purchased from Magen David Adom’s Israel national blood bank, and stored up to one week before usage. The cells were diluted 1000 times in phosphate buffered saline (PBS) solutions supplemented with 2 mM ethyleneiam inetetraacetic acid (EDTA).

Monocyte white blood cells were isolated in a two-stage process: first peripheral blood mononuclear cells (PBMCs) were isolated from blood using of Ficoll-Paque PLUS (GE Healthcare, SN.17-1440-02) in accordance with manufacturer’s instructions. Then, the monocytes were isolated from the PBMCs using a negative selection magnetic kit (EasySep for monocytes, SN. 19359) according to the manufacturer’s instructions. Cells were placed in PBS 2 mM EDTA. Afterward, the membrane of the cells was stained with WGA conjugated to FITC (50 µg/ml, Sigma #L4895-5MG), while the nucleus was stained with Hoechst 33342 (10 µg/ml, Sigma #B2261).

HT-29 cells were purchased from the ATCC. Green fluorescent protein gene was previously transfected into the cells using adenovirus vector [47]. The growth medium was Dulbecco's Modified Eagle's Medium (DMEM) (BI, SN. 01-55-1A) supplemented with 10% fetal bovine serum (FBS) (BI, SN. 04-007-1A), 4 mM L-Glutamin (BI, SN. 03-020-1B) and 1% antibiotics (BI, SN. 03-033-1B). The cells were incubated under standard cell culture conditions at 37⁰ C and 5% CO₂ in a humidified incubator until 80% confluence was achieved. In addition, the cell nucleus was fluorescently labeled with 10 μg/mL of Hoechst 33342.

3. Experimental results and discussions

3.1. Performance analysis of the method

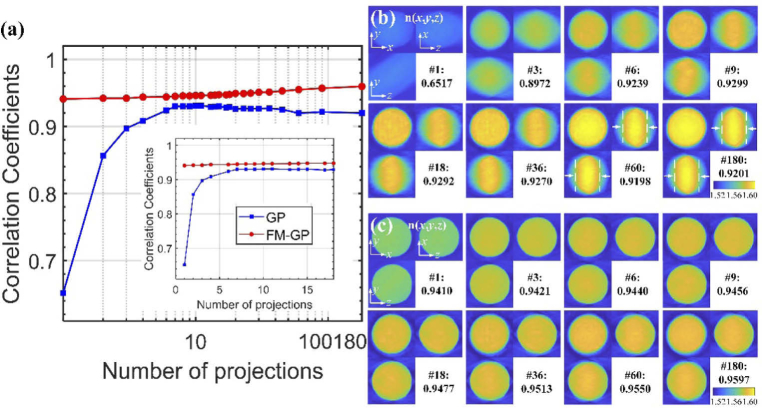
With the FM-GP iterative reconstruction method, a high-quality reconstruction of the RI can be achieved even with sparse projection coverage. We first checked the performance of the method under various angular projection by imaging a fluorescent bead. The fluorescent polystyrene bead (n = 1.587 at 633 nm) immersed in matching oil (n = 1.518) was sandwiched by two coverslips, and measured by the fluorescence module and by the tomographic module, respectively. In the experiments, the illumination angle was 61 degrees and all interferograms captured with equidistant azimuth angle. First, the 3D mask was generated from the fluorescence images. A bead having contour determined by the same mask and nominal RI was then used as reference tomogram. We calculated the correlation coefficients between this reference tomogram and the tomograms reconstructed using only sparse projections. The red curve shown in Fig. 4(a) represents the results. Orthogonal cross sections of some representative tomograms are also presented in Fig. 4(c), in which the number of projections and the corresponding coefficients are also marked. The tomogram shown on the right bottom corner of Fig. 4(c) was reconstructed from 180 illumination angles. It is almost uniformly distributed and has an average RI value of 1.588. It has a maximum correlation coefficient of 0.9597. From both the correlation coefficients values and the tomograms, it is clear that even with 9 projections, an acceptable tomogram is obtained, with a correlation coefficient of 0.9456. We thus chose to use only 9 projections in the following experiments to obtain an acceptable quality 3D RI reconstruction, which decreased the acquisition time greatly.

Fig. 4.

(a) Correlation coefficients between the 3D RI maps of a polystyrene bead, which were reconstructed using different numbers of angular projections, and the reference map. Blue curve with rectangle markers represents coefficients obtained from the conventional GP algorithm. Red curve with circle markers represents coefficients obtained from the proposed FM-GP method. The horizontal axis (number of projections) is in log scale. The inset shows the same data in normal scale on the horizontal axis. (b) Three orthogonal cross sections and the corresponding correlation coefficients of reconstructed 3D RI maps versus the projection numbers in the conventional GP algorithm. (c) Three orthogonal cross sections and the corresponding correlation coefficients of reconstructed 3D RI maps versus projection numbers in the FM-GP algorithm, showing a significant improvement in comparison to (b).

For comparison, the tomograms were also reconstructed using the conventional GP algorithm with the corresponding angular projections, but without using the fluorescence images. Taking the same reference tomogram, the calculated correlation coefficient values are plotted as a blue curve in Fig. 4(a). Figure 4(b) shows several groups of the cross sections from the tomograms. In this case, the correlation coefficient values are always lower than these obtained by our FM-GP method, using the same angular projections. In addition, a slight decrease in the correlation coefficient values was observed when the projection number exceeded 60. The main reason for this is that GP algorithm leads to higher values in the central layers, while underestimating the values towards both borders along the optical axis direction [32]. This effect becomes more obvious as indicated by the white dashed lines in Fig. 4(b) when more projections are used.

3.2. Measurement of a red blood cell

In order to demonstrate the shape-preserving capability of the tomogram reconstructed by the suggested method, we measured an RBC. Tomographic measurement of RBCs is a valuable tool in studying the structural and mechanical modifications induced by various diseases [9]. The typical shape of a healthy RBC is flat and biconcave. Traditionally, it is hard to reconstruct its accurate shape in limited-view tomography, as it requires good coverage in the angular spectrum along optical axis [6,35]. A membrane-stained RBC was first imaged by confocal imaging, and then 9 interferograms were recorded by rotating the illumination beam with 40-degree angular spacing. Figures 5(c-e) show three cross sections through the origin of the tomogram reconstructed with the regular GP algorithm (without using the fluorescence data). A central hole appears in these figures, which obviously violates the cell structural distribution. In addition, other artifacts appear in the area marked by black arrows in Figs. 5(d-e), which is a prolongation effect in the reconstruction. The distortions are due to the missing spatial information of the illumination NA [32]. On the contrary, three cross sections of the tomogram reconstructed with our FM-GP algorithm are shown in Figs. 5(f-h). The donut shape of the RBC is precisely reconstructed using the proposed method, while the distortions are successfully eliminated. From these reconstructed results, more accurate measurement of the RBC parameters, such as its volume, can be performed.

Fig. 5.

Comparison of the reconstructed 3D RI maps of a red blood cell between our method and the conventional ODT method. (a) 3D fluorescence image obtained by SDCM. (b) The corresponding 3D calculated mask. (c-e) Cross sectional slices of the reconstructed RI obtained from the conventional ODT algorithm with 9 projections. (c) x-y slice, (d) x-z slice, and (e) y-z slice, at the center. There are strong deformations breaking the true concave shape of the RBC in (d) and (e), as indicated by black arrows, which are results of missing cone problem in the conventional method. (f-h) The corresponding improved cross sectional slices of the reconstructed RI obtained from our method. This reconstruction coincides well with the true shape of the cell. Scale bars indicate 3 μm.

3.3. RI measurement of a monocyte

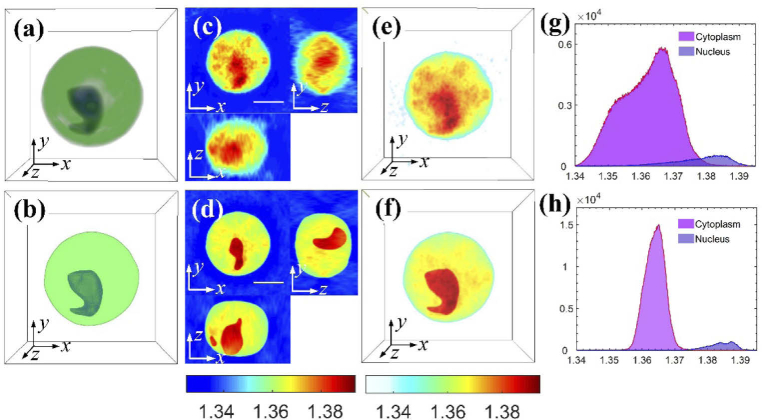
With the suggested method, segmenting subcellular organelles inside a cell and evaluating their RI values can be conducted in high precision. To demonstrate this, we measured a monocyte. The confocal imaging was performed in two channel. The contour of the cell was obtained by imaging the green fluorophores labeling the cell membrane in the green channel. The nucleus was labeled by Hoechst and imaged in the blue channel. The merged fluorescence image is shown in Fig. 6(a) and Visualization 1 ^{(1.3MB, avi)} . Figures 6(b) and Visualization 2 ^{(1.3MB, avi)} present the generated 3D masks, in which the peripheral green mask represents the cytoplasm distribution and central blue mask represents the nucleus distribution. Figure 6(c) shows the reconstructed cross sections using the regular GP algorithm, while Fig. 6(d) shows the results obtained using the proposed FM-GP algorithm. The corresponding 3D tomograms of these two cases are also shown in Fig. 6(e) and Visualization 3 ^{(1.9MB, avi)} , and in Fig. 6(f) and Visualization 4 ^{(1.8MB, avi)} , respectively. Obviously, the same kind of distortion of overestimation in the central sections and lower estimation in the outer sections appear in Figs. 6(c) and 6(e).

Fig. 6.

Comparative results of imaging a monocyte, which has distinctive difference in RI values between the cytoplasm and the nucleus. (a) Merged 3D fluorescence distribution of the cell obtained using SDCM (see Visualization 1 ^{(1.3MB, avi)} ). (b) Generated 3D masks from (a), in which the green colored mask represents the cytoplasm distribution and the blue colored mask represents the nucleus distribution (see Visualization 2 ^{(1.3MB, avi)} ). (c,e) Reconstructed RI results: (c) three cross-sectional slices, and (e) 3D RI distribution (see Visualization 3 ^{(1.9MB, avi)} ). Based on the RI value variance in different regions, both nucleus and cytoplasm values can be measured but they differ greatly from their true shapes. (d,f) The corresponding RI reconstructed with our method: (d) three cross-sectional slices, and (f) 3D RI distribution (see Visualization 4 ^{(1.8MB, avi)} ). In (d) and (f), the distributions of the nucleus and the cytoplasm are well matched with results measured by SDCM. (g) Histogram of RI values in the cytoplasm and the nucleus of the 3D RI map shown in (e). (h) Histogram of RI values in the cytoplasm and the nucleus of the 3D RI map shown in (f). Scale bars represent 5 μm.

In conventional interferometric tomography, in order to calculate the RI distributions of the cytoplasm and the nucleus, both regions could be segmented from the variance of the RI values [7,19], and then the values can be analyzed. However, usually it cannot be used for identifying the regions accurately unless there is a sharp difference in RI between them. In conventional dual-modality correlative fluorescence and interferometric tomography, both regions can be specified from Figs. 6(c) and 6(e) using their 3D masks, as shown in Fig. 6(b). However, due to distortions in the reconstructed tomogram, which result from missing angular coverage, the measured RI values have a wide margin of errors. The RI distributions of the cytoplasm and the nucleus, obtained from Fig. 6(c), are shown in Fig. 6(g). The calculated RI values are 1.3619 ± 0.0079 for the cytoplasm, and 1.3782 ± 0.0080 for the nucleus. For comparison, the tomograms presented in Figs. 6(d) and 6(f) demonstrate a better quality. The morphology of both cytoplasm and nucleus are clearly identified and coincide with those obtained from the fluorescence images. The resulting RI distributions are presented in Fig. 6(h). The corresponding RI values are 1.3639 ± 0.0031 for the cytoplasm and 1.3841 ± 0.0037 for the nucleus. These RI values have less variance than obtained using the conventional GP method, demonstrating the higher precision obtained using the proposed FM-GP method. These RI values are in agreement with our previous results obtained using angular projections with a full two-axe coverage [20] as well as with other results [46].

3.4. RI measurement of a HT-29 cell

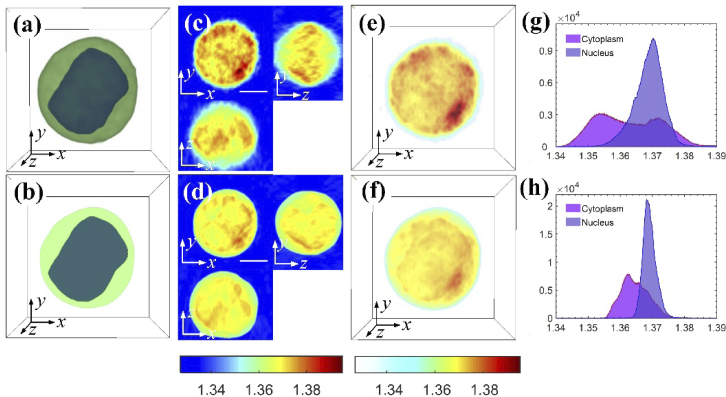
To further demonstrate the RI measuring capability of the suggested method, we measured a HT-29 human cancer cell. The two-channel fluorescence images captured are shown in Fig. 7(a) and Visualization 5 ^{(1.4MB, avi)} . Using these images, two masks were generated, as shown in Fig. 7(b) and Visualization 6 ^{(1.3MB, avi)} . The blue mask represents the nucleus and the green mask represents the cytoplasm. Figures 7(c) and 7(d) show two groups of cross sections in the tomograms reconstructed from the GP and the FM-GP algorithms, respectively. Figures 7(e) and 7(f) show the two corresponding 3D tomograms. Visualization 7 ^{(1.8MB, avi)} and Visualization 8 ^{(1.8MB, avi)} are two dynamic 3D presentations for the tomograms, respectively. The histograms of the RI values in the nucleus and the cytoplasm are shown in Fig. 7(g), for the conventional GP algorithm. The RI values are 1.3689 ± 0.0045 for the nucleus and 1.3628 ± 0.0099 for the cytoplasm. For comparison, the RI histograms of the nucleus and the cytoplasm obtained from the proposed FM-GP algorithm are shown in Fig. 7(h), and their RI values are 1.3692 ± 0.0021 and 1.3647 ± 0.0042, respectively. These values coincide well with those measured by a previous technique, combining confocal and interferometric phase imaging, developed by our group recently [38].

Fig. 7.

Comparative results of imaging a HT-29 cell, which has indistinctive difference in RI values between the cytoplasm and the nucleus. (a) Merged 3D fluorescence distribution of the cell obtained using SDCM (see Visualization 5 ^{(1.4MB, avi)} ). (b) Generated 3D masks from (a), in which the green colored mask represents the cytoplasm distribution and the blue colored mask represents the nucleus distribution (see Visualization 6 ^{(1.3MB, avi)} ). (c,e) Reconstructed RI results: (c) three cross-sectional slices, and (e) 3D RI distribution (see Visualization 7 ^{(1.8MB, avi)} ). Based on the RI value variance in different regions, both nucleus and cytoplasm values can be measured but they differ greatly from their true shapes. (d,f) The corresponding RI reconstructed with our method: (d) three cross-sectional slices, and (f) 3D RI distribution (see Visualization 8 ^{(1.8MB, avi)} ). In (d) and (f), the distributions of the nucleus and the cytoplasm are well matched with results measured by SDCM. (g) Histogram of RI values in the cytoplasm and the nucleus of the 3D RI map shown in (e). (h) Histogram of RI values in the cytoplasm and the nucleus of the 3D RI map shown in (f). Scale bars represent 5 μm.

Inside the HT-29 cell, the RI values of the nucleus and the cytoplasm are very close. Hence, it is difficult to identify these organelles from the tomogram only. As shown in Figs. 7(c) and 7(e), the high-value region looks different from the nucleus contour shown in Fig. 7(b). In this case, fluorescence labeling is essential for specifying the organelle volumes.

4. Conclusion

We have presented a dual-mode fluorescence and tomographic phase imaging technique that facilitates the segmentation of the intracellular organelles and their RI value evaluation. This method is especially helpful when using a small number of perspective interferometric projections. The membrane of the cell and its nucleus were fluorescently labeled and imaged by SDCM, combined with the same interferometric system. In contrast to the conventional correlative microscopy, where the 3D RI map is reconstructed independently, in the proposed method the morphological distributions of the subcellular organelles are involved in the tomogram reconstruction procedure. Using this new method, a high quality reconstruction can be obtained from nine projections only, which is demonstrated by comparing reconstructions of a fluorescence bead. We further demonstrated the application of the proposed method by measuring three types of human cells: an RBC, a monocyte and a cancer cell, in which accurate contour preservation and morphologic segmentation are achieved in the 3D RI maps reconstructed. In this work, we have chosen to image cells in suspension, rather than adherent cells, since the suspended cells is the more problematic case, in which small number of projections is even more critical since the cell might move over time. However, the method can work with adherent cells as well. Possible limitations of the method include the fact that the fluorescence labeling requires additional biochemical processing of the cells and may introduce phototoxicity to the samples. On the other hand, confocal fluorescence microscopes are more common than tomographic microscopes that have wide angular range. In addition, it should be noted that the present method has a low throughput as both imaging modalities are implemented sequentially. We also assume that the cell RI is not affected by the low-concentration fluorescent dyes, as typically assumed in correlative fluorescence tomography. Since the used SDCM has two imaging channels, here only the cytoplasm and nucleus are concerned. However, with more fluorescence channels and the suitable fluorescent labels, other subcellular structures can be specified. In the future, we expect the proposed technique to be a useful tool for various cellular biophysical studies.

Funding

HORIZON2020 European Research Council10.13039/501100000781 (ERC) (678316).

Disclosures

The authors declare no conflicts of interest.