Wireless Pacing Using an Asynchronous Three-Tiered Inductive Power Transfer System

Abstract

Despite numerous advancements in pacemaker technology for the treatment of cardiac arrhythmias and conduction disorders, lead-related complications associated with these devices continue to compromise patient safety and survival. In this work, we present a system architecture that has the capacity to deliver power to a wireless, batteryless intravascular pacer. This was made possible through a three-tiered, dual-sub-system, four-coil design, which operates on two different frequencies through intermittent remote-controlled inductive power transfer. System efficiency was enhanced using coil design optimization, and validated using numerical simulations and experimental analysis. Our pacemaker design was concepted to achieve inductive power transfer over a 55 mm range to a microscale pacer with a 3 mm diameter. Thus, the proposed system design enabled long-range wireless power transfer to a small implanted pacer with the capacity for intravascular deployment to the anterior cardiac vein. This proposed stent-like fixation mechanism can bypass the multitude of complications associated with pacemaker wires while wireless power can eliminate the need for repeated procedures for battery replacement.

INTRODUCTION

The application of wireless power transfer in implantable biomedical devices has great potential for improving patient outcomes. Nearly 10% of cardiac pacemaker implants experience lead-related complications.^26,36 Therefore, the elimination of device leads, the wires which carry current from a pulse generator to the stimulating electrodes, can significantly reduce complication rates in patients with pacemaker implants.

This has motivated extensive research in the development of leadless devices. However, despite the Food and Drug Administration’s (FDA) recent approval of a leadless pacemaker, new potential complications and limitations are introduced, primarily resulting from the continued inclusion of an integrated battery. These constraints include reduced patient accessibility due to large device size, the limited ability to only perform single-chamber pacing, the risk of device embolization resulting from repetitive mechanical burden on an in-chamber fixation anchor, and decreased device longevity due to a smaller battery size compared to lead-based devices.^8,27,34 Alternative approaches, including power harvesting mechanisms using motion or vibration have also been investigated; however, these techniques often demand impractical or invasive implantation, or are unable to harvest sufficient power for pacing.^4,14,17,30

The capacity to achieve wireless power delivery can alleviate many of the complications associated with existing lead-based and leadless devices. However, a primary challenge in wirelessly powered devices is in the delivery of sufficient power to a small implant over an effective range. Mid-field and far-field radio frequency power transfer have either been unable to sufficiently reduce antenna size, meet specific absorption rate (SAR) limits, or provide practical power consumption rates for a continuously operating device.^{2,5,12,13,19,24,25,37}

Various system architectures have also been designed to address the challenges of near-field RF wireless power transfer for deep tissue implants. The most common of these is the two-coil inductive power transfer (IPT) system, in which a power supply is packaged in the transmitter and the control circuitry and electrodes are contained in the receiver.^{3,12,16,24,28,29,31,38} This design encounters the challenge of delivering sufficient power while remaining below SAR limits due to large power requirements for stimulation and inherent inefficiency in an asymmetrical IPT system with a small receiver. To overcome this challenge, alternative designs have been proposed in which a charge-storage unit, such as a battery, is placed in the receiver within the same two-coil architecture.^21,23 While the addition of a battery enables power accumulation in a low-efficiency system for delivering sufficient power for deep tissue stimulation, it also entails an increase in device size that limits implant position and fixation mechanism. To avoid an increase in size while overcoming low efficiency over a long range, multi-coil approaches have been proposed in which multiple coil-to-coil wireless transmissions result in a higher power transfer efficiency to a small implant.^{18,20,22,32,43} In these multi-coil systems, there is a single source and sink plus one or more relays. The challenge of this design lies in the need to appropriately position multiple coils in the body for optimal power transfer efficiency and for multiple implants to work in sequence for successful power transfer.

In this context, we implemented a new design that utilizes the two-coil system in an asynchronous multi-tiered architecture. Remote-controlled stimulation was implemented at each level to optimize overall power output despite power delivery to a small implant. While the presented architecture utilizes a multi-coil design, each interaction is independent of the other, thus avoiding the need for multiple incisions or a long-term wearable device.

MATERIALS AND METHODS

Three-Tiered Intermittent Transmission System Design

To address the limitations of inductive power transfer, we established a three-tiered system design consisting of two independently functioning two-coil systems (Fig. 1a). We define these two systems as the “Stimulation Sub-System” (SSS) and “Charging Sub-System” (CSS). Each sub-system functions under two distinct operating frequencies to avoid system-to-system interference and inter-dependence.

FIGURE 1.

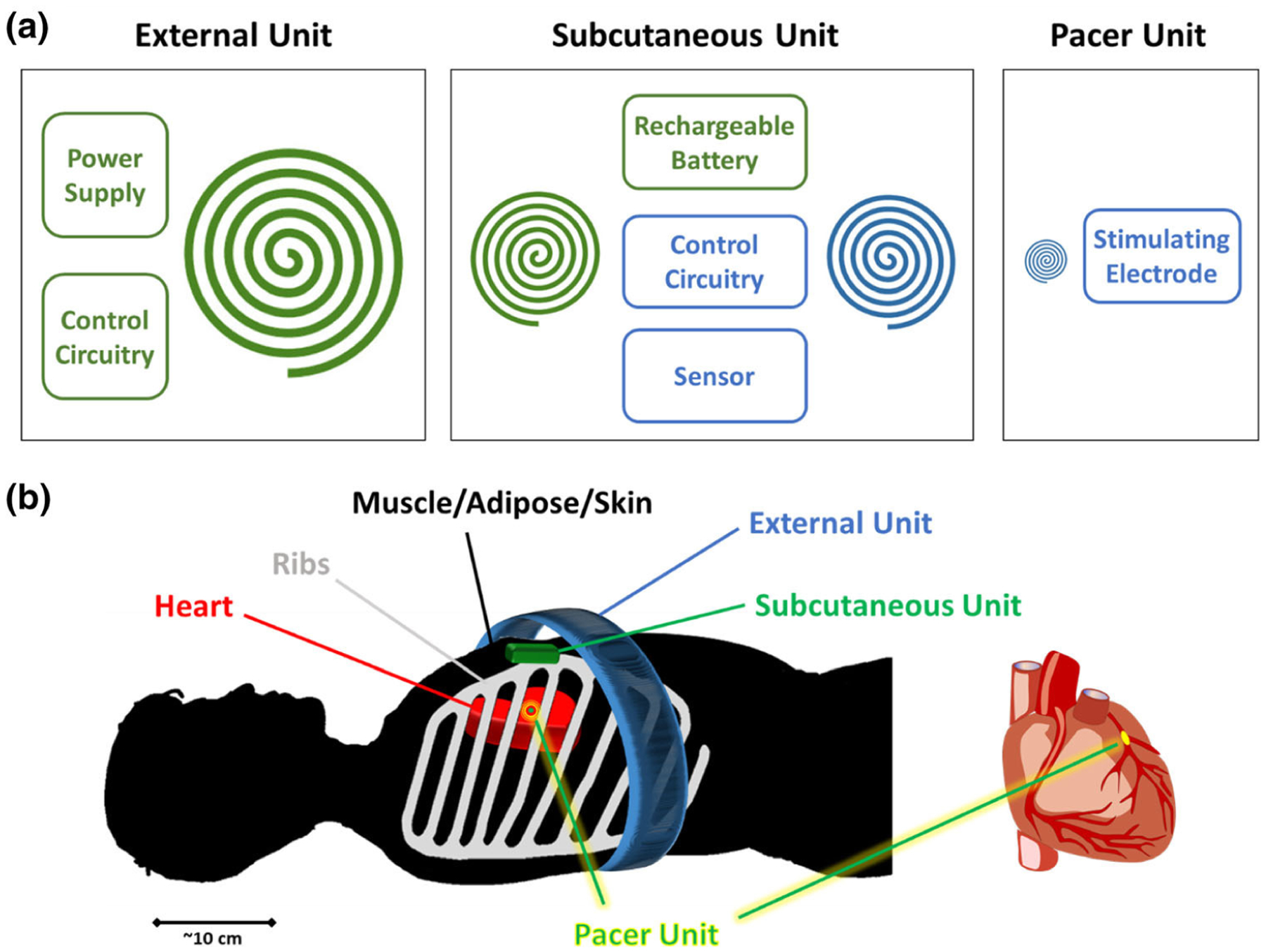
System Architecture. (a) 3-tiered, 4-coil, 2-sub-system architecture. Each unit is shown in individual boxes. Charging Sub-System (CSS) is illustrated in green and Stimulation Sub-System (SSS) is illustrated in blue. (b) The relation of external, subcutaneous, and pacer units is illustrated in the presence of skin/adipose, tissue/muscle, ribs, and heart.

The three tiers of the complete pacemaker system consists of (1) an “External Unit” to encase the transmitter coil and control circuitry of the CSS, (2) a “Subcutaneous Unit” to encase the receiver coil of the CSS, a charging circuitry, a rechargeable battery, sensors, the control circuity of the SSS, and the transmitter coil of the SSS, and (3) a “Pacer Unit” to encase the receiver coil of the SSS, a rectifier and regulator, and stimulation electrodes (Fig. 1b).

The proposed architecture utilizes intermittent wireless power transfer to independently meet the demands of each sub-system (Fig. 2). We begin with the pacer unit, the first of the implanted components in the SSS. For cardiac pacing, the device is designed for catheter-based intravascular deployment to the anterior cardiac vein (ACV). This design would require a millimeter-sized receiver coil, thus resulting in an inherently inefficient inductive power transfer system. We addressed this issue by incorporating a remote-controlled stimulation architecture as previously described.¹ As such, for a heart rate of 60 beats per minute (BPM), power would be wirelessly and intermittently transmitted from the subcutaneous unit at a pulse frequency of 1 Hz for a pulse duration of 0.2 to 1 ms. This architecture is essential for reducing power consumption, specific absorption rate, and receiver size. These conditions are optimal for the SSS, in which its pacer unit has significantly limited space available within the anatomical constraints of the ACV. A rechargeable battery in the subcutaneous unit meets the power demands of the SSS. This battery is charged through the CSS. The receiver of this sub-system is encased in the implanted subcutaneous unit, while the transmitter is encased in the external unit. This external unit is only to be worn during infrequent charging sessions. The frequency and the charging duration are dependent on the SSS power consumption, battery capacity, and efficiency of the CSS wireless transfer system.

FIGURE 2.

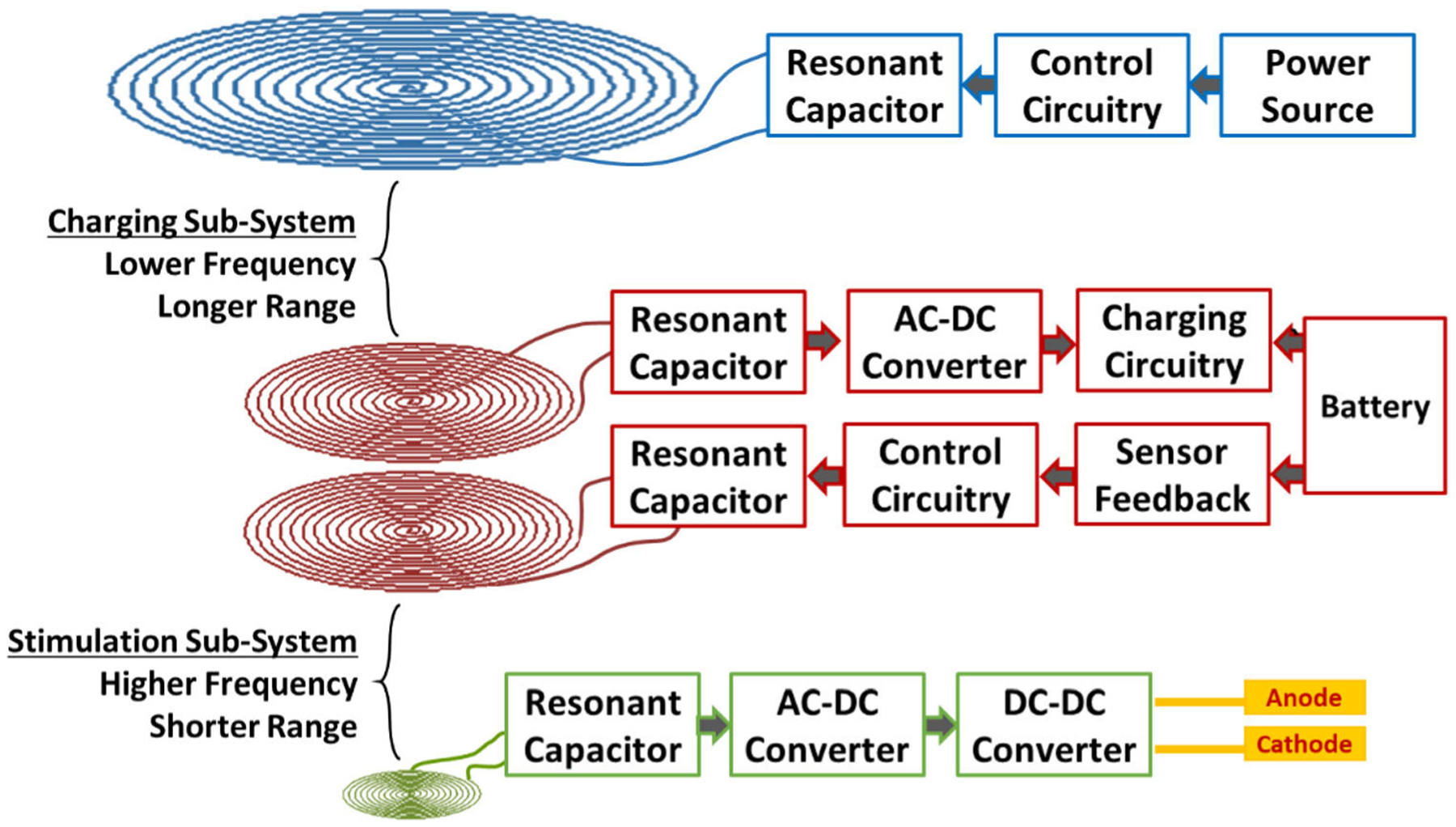
Block diagram of CSS and SSS system design, demonstrating intermittent remote-controlled stimulation of cardiac tissue over a long range.

This three-tiered, two-sub-system design ultimately entails several advantages that optimize its application in biomedical implantable devices. The ability to use different frequencies decouples the power transmission between the two sub-systems and allows for adaption to the environmental constraints encountered by each sub-system, including space availability, transmission range, and transmission frequency. In the case of the SSS, the pacer unit faces extreme anatomical constraints in the anterior cardiac vein, whereas the subcutaneous unit has more freedom underneath the skin within the anterior chest wall. In the case of the CSS, the external unit has maximum freedom in size but must also transmit power over a longer range in the setting of variations in the thickness of the chest wall and manual positioning of the chest strap by the patient. Flexibility in frequency selection is also important for meeting SAR demands in each sub-system in which the length and frequency of transmission also varies. The SSS experiences short and frequent transmission, while the CSS experiences long but infrequent transmissions.

Optimal Design for the Stimulation Sub-System

The pacer unit of the SSS is the final recipient of power in our multi-level system and encounters the most stringent constraints. We aimed to design the device to be fixated in the anterior cardiac vein, analogous to the deployment of an intravascular stent. This implant position would minimize the mechanical burden that is experienced by existing devices, which are fixated inside the contracting myocardium of the ventricular chamber. Consequently, the device was limited to the small vessel diameter of 3.8 ± 0.7 mm.³⁵ Our previous work demonstrated that the optimum design for this condition was a hollow-centered coil, formed by bending a planar circular coil into the third-dimension, thus creating a half-cylindrical coil design.¹ We further optimized our design by utilizing a planar elliptical coil with five turns of a 30 AWG wire bent into a half-cylindrical shape. A meandering structure in the tail provided additional dimension for capture of the magnetic field (Fig. 3a). The final device was 2.8 mm in diameter and 15 mm in length and allowed for blood flow through the center while remaining within the limits of the implant position.

FIGURE 3.

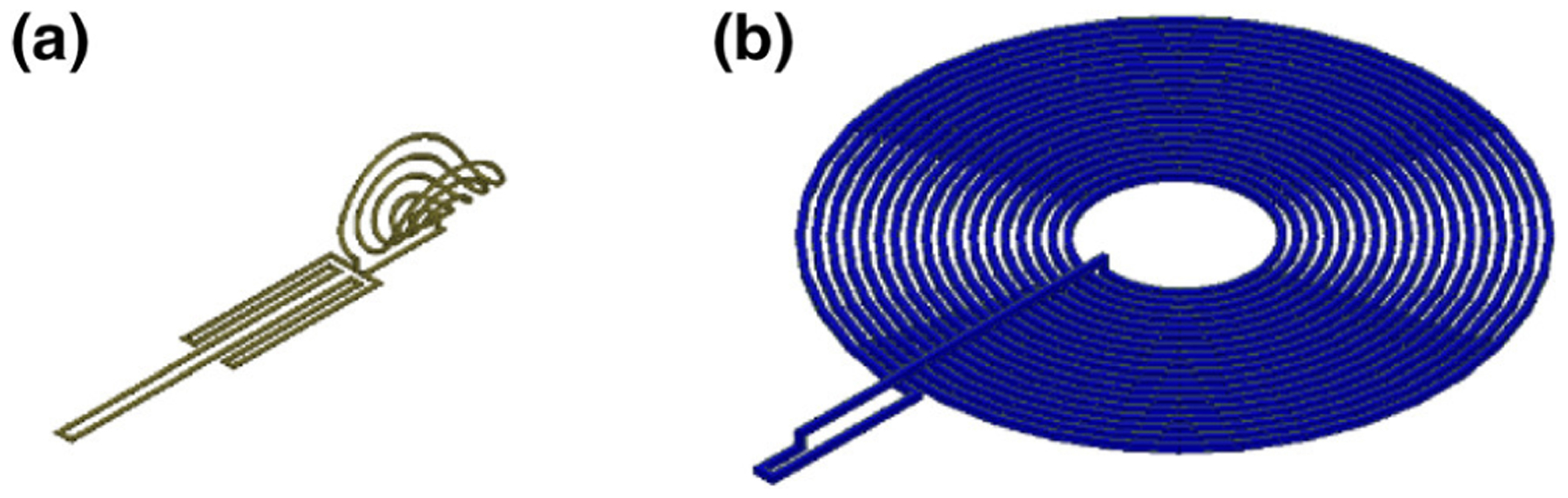
Stimulation Sub-System Coil Designs. (a) SSS receiver coil, (b) SSS transmitter coil.

The transmitter coil of the subcutaneous unit had more flexibility in size and shape due to more available space in the anterior chest wall. To minimize aesthetic side-effects, we designed the transmitter as a planar coil with a diameter of 40 mm (Fig. 3b).¹

Validation Studies for the Stimulation Sub-system

We examined the power transfer efficiency of the proposed system using two validation steps: (1) Finite Element Method (FEM) numerical simulations, and (2) in vitro studies. Previous studies have demonstrated the mean anatomical distance between the suprasternal border (transmitter position) and anterior cardiac vein (receiver position) to be 20 mm.¹ Thus, we examined the power transfer efficiency of the SSS over a 10 to 30 mm range.

The coil designs (Table 1) were modeled in Solid-works computer-aided design software. The models were imported into ANSYS Maxwell simulation software, where the transmitter coil was positioned at varying distances apart from the receiver coil. Using the Eddy Current solver in ANSYS Maxwell, we simulated the magnetic field, inductance, resistance, and coupling coefficient resulting from the 13.56 MHz alternating current (AC) in the transmitting coil and its impact on the receiving coil. The operating frequency was established in line with the Federal Communications Commission (FCC) reserved industrial, scientific and medical (ISM) radio band, and optimized based on the compromise between minimizing tissue energy absorption and maximizing power transfer efficiency.¹⁰ Tissue absorption was verified to remain below SAR limits using electric (E) field computations in ANSYS Maxwell and Eq. (1):

$$\text{SAR}=\frac{\sigma E^2}{\rho }$$ (1)

where σ is the electrical conductivity of the tissue and ρ is the mass density of the tissue.

TABLE 1.

Transmitter (Tx) and receiver (Rx) coil design parameters for the SSS.

Parameter	Tx coil (subcutaneous unit)	Rx coil (pacer unit)
Shape	Planar circular coil with N-turns	Half-cylindrical + meandering tail
Size	5 mm inner radius, 20 mm outer radius	3 mm diameter × 15 mm length
Wire gauge	26 AWG	30 AWG
# of turns	18 turns	4 turns

The coils’ internal resistance and inductance as well as the coupling coe cient between the interacting components were imported into PSPICE Electronic Circuit Optimization & Simulation software. We simulated the circuit of Fig. 4 with a 1000 Ω load at the receiver, which is representative of the impedance of a typical high-impedance pacemaker stimulation lead electrode. We measured the power transfer efficiency given an instantaneous power of 1.26 W, which is equivalent to an average power of 1.26 mW for a heart rate of 60 beats per minute (BPM) and pulse duration of 1 ms.

FIGURE 4.

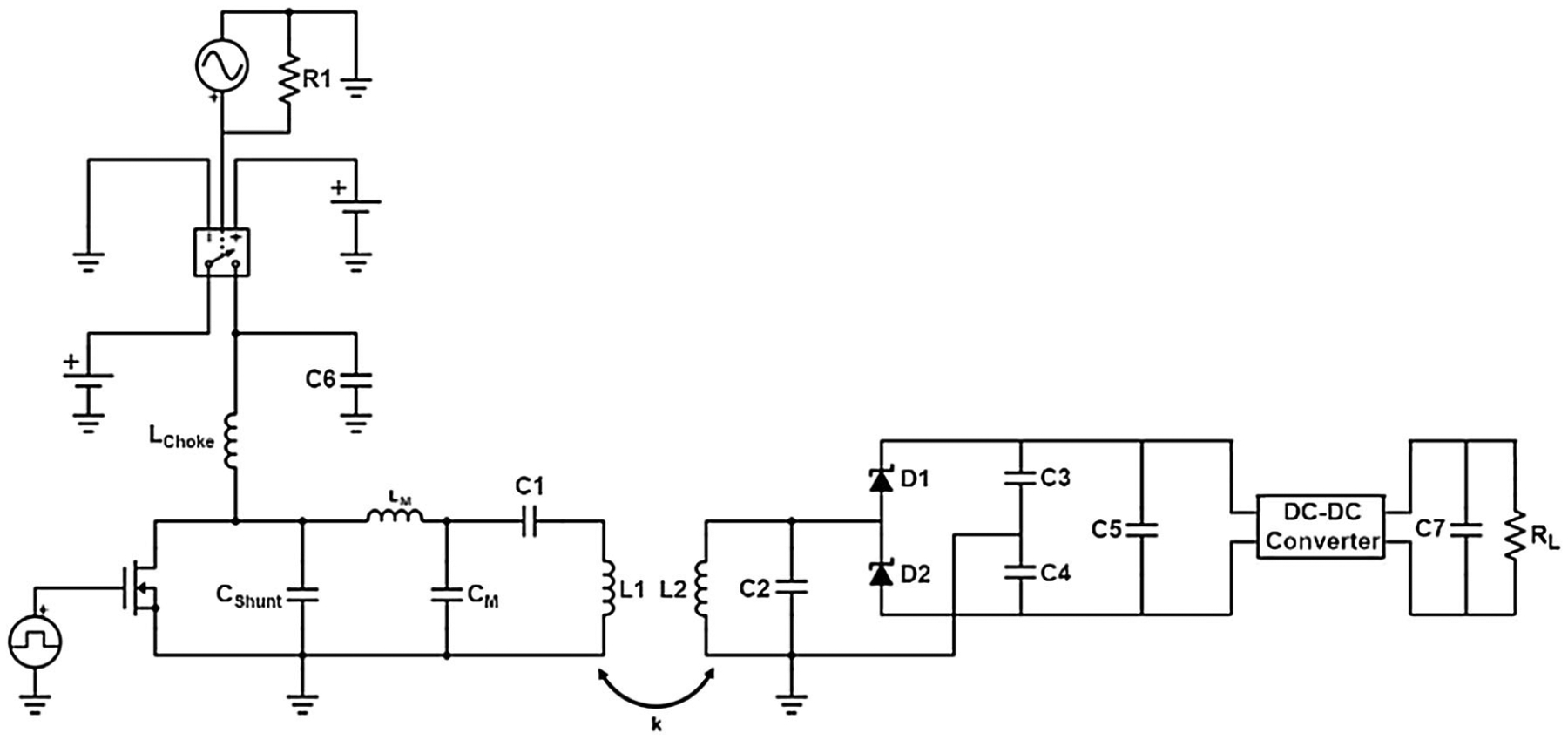
On the left, the simulated circuit model of the transmitter, consisting of a class E power amplifier (L_choke = 220 μH, C_shunt = 180 pF, and BS170 MOSFET), matching circuit, and series tank circuit. On the right, the simulated circuit model of the receiver, consisting of a parallel tank circuit, rectifier, and regulator. The circuit was modeled using coil properties and coupling coefficient obtained from the ANSYS simulations.

In vitro experiments were subsequently performed to validate simulation results. The circuit of Fig. 4 was fabricated on a printed circuit board (PCB). The transmitter and receiver were then spaced apart at a range of 10 to 30 mm with a heterogenous segment of bovine tissue, consisting of fat, muscle, and bone, positioned in between the two components. The results of the simulation analysis were then compared against the experimental data.

Optimal Design for the Charging Sub-system

The external unit of the CSS is the primary source of power in our multi-level system and encounters the least constraints. The transmitter coil design of this unit was primarily defined by practical size and weight limits of a short-term wearable chest strap. This was set to a maximum volume of 100 mm × 100 mm × 10 mm. The subcutaneous unit, shared between the CSS and SSS, determined the constraints of the CSS receiver coil. Similar to the transmitter coil of the SSS, the receiver coil of the CSS was designed as a planar coil to minimize thickness with a maximum diameter of 40 mm. The operating frequency was set to 6.78 MHz to differentiate the signal between the CSS and the SSS, while remaining within the ISM band and providing sufficient power transmission. The frequency of the CSS was selected to be lower than the SSS due to the higher efficiency possible with the lower size constraints of the transmitting and receiving coils in the CSS. The power transfer range was set to 25 mm, in line with the previously measured mean anatomical distance between the surface of the skin and the suprasternal border.³³ Finally, the load impedance was established based on the average voltage during the constant-current phase of the battery charging cycle, during which the battery is primarily charged and there is a small percent change in the battery voltage, thus allowing for calculation approximations.

These constraints were implemented in a Monte Carlo simulation to predict the optimal conditions that would yield the highest power transfer efficiency (PTE). The variables of the system were defined with a uniform distribution based on the aforementioned conditions as shown in Table 2.

TABLE 2.

Variables for optimal design and sensitivity analysis for the Tx and Rx coils of the CSS.

Variable	Distribution
Tx wire gauge	10 AWG-38 AWG
Tx inner radius	3 mm to 50 mm
Tx outer radius	3 mm to 50 mm
Tx height	1 mm to 10 mm
Rx wire gauge	18 AWG to 38 AWG
Rx inner radius	3 mm to 20 mm
Rx outer radius	3 mm to 20 mm

The variables were iteratively inserted into a series of functions to arrive at the output of PTE, as defined by Eq. (2)⁹:

$$\eta =\frac{k^2{Q}_1{Q}_{2L}}{1+k^2{Q}_1{Q}_{2L}}\cdot \frac{Q_{2L}}{Q_L},$$ (2)

where k is the coupling coefficient, Q₁ is the quality factor of the transmitter coil, Q₂ is the quality factor of the receiver coil, Q_2L = Q₂Q_L/Q₂ + Q_L, and Q_L = R_Load/2πfL₂.

The coupling coefficient is independent of the operating frequency but highly dependent on coil geometry and the relative position of coils⁹:

$$k=\frac{r_1^2{r}_2^2}{\sqrt{r_1{r}_2}{\left(\sqrt{r_1^2+D^2}\right)}^3}cos\left(\theta \right),$$ (3)

where r₁ is the diameter of the transmitter, r₂ is the diameter of the receiver, D is the distance between the transmitter and receiver, and θ is the misalignment angle.

The quality factor of the coils is determined using Eq. (4)⁶:

$$Q=\frac{2\pi fL}{R_{\text{eff}}},$$ (4)

where f is the operating frequency, L is antenna inductance, and R_eff is the effective ohmic losses.

To determine R_eff, we begin with the DC resistance of the coil, as defined by Eq. (5)⁶:

$$R_{\text{DC}}=\frac{l}{\sigma \pi a^2},$$ (5)

where l is the length of the coil, σ is the electrical conductivity of the coil, and a is the radius of the wire.

We further analyzed the ohmic losses by taking into account the impact of alternating current on coil resistance. AC resistance of a coil is a ected by two main factors. The first is the skin effect, which results in the primary distribution of current density to the surface of the current-carrying conductor. This results in an effect ive reduction in the cross-sectional area through which current travels, thus ultimately increasing resistance. Dowell presented an estimation for this effect by transforming the turns of a coil into an equivalent foil (Fig. 5d). The AC resistance of the coil for each “foil” layer as a result of skin effect is then defined by Eq. (6)⁴¹:

$$R_{\text{AC}}=R_{\text{DC}}{\xi }^{\prime }\left(\frac{\text{sinh }2{\xi }^{\prime }+\text{sin }2{\xi }^{\prime }}{\text{cosh }2{\xi }^{\prime }-\text{sin }2{\xi }^{\prime }}\right),$$ (6)

where ξ′ is defined by Eq. (7):

$${\xi }^{\prime }=\xi \sqrt{\eta },$$ (7)

in which porosity coefficient, η, is defined by Eq. (8):

$$\eta =\frac{Na}{b},$$ (8)

and ξ is defined by Eq. (9):

$$\xi =d/\delta ,$$ (9)

where skin depth, δ, is defined by Eq. (10):

$$\delta =\frac{1}{\sqrt{\pi f{\mu }_o{\mu }_r\sigma }},$$ (10)

where N is the number of turns in the coil, a is each square width, b is the window width, d is the wire diameter, f is the frequency, μ_o is the permeability of the surrounding material, μ_r is the permeability of the conductor material, and σ is the electrical conductivity of the tissue.

FIGURE 5.

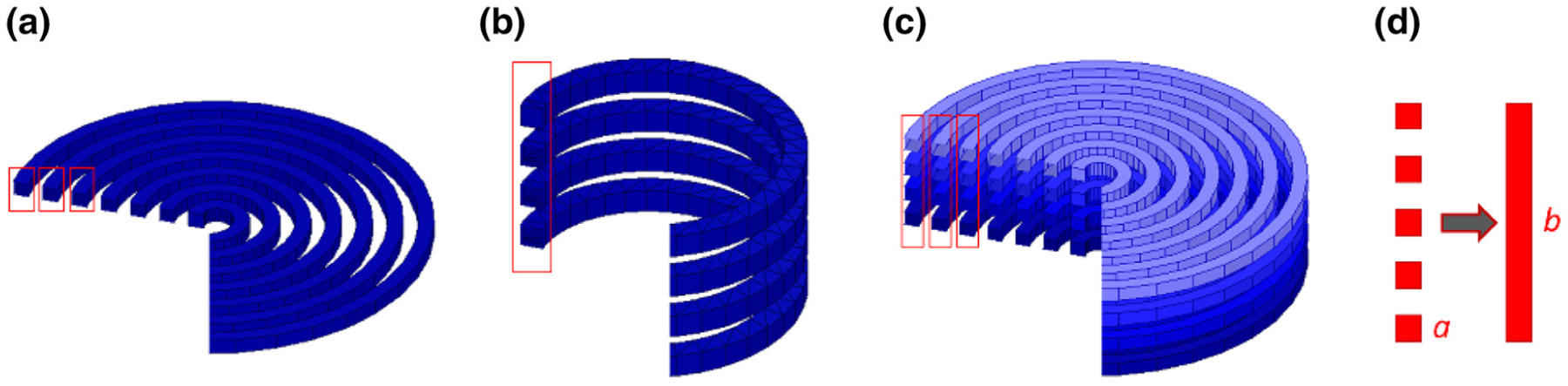
Coil Geometries. (a) a planar circular coil with N-turns, (b) a multi-layer circular coil with a single turn, (c) a multi-layer circular coil with N-turns, (d) conversion of turns of coils into an equivalent foil layer.

The second factor a ecting coil AC resistance is the proximity effect, which is a result of further redistribution of current as a result of the presence of a nearby current-carrying conductor. Using the Dowell method, the AC resistance for the mth “foil” layer as a result of the proximity effect is computed by using Eq. (11)⁴¹:

$$R_{\text{AC}}=\frac{2}{3}{R}_{\text{DC}}{\xi }^{\prime }\left(m^2-1\right)\left(\frac{\text{sinh }2{\xi }^{\prime }-\text{sin }2{\xi }^{\prime }}{\text{cosh }2{\xi }^{\prime }+\text{sin }2{\xi }^{\prime }}\right),$$ (11)

The resistance of the full length of the coil is then defined by Eq. (12):

$$R_{\text{AC}}=\sum _{m=1}^M{R}_{\text{AC},m},$$ (12)

where M is the total number of layers.

The inductance of each coil was calculated based on the coil geometry. Three potential geometries were examined for this study: (1) planar circular coil with N-turns, (2) multi-layer circular coil with a single turn, and (3) multi-layer circular coil with N-turns (Figs. 5a–5c, respectively).

The inductance for a planar circular coil with N-turns is estimated by Eq. (13)^11,39:

$$L=\frac{\left(0.3937\right){\left(N*\frac{r_{\text{i}}+r_{\text{o}}}{2}\right)}^2}{8\left(\frac{r_{\text{i}}+r_{\text{o}}}{2}\right)+11\left(r_{\text{o}}-r_{\text{i}}\right)}\mu \text{H},$$ (13)

and the inductance for a multi-layer circular coil with a single turn is estimated by Eq. (14)^11,39:

$$L=\frac{{\left(r_{\text{i}}N\right)}^2}{22.9r_{\text{i}}+25.4h}\mu \text{H},$$ (14)

and the inductance for a multi-layer circular coil with N-turns is estimated by Eq. (15)^11,39:

$$L=\frac{\left(0.31\right){\left(N*\frac{r_{\text{i}}+r_{\text{o}}}{2}\right)}^2}{6\left(\frac{r_{\text{i}}+r_{\text{o}}}{2}\right)+9h+10\left(r_{\text{o}}-r_{\text{i}}\right)}\mu \text{H},$$ (15)

where r_i is the inner coil radius (cm), r_o is the outer coil radius (cm), h is coil height (cm), d is wire diameter and spacing between turns, and

• $N=\frac{1}{2}\left(\frac{r_{\text{o}}+r_{\text{i}}}{d}+1\right)$ for a planar circular coil with N-turns

• $N=\frac{1}{2}\left(\frac{h}{d}\right)$ for a multi-layer circular coil with a single turn

• $N=\frac{1}{4}\left(\frac{r_{\text{o}}+r_{\text{i}}}{d}+1\right)\left(\frac{h}{d}\right)$ for a multi-layer circular coil with a single turn.

We also performed a correlation analysis between each variable and PTE. To perform this analysis for each of the three coil designs, all variables, except the variable of interest, were kept constant. The resulting change in PTE was then compared against the changes in the variable of interest. This process was repeated for up to 1000 random samples, followed by normalization and averaging over the selected samples. These normalized values were then plotted for each transmitter coil design to demonstrate correlations between each variable and PTE.

Finally, a sensitivity analysis was performed to determine the variable that yielded the highest effect on PTE. The sensitivity was computed by calculating the mean of the variance between each data point in the normalized datasets.

Validation Studies for the Charging Sub-system

We performed two validation studies on the output of our Monte Carlo simulation. Due to the reliance on approximations for our analytical models, we first examined the error rate of our outputs by performing a Finite Element Analysis using ANSYS Maxwell on the interaction between the Tx and Rx coils for one sample in each of the three coil designs.

Since nearly 150 million combinations were examined in the optimization analyses, in the second validation step, we evaluated the persistence of the same level of accuracy in the remaining datasets. This analysis was performed using the correlation data. We computed the variance between each data point in the normalized samples. We then used the variance of these variances to validate computational consistency in which a lower value would indicate high repeatability.

Charging Frequency and Duration

As revealed in Fig. 2, the pacer unit and subcutaneous unit of the pacemaker function based on intermittent charging intervals from the external unit. Charging frequency and duration are dependent on battery capacity and effective coupling in the CSS. We utilized the LP204965 ultrathin Lithium Polymer rechargeable battery for our pacemaker due to an optimal compromise between size and power capacity. The LP204965 carries a 1100 mAh battery capacity and 3.7 V output with dimensions of 65 mm × 49 mm × 2 mm. Charging frequency is dependent on battery capacity and device power consumption:

$$\text{Time to discharge}\left(\text{h}\right)=\frac{\text{Battery capacity}\left(\text{Ah}\right)*\text{battery voltage}\left(\text{V}\right)}{\text{Power consumption}\left(\text{W}\right)},$$ (16)

The time to discharge is thus ultimately impacted by the coupling efficiency of the SSS. Conversely, the charging duration is primarily impacted by the coupling efficiency and power output of the inductive power transfer system of the CSS:

$$\text{Time to charge}\left(\text{h}\right)=\frac{\text{Battery capacity}\left(\text{Ah}\right)}{\text{Charge rate current}\left(\text{A}\right)},$$ (17)

To measure this value, circuit simulations were performed in PSPICE software using the circuit of Fig. 4 in conjunction with the optimized coil properties obtained from Monte Carlo simulations for the CSS.

RESULTS

Stimulation Sub-system

The modeled system defined by the properties in Table 1 were simulated over a range of 10 to 30 mm distance between the transmitter and receiver coils. The resulting voltage output was plotted as shown in blue in Fig. 6. SAR calculations using Eq. (1) also revealed the SSS to be over 20 times below the FCC safety limit of 1.6 W/kg.⁷

FIGURE 6.

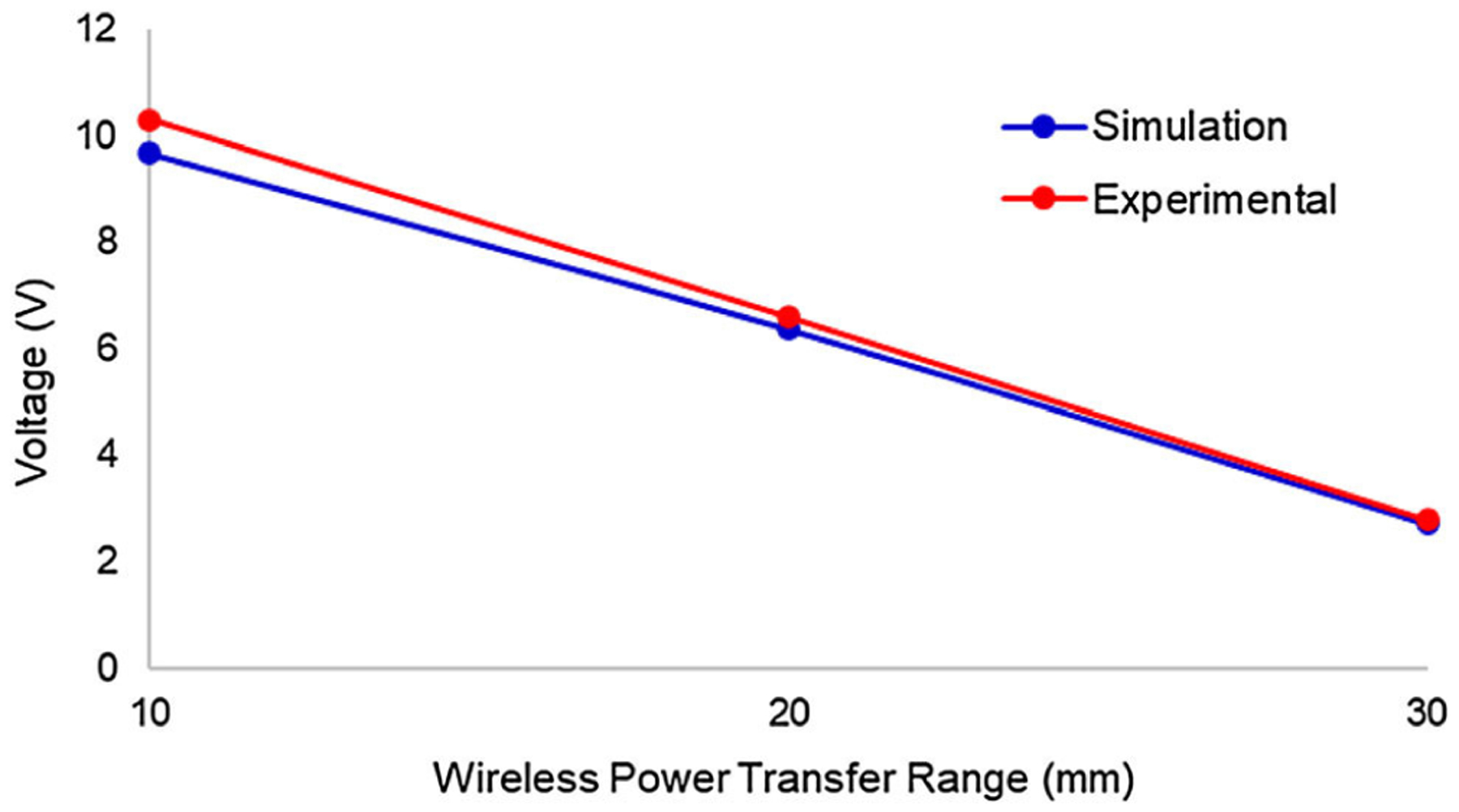
Comparison of the voltage output of the simulation data and experimental data in the wireless power transfer system of SSS demonstrates computational validation.

These results were compared against in vitro experiments over the same range as shown in red in Fig. 6. The mean percent error between the simulation and experimental data was demonstrated to be 4.31%, thus validating the numerical simulations as reliable predictors of the system operational capacity.

Charging Sub-system

Using the variable definitions in Table 2 and function definitions in Eqs. (1) to (14):

• 147,377,664 total coil design combinations were produced, with

• 9,664,704 combinations for a planar circular transmitter coil with N-turns,

• 24,204,096 combinations for a multi-layer circular transmitter coil with a single turn, and

• 113,508,864 combinations multi-layer circular transmitter coil with N-turns.

The receiver, confined to the subcutaneous unit, was only simulated as a planar circular coil with N-turns.

The optimal scenario for each coil design is shown in Table 3, with the most optimal design revealed to be a multi-layer circular transmitter coil with N-turns in combination with the planar circular receiver coil with N-turns.

TABLE 3.

Optimal design variables for the transmitter (Tx) and receiver (Rx) coils.

Tx coil type	Planar, N-turns	Multi-layer, single turn	Multi-layer, N-turns
Tx wire gauge	10 AWG	10 AWG	38 AWG
Tx inner radius	10.00 mm	45.00 mm	9.000 mm
Tx outer radius	33.31 mm	47.59 mm	36.90 mm
Tx height	2.590 mm	10.36 mm	9.000 mm
Rx coil type	Planar, N-turns	Multi-layer, single turn	Multi-layer, N-turns
Rx wire gauge	19 AWG	19 AWG	28 AWG
Rx inner radius	8.000 mm	8.000 mm	3.000 mm
Rx outer radius	19.83 mm	19.77 mm	19.32 mm

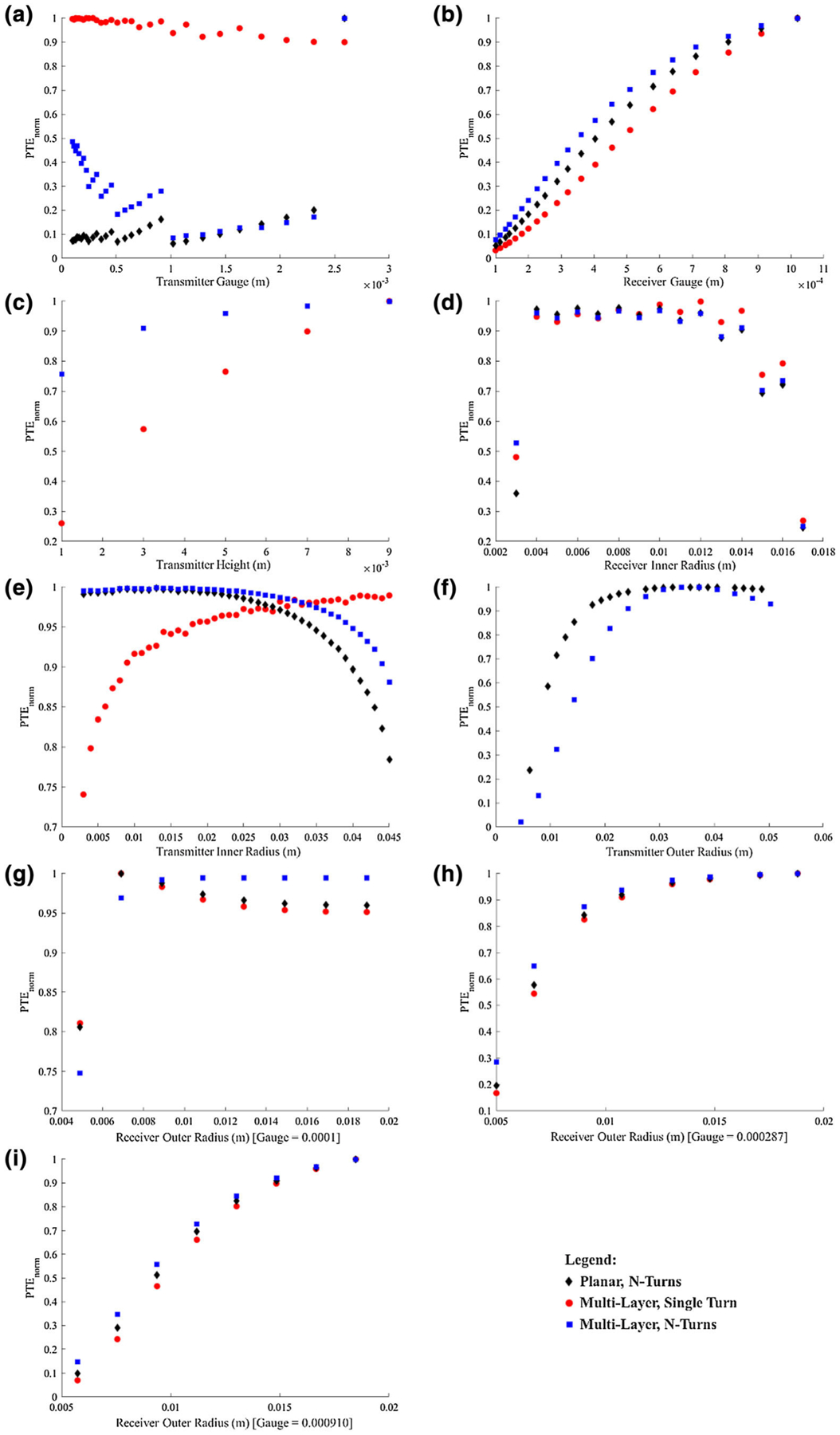
The correlations between each variable and PTE for each coil design (Fig. 7) were subsequently determined. Notably:

FIGURE 7.

Variable correlations vs. PTE for different coil designs. (a) Tx gauge, (b) Rx gauge, (c) Tx Height, (d) Rx inner radius, (e) Tx inner radius, (f) Tx outer radius (g) Rx outer radius at gauge set to 0.0001, (g) Rx outer radius at gauge set to 0.000287, (h) Rx outer radius at gauge set to 0.000910.

• For changes in transmitter wire gauge, while there was a noticeable trend between wire gauge and PTE, the correlation could not be clearly modeled to a function for any of the three coil geometries. The demonstrated step-wise pattern may be attributed to the counter-balance of the impact of resistance and the number of turns. As the number of turns increases, the efficiency would be expected to increase. However, the coil is limited by a specific inner and outer radius, thus necessitating a smaller diameter wire with decreased spacing between wire turns (thus, a rise in resistance due to decreased surface area as well as the greater impact of skin and proximity effect). As the wire diameter increases, this step wise pattern is widened due to the decreasing percent change in resistance.

• For changes in receiver wire gauge, despite variations in transmitter geometries, the correlation remained logarithmic for all three coil geometries.

• For changes in transmitter inner radius, the planar coil with N-turns geometry and the multi-layer coil with N-turns geometry had the same second-order polynomial correlation, but the multi-layer coil with a single turn followed a logarithmic function.

• For changes in receiver inner radius, the system primarily followed a second-order polynomial function for all three coil geometries; however, an outlier was present when the inner radius was very small. This outlier may be a result of increased parasitic capacitance.

• For changes in transmitter height, the correlation was primarily logarithmic for both coil geometries (note: the planar coil with N-turns geometry did not have height correlation analyses).

• For changes in transmitter outer radius, a logarithmic function was again most fitting of the data (note: the multi-layer coil with single-turn geometry did not have outer radius correlation analyses).

• For changes in the receiver outer radius, the correlation was primarily logarithmic with some minor variations between the three coil geometries. An interesting note for the receiver outer radius was the change in the correlation as a result of changes in transmitter wire gauge.

Our sensitivity analysis revealed additional information on the role of each coil variable in power transfer efficiency. As shown in Table 4, the receiver geometry plays a larger role than the transmitter geometry, with the wire gauge being the most important. The strong influence of the receiver is anticipated, based on the larger role of its properties on PTE as shown in Eq. (2). Furthermore, wire gauge was shown to affect the sensitivity of the receiver outer radius on PTE. As the diameter of the wire decreased, the sensitivity of outer radius on PTE decreased. This effect may be due to the increasing effect of number of turns and coil resistance relative to the impact of coil surface area on PTE. This phenomenon can play a large role in establishing design parameters where there are limitations on the size of the receiver coil.

TABLE 4.

Mean variance between each data point in normalized dataset.

Coil type	Planar, N-turns	Multi-layer, single turn	Multi-layer, N-turns
Tx wire gauge	0.0301	0.0013	0.0396
Tx inner radius	0.0041	0.0037	0.0014
Tx outer radius	0.0379	N/A	0.1155
Tx height	N/A	0.0880	0.0160
Rx wire gauge	0.1057	0.1037	0.1030
Rx inner radius	0.0647	0.0526	0.0540
Rx outer radius	0.0037	0.0033	0.0074
	[G2 = 38 AWG]	[G2 = 38 AWG]	[G2 = 38 AWG]
	0.0811	0.0876	0.0634
	[G2 = 29 AWG]	[G2 = 29 AWG]	[G2 = 29 AWG]
	0.1103	0.1198	0.0975
	[G2 = 19 AWG]	[G2 = 19 AWG]	[G2 = 19 AWG]

In the case of the multi-layer coil with N-turns, the transmitter geometry was uniquely shown to have a larger impact on PTE than receiver geometry, with the outer radius revealed to exhibit the largest sensitivity on PTE. This effect may stem from the large number of turns possible in the multi-layer, N-turn coil, leading to a significant increase in inductance that overcomes other variable effects.

We subsequently validated the output of our Monte Carlo simulation using numerical simulations on one sample dataset for each coil design, with the results revealing relative field strengths (Fig. 8). These models were also utilized to confirm conformity to SAR safety standards.

FIGURE 8.

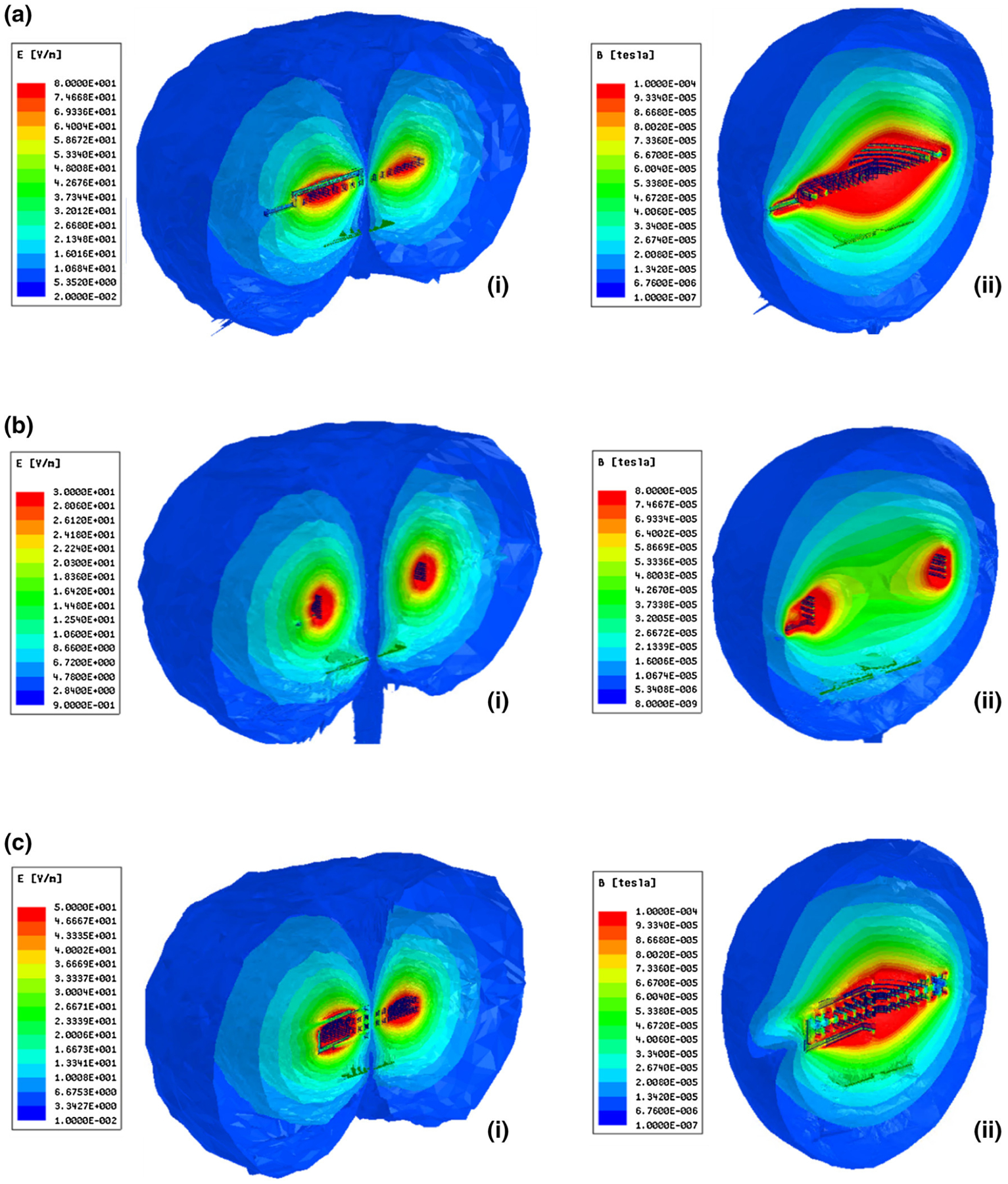
FEM results (a) Planar coil with N-turns (i) Electric (E) field (ii) Magnetic (B) field, (b) Multi-layer coil with single turn (i) E-field (ii) B-field, (c) Multi-layer coil with N-Turns (i) E-field (ii) B-field.

Percent errors between the analytical and numerical models are shown in Table 5. We observed large errors in quality factor computations, with the primary effect on Q of the multi-layer N-turn design. This is due to inherent errors in the analytical approximation for coil AC resistance using the Dowell method. This percent error has been shown to be impacted primarily by the operating frequency,⁴¹ which was kept constant for all simulations. Furthermore, it is important to note that the primary focus of this optimization study was to determine relative, rather than absolute, impact on PTE, which was the focus of our second validation study.

TABLE 5.

Comparison between analytical and numerical model results.

	Tx: planar, N-turns	Rx: planar, N-turns
Inductance	2.4%	0.8%
Quality factor	30.1%	1.7%
Coupling coefficient	4.9%
	Tx: multi-layer, single turn	Rx: planar, N-turns
Inductance	0.2%	0.7%
Quality factor	21.1%	6.7%
Coupling coefficient	9.7%
	Tx: multi-layer, N-turns	Rx: planar, N-turns
Inductance	2.4%	0.1%
Quality factor	72.2%	2.7%
Coupling coefficient	3.1%

The second validation study was performed by comparing the samples to one another to reveal consistency of the analytical model computations. The results of this analysis are shown in Table 6, indicating reliability throughout the analysis.

TABLE 6.

Variance of sample variance to examine model reliability.

Coil type	Planar, N-turns	Multi-layer, single turn	Multi-layer, N-turns
Tx wire gauge	1.175 × 10−5	9.990 × 10−7	5.732 × 10−5
Tx inner radius	3.231 × 10−5	1.292 × 10−5	1.009 × 10−5
Tx outer radius	3.741 × 10−4	N/A	2.147 × 10−4
Tx height	N/A	4.377 × 10−4	5.275 × 10−4
Rx wire gauge	2.480 × 10−5	1.162 × 10−5	7.395 × 10−5
Rx inner radius	5.629 × 10−4	4.082 × 10−4	3.586 × 10−4
Rx outer radius	6.790 × 10−8	1.996 × 10−8	2.893 × 10−6

Charging Frequency and Duration

Charging frequency and duration were computed based on power consumption levels and power transfer efficiency between each of the two sub-systems. The SSS was estimated to consume 1 mW of power to meet pacing demands at 60 BPM, in addition to 20 μW of power for an EKG sensor,¹⁵ and 10 μW for the control circuitry.⁴⁰ Using Eq. (16), the full capacity of the battery would provide sufficient power for nearly 5.5 months.

Using the system output and Eq. (17), we estimated an 8-hour charging session. This session could either be completed once every 5.5 months (e.g. overnight charging) or separated into two 4-hour charging sessions once every 2.5 months depending on patient preference and compliance. Notably, these estimations are based on maximum power consumption for a patient that is in need of continuous pacing with maximum voltage threshold of 5 V at pulse duration of 1 ms. This is in comparison to the significantly lower average voltage threshold of 0.8 V at pulse duration of 0.5 ms,²² which would result in lower power consumption. Furthermore, artificial pacing is only activated in response to detecting aberrant rhythms. In most patients, this is not continuous, thus further extending battery life.

DISCUSSION

In this work, we established a novel system architecture to enable long-range wireless power transfer to a small batteryless deep-tissue implant. Due to the need for a small receiver size within anatomical constraints, inductive power transfer systems in medical implants often encounter very low power transfer efficiency that either demands reduction in wireless power transfer range or increase in power transmission that may surpass SAR limits. We addressed these challenges by implementing an asynchronous four-coil design consisting of two independent two-coil sub-systems. While various multi-coil architectures have been proposed,^{18,20,22,32,43} their reliance on an inter-dependent relay system requires the continuous presence of all coils for power transmission to the final device.

To minimize the number of implants and surgical incisions, the stimulator of the presented system was designed to function entirely independent from the primary power source present in the external unit. This architecture was made possible through the application of remote-controlled power transfer in each sub-system, thus allowing for sufficient wireless power transfer range while avoiding multiple position-limited implants. Furthermore, despite each IPT sub-system’s low efficiency, the utilization of intermittent power transfer enables sufficient power (> 5 V with 1000 Ω impedance) for a short pulse (in this case, 1 ms) stimulation to a miniature intravascular implant over a total distance of 55 mm (20 mm SSS and 25 mm CSS), while remaining below SAR limits.

While the presented architecture has established the potential for long-range wireless power transfer to deep-tissue batteryless implants, there remain challenges in the translation of this work to clinical viability. Firstly, angular misalignment due to cardiac motion may impact power transfer efficiency. The current work aims to compensate for potential losses from misalignment by optimizing design within a controlled environment that could remain applicable under alternative conditions. In the case of the SSS, our previous work has demonstrated sufficient power transfer at up to 20° misalignment.¹ The presented coil design improvements are predicated to perform with higher efficiency, thus further increasing immunity to misalignment losses. In the case of the CSS, the large margin of safety for meeting SAR limits (according to the E-field simulations of Fig. 8) allows for increased power input to meet any potential anatomical variations in distance and misalignment.

Secondly, while the current work establishes the fundamental basis for a wireless architecture, in vivo testing of the presented system design is a vital next step for clinical translation. As part of this transition to a physical model, additional criteria may be established to ensure the absence of intra-system interference in addition to the safety currently established using the two different frequencies. This includes the presence of a shielding substrate for each coil in the subcutaneous unit as well as encryption of the transmitted signal.^25,42 Any residual mutual inductance arising from their spatial proximity may be accounted for using a variable capacitor IC, which can also be utilized to maximize efficiency resulting from changes in coupling due to cardiac motion.

Ultimately, this work establishes a fundamental basis for wireless power transfer in medical devices with a unique perspective on coil design influence on power transfer efficiency. While the communication architecture of the proposed system may seem apparent in design, its potential for providing long-range wireless power transfer to deep-tissue microscale implantable devices provides a first step towards achieving leadless biomedical implants.