Abstract
Nervous system maturation occurs on multiple levels—synaptic, circuit, and network—at divergent timescales. For example, many synaptic properties mature gradually, whereas emergent network dynamics can change abruptly. Here we combine experimental and theoretical approaches to investigate a sudden transition in spontaneous and sensory evoked thalamocortical activity necessary for the development of vision. Inspired by in vivo measurements of timescales and amplitudes of synaptic currents, we extend the Wilson and Cowan model to take into account the relative onset timing and amplitudes of inhibitory and excitatory neural population responses. We study this system as these parameters are varied within amplitudes and timescales consistent with developmental observations to identify the bifurcations of the dynamics that might explain the network behaviors in vivo. Our findings indicate that the inhibitory timing is a critical determinant of thalamocortical activity maturation; a gradual decay of the ratio of inhibitory to excitatory onset time drives the system through a bifurcation that leads to a sudden switch of the network spontaneous activity from high-amplitude oscillations to a nonoscillatory active state. This switch also drives a change from a threshold bursting to linear response to transient stimuli, also consistent with in vivo observation. Thus we show that inhibitory timing is likely critical to the development of network dynamics and may underlie rapid changes in activity without similarly rapid changes in the underlying synaptic and cellular parameters.
NEW & NOTEWORTHY Relying on a generalization of the Wilson–Cowan model, which allows a solid analytic foundation for the understanding of the link between maturation of inhibition and network dynamics, we propose a potential explanation for the role of developing excitatory/inhibitory synaptic delays in mediating a sudden switch in thalamocortical visual activity preceding vision onset.
Keywords: cortex, development, mean fields, neural networks
INTRODUCTION
The developing mammalian brain transitions through intermediate activity regimes that reflect the progression of the circuits through configurations specialized for developmental roles, including enhancing synaptic plasticity, amplification of input, and conservation of energy (Butts and Kanold 2010; Kanold and Luhmann 2010; Khazipov et al. 2013; Kirkby et al. 2013; Luhmann et al. 2016). Although the evolution of the cellular, synaptic, and circuit properties has been described throughout development, how maturation at this scale leads to changes in the emergent collective activity patterns of brain networks remains to be established. Of particular interest is an apparent disconnect between the microscopic circuit properties, which tend to gradually progress from immature to adult levels (Etherington and Williams 2011; Luhmann and Prince 1991; McCormick and Prince 1987), and the macroscopic patterns of activity, whose transitions can be abrupt (Chipaux et al. 2013; Colonnese et al. 2010; Golshani et al. 2009; Rochefort et al. 2009). An important question in development is whether such sudden “switches” in network dynamics reflect dramatic changes in the electrophysiological properties of cells or network circuits or arise as nonlinear responses of the macroscopic activity to gradual changes in microscopic parameters (Colonnese and Phillips 2018). Establishing the relationship between cellular/synaptic maturation and the emergence of new activity patterns is thus a critical component for understanding how neural circuitry becomes functional. It is also important in order to predict how neurological disorders, which often cause subtle cellular and synaptic changes, might have outsize effects during the important developmental epochs when synapses and circuits are forming (Ackman and Crair 2014; Ben-Ari 2008).
Delineating how slow developmental changes at the microscopic scale relate to the fast macroscopic transitions is a challenge for experimental approaches. Inhibiting even processes deemed nonessential can have significant effects on the network dynamics, making it particularly challenging to disentangle the respective roles of the multiple synaptic and cellular changes in the rapid functional transitions. This is where modeling and mathematical analysis become essential. Sudden changes in the activity dynamics caused by smooth changes in the underlying parameters are common properties of recurrent networks (and of nonlinear dynamical systems in general). Mathematically, these can be identified through bifurcation theory, which classifies changes in the number or stability of possible states (e.g., attractors) occurring in dynamical systems as parameters are varied. Applications of bifurcation theory to the neurosciences are abundant: they were used to account for the emergence of visual hallucinations due to cortical disinhibition (Ermentrout and Cowan 1979), perceptual bistability (Shpiro et al. 2009), neuronal bursting caused by slow adaptation of cellular excitability (Ermentrout and Kopell 1986; Izhikevich 2000), and epileptic-like activity in response to slowly increasing input levels (Touboul et al. 2011).
In this study, we apply an analytic approach where we identify bifurcations in a reduced neural population activity model to show how a gradual maturation of inhibitory timescales can account for a dramatic developmental change in cortical activity: the sudden emergence of an asynchronous thalamocortical activity regime that allows for linear responses to sensory input (Colonnese and Phillips 2018). In rat visual cortex, this switch in thalamocortical network dynamics affects both spontaneous as well as light-evoked activity (Colonnese et al. 2010; Murata and Colonnese 2018). It consists of a massive reduction in total excitability of the network as the system shifts from a developmental-plasticity mode into a linear sensory coding mode correlated with the emergence of the ability of the animal to cortically process visual stimuli, all in under 24 hours (Colonnese 2014). Day-by-day measurements in somatosensory and visual cortices have revealed a number of synaptic and circuit changes that might contribute to this switch in cortical activity. These include an increase in feedforward inhibition triggered in both cortex and thalamus, resulting in reduced inhibitory delay (Colonnese 2014; Daw et al. 2007; Minlebaev et al. 2011; Murata and Colonnese 2016), as well as more gradual increases in total inhibitory and excitatory synaptic amplitudes, increasing inhibitory effect due to reduction in the reversal potential for chloride (Glykys et al. 2009; Owens et al. 1996), changes in interneuron circuitry (Marques-Smith et al. 2016; Tuncdemir et al. 2016), patterning of thalamic firing (Lo et al. 2002; McCormick et al. 1995; Murata and Colonnese 2016, 2018), reduction of action potential threshold (Golshani et al. 2009), and changing glutamatergic receptor composition (Rumpel et al. 2004), among others.
Since inhibitory interneurons play a critical role in determining the network properties of adult thalamocortical circuits, particularly the oscillatory synchronization and bistability (Haider and McCormick 2009), we hypothesized that change in inhibition, particularly in the timing of inhibition, is a likely determinant of the rapid emergence of functional visual circuits. Although previous modeling approaches studied the role of inhibitory offset timing (Destexhe and Sejnowski 2009; Ermentrout 1998), their use of first-order differential equation models precluded analysis of the onset timescales, which are most relevant to development. Second-order differential equations modeling a noninstantaneous synaptic integration were used in a variety of models of collective neural dynamics (Jansen and Rit 1995; Wendling and Chauvel 2011). In these models, reproducing in particular oscillatory and epileptiform activity, it was shown that directly replacing second-order synapses by first-order differential equations severely limited the dynamics (Touboul et al. 2011); notably, the mode no longer showed oscillatory activity. Similar models based on second-order synapses were further developed by Liley and collaborators (Liley et al. 2010) to include synaptic reversal potentials, which may play important roles for developmental modeling because, at stages of development earlier than the switch, a significant change in GABA reversal potential arises (Chen et al. 1996). To enable us to analyze the role of changing inhibitory/excitatory strength and onset delay (two critical parameters whose impact was largely overlooked in the computational literature) on network activity, we developed a novel extension of the Wilson and Cowan (WC) model (Wilson and Cowan 1972) in which the ratio of excitatory to inhibitory current amplitudes as well as relative timing can be varied independently to determine their combined potential roles in the evolution of cortical activity.
In this work, we first review the key experimental observations that serve as a foundation of our computational study, and that our model must capture. We then introduce our extension of the WC firing rate model and identify key parameters that will serve in the analysis, notably, the ratio of the excitatory to inhibitory onset timescales, the ratio of the excitation to inhibition strength, and the amplitude of the external stimulus. This model being developed, we then carry out an extensive bifurcation analysis of the model to identify the critical changes in the dynamics of the system determined by the key parameters of input strength and relative inhibitory amplitude and delay. By using these results, we are able to identify a developmental parameter trajectory that is consistent with the experimental data across the first two postnatal weeks, including the rapid switch in activity.
Our results lend support to the hypothesis that dramatic changes in the activity of neural networks during development do not require similarly sharp changes in the cellular and synaptic properties. They also suggest that, for the case of the rat visual cortex, a speed-up in the timescale of the inhibitory neuronal response onset can account for multiple key observations on cortical activity throughout development.
MATERIALS AND METHODS
In all species and systems examined, sensory thalamocortical development can be broadly divided into two periods, which we refer to as “early” and “late,” that determine the spontaneous and evoked network dynamics (Colonnese and Phillips 2018; Dooley and Blumberg 2018; Leighton and Lohmann 2016; Luhmann and Khazipov 2018). The division between these epochs occurs before the onset of active sensory experience: birth for auditory, somatosensory, and visual systems in humans, eye-opening in the rodent visual system, and whisking in rat somatosensory cortex (Chipaux et al. 2013; Colonnese et al. 2010; Fabrizi et al. 2011). These macroscopic changes happen very fast, whereas many microscopic parameters are observed to vary smoothly during the transition between the early and late periods. To show how this can happen while reproducing the experimental data, we start by reviewing some key phenomenological aspects our model aims to reproduce. We then describe an extension of a two-population Wilson–Cowan (WC) model that allows us to parameterize the ratios of the synaptic population onset time delays and current amplitudes received by inhibitory and excitatory cells, which appear to be crucial for capturing the developmental dynamics.
Development of the Thalamocortical Loop
This study uses the rat visual cortex as the reference animal model, as its development has been studied in great detail. Experiments in rat visual cortex show that the switch between early and late periods is extremely rapid, occurring within 12 h (Colonnese 2014; Colonnese et al. 2010) between postnatal day (P)11 and P12. Both visually evoked and spontaneous activity differ qualitatively between early and late periods at multiple levels. These include the duration, amplitude, and structure of flash-evoked activity, the linearity of visual responses, the oscillatory and laminar structure of activity, the continuity of background activity, the stability of membrane potential depolarization, the sparsity of neuronal firing, and the regulation of activity by state (see (Colonnese and Phillips 2018 for review). Some of these differences may be a result of changes in activation patterns in the retina. Indeed, retinal activity transitions from intermittent waves of spontaneous activity to persistent, light-regulated activity at end of the second postnatal week (Demas et al. 2003). The processes underlying early retinal dynamics have been modeled (Hjorth et al. 2015). Here we examine the hypothesis that in addition to changes in the incoming retinal input, which manifest as changes in the patterning of activation on the order of seconds, there are changes in the thalamocortical network that modify the central responses to retinal input on the order of tens of milliseconds.
The most prominent change of central networks to retinal input is that during the early period retinal input, which does not evidence subsecond oscillations, drives 6- to 20-Hz spindle-burst oscillations in visual thalamus and cortex. These oscillations, the period of which is age dependent, synchronize firing within the cortical column (Colonnese et al. 2010; Colonnese and Khazipov 2010; Hanganu et al. 2006; Shen and Colonnese 2016) and between cortex and thalamus (Murata and Colonnese 2016; Yang et al. 2016). These oscillations disappear suddenly at the switch (P12), to be replaced by brief, graded responses to transient retinal activation and persistent stable depolarization to extended activity (Colonnese 2014; Colonnese et al. 2010). In vivo whole cell recordings show that during the early stages periods of activity are unstable and the network does not produce an “active” state, defined as a stable depolarized state, continuous during wakefulness or alternating with down-states during sleep (Fig. 1), until P12. The change to adultlike network dynamics occurs as a rapid switch between P11 and P12 (Colonnese 2014; Colonnese et al. 2010) (Fig. 1). At this age, extracellular recordings no longer reveal a prominent peak in spectral power during wakefulness, also indicating a prominent asynchronous state (Harris and Thiele 2011; Shen and Colonnese 2016). Measurements of sensory responsiveness indicate a shift from a nonlinear “bursting” regime to a graded, linear regime simultaneous with the switch from unstable/oscillatory to stable membrane currents (Colonnese et al. 2010).
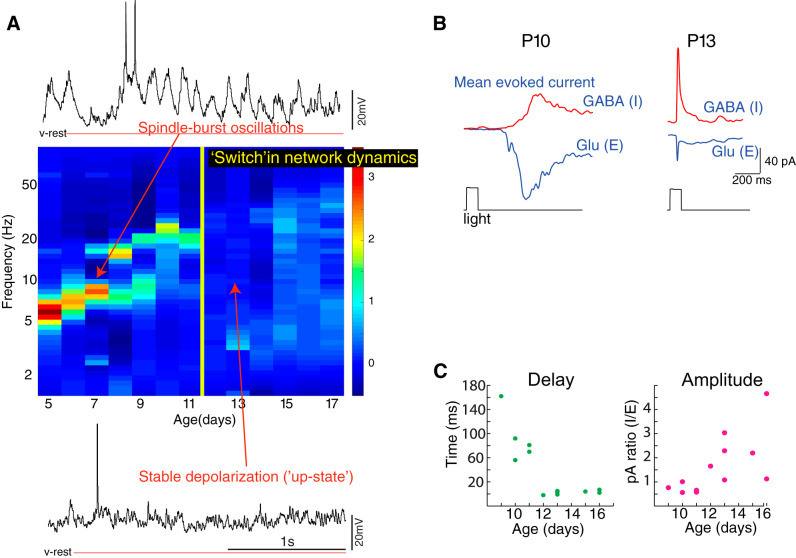
Fig. 1.
Network dynamics and inhibitory synaptic currents during development of visual thalamo-cortex (TC). A: spectral analysis of local field potentials (LFPs) reveals robust oscillatory behavior in early developing TC that increases in frequency but decreases in amplitude. Transition to an adultlike pattern occurs between postnatal day (P)11 and P12. Color graph in middle shows representative spectrograms of layer 4 LFP for each of the indicated ages, with representative whole cell currents at P7 (top, showing prominent 8-Hz oscillations in membrane potential, referred as “spindle-burst” activity) and P13 (bottom, dominated by stable depolarization referred to as an “up” or “active” state). Spectra are normalized to mean power, and the 1/f noise is removed by subtraction. Data are novel analyses derived from animals first reported in Colonnese (2014) and Colonnese and Khazipov (2010). v-rest, resting potential. B and C: whole cell voltage clamp in vivo shows that changes in inhibitory currents are strongly correlated with maturation of network dynamics. B: representative neurons at 2 ages showing mean light-evoked inhibitory (I; GABA) and excitatory [E; glutamate (Glu)] currents. Inhibitory currents at young ages are smaller and delayed relative to excitatory currents. C: development of evoked inhibitory delay (left) and amplitude (right) in visual cortex. Delay is measured as difference between excitatory and inhibitory current onset and amplitude as the ratio between the peaks of each current. Data are reproduced from Colonnese (2014).
Together these observations show that the first 2 wk of the rat’s brain development are characterized by a thalamocortical network that maintains oscillatory activity in response to input. The maturation of these early dynamics to adultlike networks occurs as a sudden transition in the network dynamics leading to an adultlike linear processing regime, asynchronous network activity, and stable depolarization during activation. As measured in somatosensory and visual cortex, the synaptic changes most closely associated with this developmental switch are an increase in the amplitude of synaptic inhibition and a decrease in its delay (Colonnese 2014; Minlebaev et al. 2011). It appears that through this process inhibition and excitation drive toward a general balance. Such measurements of feedforward inhibition in cortex suggest that changes in the timing and strength of inhibition are important, but they reflect only a limited population of total inhibition that likely evolves more gradually. We therefore take these limited measurements of inhibitory and excitatory synaptic currents as starting point to examine timing and power of inhibition during thalamocortical network development.
The Mathematical Model
To clarify the potential key role of inhibitory maturation in the developmental switch, we developed a firing rate model explicitly accounting for the synaptic timing effects. To this end, we extended the WC model to allow us to study independently the effects of excitatory and inhibitory synaptic delays, as well as their rise and decay times (Fig. 2A). Evoked inhibitory and excitatory synaptic population currents seen experimentally (Fig. 1B) display double-exponential profiles not accounted for by the instantaneous exponentially decaying currents of the classical WC model. These are well parameterized by second-order dynamical systems with double-exponential impulse responses, whose amplitude, rise, and decay times can be prescribed (see Fig. 2).
Fig. 2.
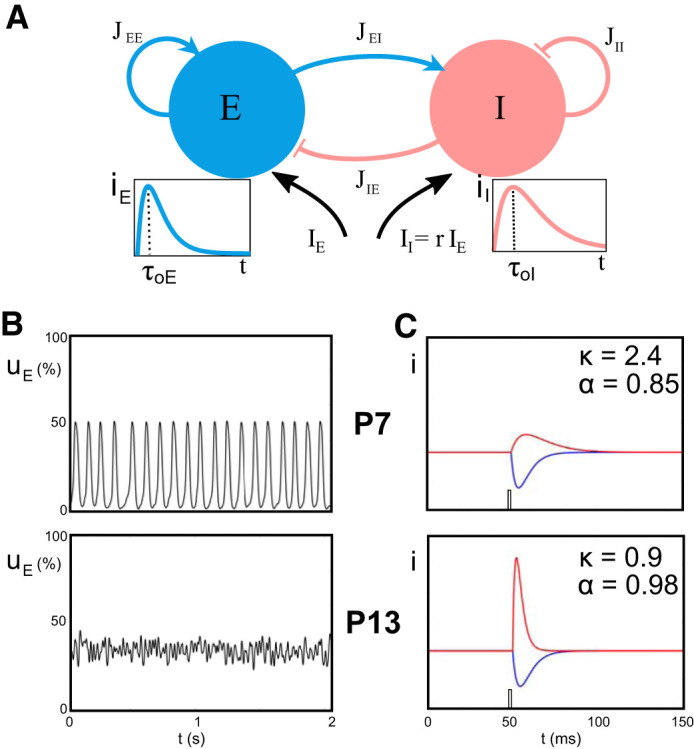
Two-population model with double-exponential synapses. A: 2 populations of neurons, 1 excitatory (E; blue) and 1 inhibitory (I; red) in interaction (coupling coefficients JEE, JEI, JIE, JII) and receiving external inputs, IE and II, respectively. Insets: the typical double-exponential responses to impulses for each population (arbitrary units), with identical peak amplitudes and respective onset delays τoE and τoI. r, ratio between the 2 inputs; t, time. B: numerical simulations of the model, with Gaussian noise stimulus, using coefficients that best approximate behavior at postnatal day (P)7 (top) and P13 (bottom). In these graphs is represented the proportion of active excitatory neurons uE as function of time t: at P7, the network displays an oscillatory behavior at around 10 Hz, whereas at P13 the activity shows a noisy stationary behavior, both being comparable to the in vivo recordings (Fig. 1). C: excitatory (blue) and inhibitory (red) synaptic currents in response to a brief impulse, in arbitrary units, with the convention that the total excitatory transmitted current (area under the curve) is normalized to 1. α, Ratio between inhibitory and excitatory responses; κ, ratio between inhibitory and excitatory current onset delays.
In detail, synaptic responses are defined as the solutions of
| (1) |
where x′ (resp. x″) denotes the first (resp. second) derivative in time of x and f(t) the input to the system. We study these equations in more detail in appendix a and recall that the solution is given by a difference of two exponentials with rates having a ratio λ = τ2/τ1; thus τ1 can be interpreted as a rise time and τ2 as a decay time, assuming τ1 > τ2. Following the approach introduced by Wilson and Cowan (Wilson and Cowan 1972), we model (uE,uI) as the fractions of cells in the excitatory (E) and inhibitory (I) populations firing at time t. Each population is assumed to satisfy an equation of type 1, with respective rise and decay times () and (), yielding the system of differential equations:
| (2) |
where the input to population E/I possibly induces an activation to the fraction of quiescent cells [1 − u_(E/I)] with a maximal rate fE/I and according to a sigmoidal transform SE/I of the total current received. The sigmoids associated to each population may have distinct thresholds θE/I and distinct slopes aE/I but are assumed to have the same functional form: SE(·) = S(aE,θE,·) and SI(·) = S(aI,θI,·) with
| (3) |
The total input received by a population E/I is given by the sum of the external current IE/I and the input of other cells, proportional to the fraction of firing cells in both populations and weighted by synaptic coefficients (Ji,j)(i,j)∈{E,I} that depend both on the level of connectivity between populations (i,j) and on the average amplitude of the postsynaptic currents.1
To reduce dimensionality, we now express time in units of (dimensionless time ), yielding a system depending on three dimensionless ratios:
| (4) |
The coefficients λE and λI determine the slope of the decay of the double-exponential synaptic responses, and κ provides a proxy for the ratio between inhibitory and excitatory current onset delay.
In fact, it can be shown (see appendix a) that the peaks of the impulse responses of the excitatory and inhibitory synapses (the onset times) can be expressed as
| (5) |
with . Equivalently, by reintroducing the standard time units, one has and , and, when λE = λI, we have .
The parameter κ is key for the problem at hand. Indeed, experimental data (Fig. 1) show a decrease of the inhibition onset delay relative to the excitatory one; hence we expect κ to decrease during development.
Moreover, the system depends upon two amplitude parameters fE and fI. Timescales of currents not only impact the timing of synaptic rise and decay, they also affect the total current transmitted, which we can quantify as the integral of the impulse synaptic response (response to a Dirac input), denoted AE and AI. We fixed fEλE = 1 to satisfy the normalization AE = 1 and denoted by α the ratio AI/AE (see appendix a):
Heuristically, when α < 1, the total current that would be received by the inhibitory population in response to a pulse of current is smaller than the total current received by the excitatory population in the same situation. In terms of this interpretable parameter, Eqs. 2 reduce to
| (6) |
where the derivatives are now taken with respect to the dimensionless time variable t̄.
To recapitulate, in our reduced model there are two key quantities that we will work with: κ that gives the ratio of the relative onset delay of inhibition and excitation and α giving the ratio of the total excitatory and inhibitory transmitted currents. In other words, heuristically, κ indicates the temporal scale of inhibition relative to excitation and α is the relative total impact strength of inhibition versus excitation. These two control the balance between excitation and inhibition in the model.
Mathematical and Computational Methods
The full mathematical framework is provided in the reference Wilson and Cowan (1972) and in the main text, while more details can be found in appendix a, b, and c. The bifurcation analysis was performed with XPPAUT (Ermentrout 2002) and MATCONT (in MATLAB environment) (Dhooge et al. 2003). The results shown in Fig. 2B, Fig. 3C, Fig. 4, Fig. 5, and Fig. 6 are based on numerical simulation where Eqs. 6 have been implemented in MATLAB and Python codes with the Euler–Maruyama method for simulating stochastic trajectories. In particular, for each set of parameters we simulated 1 s of dynamics, but frequencies [by fast Fourier transform (FFT) analysis] and amplitudes of the oscillations have been calculated only on the last 500 ms, to avoid the initial transient. Moreover, for the cases with noise, for each set of parameters we ran 10 different simulations and show the mean for the amplitudes of the oscillations in Fig. 6.
Fig. 3.
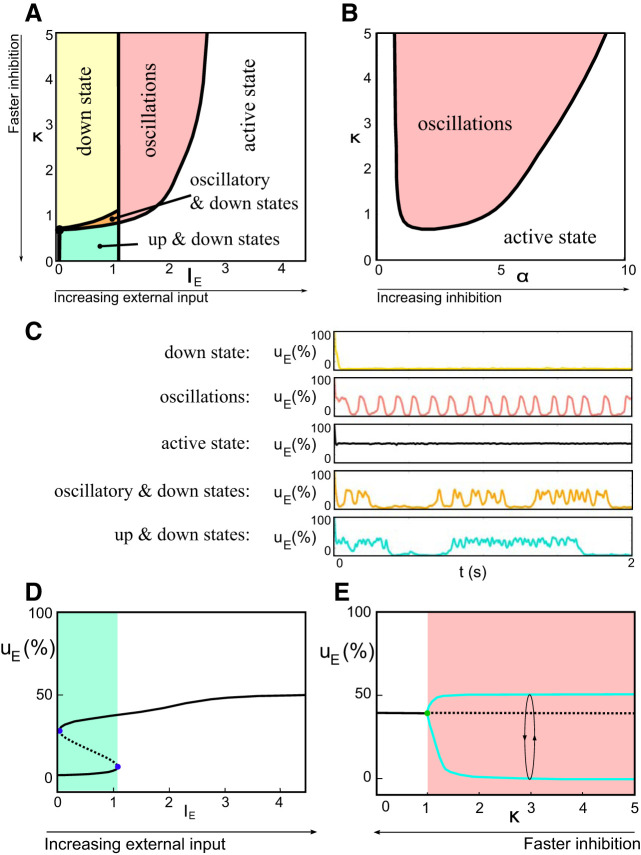
Small changes in inhibition cause large shift in dynamic regimes. A: bifurcation diagram showing dynamics as a function of external input (IE) and inhibitory timescale for a fixed ratio of inhibition to excitation α = 1. We observe 5 typical regimes: a single stable state associated with low firing rates (“down-state”); a single stable state associated with high firing rates (“active state”); a region of bistability between up- and down-states; an oscillatory regime; and a limited region with oscillations and down-states. κ, ratio between inhibitory and excitatory current onset delays. B: dynamics as a function of inhibitory amplitude and timescale for a fixed input IE = 1.5. We observe 2 regimes: oscillatory and active. C: typical time-dependent solutions for the excitatory activity uE in the different parameter regions. D: uE as a function of external input for α = 1 and κ = 0.5. Low input yields 2 stable activity states (solid lines), which suddenly shift to a single stable active state (white region) with a small increase in IE. E: uE as a function of inhibitory timescale for α = 1 and IE = 1.5. Note again “fast” shift from active state to oscillatory regime (blue lines with circle) with increasing ratio of inhibitory to excitatory timescale.
Fig. 4.
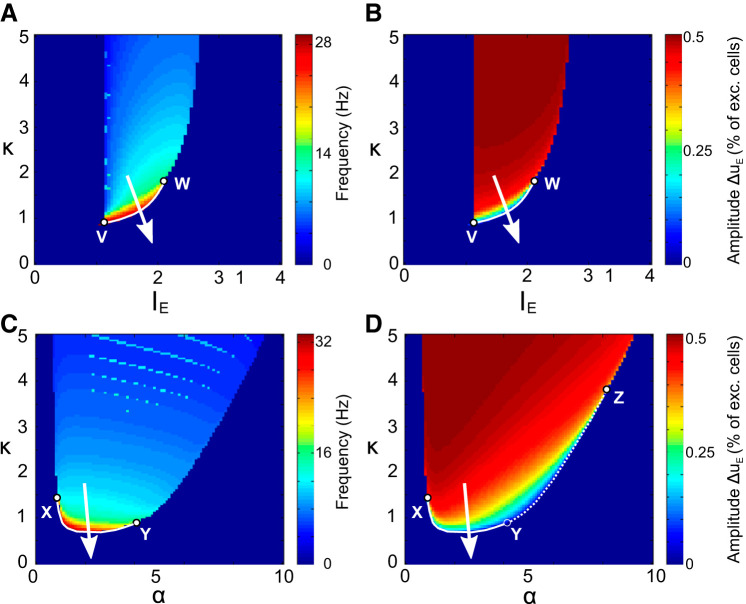
Frequency and amplitude of the oscillatory solutions. A and B refer to (IE,κ) phase space with ratio of inhibition to excitation α = 1, whereas C and D refer to (α,κ) phase space with external input IE = 1.5. In A and C the frequency is expressed in hertz after fixing excitatory synaptic rise time constant = 5 ms (thus the excitatory onset delay has the reasonable value of τoE ∼ 4.5 ms). Suitable trajectories during development should cross the white line between points V and W at the moment of the switch. In B and D, the amplitude values correspond to the difference between the maximum and the minimum of the oscillation in the excitatory population activity uE. Suitable trajectories during development should cross the white line between points X and Y at the moment of the switch (example trajectory shown as white arrow), whereas crossing the dotted white line between Y and Z would only allow for a decrease in the oscillations amplitude.
Fig. 5.
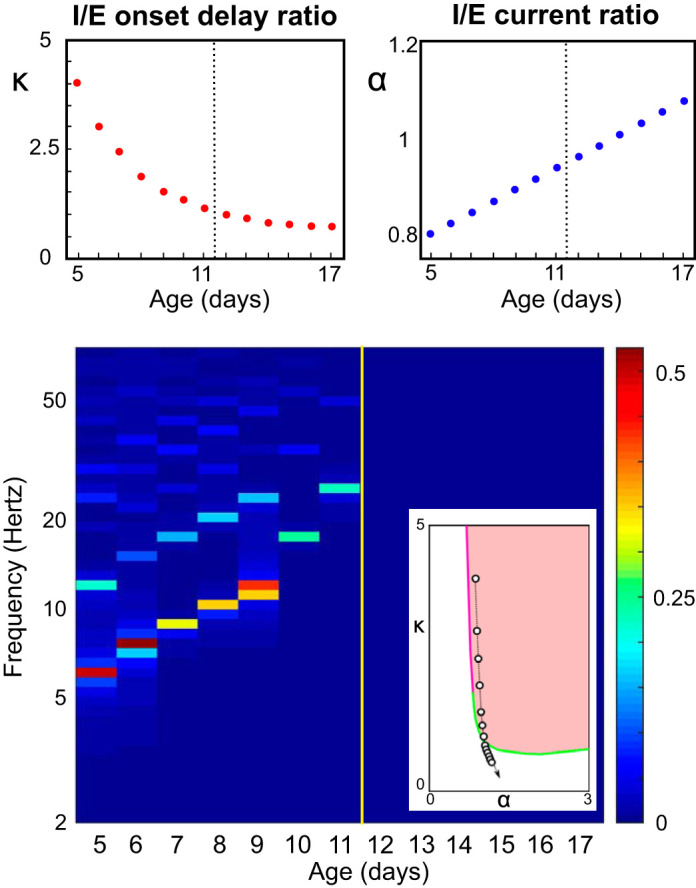
Model of the developmental switch. Top: proposed developmental trajectories for relative [inhibitory (I)/excitatory(E)] inhibitory onset delay κ and amplitude α. The black dashed vertical lines indicate the moment of the development switch, happening between postnatal day (P)11 and P12. Bottom: spectrogram of the solutions of Eq. 6 with external input IE = 1.5 and excitatory synaptic rise time constant = 5 ms, computed as the fast Fourier transform of the excitatory activity uE; same calculation and representation as used in the experimental data of Fig. 1A. Inset: the chosen trajectory in the bifurcation diagram in the 2-dimensional parameter space (α,κ). Color codes as in Fig. 3 and Fig. B2.
Fig. 6.
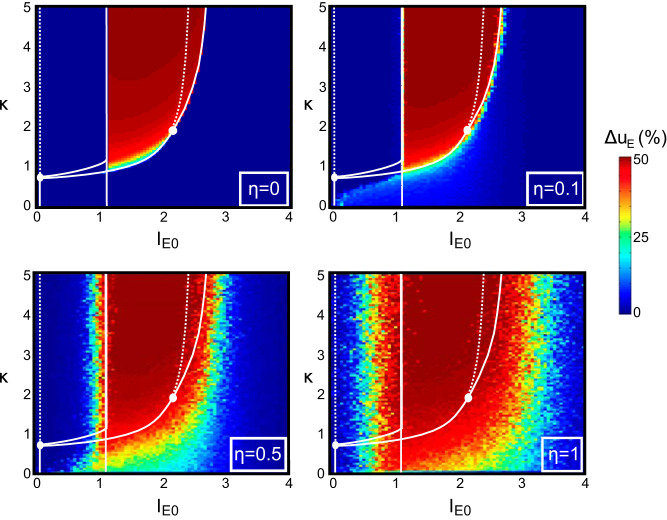
Amplitude of the oscillatory solutions in the presence of noise. We consider the effects of Gaussian noise η on the statistics of Fig. 4, namely, the difference between the maximum and the minimum values of the excitatory activity uE, in the (IE0,κ) phase space, where IE0 is average value of excitatory input and κ is onset delay. The bifurcations of the noiseless case are indicated with the same notation as in Fig. 3.
RESULTS
The patterns of activity recorded experimentally through the switch reveal multiple aspects that a model should reproduce in their spontaneous activity: a smooth increase in spontaneous oscillation frequency (condition c1); a relatively narrow oscillatory band from theta to low gamma (condition c2); a gradual decrease in oscillation amplitude (condition c3); and a sudden transition to broadband noise (asynchronous up-state) (condition c4).
Moreover, responses to brief stimuli also significantly change during development, a feature that a model accurately accounting for in vivo development should also reproduce: a transition from a highly nonlinear all-or-none response to transient inputs (condition c5) to a linear graded response reflecting the stimulus amplitude and duration (condition c6); this transition occurs at the same time as the phase transition observed for spontaneous activity.
We thus investigate the spontaneous and driven properties of this system as a function of the parameters altered during development, to assess whether, and under which conditions, the model can reproduce experimental dynamics and what these conditions tell us about the underlying biological system.
Spontaneous Dynamics
First, we characterized the possible dynamical neural activity states (attractors) of the model of Eq. 6, their nature (steady states or periodic orbits) and stability as a function of the parameters altered during development. Our assumption is that stable attractors determine the observable dynamics in our network and these should correspond to developmental epochs defined by consistent activity patterns (e.g., the early period of oscillations vs. the later period of bistability) and change qualitatively at bifurcation points that should correspond to the rapid switch observed in cortical activity. We test the role of three key parameters assumed to be significantly modified during development: κ (onset delay of inhibition relative to excitation), α (ratio of inhibitory to excitatory impulse current), and IE (level of external input to both populations).
Other parameters were set as in standard references (Wilson and Cowan 1972). In particular, we fixed aE = 1.3, θE = 4, aI = 2, and θI = 3.7. The connectivities have been fixed to JEE = 16, JII = −3, JEI = −JIE = 10. For simplicity, we consider II = rIE with r = 0.5 fixed and λE = λI = 0.8. In appendix c we show that other choices of r, λE, λI, and J do not qualitatively affect the dynamics of the system in the (α, κ, IE) space.
Strong Influence of Synaptic Transmission on Network Dynamics
As expected, the relative timescales and amplitudes of inhibition control the dynamics and substantially modify the response of the system to an input. Figure 3 shows the state (bifurcation) diagram delineating the activity behaviors of the system for various choices of synaptic parameters and input. We find that, consistent with experimental observations, our system features
-
1.
Stationary and bistable states: different combinations of κ, α, IE resulted in a stable down-state (yellow region in Fig. 3), associated with low activity akin to the inactive periods during early development when the system is between waves, or in a stable active state (white region), associated with high activity and likely akin to the up-state and awake and high-visual input states in adults. In addition, a region of bistability (blue region) for the down and active states occurs with low input and fast inhibition, likely analogous to slow-wave state of sleep and low visual input.
-
2.
Oscillatory states: intermediate values or input as well as inhibitory amplitude and delay resulted in rhythmic activation of E/I populations (pink region in Fig. 3) likely representing the oscillatory regime of young animals during retinal wave input. A small region of coexisting down-states and oscillations (orange region) was also observed.
The boundaries (bifurcations) between dynamic regimes are studied in depth in appendix b.
Model Validation and Interpretation
Phase transitions in the model activity.
The state bifurcation diagrams help us to identify parameter regimes that produce model dynamics that are compatible with the spontaneous activity observed experimentally in vivo at different stages of development. Moreover, this analysis suggests a developmental parameter trajectory that would recapitulate the day-by-day development of activity, including the rapid switch from oscillations to active state.
In detail, the oscillatory activity characteristic of immature animals (P5–P10) during retinal waves likely corresponds to the pink (and possibly orange) regions of Fig. 3, whereas the asynchronous activity characteristic of late development (≥P12) during periods of high arousal corresponds to the unique active state (white regions) and the period of low arousal and input (e.g., sleep) to the bistable (blue) parameter regions. Any trajectory in the parameter space connecting these two different scenarios (pink toward white or yellow/orange to blue) would allow a phase transition satisfying the condition (c4) listed above.
In terms of biophysical parameters, oscillations are particularly prominent for κ sufficiently large, i.e., when inhibitory currents activate after a delay that is larger than the excitatory currents (excitation leads inhibition), and only for intermediate values of input IE (too low or too high input leading to down- or up-states, respectively). Low values of κ, associated with faster inhibitory currents, yield dynamics generally consistent with later developmental stages: devoid of intrinsic oscillations during activation and producing bistable network activity during low activation.
If we consider the system under moderate activation, increasing the κ (i.e., increasing inhibitory delay) causes active states to disappear in favor of periodic dynamics as hypothesized to occur during development.
Our analysis indicates in particular that as inhibitory onset becomes faster, the network dynamics undergoes bifurcations leading the system to transition between an oscillatory regime with relatively low oscillation frequencies and large amplitudes to a regime with a stable active constant-activity state that we can interpret as an up-state. Indeed, as we can see in the two-parameter diagrams in Fig. 3A, for any given value of the external input IE there exists a critical value κc(IE) at which the system undergoes a bifurcation toward either a unique up-state regime (white region) or a bistable regime (green region). A similar transition is observed experimentally around P11–P12, characterized by a switch from an oscillatory to a prominent up-state of activity during periods of high activation. For κ < κc(IE), the system tends to settle into the active stationary state regime (pink toward white regions), except for small values of input IE for which this up-state may coexist with a down-state (orange toward green regions). Interestingly, we note that the value of the input IE acting as a transition between these two possible outcomes is independent of κ, indicating that the emergence of the down-state arises at levels of thalamic or cortical input that are independent of the inhibitory-to-excitatory current onset delay ratio. In other words, the down-state may be observed at any stage of inhibitory maturation if the feedforward input is sufficiently low, and interestingly this threshold changes near values of κ that also drive the switch from oscillatory to active states.
In vivo (Fig. 1), the amplitudes of inhibitory synaptic currents increase relative to the excitatory currents (parameterized by α in the model) during development. In the model, we observed (Fig. 3B) that, for input levels associated with oscillations at α = 1, the oscillatory region of parameters is convex, so that increasing or decreasing the relative amplitude of the inhibitory currents α, or simply decreasing the relative inhibitory onset delay κ beyond a critical value, yields a switch to nonoscillatory regimes similar to adult network responses.
Covariation of relative synaptic delays and amplitudes and developmental switch.
We identify three possible scenarios that can lead the system to transition from rhythmic to stationary activity consistent with the experimental evidence: increase of the input, decrease of the relative inhibitory onset delay (κ), and increase of the relative inhibitory current amplitude (α). To differentiate these, we can consider which scenarios are consistent with the characteristic increase in oscillation frequency observed experimentally (criterion c1; see Fig. 1A).
In experiments, a robust measurement of this acceleration was obtained by deriving the power spectrum of the recorded field potential activity, which is tightly correlated with excitatory neuron firing in superficial layers (Colonnese and Khazipov 2010). To directly compare model dynamics to the experimental measurements, we compute the fast Fourier transform of the solutions to Eq. 6 within the range of parameters covered by the above bifurcation analysis and report in Fig. 4 the two relevant quantities associated: peak frequency and amplitude. This analysis reveals that the possibility to have both an increase in oscillation frequency (condition c1 above) and a smooth decrease in oscillation amplitude (condition c3) occurs only in a specific part of the boundary between oscillations and linear regimes as shown by the white curves in Fig. 4A (linking points V and W) and Fig. 4C (between points X and Y). Both curves show a critical role for in κ in mediating a pass through the bifurcation, suggesting that the onset delay of inhibition plays a central role during the developmental switch. Thus, although changes in IE or α can underpin a sudden switch between an oscillatory and a constant-activity state, the telltale frequency acceleration near the transition specifically points toward a decrease of the relative inhibitory current onset delay κ.
Note that in the phase space the oscillation frequency increase happens only near a subset of the boundary of the oscillatory set highlighted by a solid line (mathematically associated to supercritical Hopf bifurcation, as shown in appendix b), whereas the remainder of the boundary is associated with another bifurcation (called a limit point of cycles) that does not meet our experimental criteria. Our model predicts that the corresponding oscillatory amplitude should progressively decrease and not suddenly drop as would be the case if the switch occurred by crossing the limit point of cycles. In other words, condition c3 arises naturally in the model when conditions c1 and c4 are satisfied.
Following our analysis, we can now propose a specific developmental trajectory of the parameters that reproduces development in vivo (see Fig. 1C). To follow the observed data, we qualitatively constrained the inhibitory onset timescale to decrease and the synaptic amplitude to increase with the developmental stage as seen in data. We fixed the excitatory time constant to a realistic value of = 5 ms. A specific set of age-dependent parametric trajectories depicted in Fig. 5, top, resulted in an accurate match with the experimental data: a sudden switch, at age P12, between an oscillatory state and a quasi-constant activity, together with a clear increase in oscillation frequency and decrease in amplitude approaching the switch.
Robustness to noise.
The above results were obtained in a deterministic system, which allowed us to use bifurcation theory to show sudden transitions in the network activity as a function of the excitation-to-inhibition timescale ratio and input level. However, in physiological situations, neural populations show highly fluctuating activity due to multiple sources of noise (e.g. channel noise or synaptic noise resulting from the intense bombardment of neurons from other brain areas) (Faisal et al. 2008). The role of noise in dynamical systems has been the topic of intense study (Berglund and Gentz 2006; Lindner et al. 2004). In general, large amounts of noise generally overwhelm the dynamics, whereas small noise produces weak perturbations of the deterministic trajectories away from instabilities. In the vicinity of the phase transitions (bifurcations), even small amounts of noise may significantly modify the deterministic dynamics (Buchin et al. 2016; Lindner et al. 2004; Tuckwell et al. 2009). Because of the importance of these transitions in the switch, we now look into the impact of noise on the model dynamics of Eq. 6. We assume that the various sources of noise result in random fluctuations of the current received by each population around their average value IE0 and II0 = rIE0 and model the current received by each population by the Ornstein–Uhlenbeck processes
| (7) |
where and are standard Wiener processes and η is a nonnegative dimensionless parameter quantifying the level of noise. We computed the solutions of the system and derived the statistics of the solutions for various levels of noise. The average amplitude of the variations in time of the solutions as a function of the excitatory input IE0 and excitation-to-inhibition timescale ratio κ is depicted in Fig. 6 for various values of η and fixed r = 0.5. Away from the bifurcation lines, the impact of moderate noise is reasonably negligible, and the noisy system behaves as its deterministic counterpart (plotted, e.g., in Fig. 2B), where at P7 (before the switch) the oscillating regime displays minor perturbations from the deterministic (η = 0.3, κ = 2.4, α = 0.85, IE = 1.5), and similarly the stationary up-state at P13 (after the switch) is only perturbed (η = 0.3, κ = 0.9, α = 0.98, IE = 1.5). Near transitions, we observe two effects that have a moderate, yet visible effect on the precise parameters associated to a switch. In particular, we observe that all transition lines tend to be shifted by the presence of noise, enlarging the parameter region associated with oscillations. This effect is likely due to stochastic resonance effects (arising specifically in the vicinity of heteroclinic cycles or folds of limit cycles identified in appendix b), while in the vicinity of the supercritical Hopf bifurcation already highlighted for its relationship with physiological data, coherence resonance effects due to the interaction of noise with the complex eigenvalues of that equilibrium (see Lindner et al. 2004).
We thus conclude that despite a slight quantitative shift of the parameter values associated with the switch, the qualitative behavior of the noisy system remains fully consistent with the experimental observations. Indeed, a decrease in the timescale ratio κ, possibly associated with an increase in the input, yields a transition from oscillating solutions to a stationary activity level associated with linear responses to input, which ensures that the proposed mechanism underlying the switch is robust in the presence of noise.
Response to transient inputs.
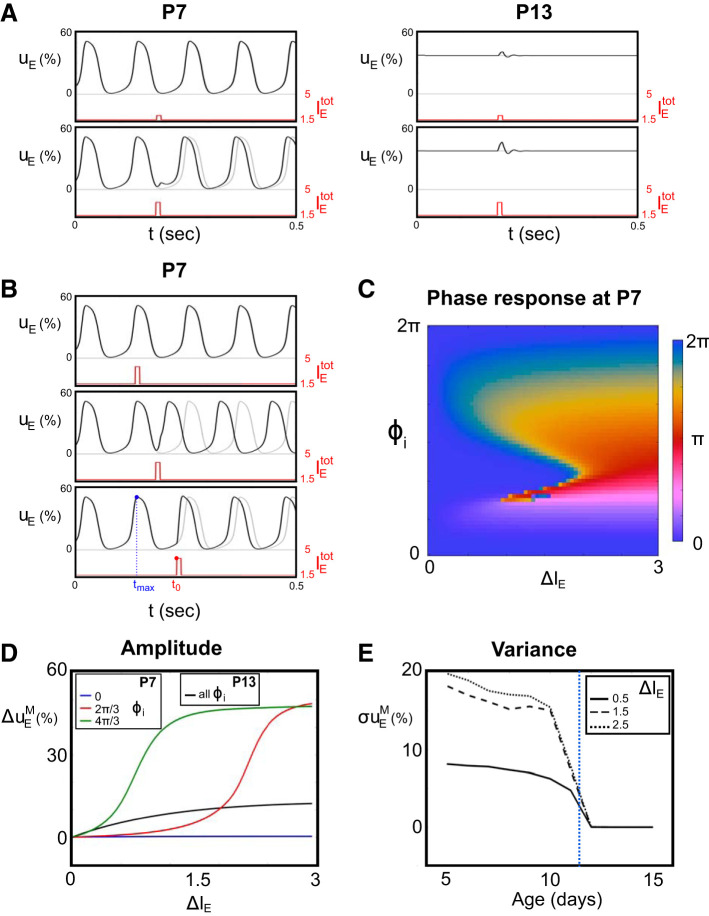
Above we showed under which constraints all conditions c1–c4 are satisfied for the model to match the experimental data on the spontaneous activity during the development. However, spontaneous activity is not the only dramatic change reported during the developmental switch: the responses to transient input, like light pulses, are also markedly modified through the switch. These phenomena, labeled conditions c5 and c6 above, can be seen as a consequence of the same bifurcations arising in the system. Having developed and identified the parametric paths in the model solely for the spontaneous activity, we wanted to see if the model and our chosen trajectory through κ, α, and IE also generate realistic responses to stimuli. We thus considered the dynamics of the system at P7 (κ = 2.4, α = 0.85, IE = 1.5) and P13 (κ = 0.9, α = 0.98, IE = 1.5) in response to brief square pulses (duration δt = 10 ms) of varying amplitude ΔIE emulating light pulses:
| (8) |
where is equal to 1 for t ∈ [t0, t0 + δt] and 0 otherwise.
At P7, the pulse causes both a transient increase in the amplitude of the excitatory activity and, more markedly, a phase shift of the spontaneous oscillations that depends on the phase at which the stimulus is applied (Fig. 7A). The amplitude of the transient response does not grow linearly with the amplitude ΔIE of the external transient. In sharp contrast, after the switch the response to the pulse is characterized by small-amplitude damped oscillations whose maximal amplitude shows a much more gradual dependence in the pulse amplitude and no specific dependence on the timing of the impulse presentation (Fig. 7A; P13). To assess, before the switch, the dependence of the response to the stimulus, we considered the phase shift Φt, implicitly defined asymptotically by
| (9) |
where is the excitatory activity for ΔIE = 0, T is the period of the oscillations, and parametrizes the initial phase shift between the beginning of the transient input and the instant of the maximum in the activity just preceding t0 (this quantity is similar to the classical phase response curve in weakly perturbed oscillators). The asymptotic phase shift Φt is shown in Fig. 7C as a function of ΔIE and ϕi. As expected, for small transient pulse amplitude, a small phase shift arises regardless of the timing. However, when ΔIE increases an unstable region appears, and the phase response becomes much more complex and varies sharply as a function of both parameters (details of the dependence are not considered here, the point being that a strong dependence arises before the switch).
Fig. 7.
Response to external input transients. We consider the response of the excitatory population when a 10-ms square input is applied to both excitatory and inhibitory populations. A: results corresponding to postnatal day (P)7 (left) and P13 (right), where model parameters are fixed as in Fig. 2 and Fig. 5, in the absence of noise, for 2 different external stimuli, ΔIE = 0.5 (top) and ΔIE = 1.5 (bottom). Solid black lines represent excitatory activity uE when an external input transient is applied (red solid lines), and dotted lines are the corresponding activity for baseline constant input. B: responses at P7 for different onset time t0 of the transient external stimuli, relative to the instant of previous maximum of activity tmax. C: the color map represents the asymptotic phase shift Φt between the excitatory activity response and the unperturbed solution, as a function of the transient amplitude ΔIE and the initial phase shift ϕi. D: maximum difference Δ in activity between perturbed and unperturbed dynamics, for different initial phase shift ϕi, in a window of 100 ms from the onset time of the external impulse (P7 and P13 model parameters). E: variance σ of the distribution over ϕi as a function of the age of the animal (parameters fixed as in Fig. 5) for different values of ΔIE. The blue dashed vertical line indicates the moment of the developmental switch, happening between P11 and P12.
This dependence in the timing of the stimulus presentation is further apparent in Fig. 7, D and E, when considering the maximal difference between perturbed and unperturbed activity in a window Δt = 100 ms induced by impulse stimuli at different phases (Fig. 7D) before the switch (P7):
| (10) |
Depending on ϕi, very different nonlinear responses can be recorded. Because of the absence of spontaneous oscillations, no such variability arises after the switch. The switch is thus associated with a dramatic drop in the variance of the response distribution as a function of the time of presentation and at all stimulus amplitudes as we cross the developmental transition (Fig. 7E). After the developmental switch (≥P12), only a transient response over the asymptotic stable solution appears, and its amplitude gradually increases with that of the external transient stimulus, independently on the precise parameters corresponding to different days in our chosen trajectory example (Fig. 7, D and E). Therefore, these results show that our simple development model in terms of a decrease of the inhibitory/excitatory onset delay κ is compatible with conditions c5 and c6.
DISCUSSION
During thalamocortical development, multiple aspects of network activity undergo dramatic changes at all scales, from microscopic to macroscopic, during spontaneous activity as well as in response to external stimuli.
Using nonlinear dynamical systems theory, we studied how underlying synaptic and circuit changes, generally slow and progressive, can give rise to abrupt transitions in the global network dynamics. In particular, we focused on one specific phenomenon, the sharp switch occurring in the rodent visual cortex that changes the pattern of spontaneous activity in under 12 h. This switch transitions a regime in which 5- to 20-Hz oscillations, called “spindle-bursts” or “delta-brushes,” are produced in response to thalamocortical input to a regime in which such input generates asynchronous irregular firing.
To infer the possible mechanism inducing such a transition, we developed a new version of the standard Wilson–Cowan model for excitatory and inhibitory population activities, enriched with double-exponential synapses. This modification allowed us to introduce new features relevant to developing neurons, specifically modulating the delay of each population’s response to input. These timescales indeed appear particularly prominent, as inhibitory and excitatory cells display a significant maturation of the profile of the synaptic responses to current pulses throughout the switch (Colonnese and Phillips 2018).
The Wilson–Cowan approach has been extensively studied in the case of mature cortical networks (Destexhe and Sejnowski 2009; Ermentrout 1998), and one of its major advantages is its simplicity yet an ability to accurately reproduce observed behaviors. Indeed, only a few biologically related parameters define the model, a massive simplification compared with more biologically accurate models. If, on one hand, this obscures a direct relationship with experimental measurements, it provides a direct understanding of the main rate-based mechanisms underlying the global dynamics of the system. In Rahmati et al. 2017, for example, another version of the Wilson–Cowan model, enhanced by short-term plasticity, was used to address another related aspect of the development, namely the emergence of sparse coding. In this work, we have shown that the decay of the inhibitory onset timescale, which we examined as a ratio to the excitatory timescale, explains the main features of the developmental switch observed experimentally. Mathematically, when the ratio between the two onset delays decreases, the dynamics of the system crosses a Hopf bifurcation arising where excitatory and inhibitory delays are of the same order of magnitude. Moreover, the model constrains directly the possible changes in electrophysiological parameters consistent with the experimental observations. In particular, we showed that an acceleration of the early oscillations and a decay of their amplitude, which occurs experimentally before the switch, predicts specific changes in timescale ratios and amplitudes. Namely, it predicts a decay of the onset delay ratio of inhibitory to excitatory currents and an increase in the relative inhibitory current amplitude. Both key phenomena were observed experimentally during development (Fig. 1).
To exhibit this result, we provide an extensive numerical analysis of the bifurcations occurring as a function of the normalized inhibitory delay together with relative inhibitory strength and the amplitude of the external input. We found that smooth progression in these parameters caused a flip from an initial oscillatory state to a constant-activity regime. Generally, this switch could be driven either by increasing the inhibitory amplitude or by reducing the inhibitory response time. However, the experimentally measured acceleration of frequency and reduction in amplitude can only be accounted for by significant changes in the inhibitory delay, suggesting it is the key parameter driving development.
Because of the natural biological variability of the parameters, it is a complex task to assess whether changes in the electrophysiological parameters are sudden or continuous. We argue that our mathematical model and analysis are relevant in both cases: in a system that does not display the bifurcation related to timescale ratios, even a sharp decrease in the inhibitory delay would not result in the observed qualitative change in network behavior because of the persistence of a stable attractor dynamic of the system.
From the biological viewpoint, this result suggests that the transition is intrinsically related to the fact that the inhibitory population response time becomes faster by a larger fraction than the excitatory response time. In other words, the inhibition speeds up fractionally faster through the switch than the excitation. This is easy to see; if we denote and as the onset timescales of the E/I populations before and after the switch, respectively, a decreasing inhibitory-to-excitatory ratio (κ) gives
Note that this is result is independent of the fact that already observed in Fig. 1C and which could theoretically occur with constant, increasing, or nonmonotonic evolutions of the ratios. Going back to experimental data, we computed the ratio of the excitatory and inhibitory onset delay and found preliminary evidence of the decay of ratios according to the above formula (Fig. 8). The data indeed show a significant decrease of the timescale ratio before the switch κb = 1.47 ± 0.05 and after the switch of κa = 0.98 ± 0.11 (mean ± standard error; 1-tailed Welch’s t test for κb > κa yields a P value: P = 0.001). However, because of the limited number of points, more data need to be collected specifically for this purpose in order to resolve the fine evolution of the ratio as a function of age.
Fig. 8.
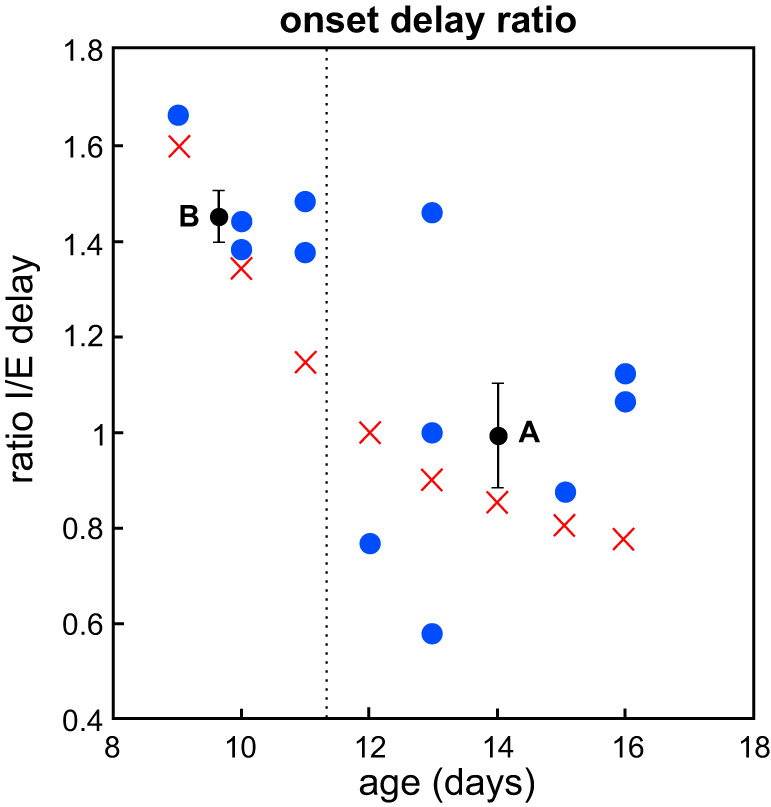
Decreasing ratio of delays. Blue points represent the experimental data of Fig. 1C expressed in terms of ratio between inhibitory and excitatory current onset (I/E) delays. The dashed line indicates the moment of the observed developmental switch, between postnatal day (P)11 and P12. Black points and error bars represent the mean values and standard error for the points before (B) and after (A) the transition. Red crosses correspond to the trajectory for onset delay κ chosen in the example of Fig. 5.
Although not designed to model the switch from discontinuous to continuous activity that occurs alongside the switch from the oscillatory to stable regimes, our results suggest that a single mechanism can cause both. Previously it has been proposed these two changes are the result of separate (though perhaps linked) circuit changes: increased inhibition drives the stabilization of thalamocortical networks, and increased input to thalamus from ascending neuromodulators and/or continuous retinal input drives continuity (Colonnese 2014; Colonnese et al. 2010; Murata and Colonnese 2018). However, our results show that even in the absence of changes in strength of input (imagined as IE − II), as long as there is some minimal excitation occurring during low-activity periods we would expect a switch from persistent down-state to a bistable up/down regime at close to the same values for κ at which we see the switch from oscillations to stable up-states. Thus periods of low input that previously resulted only in network silence now produce alternating activity and down-states, and inputs that produced oscillations now produce stable activation, which is exactly what is observed in vivo (Shen and Colonnese 2016).
Initially, we aimed to account for a qualitative change in the dynamics of cortical networks when inhibition becomes faster. Yet we were able to capture not only the main network activity features observed experimentally but also the order of magnitude of the frequency and amplitude trajectories of the oscillations without the need for fine-tuning. The exact quantitative results, however, depend on the actual parameter values. In particular, although the existence of the preswitch oscillations depends only on the ratio between the inhibitory and excitatory onset delays, the frequency of those oscillations is proportional to the absolute value of those delays. In our final quantitative simulations, we focused on the case where the excitatory current delay is kept fixed; studies based on further experimental measurements could allow consideration in more detail of the role of the absolute excitatory delay and its developmental dynamics.
Our simple model can be improved in several directions. First, our model does not distinguish distinct neural populations and the variety of their timescales within the thalamocortical loop. A direct perspective would be to make the model more precise by including various populations and changes in their timescales and relative impact. In particular, the early thalamocortical oscillations described in Fig. 1 involve the thalamus, itself showing an oscillatory activity at the same frequency as cortex, and experimental evidence shows that the intact cortico-thalamic loop is a critical component of these oscillations (Murata and Colonnese 2016). The model of early oscillation generation in the visual system we developed here suggests that unpatterned input (roughly IE − II in the model) from retina provides the drive and thalamus and cortex as a whole oscillate in response. This reproduces accurately the fact that both thalamus and cortex switch to asynchronous/tonic patterns of firing after the switch and both are the sites of reduced delay and increased amplitude of inhibition (Murata and Colonnese 2018). The value of the present results lies in showing that recurrent networks of excitatory and inhibitory neurons can be made to undergo developmental transitions similar to those observed in vivo in response to similar changes in the electrophysiological parameters. Future studies will reveal the circuit specifics of these networks during development.
A natural question arising from this study is: are there known developments of the inhibitory circuitry that could underlie the decrease in population timescale ratios predicted by our model? Evidence shows that “fast-spiking” parvalbumin-expressing interneurons, which provide rapid, persistent inhibition in the cortical network (Hu et al. 2014), gradually acquire these characteristics during the second and third postnatal weeks (Huang et al. 2007; Luhmann and Prince 1991). Furthermore, in somatosensory cortex, inhibitory circuits undergo a dramatic rearrangement, with thalamocortical axons changing their target from slower somatostatin interneurons neurons in layer 5 to parvalbumin-expressing layer 4 interneurons (Daw et al. 2007; Marques-Smith et al. 2016; Tuncdemir et al. 2016). This development of feedforward, hence faster, inhibition in cortex is accompanied by the incorporation of the inhibitory thalamic reticular nucleus within the thalamocortical loop (Murata and Colonnese 2016), which would be expected to further speed and increase the bulk inhibitory population response. Future iterations of the model could incorporate the local connectivity of each of these inhibitory subpopulations in the model, but for the current iteration, with a single rate standing in for all inhibitory types, such sequential integration of feedforward interneuron type into the network should result in an apparent quickening of the mean response as modeled here. An important question that remains largely open is to analyze the mechanisms supporting the developmental switch in spiking neural network models. Progress in this direction requires us to better understand the neural bases of the maturation of synaptic transmission to properly integrate these changes in that model. A spiking model of the developing thalamo-cortical loop would further allow addressing deeper questions such as the possible modifications in spike patterns through development and how these (in addition to firing rates only) could support appropriate information processing after the switch.
We should also emphasize that our extension of the Wilson–Cowan model to investigate temporal dynamics of inhibition has implications and applications beyond development. Disruption of inhibition, particularly mediated by fast-spiking parvalbumin neurons, has been implicated in a number of neurodevelopmental disorders (Contractor et al. 2015; Gogolla et al. 2009). These include multiple mouse models of autism and schizophrenia. Although to our knowledge direct measurements of inhibitory delay have not been published, reduced drive (Gibson et al. 2008) or density of fast-spiking parvalbumin neurons should result in net slowing down of inhibitory rise times as represented within our model. The bifurcations of this model show that even small changes in delay can result in significant changes in the oscillatory dynamics, which might inform processing deficits observed in these conditions.
GRANTS
M.T.C. is supported by the National Eye Institute (EY-022730). A.R., J.D.T., and B.S.G. acknowledge funding from ANR-10-IDEX-0001-02 PSL*. This study was performed as a part of the Basic Research Program at the National Research University Higher School of Economics (HSE) supported by the Russian Academic Excellence Project “5-100.”
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
A.R., M.T.C., J.D.T., and B.S.G. conceived and designed research; A.R., M.T.C., J.D.T., and B.S.G. performed experiments; A.R., M.T.C., J.D.T., and B.S.G. analyzed data; A.R., M.T.C., J.D.T., and B.S.G. interpreted results of experiments; A.R., M.T.C., J.D.T., and B.S.G. prepared figures; A.R., M.T.C., J.D.T., and B.S.G. drafted manuscript; A.R., M.T.C., J.D.T., and B.S.G. edited and revised manuscript; A.R., M.T.C., J.D.T., and B.S.G. approved final version of manuscript.
ACKNOWLEDGMENTS
The authors thank M. Krupa for discussions.
APPENDIX A: MATHEMATICAL DETAILS
In this appendix, we discuss some mathematical details concerning the theoretical model described in the main text. Starting from the model defined in Eq. 2 in the main text, and applying the time redefinition and the reparametrization of Eq. 4 described in the main text, we obtain the system
| (A1) |
To understand the role of the parameters κ, α, and λ’s discussed in this work, we consider here the case in which the right-hand sides of the differential equations are substituted by Dirac external impulses at time t0:
| (A2) |
Therefore the simplified differential equations for the excitatory and inhibitory activities can be written as
| (A3) |
This dynamical system can be analytically solved, and the general solutions read
| (A4) |
where θ(x) is the Heaviside theta function and c1, c2, c3, c4 integration constants. When imposing the solutions to be trivial before the external impulses [uE(t) = uI(t) = 0, t < t0], we finally obtain
| (A5) |
It is easy to verify that the areas under the curves of these responses are
| (A6) |
In the main text, we fixed the parameters fE = 1/λE and fI = 1/(κ2λI) in order to have an area AE = 1 and a ratio AI/AE = α. The parameter α can then be identified as the quantity of response of the inhibitory population to a spikelike input, with respect to the excitatory response. Moreover, from these explicit solutions it is easy to derive the exact onset delays, defined as the time at which the responses reach their maximum
| (A7) |
In Fig. A1 we have shown the effect of changing the parameters κ and λ’s on these solutions. These results justify our interpretation of κ as representing the ratio between the onset delays of excitatory and inhibitory responses (which is an exact result when λE = λI) and λ’s as the parameters regulating the decay slopes of these responses.
Fig. A1.
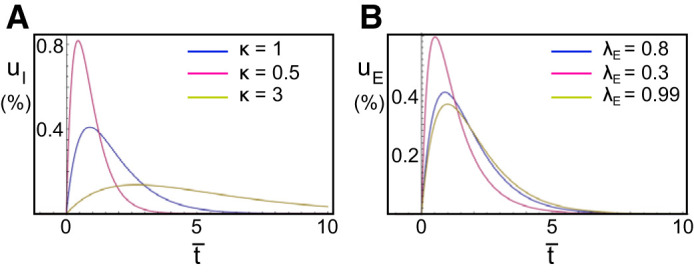
Dependence of the response activity on parameter onset delay κ and ratio of responses λ. A: the response of the inhibitory activity uI to a Dirac input at dimensionless time t̄ = 0, for different values of κ, with λI = 0.8 and α = 1. B: the same response of the excitatory activity uE for different values of λE.
APPENDIX B: CHARACTERIZATION OF THE BIFURCATIONS OF THE SYSTEM
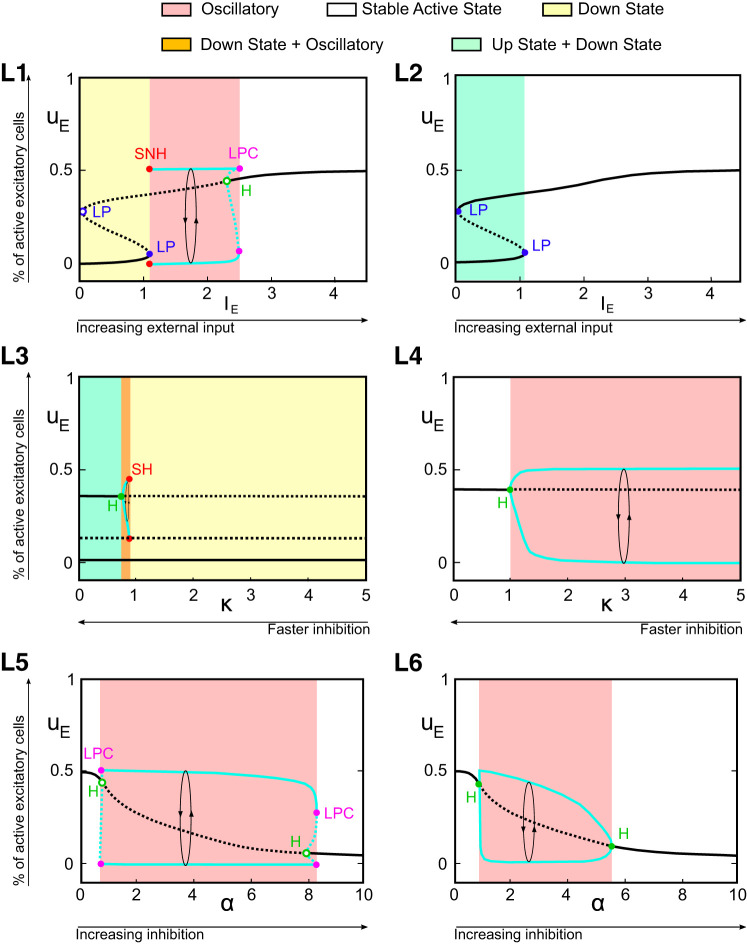
The regions of typical behavior are separated by the presence of bifurcations of fixed points and periodic orbits that were tracked numerically. For simplicity, the technical terminology was avoided in the main text, but we consistently used a color code to identify, in the transitions, each specific bifurcation, as follows:
-
•
The appearance or disappearance of stationary states was associated with saddle-node bifurcations [or limit points (LP); blue circles in Fig. B1). We distinguish two types of saddle-node bifurcations: those yielding one stable and one saddle equilibrium (circles filled in blue) and those yielding two unstable equilibria (circles filled in white, associated with the emergence of one repelling and one saddle equilibrium).
-
•
Emergence of oscillatory behaviors is related to the presence of Hopf bifurcations (green circles in Fig. B1). Locally, Hopf bifurcations give rise to periodic orbits that are either stable or not, and we have identified each case (super- or subcritical Hopf bifurcations are depicted with green- or white-filled circles, respectively).
-
•
The periodic orbits also undergo bifurcations that affect network behavior: they may disappear through homoclinic bifurcations (red points, which include both saddle-node homoclinic and saddle homoclinic), at which point of branch of periodic orbit collides with a branch of fixed points (either a saddle-node point or a saddle equilibrium) and subsequently disappears. We also observed the presence of folds of limit cycles (or limit points of cycles, in magenta), particularly important in the presence of subcritical Hopf bifurcations since they result in the presence of a stable, large-amplitude cycle.
Fig. B1.
Bifurcation diagrams in 1-dimensional parameter spaces. In all panels, we show the value of the excitatory activity uE associated with equilibria and periodic orbits (in that case, maximal and minimal values are plotted) as a function of 1 given parameter. L1 and L2 show the influence of excitatory input IE for fixed α = 1 and κ = 3 (L1) or κ = 0.5 (L2). L3 and L4 elucidate the influence of κ with α = 1 and IE = 0.75 (L3) or IE = 1.5 (L4). L5 and L6 characterize the influence of α, with IE = 1.5 and κ = 4 (L5) or κ = 1.5 (L6). Regions are colored according to the type of stable solutions. We distinguish between up- and down-states when >1 solution is present for a given choice of the parameters, whereas we call it a generically stable active state when only 1 (stable) constant solution is present. Bifurcation labels: LP, limit point; H, Hopf; SH, saddle homoclinic; SNH, saddle node homoclinic; LPC, limit point of cycles. Solid (dashed) black lines represent stable (unstable) solutions for uE. Maximal and minimal uE along cycles are depicted in cyan (solid, stable; dashed, unstable limit cycles).
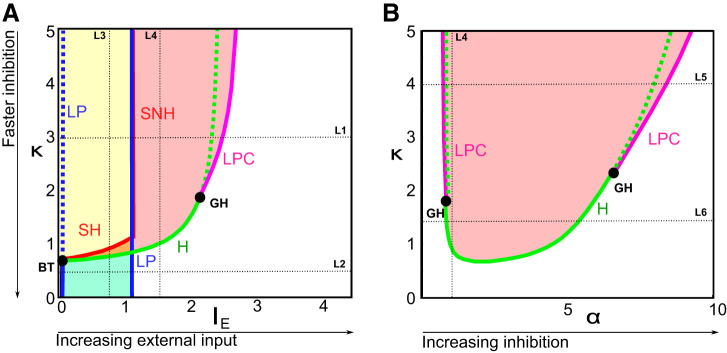
These bifurcations are structurally stable, and their continuation allowed us to construct Fig. B2 elucidating their dependence on parameters. In other words, boundaries of the regions in Fig. B2 are obtained by computing the two-parameter bifurcation diagrams of the system as inhibitory timescale and external current (κ and IE; Fig. B2A) or inhibitory timescale and inhibitory current amplitude(κ and α; Fig. B2B) are varied together. Saddle-node and Hopf bifurcation curves are distinguished in Fig. B2: the blue curve corresponds to saddle-node bifurcations and the green curve to Hopf bifurcations, with singularities located at isolated codimension-two bifurcation points. Codimension-one diagrams depicted in Fig. B1 correspond to sections of codimension-two diagrams, and we indicated the location of these sections in Fig. B2. In both panels, we observe the presence of two codimension-two bifurcation points:
Fig. B2.
Codimension-2 bifurcation diagrams. A elucidates the transitions in the network behavior as a function of input and inhibitory timescales (IE,κ) for fixed α = 1. B characterizes the network behavior as a function of amplitude and timescale of inhibition (α,κ), for fixed IE = 1.5. Color code and notations as in Fig. B1. Codimension-2 bifurcations: BT, Bogdanov–Takens; GH, generalized Hopf (Bautin). Solid and dotted blue (resp. green) lines represent respectively stable or unstable limit points (resp. Hopf bifurcations). Sections corresponding to the different panels of Fig. B1 are depicted with dotted black lines.
-
•
A Bogdanov–Takens bifurcation (BT; Fig. B2A). At this point, the Hopf bifurcation meets tangentially the saddle-node bifurcation curve and disappears, explaining in particular the transition between Fig. B1L1 (no Hopf bifurcation, on one side of the BT bifurcation) and Fig. B1L2 (on the other side of the BT bifurcation). The universal unfolding of the Bogdanov–Takens bifurcation is associated with the presence of a saddle-homoclinic bifurcation, SH curve, along which the periodic orbit disappears, colliding with a saddle fixed point. We computed this curve numerically (depicted in red in Fig. B2) and found that this curve collides with the saddle-node bifurcation associated with the emergence of down-states, at which point it turns into a saddle-node homoclinic bifurcation (namely, instead of colliding with a saddle fixed point, the family of periodic orbits now collides with a saddle-node bifurcation point). From the point of view of the observed behaviors, this transition has no visible impact. This curve accounts for the presence of SNH and SH points in Fig. B1, L1 and L3.
-
•
Bautin bifurcation points (or generalized Hopf, labeled GH), where the Hopf bifurcation switches from super- to subcritical, underpinning the variety of types of Hopf bifurcations observed in Fig. B1, particularly between L5 and L6. The universal unfolding of the Bautin bifurcation is associated with the presence of a fold of limit cycles (or limit point of cycles, LPC, depicted in magenta), that was already identified in Fig. B1, L1 and L5, which appear clearly in Fig. B2 to be those sections intersecting the LPC lines.
APPENDIX C: INDEPENDENCE OF THE RESULTS ON OTHER PARAMETERS
In the analysis discussed in the main text, we focused on the role played in our model by the three parameters κ, the ratio between the onset delays of inhibitory and excitatory currents, α, the ratio between the inhibitory and excitatory responses, and IE, the amount of external input. We fixed all other parameters of the model to standard values and observed that a decrease in κ is fundamental in explaining the features of the developmental switch: it determines a phase transition from an oscillatory regime to a stable one, with an increase in frequency and decrease in amplitudes, of the oscillations, when approaching the switch. In this appendix, we show that the scenario we discussed in the main text is not peculiar to the parameter choices we made, that no particular tuning is needed, and that, instead, the qualitative results are robust when the other parameters are allowed to vary in suitable intervals.
Connectivities
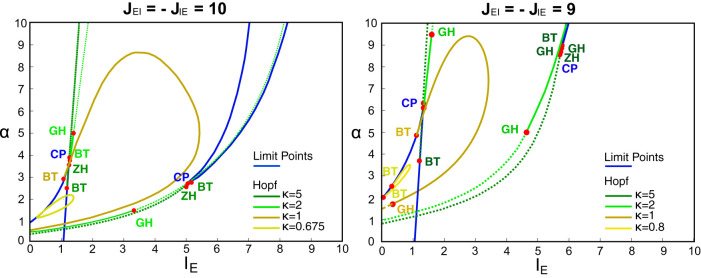
To show how this bifurcation diagram changes as function of the connectivity, as an example we show in Fig. C1 the comparison between the choice we made in the main text (JEI = −JIE = 10) and the case with JEI = −JIE = 9. Limit points and Hopf bifurcations are shown for different values of κ. Note that although LP lines are left invariant by changes in κ, Hopf bifurcations (and then the parameter region giving rise to stable oscillations) shrink when decreasing κ. Nonetheless, the dependence of the dynamics on JEI and JIE is very similar in the two cases, only the values of the parameters for which transitions happen change. For example, in the case JEI = −JIE = 9, if fixing IE = 1.5, the scenario of Fig. B1L4 cannot be reproduced for α = 1 but instead for α ≥ 1.5 for some different critical value of κ at the Hopf bifurcation. This general behavior is guaranteed for a significant interval of values for the connectivity parameters, excluding therefore the fact that our results would depend on some sort of fine-tuning. Moreover, it is easy to show that also the balanced condition JEI = −JIE is unnecessary, and it was chosen only to diminish the number of free parameters of the model.
Fig. C1.
Bifurcation diagram in the space of external input IE and current area ratio α for different onset delays κ and different values of the connectivity parameters JEI and JIE. The limit point lines are the same for all values of κ. However, the stability of the same limit points changes with the different values of κ. Solid and dotted green lines represent stable or unstable Hopf bifurcations, respectively. Codimension-2 bifurcations follow the same conventions as in Fig. B1, with ZH = zero-Hopf. For the clarity of the figure, saddle-node homoclinic, saddle homoclinic bifurcations, and limit points of cycles are not represented.
Ratio between External Inputs to Inhibitory and Excitatory Populations
In the standard Wilson and Cowan model, the external inputs to inhibitory and excitatory populations are introduced as independent. In our notation, they are related by II = rIE, therefore defining the parameter r as the ratio between the two inputs. We consider here only the case of positive r. In Fig. C2 for IE = 1.5 and α = 1 we show a two-dimensional bifurcation diagram in the (r, κ) parameter pace. As for J’s, for a significant interval of values of this ratio (), the developmental switch can occur for κ decreasing with days, with the dynamics passing from an oscillatory to a stable regime, generically through a Hopf bifurcation. For and , the transition can occur through limit point of cycles bifurcations. For the transition, if present, occurs for unnatural higher values of κ.
Fig. C2.
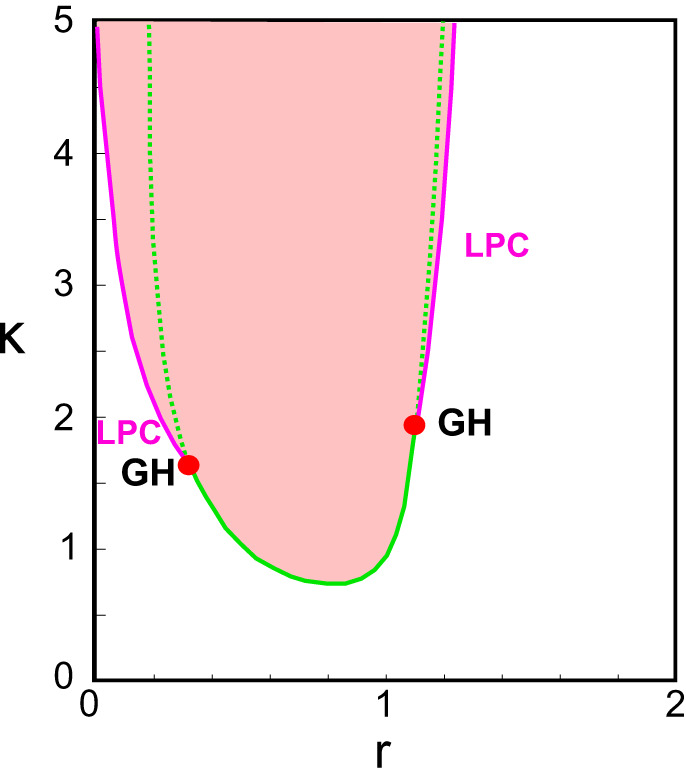
Dependence on the parameter r. Bifurcation diagrams in 2-dimensional parameter space (r,κ) for fixed IE = 1.5 and α = 1. All other parameters are fixed as specified in the main text. Color code for areas and codimension-1 and -2 bifurcations as in Fig. 3, Fig. B1, and Fig. B2.
“Decay” Time Constants
In the extension we propose of the standard Wilson and Cowan model with double-exponential synapses, we introduced four time constants (instead of the standard two). One was reabsorbed in the definition of time, whereas the others can be redefined in terms of dimensionless ratios. The main parameter κ represents roughly the ratio between the onset delays of inhibitory and excitatory delays. The parameters λE and λI, instead, can be seen as determining the slope of the decay of the synaptic responses, and by construction they are 0 < λE, λI < 1. In the analysis performed in the main text, we fixed λE = λI = 0.8. In Fig. C3 we show how once again the main qualitative result does not depend on the precise value of λ’s. In fact, in both symmetric and asymmetric cases, only the critical value of κ at the Hopf bifurcation and the precise value of the amplitude of the oscillations are affected by the λ choice.
Fig. C3.
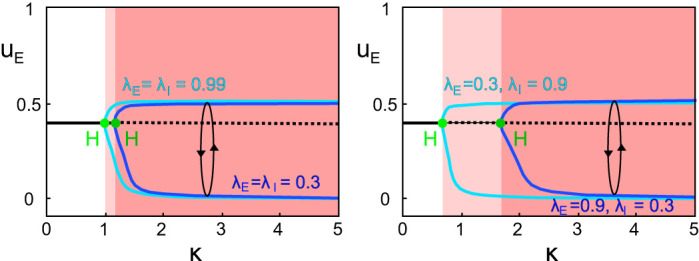
Dependence on the parameters λE and λI. Bifurcation diagrams in 1-dimensional parameter κ for fixed IE = 1.5 and α = 1. On left, we compare the 2 symmetric cases A1 (λE = λI = 0.99) and A2 (λE = λI = 0.3). On right, the 2 asymmetric cases B1 (λE = 0.3, λI = 0.9) and B2 (λE = 0.9, λI = 0.3). All other parameters are fixed as specified in the main text. Color code for areas and codimension-1 and -2 bifurcations as in Fig. 3 and Fig. B1L4, with light colors for cases A1 and B1 and darker colors for cases A2 and B2.
Footnotes
This model, although reproducing accurately the time profile of synaptic responses, does not, strictly speaking, constrain the proportions to remain between 0 and 1; to overcome this issue, for each solution we confirmed that all solutions we computed never left the interval [0, 1].
REFERENCES
- Ackman JB, Crair MC. Role of emergent neural activity in visual map development. Curr Opin Neurobiol 24: 166–175, 2014. doi: 10.1016/j.conb.2013.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Ari Y. Neuro-archaeology: pre-symptomatic architecture and signature of neurological disorders. Trends Neurosci 31: 626–636, 2008. doi: 10.1016/j.tins.2008.09.002. [DOI] [PubMed] [Google Scholar]
- Berglund N, Gentz B. Noise-Induced Phenomena in Slow-Fast Dynamical Systems: a Sample-Paths Approach. London, UK: Springer Science & Business Media, 2006. [Google Scholar]
- Buchin A, Rieubland S, Häusser M, Gutkin BS, Roth A. Inverse stochastic resonance in cerebellar purkinje cells. PLOS Comput Biol 12: e1005000, 2016. doi: 10.1371/journal.pcbi.1005000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butts DA, Kanold PO. The applicability of spike time dependent plasticity to development. Front Synaptic Neurosci 2: 30, 2010. doi: 10.3389/fnsyn.2010.00030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen G, Trombley PQ, van den Pol AN. Excitatory actions of GABA in developing rat hypothalamic neurones. J Physiol 494: 451–464, 1996. doi: 10.1113/jphysiol.1996.sp021505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipaux M, Colonnese MT, Mauguen A, Fellous L, Mokhtari M, Lezcano O, Milh M, Dulac O, Chiron C, Khazipov R, Kaminska A. Auditory stimuli mimicking ambient sounds drive temporal “delta-brushes” in premature infants. PLoS One 8: e79028, 2013. doi: 10.1371/journal.pone.0079028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colonnese MT. Rapid developmental emergence of stable depolarization during wakefulness by inhibitory balancing of cortical network excitability. J Neurosci 34: 5477–5485, 2014. doi: 10.1523/JNEUROSCI.3659-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colonnese MT, Kaminska A, Minlebaev M, Milh M, Bloem B, Lescure S, Moriette G, Chiron C, Ben-Ari Y, Khazipov R. A conserved switch in sensory processing prepares developing neocortex for vision. Neuron 67: 480–498, 2010. doi: 10.1016/j.neuron.2010.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colonnese MT, Khazipov R. “Slow activity transients” in infant rat visual cortex: a spreading synchronous oscillation patterned by retinal waves. J Neurosci 30: 4325–4337, 2010. doi: 10.1523/JNEUROSCI.4995-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colonnese MT, Phillips MA. Thalamocortical function in developing sensory circuits. Curr Opin Neurobiol 52: 72–79, 2018. doi: 10.1016/j.conb.2018.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contractor A, Klyachko VA, Portera-Cailliau C. Altered neuronal and circuit excitability in fragile X syndrome. Neuron 87: 699–715, 2015. doi: 10.1016/j.neuron.2015.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw MI, Ashby MC, Isaac JT. Coordinated developmental recruitment of latent fast spiking interneurons in layer IV barrel cortex. Nat Neurosci 10: 453–461, 2007. doi: 10.1038/nn1866. [DOI] [PubMed] [Google Scholar]
- Demas J, Eglen SJ, Wong RO. Developmental loss of synchronous spontaneous activity in the mouse retina is independent of visual experience. J Neurosci 23: 2851–2860, 2003. doi: 10.1523/JNEUROSCI.23-07-02851.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destexhe A, Sejnowski TJ. The Wilson-Cowan model, 36 years later. Biol Cybern 101: 1–2, 2009. doi: 10.1007/s00422-009-0328-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dhooge A, Govaerts W, Kuznetsov YA. MATCONT: a MATLAB package for numerical bifurcation analysis of ODEs. ACM Trans Math Softw 29: 141–164, 2003. doi: 10.1145/779359.779362. [DOI] [Google Scholar]
- Dooley JC, Blumberg MS. Developmental “awakening” of primary motor cortex to the sensory consequences of movement. eLife 7: e41841, 2018. doi: 10.7554/eLife.41841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout B. Neural networks as spatio-temporal pattern-forming systems. Rep Prog Phys 61: 353–430, 1998. doi: 10.1088/0034-4885/61/4/002. [DOI] [Google Scholar]
- Ermentrout B. Simulating, Analyzing, and Animating Dynamical Systems: a Guide to XPPAUT for Researchers and Students. Philadelphia, PA: SIAM, 2002. [Google Scholar]
- Ermentrout GB, Cowan JD. A mathematical theory of visual hallucination patterns. Biol Cybern 34: 137–150, 1979. doi: 10.1007/BF00336965. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kopell N. Parabolic bursting in an excitable system coupled with a slow oscillation. SIAM J Appl Math 46: 233–253, 1986. doi: 10.1137/0146017. [DOI] [Google Scholar]
- Etherington SJ, Williams SR. Postnatal development of intrinsic and synaptic properties transforms signaling in the layer 5 excitatory neural network of the visual cortex. J Neurosci 31: 9526–9537, 2011. doi: 10.1523/JNEUROSCI.0458-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabrizi L, Slater R, Worley A, Meek J, Boyd S, Olhede S, Fitzgerald M. A shift in sensory processing that enables the developing human brain to discriminate touch from pain. Curr Biol 21: 1552–1558, 2011. doi: 10.1016/j.cub.2011.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci 9: 292–303, 2008. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson JR, Bartley AF, Hays SA, Huber KM. Imbalance of neocortical excitation and inhibition and altered UP states reflect network hyperexcitability in the mouse model of fragile X syndrome. J Neurophysiol 100: 2615–2626, 2008. doi: 10.1152/jn.90752.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glykys J, Dzhala VI, Kuchibhotla KV, Feng G, Kuner T, Augustine G, Bacskai BJ, Staley KJ. Differences in cortical versus subcortical GABAergic signaling: a candidate mechanism of electroclinical uncoupling of neonatal seizures. Neuron 63: 657–672, 2009. doi: 10.1016/j.neuron.2009.08.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gogolla N, Leblanc JJ, Quast KB, Südhof TC, Fagiolini M, Hensch TK. Common circuit defect of excitatory-inhibitory balance in mouse models of autism. J Neurodev Disord 1: 172–181, 2009. doi: 10.1007/s11689-009-9023-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golshani P, Gonçalves JT, Khoshkhoo S, Mostany R, Smirnakis S, Portera-Cailliau C. Internally mediated developmental desynchronization of neocortical network activity. J Neurosci 29: 10890–10899, 2009. doi: 10.1523/JNEUROSCI.2012-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider B, McCormick DA. Rapid neocortical dynamics: cellular and network mechanisms. Neuron 62: 171–189, 2009. doi: 10.1016/j.neuron.2009.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanganu IL, Ben-Ari Y, Khazipov R. Retinal waves trigger spindle bursts in the neonatal rat visual cortex. J Neurosci 26: 6728–6736, 2006. doi: 10.1523/JNEUROSCI.0752-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, Thiele A. Cortical state and attention. Nat Rev Neurosci 12: 509–523, 2011. doi: 10.1038/nrn3084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hjorth JJ, Sterratt DC, Cutts CS, Willshaw DJ, Eglen SJ. Quantitative assessment of computational models for retinotopic map formation. Dev Neurobiol 75: 641–666, 2015. doi: 10.1002/dneu.22241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Gan J, Jonas P. Interneurons. Fast-spiking, parvalbumin+ GABAergic interneurons: from cellular design to microcircuit function. Science 345: 1255263, 2014. doi: 10.1126/science.1255263. [DOI] [PubMed] [Google Scholar]
- Huang ZJ, Di Cristo G, Ango F. Development of GABA innervation in the cerebral and cerebellar cortices. Nat Rev Neurosci 8: 673–686, 2007. doi: 10.1038/nrn2188. [DOI] [PubMed] [Google Scholar]
- Izhikevich E. Neural excitability, spiking and bursting. Int J Bifurcat Chaos 10: 1171–1266, 2000. doi: 10.1142/S0218127400000840. [DOI] [Google Scholar]
- Jansen BH, Rit VG. Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol Cybern 73: 357–366, 1995. doi: 10.1007/BF00199471. [DOI] [PubMed] [Google Scholar]
- Kanold PO, Luhmann HJ. The subplate and early cortical circuits. Annu Rev Neurosci 33: 23–48, 2010. doi: 10.1146/annurev-neuro-060909-153244. [DOI] [PubMed] [Google Scholar]
- Khazipov R, Colonnese M, Minlebaev M. Neonatal cortical rhythms. In: Neural Circuit Development and Function in the Brain, edited by Rubenstein J, Pakic P. San Diego, CA: Academic, 2013, p. 131–153. [Google Scholar]
- Kirkby LA, Sack GS, Firl A, Feller MB. A role for correlated spontaneous activity in the assembly of neural circuits. Neuron 80: 1129–1144, 2013. [Erratum in Neuron 81: P281, 2014.] doi: 10.1016/j.neuron.2013.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leighton AH, Lohmann C. The wiring of developing sensory circuits—from patterned spontaneous activity to synaptic plasticity mechanisms. Front Neural Circuits 10: 71, 2016. doi: 10.3389/fncir.2016.00071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liley DT, Bojak I, Dafilis MP, van Veen L, Frascoli F, Foster BL. Bifurcations and state changes in the human alpha rhythm: theory and experiment. In: Modeling phase transitions in the brain, edited by Steyn-Ross DA, Steyn-Ross M. New York: Springer, 2010. [Google Scholar]
- Lindner B, Garcıa-Ojalvo J, Neiman A, Schimansky-Geier L. Effects of noise in excitable systems. Phys Rep 392: 321–424, 2004. doi: 10.1016/j.physrep.2003.10.015. [DOI] [Google Scholar]
- Lo FS, Ziburkus J, Guido W. Synaptic mechanisms regulating the activation of a Ca2+-mediated plateau potential in developing relay cells of the LGN. J Neurophysiol 87: 1175–1185, 2002. doi: 10.1152/jn.00715.1999. [DOI] [PubMed] [Google Scholar]
- Luhmann HJ, Khazipov R. Neuronal activity patterns in the developing barrel cortex. Neuroscience 368: 256–267, 2018. doi: 10.1016/j.neuroscience.2017.05.025. [DOI] [PubMed] [Google Scholar]
- Luhmann HJ, Prince DA. Postnatal maturation of the GABAergic system in rat neocortex. J Neurophysiol 65: 247–263, 1991. doi: 10.1152/jn.1991.65.2.247. [DOI] [PubMed] [Google Scholar]
- Luhmann HJ, Sinning A, Yang JW, Reyes-Puerta V, Stüttgen MC, Kirischuk S, Kilb W. Spontaneous neuronal activity in developing neocortical networks: from single cells to large-scale interactions. Front Neural Circuits 10: 40, 2016. doi: 10.3389/fncir.2016.00040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marques-Smith A, Lyngholm D, Kaufmann AK, Stacey JA, Hoerder-Suabedissen A, Becker EB, Wilson MC, Molnár Z, Butt SJ. A transient translaminar GABAergic interneuron circuit connects thalamocortical recipient layers in neonatal somatosensory cortex. Neuron 89: 536–549, 2016. doi: 10.1016/j.neuron.2016.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Prince DA. Post-natal development of electrophysiological properties of rat cerebral cortical pyramidal neurones. J Physiol 393: 743–762, 1987. doi: 10.1113/jphysiol.1987.sp016851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Trent F, Ramoa AS. Postnatal development of synchronized network oscillations in the ferret dorsal lateral geniculate and perigeniculate nuclei. J Neurosci 15: 5739–5752, 1995. doi: 10.1523/JNEUROSCI.15-08-05739.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minlebaev M, Colonnese M, Tsintsadze T, Sirota A, Khazipov R. Early γ oscillations synchronize developing thalamus and cortex. Science 334: 226–229, 2011. doi: 10.1126/science.1210574. [DOI] [PubMed] [Google Scholar]
- Murata Y, Colonnese MT. An excitatory cortical feedback loop gates retinal wave transmission in rodent thalamus. eLife 5: e18816, 2016. doi: 10.7554/eLife.18816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murata Y, Colonnese MT. Thalamus controls development and expression of arousal states in visual cortex. J Neurosci 38: 8772–8786, 2018. doi: 10.1523/JNEUROSCI.1519-18.2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owens DF, Boyce LH, Davis MB, Kriegstein AR. Excitatory GABA responses in embryonic and neonatal cortical slices demonstrated by gramicidin perforated-patch recordings and calcium imaging. J Neurosci 16: 6414–6423, 1996. doi: 10.1523/JNEUROSCI.16-20-06414.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahmati V, Kirmse K, Holthoff K, Schwabe L, Kiebel SJ. Developmental emergence of sparse coding: a dynamic systems approach. Sci Rep 7: 13015, 2017. doi: 10.1038/s41598-017-13468-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rochefort NL, Garaschuk O, Milos RI, Narushima M, Marandi N, Pichler B, Kovalchuk Y, Konnerth A. Sparsification of neuronal activity in the visual cortex at eye-opening. Proc Natl Acad Sci USA 106: 15049–15054, 2009. doi: 10.1073/pnas.0907660106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumpel S, Kattenstroth G, Gottmann K. Silent synapses in the immature visual cortex: layer-specific developmental regulation. J Neurophysiol 91: 1097–1101, 2004. doi: 10.1152/jn.00443.2003. [DOI] [PubMed] [Google Scholar]
- Shen J, Colonnese MT. Development of activity in the mouse visual cortex. J Neurosci 36: 12259–12275, 2016. doi: 10.1523/JNEUROSCI.1903-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shpiro A, Moreno-Bote R, Rubin N, Rinzel J. Balance between noise and adaptation in competition models of perceptual bistability. J Comput Neurosci 27: 37–54, 2009. doi: 10.1007/s10827-008-0125-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touboul J, Wendling F, Chauvel P, Faugeras O. Neural mass activity, bifurcations, and epilepsy. Neural Comput 23: 3232–3286, 2011. doi: 10.1162/NECO_a_00206. [DOI] [PubMed] [Google Scholar]
- Tuckwell HC, Jost J, Gutkin BS. Inhibition and modulation of rhythmic neuronal spiking by noise. Phys Rev E Stat Nonlin Soft Matter Phys 80: 031907, 2009. doi: 10.1103/PhysRevE.80.031907. [DOI] [PubMed] [Google Scholar]
- Tuncdemir SN, Wamsley B, Stam FJ, Osakada F, Goulding M, Callaway EM, Rudy B, Fishell G. Early somatostatin interneuron connectivity mediates the maturation of deep layer cortical circuits. Neuron 89: 521–535, 2016. doi: 10.1016/j.neuron.2015.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wendling F, Chauvel P. Transition to ictal activity in temporal lobe epilepsy: insights from macroscopic models. In: Computational Neuroscience in Epilepsy, edited by Soltesz I, Staley K. New York: Academic Press, 2011, p. 356–386. [Google Scholar]
- Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J 12: 1–24, 1972. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JW, Reyes-Puerta V, Kilb W, Luhmann HJ. Spindle bursts in neonatal rat cerebral cortex. Neural Plast 2016: 3467832, 2016. doi: 10.1155/2016/3467832. [DOI] [PMC free article] [PubMed] [Google Scholar]