A fractional-order differential equation model of COVID-19 infection of epithelial cells

Abstract

A novel coronavirus disease (COVID-19) appeared in Wuhan, China in December 2019 and spread around the world at a rapid pace, taking the form of pandemic. There was an urgent need to look for the remedy and control this deadly disease. A new strain of coronavirus called Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) was considered to be responsible for COVID-19. Novel coronavirus (SARS-CoV-2) belongs to the family of coronaviruses crowned with homotrimeric class 1 fusion spike protein (or S protein) on their surfaces. COVID-19 attacks primarily at our throat and lungs epithelial cells. In COVID-19, a stronger adaptive immune response against SARS-CoV-2 can lead to longer recovery time and leads to several complications.

In this paper, we propose a mathematical model for examining the consequence of adaptive immune responses to the viral mutation to control disease transmission. We consider three populations, namely, the uninfected epithelial cells, infected cells, and the SARS-CoV-2 virus. We also take into account combination drug therapy on the dynamics of COVID-19 and its effect.

We present a fractional-order model representing COVID-19/SARS-CoV-2 infection of epithelial cells. The main aim of our study is to explore the effect of adaptive immune response using fractional order operator to monitor the influence of memory on the cell-biological aspects. Also, we have studied the outcome of an antiviral drug on the system to obstruct the contact between epithelial cells and SARS-CoV-2 to restrict the COVID-19 disease. Numerical simulations have been done to illustrate our analytical findings.

1. Introduction

The year 2020 was devastating for mankind due to COVID-19. Around 87 million people around the world were affected and 1.8 million people died during 2020 and its massacre is still persisted. The epidemic of COVID-19 causes due to SARS-CoV-2 virus. It has been observed that most of the patient of COVID-19 shows mild symptoms and can recover with their own immunity. General symptoms of COVID-19 infections are common fever, cough, odorlessness, and tastelessness. The patient suffering from comorbidity factor-like heart disease, liver, and kidney disease is more venerable to the attack of COVID-19. If a COVID-19 patient suffers from pneumonia, then an acute respiratory disease may cause his/her multiple organ failure.

It has been observed that COVID-19 patient shows minor syndromes and can get well with individual immunity. General syndromes of COVID-19 infections are common fever, cough, odorlessness, and tastelessness. The patient suffering from comorbidity factor-like heart disease, liver, and kidney disease is more venerable to the attack of COVID-19. If a COVID-19 patient suffers from pneumonia, then an acute respiratory disease may cause his/her multiple organ failure.

For COVID-19 patients Real-time PT-PCR is an accurate diagnostic tool [1]. However, viral dynamics in the COVID-19 patients is yet to be explored fully. Zhou et al. [2] determined the viral load of 17 symptomatic patients which enlightened the within-host dynamics of COVID-19 disease. It has been observed that COVID-19 replication cycles are longer than normal/seasonal flu. It has 10 days additional replication after the maturation period [2], [3], [4]. The effectiveness of the lock-down and its importance to control the damaging effects of inadequate testing has also been studied through mathematical modelling [5]. Pharmaceutical and non pharmaceutical control has also been studied to control the COVID-19 cases [6].

From the study of Zhou et al. [7] the principal infection site of the human host in COVID-19 is verified. Human epithelial cell constitute main target area for SARS-CoV-2 infection. Angiotensin-converting enzyme II (ACE2) receptor of epithelial cells plays an important role in cellular entry [7], [8]. The concentration of ACE2 receptors is higher in the tongue than in buccal and gingival tissues. These findings lead to the fact that the mucosa of the mouth could also be a potentially high-risk route of COVID-19 infection.

Thus epithelial cells of the tongue are the main routes of entry for COVID-19. Zhou [7] also reported that SARS-CoV-2 spikes S bind with ACE2 receptor of epithelial cells with high affinity. There exist several mathematical models dealing with the dynamics of this disease. These models are usually governed by a system of ordinary differential equations and include three state variables at time t, target cell, infected cells, and free virus. However, such models have been studied without the drug therapy except [9], [10].

In this paper, we have proposed a fractional variant of the following mathematical model to investigate the SARS-CoV-2 viral dynamics in human hosts:

$$\begin{array}{ccc}\hfill \frac{d{E}_s}{dt}& =& \Pi -\beta E_{s}V-{\delta }_s{E}_s,\hfill \\ \hfill \frac{d{E}_i}{dt}& =& \beta E_{s}V-{\delta }_i{E}_i,\hfill \\ \hfill \frac{dV}{dt}& =& pV(1-\frac{V}{K})-{\delta }_{v}V,\hfill \end{array}$$ (1)

with initial values $E_s\left(0\right),E_i\left(0\right),V\left(0\right)$.

We also introduce antiviral drug therapy in our proposed model. To analyze the effect of antiviral therapy we consider the drug efficacy ${ϵ}_1$ as the drug which blocks infection and ${ϵ}_2$ which acts against the production of new virions. Thus, under the therapy, the infection rate becomes $(1-{ϵ}_1)\beta$ and the production rate of virions becomes $(1-{ϵ}_2)p$. Here $0\le {ϵ}_1,{ϵ}_2\le 1$ [11]. Also ${ϵ}_1,{ϵ}_2=1$ means the drug is 100% effective and ${ϵ}_1,{ϵ}_2=0$ describes that there is no drug effect.

Fractional calculus has played a pivotal role in the modeling of several real-life problems [12], [13]. Fractional derivative operator plays a fundamental role in describing the memory effect of several models associated with many biological systems. The fractional differential equation also helps to reduce the errors from the neglected parameters in the usual modeling of real-life problems.

The tools of fractional calculus help the implementation of memory which is one of the hereditary characteristics in most of the cell biological systems. The cell biological structure like fractals is analyzed with the aid of the fractional-order derivative. Caputo and Riemann–Liouville derivatives indicate the effect of memory between an integer-order derivative and a power of time [12], [14]. Thus, a certain cytobiological system becomes more realistic by introducing memory effects in it.

Nabi et al. [15] studied a compartmental mathematical model of COVID-19 pandemic and studied the effect of fraction parameter $\alpha$ incorporating imperfect quarantine and disrespectful behaviour of citizens towards lockdown policies. In the article [16], the author formulated a compartmental mathematical model to gain a deeper understanding about the future dynamics of COVID-19 and here the authors incorporated all possible non-pharmaceutical intervention strategies and studied the control strategies in presence of control.

In this article, we use the fractional-order differential equations to explore the SARS-CoV-2 viral dynamics in the human hosts. Our main aim is to study a mathematical model involving the memory effect in a cell biological system of SARS- CoV-2 infection. We present some definitions of fractional calculus in Section 2. In Section 3, the existence of nonnegative is derived. In Section 4 the proposed fractional-order model is analyzed to find the stability of the system. In Section 5 the effect of drugs is studied, while numerical simulations are carried out in Section 6. The concluding remarks are discussed within the last section.

2. Definition of fractional calculus

In this section, we recall some definitions of fractional calculus related to our study before presenting the epidemic model in terms of fractional derivatives [17], [18].

Definition 1

The left and right sided Caputo fractional derivatives of order $\alpha (n-1\le \alpha <n)$ for a function $f\in A{C}^n[a,b]$ can be defined as:

$$\begin{array}{ccc}\hfill {}_a^C{D}_t^{\alpha }f\left(t\right)& =& \frac{1}{\Gamma (n-\alpha )}{\int }_a^t\frac{f^n\left(s\right)}{{(t-s)}^{\alpha -s+1}}ds,\hfill \\ \hfill {}_t^C{D}_b^{\alpha }f\left(t\right)& =& \frac{{(-1)}^n}{\Gamma (n-\alpha )}{\int }_t^b\frac{f^n\left(s\right)}{{(t-s)}^{\alpha -s+1}}ds.\hfill \end{array}$$ (2)

Here $\alpha$ represents the order of the derivative with $n-1<\alpha <n$, and $\Gamma$ represents the gamma function. Here $n$ is an integer and $a>0,b>0$ are constants.

Now we present fractional-order operators into the SARS-CoV-2 infection of (1) to obtain its fractional variant given by:

$$\begin{array}{ccc}\hfill D^{\alpha }{E}_s& =& \Pi -\beta E_{s}V-{\delta }_s{E}_s,\hfill \\ \hfill D^{\alpha }{E}_i& =& \beta E_{s}V-{\delta }_i{E}_i,\hfill \\ \hfill D^{\alpha }V& =& pV(1-\frac{V}{K})-{\delta }_{v}V.\hfill \end{array}$$ (3)

Here $E_s\left(t\right)$ symbolizes the concentration of uninfected epithelial cells, $E_i\left(t\right)$ denotes the concentration of infected cells, $V\left(t\right)$ the concentration of free SARS-CoV-2 virus at time $t$ along with $\alpha \in (0,1)$ and $D^{\alpha }$ is indicated as the Left-Caputo fractional derivative. But we have restricted our study to the case: $0.5<\alpha \le 1$. It is due to the fact that fractional derivatives cannot nearly define when $0<\alpha \le 0.5$.

In (3), $\Pi$ is the birth rate of epithelial cells, ${\delta }_s$ is the death rate of uninfected epithelial cells, $\beta$ is the rate of infection of epithelial cells. and ${\delta }_i$ is the death rate of infected epithelial cells. Viral replication is modelled with a logistic function with maximum carrying capacity $K$ and $p$ is the replication rate. The virus removal rate is ${\delta }_v$. The initial conditions for infection by free virus are

$$E_s\left(0\right)={\overline{E}}_s,E_i\left(0\right)={\overline{E}}_i,V\left(0\right)=\overline{V}.$$ (4)

where ${\overline{E}}_s=\frac{\Pi }{{\delta }_s}$.

3. Non-negative solution

For any infectious disease, the infection rate and disease transmission the most important factors. It has been observed that in many epidemiological models the system attains its disease-free state when the infected population disappears from the population.

We now find the existence condition for the nonnegative solution of the system (3).

Let $R_{+}^3=\{x\in R^3|x\ge 0\}$ and let $x\left(t\right)={(E_s\left(t\right),E_i\left(t\right),V\left(t\right))}^T$. We need the following generalized mean value theorem [19] to prove the non- negativeness of the solution of the system (3).

Lemma 1 Generalized Mean Value Theorem [19] —

Suppose $f\left(x\right)\in C[a,b]$ and $D_a^{\alpha }\in C(a,b]$ for $0<\alpha \le 1$ , then

$$f\left(x\right)=f\left(a\right)+\frac{1}{\Gamma \left(\alpha \right)}\left(D_a^{\alpha }f\right)\left(\xi \right){(x-a)}^{\alpha },$$

with $a\le \xi \le x,\forall x\in (a,b]$ .

Corollary 1

If $D_a^{\alpha }f\left(x\right)\ge 0,$ $\forall x\in (a,b)$ , then $f\left(x\right)$ is nondecreasing for each $x\in [a,b]$ . If $D_a^{\alpha }f\left(x\right)\le 0$ , $\forall x\in (a,b)$ , then $f\left(x\right)$ is nonincreasing for each $x\in [a,b]$ .

Theorem 1

For the system (3) , there exists a unique solution $x\left(t\right)={(E_s,E_i,V)}^T$ for $t\ge 0$ and the solution will remain within the space $R_{+}^3$ . Also the epithelial cells are all bounded by $E_{tot}$ .

Proof

We have a unique solution on $(0,+\infty )$ of the system (3) (see Theorem 3.1 Remark 3.2 [21]). Now we verify whether the non-negative orthant $R_{+}^3$ is positively invariant region. From model (3) we have

$$\begin{array}{ccc}\hfill D^{\alpha }{E}_s{|}_{E_s=0}& =& \Pi >0,\hfill \\ \hfill D^{\alpha }{E}_i{|}_{E_i=0}& =& \beta E_{s}V\ge 0,\hfill \\ \hfill D^{\alpha }{V|}_{V=0}& =& 0.\hfill \end{array}$$ (5)

Let $E_{tot}=E_s+E_i$. From Eq. (3), we have

$$D^{\alpha }{E}_{tot}=\Pi -{\delta }_s{E}_s-{\delta }_i{E}_i.$$

Since death rate of infected epithelial cells is faster than the natural death rate of susceptible epithelial cells i.e. ${\delta }_i>{\delta }_s$, therefore, at $E_{tot}=E_{max}$ we have

$$D^{\alpha }{E}_{tot}{|}_{E_{tot}=E_{max}}=\Pi -{\delta }_s{E}_s-{\delta }_i{E}_i<\Pi -{\delta }_s{E}_{max}<0.$$

Hence, according to the corollary, the total epithelial cell population including susceptible and infected epithelial cells is bounded by $E_{max}$. □

4. Equilibrium point and stability analysis

To find the equilibrium point, we assume that

$$D^{\alpha }{E}_s=D^{\alpha }{E}_i=D^{\alpha }V=0.$$ (6)

Solving the system (6), the uninfected equilibrium point $E^0$ and infected equilibrium point $E^{*}$ are found to be

• (i) $E^0(E_s^0,0,0)$, where $E_s^0=\frac{\Pi }{{\delta }_s}$,
• (ii) $E^{*}(E_s^{*},E_i^{*},V^{*})$,

where $E_s^{*}=\frac{\Pi }{\beta V^{*}+{\delta }_v},E_i^{*}=\frac{\beta E_s^{*}{V}^{*}}{{\delta }_v}$ and $V^{*}=K(1-\frac{{\delta }_v}{p})$ exist if $p>{\delta }_v$.

The Jacobian matrix for the system (3) is

$$\begin{array}{c}\hfill J\left(E\right)=\left(\begin{array}{ccc}-\beta V-{\delta }_s& 0& -\beta E_s\\ \beta V& -{\delta }_i& \beta E_s\\ 0& 0& p(1-\frac{2V}{K})-{\delta }_v\end{array}\right).\end{array}$$ (7)

At uninfected steady state $E^{*}$, the Jacobian is

$$\begin{array}{c}\hfill J\left(E^0\right)=\left(\begin{array}{ccc}-{\delta }_s& 0& -\beta \frac{\Pi }{{\delta }_s}\\ 0& -{\delta }_i& \beta \frac{\Pi }{{\delta }_s}\\ 0& 0& p-{\delta }_v\end{array}\right).\end{array}$$ (8)

For the Jacobian matrix at $E^0$, the uninfected steady state is asymptotically stable if every eigen values satisfy the conditions [20], [22] given below

$$\left|\arg \left(\lambda \right)\right|>\frac{\alpha \pi }{2}.$$ (9)

The eigenvalues are determined by solving the characteristic equation: $\det (J\left(\overline{E}\right)-\lambda I)=0$. For $E^0$ the eigenvalues are ${\lambda }_1=-{\delta }_s,{\lambda }_2=-{\delta }_i,{\lambda }_3=-({\delta }_v-p)$. Here all roots are negative if $p<{\delta }_v$.

Theorem 2

The uninfected state $E^0$ is locally asymptotically stable if $p<{\delta }_v$ .

To study the local stability of the infected steady state $E^{*}$ for $p>{\delta }_v$ we consider the linearized system of (3) at the infected state $E^{*}$. The Jacobian matrix at $E^{*}$ is given by

$$\begin{array}{c}\hfill J\left(E^{*}\right)=\left(\begin{array}{ccc}-\beta V^{*}-{\delta }_s& 0& -\beta E_s^{*}\\ \beta V^{*}& -{\delta }_i& \beta E_s^{*}\\ 0& 0& p(1-\frac{2V^{*}}{K})-{\delta }_v\end{array}\right).\end{array}$$ (10)

The characteristic equation of the linearized system (10) is

$$\Psi \left(\lambda \right)={\lambda }^3+{\xi }_1{\lambda }^2+{\xi }_2\lambda +{\xi }_3=0,$$ (11)

where

$$\begin{array}{ccc}\hfill {\xi }_1& =& ({\delta }_v+\beta V^{*})+({\delta }_v+\frac{2p{V}^{*}}{K}-p)+{\delta }_i,\hfill \\ \hfill {\xi }_2& =& ({\delta }_v+\beta V^{*})({\delta }_v+\frac{2p{V}^{*}}{K}-p)+{\delta }_i({\delta }_v+\beta V^{*}+{\delta }_v+\frac{2p{V}^{*}}{K}-p),\hfill \\ \hfill {\xi }_3& =& ({\delta }_v+\beta V^{*})({\delta }_v+\frac{2p{V}^{*}}{K}-p){\delta }_i.\hfill \end{array}$$ (12)

Using the following proposition [23] we can analyse the stability at the infected equilibrium $E^{*}$.

Proposition 1

If all eigenvalues $\lambda$ of $J\left(E^{*}\right)$ satisfy $\left|\arg \left(\lambda \right)\right|>\frac{\alpha \pi }{2}$ , then the infected steady state $E^{*}$ is asymptotically stable.

Let

$$\begin{array}{ccc}\hfill D\left(\Psi \right)& =& -\begin{array}{ccccc}1& {\xi }_1& {\xi }_2& {\xi }_3& 0\\ 0& 1& {\xi }_1& {\xi }_2& {\xi }_3\\ 3& 2{\xi }_1& {\xi }_2& 0& 0\\ 0& 3& 2{\xi }_1& {\xi }_2& 0\\ 0& 0& 3& 2{\xi }_1& {\xi }_2\end{array}\hfill \\ & =& 18{\xi }_1{\xi }_2{\xi }_3+{\left({\xi }_1{\xi }_2\right)}^2-4{\xi }_3{\xi }_1^3-4{\xi }_2^3-27{\xi }_3^2.\hfill \end{array}$$ (13)

Under the findings of [24] we have

Proposition 2

(i) If the discriminant of $\Psi \left(\lambda \right),D\left(\Psi \right)$ is positive, then the infected steady state $E^{*}$ is asymptotically stable iff Routh–Hurwitz conditions are satisfied, i.e., ${\xi }_1>0,{\xi }_2>0,{\xi }_1{\xi }_2-{\xi }_3>0$ if $D\left(\Phi \right)>0$ .

(ii) If $D\left(\Psi \right)<0,{\xi }_1\ge 0,{\xi }_2\ge 0,{\xi }_3>0,0.5<\alpha <2/3$ , then the infected steady state $E^{*}$ is asymptotically stable.

(iii) If $D\left(\Psi \right)<0,{\xi }_1>0,{\xi }_2>0,{\xi }_1{\xi }_2={\xi }_3,\alpha \in (0.5,1)$ , then the infected steady state $E^{*}$ is asymptotically stable.

(iv) If $D\left(\Psi \right)<0,{\xi }_1<0,{\xi }_2<0,\alpha >2/3$ , then the infected steady state $E^{*}$ is unstable.

We have $D\left(\Psi \right)=1.2443>0,{\xi }_1=3.0654,{\xi }_2=1.6796,{\xi }_3=0.2213,$ and ${\xi }_1{\xi }_2-{\xi }_3=4.9272>0$ for the parameter values taken from Table 1 . Thus the infected steady state $E^{*}$ satisfies the condition of Proposition 2 (i) and hence the system is asymptotically stable. Numerical simulation supports our analytical findings that the infected steady state $E^{*}$ is asymptotically stable

Table 1.

Biological variables and parameters for SARS-CoV-2 infection.

Parameters	Description	Value (day${}^{-1}$)
Dependent variables
$E_s$	Uninfected epithelial cell population	_
$E_i$	Infected epithelial cell	_
$V$	Initial density of SARS-CoV-2 RNA	_
Parameters
$\Pi$	Growth rate of epithelial cells	2900
${\delta }_s$	Natural death rate of epithelial cells	0.61
$\beta$	Rate of infection	0.000397
${\delta }_i$	Blanket death rate of epithelial cells	2
$p$	Replication rate of virus	2.1-8.7
$K$	Carrying capacity	fitted
${\delta }_v$	Death rate of free virus	0.6-2.3

5. Model of SARS-CoV-2 with drug

To understand the various dynamics of antiviral drug therapy in the system (3) we incorporate two drug efficacy parameter ${ϵ}_1$ and ${ϵ}_2$ in blocking new infection and production of new virions. When the drug efficacy ${ϵ}_1,{ϵ}_2=1$, the drugs are 100% efficient. The fractional model with drug therapy can be formulated as

$$\begin{array}{ccc}\hfill D^{\alpha }{E}_s& =& \Pi -(1-{ϵ}_1)\beta E_{s}V-{\delta }_s{E}_s,\hfill \\ \hfill D^{\alpha }{E}_i& =& (1-{ϵ}_1)\beta E_{s}V-{\delta }_i{E}_i,\hfill \\ \hfill D^{\alpha }V& =& (1-{ϵ}_2)pV(1-\frac{V}{K})-{\delta }_{v}V,\hfill \end{array}$$ (14)

where $D^{\alpha }$ is the Caputo fractional derivative of order $\alpha$, $0<\alpha \le 1$.

Theorem 3

The system (14) attains its uninfected equilibrim point

$${\overline{E}}^0=({\overline{E}}_s^0,0,0)$$ (15)

for all values in the system when $R_0<1$ and when $R_0>1$ , there exist a unique infected equilibrium point

$${\overline{E}}^{*}=({\overline{E}}_s^{*},{\overline{E}}_i^{*},{\overline{V}}^{*}),$$ (16)

where

$$\begin{array}{ccc}\hfill {\overline{E}}_s^{*}& =& \frac{\Pi }{(1-{ϵ}_1)\beta {\overline{V}}^{*}+{\delta }_v},\hfill \\ \hfill {\overline{E}}_i^{*}& =& \frac{(1-{ϵ}_1)\beta E_s^{*}{V}^{*}}{{\delta }_v},\hfill \\ \hfill {\overline{V}}^{*}& =& K(1-\frac{{\delta }_v}{(1-{ϵ}_2)p}).\hfill \end{array}$$ (17)

The stability analysis of the model (14) is similar to that of the model (3). Thus, we omit this part, but we present the following remarks.

Remark 1

• i.The uninfected equilibrium $E^0$ is locally asymptotically stable if $p<{\delta }_v$.
• ii.The infected equilibrium $E^{*}$ is locally asymptotically stable if $p>{\delta }_v$.

6. Numerical simulation

In this section, the numerical solution is given to support the analytical findings of the models (3) and (14). The biological parameters are described in Table 1. To illustrate and verify the effect of the fractional order parameter $\alpha$ on the model dynamics, we consider different values of $\alpha \in [0.5,1]$.

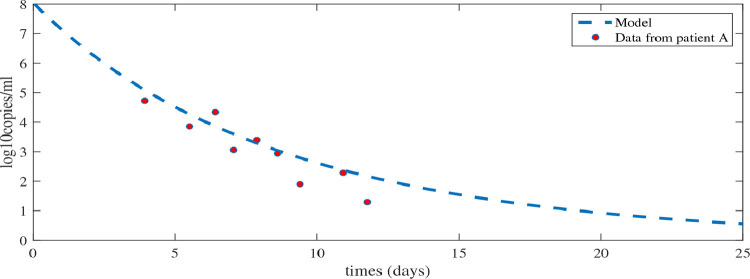
We have studied the SARS-CoV-2 viral load. Here the data are taken from Wolfel et al. [25]. The daily reported and measured viral load for patients was collected from a hospital in Munich, Germany. We considered one data set for this study. The dataset fitted in the solution curve of viral load ($V\left(t\right)$) is shown in Fig. 1. The fixed parameter $\Pi ,{\delta }_s,{\delta }_i,$ are taken from Table 1. From the initial condition we have estimated the parameters $\beta ,r,K$ and ${\delta }_v$.

Fig. 1.

Best fits of model (3) to the viral load data in patients from Germany [25].

Here $\beta ,p$ show a significant positive correlation with $K$. The replication rate of the virus will enhance infection process. Also immune suppression rates are positively correlated with the highest viral load and the death rate of infected cells and the death rate of the virus reflect a negative correlation with $K$. This reveals that $\beta$ and $p$ play a crucial role in controlling the viral load (see Fig. 1 ).

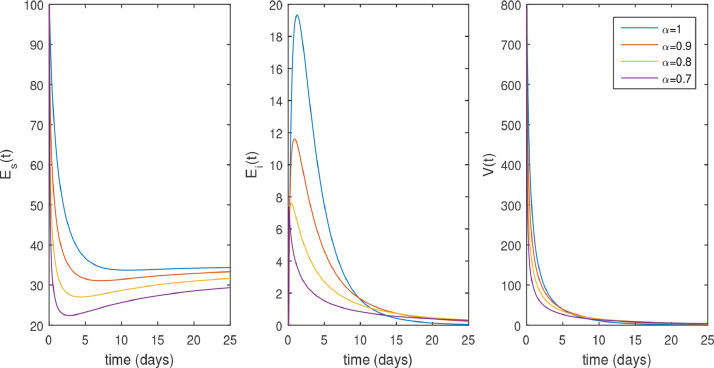
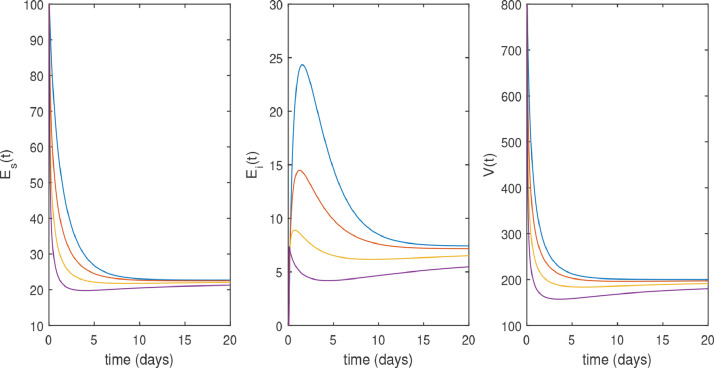
In Figs. 2 and 3 , the numerical solution of the model (3). Fig. 2 shows that the system converges to its uninfected state, $E^0$ for different values of $\alpha$ when $p<{\delta }_{\nu }$. The converges of the uninfected equilibrium point $E^0$ is predicted in (2). Fig. 3 shows the dynamics of SARS-CoV-2, when $p>{\delta }_v$. Fig. 3 shows the faster convergence to its infected equilibrium point due to the smallest values of $\alpha$. This figure also shows that the peak of the infection is reduced in the fractional order case and the disease takes a long time to be eradicated.

Fig. 2.

Trajectories of 3 model variables without drug therapy with $\alpha =0.7,0.8,0.9,1.0$ along the time t (days), $p=2.5<{\delta }_v=2.6$.

Fig. 3.

Trajectories of 3 model variables without drug therapy with $\alpha =0.7,0.8,0.9,1.0$ along the time t (days), $p=2.7>{\delta }_v=2.6$.

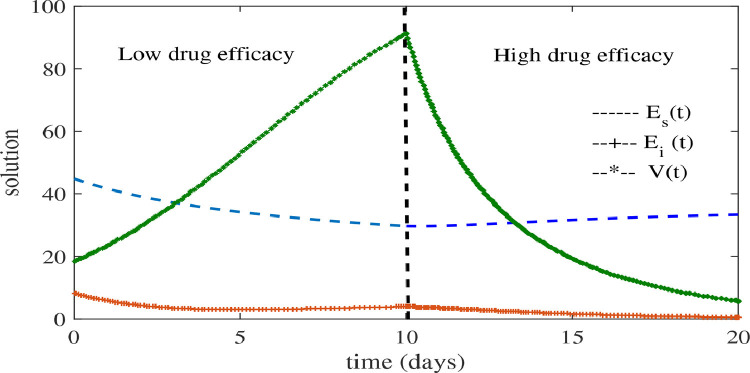
To compare the effect of the effectiveness of the drugs in the fractional SARS-CoV-2 model with drug therapy (14), we consider the different values of ${ϵ}_1$ and ${ϵ}_2$ for the different time schedules. We keep low efficacy of drug therapy for $t\le 10$ days with ${ϵ}_1={ϵ}_2=0.02$ and after 10 days we consider higher drug efficacy (${ϵ}_1={ϵ}_2=0.8$). The comparison of drug efficacy is shown in Fig. 4 . We can see that before 10 days the system converges to its infected state ${\overline{E}}^{*}$ according to (16). When we increase the drug efficacy after 10 days the system converges to its uninfected state. This result is obvious because the infected cells $E_i\left(t\right)$ and virus $V\left(t\right)$ decreases with respect to time $t$ when high drug efficacy is introduced.

Fig. 4.

Numerical solutions of fractional order SARS-CoV-2 model with the drug therapy. Comparison of the efficacy in different time intervals for ${ϵ}_1={ϵ}_2=0.02$ (small) for $t\le 10$ days and ${ϵ}_1={ϵ}_2=0.9$ (high) for $t>10$ days when $R_0>1$ keeping $\alpha =1$ and $T=20$ days.

7. Conclusion

In this paper, we have proposed a fractional-order mathematical model for SARS-CoV-2/COVID-19. The model consisting of ordinary differential equations can only describe an instantaneous process that depends on the time scale under consideration. On the other hand, the fractional-order model additionally addresses the property of memory and the range of memory parameter ($\alpha$) and describe the memory effects in a cell biological structure. It is found that the fractional-order system moves to its stable position faster than the corresponding integer-order model system. Here $\alpha$ plays a pivotal role to understand the memory effects within a cell biological system. It is also observed that with the lower value of $\alpha$, the system converges to its stability more quickly.

Under certain constraint, the fractional-order system (3) possesses uninfected equilibrium $E^0$ and infected equilibrium $E^{*}$. We have found sufficient circumstances for stability for the given parameter set as in Table 1 (see Theorem 2). Numerical simulations confirm our analytical findings for the parameters taken from Table 1 related to the analytical finding of the stability condition. Also, the model is successfully explored by varying the memory of cells. Furthermore, considering the drug efficacy in the model, we can see decrease in the infected cell population and viral load with high drug efficacy in comparison to low drug efficacy. Hence, we can conclude that the fractional-order model is appropriate than its associated integer-order model.

CRediT authorship contribution statement

Amar Nath Chatterjee: Conceptualization, Formal analysis, Methodology, Writing - original draft, Writing - review & editing. Bashir Ahmad: Conceptualization, Project administration, Supervision, Writing - original draft, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.