Integrating social and cognitive aspects of belief dynamics: towards a unifying framework

Abstract

Belief change and spread have been studied in many disciplines—from psychology, sociology, economics and philosophy, to biology, computer science and statistical physics—but we still do not have a firm grasp on why some beliefs change more easily and spread faster than others. To fully capture the complex social-cognitive system that gives rise to belief dynamics, we first review insights about structural components and processes of belief dynamics studied within different disciplines. We then outline a unifying quantitative framework that enables theoretical and empirical comparisons of different belief dynamic models. This framework uses a statistical physics formalism, grounded in cognitive and social theory, as well as empirical observations. We show how this framework can be used to integrate extant knowledge and develop a more comprehensive understanding of belief dynamics.

1. Introduction

Why do individuals change some beliefs quickly in the light of new information while they fiercely resist changing other beliefs? Why do some beliefs spread faster than others? Why do societies sometimes come to consensus about an issue and at other times splinter in clusters with widely different beliefs? Questions about belief dynamics have long occupied scholars across a wide range of disciplines and have been studied on individual and societal levels. At the individual level, researchers in psychology, biology, evolutionary anthropology, political science and philosophy have studied cognitive processes that underlie belief dynamics, including individual and social learning, social judgement and decision-making, social influence, and belief formation and change. At the societal level, researchers in disciplines ranging from sociology and economics to statistical physics and computer science have focused on the spread of beliefs in social networks, and the two-way relationship between the structure of these networks and people's beliefs.

A comprehensive grasp of processes and outcomes of belief dynamics and how they can be influenced is still elusive, for at least three reasons. First, while most researchers agree that beliefs form and change through a dynamic interplay of social network structure and cognitive processes, most disciplines focus predominantly on only one of these aspects. This makes it difficult to adequately capture the underlying complex social-cognitive system, leading to crucial gaps in our understanding of belief dynamics. For example, models of belief dynamics can predict the emergence of full consensus or strong polarization [1], but they generally cannot predict for which beliefs a society will reach consensus and for which beliefs polarization will increase. Similarly, these models often cannot predict why some beliefs are more or less easy to change. Here, we propose that the key to understanding these puzzles might be to integrate social and cognitive components of the complex system underlying belief dynamics (figure 1) into a single unifying quantitative framework.

Figure 1.

Main structural and process components of belief dynamics. Each individual has a network of individual beliefs, here represented as probability distributions over possible belief states (described in §§2.1.1 and 3.1.1). Each individual is also embedded in a social network (§§2.1.2 and 3.1.2). When considering a belief about a particular issue (or ‘focal belief’), individuals form cognitive representations of what their own related individual beliefs are and what relevant others in their social network believe (§§2.2.1 and 3.2.1), using different integration strategies (here we use averaging strategy as an example). When the focal belief diverges from other individual and social beliefs, individuals may experience dissonance (§§2.2.2 and 3.2.2). To resolve it, they might update their beliefs (either belief distributions or connections between their beliefs), or they might update their social network connections (§§2.2.3 and 3.2.3). This in turn modifies the structure of individual beliefs and social networks, starting another round of belief dynamics.

Second, there is little comparison of different models of belief dynamics, both within and especially between disciplines (for a rare exception, see [2]). On the theoretical level, there are few investigations to what extent different models share similar assumptions and to what extent these different models can be integrated. On the empirical level, models are seldomly tested against each other, resulting in insufficient understanding of which models are actually better in capturing real-world belief dynamics. Many models are developed on an abstract level that does not lend itself to empirical measurement, or they remain untested because they are developed within fields that do not traditionally conduct empirical studies. Coupled with relatively scarce communication between different fields, this leads to a slow build up to fundamental principles of belief dynamics. Here, we review insights from different disciplines organized according to the structural and process components of belief dynamics identified in figure 1. We go beyond several excellent reviews that focus mostly on developments within a single discipline [1,3–7] and follow examples of reviews that cross interdisciplinary boundaries [8–11]. In particular, we review research efforts in areas that are essential to understanding the complex system underlying belief dynamics but are typically not considered in this literature, such as the work on cognitive representations of beliefs and social networks, and on the many simple strategies people use to integrate information about their own and others' beliefs.

Third, there is a lack of quantitative modelling frameworks that could be used to adequately integrate both cognitive and social network aspects and make empirically testable predictions about belief dynamics. Typically, models rich in cognitive and social detail tend to be formulated verbally, while quantitative models tend to lack sufficient realism. Agent-based models are well positioned to fill this gap [12–15]. Here, we propose a quantitative framework that is rich in cognitive and social details yet also simple enough to provide quantitative predictions for integrating these details. The framework integrates the main structural and process components of belief dynamics (figure 1) and enables systematic theoretical and empirical comparisons of different implementations (box 1 and figure 2).

Box 1. Quantitative implementation of the integrative framework for models of belief dynamics.

Consider a network with N nodes, each corresponding to an individual. Each node i is connected to K_i other nodes by links which can be directed or undirected, and have unit or other weights. Each node i is assigned a focal belief σ_i, an individual field, ${\mathit{h}}_i^{\mathrm{ind}}$, and a social field, ${\mathit{h}}_i^{\mathrm{soc}}$. The focal belief is an m-component belief state vector ${\mathit{\sigma }}_i=p_{i,\alpha }$, α = 1, …, m, where the vector components (indexed by α) correspond to m possible belief states on a particular issue. In terms of its m components, the vector is written as

$${\mathit{\sigma }}_i=(\hspace{0.17em}{p}_{i1},\hspace{0.17em}{p}_{i2},\hspace{0.17em}\dots ,\hspace{0.17em}{p}_{im}),$$ 1.1

where p_i,α ∈ [0, 1], ${\sum }_{\alpha =1}^m\hspace{0.17em}{p}_{i,\alpha }=1$, are probabilities or weights assigned to each belief state. (For the ease of readability, the time dependence of the quantities σ_i, as well as ${\mathit{d}}_i^{\mathrm{ind}},{\mathit{d}}_i^{\mathrm{soc}}$, h_i and H_i to be defined below, is understood.)

We represent one's orientation with respect to a given issue by one's internal individual field [16] that consists of all of the individual's beliefs relevant for the focal belief under consideration. The individual field for individual i is represented by an m-component vector ${\mathit{h}}_i^{\mathrm{ind}}$. Components of ${\mathit{h}}_i^{\mathrm{ind}}$ denote probabilities or weights corresponding to the same belief states as in vector σ_i. Similarly, we represent perceived orientation of one's social contacts regarding the given issue, or social field, as m-component vector ${\mathit{h}}_i^{\mathrm{soc}}$, whose components denote the probabilities that one's social contacts assume different belief states.

The framework can incorporate different strategies for cognitive representations, that is integrating many different individual beliefs and perceived social contacts' beliefs into the individual and the social field, respectively. Common examples of integration strategies include a random updating rule, h_i = σ_j, where σ_j is a randomly chosen other own belief or social contact, as in classic voter models [17,18]; different averaging strategies over other own beliefs or perceived beliefs of social contacts, ${\mathit{h}}_i={\sum }_{\hspace{0.17em}j\ne i}^{K_i}{l}_{ij}\hspace{0.17em}{\mathit{\sigma }}_j$, where ${\sum }_j{l}_{ij}=1$ [19,20]; majority rule (or more generally, conformism, ${\mathit{h}}_i=\mathrm{sgn}\left({\sum }_{\hspace{0.17em}j=1}^{K_i}{\mathit{\sigma }}_j\right)$) and other frequency-dependent strategies [21,22]; as well as various non-compensatory and other strategies such as a similarity-based rules (as in bounded confidence models) [23], importance- or expertise-based rules (as is frequently observed in humans and other animals) [24,25], h_i = σ_e, where chosen σ_e stays fixed over time, validity, or recognition-based rules [26].

A simple but reasonable choice for modelling the dissonance about individual beliefs ${\mathit{d}}_i^{\mathrm{ind}}=d_{i,\alpha }^{\mathrm{ind}}$ experienced by individual i when considering a particular belief state α (modelled as a component of state vector ${\mathit{\sigma }}_i=p_{i,\alpha }$) is

$$d_{i,\alpha }^{\mathrm{ind}}=({\mathit{\delta }}_{\alpha }-{\mathit{h}}_i^{\mathrm{ind}}{)}^2,\alpha =1,\hspace{0.17em}\dots ,\hspace{0.17em}m,$$ 1.2

where the components of the ‘sampling vector’ ${\mathit{\delta }}_{\alpha }$ are Kronecker δ-functions

$${\mathit{\delta }}_{\alpha }={\delta }_{\alpha ,{\alpha }^{\mathrm{\prime }}}=\{\begin{array}{ll}1& \mathrm{if}\hspace{0.17em}{\alpha }^{\mathrm{\prime }}=\alpha \\ 0& \mathrm{if}\hspace{0.17em}{\alpha }^{\mathrm{\prime }}\ne \alpha \hspace{0.17em}.\end{array}\hspace{0.17em}$$ 1.3

The social dissonance ${\mathit{d}}_i^{\mathrm{soc}}=d_{i,\alpha }^{\mathrm{soc}}$ is calculated similarly. In (1.3), α is held fixed and α′ runs from 1 to m. We employ here the usual vector notation in which the square of a vector is a dot (or inner) product of the vector with itself: ${\mathit{v}}^2=\mathit{v}\cdot \mathit{v}$.

To get a probability distribution over possible belief states for each node, we define the total dissonance function for individual i as

$${\mathit{H}}_i=(1-w){\mathit{d}}_i^{\mathrm{ind}}+w{\mathit{d}}_i^{\mathrm{soc}},$$ 1.4

or expressed in terms of components,

$$H_{i,\alpha }=(1-w)d_{i,\alpha }^{\mathrm{ind}}+w{d}_{i,\alpha }^{\mathrm{soc}},$$ 1.5

where the parameter w ∈ [0, 1] controls the relative weights of dissonance due to individual versus social considerations.

Finally, we compute the updated components of the probability vector σ_i from the dissonance function (1.5) using the softmax function

$$p_{i,\alpha }=\frac{{\mathrm{e}}^{-\beta H_{i,\alpha }}}{{\sum }_{\alpha =1}^m{\mathrm{e}}^{-\beta H_{i,\alpha }}},$$ 1.6

where β = [0, ∞) is a parameter that measures the ‘noisiness’ of the belief updating process: larger β values correspond to smaller noise and more attentiveness (as noted in the main text, β corresponds to an inverse temperature in physics applications).

Figure 2.

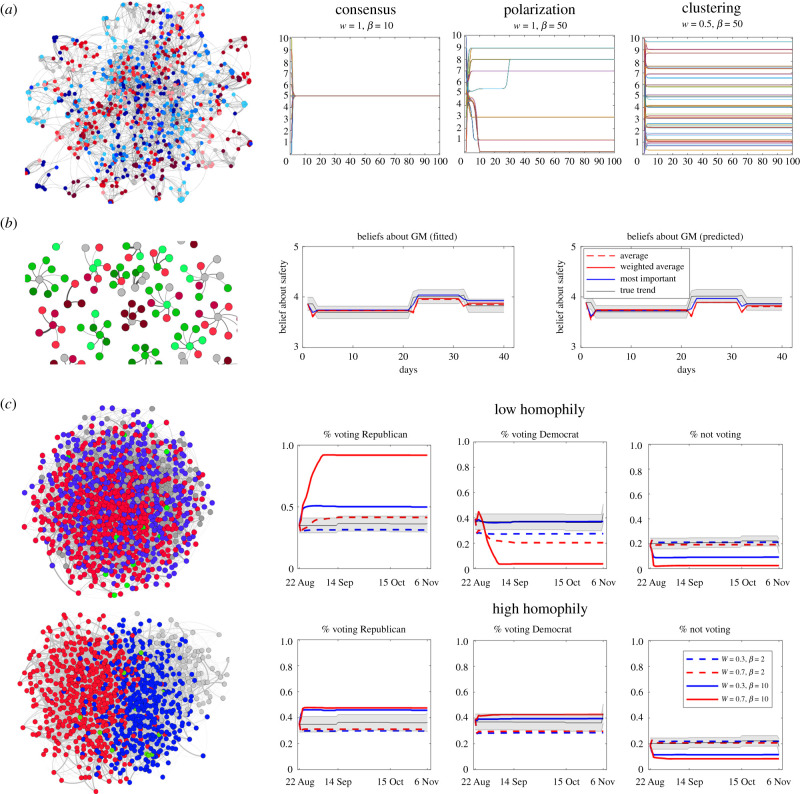
Examples of theoretical and empirical tests of models constructed using the integrative framework. The leftmost subpanels show the networks used and the node colours represent different belief states at the initial time point. (a) The results of theoretical simulations with random initial conditions and individual field distributions. Depending on the values of parameters w and β (shown at the top of each graph), patterns resembling consensus, polarization and clustering occur in otherwise identical social networks. (b) Results from models of empirical changes in beliefs about safety of GM food, observed in a national longitudinal survey that measured them six times over the course of several months. Different models used different rules for integrating relevant individual beliefs and perceived social contacts' beliefs into individual and social fields (averaging rule, importance-weighted averaging or only the most important belief/contact). We compare predictions of models assuming different rules (coloured lines) with the true, survey-measured trend (black line, with grey ribbon denoting 95% CI). (c) How the framework can be used to extrapolate empirical survey findings on political preferences and network connections to broader populations. Here we simulated networks of voters (red, Republicans; blue, Democrats; green, other; grey, non-voters) in the 2018 elections in Ohio assuming majority integration rule and lower (top subpanels) or higher (bottom subpanels) homophily. The predictions based on different combinations of parameters (different coloured lines in plots) are compared to survey-measured trends (black lines, with grey ribbon denoting empirical 95% CI). See box 1 and text for more details.

2. Main components of belief dynamics

2.1. Structural components

Structurally, the complex system underlying belief dynamics consists of two main components: individual beliefs and their connections, and people's social contacts and the relationships between them.

2.1.1. Individual beliefs

Individual beliefs are essential components of belief dynamics, but there is little consensus on how they should be defined, measured and modelled. Here, we adopt an inclusive definition of beliefs that encompasses conceptualizations used in different fields, including beliefs as assumptions about states of the world (e.g. ‘vaccination is safe for children’, ‘I believe there is a 30% chance of rain tomorrow’), views on moral and political issues (e.g. ‘genetically modified foods are against nature’, ‘a free market is good for everyone’), evaluations or cognitive aspects of attitudes (e.g. ‘cats are fun’, ‘this politician is trustworthy’ [27,28]) or as own preferences (e.g. ‘I prefer having more time to earning more money’, ‘I like summers more than winters'). Support for a belief can be measured on different scales, from dichotomous true–false or agree–disagree, to rating scales with several points, to subjective probabilities and probability distributions. Different domains emphasize different ways of belief measurement: rating scales are often used in social psychology and political science [29,30], while subjective probabilities are relatively more often used in economics [19,31,32], philosophy [33,34], artificial intelligence [35], and judgement and decision-making [36–39]. Some theories in the attitude literature combine both evaluations of beliefs and their subjective probabilities [40–43]. Most extant models consider changes of a single belief over time, but beliefs develop and change together with many other related individual beliefs. One way to model this structure is to use a network analogy and study changes of many interconnected beliefs simultaneously [44–49]. Empirical tests of full network models are difficult as they require extensive data collections on many beliefs changing over time to fit the parameters (but see [50]). However, models can at least assume that some summary value of other beliefs influences changes of any individual belief. A number of plausible cognitive integration strategies that can produce such summary values have been proposed (see §2.2.1).

2.1.2. Social networks

Information from people's social environment is an important contributor to the complexity of belief formation and change. The relevant social environments can include many different social contacts, from friends and family, online communities, media figures, to companies, educators, health workers and politicians. Social contacts are embedded in ever-evolving social networks that to a large part determine what information is spread and to whom. The importance of social networks for understanding how beliefs change has long been acknowledged, with Durkheim highlighting already in 1893 [51] the need to study individuals within their social networks. Moreno introduced the first network visualizations and methods for measuring them in 1951 [52]. Since then, a large number of network properties important for belief dynamics have been identified (for overviews, see [5,53–57]). Some of the most frequently studied properties are various measures of centrality (i.e. structural importance) of individuals [58,59], strength and length of paths between them (e.g. how long does it take on average for information to flow from one individual to another individual in the social network) [60], balance of relationships in which they are embedded (e.g. are two friends of an individual generally also friends) [61] and homophily (i.e. the tendency to have friends who hold similar beliefs) [62]. For example, homophily may constrain the spread of beliefs and behaviours such as smoking, obesity and even divorce [63–65], and the resulting beliefs can influence processes such as network updating that in turn influence homophily [66]. A related concept is echo chambers in which beliefs are amplified or reinforced by communication to similar others and repetition of what one already believes [67,68].

2.2. Process components

Complex social systems with similar belief and network structures can still give rise to different patterns of belief dynamics because of various cognitive processes operating on these structures. The way people represent their individual beliefs and social networks, the dissonance they feel regarding them and their strategies for updating their beliefs and network links can all contribute to different belief dynamics. In the following sections, we will discuss each of these processes in turn, even though in reality, these processes often occur in parallel and influence each other.

2.2.1. Cognitive representation of individual beliefs and social networks

Most models of belief dynamics outside psychology assume that people have stable and accurate cognitive representations of their own beliefs and beliefs of their social contacts. However, research in cognitive psychology suggests that people often do not have readily formed beliefs about different issues, but must (re)construct them on the spot based on different individual considerations that come to mind [69,70]. These considerations can include other related beliefs, values, assumptions and preferences. Which ones are activated depends on their inter-relationships, memory processes such as priming and forgetting, and processes of self-deception [71,72]. Similarly, people might not have a ready-made representation of what others in their social networks believe. These social beliefs have to be formed by integrating available samples from one's social environment and other relevant considerations. They are affected by memory processes [73,74] as well as by one's social contacts’ impression management [75] and other signalling strategies [76–79].

The many relevant individual and social considerations need to be integrated into an overall cognitive representation of one's own and others’ beliefs about an issue. Many disciplines study integration of either personal considerations or information from social networks, but rarely both, although they might involve similar processes. For example, when considering whether it is safe to eat genetically modified (GM) food, one might integrate other relevant individual beliefs about GM food (e.g. whether GM food is natural and whether it is harmful for the environment) as well as various relevant social beliefs (e.g. what scientists and one's own friends think about it). One can then try to derive a summary of those beliefs, which can be relatively precise or just a general impression of how one feels about an issue.

Some approaches to studying integration processes are primarily normative, suggesting that integration should be done to achieve a coherent set of beliefs. A standard normative approach is Bayesian learning, which assumes that individuals integrate their beliefs optimally given an underlying model of the world that includes their own and others' beliefs, in line with Bayesian calculus. Bayesian approaches to information integration have been intensively explored in artificial intelligence [35], cognitive science [80,81] and economics [32,82]. Furthermore, several logical approaches to information integration have been developed in the context of belief dynamics [83–85]. Dynamic epistemic logic [84,85] assumes plausibility models through which individuals consider different worlds as possible candidates for the actual world, where each world has a plausibility order in relation to the other worlds. In its simplest form, beliefs are summarized by removing non-plausible worlds from the total set of worlds. Some approaches combine logical integration and specific social network structures [86,87]. These theories include information about what others believe and analyse what brings about belief change.

Other approaches to studying integration processes are primarily descriptive, aiming to explain cognitive strategies. These approaches are motivated by observations that people tend to use relatively simple strategies that can work with limited information and cognitive capacity, sometimes approximating the results of normative ideals [5,19,24–26,88]. One prominent class of strategies are frequency-dependent strategies. These strategies give advantage to those beliefs that are supported by a certain number or fraction of one's social contacts, or of one's personal considerations about an issue. The most studied rule in this class is the majority rule [89–93] and its plurality variants (for more than two options) that can be used both for integrating one's own considerations (e.g. tallying [94,95]) and external social information [96]. Across many disciplines, rules using other thresholds have been studied empirically and theoretically, including minority rule, unanimity rule and others (in political science [89,90]; economics [97]; sociology [92,98,99]; law [100]; organizational science [101]; evolutionary anthropology,[102]; animal learning [103]; psychology [93,104–107]; machine learning, e.g. [108]; and statistical physics [21,91]).

Another prominent class of descriptive approaches for information integration are averaging strategies (and the closely related weighted additive rules). In psychology, they have been studied as rules for integrating personal considerations about an issue using different weighting schemes [95,109], as well as for integrating social information in belief change [110], advice taking [111] and social judgement [110,112]. In other disciplines, they have been studied mostly for integrating social information. For example, DeGroot learning [19] and its variants [20] studied in sociology and economics involve weighted averaging of one's own and neighbours’ beliefs [65,113–116]. Several rules studied in statistical physics, such as voter rule, Ising and Potts models, etc. are essentially averaging rules as well [17,18,117]. Random or ‘unbiased’ copying that is often used as a benchmark in evolutionary anthropology is also an averaging rule in the long run [22]. Epidemiological models of belief dynamics, where individuals are described with a certain probability of getting ‘infected with’ and ‘recovering from’ a belief can also be thought of as examples of averaging [118].

A final prominent group of descriptive approaches to information integration are various non-compensatory strategies. Unlike frequency-dependent and averaging rules, they do not take into account all personal considerations or social contacts, but choose just one or a smaller subset based on particular properties of these considerations or contacts. For example, when people follow a take-the-best rule, they rely on a single best consideration, disregarding all others [119]. Similarly, they might disregard other considerations when following memory-based cues such as recognition [119], perceptual or memory fluency [120–122], or familiarity [123,124]. When it comes to integrating social information, many non-compensatory model-based strategies have been described in humans and other animals [125–127]. Prominent examples are strategies that entail following a leader, a perceived expert, a close friend, a family member, a successful individual or the most trusted individual. Variants of model-based strategies also exist in bounded confidence models in which an individual is more likely to interact and copy a person with similar opinions. As the similarity of opinions changes over time, so does the likelihood that any two individuals will influence one another [23,128,129]. The classic model of dissemination of culture [130] uses similar assumptions: probability of interaction between two agents is proportional to the similarity of opinions of these agents.

All of these simple strategies are plausible ways of integrating information both when forming one's own beliefs and when forming beliefs about others, and most likely people use all of them in different contexts. However, current models of belief dynamics typically assume only one type of strategy (e.g. a majority rule or simple averaging as in figure 1), and there is a lack of theoretical and empirical comparisons of signatures of different strategies. The framework we propose in §3 enables such comparisons.

2.2.2. Dissonance

If one's existing individual or social beliefs about an issue are not in line with new information or beliefs about the issue, one might experience dissonance [131,132]. Dissonance of individual or social beliefs is often expressed in terms of inconsistency or imbalance between different beliefs people have [132,133]. Formal models of dissonance related to individual beliefs have been implemented within the literature on neural networks [44,45,134], as well as within a statistical physics framework [46–48]. Dissonance of social beliefs can be represented as imbalance in perceived beliefs in one's overall social network [135–137] and modelled in the same way as dissonance of individual beliefs, but it has also been conceptualized as a discomfort because of acting inconsistently in a social setting [138,139], or as a feeling of not belonging [140].

To adequately measure dissonance, one would ideally like to elicit and measure all beliefs that are relevant for the issue of interest. This ideal goal can in practice be approximated by relying on extant empirical research and theories of what considerations might be important for beliefs about a particular issue (e.g. moral values such as fairness, care or freedom might be important for beliefs about some science-related and political issues) [141,142], eliciting beliefs using different ways of asking people what considerations about an issue come to mind [143–145]. Measured dissonance can be compared with feelings of felt dissonance or felt ambivalence [146–148], a psychological state that has been described as being uncomfortable, uneasy and bothered [44,61,132,133,135,149,150]. Of note, even though measured dissonance might be strong, it does not have to result in a corresponding belief change. Actual belief change will depend on how much attention one pays to the inconsistent beliefs, which in turns depends on the presence of other distractors, noise in the perception process and subjective importance of the beliefs [132,146].

2.2.3. Belief and network updating

People might resolve dissonance in at least two ways. The first is to change their own individual beliefs to fit better with their important values or with perceived beliefs of their social contacts [62,65,151–153]. One might also try to make one's individual beliefs as dissimilar as possible from beliefs of individuals one dislikes [48,131,154].

People can also try to resolve the dissonance by changing the connections between their different beliefs, and/or between themselves and their social contacts [61,155]. There is substantially less research on such network updating strategies than on belief updating strategies, in particular when it comes to updating links between one's own beliefs. Models of belief dynamics with a social network updating component started to occur relatively recently, partially building on the literature studying behavioural games on adaptive networks [156]. An early example is the coevolving voter model [157], where a single parameter determines whether an individual adopts a belief of a random neighbour, or replaces one of their social connections with a connection to an individual with the same belief as them. Recent empirical and modelling work has also shown that individuals in social networks can dynamically modify their local connections in an adaptive way in response to changing environments, making individual and collective beliefs more accurate [158]. In any case, updated beliefs and network links change the structure of the social networks in which people are embedded, starting another round of belief dynamics. In figure 1, we show an example of belief updating strategy (to the left) and social network updating strategy (to the right).

3. An integrative framework for modelling belief dynamics

In this section, we propose a unifying quantitative framework that builds upon the structural and process components of belief dynamics reviewed in the previous sections. The framework uses a statistical physics formalism [1], grounded in cognitive and social theory and observations [16,47,159]. This formalism enables the construction and comparison of models with different assumptions about individual and social factors that influence belief formation, change and spread. Its main advantage is that it can express a large number of different models and reproduce a variety of empirically observed patterns of belief spread, using only a few components. Each of its variables and parameters can be either directly observed or estimated from empirical data, and can be given a plausible psychological meaning reflecting factors that have been recognized as important for belief dynamics. In what follows, we outline how our framework incorporates the main aspects of belief dynamics reviewed in the previous sections (see also figure 1). We then provide two empirical examples of using the framework to model real-world beliefs, one about beliefs on scientific issues such as GM food and the other about beliefs on political issues such as voting for different political candidates.

3.1. Structural components

3.1.1. Individual beliefs

We adopt a widely used statistical physics approach [1], where a specific belief under consideration by individual i (here we call it ‘focal belief’, for example, a belief about safety of GM food) is represented by a discrete-valued variable σ_i that is traditionally (for historical reasons) called a spin. Depending on the issue in question, the variable σ_i can take anywhere from two (yes/no, agree/disagree) to many (e.g. ranging from strongly agree to strongly disagree) values corresponding to different belief states. Belief states can be measured by attitude questions or approximated from behaviours (e.g. past records about voting or purchases). The spin σ_i is usually treated as a scalar variable which can change its state among a discrete or continuous set of possibilities over time, but at any given time is found in one state only. We introduce a more general vector approach (see box 1), where beliefs are represented as probability distributions over a range of possible levels of acceptance of a given belief (figure 1, part 1.1). This approach includes the usual scalar spin models as a special case. Vector models of cultural dynamics have been studied by others [130], but the nature and implementation of those are different from that discussed here. Our conceptualization of beliefs is also similar to quantum and Markov models of belief change during evidence accumulation [160]. The latter models, however, do not include a social network component and typically apply only to relatively short time scales.

An example of our general vector approach is the one in which an individual fills out a survey and is asked to choose between five possible belief states regarding the issue in question: strongly agree, agree, neutral/do not know, disagree, strongly disagree. For example, one might believe that on a scale from 1 to 5, the safety of eating GM food is around 4. We define a vector σ_i with (in this example) five components that describe probabilities or weights which are assigned to each of the belief states—so the sum of all components of σ_i at any time is equal to one. For example, one might answer ‘agree’ to a survey question, but might feel one's true belief state is somewhere in between ‘agree’ and ‘strongly agree’, in which case the vector (0.25, 0.75, 0, 0, 0) is a more accurate representation. Depending on how fine-grained the different choices are, the framework can accommodate both discrete (or categorical) and continuous representations of beliefs. For example, one's beliefs about the safety of GM food can be described as assigning a probability of choosing each of the points on a scale from very unsafe to very safe. In a similar manner, one's beliefs about different political options might be described as 20% support for policies espoused by party A and 80% for those of party B.

3.1.2. Social networks

Individuals are represented by nodes on a social network. Each node can be assigned one or more beliefs represented as probability distributions (figure 1, part 1.2). Weighted links connect two nodes, i and j (or neighbours) and represent the degree of information flow between the two. The strength and sign of the interaction between two nodes is denoted by a positive or a negative link weight. A positive link weight between two neighbours indicates a tendency for individuals i and j to want to agree, while a negative weight indicates that a change in i's belief induces a change in the opposite direction in j. For example, when we generally like someone, we tend to agree with them on specific beliefs, but when we dislike someone, we might disagree even on things that we otherwise do not have much stake in (or might even have been sympathetic to otherwise). Moreover, the graph can be directed, meaning that the communication between two individuals is only one way, or else two way but with different link weights in each direction. These social networks can be measured objectively using sociometric methods or subjectively using people's perceived associations between their social contacts.

3.2. Process components

3.2.1. Cognitive representations of beliefs and social networks

Starting from some initial belief states, beliefs evolve in time according to specific dynamical rules. These rules depend on interactions with both the individual beliefs that one holds and with one's social beliefs, or perceived beliefs of others around them. As mentioned, the focal belief under consideration is represented by the vector σ_i. The framework includes other internal beliefs related to that focal belief, which are assumed to form individual field ${\mathit{h}}_i^{\mathrm{cog}}$, as well as perceived beliefs of social contacts, assumed to form one's social field ${\mathit{h}}_i^{\mathrm{soc}}$ (see box 1 and figure 1, part 2.1).

An individual can use different strategies (e.g. frequency-dependent or averaging rules) to integrate internal beliefs into their individual field ${\mathit{h}}_i^{\mathrm{ind}}$, and perceived social contacts' beliefs into their social field ${\mathit{h}}_i^{\mathrm{soc}}\hspace{0.17em}$(see box 1). For example, when forming one's belief about GM food or a political candidate, one might consider only the most important relevant belief (e.g. whether scientists agree that GM food is safe, or whether a political candidate supports abortion), or combine many other relevant beliefs in an average overall impression. The choice of strategy will depend on the particular task and cultural context, as well as on one's own cognitive capacities and personal preferences. These strategies can be probed directly through survey and experimental measurement, or can be inferred by comparing predictions of models implemented in the framework.

3.2.2. Dissonance

When a belief does not fit well with one's individual and/or social field, one can experience dissonance (figure 1, part 2.2). In our framework, these dissonances ${\mathit{d}}_i^{\mathrm{ind}}$and ${\mathit{d}}_i^{\mathrm{soc}}$ correspond to the squared difference between probability (or support) distributions that are currently assigned to different beliefs. This difference is then used to calculate a new belief distribution that would best minimize the dissonance, using a Boltzmann entropy framework (equivalent to the softmax function often used in decision theory, box 1). For example, if through an educational campaign one learns that a valued, trustworthy person or organization believes GM food is safe to eat, this might push one towards believing that GM food is safe; and vice versa if one learns that an untrustworthy source supports GM food.

While attempting to minimize the ovearll dissonance, individuals can experience a tension between minimizing their individual and social dissonance [131,132]. Across different people and issues, one or the other type of dissonance can be more important. In our framework, this is represented by the parameter w, which weights the social relative to the individual dissonance (box 1). For example, a higher value of w would mean that one prefers to be aligned in their political preferences with their family and friends (and minimize dissonance related to social beliefs) even if their chosen political candidate does not behave in line with one's moral values (so one must tolerate some dissonance of individual beliefs).

The effect of dissonance on the evolution of beliefs is expected to be strongest for those who have the most certainty about their own beliefs and those of their neighbours. In our framework, this certainty is modelled by the (inverse of the) parameter β. This parameter is a measure of ‘noisiness’ or uncertainty which can arise from several sources, such as errors in recollecting or reconstructing own and others' beliefs relevant to the focal belief, as well as misjudging or not paying sufficient attention to one's own dissonance. The unpredictability is represented as temperature in statistical physics models, with zero temperature corresponding to the complete absence of noise. In our model, temperature corresponds to 1/β (box 1). The higher the temperature (i.e. the smaller β is), the greater the level of uncertainty and, therefore, the less of an effect dissonance has on belief updating. For example, one might receive facts showing GM food is safe to eat, but if one does not pay sufficient attention to how these facts actually relate to one's other beliefs, the facts might not have much effect. By contrast, paying much attention to an issue can also make belief change less likely, because one is also aware of the dissonance that such belief change might cause (e.g. one might not change one's negative beliefs about GM food, because most people in one's social circle hold negative beliefs towards GM good).

Both parameters w and β can be estimated from data or approximated by empirical measurements of subjective relative importance of staying aligned with one's own or with one's social network's beliefs (for w), and of attention and subjective certainty (for β).

3.2.3. Belief and network updating.

Dissonance can be reduced by modifying one's own beliefs, but it can also be alleviated by changing or cutting links to beliefs and individuals that disagree with one's firmly held belief (figure 1, part 2.3). Our framework allows for modelling different processes of network updating, which can include random rewiring of edges, rewiring based on some threshold of similarity between any two spins, rewiring aimed at preserving balance in triads of spins or the overall network, and other processes. For example, the model can assume that one disconnects, over time, social contacts with very different political beliefs. This will in turn reduce the social dissonance one feels from holding beliefs that are not shared by one's social network.

3.3. Implementing and testing models within the framework

Models formulated within the framework can reproduce commonly observed outcomes of belief dynamics as well as empirically measured beliefs about real-world issues. Our first implementation (figure 2a) corresponds to theoretical tests of the framework: we initially assign every individual one of m belief states (1, 0, 0, … , 0, 0), (0, 1, 0, … , 0, 0), … , (0, 0, 0, … , 0, 1), chosen randomly and independently of all neighbours, as well as one's own individual field $h_i^{\mathrm{ind}}$. In all implementations shown here, the belief updating is done synchronously; at every time step, all agents simultaneously measure the distance of all possible future belief states (represented by ${\mathit{\delta }}_{\alpha }$, where α is an index for the different belief states). The three patterns in figure 2a, showing consensus, polarization and clustering, were produced by varying only the parameters w and β, and keeping the network structure and the belief updating rule the same. The networks were generated by stochastic block models with low homophily, where individuals were parts of social circles loosely connected to each other and their initial beliefs were assigned randomly (figure 2a, leftmost subpanel). At each time step, individuals updated their beliefs using a simple unweighted average of beliefs of their social contacts. When both the weight w on the dissonance due to social beliefs and the noise strength were relatively high (w = 1, β = 10, left panel), populations always reached consensus. With the same high w but much lower levels of noise (w = 1, β = 50, middle panel), patterns akin to polarization emerged in around 10% of the runs. Finally, when dissonances due to individual and social beliefs were weighted equally (w = 0.5) and with the same level of low noise (β = 50, right panel), individuals clustered into subgroups, with similar beliefs within each subgroup but differing beliefs between subgroups. Further study of different combinations of the parameters w and β implemented on different social network structures and with different cognitive integration strategies will enable comparisons between the predictions of many other different models.

What ultimately matters most is how well these models explain empirically observed belief trends. We provide two empirical examples. One example (figure 2b) involves beliefs about safety of GM food, empirically measured two times in each of the three waves of a longitudinal survey on a national sample of N = 531 participants [161]. Besides this focal belief, in each wave, participants also reported 12 other beliefs about their individual moral issues related to GM food [162], and perceived beliefs of different social groups (family, online community, scientists, doctors, etc.). They also reported the subjective importance of each moral and social belief for the focal belief. In our modelling framework, the focal belief and other relevant moral and social beliefs are represented as vectors of probabilities that an individual is in each of seven possible belief states (ranging from 1, completely disagree, to 7, completely agree). Participants are connected with directed links to each of the social groups mentioned (see the leftmost panel of figure 2b). Moral and social beliefs are updated to new measured values after each survey wave, and integrated into individual and social fields using one of three integration rules: simple average of belief vectors, weighted average where each belief vector is weighted by the stated importance of that belief (as measured in the survey) or the most important belief. The focal belief is not updated to empirically measured values but is instead calculated at each time point from the model (see box 1). The difference (root-mean-squared deviation) between modelled and empirically measured focal beliefs is used as an indicator of model fit.

The framework can be used to model the effects of outside information. The study on GM food (figure 2b) included an experimental intervention in the second wave, in which different groups of participants received scientific information about the safety of GM food, alone or combined with information about relevant social and moral beliefs (for example, about the scientific consensus, or about fairness regarding small farmers). In the model, this intervention is represented as changes in relevant measured social and moral beliefs (for example, in beliefs about scientists, or beliefs about fairness). These changes might cause dissonance between the focal belief and other individual and social beliefs, which can be resolved by changing the focal belief depending on the importance of each type of dissonance (parameter w) and the attention paid to the belief updating process (parameter β). Parameters w and β are fitted with a grid search procedure (ranges: 0 ≤ w ≤ 1, and 0 ≤ β ≤ 100) for each time point on a random half of the participants, so that they minimize the deviation between modelled and actually measured focal beliefs (inspection of the deviations showed that only one parameter combination minimized the deviation between model and data). Here we present belief trends in the group of participants who received only the basic scientific information about the safety of GM food (figure 2b; for further results, see [161]). On average across time points, parameters w and β for this group are estimated at 0.57 and 23, respectively, suggesting a stronger weight on social dissonance and a moderate amount of uncertainty in belief updating process. These same parameters are then used to predict the data for the other, unseen, half of participants. Across 50 random half-splits, we find that our models predict this unseen data well (figure 2b, right panel). When comparing models assuming different integration rules, we find that this group of participants do not seem to consider all potentially relevant moral and social beliefs, but seem to rely on one most important belief, as reflected in lower root-mean-squared deviations and higher correlations of predicted trends for the most important rule (0.07 and 0.85, respectively) compared to the simple average rule (0.12 and 0.58) and weighted average rule (0.12 and 0.60; see [161] for more details and further insights from this study).

Another example (figure 2c) comes from a survey of voting beliefs conducted in three waves before the 2018 US election for House of Representatives, on a national probabilistic panel sample of more than 4000 participants [163]. In each wave, they reported four focal beliefs about their voting behaviour on a scale from 0 to 100: that they will (i) vote Republican, (ii) vote Democrat, (iii) vote for another party, or (iv) not vote at all, with the requirement that the four estimates sum to 100. They also reported the percentage of their social circle that they estimated will vote for each party or not vote. We use these data to construct simulated networks of 1000 potential voters in the 2018 elections in different states (figure 2c shows the example for Ohio). To assign network connections, we use survey estimates of the structure of social circles for supporters of different candidates, and assign to each simulated voter a social circle that is either somewhat or very similar (low versus high homophily) to themselves in terms of political orientation and other demographic characteristics (age, race, income and education). To achieve similar intercorrelations of these characteristics in the simulated sample as in reality, we construct copulas based on the survey and population-level data. We calculate the social field as the majority of beliefs in one's social circle. To assign initial focal beliefs to each potential voter in this simulated network, we use probabilities of different states derived from the first wave of survey data, and then calculate beliefs in each subsequent time step based on the model (see box 1 and code in electronic supplementary material). Each of these beliefs is represented as a vector of probabilities that a participant is in each of four possible states: voting Republican, Democrat, other party or not voting. The individual field is composed of four equivalent vectors representing their actual voting behaviour in 2016 (describing whether they voted for the Republican, Democrat, or other candidate, or did not vote at all). The individual field is assumed to be updated three times in the pre-election period, following important events that could have swayed public opinion: ‘Sharpiegate’ on 4 September [164], Kavanaugh accusations becoming public around 14 September [165] and Pittsburg synagogue shooting on 27 October [166]. We assumed that the first and the third event reduced the support for Republicans, while the second polarized public opinion so that everyone became more convinced about their prior political choice.

We compare trajectories of voting beliefs derived from this simulated network of potential voters with empirical trajectories measured on actual survey participants, using different assumptions about the underlying social and cognitive processes. First, we investigate the effect of assumed homophily of the social network. Results shown in figure 2c suggest that the high homophily assumption (lower panel) produces modelled trends that better correspond to empirical trends than the low homophily assumption (upper panel). The lower panel (high homophily version, which fits the data better) of figure 2c suggests that voting for Democrats is better explained by higher level of attentiveness (in the middle figure in the lower panel, full lines—higher β—are closer to the black line that represents true trajectory), while voting for Republicans and not voting is better explained by lower level of attentiveness (in the first and last figures in the lower panel, dashed lines—lower β—are closer to the black line).

These findings illustrate that our modelling framework enables comparison of models using different assumptions about social networks, strategies for belief integration, relative importance of dissonance related to individual and social beliefs, and attentiveness to the updating process. This kind of modelling could be used to gain insights into belief dynamics in different contexts (to the extent that they can be compared), for instance, to assess in advance the impacts of different educational interventions designed to increase public science literacy, or to explore and predict a variety of societal trends and understand their underlying mechanisms.

4. Conclusion and outlook

In this paper, we reviewed a range of findings and models about belief dynamics from different disciplines and proposed a quantitative framework that could be used to compare the many different existing models theoretically and empirically. In this section, we discuss the outlook for the study of belief dynamics in relation to the three challenges we identified in the introduction: integration of network structure and cognitive processes, model comparison and the need for an integrative quantitative framework that makes testable predictions about belief dynamics.

Understanding belief dynamics requires insights and integration of many theoretical and empirical findings on cognitive and network components of belief dynamics, studied in many different disciplines. Our review of the literature is only a first step in this direction. To stimulate further integrative efforts, we outline a quantitative framework based on a statistical physics formalism that enables studying how these components together give rise to different patterns of belief dynamics.

A main advantage of our framework is that it allows for comparison of different models within the same computational formalism. By implementing different assumptions of models in the extant literature, we can compare how well they predict empirical patterns of belief dynamics. These predictions can be assessed on individual and group levels. Given that belief dynamics is a complex system involving interacting and changing structural and process components, accurate predictions of individuals' beliefs might be difficult to achieve. However, even when individual-level predictions of belief change are beyond reach, the framework can be used to understand and predict system level characteristics and trajectories [12].

Models of belief dynamics are often quantitative, but their predictions have so far rarely been confronted with empirical data other than in a qualitative fashion, mostly by visually assessing the match between predictions and data. The focus on qualitative pattern matching makes it somewhat difficult to compare how well different models predict empirical patterns such as polarization and consensus. There are examples where researchers have fitted belief dynamics models to empirical data, but these investigations usually only focus on some aspects, either cognitive or social, of the whole system of belief dynamics. The framework we propose can provide predictions based on the interplay of these aspects and assess the quantitative fit to empirical data.

The study of belief dynamics depends on the availability of suitable data. In order to capture the full dynamics of belief change, researchers need information gathered over time about not only individual beliefs, but also about the structure of the social network. The lack of suitable data is perhaps one of the main contributors to the lack of progress in understanding belief dynamics. However, during the last decade or so, we have seen the emergence of unprecedented data collection opportunities for social scientists. By combining techniques developed within computational social science with traditional experiments and surveys, researchers can develop more complete datasets suitable for model comparison, if privacy and security concerns can be adequately addressed.

Future research could consider several extensions to the framework. For example, we treated the various related beliefs in an aggregated manner. In order to fully understand belief dynamics, beliefs relevant for a certain focal belief should be treated as a network of beliefs [46] with weights between the belief nodes that can be updated over time. Although the idea of belief networks has a long history in psychology [132,167], formal theories that can provide predictions of how the network structures of individual beliefs affect belief dynamics and related behaviours have only been developed relatively recently [44,45,134]. For example, Dalege et al. [46,47] have developed a quantitative model of belief networks that underlie people's attitudes towards different issues. Other models combine the structure of the internal belief network and the social network: Rodriguez et al. [49] developed a model of belief dynamics where each individual is endowed with a network of interacting beliefs that changes through interaction with other individuals in a social network. However, empirical tests of network models are still rare, as fitting them requires large longitudinal data on a number of different beliefs. One recent example of such an empirical test showed that a model combining networks of individual and social beliefs can predict changes in science-related beliefs [50]. We have also not considered the relation between measured beliefs and actual behaviour. In some situations, perceived behavioural control [41] or external factors in the environment rather than internal belief dynamics might affect individuals' behaviour. Another challenge is modelling more precisely how different educational interventions affect beliefs by acting on specific structural and process components of belief dynamics, and how we can compare interventions in different contexts. Finally, the problems of identification and mimicry of different models of belief dynamics need to be studied more extensively. We hope that this review and framework will enable further study of these and other questions and contribute to a better understanding of dynamics of beliefs about science, health, politics and other issues arising in human societies.

Ethics

Collection of data in empirical examples has been approved by the University of New Mexico (no. 16018) and the University of Sothern California (no. UP-14-00148) Institutional Review Boards. Informed consent was obtained before the beginning of each study by the study authors.

Data accessibility

Data used in examples and the modelling code are available for download at the link provided in the electronic supplementary material.

Authors' contributions

All authors contributed equally to writing of the manuscript. M.G., H.O., T.v.d.D. and D.L.S. contributed the empirical examples.

Competing interests

We declare we have no competing interests.

Funding

M.G., H.O. and J.D. were supported in part by grants from the National Science Foundation (DRMS-1757211, DRMS-1949432 and BCS-1918490), M.G., T.v.d.D. and D.L.S. were supported in part by a grant from the National Institute of Food and Agriculture (NIFA-2018-67023-27677) and J.D. was supported in part by the Marie Curie Fellowship. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding agencies.