The scaling of ground reaction forces and duty factor in monitor lizards: implications for locomotion in sprawling tetrapods

Abstract

Geometric scaling predicts a major challenge for legged, terrestrial locomotion. Locomotor support requirements scale identically with body mass (α M¹), while force-generation capacity should scale α M^2/3 as it depends on muscle cross-sectional area. Mammals compensate with more upright limb postures at larger sizes, but it remains unknown how sprawling tetrapods deal with this challenge. Varanid lizards are an ideal group to address this question because they cover an enormous body size range while maintaining a similar bent-limb posture and body proportions. This study reports the scaling of ground reaction forces and duty factor for varanid lizards ranging from 7 g to 37 kg. Impulses (force×time) (α M^0.99−1.34) and peak forces (α M^0.73−1.00) scaled higher than expected. Duty factor scaled α M^0.04 and was higher for the hindlimb than the forelimb. The proportion of vertical impulse to total impulse increased with body size, and impulses decreased while peak forces increased with speed.

1. Introduction

Inevitable consequences of body size and shape impose a major challenge for terrestrial locomotion. Given that muscle force and bone strength are proportional to cross-sectional area (L²), while mass is proportional to volume (L³), geometrically similar animals should experience relatively greater muscle and bone stresses with increasing body size. Mammals hold their limbs parasagittally and partially compensate for this challenge by transitioning from a crouched (bent-leg) posture in small mammals to a more upright (straight-leg) posture in larger mammals (up to around 300 kg) with greater average joint angles at larger body sizes, decreasing the ratio of muscle impulse necessary to produce a given ground reaction impulse (an increased limb muscle mechanical advantage) [1]. This strategy is not generally used by sprawling tetrapods such as amphibians and reptiles, although lizards do vary their locomotor posture, sometimes becoming bipedal at high speed [2–4]. It has been proposed that larger sprawling tetrapods may also adjust posture with size and speed [2,3,5–8], but the limbs of varanids do not become more upright with increasing body size [9]. Furthermore, although numerous studies have reported ground reaction forces (GRFs) for sprawling tetrapods (e.g. [10–15]), little is known about the scaling of locomotor forces in these animals.

Varanid lizards are an ideal group in which to study how animals respond to the biomechanical problems of body size because they range from 5 g to 100 kg [16] while maintaining similar postures [9,16,17] and body proportions [18]. Femoral adduction and knee and ankle joint angles did not vary significantly with size (40 g–8 kg) in a previous study on varanids [9]. Larger varanids have previously been shown to compensate for the predicted size-dependent loss of muscle force by possessing pelvic [17] and pectoral muscles [19] of greater mass and physiological cross-sectional area, reduced locomotor speeds [20], increased duty factors and modest changes in femoral kinematics [9].

This study investigates GRFs and stride parameters in varanid lizards against two null hypotheses for the scaling of locomotor forces with body mass. Under a null hypothesis based on body support requirements, peak vertical forces will increase α M¹ to support the increased body masses of larger animals locomoting at dynamically similar speeds [1,21], while the inverted pendulum model predicts that impulses would increase α M^1.167 (force × time: M¹ * (M^1/3)^1/2) [22,23]. Alternatively, a null hypothesis based on muscular force production suggests that, under purely geometric scaling, peak forces will only increase α M^2/3 because muscle force is proportional to cross-sectional area. In both cases, peak forces should increase with speed, while impulses remain constant [24]. If forces scale according to the body support hypotheses, stress (force/area) will increase α M¹ – M^0.67 = M^1/3, leading to dangerously low skeletal safety factors and relatively lower muscle forces in larger animals [16,21]. If peak forces scale with a lower exponent than body mass instead, how can larger animals locomote effectively?

2. Material and methods

GRFs were collected for 28 lizards from 12 species (table 1) [25,26] covering almost the entire possible body size range. Two hundred and seventeen individual strides were recorded across speeds ranging from 0.96 to 4.05 m s⁻¹, comprising 105 forelimb and 112 hindlimb trials. Forces were collected at 1000 or 10 000 Hz with a custom-built force-plate [12], a force-plate based on a Nano17 load cell (ATI Industrial Automation, Apex, NC, USA), or an IP65 gamma force-plate (ATI Industrial Automation). All animals (except V. komodoensis, which were zoo animals) were wild caught. Force-plates were calibrated using equal weights. Trials with aberrant gaits, or incomplete foot contacts were excluded. Methods were approved under ethics SBS/195/12/ARC (QLD), ANA16104 (QLD), ANE1934 (QLD), ANE2054 (QLD), A2450 (QLD), ANE2054 (QLD) and RA/3/100/1188 (WA), and lizards were collected under permits WISP11435612 (QLD) and SF009075 (WA), 08-001092-5 (WA) and WA0001919 (QLD).

Table 1.

Species investigated in the study. ¹[25]; ²[26]; ³mean of other species studied.

species	N (individuals)	body mass (g)	n (strides)	species max speed (m s−1)
V. brevicauda	3	7.00 ± 1.91	9	1.591
V. caudolineatus	3	11.06 ± 2.28	15	2.341
V. eremius	1	11.8	6	3.711
V. semiremex	1	49.9	5	3.493
V. acanthurus	1	52.7	11	3.051
V. hammersleyensis	1	63.7	2	2.831
V. tristis	3	186.5 ± 79	38	3.951
V. rosenbergi	2	662 ± 385	19	2.76
V. panoptes	5	1328.3 ± 650.2	92	5.91
V. spenceri	1	2098	1	3.493
V. varius	4	2311 ± 872.3	50	4.031
V. komodoensis	3	26 550 ± 5310	18	4.692

Dorsal and lateral videos were captured using high-speed cameras (Fastec IL3-100; 1280 × 1024 pixels, Fastec Imaging Corporation, San Diego, CA, USA) recording at 250 fps. Forces and videos were synchronized and strides identified using custom MATLAB (Mathworks, Natick, MA, USA) programs and an internal trigger. GRFs were analysed from footfall to toe-off and smoothed using a fourth-order, zero-lag Butterworth low-pass filter. Force polarities were transformed so that positive values indicate ground support (GRF_Z), cranially directed forces (GRF_X), and medially directed forces (GRF_Y) relative to the body (figure 1e). Total force magnitude [1,27] was calculated as in the below equation

$$\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_{\mathrm{TOT}}=\sqrt{(|\mathrm{GR}{\mathrm{F}}_X{|}^2+\hspace{0.17em}{|\mathrm{GR}{\mathrm{F}}_Y|}^2+{|\mathrm{GR}{\mathrm{F}}_Z|}^2)}$$ 2.1

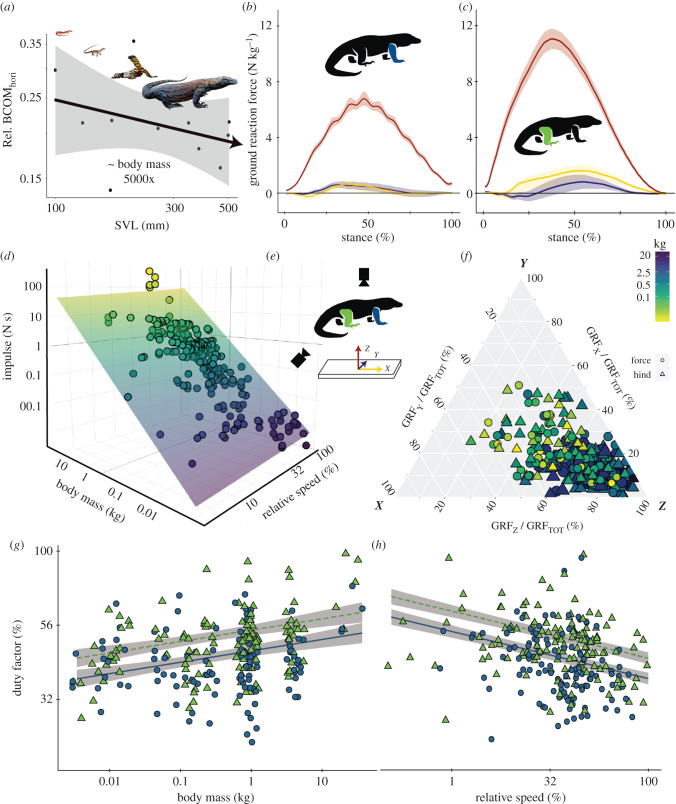
Figure 1.

GRFs and duty factor in monitor lizards. (a) Caudal displacement of the horizontal body centre of mass (electronic supplementary material, figure S4). Average forelimb (b) and hindlimb (c) GRFs of monitor lizards recorded on a force-plate (e) for vertical (Z, red), cranial–caudal (X, yellow) and medial–lateral (Y, purple) directions. (d) Total GRF impulse varied with body mass and relative speed. (f) Relative proportion of X, Y and Z impulses varied with body mass and fore versus hindlimb. Duty factor increased with body mass (g) but decreased with relative speed (h) and was higher for the hindlimb (green triangles) than the forelimb (blue circles). Shading in (g,h) indicates 95% confidence intervals (a,d,g,h) are depicted on log scales.

Impulses were time integrals of force. For cranial, caudal, medial and lateral impulses, forces were separated into positive and negative regions before integration.

The average speed was estimated by quantifying the two-dimensional (2D) motion of a single dorsal point using DeepLabCut, a machine-learning video tracking software [28]. Speeds were converted to relative speed based on the maximum sprint speed for each species (table 1). Relative speed [29] was used instead of dynamic speed (Froude number) because, although dynamic speed is useful for identifying similar gaits among diverse species [23] and was well-correlated with relative speed in our dataset (electronic supplementary material, figure S4), it has been shown to be of limited utility in predicting similar gaits in closely related lizards [30] and it is not obvious which characteristic length would best capture the dynamics of sprawling locomotion.

All analyses were conducted using R 3.6.3 (R Development Core Team, 2020). The relationships between force parameters and body mass, relative speed and limb (forelimb versus hindlimb) were assessed using mixed-effects models employing the lmer.R function from the lme4 and lmerTest packages including subject as a random factor [31,32]. All continuous variables were log-transformed. In all cases, a full-interaction model was initially constructed. If the interaction terms were not significant, a reduced model with no interaction terms was used instead, provided that an ANOVA test found no significant difference between these models. When full models were used, non-significant variables were successively dropped from the model using the update.R function as long as each, successive model was not significantly different from the previous one using an ANOVA test (electronic supplementary material, table S1). Individual regressions for body mass and relative speed (table 2) were calculated using sim_slopes.R, and plotted using interact_plot.R [33]. Percentage differences between fore and hindlimb parameters were calculated as the ratio of the inverse logs from the regression intercept values.

Table 2.

Scaling coefficients for stride parameters versus body mass and speed. Values represent independent fixed-effects regression coefficients and 95% confidence intervals calculated from linear mixed-effects models (electronic supplementary material, table S1).

parameter	limb	versus log10 body mass (kg)		versus log10 relative speed
		slope	intercept	slope	intercept
duty factor	combined	0.038 ± 0.024		−0.161 ± 0.035
	fore		1.554		1.554
	hind		1.624		1.624
total impulse  $\int \hspace{0.17em}\mathrm{GR}{\mathrm{F}}_{\mathrm{Tot}}$	combined			−0.334 ± 0.146
	fore	1.14 ± 0.105	−0.624		−0.624
	hind	1.260 ± 0.105	−0.370		−0.370
total peak force	combined		−0.720		−0.720
	fore	0.852 ± 0.186		0.327 ± 0.506
	hind	0.728 ± 0.184		−0.270 ± 0.396
vertical impulse  $\int \hspace{0.17em}\mathrm{GR}{\mathrm{F}}_Z$				−0.379 ± 0.153
	fore	1.191 ± 0.106	−0.441		−0.441
	hind	1.316 ± 0.105	−0.693		−0.693
vertical peak force	combined			0.211 ± 0.122
	fore	0.890 ± 0.069	0.707		0.707
	hind	0.999 ± 0.067	0.886		0.886
cranial impulse  $\int +\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_X$	combined	1.058 ± 0.190
	fore		−1.889
	hind		−1.417
cranial peak force$+\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_X$	combined	0.809 ± 0.134	0.073
caudal impulse  $\int -\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_X$	combined	0.982 ± 0.204
	fore		−2.130
	hind		−1.939
caudal peak force  $-\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_X$	combined	0.812 ± 0.101
	fore		−0.195
	hind		−0.053
medial impulse  $\int +\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_Y$	combined	1.084 ± 0.198
	fore		−1.567
	hind		−1.194
medial peak force  $+\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_Y$	combined	0.812 ± 0.128		0.531 ± 0.317
	fore		0.303		0.303
	hind		0.120		0.120
lateral impulse  $\int -\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_Y$	combined		−1.904
	fore	0.986 ± 0.232
	hind	1.337 ± 0.226
lateral peak force  $-\hspace{0.17em}\mathrm{GR}{\mathrm{F}}_Y$	combined	0.922 ± 0.110
	fore		−0.129
	hind		−0.133
stance time	combined	0.297 ± 0.053		−0.624 ± 0.089
	fore		1.402		1.402
	hind		1.463		1.463
swing time	combined	0.184 ± 0.033		−0.285 ± 0.052
	fore		1.259		1.259
	hind		1.326		1.326

To check for an influence of phylogeny, slopes and confidence intervals of linear regressions for species means of each parameter were compared with phylogenetic independent contrasts (electronic supplementary material, figure S1), calculated using the pic.R function [34] and the maximum-likelihood varanid tree built from 1030 bp of the NADH-2 gene [35]. To investigate the scaling of the position of the horizontal centre of mass, data from the two-scale method [36] (electronic supplementary material, figure S5) were analysed (figure 1a).

3. Results

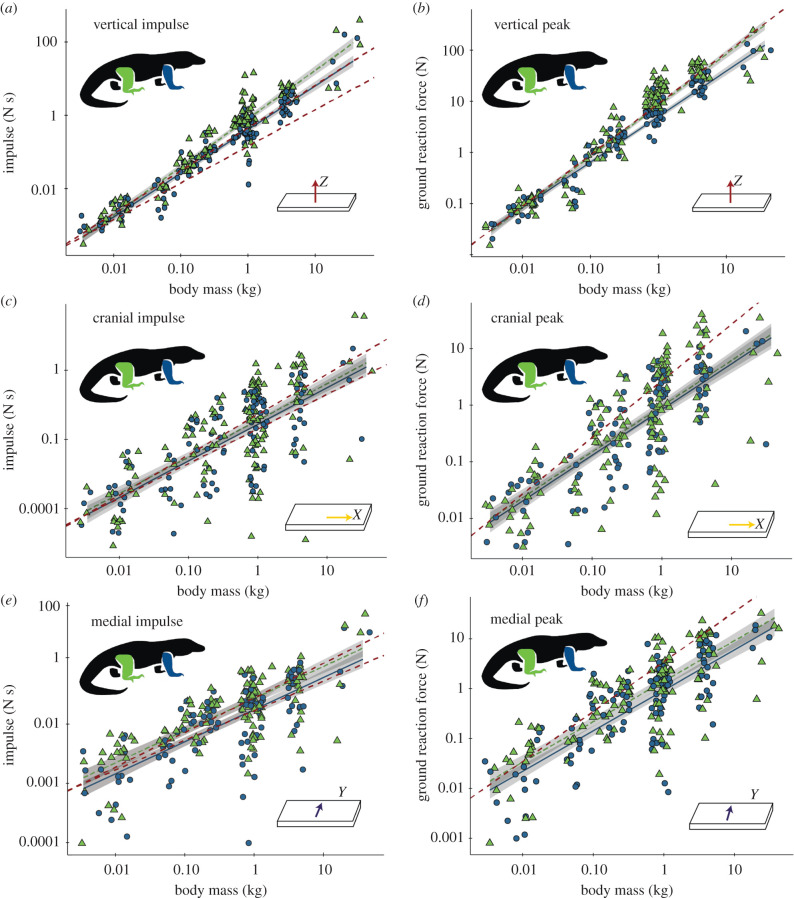
Ground reaction peak forces (figure 2) and impulses (figures 1d and 2) scaled differently with body mass and relative speed (table 2). Overall, impulses scaled with slopes greater than 1 while peak forces scaled with slopes less than 1 when regressed against body mass (figure 2). When significant relationships between speed and forces were detected, impulses decreased and peak forces increased with speed (table 2). Total and vertical impulses increased with body mass (vertical impulse slopes: 1.19 ± 0.11 forelimb; 1.32 ± 0.11 hindlimb), decreased with relative speed (slope: −0.38 ± 0.15), and varied with limb, and the interaction with body mass and limb, while relative speed did not significantly affect either cranial–caudal or medial–lateral impulses (electronic supplementary material, table S1). Vertical, total and lateral impulses scaled with a steeper slope against body mass for the hindlimb than the forelimb (table 2 and figure 2), and were also absolutely higher in the hindlimb in vertical, total, caudal, cranial and medial impulses (77.8%, 77.8%, 58.4%, 31.8% and 134.4%, respectively) (table 2). Total and vertical impulses decreased with speed. Vertical impulses ranged from 0.014 to 12 times body weight (mean 0.83).

Figure 2.

Scaling of ground reaction impulse and peak force in monitor lizards. Impulse and peak forces for vertical (a,b), caudal (c,d) and lateral (e,f) directions shown on log-log plots with regression lines from mixed-effects models for the hindlimbs (green triangles) and the forelimbs (blue circles). Regression equations are listed in table 2. Red dashed lines indicate slopes of 1 (peak graphs), and 1 and 1.167 (impulse graphs). Shading indicates 95% confidence intervals.

Total, vertical, lateral, medial, caudal and cranial peak forces increased significantly with body mass (figure 2 and table 2; electronic supplementary material, figure S2). Relative speed also had a significant positive effect on total, vertical, cranial and medial peak forces (electronic supplementary material, table S1 and figure S3). Every interaction term had a substantial effect on total peak force, and vertical peak force also depended on limb, perhaps reflecting differing relationships between individual force components, body mass, speed, and limb. Peak vertical, caudal and medial forces were higher for the hindlimb (51.4%, 41.3%, 51.4%, respectively), but hindlimb and forelimb peak forces were similar for lateral and total forces (table 2). Forelimb total peak forces also increased with a steeper slope than those of the hindlimb (table 2). Vertical peak forces ranged from 1.09 to 49.15 times body weight (mean 9.69).

Duty factor was found to be significantly related to body mass, speed and limb (electronic supplementary material, table S1). Duty factor increased with body mass (slope: 0.04 ± 0.02) and decreased with relative speed (slope: −0.16 ± 0.04) (figure 1g,h). The duration of both stance and swing phases increased with body mass and decreased with speed (table 2). The mean duty factor was higher for hindlimb trials (49.8) than forelimb trials (42.6) (table 2). The proportion of total impulse due to vertical forces decreased significantly (electronic supplementary material, table S1) with body mass (figure 1f). Hindlimb to forelimb ratios of raw impulses scaled to body mass were 2.23 (vertical), 2.11 (cranial), 1.59 (caudal), 1.19 (lateral) and 2.03 (medial).

4. Discussion

This study reports the scaling of GRFs from varanid lizards ranging over about three and a half orders of magnitude in body mass. The main findings of this study were that ground reaction impulses scaled against body mass roughly as expected by the inverted pendulum model (∼M^1.167), while peak forces scaled with body size less than predicted by the body support hypothesis (peak < M¹), but greater than the force production hypothesis (peak > M^2/3). Duty factor was found to increase with body mass, indicating that larger varanids extend body support over a longer stance phase with lower peak forces. Future research examining the scaling of muscle moment arms and muscle gearing is needed to determine how GRFs are produced, but taken in the context of previous work, these results may suggest that varanids compensate for the biomechanical challenges of size by using two simultaneous strategies: (i) increasing duty factor to keep peak GRFs below critical levels and attenuate the consequences of the body support hypothesis, and (ii) allometric increases in muscle force-generation capacity and bone strength to circumvent the consequences of the force-generation hypothesis.

Scaling exponents of vertical and lateral impulses are steeper than predicted by the body support model, even when taking duty factor into account, whereas other impulses scale with expectations. Predictions based on the inverted pendulum model suggest that vertical ground reaction impulse should scale as M^1.167 in animals with limbs oriented in the parasagittal plane [22]. We found that forelimb vertical impulse scaling agrees well with this prediction when duty factor is taken into account, while hindlimb impulse scales more steeply (M^1.32–M^0.04 = M^1.28 hindlimb; M^1.19–M^0.04 = M^1.15 forelimb). This may suggest that the forelimbs of sprawling tetrapods follow the inverted pendulum model more closely than the hindlimbs, which could be related to differences in locomotor mechanics and roles (propulsion versus changing direction) between girdles, or indicate increasing dominance of the hindlimb in body support at larger body masses. After correcting for duty factor, cranial–caudal impulses scale α M^∼1, suggesting that larger sprawling tetrapods do not use proportionally more braking or propulsive forces. Medial impulse scales α M^∼1.04 after taking duty factor into account, while lateral impulse of the hindlimb scales α M^∼1.3, suggesting that these side-to-side forces may become more important at larger body sizes. The pattern of lateral undulation changes with speed [37–40] and may vary with body size. Proportionally, higher lateral GRFs and/or magnitudes of lateral undulation in larger sprawling animals may distribute peak forces away from the vertical, enabling them to generate sufficient locomotor force without dangerously high bone stresses in any one direction.

Vertical peak forces scale with greater slopes than expected from the force production hypothesis (α M^0.67) even when duty factor is taken into account (M^01.00 – M^0.04 = M^0.96 hindlimb; M^0.89 – M^0.04 = M^0.85 forelimb), suggesting that increased duty factor cannot, by itself, explain high peak force scaling exponents. The finding that peak forces exceed the force and stress limits predicted by geometric scaling is anticipated by previous work [17,19] which shows positive allometry in the musculoskeletal system of varanids. Varanid muscles show positive allometry in mass (slope: 1.43 forelimb, 1.07 hindlimb) and physiological cross-sectional area (slope: 0.88 forelimb, 0.76 hindlimb) [17,19]. Although in vivo bone strains have not been measured in varanids, varanid bone diameters scale with positive allometry [41,42], and with a higher exponent than those of iguanids [42]. Although varanids retain largely similar body proportions and postures at different body sizes, small differences in anatomy and posture may have substantial effects on local stresses. Future biomechanical modelling studies may show that locomotor forces are distributed less vertically in larger sprawling tetrapods, allowing proportionally less-robust bones and muscles to generate sufficient locomotor forces.

GRFs were found to be hindlimb-dominant, with the hindlimb providing greater peak force than the forelimb in all directions (table 2). Although no significant differences were detected, peak cranial–caudal and medio-lateral forces occurred earlier in hindlimb compared to forelimb strides (figure 1a–c), suggesting that the hindlimb may transition into the propulsive phase earlier than the forelimb, perhaps reflecting partial division of labour between the hindlimb (propulsion) and forelimb (changing direction) [43]. Greater medial peak forces and impulse were reported in the forelimb than hindlimb for V. exanthematicus during high-speed running [10], but greater medial peak forces and impulses were found in the hindlimb across multiple varanid species in this study. This suggests that medial impulse may become increasingly forelimb-dominated at higher speeds, but relative speed did not predict medial impulse in our dataset (electronic supplementary material, table S1). For all variables in which the fixed effect regression slope for body mass differed between the hindlimb and forelimb (vertical impulse, vertical peak force and propulsive peak force), the hindlimb became increasingly dominant at larger body sizes. This is likely related to the location of the whole-body centre of mass, which moves caudally with increased body size in varanids (figure 1a) [36]. Although the hindlimb produced more vertical impulse than the forelimb at all speeds (table 2), hindlimb vertical impulses did not increase more steeply than forelimb impulse with speed, which is inconsistent with studies on cheetahs, greyhounds [44] and horses [45], and may reflect the fact that although sprawling tetrapods adjust their gait with speed [2], the transitions are not regular and abrupt as in mammals [24,46].

How locomotion changes with body size has been most commonly studied in upright mammals and birds [22,24], yet sprawling postures are characteristic of current and extinct tetrapod lineages and sprawling locomotion was widespread in stem amniotes [47] and prior to the Triassic [48]. These results provide insight into selective pressure in the evolution of terrestrial locomotion, particularly how size affects locomotion in sprawling tetrapods. They may also lead to better reconstruction of extinct species, and help to explain how larger extinct forms dealt with the biomechanical challenges of locomotion at greater body size.

Ethics

Methods were approved under ethics SBS/195/12/ARC (QLD), ANA16104 (QLD), ANE1934 (QLD), ANE2054 (QLD), A2450 (QLD), ANE2054 (QLD) and RA/3/100/1188 (WA), and lizards were collected under permits WISP11435612 (QLD) and SF009075 (WA), 08-001092-5 (WA) and WA0001919 (QLD).

Data accessibility

Raw data and code are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.rn8pk0p82 [49].

Authors' contributions

R.L.C. participated in study design, collected data, analysed the data and wrote the manuscript. T.J.M.D. participated in study design, collected data and helped revise the manuscript. R.I. collected data. D.R. collected data. C.J.C. participated in study design, created tools for data analysis, collected data and helped revise the manuscript. All authors contributed to manuscript revision, gave final approval for publication and are accountable for the work performed.

Competing interests

We declare we have no competing interests.

Funding

Funding was provided by the Australian Research Council (DE120101503, DP180100220), National Science Foundation (1256065) and the Natural Sciences and Engineering Research Council of Canada.