Abstract
Stereotactic body radiation therapy (SBRT) has demonstrated high local control rates in early stage non-small cell lung cancer (NSCLC) patients who are not ideal surgical candidates. However, distant failure after SBRT is still common. For patients at high risk of early distant failure after SBRT treatment, additional systemic therapy may reduce the risk of distant relapse and improve overall survival. Therefore, a strategy that can correctly stratify patients at high risk of failure is needed. The field of radiomics holds great potential in predicting treatment outcomes by using high-throughput extraction of quantitative imaging features. The construction of predictive models in radiomics is typically based on a single objective such as overall accuracy or the area under the curve (AUC). However, because of imbalanced positive and negative events in the training datasets, a single objective may not be ideal to guide model construction. To overcome these limitations, we propose a multi-objective radiomics model that simultaneously considers sensitivity and specificity as objective functions. To design a more accurate and reliable model, an iterative multi-objective immune algorithm (IMIA) was proposed to optimize these objective functions. The multi-objective radiomics model is more sensitive than the single-objective model, while maintaining the same levels of specificity and AUC. The IMIA performs better than the traditional immune-inspired multi-objective algorithm.
Keywords: Lung SBRT, Radiomics, Multi-objective learning, Pareto-optimal solution
1. Introduction
With the development of modern imaging and radiation delivery techniques, dose escalation with stereotactic body radiation therapy (SBRT) has emerged as the standard of care for inoperable early stage non-small cell lung cancer (NSCLC) (Høyer, 2008; van Baardwijk et al., 2012; Timmerman et al., 2010). Primary local control rates higher than 95% were achieved for this tumor type after 3 years of 3-fraction SBRT (Timmerman et al., 2010) Nevertheless, early stage distant failure was still common with a 3-year rate of 22.1%. A recent update on the RTOG 0236 experience showed 5-year distant failure rates of 31% (Timmerman et al., 2014). Additionally, distant failure often occurs shortly after definitive treatment of the primary tumor. Distant failure is considered as an important oncologic event because it closely correlates with mortality. For patients at high risk of early distant failure, additional systemic therapy after SBRT may reduce this risk and improve overall survival. However, because this population is often in relatively poor health, the therapy-related toxicity could increase mortality. Therefore, a strategy that can correctly predict patients with high risk distant failure in early cancer stages is needed.
By quantitatively analyzing large amounts of information from medical images, the field of radiomics holds great potential to predict treatment outcome (Freeman et al., 2015; Gillies et al., 2015; Lambin et al., 2012; Wu et al., 2016a). In a recent study (Freeman et al., 2015), the radiomics features extracted from joint FDG-PET and MRI were used to predict lung metastasis risk in soft-tissue sarcomas. After constructing the multivariable model using logistic regression, the AUC was found to be equal to 0.984. Hawkins et al. (Hawkins et al., 2014) applied radiomics features extracted from CT images to predict survival time in NSCLC with an accuracy of 77.5%. In a study by Coroller et al. (Coroller et al., 2015), CT based radiomics features were added to the clinical model to predict distant metastasis in lung adenocarcinoma, and the performance was significantly improved.
Most currently available radiomics methods adopt a single objective, such as overall accuracy or AUC, as the objective function to construct the predictive model. Many applications adopted accuracy as the objective function and utilized a cross-validation strategy to train the predictive models (Wu et al., 2016b; Tan et al., 2013; Mu et al., 2015; Huynh et al., 2016). In (Freeman et al., 2015), AUC was taken as the objective function to train the model by repeated bootstrap samples for predicting lung metastasis in soft-tissue sarcomas of the extremities. In (Huang and Dun, 2008), a distributed particle swarm optimization (PSO) strategy was used to train the SVM predictive model. In this method, the training process was considered as a combinatorial optimization problem and the objective was to maximize the accuracy by combining different parameters. Similarly, clonal selection algorithm (CSA) and genetic algorithm were also utilized to train the predictive models (Ding and Li, 2009; Cho et al., 2006; Avci, 2009; Wu et al., 2009). In treatment outcome prediction applications, treatment outcome data is often imbalanced (i.e., with and without distant failure after SBRT in NSCLC). Thus, overall accuracy alone may not be a good measure for the predictive models, especially when positive and negative events are imbalanced in training datasets. For example, the number of patients with distant failure in lung SBRT is lower than that of patients without distant failure. Although the accuracy can be high as it is used as the objective function, sensitivity can be low. An extreme example is shown in table 1. Assuming 20 samples, TP indicates true positives, FN indicates false negatives, FP indicates false positives, and TN indicates true negatives. According to the predictive results in Eq. (1) ~ (3), despite high accuracy and specificity, sensitivity is only 0.33. In this case, the model may misclassify patients with distant failure into the category without distant failure. Despite high accuracy and specificity, the model does not provide enough information to stratify patients at high risk of distant failure eligible for additional systematic therapy. In contrast, a high specificity model is required to minimize false positives among high-risk patients receiving adjuvant systemic therapy, which could lead to treatment-related toxicity. Therefore, the predictive model has to be both sensitive and specific. Although the AUC provides a better measure than overall accuracy by taking both sensitivity and specificity into account, it also summarizes the test performance over regions of the ROC space that would rarely be used. In addition, final prediction is determined by the threshold that needs to be manually selected.
Table 1.
Illustration of imbalanced dataset for prediction results.
| Positive | Negative | |
|---|---|---|
| Positive | TP=1 | FN=2 |
| Negative | FP=2 | TN=15 |
| (1) |
| (2) |
| (3) |
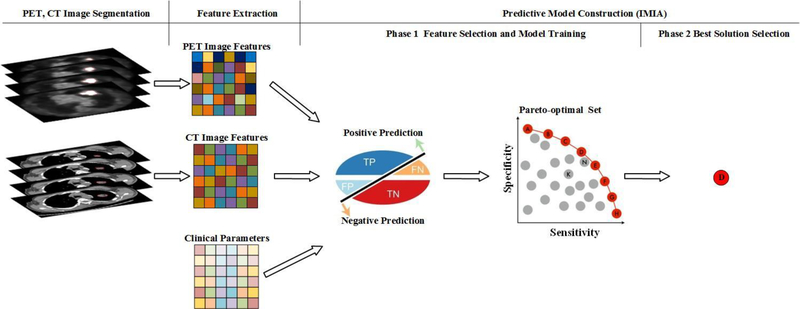
To overcome the limitation of the conventional single-objective model, we proposed a multi-objective radiomics model that simultaneously considers both sensitivity and specificity as the objective functions. Additionally, an iterative multi-objective immune algorithm (IMIA) was proposed to train the model and render it more accurate and reliable. IMIA consists of two phases: (1) generating a Pareto-optimal solution set; (2) selecting the best of all feasible solutions according to the predictive results. The workflow of the multi-objective radiomics model is illustrated in figure 1. In this model, tumors were first segmented in PET and CT images. Image features such as intensity, texture, and geometry features were then extracted. In the following step, clinical parameters were combined with quantitative imaging features to construct the predictive model using IMIA. Another advantage of our proposed model is the flexibility to select the best solution according to the clinical needs because multiple solutions are generated in multi-objective radiomics. Of course, in the ideal situation, a model will have both very high sensitivity and specificity, but this is rarely achievable; instead, models can be optimized to the need; for example, in newborn screening, missing a correctable metabolic defect can be catastrophic, and the intervention is non-toxic, so a model with very high sensitivity can be employed that sacrifices some specificity. However, if the intervention is high risk or has significant toxicity and the benefit has not been established, such as the administration of cytotoxic chemotherapy to otherwise locally-staged lung cancer patients treated with SBRT, specificity for distant metastases potential can be given a higher priority than sensitivity to maximize the likelihood that the intervention is applied to the population most likely to benefit from it.
Figure 1.
Multi-objective radiomics workflow.
2. Material and Method
2.1. Patients, clinical parameters and images
This study included 52 patients in early IA and IB stages, who had received SBRT from 2006 to 2012. The follow-up range was from 6 to 64 months, with a median follow-up time of about 18 months. Twelve (23.1%) of these patients had distant failure.
Clinical parameters were extracted from clinical charts and were categorized into four groups: (1) demographic parameters; (2) tumor characteristics; (3) treatment parameters; and (4) pretreatment medications (table 2). Each parameter can be used as an independent feature for the predictive model.
Table 2.
Clinical parameters.
| Demographic parameters | Tumor characteristics | Treatment parameters | Pretreatment medicine |
|---|---|---|---|
| Age | Primary diagnosis | Number fractions | Antiinflammatories |
| Ethnicity | Central tumor or not | Dose per fraction | Anitdiabetic |
| Gender | Tumor size | BED | Metformin |
| Histology | Statin | ||
| Location | ACE inhibitor | ||
| Stage | ASA | ||
Abbreviation – BED: biological equivalent dose; ACE inhibitor: Angiotensin-converting-enzyme inhibitor; ASA: Acetylsalicylic acid.
CT and PET images used in this study were all from pre-treatment scans. The median interval between PET/CT scan and SBRT treatment was 1 month (within 2 weeks to 2 months for more than 80% of patients). They were acquired by the SIEMENS Biograph 64/1094 (Siemens Medical Solution, Malvern, PA), the Philips Gemini TF/Dual GS (Philips Healthcare, Andover, MA), or the GE Discover ST (GE Healthcare, Waukesha, WI). The CT volume was composed of 274 to 355 slices (3.26 mm ~5.00 mm thick) of 512 × 512 pixels (0.98 × 0.98 mm or 1.17 × 1.17 mm). The PET volume was also composed of 274 to 355 slices (2.43~5.00mm thick) of 168 × 168 pixels, 144 × 144 pixels, or 128 × 128 pixels (4.00 × 4.00 mm or 5.00 × 5.00 mm).
2.2. Tumor segmentation
Before extracting the image features, tumors need to be segmented. In this work, tumors were segmented in a semi-automatic way, as follows.
For the segmentation only, the slices containing tumors were denoised using the fast non-local mean image denoising method (Darbon et al., 2008) to avoid the influence of noise. The middle slice was segmented using the object information based interactive segmentation method (OIIS) (Zhou et al., 2013a). In the OIIS, initial segmentation of the potential regions of interest was performed by a mean-shift method (Cheng, 1995) and the final segmentation was obtained by merging the similar regions according to the similarity determined by the Bhattacharyya coefficient (Kailath, 1967). The accuracy of OIIS has been validated in a previous study, where the F-score was above 0.98. Once the central slice was segmented, the other slices were segmented by the well-known OTSU method (Otsu, 1975) that considers the similarity between two adjacent slices. The segmentation results for PET and CT images are shown in figure 2. The segmented tumors are marked in red.
Figure 2.
Tumor segmentation results for PET and CT images. (a)-(c) Examples of PET image segmentation results in one patient; (d)-(f) CT image segmentation results.
2.3. Image feature extraction
Intensity, texture, and geometry features were extracted for PET and CT images (table 3). All features were extracted in the segmented 3D tumors. For PET images, the standardized uptake value (SUV) was calculated before extracting the features (Adams et al., 2010).
Table 3.
Image features.
| Intensity features | Texture features | Geometry features |
|---|---|---|
| Minimum | Energy | Volume |
| Maximum | Entropy | Major diameter |
| Mean | Correlation | Minor diameter |
| Stand deviation | Contrast | Eccentricity |
| Sum | Texture Variance | Elongation |
| Median | Sum-Mean | Orientation |
| Skewness | Inertia | Bounding Box Volume |
| Kurtosis | Cluster Shade | Perimeter |
| Variance | Cluster Prominence | |
| Homogeneity | ||
| Max-Probability | ||
| Inverse Variance | ||
For the intensity features, the mean, median, standard deviation, maximum and minimum value, skewness, kurtosis, and variance were calculated based on the intensity histogram. Skewness is used to describe the degree of distribution asymmetry around its mean. The skewness value can be either positive or negative and is expressed as:
| (6) |
Kurtosis indicates the flatness or the spikiness of the signal and is defined as:
| (7) |
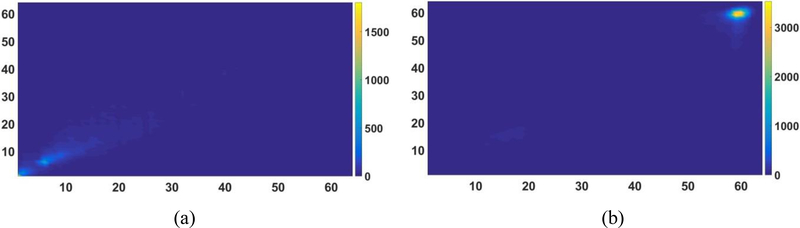
Before calculating the texture features, the gray level co-occurrence matrix (GLCM) was constructed. The GLCM is a square matrix with the number of rows and columns equaling the quantized gray level denoted by Ng. Each element p(i, j) in GLCM represents the number of times a pixel of gray level i occurs with a neighbor pixel of gray level j in the image at a particular displacement distance and angle (Yang et al., 2012). We used histograms with 64 bins and constructed GLCM using 3D analysis of the tumor region with 26 neighboring voxels and 13 directions of the 3D space. An example of the constructed GLCM for PET and CT is shown is figure 3. Twelve texture features were then calculated and defined as follows.
Figure 3.
Example of the constructed GLCM. (a) GLCM for PET; (b) GLCM for CT.
-
Energy is defined as
(8) Energy is a measure of image homogeneity and a higher energy value indicates a more homogeneous image.
-
Entropy is defined as
(9) Entropy is used to measure the randomness of the image intensity distribution.
- Correlation is defined as
where μ is the mean value and σ is the standard deviations. Correlation is a measure of the linear dependency of gray levels on those of either neighboring voxels or specified points.(10) -
Contrast is defined as
(11) Contrast is a measure of the local variations within an image and is highly correlated with the difference between the highest and the lowest values of a continuous set of voxels.
-
Variance is defined as
(12) Variance is used to measure the variation around the mean value.
- Sum-Mean is defined as
(13) -
Inertia is defined as
(14) Inertia is used to measure the local variation between a voxel and its neighbors.
-
Cluster Shade is defined as
(15) Cluster shade is taken as the measurement of the matrix skewness.
-
Cluster Tendency is defined as
(16) Cluster Tendency is used to measure asymmetry.
-
Homogeneity is defined as
(17) Homogeneity is used to measure the closeness of the elements in p(i, j) to the diagonal.
- Max-Probability is defined as
(18) -
Inverse Variance is defined as
(19) Inverse variance is also used to measure the homogeneity of an image.
Geometry features describe the shape, size, or relative position of the tumor (Tan et al., 2013). The major diameter is defined as the major axis length or longest diameter, while the minor diameter is the shortest diameter. Eccentricity is the aspect ratio, defined as the ratio of the length between the major and the minor axis. The features after z-score normalization are reported in figure 4.
Figure 4.
Features from PET, CT images, and clinical parameters after z-score normalization.
2.4. Predictive model
The Support Vector Machine (SVM) was used to construct the predictive model. SVM can find the optimal separating hyperplane between classes by solving a constrained quadratic optimization problem (Zhou et al., 2016). Assuming that {xi, yi}, i = 1, ⋯, n represents the training set with xi as the input vector and yi ∈ {−1,1} as the label. For linear SVM, we assume that the classification function is
| (20) |
where w represents the normal vector of the hyperplane, and b is the bias term of the separating hyperplane. The objective function is
| (21) |
For nonlinear SVM, kernel denoted by k(xi, x) is introduced. In addition, a penalty parameter C is introduced to reduce the effect of the outliers. Hence, the objective function is
| (22) |
| (23) |
where ξi represents the non-negative slack variables. The problem above can be solved by introducing the Lagrange dual function as:
| (24) |
where α is the vector of the dual variables corresponding to each separation constraint and ri is the weight of ξi. After the transformation, the new objective function is expressed as:
| (25) |
| (26) |
where xi and xj are samples i and j, respectively. After obtaining the optimal solutions for Eq. (25), the predictive model was constructed. In the test stage, we assume x is a test sample and the discriminant function is expressed as:
| (27) |
As shown in a previous study (Levman et al., 2008), the radial basis function (RBF) kernel is recommended as a primary choice and was used as:
| (28) |
where γ is a shape parameter that determines the smoothness of the boundary between the groups in the original object space. To obtain the optimal predictive model, the parameters C and γ are trained by the proposed training algorithm, which will be described in the following sections.
2.5. Multi-objective radiomics model
After extracting the features, we selected those that would improve model performance and reduce computational complexity. In addition, the model parameters described earlier were also trained to achieve optimal performance. Because feature selection may influence the model parameter training, feature selection and model parameter training should be conducted simultaneously (Huang and Dun, 2008). In this work, combinatorial optimization, defined as finding an optimal object from a finite set of objects (Nemhauser and Wolsey, 1988), was utilized for feature selection. During optimization, each feature has a binary label “0” or “1”. In a solution obtained by the IMIA algorithm described in section 2.6, a feature is selected if it has a label “1”. If the label is “0”, then the corresponding feature is not selected.
We assume that the model parameters are denoted by α = {α1, ⋯, αM}, where M is the number of model parameters. All the features are denoted by β = {β1, ⋯, βN}, where N is the number of features. The objective functions include both sensitivity and specificity, denoted by fsen, fspe, respectively, as:
| (29) |
| (30) |
where TP is the number of true positives, TN is the number of true negatives, FP is the number of false positives, and FN is the number of false negatives (Zhou et al., 2013a). The goal of the proposed model is to simultaneously maximize fsen and fspe to obtain the Pareto-optimal solutions:
| (31) |
The best predictive result is selected according to the clinical needs. The solution corresponding to the selected features and model parameters can also be obtained. In the following subsection, a new algorithm named as IMIA was described to solve the multi-objective optimization problem.
2.6. Iterative multi-objective immune algorithm
Because two objective functions are defined in equation (31), a multi-objective optimization algorithm is needed. Multi-objective evolutionary algorithms (MOEA) have recently shown superior performance for multi-objective optimization (Deb, 2001).We selected the artificial immune system (AIS) inspired MOEA, a highly distributed, adaptive, self-organizing algorithm with learning characteristics, memory features (Zhou et al., 2013b), and improved performance. Moreover, to improve the accuracy and reliability of the predictive model, an enhanced AIS inspired algorithm called IMIA was proposed. IMIA consists of two phases: (1) Generating the Pareto-optimal solution set; (2) selecting the best solution according to the clinical needs. The first phase includes the following key steps:
Step 1: Initialization
Because feature selection and model parameter training are performed simultaneously, a hybrid initialization of the selected features and model parameters is needed. In MOEA, an initial solution set is always needed. In our method, the initial solution set was generated randomly. One particular solution consists of a group of binary or integer values, named as “individuals”. Each individual in one particular solution represents one feature or one model parameter. The features are encoded by a binary encoding method. A value of “1” indicates that the corresponding feature has been selected, while “0” denotes that the corresponding feature has not been selected. Model parameters are optimized directly because the value is continuous. We use Gmax to denote the maximal number of generations and D(j) = {d1, ⋯, dP}, j = 0 to denote a solution set, where di, i = 1, ⋯, P is the particular solution.
Step 2: Clonal operation
We used proportional cloning to keep the best solutions (Gong et al., 2008). The solution with a larger crowding-distance was reproduced multiple times, with the clonal time qi for each solution calculated as:
| (32) |
where nc is the expectant value of the clonal solution set and ⌈ ⌉ is the ceiling operator. δ(di, D) represents the crowding distance of the particular solution di, calculated as:
| (33) |
where and are the maximal and minimal value of the ith objective function and δi(d, D) is calculated as (Gong et al., 2008):
| (34) |
After performing the clonal operation for each solution, all the newly generated solutions constitute the cloned solution set denoted by C(j).
Step 3: Mutation operation
To generate better solutions, the mutation operation is performed on the cloned solution set C(j). Assume that the mutation probability is denoted by MP. For each individual in one particular solution, a random mutation probability (RPi) is first generated. If MP > RPi, the mutation will be performed. After completing the mutation operation for each solution, all the new particular solutions form the mutated solution set M(j). The original solution set D(j) and M(j) are combined to get a new solution set denoted by F(j).
Step 4: Deleting operation
The same solutions may exist in the new generated solution set F(j) after performing the two steps described above. To avoid a reduction of the search space for the same solutions, only the unique one is kept. The remaining solutions constitute the new solution set DF(j). If size(DF(j)) < P, step 2 should be applied; otherwise, step 5 should be applied.
Step 5: Updating solution set
To maintain the size of the solution set, P particular solutions are selected from the solution set DF(j). Before performing any updates, the performance of each solution is evaluated. Model parameters C and γ in SVM are extracted from each particular solution to construct the model. The samples with the selected features in one solution are used to calculate fsen and fspe through 5-cross-validation. In most traditional MOEAs, the crowding distance is used to update the solution set to increase the diversity of the Pareto-optimal solutions (Deb et al., 2002). In our study, we proposed obtaining the Pareto-optimal set with a higher AUC as it is one of the most important criteria to evaluate the performance of a model or system. Therefore, in this step the solution in D(j) is sorted in the descending order using the fast nondominated sorting approach (Deb et al., 2002), according to the AUC of each solution. The P solutions are chosen from solution set DF(j)to constitute the new solution set UD(j). An example of the workflow is illustrated in figure 5. First, the two best non-dominated solution sets F1 and F2 are selected. If all the solutions from F3 are selected, the present solution number will be exceeded. Therefore, only some of the solutions are selected according to AUC sorting, and the new solution set is generated.
Figure 5.
AUC based non-dominated sorting.
Step 6: Termination
If j ≥ Gmax, UD(j) is considered as the output and the algorithm ends; Otherwise, let j = j + 1 and D(j) = UD(j), and go to step 2.
In the second phase, the best solution is selected after generating the Pareto-optimal solution set. In this work, the best solution is selected according to sensitivity, specificity, and AUC. Assume that the thresholds for sensitivity and specificity are denoted by Tsen and Tspe, respectively. The Pareto-optimal solution is denoted by D = {D1,D2, ⋯, DP} and the corresponding sensitivity, specificity, and AUC for each solution Di, i = 1,,2, ⋯, P are denoted by , , , i = 1,2, ⋯, P, respectively. The procedure to select the best solution is described as follows.
Step 1: For each particular solution Di, i = 1,2, ⋯, P, if , and , it is selected as the candidate solution. All the selected solutions constitute the candidate set, which is denoted by , where Q is the number of selected solutions.
Step 2: The best solution is selected with the highest AUC in DC.
As compared with the most commonly available immune-inspired algorithm, the deleting operation is a new step in IMIA; after performing clonal and mutation operations, the same solutions may exist in a solution set, narrowing the search space. After performing the deleting operation, additional solutions can be added into the solution set, increasing the diversity of the solution set and the chances of obtaining better solutions.
3. Experimental results
3.1. Experimental setup
The multi-objective radiomics model and the IMIA were evaluated for distant failure prediction in lung SBRT patients. The traditional immune multi-objective algorithm (TIMA) was used for comparison. Two differences between TIMA and IMIA are listed as follows: (1) TIMA does not have a deleting operator; (2) when updating the population in TIMA, the fast non-dominated sorting was calculated according to the crowding distance (Deb et al., 2002). In IMIA, the population was sorted according to the AUC.
Furthermore, we compared the proposed model with a single-objective model, with the AUC as the single objective function. For fair comparison, the optimization strategy employed in the single objective with AUC (SO-AUC) is also an immune-inspired algorithm that consists of the following steps: 1) Initialization. This step is based on hybrid initialization as for IMIA. 2) Clonal operation. Proportional cloning also was used. 3) Mutation operation, as for IMIA. 4) Evaluation and selection. In this step, AUC was considered as the objective function to update the population. 5); Termination test. In this step, the individual with the highest AUC was considered as the final output.
The population number was set to 100 in all three methods, while the maximal generation number was set to 200. In the clonal operator, nc was set to 200. In the mutation operator, the mutation probability was set to 0.9. The five-folder cross-validation was performed. To study the influence of the different features, seven combinations of the three feature groups (clinical parameters, and PET and CT imaging features) were used to build the predictive models. Sensitivity, specificity, and AUC were used to evaluate the performance of the different models and compared with the unpaired t test at a significance level of 0.05. All experiments were performed 10 times, including the calculation of the mean and standard deviation for each evaluation criteria.
3.2. Results
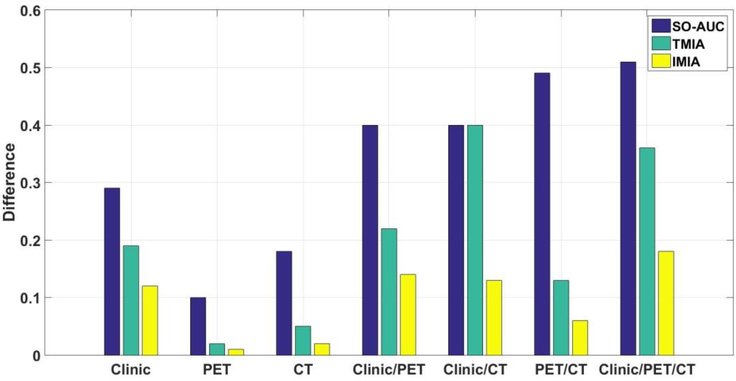
Sensitivity, specificity, and AUC for different methods are summarized in table 4. As compared with SO-AUC, IMIA can obtain similar specificity and AUC results, but greater sensitivity. The difference between sensitivity and specificity for the three methods is reported for seven combinations (figure 6). The difference between sensitivity and specificity in IMIA is smaller than SO-AUC in all cases, and smaller than TMIA in most of cases. IMIA can obtain better performance than TMIA for most combinations of the three evaluation criteria. The p-values of the unpaired t test between IMIA and each of other two methods for three evaluation criteria are shown in table 5. These results show that there is a statistically significant difference between IMIA and each of other two methods for sensitivity, specificity and AUC in all seven combinations. For the different predictive methods, the highest prediction accuracy based on the AUC measure is achieved when all the features (clinical parameters, PET feature, and CT feature) are combined.
Table 4.
Results of different prediction methods.
| Modality | Method | Sensitivity | Specificity | AUC |
|---|---|---|---|---|
| Clinic | SO-AUC | 0.59±0.14 | 0.88±0.05 | 0.84±0.01 |
| TMIA | 0.63±0.09 | 0.82±0.04 | 0.76±0.05 | |
| IMIA | 0.76±0.03 | 0.88±0.02 | 0.81±0.04 | |
| PET | SO-AUC | 0.65±0.15 | 0.75±0.06 | 0.78±0.03 |
| TMIA | 0.70±0.04 | 0.72±0.03 | 0.69±0.04 | |
| IMIA | 0.76±0.08 | 0.75±0.08 | 0.75±0.04 | |
| CT | SO-AUC | 0.68±0.11 | 0.86±0.04 | 0.82±0.02 |
| TMIA | 0.79±0.05 | 0.84±0.03 | 0.80±0.03 | |
| IMIA | 0.81±0.06 | 0.79±0.05 | 0.78±0.03 | |
| Clinic and PET | SO-AUC | 0.54±0.06 | 0.94±0.02 | 0.86±0.04 |
| TMIA | 0.75±0.01 | 0.97±0.02 | 0.84±0.03 | |
| IMIA | 0.77±0.04 | 0.91±0.04 | 0.82±0.06 | |
| Clinic and CT | SO-AUC | 0.54±0.14 | 0.94±0.02 | 0.85±0.06 |
| TMIA | 0.58±0.01 | 0.98±0.02 | 0.68±0.03 | |
| IMIA | 0.77±0.04 | 0.90±0.03 | 0.83±0.05 | |
| PET and CT | SO-AUC | 0.47±0.14 | 0.96±0.05 | 0.84±0.02 |
| TMIA | 0.73±0.04 | 0.86±0.08 | 0.75±0.07 | |
| IMIA | 0.75±0.01 | 0.81±0.04 | 0.81±0.04 | |
| Clinic, PET and CT | SO-AUC | 0.46±0.12 | 0.97±0.03 | 0.87±0.02 |
| TMIA | 0.62±0.06 | 0.98±0.03 | 0.84±0.04 | |
| IMIA | 0.76±0.03 | 0.94±0.03 | 0.83±0.04 | |
Figure 6.
Difference in sensitivity and specificity between SO-AUC, TMIA, and IMIA.
Table 5.
Results of p-values compared between IMIA and TMIA or SO-AUC for three evaluation criteria in seven combinations
| Method | Criterion | Clinic | PET | CT | Clinic/PET | Clinic/CT | PET/CT | Clinic/PET/CT |
|---|---|---|---|---|---|---|---|---|
| TMIA | Sensitivity | p=0.002 | p=0.03 | p=0.007 | p<0.0001 | p<0.0001 | p<0.0001 | p<0.0001 |
| Specificity | p=0.003 | p=0.003 | p<0.001 | p=0.007 | p=0.01 | p<0.0001 | p<0.04 | |
| AUC | p=0.02 | p<0.001 | p=0.001 | p<0.0001 | P<0.0001 | p=0.01 | p=0.007 | |
| SO-AUC | Sensitivity | p<0.001 | p=0.006 | p=0.008 | p=0.007 | P<0.0001 | p<0.0001 | p<0.0001 |
| Specificity | p<0.0001 | p=0.007 | p=0.005 | p<0.0001 | p<0.0001 | p<0.0001 | p<0.02 | |
| AUC | p<0.001 | p<0.001 | p=0.004 | p<0.0001 | P<0.0001 | p=0.04 | p=0.03 | |
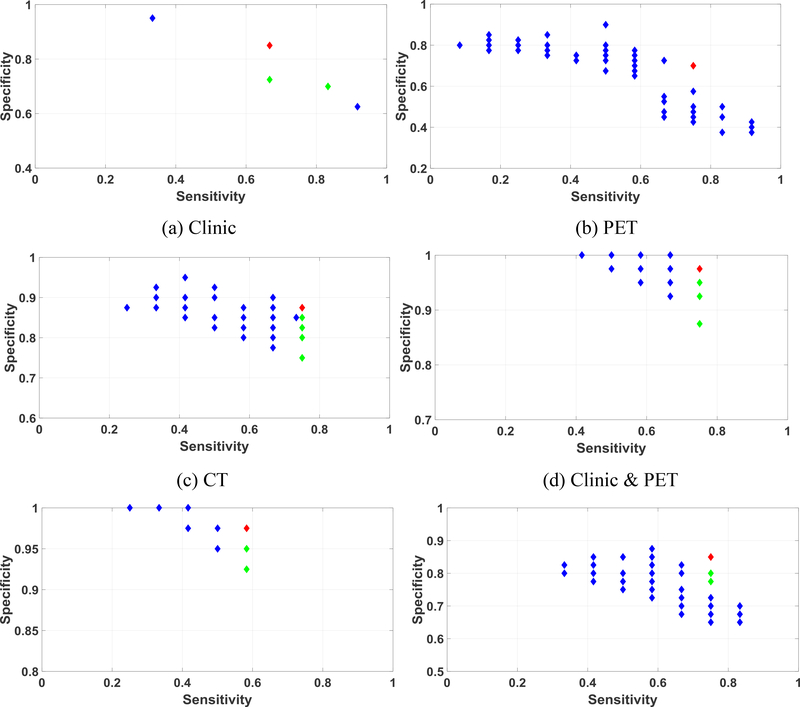
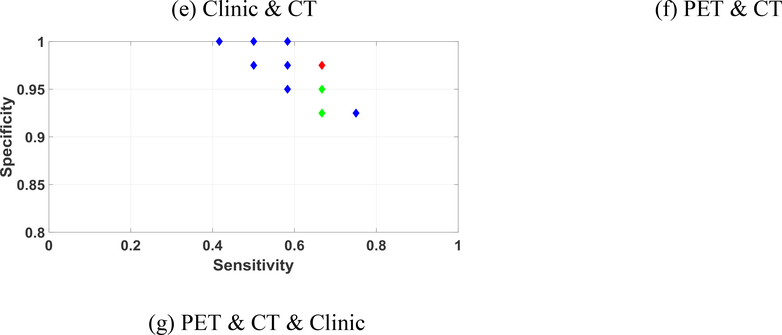
One group of the Pareto-optimal solution set and the selected final solution in IMIA is shown in figure 7. The selected final solution was marked in red, while the selected feasible solutions were marked in green. The unselected labels were marked in blue. The best solutions for all combinations were in the Pareto-optimal surface. Meanwhile, figure 8 shows one group of the Pareto-optimal solution set for TMIA. The number of Pareto solutions in TMIA is less than IMIA shown in figure 8. This is because TMIA keeps the same solutions, which reduces the diversity of feasible solutions.
Figure 7.
Pareto-optimal solution set and best solution selection for IMIA using different combinations of the feature sets. Red label: final selected solution; Green labels: selected feasible solutions; Blue labels: unselected solutions. Note that the ranges of the x and y axes are different in each figure.
Figure 8.
Pareto-optimal solution set and best solution selection for TMIA using different combinations of the feature sets. Red label: final selected solution; Green labels: selected feasible solutions; Blue labels: unselected solutions. Note that the ranges of the x and y axes are different in each figure.
4. Discussion and Conclusions
A multi-objective radiomics model was proposed to predict distant failure in early stage NSCLC treated with SBRT and overcome the disadvantages of the single objective predictive model in radiomics. Both sensitivity and specificity were simultaneously considered as the objects to guide the predictive model construction. Moreover, an iterative multi-objective immune algorithm (IMIA) was developed to train the model and increase accuracy and reliability. As compared with the traditional method, the deleting operation was added in IMIA, and AUC was adopted as a non-dominated sorting criterion upon updating of the solution set. The solution set diversity can be kept when adding the deleting operation in IMIA. With this approach more optimal solutions were obtained. In addition, because AUC is used as a criterion to update the solution set, the solution with higher AUC was also kept.
Several studies have attempted to predict distant failure after SBRT (Clarke et al., 2012; Timmerman et al., 2014; Zhou et al., 2016), although they mainly focused on individual factors or clinical parameters (Zhou et al., 2016). In this work, we combined image features and clinical parameters to improve the prediction accuracy for distant failure in lung SBRT. For seven combinations of the input features, we showed they can perform better than single group features. The best performance was obtained when all three group features were combined within the three methods because the addition of new group features allowed the selection of positive features, improving the performance of all the predictive models. As part of the goal of this work is to investigate the influence of different imaging modalities for the prediction accuracy, we segmented tumors in CT and PET separately and then extracted features from each imaging modality for different predictive models. This allows us to examine the prediction performance of each imaging modality by solely using its own information. Due to the image resolution difference between PET and CT, the two segmentations could be slightly different. We may obtain a single segmented volume by co-segmentation of anatomical and functional images (Bagci et al., 2013). The influence of different segmentation strategies is warranted in a future study.
To validate the performance of the proposed model and IMIA in the short term, independent patient cohorts from other institutions are needed. However, data sharing from another institution is still a challenge due to many practical and regulatory issues. Alternatively, rather than asking for submission of patient clinical and imaging data from potential collaborators, we may share our model to them for validation internally, and thus no patient data will be required to leave their institutions. We are planning to implement this strategy in a future study. Ultimately, an optimized and robust model will need to be validated in a prospective study. In addition, in the currently proposed method, the best solution was selected from the Pareto-optimal set by setting the thresholds for sensitivity and specificity. However, the manual setting of an optimal threshold is challenging, indicating the need for automatic selection.
Acknowledgements
This work was supported in part by the American Cancer Society (RSG-13-326-01-CCE and ACS-IRG-02-196) and US National Institutes of Health (5P30CA142543). The authors would like to thank Dr. Damiana Chiavolini for editing the manuscript.
Reference
- Adams MC, Turkington TG, Wilson JM and Wong TZ 2010. A systematic review of the factors affecting accuracy of SUV measurements American Journal of Roentgenology 195 310–20 [DOI] [PubMed] [Google Scholar]
- Avci E 2009. Selecting of the optimal feature subset and kernel parameters in digital modulation classification by using hybrid genetic algorithm–support vector machines: HGASVM Expert Systems with Applications 36 1391–402 [Google Scholar]
- Bagci U, Udupa JK, Mendhiratta N, Foster B, Xu Z, Yao J, Chen X and Mollura DJ 2013. Joint segmentation of anatomical and functional images: Applications in quantification of lesions from PET, PET-CT, MRI-PET, and MRI-PET-CT images Medical image analysis 17 929–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y 1995. Mean shift, mode seeking, and clustering Ieee T Pattern Anal 17 790–9 [Google Scholar]
- Cho M-Y, Lee T-F, Kau S-W, Shieh C-S and Chou C-J Innovative Computing, Information and Control, 2006. ICICIC’06. First International Conference on,2006), vol. Series 1): IEEE; ) pp 26–30 [Google Scholar]
- Clarke K, Taremi M, Dahele M, Freeman M, Fung S, Franks K, Bezjak A, Brade A, Cho J and Hope A 2012. Stereotactic body radiotherapy (SBRT) for non-small cell lung cancer (NSCLC): is FDG-PET a predictor of outcome? Radiotherapy and Oncology 104 62–6 [DOI] [PubMed] [Google Scholar]
- Coroller TP, Grossmann P, Hou Y, Velazquez ER, Leijenaar RT, Hermann G, Lambin P, Haibe-Kains B, Mak RH and Aerts HJ 2015. CT-based radiomic signature predicts distant metastasis in lung adenocarcinoma Radiotherapy and Oncology 114 345–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darbon J, Cunha A, Chan TF, Osher S and Jensen GJ Biomedical Imaging: From Nano to Macro, 2008. ISBI 2008. 5th IEEE International Symposium on,2008), vol. Series): IEEE; ) pp 1331–4 [Google Scholar]
- Deb K 2001. Multi-objective optimization using evolutionary algorithms vol 16: John Wiley & Sons; ) [Google Scholar]
- Deb K, Pratap A, Agarwal S and Meyarivan T 2002. A fast and elitist multiobjective genetic algorithm: NSGA-II IEEE transactions on evolutionary computation 6 182–97 [Google Scholar]
- Ding S and Li S Knowledge Acquisition and Modeling, 2009. KAM’09. Second International Symposium on,2009), vol. Series 2): IEEE; ) pp 17–20 [Google Scholar]
- Freeman C, Skamene S and El Naqa I 2015. A radiomics model from joint FDG-PET and MRI texture features for the prediction of lung metastases in soft-tissue sarcomas of the extremities Physics in medicine and biology 60 5471. [DOI] [PubMed] [Google Scholar]
- Gillies R J, Kinahan P E and Hricak H 2015. Radiomics: Images Are More than Pictures, They Are Data Radiology 151169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong M, Jiao L, Du H and Bo L 2008. Multiobjective immune algorithm with nondominated neighbour-based selection Evolutionary Computation 16 225–55 [DOI] [PubMed] [Google Scholar]
- Hawkins SH, Korecki JN, Balagurunathan Y, Gu Y, Kumar V, Basu S, Hall LO, Goldgof DB, Gatenby RA and Gillies RJ 2014. Predicting outcomes of nonsmall cell lung cancer using CT image features IEEE Access 2 1418–26 [Google Scholar]
- Høyer M 2008. Improved accuracy and outcome in radiotherapy of lung cancer Radiotherapy and Oncology 87 1–2 [DOI] [PubMed] [Google Scholar]
- Huang C-L and Dun J-F 2008. A distributed PSO–SVM hybrid system with feature selection and parameter optimization Appl Soft Comput 8 1381–91 [Google Scholar]
- Huynh E, Coroller TP, Narayan V, Agrawal V, Hou Y, Romano J, Franco I, Mak RH and Aerts HJ 2016. CT-based radiomic analysis of stereotactic body radiation therapy patients with lung cancer Radiotherapy and Oncology 120 258–66 [DOI] [PubMed] [Google Scholar]
- Kailath T 1967. The divergence and Bhattacharyya distance measures in signal selection IEEE transactions on communication technology 15 52–60 [Google Scholar]
- Lambin P, Rios-Velazquez E, Leijenaar R, Carvalho S, van Stiphout RG, Granton P, Zegers CM, Gillies R, Boellard R and Dekker A 2012. Radiomics: extracting more information from medical images using advanced feature analysis European Journal of Cancer 48 441–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levman J, Leung T, Causer P, Plewes D and Martel A L 2008. Classification of dynamic contrast-enhanced magnetic resonance breast lesions by support vector machines Medical Imaging, IEEE Transactions on 27 688–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mu W, Chen Z, Liang Y, Shen W, Yang F, Dai R, Wu N and Tian J 2015. Staging of cervical cancer based on tumor heterogeneity characterized by texture features on 18F-FDG PET images Physics in medicine and biology 60 5123. [DOI] [PubMed] [Google Scholar]
- Nemhauser GL and Wolsey LA 1988. Integer programming and combinatorial optimization Wiley, Chichester. GL Nemhauser, MWP Savelsbergh, GS Sigismondi (1992). Constraint Classification for Mixed Integer Programming Formulations. COAL Bulletin 20 8–12 [Google Scholar]
- Otsu N 1975. A threshold selection method from gray-level histograms Automatica 11 23–7 [Google Scholar]
- Tan S, Kligerman S, Chen W, Lu M, Kim G, Feigenberg S, D’Souza WD, Suntharalingam M and Lu W 2013. Spatial-temporal [18 F] FDG-PET features for predicting pathologic response of esophageal cancer to neoadjuvant chemoradiation therapy International Journal of Radiation Oncology* Biology* Physics 85 1375–82 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmerman R, Paulus R, Galvin J, Michalski J, Straube W, Bradley J, Fakiris A, Bezjak A, Videtic G, Johnstone D, Fowler J, Gore E and Choy H 2010. Stereotactic Body Radiation Therapy for Inoperable Early Stage Lung Cancer Jama-J Am Med Assoc 303 1070–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmerman RD, Hu C, Michalski J, Straube W, Galvin J, Johnstone D, Bradley J, Barriger R, Bezjak A, Videtic GM, Nedzi L, Werner-Wasik M, Chen Y, Komaki RU and Choy H 2014. Long-term Results of RTOG 0236: A Phase II Trial of Stereotactic Body Radiation Therapy (SBRT) in the Treatment of Patients with Medically Inoperable Stage I Non-Small Cell Lung Cancer Int J Radiat Oncol 90 S30–S [Google Scholar]
- van Baardwijk A, Tomé WA, van Elmpt W, Bentzen SM, Reymen B, Wanders R, Houben R, Öllers M, Lambin P and De Ruysscher D 2012. Is high-dose stereotactic body radiotherapy (SBRT) for stage I non-small cell lung cancer (NSCLC) overkill? A systematic review Radiotherapy and Oncology 105 145–9 [DOI] [PubMed] [Google Scholar]
- Wu C-H, Tzeng G-H and Lin R-H 2009. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression Expert Systems with Applications 36 4725–35 [Google Scholar]
- Wu J, Aguilera T, Shultz D, Gudur M, Rubin DL, Loo BW Jr., Diehn M and Li R 2016a. Early-Stage Non-Small Cell Lung Cancer: Quantitative Imaging Characteristics of (18)F Fluorodeoxyglucose PET/CT Allow Prediction of Distant Metastasis Radiology 281 270–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu W, Parmar C, Grossmann P, Quackenbush J, Lambin P, Bussink J, Mak R and Aerts HJ 2016b. Exploratory study to identify radiomics classifiers for lung cancer histology Frontiers in oncology 6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Tridandapani S, Beitler JJ, David SY, Yoshida EJ, Curran WJ and Liu T 2012. Ultrasound GLCM texture analysis of radiation-induced parotid-gland injury in head-and-neck cancer radiotherapy: an in vivo study of late toxicity Medical physics 39 5732–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Z-G, Liu F, Jiao L-C, Li L-L, Wang X-D, Gou S-P and Wang S 2013a. Object information based interactive segmentation for fatty tissue extraction Computers in biology and medicine 43 1462–70 [DOI] [PubMed] [Google Scholar]
- Zhou Z-G, Liu F, Jiao L-C, Zhou Z-J, Yang J-B, Gong M-G and Zhang X-P 2013b. A bi-level belief rule based decision support system for diagnosis of lymph node metastasis in gastric cancer Knowledge-Based Systems 54 128–36 [Google Scholar]
- Zhou Z, Folkert M, Cannon N, Iyengar P, Westover K, Zhang Y, Choy H, Timmerman R, Yan J and Xie X-J 2016. Predicting distant failure in early stage NSCLC treated with SBRT using clinical parameters Radiotherapy and Oncology [DOI] [PMC free article] [PubMed] [Google Scholar]