Abstract
Virtual environments have been widely used in motor neuroscience and rehabilitation, as they afford tight control of sensorimotor conditions and readily afford visual and haptic manipulations. However, typically, studies have only examined performance in the virtual testbeds, without asking how the simplified and controlled movement in the virtual environment compares to behavior in the real world. To test whether performance in the virtual environment was a valid representation of corresponding behavior in the real world, this study compared throwing in a virtual set-up with realistic throwing, where the task parameters were precisely matched. Even though the virtual task only required a horizontal single-joint arm movement, similar to many simplified movement assays in motor neuroscience, throwing accuracy and precision were significantly worse than in the real task that involved all degrees of freedom of the arm; only after 3 practice days did success rate and error reach similar levels. To gain more insight into the structure of the learning process, movement variability was decomposed into deterministic and stochastic contributions. Using the tolerance-noise-covariation decomposition method, distinct stages of learning were revealed: While tolerance was optimized first in both environments, it was higher in the virtual environment, suggesting that more familiarization and exploration was needed in the virtual task. Covariation and noise showed more contributions in the real task, indicating that subjects reached the stage of fine-tuning of variability only in the real task. These results showed that while the tasks were precisely matched, the simplified movements in the virtual environment required more time to become successful. These findings resonate with the reported problems in transfer of therapeutic benefits from virtual to real environments and alert that the use of virtual environments in research and rehabilitation needs more caution.
NEW & NOTEWORTHY This study compared human performance of the same throwing task in a real and a matched virtual environment. With 3 days’ practice, subjects improved significantly faster in the real task, even though the arm and hand movements were more complex. Decomposing variability revealed that performance in the virtual environment, despite its simplified hand movements, required more exploration. Additionally, due to fewer constraints in the real task, subjects could modify the geometry of the solution manifold, by shifting the release position, and thereby simplify the task.
Keywords: noise, skill learning, throwing, variability, virtual environment
INTRODUCTION
Virtual environments have been widely employed for motor learning, both in basic neuroscience research and in rehabilitation (Burdea and Coiffet 2003; Henderson et al. 2007; Holden and Todorov 2002; Krakauer et al. 1999; Saposnik and Levin 2011; Shadmehr and Mussa-Ivaldi 1994). In a typical virtual environment, subjects see a visual display of a target or an object together with their online measured movements in the context of a task, such as reaching to a target. Interaction with the objects in the virtual workspace can be enhanced with haptic joysticks, sensing gloves, or robotic manipulanda that feed forces that are created in the virtual environment back to the user. In rehabilitation, virtual environments have been embraced, as they can create motivating games with adjustable parameters together with precise and automatized documentation of performance improvements. They also afford the therapist to simplify the task and titrate the difficulty according to the individual’s needs.
In basic motor neuroscience research, virtual environments have served as platforms in which functional behaviors can be simplified to those features that are of interest to address a scientific question. In the spirit of scientific reduction, unnecessary variability and “clutter” can be eliminated to allow cleaner experimental assays. Visual and haptic interfaces with (close-to) real-time interaction afford studying the effect of various types of feedback to the subject, both realistic or experimentally manipulated, such as augmenting the error, adding or attenuating noise, or creating sensory conflicts (Caballero and Rombokas 2019; Chu et al. 2013; Di Fabio and Badke 1991; Hasson et al. 2016; Sharp et al. 2011; Wei et al. 2005). Typically, the movements in a virtual environment are constrained to involve fewer degrees of freedom to focus on the chosen scientific questions. For example, a prominent paradigm in recent research on motor adaptation has been reaching of a two-joint limb in the horizontal plane (Bagesteiro and Sainburg 2003; Diedrichsen et al. 2005; Georgopoulos et al. 1982; Karniel and Mussa-Ivaldi 2003; Shadmehr and Mussa-Ivaldi 1994). This simple pointing task eliminated redundancy in the joint degrees of freedom, the effect of gravity and surface friction, and also “perturbations” from contact with objects. Numerous insights have resulted from this line of research, such as characteristics of the adaptation process and the role of internal models. It is fair to say that these findings are assumed to “scale up” to more complex, i.e., realistic behavior. Therefore, it is surprising that it has yet remained untested whether the principles of control and adaptation hold up in a matching behavior in a more realistic environment. The present study is a first step to compare how humans learn an equivalent motor task in a virtual and a real environment.
Our study examined a simple throwing task to compare performance in a virtual testbed with that in a realistic but closely matched task. All task parameters were identical to the best of our abilities, i.e., target size and distance, ball size, and weight, ball flight properties. However, the throwing movements themselves differed: in the virtual set-up, they were controlled single-joint forearm movements with hand opening for ball release, while the real task involved full arm movements in three dimensional (3D) space and a ball release with hand and fingers. We chose throwing as our testbed, as it is a demanding sensorimotor skill that requires practice. As it is also a fundamental skill that humans have developed over evolutionary time, it has received considerable attention in motor neuroscience, biomechanics, developmental psychology, and evolutionary biology (Calvin 1982; Crozier et al. 2019; Haywood and Getchell 2019; Lombardo and Deaner 2018; Maselli et al. 2019). However, the analysis of unconstrained overarm throwing is challenging and reliable kinematic measures are hard to come by. Hence, most studies simplified the skill to afford sensitive and reliable measures and mechanical modeling.
For example, a biomechanical analysis of throwing examined a two-degree-of-freedom model arm to determine the timing limits of ball release and argued, on the basis of a number of assumptions, that the timing window for an optimal throw is as short as 2 ms (Chowdhary and Challis 1999). Using a dart throwing action confined to the sagittal plane as their testbed, Nasu et al. (2014) similarly reported an extremely short timing window for accurate ball releases. In contrast, Smeets et al. demonstrated, also in a simplified dart-throwing task that it is less the timing but more the sensitivity to velocity errors that characterizes movement strategies of experts (Smeets et al. 2002). A mathematical analysis of overarm and underarm throwing, also confined to two dimensions, demonstrated that different regions in the space spanned by the two release variables have different sensitivity to error and noise (Venkadesan and Mahadevan 2017). Common to these and other studies is that they all simplified the full throwing action to gain insight into the control demands of this complex sensorimotor skill.
In the same vein, Sternad and colleagues developed a throwing task in a virtual environment that reduced the throwing action to a simple forearm extension in the horizontal plane, where opening the hand released the virtual ball that aimed to hit a virtual target (Cohen and Sternad 2009; Müller and Sternad 2004, 2009). Despite this simplicity, this virtual task maintained the essential redundancy in throwing: position and velocity at ball release fully determined the ball trajectory and its hitting accuracy. On the basis of a simplified model of the task, the solution space was mathematically derived and rendered a solution manifold that comprised a set of strategies with the same zero error. The core result of these studies was that not only the mean error decreased with practice, but that the distribution of release variables also changed with respect to the solution manifold. Three “costs” were defined that could quantify stages in motor learning from the distribution of release variables. Specifically, the initial exploration of the solution space to find the most error-insensitive strategy was quantified by “tolerance-cost” (more details below). Further improvement was achieved by exploiting covariation between execution variables (covariation-cost) and, to a lesser extent, by reducing the stochastic dispersion or noise (noise-cost) (Abe and Sternad 2013; Chu et al. 2016; Cohen and Sternad 2009; Müller and Sternad 2004; Van Stan et al. 2017).
The present study employed this decomposition method to compare motor learning of throwing in a virtual and a real environment. Subjects either performed a virtual task or a real task in which all physical parameters were matched, such that performance could be evaluated with exactly the same metrics. Importantly, the two task versions involved different arm and hand movements: the virtual task reduced the throwing action to a single-joint elbow flexion in the horizontal plane, while real throwing involved the entire arm and hand with all its degrees of freedom. Further, the virtual workspace displayed a two-dimensional (2D) top-down view of the target, rather than a 3D perspective with depth information. Hence, the objective of this study was to evaluate the effect of this experimental reduction and critically question whether findings in such virtual settings can “scale up” to more realistic behaviors.
Two groups of subjects practiced the real and virtual throwing task over 3 days and performance error and variability were compared. Counter to the expectation that simplified movements may reduce the coordinative challenge, results showed that the virtual task performance was significantly worse and only approached the real performance after 3 days of practice. The variability decomposition revealed that finding the error-tolerant solution took longer in the virtual task and was the main contributor to this difference. Only in the real task did subjects reach a stage where they could fine-tune their throws. One potentially important factor to this superior task performance in real throwing was that subjects had some leeway to position the ball release and could, thereby, slightly modify the solution manifold in favor of successful throws.
METHODS
Participants.
A total of 16 healthy right-handed undergraduate and graduate students (10 female, 6 male, mean age 23.4 yr) participated in the two experiments. Eight subjects were randomly assigned to the virtual task, and eight subjects were assigned to the real task. All subjects were informed about the procedures and gave written consent before the data collection; they received $30 compensation upon completion of the three practice sessions. The protocol was approved by the Institutional Review Board at Northeastern University.
Experimental paradigms.
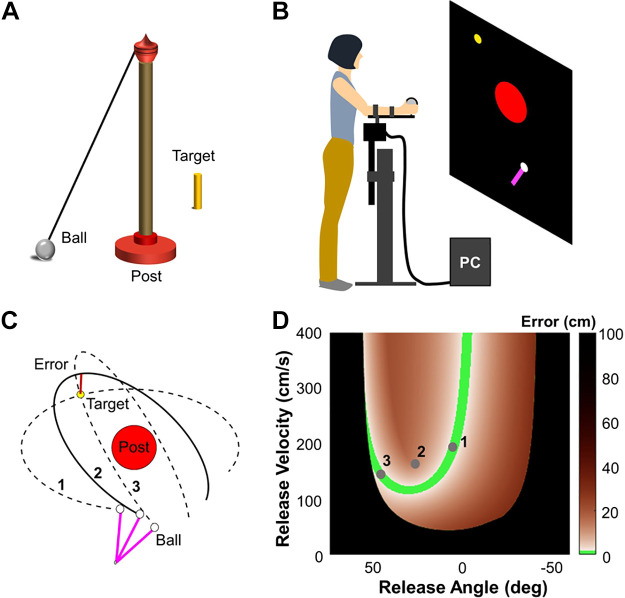
The basic experimental task was inspired by the British pub game skittles, which is similar to the playground game tetherball in the United States. In the skittles game, subjects throw a ball tethered to a vertical post and aim to knock down a target skittle on the other side of the post (Fig. 1A). This study used two sets of equipment to compare motor learning in a virtual and a real environment.
Figure 1.
Skittles game and the virtual environment. A: schematic depiction of the real skittles game in three dimensions. B: experimental setup of the virtual skittles. The subject stands 1.5 m in front of a back projection screen with her forearm rested on a horizontal lever arm, and the pivot is aligned with the elbow joint. A wooden ball is attached at the distal end of the lever arm. C: top-down view of the workspace. The red and yellow circles represent the center post and target, respectively; the purple bar shows the position of the lever arm at the moment of release. Three exemplary ball trajectories are plotted as solid or dashed black lines. The performance error is defined by the minimum distance between the ball trajectory and the target. D: solution space and solution manifold of the virtual task. The brown shading indicates the performance error, and the green band is the solution manifold, with the three points corresponding to the three ball releases in C.
Virtual skittles.
The virtual set-up was identical to what was used in previous studies (e.g., Hasson et al. 2016; Zhang et al. 2018). Subjects stood in front of a back-projection screen at a distance of 1.5 m and rested their dominant arm on a horizontal manipulandum adjusted to a comfortable height (Fig. 1B). The single-degree-of-freedom lever arm restricted their movements to rotations around the elbow joint in the horizontal plane. This simplification of the movement enabled fast recording and rendering of the movement in the virtual environment with minimal delay. Angular rotations of the manipulandum were recorded by an optical encoder with a sampling frequency of 1,000 Hz (BEI Sensors, Goleta, CA); the forearm movements were shown in real time on the screen as a purple bar rotating around a pivot. A wooden ball was affixed to the distal end of the manipulandum with a small force sensor attached to it (Interlink Electronics, Camarillo, CA). Subjects grasped this ball by closing their fingers onto the force sensor. To throw the virtual ball, subjects flexed their forearm and opened their hand as in a forearm Frisbee throw. Releasing the finger from the force sensor initiated the ball flight. After release, the subject saw the ball traversing an elliptic trajectory around the post (Fig. 1C). To ensure that subjects understood the task and the ball trajectories as shown on the screen, the experimenter showed the subject a small table version of the real skittles game and demonstrated the ball release and how it traversed the post to hit a target skittle.
The ball trajectory was calculated on the basis of the online-measured angular position and velocity of the manipulandum at the moment when the finger lifted from the force sensor. Throwing performance was described by the error defined as the minimum distance between the center of the target and the ball trajectory (Fig. 1C). If the ball hit the target, i.e., the distance between the closest point on the ball trajectory and the target center was smaller than 1.77 cm, the target turned from yellow to green, indicating a successful hit.
The task was projected as a 2D top-down view on the back projection screen (200 cm × 200 cm) in front of the subject (Fig. 1B). The large red circle depicted the top-down view of the post with a diameter of 25 cm; the smaller yellow circle represented the target with a diameter of 2.54 cm. The white circle at the end of the purple bar was the ball to be thrown (diameter 2.54 cm). The purple bar corresponded to the subject’s forearm/manipulandum movement in real time. The length of the lever arm on the screen was l = 30 cm, and the pivot of the lever was at the bottom end located at [−10 cm, −65 cm]; the origin of the workspace was defined at the center of the post [0 cm, 0 cm]. The target was located at [−30 cm, 30 cm].
Redundancy.
Throwing performance was quantified by the error between the ball trajectory and the target center. The redundancy of this task is illustrated in Fig. 1C, which shows three ball trajectories and their error to the target. While the black line represents a trajectory that passed by the target with a non-zero error, the two dashed ball trajectories both traversed the center of the target with zero error, even though they were released with two different angles and velocities. This exemplifies that zero error could be achieved with different combinations of release angles and velocities. Mathematically, these zero-error solutions constitute an infinite set and define the solution manifold. A visual summary of this redundancy is shown in Fig. 1D: The space is spanned by the two execution variables, angle and velocity of the hand at release, that fully determine the error. The green band represents the solution manifold, including small errors within the threshold that defined a successful hit (indicated by the target turning green). The orange color shades indicate different magnitudes of error associated with the different combinations of release angles and velocities. The black boundary demarcates areas for ball releases that hit the red post. The geometry of the solution space and solution manifold is determined by the location of the target (Zhang et al. 2018).
Physical model and definition of execution and result variables.
This top-down projection simplified the physics of the task to a 2D system, where the ball was suspended by two orthogonal, massless springs (Fig. 2A). The equilibrium point of the ball was at the origin, the center of the post. The angle, tangential velocity and the x-y positions of the ball at the moment of release r were calculated as:
| (1) |
| (2) |
| (3) |
| (4) |
where θr, vr, xr and yr are the angle, tangential velocity, and x-y position of the ball at the moment of release; θp and are the angular position and velocity around the pivot measured by the optical encoder; xp and yp are the x-y position of the pivot, and l is the length of the lever arm (Fig. 2A).
Figure 2.
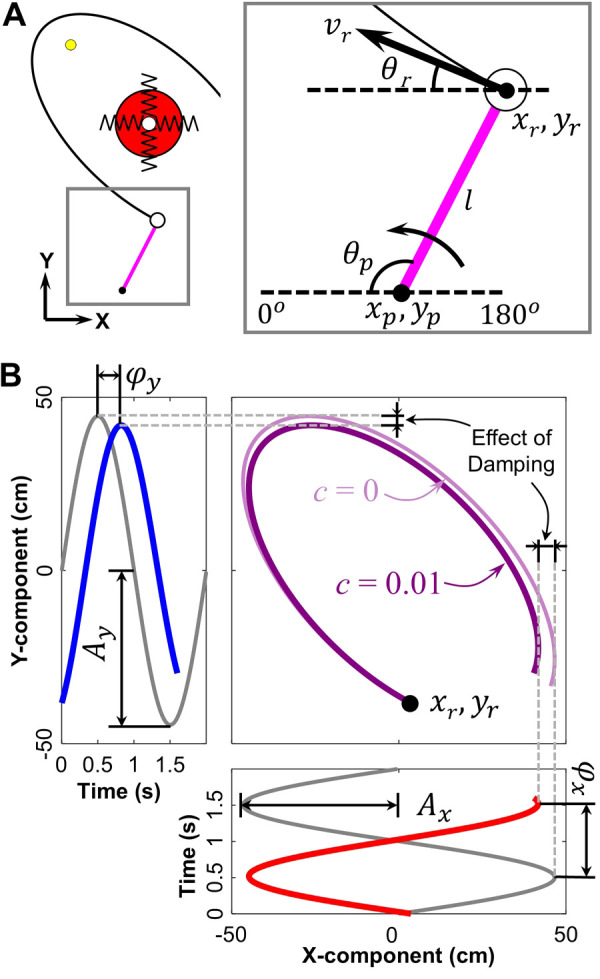
Calculation of the ball trajectory. A: top-down view on the workspace, the springs visualize that the ball trajectory was modeled by two orthogonal springs. Execution variables of the ball trajectory in the two-dimensional (2D) workspace: xp, yp is the 2D position of the lever arm’s pivot; θp is the angle of the lever arm; l is the length of the lever arm; xr and yr is the 2D position of the ball release; vr and θr are execution variables used to calculate the ball trajectory. The thick arrow indicates the direction of the arm movement for the throw. B: simulation of the ball trajectory. Gray curves denote y = Ax sin(x) and y = Ay sin(x). Red and blue curves are the x- and y-component of the ball trajectory with a phase shift and added damping, producing the trajectories in the x-y workspace. The dark purple trajectory is the resulting ball trajectory, whereas the light purple trajectory shows the trajectory without damping for reference.
The equations of motion for the ball xB and yB were simulated starting at release using two sinusoids in the x- and y-dimensions:
| (5) |
| (6) |
Note that two sinusoids with a non-zero phase difference plotted orthogonally against each other describe an ellipse in a so-called Lissajous plot. Ax and Ay describe the amplitudes and φx and φy describe the initial phases of the two sine waves. The exponential terms introduce damping defined by τ. Figure 2B displays two sinusoids on orthogonal axes in gray; the red and blue curves are phase-shifted and lightly damped. The purple curves combine the sinusoids in a Lissajous plot; the light purple is the undamped ball trajectory, while the dark purple curve is the damped ball trajectory; the latter is used in the experiment. The simulation stopped at 1.6 s after ball release. The following equations show how the amplitudes and phases were determined:
| (7) |
| (8) |
| (9) |
| (10) |
The natural frequency of the system ω and the time constant τ that introduced damping into the ball flight were defined as follows:
| (11) |
| (12) |
In the experiment, the spring constant was set to k = 6.7 g/cm, the mass of the ball was m = 68 g, and the damping ratio was set to c = 0.01.
In both the virtual and the real task, there were four execution variables that fully determined the single result variable error: angular position hr, tangential velocity of the hand vr and the x-y-coordinates of the ball at the moment of release, xr, yr (Fig. 2A). In the virtual task, the x-y position of the ball was constrained to the circular path of the hand fixed to the paddle and could be calculated on the basis of the angular position and its derivative with Eqs. 3 and 4. Hence, two variables, θp and , were sufficient to determine the ball trajectory. Note that in this study, the solution space was calculated with θr and vr instead of θp and as in previous studies to exactly match the calculations in the real and virtual skittles task. Note that the two coordinate systems can be affine transformed to each other as in Eqs. 1 and 2. Although such a coordinate transformation can affect variability analyses that are based on covariance analysis, such as principal component analysis and the uncontrolled manifold analysis, this affine transformation has negligible effects on the tolerance-noise-covariation (TNC) decomposition (Cohen and Sternad 2009; Sternad et al. 2010).
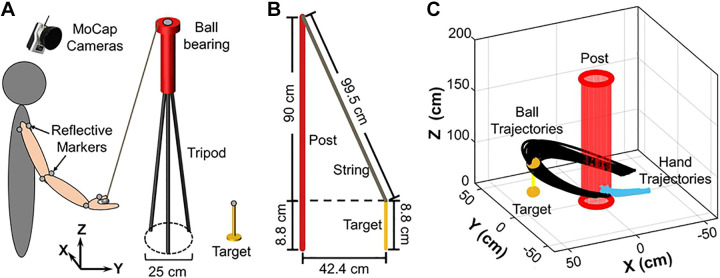
Real skittles.
Subjects stood in front of a table upon which the skittles apparatus was placed. A vertical post mounted on a tripod stood centered on the table (Fig. 3, A and B), and the physical configuration exactly matched that of the virtual skittles: The center of the post defined the origin of the work space [0 cm, 0 cm] and the target was located at [−30 cm, 30 cm]. The diameter of the bottom of the tripod was 25 cm, the height of the post, including the tripod, was 98.8 cm. The target height was 8.8 cm, and its diameter was 1.0 cm; it was mounted on a spring, so that the ball could knock over the target without it falling off the table. The radial distance of the target to the post was 42.4 cm (as in the virtual workspace). A steel ball (mass: 68 g, diameter: 2.54 cm) was attached to an inelastic, light-weight nylon string (length: 99.5 cm) connected to the top of the post; steel ball bearings were added to minimize friction. The string was slightly longer than the post to ensure that the vertical elevation of the ball from the table surface remained relatively small to afford the projection of the ball trajectory onto the 2D horizontal plane as explained below. This allowed an exact match of the data analyses.
Figure 3.
Experimental setup of the real skittles in the laboratory. A: the subject stood close to a table of regular height with the skittles game placed on the table top. Nine reflective markers (represented by gray circles) were attached to the subject’s right arm, the top of the post, and the top of the target skittle. The ball was also covered with reflective tape and identified as a marker. Twelve motion capture cameras recorded the three-dimensional position of the markers. B: dimensions of the real skittles task. The red, yellow, and gray lines represent post, target, and string, respectively. Note that the string was 1.5 cm longer than the post. This ensured that when the subject deflected the ball and string, the ball remained close to the table surface. This facilitated the projection of the ball onto the two-dimensional surface in the analysis. C: exemplary hand and ball trajectories plotted in three-dimensional space.
Subjects performed the throwing movements by grasping the real ball (with two or three fingers) and throwing it around the center post. To create “real throwing,” the arm was free to move, and only the release location was specified by the experimenter. To record the subjects’ hand and arm movements in the real skittles game, eight reflective markers were attached to typical landmarks on the subject’s right arm: acromion and coracoid process of the scapula (two markers), medial and lateral epicondyle of the humerus (two markers), dorsal side of the wrist (one marker), dorsal side of the proximal phalanges of the thumb (one marker). For the present analyses, only the markers on the thumb were considered. The ball was covered with reflective tape to record the ball trajectory. Two markers identified the locations of the post (top) and the target (top). The 3D positions of all markers were recorded by 12 cameras placed above the subject just below the high ceiling (Qualisys, Göteborg, Sweden). The sampling rate was 200 Hz. Figure 3C shows a 3D rendering of the hand and ball trajectories around the post. The short segment of the hand trajectories was described by the marker on the thumb before ball release (blue).
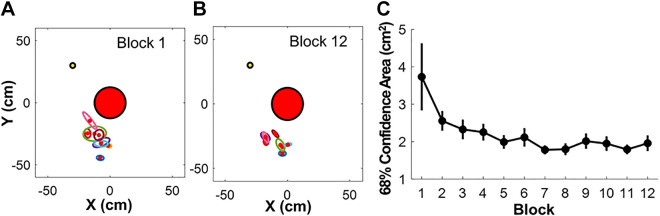
To constrain the many ways of throwing the real ball, subjects were instructed to stand at a fixed position in front of the table and start each throw by holding the ball above a marked position on the table (0 cm, −35 cm) until they were cued by the experimenter to initiate a throw. As subjects tended to first perform a backward movement preparing for the ball release, the actual release position varied slightly across subjects and blocks (see Fig. 4). Subjects were instructed to hit the target with the ball while keeping the string taut; given the weight of the ball, this was almost always satisfied. Hitting error was quantified by the minimum distance between the center of the ball and the center of the target; a throw was classified as successful when the distance of the ball to the target was smaller than the threshold of 1.77 cm, i.e., when the ball (diameter 2.54 cm) contacted the target (diameter 1 cm). After each throw, the subjects grasped the ball again and returned to the same starting position, waiting for the next cue from the experimenter.
Figure 4.
Release positions in the real skittles task. A: distributions of release points for all eight subjects in Block 1; each ellipse represents the 68% confidence region of 30 releases for one subject. B: confidence ellipses of release points of all eight subjects in Block 12. C: change of 68% confidence area from Block 1 to Block 12, indicating that the release positions were increasingly better controlled following the instructions; the error bars represent standard errors across subjects.
Each subject practiced the virtual or the real task on three successive days with 120 trials on each day. Each session was parsed into four blocks of 30 throws, with a break of 1 min between each block.
Analysis of the ball trajectory in the real task.
To afford data analysis in comparable fashion in both virtual and real skittles, the data from the real skittles task needed more prior processing. Specifically, the 3D ball trajectory was reduced to 2D to afford identical analysis of variability in both the real and the virtual task.
As in the virtual set-up, the real ball trajectory was fully determined by the position and velocity at the time of ball release. To optimize the comparison of the two tasks, the 3D kinematics of the ball was first projected onto 2D table plane, similar to the virtual model task. In addition, the position of the hand at ball release was, in principle, free to vary in two dimensions, as the hand movements were not constrained to the circular path of the manipulandum around the pivot. However, to match the ball releases in the real and virtual task, the experimenter specified the release position to the subject with a point on the table. Although this location was visible, subjects still had some leeway as to when and where to release the ball. Figure 4, A and B shows the release positions of the eight subjects at the beginning (Block 1) and end of practice (Block 12). Each subject’s ball releases are indicated by a confidence ellipse calculated for all trials in a block; as can be seen, they slightly varied between individuals and across blocks, but the size of the confidence ellipse decreased with practice and attenuated variations (Fig. 4C). As will be noted below, the different release positions created small variations to the solution manifold. As illustrated in the virtual task, xr and yr represented the release position, θr was the release angle, and vr was the scalar value of the tangential velocity at release (Fig. 2A). Again, to match the two task scenarios and reduce the two variables to one, the mean position of releases was determined and fixed for each block of 30 trials. The equations of motion of the ball in the horizontal plane were identical to those of the virtual skittles model (Eq. 5–12).
To determine the moment of release from the motion capture data (note there was no thresholded force sensor on the ball), the distance between the thumb marker and the ball marker was calculated; the instant of release was determined when the separation velocity of those two markers exceeded 0.30 cm/s for the first time. However, further adjustments had to be made, as often the fingers accelerated the ball at release. More details may be found in appendix a.
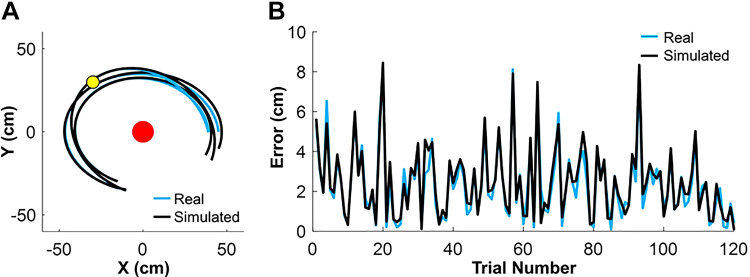
To further match the two environments, the spring constant k and the damping ratio c had to be determined for the real task. To do so, the ball trajectories were generated for each trial based on Eqs. 5–12 using the measured execution variables; the simulations used different k and c values sweeping through the ranges: k∈[0.1,0.9] and c∈[0,0.1]. Those values of k and c were chosen that minimized the summed Euclidian distance of the real trajectory and the simulated trajectory. To avoid artifacts from the energy loss during the ball-target collision, only the portions of ball trajectories between ball release and target contact were considered. Figure 5A shows three real and the three best-fitting trajectories simulated with the optimal k and c values. The average Euclidean difference between the error in the real and simulated ball trajectories was 0.34 cm, ranging between 0.12 and 0.57 cm. The estimated spring constants k of all eight participants ranged from 6.4 g/cm to 6.8 g/cm, with an average of 6.7 g/cm; the estimated damping ratios c ranged from 0.001 to 0.01. Note that the damping ratio had only little effect on the ball trajectory, as it was small and represented only one quarter of a full cycle around the post. Figure 5B compares the distance errors calculated from 120 simulated and the real ball trajectories of one subject. This simulation not only estimated the model parameters, but also validated the 2D projected data from the real skittles. Note that these calculations in the real set-up were performed before the virtual experiment, and the estimated parameters were entered into the virtual model to achieve maximum similarity.
Figure 5.
Real and simulated ball trajectories and performance error of the real skittles task. A: real and simulated trajectories of three throws from an exemplary subject, based on the estimated ball release. Coincidence of trajectories illustrate the veridical estimates. B: calculated performance error with real and simulated ball trajectory of 120 trials from the same subject.
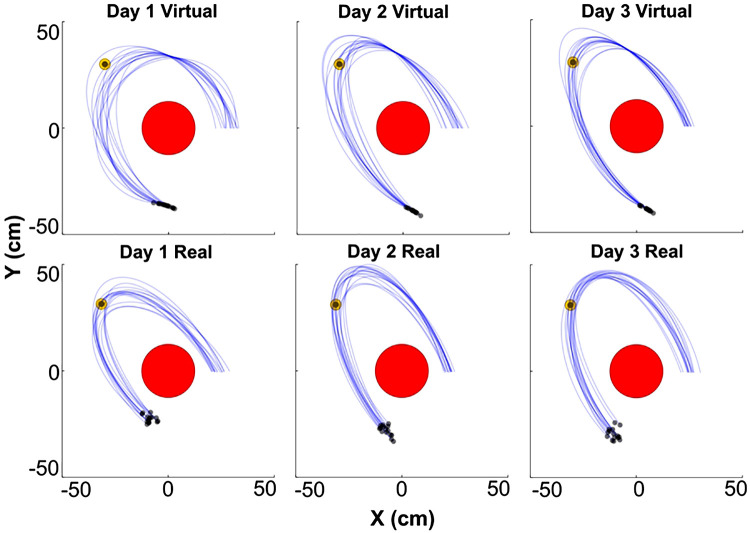
Figure 6 shows 15 ball trajectories of two representative subjects, one from the virtual group and one from the real group, across day 1, day 2 and day 3. The 15 trajectories were taken from the end of Block 2 of each day. As can be seen, in both conditions, the 15 successive throws generate a bundle with similar, yet variable, ball trajectories that traverse inside and outside of the target. The release position on day 1 is visibly different than on days 2 and 3 in both conditions. Overall, the ball trajectories appear more variable in the virtual condition. On the basis of these ball trajectories, the descriptive performance measures error and success rate could be calculated in analogous fashion for both the real and virtual tasks.
Figure 6.
Ball trajectories of two representative subjects in the virtual (top) and real (bottom) tasks across the 3 days of practice. The blue curves represent 15 ball trajectories from each day, the red circle is the center post, the small yellow circle is the target, and black dots are the release point.
Tolerance-noise-covariation analysis.
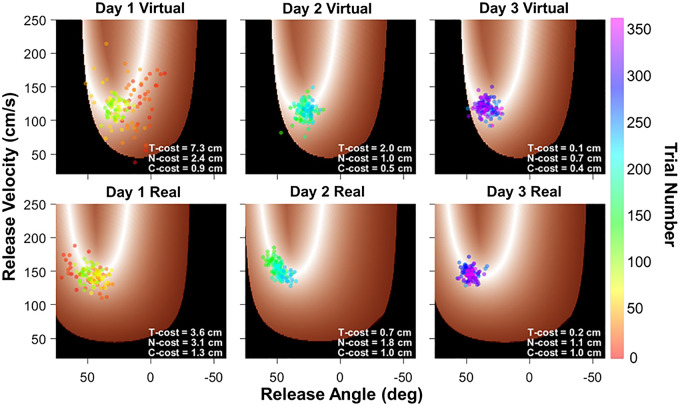
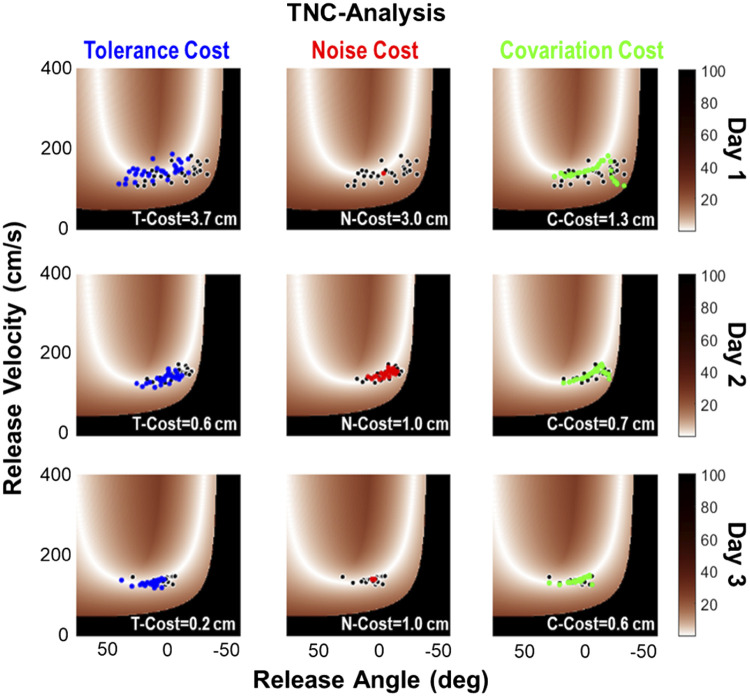
To provide a more fine-grained characterization of the potential performance differences between the real and the virtual skittles task, the variability in the redundant execution space was decomposed using the TNC-analysis. To track how performance changed, the distribution of the variables was parsed into three contributions or costs: tolerance, noise, and covariation (Cohen and Sternad 2009). This analysis was conducted on each block of 30 trials. Figure 7 shows performance of the same two subjects as in Fig. 6 from day 1, day 2, and day 3, one subject for the virtual and one subject for the real task; each point represents a single throw. Calculation details for the TNC-costs are provided in appendix b, as this method was already applied in several previous studies (Cohen and Sternad 2009; Sternad et al. 2010; Van Stan et al. 2017).
Figure 7.
Solution spaces in the virtual (top) and real (bottom) task. The white color denotes the solution manifold; black denotes throws that hit the center post. The data points from the same two subjects as in Fig. 6 are shown in each task. The color of the throws denotes the trial number, showing how the throws change with respect to the solution manifold across practice. Note that the virtual and real task show slightly different geometries of the solution manifolds. For each panel, the values of the tolerance-noise-covariation costs are listed.
The color scale of the data points indicates trial number, illustrating how the sequence of throws traversed through the space on each practice day. After a large spread on day 1, especially in the virtual task, the data started to settle on a location of the solution manifold on day 2. This traversal in the solution space is captured by tolerance-cost. The data in real skittles also show an alignment with the solution manifold, a feature that is quantified in covariation-cost. Day 3 shows some further clustering and reducing of noise, i.e., optimizing noise-cost, although this is not as pronounced as other experiments revealed (Cohen and Sternad 2009). Compared with these previous studies, the practice time in the current experiment was relatively short, and the reduction of noise and covariation tended to occur in later stages of practice. Figure 6 shows the values of the three costs in each panel. For example, T-cost = 7.3 cm means that the set of throws could improve by 7.3 cm in accuracy if the data distribution had been shifted to better overlap with the solution manifold (see appendix a).
Note that the solution manifolds in Fig. 7 are slightly different for the two tasks. This is because the real game allowed some variation of the x-y hand position at ball release, as the hand movements were not constrained to a circular path. This release position affected the geometry of the solution manifold. Therefore, the mean release position was estimated for each practice block and used to create the solution space for each block of trials separately. In addition, the average k and c values were calculated per block as they also changed slightly. These small variations of the parameters modified the geometry of the execution space and the solution manifold, as can be seen in Fig. 7. Specifically, the solution manifolds in the real task tended to be further away from the boundary that resulted in post hits (black area).
Note that, in principle, the TNC analysis could have been performed on the full three-dimensional data of the real skittles task with four execution variables, release position in x- and y-dimensions, release angle, and release velocity. However, the x-y coordinates of the release position were not independent from the release angle, since the ball trajectory was constrained to a circular arc by the pendular string. As the release positions of each individual were relatively consistent, the analysis could fix the mean release position and reduce the execution variables to the same variables as in the virtual task and, thereby, facilitate comparison across the two tasks.
Statistical analyses.
First descriptive metrics were error, variability of error, and success rate. Since the distributions of performance error were skewed and leptokurtic, the median and interquartile range (IQR) of the performance error were used to characterize the first and second moment of the error. Success rate, median of error, and IQR of error were obtained for each subject per block. Note that by definition, for each error, the ball trajectory, i.e., the execution variables, could be different. The dispersion of error is not equivalent to the dispersion of the ball trajectories. However, the error and its dispersion determined the degree of accomplishment of the task, and it was, therefore, a meaningful metric. Because of this redundancy, the calculation of the TNC costs extracted different features of performance. Noise cost may be closest to the conventional variability metric.
To characterize how performance changed with practice, all dependent measures were submitted to a repeated-measures 2 (group) × 12 (block) ANOVAs, with practice Block as a within-subject factor and Group as a between-subject factor. Greenhouse-Geisser corrections were applied to the within-subject effect when the sphericity assumption was violated (Kirk 1982). Since the sample size of the experiment was relatively small (8 participants in each group), a bootstrapping method was also applied. To simulate the process of a two-factor repeated-measures ANOVA, all data of 12 blocks from all subjects were first pooled. Second, 12 levels of data were randomly sampled with replacement (creating blocks of data). Third, two data sets of eight subjects were randomly sampled with replacement (creating a real vs. a virtual group). Fourth, a repeated-measures 2 (group) × 12 (block) ANOVA was conducted on these sampled groups and the F values were calculated. Fifth, steps 1–4 were repeated 1,000,000 times to create a distribution of F values. Sixth, the F values from the repeated-measures ANOVA of the actual observed groups were compared with the distribution of F values from the bootstrapped data sets. The P value was calculated as the ratio of the number of samples from the bootstrapped F distribution that exceeded the observed F value divided by the total bootstrap number (1,000,000).
Further, planned comparisons using two-sample t tests between the virtual and real groups on each block were applied on success rate, error, and IQR of error. To do so, another bootstrapping method was applied. For each block, all 16 subjects were pooled, and two sets of eight subjects’ data were randomly sampled without replacement. The differences between the means of two data sets were calculated. This process was repeated 1,000,000 times to obtain a distribution of differences between the means. The P value was determined as the ratio between the number of values from the bootstrapped mean differences that exceeded the observed mean difference divided by the total bootstrap number. Pearson correlations were computed between the performance error and each TNC-cost for each individual.
Supplemental data are available at https://doi.org/10.6084/m9.figshare.12100761.
RESULTS
Two groups of subjects performed the virtual and real throwing task, which entailed throwing a ball suspended from a vertical post like a pendulum and aiming it to hit a target on the other side of the post. Each subject performed 3 days of practice with 4 blocks of 30 throws each day. Performance and learning were evaluated with descriptive error and success metrics and with a decomposition of variability that afforded more insight into the learning process.
Success rate, error and variability of error.
The performance metrics, success rate, mean performance error, and the interquartile range (IQR) of error of all subjects across the 12 blocks are shown in Fig. 8. The plots show averages and standard errors across subjects for each block, together with the individual data (in more transparent lines). The first repeated-measures 2 × 12 ANOVA on success rate revealed a significant main effect of Block, F(5.39,75.45) = 10.40, which was also significant with bootstrapping P < 0.001, showing that both groups improved with practice. However, the real group’s performance was significantly better overall, F(1, 14) = 10.55, with P = 0.008 using bootstrapping: the success rates in the real task increased from 31.67% ± 4.50% in Block 1 to 60.00% ± 4.08% in Block 12, while in the virtual task only from 17.08% ± 4.65% to 48.75% ± 3.88%. There was no significant interaction; bootstrapping rendered P = 0.92. Figure 8A shows this clear separation between the virtual and the real group across all practice sessions, although pairwise significant differences were only identified in Blocks 1, 3, 5, 7 and 8, as indicated by an asterisk.
Figure 8.
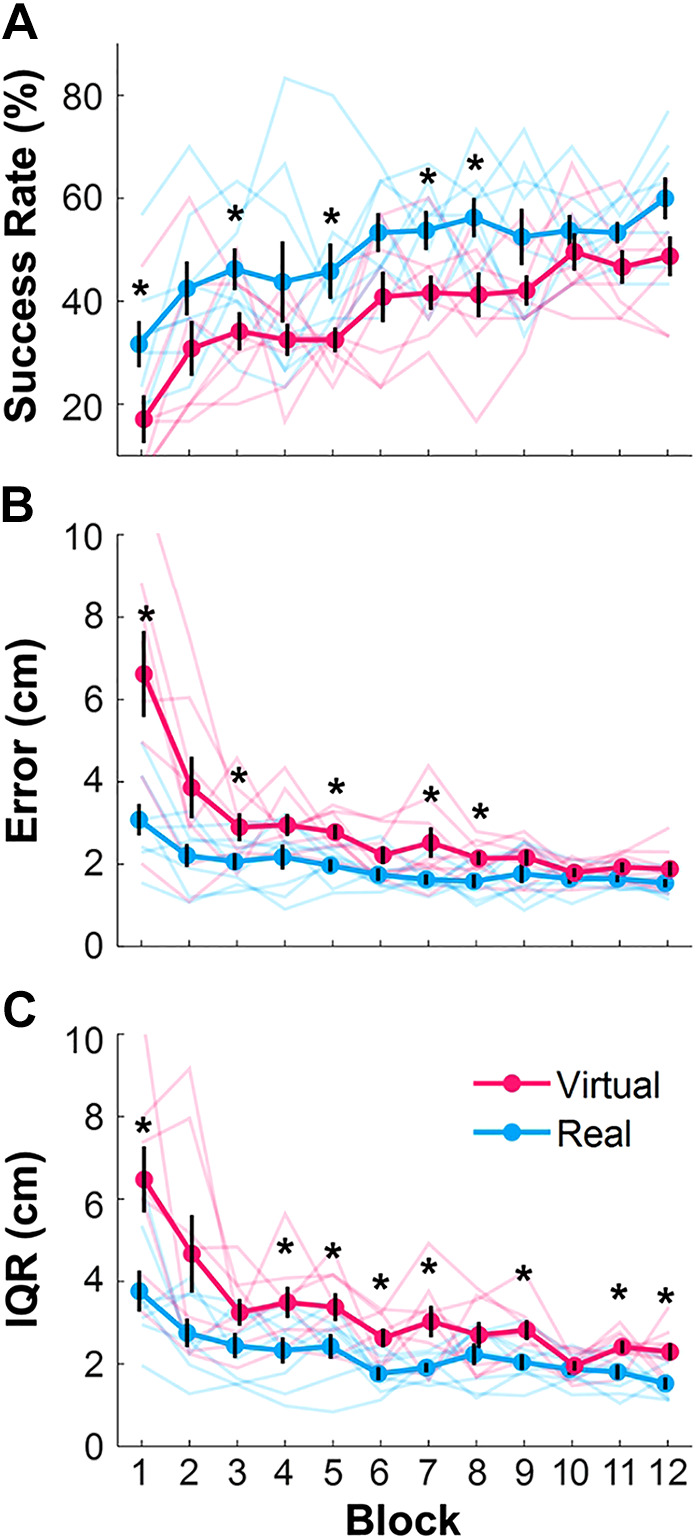
Performance in the real and virtual skittles task. A: average success rates across all subjects per block in the real and virtual skittles across 12 blocks of practice. Asterisks denote significant differences between virtual and real blocks. B: average performance error of the real and virtual skittles decreased across 12 blocks of practice. C: interquartile range of error of the real and virtual skittles decreased with practice. Error bars represent standard errors across subjects. The solid lines represent the means and the errors of the standard deviations across subjects. The transparent lines show all eight subjects.
The same ANOVA on error revealed a significant interaction between Group and Block, F(2.10,29.39) = 4.36, with P < 0.001 when using bootstrapping. The real group decreased the error from 3.1 ± 0.4 cm in Block 1 to 1.5 ± 0.1 cm in Block 12, while subjects in the virtual group started with higher errors: 6.6 ± 1.1 cm and decreased them to the same approximate level as the real group in Block 12 with 1.9 ± 0.2 cm. Planned pairwise tests for each Block detected significant differences in Blocks 1, 3, 5, 7, and 8. The main effect of Block was also significant, F(2.10,29.39) = 15.79, with P < 0.001 when using bootstrapping, showing that both groups decreased their errors (Fig. 7B). The significant effect of Group, F(1,14) = 17.42, with P = 0.001 when using bootstrapping, showed again the advantage of the real group: their errors decreased from 3.1 ± 0.4 cm in Block 1 to 1.5 ± 0.1 cm in Block 12, while subjects in the virtual group started with higher errors: 6.6 ± 1.1 cm and decreased them to approximate the real group in Block 12 with 1.9 ± 0.2 cm.
The ANOVA on the variability of errors, or IQR, again rendered a significant main effect of Block, F(3.35,46.92) = 14.02, with P < 0.001 when using bootstrapping; the IQR of the real group decreased from 3.8 ± 0.5 cm to 1.5 ± 0.1 cm, while the virtual group started much higher and decreased from 6.5 ± 0.8 cm to 2.3 ± 0.2 cm. There was also a significant main effect of Group, P = 0.001, providing evidence that the real group had consistently smaller variability than the virtual group. There was no interaction between Block and Group, P = 0.082 with bootstrapping. Planned comparisons identified significant differences in Blocks 1, 4, 5, 6, 7, 9, 11 and 12.
While all three performance measures revealed differences, the advantage of the real set-up manifested most pronouncedly in the variability measures. This motivated further analyses of the distributions of the data in each block.
Variability analysis: tolerance, noise, and covariation.
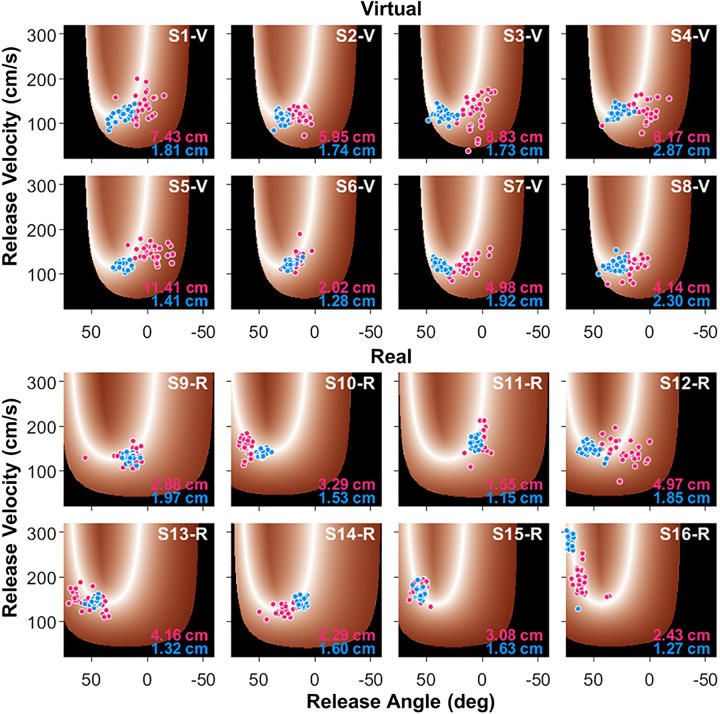
T-cost, N-cost, and C-cost were estimated from the distributions of the 30 trials of each block in the solution space, separately for each subject. Showing all 16 subjects, Fig. 9, top, shows 8 subjects in the virtual task, and Fig. 9, bottom, shows 8 subjects in the real task. Each panel shows one subject with trials from Block 1 (denoted with red dots) and trials from Block 12 (denoted with blue dots). The values in the bottom right corner are the average error of each block. All virtual subjects started their performance with a larger variability and with release angles closer to 0°, which corresponded to θr in Fig. 2A. In Block 12, the trials were more clustered around the solution manifold and were associated with smaller errors. In the real task, the individuals showed larger individual differences in how performance was improved. However, in Block 12, all subjects displayed very tightly clustered throws close to the solution manifold. Note that their solution manifold differed from the virtual task and also slightly between each other, although not very much. One noticeable difference is that the solution manifold has a second branch on the left, potentially allowing more throwing possibilities.
Figure 9.
Exemplary results from all 16 subjects in the virtual and real tasks. Top: subject 1 to subject 8 in the virtual task. Bottom: subject 9 to subject 16 in the real task. For each subject, the 30 throws on Block 1 are shown in red, and the 30 throws of Block 12 are shown in blue. The values of average performance error are listed in the bottom right corner of each panel. As to be expected, the real throwing performance shows more differences in strategy between subjects that, on the whole, all lead to better performance.
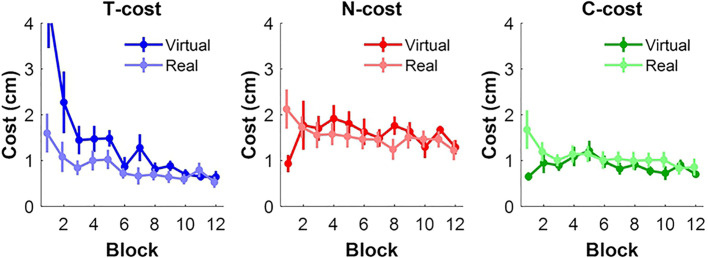
Figure 10, A and B show the average costs of each of the three components for the 12 blocks, both in the virtual and real task. The mean values across subjects and its standard errors are plotted across blocks. In the virtual task, T-cost declined with practice, while N-cost and C-cost remained at a relatively steady level throughout practice. T-cost was initially high, reflecting initial exploration until the right release variables were found. After Block 2 or 3, however, T-cost dropped to a floor value without much further reduction for the remainder of practice. While unchanging, N-cost was consistently higher than C-cost. After the initial drop of T-cost, N-cost made a slightly higher contribution to the performance error. In contrast, in the real task, the three costs declined in parallel throughout the blocks. T-cost made the lowest contribution, and again, N-cost was consistently higher than C-cost. Note that the y-axis range was adjusted to highlight the differential contributions of the costs in the real task, which would have been invisible when applying the same axis as in the virtual task.
Figure 10.
Results of the tolerance-noise-covariation analysis. A and B: T-cost, N-cost, and C-cost in the real and virtual tasks; error bars indicate standard errors across subjects. Note that the y-axes are different for the real and virtual task for better visibility. C and D: rank orders of the three costs in the 12 blocks of practice. Number of subjects for each cost that made the greatest contribution to error (rank 1). E and F: rank orders of the three costs in the 12 blocks of practice. Number of subjects for each cost that made the smallest contribution to error.
One way to compare the different contributions of the three costs was to examine the rank ordering of the three costs in each block for each individual. Figure 10, C–F summarizes these rank orders across blocks: the numbers of subjects for which a given cost had the largest contribution (rank 1) are shown in Fig. 10, C and D for the virtual and the real task, respectively; the numbers of subjects for which a given cost made the least contribution (rank 3) are shown in Fig. 10, E and F. Comparing the relative numbers for rank 1 revealed some similarity. In the virtual task, in 6 out of 8 subjects T-cost (denoted in blue) was highest in Block 1; from Block 3 to Block 12, N-cost (denoted in red) became the largest contributor; C-cost contributed very rarely, indicating that subjects did not optimize covariation. In the real task, T-cost was visibly less pronounced, and N-cost always had the highest numbers of rank 1. When examining rank 3, the lowest contributions to performance, C-cost and T-cost, were equally represented in the virtual group. In the real group, T-cost made the smallest contribution to the performance error from the beginning of practice, implying that exploration played a subordinate role.
In another comparison, the three costs were contrasted in pairwise fashion to identify differences in strategies in the virtual and real task (Fig. 11). Three two-way ANOVAs were applied on the three costs. T-cost resulted in a significant effect of Block, F(2.60,36.45) = 11.03, P < 0.001 with bootstrapping, and Group, F(1,14) = 7.65, P = 0.014 with bootstrapping, with a significant interaction between Group and Block, F(2.60,36.45) = 3.79, P = 0.008 with bootstrapping. These results signified that T-cost decreased with practice in both groups, but the virtual group started with a higher error. Neither N-cost nor C-cost showed any significant improvements with practice, or differences between groups. In summary, the comparisons of the three components revealed that the different performance errors of the two groups were caused by differences in T-costs. Note for direct comparison the y-axes are now identical (even though one data point was lost for the T-cost figure).
Figure 11.
Pairwise comparison of T-cost, N-cost, and C-cost in real and virtual environments. The three panels show mean T-costs (left), N-costs (middle), and C-costs (right) across 12 practice blocks for the real and virtual tasks, respectively; the error bars are standard errors across subjects. For direct comparison, the y-axes for all three costs are identical, even though one data point was cut off for the T-cost panel (see Fig. 10).
To further quantify the contribution of the three costs to performance improvement in each individual, Pearson correlations between error and T-, N-, and C-cost were performed for each subject across 12 blocks, respectively. The results are summarized in Table 1. In both groups, T-cost showed highly significant positive correlations with error in most individuals. However, in the real task only, 4 out of 8 subjects also showed positive correlations in N-cost and C-cost. These results indicate that while T-cost mainly drove the performance improvement in both conditions, the real task also allowed for noise reduction and covariation, N-cost, and C-cost, to add to improvements.
Table 1.
Pearson correlation between performance error and T-, N-, and C-costs for all 16 subjects
| Subject | T-cost |
N-cost |
C-cost |
||||
|---|---|---|---|---|---|---|---|
| r | Sig | r | Sig | r | Sig | ||
| Virtual | 1 | 0.985 | *** | −0.380 | 0.087 | ||
| 2 |
0.950 | *** | −0.561 | −0.159 | |||
| 3 |
0.975 | *** | 0.141 | 0.278 | |||
| 4 |
0.995 | *** | −0.357 | −0.161 | |||
| 5 |
0.995 | *** | −0.483 | −0.294 | |||
| 6 |
0.845 | *** | 0.338 | 0.265 | |||
| 7 |
0.980 | *** | −0.051 | −0.001 | |||
| 8 |
0.794 | ** | 0.298 | 0.157 | |||
| Mean |
0.940 | −0.132 | 0.022 | ||||
| Std |
0.077 | 0.360 | 0.212 | ||||
| Real | 9 | 0.827 | ** | 0.685 | * | 0.594 | * |
| 10 |
0.732 | ** | 0.052 | 0.260 | |||
| 11 |
0.788 | ** | −0.002 | 0.096 | |||
| 12 |
0.792 | ** | 0.655 | * | 0.927 | *** | |
| 13 |
0.889 | *** | 0.797 | ** | 0.572 | ||
| 14 |
0.635 | * | 0.579 | * | 0.107 | ||
| 15 |
0.836 | ** | 0.493 | 0.612 | * | ||
| 16 |
0.181 | −0.003 | 0.787 | ** | |||
| Mean |
0.710 | 0.407 | 0.494 | ||||
| Std | 0.227 | 0.336 | 0.308 | ||||
The asterisks represent the level of significance:
0.01 < P < 0.05,
0.001 < P < 0.01,
P < 0.001.
DISCUSSION
Over the past few decades, numerous studies in movement neuroscience and in physical therapy have employed virtual reality set-ups as they allow sophisticated manipulations and measurements that were impossible in real testbeds. In parallel, physical therapy has adopted virtual reality as a means to deliver motivating games that allow quantitative measures of performance, multisensory feedback, and individualized challenges in salient and enriched environments (Levac et al. 2019; Levin et al. 2015; Saposnik and Levin 2011). However, the evident expectation that the skills acquired during virtual rehabilitation transfer to the real environment has not found much support (Anglin et al. 2017; de Mello Monteiro et al. 2014; Levac et al. 2019; Quadrado et al. 2019). These results raised the concern that movements in a virtual world may not faithfully represent determinants of movements in the real world.
Similarly, motor neuroscience has embraced virtual environments, but with a different goal: Virtual testbeds reduce the complex behavior and can isolate and tailor movements to address a scientific question. Numerous studies on reaching in the horizontal plane have studied adaptations to visuo-motor rotations and perturbing force-fields and have revealed detailed results on error correction, generalization, and time scales of learning (Shadmehr and Mussa-Ivaldi 1994; Shadmehr et al. 2010). However, it needs to be noted that the limb movements were reduced to two or maximally three joints moving in the horizontal plane with minimal friction from the surface. The visual workspace presented a point target together with a cursor representing the end-effector movements against an empty 2D background. The task is void of any contact with an object. How does this virtual aiming relate to realistic functional behavior? Importantly, do the results in this virtual assay “add up” or “scale up” to understand real behavior in its full complexity?
While experimental reduction as a scientific method should not be called into doubt, these questions, nevertheless, deserve more attention. With this concern in mind, the present study examined a throwing task both in a virtual and a real environment. While the arm, hand, and finger movements differed in several ways, the physical parameters of the task were matched as exactly as possible. Do observations in the reduced virtual paradigm match those in a more realistic context? Our findings showed clearly that the performance outcomes were significantly better in the real task, at least on the first 2 days of practice. The success rate was better, the errors were lower and, most clearly, the variability was less in 8 out of 12 blocks. To go beyond these descriptive outcome measures, this study also examined changes in variability, specifically using a decomposition method developed by our group (Cohen and Sternad 2009). Significant differences emerged that provided more insight how strategies differed between the two testbeds.
Estimation of release variables in real throwing.
Before further discussion, the difficulties of estimating the variables at ball release in real throwing need to be highlighted. Real throwing affords subtle adjustments in finger forces and stiffness when throwing a ball (Hore and Watts 2011). Therefore, several previous studies on naturalistic throwing, could not estimate the release variables as accurately and reliably as desired. For example, in a study on dart throwing, simplified to the sagittal plane, the measured position of the dart at the target board differed from the one simulated with the release variables by up to 20 cm (Smeets et al. 2002). This was five times the actual error dispersion and the actual and simulated target position only had a correlation coefficient between 0.6 and 0.9. These deviations were not only introduced by environmental parameters, but probably by inaccuracies in measuring the dart release. Similarly, the dart throwing simulation by Nasu et al. (2014) had an estimation error of 18.5 mm at the target, which was about two times of the diameter of the bull’s eye. The authors applied different velocity thresholds to detect the release for each individual, but the criteria could not be firmly established. The interaction forces between the fingers and the projectile are difficult to measure and have been largely neglected in these experimental estimates. As detailed in appendix a, the present study developed methods to improve the estimation accuracy of the time of ball release and the values of the release variables.
Virtual task requires more exploration.
The most striking result is that performance started with much higher errors in the virtual task and decreased slowly to reach the same level as the real task, but only after 3 days. The variability analysis revealed that tolerance-cost started much higher in the real task, while in the virtual task it started with similar values as noise- and covariation-costs. To reiterate, tolerance-cost quantifies how much the average error could have improved if the data distribution were translated to another location in solution space, without any other transformation. Hence, tolerance-cost evaluates to what degree the data distribution is not at the most error-tolerant area and still explores the solution space. Arguably, exploration, the early stage of learning, is a “mapping out” of the result space. Several studies have focused on this first stage of the learning process (Button et al. 2008; Goodman et al. 2004; Ivaldi et al. 2014; McDonald et al. 1995; Wilson et al. 2014). For example, Wu and colleagues presented data that suggested that the initial variability determined individual learning rates, although several subsequent studies could not replicate this result (Cardis et al. 2018; He et al. 2016; Singh et al. 2016; Sternad 2018; Wu et al. 2014). Wilson et al. (2016) have provided evidence for both a directed search and a chance-based gathering of information. However, endeavors to disentangle the different exploration strategies based on random noise or directed gradient descent were typically hamstrung by the fact that the result space had to be known. In fact, the virtual task has been developed with the goal to allow this mathematical analysis of the solution space. It then facilitated the task-based analysis with the TNC-decomposition to provide an inroad to quantify exploration by the tolerance-cost. Note that related variability decomposition methods, the uncontrolled manifold (or UCM) analysis and the GEM analysis only focus on the covariation and noise components and do not capture the translations across the solution space (Cusumano and Cesari 2006; Latash et al. 2002; Sternad 2018); for a comparative summary, see Müller and Sternad (2009) and Sternad et al. (2010).
Returning to the comparison between the real and the virtual task, covariation-cost and noise-cost were lower and declined very slowly. It is further worth noting that also covariation-cost and noise-cost showed significant correlations with performance error in the real skittles, while in the virtual skittles, none of the subjects gave any indication that these components mattered. As seen in previous studies on the same task, but with longer practice, covariation did become a significant contributor to performance improvements, but only much later in practice (Abe and Sternad 2013; Cohen and Sternad 2009; Van Stan et al. 2017). Noise has been the hardest component to reduce, and many days of practice or additional interventions are needed (Hasson et al. 2016; Huber et al. 2016).
The notion that learning proceeds in stages is not new in learning theory, and several other proposals have been made (Bernstein 1967; Posner et al. 2004). A number of studies have pointed out that learning of a given task is not a single process but involves a complex system with more than one timescale. Wenderoth and Bock (2001) showed multiple timescales in a bimanual rhythmic task, similar to work by Park and colleagues (Park et al. 2013; Park and Sternad 2015). These studies extracted different task-relevant metrics that all showed a different time course of improvement across practice. In contrast, Smith et al. used a single behavioral variable but showed that by including a second timescale in the iterative learning model, they could account for observations, such as savings (Smith et al. 2006). The TNC analysis may offer another analysis tool that can differentiate different stages and strategies based on the type of changes in variability.
Differences between the real and the virtual task.
As emphasized in the methods, the physical parameters of the two tasks were identical, but there were several differences in terms of movement execution and the perceived environment. To start with the obvious, the real set-up was in three dimensions, where depth perception was required—or helped—to see and aim for the target. In the virtual task, subjects saw a bird’s-eye 2D view of the task without perspectival distortion, with all the objects represented by circles of different colors and diameters. In the real task, the feedback about throwing accuracy was a real collision between the ball and target, whereas in the virtual set-up, a color change of the target signaled success. However, subjects had a clear view of the distance between ball trajectory and virtual target.
Importantly, the movements differed in several aspects: in the virtual set-up, the forearm was constrained to the circular path around the pivot. In contrast, in the real task, subjects used their entire arm with all joint degrees of freedom. Nevertheless, the hand trajectory was also constrained to a circular path around the post before ball release as the pendulum string had to remain taut. Finally, the ball release in real throwing required fine-grained coordination between the fingers, including complex interaction forces between the fingers and the ball, while in the virtual task, a simple extension of the index finger was sufficient to release the virtual ball. The complex finger-ball forces were detailed by Hore et al., who concluded that skilled throwers modulate their finger stiffness based on an internal model of the interaction forces to determine the release velocity (Hore et al. 1999; Timmann et al. 1999). Note that it was not our objective to equate the arm movements in the real and virtual tasks. We only strove to equalize only the tasks to evaluate the effect of the reductions or simplifications of the movements. So why is real throwing with all its complexity still more accurate? Several reasons may account for the observed advantage.
Redundancy of multi-joint coordination may help.
Because of the less constrained arm movements, subjects may have exploited the redundancy of the multijoint arm to better adjust the position and velocity of the hand at ball release. Further, the redundancy in hand-finger joints may also have afforded fine-grained adjustments of their hand and finger coordination to throw the ball. Following Hore et al., subjects may have included finger stiffness to fine-tune the ball throw (Hore and Watts 2011). While from a scientific perspective, controlling the complex arm, hand and finger may appear more challenging, awareness of the null space of the arm and hand may be acquired from everyday experience. Even though people have more experience in real throwing, anecdotal and scientific evidence provides ample documentation that throwing is not easy. The results suggest that operating in a virtual environment may even be more demanding and may need more exploration and familiarization.
Geometry of the solution manifold.
A seemingly subtle but interesting point is that in the real task, the solution space is not completely fixed. The geometry of the solution manifold is determined by two factors: the location of the target and the location of ball release. In the virtual task, the hand trajectory was strictly confined to the circular arc with its pivot fixed; hence, the geometry of the solution space was fixed. The subject could only adjust the velocity profile of the hand trajectory and, of course, the moment of release. In contrast, in real throwing the subject’s hand trajectory was confined to an arc around the center post, as they held the ball attached to a string that needed to be taut. Even though subjects were instructed to release the ball at a fixed position, they could and did adjust the ball release position slightly. Figure 4 shows that even though subjects were instructed to release the ball at a designated position, they varied in their choice and some variability remained within and between subjects. These seemingly small positional adjustments shaped the solution manifold as seen in Figs. 7 and 9, which show representative data from real and virtual throwing with their respective solution spaces. Despite the identical placement of the target with respect to the post and the designated position of ball release, the solution manifold differed slightly. In particular, a left branch appeared creating potentially more options for throws without hitting the post. A similar observation was reported in a study on realistic target-oriented throwing by Wilson et al. (2016). The small variations in release position might reflect that subjects created this possibility to increase their success rate. However, the results showed only one subject (S16-R) actually used this branch and 3 subjects were close (S10-R, S13-R, and S15-R). Although this raises an interesting issue of how subjects may shape their solution manifold when they are free to choose the ball release location, the current data seem to be relatively little influenced by it. To directly address this question, subjects would need to be instructed to find their preferred release position.
Summary and implications for research and rehabilitation.
Virtual environments have found increasing use in research and rehabilitation, although for different purposes. While physical therapy has employed them as motivating games that also enabled precise measurements and titration of task difficulty, motor neuroscience has used them to create simple testbeds for addressing focused scientific questions, while eliminating uncontrolled variability. This reductionistic strategy parallels the modeling process that distills without replicating the full system. In this spirit, many experimental paradigms in motor neuroscience have “modeled” real behaviors: reaching has been reduced to aiming in the horizontal plane (Wang and Sainburg 2007), and grasping has been reduced to pressing on an object or holding an object with precisely known physical properties (Zatsiorsky and Latash 2008). Both paradigms are far from the complexity of behaviors with natural objects. Also walking and running are typically examined on a treadmill to eliminate uneven ground and changing velocity, and to facilitate recording (Alton et al. 1998; Dingwell et al. 2001; Ochoa et al. 2017). Inevitably, all these experimental settings lose something of the real world that could be important for the scientific question. While this scientific approach is widely accepted, the question still remains how the findings relate to the task that gave rise to the model testbed: be it reaching, grasping, walking, or throwing.
This study compared a real and virtual version of throwing, where the task requirements were precisely matched, but the movements remained different. The main and somewhat unexpected result was that hitting performance in the real setting with a full arm and hand movements was significantly better. Real throwing required a significantly shorter learning period and earlier involvement of more fine-tuned processes of covariation and noise reduction. Perhaps, virtual learning tasks should consider longer practice sessions. Further, despite the close match of the physical task parameters, differences in movement execution engendered subtle differences in the solution space that revealed potential opportunities for control. This was not trivial as the more complex, real environment seemed to pose more challenge for movement control. It may be of interest to include this aspect into the virtual setting and test its influence on performance.
Given the widespread use of virtual environments in motor neuroscience, these results raise some caveats for the unreflected generalization of findings to complex real-world actions. Virtual environments may present initial hurdles, such that subjects do not find their best strategy or, relevant for physical therapy, they do not practice, a strategy that is transferable to activities of daily living. For example, in unconstrained settings, skilled throwers may not only align their trajectories with the solution manifold, but also shape and exploit the geometry to fit their preferences. Therefore, caution should be applied to basic research on motor control: the results in simplified settings may not scale up as expected. After all, the human neuromotor system is a highly complex, nonlinear, hierarchical system. Perhaps, despite all the recognized advantages of reductionistic science, it is also worth studying more complex behaviors.
GRANTS
This research was supported by the National Institutes of Health through Grants R01-HD087089, R01-NS120579, R01-HD045639, and R21-DC013095, which were awarded to D. Sternad.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
Z.Z. and D.S. conceived and designed research; Z.Z. performed experiments; Z.Z. analyzed data; Z.Z. and D.S. interpreted results of experiments; Z.Z. prepared figures; Z.Z. and D.S. drafted manuscript; Z.Z. and D.S. edited and revised manuscript; Z.Z. and D.S. approved final version of manuscript.
APPENDIX A: DETERMINATION OF ANGLE AND VELOCITY AT BALL RELEASE
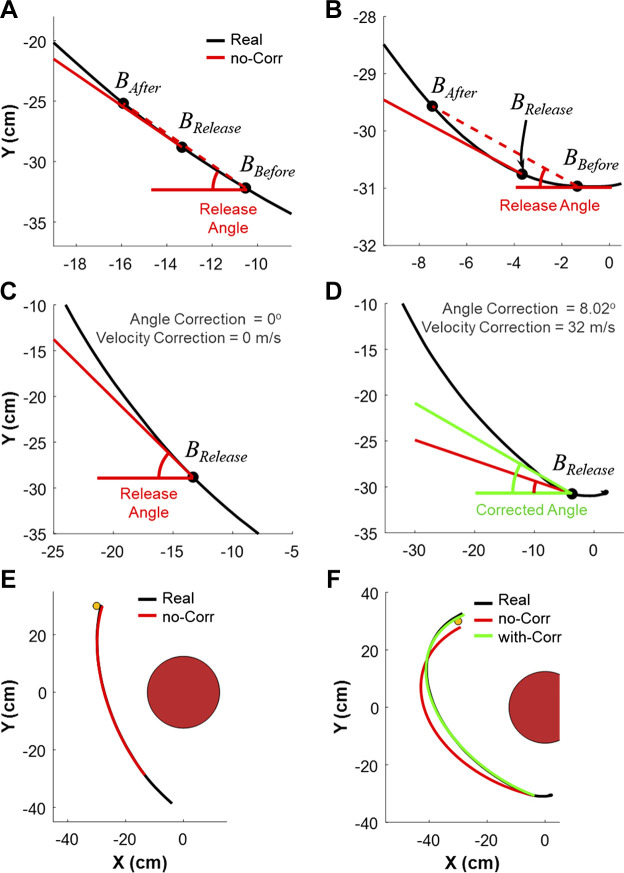
Several previous studies examined real-life throwing with similar research goals as this study and determined the execution variables of the hand at ball release (e.g., Nasu et al. 2014; Smeets et al. 2002). Despite interesting analyses and results, these studies had to report significant differences in the accuracy of the real ball trajectory and the ball trajectory simulated with the estimated execution variables. Although these discrepancies can be ascribed to air resistance, ball spin, or deviations from the saggital plane, they also arise from inaccuracies in determining the actual variables at release that generated the ball trajectory. Given the detailed analyses based on the relation between execution and result variables, this is a critical factor for the reliability of the results and conclusions. Unlike in the virtual set-up, where the ball release variables are defined at the moment of ball release, the ball trajectory in the real throw is also influenced by the potential exchange of forces between the fingers and the ball. In this study, we introduced a correction of the kinematics when the ball trajectory was significantly modified by finger forces.
The first step in the analysis of the ball release variables was to determine the moment of release using the motion capture data (note: there was no force sensor). Given that reflective markers were on both the ball and the thumb, the relative distance and the velocity between these two markers was the basis for calculation. The instant of release was determined when the separation velocity of those two markers exceeded 0.30 cm/s for the first time. This threshold was empirically determined and held constant across all subjects [note that individual adaptations had to be applied in Nasu et al. (2014)]. However, the angle and velocity of the ball at this moment were not necessarily the best predictor for the ball trajectory.
Figure A1 illustrates the calculations for two ball trajectories in the x-y plane: one trajectory showed no marked change in direction (left column); for the second trajectory the fingers exerted forces to the ball at release such that the ball trajectory made a sharp turn and increased its velocity at release (right column). To begin, on the basis of the x-y position at the release moment BRelease, two points 30 ms before and after release, BBefore and BAfter, were determined on the measured ball trajectory (black line in Fig. A1). Connecting these two points (red dashed line) defined the angle of release if no force were imparted onto the ball at release. Figure A1A shows an example segment where angle and velocity changed only negligibly and the solid and dashed line were almost overlapping. Figure A1B illustrates how the real trajectory could deviate markedly, leading to erroneous release angle estimates. The solid red line illustrates the release angle and velocity by shifting the red dashed line to start at BRelease. To calculate the scalar velocity of ball release, all samples between BBefore and BAfter were examined to avoid the confounding effect of equipment noise in the estimation. The Euclidian distances from BRelease to all the points between BBefore and BAfter were determined and a regression of those distances over time gave the scalar velocity of the ball at release.
Figure A1.
Estimation of release angle and velocity accounting for the force that fingers exerted on the ball. A: exemplary trajectory with negligible force at release in black; the red dashed line between BBefore and BAfter determines the angle of the ball at release. B: exemplary trajectory (black) and release angle (red dashed line) with nonnegligible force at release. As the release angle differed from the actual ball trajectory, the red solid line shows the angle of release translated to the actual location of release. C and D: real and corrected ball angle and velocity at release as determined in A and B. E and F: real and corrected ball trajectories as in A and B shown in the x-y workspace; the yellow dot is the target.
The correction used an optimization approach, in which the ball trajectory for each trial was simulated with different release angles and release velocities sweeping through the ranges: and , with 100 test values evenly separated for each variable. The simulation error of each pair of and was determined as the average Euclidian distance between the simulated and real trajectories from the release to the point of minimum distance to the target. The values of and , which minimized the simulation error, were chosen as the “veridical” release variables. For subjects with small exerted force, as depicted in the left column of Fig. A1, the angle and velocity corrections were zero. In Fig. A1E, the simulation error was small: 0.15 cm. For subjects with nonnegligible force as in the right column, a correction was applied. For instance, in Fig. A1F, the correction reduced the average simulation errors for this trajectory from 4.45 cm to 0.30 cm.
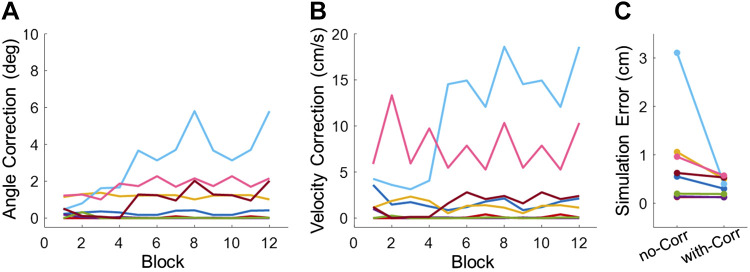
A summary of all corrections of angle, velocity, and errors are presented in Fig. A2. The 8 subjects in the real group displayed different degrees of angle and velocity corrections (Fig. A2, A and B). While 3 subjects had very small angle and velocity corrections, there were 5 subjects who had nonnegligible errors compared with the original simulated trajectories. After the corrections on angle and velocity, the simulation errors significantly decreased (Fig. A2C).
Figure A2.
Correction of execution variables for all subjects. Each colored line represents the mean correction of one subject for each block. A: angle correction for all subjects across blocks. B: velocity correction for all subjects across blocks. C: average simulation error with/without angle and velocity correction.
APPENDIX B: TOLERANCE-NOISE-COVARIATION ANALYSIS
This analysis was conducted in execution space, spanned by release angle and velocity, where sets of 30 trials were analyzed with respect to their contribution to performance error (see also Cohen and Sternad 2009; Sternad et al. 2010). Figure B1 illustrates the analysis with the distributions of one block of trials on the 3 days of practice: the first column shows the operations for the estimation of tolerance-cost, or T-cost, the second column shows noise-cost, or N-cost, and the third column shows covariation-cost, or C-cost. In each panel, the black data points represent the veridical distributions of the 30 trials, and the colored data points show the transformed data that optimize each cost defined as follows.
Figure B1.
Illustration of the algorithm for calculating tolerance-cost, covariation cost, and noise cost over 3 days. The black points are the actual data, while the colored points are the transformed data for the respective operations. The data set with the best mean error is depicted. The cost is determined by subtracting the mean error from the ideal data set from the actual data, in units of centimeters (shown for each example data set).
Calculation of tolerance cost.
T-cost is the cost to overall performance for not being in the most error-tolerant area of the execution space. T-cost was estimated by generating an optimized data set in which the mean release angle and the mean release velocity were shifted in execution space to the location that yielded the best overall mean error. The distribution along each axis was preserved during this process. In the numerical procedure, the center point of the distribution was identified as the mean of the distribution of the x-axis (angle) and the y-axis (velocity). The angles tested as centers were limited to those between 0 and 180°; the velocity values tested as centers were limited to 50–400 cm/s. Then, the data set was shifted on a grid of 1,500 × 1,500 possible center points. The optimization procedure shifted the data set through every possible center point and evaluated its mean result at each location. When data points extended beyond the grid limits, the values were calculated on the extended execution space. The location that produced the best (lowest) mean error was compared with the mean error of the actual data set; the algebraic difference between the two mean error values defined T-cost in units of centimeters. Figure B1 shows the shifted data leading to the optimal result versus the actual data.
Calculation of noise cost.
N-cost is the cost to overall performance due to nonoptimal stochastic dispersion in execution space. N-cost was estimated by generating an optimal data set, in which the observed variability was scaled to achieve the least possible mean error, while leaving the angle-velocity pairings and overall mean unchanged. Although one would initially expect all data sets to be optimally reduced to a single point, note that each data set was evaluated in terms of its result or error. Therefore, the mean of a data set would not always fall directly on the solution space and were not always optimal. In the numerical procedure, the radial distance of each data point of the distribution was determined and divided into 100 steps. Subsequently, all data points were pulled toward the mean at 1% intervals and the mean error was evaluated at each interval. The algebraic difference between the mean error evaluated for each step and the actual mean error was calculated. The scaling step that produced the lowest mean error was the optimal data set; the algebraic difference of the mean error between this transformed set and the original data set defined N-cost. Figure B1 shows the optimal scaled distribution denoted in red against the actual data denoted in black.
Calculation of covariation cost.
C-cost is the overall cost to performance due to insufficient alignment with the solution manifold; i.e., not exploiting the redundancy in the execution space. C-cost was estimated by generating an optimized data set, in which the marginal distribution of the angle and velocity values were not modified, but the individual trial-by-trial pairings were recombined. Using a greedy hill climbing algorithm, data were pairwise matched and the mean error for each transformed data set was evaluated (Russell and Norvig 2002). Specifically, all angle-velocity pairs were rank-ordered from lowest error (best) to highest error (worst); i = 1, 2, 3… 30, since all data sets comprised 30 trials. Subsequently, the worst performing angle (i = 30) was paired with velocity (i = 29), and velocity (i = 30) was paired with angle (i = 29); the mean results of the new error for i = 30 and i = 29 were compared with the original mean error of the two trials. If the error improved over the original, the swap was accepted. As a next step, angle (i = 30) was swapped with angle (i = 28), and the resulting mean error of the two trials was evaluated. If the mean result improved, the swap was accepted. This continued until angle (i = 30) was compared with angle (i = 1); i.e., angle (i = 30) was swapped with angle (i = 1). After this sequence of 29 comparisons, the same sequence was repeated with angle (i = 99); therefore, the batch consisted of 29 × 29 = 841 comparisons. The number of profitable swaps was recorded for each batch, and the procedures were repeated on the improved set until no further swaps could be made. The algebraic difference between the mean error of this optimized data set and the original data set defined C-cost. Figure B1 shows the transformed data set with the best covariation result denoted in green against the actual data denoted in black.
REFERENCES
- Abe MO, Sternad D. Directionality in distribution and temporal structure of variability in skill acquisition. Front Hum Neurosci 7: 225, 2013. doi: 10.3389/fnhum.2013.00225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alton F, Baldey L, Caplan S, Morrissey MC. A kinematic comparison of overground and treadmill walking. Clin Biomech 13: 434–440, 1998. doi: 10.1016/S0268-0033(98)00012-6. [DOI] [PubMed] [Google Scholar]
- Anglin J, Saldana D, Schmiesing A, Liew S. Transfer of a skilled motor learning task between virtual and conventional environments. 2017 IEEE Virtual Reality (VR). Los Angeles, CA, March 18–22, 2017. [Google Scholar]
- Bagesteiro LB, Sainburg RL. Nondominant arm advantages in load compensation during rapid elbow joint movements. J Neurophysiol 90: 1503–1513, 2003. doi: 10.1152/jn.00189.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein N. The Coordination and Regulation of Movements. Oxford, UK: Pergamon Press, 1967. [Google Scholar]
- Burdea G, Coiffet P. Virtual Reality Technology. New York: John Wiley, 2003, vol 1. [Google Scholar]
- Button C, Chow J, Rein R. Exploring the perceptual-motor workspace: new approaches to skill acquisition and training. In: Handbook of Biomechanics and Human Movement Science, edited by Hong Y, Bartlett R. Abingdon-on-Thames, UK: Routledge, 2008, p. 550–565. [Google Scholar]
- Caballero DE, Rombokas E. Sensitivity to conflict between visual touch and tactile touch. IEEE Trans Haptics 12: 78–86, 2019. doi: 10.1109/TOH.2018.2859940. [DOI] [PubMed] [Google Scholar]
- Calvin W. Did throwing stones shape hominid brain evolution? Ethol Sociobiol 3: 115–124, 1982. doi: 10.1016/0162-3095(82)90010-3. 6632930 [DOI] [Google Scholar]
- Cardis M, Casadio M, Ranganathan R. High variability impairs motor learning regardless of whether it affects task performance. J Neurophysiol 119: 39–48, 2018. doi: 10.1152/jn.00158.2017. [DOI] [PubMed] [Google Scholar]
- Chowdhary AG, Challis JH. Timing accuracy in human throwing. J Theor Biol 201: 219–229, 1999. doi: 10.1006/jtbi.1999.1024. [DOI] [PubMed] [Google Scholar]
- Chu VW, Park SW, Sanger TD, Sternad D. Children with dystonia can learn a novel motor skill: strategies that are tolerant to high variability. IEEE Trans Neural Syst Rehabil Eng 24: 847–858, 2016. doi: 10.1109/TNSRE.2016.2521404. [DOI] [PubMed] [Google Scholar]
- Chu VW, Sternad D, Sanger TD. Healthy and dystonic children compensate for changes in motor variability. J Neurophysiol 109: 2169–2178, 2013. doi: 10.1152/jn.00908.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen RG, Sternad D. Variability in motor learning: relocating, channeling and reducing noise. Exp Brain Res 193: 69–83, 2009. doi: 10.1007/s00221-008-1596-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen RG, Sternad D. State space analysis of timing: exploiting task redundancy to reduce sensitivity to timing. J Neurophysiol 107: 618–627, 2012. doi: 10.1152/jn.00568.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crozier D, Zhang Z, Park SW, Sternad D. Gender differences in throwing revisited: sensorimotor coordination in a virtual ball aiming task. Front Hum Neurosci 13: 231, 2019. doi: 10.3389/fnhum.2019.00231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cusumano JP, Cesari P. Body-goal variability mapping in an aiming task. Biol Cybern 94: 367–379, 2006. doi: 10.1007/s00422-006-0052-1. [DOI] [PubMed] [Google Scholar]
- de Mello Monteiro CB, Massetti T, da Silva TD, van der Kamp J, de Abreu LC, Leone C, Savelsbergh GJ. Transfer of motor learning from virtual to natural environments in individuals with cerebral palsy. Res Dev Disabil 35: 2430–2437, 2014. doi: 10.1016/j.ridd.2014.06.006. [DOI] [PubMed] [Google Scholar]
- Di Fabio RP, Badke MB. Stance duration under sensory conflict conditions in patients with hemiplegia. Arch Phys Med Rehabil 72: 292–295, 1991. [PubMed] [Google Scholar]
- Diedrichsen J, Hashambhoy Y, Rane T, Shadmehr R. Neural correlates of reach errors. J Neurosci 25: 9919–9931, 2005. doi: 10.1523/JNEUROSCI.1874-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingwell JB, Cusumano JP, Cavanagh PR, Sternad D. Local dynamic stability versus kinematic variability of continuous overground and treadmill walking. J Biomech Eng 123: 27–32, 2001. doi: 10.1115/1.1336798. [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, Massey JT. On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J Neurosci 2: 1527–1537, 1982. doi: 10.1523/JNEUROSCI.02-11-01527.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman JS, Wood RE, Hendrickx M. Feedback specificity, exploration, and learning. J Appl Psychol 89: 248–262, 2004. doi: 10.1037/0021-9010.89.2.248. [DOI] [PubMed] [Google Scholar]
- Hasson CJ, Zhang Z, Abe MO, Sternad D. Neuromotor noise is malleable by amplifying perceived errors. PLOS Comput Biol 12: e1005044, 2016. doi: 10.1371/journal.pcbi.1005044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haywood K, Getchell N. Life Span Motor Development. Champaign, IL: Human Kinetics, 2019. [Google Scholar]
- He K, Liang Y, Abdollahi F, Fisher Bittmann M, Kording K, Wei K. The statistical determinants of the speed of motor learning. PLoS Comput Biol 12: e1005023, 2016. doi: 10.1371/journal.pcbi.1005023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson A, Korner-Bitensky N, Levin M. Virtual reality in stroke rehabilitation: a systematic review of its effectiveness for upper limb motor recovery. Top Stroke Rehabil 14: 52–61, 2007. doi: 10.1310/tsr1402-52. [DOI] [PubMed] [Google Scholar]
- Holden M, Todorov E. Use of virtual environments in motor learning and rehabilitation. In: Handbook of Virtual Environments: Design, Implementation, and Applications, edited by Stanney KM. Mahwah, NJ: Erlbaum, 2002, p. 999–1026. [Google Scholar]
- Hore J, Watts S. Skilled throwers use physics to time ball release to the nearest millisecond. J Neurophysiol 106: 2024–2033, 2011. doi: 10.1152/jn.00059.2011. [DOI] [PubMed] [Google Scholar]
- Hore J, Watts S, Tweed D. Prediction and compensation by an internal model for back forces during finger opening in an overarm throw. J Neurophysiol 82: 1187–1197, 1999. doi: 10.1152/jn.1999.82.3.1187. [DOI] [PubMed] [Google Scholar]
- Huber ME, Kuznetsov N, Sternad D. Persistence of reduced neuromotor noise in long-term motor skill learning. J Neurophysiol 116: 2922–2935, 2016. doi: 10.1152/jn.00263.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivaldi S, Lyubova N, Droniou A, Padois V, Filliat D, Oudeyer P, Sigaud O. Object learning through active exploration. IEEE Trans Auton Ment Dev 6: 56–72, 2014. doi: 10.1109/TAMD.2013.2280614. [DOI] [Google Scholar]
- Karniel A, Mussa-Ivaldi FA. Sequence, time, or state representation: how does the motor control system adapt to variable environments? Biol Cybern 89: 10–21, 2003. doi: 10.1007/s00422-003-0397-7. [DOI] [PubMed] [Google Scholar]
- Kirk R. Experimental Design. New York: John Wiley & Sons, 1982. [Google Scholar]
- Krakauer JW, Ghilardi MF, Ghez C. Independent learning of internal models for kinematic and dynamic control of reaching. Nat Neurosci 2: 1026–1031, 1999. doi: 10.1038/14826. [DOI] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schöner G. Motor control strategies revealed in the structure of motor variability. Exerc Sport Sci Rev 30: 26–31, 2002. doi: 10.1097/00003677-200201000-00006. [DOI] [PubMed] [Google Scholar]
- Levac DE, Huber ME, Sternad D. Learning and transfer of complex motor skills in virtual reality: a perspective review. J Neuroeng Rehabil 16: 121, 2019. doi: 10.1186/s12984-019-0587-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin MF, Weiss PL, Keshner EA. Emergence of virtual reality as a tool for upper limb rehabilitation: incorporation of motor control and motor learning principles. Phys Ther 95: 415–425, 2015. doi: 10.2522/ptj.20130579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lombardo M, Deaner R. Born to throw: the ecological causes that shaped the evolution of throwing in humans. Q Rev Biol 93: 1–16, 2018. doi: 10.1086/696721. [DOI] [Google Scholar]
- Maselli A, Dhawan A, Russo M, Cesqui B, Lacquaniti F, d'Avella A. A whole-body characterization of individual strategies, gender differences, and common styles in overarm throwing. J Neurophysiol 122: 2486–2503, 2019. doi: 10.1152/jn.00011.2019. [DOI] [PubMed] [Google Scholar]
- McDonald PV, Oliver SK, Newell KM. Perceptual-motor exploration as a function of biomechanical and task constraints. Acta Psychol (Amst) 88: 127–165, 1995. doi: 10.1016/0001-6918(93)E0056-8. [DOI] [PubMed] [Google Scholar]
- Müller H, Sternad D. Decomposition of variability in the execution of goal-oriented tasks: three components of skill improvement. J Exp Psychol Hum Percept Perform 30: 212–233, 2004. doi: 10.1037/0096-1523.30.1.212. [DOI] [PubMed] [Google Scholar]
- Müller H, Sternad D. Motor learning: changes in the structure of variability in a redundant task. In: Progress in Motor Control, edited by Sternad D. New York: Springer, 2009, p. 439–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasu D, Matsuo T, Kadota K. Two types of motor strategy for accurate dart throwing. PLoS One 9: e88536, 2014. doi: 10.1371/journal.pone.0088536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ochoa J, Sternad D, Hogan N. Treadmill vs. overground walking: different response to physical interaction. J Neurophysiol 118: 2089–2102, 2017. doi: 10.1152/jn.00176.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SW, Dijkstra TM, Sternad D. Learning to never forget: time scales and specificity of long-term memory of a motor skill. Front Comput Neurosci 7: 111, 2013. doi: 10.3389/fncom.2013.00111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SW, Sternad D. Robust retention of individual sensorimotor skill after self-guided practice. J Neurophysiol 113: 2635–2645, 2015. doi: 10.1152/jn.00884.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner M, Snyder C, Solso R. Attention and cognitive control. In: Cognitive Psychology: Key Readings, edited by Balota DA, Marsh EJ. New York: Psychology Press, 2004, p. 205–223. [Google Scholar]
- Quadrado VH, Silva TDD, Favero FM, Tonks J, Massetti T, Monteiro CBM. Motor learning from virtual reality to natural environments in individuals with Duchenne muscular dystrophy. Disabil Rehabil Assist Technol 14: 12–20, 2019. doi: 10.1080/17483107.2017.1389998. [DOI] [PubMed] [Google Scholar]
- Russell S, Norvig P. Artificial Intelligence. New York: Prentice Hall, 2002. [Google Scholar]
- Saposnik G, Levin M; Outcome Research Canada (SORCan) Working Group . Virtual reality in stroke rehabilitation: a meta-analysis and implications for clinicians. Stroke 42: 1380–1386, 2011. doi: 10.1161/STROKEAHA.110.605451. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci 33: 89–108, 2010. doi: 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- Sharp I, Huang F, Patton J. Visual error augmentation enhances learning in three dimensions. J Neuroeng Rehabil 8: 52, 2011. doi: 10.1186/1743-0003-8-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh P, Jana S, Ghosal A, Murthy A. Exploration of joint redundancy but not task space variability facilitates supervised motor learning. Proc Natl Acad Sci USA 113: 14414–14419, 2016. doi: 10.1073/pnas.1613383113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smeets JB, Frens MA, Brenner E. Throwing darts: timing is not the limiting factor. Exp Brain Res 144: 268–274, 2002. doi: 10.1007/s00221-002-1072-2. [DOI] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: e179, 2006. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternad D. It’s not (only) the mean that matters: variability, noise and exploration in skill acquisition. Curr Opin Behav Sci 20: 183–195, 2018. doi: 10.1016/j.cobeha.2018.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sternad D, Park SW, Müller H, Hogan N. Coordinate dependence of variability analysis. PLoS Comput Biol 6: e1000751, 2010. doi: 10.1371/journal.pcbi.1000751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Timmann D, Watts S, Hore J. Failure of cerebellar patients to time finger opening precisely causes ball high-low inaccuracy in overarm throws. J Neurophysiol 82: 103–114, 1999. doi: 10.1152/jn.1999.82.1.103. [DOI] [PubMed] [Google Scholar]
- Van Stan JH, Park SW, Jarvis M, Mehta DD, Hillman RE, Sternad D. Measuring vocal motor skill with a virtual voice-controlled slingshot. J Acoust Soc Am 142: 1199–1212, 2017. doi: 10.1121/1.5000233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkadesan M, Mahadevan L. Optimal strategies for throwing accurately. R Soc Open Sci 4: 170136, 2017. doi: 10.1098/rsos.170136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Sainburg RL. The dominant and nondominant arms are specialized for stabilizing different features of task performance. Exp Brain Res 178: 565–570, 2007. doi: 10.1007/s00221-007-0936-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Y, Patton J, Bajaj P, Scheidt R. A real-time haptic/graphic demonstration of how error augmentation can enhance learning. IEEE International Conference on Robotics and Automation (ICRA). Barcelona, Spain, April 18–22, 2005. [Google Scholar]
- Wenderoth N, Bock O. Learning of a new bimanual coordination pattern is governed by three distinct processes. Mot Contr 5: 23–35, 2001. doi: 10.1123/mcj.5.1.23. [DOI] [PubMed] [Google Scholar]
- Wilson AD, Weightman A, Bingham GP, Zhu Q. Using task dynamics to quantify the affordances of throwing for long distance and accuracy. J Exp Psychol Hum Percept Perform 42: 965–981, 2016. doi: 10.1037/xhp0000199. [DOI] [PubMed] [Google Scholar]
- Wilson RC, Geana A, White JM, Ludvig EA, Cohen JD. Humans use directed and random exploration to solve the explore-exploit dilemma. J Exp Psychol Gen 143: 2074–2081, 2014. doi: 10.1037/a0038199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu HG, Miyamoto YR, Gonzalez Castro LN, Ölveczky BP, Smith MA. Temporal structure of motor variability is dynamically regulated and predicts motor learning ability. Nat Neurosci 17: 312–321, 2014. doi: 10.1038/nn.3616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Multifinger prehension: an overview. J Mot Behav 40: 446–476, 2008. doi: 10.3200/JMBR.40.5.446-476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Guo D, Huber ME, Park SW, Sternad D. Exploiting the geometry of the solution space to reduce sensitivity to neuromotor noise. PLoS Comput Biol 14: e1006013, 2018. doi: 10.1371/journal.pcbi.1006013. [DOI] [PMC free article] [PubMed] [Google Scholar]