The effect of visual uncertainty on implicit motor adaptation

Abstract

Sensorimotor adaptation is influenced by both the size and variance of error information. In the present study, we varied visual uncertainty and error size in a factorial manner and evaluated their joint effect on adaptation, using a feedback method that avoids inherent limitations with standard visuomotor tasks. Uncertainty attenuated adaptation, but only when the error was small. This striking interaction highlights a novel constraint for models of sensorimotor adaptation. Sensorimotor adaptation is driven by sensory prediction errors, the difference between the predicted and actual feedback. When the position of the feedback is made uncertain, motor adaptation is attenuated. This effect, in the context of optimal sensory integration models, has been attributed to the motor system discounting noisy feedback and thus reducing the learning rate. In its simplest form, optimal integration predicts that uncertainty would result in reduced learning for all error sizes. However, these predictions remain untested since manipulations of error size in standard visuomotor tasks introduce confounds in the degree to which performance is influenced by other learning processes such as strategy use. Here, we used a novel visuomotor task that isolates the contribution of implicit adaptation, independent of error size. In two experiments, we varied feedback uncertainty and error size in a factorial manner. At odds with the basic predictions derived from the optimal integration theory, the results show that uncertainty attenuated learning only when the error size was small but had no effect when the error size was large. We discuss possible mechanisms that may account for this interaction, considering how uncertainty may interact with the relevance assigned to the error signal or how the output of the adaptation system in terms of recalibrating the sensorimotor map may be modified by uncertainty.

NEW & NOTEWORTHY Sensorimotor adaptation is influenced by both the size and variance of error information. In the present study, we varied visual uncertainty and error size in a factorial manner and evaluated their joint effect on adaptation, using a feedback method that avoids inherent limitations with standard visuomotor tasks. Uncertainty attenuated adaptation but only when the error was small. This striking interaction highlights a novel constraint for models of sensorimotor adaptation.

INTRODUCTION

Multiple learning processes contribute to successful goal-directed actions in response to changes in physiological states and environments (1–7). Among these processes, implicit motor adaptation is of primary importance, helping ensure that the sensorimotor system remains well calibrated. This adaptive process is assumed to be driven by sensory prediction error (SPE), the difference between the predicted feedback from a motor command and the actual sensory feedback (8, 9).

The behavioral change in response to a SPE, or rate of implicit adaptation, is constrained by various properties of the feedback signal. One constraint is related to the temporal properties of the feedback. For example, the rate of adaptation is strongest when feedback is provided throughout the entire movement (7, 10–12). In contrast, the rate is attenuated when the feedback is limited to the end point of the movement and further attenuated when it is delayed (13–17).

A second constraint is related to spatial properties of the feedback. One example here is related to the size of the error signal and how this may impact the inferred relevance by our nervous system (18–21), with greater weight given to errors that are deemed to be behaviorally relevant. Numerous studies have observed reduced learning rates in response to large errors (21–23), with this effect interpreted as the motor system attributing these errors to irrelevant extrinsic sources, thereby discounting these low probability events. For example, it may not be advantageous for the motor system to recalibrate for a missed basketball shot because of a sudden large gust of wind. Whereas variation in error size changes the mean of the feedback signal, other manipulations change the standard deviation or uncertainty of the feedback. For example, the visual feedback can be signaled by either a cursor (small standard deviation, low spatial uncertainty) or a cloud of dots (large standard deviation, high spatial uncertainty), with increases in spatial uncertainty accompanied by decreases in adaptation rate (24–28).

A parsimonious account of these effects builds on the theoretical framework of optimal integration (29). In the context of sensorimotor adaptation, the learning rate is based on a weighted signal composed of the feedback and the feedforward prediction. Uncertainty, either from temporal delay or spatial variability reduces the weight given to the feedback signal and, as such, reduces the rate of adaptation (24, 28, 30). Moreover, variation in error size may also be interpreted as a source of uncertainty in terms of error relevance. Thus a small error, deemed to be highly relevant to the motor system, is given more weight during learning, whereas a large error, with questionable relevance, is discounted.

To date, tests of optimal integration have relied on standard visuomotor tasks in which the perturbation involves introducing a mismatch between visual feedback and the position of the hand (e.g., cursor rotated by 45° from true hand position). These tasks have been shown to conflate different learning processes and, in particular, implicit sensorimotor adaptation and explicit (strategic) aiming (2, 7, 31, 32). Since these processes work in tandem, modifying the sensorimotor map in a similar direction, it is difficult to evaluate how uncertainty impacts implicit adaptation per se. Moreover, when the visual feedback is contingent on the participant’s performance, the size of the error and task outcome tend to be confounded with the learning phase: Large errors are frequent early in learning and small errors are frequent late in learning.

To bypass these concerns, we revisited the effect of visual uncertainty on sensorimotor adaptation by using noncontingent, clamped visual feedback (33). As with standard visuomotor rotation tasks, participants reach to a visual target, with the position of the hand occluded. Visual feedback of hand position is usually provided in the form of a cursor. The radial position of the cursor is locked to that of the hand, similar to standard adaptation tasks. The key feature, though, is that with clamped feedback, the angular position of the cursor is invariant with respect to the target. Despite being fully informed of the manipulation and instructed to always reach directly to the target, the participant’s behavior exhibits all of the hallmarks of implicit adaptation, with the heading angle gradually shifting in the direction opposite to the clamped feedback (33–38). Presumably, this change is driven in an obligatory manner (39) because the implicit adaptation system interprets the discrepancy between the target and feedback cursor as a SPE.

In the present experiments, we manipulate both the size (mean) and uncertainty (variance) of the “clamped” visual feedback in a factorial manner. By using the clamp method, we can hone in on the effect of uncertainty on implicit adaptation, eliminating possible contributions from other learning processes. In this way, we test a core prediction of the basic optimal integration model, namely that the effect of increasing uncertainty should be independent of the size of the error. However, previous studies that have used methods to isolate implicit adaptation have revealed a surprising rigidity to this process: Adaptation is largely invariant over a wide range of errors (33, 35), perturbation schedules (40), and task goals (39). This leaves open the possibility that, when adaptation is isolated, visual uncertainty may have a negligible effect on learning. Moreover, the clamp method provides a unique opportunity to assess the impact of uncertainty for a fixed visual perturbation, where the error size is held constant over the course of learning.

METHODS

Participants

A total of 120 participants (52 females, mean age = 20.3 ± 2.1 yr) were recruited for two experiments. The sample sizes were based on previous studies using noncontingent visual feedback to study sensorimotor adaptation (33, 35, 36). All participants were right-handed, as verified with the Edinburgh Handedness Inventory (41), provided written informed consent to the study and received course credit or financial compensation for their participation. The experimental protocol was approved by the Institutional Review Board at the University of California, Berkeley.

Reaching Task

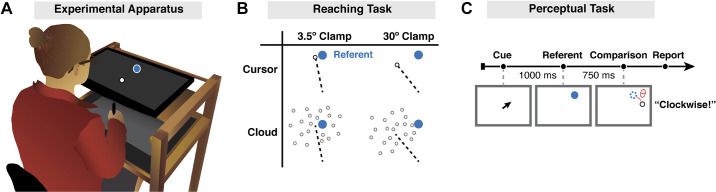
The participant was seated at a custom-made table that housed a horizontally mounted LCD screen (53.2 cm by 30 cm, ASUS), positioned 27 cm above a digitizing tablet (49.3 cm by 32.7 cm, Intuos 4XL; Wacom, Vancouver, WA) (Fig. 1A). Stimuli were projected onto the LCD screen. The experimental software was custom written in Matlab, using the Psychtoolbox extensions (42).

Figure 1.

Experiment methods. A: experimental apparatus and setup. B: schematic overview of the 2 × 2 design in experiment 1. The target (blue dot) was blanked from the screen before participants initiated their reach. Feedback was only presented at the endpoint, in the form of a cursor (white dot) or cloud of dots. The dotted line is included to graphically highlight the two clamp angles (not drawn to scale), pointing from the start position to the centroid of the feedback. C: trial sequence for the visual discrimination task. The centroid of the comparison stimulus (cursor or cloud) was positioned clockwise or counterclockwise relative to the target location at an angle (θ) equal to 1 of 5 rotation angles (see text). In the example shown, the comparison stimulus is a cursor (white circle) shifted 5° clockwise from the referent stimulus (position depicted in blue outline but not visible on the screen). The participants reported whether they perceived the centroid to be clockwise or counterclockwise relative to the remembered target location.

The participant performed center-out planar reaching movements by sliding a modified air hockey “paddle” containing an embedded stylus. The tablet recorded the position of the stylus at 200 Hz. The monitor occluded direct vision of the hand, and the room lights were extinguished to minimize peripheral vision of the arm. The participant was asked to move from a start location at the center of the workspace (indicated by a white annulus, 0.6-cm diameter) to a visual target (blue circle, 0.6-cm diameter). The target could appear at one of four locations around a virtual circle (45°, 135°, 225°, and 335°), with a radial distance of 8 cm from the start location.

At the beginning of each trial, the white annulus was present on the screen, indicating the start location. The participant was instructed to move the stylus to the start location. Feedback of hand position was indicated by a solid white cursor (diameter 0.3 cm), only visible when the hand was within 2 cm of the start location. Once the start location was maintained for 500 ms, the white cursor corresponding to the participant’s hand position was turned off. The blue target appeared for only 250 ms and then blanked before the onset of movement. The participant was instructed to rapidly slide the stylus, attempting to “slice” through the position at which the target had appeared. We opted to blank the target before movement to prevent the target from providing a visual reference point for comparison with the end point feedback (see below; also Ref. 24). To ensure rapid movements, the auditory message, “too slow” was played if the movement time exceeded 300 ms. No intertrial interval was imposed.

Experimental Feedback Conditions

Visual feedback was limited to end point feedback and remained visible for 500 ms. The feedback was presented when the movement amplitude exceeded 8 cm. The radial position of the feedback was always at the distance of the target (8 cm). The angular position of the feedback was either veridical (hand position at 8-cm amplitude) or displaced from the target by a prespecified angle (clamped perturbation). The form of the feedback was either a single white cursor (low uncertainty) or a cloud of dots (high uncertainty) (Fig. 1B). For the latter, the feedback signal was composed of a cloud of dots (25 gray 0.3-cm diameter circles) with the position of each dot pseudorandomly drawn from a two-dimensional isotropic Gaussian distribution with a standard deviation of 10° and with a minimal distance of 0.3 cm between dots (i.e., dots do not overlap). The center of mass of the cloud was controlled to be at the desired clamp angle on perturbation trials. The luminance of the 25 dots was adjusted such that their sum was equal to the luminance of the cursor. In addition to trials with veridical and clamped feedback, there were also trials with no feedback.

Experiment 1

Experiment 1 (4 groups, n = 24/group) was designed to examine the impact of visual uncertainty on sensorimotor adaptation when the error signal remained invariant for the duration of the experiment. A 2 × 2 factorial design was employed, with one factor based on error size (3.5° or 30° clamped displacement of feedback relative to target) and the other based on certainty (cursor or cloud) (Fig. 1B). Participants were randomly assigned to one of the four conditions, and within each group, the direction of the rotation (clockwise or counterclockwise relative to the target) was counterbalanced. By using a fixed perturbation for each participant for the duration of the experiment, we could observe the learning function to near asymptotic performance.

The experiment consisted of 700 trials, divided into 5 blocks: no feedback baseline (20 trials), veridical feedback baseline (60 trials), clamped feedback perturbation (600 trials), no feedback postperturbation (12 trials), and veridical feedback postperturbation (8 trials). The initial baseline trials were included to familiarize the participants with the apparatus and provide veridical feedback to minimize idiosyncratic directional biases. Before the error clamp block, participants were informed about the nature of the perturbation, with the instructions emphasizing that the position of the feedback was independent of their hand movement. There were also three trials to demonstrate the invariant nature of the feedback. For each of these three trials, the target appeared at the 90° location (straight ahead), and on successive trials, the experimenter instructed the participant to “Reach straight to the left” (180°), “Reach straight to the right” (0°), and “Reach backward towards your torso” (270°). The visual feedback appeared at 90° with respect to the target for all three trials. This was followed by the 600-trial error clamp block. The final two blocks were no feedback (no visual feedback present) and veridical feedback washout blocks, where the participant was instructed to reach directly to the target.

Experiment 1 Reaching Data Analysis

The primary dependent variable was end point hand angle, defined as the angle of the hand relative to the target when movement amplitude reached 8 cm from the start position (i.e., angle defined by two lines, one from the start position to the target and the other from the start position to the hand). A hand angle of 0° corresponds to a reach directly to the target. Analyses were also performed using heading angle at peak radial velocity, which is ∼1 cm into the reach. These analyses yielded essentially the same results; as such, we only report the results from the end point hand angle analyses. To aid visualization, the hand angle values for the groups with counterclockwise rotations were flipped, such that a positive heading angle corresponds to an angle in the direction of expected adaptation (the opposite direction of the rotated, clamped feedback).

Trials in which the observed hand angles deviated by >3.5 SD from a moving mean based on a five-trial window were excluded from further analysis (<1% of all trials and between 0 and 2.3% of trials removed for each participant). These outlier trials were assumed to reflect attentional lapses or trials in which the participant attempted to anticipate the target location.

Movement cycles consisted of four consecutive reaches (1 reach per 4 target locations). The mean heading angle for each cycle was calculated and baseline subtracted to assess adaptation relative to (small) idiosyncratic biases. Baseline was defined as the last five cycles of the veridical feedback baseline block (cycles 16–20).

We used three primary measures of adaptation: early adaptation rate, late adaptation, and aftereffect. Following Kim et al. (35), early adaptation rate was operationalized as the average change in hand angle per cycle, with the analysis conducted over cycles three to seven of the perturbation block. (Given the somewhat arbitrary range selection, we also calculated the same dependent variable using the first 10 cycles of the perturbation block and observed the same pattern of results.) Late adaptation was operationalized as the average mean hand angle over the last 10 cycles of the perturbation block (cycles 161–170) (33, 35). The aftereffect was operationalized as the average mean hand angle over the first cycle of the no-feedback washout block. Note that we opted to use these behavioral measures rather than obtain parameter estimates from exponential fits since the latter approach gives considerable weight to the asymptotic phase of performance and is less sensitive to early differences in rate.

We used the Shapiro-Wilk test and Levene’s test to assess normality and homogeneity of variance, respectively, in the distribution of these dependent variables. These tests revealed a number of violations. As such, we opted to employ a more conservative nonparametric permutation test in all of the comparisons reported below (43–45). For these tests, we used 1,000 permutations and calculated the permutation P value using the aovperm and perm.t.test functions in the R statistical package (46).

For each condition, we first assessed if the perturbed feedback produced adaptation, using a paired permutation test to compare the aftereffect measure to baseline performance (average hand angle of last 5 cycles of veridical feedback). To examine the effect of visual uncertainty on motor adaptation, and how this effect varied with error size, the rate of early adaptation, the magnitude of late adaptation, and the magnitude of aftereffect were evaluated separately with a two-way permutation ANOVA. Post hoc unpaired permutation tests were used in all post-hoc comparisons, with the P values Bonferroni corrected (P_perm,bf) to assess group differences.

We also conducted two additional tests to compare performance during different phases of the experiment. First, we evaluated whether implicit adaptation was maintained from late adaptation to the aftereffect block, performing a two-way permutation ANOVA. Second, we evaluated whether visual uncertainty had a similar effect for early and late phases of adaptation using a permutation linear mixed effect model, with fixed factors (learning phase, clamp size, and feedback type) and a random factor (Participant ID).

Visual Discrimination Task

To quantify the effect of our uncertainty manipulation, a subset of the participants in experiment 1 (n = 64) were tested on a perceptual task, comparing position acuity for displays containing a single dot or a cloud of dots (Fig. 1C). For these participants, the visual discrimination task was performed before the reaching task.

We used a two-alternative, forced choice visual discrimination task. Each trial began with the presentation of an arrow at the center of the screen that pointed towards one of two possible target locations (45° or 135°) for 1,000 ms. Once the arrow disappeared, a blue dot (0.6-mm diameter) was immediately presented at the cued location. This defined the reference position. The referent remained visible for 250 ms, followed by a blank screen for 750 ms. The comparison stimulus was then presented for 500 ms. Using a within-subject design, there were 20 comparison values: 10 displacement sizes (± 0.3°, 0.8°, 1.5°, 2.5°, or 5°) × 2 forms (cursor or cloud, using the same specifications for each as in the reaching phase of the study). Following the offset of the comparison stimulus, the participant vocally indicated if the center of the comparison stimulus was shifted clockwise or counterclockwise relative to the target location. The experimenter entered the participant’s choice with a key press, concluding the trial. A right arrow response was used for clockwise choices and left arrow for counterclockwise choices.

To maintain a similar task context between the visual discrimination task and the reaching task, participants were not asked to maintain fixation. However, we recognize that the attentional demands in the two tasks were quite different. In this visual discrimination task, participants attended to the comparison stimulus to provide an accurate directional judgement relative to the referent, whereas in the reaching task, participants ignored the visual feedback (per the task instructions).

Visual Discrimination Data Analysis

To examine how visual uncertainty influences perception, we fitted psychometric functions to the participants’ verbal reports from the location discrimination task in experiment 1. The psychometric function was defined as the probability of reporting “counterclockwise” for each displacement size, x. We fit the judgment data with a cumulative density function of a normal distribution expressed as φ(x):

$$\phi \left(x\right)=\frac{1}{{\sigma }_v\sqrt{2\pi }}\underset{-\infty }{\overset{x}{{\displaystyle \int }}}ex{p}^{\frac{-{\left(x^{\prime }-\mu \right)}^2}{2{\sigma }_v^2}}d{x}^{\prime }$$ (1)

From this function, we obtained the point of subjective equality, μ, the mean of the underlying Gaussian distribution, as an estimate of the participant’s bias. As a measure of visual uncertainty, we used the difference threshold σ_v, the standard deviation of the underlying Gaussian distribution. A larger difference threshold is indicative of more variance (and uncertainty) in the perceptual judgments. Pairwise permutation t tests were performed on these two variables to assess within-participant differences in directional bias and visual uncertainty for the cursor and cloud conditions.

Experiment 2

In experiment 2, the size and direction of the clamped perturbation were varied from trial to trial, allowing us to examine the effect of uncertainty across a wider range of error sizes. A within-subject design was employed (n = 24), with each participant tested in two sessions. In one session, the feedback consisted of a cursor (i.e., a single dot), and in the other, the feedback was composed of the cloud of dots. The order of the two types of feedback was counterbalanced across participants, with a gap of 1–3 days between sessions. Testing was spread over two sessions to allow us to collection sufficient observations for each error size. Each participant was assigned to reach to a single target, chosen from one of three possible locations (45°, 135°, and 225°). The same target location was used for both sessions.

There were four blocks in each session for a total of 1,465 trials per session: No feedback baseline (10 trials), veridical feedback baseline (20 trials), clamped feedback perturbation (1,425 trials), and no-feedback postperturbation (10 trials). During the perturbation block, there were 19 possible positions for the center of the feedback: 0°, ±1.5°, ±3.5°, ±10°, ±18°, ±30°, ±45°, ±60°, ±75°, and ±90°, with the ± indicating that the perturbation could either be clockwise or counterclockwise from the target. There were 75 trials for each condition, with the size of the perturbation selected at random for each trial.

All other aspects of the experiment were the same as in experiment 1. Participants were informed of the nature of the clamped feedback before the perturbation block. The instructions (together with demonstration trials) emphasized that the feedback position was not contingent on their movement. They were told that the position of the feedback would be randomly determined and that they should ignore it.

Experiment 2 Reaching Data Analysis

Hand angles were measured as in experiment 1, with each value baseline corrected (subtraction of mean hand angle during last 5 trials of the feedback baseline block). The primary analysis focused on trial-to-trial changes (Δ) in hand angle (difference in hand angle between trial n + 1 and trial n), looking at these values as a function of the clamp size and feedback type on trial n. Since each participant performed both clockwise and counterclockwise error clamps, we collapsed the data over direction for a given perturbation size, providing a more stable estimate of the Δ hand angle for each condition based on 150 trials/perturbation size, except for the 0° condition which had only 75 trials. Trials in which the change in hand angle deviated by >3.5 SD were excluded from further analyses (<1% of all trials and between 0 and 0.8% of trials removed for each participant).

To evaluate the interaction between error size and visual uncertainty on adaptation, the Δ hand angle values were submitted to a mixed effect model: error size and visual uncertainty were the within-subject fixed factors, and participant was the random factor (Satterthwaite’s degree of freedom reported). Data from the 0° clamp condition were excluded since no a priori differences were expected between the cursor and cloud for this condition [confirmed using a permutation test: t(23) = –0.25, P_perm = 0.56, d = 0.05]. As a finer grain post hoc analysis, each of the 10 rotation sizes were submitted to 10 planned permutation tests, comparing trial-by-trial adaptation between the cursor and cloud conditions. Since the main goal of this study is to identify error sizes where visual uncertainty has an effect on adaptation, applying a Bonferroni family-wise error correction on 10 planned comparisons would lead to a loss in power. We therefore corrected for multiple comparison using the less stringent Benjamini-Hochberg Procedure (P_perm,BH) with a false discovery rate of 0.05 (R package: FSA).

Measures of Effect Size

Cohen’s d (for between-subjects design), Cohen’s d_z (for within-subjects design), and eta squared (for between-subjects ANOVA) were provided as standardized measures of effect size (47). To evaluate key null effects, we calculated the Bayes factor ($B{F}_{0^{+}}$) for the t values, using the ratio between the likelihood of two hypotheses (i.e., the likelihood that the data support the null hypothesis over the likelihood that the data support the alternative hypothesis). As such, a Bayes factor >1 is an indication that the data favors the null, with the magnitude reflecting the effect size. As a rule of thumb, Bayes factors between 1 and 3, 3 and 10, and above 10 are considered to provide weak, moderate, and strong support for the null hypothesis, respectively (48, 49).

RESULTS

In experiment 1, we asked whether visual uncertainty affects implicit motor adaptation for both small (3.5°) and large (30°) errors. We manipulated uncertainty by presenting end point feedback in the form of a cursor (low uncertainty) or cloud of dots (high uncertainty).

Experiment 1: Perceptual Discrimination Task

To verify that perceived location is more uncertain with the cloud displays, a subset of participants performed a visual discrimination task before completing the reaching task. For this task, participants compared the relative position of stimuli in two successively presented displays. The first display showed a single dot; the second showed either a single dot or a cloud of dots. The participant judged if the position of the second dot or centroid of the cloud was shifted clockwise or counterclockwise relative to the position of the dot in the first display.

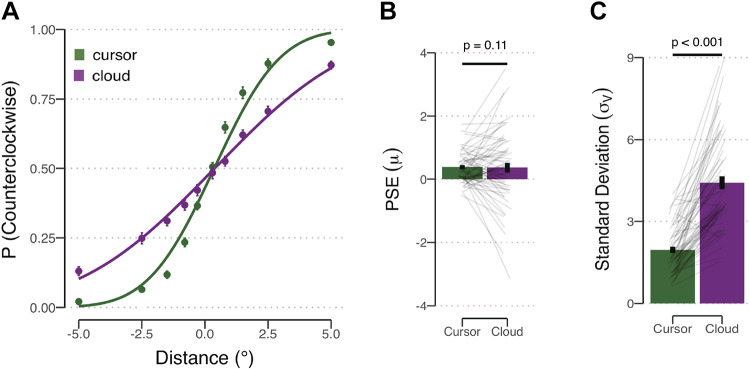
As can be seen in Fig. 2A, while participants were mostly correct in assessing the relative positions of both visual stimuli, performance was more variable in the cloud condition compared with the dot condition. To quantify these effects, we estimated the directional bias (μ) and the difference threshold (σ_v) for each individual in the dot and cloud conditions. Four individuals were excluded from this analysis because their psychometric functions in the cloud condition were too flat to allow the fitting procedure to converge (reflecting poor overall performance). As such, the results reported below underestimate the difference in location acuity between the two conditions.

Figure 2.

Visual discrimination task. A: proportion of counterclockwise reports as a function of the centroid of the comparison stimulus. Positive values on the x-axis correspond to shifts in the counterclockwise direction. Estimated psychometric functions are the thick lines based on group averaged data for the cursor (green) and cloud (purple) groups. B and C: mean bias and threshold estimates for the cursor and cloud conditions. Error bars represent SE, and thin gray lines represent individuals’ data. P values from within-subject t tests are shown. PSE, point of subjective equality.

To test whether there were systematic directional biases, we compared the mean bias estimates to 0° (Fig. 2B). In both conditions, there was a small bias to judge the comparison display as shifted in the counterclockwise direction relative to the referent display {cursor: t(58) = 5.71, P_perm < 0.001, [0.25°, 0.52°], d_z = 0.74; cloud: t(58) = 2.33, P_perm = 0.022, [0.05°, 0.68°], d_z = 0.30}. The degree of bias did not differ between conditions {t(58) = 0.13, P_perm = 0.87, [–0.27°, 0.31°], d_z = 0.02}.

To test whether the cursor and cloud yield different levels of visual uncertainty, we compared the difference threshold estimates for the two conditions (Fig. 2C). The estimate was considerably higher for the cloud group compared with the cursor group {t(58) = –11.66, P_perm < 0.001, [–2.88°, –2.03°], d_z = 1.52}. The mean difference thresholds were 1.96° and 4.41° for the cursor and cloud conditions, respectively. Thus the results confirm that participants are more variable in judging the centroid position of a cloud of dots compared with the position of a single dot, a critical assumption underlying our manipulation of visual uncertainty in the reaching experiments.

Experiment 1: Reaching Task

Participants were randomly assigned to one of four groups for the reaching task. After baseline blocks to familiarize the participants with the apparatus and basic trial structure, we presented clamped visual feedback, using either a cursor or a cloud. To assess implicit adaptation, we measured the mean hand angle over the course of the perturbation block and during a subsequent washout block in which no feedback was provided (Fig. 3A).

Figure 3.

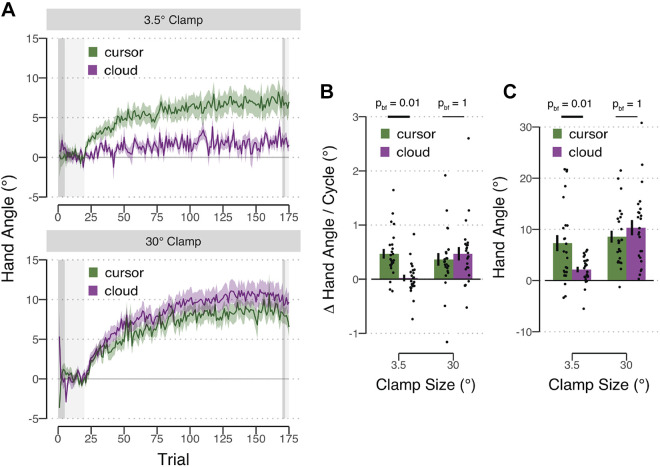
Reaching results for experiment 1. A: mean time course of hand angles for the cursor (green) and cloud (purple) groups, presented with either a 3.5° (top) and 30° (bottom) clamp during the error clamp block. Hand angle is presented relative to the target (light gray horizontal dashed line) during no feedback (dark gray background), veridical feedback (light gray background), and error clamp trials (white background). Shaded region denoting SE. B: early adaptation rate, operationalized as the average change in hand angle per cycle over cycles 3–7 in the error clamp block. C: late adaptation, operationalized as average hand angle over the last 10 cycles in the error clamp block. Bonferroni (bf) corrected P values from between-subject t tests are shown.

On clamped visual feedback trials, the participants’ hand gradually deviated in the direction opposite to the feedback, and eventually reached an asymptote. Given that the participants were fully informed about the noncontingent nature of the clamped feedback, as well as the repeated emphasis in the instructions to ignore the feedback, we assumed that the change in hand angle is implicit. This assumption is strengthened by the fact that the hand angle remained similar between the end of the adaptation trials and start of the no feedback aftereffect trials [main effect of clamp size: F(1,92) = 0.11, P_perm = 0.75, η² < 0.01; main effect of uncertainty: F(1,92) = 0.05, P_perm = 0.83, η² < 0.01; interaction: F(1,92) = 0.41, P_perm = 0.83, η² < 0.01; difference between late adaptation and aftereffect for all groups: P_perm > 0.06]; when other processes contribute to the behavioral change, there is a rapid decrease in hand angle in the initial aftereffect trials (1, 7).

To quantify how much implicit adaptation was elicited by the clamped visual feedback, we first examined the aftereffect results, asking if the mean hand angle was systematically different from 0° in the washout block. The two cursor groups and the 30° cloud group showed implicit adaptation as evidenced by a systematic aftereffect in which the hand angle was shifted in a direction opposite to that of the clamp {3.5° cursor: t(22) = 3.98, P_perm = 0.002, [3.31°, 9.80°], d_z = 0.85; 30° cursor: t(22) = 7.55, P_perm = 0.002, [5.44°,9.66°], d_z = 1.5; 30° cloud: t(22) = 8.82, P_perm < 0.001, [6.43°, 11.22°], d_z = 1.59}. In contrast, the 3.5° cloud group did not show significant adaptation {t(22) = 1.66, P_perm = 0.08, [–0.40°, 3.72°], d_z = 0.34}.

We next compared the aftereffect data for the four conditions. There was a significant effect of clamp size with the large clamp conditions producing larger adaptation [F(1,92) = 14.04, P_perm = 0.01, η² = 0.12]. The effect of feedback type was not significant [F(1,92) = 2.33, P_perm = 0.13, η² = 0.02]. Critically, there was a significant interaction of these factors [F(1,92) = 6.44, P_perm = 0.01, η² = 0.06]. Bonferroni corrected post hoc analyses revealed that visual uncertainty attenuated adaptation when the clamp size was small {3.5° groups: t(22) = 2.63, P_perm,bf = 0.02, [1.15°, 8.63°], d = 0.76; 3.5° cursor: [6.55°, 7.69°]; 3.5° cloud: [1.66°, 4.88°]} but not when the clamp size was large {30° groups: t(22) = –0.80, P_perm,bf = 1, [–4.29°, 1.86°], d = 0.23, $B{F}_{0^{+}}$ = 2.69 in favor of the null; 30° cursor: [8.01°, 4.80°]; 30° cloud: [9.23°, 5.76°]}. We note that overall adaptation in the current study, even in the cursor condition, is attenuated compared with previous studies using the clamp method. Late adaptation to the cursor is between 7° and 9°, values that are much lower than the 20–30° asymptotes observed in previous studies (33, 35). We suspect the lower values observed here reflect two methodological changes adopted in the current study, the use of end point feedback and the blanking of the target after 250 ms. Both of these factors have been shown to attenuate adaptation (6, 7, 10–12).

We then examined the learning functions, asking how visual uncertainty influenced the rate of early adaptation and the magnitude of late adaptation (Figs 3, B and C). For each dependent variable, we used a 2 × 2 between-subject ANOVA with factors clamp size (3.5° and 30°) and feedback type (cursor and cloud). For early adaptation, neither the effect of clamp size [F(1,92) = 2.93, P_perm = 0.08, η² = 0.03] nor feedback type [F(1,92) = 2.90, P_perm = 0.09, η² = 0.03] was significant. However, there was a significant interaction of these factors [F(1,92) = 7.53, P_perm = 0.005, η² = 0.07]. Bonferroni-corrected post hoc analyses revealed that visual uncertainty attenuated adaptation when the clamp size was small {3.5° groups: t(46) = 4.16, P_perm,bf = 0.01, [0.23°, 0.67°], d = 1.20; 3.5° cursor: [0.29°, 0.65°]; 3.5° cloud: [–0.11°, 0.15°]} but not when the clamp size was large {30° groups: t(46) = −0.62, P_perm,bf = 1, [–0.45°, 0.24°], d = 0.17, $B{F}_{0^{+}}$ = 2.97 in favor of the null; 30° cursor: [0.12°, 0.61°]; 30° cloud: [0.21°, 0.73°]}.

A similar pattern was observed for late adaptation: The clamp size × feedback interaction was significant [F(1,92) = 7.55, P_perm = 0.006, η² = 0.07], with the post hoc analyses again showing that visual uncertainty attenuated adaptation when the clamp size was small {3.5° groups: t(46) = 3.10, P_perm,bf = 0.002, [1.81°, 8.51°], d = 0.89} but not when the clamp size was large {30° groups: t(46) = –0.93, P_perm,bf = 1, [–5.57°, 2.04°], d = 0.27, $B{F}_{0^{+}}$ = 2.44 in favor of the null}. There was also a main effect of clamp size [F(1,92) = 14.04, P_perm = 0.008, η² = 0.12], with higher asymptotic levels reached for the large clamp (30° cursor: [6.15°, 11.00°]; 30° cloud: [7.26°, 13.41°]) compared with the small clamp (3.5° cursor: [4.05°, 10.57°]; 3.5° cloud: [1.03°, 3.27°]). The main effect of feedback type was not significant [F(1,92) = 1.83, P_perm = 0.19, η² = 0.02].

In summary, visual uncertainty had a large effect when the clamp size was small clamp but a negligible effect when the clamp size was large. Moreover, the effect of uncertainty did not seem to increase or diminish over the course of learning, evident by the persistent size by feedback type interaction observed during both early and late adaptation, and consistent with the nonsignificant interaction in the three-way ANOVA involving clamp size × feedback type × learning phase [F(1,92) = 3.23, P_perm = 0.09, η² = 0.01].

Experiment 2: Reaching Task

In the second experiment, we sampled a larger range of error sizes to take a more detailed look at how uncertainty is impacted by error size. Using a within-subject design, we manipulated visual uncertainty by again providing either cursor or cloud feedback, and now crossed that with a large range of clamp sizes (0 to ± 90°). The main dependent variable was the trial-to-trial change in hand angle (Δ hand angle). Positive values indicate a change in hand angle opposite to the direction of the error clamp (i.e., adaptation).

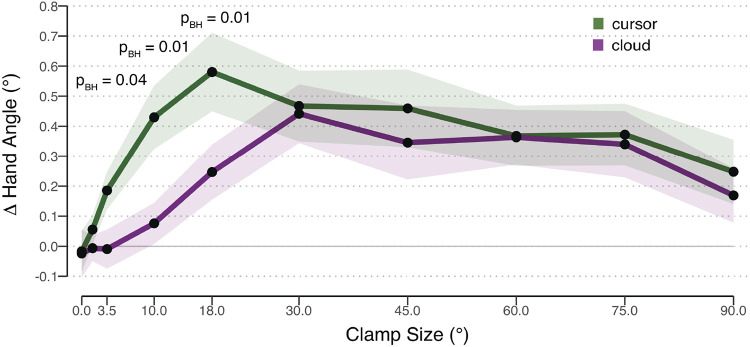
Qualitatively, the shape of each function was bipartite, consisting of a roughly linear zone (up to ∼18–30°), followed by an extended saturation zone (Fig. 4). To statistically evaluate these data, we asked if the Δ hand angle value for each condition (10 error sizes × 2 types of feedback) was significantly different than zero. For the cursor condition (green line), trial-by-trial adaptation was significant for all clamp sizes [all t(23) > 2.31, P_perm < 0.022, d > 0.47] except for the 0° [t(23) = –0.25, P_perm = 0.97, d = 0.05] and 1.5° conditions [t(23) = 1.14, P_perm = 0.23, d = 0.23]. In contrast, for the cloud condition, only clamp sizes ≥18° elicited significant implicit adaptation [all t(23) > 1.86, P_perm < 0.02, d > 0.38]. The trial-to-trial Δ hand angle was not significant when the error was 0° [t(23) = –0.30, P_perm = 0.75, d = 0.06], 1.5° [t(23) = –0.15, P_perm = 0.50, d = 0.03], 3.5° [t(23) = –0.15, P_perm = 0.78, d = 0.03], and 10° [t(23) = 1.11, P_perm = 0.36, d = 0.23].

Figure 4.

Results for experiment 2. Change (Δ) in hand angle on trial n + 1 as a function of the clamped feedback on trial n. Feedback was either given in form of a cursor (green) or cloud (purple). Data represent mean corrections across participants. Shaded region represents SE. Benjamini-Hochberg (BH)-corrected P values from significant within-subject t tests between cursor and cloud are shown.

The interaction between error size and uncertainty is evident in Fig. 4 [χ(8, 24) = 15.64, P = 0.04, η² = 0.03]: cursor and cloud functions show considerable divergence when the errors are <30°, consistent with the observation in experiment 1 that visual uncertainty attenuates adaptation for small clamp sizes. However, cursor and cloud converge when errors are larger than 30°. To statistically compare the two types of feedback, paired t tests were performed for each clamp size, correcting for multiple comparisons. The cursor elicited a stronger adaptive response than the cloud for clamp sizes of 3.5° [t(23) = 2.69, P_perm,BH = 0.04, d_z = 0.55, $B{F}_{0^{+}}$ = 0.18], 10° [t(23) = 3.77, P_perm,BH = 0.02, d_z = 0.77, $B{F}_{0^{+}}$ = 0.06], and 18° [t(23) = 3.13, P_perm,BH = 0.02, d_z = 0.64, $B{F}_{0^{+}}$ = 0.13] conditions. The mean Δ hand angle was also larger in response to the cursor in the 1.5° condition, but this effect was not significant [t(23) = 0.85, P_perm,BH = 0.50, d_z = 0.17, $B{F}_{0^{+}}$ = 2.38 in favor of the null]. There were no differences in the adaptive response to cursor or cloud feedback in response to clamp sizes greater or equal to 30° [all t(23) < 1.29, P_perm,BH > 0.37, d_z < 0.30, $B{F}_{0^{+}}$ > 1.9 in favor of the null].

In summary, the results of experiment 2 provide further evidence that visual uncertainty attenuates adaptation in response to small clamp sizes but had a negligible effect on the response to large clamp sizes.

DISCUSSION

The rate of learning in sensorimotor adaptation tasks depends on various properties of the feedback such as the size of the error, the variability of the signal, and its inferred relevance (21, 24, 28). However, the interpretation of these results is complicated by limitations in the methods used in standard adaptation tasks. First, multiple learning systems have been shown to play a substantial role in performance, making it difficult to evaluate how uncertainty impacts implicit adaptation. Second, when a constant perturbation is paired with feedback contingent on the participant’s performance, the size of the error and the phase of learning are confounded. Here, we exploited unique features of the clamp method (33) to systematically examine the effect of visual uncertainty on implicit visuomotor adaptation. Convergent results from two experiments show that uncertainty attenuated learning but only when the error size was small. These observations reveal a novel interaction between the quality and the relevance of errors that jointly constrain the rate and extent of sensorimotor adaptation.

These conclusions are predicated on the assumption that clamped feedback engages processes similar to those underlying implicit adaptation elicited in standard visuomotor tasks with contingent feedback, as well as by perturbations that arise more naturally in the environment (e.g., an uneven surface or a heavy jacket). As noted in the introduction, the clamp method mitigates certain confounds inherent in standard visuomotor adaptation tasks, while allowing the experimenter to maintain control over error size. Although this method is certainly quirky (participants told to ignore an invariant, noncontingent “feedback” signal), the task is simple, and the adaptive response is robust. While future work may be warranted to look at the interaction of visual uncertainty and error size in more naturalistic settings, we expect that the same pattern would be observed given the close correspondence in behavior elicited by clamped and contingent feedback (21, 33–35, 38). For example, with both types of feedback, the size of the response scales with the size of the perturbation over a limited range before saturating at a comparable asymptotic level (1, 21, 33, 35, 50–53). Given these similarities, we expect the attenuating effect of visual uncertainty would be restricted to small errors even in a standard adaptation task.

This effect of visual uncertainty has been interpreted through the lens of optimal integration (29). By this model (Fig. 5A), the learning rate is a weighted composition of feedback and feedforward sources (24, 28, 30), with these weights determined by the relative uncertainties in each source. For a given level of uncertainty, the optimal integration model predicts the size of the trial-to-trial correction will increase in proportion with the size of the error, with the slope corresponding to the learning rate. Less weight would be given to an unreliable feedback signal, resulting in a lower slope (Fig. 5A). While this model captures the effect of visual uncertainty for small errors, it fails to account for the negligible effect of visual uncertainty on large errors observed in the present studies.

Figure 5.

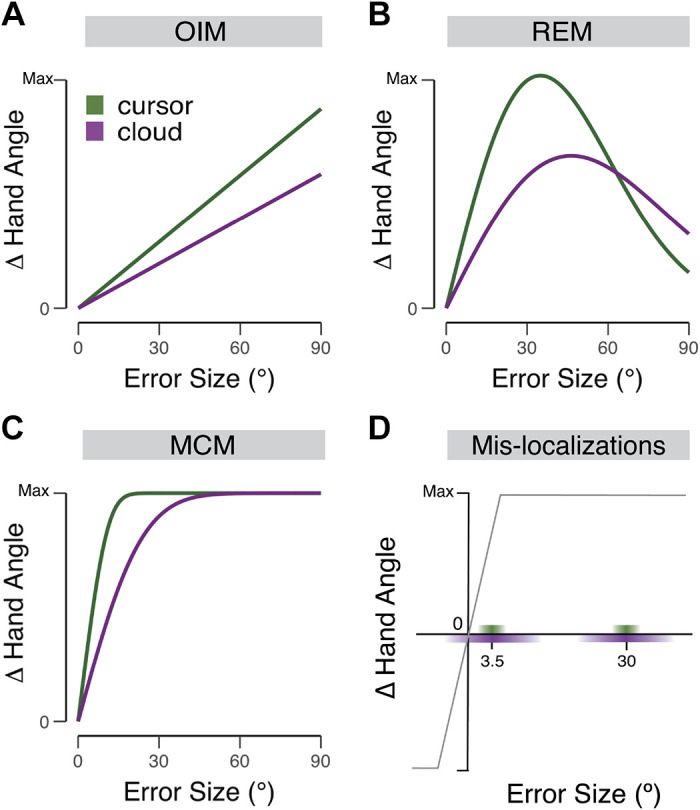
Schematic hypotheses of the effect of visual uncertainty on visuomotor adaptation. A–C: predicted trial-by-trial change in hand angle as a function of error size and visual uncertainty (cursor = certain feedback; cloud = uncertain feedback) for the optimal integration model (OIM; A), relevance estimation model (REM; B), and motor correction model (MCM; C). D: the motor correction model assumes that the update function is composed of a linear zone, where motor updates are proportional to the size of the error, and a saturation zone, estimated to start around 5°, over which the size of the motor update is invariant. The saturation level of the colored bars on the x-axis depict the distribution of perceived locations for the low uncertainty (cursor, green) and high uncertainty (cloud, purple) conditions. For a large 30° error, the perceived location of the error always falls in the saturation zone and thus adaptation is similar for the cursor and cloud conditions. For the small 3.5°, uncertainty will impact the size of the update, including sign flips when the perceived location of the error is of the opposite sign as the actual error.

Different hypotheses may account for this interaction between error size and visual uncertainty. One account builds on the relevance hypothesis (21, 54), the idea that that the motor system gives more weight to small errors relative to large errors. Relevance estimation (Fig. 5B) predicts that the rate of adaptation will fall off with increases in error size, an effect observed in experiment 2 (see Refs. 21–23). This falloff with size should occur for feedback signals that are either low (cursor) or high (cloud) in terms of uncertainty. However, the model predicts that the effect of uncertainty will diminish with size. In the extreme, the rate of learning would reach zero, and as such, by definition, the rate would no longer be impacted by uncertainty.

More interesting is to consider why the effect of uncertainty should have a differential effect on small and large errors. Relevance estimation, at least in terms of error size, captures the notion that the motor system is estimating the source of the error. Small errors, attributed to a miscalibration in the sensorimotor system, require correction, and the weight given to them will fall off with increasing uncertainty. Large errors, on the other hand, get discounted because they may be attributed to an external source. Paradoxically, an uncertain large error is likely to reduce the rate of discounting since the uncertainty is likely to also impact the likelihood that the error will be attributed to an external source. By this view, we would expect to observe a crossover point (Fig. 5B) where the response to a large (mean) error is greater to a high uncertainty signal compared with a low uncertainty signal (i.e., the cursor condition would decay faster to zero at a smaller error size compared with the cloud condition). While the functions approach each other in experiment 2, there were no obvious signs of a crossover in the group data (Fig. 4) nor was this predicted pattern evident in an analysis of individual data (Supplemental Fig. S1: see https://doi.org/10.6084/m9.figshare.13150715.v1; Supplemental Fig. S2: see https://doi.org/10.6084/m9.figshare.13150667.v1). Moreover, the functions did not approach a learning rate of zero, even for errors as large as 90°, a result that seems inconsistent with the predictions of the relevance estimation model.

Our prior work with the clamp method has motivated an alternative model of adaptation, one that is also consistent with the observed interaction between error size and uncertainty. The motor correction model emphasizes that constraints on adaptation rates arise from limitations with the degree of plasticity or change that can occur within the sensorimotor system from one trial to the next (35). As with the relevance estimation model, the motor correction model assumes a linear scaling of change for small errors. However, the system eventually reaches a saturation point, corresponding to the maximum degree of plasticity in response to an error. Beyond this saturation point, the update value remains at this maximum for errors out to 90°, eventually decaying back to no correction around 135°–180° (33, 35). A core feature of this model is that it can account for the relatively invariant implicit adaptation functions over a large range of errors, an observation at odds with optimal integration and relevance estimation models and consistent with results from standard adaptation tasks showing a common asymptotic value over a wide range of errors (1).

The architecture and operation of the motor correction model require minimal modification to account for the effect of uncertainty. One possibility would be to posit that the motor system performs a form of optimal integration, adjusting the gain on motor output based on varying levels of visual uncertainty. As such, visual uncertainty would attenuate the motor correction function but still reach the same saturation point, albeit at a larger error size (Fig. 5C). This prediction is consistent with visual uncertainty increasing the saturation point from ∼18° in the cursor condition to ∼30° in the cloud condition (Fig. 4).

Alternatively, the main effect of uncertainty in the visual feedback may be to alter the perceived location of the feedback on a given trial. That is, the motor system may make a point estimate of the location of the feedback and use this estimate to determine the required correction in the sensorimotor map, with the update function unaffected by uncertainty (Fig. 5D). Adaptation to large errors would be unaffected by uncertainty since the perceived locations would largely fall within the saturation zone and therefore elicit the maximum motor correction. In contrast, uncertainty would attenuate adaptation to small errors for two related reasons. First, the sum effect of normally distributed errors would result in attenuation given that misperceptions associated with large errors end up in the saturated zone, whereas misperceptions associated with small errors are in the linear zone. Second, with a broad distribution of perceived locations (high visual uncertainty), the feedback will on some trials be mis-localized to the opposite side of the target, eliciting a motor correction with the opposite sign.

Even though the interaction between error size and visual uncertainty rules out the simple optimal integration model, the current data do not definitively discriminate between the relevance estimation and motor correction models. The absence of a consistent crossover effect even with errors as large as 90° is at odds with the prediction unique to the relevance estimation model. However, this effect may be difficult to detect in group-level data that pool together individuals with different crossover points, and the individual functions may be too noisy to reliably estimate crossover points, should they exist. As such, we believe both the relevance estimation and motor correction models remain viable candidates that account for the effect of visual uncertainty on adaptation.

It is, of course, possible that the core ideas from both of these models will be a part of a more comprehensive model. The models differ in the processing stage at which uncertainty impacts adaptation. For relevance estimation, the effect is in terms of the input (i.e., error signal) to the learning process, namely a gain modulating the error signal. In contrast, for the motor correction model, the effect is in terms of the output of the system, either in terms of a gain modulating how the system updates the sensorimotor map, or as a consequence of trial-by-trial adaptation in response to (mis)localized errors.

This last point is a key distinction: optimal integration, relevance estimation, and attenuated motor corrections all assume that the adaptation system is sensitive to distributional information about the feedback, adjusting its parameters in the face of variation in uncertainty. In contrast, the mis-localization motor correction model posits that the adaptation system is inflexible, doggedly recalibrating the sensorimotor map based on its estimate of the perceived location of the feedback. Such rigidity has also been observed in accounts of how adaptation is affected (or not affected) by errors of different sizes (1, 33), perturbation schedules (40), and task demands (39). The effects of uncertainty, or lack thereof, adds to the growing list of examples where the motor system behaves in a rigid manner, insensitive to higher level statistics embedded within the environment.

GRANTS

J.S.T. was funded by a 2018 Florence P. Kendall Scholarship from the Foundation for Physical Therapy Research. This work was supported by National Science Foundation Grant 1934650 and National Institutes of Health Grants K12-HD-055931 (to H.E.K.) and NS-105839 and NS-116883 (to R.B.I.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.S.T., G.A., H.E.K., D.E.P., Z.W., and R.B.I. conceived and designed research; J.S.T. performed experiments; J.S.T. analyzed data; J.S.T., G.A., H.E.K., D.E.P., Z.W., and R.B.I. interpreted results of experiments; J.S.T. prepared figures; J.S.T. drafted manuscript; J.S.T., G.A., H.E.K., D.E.P., Z.W., and R.B.I. edited and revised manuscript; J.S.T., G.A., H.E.K., D.E.P., Z.W., and R.B.I. approved final version of manuscript.