IsoResolve: predicting splice isoform functions by integrating gene and isoform-level features with domain adaptation

Abstract

Motivation

High resolution annotation of gene functions is a central goal in functional genomics. A single gene may produce multiple isoforms with different functions through alternative splicing. Conventional approaches, however, consider a gene as a single entity without differentiating these functionally different isoforms. Towards understanding gene functions at higher resolution, recent efforts have focused on predicting the functions of isoforms. However, the performance of existing methods is far from satisfactory mainly because of the lack of isoform-level functional annotation.

Results

We present IsoResolve, a novel approach for isoform function prediction, which leverages the information from gene function prediction models with domain adaptation (DA). IsoResolve treats gene-level and isoform-level features as source and target domains, respectively. It uses DA to project the two domains into a latent variable space in such a way that the latent variables from the two domains have similar distribution, which enables the gene domain information to be leveraged for isoform function prediction. We systematically evaluated the performance of IsoResolve in predicting functions. Compared with five state-of-the-art methods, IsoResolve achieved significantly better performance. IsoResolve was further validated by case studies of genes with isoform-level functional annotation.

Availability and implementation

IsoResolve is freely available at https://github.com/genemine/IsoResolve.

Supplementary information

Supplementary data are available at Bioinformatics online.

1. Introduction

A central goal of functional genomics is to accurately annotate the function of genes and their encoded proteins (Severing et al., 2011), which is fundamental for advancing the understanding of important biological processes (Schmitz et al., 2012), such as cell differentiation (Mathys et al., 2019; Xu et al., 2019), tissue development and disease progression (Chen and Crowther, 2012; Guan et al., 2010; Liu et al., 2020a,b). Much progress has been made in predicting gene functions by mining heterogeneous functional genomics data with computational approaches. A binomial model in combination with Markov random field propagation was proposed to predict protein functions by mining protein interaction data (Letovsky and Kasif, 2003). The computational prediction of cancer gene functions was systematically discussed in a review (Hu et al., 2007). Gene functions in a hierarchical context were predicted using an ensemble of support vector machines (Guan et al., 2008). By formulating the prediction of gene function as a multilabel learning problem, a decision tree-based method was established (Schietgat et al., 2010). Very recently, a method integrating sequence and protein–protein interaction networks with a learning-to-rank framework was proposed (You et al., 2019). The semantic similarity based on compressed Gene Ontology (GO) terms was shown to be promising for gene function prediction (Zhao et al., 2019).

A major limitation of gene function prediction is that available methods treat a gene as a single entity, neglecting the fact that a single gene may produce multiple isoforms through alternative splicing (Baralle et al., 2017; Dominguez et al., 2016; Song et al., 2017; Weyn-Vanhentenryck et al., 2018) and that the functions of isoforms may be largely different and even opposing (Menon et al., 2011; Pan et al., 2008). For example, the principal isoform of CASP3 consists of seven exons. Alternative splicing generates a shorter isoform CASP3-s resulting from the deletion of Exon 6, which leads to an altered open reading frame and a peptide with altered amino acid sequences. CASP3-s is anti-apoptotic while the principal isoform is pro-apoptotic (Vegran et al., 2006). TRPM3 belongs to the transient receptor potential ion channel family. The two isoforms TRPM3α1 and TRPM3α2 of the same gene were studied and it was found that their ion selectivities were disparate (Oberwinkler et al., 2005). The permeability of TRPM3α1 for Ca²⁺ and Mg²⁺ was very poor, while TRPM3α2 could be easily permeated by these divalent cations. The pairs of isoforms for several genes including Anxa6, Calu and Ptbp1 were analyzed and it was shown that one isoform of each gene was associated with breast cancers while the other was not (Menon et al., 2011). The structural differences between the paired isoforms were further revealed by detailed 3D protein structure modeling with I-TASSER (Yang et al., 2015). By assaying and comparing the protein–protein interaction profiles of splice isoforms of a large number of genes, it was found that the majority of isoform pairs shared less than 50% of their interactions. This finding strongly supports the high functional diversity among isoforms (Yang et al., 2016). Therefore, functional annotation at the gene level has the intrinsic limitation that functional differences among isoforms are ignored.

To address this issue, several methods have been proposed to predict isoform functions. In our earlier work, multiple instance learning (MIL)-based support vector machines (mi-SVMs) was introduced to predict isoform functions for mice and humans (Eksi et al., 2013; Panwar et al., 2016). The instance-oriented multiple instance label propagation (iMILP) method was developed in the MIL framework and was used to annotate isoform functions for humans (Li et al., 2014). The MIL-based weighted logistic regression model (WLRM) was shown to be accurate in predicting the functions of human coding isoforms (Luo et al., 2017). Based on domain adaptation (DA), a deep learning approach DeepIsoFun (Shaw et al., 2019) was developed, which outperformed the previous methods including mi-SVM, iMILP and WLRM. DA is capable of transferring knowledge of function prediction models in the gene domain (also called the source domain in general) to the prediction of isoform functions (the isoform domain, also called the target domain) (Shaw et al., 2019). IsoFun (Yu et al., 2020a,b) and DisoFun (Wang et al., 2020a,b) were proposed based on random walks and matrix factorization (Yu et al., 2020a,b), respectively. A novel isoform function prediction method DIFFUSE was established by combining deep learning and conditional random field techniques (Chen et al., 2019). Although significant progress has been made in isoform function prediction, the performance of current methods is still limited. Therefore, computational methods that can predict isoform functions with improved accuracy are still needed.

In this article, we present IsoResolve, a DA-based approach to predict isoform functions. IsoResolve takes both gene-level and isoform-level features, and annotated gene functions as input. Because gene-level features and isoform-level features have different distributions (Hibbs et al., 2007; Trapnell et al., 2012), IsoResolve treats them as two different domains. It then uses DA (Nikzad-Langerodi et al., 2018) to project the two domains into a latent variable (LV) space in such a way that the projections of gene and isoform features in the LV space are of similar distribution. This ensures that the information in gene function prediction models can be leveraged to build isoform function prediction models. Both DeepIsoFun and IsoResolve are based on DA. DeepIsoFun uses a neural network autoencoder to generate feature embedding of original gene and isoform features (Shaw et al., 2019), whereas our method uses a partial least squares (PLS)-based DA approach to project features in the two domains.

We apply IsoResolve to three datasets with both gene- and isoform-level features. We evaluate its performance in predicting biological functions (GO terms). We investigate how the GO term size and category influence the performance. Because of the lack of isoform-level function annotation data, the performance of our model is validated with single isoform genes (SIGs) for which the functions are known (the same as their parental genes). Gene-level function prediction performance is evaluated for multi-isoform genes (MIGs) for which isoform-level functions are unavailable. We evaluate the robustness of our method to information leak caused by paralog genes. We compare IsoResolve with state-of-the-art methods. Finally, we illustrate that our method is able to identify isoform functions by using case studies where gene functions are annotated at the isoform level.

2. Materials and methods

2.1. IsoResolve

In the context of isoform function prediction, a gene may contain multiple isoforms with different functions. Given a biological function represented by a GO term, a gene is positive if it is annotated to the term and negative otherwise. The assumptions of isoform function prediction are that: (i) for a positive gene, at least one of its isoforms should carry out the given function under consideration, and (ii) for a negative gene, none of its isoforms carries out the function.

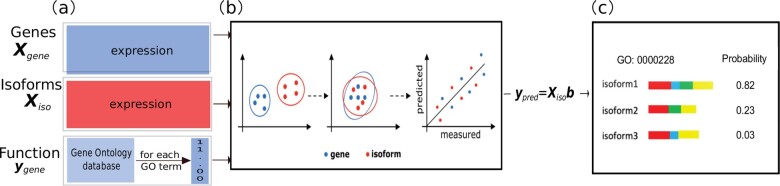
The schematic of IsoResolve is shown inFigure 1. Briefly, IsoResolve implements DA (Nikzad-Langerodi et al., 2018) to predict isoform functions by leveraging gene function prediction models. This is motivated by the assumption that the information learned from gene function prediction can be leveraged for isoform function prediction. It is detailed in the following section.

Fig. 1.

Schematic of IsoResolve. (a) IsoResolve takes gene-level expression features (${\mathit{X}}_{\text{gene}}$), isoform-level expression features (${\mathit{X}}_{\text{iso}}$) and annotated gene functions in the GO database as input. The gene label vector ${\mathit{y}}_{\text{gene}}$ is calculated for each GO term separately. (b) By means of DA, IsoResolve projects gene-level features (blue) and isoform-level features (red) into a latent variable (LV) space such that the projections of gene and isoform features in the LV space have similar distribution, which ensures that the information in gene function prediction models (relationship between gene-level features and gene functions) can be leveraged to predict isoform functions. (c) After building the model ${\mathit{y}}_{\text{pred}}$=${\mathit{X}}_{\text{iso}}\mathit{b}$, the functions (GO terms) of isoforms of the same gene can be predicted and differentiated. The red, blue, green and yellow rectangles represent exons in the isoform. Each rectangle represents a single exon while each isoform is made up of multiple exons. For example, Isoform 1 consists of four exons, while both Isoform 2 and 3 contains three exons

2.1.1. Input data in both the gene and isoform domains

The input for our method includes data from both the gene and isoform domains. For a given dataset, assume that it contains m genes and n isoforms. In our study, we consider gene or isoform expression as features. Let r denote the number of features. As expression is calculated from RNA-seq data of samples, r is the same as the number of samples in a given dataset.

Gene-level features. Let an m × r matrix ${\mathit{X}}_{\text{gene}}$ represent the feature matrix for genes, where a row is a gene and a column is a feature. The label of the gene is determined by functional annotation. For a given function (a GO term) under investigation, the label of each gene is stored in an m-dimensional vector ${\mathit{y}}_{\text{gene}}$, where its value is 1 if the gene is annotated to the function and 0 otherwise.

Isoform-level features. Let an n × r matrix ${\mathit{X}}_{\text{iso}}$ represent the feature matrix for isoforms, where a row is an isoform and a column is a feature. Assume that l of n isoforms are from SIGs that contain a single isoform. The functions of these isoforms are the same as those of their parental genes. Let an l × r matrix ${\mathit{X}}_{\text{iso}}^s$ denote the feature matrix of this subset of isoforms. Their labels are stored in an l-dimensional vector ${\mathit{y}}_{\text{iso}}^s$.

The same set of expression features are used to construct ${\mathit{X}}_{\text{gene}},\hspace{0.17em}{\mathit{X}}_{\text{iso}}$ and ${\mathit{X}}_{\text{iso}}^s$. So these three feature matrices have the same number of columns. Let X be the concatenated feature matrices of ${\mathit{X}}_{\text{gene}}$ and ${\mathit{X}}_{\text{iso}}^s$ and y denote the concatenated label vector of ${\mathit{y}}_{\text{gene}}$ and ${\mathit{y}}_{\text{iso}}^s$.

2.1.2. The algorithm to leverage gene function prediction models for isoform function prediction

The core of IsoResolve is to leverage the information of gene function prediction models for the prediction of isoform functions. The algorithm of IsoResolve is described in detail below.

1. IsoResolve predicts isoform function with a partial least square model

   In IsoResolve, a PLS model is used to predict isoform functions as follows:

   $${\mathit{y}}_{\text{pred}}={\mathit{X}}_{\text{iso}}\mathit{b},$$ (1)

   where b represents the vector of regression coefficients and ${\mathit{y}}_{\text{pred}}$ stands for the predicted score of isoforms. The higher ${\mathit{y}}_{\text{pred}}$ is, the more likely the isoform is to carry out the function under consideration. Based on the theory of PLS, b is calculated as:

   $$\mathit{b}=\mathit{W}{({\mathit{P}}^T\mathit{W})}^{-1}\mathit{q}$$ (2)

   where W is an r × k matrix (k denotes the dimension of the LV space). Each column of W is an $r\times 1$ weight vector, denoted by ${\mathit{w}}_{\text{iso}}$ with which the projection of input feature data into the LV space is calculated. P is an r × k matrix. In PLS, each column of P is called a loading vector, with the element reflecting the importance of each feature. q is a $k\times 1$ vector, with the element describing the importance of each latent variable (Abdi, 2010). P and q can be calculated based on W with conventional PLS (Abdi, 2010).

   From Equations (1) and (2), building isoform function prediction models requires the calculation of ${\mathit{w}}_{\text{iso}}$, which is detailed in the section below.

2. Formulating ${\mathit{w}}_{\mathit{iso}}$ as the solution to an optimization problem that minimizes the difference between gene features and isoform features in the LV space

   IsoResolve projects ${\mathit{X}}_{\text{gene}}$ and ${\mathit{X}}_{\text{iso}}$ into the same LV space. Let ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ be the projections of gene and isoform feature matrices on the direction of w, which are calculated as:

   $${\mathit{t}}_{\text{gene}}={\mathit{X}}_{\text{gene}}\mathbf{w},$$ (3)

    

   $${\mathit{t}}_{\text{iso}}={\mathit{X}}_{\text{iso}}\mathit{w}.$$ (4)
   The solution to w, denoted by ${\mathit{w}}_{\text{PLS}}$, is calculated by solving the following optimization problem in PLS (Nikzad-Langerodi et al., 2018):

   $${\mathit{w}}_{\text{PLS}}=\underset{\mathit{w}}{\arg \min }\left|\right|\mathit{X}-\mathit{y}{\mathit{w}}^T|{|}_F^2$$ (5)
   In IsoResolve, ${\mathit{w}}_{\text{iso}}$ is derived by minimizing the distributional difference between ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$. The reason is that the more similar the two projections are, the more information the isoform function prediction can leverage from gene function prediction models. That is, ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ are required to obey the same distribution. Because it is challenging to ensure ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ to have exactly the same distribution, we instead require ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ to have the same mean and approximately the same variance as an alternative solution previously proposed in Nikzad-Langerodi et al. (2018). ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ are therefore mean-centered so that they have the same mean (both are zero). To make them have equal variances, the difference between their variances must be minimized. To compute ${\mathit{w}}_{\text{iso}}$, we extend the objective function in Equation (5) to the following (Nikzad-Langerodi et al., 2018):

   $${\mathit{w}}_{\text{iso}}=\underset{\mathit{w}}{\arg \min }\left|\right|\mathit{X}-\mathit{y}{\mathit{w}}^T|{|}_F^2+\lambda |\mathit{var}({\mathit{t}}_{\text{gene}})-\mathit{var}({\mathit{t}}_{\text{iso}})|$$ (6)

   where var($·$) means the calculation of variance and the second term $\lambda |\mathit{var}({\mathit{t}}_{\text{gene}})-\mathit{var}({\mathit{t}}_{\text{iso}})|$ is used to penalize the difference in the variances between ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$. λ is a factor that controls to what extent the penalty is imposed. A larger λ leads to a higher penalty. λ is a tuning parameter in IsoResolve. In Equation (6), the variances of ${\mathit{t}}_{\text{gene}}$ and ${\mathit{t}}_{\text{iso}}$ are calculated as:

   $$\mathit{var}({\mathit{t}}_{\text{gene}})=\frac{{\mathit{w}}^T{\mathit{X}}_{\text{gene}}^T{\mathit{X}}_{\text{gene}}\mathit{w}}{m-1},$$ (7)

    

   $$\mathit{var}({\mathit{t}}_{\text{iso}})=\frac{{\mathit{w}}^T{\mathit{X}}_{\text{iso}}^T{\mathit{X}}_{\text{iso}}\mathit{w}}{n-1}.$$ (8)

3. Computing W, P and q

   Inserting Equations (7) and (8) into Equation (6), we obtain the following optimization problem.

   $$\begin{array}{cc}\hfill & {\mathit{w}}_{\text{iso}}=\underset{\mathit{w}}{\arg \min }\left|\right|\mathit{X}-\mathit{y}{\mathit{w}}^T|{|}_F^2\hfill \\ \hfill & \hspace{1em}\hspace{1em}+\lambda |\frac{1}{m-1}{\mathit{w}}^T{\mathit{X}}_{\text{gene}}^T{\mathit{X}}_{\text{gene}}\mathit{w}-\frac{1}{n-1}{\mathit{w}}^T{\mathit{X}}_{\text{iso}}^T{\mathit{X}}_{\text{iso}}\mathit{w}|\hfill \end{array}$$ (9)

   where m and n denote the numbers of genes and isoforms, respectively. By taking the derivative with respect to ${\mathit{w}}^T,\hspace{0.17em}{\mathit{w}}_{\text{iso}}$ can be computed in the closed form below:

The ${\mathit{w}}_{\text{iso}}$ calculated above represents the first column vector of W in Equation (2) (corresponding to the first dimension of the LV space). Based on ${\mathit{w}}_{\text{iso}}$, the first column vector of P and the first element of q can be calculated (see details in Supplementary Note S1). Then, the remaining k–1 column vectors of W and P and the remaining k–1 elements of q can be obtained iteratively (Supplementary Note S1). With the obtained W, P and q, the regression coefficient vector b can then be calculated with Equation (2), and the score for an isoform to carry out a function can be computed with Equation (1).

Next, we convert the score predicted with Equation (1) to a probabilistic value in the range of [0, 1] with the logistic function. Let ${\mathit{y}}_{\text{pred},i}$ represent the predicted score for the ith isoform in the test set. Its probability for carrying out a biological function is calculated as:

$$\begin{array}{cc}\hfill & {\text{Prob}}_i=\frac{1}{1+e^{-{\mathit{y}}_{\text{pred},i}}}\hfill \end{array}$$ (10)

2.2. Datasets

We evaluate the performance of our method in isoform function prediction on three datasets. The numbers of genes, isoforms and features for each dataset are provided in Supplementary Table S1.

Dataset A is described in Shaw et al. (2019). From an initial set of 4643 RNA-Seq experiments obtained from the short-read archive (SRA) database, the authors selected only samples with 50–100 million reads, discarded samples with the alignment ratio of reads lower than 0.7, and filtered poorly covered genes and corresponding isoforms. 1735 RNA-seq experiments of human samples from various biological conditions were retained. It contains 47 393 isoforms and 19 352 genes, in which 9039 are SIGs and 10 313 are MIGs. Gene-level features were calculated as the sum of expression of its isoforms (Shaw et al., 2019).

Dataset B is described in Eksi et al. (2013), with 811 mouse RNA-seq experiments downloaded from the SRA database. The experiments with fewer than 10 million reads or with a mapping rate of reads less than 50% were filtered. Isoforms that were detected in fewer than half of the experiments were removed. After the preprocessing, 365 experiments were kept. Each experiment contained 19 201 genes and 24 274 isoforms. The numbers of SIGs and MIGs were 15 974 and 3227, respectively. The sum of isoform expression was calculated as gene-level expression (Shaw et al., 2019).

Dataset C is our newly compiled data from the Genotype-Tissue Expression (GTEx) Project (https://gtexportal.org/home/) (Lonsdale et al., 2013). In this project, RNA-seq experiments were performed for samples from 30 tissues. There are multiple samples for each tissue. We downloaded the RNA-seq expression data (version v6) of 8555 samples covering the 30 tissues including lung, kidney, blood, etc. The unit of expression level is Fragments Per Kilobase of exon per Million fragments mapped (FPKM). The data were quality controlled with the following procedure. First, in each tissue, only the isoforms that were expressed (FPKM>1) in more than half of the samples were retained. Then, we kept the isoforms that were detected in at least one tissue. This resulted in 17 425 genes and 64 779 isoforms. Of all genes, 4287 are SIGs and 13 138 are MIGs. The isoform expression matrix contains 8555 features (e.g. RNA-seq samples), which is of very high dimension and makes it very time-consuming to build isoform function prediction models for a large number of functions as done in our work. We therefore reduced the dimensionality of the isoform expression data with principal component analysis (PCA). PCA was applied to the expression data of each tissue and the principal components (PCs) were sorted in descending order by their variances. Then a number of the top-ranked PCs were selected in such a way that these PCs explained $\ge$90% of the variance of the original data. Combining the PCs for each tissue, we obtained 159 PCs, which were used as features for this dataset. Gene-level features were computed as the sum of isoform-level features.

2.3. Parameter optimization of IsoResolve

As described previously, IsoResolve has two parameters. The first is the maximal allowed number of dimensions of the latent variables (LVs) space, denoted by k. The optimal number of LVs is often less than 20 (Filzmoser et al., 2009). In our study, we set k to 20 to search for optimal models. The second parameter is the penalty factor, denoted by λ, which controls to what extent the distributional difference between the LV projected from gene-level features and that from isoform-level features is penalized (discussed in Section 2.1.2). We considered a wide range of $\lambda \in$ [0.001, 0.01, 0.1, 1, 10, 100]. We found that k and λ have significant effects on the performance on the function prediction. Taking the function (GO: 0055085) as an example, we showed the prediction performances at different k and λ values based on Dataset A (Supplementary Fig. S1). As can be seen, the parameter λ and k have different degrees of influence on the prediction ability. For this example, k leads to better performance when it is in the range from 8 to 10 and λ results in better performance when its value is 0.1 or 10. For each function (i.e. a GO term), the grid search method was used to determine the optimal values of k and λ based on five-fold cross validation.

3. Results and discussion

Currently, the best performing method for isoform function prediction based on expression is shown to be DeepIsoFun and its highest accuracy is achieved on Dataset A (Shaw et al., 2019). The authors dedicated the majority of the analysis to Dataset A because of its high quality. Therefore, in this section, we first focused our analysis and compared IsoResolve with DeepIsoFun on Dataset A. Next, we compared the performance of IsoResolve with the other state-of-the-art methods including DisoFun, IsoFun, WLRM and mi-SVM on the three datasets. Following the same five-fold cross-validation method used in Eksi et al. (2013) and Shaw et al. (2019), we partitioned the data based on genes rather than isoforms to ensure that all isoforms of the same gene belong to the same group to avoid information leak and overfitting.

3.1. Performance of IsoResolve

3.1.1. Performances for GO terms of different sizes and functional categories

The GO term size and category have been shown to impact the performance of isoform function prediction (Eksi et al., 2013; Shaw et al., 2019). The number of genes that are annotated to a GO term is called the GO term size. The GO database contains terms of three main categories, namely, biological process (BP), cellular component (CC) and molecular function (MF).

Ideally, our model should be evaluated for isoform-level functional prediction. However, as isoform-level functions are not available for many genes, we follow the conventional practice (Eksi et al., 2013; Shaw et al., 2019) and investigate the impact of GO term sizes and the main category on the performance of our method at the gene level. For each function (GO term), the maximum score of its isoforms is taken as the score of the gene. For a given function, the gold standard of positive (annotated to the term) and negative (not annotated to the term) genes is constructed using the basic version of the GO database.

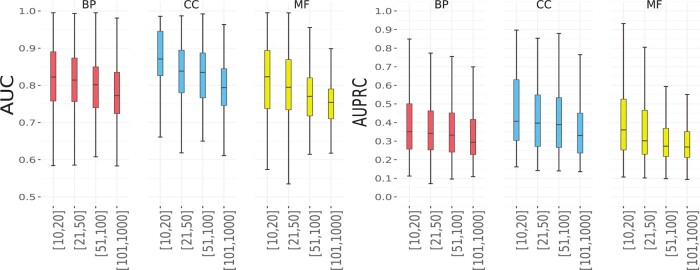
We tested the performance of IsoResolve on Dataset A. There are a total of 4272 GO terms. The numbers of BP, CC and MF terms are 2178, 699 and 1395, respectively. For each GO term, both AUC and AUPRC were calculated to evaluate the performance. For AUPRC, its baseline [equal to the percentage of positives in a dataset, see details in Saito et al. (2015)] varies among different GO terms because the number of positives, i.e. the number of genes annotated to each GO term, vary from term to term. The results for different terms can therefore not be compared. Therefore, the baseline needs to be set to the same for fair comparison of prediction performance between GO terms. Shaw et al. has unified the baseline of all terms to 0.1 in the previous work (Shaw et al., 2019). For fair comparison of our model with that in Shaw et al. (2019), we also used the same baseline 0.1. Because the maximal GO term size considered in this study was 1000, the number of negatives (unannotated genes to a GO term) exceeds that of positives. Therefore, for each GO term, we randomly selected a subset of negatives such that their number was 9 times that of the positives to have a baseline of 0.1. The average AUC values obtained by our method were 0.812, 0.845 and 0.795 for the BP, CC and MF categories, respectively. The average AUPRC values for the three categories were 0.327, 0.381 and 0.298, respectively. These results suggest that all the different categories of GO terms could be predicted well, which is consistent with the observation in Shaw et al. (2019).

As the GO term size has been shown to affect prediction performance, we followed the work (Chen et al., 2019) and divided the GO terms in each category into four groups with different size ranges, which were [10, 20], [21, 50], [51, 100] and [101, 1000], respectively. For each category, the AUC and AUPRC values in each group of terms of different sizes are shown in Figure 2. In terms of both AUC and AUPRC, we found that the performance of IsoResolve decreased as the GO term size increases for the three categories. This trend is the same as that observed in previous studies on isoform function prediction (Shaw et al., 2019). A potential reason is that GO terms with larger sizes represent more heterogeneous functions and are therefore more difficult to predict than smaller terms.

Fig. 2.

Performance of IsoResolve on GO terms with different sizes in the BP, CC and MF categories

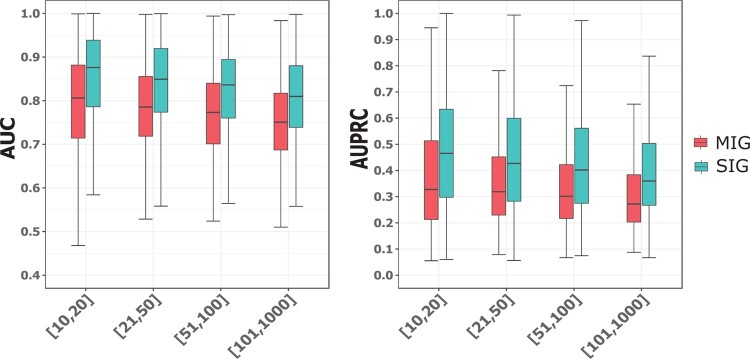
3.1.2. Performances for SIGs and MIGs

We assessed the prediction performances for SIGs and MIGs. As SIGs contain only one isoform, they were used to assess the performance in isoform-level function prediction. For MIGs, because their isoform-level functions were not available, we assessed the performance in gene-level function prediction instead. That is, for each GO term, the predicted score of the MIG was computed as the maximum of the scores of all its isoforms following the convention (Chen et al., 2019; Eksi et al., 2013). For this analysis, we divided the GO terms in each main category into four groups with different size ranges, which were [10, 20], [21, 50], [51, 100] and [101, 1000]. For BP terms, we observed a trend that the prediction performances for both SIGs and MIGs in terms of AUC and AUPRC decreases with increasing GO term size (Fig. 3). The average AUC values for SIGs in the four groups of GO terms were 0.872, 0.849, 0.839 and 0.813, respectively. Correspondingly, the average AUC values for MIGs were 0.804, 0.782, 0.771 and 0.753. This trend held for CC and MF terms (Supplementary Fig. S2).

Fig. 3.

Performance of IsoResolve for SIGs and MIGs for the four groups of BP terms with different size ranges

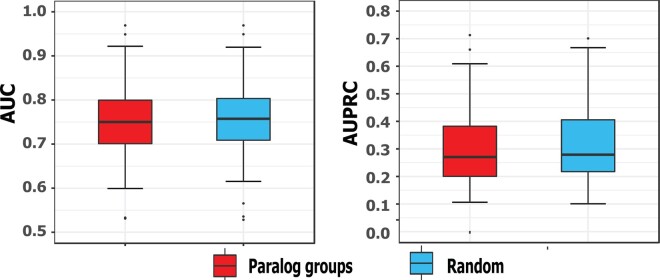
3.1.3. IsoResolve is robust to information leak from paralog genes

During cross validation, it may occur that some genes from one paralog group are in the training set and the remaining from the same group are in the test set. This could lead to information leak and makes the prediction performance of our method better than what it should be. We therefore tested whether the good performance of our method resulted from information leak. This could potentially cause information leak and thus overfitting of our models because paralog genes could be similar in sequences and functions. Following the method described in Eksi et al. (2013), we partitioned all genes in such a way that the genes from the same paralog groups were partitioned into the same fold in five-fold cross-validation to avoid information leak. The paralog genes were obtained from Ouedraogo et al. (2012). We identified 903, 665 and 863 paralog gene groups for Dataset A, Dataset B and Dataset C, respectively. The paralog genes expressed in Dataset A, Dataset B and Dataset C are provided in Supplementary Tables S2–S4, respectively. GO slim terms that represent a broad range of key biological functions were used in this experiment. We used the set of 150 GO slim terms provided in Shaw et al. (2019). It is assumed that the term with less than five annotated genes represent very specific functions and is not appropriate for model training and testing (Shaw et al., 2019). We removed such terms and obtained 96 GO slim terms for isoform function prediction. We performed the cross-validation experiments ten times and each time the paralog groups were partitioned randomly into five-folds. The mean and standard deviation of AUC and AUPRC for paralog-based cross-validation and conventional cross-validation are shown in Supplementary Table S5. First, we found that the standard deviation of AUC and AUPRC for both ways of cross-validation are small, suggesting that the performance are robust regardless of how genes were partitioned. Second, we found that the performance for the partition based on paralogs was slightly lower than but comparable to that based on random partition (Fig. 4 for Dataset A, Supplementary Fig. S3 for Dataset B and C), being consistent with the results in the previous work (Eksi et al., 2013). These results suggest that our method is robust to information leak from paralog genes.

Fig. 4.

Comparison of the performance achieved by partitioning the genes according to paralog groups with that by partitioning the genes randomly on Dataset A

3.2. Comparison with DeepIsoFun

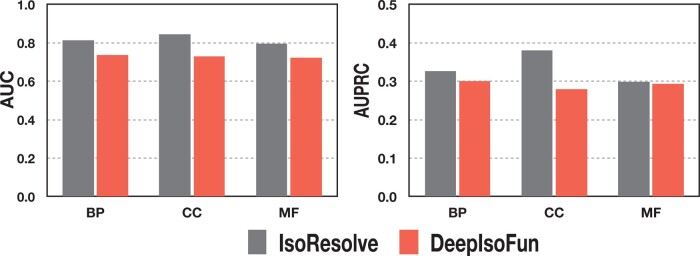
DeepIsoFun was shown to be of the highest accuracy in isoform function prediction, and its performance was evaluated extensively for the 4272 GO terms on Dataset A (Shaw et al., 2019). To comprehensively compare our method with DeepIsoFun, we also evaluated the performance of IsoResolve for the 4272 GO terms on Dataset A. The comparison of the performance between IsoResolve and DeepIsoFun is shown in Figure 5. The average AUC values obtained by DeepIsoFun for the three GO categories were 0.735, 0.728 and 0.722, respectively. In contrast, the corresponding average AUC values of our method are 0.812, 0.845 and 0.795, respectively. The improvements of our method over DeepIsoFun were 32.8, 51.3 and 32.9%, respectively (against the baseline 0.5; the improvement is calculated as (b - a)/(a - 0.5), where b and a represent the AUC of IsoResolve and DeepIsoFun, respectively). The average AUPRC values were 0.301, 0.279 and 0.294 for DeepIsoFun, and were 0.327, 0.381 and 0.298 for our method. The improvements of our method were 12.9, 57.0 and 2.06%, respectively (against the 0.1 baseline). In addition, we also compared IsoResolve with DeepIsoFun on their performance for SIG and MIG level in terms of AUC (Supplementary Fig. S4). We found that our method also performed better.

Fig. 5.

Comparison between IsoResolve and DeepIsoFun for the three categories of terms: BP, CC and MF

3.3. Comparison of IsoResolve with state-of-the-art methods

In addition to DeepIsoFun, the state-of-the-art methods for predicting isoform functions based on expression profiles include DisoFun, IsoFun, WLRM and mi-SVM. IsoFun (Yu et al., 2020a,b) was proposed based on random walks and DisoFun (Wang et al., 2020a,b) was proposed based on matrix factorization. WLRM formulates isoform function prediction into a logistic regression model in which a weight is introduced to the isoform of each positive gene (Luo et al., 2017). mi-SVM is an extension of SVM to deal with the MIL problem. It was introduced to predict isoform functions in our previous work (Eksi et al., 2013). DeepIsoFun was compared with our method in Section 3.2 and was therefore not considered here. iMILP was not considered because it treats isoform function as a three-class classification problem and thus cannot be fairly compared. DIFFUSE was also not compared because it requires both expression and sequence/domain as input (Chen et al., 2019).

We compared the performance of IsoResolve with that of the four methods on the three datasets. We used GO slim terms (described in Section 3.1.3) for testing. The results in terms of the average AUC and AUPRC over all the terms are shown in Table 1. The average AUC values obtained by IsoResolve on Datasets A, B and C were 0.780, 0.741 and 0.742, respectively, which were higher than those obtained by DisoFun, IsoFun, WLRM and mi-SVM. For Dataset A, the improvements in AUC by IsoResolve compared with DisoFun, IsoFun, WLRM and mi-SVM were 39.3, 61.8, 85.4 and 97.2%, respectively (against the baseline of 0.5). The improvements in AUC compared with that of the other four methods were 31.7, 54.5, 73.4, 81.2% and 28.0, 63.5, 83.3, 87.6% on Dataset B and C, respectively. In terms of AUPRC, our method also outperformed the other four methods. Taking Dataset A as an example, the average AUPRC value obtained by IsoResolve was 0.348, which was higher than 0.248 (DisoFun), 0.213 (IsoFun), 0.192 (WLRM) and 0.198 (mi-SVM). These results suggest that our method is promising for isoform function prediction.

Table 1.

Comparison of IsoResolve with state-of-the-art methods

Method	Dataset A		Dataset B		Dataset C
	AUC	AUPRC	AUC	AUPRC	AUC	AUPRC
IsoResolve	0.780	0.348	0.741	0.258	0.742	0.293
DisoFun	0.701	0.248	0.683	0.215	0.689	0.224
IsoFun	0.673	0.213	0.656	0.194	0.648	0.181
WLRM	0.651	0.192	0.639	0.182	0.632	0.165
mi-SVM	0.642	0.198	0.633	0.209	0.629	0.184

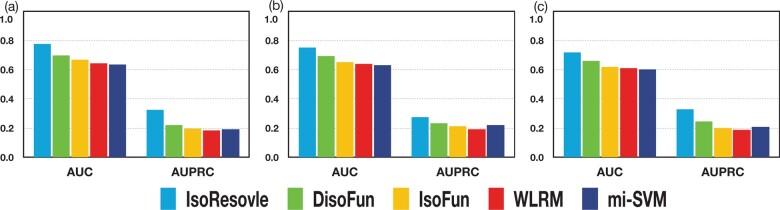
Next, we compared the five methods based on the performance for SIGs because the functions of SIGs are actually at the isoform level. We computed the prediction performance for IsoResolve, DisoFun, IsoFun, WLRM and mi-SVM for SIGs. The AUC and AUPRC values are shown in Figure 6. For the three datasets, IsoResolve achieved better performance than the other four methods, suggesting that our method was most accurate in predicting isoform-level functions.

Fig. 6.

Comparison of the performance for SIGs in terms of AUC and AUPRC on (a) Dataset A, (b) Dataset B and (c) Dataset C

3.4. Case studies

We further tested the performance of IsoResolve on a small-scale dataset of genes with annotated isoform functions described in the work (Shaw et al., 2019). The authors proposed to validate isoform function prediction models by testing whether the isoforms of genes annotated with opposite functions can be differentiated (Shaw et al., 2019). Specifically, the authors focused on the biological function regulation of apoptosis process whose two child GO terms, i.e. pro-apoptosis (GO: 0043065) and anti-apoptosis (GO: 0043066), represent opposite functions. A total of 18 multi-isoform genes annotated with both pro-apoptosis and anti-apoptosis functions were identified. Using the same method as described in Shaw et al. (2019), we evaluated whether the pro- and anti-apoptosis functions of isoforms of these 18 genes could be differentiated by our method. An isoform was predicted to carry out a function if its probability predicted by IsoResolve was higher than 0.5 and vice versa. The results are shown in Supplementary Table S6. IsoResolve was able to predict the Regulation of apoptosis function for the isoforms of all 18 genes (100% recall), the pro-apoptosis function for the isoforms of 17 genes (94.4% recall) and the anti-apoptosis function for the isoforms of 17 genes (94.4% recall). As a comparison, the recall values for these three functions achieved by DeepIsoFun were 94.4%, 72.2% and 77.7%, respectively, which were lower than those of our method (Supplementary Table S6) [note that the results for mi-SVM and WLRM are not shown here because they were less accurate than DeepIsoFun (Shaw et al., 2019)]. Furthermore, we found that our method successfully differentiated the pro- and anti-apoptosis functions among isoforms of 14 genes. In contrast, DeepIsoFun differentiated the functions for only eight genes, indicating that our method is more accurate in recognizing genes with functionally differentiated isoforms.

Further, motivated by the principle that structures determine functions, we investigated whether functionally differentiated isoforms may have different 3-dimensional (3D) structures. Taking the two isoforms (NM_001318095 and NM_000600) with differentiated functions of IL6 (Supplementary Table S6) as an example, we built their three-dimensional models with I-TASSER (Yang et al., 2015), which is the state-of-the-art software to model 3D structures of proteins. First, the TM-score of the 3D models of the two isoforms were 0.653 and 0.622, respectively, indicating that the models were accurate (note: 3D models with TM-score > 0.5 are considered accurate). Second, we found that the 3D models of the two isoforms were clearly different from each other (Supplementary Fig. S5), being consistent with their differentiated functions. Another example is DNAJA1 with functionally differentiated isoforms, the 3D models of its two isoforms NM_001539 and NM_001314039 were accurate, with TM-score equal to 0. 615 and 0. 645 (Supplementary Fig. S5), respectively. Their 3D models were largely different, supporting the difference in their functions.

4. Conclusion

Gene-level function prediction is of limited precision because it treats a gene as a single entity, without differentiating isoforms that may carry out different or even opposite biological functions. In recent years, significant effort has been dedicated to the prediction of isoform functions, aiming for gene function annotation at a finer resolution. Isoform function prediction is challenging because of the lack of experimentally verified functions annotated to isoforms. To address this challenge, methods including mi-SVM, WLRM, isoFun, DisoFun and DeepIsoFun, have been proposed to predict isoform functions. These methods have been proven promising in predicting isoform functions.

We are motivated to further improve the performance in predicting isoforms. We propose IsoResolve, which is able to leverage the information of gene function prediction models for isoform function prediction with DA. We show that our method is superior to state-of-the-art methods on three datasets. The overall performance of IsoResolve in functional prediction is more accurate. Based on mi-SVM described in Eksi et al. (2013), it is observed that the prediction performance for MIGs is higher than that of SIGs. However, the prediction performance for SIGs is higher than MIGs based on IsoResolve. One possible reason why we have observed this difference is that in mi-SVM, the selection of ’witness’ (i.e. the positive isoform) in MIGs is iteratively optimized so as to be separated from negative isoforms based on the multiple-instance learning framework, which may lead to better accuracy for MIGs. In contrast, because IsoResolves does not optimize the selection of positive isoforms in MIGs, its performance for MIGs is relative lower than that for SIGs. Integrating positive isoform selection with IsoResolve might improve isoform function prediction model, which is interesting and would be studied in our future work. We also illustrate that our method performs better in identifying genes with functionally differentiated isoforms in a case study of pro- and anti-apoptosis function. A possible explanation for the high accuracies of our method is that it is able to effectively leverage the knowledge gained from gene function prediction models and that the PLS model used in IsoResolve has the built-in ability to deal with high dimensional and multi-correlated features for extracting latent variables that are predictive of biological functions.

Though beyond the scope of this work, our method can be further improved in several ways including data denoising, because large datasets involving many tissues and biological conditions may be of high noise level. In addition, because many features are redundant and may be irrelevant to the functions of isoforms, developing feature selection methods for isoform function prediction could be valuable to this field. Further, integrating other types of genomic data in addition to gene expression used in this study could be a promising way to build more accurate models as heterogeneous data may complement each other and thus provide additional predictive value for isoform function prediction. In fact, in addition to expression, sequence and domain features of isoforms were integrated in the DIFFUSE method (Chen et al., 2019), and the results were better than ours. Though, our method based on only expression data was comparable to that of DIFFUSE. In the future, an important question to consider is to design methods that can effectively integrate different types of data to improve isoform function prediction. There are two main strategies. The first is to combine different types of input features such as sequence, expression and domain into a single feature matrix, followed by building a model on the combined feature matrix. The second is to build an isoform function prediction model based on each type of feature and then integrate the prediction results of each individual model. Integrating heterogeneous feature data face several challenges: (i) Missing values may exist for some types of feature data; how to handle missing data to maximize the usability of data is a challenge. (ii) The characteristics and levels of noise in different types of data is different, making it challenging to design methods that can cope with such heterogeneous noise. (iii) In the context of limited availability of isoform-level function annotation, how to determine the weight of different types of data and how to design methods to identify a set of predictive features (Liu et al., 2020a,b; Pes, 2017) are also challenging. It is our expectation that more powerful methods for the isoform function prediction will be developed in the future and that the isoform-level annotation of functions will advance our understanding of biological processes and disease pathways.