Rapid and accurate structure-based therapeutic peptide design using GPU accelerated thermodynamic integration

Abstract

Peptide-based therapeutics are an alternative to small molecule drugs as they offer superior specificity, lower toxicity, and easy synthesis. Here we present an approach that leverages the dramatic performance increase afforded by the recent arrival of GPU accelerated thermodynamic integration (TI). GPU TI facilitates very fast, highly accurate binding affinity optimization of peptides against therapeutic targets. We benchmarked TI predictions using published peptide binding optimization studies. Prediction of mutations involving charged side-chains was found to be less accurate than for non-charged, and use of a more complex 3-step TI protocol was found to boost accuracy in these cases. Using the 3-step protocol for non-charged side-chains either had no effect or was detrimental. We use the benchmarked pipeline to optimize a peptide binding to our recently discovered cancer target: EME1. TI calculations predict beneficial mutations using both canonical and non-canonical amino acids. We validate these predictions using fluorescence polarization and confirm that binding affinity is increased. We further demonstrate that this increase translates to a significant reduction in pancreatic cancer cell viability.

1 |. INTRODUCTION

Proteins often carry short linear peptide segments that are recognized by globular domains. It is estimated that this type of interaction accounts for 15%−40% of known protein–protein mediations.¹ A large number of these complexes now have 3D structures available in the Protein Data Bank (PDB) and thus can be subjected to computational protein design techniques. Such techniques can be used to design inhibitors of the biological interaction with a view to producing a therapeutic outcome. Peptide fragments at protein–protein interfaces can be extracted and used as peptide inhibitors of protein–protein interactions (PPIs).² Such peptides often have suboptimal binding affinity and require substantial optimization to achieve efficacy at therapeutically viable concentrations.

Peptide therapeutics are currently undergoing a huge expansion and the market size is predicted to continue its increase into the fore-seeable future.³ The most recent published estimate for the number of peptides in clinical and pre-clinical development is 140 and 500, respectively.⁴ Given this intense activity, methods for optimizing peptide affinity are of major interest.

Recently we reported a number of new drug targets and peptide drug leads discovered by screening a human peptide library of 50 000 peptides for effects on pancreatic cancer cell (RWP1) proliferation.⁵ One of the peptides that significantly reduced cell viability mapped to a fragment of MUS81 at the interface with its interaction partner EME1. The MUS81–EME1 complex is an endonuclease that recognizes specific DNA structures at replication forks. It cleaves these structures to rescue forks that become stalled during replication. It has a large interface with a buried surface area of 7094 Ų. The peptide identified in screening is the C-terminal end of MUS81 (residues 538–551), and it interacts with both the C-terminal domain of EME1, and with other parts of MUS81 C-terminal domain. This part of the protein is thought to be involved in DNA recognition⁶ and thus disrupting it likely result in loss of function and replication forks remain stalled, hampering proliferation. MUS81–EME1 is involved in DNA repair; as DNA repair is one of cancer cells’ most notable vulnerability, its inhibition is a possible venue for cancer therapy.⁷ A high-resolution crystal structure is available for the MUS81–EME1 complex (PDB ID: 2ZIX).⁶ The availability of a structure provides the opportunity to undertake rational in silico design in order to optimize the binding affinity and boost potency.

Here we describe a computational approach for designing peptides with optimized binding affinity. A schematic of the method pipeline is shown in Figure 1. The method was developed by first benchmarking on cases with experimental kD values—sourced from the literature.^8,9 We apply the optimized pipeline to the MUS81 peptide and successfully increase the binding affinity, leading to a significant reduction in pancreatic cancer cell viability.

FIGURE 1.

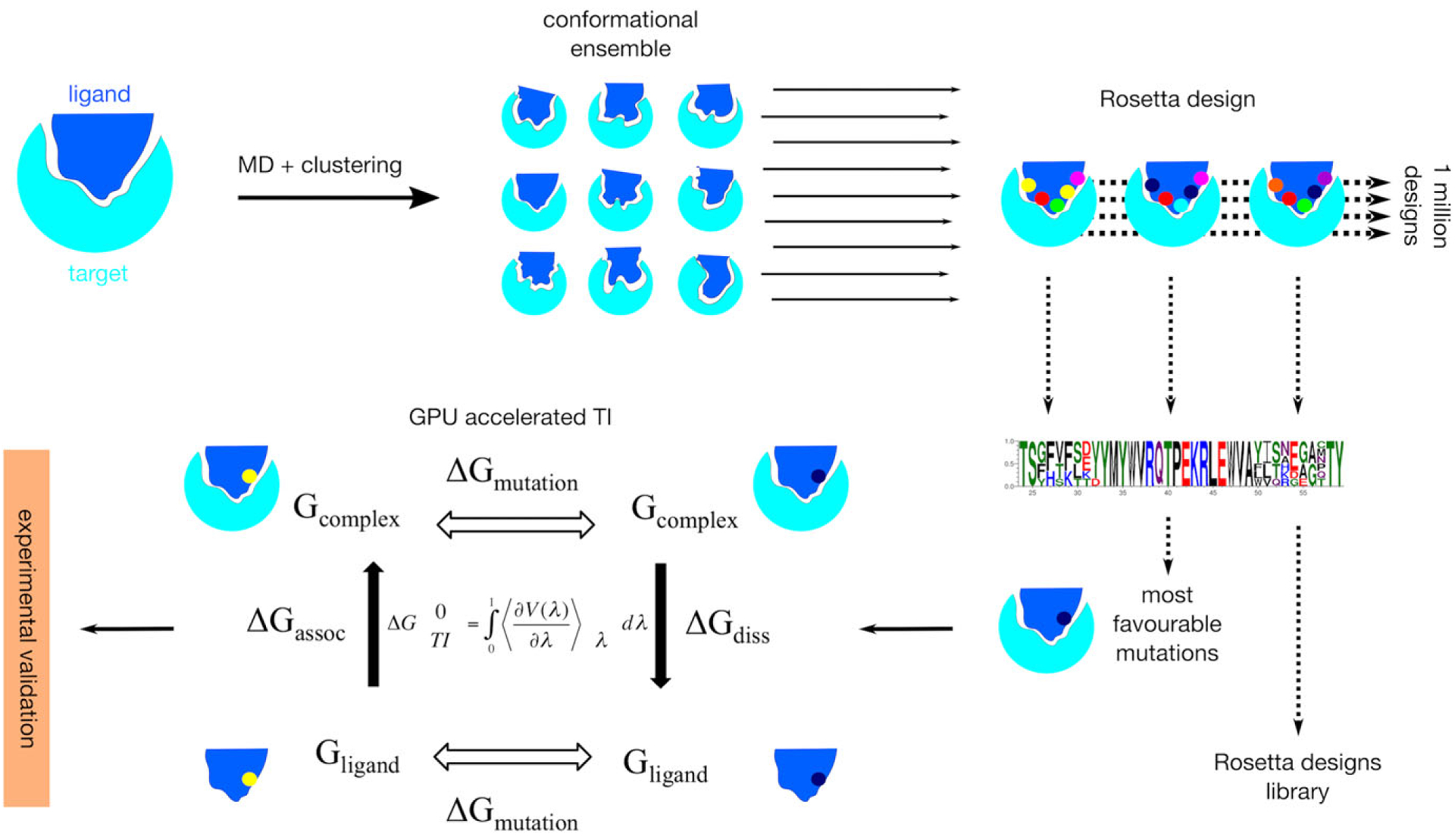
Schematic of the workflow from a ligand–target complex starting structure through to experimental validation of predicted mutations. An ensemble of conformations is first generated by clustering molecular dynamics trajectories. Each member of the ensemble is then subject to Rosetta design. Highly favorable Rosetta predictions are then further evaluated using GPU accelerated thermodynamic integration, and the results from this are experimentally validated. Four sets of calculations are performed in the thermodynamic integration step. Micro-canonical ensembles are generated for both wild type and mutated ligands (ΔG_mut) in bound and unbound states (ΔG_assoc and ΔG_diss). Output energies are integrated using the equation shown to derive ΔG

Our approach takes coarse mutation predictions suggested by Rosetta¹⁰ and refines the design using thermodynamic integration (TI). TI and free energy perturbation (FEP) are currently among the most accurate computational techniques for free energy calculation. They have been consistently shown to match experimental binding free energy values with minimal error.^11–14 Drug–target,¹² protein–protein,¹⁵ protein–DNA,¹⁶ and protein–peptide^17,18 interaction energies have all been accurately predicted using TI. Until recently, performing anything more than a very small number of TI calculations was prohibitively resource intensive. Usually it was necessary to run very short simulations and severely limit the number of replicates. However, the very recent arrival of GPU accelerated TI¹⁹ has dramatically increased capabilities in this regard. It is now possible to test dozens of mutations over significant time-scales and perform many replicates. Depending on system size this can be carried out on the order of 1 week using GPU resources typically available to academic institutions. We utilize this dramatic increase in power to construct a highly accurate yet very rapid peptide optimization method.

2 |. MATERIALS AND METHODS

2.1 |. Model preparation and MD simulation

PDB structures: X, Y, Z containing peptide-target complexes were retrieved from the PDB. Water molecules and other ions and ligands were removed. The remaining structures were prepared for Amber MD simulation using the WHATIF web interface to build in any missing atoms.²⁰ Correct protonation states were identified and annotated. The models were subsequently energy minimized using a combination of steepest descent and conjugate gradient methods. Following this they were equilibrated and heated over 100 ps to 300 K and positional restraints were gradually removed. Restraints were completely removed and full equilibration was achieved after a further 12 ns of MD. Root mean square deviation (RMSD) was calculated to determine convergence. Following equilibration, a 50 ns trajectory was produced for the analysis. Simulations were carried out in explicit solvent comprising a 12 nm³ box of TIP3P water using TLEAP in AMBER16.²¹ Sodium counter-ions were added for overall charge neutrality and periodic boundary conditions were applied. Bonds to hydrogen were constrained using SHAKE²² and a 2 fs time step was used. The particle mesh Ewald²³ algorithm was used to treat long-range electrostatic interactions and the cut-off for non-bonded interactions was set at 12.0 Å. The AMBER ff14SB force field was used for natural amino acid, and the parameters of NCAA were adapted from Forcefield_NCAA developed by Floudas’ group.²⁴ Na⁺ and Cl⁻ counter-ions were added to neutralize the overall system net charge. All the topology files and structures were visually inspected after fully setting up. A Berendsen thermostat and barostat was used throughout for both temperature and pressure regulation.²⁵ During calculations a snapshot was saved every 2 ps. Clustering of the 50 ns production trajectory was carried out using the MMTSB toolset²⁶ (kclust tool) to produce a manageably sized, representative ensemble for design calculations. Radius was set to 2.0 Å and maxerr to 1. This generated a set of backbones representative of the space sampled during the simulation. These, together with the original crystal structure, were used as the models for mutation calculations using Rosetta. Input files and scripts can be found here: https://gitlab.com/kimlab/rapid.

2.2 |. Rosetta calculations

Rosetta modeling calculations were carried out using the Python based interface: PyRosetta.²⁷ The native complex PDB files were first reformatted for compatibility with Rosetta, followed by calculation of the native Rosetta energy score using the “full atom” scoring function. This calculation was repeated 100 times to obtain an average energy score and SD. Each interface side chains were then separately mutated to each of the 20 CAAs and the energy score recalculated. Again each variant was repeated 100 times to obtain averaged scores. For both native and all of the mutant variants, energy score calculations were preceded by full repacking of all side-chains using the “packmover2” function. This searches for the lowest energy configuration of rotamers using the Dunbrack library.²⁸ Sampling of rotamers is necessarily discretized and sampling from the Dunbrack library was set to include additional rotamers at two full standard deviations from the mean chi angle. Differences between native and mutant scores were calculated and negative energy change values were used to generate logos using WebLogo.²⁹ A PDB structure was also generated for each of the mutations to aid manual curation of the output. Calculation of mutations to NCAAs followed the same protocol as for CAAs. Parameters for NCAAs were not included in the Rosetta package, so a previously validated set of 114 parameterized NCAAs with backbone dependent rotamer libraries was obtained and used.³⁰ Input files and scripts can be found here: https://gitlab.com/kimlab/rapid.

2.3 |. Manual curation

Because TI is very computationally expensive, it is prudent to manually curate the Rosetta output before proceeding to this step. Mutations where negative change in the energy score does not make sense structurally and biochemically can be eliminated. Visual inspection of each such mutation was carried by loading the structures output by Rosetta into Chimera³¹ and PyMol.³² Hydrogen bonds, electrostatic interactions and relevant inter-chain atom-atom distances were displayed. These features—together with shape complementarity—were used to decide predicted beneficial mutation was valid. A common example of elimination was mutation to large hydrophobic residues that had no atoms less than 5 Å from the target protein. Another issue was an apparent Rosetta scoring function bias toward GLY and ALA. Approximately 70% of the candidates from Rosetta were removed at this step.

2.4 |. Thermodynamic integration calculations

Mutations with negative energy score changes that survived visual inspection were subject to TI calculations. TI computes the free energy difference between two states, in this case between the target in complex with the peptide and the same target in complex with a mutated version of the peptide. Destabilizing mutations result in significant conformational changes that make the TI approach unsuitable, as it is then very difficult to sample enough phase space to get converged output. For this reason, apo proteins with a backbone RMSD to the average that exceeded 4.0 Å were not allowed to proceed to full TI. For each ΔG_mut process there are three main stages: (1) Partial charges are gradually switched off. (2) vdW transformation: the native residue is gradually phased out and the mutant residue simultaneously phased in. (3) Partial charges are gradually switched back on again. The calculation is separated in this way because having a nonzero charge on an atom—while the vdW interactions with its surrounding are getting weaker—leads to simulation instability. For each stage, the system is first minimized and equilibrated. The equilibration step involves simulating both wild-type and mutant variants in the apo state. TI is unsuitable for measuring significant reductions in stability due to the associated increase in conformational variation. Destabilizing variants would thus be discarded, although no significant destabilization was detected, likely due to the surface location (destabilizing mutations tend to be core residues). Following equilibration, for each of stages 1–3, graduation is achieved by performing separate simulations at discrete points denoted “lambda” in the transformation. This series of predetermined windows provides the “coupled potential function” and the integration is carried out over the average of the lambda derivative of the coupled potential function at given &lambda values. TI calculations were carried out using largely the same simulation conditions described above in Model preparation and MD simulation. However, bonds to hydrogen were not constrained using SHAKE²² during TI calculations, so a 1 fs time step was necessary to capture this fast motion (in the original simulation SHAKE was switched on and a 2 fs time step was allowed). Mutant transformations were simulated for both the un-complexed protein in water and in complex with the target. Nine windows were used for each transformation. This was carried out for each of the three main stages, namely charges switched off, phasing, charges switched back on. This means a total of 54 MD simulations are required for each full TI calculation. In the vdW transformation step simulations, softcore potentials are used, which modify the Lennard–Jones equation to prevent the origin singularity type of free energy divergence from occurring.³³ The multisander capability in Amber was used to create two groups—corresponding to the start and end states. A mixing parameter λ was used to interpolate between perturbed and unperturbed potential functions.

One-step TI calculations were carried out using AMBER16 GPU TI calculations. A time step of 1 fs was used for the integration of the equations of motion and a cutoff of 9 Å was used for Long-range electrostatic interactions with the particle-mesh Ewald method (PME). In one-step TI calculations, the whole mutated residues were treated with softcore potentials, and the electrostatic and van der Waals forces were modified simultaneously. About 11 λ windows were set up for the peptide and complex, respectively, where the λ value changed from 0.0 to 1.0 with Δλ = 0.1. All the starting structures were first minimized and relaxed at 300 K in the NVT ensemble. The initial conformations for each λ window were sequentially generated with 1.4 ns pre-equilibration for each λ-value where the pre-equilibrated conformation of the current λ window was used as the starting conformation of the next λ window for production. A fairly long TI simulation of 5 ns was performed for each λ window for every mutation. The first 1 ns data were discard as equilibration and the last 4 ns data were collected for data analysis at a sampling frequency of 500 fs. Each simulation was repeated 10 times to calculate the ensemble-averaged values. More information of the recommended setup protocol can be found in the Ref. 19. Input files and scripts can be found here: https://gitlab.com/kimlab/rapid.

2.5 |. Purification of protein

The EME1 cDNA clone was obtained from Openfreezer in Gateway Entry vector. The clone was then transferred into a pET-53-DEST by Gateway LR clonase (Invitrogen). Destination vectors were transformed into Escherichia coli BL21(DE3) and cultivated to express proteins. Protein expression was induced by 0.5 mM of Isopropyl β-D-1-thiogalactopyranoside at mid-log phase. After growing the culture overnight at 16°C, cells were harvested by centrifugation at 14 000g for 10 min. Cells were lysed with a sonicator and proteins were purified using Ni-NTA agarose (Qiagen) according to the product manual. Concentration of the purified proteins was determined by measuring the absorption at 280 nm using their extinction coefficients.

2.6 |. Peptide synthesis

The peptides were synthesized as previously described.⁵ Briefly, peptides were synthesized on a Liberty Blue Microwave peptide synthesizer (CEM Corporation) using Fmoc chemistry. Peptides were N-terminally extended based on their source protein. Met residues were substituted by isosteric norleucine to avoid oxidation. The coupling with N,N′-diisopropylcarbodiimide/ethyl 2-cyano-2-(hydroxyimino) acetate (OXYMA) was performed for 4 min at 90°C for all residue except for Cys and His, for which the reaction was carried out for 10 min at 50°C. Removal of Fmoc group was conducted at 90°C for 2 min for sequences containing no Cys or Asp. All deprotection cycles after Asp and Cys were conducted at room temperature to avoid racemization and aspartimide formation. Low loading Rink Amide MBHA resin (Merck) was used for the synthesis of amidated peptides and Wang resins were used for the synthesis of peptides with free carboxy termini. The peptides were cleaved from the resin and deprotected with a mixture of 90.0% (v/v) trifluoroacetic acid (TFA) with 2.5% water, 2.5% triisopropyl-silane, 2.5% 2,2′-(ethylenedioxy)diethanethiol, and 5% thioanisol. Peptides were purified on a preparative (25 mm × 250 mm) Atlantis C3 reverse phase column (Agilent Technologies) in a 90 min gradient of 0.1% (v/v) trifluoroacetic acid in water and 0.1% trifluoroacetic acid in acetonitrile, with a 10 mL/min flow rate. The fractions containing peptides were analyzed on Agilent 6100 LC/MS spectrometer with the use of a Zorbax 300SB-C3 PoroShell column and a gradient of 5% acetic acid in water and acetonitrile. Fractions that were more than 95% pure were combined and freeze dried.

2.7 |. Fluorescence polarization assay

We carried out binding assays with fluorescence polarization using recombinant proteins and fluorescently labeled synthetic peptides. Synthetic peptides were labeled with Alexa Fluor 488 Hydrazide dye according to the manufacturer’s protocol (Thermofisher Scientific). Fluorescence measurements were made using a BMG PHERAstar FS fluorescence polarization spectrometer with the set gain adjustment at 35 mP (3D Facility, Faculty of Medicine, University of Toronto) with fixed excitation (485 nm) and emission (520 nm) wavelength filters. For saturation curves, a fixed concentration of the fluorescently labeled peptide probe (1 μM) was incubated with increasing concentrations of target proteins (0–25 μM). All measurements were taken at room temperature (25°C) 25 mM Tris, 150 mM NaCl, and 5 mM BME at pH 7.0, after 20 min of equilibration. Saturated values could not be obtained because a higher concentration of purified protein was not possible (maximum concentration is 30 μM). The protein seems to be insoluble at higher concentrations, making it impossible to go higher than 30 μM. K_d values were obtained by performing a sigmoidal curve fitting using the log10 of protein concentrations (Origin Pro 9.0 software).

2.8 |. Cell viability assay

Cells were trypsinized from subconfluent cultures and were suspended in culture then seeded into triplicate wells of a 96-well plate (100 μL per well) at a density of 1.5 × 10⁴ per well at standard culture conditions of 5% CO₂ in air at 37°C. Cells were treated with various concentrations of synthetic lipidated peptides for 72 hr. Alamar Blue reagent was added to each well (10 μL) and optical density of the plate was measured at 540 and 630 nm with a standard spectrophotometer at 1, 2, and 4 hr after adding Alamar Blue. A dose-response curve was generated with different concentrations of the peptides (0–25 μM). Cell viability at the highest concentration of peptides (25 μM) and 1 hr reading after adding Alamar Blue reagent was used to produce the graph.

3 |. RESULTS

To benchmark our TI protocol, we first selected the murine double minute 2 (MDM2):p53 complex. This is arguably the clearest example of success in designing a peptide inhibitor based on motif interactions. Over-expression of the MDM2 and murine double minute X (MDMX) proteins causes a decrease in p53 apoptotic activity through a short alpha helix with the motif FxxxWxxL. P53 is probably the most important tumor suppressor, and thus disrupting this interaction carries huge potential for recovering p53 functionally and promoting apoptosis in cancer cells. Since the first characterization of the motif, this complex has been intensely studied and many strategies have been applied with different levels of success to identify potential inhibitors. Examples include classical screening of small molecules, structural rational design, and phage display, among others. The most successful molecule from these efforts is a modified version of the natural peptide, ALRN-6924.^34,35 This stapled peptide has proved its capacity to restore p53 activity in vitro and in vivo, and it is currently in clinical trials.³⁶ It is an ideal test case for our structure-based approach because (a) it is a peptide–target interaction with therapeutic potential; (b) there are mutational binding energy changes reported for all the positions; and (c) there is a high-resolution structure available. The best structure available to test our approach is the complex of MDM2-PMI. PMI is a high affinity peptide, identified by screening 12-mer peptide phage library against site-specifically biotinylated p53-binding domains of human MDM2 and MDMX.³⁷ It has been a potential template to develop a high affinity peptide inhibitor to target p53.⁸ Usefully, ΔΔG values for Alanine substitutions at all positions have already been measured.⁸

A high-resolution crystal structure was obtained from the Protein Data Bank (PDB ID: 3EQS). The missing C-terminal Proline was modeled using tleap and structure was relaxed using 5 ns of molecular dynamics (MD). The resulting trajectory was then clustered by conformation and the most representative backbone of the ensemble was then used as a starting point for the TI calculations. Amber 16 was used to perform the MD and TI calculations. A recent study suggested that its TI performance is equivalent to the commercial tool FEP+ in Schrödinger Suites, which is considered to be current state-of-the-art in this arena.³⁸

Initial runs were performed over 15 ns per lambda, using a 1-step protocol, and taken as the mean of five replicates. Using this approach, we were able to correctly predict and evaluate a significant number of experimentally determined mutations. With the exception of E5A, TI calculation results show very good correlation with experimental values (Figure 2A). P12A is likely very mobile as it is the last residue of the C-terminus and was not resolved in the X-ray crystal structure.³⁷ This was confirmed by the dispersion energies obtained for the Hamilton function across the different lambdas registered during the simulations.

FIGURE 2.

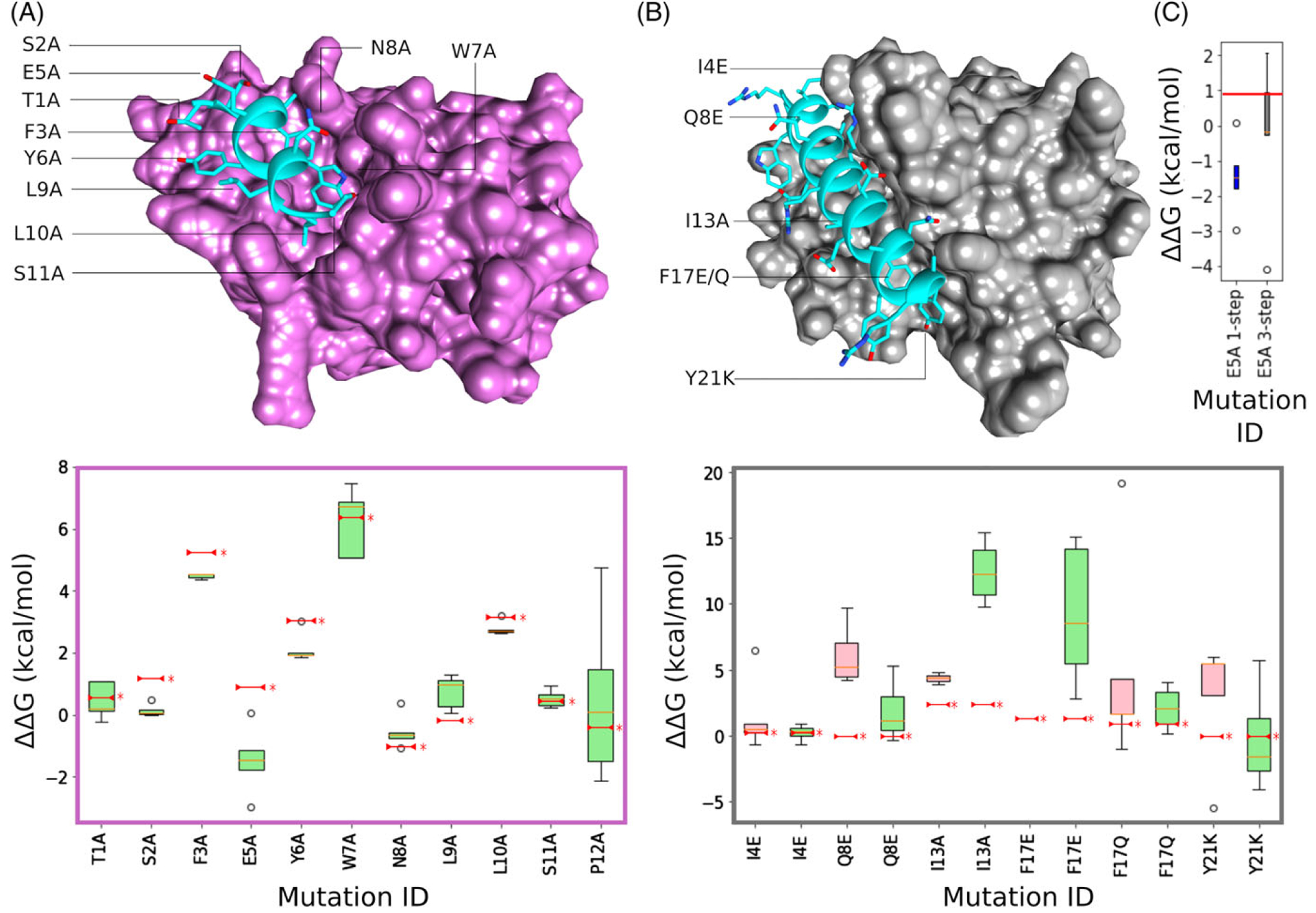
Atomistic structures and TI binding energy change box plots for benchmarking cases MDM2–PMI and MCL2–Bim. (A) PMI peptide (blue) in complex with MDM2 (pink). Box plot below structure shows changing binding energy for each mutation with five TI replicates in each distribution. Published experimental values are marked by a red line and *. (B) Bim peptide (blue) in complex with MCL2 (gray). Associated box plot below shows distributions for both 1-step (red) and 3-step (green) protocols. (C) Box plot showing improved TI prediction using 3-step protocol for MDM3–PMI E5A mutation (red line = published experimental value)

E5A is a different story as it involves a charge change. The handling of charges is widely recognized as problematic for alchemical free energy calculations and a tractable solution has yet to be proposed.³⁹ In the context of peptide design, it is necessary only to correctly predict whether a mutation will have a damaging or beneficial effect, that is, produce a positive or negative ΔΔG. In order to investigate the optimal parameters for calculating charge change mutation ΔΔG using TI, we explored the literature for a test case with a greater number of mutations involving charged residues. The complex formed by the Bim peptide and MCL-1 target was chosen on the basis that experimental kD measurements were available for four charge change mutations⁹ and a low-resolution crystal structure of the system was available in the PDB.⁴⁰ This structure was processed in the same manner as MDM2-PMI, using MD to generate a relaxed system and clustering to extract a structure representing the dominant conformational state. TI calculations were carried out on six mutants, four of which involved a charge change. The results of TI calculations using different protocols and parameters are shown in Figure 2B.

Initial runs were performed over 15 ns, using a 1-step protocol, and taken as the mean of five replicates. All five replicas of a given mutation were then run in parallel using both 1-step and 3-step protocols. In the 3-step protocol, charges were turned off over a separate series of lambdas before the transition between side chains. A separate set of calculations were then carried out to gradually switch the mutated side chain charges back on. Conversely, the 1-step approach involves transitioning to the mutant side chain with charges switched on.

Using the mean of five replicates, the first round of TI calculations using the 1-step protocol showed mixed success in correctly predicting positive or neutral energy change. Performing additional post-processing on the TI output lead to some improvement. Post-processing consisted of plotting each lambda and removing outliers, followed by removing the first nanosecond of production before integration. However, Q8E and Y21K mutations bore little resemblance to experimental values, and the F17E mutation consistently lead to complex dissociation. TI calculations were then repeated using the 3-step protocol. Q8E and Y21K mutation values were much closer to experimental values and F17E did not dissociate. Interestingly, the I13A mutation performed significantly worse using the 3-step protocol. This suggests that for mutations that do not involve a charge change, the 1-step protocol might be preferred. F17Q, the other uncharged mutation, saw no significant difference between 1-step and 3-step approaches. In addition to different step protocols, a variety of equilibration and production times were tested. Surprisingly, longer timescale of either yielded no significant improvements (Supporting Information Figure S1).

In light of results indicating that the 3-step protocol improves charge-change mutation calculation, it was applied to the problematic E5A in the PMI-MDM2 system. The results in Figure 2C show significant improvement in accuracy, supporting this set of conditions as optimal for charge change cases. Applying the 3-step protocol to PMI-MDM2 cases with no charge change produced a decrease in performance. This further supported that the 3-step protocol should be avoided for mutations that do not involve a charge change.

Having satisfactorily benchmarked the approach using cases from the literature, we next applied the methodology to a peptide we had previously shown binds to EME1, disrupting the MUS81–EME1 complex and reducing cell viability in cancer cell lines.⁵ The MUS81–EME1 complex interface is large (buried surface area 7094 Å) and EME1 is comprised of two domains connected by a flexible linker. The C-terminal MUS81 peptide (residues 538–551, amino acid sequence: RTLSQLYCSYGPLT) found to inhibit this interaction only interacts with the C-terminal domain of EME1. All but this domain was removed (residues 305–455) for simulations to minimize the computational cost. To get an interesting set of mutations to test with TI, Rosetta was used to predict potentially beneficial mutations by scanning all single point mutations over the MUS81 peptide.

The structure was first relaxed with MD to generate an ensemble representing the conformational exploration of MUS81–EME1. Ensemble members were then subject to the introduction of single mutations by Rosetta. Rosetta score for each mutation was compared with the native structure score and mutations producing a lower energy score were visually inspected. After discarding visually poor candidates, thermodynamic integration calculations were conducted on the remaining best (most frequently predicted) mutations to more accurately assess mutation effect. Visually poor candidates were mostly comprised of Rosetta predictions for large hydrophobic residues that project away from the target into the solvent. MUS81–EME1 binding was found to be well optimized and the only MUS81 mutation predicted to improve binding significantly was S546 W (Figure 3). In order to optimize further, non-canonical amino acids (NCAA) were also tested (Supporting Information Table S1). NCAA diversity allows more nuanced design of surface shape, core packing, and hotspot interaction geometry.

FIGURE 3.

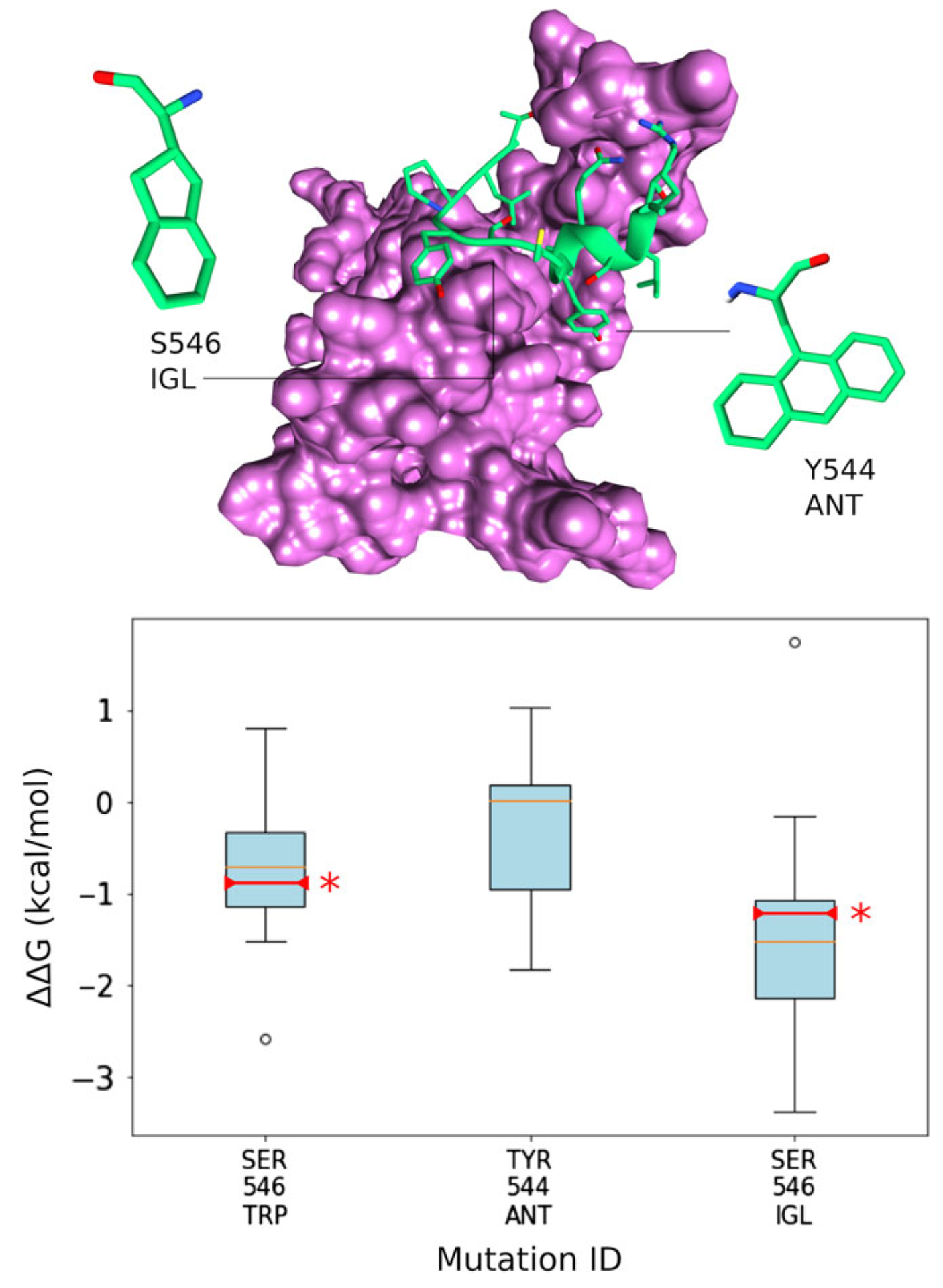
MUS81–EME1 atomistic structure and box plots showing TI predictions of canonical and non-canonical amino acid mutation. EME1 is depicted in pink and the MUS81 fragment peptide is shown in green. Subsequent experimental validation of predictions is marked on the box plots by a red line and *

To ensure the best chance of successfully incorporating different sized amino acids, different target conformational states were generated. The EME1 target structure was subjected to 50 ns × 10 replicates of molecular dynamics (MD). The resulting trajectories were then clustered by conformation to generate a representative backbone ensemble. Proteins are dynamic and usually explore many different conformations. Generating a representative ensemble of backbones therefore increases the chances of finding complementary interface geometry when mutations are introduced. Each backbone was treated equally although it should be noted that their root conformational clusters were not equally populated. Using this approach, another mutation was predicted to improve binding affinity: S546IGL. This large hydrophobic residue is shown in atomistic stick representation in Figure 3. A Y544ANT mutation, predicted by Rosetta, failed to show improvement at the TI step.

In order to experimentally validate these predictions fluorescence polarization (FP) assays were carried out (Figure 4A). The resulting K_d changes were converted to ΔΔG (kcal/mol) and marked on Figure 3 TI calculation boxplots. Experimental validation of Y544ANT was not possible as this mutation rendered the peptide insoluble. Experimental values were in close agreement with computational predictions. Serine 546 mutations to Tryptophan and the non-canonical IGL confirmed significant improvements in binding affinity. Changes in cell viability were also measured to assess the effects of candidate peptide’s disruption to the MUS81–EME1 complex. Specifically, we investigated effects on pancreatic adenocarcinoma RWP1 cells and HEK293T cells. Overall the results confirm binding energy measurements, particularly for HEK293T viability, which correlate well with experimental K_ds (Figure 4B). We note here that inhibition of MUS81–EME1 has significant effects on both cell lines, with effects being much stronger on RWP1. As MUS81–EME1 is involved in DNA repair, a known vulnerability of strongly proliferating cells, such inhibition may be a venue for cancer treatment.

FIGURE 4.

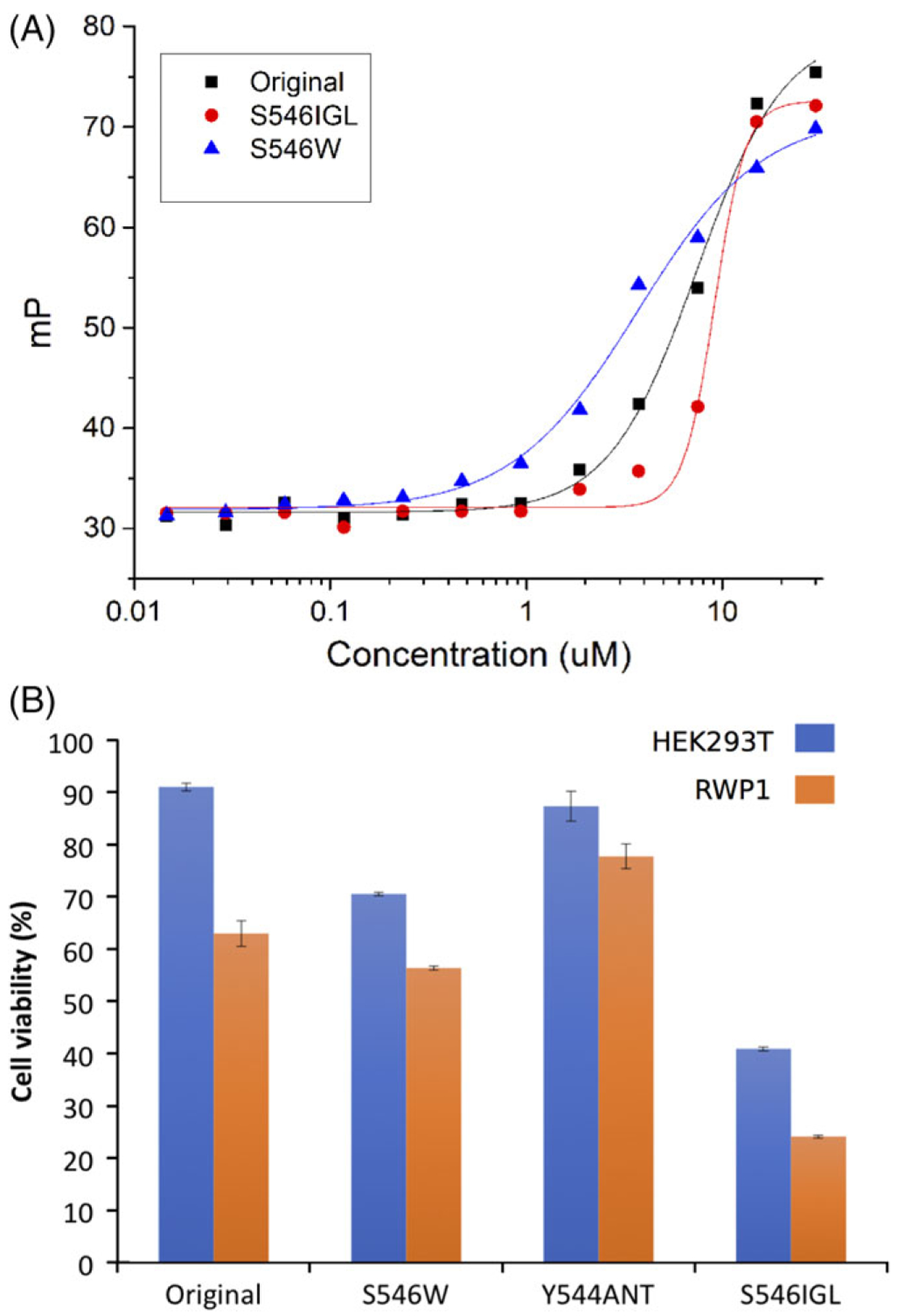
Fluorescence polarization and Alamar blue cell viability assays. Fluorescence polarization binding curves of Mus81 original, S546 W and S546IGL peptides to the EME-1 protein. All measurements were taken at room temperature (25°C), 25 mM Tris, 150 mM NaCl, and 5 mM BME at pH 7.0, after 20 min of equilibration. Experimental validation of the effect of Mus81 peptides on cell viability, as measured by the Alamar blue assay. Cells were treated with various concentrations of Mus81 original, S546W, Y544ANT, and S546IGL peptides for 72 hr (data shown using 50 μM of peptides). Orange bars represent effects of peptides on cancer (RWP1) cells and blue bars represent effects on HEK293T cells. Experiments were done in triplicate. Data represent mean values

Various statistical analyses of TI prediction relationships to experiment values were carried out for each of the systems under investigation (Table 1). Root mean square (RMS) error is expectedly large in cases involving charged residue changes. This is even more starkly reflected by the mean unsigned error (MUE), where the error increases according to the number of charge changes. Correlations also reflect the ability to handle charge changes and strongly show the utility of the 3-step protocol. Area under ROC curve (AUC) shows that our ability to predict whether or not a mutation is destabilizing is approximately halved for the charge change dominated case, but that the 3-step protocol recovers approximately 50% of accuracy (Table 2).

TABLE 1.

Speed of AMBER16 GPU TI simulations on single tesla P100 GPU card

Transformation	Total atoms (complex)	Total atoms (peptide)	Time (complex)/λ window (hr)	Time (peptide)/λ window (hr)
TYR → BUG	28 537	7598	1.67	0.95
THR → ANT	29 300	8736	1.67	0.96
IGL → SER	27 159	7960	1.53	0.94

TABLE 2.

Statistical analysis

	MDM2	Bim 1-step	Bim 3-step	MUS81
Root mean square error	4.25	5.54	6.53	1.08
Mean unsigned error	1.07	4.03	2.58	0.8
Pearson’s r	0.9	0.13	0.92	0.89
Spearman’s P	0.67	0.05	0.9	-
Area under ROC curve	0.81	0.43	0.66	0.51

4 |. DISCUSSION

Robust and reliable free energy methods for the prediction of protein–peptide binding affinity are of high value to the drug discovery process. Aided by the significant speedup of GPUs, rigorous free energy calculations can be applied to the rational design of peptide therapeutics. GPU-accelerated AMBER TI code was recently enabled from the Merck–Rutgers collaboration and demonstrated reliable and reproducible predictions on a drug discovery relevant dataset. Here, we applied this approach to peptide therapeutic design and assessed the performance of peptide–protein binding using AMBER16 in combination with Rosetta.

Employing the 3-step protocol triples the resources required for each TI calculation. Currently there is little consensus over whether the 3-step protocol affords improvement in accuracy over the 1-step approach. Our results suggested that the 3-step protocol produces significant accuracy improvements for mutations involving charged residues. This is intuitive given that switching charges on and off in steps one and three reduces the chance of severe clash with extreme lambda values.

Surprisingly however, while the 3-step protocol increases accuracy for charged residues, we have noticed a large deviation from the experimental values for big hydrophobic residues (Figure 2 and Supporting Information Figure S1). These results suggest that the 1-step protocol is recommended where a big hydrophobic residue is involved. The three-step protocol apparently does not converge well for those cases (Supporting Information Figure S2), making it necessary to extend the sampling further than the regular one-step protocol to reach convergence.

This study indicates that high terminal flexibility can cause problems for TI calculation. The P12A mutation was a good example of this, not having a clear anchoring interaction and being slightly exposed to the solvent. Such instability is not exclusive the proline as all mutated resides show the same behavior. This made it difficult to sample a representative set of conformations for the system states, a key requirement for accurate TI results. It is suggested therefore that for such cases, more conformational sampling may be required to achieve convergence of the simulations and optimal accuracy. However, in the P12A case, doubling the simulation time did not produce stable results. It is likely that the key states involved at this position are not well defined or not accessible in a reasonable time scale. In such situations, an ad hoc solution may be applied for binding energy predictions with experimental accuracy.

Our results indicate that different conditions can be proscribed, depending on the type of mutation under consideration. In particular, where a mutation is accompanied by a change in charge, the 3-step protocol should be used, though lengthening equilibration or production simulation times produces little improvement in accuracy. Conversely, if the mutation does not involve charge change, the 3-step protocol should always be avoided, and the time-scale and number of replicates can likely be limited to x and y respectively to most efficiently utilize the available resources.

We believe the increase in speed afforded by GPU accelerated TI, and consequent robustness, will help drive decisions in medicinal chemistry and accelerate the pace of drug discovery.