Correcting signal biases and detecting regulatory elements in STARR-seq data

Abstract

High-throughput reporter assays such as self-transcribing active regulatory region sequencing (STARR-seq) have made it possible to measure regulatory element activity across the entire human genome at once. The resulting data, however, present substantial analytical challenges. Here, we identify technical biases that explain most of the variance in STARR-seq data. We then develop a statistical model to correct those biases and to improve detection of regulatory elements. This approach substantially improves precision and recall over current methods, improves detection of both activating and repressive regulatory elements, and controls for false discoveries despite strong local correlations in signal.

Gene regulation is of foundational importance to nearly all biological processes, and variation in gene regulatory activity plays a major role in human disease risk (Lee and Young 2013; Parker et al. 2013; Finucane et al. 2015). A major step toward measuring regulatory activity across the human genome has been the development of high-throughput reporter assays such as STARR-seq (Arnold et al. 2013) that allow regulatory element activity to be quantified with high-throughput sequencing rather than with optical detection of a fluorescent or luminescent signal.

High-throughput reporter assays create substantial analytical challenges that are distinct from other sequencing-based genomic assays. There is significant local variation in high-throughput reporter assay signal. We show here that, across data from several laboratories, most of that variation can be explained by features of the underlying genomic sequence and experimental procedures rather than by regulatory element activity. For example, nucleotide composition can alter PCR efficiency leading to under- and overrepresentation of some sequences. Meanwhile, highly repetitive sequences often do not align uniquely to the human reference genome, also biasing signal estimates. Additional analytical challenges include that STARR-seq signals can be both positive and negative, reflecting activation and repression, and the boundaries of regulatory elements are typically unknown and must therefore be estimated from the data. Those challenges together impact signal representations, hinder estimation of regulatory element activity, and cause false positives and false negatives when left unaddressed.

Taken together, key requirements of statistical methods to analyze STARR-seq data are the ability to identify and estimate the effect of both activating and repressing regulatory elements while also correcting for underlying sequence biases in high-throughput reporter assays. A statistical model was recently introduced that corrects technical biases and detects regulatory elements in STARR-seq, but the model is limited to detecting only activating regulatory elements (Lee et al. 2020). Considering repression is a crucial gene regulation mechanism (Courey and Jia 2001), overlooking repressive elements may limit understanding of gene regulation with STARR-seq. To overcome that challenge, our correcting reads and analysis of differentially active elements (CRADLE) model takes a two-step approach. First, CRADLE uses a generalized linear regression model to estimate and correct major biases that we have identified in STARR-seq data. Next, CRADLE detects regions with statistically significant regulatory activity from the bias-corrected signals while rigorously controlling FDR. In doing so, CRADLE substantially improves the use of STARR-seq by providing a robust estimation of regulatory activity and improved visualization of raw signals.

Results

DNA sequence biases STARR-seq signals

To identify sources of signal variance in STARR-seq, we analyzed data from two whole-genome STARR-seq studies completed in different laboratories and in different human cell models: A549 (Johnson et al. 2018) and HeLa-S3 cells (Muerdter et al. 2018). Each study followed a similar protocol in which an input STARR-seq library was generated by cloning randomly fragmented genomic DNA into the 3′ untranslated region (UTR) of a reporter gene. The input library was then assayed by transfecting it into cultured human cells where the cloned DNA fragments regulate their own transcription into mRNA. The expression of each random fragment as mRNA was then measured with high-throughput sequencing. Finally, regulatory activity was estimated by comparing the expression of each fragment in the output library relative to its abundance in the input library.

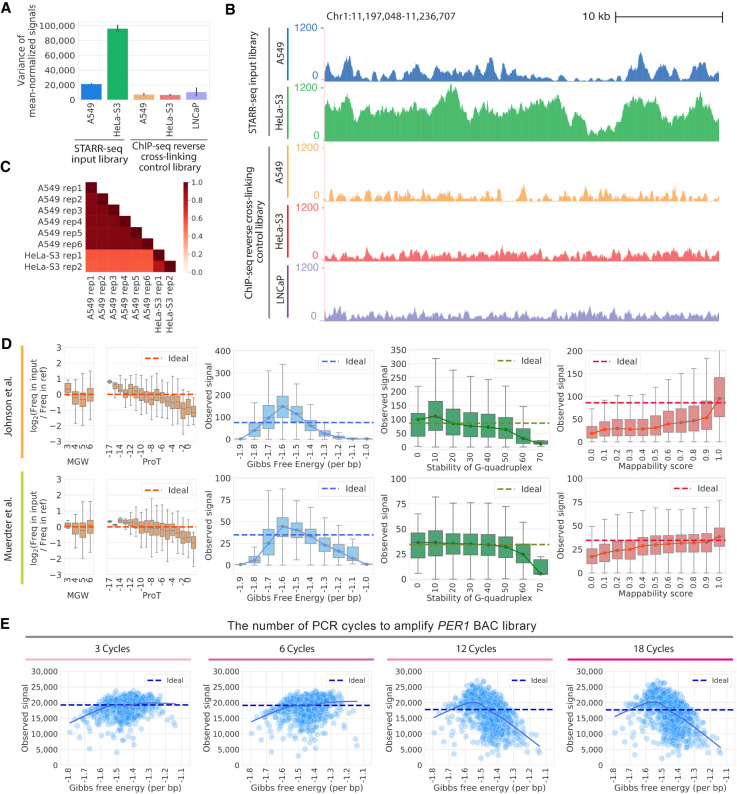
The STARR-seq input libraries showed substantially more signal variance than is observed in the controls for other genomic assays such as for ChIP-seq (Fig. 1A,B; The ENCODE Project Consortium 2012). That variance in STARR-seq input signal was consistent across replicates and between studies (Fig. 1C), more so than for ChIP-seq input signal (Supplemental Fig. S1). Here, we analyzed four potential sources of variance in STARR-seq signal: (1) DNA structure influencing DNA fragmentation, cloning or other enzymatic reactions, thus affecting which DNA fragments are available in the assay library (Poptsova et al. 2014); (2) differences in the Gibbs free energy of DNA fragments influencing multiplex PCR efficiency, leading to preferential amplification of some fragments (Cheung et al. 2011; Benjamini and Speed 2012; Hansen et al. 2012; Jiang et al. 2015; Love et al. 2016; Teng and Irizarry 2017); (3) G-quadraplexes in the genome impairing amplification by DNA polymerase (Chambers et al. 2015; Rhodes and Lipps 2015); and (4) biases resulting from differences in the mappability of short read sequences to the reference human genome, for example, owing to repetitive sequences (Derrien et al. 2012).

Figure 1.

Technical biases affect STARR-seq signal. (A) STARR-seq input libraries have higher signal variance than ChIP-seq input control libraries. Variance in per base signal in individual RPKM-normalized libraries are plotted for Chromosome 1. The error bars indicate variance between replicates. The number of replicates plotted is as follows: six replicates for STARR-seq A549 data; two replicates for STARR-seq HeLa-S3 data; three replicates for ChIP-seq A549 data; two replicates for ChIP-seq HeLa-S3 data; three replicates for ChIP-seq LNCaP data. (B) Representative browser signal tracks are shown for STARR-seq and ChIP-seq input libraries (Chr 1: 11,197,048–11,236,707). Signals are RPKM-normalized. (C) Pearson's correlations of STARR-seq input library signals in 1-bp windows along Chromosome 1. (D) DNA sequence biases impact STARR-seq signals. STARR-seq signals are plotted for 500-bp windows with varying degrees of bias for the following physical properties of DNA: fragment-end DNA structures, Gibbs free energy, G-quadruplex structure, and mappability. Whiskers extend 1.5 times the interquartile range. Center lines in the boxes show the medians. In plots of fragment-end bias, minor groove width (MGW) and propeller twist (ProT) are plotted and the ideal is log₂(Freq in input/Freq in ref)=0. In plots of other biases, the ideal line is the median signal. (E) PCR amplification introduces bias into STARR-seq libraries. The impact of Gibbs free energy bias is shown for PER1 BAC libraries amplified with different numbers of PCR cycles (3, 6, 12, and 18 cycles). Each point represents the sum of signals in a 500-bp window from three technical replicates. The solid line is a lowess fit line. The dashed ideal line is the median signal across all windows.

We found evidence that each source of bias influences the signal observed when sequencing STARR-seq libraries. To model biases attributed to DNA secondary structure, we computationally estimated the minor groove width (MGW) and propeller twist (ProT) at the 5′ ends of DNA fragments (Zhou et al. 2013). We analyzed 5′ ends of DNA fragments because they are not modified in the end-repairing process of generating STARR-seq libraries (Poptsova et al. 2014). We observed distinct biases in 5′ MGW and ProT (Fig. 1D). Consistent with signal biases caused by preferential fragmentation, ApG and GpG dinucleotides are most underrepresented at the 5′ ends of STARR-seq fragments, which were previously reported to be less prone to shearing (Supplemental Fig. S2; Poptsova et al. 2014). To estimate biases caused by differences in the thermodynamic stability of complementary DNA strands, G-quadruplex structure, and mappability, we binned the genome into 500-bp windows. We then used data from previous studies to estimate the Gibbs free energy of the duplexed DNA strands (Protozanova et al. 2004), stability of G-quadruplex structure (Chambers et al. 2015), and the fraction of redundant mappable positions in the reference genome for each window (Fig. 1D; Derrien et al. 2012). Fragments with the highest Gibbs free energy, highly stable G-quadruplex structure, and low mappability all had substantially depleted STARR-seq signals. Those trends were consistent across both whole-genome STARR-seq studies (Johnson et al. 2018; Muerdter et al. 2018).

To evaluate whether biases in estimated Gibbs free energy are caused by differences in PCR amplification efficiency, we generated DNA fragment libraries from a bacterial artificial chromosome (BAC) using between three and 18 cycles of PCR. The BAC contained 211 kb surrounding the PER1 gene on human Chromosome 17. DNA fragments with extreme Gibbs free energy were depleted from the final library, and particularly so after 12 or more PCR cycles (Fig. 1E). That observation also indicates that signal from output STARR-seq libraries will have more severe PCR-related biases than that from input libraries owing to the additional 15–16 PCR cycles used (Johnson et al. 2018; Muerdter et al. 2018), and that minimizing PCR can substantially reduce this source of bias.

Modeling biases in STARR-seq signal guides improved experimental designs

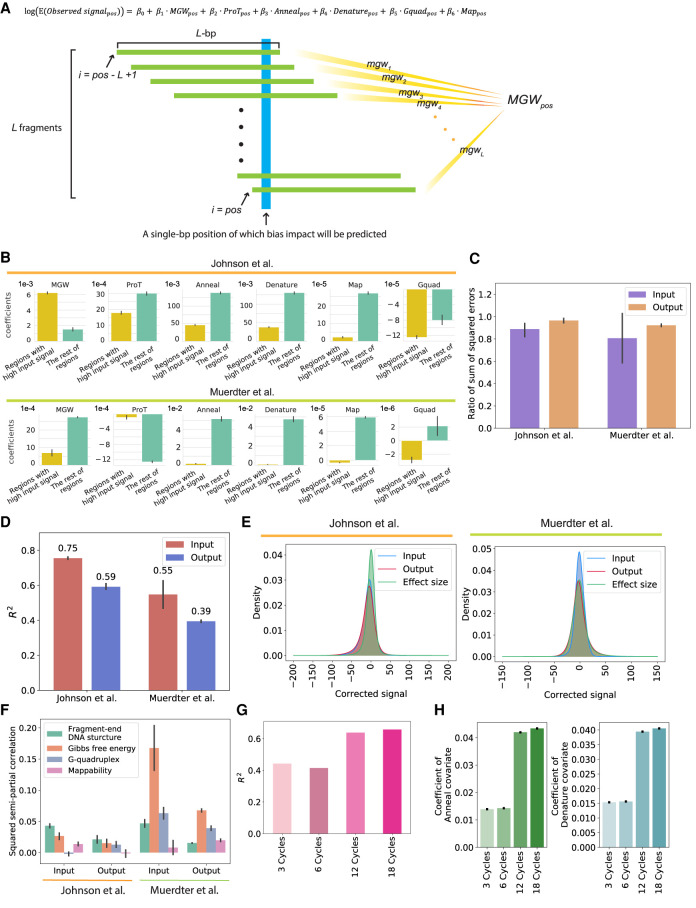
To model the aforementioned biases in STARR-seq signal, we developed a generalized linear regression model (GLM) with covariates to model DNA structure (Zhou et al. 2013) in fragment ends, annealing and denaturing efficiency of DNA fragments related to their Gibbs free energy (Protozanova et al. 2004), stability of G-quadruplex structure (Chambers et al. 2015), and mappability (Derrien et al. 2012) as a reduced set of independent variables (Fig. 2A). We then fit that model to predict biases in STARR-seq signals across the genome (Fig. 2A). To improve model fit, particularly at the extremes of STARR-seq signal, we separately modeled regions with high STARR-seq signal that we observed to have significantly different coefficients for biases related to the fragment Gibbs free energy (Fig. 2B). We used a biased structured sampling approach to better fit the tails of the signal distribution (Fig. 2C; Methods). The model fit was robust to the specific thresholds used in the biased structured sampling approach (Supplemental Fig. S3). Together, these adjustments improve model fit at the extremes of STARR-seq signal where biases are most strong and thus most likely to impact analysis.

Figure 2.

The CRADLE GLM approach accurately predicts signal bias. (A) Equation of the GLM to predict the impact of technical biases and approach used by CRADLE to calculate bias covariates. To estimate bias effects for each position (blue), we used a window centered on that position that was twice the median fragment length, L. We assume L number of fragments (green) in a window and that each fragment is L-bp in length. To calculate each bias covariate for the position, we combined quantitative measures from L fragments. (pos) Single-bp position; (MGW_pos) minor grove width; (ProT_pos) propeller twist; (Anneal_pos) annealing efficiency; (Denature_pos) denaturation efficiency; (Gquad_pos) G-quadruplex structure; (Map_pos) mappability. (B)–(F) The results from the GLM fitted with Johnson et al. (2018) STARR-seq data (six input libraries and five 0-h dex-treated output libraries) and Muerdter et al. (2018) STARR-seq data (two input libraries and two no-inhibitor-treated output libraries). For C–F, the results were visualized for Chromosome 1. (B) Coefficients in input libraries for regions with signals above and below the 90th percentile (“Regions with high input signal” and “The rest of regions,” respectively). (C) Ratio of the sum of squared errors with structured sampling to the sum of squared errors with random sampling are plotted for regions with extremely high signals (above the 99th percentile). (D) Variance explained by CRADLE are plotted. The R² values are from GLMs fitted with input and output STARR-seq libraries. The error bars indicate variance between replicates. (E) Distribution of GLM residuals and the STARR-seq effect sizes are shown after correction. (F) Squared semipartial correlations are shown for fragment-end, Gibbs free energy, G-quadruplex, and mappability covariates. The error bars indicate variance between replicates. (G) The R² values of the GLMs are shown for PER1 BAC libraries amplified with different numbers of PCR cycles. (H) Coefficients of anneal and denature covariates are shown for the GLM fitted with PER1 BAC libraries. The error bars show a 95% confidence interval.

Overall, the GLM fit the observed signals with R² up to 0.75 for input STARR-seq libraries (Fig. 2D). The model fit output libraries less well than the input libraries, owing in part to regulatory activity also contributing to differences in STARR-seq signal. Still, the GLM showed comparable performance to using input library in predicting biases of output library, despite the high degrees of freedom (Supplemental Fig. S4). The GLM had significantly better fit than the model that simply binned genome and used GC content in each bin as a covariate (Supplemental Fig. S5). We think the improved fit of the GLM over the simple GC-content model is partially a result of the nonlinear relationship of GC content and signal (Fig. 1D). Residuals from the model approximately follow a normal distribution (Fig. 2E), supporting model fit. We also estimated the extent to which each covariate independently explained variation in STARR-seq signal (Fig. 2F). Overall, the median of the explained variation across the two studies showed fragment-end sequences, and Gibbs free energy explained the greatest amount of signal variation. In the data from Johnson et al. (2018), G-quadruplex bias in the input STARR-seq library and mappability bias in the output STARR-seq library had a negative marginal contribution to total predictive power but the effects were minor. Meanwhile, in the data set of Muerdter et al. (2018), Gibbs free energy was the major contributor to signal biases, showing relatively large variance between replicates. This shows distinctive bias effects in the two input libraries, which aligns with relatively small correlation between two signals compared to Johnson et al. (Fig. 1C). These findings indicate that most of the variance in STARR-seq signal can be attributed to technical biases; it is important to model distinct relative contributions of those biases in different STARR-seq library preparations.

Most of the parameters we modeled are not readily mitigated by modifying experimental procedures. As examples, reducing PCR cycles may not be feasible when template is limited, and DNA fragmentation is required for STARR-seq. Therefore, we investigated whether the GLM can instead statistically correct biases in STARR-seq signal. First, we fit the aforementioned GLM (Fig. 2A) to fragment sequencing libraries generated with different numbers of PCR cycles and calculated the amount of variance explained by the GLM. Consistent with our earlier observation that additional PCR cycles increased Gibbs free energy bias (Fig. 1E), the model explained more signal variance when more PCR cycles were used (Fig. 2G). There was also a monotonic increase in the coefficients for fragment annealing and denaturing efficiency based on the Gibbs free energy (Fig. 2H). Those results show that the GLM can correct different amounts of bias resulting from different experimental designs.

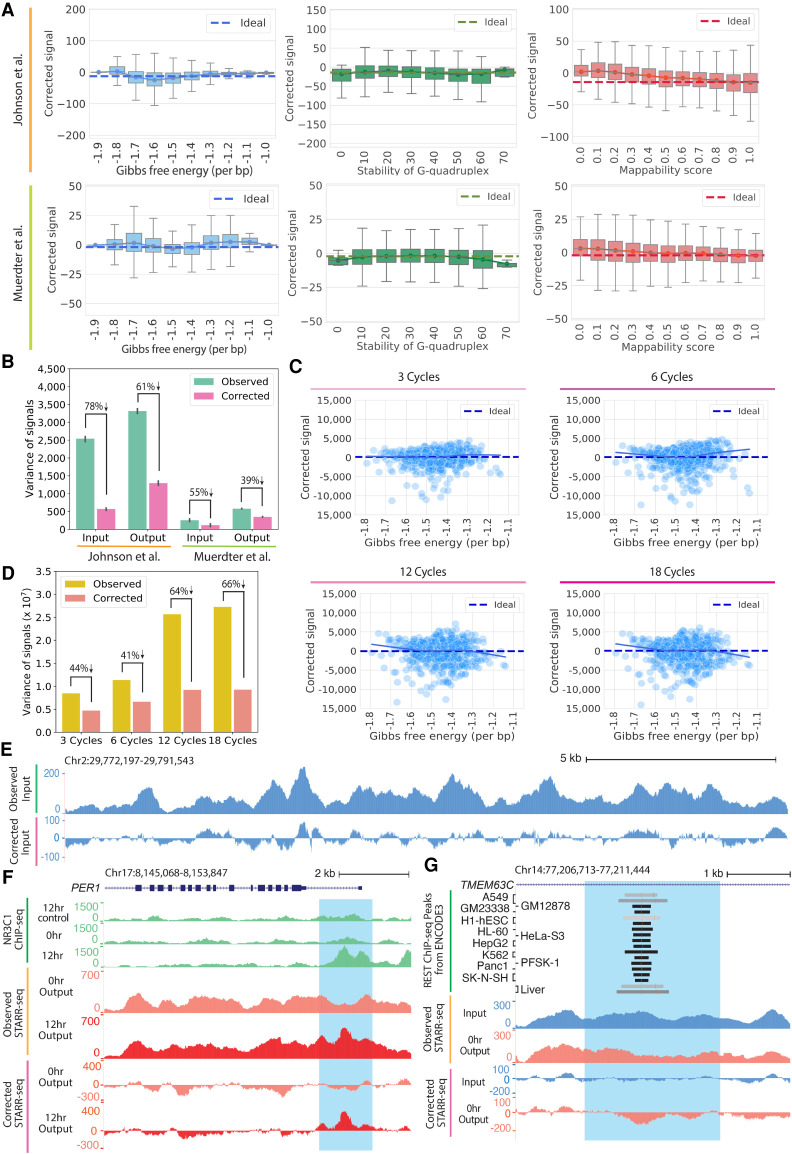
Removing technical biases in STARR-seq improves visualization

Visualizing signals from functional genomic assays is often a critical step in quality control, experiment interpretation, integrative analysis, and hypothesis generation. Because substantial signal variation in STARR-seq is attributed to the underlying DNA sequence, however, it is challenging to gain useful information from visual inspection of uncorrected STARR-seq signals. That visualization can be substantially improved by instead using the residuals from the GLM. For example, across the two genome-wide studies analyzed here (Johnson et al. 2018; Muerdter et al. 2018), the GLM reduced signal variance by between 40% and 80%, resulting in approximately zero-centered corrected signals (Fig. 3A,B). Further demonstrating generality across specific experimental procedures, the GLM also effectively corrected biases caused by different amounts of PCR (Fig. 3C,D). An example of the resulting correction for a 19-kb region is shown in Figure 3E, where the GLM residuals allow for clearer visual identification of elements with activating or repressive regulatory effects. For example, a region near the PER1 gene that is well known to have activating regulatory activity in response activation of the glucocorticoid receptor (NR3C1) (Reddy et al. 2012; Johnson et al. 2018) showed much clearer indication of activity after correction (Fig. 3F). Similarly, an example of a repressive element that is bound by the REST repressor (The ENCODE Project Consortium 2012) is also better represented in corrected signals compared to uncorrected observed signals (Fig. 3G). To generalize the argument that correcting biases better reflects regulatory activity, we compared observed and corrected signal for NR3C1-binding regions and REST-binding regions that had corresponding motifs (Supplemental Fig. S6; The ENCODE Project Consortium 2012). Overall, corrected signal provides more stable background signal and shows clearer regulatory activity (Supplemental Fig. S6). Together, these results show that our model accounts for a substantial variation of signals in STARR-seq data and improves visualization of signals.

Figure 3.

The CRADLE GLM approach corrects technical bias. (A) STARR-seq signals are plotted for 500-bp windows along Chromosome 1 after removing technical bias with CRADLE. Signal is balanced despite varying degrees of technical biases. The ideal line is the median corrected signal. Whiskers extend 1.5 times the interquartile range. Center lines in the boxes show the medians. (B) Variance in observed signals and CRADLE-corrected signals in 1-bp windows are shown along Chromosome 1. The error bars indicate variance between replicates; six input libraries and five 0-h dex-treated output libraries in Johnson et al. (2018) are plotted; two input libraries and two no-inhibitor-treated output libraries in Muerdter et al. (2018) are plotted. (C) STARR-seq signals are shown for PER1 BAC libraries amplified with different numbers of PCR after removing technical bias with CRADLE. Each point represents the sum of corrected signals in a 500-bp window from three technical replicates. The solid line is a lowess fit line. The dashed ideal line is the median signal across all windows. (D) Variance in observed signals and CRADLE-corrected signals in 1-bp windows are shown after correcting the PER1 BAC libraries. (E) Representative signal tracks are shown for STARR-seq input libraries before and after CRADLE correction (Chr 2: 29,772,197–29,791,543). (F) STARR-seq and ChIP-seq signal tracks are shown in the dex-responsive PER1 locus. Observed and corrected signal of Johnson et al. (2018) are presented for 0-h dex-treated (untreated) and 12-h dex-treated output libraries. ChIP-seq signal tracks are not corrected. The highlighted region (Chr 17: 8,151,204–8,152,809) is a known dex-responsive activating regulatory element. (G) STARR-seq signal tracks are shown for the TMEM63C locus. Observed and corrected signal of Johnson et al. (2018) are presented for input and 0-h dex-treated output libraries. The highlighted region (Chr 14: 77,207,895–77,210,261) contains a REST motif and is occupied by REST in multiple cell types.

Correcting biases improves detection of regulatory signals embedded in STARR-seq data

To next detect genomic regions with significant STARR-seq activity, we developed a new method that rigorously models two key features of the assay. First, STARR-seq measures both activation and repression of reporter gene expression (Johnson et al. 2018), thus being able to detect both activation and repression is important. Second, local STARR-seq signals are highly correlated (e.g., Fig. 3E). That correlation, if not appropriately considered, can lead to nonconservative control of type I errors if not modeled (Lun and Smyth 2014).

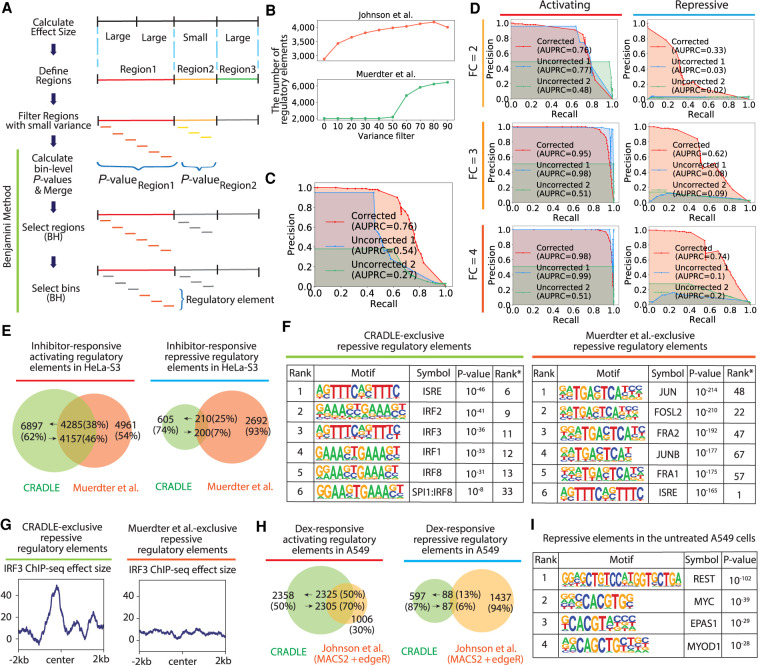
To overcome those challenges, we developed a two-step statistical approach to merge locally correlated signals while maintaining well-calibrated control of the false discovery rate (FDR) (Fig. 4A). Briefly, our approach first detects signals in broad genomic regions and then identifies more specific sources of signal variation within those regions. The approach is based on previous work from Benjamini (Benjamini and Hochberg 1995; Benjamini and Bogomolov 2014). To increase power of detecting regulatory elements, we also used independent filtering to remove regions without enough signal variation to reject the null (Fig. 4A,B; Bourgon et al. 2010).

Figure 4.

Detection of regulatory elements with CRADLE. (A) CRADLE regulatory element pipeline is shown in diagram. Effect sizes are calculated in windows of uniform length. Contiguous windows with similar effect sizes are merged into regions before filtering regions with small variance. Regions are binned and a statistical test is performed on each bin to compare corrected input and output signals. Bin-level P-values are merged to generate a region-level P-value before performing a region-level Benjamini–Hochberg (BH) procedure. Regions selected by the first BH procedure were used to perform a bin-level BH procedure to identify regulatory elements. (B) The number of detected regulatory elements is dependent on the variance filter. (C,D) Precision recall curves, using corrected and uncorrected signals in the simulation study. To detect regulatory elements with uncorrected signals, two statistical approaches were used: (1) fitting uncorrected signals to Poisson GLM and performing Wald test (“Uncorrected 1”) and (2) using a Poisson distribution with the mean of uncorrected input signals as a null distribution and testing the significance of the mean of uncorrected output signals (“Uncorrected 2”). (C) Precision recall curve when signals are simulated with mixed fold change (2, 3, 4) and a mix of activating and repressive elements. (D) Precision recall curve when signals are simulated with a fixed fold change (FC) and with a fixed regulatory activity (either activating or repressive). (E–G) Comparison of inhibitor-responsive regulatory elements detected by CRADLE and Muerdter et al. (2018). (E) The Venn diagram shows the overlap of regulatory elements detected by both studies. (F) Transcription factor motif enrichment is shown for inhibitor-responsive repressive regulatory elements exclusively detected by each study. Rank* is the rank of motif in the other study. (G) The mean of IRE3 ChIP-seq effect size is plotted for inhibitor-responsive repressive regulatory elements exclusively detected by each study. (H) The Venn diagram shows the overlap of dex-responsive activating and repressive regulatory elements detected by CRADLE and Johnson et al. (2018). (I) Transcription factor motif enrichment in A549 steady-state repressive regulatory elements detected by CRADLE.

To show the benefit of correcting technical biases when detecting regulatory elements in STARR-seq data, we simulated whole-genome STARR-seq signals with embedded activating and repressive regulatory elements across a range of effect sizes (Fig. 4C,D). We then used the method described above to detect regulatory elements in corrected or uncorrected signals. When detecting regulatory elements with uncorrected signals, we used statistical tests based on a Poisson distribution to avoid unfairly reducing the performance by violating key assumptions of a t-test. Specifically, we used two approaches: (1) fitting uncorrected signals to a Poisson GLM and Wald tests to reject the null (“Uncorrected 1”), and (2) using a Poisson distribution with the mean of uncorrected input signals as a null distribution and testing for a significant difference in the means of uncorrected output signals (“Uncorrected 2”).

Overall, correcting biases with the GLM substantially improved the precision of detecting regulatory signals, especially at more stringent detection thresholds (Fig. 4C,D). In contrast, the majority of regulatory elements with uncorrected signals were false positives (Supplemental Fig. S7). Performance improvement was particularly pronounced when detecting repression (Fig. 4D), where the area under the precision recall curve (AUPRC) increased by 0.64 when correcting signals.

Overall, repressive signals are more difficult to detect. In the repression simulation with corrected signals, recall and precision were worse than in the activation simulation by as much as 0.43 in AUPRC. The decreased AUPRC was mainly a result of small simulated output signals of repressive regulatory elements that were largely filtered out by the overall variance filter. However, this simulation result still shows correcting technical biases helps to decrease false positives in detecting both activation and repression.

Improved detection of regulatory elements in STARR-seq data

We used the CRADLE method described above to call regulatory elements in data from two published whole-genome STARR-seq studies (Johnson et al. 2018; Muerdter et al. 2018). Muerdter et al. (2018) measured differential regulatory activity in response to inhibitors that blocked interferon response. The study reported 12,010 inhibitor-responsive regulatory elements with 2892 repressive elements, with their analysis pipeline that used binomial distribution and hypergeometric tests (Arnold et al. 2013; Muerdter et al. 2018). CRADLE detected a similar number of regulatory elements at 20% FDR (N = 11,997), 815 of which were repressive (Supplemental Table S1). Although the activating elements detected by each method had overlap up to 46%, repressive elements were largely different between the methods (Fig. 4E).

To investigate the biological properties of regulatory elements detected exclusively by each method, we used motif enrichment analysis to detect potential biologically important sequence signals in the nonoverlapping sets of regulatory elements. Motifs for interferon-responsive transcription factors (TFs) were most strongly enriched in the CRADLE-exclusive repressive elements (Fig. 4F; Supplemental Table S2). In contrast, activator-protein 1 (AP-1) TF motifs were most significantly enriched in the repressive elements unique to the Muerdter et al. (2018) analysis, with interferon response motifs ranked lower by enrichment (Fig. 4F; Supplemental Table S3). The motifs enriched in shared repressive regulatory elements of CRADLE and Muerdter et al. (2018) overall corresponded with the motifs enriched in CRADLE-exclusive repressive regulatory elements (Supplemental Tables S2, S4). In addition, the CRADLE-exclusive repressive elements showed higher enrichment for IRF3 ChIP-seq signal (Fig. 4G). We noted that CRADLE estimated positive effects for 1704 repressive elements uniquely detected by Muerdter et al. (Supplemental Fig. S8; Muerdter et al. 2018), suggesting they are false positives attributed to the biases in STARR-seq signal. Indeed, subsequent motif analysis of those repressive elements with positive effects revealed enriched NF-kB motifs, not corresponding to the experimental design.

The Johnson et al. (2018) study used STARR-seq to measure changes in regulatory activity in response to the dexamethasone (dex) across time. The study used MACS2 (Zhang et al. 2008) and edgeR (Robinson et al. 2010) together to identify 4835 dex-responsive regulatory elements at 0.05 FDR with 3311 activating elements. With the data from Johnson et al. (2018), we used CRADLE to detect regulatory elements both in untreated A549 cells and in response to dex at the same 0.05 FDR (Supplemental Tables S5, S6). That analysis identified 10% more dex-responsive regulatory elements (N = 5368) than the methods used by Johnson et al. (2018), with 4683 activating and 685 repressive dex-responsive regulatory elements (Supplemental Table S6). As with the comparison to the Muerdter et al. (2018) analysis, we observed little overlap in repressive elements whereas activating elements showed up to 70% overlap (Fig. 4H). Overall, those repressive regulatory elements identified by CRADLE in each study had higher control library signals than activating regulatory elements, demonstrating CRADLE requires a region to have enough coverage to be reliably detected as repressive (Supplemental Fig. S9).

To validate the newly identified repressive elements, we again used motif enrichment analysis to identify potential sequence signals consistent with repressive elements. The motif for the RE1-silencing transcription factor (REST), a well-characterized repressive factor (Chong et al. 1995), was most enriched in repressive regulatory elements in untreated A549 cells (Fig. 4I; Supplemental Table S7). Meanwhile, the motif enrichment in dex-responsive regulatory elements exclusively detected from CRADLE corresponded to previous findings about NR3C1 biology. Namely, for the dex-responsive activating regulatory elements, the NR3C1 DNA binding motif was most enriched followed by cofactor AP-1 transcription family (Supplemental Table S8), corresponding to the motifs enriched in the shared dex-responsive activating regulatory elements (Supplemental Table S9). For the dex-responsive repressive regulatory elements, the AP-1 motif was most enriched, consistent with the role of AP-1 in NR3C1-mediated activation and repression (Supplemental Table S10; Gupte et al. 2013; Johnson et al. 2018; McDowell et al. 2018).

We also validated some of the 240 A549 steady-state REST-binding repressive regulatory elements using two independent studies (Supplemental Fig. S10; van Arensbergen et al. 2019; Doni Jayavelu et al. 2020). Although neither of these studies used A549 cells, we assumed the repressive activity of the REST-binding repressive regulatory elements could be validated in other cell models because REST is a common repressor in diverse cell lines. We intersected the REST-binding repressive regulatory elements with the regions tested by Doni Jayavelu et al. (2020) that used massively parallel reporter assay (MPRA) test repressive activity and observed 30 elements in common (Supplemental Fig. S10). Of those, 27 elements (90%) had repressive activity in Doni Jayavelu et al. (2020), whereas two elements did not have coverage and one element did not show repressive activity. The one nonrepressive element is likely a result of the small overlap with their tested region (27 bp) that did not cover the REST motif. We also compared our repressive element calls with the data from a genome-wide survey of regulatory elements (SuRE) signal (van Arensbergen et al. 2019). The SuRE signal in the REST-binding repressive regulatory elements showed repression in that study that was significantly different from both random and activator-binding elements (Supplemental Fig. S10).

Discussion

We showed that a substantial fraction of the variation in STARR-seq signal can be explained by DNA sequence features that are related to experimental artifacts rather than regulatory element activity. Overall, biases in PCR amplification had some of the strongest impacts on sequence biases in STARR-seq, and we show here that minimizing the amount of PCR can reduce variation in signals. DNA structure bias at the ends of fragments is possibly caused by preferential fragmentation, cloning, or efficiency as an enzymatic substrate. The efficiency of adding adaptors in cloning or in reverse transcription could be also affected by DNA sequences or structures at fragment ends (Zheng et al. 2011). Potential opportunities to mitigate those biases could include using multiple enzymes from different species that have different sequence biases or further refinement of reaction conditions. Similarly, increasing read length could mitigate mappability-induced biases by decreasing the mappable space in the genome; G-quadruplex structure bias might be alleviated by optimizing experimental conditions to destabilize those structures. However, mitigating technical biases using a statistical model is much faster and easier. We showed the GLM had significant predictive power that led to substantially stabilized STARR-seq signals. Indeed, corrected signals showed noticeably reduced variance and improved visualization of regulatory activity.

With corrected signals from the GLM, we detected regulatory elements with substantially improved accuracy compared to previous models. CRADLE especially improved the identification of repressive regulatory elements that were challenging to detect previously, as we showed via simulations, comparisons to other studies, and through investigation of DNA binding motifs for repressive factors. That improvement will allow for a more complete understanding of the diversity of regulatory element activity across the human genome.

Lee et al. (2020) also recently addressed the need to model biases in STARR-seq to improve detection of regulatory elements. Conceptually, both approaches model physical characteristics of genomic sequence that substantially influence STARR-seq signal and develop novel peak calling approaches. In terms of implementation, there are differences in model parameters (e.g., how CRADLE models PCR biases), model fitting (e.g., weighted sampling of the tails of the coverage distribution), and peak calling methods. In terms of performance evaluation, we evaluated CRADLE over a broader range of simulations, and in doing so we showed that the reported False Discovery Rates are well-calibrated. We also showed that CRADLE is especially able to detect repressed regulatory elements.

Our work on CRADLE also opens up the possibility of developing analogous statistical models for other high-throughput sequencing technologies. Many high-throughput sequencing technologies share common experimental steps that cause technical biases in STARR-seq. In that regard, CRADLE exemplifies how those biases can be statistically modeled and corrected, thus allowing effect estimation and peak calling from data with a mean of zero. Of course, each sequencing technology may have assumptions that are distinct from STARR-seq and have other major bias effects that were not modeled in CRADLE. For example, antibody specificity might be one of the major bias sources in ChIP-seq. More studies need to be done to determine the scope of the applicability of CRADLE.

Methods

Downloaded data

For STARR-seq data, we downloaded FASTQ files of whole-genome STARR-seq that used A549 and HeLa-S3 cells from Johnson et al. (2018) and Muerdter et al. (2018), respectively. Those files were downloaded from NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) repository (Barrett et al. 2013) with accession codes available in those studies (GSE114063, GSE100432).

For ChIP-seq data (The ENCODE Project Consortium 2012; Davis et al. 2018), we downloaded ChIP-seq FASTQ files with following GEO accession codes: GSE91296 for A549 control ChIP-seq; GSE91275 for A549 0-h dex-treated NR3C1 ChIP-seq; GSE91235 for A549 12-h dex-treated NR3C1 ChIP-seq; GSE92032 for HeLa-S3 control ChIP-seq; GSE101280 for A549 REST control ChIP-seq; GSE101362 for A549 REST ChIP-seq; GSM935570 for HeLa-S3 IRF3 ChIP-seq; GSM935339 for HeLa-S3 IRF3 control ChIP-seq.

Processing of high-throughput sequence data

FASTQs files were aligned to the human genome reference assembly hg38 with Bowtie 2 (version 2.3.4.3) (Langmead and Salzberg 2012), using the ‐‐sensitive option and requiring a MAPQ of at least 30. Fragments were discarded if they are aligned to gap, centromere, and telomere that are available in UCSC Gap and Centromere Table Browser (Hinrichs et al. 2006) and ENCODE blacklist regions (Amemiya et al. 2019). Alignment of paired-end data sets were further restricted to require properly paired alignments. Unnormalized and RPKM-normalized (‐‐binSize 1) bigWig files were generated by bamCoverage subcommand in deepTools (version 3.0.1) (Ramírez et al. 2016) using ‐‐extendReads. The reported average fragment length was used to extend reads when generating single-end bigWigs. Unnormalized and normalized bigWig files were used for CRADLE inputs files and for visualizing signals in genome browser tracks, respectively. A549 ATAC-seq FASTQs were processed as above but were aligned to hg19 and required a less stringent MAPQ score (≥5). Peaks were called for ChIP-seq data sets using MACS2 (Zhang et al. 2008) with an FDR threshold of 0.05. For NR3C1-binding sites, we first called peaks using MACS2 (Zhang et al. 2008), independently for 0-h dex-treated NR3C1 ChIP-seq samples and 12-h dex-treated NR3C1 ChIP-seq samples with respective control ChIP-seq samples. Then we merged those peaks and used edgeR (Robinson et al. 2010) to perform differential testing at FDR 0.05 and selected peaks with positive effect size to detect NR3C1-binding regions. The coordinates of autosomal inhibitor-responsive regulatory elements previously reported in hg19 (Muerdter et al. 2018) were converted to hg38 with liftOver (Hinrichs et al. 2006).

PER1 BAC library preparation and sequencing

Purified PER1 bacterial artificial chromosomes (BACs) (CH17-212C17; Chr 17: 7,981,103–8,192,310) were harvested from Escherichia coli using standard protocols. Following DNA shearing using the Covaris S2 instrument, the BAC DNAs were size-selected using solid phase reversible immobilization (SPRI) beads. STARR-seq insert libraries were prepared using the NEBNext DNA Library Prep Master Mix kit and 50 ng of template DNA. Adapted DNAs were enriched in triplicate reactions via 3, 6, 12, or 18 cycles of PCR using the NEB Q5 PCR kit. The resulting libraries were characterized on the Agilent Tape Station before 50 cycles of paired-end sequencing on the Illumina MiSeq platform. FASTQs were aligned as above. We checked duplicated rate for each cycle using Picard (MarkDuplicates, version 2.14.0). The mean duplicate rate for each cycle is as follows: 0.3% in Cycle 3; 0.5% in Cycle 6; 1.3% in Cycle 12; 1.9% in Cycle 18.

Data processing for bias covariates

To obtain DNA structure parameters for fragment-end bias, we estimated minor groove width (MGW) and propeller twist (ProT) for all 5-mers (total 1024 sequences) using DNAshape (Zhou et al. 2013). For Gibbs free energy parameters, we used the estimated Gibbs free energy for all dimers (Protozanova et al. 2004). For G-quadruplex structure parameters, we used bigWig files that reported stability of G-quadruplex structure in the whole genome with accession code GSE63874 in GEO (Chambers et al. 2015). For mappability scores, we downloaded the human mappability score bigWig files for 36-mer and 50-mer (Derrien et al. 2012), using accession codes (ENCSR821KQV, ENCSR093EEM) in ENCODE (The ENCODE Project Consortium 2012; Davis et al. 2018). For those G-quadruplex structure bigWig and mappability bigWig files, the genomic coordinates were in hg19 assembly, so we used the liftOver tool (Hinrichs et al. 2006) to convert them to hg38.

Measuring technical biases in STARR-seq libraries

To investigate fragment-end bias, we counted the frequency of 5-mers starting 2 bp upstream of the 5′ end of positive strands of fragments in STARR-seq input libraries (Johnson et al. 2018; Muerdter et al. 2018). To identify enriched fragmentation sites, we compared that observed 5-mer frequency distribution to that observed in the reference genome (hg38) excluding gaps, centromeres, telomeres that are available in UCSC Gap and Centromere Table Browser (Hinrichs et al. 2006), and ENCODE blacklist regions (Amemiya et al. 2019). To examine Gibbs free energy, G-quadruplex structure, and mappability bias, we binned human Chromosome 1 into 500-bp windows using a 250-bp stride. We estimated the amount of potential technical bias in a window by calculating the mean of per base measure of those biases using previously reported values: Gibbs free energy value (Protozanova et al. 2004); the percent of mismatch for G-quadruplex structure bias (Chambers et al. 2015); and mappability score (Derrien et al. 2012). This analysis was limited to the PER1 BAC when estimating Gibbs free energy bias in the PER1 BAC library.

Correcting technical biases in STARR-seq

We used the technical bias covariates in a general linearized model (GLM) with a Poisson distribution and log link to correct STARR-seq signals. An estimate of the 90th percentile of observed coverage in input libraries (Isig_P90) was calculated using 1-kb bookended regions. To ensure the GLM models effects across the range of observed signals, we trained the model using a structured sampling strategy to select bookended regions without replacement such that the final training set is approximately 10⁶ bases in length. We evenly partitioned the training set to fit regions with input signal above and below Isig_P90. The set of regions below Isig_P90 were further evenly partitioned into the following percentile bins of observed coverage: [0, 20); [20, 40); [40, 60); [60, 80); [80, 90). To ensure representation across the upper tail of the STARR-seq signal distribution, regions above Isig_P90 were asymmetrically partitioned as follows: 62.5% of regions were evenly divided into the following percentile bins of observed coverage, [90, 92); [92, 94); [94, 96); [96, 98); [98, 99), whereas the remaining 37.5% of regions were binned into the 99th percentile of coverage. With Muerdter et al. (2018) data, we empirically found preferentially sampling Chromosome X in the last two bins improved performance.

Single base positions with observed input signal (Isig_pos) above and below Isig_P90 were independently fit to the GLM. To predict the total bias effects at each single base position, we used windows twice the length of the median fragment length (L) centered on the position of interest (Fig. 2A). We assumed each position was covered by L number of hypothetical fragments of L bp length with each overlapping by a single base. We then multiplied the same bias covariates for all fragments in that window with each covariate to the power of a unique beta as follows:

$$\begin{array}{ccc}\mathrm{Observed}\mathrm{signa}{\mathrm{l}}_{pos}& \sim \prod _{i=pos-L+1}^L& MG{W}_i^{{\beta }_1\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_1^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\\ & & \cdot Pro{T}_i^{{\beta }_2\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_2^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\\ & & \cdot Annea{l}_i^{{\beta }_3\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_3^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\\ & & \cdot Denatur{e}_i^{{\beta }_4\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_4^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\\ & & \cdot Gqua{d}_i^{{\beta }_5\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_5^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\\ & & \cdot Ma{p}_i^{{\beta }_6\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_6^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)}\end{array}$$ (1)

Each beta coefficient represents the relative effect of each bias predictor. Here, we assumed the set of betas is the same for all overlapping fragments. Then in log space, observed signal can be estimated with using the sums of bias covariates in the GLM as follows:

$$\begin{array}{ccc}& & \log (E\left(\mathrm{Observed}\mathrm{signa}{\mathrm{l}}_{pos}\right))=\\ & & \left({\beta }_1\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_1^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(MG{W}_i\right)\\ & & +\left({\beta }_2\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_2^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(Pro{T}_i\right)\\ & & +\left({\beta }_3\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_3^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(Annea{l}_i\right)\\ & & +\left({\beta }_4\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_4^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(Denatur{e}_i\right)\\ & & +\left({\beta }_5\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_5^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(Gqua{d}_i\right)\\ & & +\left({\beta }_6\cdot I(Isi{g}_{pos}<Isi{g}_{P90})+{\beta }_6^{\mathrm{\prime }}\cdot \left(1-I(Isi{g}_{pos}<Isi{g}_{P90})\right)\right){\sum }_{i=pos-L+1}^L\log \left(Ma{p}_i\right)\end{array}$$ (2)

MGW and ProT values were calculated using DNAshape (Zhou et al. 2013) for the two 5-mers starting from 2 bp external to both 5′ ends of each hypothetical fragment. MGW_i and ProT_i was obtained by multiplying those two MGW and ProT values, respectively.

We used the nearest-neighbor model (SantaLucia 1998; Protozanova et al. 2004) to estimate the Gibbs free energy of each hypothetical fragment. To estimate the relative melting temperature (T_m) of each fragment, we divided Gibbs free energy of a hypothetical fragment by the number of dimers in that hypothetical fragment and by the fixed entropy value (Protozanova et al. 2004). T_m values were normalized to range of [0, 1]. To model the nonlinear dependency of annealing and denaturing efficiencies to T_m, normalized T_m values in the ith fragment (T_m,i) were mapped to two exponential functions as follows:

$$\begin{array}{c}\mathrm{Annea}{\mathrm{l}}_i=\left(e^{T_{m,i}}-\frac{{10}^6-e}{{10}^6-1}\right)/\left(\frac{{10}^6-1}{1-e}\right)\\ \mathrm{Denatur}{\mathrm{e}}_i=\left(e^{-T_{m,i}}-\frac{{10}^6-e}{{10}^6-1}\right)/\left(\frac{{10}^6-1}{1-e}\right)\end{array}$$ (3)

Those mapped values were used for Anneal_i and Denature_i in the GLM Model.

To obtain Gquad_i for each hypothetical fragment, we used the maximum of G-quadruplex structure stability value in that sequence (Chambers et al. 2015). To obtain Map_i for each hypothetical fragment, we used a k-mer mappability score file (Derrien et al. 2012), where k-mer is a sequencing length, and multiplied the mappability scores of both ends of a fragment.

After fitting the GLM, the bias predicted by the model at each base position was removed by subtracting the estimated bias effect from the observed signal. To avoid false positives, positions with fewer than 10 observed overlapping fragments and with no signal in output libraries are not reported in the corrected signal file. The minimum number of observed overlapping fragments required for a position to be reported is parameterized (-mi) in the correctBias subcommand in CRADLE.

Modeling technical biases in STARR-seq libraries with only GC content

To show our sophisticated approach of modeling bias has better fit than simply modeling GC content, we took the following approach. We binned the genome with nonoverlapping sliding windows with six different window sizes ranging from 10 to 1000 bp. We randomly selected approximately 10⁶ bases in length for a training set. Then with the training set, we calculated GC content in each bin for which the size corresponded to the chosen window size and used the GC content as a covariate in fitting GLM with Poisson distribution and log link. We independently fitted each replicate in the GLM. Then we used the resulting coefficients (intercept and the coefficient of GC content) to estimate the bias impact for the regions that were not in the training set.

Normalizing signals in STARR-seq

To make the corrected signals from the GLM comparable between replicates, for example, by correcting for overall differences in sequencing, we normalized STARR-seq signals between replicates using linear regression. We used the training set sampled as mentioned above and regressed per-nucleotide signal from each library against a common replicate of the input library. We estimated the slope in the linear regression and divided observed signals in each library by that slope estimate.

Evaluating model fit

To determine how well the CRADLE GLM explained variance in observed signal, we calculated R² with observed and predicted signals across Chromosome 1 for each STARR-seq library. To calculate R², we fitted the GLM in CRADLE and calculated the sum of squares (SSQ) by adding up squared residuals. Then, we calculated total SSQ, the sum of the squared difference of observed signals and the mean signal. By using the SSQ and total SSQ, we calculated R² with the following equation:

$$R^2=1-\left(\text{SSQ}/\text{total}\text{SSQ}\right).$$

Evaluating the contribution of each covariate to model fit

To estimate the contribution of each bias type, we calculated semipartial correlations for Chromosome 1 using the GLM. To assess each technical bias type, we excluded bias covariates that model corresponding bias type in fitting the GLM. For example, we excluded “anneal” and “denature” covariates when assessing Gibbs free energy bias impact. The R² of these models were calculated as above and subtracted from the R² of the full model.

Calling regulatory elements with CRADLE

Genomic regions possessing regulatory activity were identified using a modified Benjamini method (Benjamini and Bogomolov 2014). We first binned the genome into windows (1.5 × L) and determined the effect size of each window by subtracting the mean corrected signal in input libraries from the mean corrected signal in output libraries. Each window was classified to one of the three types, using the following standard:

• Type(window_x) = 1 if (effect size > 0 and |effect size| > 99th percentile of absolute effect sizes),

• Type(window_x) = −1 if (effect size < 0 and |effect size| > 99th percentile of absolute effect sizes),

• Type(window_x) = 0 otherwise.

The threshold of the 99th percentile of absolute effect sizes was chosen to classify windows because the majority of windows are not expected to encode regulatory activity. Contiguous windows of the same type, including Type 0, were merged to form regions for statistical testing. These regions were then binned with nonoverlapping bins of which the length is 1/6 × L. In each bin, the input and output STARR-seq signals were compared using Welch's t-test (Welch 1947) to account for potential differences in variance. Individual bin-level P-values from the same region were merged to a region-level P-value via the method of Simes (1986). To increase our power to detect potential regulatory regions for final testing, regions with small overall variance were removed from further analysis independently of the statistical test used (Bourgon et al. 2010). Specifically, we ranked regions according to their overall variance and then applied the overall variance filter that removed 0%–90% of regions with low variance using 10% intervals. P-values for regions passing each threshold were subjected to the first BH procedure (Benjamini and Hochberg 1995) using a parameterized FDR value (-fdr). Then, we chose the threshold of the overall variance filter that returned the greatest number of selected regions from the first BH procedure. To identify bins that have regulatory activity, bin-level P-values from the Welch's t-test in the selected regions were then subjected to the second BH procedure with new FDR adjusted by the following:

$$\mathrm{New}\mathrm{FDR}=\left(\mathrm{predetermined}\mathrm{FDR}\right)\times \left(\frac{\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{selected}\mathrm{regions}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{regions}}\right).$$

Contiguous bins that encode regulatory activity with the same sign of effect sizes were merged in the final output and the minimum P-value was reported.

Simulation of STARR-seq signals

To evaluate the performance of CRADLE, we simulated STARR-seq signals that maintained the observed sequence biases and expected variance across replicates. STARR-seq signals were simulated using a negative binomial distribution and mean-variance relationships estimated independently for input and output libraries from previously published STARR-seq data (Johnson et al. 2018). Simulated input and output signal matrices generated using 300-bp bookended windows along Chromosome 1 were used to estimate mean-dispersion relationship in DESeq2 (Love et al. 2014) before interpolation with the Scipy.interpolate.interp1d command in Python. To generate a set of predefined regulatory elements (N = 50,504), we randomly sampled ∼0.5% of total windows requiring that the selected windows be in at least the 70th percentile of coverage in the published input libraries. For each predefined regulatory element, we randomly assigned an absolute fold change [2, 3, or 4] and regulatory activity type [activating or repressing]. Predefined sets of regulatory elements with a specific fold change and regulatory activity type were generated as above using the specified fold change and regulatory activity types as described in text.

Five simulated STARR-seq input and output signals were generated using a negative binomial distribution. The mean parameters used to generate the simulated input and output signals were determined by calculating the mean window counts using the published input libraries (Johnson et al. 2018). The variance parameters were determined using either the input or output interpolation analyses described above. The mean parameters used to generate the simulated output signals were adjusted for predefined regulatory elements windows by multiplying or dividing the mean signal by the predetermined fold change and determining the corresponding variance parameter.

Detecting regulatory elements in simulated data

To evaluate the effect of correcting STARR-seq signals on identifying regulatory elements, we used CRADLE to call regulatory elements before and after correcting biases in the simulated data sets. Owing to the normality assumption in Welch's t-test, we modified the CRADLE approach described above to call regulatory activity in uncorrected simulated signals. In place of the Welch's t-test, we used two alternative statistical approaches to compare uncorrected simulated input and output signals. First, we used a Poisson GLM as follows:

$$\begin{array}{cc}\log \left(E\right(\mathrm{signa}{\mathrm{l}}_i\left)\right)={\beta }_0+{\beta }_1\times \left(\mathrm{data}\mathrm{typ}{\mathrm{e}}_i\right)& \mathrm{data}\mathrm{type}=\left\{\begin{array}{cc}0& \mathrm{if}\mathrm{signa}{\mathrm{l}}_i\mathrm{is}\mathrm{from}\mathrm{input}\mathrm{libray}\\ 1& \mathrm{if}\mathrm{signa}{\mathrm{l}}_i\mathrm{is}\mathrm{from}\mathrm{output}\mathrm{libray}\end{array}\right\}\end{array}$$ (4)

We then performed the Wald test for β₁ with f distribution. Second, we followed a similar approach as used by MACS2 (Zhang et al. 2008). We used the mean input bin signal as the mean parameter in a Poisson distribution to calculate a P-value for the mean output bin signal. We called regulatory activity in corrected simulated signals as described above.

Motif enrichment analysis

Motif enrichment analysis was performed using the findMotifsGenome subcommand in the HOMER (Heinz et al. 2010) 4.10.1 software suite using the following parameters: -size given -mis 3 -mset vertebrates.

Plotting heatmaps

Heatmaps were plotted using deepTools command “computeMatrix” using a reference-point and “plotHeatmap” (Ramírez et al. 2016). In both cases, we specified single-nucleotide resolution using the option ‐‐binSize 1.

TF occupancy in CRADLE regulatory elements

To determine whether regulatory elements called by CRADLE are bound by TFs, we used the CRADLE pipeline to detect A549 steady-state activating and repressive regulatory elements from a previously published study (Johnson et al. 2018). We used the findMotifsGenome subcommand in the HOMER suite (version 4.10.1) (Heinz et al. 2010) with the parameters, -size given -mis 0 -mset vertebrates -find, to detect REST motifs in each repressive element and FOSL2, JUNB, and GABPA motifs in activating elements. For each element that encoded a specified motif, we intersected those elements with ENCODE ChIP-seq peaks for the corresponding TF in A549 cells (The ENCODE Project Consortium 2012; Davis et al. 2018).

Validation of REST-occupied repressive regulatory elements

Regions tested by Doni Jayavelu et al. (2020) in K562 cells (N = 7440) were intersected with repressive regulatory elements identified by CRADLE in A549 cells that also contained a REST motif and were bound by REST in the same cell line (N = 240) (The ENCODE Project Consortium 2012). Reported fold change values in K562 cells were compared for the intersection set except the two elements without coverage (N = 28), regions predicted by Doni Jayavelu et al. (2020) to be repressive elements (N = 3001), and control regions (N = 40).

Signals from a genome-wide Survey of Regulatory Elements (SuRE) in HepG2 and K562 cells (van Arensbergen et al. 2019) were compared in specific sets of regulatory elements identified by CRADLE in A549 cells. These regulatory elements included activating regulatory elements that contained either a FOSL2, GABPA, or JUNB motif and were bound by the corresponding TF in A549 (The ENCODE Project Consortium 2012) or repressive elements that likewise contained a REST motif and were bound by REST (N = 240) (The ENCODE Project Consortium 2012). A549 regulatory elements that contained a SNP in the genomes assayed in the SuRE study were excluded on a per genome basis. The minimum and maximum number of SNP-filtered elements compared for each TF are as follows: FOSL2 N = 650-651; GABPA N = 401-402; JUNB N = 723; REST N = 102.

We randomly generated a set of regions (N = 240) of fixed length (430 bp) controlling for accessibility (The ENCODE Project Consortium 2012) and dinucleotide composition. The fixed length was set to the median length of the compared repressive elements. In generating random regions, we excluded regions that overlapped gaps, centromeres, and telomeres that are available in UCSC Gap and Centromere Table Browser (Hinrichs et al. 2006) and ENCODE blacklist regions (Amemiya et al. 2019), or the following features defined by ChromHMM (Ernst and Kellis 2017) in K562 and HepG2 cells: promoters, promoter flanking regions, enhancers, CTCF enriched sites, and repressed regions. After applying the SNP-filter described above, we obtained 94 random regions.

Data access

The PER1 BAC data sets generated in this study have been submitted to NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE149914.

CRADLE is implemented in Python, and the source code is available in the Supplemental Code. CRADLE can be freely downloaded either from GitHub (https://github.com/ReddyLab/CRADLE) or pip (pip install cradle; https://pypi.org/project/CRADLE/). Instructions for installing and running CRADLE are available on the CRADLE GitHub page.

Competing interest statement

The authors declare no competing interests.