Abstract
Producing manual, pixel-accurate, image segmentation labels is tedious and time-consuming. This is often a rate-limiting factor when large amounts of labeled images are required, such as for training deep convolutional networks for instrument-background segmentation in surgical scenes. No large datasets comparable to industry standards in the computer vision community are available for this task. To circumvent this problem, we propose to automate the creation of a realistic training dataset by exploiting techniques stemming from special effects and harnessing them to target training performance rather than visual appeal. Foreground data is captured by placing sample surgical instruments over a chroma key (a.k.a. green screen) in a controlled environment, thereby making extraction of the relevant image segment straightforward. Multiple lighting conditions and viewpoints can be captured and introduced in the simulation by moving the instruments and camera and modulating the light source. Background data is captured by collecting videos that do not contain instruments. In the absence of pre-existing instrument-free background videos, minimal labeling effort is required, just to select frames that do not contain surgical instruments from videos of surgical interventions freely available online. We compare different methods to blend instruments over tissue and propose a novel data augmentation approach that takes advantage of the plurality of options. We show that by training a vanilla U-Net on semi-synthetic data only and applying a simple post-processing, we are able to match the results of the same network trained on a publicly available manually labeled real dataset.
Keywords: Image compositing, chroma key, tool segmentation
I. Introduction
Surgical instrument labeling is a generic problem in Computer-Assisted Interventions (CAI) [1]–[6]. Locating an instrument’s contour within a surgical scene has a wealth of potential applications. It is already, or in some cases is bound to become, an essential building block of many key clinical applications in Surgical Data Science [7]. To name a few: placing informative overlays on the screen or performing augmented reality without occluding instruments, subtracting surgical tools from the scene when building a tissue panorama, surgical workflow analysis, skills analysis and error detection, automatic endoscope camera calibration, visual servoing, surgical task automation, feature matching for 3D reconstruction, and in general any approach that takes advantage of real-time segmentation as a way of tracking a target across frames.
Early approaches for tool recognition either used positioning sensors (robotic surgery) [8] or embedded additional sensors [9] within the instruments. However, attempts to do so have shown many drawbacks besides a limited accuracy [10], [11]. In addition to the difficulties created by the added complexity due to the workflow alteration, additional sensors or tool modifications have to be able to overcome the harsh conditions of the instrument sterilization process [12].
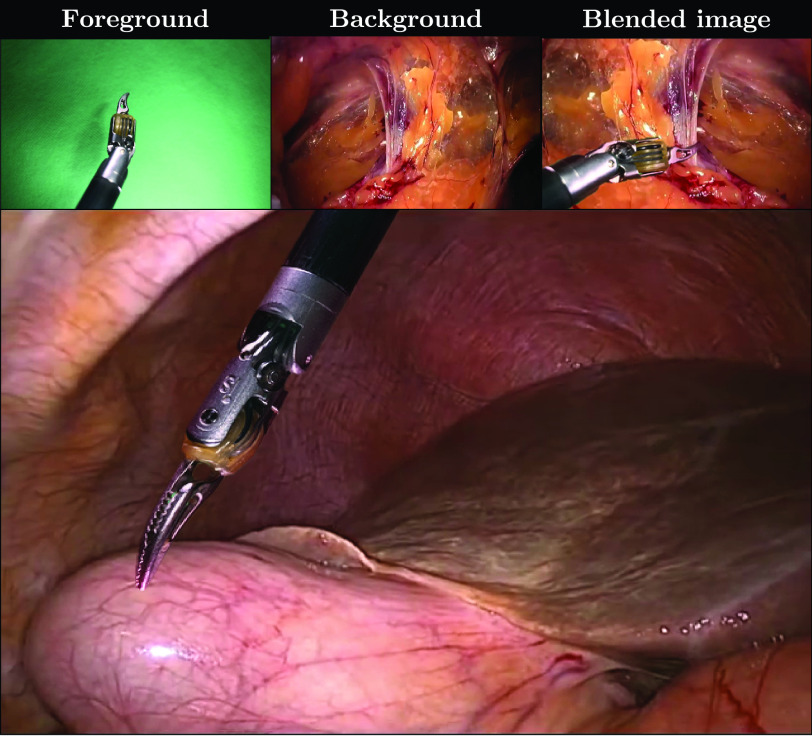
Recent machine learning advances have shown extraordinary progress in visual recognition. Yet, in the medical context in general, and for our task in particular, progress is typically restrained by the scarcity of available fine-grained annotations required for training purposes, and by the limited practicality and cost of creating such annotations at scale. In this paper, we explore the feasibility of using a chroma key (see Fig. 1 and supplementary material Fig. 2 and 3) to automatically generate large quantities of semi-synthetic yet realistic “ground truth” images and labels. As opposed to synthetic data, our generated images come from compositing real images. Hence, we refer to them as semi-synthetic. We use them to train a deep neural network for surgical tool segmentation. Given the proposed setup in Fig. 1, the key methodological challenge is the blending of instruments recorded over the chroma key onto tissue frames in such a way that the segmentation learned based on this semi-synthetic images generalizes to real clinical data. Stemming from this methodological challenge, it is a research question whether it is necessary to blend realistic images for learning the segmentation, or in contrast, it can be learned without the need for deploying sophisticated domain-specific blending mechanisms.
Fig. 1.
Blending process (top row). Blended image sample (bottom picture). Inspired by chroma key compositing in the movie industry, we show that segmentation models can be trained exclusively on a semi-synthetic dataset based on superimposition and data augmentation (as shown in the blended image above), achieving a comparable accuracy to those trained on manually annotated images. We demonstrate that the difficulty to synthesize a realistic border represents less of a problem for learning purposes when our stochastic mix of known blending methods (called mix-blend) is employed to superimpose objects, allowing for state-of-the-art segmentation performance.
Fig. 2.

Overview of the semi-synthetic generation method. We illustrate both the concept of source image and the process to generate semi-synthetic images. For an image to be considered as source image, it must fulfill two conditions. First, its labeling must be available or easier than a manual annotation of the tool in a real endoscopic image. Second, it must be a close approximation of a real clinical image so that when complementary source images are blended, the result is close to a real endoscopic image. The automatic segmentation of source images is hue-based for 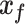 (detailed in section IV-C) and trivial for
(detailed in section IV-C) and trivial for 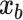 . We assume that the correct way to blend complementary source images to form a real clinical image is unknown. In this figure, three possible ways to do it are illustrated. A green arrow is shown to highlight a part of the semi-synthetically generated image, the border of the tool, and the tooltip itself, whose appearance differs depending on the choice of blending function (best viewed in the electronic version of the manuscript).
. We assume that the correct way to blend complementary source images to form a real clinical image is unknown. In this figure, three possible ways to do it are illustrated. A green arrow is shown to highlight a part of the semi-synthetically generated image, the border of the tool, and the tooltip itself, whose appearance differs depending on the choice of blending function (best viewed in the electronic version of the manuscript).
Fig. 3.

Multi-blend training iteration: in every training iteration a pair foreground-background is chosen and blended with one of the 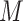 blending functions we decide to employ. To comply with (8), all
blending functions we decide to employ. To comply with (8), all 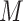 blending functions have to be chosen at least once during the training for each combination of
blending functions have to be chosen at least once during the training for each combination of 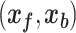 present in the dataset. After a training instance (image plus label) has been generated, it is passed to
present in the dataset. After a training instance (image plus label) has been generated, it is passed to 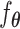 (see eq. 1). Mix-blend training iteration: following (11), the forward and background images randomly chosen from the training set are blended
(see eq. 1). Mix-blend training iteration: following (11), the forward and background images randomly chosen from the training set are blended 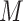 times, one per blending function approximator (
times, one per blending function approximator (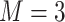 in our implementation). Then, a weighted sum of all the blended images is performed with random weights
in our implementation). Then, a weighted sum of all the blended images is performed with random weights 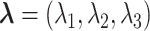 sampled from a Dirichlet distribution (see Fig. 1 in the supplementary material). As we model
sampled from a Dirichlet distribution (see Fig. 1 in the supplementary material). As we model 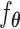 as a neural network, this figure illustrates the way of adding a training instance into each iteration’s mini-batch.
as a neural network, this figure illustrates the way of adding a training instance into each iteration’s mini-batch.
The paper is structured as follows. First, we comment on recent related articles that target different forms of image compositing to learn different tasks. We continue to explain our formalization of the learning problem and how this leads to the generation of the semi-synthetic training instances used to learn the segmentation. Then, we introduce a training strategy that adapts to our modelling of the images and way of blending. The material’s section contains a detailed description of the data used for the experiments and how we record it. In the implementation section, we develop on data augmentation, specific blending modes employed, and network training protocol. Finally, we explain the different experiments carried out to evaluate the performance of our methods, and discuss the results obtained.
Contributions. We propose a novel technique and theoretical framework to synthesize ground truth images and labels for image segmentation problems. We focus on instrument segmentation in endoscopic scenes. Our method relies on two sources of data: Sample instruments recorded over a chroma key; and images that only contain background tissue. In order to merge these two pieces of information we rely on existing blending methods and propose mix-blend. This novel blending approach relies on the probabilistic combination of a set of simple blending functions that act as a basis for blending. Furthermore, we introduce a Monte Carlo method to generate the blended training samples on the fly (during training), which fits well with Stochastic Gradient Descent (SGD) optimization solvers. This approach allows us to learn the segmentation without the need for advanced domain adaptation techniques. We also make public all our newly created datasets including: our semi-synthetic tool segmentation dataset containing 100K labeled images, our chroma key foreground dataset (14K labeled images), our background tissue dataset (6K images from 50 surgical procedures), and our real clinical testing set (514 manually labeled images from 20 surgical procedures).
II. Related Work
A number of classical surgical tool segmentation methods have been proposed with promising results, see e.g. [1], [2]. Recently, data-driven approaches based on Convolutional Neural Networks [3]–[5] have shown to be the leading technique to estimate an instrument-background segmentation of surgical scenes [13]. Despite the availability of such powerful methods, the tool segmentation task still represents a challenge due to a lack of large-scale fine-grained annotated datasets. As pointed out in the conclusions of the 2017 Robotic Instrument Segmentation Challenge [13], current instrument segmentation datasets, such as the one used in the challenge (only around 3K annotated images), are severely limited by the amount of data. In contrast, general-purpose computer vision datasets possess hundreds of thousands or millions of images (e.g. COCO, 330K manually segmented images). In order to circumvent the need for similar quantities of manual annotations, recent works have explored ways of reducing human effort. This has been of interest in both the computer vision industry [14]–[18] and the CAI community [6], [19]–[22]. There are two fundamental approaches to alleviate the manual effort. Either reducing the number of annotations needed or allowing for faster manual labeling. In the following paragraphs, we give an overview of both.
In [20], Maier-Hein et al. explored crowd-sourcing as a means of correcting weak labels generated from a small amount of annotated images (MICCAI Endoscopic Vision Challenge 2015). In their proposal, workers were provided with endoscopic images and corresponding estimated segmentations, which they had to correct with an interactive tool. The estimated segmentations were generated by an atlas forest (AF) method [23]. The authors trained an uncertainty estimator based on the predictions of the forest to regress confidence maps, providing the workers with only those areas of low confidence for correction. Although the results are encouraging, this method still requires an interactive segmentation setup and manual pixel-wise annotations. In another attempt to reduce the labeling effort, Nwoye et al.
[6] have recently suggested to use per-frame instrument presence classification labels as weak supervision for segmentation. Although they have shown promising performance for localization, it is still very challenging for these methods to provide a pixel-wise accurate segmentation of the instruments, which is crucial for applications such as visual servoing for surgical task automation. Besides, a labeled dataset for tool presence is mandatory. Another approach to alleviating the manual labeling effort is to employ unlabeled data to learn the endoscopic image domain representation. Ross et al.
[22] proposed to learn re-colorization as a pre-training task. They convert endoscopic images to CIELab and train a convolutional network in a fake/real adversarial scheme to regress the colour channels 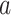 and
and 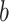 , giving L as an input. This auxiliary task allows them to reduce the amount of manually annotated data considerably. While showing promising results, pixel-wise annotations are still required. Alternatively to pre-training on a different auxiliary task, Yu et al.
[24] proposed to reduce the amount of labeling by exploiting temporal consistency present in surgical videos. In their work, a teacher network uses past and future video frames to produce a classification estimation for the current video frame. The teacher network is then employed to generate a larger dataset of weak labels based on unlabeled data, from which the student network learns, using the same information as input that is employed at testing time.
, giving L as an input. This auxiliary task allows them to reduce the amount of manually annotated data considerably. While showing promising results, pixel-wise annotations are still required. Alternatively to pre-training on a different auxiliary task, Yu et al.
[24] proposed to reduce the amount of labeling by exploiting temporal consistency present in surgical videos. In their work, a teacher network uses past and future video frames to produce a classification estimation for the current video frame. The teacher network is then employed to generate a larger dataset of weak labels based on unlabeled data, from which the student network learns, using the same information as input that is employed at testing time.
Recently, generative methods [12], [25] have shown potential to address the data scarcity problem in endoscopic vision. Alternatively to just reducing the number of labels or time required for dataset curation, dataset synthesis has emerged as an inexpensive approach to generate annotated images automatically. The work of Heimann et al. [19] proposed to synthetically embed an ultrasound (US) transducer into fluoroscopy images to generate a training set. The aim was to detect the in-plane probe’s position, orientation, and scale. To do so, the authors performed a computer tomography (CT) of a US probe and embedded it into real CT patient volumes, automatically generating radiographs and ground truth by a forward projection of the CT that contains the synthetically embedded US probe. A similar approach has been recently presented in [26], where authors show different aspects of the simulation that are key to bridge the gap between synthetic and real data.
In a non-medical context, there is an established research direction that aims to overcome the lack of annotated data using the so-called virtual setups or synthetically rendered scenes [27]. This approach is extremely challenging [28], [29]. As suggested by [30], many aspects have to be taken into account to synthesize high-quality scenes, often requiring advanced domain adaptation techniques to bridge the gap between synthetic and real data. To address the generalization difficulty addressed by virtually rendered setups, a new research stream focuses on compositing as opposed to rendering [15]–[18], [31]. In this line of research, training images are composed by a combination of visual elements coming from different sources. Augmentation techniques related to compositing, such as mixup where pairs of images are alpha-blended [32], have also been developed to improve generalization. In [31], authors proposed a method to embed synthetic objects of known geometry into real pictures. Although they manage to generate photo-realistic semi-synthetic images, their approach relies on a fine-grained model of the 3D scene geometry and the lighting conditions, which is not available in endoscopic videos.
Orthogonal to those techniques that aim to maximize the realism of training data, domain randomization [33] has emerged as a powerful technique to bridge the gap between simulation and target domain by doing exactly the opposite. The aim is to alter the synthetic data in a stochastic manner such that the deep networks concentrate on the essential features to solve the task. Reality is modelled as yet another variation of the source domain. In medical imaging, domain randomization has recently also shown promising results [34]. Toth et al. have successfully used this technique for 3D/2D cardiac model-to-X-ray registration, showing that unrealistic perturbations of the training data are useful to train a model for the task just based on synthetic training data.
In computer vision, image compositing is one of the possible approaches to perform domain randomization. This has been recently shown by several authors [15], [35]. In [15], Dwibedi et al. proposed to use automatic compositing to build a dataset for training a deep learning object detector. Even though image compositing approaches seem promising, they suffer from a recurrent issue, the unintended embedding of artificial features derived from the blending process into the synthetic images. This creates a bias in the dataset. That is, if all the objects that we are trying to detect are blended using the same method, let us say, a crude cut-and-paste, they are all subject to have a particular boundary derived from the cut-and-paste process. As objects in real images do not present these features, generalization is highly affected [15]. To alleviate this, Dwibedi et al.
[15] propose to synthesize every training image several times, using the same objects and background, but a different method to superimpose the objects. This way of modelling the blending, and the learning problem it leads to, represent a particular case of the formulation we introduce in section III for the problem. We compare this method to ours and propose an alternative approach to model the combination of blending algorithms. Although the approach in [15] shows an improvement of accuracy over a trivial cut-and-paste, it is still limited by the 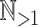 deterministic blending methods chosen, whose features can also be learned by a deep network. Tripathi et al.
[18] propose an alternative approach to prevent the network from exploiting blending artifacts to detect foreground objects. They blend all the objects with a single method, the standard alpha-blending, but introduce artifacts in the background. These artifacts (called flying distractors) consist of parts of other backgrounds, cut with the shape of a foreground object, and blended into the scene. This approach also fits well within our theoretical framework in section III, as we are not limited to use a foreground-background image pair to create our semi-synthetic images, but can also use two backgrounds with one of them having the segmentation annotation of another foreground image, leading to the solution proposed by [18]. Hence, flying distractors are also included in our semi-synthetic dataset, blending them with our Monte Carlo method to generate training samples.
deterministic blending methods chosen, whose features can also be learned by a deep network. Tripathi et al.
[18] propose an alternative approach to prevent the network from exploiting blending artifacts to detect foreground objects. They blend all the objects with a single method, the standard alpha-blending, but introduce artifacts in the background. These artifacts (called flying distractors) consist of parts of other backgrounds, cut with the shape of a foreground object, and blended into the scene. This approach also fits well within our theoretical framework in section III, as we are not limited to use a foreground-background image pair to create our semi-synthetic images, but can also use two backgrounds with one of them having the segmentation annotation of another foreground image, leading to the solution proposed by [18]. Hence, flying distractors are also included in our semi-synthetic dataset, blending them with our Monte Carlo method to generate training samples.
III. Methods
A. Semi-Synthetic Learning
As it is customary in data-driven segmentation, we aim to solve for a mapping 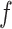 such that
such that 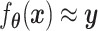 , where
, where 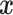 is an input image,
is an input image, 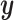 the segmentation mask corresponding to
the segmentation mask corresponding to 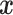 , and
, and 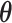 a vector of parameters. The parameters
a vector of parameters. The parameters 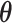 are sought as an approximate solution of the following Expected Risk Minimization problem:
are sought as an approximate solution of the following Expected Risk Minimization problem:
 |
where 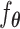 is a parametric function (the segmentation network in our implementation),
is a parametric function (the segmentation network in our implementation), 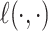 represents our real-valued loss function, and
represents our real-valued loss function, and 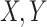 are modelled as two random variables of unknown joint probability distribution
are modelled as two random variables of unknown joint probability distribution 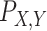 . For the sake of simplicity, as we focus on how our modelling of
. For the sake of simplicity, as we focus on how our modelling of  changes the optimization problem, regularization terms are omitted across this section.
changes the optimization problem, regularization terms are omitted across this section.
In practice, limited by a training set, we typically approximate the true joint probability distribution 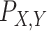 of our training set by the following empirical probability measure
of our training set by the following empirical probability measure  :
:
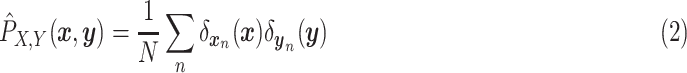 |
where 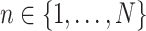 ,
, 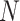 represents the number of training samples, and
represents the number of training samples, and 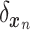 and
and 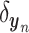 stand for Dirac measures centered at
stand for Dirac measures centered at 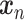 and
and 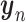 respectively. Based on (2), the learning problem (1) becomes:
respectively. Based on (2), the learning problem (1) becomes:
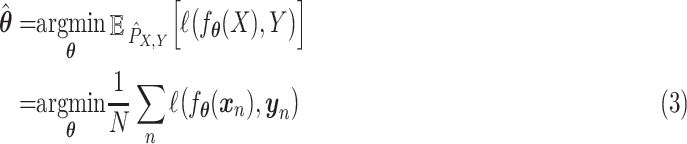 |
However, generating pairs 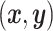 by recording real clinical images and manually labeling is exceedingly time-consuming, leads to inaccurate labels and amounts of data that are far from computer vision industry standards. Nonetheless, we observe that in our problem of instrument-background segmentation, the foreground of an image could be overlaid onto the background of another, and still form a plausible image. This gives us the intuition that an image could be segmented into several components (including but not limited to foreground and background) that could be blended to form new images. As such, we consider an image
by recording real clinical images and manually labeling is exceedingly time-consuming, leads to inaccurate labels and amounts of data that are far from computer vision industry standards. Nonetheless, we observe that in our problem of instrument-background segmentation, the foreground of an image could be overlaid onto the background of another, and still form a plausible image. This gives us the intuition that an image could be segmented into several components (including but not limited to foreground and background) that could be blended to form new images. As such, we consider an image 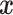 as a realization of a random variable
as a realization of a random variable 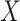 modelled as
modelled as 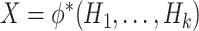 where
where 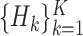 are
are 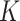 random variables capturing the different components of information (e.g. background, foreground instrument). Observations (called source images throughout the text) of these random variables represent the sources of any given
random variables capturing the different components of information (e.g. background, foreground instrument). Observations (called source images throughout the text) of these random variables represent the sources of any given 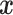 , and
, and 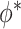 is an ideal blending function that renders the final image with all its components. This model is particularly advantageous if:
is an ideal blending function that renders the final image with all its components. This model is particularly advantageous if:
-
1)
Labeling samples of
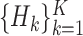 is easier than labeling samples of
is easier than labeling samples of 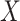 .
. -
2)
We are able to blend segmented complementary source images and their labels to form new valid training pairs
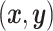 .
.
The idea of seeing an endoscopic image as made of 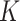 source images that are easier to segment than real clinical images themselves is illustrated in Fig. 2. In our case, we assume that we are able to segment any given
source images that are easier to segment than real clinical images themselves is illustrated in Fig. 2. In our case, we assume that we are able to segment any given 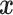 into
into 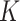 source images, where
source images, where  is the number of classes. In the case of binary tool segmentation, we focus on
is the number of classes. In the case of binary tool segmentation, we focus on 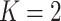 , foreground (surgical instruments) and background (tissue). Furthermore, we hypothesize that any combination of complementary source images is equally likely to form a plausible endoscopic image. This proposal corresponds to modelling
, foreground (surgical instruments) and background (tissue). Furthermore, we hypothesize that any combination of complementary source images is equally likely to form a plausible endoscopic image. This proposal corresponds to modelling 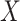 as:
as:
 |
where 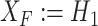 and
and 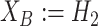 are assumed to be independent random variables whose observations are foregrounds
are assumed to be independent random variables whose observations are foregrounds 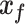 and backgrounds
and backgrounds 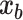 .
.
The way of modelling 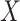 in (4) requires us to know the ideal blending function
in (4) requires us to know the ideal blending function 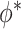 . As this is not the case, we opt to model blending in a probabilistic manner. The composited labels
. As this is not the case, we opt to model blending in a probabilistic manner. The composited labels 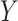 are trivially obtained by keeping the foreground labels
are trivially obtained by keeping the foreground labels 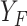 irrespective of the blending function (see Fig. 2). Therefore, we define
irrespective of the blending function (see Fig. 2). Therefore, we define 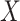 and
and 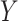 as:
as:
 |
where 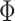 is now a random variable whose observations
is now a random variable whose observations 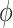 are blending functions. Such modelling leads to the following joint probability measure:
are blending functions. Such modelling leads to the following joint probability measure:
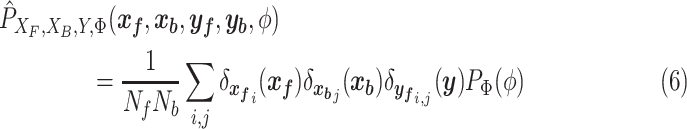 |
where 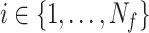 ,
, 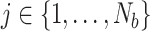 ,
,  and
and 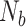 are the number of foregrounds and backgrounds, and
are the number of foregrounds and backgrounds, and 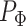 represents the probability measure for
represents the probability measure for 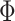 .
.
Given the framework presented in (5) and (6), we can now define 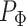 in a number of ways. A possible approach is to arbitrarily choose a pool of blending methods to create our training images (as informally proposed in [15] for object detection), which is equivalent to defining
in a number of ways. A possible approach is to arbitrarily choose a pool of blending methods to create our training images (as informally proposed in [15] for object detection), which is equivalent to defining 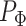 by:
by:
 |
where 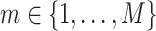 ,
, 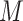 is the number of blending functions that we arbitrarily decide to define, and
is the number of blending functions that we arbitrarily decide to define, and  stands for Dirac measures centered at
stands for Dirac measures centered at 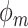 . This initial definition of
. This initial definition of 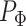 allows for either deterministic (
allows for either deterministic (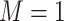 ) or probabilistic (
) or probabilistic ( ) blending, and turns our learning problem (1) into:
) blending, and turns our learning problem (1) into:
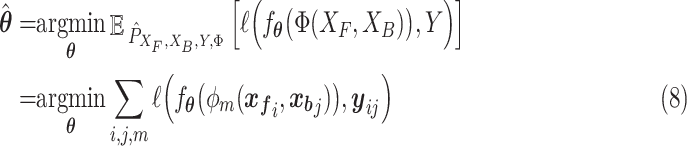 |
The training scheme in (8), which we denote as multi-blend, is illustrated in Fig. 3, and formalizes the heuristic proposed experimentally by [15].
In the case of 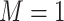 , all images in the training set are blended using the same method. If not chosen carefully, features of the blending could be erroneously learned during training, leading to poor generalization to real images.
, all images in the training set are blended using the same method. If not chosen carefully, features of the blending could be erroneously learned during training, leading to poor generalization to real images.
Using several blending functions (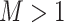 ) is a way to introduce robustness. Every pair (
) is a way to introduce robustness. Every pair (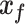 ,
, 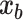 ) added to the training set is blended
) added to the training set is blended 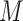 times, and
times, and  images are added to the training set. The intuition is that by having images whose only difference is the blending approach (as they have the same
images are added to the training set. The intuition is that by having images whose only difference is the blending approach (as they have the same 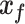 and
and 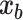 ) we could potentially induce
) we could potentially induce  to be blending invariant.
to be blending invariant.
Departing from the approach in [15] formalised above, rather than minimizing the risk functional defined only by a fixed set of 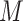 blending functions, we now propose to delve into blending invariance by modelling
blending functions, we now propose to delve into blending invariance by modelling 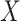 as:
as:
 |
where 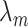 is the
is the 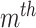 component of a vector of positive reals
component of a vector of positive reals 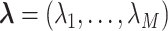 s.t.
s.t. 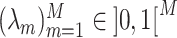 ,
, 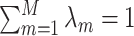 , and
, and 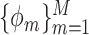 is a basis of blending functions in our model. We model
is a basis of blending functions in our model. We model 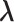 as an observation of a random variable
as an observation of a random variable 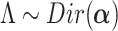 , parameterized by a vector of strictly positive reals
, parameterized by a vector of strictly positive reals 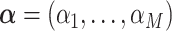 s.t.
s.t.
 |
where 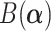 is the multivariate beta function. This modelling of
is the multivariate beta function. This modelling of 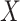 is a fundamental difference to [15]. It allows us to generate an infinite amount of images for a given pair foreground-background. In contrast, in [15], a particular combination of objects, which would be equivalent to our foreground-background pairs, can lead only to
is a fundamental difference to [15]. It allows us to generate an infinite amount of images for a given pair foreground-background. In contrast, in [15], a particular combination of objects, which would be equivalent to our foreground-background pairs, can lead only to 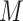 blended images (as many as blending functions employed). That is, we explore a wider space of blending functions.
blended images (as many as blending functions employed). That is, we explore a wider space of blending functions.
Following our choice of probability measure for 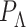 , and hence for
, and hence for 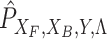 , our learning problem (1) turns into:
, our learning problem (1) turns into:
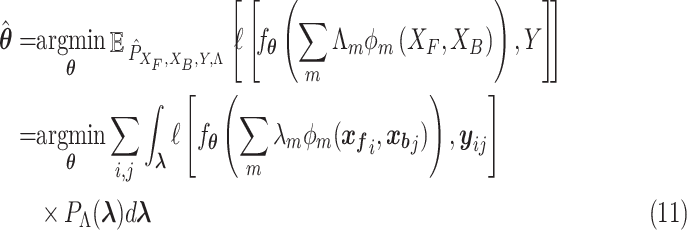 |
where 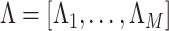 . The training strategy presented in (11) requires the computation of the loss over all the combinations of foreground-background
. The training strategy presented in (11) requires the computation of the loss over all the combinations of foreground-background 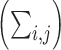 for all the possible weighted sums (
for all the possible weighted sums (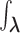 ) of blended images. Although this is unfeasible, in practice, foregrounds, backgrounds, and weights
) of blended images. Although this is unfeasible, in practice, foregrounds, backgrounds, and weights 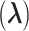 can be (and are) randomly sampled during the training of the network with SGD. In that case the network training process is therefore solving the following optimization problem:
can be (and are) randomly sampled during the training of the network with SGD. In that case the network training process is therefore solving the following optimization problem:
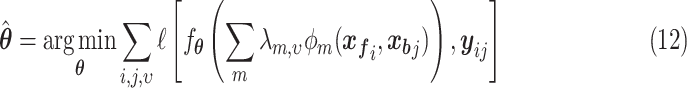 |
where 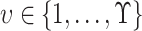 ,
, 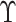 is the number of samples of
is the number of samples of 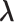 drawn according
drawn according 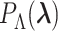 during training for each combination foreground-background, and
during training for each combination foreground-background, and 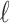 represents the pixel-wise cross-entropy loss employed by our segmentation network during training.
represents the pixel-wise cross-entropy loss employed by our segmentation network during training. 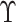 is proportional to the number of optimization steps or training iterations selected. We refer to the learning strategy in (12) as mix-blend learning (see Fig. 3 and supplementary material Fig. 1).
is proportional to the number of optimization steps or training iterations selected. We refer to the learning strategy in (12) as mix-blend learning (see Fig. 3 and supplementary material Fig. 1).
B. Post-Processing
In our method, the foreground images 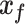 are recorded in a loosely controlled and somewhat artefactual setup. The illumination conditions (LED light source), recording devices (mobile phone and DSLR), and camera viewpoints to record the instruments are different from those seen in real clinical videos. In addition, we just recorded a small sample of instruments (see supplementary material Fig. 4). One could argue that mimicking the clinical setup by recording with different endoscopes, a laparoscopic phantom, and a large number of surgical instruments could lead to more realistic blended images and better performance. However, there is no guarantee, that after creating such setup, a domain gap would not still exist between semi-synthetic data and real clinical videos. What is guaranteed is that the method would be less flexible. Hence, we opt to mitigate the expected domain gap between our trivial setup and real clinical videos with post-processing.
are recorded in a loosely controlled and somewhat artefactual setup. The illumination conditions (LED light source), recording devices (mobile phone and DSLR), and camera viewpoints to record the instruments are different from those seen in real clinical videos. In addition, we just recorded a small sample of instruments (see supplementary material Fig. 4). One could argue that mimicking the clinical setup by recording with different endoscopes, a laparoscopic phantom, and a large number of surgical instruments could lead to more realistic blended images and better performance. However, there is no guarantee, that after creating such setup, a domain gap would not still exist between semi-synthetic data and real clinical videos. What is guaranteed is that the method would be less flexible. Hence, we opt to mitigate the expected domain gap between our trivial setup and real clinical videos with post-processing.
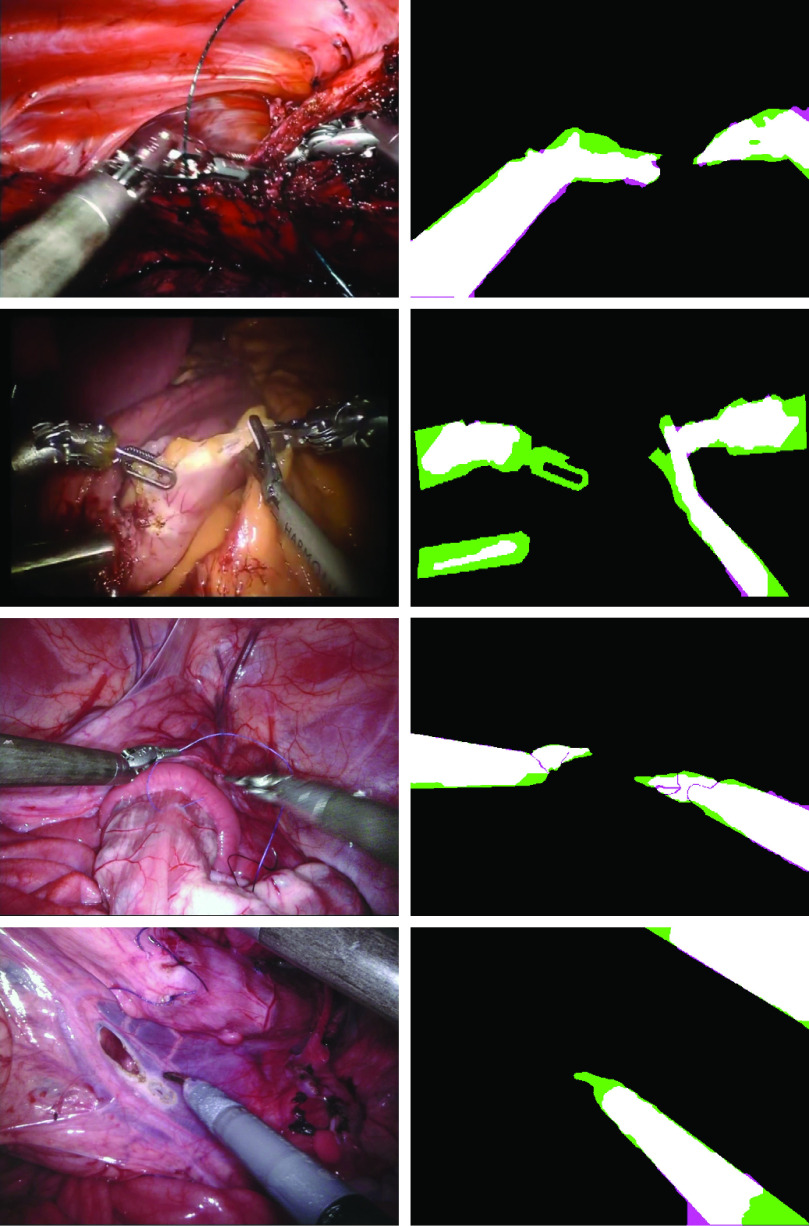
Fig. 4.
Exemplary segmentations of the RoboTool dataset (two top rows) and EndoVis2017 dataset (two bottom rows) segmented with our mix-blend method. The best/median/worst cases for each testing dataset are shown in figures 8–10 of the supplementary material. Confusion images are displayed on the right column. True positive (white), true negative (black), false positive (magenta), and false negative (green).
GrabCut [36] is a well-known semi-automatic segmentation technique that may be employed for post-processing (without needing to provide manual scribbles). The probability map generated by our neural network may replace the usual manual scribble that is employed to initialize the Gaussian mixture models of GrabCut. We assume that network estimated probabilities < 0.2 represent sure background, and ≥ 0.8 sure foreground. The segmentation of pixels for which the network prediction is considered certain is not modified by GrabCut. Provided the seeding process proves reliable, by expanding the segmentation from these certainty zones according to colour contrast present in the specific image, GrabCut enables to bridge relatively minor domain gaps.
IV. Materials
In order to implement the training schemes in (8) and (11), we need to devise:
-
1)
A way to obtain source images, where source images denotes images that are easy to segment into
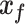 and
and 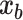 .
. -
2)
A set of blending methods
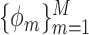 that allows us to combine
that allows us to combine  and
and 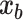 to form new images.
to form new images.
In this work, we propose to obtain two types of source images, foregrounds and backgrounds.
A. Background Dataset Collection
Although recording videos containing just tissue may be possible prospectively, for this work and without loss of generality, we have obtained all backgrounds from freely available surgical procedures on the Internet, as done in other computer vision datasets [37]. We manually select frames that only contain human tissue from video sequences of different surgical procedures. Segmenting these background source images into components is trivial. There is no foreground component in them, just background tissue. Hence, they represent our 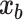 . We have collected 6130 images from 50 laparoscopic interventions (exemplar images illustrated in fig. 5 of the supplementary material). The background images included in this dataset contain some degree of tool-tissue interaction. They display direct interactions, such as tissue being pulled (with the tools out of the camera view), and also indirect artefacts, such as those inflicted by the instruments on the background tissue. Examples of the latter are shadows, blood, debris, and smoke. Nonetheless, it should be noted that there may be a certain type of interaction between instruments and tissue that we may not be able to reproduce via image compositing. This may impact the generalization ability of the model. However, as our clinical testing set (RoboTool) contains these interactions, the results shown in section VII already account for the impact of this limitation. A possible workaround is to add a small amount of manually annotated images displaying special tool-tissue interactions that cannot be observed otherwise. Once we have the tools segmented out from those images, we can refill the tool pixels with other background images as we do for our flying distractors. Then, these backgrounds become fully functional as those that do not contain any tools. The background images used to build the semi-synthetic training dataset are not present in any of the testing sets employed.
. We have collected 6130 images from 50 laparoscopic interventions (exemplar images illustrated in fig. 5 of the supplementary material). The background images included in this dataset contain some degree of tool-tissue interaction. They display direct interactions, such as tissue being pulled (with the tools out of the camera view), and also indirect artefacts, such as those inflicted by the instruments on the background tissue. Examples of the latter are shadows, blood, debris, and smoke. Nonetheless, it should be noted that there may be a certain type of interaction between instruments and tissue that we may not be able to reproduce via image compositing. This may impact the generalization ability of the model. However, as our clinical testing set (RoboTool) contains these interactions, the results shown in section VII already account for the impact of this limitation. A possible workaround is to add a small amount of manually annotated images displaying special tool-tissue interactions that cannot be observed otherwise. Once we have the tools segmented out from those images, we can refill the tool pixels with other background images as we do for our flying distractors. Then, these backgrounds become fully functional as those that do not contain any tools. The background images used to build the semi-synthetic training dataset are not present in any of the testing sets employed.
B. Foreground Dataset Collection
To extract foreground components, we collect a pool of instruments and place them over a chroma key (see Fig. 2 and 3 in the supplementary material). These images represent our second type of source images. In this scenario, we can reproduce many different lighting conditions and viewpoints. As the chroma key is monochromatic (green), we can automatically segment 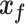 (tools), and discard the green background component. We have recorded two subsets, each one with a different camera. To facilitate segmentation, the chroma key has to be properly illuminated. This way, the amount of shadows on the chroma fabric is minimized. The number of instruments per image varies from one to three (out of a total of 17 instruments recorded). The two recording devices employed are a mobile phone camera, whose subset contains 13613 frames of size
(tools), and discard the green background component. We have recorded two subsets, each one with a different camera. To facilitate segmentation, the chroma key has to be properly illuminated. This way, the amount of shadows on the chroma fabric is minimized. The number of instruments per image varies from one to three (out of a total of 17 instruments recorded). The two recording devices employed are a mobile phone camera, whose subset contains 13613 frames of size 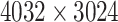 pixels that display a single instrument over the chroma key, and a DSLR camera, whose subset contains 567 frames of size
pixels that display a single instrument over the chroma key, and a DSLR camera, whose subset contains 567 frames of size 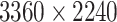 pixels.
pixels.
Although being able to record foregrounds with a commercial phone or a DSLR adds flexibility to the method, a possible approach to reduce the domain gap between synthetic and real data could be to record the foregrounds with the target imaging system. This requires having access to the exact imaging device used in practice, and generalization to other make and models (and their evolution in time) may still be limited. Nonetheless, it would be interesting for future work to examine the generalization performance when recording with different endoscopes.
C. Foreground Dataset Segmentation
Images are converted to HSV and thresholded to capture the green pixels that belong to the background. The mask generated by the HSV threshold is provided as a unitary term prior to GrabCut [36]. These automatic segmentations are quality controlled by means of visual inspection. Those few with obvious inaccuracies due to a GrabCut failure (e.g. green area captured as tool or instrument missing parts) are excluded.
As thresholding is such a simple technique, different levels of lighting affect the quality of the results significantly. It is convenient to tune the HSV threshold right before recording so that it can be adjusted to the lighting conditions of the scene and avoid tedious postprocessing. To reduce noise in the automatically-generated tool segmentation masks, our interface allows specifying the number of instruments being recorded so only those HSV-thresholded pixels that lie inside the largest  connected components are kept, where
connected components are kept, where 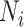 is the number of instruments.
is the number of instruments.
D. Semi-Synthetic Dataset: Training and Validation
Although our image synthesis method may be performed on-the-fly, we precompute 100K images blended with all our basis (see section V-B) to speed up our semi-synthetic training. Only the Dirichlet random weighted sum (eq. 9) is performed on-the-fly. For validation, we precompute a small semi-synthetic dataset of 500 images that use 392 foregrounds recorded over a red chroma key, and 428 backgrounds that were kept aside from the background dataset. This small semi-synthetic dataset is just used as a baseline for early stopping. That is, as stopping criteria for the training on semi-synthetic data.
E. EndoVis2017 (Existing Real Pre-Clinical Dataset): Testing Set
For evaluation, we use the images coming from the training set given at the 2017 Robotic Instrument Segmentation Challenge [13]. As these images come from recordings made with the da Vinci Surgical System (dVSS) and have been manually labeled, we refer to them as real data (as opposed to semi-synthetic data, which is the one we generate with our method). We use the training set of the challenge for evaluation (annotations are widely available). This dataset comes with eight video sequences. In order to generate baseline results for comparison with our method, we use the same protocol of the challenge. We perform cross-validation with eight folds. In each fold, the testing set contains only one video. The remaining seven videos are used for training and validation (10% of the video frames in these seven videos are left for early stopping, 90% for training). The only cross-validation performed during our experiments is that mentioned in this section, aimed at evaluating the baseline performance on the EndosVis2017 dataset.
F. RoboTool (New Real Clinical Dataset): Testing Set
We make public our newly created real clinical testing set called RoboTool (see fig. 6 of the supplementary material), containing 514 manually annotated images extracted from the videos of 20 freely available surgical procedures. For those baseline experiments where a network is trained on RoboTool, the validation set used for early stopping consists of 51 images that have not been seen in training and come from other surgical procedures different from the 20 employed to build this dataset.
V. Implementation of the Methods
All semi-synthetic data and code corresponding to the implementation of the methods is made available in open access.1
A. Data Augmentation and Standardization
After obtaining images for the foreground (based on chroma key) and background (from the Internet), and prior to their superimposition, we augment and standardize them as detailed in the following paragraphs. This step is not detailed in our mathematical model in section III for the sake of conciseness, although the extension of the model to account for it is trivial.
We perform different augmentations on foreground, background, and blended images. Foreground tools are randomly zoomed, rotated, and vertically and horizontally flipped and shifted. All these operations are performed while keeping the tools connected to the border of the image. In addition, foregrounds have synthetic blood droplets and tissue debris blended onto the tools (see fig. 7 of the supplementary material). Their brightness is also randomly altered. Background augmentations comprise horizontal and vertical flips, brightness changes, and random rotations of 90 degrees. Blended images are augmented with a set of techniques from Albumentations [38]. Namely, cutouts, synthetic smoke and shadows, JPEG compression, RGB and HSV shifts, noise (multiplicative, Gaussian, ISO), and blur (Gaussian, motion, median). In addition to these, backgrounds are also augmented with flying distractors and endoscopic padding. Flying distractors are cutouts of other backgrounds blended with the shape of a random foreground tool. For any given training image, the blending function used to superimpose the foreground tools is also used to blend the flying distractors. Endoscopic padding consists of simulating the black border occasionally present in endoscopic images. We randomly pad the images enclosing the frame with a rectangular or circular shape. Gaussian noise is randomly added to the black padding. A set of exemplary semi-synthetic images is shown in fig. 7 of the supplementary material.
Prior to the blending, the augmented pairs 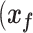 ,
,  ) are resized to our standardized width, 640-pixel (i.e. original aspect ratio is kept). A random crop is performed on the element of the pair of larger height so that both display the same height. After this step, both
) are resized to our standardized width, 640-pixel (i.e. original aspect ratio is kept). A random crop is performed on the element of the pair of larger height so that both display the same height. After this step, both 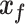 and
and  have the same resolution. This facilitates the blending of tools onto tissue (
have the same resolution. This facilitates the blending of tools onto tissue (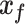 over
over 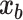 ), described below.
), described below.
B. Blending
In equations (8) and (11), we defined two ways of learning 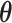 for our instrument-background segmentation function
for our instrument-background segmentation function 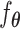 . Both approaches rely on the existence of a set of blending functions
. Both approaches rely on the existence of a set of blending functions 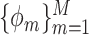 that we can evaluate to obtain a training image from a pair of
that we can evaluate to obtain a training image from a pair of 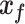 and
and 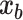 . In our implementation, we evaluate these functions using
. In our implementation, we evaluate these functions using 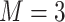 blending or superimposition algorithms:
blending or superimposition algorithms:
-
•
Trivial blending. The pixels activated in the tool mask are copied from
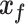 onto
onto 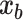 to form the final blend
to form the final blend 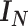 .
. -
•
Gaussian feathering. The foreground segmentation mask
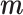 is eroded (
is eroded (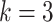 ) and blurred (
) and blurred (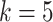 ). The final image is generated as
). The final image is generated as 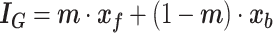 , where
, where 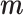 represents the mask after erosion and blurring.
represents the mask after erosion and blurring. -
•
Laplacian pyramid blending [39]. A Laplacian pyramid is constructed for both images. A Gaussian pyramid is built for the region occupied by
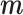 . Then, Laplacian pyramids are combined using the nodes of the Gaussian pyramid as weights and collapsed to form the blended image
. Then, Laplacian pyramids are combined using the nodes of the Gaussian pyramid as weights and collapsed to form the blended image 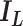 .
.
Given these blending basis, our implementation of multi-blend learning (8) consists of populating our training set with three images (one per blending method) for each pair 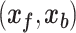 .
.
For our implementation of mix-blend
(11) we choose the same (to be able to compare results) combinations of 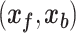 selected for the experiments of (8). However, in contrast to (8), when the optimization problem (11) is solved with SGD, the training samples included in each mini-batch are generated on the fly. To generate each sample we select a pair of
selected for the experiments of (8). However, in contrast to (8), when the optimization problem (11) is solved with SGD, the training samples included in each mini-batch are generated on the fly. To generate each sample we select a pair of 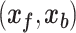 , blend it
, blend it  times, draw a random sample
times, draw a random sample 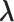 (vector of three weights, one per blending method) from
(vector of three weights, one per blending method) from 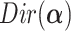 with
with 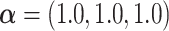 , and perform a weighted sum of the
, and perform a weighted sum of the 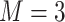 blended images.
blended images.
C. Network Architecture and Training Protocol
As the leading approach of the 2017 Robotic Instrument Segmentation Challenge [13] was a U-Net [40], this encoder-decoder architecture was chosen to model our instrument segmentation function  .
.
We train all the networks using the same protocol. A fixed learning rate (LR) of 0.001. A batch size of 32 because it is the maximum our GPU can fit. Early stopping (ES) is used to bound the duration of our training. The ES baseline is always the validation set of each experiment. The minimum delta is set to 0.01 of absolute average mIoU and the patience to 20 epochs.
All our networks are trained with SGD with momentum 0.9 and the widely used pixel-wise cross-entropy as loss function:
 |
where 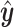 is the predicted segmentation label,
is the predicted segmentation label, 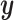 is the ground truth label,
is the ground truth label, 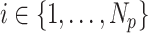 where
where 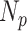 is the number of pixels, and
is the number of pixels, and 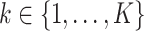 where
where 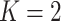 is the number of classes.
is the number of classes.
VI. Evaluation
Although metrics such as the Frechet Inception Distance (FID) [41] could be useful to evaluate the similarity between the generated and real data, in this work, we are not aiming to create photo-realistic images, but rather to train a network that generalizes well to real data for the tool segmentation task. In fact, the generated semi-synthetic images contain flying distractors (see section V-A), which are cutouts blended with the shape of a tool and the texture of a background. These artefacts are not present in real images, but they help to learn the segmentation by encouraging the network to not learn the blending as a feature to detect tools. Therefore, evaluating the realism of the semi-synthetic images would not lead to a meaningful result. Our evaluation focuses on assessing the quality of the tool segmentation. For such purpose, we employ the widely used intersection over union (IoU), also called Jaccard index.
For a single video frame, we compute the IoU 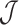 between the binarized (threshold ≥ 0.5, background = 0, tool = 1) probability prediction
between the binarized (threshold ≥ 0.5, background = 0, tool = 1) probability prediction 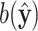 and the ground truth
and the ground truth 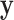 (which is already a binary image). That is:
(which is already a binary image). That is:
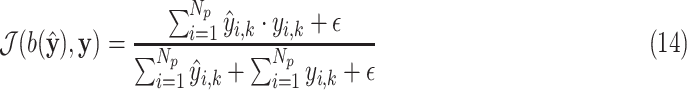 |
where 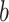 denotes the binarization function,
denotes the binarization function, 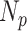 is the number of pixels in the image,
is the number of pixels in the image, 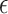 is the machine epsilon, and
is the machine epsilon, and 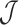 bounds our scores to the interval [0, 1]. To report the IoU for a video sequence, we average the metric
bounds our scores to the interval [0, 1]. To report the IoU for a video sequence, we average the metric 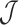 across all the frames. All the results are given in percentage.
across all the frames. All the results are given in percentage.
VII. Results and Discussion
In our first experiment, we train eight networks. Each one is trained on seven videos of the EndoVis2017 dataset, and tested on the remaining video (see results per video in table I of the supplementary material). This experiment leads to an average mIoU across experiments of 81.6 [69.7, 89.6] (confidence interval [5%, 95%]). At first sight, it could seem as if the binary segmentation of surgical tools is a solved problem. However, when we test a network trained on all the EndoVis2017 videos on RoboTool (our real clinical dataset presented in section IV-F), the performance drops to 66.6 [43.0, 87.2], suggesting some overfitting to the recording conditions of the challenge dataset. For a fair comparison with the proposed method, we apply post-processing to the output of the network trained on EndoVis2017 (table I), pushing the average mIoU on RoboTool to 69.4 [37.7, 91.8]. We also performed the inverse experiment, training on RoboTool and testing on EndoVis2017. This led to an average mIoU of 73.8 [56.3, 86.6]. These results suggest that networks trained on these small manually labeled datasets (coming from a small number of recorded interventions) do not generalize as well as it could be expected. All the results for training and testing on real data are presented in table I.
TABLE I. Baseline Results. Training and Evaluating on Manually Labeled Real Data. No Semi-Synthetic Data nor Blending Technique has Been Used to Generate the Results on This Table. In the First Line of the Results, When Training and Testing on EndoVis2017, Leave One Out is Used, Following the Protocol of the EndoVis2017 Challenge (See Section IV-E).
| Training dataset | Post-processing | Testing dataset | IoU [5%, 95%] |
|---|---|---|---|
| EndoVis2017 | None | EndoVis2017 | 81.6 [69.7, 89.6] |
| RoboTool | None | EndoVis2017 | 73.8 [56.3, 86.6] |
| RoboTool | GrabCut | EndoVis2017 | 80.5 [55.8, 94.1] |
| EndoVis2017 | None | RoboTool | 66.6 [43.0, 87.2] |
| EndoVis2017 | GrabCut | RoboTool | 69.4 [37.7, 91.8] |
In the context of generating a dataset that can allow for the learning of the tool segmentation, crisp borders induced by simple copy-pasting represent a spurious feature that the network would exploit as a mean to solve for the segmentation of the tools in semi-synthetic data. To address this challenge, we analyze the performance of each blending method individually, and compare the different approaches to combine them. For doing this, we train on semi-synthetic data, and test on the two real datasets, EndoVis2017 and RoboTool. We carry out this comparison by training networks with identical 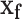 and
and 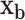 while changing the blending method. Our results indicate that Laplacian blending is superior to both trivial and Gaussian blending. Surprisingly, it also outperforms multi-blend by four percentage points, suggesting that the inclusion of either trivial, Gaussian, or both blending modes is counterproductive. In contrast, mix-blend outperforms Laplacian by 4 percentage points and multi-blend by 8 percentage points. This result supports our theoretical claim that multi-blend is just a particular corner case of mix-blend with
while changing the blending method. Our results indicate that Laplacian blending is superior to both trivial and Gaussian blending. Surprisingly, it also outperforms multi-blend by four percentage points, suggesting that the inclusion of either trivial, Gaussian, or both blending modes is counterproductive. In contrast, mix-blend outperforms Laplacian by 4 percentage points and multi-blend by 8 percentage points. This result supports our theoretical claim that multi-blend is just a particular corner case of mix-blend with 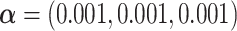 . The top performing results of our proposed mix-blend learning (see table II) also suggest that varying the blending method helps to boost segmentation accuracy when jumping from semi-synthetic to real data. This effect has also been observed by Dwibedi et al. in [15]. We believe the reason why mix-blend learning – eq. 12 – achieves higher IoU than multi-blend – eq. 8 – is because it explores a larger (infinite) variety of possible blendings (not just the
. The top performing results of our proposed mix-blend learning (see table II) also suggest that varying the blending method helps to boost segmentation accuracy when jumping from semi-synthetic to real data. This effect has also been observed by Dwibedi et al. in [15]. We believe the reason why mix-blend learning – eq. 12 – achieves higher IoU than multi-blend – eq. 8 – is because it explores a larger (infinite) variety of possible blendings (not just the 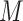 basis), delving deep into the invariance to the blending mechanism.
basis), delving deep into the invariance to the blending mechanism.
TABLE II. Ablation Study of Blending Methods. Training on Semi-Synthetic Data and Testing on Unseen Real Data.
| Training dataset (blending) | Testing dataset | IoU [5%, 95%] |
|---|---|---|
| Semi-synthetic (Trivial) | EndoVis2017 | 53.7 [44.3, 66.6] |
| Semi-synthetic (Gaussian) | 55.2 [44.8, 70.4] | |
| Semi-synthetic (Laplacian) | 68.3 [52.4, 83.1] | |
| Semi-synthetic (Multi-blend) [15] | 64.3 [49.2, 79.8] | |
| Semi-synthetic (Mix-blend) | 72.8 [56.5, 87.8] | |
| Semi-synthetic (Trivial) | RoboTool | 48.4 [38.2, 65.5] |
| Semi-synthetic (Gaussian) | 48.7 [38.2, 65.7] | |
| Semi-synthetic (Laplacian) | 54.3 [40.4, 75.6] | |
| Semi-synthetic (Multi-blend) [15] | 51.7 [39.5, 74.5] | |
| Semi-synthetic (Mix-blend) | 56.1 [40.2, 77.5] |
The last part of our study is on bridging the gap between synthetic and real data. We show that by using simple post-processing, we are able to push the performance of our semi-synthetic mix-blend method to reach the same accuracy as a network trained on real data. Training on EndoVis2017 and testing on RoboTool (our real clinical dataset with 20 surgical procedures) we achieve 66.6 [43.0, 87.2]. With GrabCut post-processing this increases to 69.4 [37.7, 91.8]. Training on semi-synthetic data with mix-blend, we achieve 56.1 [40.2, 77.5] on RoboTool. With GrabCut post-processing we reach 68.1 [42.6, 92.5] (see exemplary segmentations in Fig. 4). All the results of our complete pipeline trained on semi-synthetic data and evaluated on real data are shown in table III. Figures 8, 9, and 10 of the supplementary material facilitate the visual comparison of results at several percentile levels for the different methods (best/median/worst cases). In fig. 8 of the supplementary material, we show the baseline results (training on a real dataset, and testing on a different real dataset). In fig. 9 and 10 of the supplementary material, we show the best/median/worst cases when training on semi-synthetic data and testing on real datasets RoboTool and EndoVis2017.
TABLE III. Results of Our Proposed Blending Method in Combination With Post-Processing.
| Training dataset | Post-processing | Testing dataset | IoU [5%, 95%] |
|---|---|---|---|
| Semi-synthetic (Mix-blend) | GrabCut | EndoVis2017 | 83.3 [62.7, 93.9] |
| Semi-synthetic (Mix-blend) | GrabCut | RoboTool | 68.1 [42.6, 92.5] |
VIII. Conclusion
We have shown a new method to automatically generate labels for surgical tool segmentation. Synthetically generating the whole surgical scene is a very challenging problem. However, just performing a simple semi-synthetic blending that explores the mix of a set of blending basis, and applying post-processing, we are able to train a convolutional neural network that achieves an analogous performance to that of a network trained on currently available manually labeled datasets such as EndoVis2017. Future work includes the exploration of domain adaptation techniques that could potentially push further the results obtained by the semi-synthetic blending.
Acknowledgment
The authors would like to thank NVIDIA for the donated GeForce GTX TITAN X GPU.
Funding Statement
This work was supported in part by the Wellcome under Grant 203148/Z/16/Z, Grant 203145Z/16/Z, and Grant WT101957; in part by the Engineering and Physical Sciences Research Council (EPSRC) under Grant NS/A000049/1, Grant NS/A000050/1, Grant NS/A000027/1, and Grant EP/L016478/1; and in part by the European Union’s Horizon 2020 Research and Innovation Program through the Marie Skłodowska-Curie Grant under Agreement TRABIT 765148. The work of Tom Vercauteren was supported by the Medtronic/RAEng Research Chair under Grant RCSRF1819\7\34.
Footnotes
Contributor Information
Luis C. Garcia-Peraza-Herrera, Email: luis.herrera.14@ucl.ac.uk.
Lucas Fidon, Email: lucas.fidon@kcl.ac.uk.
Claudia D’Ettorre, Email: c.dettorre@ucl.ac.uk.
Danail Stoyanov, Email: danail.stoyanov@ucl.ac.uk.
Tom Vercauteren, Email: tom.vercauteren@kcl.ac.uk.
Sébastien Ourselin, Email: sebastien.ourselin@kcl.ac.uk.
References
- [1].Rieke N.et al. , “Real-time online adaption for robust instrument tracking and pose estimation,” in Proc. MICCAI, 2016, pp. 422–430. [Google Scholar]
- [2].Ye M., Zhang L., Giannarou S., and Yang G.-Z., “Real-time 3D tracking of articulated tools for robotic surgery,” in Proc. MICCAI, 2016, pp. 386–394. [Google Scholar]
- [3].García-Peraza-Herrera L. C.et al. , “Real-time segmentation of non-rigid surgical tools based on deep learning and tracking,” in Proc. CARE Workshop, Held Conjunct (MICCAI), 2016, pp. 84–95. [Google Scholar]
- [4].Pakhomov D., Premachandran V., Allan M., Azizian M., and Navab N., “Deep residual learning for instrument segmentation in robotic surgery,” in Proc. MLMI, 2019, pp. 566–573. [Google Scholar]
- [5].Shvets A. A., Rakhlin A., Kalinin A. A., and Iglovikov V. I., “Automatic instrument segmentation in robot-assisted surgery using deep learning,” in Proc. 17th IEEE Int. Conf. Mach. Learn. Appl. (ICMLA), Dec. 2018, pp. 624–628. [Google Scholar]
- [6].Nwoye C. I., Mutter D., Marescaux J., and Padoy N., “Weakly supervised convolutional LSTM approach for tool tracking in laparoscopic videos,” Int. J. Comput. Assist. Radiol. Surgery, vol. 14, no. 6, pp. 1059–1067, Jun. 2019. [DOI] [PubMed] [Google Scholar]
- [7].Maier-Hein L.et al. , “Surgical data science for next-generation interventions,” Nature Biomed. Eng., vol. 1, no. 9, pp. 691–696, Sep. 2017. [DOI] [PubMed] [Google Scholar]
- [8].Kwartowitz D. M., Miga M. I., Herrell S. D., and Galloway R. L., “Towards image guided robotic surgery: Multi-arm tracking through hybrid localization,” Int. J. Comput. Assist. Radiol. Surgery, vol. 4, no. 3, pp. 281–286, May 2009. [DOI] [PubMed] [Google Scholar]
- [9].Haase S., Wasza J., Kilgus T., and Hornegger J., “Laparoscopic instrument localization using a 3-D time-of-flight/RGB endoscope,” in Proc. IEEE Workshop Appl. Comput. Vis. (WACV), Jan. 2013, pp. 449–454. [Google Scholar]
- [10].Reiter A., Allen P. K., and Zhao T., “Feature classification for tracking articulated surgical tools,” in Proc. MICCAI, 2012, vol. 15, no. 2, pp. 592–600. [DOI] [PubMed] [Google Scholar]
- [11].da Costa Rocha C., Padoy N., and Rosa B., “Self-supervised surgical tool segmentation using kinematic information,” Feb. 2019, arXiv:1902.04810. [Online]. Available: http://arxiv.org/abs/1902.04810
- [12].Pakhomov D., Shen W., and Navab N., “Towards unsupervised learning for instrument segmentation in robotic surgery with cycle-consistent adversarial networks,” Jul. 2020, arXiv:2007.04505. [Online]. Available: http://arxiv.org/abs/2007.04505
- [13].Allan M.et al. , “2017 robotic instrument segmentation challenge,” Feb. 2019, arXiv:1902.06426. [Online]. Available: http://arxiv.org/abs/1902.06426
- [14].Zhou B., Khosla A., Lapedriza A., Oliva A., and Torralba A., “Learning deep features for discriminative localization,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp. 2921–2929. [Google Scholar]
- [15].Dwibedi D., Misra I., and Hebert M., “Cut, paste and learn: Surprisingly easy synthesis for instance detection,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Oct. 2017, pp. 1310–1319. [Google Scholar]
- [16].Georgakis G., Mousavian A., Berg A. C., and Kosecka J., “Synthesizing training data for object detection in indoor scenes,” Feb. 2017, arXiv:1702.07836. [Online]. Available: http://arxiv.org/abs/1702.07836
- [17].Dvornik N., Mairal J., and Schmid C., “Modeling visual context is key to augmenting object detection datasets,” in Proc. ECCV, 2018, pp. 364–380. [Google Scholar]
- [18].Tripathi S., Chandra S., Agrawal A., Tyagi A., Rehg J. M., and Chari V., “Learning to generate synthetic data via compositing,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2019, pp. 461–470. [Google Scholar]
- [19].Heimann T., Mountney P., John M., and Ionasec R., “Real-time ultrasound transducer localization in fluoroscopy images by transfer learning from synthetic training data,” Med. Image Anal., vol. 18, no. 8, pp. 1320–1328, Dec. 2014. [DOI] [PubMed] [Google Scholar]
- [20].Maier-Hein L.et al. , “Crowd-algorithm collaboration for large-scale endoscopic image annotation with confidence,” in Proc. MICCAI, 2016, pp. 616–623. [Google Scholar]
- [21].Vardazaryan A., Mutter D., Marescaux J., and Padoy N., “Weakly-supervised learning for tool localization in laparoscopic videos,” in Proc. LABELS, 2018, pp. 169–179. [Google Scholar]
- [22].Ross T.et al. , “Exploiting the potential of unlabeled endoscopic video data with self-supervised learning,” Int. J. Comput. Assist. Radiol. Surgery, vol. 13, no. 6, pp. 925–933, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [23].Zikic D., Glocker B., and Criminisi A., “Atlas encoding by randomized forests for efficient label propagation,” in Proc. MICCAI, 2013, pp. 66–73. [DOI] [PubMed] [Google Scholar]
- [24].Yu T., Mutter D., Marescaux J., and Padoy N., “Learning from a tiny dataset of manual annotations: A teacher/student approach for surgical phase recognition,” in Proc. IPCAI, 2019, pp. 1–13. [Google Scholar]
- [25].Pfeiffer M.et al. , “Generating large labeled data sets for laparoscopic image processing tasks using unpaired image-to-image translation,” in Proc. MICCAI, 2019, pp. 119–127. [Google Scholar]
- [26].Unberath M.et al. , “Enabling machine learning in X-ray-based procedures via realistic simulation of image formation,” Int. J. Comput. Assist. Radiol. Surg., vol. 14, no. 9, pp. 1517–1528, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Su H., Qi C. R., Li Y., and Guibas L. J., “Render for CNN: Viewpoint estimation in images using CNNs trained with rendered 3D model views,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Dec. 2015, pp. 2686–2694. [Google Scholar]
- [28].Peng X., Sun B., Ali K., and Saenko K., “Learning deep object detectors from 3D models,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Dec. 2015, pp. 1278–1286. [Google Scholar]
- [29].Chen W.et al. , “Synthesizing training images for boosting human 3D pose estimation,” in Proc. 4th Int. Conf. 3D Vis. (DV), Oct. 2016, pp. 479–488. [Google Scholar]
- [30].Movshovitz-Attias Y., Kanade T., and Sheikh Y., “How useful is photo-realistic rendering for visual learning?,” in Proc. ECCV, 2016, pp. 202–217. [Google Scholar]
- [31].Karsch K., Hedau V., Forsyth D., and Hoiem D., “Rendering synthetic objects into legacy photographs,” in Proc. SIGGRAPH Asia Conf. (SA), 2011, pp. 1–12. [Google Scholar]
- [32].Zhang H., Cisse M., Dauphin Y. N., and Lopez-Paz D., “Mixup: Beyond empirical risk minimization,” in Proc. ICLR, 2018, pp. 1–13. [Google Scholar]
- [33].Tobin J., Fong R., Ray A., Schneider J., Zaremba W., and Abbeel P., “Domain randomization for transferring deep neural networks from simulation to the real world,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. (IROS), Sep. 2017, pp. 23–30. [Google Scholar]
- [34].Toth D., Cimen S., Ceccaldi P., Kurzendorfer T., Rhode K., and Mountney P., “Training deep networks on domain randomized synthetic X-ray data for cardiac interventions,” in MIDL, 2019, pp. 468–482.
- [35].Tremblay J.et al. , “Training deep networks with synthetic data: Bridging the reality gap by domain randomization,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Workshops (CVPRW), Jun. 2018, pp. 969–977. [Google Scholar]
- [36].Rother C., Kolmogorov V., and Blake A., “‘GrabCut’: Interactive foreground extraction using iterated graph cuts,” in Proc. SIGGRAPH, 2004, p. 309. [Online]. Available: http://portal.acm.org/citation.cfm?doid=1186562.1015720 [Google Scholar]
- [37].Lin T.-Y.et al. , “Microsoft coco: Common objects in context,” in Proc. Eur. Conf. Comput. Vis., 2014, pp. 740–755. [Google Scholar]
- [38].Buslaev A., Iglovikov V. I., Khvedchenya E., Parinov A., Druzhinin M., and Kalinin A. A., “Albumentations: Fast and flexible image augmentations,” Information, vol. 11, no. 2, p. 125, Feb. 2020. [Online]. Available: https://www.mdpi.com/2078-2489/11/2/125 [Google Scholar]
- [39].Burt P. J. and Adelson E. H., “A multiresolution spline with application to image mosaics,” ACM Trans. Graph., vol. 2, no. 4, pp. 217–236, Oct. 1983. [Google Scholar]
- [40].Ronneberger O., Fischer P., and Brox T., “U-Net: Convolutional networks for biomedical image segmentation,” in Proc. MICCAI, 2015, pp. 234–241. [Google Scholar]
- [41].Heusel M., Ramsauer H., Unterthiner T., Nessler B., and Hochreiter S., “GANs trained by a two time-scale update rule converge to a local Nash equilibrium,” Jun. 2017, arXiv:1706.08500. [Online]. Available: http://arxiv.org/abs/1706.08500