Role of bacterial RNA polymerase gate opening dynamics in DNA loading and antibiotics inhibition elucidated by quasi-Markov State Model

Significance

The initiation of bacterial transcription requires DNA loading via flexible loading gate of the RNA polymerase complex, consisting of the clamp and β-lobe domain. While the clamp is important in transcription initiation, the role of β-lobe remains unclear. Using quasi-Markov State Models (qMSMs) constructed from molecular dynamics simulations, we showed that the opening of β-lobe is orders of magnitude faster than that of the clamp, which depends on the structure of Switch 2. Strikingly, opening of the β-lobe is sufficient geometrically to accommodate DNA loading even when the clamp is partially closed. These two observations highlight β-lobe’s critical role allowing DNA loading during initiation. Thus, β-lobe is a promising target for antibiotics. qMSM also provides a promising tool investigating biomolecular dynamics.

Abstract

To initiate transcription, the holoenzyme (RNA polymerase [RNAP] in complex with σ factor) loads the promoter DNA via the flexible loading gate created by the clamp and β-lobe, yet their roles in DNA loading have not been characterized. We used a quasi-Markov State Model (qMSM) built from extensive molecular dynamics simulations to elucidate the dynamics of Thermus aquaticus holoenzyme’s gate opening. We showed that during gate opening, β-lobe oscillates four orders of magnitude faster than the clamp, whose opening depends on the Switch 2’s structure. Myxopyronin, an antibiotic that binds to Switch 2, was shown to undergo a conformational selection mechanism to inhibit clamp opening. Importantly, we reveal a critical but undiscovered role of β-lobe, whose opening is sufficient for DNA loading even when the clamp is partially closed. These findings open the opportunity for the development of antibiotics targeting β-lobe of RNAP. Finally, we have shown that our qMSMs, which encode non-Markovian dynamics based on the generalized master equation formalism, hold great potential to be widely applied to study biomolecular dynamics.

RNA polymerase (RNAP) is the enzyme responsible for transcription. Upon promoter binding, the multistep process of promoter melting occurs, whereby the promoter double-stranded DNA (dsDNA) is being separated into two single-stranded DNAs (ssDNAs). The recognition between holoenzyme (RNAP and σ-factor) and promoter DNA consists of a series of intermediate states that varies with the species, the promoter sequence, transcription factors, and environmental stress (1–4). For instance, a cryogenic electron microscopy (cryo-EM) study of the promoter melting of Mycobacterium tuberculosis (Mtb) holoenzyme reveals two stable intermediates (5). However, when Escherichia coli holoenzyme is in complex with the transcription activator protein TraR, the populations of promoter melting intermediates would increase, enabling the capture of as many as seven intermediate structures by cryo-EM (3). Importantly, it is widely acknowledged that partial or complete closure of the clamp is required for the stabilization of the initial holoenzyme–dsDNA complex (closed complex/RPc) (3, 5–7). Lastly, the clamp must be closed in the open complex (Rpo) to stabilize the separated DNA (8–10).

The crab claw conformation of RNAP consists of two highly flexible pincers, the clamp and β-pincers (β-protrusion and β-lobe) (8, 9, 11), which are important for transcription initiation (12). Indeed, the overall crab claw conformation of RNAP is highly conserved in all prokaryotes (11). During promoter melting, the dsDNA must be separated before being loaded into the active site to form the transcription bubble. In the first step, the holoenzyme binds to the promoter, followed by the separation of the −10 element by β-protrusion and σ-factor (3, 6, 13). Then, the downstream element of the promoter DNA, either in the dsDNA or ssDNA form, must be loaded into the inner cleft of RNAP via the loading gate, which constitutes the space between the clamp and the β-lobe (12) (Fig. 1A). To accommodate the large conformational changes of DNA during its loading through the loading gate into the RNAP inner cleft (12), the gate needs to be first opened and then closed. The current literature suggests that gate opening is essentially synonymous with clamp opening (12), while the dynamics of promoter melting involving the conformational changes of the loading gate, particularly the role of β-lobe remain elusive.

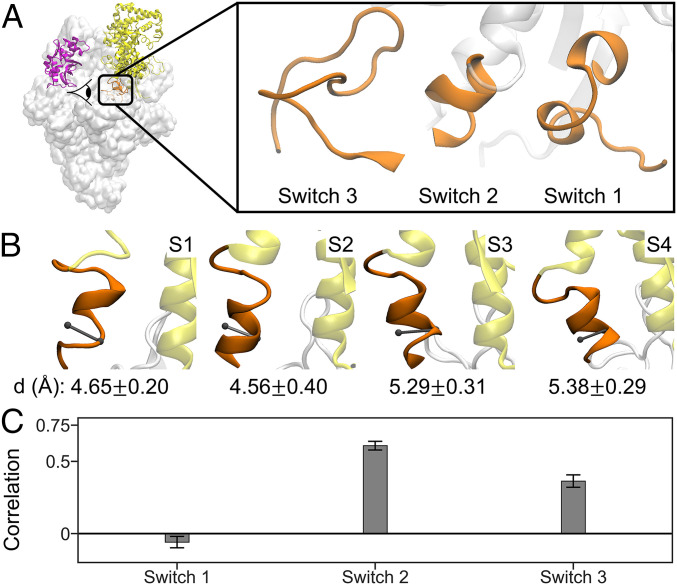
Fig. 1.

qMSM identifies four metastable states corresponding to the opening and closing of RNAP clamp domain. (A) The overall cartoon representation of bacterial holoenzyme and its domains, clamp, β-lobe, and Switch 2 region are shown as yellow, magenta, and orange, respectively. (B) Four macrostates of the clamp domain of RNAP are identified by MSM. The metastable states are represented as clamp opening/closing angles and rmsd of Switch 2 region (β’611 to 620) aligned to the Switch 2 region of the closed clamp in the crystal structure. The clamp opening/closing angle ($\text{Θ}$) is defined as the torsion angle between four centers of mass of C-α of residues 1) ω 60 to 68, 2) β’1461 to 1468, 3) β1031 to 1033 and β’620 to 622, and 4) β’568 to 573 and is offset by the angle of closed clamp crystal structure ($\text{Θ}-{\text{Θ}}_{\text{closed}}$). (C) The transition time between metastable states and the stationary population of each state is shown. The transitions between S1 and S2, as well as S3 and S4, are fast. The transitions between S1 or S2 to either S3 or S4 are slow, as indicated by the higher free-energy barrier. The full list of transition times is shown in SI Appendix, Table S1.

Previous transcription initiation studies have been focused on the clamp opening and closure (12), even though β-lobe is an indispensable component of the loading gate. This is likely due to the deceivingly stable conformation of β-lobe, while the clamp clearly adopts different conformations in the crystal and cryo-EM structures during promoter melting (3, 5, 6, 14). However, the larger B-factors (protein flexibility) of the β-lobe in these structures suggest that it is more flexible than the clamp (15–17). Thus, the β-lobe conformation reported in these structures could be an apparent average of a highly flexible domain (15, 17–19). Hence, both clamp and β-lobe need to be considered to elucidate the mechanisms of the DNA loading during initiation. Furthermore, dynamic transitions between resolved intermediate states at atomic resolution during promoter melting remain unresolved. The importance of the β-lobe was hypothesized in the recent cryo-EM study of Mtb RNAP during promoter melting (5). In this study, a cryo-EM structure of an intermediate of promoter melting with DNA loaded was captured even though the clamp is locked in a partially closed conformation by an inhibitor, suggesting β-lobe’s important role (instead of the clamp) in the first steps of dsDNA loading. Revealing these processes can provide mechanistic insights on how the clamp and β-lobe serve as the pincers of the loading-gate coordinate to allow efficient DNA loading.

The clamp domain has been the target for antibiotics such as Fidaxomicin, Lipiarmicin, Myxopyronin (Myx), Corallopyronin (Cor), and Squaramides with strong efficacies on inhibiting bacterial gene-transcription initiation (2, 8, 20, 21). These antibiotics all bind to the Switch regions, which lie at the base of the clamp and function to modulate clamp opening (8, 9). Myx, Cor, and Squaramides bind to the Switch 2 region and confine the clamp in a partially closed conformation (5, 20–22). Hence, inhibition of the Switch 2 region by these antibiotics have been shown to disrupt clamp motion and transcription initiation (20, 21). Furthermore, this class of inhibitors has been shown to have negligible effects on the activity of eukaryotic RNAP (20) so that it can be used as an antibiotics for human use. Even though structural studies have described the binding interactions between RNAP and Myx, the dynamic processes for antibiotics to recognize RNAP remain unclear (20, 21). Interestingly, these antibiotic-bound structures are all locked at the unfolded configuration of the Switch 2 region (8, 20, 21), which is different from the folded configuration of the Switch 2 region in the apo holoenzyme structures with the clamp being open or closed. Based on these observations from static structures, two distinct recognition mechanisms between antibiotics and RNAP can be proposed. In the conformational selection mechanism (23–31), the Switch 2 region can oscillate between folded and unfolded conformations, and the antibiotics then selectively bind to an unfolded conformation and subsequently trap the RNAP in a conformation with the clamp partially closed. In the induced fit model (23–31), antibiotics bind to a folded Switch 2 region, and this binding further induces the unfolding of the Switch 2 region, hence, stabilizing the RNAP-antibiotics bound complex. To resolve these competing recognition mechanisms, it is important to understand the dynamics of molecular recognition of the Switch 2 region by antibiotics. Understanding these recognition mechanisms can provide insights to improve the antibiotics design targeting the bacterial RNAP clamp motion.

To complement experiments, all-atom molecular dynamics (MD) simulations in the explicit solvent provide a powerful approach to modeling protein dynamics at atomic resolution. However, the timescale accessible to MD simulations of biomolecular complexes, such as RNAP (at microseconds or shorter), remains orders of magnitude shorter than that of functional conformational changes of interest (often at milliseconds or longer). Markov State Model (MSM) is a popular method that can bridge this timescale gap (32–41), in which continuous dynamics are modeled as Markovian transitions among metastable conformational states at discrete time intervals (lag times). MSMs have been widely applied to study protein conformational changes (40, 42–58), including those involved in the elongation of multisubunit RNAP (44, 55, 57–62). MSMs must be constructed with long enough lag times to allow Markovian interstate transitions. This imposes a main challenge for MSM studies of RNAP since the lag time is bound by the length of relatively short MD simulations to estimate transition probabilities. To address this challenge, we recently developed the quasi-MSM (qMSM) method based on the generalized master equation formalism, which encodes non-Markovian dynamics into memory kernel functions (63). qMSM provides a promising approach to studying the global conformational changes involved in the RNAP loading-gate motion.

In this work, we elucidated the dynamics of the loading-gate opening modulated by both the clamp and the β-lobe. To simulate the loading-gate dynamics that occur at a millisecond timescale (9), we constructed qMSM from an aggregation of 61.2-µs all-atom MD simulations of the holoenzyme (∼540,000 atoms). We determined that the clamp domain is the rate-limiting step of the loading-gate opening and closing, as the clamp opening and closing is four orders of magnitude slower than the β-lobe. Our qMSM reveals two intermediate states of clamp closing, one of which is bound by antibiotics. Myx (an inhibitor of clamp domain) recognizes RNAP via the conformational selection model for a metastable partially closed state containing an unfolded Switch 2 region. We further elucidated the complete molecular mechanisms by which the clamp domain opens and closes. Excitingly, we discovered that β-lobe is critical to promoter melting. Our results clearly demonstrated the coordination of both clamp and β-lobe to control the loading gate and generate a sufficiently opened loading gate for DNA loading.

Results and Discussions

Construction and Validation of qMSM for the Loading-Gate Dynamics of RNAP.

To understand the functional dynamics of the loading gate of Thermus aquaticus (Taq) holoenzyme, we followed our previously published protocol (61) to construct MSMs from extensive all-atom MD simulations. The loading-gate opening is a complex global conformational change involving opening as well as swiveling of both the clamp and β-lobe. These complex motions render the initial pathways highly difficult to obtain in order to fully sample the multidimensional flexibility of both pincers. To address this challenge, we adopted the two-basin Gō-model coarse-grained MD simulations (CG-MD) (64) to efficiently drive the loading-gate opening/closing via Gō potential, while fully exploring the dynamics of clamp and β-lobe (see Methods and SI Appendix, section 2.1). Indeed, our residue-based CG-MD simulations successfully sampled transitions between the open and closed RNAP clamp conformations (SI Appendix, Fig. S1A). We then back mapped representative CG-MD structures to all-atom structures and initiated MD simulations (accumulated 61.2-µs all-atom MD simulations of the system with ∼540,000 atoms, see Methods for details). To construct MSMs, we applied the time-lagged independent component analysis (tICA) (65–67) to reduce the high dimensional MD conformations to three collective variables and subsequently grouped them into 100 microstates using the k-center clustering (68). Please refer to Methods for more details of microstate MSM construction and validation.

To interpret biological mechanisms underlying loading-gate opening, we utilized our recently developed qMSM (63) method to build a model containing only four metastable macrostates (state S1 to S4 in Fig. 1) via kinetic lumping from 100 microstates (see Methods). To describe the slow timescale of complex biomolecular conformational changes (occurring at millisecond timescale), Markovian MSMs were typically built with hundreds of microstates, making the interpretation of biological significance highly difficult. Here, qMSM, which can recover the slow timescale only with a few numbers of states, is utilized to describe the slow opening and closing of the loading gate. Different from MSM, qMSM considers non-Markovian dynamics via time-dependent memory kernels ($\mathit{K}\left(\tau \right)$) using the generalized master equation (Eq. 1). For our system, the memory kernels are shown to relax at ${\text{τ}}_{\text{K}}=30$ns (see Methods and SI Appendix, Fig. S6A), and qMSM built at ${\text{τ}}_{\text{K}}$ can accurately predict the dynamics as compared with MD simulations (SI Appendix, Fig. S6C). Strikingly, we show that qMSM greatly outperforms four-state MSMs, which failed the Chapman–Kolmogorov test even when built with a lag time as long as 100 ns (SI Appendix, Fig. S6B) and predicted faster dynamics than all-atom MD simulations (SI Appendix, Fig. S6 C and D).

Dynamics of Opening and Closing of Clamp and β-Lobe Revealed by qMSM.

To examine the inherent oscillations of the opening and closing of the clamp and β-lobe, we employed the apo structure of T. aquaticus holoenzyme in the absence of DNA to cover all possible conformations. We conducted a qMSM study on the holoenzyme to reveal the timescale of the clamp and the β-lobe opening. Using qMSM, we identified four metastable states that correspond to different clamp conformations, indicating that clamp domain motion constitutes the slowest motions of the holoenzyme (Fig. 1B). We observed that the estimated equilibrium populations consist mostly of the state with open clamp [S1: 71.4%, similar with Protein Data Bank (PDB) ID 5TJG (6)]. This is consistent with the crystal structures of holoenzyme that are captured in the open clamp conformation (2, 69). The remaining conformations consist of the partially closed clamp α-helical Switch 2 (S2), the partially closed clamp π-helical Switch 2 (S3), and closed clamp state (S4, similar with PDB ID: 4XLN (7)) constituting 16.7, 7.7, and 4.2% of the total equilibrium population, respectively (Fig. 1C). We note that the closed clamp state is the minority in the RNAP holoenzyme system, which is consistent with single molecule fluorescence resonance energy transfer (sm-FRET) experiments (9). In addition, the closed clamp conformation is observed by crystallography and cryo-EM only when RNAP is in complex with DNA (7). This implies that the binding of DNA helps to close the clamp. Interestingly, we identified two partially closed intermediate states (S2 and S3) which have not been captured previously in the crystal structures of the holoenzyme but play an important role for antibiotic binding as we will discuss in the next section. We found that the clamp conformations of these two intermediate states are similar but differ by the conformations of the Switch 2 region (a helical motif positioned directly under the clamp domain, see Fig. 1 A and B). In S2, the Switch 2, which resembles the open-state S1, is in α-helix conformation (Fig. 2B). In sharp contrast, the conformations of Switch 2 in S3, which resemble the closed-state S4, are in the bulkier π-helix conformations (Fig. 2B).

Fig. 2.

Switch 2 region under the clamp acts as a hinge of the clamp domain opening and closing. (A) Switch regions are located under the clamp domain. There are three switch regions, Switch 1, Switch 2, and Switch 3, which are adjacent to each other. The viewing angle of the switch regions is shown by eye symbol in the left figure. (B) Diameter of the α-helix of the Switch 2 region in each metastable state is shown. The viewing direction of these figures is perpendicular to the viewing direction of A and into the protein core. The diameter is the distance between center of mass of C-α atoms of residue β’615 and 619 and C-α atom of residue β’617. Small diameter of helix at ∼4.5 Å indicates α-helical conformation, while large diameter of helix at ∼5.2 Å indicates π-helical conformation. (C) Pearson’s correlation coefficient of the clamp opening/closing angle with the rmsd of Switch 1, 2, 3 regions aligned to the C-α atoms of the individual Switch regions in the closed-clamp crystal structure. For the calculation of rmsd of switch regions, the C-α atoms of the following residues are included: 1) β’1431 to 1443 for Switch 1, 2) β’610 to 620 for Switch 2, and 3) β1010 to 1032 for Switch 3. Based on correlation analysis, only conformational change of Switch 2 is strongly correlated with the clamp opening/closing motion. The error bars were obtained by bootstrapping of independent trajectories.

Interestingly, among the three switch regions (Switch 1 to 3, Fig. 2A), we found that only the local refolding of the Switch 2 region is strongly correlated with the global conformational changes of the clamp closing (Fig. 2C). Our results demonstrate the critical role of the Switch 2 region in clamp opening and closing. We also examine the interactions of the Switch 2 region that regulate the clamp domain closing. The helical structure of Switch 2 (β’610 to 620) in each state is stabilized by the interactions between Switch 2 and its surroundings, particularly Switch 1 (β’1431 to 1443) and Switch 3 (β’1010 to 1032) (SI Appendix, Fig. S8 and Table S2). Switch 1 and Switch 3 regions are adjacent to Switch 2 and are also located directly under the clamp domain (Fig. 2A). Especially in S1 and S2, Switch 2 mostly interacts with Switch 1, while Switch 2 mostly interacts with Switch 3 in S3 and S4 (SI Appendix, Fig. S8 and Table S2). These observations suggest that the helical structure and interactions experienced by the Switch 2 region affect its relative position, which then determines the conformation of the RNAP clamp.

Further analysis of structures in metastable states identified by qMSM revealed residues that are important for the stabilization of Switch 2 helical conformation. In particular, residues βR1031, β’L619, and βQ1019 form specific interactions that stabilize the π-helix conformation in S3 and S4 (SI Appendix, Fig. S8 C and D and Table S2). Therefore, we predict that replacement of these two residues with those ones with shorter sidechains (e.g., β’Q1019A) will lead to the disruption of the π-helix and negatively impact transcription initiation. Indeed, previous experimental study shows that mutants of residues βR1031 and β’L619 (βR1269H and β’L343I in E. coli RNAP) exhibited impairment of promoter melting at early stage (70).

We further elucidate the timescale of the clamp opening and closing, which is shown to be in milliseconds from our qMSM. By calculating the mean first passage time (MFPT) between pairs of metastable states (SI Appendix, Table S1), we determined that the transition between the states with similar conformation of Switch 2 are fast: that is, transitions between open (S1) and S2 or between S3 and closed (S4) (Fig. 1C). On the other hand, the transitions between states with different conformations of Switch 2 are slow: that is, transitions from S1/S2 to S3/S4 (Fig. 1C and SI Appendix, Table S1). These observations indicate that the rate-limiting step of clamp closing corresponds to the conformational change of Switch 2 region that occurs at ∼2 ms (i.e., local refolding from α- to π-helix, Fig. 2B), which is consistent with the strong correlation between clamp domain movement and local refolding of Switch 2 (Fig. 2C). These observations agree with the previous hypothesis that the Switch 2 region acts as the hinge under the clamp that regulates the clamp domain (8, 20).

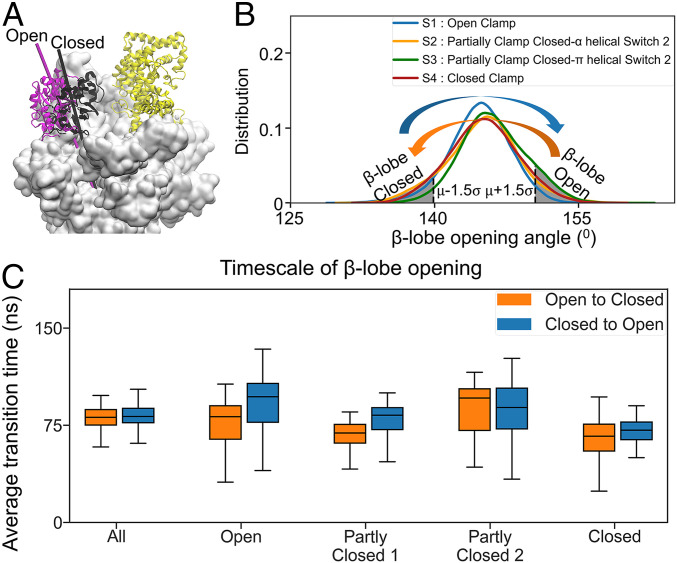
In our simulations, the β-lobe is more dynamic and flexible than previously suggested by structural studies (15–17), underlining its potential role in the promoter melting not reported before. To understand the role of β-lobe during promoter melting, we further analyzed the β-lobe conformations in our qMSM metastable states and observed that the opening of β-lobe is much faster than the clamp. First, we noticed that the distributions of β-lobe opening angles are similar in all four metastable states (Fig. 3B), suggesting that β-lobe’s opening and closing may occur in all states. Then, we calculated the timescale of β-lobe opening and closing, which are consistently at the timescale of 100 ns in all metastable states (Fig. 3C and SI Appendix, Fig. S9B). These results indicate that β-lobe is much more flexible than the clamp domain and can dynamically oscillate between the open and closed states at significantly faster (four orders of magnitudes) timescales than that of the clamp. The clamp opening is a much slower process, as it requires substantial local refolding of the secondary structure of the Switch 2 region. However, the β-lobe is connected to the rest of RNAP only by two coil chains, thus exhibiting substantially higher flexibility than the clamp. This observation is also consistent with the crystal structures of holoenzyme, where the B-factor of β-lobe is always larger than that of the clamp (15–17). Overall, our qMSM study reveals atomistic details on the dynamics of the loading gate that could not be revealed by structural studies alone. This includes the vast difference in the timescale of the opening between the clamp and β-lobe, implicating their functional significance and the structural changes of the Switch 2 helix accounting for the opening and closing of the clamp.

Fig. 3.

β-Lobe is a highly dynamic domain compared to clamp. (A) The open and closed conformations of β-lobe are shown as magenta and black, respectively. The β-lobe opening angle is defined as the dihedral angle formed by the center of mass of four groups of residues represented by the C-α atoms: 1) β’877 to 889, 2) β’938 to 943, 3) β’786 to 793, and 4) β142 to 325. (B) Distribution of β-lobe opening angle in each metastable state is shown. The open β-lobe state consists of structures having β-lobe opening angle larger than μ + 1.5σ, where μ and σ is the average and SD of all MD trajectories. The closed β-lobe state consists of the structures having β-lobe opening angle smaller than μ − 1.5σ. (C) Average transition time values of β-lobe opening in all the dataset and each metastable state. The opening of the β-lobe is two to three orders of magnitude faster than the clamp opening.

Elucidation of the Clamp Domain Dynamics Reveals the Recognition Mechanisms of Myx.

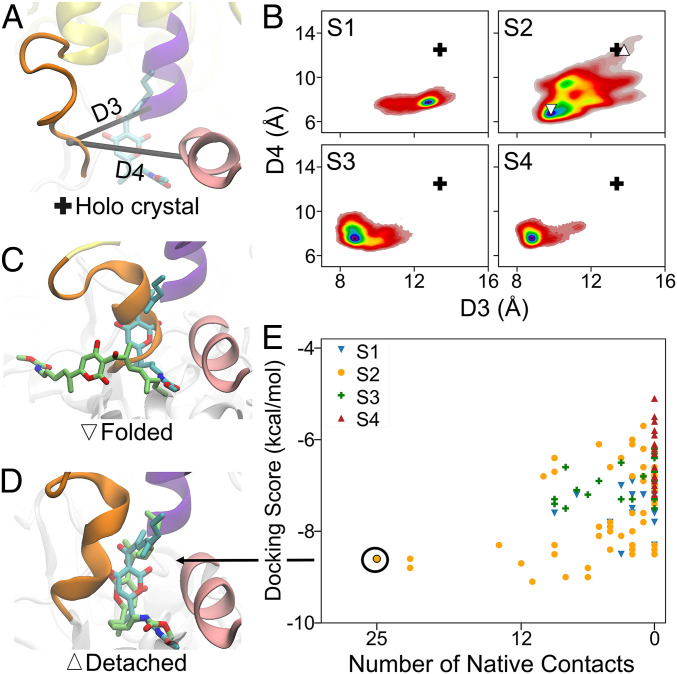
Our discovery of the atomistic mechanisms of clamp closing involving Switch 2 allows us to further explore the mechanisms by which a class of antibiotics such as Myx inhibit the initiation of transcription. We first showed that partially unfolded Switch 2 is transient only in a partially closed state (S2), and this unfolded conformation can sufficiently accommodate binding to Myx. We further analyze the Switch 2 structures in each qMSM metastable state. First, we calculate the distances between β’617 to 620 of Switch 2 and β’1466 to 1467 or β1084 to 1085, corresponding to D3 or D4, respectively (Fig. 4A). D3 is the distance between the centers of mass of C-α atoms of β’617 to 620 (part of Switch 2) and β1084 to 1085. D4 is calculated as the distance between the centers of mass of C-α atoms of β’617 to 620 (part of Switch 2) and β’1466 to 1467. As shown in the crystal structures, the binding pocket of Myx is formed by the unfolding of the Switch 2 region and these two helices (Fig. 4A) (20–22). Thus, for Myx to bind, enough space needs to be created between Switch 2 and these helices, which is shown by relatively large values D3 and D4 in the cocrystal structure of Myx bound to RNAP (+ symbol in Fig. 4 A and B). Our qMSM reveals that, only in S2, a fraction of the Switch 2 structures display sufficiently large D3 and D4, corresponding to the detached and partially unfolded Switch 2 region (Fig. 4B).

Fig. 4.

Spontaneous detachment or unfolding of Switch 2 region only occurs in a partially closed state, S2, which allows binding of Myx. (A) The structure of Switch 2 region when bound to Myx is shown. Switch 2, helix 1084 to 1090, helix β’1463 to 1467 are shown in orange, purple, and pink cartoon. Myx is shown as cyan sticks representation. D3 or D4 are the distance between center of mass represented by C-α atoms of β’617 to 620 (part of Switch 2) and β1084 to 1085 (D3) or β’1466 to 1467 (D4), respectively. (B) The free-energy landscape represented as D3 and D4 are shown for each metastable state. The plus sign (+) represents the cocrystal structure of RNAP bound with Myx (PDB ID: 3DXJ). The detached and folded Switch 2 structure in S2 is shown as (Δ) and ($\nabla$). (C) The docking pose of Myx to a folded ($\nabla$) Switch 2 is shown as lime sticks representations. (D) The docking pose of Myx to a detached (Δ) Switch 2 is shown as lime sticks representation, which also corresponds to the best docking pose (largest number of native contacts). In Fig. A , C, and D, and in both C and D, Myx in the cocrystal structure (PDB ID: 3DXJ) is overlaid and shown as cyan sticks representation. (E) Docking results of Myx to RNAP conformations in each metastable state are plotted as docking score and number of native contacts.

To further determine if the observed partially unfolded structures can indeed accommodate binding of Myx, we performed molecular docking to the transient partially unfolded (selected from qMSM) and folded structures (observed in crystal structures). Indeed, only docking to the structures from S2 results in a binding pose similar to the cocrystal structure, as indicated by a large number of native contacts (orange dots in Fig. 4E). Specifically, only binding to the detached (or unfolded) Switch 2 structure from S2, where both D3 and D4 are as large as the cocrystal structure (Δ symbol in Fig. 4B; orange dots in SI Appendix, Fig. S11D). Evidently, the best docking pose with the largest number of native contacts is strikingly similar to the cocrystal structure (Fig. 4D) and has several similar interactions with the cocrystal structure: that is, Myx with residue β’1463, β’1467, β1084, and β’621 (SI Appendix, Fig. S11 A and B). On the other hand, folded Switch 2 structure does not provide sufficient space for the binding of Myx, as Myx binds outside of the supposed binding pocket ($\nabla$ symbol in Fig. 4 B and C) yielding docking poses dissimilar to the cocrystal structure (brown dots in SI Appendix, Fig. S11D).

The above observations suggest a conformational selection recognition mechanism of the antibiotics. In this mechanism, Myx initially binds to the partially unfolded Switch 2 region, especially only in one of the partially closed clamp states: S2, where a binding pocket can form spontaneously in RNAP. The binding of Myx will confine the clamp in a partially closed clamp conformation and hinders it to either close or open (8, 9). Notably, there are consistent interactions between Myx and residues in RNAP in the initial bound conformation (SI Appendix, Fig. S11 A and B). We expect that upon initial binding, additional structural adjustments will further optimize these interactions to fully resemble the cocrystal structures.

Previous experimental results support the conformational selection mechanism of Myx that we proposed here. In particular, our model suggests that mutation of a phenylalanine, F614, derived from a published experimental study (21), a Switch 2 region residue that is in contact with the βL1088 and β’A1438, to a less bulky alanine may reduce the hydrophobic interactions and thus increase the chance of Switch 2 unfolding. This may subsequently result in more available space in the binding pocket and thus higher affinity for the binding of Myx. Indeed, previous in vitro IC50 measurement has validated this prediction and shown that mutation at β’F614A (F614A) causes hypersensitivity to Myx (21). To further investigate the binding of Myx to the F614A mutant, we also performed docking of Myx to the Switch 2 region with F614A mutation of structures from S2 (both folded and detached/unfolded). Docking to the unfolded and detached F614A conformations results in a larger number of docking poses that are more similar to the cocrystal structure (a large number of native contacts of light blue dots, SI Appendix, Fig. S11D). This implies that F614A does allow for more favorable binding with Myx by providing more space in the binding pocket. Interestingly, docking to the folded F614A conformations does not result in shift of fraction of native contact compared with the wild type (dark blue dots, SI Appendix, Fig. S11D). Thus, we anticipate that F614A only affects the partially unfolded structures, and unfolding is required to cause hypersensitivity of F614A. This result further supports the conformational selection mechanism. Furthermore, it has been shown that Myx cannot inhibit transcription initiation if the transcription bubble has already been formed in RPo complex (20, 21). In this complex, the clamp and Switch 2 are locked in closed conformation. Thus, the conformational selection mechanism of Myx recognition can explain this experimental result, since Myx binding requires the transition of the clamp domain to the partially closed conformation.

The Role of β-Lobe on Promoter DNA Loading.

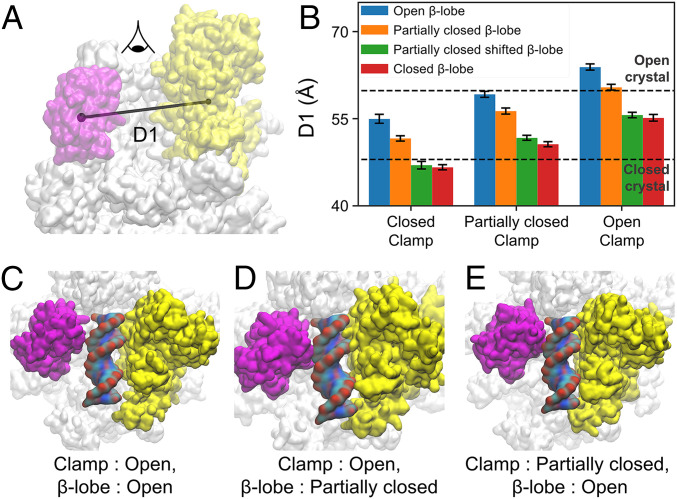
We next inspected the loading-gate (i.e., the space between β-lobe and clamp) conformations that can accommodate dsDNA loading. To achieve this, we modeled dsDNA in the loading-gate conformations with different degrees of opening (Fig. 5 A and B). We found that even when the clamp is partially closed, opening of the β-lobe is sufficient to accommodate dsDNA. To select representative conformations, we grouped the clamp and β-lobe conformations from our MD simulations into three and four states, respectively, according to structural similarities based on the principal component analysis (PCA) (see Methods and SI Appendix, section 7 for details). As a result, the clamp conformations are clustered to open, partially closed, and closed conformations (reference SI Appendix, Fig. S12A and section 7 for details), while the β-lobe conformations are grouped into the open, partially closed, partially closed shifted, and closed conformations (reference SI Appendix, Fig. S13A and section 7 for details). Combining these two sets of conformations results in 12 combinations of clamp and β-lobe conformations (Fig. 5B). We adopted the distance between the clamp and the β-lobe to describe the openness of the loading gate (D1 in Fig. 5A). We then examined if the loading gate in these 12 conformations has sufficient space to allow the loading of dsDNA. Interestingly, we found that only three combinations of clamp and β-lobe conformations can allow the loading of the dsDNA: open clamp and open β-lobe, open clamp and partially closed β-lobe, and partially closed clamp and open β-lobe (Fig. 5 C–E). In contrast, dsDNA will experience steric clashes when it passes through the loading gate in all other combinations of clamp and β-lobe conformations (SI Appendix, Figs. S14 and S15). At the beginning of the promoter melting, the clamp has to be closed or at least partially closed (3, 5–7). Then, dsDNA of the downstream promoter must pass through the loading gate representing the space between the clamp and β-lobe to enter the inner cleft of RNAP. Based on our results, either the clamp or β-lobe needs to open to provide enough space for the loading of the promoter dsDNA. If the clamp is already in a partially closed state at the beginning of the promoter melting, the opening of β-lobe will be sufficient to facilitate dsDNA loading geometrically.

Fig. 5.

Opening of β-lobe is sufficient for DNA loading even when the clamp is partially closed. (A) D1 is the distance between center of mass of clamp and β-lobe. The atoms included for the calculation of center of mass is the same as the ones included for PCA. (B) Merging the clustering in A and B results in 12 combinations of clamp and β-lobe conformations. The D1 values for the structure closest to the cluster centers from each combination are shown as bar graph. There are three combinations of clamp and β-lobe conformation that can accommodate dsDNA, which are (C) open and open, (D) open and partially closed, (E) partially closed and open, respectively.

Our proposed mechanism is supported by the cryo-EM of Mtb holoenzyme with promoter dsDNA already loaded to the inner cleft and Cor bound (5). Since Cor confines the clamp domain in the partially closed conformation, this cryo-EM structure suggests that clamp opening may not be required during the initial loading of dsDNA. We note that our proposed mechanism only explains the initial loading of dsDNA during promoter melting, where the transcription bubble has not been fully formed. In the later stage of the promoter melting, the loaded dsDNA will be separated into single-stranded DNA, and this step may require clamp opening. Furthermore, we also note that the structure of the promoter dsDNA may be more complicated than the DNA model used here, where the upstream promoter DNA (position −100) was found to wrap around the E. coli RNAP during promoter melting (71, 72). In this situation, opening of the clamp was required even at the beginning of promoter melting. Thus, as mentioned, different species of bacteria may follow different promoter melting pathways and have different free-energy landscapes of the promoter melting. Nonetheless, the β-lobe is always more flexible than the clamp across different bacterial species as observed by the B-factors in crystal and cryo-EM structures (15–17), suggesting that opening of the β-lobe is always easier than the clamp. Therefore, it is important to consider β-lobe during the promoter melting. Importantly, these findings highlight the importance of β-lobe during transcription initiation, which open opportunities to the development of antibiotics that target β-lobe. Interestingly, a recent cryo-EM study suggests that an antibiotic, Sorangicin, may inhibit the bacterial transcription via affecting the movement of β-lobe through allosteric interactions (73).

Conclusions

In this study, we have applied qMSM built from extensive all-atom MD simulations of bacterial RNAP to elucidate the dynamics of DNA loading-gate opening and closing. Using qMSM, we have determined that the timescale of the β-lobe opening is orders of magnitude faster than the clamp, suggesting the significant role of β-lobe during the DNA loading owing to its much higher mobility for gate opening or closing. Moreover, we discovered that the opening of the β-lobe is geometrically sufficient to allow initial loading of promoter dsDNA during the promoter melting, even when the clamp is in the partially closed conformation. Furthermore, we have shown that the clamp domain opening is mostly regulated by local refolding of the Switch 2 region from an α-helix to a π-helix. We further show that the spontaneous refolding and detachment of Switch 2 occurring in a partially closed clamp state provide enough space to allow binding of the antibiotic Myx via a conformational selection mechanism. Considering that the clamp, β-lobe, and Switch regions are conserved features in all prokaryotic species, we expect that the findings in this work could be generalized to other species of bacteria. Our qMSM, which adopts the memory kernels based on the generalized master equation, provides a promising approach in generating models containing a handful of states that can greatly facilitate the interpretation of the biological mechanisms. Overall, our work yields insights into the loading-gate dynamics and highlight the undiscovered role of β-lobe, which provides a potential target for future development of antibiotics.

Methods

All-Atom MD Simulation Setup for RNAP Structures with Open and Closed Clamp.

The open clamp conformation of the holoenzyme (RNAP and σ^A factor) was obtained from the crystal structure of T. aquaticus RNAP holoenzyme in complex with downstream-fork promoter [PDB ID: 5TJG (6)]. The closed clamp structure was modeled from crystal structures of Taq RNAP holoenzyme bound to the complete transcription bubble [PDB ID: 4XLN (7)]. The DNA chains are removed from the crystal structure in all the following MD simulations. For both crystal structures, residues 162 to 452 of β’ domain were replaced by the GAG sequence. The part replaced is not conserved and located far from the inner surface of the clamp domain. The modeled structures were solvated in a dodecahedron simulation box, and additional Na⁺ and Cl⁻ ions were added to neutralize the system and reach the 0.15 M salt concentration. The total number of atoms in the simulation box is consistently set to be 543,237 for all all-atom MD simulations initiated from different structures. GROMACS 4.5 simulation package (74) and AMBER 99SB-ILDN force field (75) are used for all-atom MD simulations. Please refer to SI Appendix, section 1: “All-atom MD simulation set-up” for more details of the system setup and all-atom MD simulations.

Microstate-MSM Construction and Validation.

We followed our previously published protocol (61) to construct microstate MSM to investigate the opening/closing dynamics of the RNAP loading gate as described below:

• (a)Initial pathways connecting the open and closed RNAP clamp conformations: We obtained initial pathways using a coarse-grained (AICG2+) model (64, 76), in which each bead represents an amino acid residue and the two-basin Gō potential was applied to drive the conformational change between two desired structures of interest. As shown in SI Appendix, Fig. S1A, we performed five CG-MD simulations using the CafeMol software (77) for each direction of transition, that is, closed to open and open to closed, of RNAP clamp conformation (reference SI Appendix, section 2.1 for details of CG-MD simulations). We chose 86 CG-MD conformations (SI Appendix, Fig. S1B) to further reconstruct them to all-atom conformations using the back-mapping algorithm based on restrained MD simulations (78). Please refer to SI Appendix, Fig. S2 and section 2.2 for more details of the back-mapping procedure.
• (b)All-atom MD sampling along the initial pathways: We performed extensive sampling that results in an MD dataset consisting of 306 200-ns MD simulations initiated from conformations along the initial pathways as well as from open and closed RNAP clamp structure (∼61.2-µs MD simulations in total, reference SI Appendix, section 2.2 for more details).
• (c)tICA (65–67) for dimensionality reduction: We applied the force distribution analysis (FDA) (79) to identify a set of pairwise atomic distances that correlate with the RNAP clamp motion; that is, those that experience the most different force distributions between the open and closed clamp (reference SI Appendix, section 2.3 for details of FDA analysis). We further merged these atom-pair distances with those between RNAP motifs that have been previously suggested to be correlated with the clamp motion (20, 80, 81). As a result, we obtained a list of 1,770 pairwise distances (involving C-α atoms from residues in the clamp, β-lobe, β-protrusion, Switch regions, and active site, reference SI Appendix, Fig. S4) to input to the tICA analysis. We have further validated our selection of atom-pair distances by showing that it outperforms a series of alternative atom-pair distances by systematically removing certain atom pairs from the list (SI Appendix, Fig. S3B). The hyperparameters for the tICA analysis (i.e., three tICs and tICA relaxation time of 10 ns) and clustering [i.e., 100 microstates via k-center clustering (68)] were obtained by the generalized matrix Rayleigh quotient (82) method (reference SI Appendix, Fig. S5 A–C and section 2.4 for details).
• (d)We validated the 100-microstate MSM by the Chapman–Kolmogorov test, where we showed that the residence probabilities from individual microstate predicated by the microstate MSM agrees with those directly computed from all-atom MD simulations (reference SI Appendix, Fig. S5E and section 2.5).

Macrostate qMSM Construction and Validation.

To facilitate the interpretation of biological mechanisms, we applied our recently developed qMSM (63) algorithm to construct a model containing only four states (S1 to S4). To construct qMSM, we first performed the kinetic lumping to group 100 microstates into four macrostates using the PCCA+ (83, 84) algorithm. We chose four macrostates because a stable gap is observed between the third and fourth slowest implied timescale (SI Appendix, Fig. S5D). Our qMSM applies the generalized master equation formalism to encode the non-Markovian dynamics in time-dependent memory kernels ($\mathit{K}\left(\tau \right)$):

$$\dot{\mathit{T}}\left(t\right)=\mathit{T}\left(t\right)\dot{\mathit{T}}\left(0\right)+\underset{0}{\overset{\min \left\{t,\hspace{0.17em}{\tau }_K\right\}}{{\displaystyle \int }}}\mathit{T}\left(t-\tau \right)\mathit{K}\left(\tau \right)d\tau ,$$ [1]

where ${\tau }_K$ refers to the memory kernel relaxation time (or characteristic decay time), $\mathit{K}\left(t>{\tau }_K\right)\approx 0$, and $\mathit{T}\left(t\right)$ is the transition probability matrix (TPM). To numerically compute $\mathit{K}\left(t\right)$ at $t=n\mathrm{\Delta }t$ ($\mathrm{\Delta }t$ = 1 ns), we utilized a discretized form of the generalized master equation (SI Appendix, Eqs. S1 and S2) (63). We chose ${\text{τ}}_{\text{K}}=30$ ns because the mean integration of memory kernel converges at this lag time (SI Appendix, Eq. S5 and Fig. S6A). Please refer to SI Appendix, section 3 for additional details of qMSM construction.

We validated our qMSM using the Chapman–Kolmogorov test by showing that the qMSM with ${\text{τ}}_{\text{K}}=30$ ns can accurately predict residence probabilities for all four states (SI Appendix, Fig. S6C). In sharp contrast, we showed that the four-macrostate MSM without considering the memory kernels is not Markovian even with a lag time up to ∼100 ns (SI Appendix, Fig. S6B). We further showed that these first-order MSMs predict significantly faster dynamics than those of the MD simulations in the Chapman–Kolmogorov test (SI Appendix, Fig. S6 C and D) and also predicted substantially shorter MFPTs than qMSM (SI Appendix, Fig. S7 B and D). To compute MFPTs and to identify major pathways for RNAP clamp closing by the transition path theory (85, 86), we utilized the TPM:$T\left(\tau =5 \text{μ}\mathrm{s}\right)$ obtained from the discretized generalized master equation in our qMSM (reference SI Appendix, section 4 for additional details). We note that the inclusion of memory functions does not increase the number of states in qMSMs. Instead, rather than using the TPM as in MSMs, qMSMs model the dynamics using the transition tensors (63). As a result, qMSMs has substantial advantages over MSMs in interpreting biological mechanisms by yielding models with a handful of states.

Molecular Docking of Myx to RNAP.

To determine which conformations of Switch 2 can accommodate the binding of Myx, we performed molecular docking to several representative structures from each metastable state. For the structures from S2, we separated the unfolded and detached Switch 2 conformations from the folded ones. To check the similarity of the docking poses to the cocrystal structures of Taq holoenzyme and Myx, we defined and calculated the number of native contacts for each docking pose. The number of native contacts is the number of interactions between Taq holoenzyme and Myx in a docking pose which is also found in the cocrystal structure [PDB ID: 3DXJ (20)] (reference SI Appendix, section 6 for further details of molecular docking).

Selection of Representative Loading-Gate Conformations and Modeling of dsDNA.

To determine which conformation of clamp and β-lobe geometrically allow dsDNA loading, we selected representative structures from our MD simulations based on the degree of opening of the clamp and β-lobe conformations. First, we performed PCA (87) of clamp and β-lobe separately, to characterize the clamp and β-lobe opening motions (reference SI Appendix, section 7 for details of PCA). Based on the PCA results, we performed independent k-means clustering to group clamp and β-lobe conformations to three and four clusters, respectively (Fig. 5 and SI Appendix, Figs. S12A and S13A). By merging the results from the two sets of clustering, we obtained 12 clusters of different combinations of clamp and β-lobe conformations (Fig. 5B). For each cluster, we selected the structure closest to the cluster center and modeled dsDNA in the loading gate using the PyMOL Molecular Graphics System, Version 2.0 Schrödinger (SI Appendix, Figs. S14 and S15). The steric clash for each of the models was checked by MDWeb webserver (88).

Data Availability

MD simulation trajectories have been deposited in Open Science Framework (DOI: 10.17605/OSF.IO/HK9F7) (89).