Plug-and-Play Methods for Magnetic Resonance Imaging: Using Denoisers for Image Recovery

Abstract

Magnetic Resonance Imaging (MRI) is a non-invasive diagnostic tool that provides excellent soft-tissue contrast without the use of ionizing radiation. Compared to other clinical imaging modalities (e.g., CT or ultrasound), however, the data acquisition process for MRI is inherently slow, which motivates undersampling and thus drives the need for accurate, efficient reconstruction methods from undersampled datasets. In this article, we describe the use of “plug-and-play” (PnP) algorithms for MRI image recovery. We first describe the linearly approximated inverse problem encountered in MRI. Then we review several PnP methods, where the unifying commonality is to iteratively call a denoising subroutine as one step of a larger optimization-inspired algorithm. Next, we describe how the result of the PnP method can be interpreted as a solution to an equilibrium equation, allowing convergence analysis from the equilibrium perspective. Finally, we present illustrative examples of PnP methods applied to MRI image recovery.

I. Introduction

Magnetic Resonance Imaging (MRI) uses radiofrequency waves to non-invasively evaluate the structure, function, and morphology of soft tissues. MRI has become an indispensable imaging tool for diagnosing and evaluating a host of conditions and diseases. Compared to other clinical imaging modalities (e.g., CT or ultrasound), however, MRI suffers from slow data acquisition. A typical clinical MRI exam consists of multiple scans and can take more than an hour to complete. For each scan, the patient may be asked to stay still for several minutes, with slight motion potentially resulting in image artifacts. Furthermore, dynamic applications demand collecting a series of images in quick succession. Due to the limited time window in many dynamic applications (e.g., contrast enhanced MR angiography), it is not feasible to collect fully sampled datasets. For these reasons, MRI data is often undersampled. Consequently, computationally efficient methods to recover high-quality images from undersampled MRI data have been actively researched for the last two decades.

The combination of parallel (i.e., multi-coil) imaging and compressive sensing (CS) has been shown to benefit a wide range of MRI applications [1], including dynamic applications, and has been included in the default image processing frameworks offered by several major MRI vendors. More recently, learning-based techniques (e.g., [2]–[6]) have been shown to outperform CS methods. Some of these techniques learn the entire end-to-end mapping from undersampled k-space or aliased images to recovered images (e.g., [4]). Considering that the forward model in MRI changes from one dataset to the next, such methods have to be either trained over a large and diverse data corpus or limited to a specific application. Other methods train scan-specific convolutional neural networks (CNN) on a fully-sampled region of k-space and then use it to interpolate missing k-space samples [5]. These methods do not require separate training data but demand a fully sampled k-space region. Due to the large number of unknowns in CNN, such methods require a fully sampled region that is larger than that typically acquired in parallel imaging, limiting the acceleration that can be achieved. Other supervised learning methods are inspired by classic variational optimization methods and iterate between data-consistency enforcement and a trained CNN, which acts as a regularizer [3]. Such methods require a large number of fully sampled, multi-coil k-space datasets, which may be difficult to obtain in many applications. Also, since CNN training occurs in the presence of dataset-specific forward models, generalization from training to test scenarios remains an open question [6]. Consequently, the integration of learning-based methods into physical inverse problems remains a fertile area of research. There are many directions for improvement, including recovery fidelity, computational and memory efficiency, robustness, interpretability, and ease-of-use.

This article focuses on “plug-and-play” (PnP) algorithms [7], which alternate image denoising with forward-model based signal recovery. PnP algorithms facilitate the use of state-of-the-art image models through their manifestations as image denoisers, whether patch-based (e.g., [8]) or deep neural network (DNN) based (e.g., [9]). The fact that PnP algorithms decouple image modeling from forward modeling has advantages in compressive MRI, where the forward model can change significantly among different scans due to variations in the coil sensitivity maps, sampling patterns, and image resolution. Furthermore, fully sampled k-space MRI data is not needed for PnP; the image denoiser can be learned from MRI image patches, or possibly even magnitude-only patches. The objective of this article is two-fold: i) to review recent advances in plug-and-play methods, and ii) to discuss their application to compressive MRI image reconstruction.

The remainder of the paper is organized as follows. We first detail the inverse problem encountered in MRI reconstruction. We then review several PnP methods, where the unifying commonality is to iteratively call a denoising subroutine as one step of a larger optimization-inspired algorithm. Next, we describe how the result of the PnP method can be interpreted as a solution to an equilibrium equation, allowing convergence analysis from the equilibrium perspective. Finally, we present illustrative examples of PnP methods applied to MRI image recovery. For an extended version of this paper that contains additional references and more in-depth discussions on a variety of topics, see [10].

II. Image recovery in compressive MRI

In this section, we describe the standard linear inverse problem formulation in MRI. We acknowledge that more sophisticated formulations exist (see, e.g., the article by Mariya Doneva in this issue for a more careful modeling of physics effects). Briefly, the measurements are samples of the Fourier transform of the image, where the Fourier domain is often referred to as “k-space.” The transform can be taken across two or three spatial dimensions and includes an additional temporal dimension in dynamic applications. Furthermore, measurements are often collected in parallel from C ≥ 1 receiver coils. In dynamic parallel MRI with Cartesian sampling, the time-t k-space measurements from the i^th coil take the form

$${\mathit{y}}_i^{(t)}={\mathit{P}}^{(t)}\mathit{F}{\mathit{S}}_i{\mathit{x}}^{(t)}+{\mathit{w}}_i^{(t)},$$ (1)

where ${\mathit{x}}^{(t)}\in {\mathbb{C}}^N$ is the vectorized 2D or 3D image at discrete time t, ${\mathit{S}}_i\in {\mathbb{C}}^{N\times N}$ is a diagonal matrix containing the sensitivity map for the i^th coil, $\mathit{F}\in {\mathbb{C}}^{N\times N}$ is the 2D or 3D discrete Fourier transform (DFT), the sampling matrix ${\mathit{P}}^{(t)}\in {\mathbb{R}}^{M,N}$ contains M rows of the N × N identity matrix, and ${\mathit{w}}_i^{(t)}\in {\mathbb{C}}^M$ is additive white Gaussian noise (AWGN). Often the sampling pattern changes across frames t. The MRI literature often refers to R ≜ N/M as the “acceleration rate.” The AWGN assumption, which does not hold for the measured parallel MRI data, is commonly enforced using noise pre-whitening filters, which yields the model (1) but with diagonal “virtual” coil maps S_i [11].

MRI measurements are acquired using a sequence of measurement trajectories through k-space. These trajectories can be Cartesian or non-Cartesian in nature. Cartesian trajectories are essentially lines through k-space. In the Cartesian case, one k-space dimension (i.e., the frequency encoding) is fully sampled, while the other one or two dimensions (i.e., the phase encodings) are undersampled to reduce acquisition time. Typically, one line, or “readout,” is collected after every RF pulse, and the process is repeated several times to collect adequate samples of k-space. Non-Cartesian trajectories include radial or spiral curves, which have the effect of distributing the samples among all dimensions of k-space. Compared to Cartesian sampling, non-Cartesian sampling provides more efficient coverage of k-space and yields an “incoherent” forward operator that is more conducive to compressed-sensing reconstruction. But Cartesian sampling remains the method of choice in clinical practice, due to its higher tolerance to system imperfections and an extensive record of success.

Since the sensitivity map, S_i, is patient-specific and varies with the location of the coil with respect to the imaging plane, both S_i and x^(t) are unknown in practice. Although calibration-free methods have been proposed to estimate S_ix^(t) or to jointly estimate S_i and x^(t), it is more common to first estimate S_i through a calibration procedure and then treat S_i as known in (1). Stacking $\left\{{\mathit{y}}_i^{(t)}\right\}$, $\left\{{\mathit{x}}^{(t)}\right\}$, and $\left\{{\mathit{w}}_i^{(t)}\right\}$ into vectors y, x, and w, and packing {P^(t)FS_i} into a known block-diagonal matrix A, we obtain the linear inverse problem of recovering x from

$$\mathit{y}=\mathit{Ax}+\mathit{w},\mathit{w}~\mathcal{N}(\mathbf{0},{\sigma }^2\mathit{I}),$$ (2)

where $\mathcal{N}(\mathbf{0},{\sigma }^2\mathit{I})$ denotes a circularly symmetric complex-Gaussian random vector.

III. Signal Recovery and Denoising

The maximum likelihood (ML) estimate of x from y in (2) is ${\widehat{\mathit{x}}}_{\mathrm{ml}}\triangleq {\mathrm{arg\; max}}_{\mathit{x}}p(\mathit{y}|\mathit{x})$, where p(y|x), the probability density of y conditioned on x, is known as the “likelihood function.” The ML estimate is often written in the equivalent form ${\widehat{\mathit{x}}}_{\mathrm{ml}}={\mathrm{arg\; min}}_{\mathit{x}}\{-\ln p(\mathit{y}|\mathit{x})\}$. In the case of σ²-variance AWGN w, we have that $-\ln p(\mathit{y}|\mathit{x})=\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\mathrm{const}$, and so ${\widehat{\mathit{x}}}_{\mathrm{ml}}={\mathrm{arg\; min}}_{\mathit{x}}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2$, which can be recognized as least-squares estimation. Although least-squares estimation can give reasonable performance when A is tall and well conditioned, this is rarely the case under moderate to high acceleration (i.e., R > 2). With acceleration, it is critically important to exploit prior knowledge of signal structure.

The traditional approach to exploiting such prior knowledge is to formulate and solve an optimization problem of the form

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\varphi (\mathit{x})\right\},$$ (3)

where the regularization term ϕ(x) encodes prior knowledge of x. In fact, $\widehat{\mathit{x}}$ in (3) can be recognized as the maximum a posteriori (MAP) estimate of x under the prior density model p(x) ∝ exp(−ϕ(x)). To see why, recall that the MAP estimate maximizes the posterior distribution p(x|y). That is, ${\widehat{\mathit{x}}}_{\text{map}}\triangleq {\mathrm{arg\; max}}_{\mathit{x}}p(\mathit{x}|\mathit{y})={\mathrm{arg\; min}}_{\mathit{x}}\{-\ln p(\mathit{x}|\mathit{y})\}$. Since Bayes’ rule implies that ln p(x|y) = ln p(y|x) + ln p(x) − ln p(y), we have

$${\widehat{\mathit{x}}}_{\mathrm{map}}=\arg \underset{\mathit{x}}{\min }\{-\ln p(\mathit{y}|\mathit{x})-\ln p(\mathit{x})\}.$$ (4)

Recalling that the first term in (3) (i.e., the “loss” term) was observed to be −ln p(y|x) (plus a constant) under AWGN noise, the second term in (3) must obey ϕ(x) = −ln p(x) + const. We will find this MAP interpretation useful in the sequel.

It is not easy to design good regularizes ϕ for use in (3). They must not only mimic the negative log signal-prior, but also enable tractable optimization. One common approach is to use ϕ(x) = λ‖Ψx‖₁ with Ψ^H a tight frame (e.g., a wavelet transform) and λ > 0 a tuning parameter [12]. Such regularizes are convex, and the ℓ₁ norm rewards sparsity in the transform outputs Ψx when used with the quadratic loss.

Particular insight comes from considering the special case of A = I, where the measurement vector in (2) reduces to an AWGN-corrupted version of the image x, i.e.,

$$\mathit{z}=\mathit{x}+\mathit{w},\mathit{w}~\mathcal{N}(\mathbf{0},{\sigma }^2\mathit{I}).$$ (5)

The problem of recovering x from noisy z, known as “denoising,” has been intensely researched for decades. While it is possible to perform denoising by solving a regularized optimization problem of the form (3) with A = I, today’s state-of-the-art approaches are either algorithmic (e.g., [8]) or DNN-based (e.g., [9]). This begs an important question: can these state-of-the-art denoisers be leveraged for MRI signal reconstruction, by exploiting the connections between the denoising problem and (3)? As we shall see, this is precisely what the PnP methods do.

IV. Plug-and-Play Methods

In this section, we review several approaches to PnP signal reconstruction. What these approaches have in common is that they recover x from measurements y of the form (2) by iteratively calling a sophisticated denoiser within a larger optimization or inference algorithm.

A. Prox-based PnP

To start, let us imagine how the optimization in (3) might be solved. Through what is known as “variable splitting,” we could introduce a new variable, v, to decouple the regularizer ϕ(x) from the data fidelity term $\frac{1}{2{\sigma }_2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2$. The variables x and v could then be equated using an external constraint, leading to the constrained minimization problem

$$\widehat{\mathit{x}}=\underset{\mathit{x}\in {\mathbb{C}}^N}{\mathrm{arg\; min}}\underset{\mathit{v}\in {\mathbb{C}}^N}{\min }\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\varphi (\mathit{v})\right\}\text{subject to}\mathit{x}=\mathit{v}.$$ (6)

Equation (6) suggests an algorithmic solution that alternates between separately estimating x and estimating v, with an additional mechanism to asymptotically enforce the constraint x = v.

The original PnP method [7] is based on the alternating direction method of multipliers (ADMM) [13]. For ADMM, (6) is first reformulated as the “augmented Lagrangian”]

$$\underset{\mathit{x},\mathit{v}}{\min }\underset{\mathit{\lambda }}{\max }\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\varphi (\mathit{v})+\mathrm{Re}\{{\mathit{\lambda }}^{\text{H}}(\mathit{x}-\mathit{v})\}+\frac{1}{2\nu }\Vert \mathit{x}-\mathit{v}{\Vert }^2\right\},$$ (7)

where λ are Lagrange multipliers and ν > 0 is a penalty parameter that affects the convergence speed of the algorithm, but not the final solution. With u ≜ νλ, (7) can be rewritten as

$$\underset{\mathit{x},\mathit{v}}{\min }\underset{\mathit{u}}{\max }\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\varphi (\mathit{v})+\frac{1}{2\nu }\Vert \mathit{x}-\mathit{v}+\mathit{u}{\Vert }^2-\frac{1}{2\nu }\Vert \mathit{u}{\Vert }^2\right\}.$$ (8)

ADMM solves (8) by alternating the optimization of x and v with gradient ascent of u, i.e.,

$${\mathit{x}}_k=\mathit{h}({\mathit{v}}_{k-1}-{\mathit{u}}_{k-1};\nu )$$ (9a)

$${\mathit{v}}_k={\mathrm{prox}}_{\varphi }({\mathit{x}}_k+{\mathit{u}}_{k-1};\nu )$$ (9b)

$${\mathit{u}}_k={\mathit{u}}_{k-1}+({\mathit{x}}_k-{\mathit{v}}_k),$$ (9c)

where h(z; ν) and prox_ϕ(z; ν), known as “proximal maps,” are defined as

$${\mathrm{prox}}_{\varphi }(\mathit{z};\nu )\triangleq \underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\varphi (\mathit{x})+\frac{1}{2\nu }\Vert \mathit{x}-\mathit{z}{\Vert }^2\right\}$$ (10)

$$\mathit{h}(\mathit{z};v)\triangleq \underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2+\frac{1}{2\nu }\Vert \mathit{x}-\mathit{z}{\Vert }^2\right\}={\mathrm{prox}}_{\Vert \mathit{y}-\mathit{Ax}{\Vert }^2/(2{\sigma }^2)}(\mathit{z};\nu )$$ (11)

$$={\left({\mathit{A}}^{\text{H}}\mathit{A}+\frac{{\sigma }^2}{\nu }\mathit{I}\right)}^{-1}\left({\mathit{A}}^{\text{H}}\mathit{y}+\frac{{\sigma }^2}{\nu }\mathit{z}\right).$$ (12)

Under some weak technical constraints, it can be proven [13] that when ϕ is convex, the ADMM iteration (9) converges to $\widehat{\mathit{x}}$ x, the global minimum of (3) and (6).

From the discussion in Section III, we immediately recognize prox_ϕ(z; ν) in (10) as the MAP denoiser of z under AWGN variance ν and signal prior p(x) ∝ exp(−ϕ(x)). The key idea behind the original PnP work [7] was, in the ADMM recursion (9), to “plug in” a powerful image denoising algorithm like “block-matching and 3D filtering” (BM3D) [8] in place of the proximal denoiser prox_ϕ(x; ν) from (10). If the plug-in denoiser is denoted by “f,” then the PnP ADMM algorithm becomes

$${\mathit{x}}_k=\mathit{h}({\mathit{v}}_{k-1}-{\mathit{u}}_{k-1};\nu )$$ (13a)

$${\mathit{v}}_k=\mathit{f}({\mathit{x}}_k+{\mathit{u}}_{k-1})$$ (13b)

$${\mathit{u}}_k={\mathit{u}}_{k-1}+({\mathit{x}}_k-{\mathit{v}}_k).$$ (13c)

A wide variety of empirical results (see, e.g., [7,14,15]) have demonstrated that, when f is a powerful denoising algorithm like BM3D, the PnP algorithm (13) produces far better recoveries than the regularization-based approach (9). Although the value of ν does not change the fixed point of the standard ADMM algorithm (9), it affects the fixed point of the PnP ADMM algorithm (13) through the ratio σ²/ν in (12).

The success of PnP methods raises important theoretical questions. Since f is not in general the proximal map of any regularizer ϕ, the iterations (13) may not minimize a cost function of the form in (3), and (13) may not be an implementation of ADMM. It is then unclear if the iterations (13) will converge. And if they do converge, it is unclear what they converge to. The consensus equilibrium framework, which we discuss in Section V, aims to provide answers to these questions.

The use of a generic denoiser in place of a proximal denoiser can be translated to non-ADMM algorithms, such as FISTA, primal-dual splitting (PDS), and others, as in [16]–[18]. Instead of optimizing x as in (13), PnP FISTA [16] uses the iterative update

$${\mathit{z}}_k={\mathit{s}}_{k-1}-\frac{\nu }{{\sigma }^2}{\mathit{A}}^{\text{H}}({\mathit{As}}_{k-1}-\mathit{y})$$ (14a)

$${\mathit{x}}_k=\mathit{f}({\mathit{z}}_k)$$ (14b)

$${\mathit{s}}_k={\mathit{x}}_k+\frac{q_{k-1}-1}{q_k}({\mathit{x}}_k-{\mathit{x}}_{k-1}),$$ (14c)

where (14a) is a gradient descent (GD) step on the negative log-likelihood $\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2$ at x = s_k−1 with step-size $\nu \in (0,{\sigma }^2\Vert \mathit{A}{\Vert }_2^{-2})$, (14b) is the plug-in replacement of the usual proximal denoising step in FISTA, and (14c) is an acceleration step, where it is typical to use $q_k=(1+\sqrt{1+4q_{k-1}^2})/2$ and q₀ = 1.

Comparing PnP ADMM (13) to PnP FISTA (14), one can see that they differ in how the data fidelity term $\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2$ is handled: PnP ADMM uses the proximal update (12), while PnP FISTA and PnP PDS use the GD step (14a). In most cases, solving the proximal update (12) is much more computationally costly than taking a GD step (14a). Thus, with ADMM, it is common to approximate the proximal update (12) using, e.g., several iterations of the conjugate gradient (CG) algorithm or GD, which should reduce the per-iteration complexity of (13) but may increase the number of iterations. But even with these approximations of (12), PnP ADMM is usually close to “convergence” after 10-50 iterations (e.g., see Figure 4).

An important difference between the aforementioned flavors of PnP is that the stepsize ν is constrained in FISTA but not in ADMM or PDS. Thus, PnP FISTA restricts the range of reachable fixed points relative to PnP ADMM and PnP PDS.

B. The balanced FISTA approach

In Section III, when discussing the optimization problem (3), the regularizer ϕ(x) = λ‖Ψx‖₁ was mentioned as a popular option, where Ψ is often a wavelet transform. The resulting optimization problem,

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }_2^2+\lambda \Vert \mathbf{\Psi }\mathit{x}{\Vert }_1\right\},$$ (15)

is said to be stated in “analysis” form (see [19] in this special issue). The proximal denoiser associated with (15) has the form

$${\mathrm{prox}}_{\varphi }(\mathit{z};\nu )=\underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\lambda \Vert \mathbf{\Psi }\mathit{x}{\Vert }_1+\frac{1}{2\nu }\Vert \mathit{x}-\mathit{z}{\Vert }^2\right\}.$$ (16)

When Ψ is orthogonal, it is well known that prox_ϕ(z; ν) = f_tdt(z; λν), where

$${\mathit{f}}_{\mathrm{tdt}}(\mathit{z};\tau )\triangleq {\mathbf{\Psi }}^H\text{soft-thresh}(\mathbf{\Psi }\mathit{z};\tau )$$ (17)

is the “transform-domain thresholding” denoiser with ${[\mathrm{soft-thresh}(\mathit{u},\tau )]}_n\triangleq \max \{0,\frac{|u_n|-\tau }{u_n}\}{u}_n$. The denoiser (17) is very efficient to implement, since it amounts to little more than computing forward and reverse transforms.

In practice, (15) yields much better results with non-orthogonal Ψ, such as when Ψ^H is a tight frame (see, e.g., the references in [20]). In the latter case, Ψ^HΨ = I with tall Ψ. But, for general tight frames Ψ^H, the proximal denoiser (16) has no closed-form solution. What if we simply plugged the transform-domain thresholding denoiser (17) into an algorithm like ADMM or FISTA? How can we interpret the resulting approach? Interestingly, as we describe below, if (17) is used in PnP FISTA, then it does solve a convex optimization problem, although one with a different form than (3). This approach was independently proposed in [12] and [20], where in the latter it was referred to as “balanced FISTA” (bFISTA) and applied to parallel cardiac MRI. Notably, bFISTA was proposed before the advent of PnP FISTA. More details are provided below.

The optimization problem (15) can be stated in constrained “synthesis” form as

$$\widehat{\mathit{x}}={\mathbf{\Psi }}^H\widehat{\mathit{\alpha }}\text{for}\widehat{\mathit{\alpha }}=\underset{\mathit{\alpha }\in \mathrm{range}(\mathbf{\Psi })}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{A}{\mathbf{\Psi }}^H\mathit{\alpha }{\Vert }_2^2+\lambda \Vert \mathit{\alpha }{\Vert }_1\right\},$$ (18)

where α are transform coefficients. Then, as β → ∞ below, (18) can be expressed in the unconstrained form

$$\widehat{\mathit{x}}={\mathbf{\Psi }}^H\widehat{\mathit{\alpha }}\text{for}\widehat{\mathit{\alpha }}=\underset{\mathit{\alpha }}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{A}{\mathbf{\Psi }}^H\mathit{\alpha }{\Vert }_2^2+\frac{\beta }{2}\Vert {\mathit{P}}_{\mathbf{\Psi }}^{\perp }\mathit{\alpha }{\Vert }_2^2+\lambda \Vert \mathit{\alpha }{\Vert }_1\right\}$$ (19)

with projection matrix ${\mathit{P}}_{\mathbf{\Psi }}^{\perp }\triangleq \mathit{I}-\mathbf{\Psi }{\mathbf{\Psi }}^{\text{H}}$. In practice, it is not possible to take β → ∞ and, for finite values of β, the problems (18) and (19) are not equivalent. However, problem (19) under finite β is interesting to consider in its own right, and it is sometimes referred to as the “balanced” approach. If we solve (19) using FISTA with step-size ν > 0 (recall (14a)) and choose the particular value β = 1/ν then, remarkably, the resulting algorithm takes the form of PnP FISTA (14) with f(z) = f_tdt(z; λ). This particular choice of β is motivated by computational efficiency (since it leads to the use of f_tdt) rather than recovery performance. Still, as we demonstrate in Section VI, it performs relatively well.

C. Regularization by denoising

Another PnP approach, proposed by Romano, Elad, and Milanfar in [21], recovers x from measurements y in (2) by finding the $\widehat{\mathit{x}}$ that solves the optimality condition¹

$$\mathbf{0}=\frac{1}{{\sigma }^2}{\mathit{A}}^T(\mathit{A}\widehat{\mathit{x}}-\mathit{y})+\frac{1}{\nu }(\widehat{\mathit{x}}-\mathit{f}(\widehat{\mathit{x}})),$$ (20)

where f is an arbitrary (i.e., “plug in”) image denoiser and ν > 0 is a tuning parameter. In [21], several algorithms were proposed to solve (20). Numerical experiments in [21] suggest that, when f is a sophisticated denoiser (like BM3D) and ν is well tuned, the solutions $\widehat{\mathit{x}}$ to (20) are state-of-the-art, similar to those of PnP ADMM.

The approach (20) was coined “regularization by denoising” (RED) in [21] because, under certain conditions, the $\widehat{\mathit{x}}$ that solve (20) are the solutions to the regularized least-squares problem

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{\mathrm{arg\; min}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2+{\varphi }_{\mathrm{red}}(\mathit{x})\right\}\text{with}{\varphi }_{\mathrm{red}}(\mathit{x})\triangleq \frac{1}{2\nu }{\mathit{x}}^{⊺}(\mathit{x}-\mathit{f}(\mathit{x})),$$ (21)

where the regularizer ϕ_red is explicitly constructed from the plug-in denoiser f. But what are these conditions? Assuming that f is differentiable almost everywhere, it was shown in [22] that the solutions of (20) correspond to those of (21) when i) f is locally homogeneous² and ii) f has a symmetric Jacobian matrix (i.e., [Jf(x)]^⊺ = Jf(x) ∀x). But it was demonstrated in [22] that these properties are not satisfied by popular image denoisers, such as the median filter, transform-domain thresholding, NLM, BM3D, TNRD, and DnCNN. Furthermore, it was proven in [22] that if the Jacobian of f is non-symmetric, then there does not exist any regularizer ϕ under which the solutions of (20) minimize a regularized loss of the form in (3).

One may then wonder how to justify (20). In [22], Reehorst and Schniter proposed an explanation for (20) based on “score matching”, which we now summarize. Suppose we are given a large corpus of training images ${\left\{{\mathit{x}}_t\right\}}_{t=1}^T$, from which we could build the empirical prior model

$$\widehat{p_{\text{x}}}(\mathit{x})\triangleq \frac{1}{T}\sum _{t=1}^T\delta (\mathit{x}-{\mathit{x}}_t),$$

where δ denotes the Dirac delta. Since images are known to exist outside ${\left\{{\mathit{x}}_t\right\}}_{t=1}^T$, it is possible to build an improved prior model $\widetilde{p_{\text{x}}}$ using kernel density estimation (KDE), i.e.,

$$\widetilde{p_{\text{x}}}(\mathit{x};\nu )\triangleq \frac{1}{T}\sum _{t=1}^T\mathcal{N}(\mathit{x};{\mathit{x}}_t,\nu \mathit{I}),$$ (22)

where ν > 0 is a tuning parameter. If we adopt $\widetilde{p_{\text{x}}}$ as the prior model for x, then the MAP estimate of x (recall (4)) becomes

$$\widehat{\mathit{x}}=\arg \underset{\mathit{x}}{\min }\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2-\ln \widetilde{p_{\text{x}}}(\mathit{x};\nu )\right\}.$$ (23)

Because $\text{ln}\widetilde{p_{\text{x}}}$ is differentiable, the solutions to (23) must obey

$$\mathbf{0}=\frac{1}{{\sigma }^2}{\mathit{A}}^{⊺}(\mathit{A}\widehat{\mathit{x}}-\mathit{y})-\nabla \ln \widetilde{p_{\text{x}}}(\widehat{\mathit{x}};\nu ).$$ (24)

A classical result known as “Tweedie’s formula” says that

$$\nabla \ln \widetilde{p_{\text{x}}}\left(\mathit{z};\nu \right)=\frac{1}{\nu }\left({\mathit{f}}_{\mathrm{mmse}}\left(\mathit{z};\nu \right)-\mathit{z}\right),$$ (25)

where f_mmse(·;ν) is the minimum mean-squared error (MMSE) denoiser under the prior $\mathit{x}~\widehat{p_{\text{x}}}$ and ν-variance AWGN. That is, f_mmse(z) = E{x|z}, where $\mathit{z}=\mathit{x}+\mathcal{N}\left(\mathbf{0},\nu \mathit{I}\right)$ and $\mathit{x}~\widehat{p_{\text{x}}}$. Applying (25) to (24), the MAP estimate $\widehat{\mathit{x}}$ under the KDE prior $\widetilde{p_{\text{x}}}$ obeys

$$\mathbf{0}=\frac{1}{{\sigma }^2}{\mathit{A}}^{⊺}(\mathit{A}\widehat{\mathit{x}}-\mathit{y})+\frac{1}{\nu }(\widehat{\mathit{x}}-{\mathit{f}}_{\mathrm{mmse}}(\widehat{\mathit{x}};\nu )),$$ (26)

which matches the RED condition (20) when f = f_mmse(·;ν). Thus, if we could implement the MMSE denoiser f_mmse for a given training corpus ${\left\{{\mathit{x}}_t\right\}}_{t=1}^T$, then RED provides a way to compute the MAP estimate of x under the KDE prior $\widetilde{p_{\text{x}}}$.

Although the MMSE denoiser f_mmse can be expressed in closed form (see [22, eqn. (67)]), it is not practical to implement for large T. Thus the question remains: Can the RED approach (20) also be justified for non-MMSE denoisers f, especially those that are not locally homogeneous or Jacobian-symmetric? As shown in [22], the answer is yes. Consider a practical denoiser f_θ parameterized by tunable weights θ (e.g., a DNN). A typical strategy is to choose θ to minimize the mean-squared error on ${\left\{{\mathit{x}}_t\right\}}_{t=1}^T$, i.e., set $\widehat{\mathit{\theta }}={\mathrm{arg\; min}}_{\mathit{\theta }}\text{E}\{\Vert \mathit{x}-{\mathit{f}}_{\mathit{\theta }}(\mathit{z}){\Vert }^2\}$, where the expectation is taken over $\mathit{x}~\widehat{p_{\text{x}}}$ and $\mathit{z}=\mathit{x}+\mathcal{N}\left(\mathbf{0},\nu \mathit{I}\right)$. By the MMSE orthogonality principle, we have

$$\text{E}\{\Vert \mathit{x}-{\mathit{f}}_{\mathit{\theta }}(\mathit{z}){\Vert }^2\}=\text{E}\{\Vert \mathit{x}-{\mathit{f}}_{\mathrm{mmse}}(\mathit{z};\nu {\Vert }^2\}+\text{E}\{\Vert {\mathit{f}}_{\mathrm{mmse}}(\mathit{z};\nu -{\mathit{f}}_{\mathit{\theta }}(\mathit{z}){\Vert }^2\},$$ (27)

and so we can write

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\mathrm{arg\; min}}\text{E}\{\Vert {\mathit{f}}_{\mathrm{mmse}}(\mathit{z};\nu )-{\mathit{f}}_{\mathit{\theta }}(\mathit{z}){\Vert }^2\}$$ (28)

$$=\underset{\mathit{\theta }}{\mathrm{arg\; min}}\text{E}\left\{\Vert \nabla \ln \widetilde{p_{\text{x}}}(\mathit{z};\nu )-\frac{1}{\nu }(\mathit{z}-{\mathit{f}}_{\mathit{\theta }}(\mathit{z})){\Vert }^2\right\},$$ (29)

where (29) follows from (25). Equation (29) says that choosing θ to minimize the MSE is equivalent to choosing θ so that $\frac{1}{\nu }\left(\mathit{z}-{\mathit{f}}_{\mathit{\theta }}\left(\mathit{z}\right)\right)$ best matches the “score” $\nabla \ln \widetilde{p_{\text{x}}}\left(\mathit{z};\nu \right)$.

In summary, the RED approach (20) approximates the KDE-MAP approach (24)–(26) by using a plug-in denoiser f to approximate the MMSE denoiser f_mmse. When f = f_mmse, RED exactly implements MAP-KDE, but with a practical f, RED implements a score-matching approximation of MAP-KDE. Thus, a more appropriate title for RED might be “score matching by denoising.”

Comparing the RED approach from this section to the prox-based PnP approach from Section IV-A, we see that RED starts with the KDE-based MAP estimation problem (23) and replaces the $\widehat{p_{\text{x}}}-\mathrm{based}$ MMSE denoiser f_mmse with a plug-in denoiser f, while PnP ADMM starts with the ϕ-based MAP estimation problem (3) and replaces the ϕ-based MAP denoiser prox_ϕ from (10) with a plug-in denoiser f. It has recently been demonstrated that, when the prior is constructed from image examples, MAP recovery often leads to sharper, more natural looking image recoveries than MMSE recovery [23]. Thus it is interesting that RED offers an approach to MAP-based recovery using MMSE denoising, which is much easier to implement than MAP denoising [23].

Further insight into the difference between RED and prox-based PnP can be obtained by considering the case of symmetric linear denoisers, i.e., f(z) = Wz with W = W^T, where we will also assume that W is invertible. Although such denoisers are far from state-of-the-art, they are useful for interpretation. It is easy to show [24] that f(z) = Wz is the proximal map of $\varphi \left(\mathit{x}\right)=\frac{1}{2\nu }{\mathit{x}}^{⊺}\left({\mathit{W}}^{-1}-\mathit{I}\right)x$, i.e., that prox_ϕ(z; ν) = Wz, recalling (10). With this proximal denoiser, we know that the prox-based PnP algorithm solves the optimization problem

$${\widehat{\mathit{x}}}_{\text{pnp}}={\mathrm{arg\; min}}_{\mathit{x}}\left\{\frac{1}{2{\sigma }^2}\Vert y-\mathit{Ax}{\Vert }^2+\frac{1}{2\nu }{\mathit{x}}^{⊺}({\mathit{W}}^{-1}-\mathit{I})\mathit{x}\right\}.$$ (30)

Meanwhile, since f(z) = Wz is both locally homogeneous and Jacobian-symmetric, we know from (21) that the RED under this f solves the optimization problem

$${\widehat{\mathit{x}}}_{\text{red}}={\mathrm{arg\; min}}_{\mathit{x}}\left\{\frac{1}{2{\sigma }^2}\Vert \mathit{y}-\mathit{Ax}{\Vert }^2+\frac{1}{2\nu }{\mathit{x}}^{⊺}(\mathit{I}-\mathit{W})\mathit{x}\right\}.$$ (31)

By comparing (30) and (31), we see a clear difference between RED and prox-based PnP. Section V-B compares RED to prox-based PnP from yet another perspective: consensus equilibrium.

So far, we have described RED as solving for $\widehat{\mathit{x}}$ in (20). But how exactly is this accomplished? In the original RED paper [21], three algorithms were proposed to solve (20): GD, inexact ADMM, and a “fixed point” heuristic that was later recognized [22] as a special case of the proximal gradient (PG) algorithm. Generalizations of PG RED were proposed in [22]. The fastest among them is the accelerated-PG RED algorithm, which uses the iterative update³

$${\mathit{x}}_k=\mathit{h}({\mathit{v}}_{k-1};\nu /L)$$ (32a)

$${\mathit{z}}_k={\mathit{x}}_k+\frac{q_{k-1}-1}{q_k}({\mathit{x}}_k-{\mathit{x}}_{k-1})$$ (32b)

$${\mathit{v}}_k=\frac{1}{L}\mathit{f}({\mathit{z}}_k)+\left(1-\frac{1}{L}\right){\mathit{z}}_k,$$ (32c)

where h was defined in (12), line (32b) uses the same acceleration as PnP FISTA (14b), and L > 0 is a design parameter that can be related to the Lipschitz constant of ϕ_red(·) from (21) (see [22, Sec.V-C]). When L = 1 and q_k = 1 ∀k, (32) reduces to the “fixed point” heuristic from [21]. To reduce the implementation complexity of h, one could replace (32a) with the GD step

$${\mathit{x}}_k={\mathit{x}}_{k-1}-\frac{\nu }{L{\sigma }^2}{\mathit{A}}^{\text{H}}(\mathit{A}{\mathit{v}}_{k-1}-\mathit{y}),$$ (33)

which achieves a similar complexity reduction as when going from PnP ADMM to PnP FISTA (as discussed in Section IV-A). The result would be an “accelerated GD” form of RED. Convergence of the RED algorithms will be discussed in Section V-B.

V. Understanding PnP through Consensus Equilibrium

The success of the PnP methods in Section IV raises important theoretical questions. For example, in the case of PnP ADMM, if the plug-in denoiser f is not the proximal map of any regularizer ϕ, then it is not clear what cost function is being minimized (if any) or whether the algorithm will even converge. Similarly, in the case of RED, if the plug-in denoiser f is not the MMSE denoiser f_mmse, then RED no longer solves the MAP-KDE problem, and it is not clear what RED does solve, or whether a given RED algorithm will even converge. In this section, we show that many of these questions can be answered through the consensus equilibrium (CE) framework [18,22,24,25]. We start by discussing CE for the PnP approaches from Section IV-A and follow with a discussion of CE for the RED approaches from Section IV-C.

A. Consensus equilibrium for prox-based PnP

Let us start by considering the PnP ADMM algorithm (13). Rather than viewing (13) as minimizing some cost function, we can view it as seeking a solution $({\widehat{\mathit{x}}}_{\text{pnp}},{\widehat{\mathit{u}}}_{\text{pnp}})$ to

$${\widehat{\mathit{x}}}_{\text{pnp}}=\mathit{h}({\widehat{\mathit{x}}}_{\text{pnp}}-{\widehat{\mathit{u}}}_{\text{pnp}};\nu )$$ (34a)

$${\widehat{\mathit{x}}}_{\text{pnp}}=\mathit{f}({\widehat{\mathit{x}}}_{\text{pnp}}+{\widehat{\mathit{u}}}_{\text{pnp}}),$$ (34b)

which, by inspection, must hold when (13) is at a fixed point. Not surprisingly, by setting x_k = x_k−1 in the PnP FISTA algorithm (14), it is straightforward to show that it too seeks a solution to (34). It is easy to show that the PnP PDS algorithm [17] seeks the same solution. With (34), the goal of the prox-based PnP algorithms becomes well defined! The pair (34) reaches a consensus in that the denoiser f and the data fitting operator h agree on the output ${\widehat{\mathit{x}}}_{\text{pnp}}$. The equilibrium comes from the opposing signs on the correction term ${\widehat{\mathit{u}}}_{\text{pnp}}$: the data-fitting subtracts it while the denoiser adds it.

By viewing the goal of prox-based PnP as solving the equilibrium problem (34), it becomes clear that other solvers beyond ADMM, FISTA, and PDS can be used. For example, it was shown in [25] that the PnP CE condition (34) can be achieved by finding a fixed-point of the system⁴

$$\underset{\_}{\mathit{z}}=(2\mathcal{G}-\mathit{I})(2\mathcal{F}-\mathit{I})\underset{\_}{\mathit{z}}$$ (35)

$$\underset{\_}{\mathit{z}}=\left[\begin{array}{c}{\mathit{z}}_1\\ {\mathit{z}}_2\end{array}\right],\mathcal{F}(\underset{\_}{\mathit{z}})=\left[\begin{array}{c}\mathit{h}({\mathit{z}}_1;\nu )\\ \mathit{f}({\mathit{z}}_2)\end{array}\right],\text{and}\mathcal{G}(\underset{\_}{\mathit{z}}\text{)=}\left[\begin{array}{c}\frac{1}{2}({\mathit{z}}_1+{\mathit{z}}_2)\\ \frac{1}{2}({\mathit{z}}_1+{\mathit{z}}_2)\end{array}\right].$$ (36)

There exist many algorithms to solve (35). For example, one could use the Mann iteration

$${\underset{\_}{\mathit{z}}}^{(k+1)}=(1-\gamma ){\underset{\_}{\mathit{z}}}^k+\gamma (2\mathcal{G}-\mathit{I})(2\mathcal{F}-\mathit{I}){\underset{\_}{\mathit{z}}}^{(k)},\text{with}\gamma \in (0,1),$$ (37)

when $\mathcal{F}$ is nonexpansive. The paper [25] also shows that this fixed point is equivalent to the solution of $\mathcal{F}(\underset{\_}{\mathit{z}})=\mathcal{G}(\underset{\_}{\mathit{z}})$, in which case Newton’s method or other root-finding methods could be applied.

The CE viewpoint also provides a path to proving the convergence of the PnP ADMM algorithm. Sreehari et al. [14] used a classical result from convex analysis to show that a sufficient condition for convergence is that i) f is non-expansive, i.e., ‖f(x) − f(y)‖ ≤ ‖x − y‖ for any x and y, and ii) f(x) is a subgradient of some convex function, i.e., there exists φ such that f(x) ∈ ∂φ(x). If these two conditions are met, then PnP ADMM (13) will converge to a global solution. Similar observations were made in other recent studies, e.g., [24]. That said, Chan et al. [15] showed that many practical denoisers do not satisfy these conditions, and so they designed a variant of PnP ADMM in which ν is decreased at every iteration. Under appropriate conditions on f and the rate of decrease, this latter method also guarantees convergence, although not exactly to a fixed point of (34) since ν is no longer fixed.

Similar techniques can be used to prove the convergence of other prox-based PnP algorithms. For example, under certain technical conditions, including non-expansiveness of f, it was established [18] that PnP FISTA converges to the same fixed-point as PnP ADMM.

B. Consensus equilibrium for RED

Just as the prox-based PnP algorithms in Section IV-A can be viewed as seeking the consensus equilibrium of (34), it was shown in [22] that the proximal-gradient and ADMM-based RED algorithms seek the consensus equilibrium $({\widehat{\mathit{x}}}_{\text{red}},{\widehat{\mathit{u}}}_{\text{red}})$ of

$${\widehat{\mathit{x}}}_{\text{red}}=\mathit{h}({\widehat{\mathit{x}}}_{\text{red}}-{\widehat{\mathit{u}}}_{\text{red}};\nu )$$ (38a)

$${\widehat{\mathit{x}}}_{\text{red}}={\left(\left(1+\frac{1}{L}\right)\mathit{I}-\frac{1}{L}\mathit{f}\right)}^{-1}({\widehat{\mathit{x}}}_{\text{red}}+{\widehat{\mathit{u}}}_{\text{red}})$$ (38b)

where h was defined in (12) and L is the algorithmic parameter that appears in (32).⁵ Since (38) takes the same form as (34), we can directly compare the CE conditions of RED and prox-based PnP.

Perhaps a more intuitive way to compare the CE conditions of RED and prox-based PnP follows from rewriting (38b) as ${\widehat{\mathit{x}}}_{\mathrm{red}}=\mathit{f}\left({\widehat{\mathit{x}}}_{\mathrm{red}}\right)+L{\widehat{\mathit{u}}}_{\mathrm{red}}$, after which the RED CE condition becomes

$${\widehat{\mathit{x}}}_{\text{red}}=\mathit{h}({\widehat{\mathit{x}}}_{\mathrm{red}}-{\widehat{\mathit{u}}}_{\text{red}};\nu )$$ (39a)

$${\widehat{\mathit{x}}}_{\mathrm{red}}=\mathit{f}({\widehat{\mathit{x}}}_{\mathrm{red}})+L{\widehat{\mathit{u}}}_{\mathrm{red}},$$ (39b)

which involves no inverse operations. In the typical case of L = 1, we see that (39) matches (34), except that the correction ${\widehat{\mathit{u}}}_{\text{red}}$ is added after denoising in (39b) and before denoising in (34b).

Yet another way to compare the CE conditions of RED and prox-based PnP is to eliminate the ${\widehat{\mathit{u}}}_{\text{red}}$ variable. Solving (39b) for ${\widehat{\mathit{u}}}_{\text{red}}$ gives

$${\widehat{\mathit{u}}}_{\text{red}}=\frac{\nu }{{\sigma }^2}{\mathit{A}}^{\text{H}}(\mathit{y}-\mathit{A}{\widehat{\mathit{x}}}_{\text{red}}),$$ (40)

which mirrors the expression for ${\widehat{\mathit{u}}}_{\text{pnp}}$. Then plugging ${\widehat{\mathit{u}}}_{\text{red}}$ back into (39b) and rearranging, we obtain the fixed-point equation

$${\widehat{\mathit{x}}}_{\text{red}}=\mathit{f}({\widehat{\mathit{x}}}_{\text{red}})+\frac{L\nu }{{\sigma }^2}{\mathit{A}}^{\text{H}}(\mathit{y}-\mathit{A}{\widehat{\mathit{x}}}_{\text{red}}),$$ (41)

or equivalently

$$\frac{L\nu }{{\sigma }^2}{\mathit{A}}^{\text{H}}(\mathit{A}{\widehat{\mathit{x}}}_{\text{red}}-\mathit{y})=\mathit{f}({\widehat{\mathit{x}}}_{\text{red}})-{\widehat{\mathit{x}}}_{\text{red}},$$ (42)

which says that the data-fitting correction (i.e., the left side of (42)) must balance the denoiser correction (i.e., the right side of (42)).

The CE framework also facilitates the convergence analysis of RED algorithms. For example, using the Mann iteration, it was proven in [22] that when f is nonexpansive and L > 1, the PG RED algorithm converges to a fixed point.

VI. Demonstration of PnP in MRI

A. Parallel cardiac MRI

We now demonstrate the application of PnP methods to parallel cardiac MRI. Because the signal x is a cine (i.e., a video) rather than a still image, there are relatively few options available for sophisticated denoisers. Although algorithmic denoisers like BM4D have been proposed, they tend to run very slowly, especially relative to the linear operators A and A^H. For this reason, we first trained an application specific CNN denoiser for use in the PnP framework. The architecture of the CNN denoiser, implemented and trained in PyTorch, is shown in Figure 1.

Fig. 1.

The architecture of the CNN-based cardiac cine denoiser operating on spatiotemporal volumetric patches.

For training, we acquired 50 fully sampled, high-SNR cine datasets from eight healthy volunteers. Thirty three of those were collected on a 3 T scanner⁶ and the remaining 17 were collected on a 1.5 T scanner. Out of the 50 datasets, 28, 7, 7, and 8 were collected in the short-axis, two-chamber, three-chamber, and four-chamber view, respectively. The spatial and temporal resolutions of the images ranged from 1.8 mm to 2.5 mm and from 34 ms to 52 ms, respectively. The images size ranged from 160 × 130 to 256 × 208 pixels and the number of frames ranged from 15 to 27. For each of the 50 datasets, the reference image series was estimated as the least-squares solution to (1), with the sensitivity maps S_i estimated from the time-averaged data using ESPIRiT. We added zero-mean, complex-valued i.i.d. Gaussian noise to these “noise-free” reference images to simulate noisy images with SNR of 24 dB. Using a fixed stride of 30×30×10, we decomposed the images into patches of size 55×55×15. The noise-free and corresponding noisy patches were assigned as output and input to the CNN denoiser, with the real and imaginary parts processed as two separate channels. All 3D convolutions were performed using 3 × 3 × 3 kernels. There were 64 filters of size 3 × 3 × 3 × 2 in the first layer, 64 filters of size 3 × 3 × 3 × 64 in the second through fourth layers, and 2 filters of size 3 × 3 × 3 × 64 in the last layer. We set the minibatch size to four and used the Adam optimizer with a learning rate of 1 × 10⁻⁴ over 400 epochs. The training process was completed in 12 hours on a workstation equipped with a single NVIDIA GPU (GeForce RTX 2080 Ti).

For testing, we acquired four fully sampled cine datasets from two different healthy volunteers, with two image series in the short-axis view, one image series in the two-chamber view, and one image series in the four-chamber view. The spatial and temporal resolutions of the images ranged from 1.9 mm to 2 mm and from 37 ms to 45 ms, respectively. For the four datasets, the space-time signal vector, x, in (2) had dimensions of 192 × 144 × 25, 192 × 144 × 25, 192 × 166 × 16, and 192 × 166 × 16, respectively, with the last dimension representing the number of frames. The datasets were retrospectively downsampled at acceleration rates, R, of 6, 8, and 10 using pseudo-random sampling [26]. A representative sampling pattern used to undersample one of the datasets is shown in Figure 2. The data were compressed to C = 12 virtual coils for faster computation. The measurements were modeled as described in (1), with the sensitivity maps, S_i, estimated from the time-averaged data using ESPIRiT.

Fig. 2.

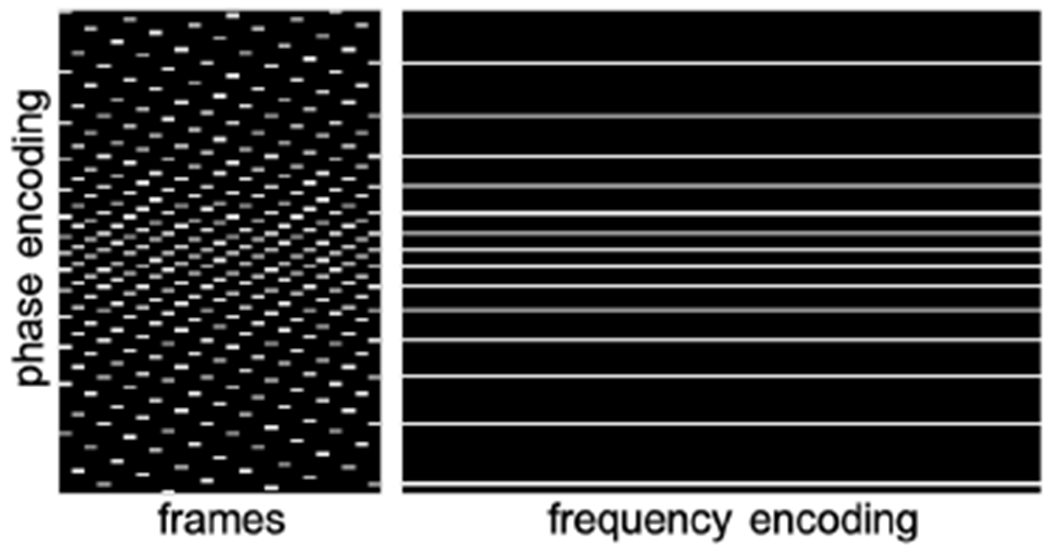
Two different views of the 3D sampling pattern used to retrospectively undersample one of the four test datasets at R = 10. The undersampling was performed only in the phase encoding direction and the pattern was varied across frames. In this example, the number of frequency encoding steps, phase encoding steps, and frames are 192, 144, and 25, respectively.

For compressive MRI recovery, we used PnP ADMM from (13) with f(·) as the CNN-based denoiser described above; we will refer to the combination as PnP-CNN. We employed a total of 100 ADMM iterations, and in each ADMM iteration, we performed four steps of CG to approximate (12), for which we used σ² = 1 = ν. We compared this PnP method to three CS-based methods: CS-UWT, CS-TV,⁷ and a low-rank plus sparse (L+S) method (see, e.g., [27]). We also compared to PnP-UWT and the transform-learning (see the overview by Wen, Ravishankar, Pfister, and Bresler in this special issue) method LASSI [28].

For PnP-UWT, we used PnP FISTA from (14) with f(·) implemented as f_tdt given in (17), i.e., bFISTA. A three-dimensional single-level Haar UWT was used as Ψ in (17). For CS-TV, we used a 3D finite-difference operator for Ψ in the regularizer ϕ(x) = ‖Ψx‖₁, and for CS-UWT, we used the aforementioned UWT instead. For both CS-TV and CS-UWT, we used monotone FISTA [29] to solve the resulting convex optimization problem (3). For L+S, the method by Otazo et al. [27] was used. The regularization weights for CS-UWT, PnP-UWT, CS-TV, and L+S were manually tuned to maximize the reconstruction SNR (rSNR)⁸ for Dataset #3 at R = 10. For LASSI we used the authors’ implementation at https://gitlab.com/ravsa19/lassi, and we did our best to manually tune all available parameters.

The rSNR values are summarized in Table I. For all four datasets and three acceleration rates, PnP-CNN exhibited the highest rSNR with respect to the fully sampled reference. Also, compared to the CS methods and PnP-UWT, which uses a more traditional denoiser based on soft-thresholding of UWT coefficients, PnP-CNN was better at preserving anatomical details of the heart; see Figure 3. The performance of PnP-UWT was similar to that of CS-UWT. Figure 4 plots NMSE as a function of the number of iterations for the CS and PnP methods. Since the CS methods were implemented using CPU computation and the PnP methods were implemented using GPU computation, a direct runtime comparison was not possible. We did, however, compare the per-iteration runtime of PnP ADMM for two different denoisers: the CNN and UWT-based f_tdt described earlier in this section. When the CNN denoiser was replaced with the UWT-based f_tdt, the per-iteration runtime changed from 2.05 s to 2.1 s, implying that the two approaches have very similar computational costs. The extended version of this paper [10] shows the results of experiments that investigate the effect of σ²/ν on the final NMSE and the convergence rate. Overall, final NMSE varies less than 0.5 dB for σ²/ν ∈ [0.5, 2] for all four datasets and all three acceleration rates, and the convergence rate is nearly the same. The extended version also explores the use of CG versus GD when solving (12) in PnP ADMM. The results suggest that 1 to 4 inner iterations of either method are optimal; more inner iterations slows the overall convergence time. The results in this section, although preliminary, highlight the potential of PnP methods for MRI recovery of cardiac cines. By optimizing the denoiser architecture, the performance of PnP-CNN may be further improved.

Table I.

rSNR (dB) of MRI cardiac cine recovery from four test datasets.

Acceleration	CS-UWT	CS-TV	L+S	LASSI	PnP-UWT	PnP-CNN
Dataset #1 (short-axis)
R = 6	30.10	29.03	30.97	27.09	30.18	31.82
R = 8	28.50	27.35	29.65	25.91	28.60	31.25
R = 10	26.94	25.78	28.29	24.98	27.06	30.46
Dataset #2 (short-axis)
R = 6	29.23	28.27	29.73	25.87	29.29	30.81
R = 8	27.67	26.65	28.23	24.54	27.75	30.17
R = 10	26.12	25.11	26.89	23.61	26.22	29.21
Dataset #3 (two-chamber)
R = 6	27.33	26.38	27.83	24.97	27.38	29.36
R = 8	25.63	24.63	26.30	23.52	25.69	28.50
R = 10	24.22	23.24	24.93	22.51	24.28	27.49
Dataset #4 (four-chamber)
R = 6	30.41	29.63	30.62	27.62	30.60	32.19
R = 8	28.68	27.76	29.00	26.33	28.94	31.42
R = 10	27.09	26.18	27.60	25.24	27.37	30.01

Fig. 3.

Results from cardiac cine Dataset #1 at R = 10. Top row: a representative frame from the fully sampled reference and various recovery methods. The green arrow points to an image feature that is preserved only by PnP-CNN and not by other methods. Middle row: error map ×6. Bottom row: temporal frame showing the line drawn horizontally through the middle of the image in the top row, with the time dimension along the horizontal axis. The arrows point to the movement of the papillary muscles, which are more well-defined in PnP-CNN.

Fig. 4.

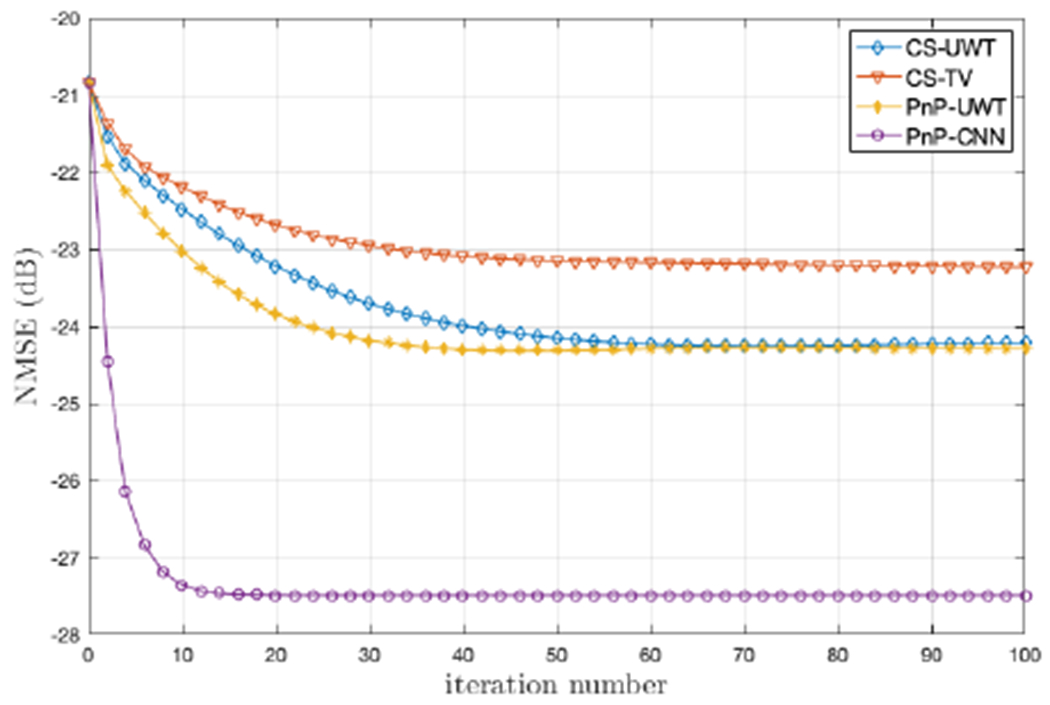
NMSE versus iteration for two PnP and two CS algorithms on the cardiac cine recovery Dataset #3 at R = 10.

B. Single-coil fastMRI knee data

In this section, we investigate recovery of 2D knee images from the single-coil fastMRI dataset [30]. This dataset contains fully-sampled k-space data that are partitioned into 34742 training slices and 7 135 testing slices. The Cartesian sampling patterns from [30] were used to achieve acceleration rate R = 4.

We evaluated PnP using the ADMM algorithm with a learned DnCNN [9] denoiser. To accommodate complex-valued images, DnCNN was configured with two input and two output channels. The denoiser was then trained using only the central slices of the 3 T scans without fat-suppression from the training set, comprising a total of 267 slices (i.e., < 1% of the total training data). The training-noise variance and the PnP ADMM tuning parameter σ²/ν were manually adjusted in an attempt to maximize rSNR.

PnP was then compared to the TV and U-Net baseline methods described and configured in [30]. For example, 128 channels were used for the U-Net’s first layer, as recommended in [30]. We then trained three versions of the U-Net. The first version was trained on the full fastMRI training set⁹ with random sampling masks. The second U-Net was trained on the full fastMRI training set, but with a fixed sampling mask. The third U-Net was trained using only the central slices of the 3 T scans without fat-suppression (i.e., the same data used to train the DnCNN denoiser) and with a fixed sampling mask.

To evaluate performance, we used the central slices of the non-fat-suppressed 3 T scans from the validation set, comprising a total of 49 slices. The evaluation considered both random sampling masks and the same fixed mask used for training. The resulting average rSNR and SSiM scores are summarized in Table II. The table shows that PnP-CNN performed similarly to the U-Nets and significantly better than TV. in particular, PnP-CNN achieved the highest rSNR score with both random and fixed testing masks, and the U-Net gave slightly higher SSIM scores in both tests. Among the U-Nets, the version trained with a fixed sampling mask and full data gave the best rSNR and SSiM performance when testing with the same mask, but its performance dropped considerable when testing with random masks. Meanwhile, the U-Net trained with the smaller data performed significantly worse than the other U-Nets, with either fixed or random testing masks. And although this latter U-Net used exactly the same training data as the PnP-CNN method, it was not competitive with PnP-CNN. Although preliminary, these results suggest that i) PnP methods are much less sensitive to deviations in the forward model between training and testing, and that ii) PnP methods are effective with relatively small training datasets.

TABLE II.

rSNR and SSIM for fastMRI single-coil test data with R = 4.

	Random testing masks		Fixed testing mask
	rSNR (dB)	SSIM	rSNR (dB)	SSIM
CS-TV	17.56	0.647	18.16	0.654
U-Net: Random training masks, full training data	20.76	0.772	20.72	0.768
U-Net: Fixed training mask, full training data	19.63	0.756	20.82	0.770
U-Net: Fixed training mask, smaller training data	18.90	0.732	19.67	0.742
PnP-CNN	21.16	0.758	21.14	0.754

VII. Conclusion

PnP methods present an attractive avenue for compressive MRI recovery. In contrast to traditional CS methods, PnP methods can exploit richer image structure by using state-of-the-art denoisers. To demonstrate the potential of such methods for MRI reconstruction, we used PnP to recover cardiac cines and knee images from highly undersampled datasets. With application-specific CNN-based denoisers, PnP was able to significantly outperform traditional CS methods and to perform on par with modern deep-learning methods, but with considerably less training data. The time is ripe to investigate the potential of PnP methods for a variety of MRI applications.