Nearest-neighbour transition-state analysis for nucleic acid kinetics

Abstract

We used stopped-flow to monitor hypochromicity for 43 oligonucleotide duplexes to study nucleic acid kinetics and extract transition-state parameters for association and dissociation. Reactions were performed in 1.0 M NaCl (for literature comparisons) and 2.2 mM MgCl₂ (PCR conditions). Dissociation kinetics depended on sequence, increased exponentially with temperature, and transition-state parameters inversely correlated to thermodynamic parameters (r = −0.99). Association had no consistent enthalpic component, varied little with temperature or sequence, and poorly correlated to thermodynamic parameters (r = 0.28). Average association rates decreased 78% in MgCl₂ compared to NaCl while dissociation was relatively insensitive to ionic conditions. A nearest-neighbour kinetic model for dissociation predicted rate constants within 3-fold of literature values (n = 11). However, a nearest-neighbour model for association appeared overparameterized and inadequate for predictions. Kinetic predictions were used to simulate published high-speed (<1 min) melting analysis and extreme (<2 min) PCR experiments. Melting simulations predicted apparent melting temperatures increase on average 2.4°C when temperature ramp rates increased from 0.1 to 32°C/s, compared to 2.8°C reported in the literature. PCR simulations revealed that denaturation kinetics are dependent on the thermocycling profile. Simulations overestimated annealing efficiencies at shorter annealing times and suggested that polymerase interactions contribute to primer-template complex stability at extension temperatures.

INTRODUCTION

Currently, paradigms for the analysis and design of nucleic acid systems typically use sequence-specific thermodynamic properties predicted by nearest-neighbour (NN) models (1). However, in many applications, thermodynamic considerations serve only to approximate system-specific behaviour that would be better described by kinetic analysis.

For example, the COVID-19 pandemic has highlighted the importance of rapid molecular testing for pathogen detection (2). Toward that aim, recent studies have demonstrated that common molecular diagnostic tools, such as RT-PCR and DNA melting analysis, can be performed in minutes-to-seconds (3,4). However, the design of rapid diagnostic assays is hindered because these nucleic acid systems are dominated by transient states, and current design paradigms provide little guidance for optimizing assays for speed. The underlying buffer, temperature, and sequence dependence of kinetics should be considered rather than thermodynamics.

Early studies on nucleic acid kinetics led to many developments including the ‘nucleation and zipper’ model for helix propagation and revealed that association and dissociation are second-order and first-order kinetic processes, respectively (5). Several studies indicate that secondary-structures, off-target hybridization, and metastable intermediate states can substantially influence association kinetics (6–9). A few investigations demonstrated that nucleic acid kinetics fit a transition-state theory model (8,10,11), and some researchers have suggested that a NN kinetic analogue may provide accurate predictions (10,12,13). Nevertheless, we lack models for quantitatively characterizing nucleic acid kinetics.

Here, we investigate how oligonucleotide sequence and buffer conditions influence temperature-dependent association and dissociation kinetics using a transition-state theory framework. To validate the experimental approach, we studied duplex sequences used previously to derive the unified NN thermodynamic parameters (14) and compare kinetic experiments to prior equilibrium melting studies. Then, we use the NN model to predict kinetics for sequences reported in the literature and simulate both extreme PCR thermocycling and high-speed melting analysis, comparing simulations to previously published data.

MATERIALS AND METHODS

Oligonucleotide design and quantification

We selected sequences from 108 duplexes previously used to derive the unified nearest-neighbour thermodynamic parameters for Watson-Crick base-pairs. Melting experiments have demonstrated that the two-state melting model accurately describes thermodynamics for these sequences (15). However, many of the original sequences have predicted secondary structures or form stable hetero- or homo-dimers that are kinetically relevant under experimental conditions. Therefore, 43 duplexes (Supplementary Table S1) with minimal predicted additional hybridization products near the duplex melting temperatures (T_Ms) were selected (16). Sequences were 6–16 nucleotides, 0–83% GC-content, and had predicted T_Ms between 20 and 52°C at 0.5 μM in 1.0 M NaCl.

Sequences were synthesized and HPLC purified by Integrated DNA Technologies. Oligonucleotides were suspended in 10 mM Tris, pH 8.0, 0.1 mM ethylenediaminetetraacetic acid, and quantification was performed on a Nanodrop One^C (Thermo Scientific) using predicted oligonucleotide extinction coefficients (17).

Stopped-flow experiments

Kinetic experiments were performed on an SFM-300X stopped-flow instrument (Bio-Logic). A temperature probe with a reported precision of ±0.1°C monitored the sample temperature which was controlled by a circulating water bath. Reactions had either a 2.0 or 13.5 ml/s flow rate with an estimated deadtime of 15.1 or 2.2 ms, respectively. Duplex formation was monitored via UV absorbance at 260 nm. A xenon-mercury lamp and monochromator were used to illuminate the sample at 260 nm in a 1.0 cm pathlength cuvette. Absorbance was recorded by a photomultiplier tube through a 311 nm short-pass filter. A blank (no DNA) absorbance measurement was recorded at each experimental temperature.

Reactions were initiated by mixing complementary oligonucleotides. Duplex formation was monitored at 4–5 oligonucleotide concentrations at each temperature. Each strand's concentration was varied to produce reactions with both equal concentrations and each strand in excess. The specific range of concentrations used for each sequence was selected based on the predicted hypochromicity (17), extinction coefficients, predicted thermodynamic stability, and the synthetic yield. Oligonucleotide concentrations varied between 0.4 and 3 μM and reactions were carried out at five or more temperatures near the T_M so that both association and dissociation kinetics contributed to the observed reaction rates. For each combination of concentration and temperature, we acquired 5–10 repeated measurements. Experimental conditions for each sequence are listed in Supplementary Table S1.

Two experimental buffers were used, a 20 mM cacodylate, pH 7.0, 1.0 M NaCl buffer (identical conditions to previously reported equilibrium melting studies), and a 50 mM Tris, pH 8.3, 2.2 mM MgCl₂ buffer (typical rapid cycle PCR conditions). In addition, a single sequence, 5′-CACGGCTC-3′, was used to explore how magnesium concentration (0.7–4.2 mM), 10% (v/v) dimethyl sulfoxide (DMSO), and 1× LCGreen⁺ (BioFire Defense) fluorescent DNA dye influence reaction kinetics in the PCR buffer. All buffers were degassed before use by vacuum at 70°C for 20 min.

Stopped-flow data analysis

Each experiment was corrected for the estimated instrument deadtime, and repeated measurements were averaged. The standard deviation of each experiment was estimated as the standard deviation of the residuals after fitting to the function . All experiments for each duplex sequence were then simultaneously fit to Reaction Scheme 1 and Equations (1–3) using the standard deviations to weight each data set. In the reversible Reaction Scheme 1, S₁ and S₂ are the complementary single strand concentrations, D is the duplex concentration, k_a is the biomolecular rate constant for association, and k_d is the unimolecular rate constant for dissociation.

The rate constant at every temperature was calculated via the Eyring equation (18) (Equation 1) where k is the temperature-dependent rate constant, κ is the transmission coefficient (assumed to be κ = 1), k_b is the Boltzmann constant, T is the temperature in kelvin, h is Planck's constant, R is the gas constant, ΔG^‡ is the activation free energy for either association or dissociation, c^⊖ is the standard concentration (1 mol l⁻¹), and m is the molecularity (m = 1 or 2 for dissociation or association, respectively).

(1)

ΔG^‡s are calculated from the temperature and activation enthalpies and entropies, ΔH^‡ and ΔS^‡ that are assumed to be temperature independent (Equation 2).

(2)

Equation (3) describes the time-dependent absorbance signal, A(t), as the sum of the absorbance of all species using the predicted extinction coefficients for each strand (ϵ₁ and ϵ₂), the hypochromicity (p, restricted between 0.6 and 1 for fitting), the cuvette path length (L = 1 cm), and a small absorbance offset (A₀).

(3)

Initial estimates for activation entropies and enthalpies were derived from linearization of the Eyring equation (19) after preliminary fitting to Equation (3) and the differential equations of Reaction Scheme 1 to obtain k_a and k_d at each experimental temperature. Then, all data was fit to Reaction Scheme 1 and Equations (1–3) to simultaneously derive the activation enthalpies and entropies for association and dissociation (ΔH^‡_a, ΔS^‡_a, ΔH^‡_d and ΔS^‡_d), hypochromicity (p), and small absorbance offsets (A₀s) for each experiment. Errors on model parameters are reported by confidence contour analysis using a threshold of a 5% increase in the sum of squared errors (20). Correlations are reported as the Pearson correlation coefficient. All data and statistical analyses were performed in MATLAB™ version R2020a (MathWorks). Nonlinear regression was performed using the trust-region-reflective algorithm and ordinary differential equations were numerically integrated via ode15s.

Nearest-neighbour model

We derived kinetic NN parameters analogous to the unified thermodynamic NN model (14). Equation (4) was used for NN predictions, where ΔG^‡(total) is the total free energy for a duplex sequence, ΔG^‡(initiation) is the initiation free energy, ΔG^‡(terminal AT) is a correction for sequences with terminal AT base-pairs (m is the number of terminal A–T pairs in the sequence), n_i is the number of occurrences of the ith NN in the sequence, and ΔG^‡(i) is the free energy of the ith NN parameter. An example calculation is presented in the supplemental data file accompanying this article.

(4)

NN kinetic parameters and associated errors were calculated using the regress function in MATLAB by randomly resampling 10 000 sets of 30 of the 43 sequences. The means and standard deviations are reported.

We identified previous studies that report either transition-state parameters or rate constants for association or dissociation in 1.0 M NaCl (7,8,11,21–23) to compare to kinetic NN predictions. To ensure that comparisons were reasonable, we excluded any study performed with immobilized or modified oligonucleotides. If only rate constants and experimental temperatures were reported, we calculated transition-state parameters via linearization of Equations (1 and 2). For predictions of self-complementary sequences, we applied a symmetry penalty of –1.4 cal/mol/K to ΔS^‡_a (14). One study reported kinetic parameters for a sequence we investigated, and that sequence was excluded from the comparison (11). Lomzov et al. reported two sets of rate constants using two different models to analyse experiments (7). Reported rate constants either included the inhibitory effects of secondary-structures or removed the effects of secondary-structure and report rate constants for duplex formation from complementary-strands only. Because the NN kinetic predictions are for duplexes, and cannot model the effects of secondary structures, predictions were compared to rate constants reported for duplex formation. Additionally, all k_as reported in the literature were compared to predictions from a recently developed algorithm by Zhang et al. (24). However, this algorithm specifically accounts for alternative structures (e.g. secondary structure) when predicting kinetics. Therefore, predicted k_as from Zhang et al. were compared to rate constants reported by Lomzov et al. that included the effects of secondary structure.

A thermodynamic NN parameter set was calculated according to Equation (5), where ΔG is the thermodynamic free energy. Identical calculations were performed to derive the thermodynamic enthalpies and entropies, ΔH and ΔS.

(5)

High-speed melting and PCR thermocycling simulations

We simulated nucleic acid kinetics in high-speed melting (25) and extreme PCR thermocycling (26) experiments from previous publications. High-speed melting simulations used Equations (1–2) and Reaction Scheme 1. For PCR simulations, Reaction Scheme 1 was modified to include two primer sequences that compete with and are complementary to the two template strands (Supplemental Reaction Scheme 1). The system of ordinary differential equations derived from Reaction Scheme 1 was solved piecewise at every experimental time-temperature measurement (10 ms for high-speed melting and 9–74 ms for extreme PCR).

Pryor et al. investigated high-speed melting and the effects of varying the temperature ramp rate between 0.1 and 32°C/s on apparent duplex T_Ms and the ability to discriminate between different genotypes using 4 target sequences (25). This study was performed in a buffer containing 20 mM Tris, 30 mM KCl, 4.5 mM MgCl₂, 1.5 mM dNTPs (total), 2% DMSO, 1.0 mM betaine, 0.04% Tween-20, 1× LCGreen+, 1X Titanium Taq DNA polymerase, and 500 ng/μl bovine serum albumin. The template concentration for simulations was 200 nM to approximate the amount of PCR product synthesized from 1 μM of each primer after 40 cycles. We also compared T_M predictions for the targets to T_Ms predicted from uMelt using the unified NNs adjusted for ionic conditions and DMSO (27).

Millington et al. investigated the effect of annealing and denaturation times on extreme PCR efficiency with two different target sequences and primer sets (26). To study the reactions, two ‘threshold temperatures,’ were estimated at which 98% of duplexes were either denatured or annealed to primers determined by melting analysis. Then, they varied the time the sample spent above or below the threshold temperature while holding all other assay parameters constant and assumed differences in the quantification cycle (C_q) were the direct result of changes in the efficiency of either the denaturation or annealing step. The PCR buffer had ionic conditions equivalent to our 2.2 mM MgCl₂ buffer but included 3 mM MgCl₂ and 0.8 mM dNTPs (total), 1× LCGreen+, 1.6 μM Klentaq, 5 μM each primer, 300 copies/μl human genomic DNA, and 500 ng/μl bovine serum albumin. The time–temperature data in this study was collected from a thermocouple inside a mock sample capillary placed next to the reaction capillary (28). For simulations, the initial concentrations were the experimental primer and template concentrations.

Simulation of the PCR experiments do not include steps to model polymerase binding and nucleotide incorporation each cycle. Instead, at extension temperatures (72°C for annealing and 68°C for denaturation experiments) the simulations convert the maximum concentration of primers bound to templates during annealing to template duplexes for the next step.

C _qs for simulations were calculated by first determining the average C_qs for experiments with no observed inhibition (29.7 for ≥1 s annealing and 24.4 for ≥0.5 s denaturation times). Then, assuming the experiments were 100% efficient, the template concentration (N_q) at C_q was calculated by Equation (6). The simulation C_qs are then the cycle in which the number of template molecules exceeds N_q.

(6)

RESULTS

Stopped-flow experiments

For all duplex sequences and buffer conditions, ΔH^‡_d and ΔS^‡_d were positive as expected for a typical dissociation reaction (Supplementary Table S2). For the association reaction, all but one sequence had negative ΔS^‡_as, and ΔH^‡_as varied between small negative and positive values (–6.6 to 9.1 kcal/mol). Confidence contour analysis revealed that parameters for the dissociation transition-state were well constrained, but parameters for association were not (Supplementary Figure S1). Because the best fit values for ΔH^‡_a were small, with large error estimates within a range crossing zero, we refit all data to a modified version of Equation (1) where ΔH^‡_a = 0 (Supplementary Table S3). With and without nonzero ΔH^‡_a, fits for most sequences were equivalent (Figure 1, Supplementary Figure S2) due to the small temperature dependence of association. Unless indicated otherwise, all results are from the model wherein ΔH^‡_a = 0.

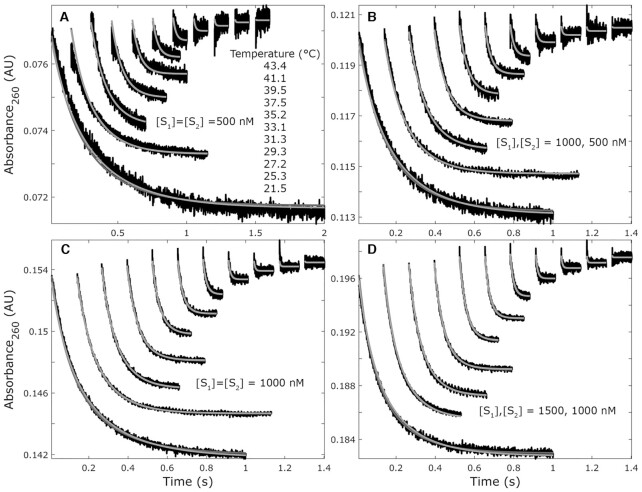
Figure 1.

Hybridization kinetics and model fitting for the sequence 5′-AGCGTAAG-3′ and its complement in 1.0 M NaCl between 21.5 and 43.4°C. Reactions are shifted vertically by small absorbance offsets from fitting and higher temperature reactions are shifted rightward for clarity. The reaction temperatures in panel A apply to B–D as well. Model fits are shown for ΔH^‡_a = 0 (light grey) and ΔH^‡_a ≠0 (dark gray). (A) Reactions with initial strand concentrations of 500 nM. (B) Reactions with initial strand concentrations [S₁] = 1000 nM, [S₂] = 500 nM. (C) Reactions with initial strand concentrations of 1000 nM. (D) Reactions with initial strand concentrations [S₁] = 1500 nM, [S₂] = 1000 nM. Not shown are reactions with initial strand concentrations of [S₁] = 500 nM, [S₂] = 1000 nM which were all fit simultaneously. As the reaction temperatures increase, equilibration is faster primarily because of increased dissociation rates. Panel C is recreated in Supplemental Figure S2 to better highlight the differences in the two model fits.

At 37°C, ΔG^‡_d was inversely correlated to thermodynamic ΔG (r = –0.99 P < 10⁻³⁹, r = –0.98 P < 10⁻²⁹ for data in NaCl and MgCl₂, respectively) but ΔG^‡_a was not (r = –0.28 P = 0.07, r = –0.09 P = 0.56). Reactions for all 43 sequences in 1.0 M NaCl were compared to previously published thermodynamic data determined by equilibrium melting. Using the models with and without ΔH^‡_a, thermodynamic parameters derived from kinetics agree well with prior equilibrium melting experiments (comparisons A and B in Table 1). Thermodynamic parameters for five sequences deviated by >20% compared to prior equilibrium melting experiments. Most (34/43) sequences were slightly less stable than reported by equilibrium melting experiments (avg. –4.6% decrease in ΔG). The hypochromicity for sequences varied between 0.79 and 0.93 and were 0–16% different (avg. = 4.7%) from a predictive algorithm (17).

Table 1.

Average Difference in 1.0 M NaCl

Comparison	Condition 1	Condition 2	ΔH (%)a	ΔS (%)a	ΔG (%)a	T M (°C)
Experimental
(A) 43 Oligos	Kinetics (ΔH‡a ≠ 0)	Equilibrium meltingb	10.2	11.5	4.6	-
(B) 43 Oligos	Kinetics (ΔH‡a = 0)	Equilibrium meltingb	9.4	10.5	4.6	-
Transition state NNs
(C) 43 Oligos	Kinetic NNs	Experimental	4.2	5.8	1.1	-
(D) 3 Oligos	Kinetic NNs	Literaturec	8.6	14.3	7.0	-
Thermodynamic NNs
(E) 10 NNs	Kinetics NNs	Unified NNsd	20	24	7.1	-
(F) 108 Oligos	Kinetic NNs	Equilibrium meltingb	10.5	11.7	6.8	2.8
(G) 108 Oligos	NNs from equilibrium meltinge	Equilibrium meltingb	8.2	9.4	5.8	2.3

^a% differences are calculated using (∑|X₁– X₂|/(X₁+ X₂)/2)/n where X₁ and X₂ are conditions 1 and 2, and n is the number of comparisons.

^bData from equilibrium melting experiments are listed in the supplementary material of Allawi et al. (1997).

^cReported in Lomzov et al. (2012), Williams et al. (1989) and Freier et al. (1983).

^dUnified NNs are reported in SantaLucia et al. (2004).

^eNNs are calculated from the subsample of equilibrium melting experiments reported in Allawi et al. (1997) for the 43 sequences studied here.

Association rates varied little between sequences and had a small temperature dependence. k_a was between 0.07 and 3.3 × 10⁷ M⁻¹ s⁻¹ for all sequences across all temperatures in all buffers (Supplementary Figure S3A). With ΔH^‡_a ≠ 0, some oligos exhibited anti-Arrhenius behaviour, and rate constants decreased with increasing temperature. Despite this, the temperature dependence of k_as was still small and approximately linear, with little indication of the exponential relationship predicted by Equation (1) (Supplementary Figure S3B). With ΔH^‡_a ≠ 0, k_a still increased <2-fold with temperature for all but 7 of 90 sequence and buffer conditions. Conversely, dissociation rates exhibited an exponential temperature dependence and increased with increasing temperature between 1 and 6 orders of magnitude (Supplementary Figure S3C and D). Overall, transition-state parameters for association were dependent on GC-content and length (Figure 2A and B), whereas for dissociation they were more dependent on sequence length (Figure 2C and D).

Figure 2.

The dependence of ΔG^‡s at 37°C on GC content and length for association (A, B) and dissociation (C, D) in 1.0 M NaCl (black) and 2.2 mM MgCl₂ (grey). ΔG^‡_a is correlated to GC content (r = –0.49, P < 10⁻³ for 1.0 M NaCl and r = –0.75, P < 10⁻⁸ for 2.2 mM MgCl₂), and length (r = 0.57, P < 10⁻⁴ and r = 0.66, P < 10⁻⁵). By comparison, ΔG^‡_d is correlated to length (r = 0.84, P < 10⁻¹¹ and r = 0.78, P < 10⁻⁹) but not GC content (r = –0.13, P = 0.39 and r = –0.04, P = 0.79). ΔG^‡s vary more between sequences for dissociation, but differences in ionic conditions have a larger effect on association.

Ionic conditions had a large influence on ΔG^‡_as, which increased 0.5–1.6 kcal/mol from 1.0 M NaCl to 2.2 mM MgCl₂ and k_as correspondingly decreased 55–94%. The difference in ΔG^‡_a at 37°C between ionic conditions correlates more to GC-content (r = –0.83, P < 10⁻¹¹) than length (r = 0.52, P < 10⁻³) and higher GC-content sequences are less affected by decreased ionic concentrations. ΔH^‡_ds and ΔS^‡_ds increased an average of 7.0% and 10.3% in 2.2 mM MgCl₂ compared to 1.0 M NaCl. ΔG^‡_ds decreased an average of –1.0% going from 1.0 M NaCl to 2.2 mM MgCl₂ at 37°C, but differences were greater when extrapolated to higher temperatures.

Using one duplex sequence, we investigated the effects of common PCR additives on nucleic acid kinetics. Increasing MgCl₂ from 0.7 to 4.2 mM decreased ΔG^‡_a from 9.0 to 8.1 kcal/mol and increased k_a from 0.31 to 1.3 × 10⁷ M⁻¹ s⁻¹ at 37°C (Supplementary Figure S4A). However, k_d was practically unaffected by any change in ionic conditions (Supplementary Figure S4B). Conversely, the addition of 10% DMSO destabilized the duplex by increasing the dissociation rate but association was unaffected. The addition of 1× LCGreen increased association rates (equivalent to increasing MgCl₂ from 2.2 to 4.2 mM) and decreased dissociation rates.

NN models and predictions

NNs for dissociation kinetics are reported for 1.0 M NaCl (Table 2) and 2.2 mM MgCl₂ (Supplementary Table S4). The NNs accurately predict experimentally determined ΔH^‡_d, ΔS^‡_d and ΔG^‡_d for the 43 duplexes in 1.0 M NaCl and predict k_ds within 1.1 ± 0.5-fold (comparison C in Table 1). Similarly, transition-state parameters were accurately predicted for the n = 3 sequences from the literature reported in 1.0 M NaCl (comparison D in Table 1) (7,21,22). Reported k_ds (at n = 11 temperatures) for those same sequences from the literature were between 6 × 10⁻⁶ to 4 × 10³ s⁻¹ and predictions were within 3-fold (Figure 3A, Supplementary Table S5). In 2.2 mM MgCl₂, the predicted ΔH^‡_d, ΔS^‡_d and ΔG^‡_d for 43 sequences were 3.3, 4.4 and 1.2% different from experiments and k_ds were predicted within 1.0 ± 0.4-fold using the NNs in Supplementary Table S4.

Table 2.

Nearest-neighbour Kinetic Parameters in 1.0 M NaCl

Dissociationa			Associationa
NN parametersb	ΔH‡d (kcal/mol)	ΔS‡d (cal/mol/K)	ΔG‡d (kcal/mol)	ΔS‡a (cal/mol/K)	ΔG‡a (kcal/mol)
AA/TT	9.2 ± 0.6	26.5 ± 1.8	1.03 ± 0.04	–0.08 ± 0.11	0.03 ± 0.03
AT/TA	8.6 ± 1.7	24.2 ± 5.3	1.09 ± 0.09	–0.16 ± 0.23	0.05 ± 0.07
TA/AT	5.6 ± 1.4	15.8 ± 4.3	0.71 ± 0.10	–0.41 ± 0.22	0.13 ± 0.07
CA/GT	11.9 ± 1.4	33.5 ± 4.4	1.51 ± 0.10	–0.35 ± 0.21	0.11 ± 0.07
GT/CA	9.6 ± 1.6	25.9 ± 5	1.56 ± 0.10	–0.02 ± 0.20	0.01 ± 0.06
CT/GA	10.2 ± 1.2	28.9 ± 3.6	1.26 ± 0.09	–0.29 ± 0.27	0.09 ± 0.08
GA/CT	8.1 ± 1.3	21.7 ± 4.0	1.37 ± 0.08	–0.22 ± 0.20	0.07 ± 0.06
CG/GC	14.5 ± 1.5	40.7 ± 4.9	1.87 ± 0.12	0.08 ± 0.29	–0.02 ± 0.09
GC/CG	11.2 ± 1.7	29.2 ± 5.5	2.13 ± 0.08	–0.02 ± 0.24	0.01 ± 0.07
GG/CC	9.8 ± 1.3	26.6 ± 4.2	1.57 ± 0.09	0.47 ± 0.16	–0.15 ± 0.05
Initiation	–14.8 ± 4.2	–66.8 ± 13.3	5.87 ± 0.32	–25.1 ± 0.7	7.79 ± 0.21
Terminal AT	–1.0 ± 1.0	–2.3 ± 3.1	–0.29 ± 0.05	0.32 ± 0.15	–0.10 ± 0.05

^aMean values and standard deviations are the average of resampling 10 000 sets of 30 out of 43 sequences and calculating NNs. ΔG^‡s are calculated at 37°C.

^bNNs are reported (5′-3′)/(3′-5).

Figure 3.

(A) NN kinetic predictions accurately predict reported dissociation rate constants (avg. 1.7 ± 0.9 fold difference) in the literature using 1.0 M NaCl (B) Correlation of reported association rate constants in the literature to NN kinetic predictions (X’s), GC content (open circles), and the predictive algorithm of Zhang et al. (squares). All values are in 1.0 M NaCl and the GC-content predictions are calculated using Equation (7). See also Supplementary Tables S5 and S6.

NNs for association (Table 2, Supplementary Table S4) are dominated by initiation factors due to the small differences in the ΔS^‡_as for sequences (avg. = –25.7 ± 0.9 cal/mol/K), and the standard deviations for ΔS^‡_a and ΔG^‡_a NNs are similar in magnitude to the values themselves. The NN parameters predict ΔS^‡_as and ΔG^‡_as no better than assuming ΔS^‡_a = –25.7 cal/mol/K for our experiments and n = 9 sequences in 1.0 M NaCl reported in the literature (7,8,11,21–23) (Supplementary Table S6). Predictions for literature k_as (n = 17) were also poor, with an average difference between experiment and prediction of 35 ± 30% compared to 61 ± 37% using ΔS^‡_a = –25.7 cal/mol/K and 83 ± 49% from a recently published predictive algorithm (24).

The NN parameters predict that association rates decrease as a function of sequence length, although prior research demonstrates rate constants increase with length for sequences >100 nucleotides (29). This is due in part to significant correlation between low GC-content and length for the sequences studied (r = –0.61; P <10⁻⁴, Supplementary Figure S5). Therefore, we derived parameters for a simple alternative model to predict association kinetics (Equation 7) that only depends on GC-content for use in PCR and melting simulations.

(7)

In Equation (7), ΔS^‡_a is a function of the fraction of GC base-pairs in the duplex, f_GC. ΔS^‡_a(GC) = –24.7 (in 1.0 M NaCl) and –26.4 (in 2.2 mM MgCl₂) cal/mol/K are the predicted ΔS^‡_as for sequences with no AT base-pairs. ΔS^‡_a(AT) = –26.9 and –31.5 cal/mol/K are the predicted ΔS^‡_a for sequences with no GC-base-pairs in 1.0 M NaCl and 2.2 mM MgCl₂, respectively. Predictions for literature k_as are similar to those from NNs (Figure 3B) and are on average 50 ± 49% different.

We calculated thermodynamic NNs with Equation (5) to compare to prior equilibrium melting studies and unified thermodynamic NNs. The 10 thermodynamic NN parameters for ΔG derived from kinetic experiments are similar to the unified NN set (Table 1, comparison E) but tend to underestimate stability in comparison. However, differences are greater for ΔH and ΔS and initiation factors (Supplementary Table S7). NN parameters from kinetics predict the ΔH, ΔS, ΔG and T_M of the 108 oligos used to derive the unified NN parameters (15) with similar accuracy as NNs derived from the subsample of equilibrium melting experiments for the same 43 duplexes (Table 1, comparisons F and G). Thermodynamic NNs derived from either kinetic or thermodynamic data for the 43 duplexes reveal similar uncertainties and errors in comparison to the unified NNs (Supplementary Table S7) due to the limited NN-content (Supplementary Tables S8 and S9) and length variability of the duplexes.

High-speed melting and PCR thermocycling simulations

To further test our kinetic predictions, we used parameters obtained with 2.2 mM MgCl₂ to simulate published high-speed melting and extreme PCR experiments. Simulations used NN parameters and Equation (7) to predict dissociation and association kinetics, respectively. Compared to high-speed melting simulations (Figure 4A), experimentally determined T_Ms were on average 2.0 ± 0.6°C different for the (n = 4) wild-type sequences at (n = 9) different ramp rates, compared to 1.9 ± 1.1°C predicted by uMelt with salt and DMSO-adjusted unified NNs (Figure 4B). Kinetic predictions were systematically lower than experiments, whereas uMelt overestimated 32 of 36 experimental T_Ms. The general trend observed in the data was recapitulated in simulations: as ramp rates increased, predicted T_Ms increased logarithmically between 0.1 and 32°C/s, an average of 2.4 ± 0.3°C versus 2.8 ± 0.5°C reported experimentally. Furthermore, faster ramp rates increased the sharpness of the melt transition for both experiments and simulations.

Figure 4.

(A) Simulations of high-speed melting for genotyping F2 c.*97G>A performed in Pryor et al. (2017). Both wildtype (black) and homozygous mutant (grey) variants are shown. Simulated melting curves for each variant are at 0.25, 1, 4, and 16°C/s ramp rates. As the rate increases, the melting curves shift to higher temperatures and the melting transitions become sharper. (B) Experimental (grey circles) and kinetic simulation T_Ms (black circles) for the wildtype increase logarithmically with the melting rate, while thermodynamic predictions from uMelt (black X’s) are constant.

We simulated nucleic acid kinetics during thermocycling for two sets of extreme PCR experiments that varied the time spent for annealing or denaturation. For annealing experiments, the predicted per cycle efficiencies range from 95.6% to 100% (avg. efficiency = 99.7 ± 0.9% for both primers) at 5 s (Figure 5A) and decrease at shorter annealing times. At 0.1 s (Figure 5B), the primer with lower GC-content had a per cycle efficiency between 83.4–92.8% (avg. = 90.5 ± 1.7%) compared to 89.2–97.3% (avg. = 95.9 ± 1.5%) for the other primer. Experimental C_qs were on average 29.7± 0.3 from 1 to 5 s and increased to 34.7 by 0.1 s. The simulations are in concordance with experiments but exhibit less inhibition at shorter times. Predicted C_qs are 30 from 0.5–5 s and increase to 32 at 0.1 s. Simulations for duplicate experiments predict identical C_qs and show little variation. Analysis of the thermocycling profiles demonstrate that at shorter annealing times the minimum sample temperature increased by approximately 7°C. However, the difference in the minimum temperature for the longest and shortest annealing times should not appreciably alter the kinetics as k_as change only slightly (2% decrease at lower temperatures) and k_ds are 8–9 orders of magnitude lower than pseudo first-order k_as (calculated with 5 μM primer concentrations) at annealing temperatures.

Figure 5.

One cycle of simulated PCR for a 75 base-pair target surrounding rs#11078849 using the 5 s (A) and 0.1 s (B) annealing times of Millington et al. (2019). Kinetic simulations for the higher (black solid line) and lower (grey solid line) GC-content primers, as well as thermodynamic simulations that assume equilibrium at every temperature predicted by salt adjusted unified NNs (dashed lines). The time-temperature trace is the black dotted line, and the Y-axis corresponds to % duplex association or temperature. Both kinetic and thermodynamic predictions suggest that the primer–template complexes dissociate prior to reaching typical extension temperatures of 68–75°C.

Interestingly, simulations for the primer-template complexes predict 84–99% dissociation at typical extension temperature range (68–75°C). This does not seem to be an error in the kinetic predictions as simulations using salt adjusted unified NNs assuming an instantaneous equilibrium at every temperature also demonstrate that the primer-template complexes are unfavourable above 67°C (Figure 5). An explanation is suggested by Datta et al. who investigated Klentaq binding to duplexes under similar ionic conditions. They reported ΔGs of about –10 kcal/mol between 60 and 70°C (30), enough to stabilize the primer-template complex at extension temperatures.

For denaturation experiments, C_qs did not change when the denaturation time was reduced from 15 to 0.5 s, but increased from 24–25 to 30.4 and 32.3 for the two duplicate experiments at 0.1 s. However, simulations predict C_qs of 26 up until 0.2 s, and at 0.1 s C_qs only increase to 27. Analysis of the experimental time-temperature profiles reveals that the maximum sample temperature each cycle decreased more than 15°C as denaturation times decreased from 15 to 0.1 s (Supplementary Figure S6). In contrast to annealing experiments, this decrease could negatively impact denaturation efficiencies due to the exponential temperature dependence of dissociation.

To illustrate this, we resimulate the experiments but shift the temperature of the thermocycling profiles by –4.3°C. The shift of –4.3°C is more than the difference between the experimental and predicted T_Ms (1.5°C) but allows simulation to highlight the sensitivity of dissociation kinetics to temperature during PCR. This discrepancy may also be due to the high experimental concentrations of Klentaq (1.6 μM) stabilizing the duplex and increasing the required denaturation temperature (31). At 0.1 s, the duplex now fails to dissociate completely for most cycles. Despite having very similar time-temperature profiles, the two duplicate experiments exhibit very different per cycle efficiencies that ranged between 16% and > 99% (Figure 6A). The denaturation step is sensitive to small temperature variations and efficient (>99%) denaturation is rarely achieved (Figure 6B). Furthermore, the maximum template dissociation for inefficient cycles generally occurs not at the temperature peak, but as the sample cools toward annealing temperatures. The average per cycle efficiencies at 0.1 s for the temperature-shifted experiments are 79 ± 22% and 71 ± 28% for duplicate experiments. The predicted C_qs are 31 and 27 compared to 32.3 and 30.4 from experiments.

Figure 6.

(A) Simulated denaturation efficiencies for each cycle during the amplification of a 60 base-pair fragment of AKAP10. Predictions were based on experimental temperature and time data for duplicate experiments (black, grey) reported by Millington et al. (2019) that were adjusted by –4.3°C. Samples were denatured each cycle for 100 ms after attaining a threshold temperature, during which time the temperature continued to rise. The threshold temperature was determined in separate experiments as the temperature at which duplexes were 98% dissociated after melting analysis at a 0.3°C/s ramp rate. (B) The two time-temperature traces corresponding to Panel A. Predicted time points for 99% dissociation are circled and is achieved only in some cycles that reach higher temperatures. The temperature threshold needed for efficient denaturation in simulations is shown as a horizontal black dashed line.

DISCUSSION

We found that a transition-state theory model describes dissociation kinetics well but exaggerates the temperature dependence of association kinetics. A reduced model with no enthalpic barrier for the transition-state more accurately described association. Annealing is an entropically unfavourable process with little to no enthalpic barrier and temperature dependence. Melting is entropically driven, enthalpically unfavourable, and exhibits an exponential temperature dependence. Overall, the thermal stability of sequences was slightly less than reported from prior equilibrium melting studies, perhaps due to the comparatively limited temperature and concentration ranges we investigated.

Sequences had either small positive or negative ΔH^‡_as and one sequence had a small positive ΔS^‡_a in 2.2 mM MgCl₂. The inconsistency of sign with duplex sequence and reaction conditions for ΔH^‡_a and ΔS^‡_a has been found in other studies, and may be due to secondary structures, intermediate states, and the experimental temperature range (6,8,9,11). In this study, sequences were selected to have minimal secondary structure, and error analysis showed ΔH^‡_as and ΔS^‡_as were only weakly constrained. Thus, investigators should be cautious interpreting experiments with a transition-state model, which can force an exponential temperature dependence that may not be observed. Others have critiqued the use of transition-state theory citing its incompatibility with the observed viscosity dependence of association and proposed alternative models (29).

Changes in buffer conditions alter association and dissociation kinetics differently. The association rates increased 4-fold as MgCl₂ increased from 0.7 to 4.2 mM. Conversely, dissociation kinetics decreased at higher ionic concentrations, but were less affected in comparison. Prior studies found association rates depend on ionic conditions, but dissociation was either independent or only slightly influenced (22,32,33). Within the typical range of MgCl₂ concentrations used in PCR, increasing ionic conditions improves the speed of the annealing step without compromising denaturation rates.

Conversely, DMSO increases dissociation kinetics but does not alter association. In this way, inclusion of DMSO in PCR buffers will lower the T_Ms of difficult to melt sequences without compromising annealing rates, although the annealing temperature may need to be lowered. The DNA dye, LCGreen+, both increased association and decreased dissociation kinetics. However, this effect may be exaggerated here in comparison to PCR, because during a PCR, a large amount of background nucleic acid may be present that effectively sequesters dye molecules, decreasing the concentration available to interact with the specific PCR product.

All sequences studied were previously investigated in equilibrium melting studies used to derive the unified thermodynamic NN parameters. Comparison between literature and thermodynamic parameters from kinetic experiments validates both our stopped-flow experimental approach and the NN kinetic parameters. With transition-state parameters for each sequence, we applied the NN framework to derive kinetic NNs for association and dissociation, which were then used to calculate thermodynamic NNs. These correspond well to the unified NN parameters, albeit with notably increased errors due to experimental differences, and the limited variability in length and NN-content between sequences we studied. Thermodynamic predictions from kinetics were consistent with equilibrium melting studies. More importantly, the NN parameters for dissociation accurately predicted reported k_ds that spanned 9 orders of magnitude.

On the other hand, a NN model for association appears overparameterized and initiation factors dominate predictions. The predicted k_as are typically within 2-fold of literature values but NNs predict a length dependence incompatible with prior experiments for much longer sequences (>100 nucleotides). Therefore, we derived a simplified model that only considers the GC-content of sequences for use in simulations.

We did not identify prior literature reporting nucleic acid kinetic parameters in 2.2 mM MgCl₂, and therefore chose to test kinetic predictions by comparison to high-speed melting and extreme PCR thermocycling experiments. Our results simulating the high-speed melting experiments in Pryor et al. are in concordance with experiments and show that apparent T_Ms increase logarithmically as a function of the temperature ramp rate. Kinetic simulations improve T_M estimates by correctly predicting how apparent T_Ms change with temperature ramp rates. Like the experimental data, our simulations show that at faster ramp rates the melting transition becomes sharper, suggesting increased genotype discrimination between wild-type and homozygous mutants. Kinetic simulations can improve apparent T_M predictions for melting analysis assays by utilizing assay-specific knowledge of sequences and temperature ramp rates.

PCR simulations accurately predicted that annealing efficiencies decrease at shorter hold times but suggested the decrease would be less severe than experiments. For comparison, we assumed experiments with the lowest C_qs were 100% efficient, but the lowest experimental C_qs for annealing (≈30) are much higher than denaturation (≈24–25) suggesting that this may be incorrect. Both the longer primer and template are predicted to have unstable secondary-structures at annealing temperatures (ΔG = –0.2 to 2.1 kcal/mol at 46–62°C) which can reduce association kinetics by an order of magnitude (9). This could explain the high experimental C_qs and contribute to the discrepancy. Simulations that assume a 50% reduction in association for both the primer–template complex (with the longer primer) and template reannealing match experimental C_qs with an average error of 0.4 ± 0.2 cycles.

In the denaturation experiments of Millington et al., melting analysis first identified a threshold temperature of 79.8°C where 98% of products were melted. Then, extreme PCR experiments controlled the time spent above the threshold temperature, and as this time decreased, so did the denaturation efficiency. However, analysis of the experimental thermocycling profiles and kinetic simulations (Figure 6 and Supplementary Figure S6), did not demonstrate any time requirement above 79.8°C to maintain >99% efficiency. On the contrary, the temperature-shifted simulations suggest that efficient denaturation in the original experiments was achieved only for cycles that reached a higher temperature threshold (≈82.3°C). Analysis is complicated by the instrument temperature control scheme itself. The decrease in maximum temperature is because the sample moves between water baths at fixed temperature setpoints to rapidly change temperature. As the time spent in the denaturation bath decreased, the maximum sample temperature both decreased and had more intercycle variability. Therefore, both the time spent at denaturation and maximum sample temperature are inherently correlated in the study. An alternative temperature control scheme would be more appropriate for a PCR-based study of denaturation.

Despite this, simulations reveal the underlying system dynamics. The discrepancy between the threshold temperatures determined via melting experiments (79.8°C) and PCR simulations (82.3°C) is predicted by Pryor et al., which showed apparent T_Ms increase with temperature ramping rates. The melting experiments used to determine the threshold temperature were performed at near-equilibrium rates of 0.3°C/s, but extreme PCR heating rates were as high as 80°C/s. Melting simulations predict a 2.3°C increase in the apparent T_M between the melting analysis and extreme PCR experiments. Therefore, the increase in C_qs at shorter denaturation times is due to the sample not reaching a high enough temperature for the selected ramp rate. However, due to the exponential dependence of dissociation rates on temperature, reaching the temperature threshold is characteristic of high efficiency cycles, but not an explicit requirement. Efficiencies could be restored by reducing the temperature ramp rate or increasing the temperature achieved. Additionally, faster temperature cycling could increase both assay speeds and efficiencies so long as an appropriately higher temperature is reached.

The mode of PCR failure is different between compromised annealing and compromised denaturation. Experiments and simulations both demonstrate that when PCR inhibition increases due to suboptimal thermocycling, failure in denaturation is more severe and manifests as greater intercycle and interreplicate variability. Decreased annealing efficiencies, on the other hand, result in more reproducible C_qs and assay efficiencies. However, this does not consider the effects of nonspecific primer binding and extension.

For PCR assays targeting short amplicons, fast and efficient denaturation is best achieved by reaching, but not holding, a temperature threshold determined by sequence, buffer conditions, and the thermocycling speed. Practically, fast temperature ramping may be limited by instrumentation, and thus the fastest consistent denaturation may be achieved with a hold time (or slower ramp rate) at a lower temperature. Kinetic simulations reveal that common equilibrium descriptions of PCR are not applicable to fast assays. Investigations of rapid-cycle PCR have also demonstrated the inappropriateness of applying equilibrium paradigms to describe fast PCR assays (34). A guide for using kinetic predictions and simulations to design rapid PCR assays is included in the supplemental data file accompanying this article.

One critical aspect of association kinetics that we did not study is the effect of mismatches. A recent study investigated how single, double, and triple mismatches influence duplex stability and found that many combinations of multiple mismatches are surprisingly stable (35). Understanding how mismatches alter nucleic acid association and dissociation kinetics will improve our understanding of nucleic acid systems and enable more sophisticated simulations that consider nonspecific oligonucleotide binding and secondary structures.

The NN model accurately predicted temperature and sequence dependent dissociation kinetics but has limitations. Comparison of both kinetic NNs and NNs from the subsample of equilibrium melting experiments to the unified NNs suggests that the accuracy of kinetic NNs is limited by the comparatively skewed distribution of NNs presented in sequences. The incorporation of additional sequences to balance the frequency of NNs in the data set should improve parameters. The NN model itself excludes any influence by next-nearest-neighbours, although other work suggests these effects are small (13). Furthermore, the NN model neglects cooperativity, which may influence dissociation rates for longer sequences. Nonetheless, this study demonstrates the validity of the NN model for predicting dissociation kinetics.

Dissociation kinetics exhibit a dramatic sequence dependence, and the rates for two oligonucleotides can be several orders of magnitude different at any given temperature. This has been experimentally demonstrated by rapid CoLD-PCR, which exploits differences in dissociation rates to enrich amplification of variant DNA sequences (36). Extreme PCR thermocycling speeds are expected to further increase relative variant amplification in CoLD-PCR, similar to the improved discrimination seen with high-speed melting. Although association kinetics are also sequence-dependent, k_as change relatively little in comparison to k_ds. Dissociation kinetics dominate oligonucleotide thermodynamics, and the dissociation rate changes orders of magnitude with temperature. Predicting and simulating the kinetics of nucleic acid systems can elucidate system-specific behaviour and assay failure modes. Kinetic simulations can be used as a valuable tool in nucleic acid analysis and design, which could be readily integrated with existing models of enzyme-nucleic acid dynamics to elucidate the kinetics of more complex nucleic-acid based systems.

DATA AVAILABILITY

Oligonucleotide sequences and transition-state parameters are listed in the online supplemental data file accompanying this article.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

BioFire Diagnostics [50502787]. Funding for open access charge: CTW.

Conflict of interest statement. None declared.