Abstract
In aspiring to be discerning epidemiologists, we must learn to think critically about the fundamental concepts in our field and be able to understand and apply many of the novel methods being developed today. We must also find effective ways to teach both basic and advanced topics in epidemiology to graduate students, in a manner that goes beyond simple provision of knowledge. Here, we argue that simulation is one critical tool that can be used to help meet these goals, by providing examples of how simulation can be used to address 2 common misconceptions in epidemiology. First, we show how simulation can be used to explore nondifferential exposure misclassification. Second, we show how an instructor could use simulation to provide greater clarity on the correct definition of the P value. Through these 2 examples, we highlight how simulation can be used to both clearly and concretely demonstrate theoretical concepts, as well as to test and experiment with ideas, theories, and methods in a controlled environment. Simulation is therefore useful not only in the classroom but also as a skill for independent self-learning.
Keywords: dependent misclassification, education, nondifferential misclassification, P value, simulation
Epidemiology has been rapidly advancing methodologically over the past 2 decades. As a result, faculty are increasingly being called upon to teach graduate students more complex statistical, methodological, and theoretical topics in a short time span. The volume and complexity of these newer topics makes it difficult to enable a deeper understanding of basic concepts. Even in cases where deep dives are possible, it has been our experience that students can easily absorb a concept using traditional teaching methods but struggle when pressed to explain them in their own words or questioned on the details. Therefore, tools that facilitate teaching of epidemiologic methods within classroom settings, as well as lifelong, independent self-learning, would be of great benefit to the epidemiologic community.
Simulation is one such tool (1–3). In epidemiology, simulation is most commonly applied when assessing or comparing the performance of methods (e.g., estimators) in terms of bias or precision under known conditions. However, it can also be used to demonstrate many fundamental principles of data analysis, including study design, bias, and error, in a clear and systematic way. Additionally, simulation can be used to develop a deeper understanding of the scientific method, since theories, methods, or hypotheses can be subjected to experiments in a well-controlled, simulated environment.
Indeed, we see many potential applications for simulation in epidemiologic education, yet in our experience we find that few students are formally taught simulation methods (although we recognize that this is not universally true). For some, this leads to the idea that simulation is difficult, when in fact simple, illuminating simulations of epidemiologic concepts often require only a few lines of software code. Here, we provide several short examples of how one might use simulation as an educational tool in epidemiology, with the ultimate goal of demonstrating the importance of teaching simulation as an essential applied skill for an epidemiologist and how simple very insightful simulations can be to program.
THE MONTE CARLO METHOD
In most epidemiologic settings, simulations rely on the Monte Carlo method. In its modern form, this method was developed to solve intractable calculations in large, complex physics systems (4). The method allows us to study systems empirically by sampling from a model that defines the system. In epidemiology, an example system might be the members of a target population with a particular exposure and outcome that were “assigned” by some unknown data-generating mechanism. Sampling occurs by drawing from a set of predefined probability distributions that describe the important features of the system. For example, we simulate individuals, meant to represent members of our target population, and attempt to recreate a possible data-generating mechanism for those individuals. We might draw a binary exposure and a binary confounder from a Bernoulli distribution and combine information on the relationship between the exposure/confounders and outcome to build a normally distributed continuous outcome. Within the sampled units or individuals, the calculations become manageable, enabling us to approximate the targeted solution.
As a general rule, the Monte Carlo sample size, or the number of times the simulation is run (as opposed to the size of each independent sample within a simulation), should be as large as is required to see no change in results upon an increase in sample size. The versatility of the Monte Carlo method is demonstrated in its many uses. Below, we show how simulation can be used to gain some insight on 2 issues encountered when learning epidemiologic methods that can be challenging for students to understand in a nuanced way, as a means of demonstrating how simulations could be developed for many concepts students are learning.
The first involves a simulation of nondifferential misclassification. It is often taught that nondifferential misclassification results in bias toward the null. This is often the case; however, there are settings where this rule may not hold—for example, when dependence between the nondifferential misclassification of 2 variables results in the net bias being away from the null. We further use this example to illustrate the difference between bias and error (5).
The second simulation example aims to provide some intuitive insight on interpreting a P value. P values continue to be a source of confusion and consternation in the empirical sciences and can be intimidating for students entering the field (6). This is particularly true when students are taught P values technically, using abstract mathematical representations or mechanical demonstrations based on probability tables. In our view, the issue is exacerbated when students are given canned phrases to use to explain P values—especially when these phrases are technically wrong (7). Using simulation, we show how distributions that generate P values are constructed. Importantly, in following the steps required to simulate this distribution, one can more easily see the logic behind a P value and thus interpret it with less difficulty.
All simulations presented in this paper were carried out using R, version 3.6.1 (R Foundation for Statistical Computing, Vienna, Austria). Software code for all examples can be found in the Web Appendix (available at https://doi.org/10.1093/aje/kwaa232) or on GitHub (8).
EXAMPLE 1: NONDIFFERENTIAL MISCLASSIFICATION
A fundamental topic in epidemiology that students must grapple with is the sources of systematic bias commonly found in our studies. One bias that is relevant regardless of study design is information bias—that is, the bias that arises from errors in the measurement of variables included in our analysis. Information bias can be caused by measurement error in continuous variables or misclassification of categorical variables. For simplicity’s sake, we will hereafter use the term misclassification to mean either misclassification or measurement error. When misclassification occurs, an important consideration is whether that misclassification is differential (whether the error is dependent on another key analytical variable) or nondifferential (not dependent on another key analytical variable).
A distinction routinely taught in introductory epidemiology courses is that nondifferential misclassification will bias a point estimate toward the null, whereas bias due to differential misclassification is less predictable. Students are often shown a pair of 2 × 2 tables which demonstrate the 2 scenarios. Suppose an instructor wants to provide her students with a more nuanced understanding. Specifically, she wants to provide simulated examples showing what the direction and magnitude of the bias can be under a variety of scenarios: 1) when there is nondifferential misclassification in only a binary exposure; 2) when there is nondifferential misclassification in only a continuous confounder; 3) when there is nondifferential misclassification in both the exposure and the confounder and the errors are independent; and 4) when there is nondifferential misclassification in both the exposure and the confounder and the errors are dependent. Dependent misclassification arises when there is correlation between the errors in 2 variables, perhaps because there is another variable which is related to the errors in both variables (as can commonly happen when the 2 variables are measured by the same questionnaire) (9, 10). One expects bias toward the null under scenario 1, but the nonbinary nature of the confounder and the dependent misclassification in scenario 4 make the direction of the bias less certain in scenarios 2–4 (9, p. 139; 11). The instructor additionally wants to communicate that the statements regarding bias are in expectation (i.e., bias is the difference between the truth and the average point estimate over a large number of studies) and may not be the case in any given single study (9, p. 14; 25). The error in a given study (i.e., the difference between the truth and the point estimate for that study) could be in the opposite direction of the bias.
To help her students parse this new layer of knowledge, the instructor sets up a simple causal diagram with an exposure affecting an outcome and 2 confounders affecting both (Figure 1A), which is then extended for misclassification (Figures 1B and 1C) (11). The instructor then has the students generate a simulation based on that diagram, by carrying out the following steps.
Figure 1.
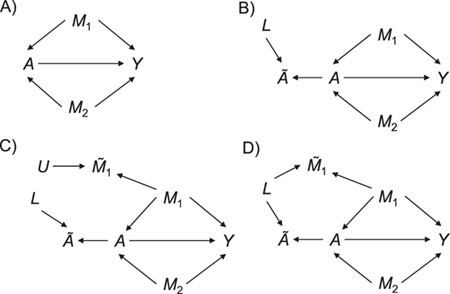
Causal diagrams guiding a student’s simulation of nondifferential misclassification. A) No misclassification; B) nondifferential misclassification of exposure 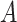 (with no misclassification of confounder
(with no misclassification of confounder 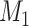 ); C) nondifferential misclassification of
); C) nondifferential misclassification of 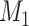 that is independent of the nondifferential misclassification of
that is independent of the nondifferential misclassification of 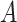 ; D) nondifferential misclassification of
; D) nondifferential misclassification of 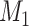 that is dependent on the nondifferential misclassification of
that is dependent on the nondifferential misclassification of 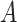 .
.
Step 1: Simulate the truth under no misclassification (Figure 1A).
Generate a sample of 1,000 individuals. Assign each individual 2 continuous confounders (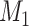 and
and 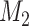 , log-normally distributed with
, log-normally distributed with 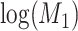 and
and 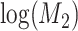
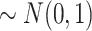 ) and a binary exposure (
) and a binary exposure (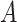 , with
, with 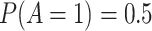 ), which is affected by the confounders (both with an odds ratio of 2). Then assign a continuous outcome (
), which is affected by the confounders (both with an odds ratio of 2). Then assign a continuous outcome (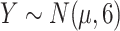 ), with mean μ dependent on exposure and confounders, as such:
), with mean μ dependent on exposure and confounders, as such:
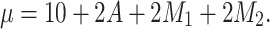 |
Step 2: Introduce nondifferential exposure misclassification (Figure 1B).
Randomly draw a continuous variable 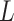 from a standard normal distribution. Among those truly exposed, select individuals to have a misclassified exposure (
from a standard normal distribution. Among those truly exposed, select individuals to have a misclassified exposure (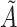 ) if their realization of
) if their realization of 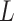 is above the 85th percentile (this sets the sensitivity to be 85%). Among those truly unexposed, select individuals to have a misclassified exposure (
is above the 85th percentile (this sets the sensitivity to be 85%). Among those truly unexposed, select individuals to have a misclassified exposure (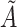 ) if their realization of
) if their realization of 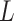 is above the 95th percentile (this sets the specificity to be 95%).
is above the 95th percentile (this sets the specificity to be 95%).
Step 3: Introduce confounder misclassification.
To induce measurement error in 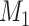 with errors independent of the errors in
with errors independent of the errors in 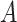 (Figure 1C), generate a random variable
(Figure 1C), generate a random variable 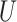 which is uniformly distributed in the range
which is uniformly distributed in the range 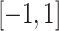 . Then, transform
. Then, transform  such that
such that  . To induce measurement error in
. To induce measurement error in  with errors dependent with the errors in
with errors dependent with the errors in 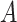 (Figure 1D), transform
(Figure 1D), transform 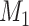 such that
such that 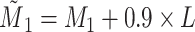 , where
, where 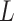 is the same random normal variable that was used to create the exposure misclassification.
is the same random normal variable that was used to create the exposure misclassification.
Step 4: Repeat steps 1–3 many times. In each simulation, estimate the mean difference (using a linear model adjusting for 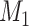 and
and 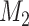 ) when there is no misclassification, when just the exposure is misclassified, when just
) when there is no misclassification, when just the exposure is misclassified, when just 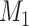 is misclassified, and when both
is misclassified, and when both 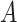 and
and 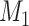 are misclassified. Examine the distributions of the point estimates. To estimate bias, compare the mean difference from the scenarios with misclassification against the true mean difference of 2 and then average across the simulations.
are misclassified. Examine the distributions of the point estimates. To estimate bias, compare the mean difference from the scenarios with misclassification against the true mean difference of 2 and then average across the simulations.
Note that the chosen parameters above are arbitrary, and we invite readers to explore how changing those parameters might affect what is observed, in a manner similar to what is shown in Table 1. See also Table 2, which summarizes various checks on the simulation and validates that the expected relationships are present (e.g., that the errors in 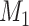 are dependent with the errors in
are dependent with the errors in 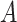 ). Additionally, there are other ways to simulate misclassification; what we present above is only a single example of how one could generate these scenarios.
). Additionally, there are other ways to simulate misclassification; what we present above is only a single example of how one could generate these scenarios.
Table 1.
How Bias Varies if Select Simulation Parameters Are Varied While Holding the Other Parameters Constant at Their Main Analysis Value, for the Scenario Where Exposure and Confounder Are Nondifferentially Misclassified and the Errors Are Dependenta
| Parameter | Main Analysis Value | Value Examined | Direction of Bias | Magnitude of Bias |
|---|---|---|---|---|
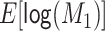 , , 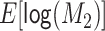
|
0 | −2 | Toward the null | −0.257 |
| −1 | Away from the null | 0.094 | ||
| 0 | Away from the null | 0.603 | ||
| 1 | Away from the null | 1.036 | ||
| 2 | Away from the null | 1.259 | ||
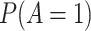
|
0.50 | 0.25 | Away from the null | 0.438 |
| 0.50 | Away from the null | 0.603 | ||
| 0.75 | Away from the null | 0.768 | ||
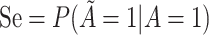
|
0.85 | 0.50 | Away from the null | 0.700 |
| 0.75 | Away from the null | 0.648 | ||
| 0.85 | Away from the null | 0.603 | ||
| 0.95 | Away from the null | 0.436 | ||
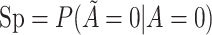
|
0.95 | 0.50 | Toward the null | −0.122 |
| 0.75 | Away from the null | 0.176 | ||
| 0.85 | Away from the null | 0.362 | ||
| 0.95 | Away from the null | 0.603 | ||
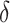 , where , where 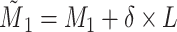
|
0.90 | −0.90 | Toward (past) the null | −2.184 |
| −0.50 | Toward the null | −1.748 | ||
| 0.50 | Toward the null | −0.036 | ||
| 0.90 | Away from the null | 0.603 | ||
| 1.50 | Away from the null | 1.282 |
Abbreviations: SD, standard deviation; Se, sensitivity; Sp, specificity.
a Notation: 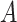 , correctly measured exposure;
, correctly measured exposure; 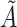 , misclassified exposure;
, misclassified exposure; 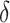 , coefficient determining amount of misclassification in
, coefficient determining amount of misclassification in 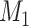 ; E(X), expected value of variable X;
; E(X), expected value of variable X; 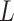 , variable used to induce misclassification;
, variable used to induce misclassification; 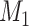 , correctly measured confounder 1;
, correctly measured confounder 1; 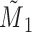 , misclassified confounder 1;
, misclassified confounder 1; 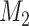 , confounder 2; P(X), probability of X; SD(X), standard deviation of X.
, confounder 2; P(X), probability of X; SD(X), standard deviation of X.
Table 2.
Results From Tests of the Expected Relationships Between Variables in the Simulation Where There Was Dependence Between the Errors in the Nondifferentially Misclassified Binary Exposure and the Continuous Confoundera
| Test | Expected Answer | Reasoning | Parameters Estimated | Value |
|---|---|---|---|---|
Does the sensitivity of 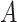 vary across the distribution of vary across the distribution of 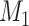 ?b ?b
|
No |
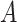 is nondifferentially misclassified. is nondifferentially misclassified. |
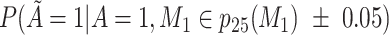
|
0.850 |
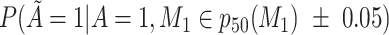
|
0.849 | |||
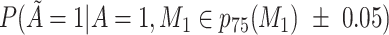
|
0.851 | |||
Does the specificity of 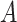 vary across the distribution of vary across the distribution of 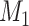 ?b ?b
|
No |
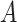 is nondifferentially misclassified. is nondifferentially misclassified. |
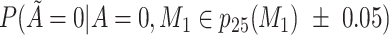
|
0.950 |
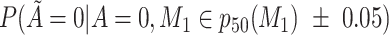
|
0.950 | |||
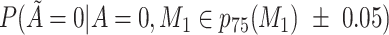
|
0.949 | |||
Does the sensitivity of  vary across error in vary across error in  , i.e., , i.e.,  ? ? |
Yes | Error in 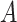 is dependent on error in is dependent on error in 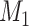 . . |
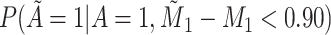
|
1.000 |
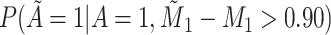
|
0.054 | |||
Does the specificity of 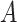 vary across error in vary across error in 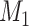 , i.e., , i.e.,  ? ? |
Yes | Error in 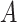 is dependent on error in is dependent on error in 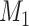 . . |
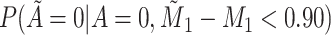
|
1.000 |
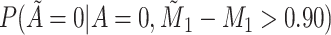
|
0.683 | |||
Does bias in 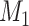 , , 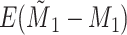 , vary across levels of , vary across levels of 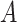 ? ? |
No |
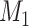 is nondifferentially misclassified. is nondifferentially misclassified. |
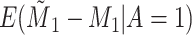
|
−0.000 |
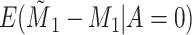
|
0.001 | |||
Does bias in 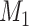 , , 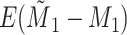 , vary across levels of , vary across levels of 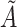 in participants with in participants with 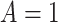 ? ? |
Yes | Error in 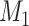 is dependent on error in is dependent on error in 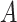 . . |
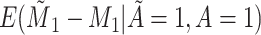
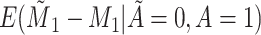
|
−0.248 1.399 |
Does bias in 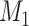 , , 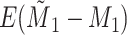 , vary across levels of , vary across levels of 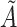 in participants with in participants with 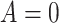 ? ? |
Yes | Error in 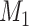 is dependent on error in is dependent on error in 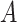 . . |
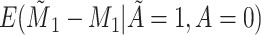
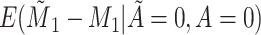
|
1.856−0.098 |
a Notation: 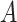 , correctly measured exposure;
, correctly measured exposure; 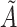 , misclassified exposure; E(X), expected value of variable X;
, misclassified exposure; E(X), expected value of variable X; 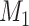 , correctly measured confounder 1;
, correctly measured confounder 1; 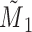 , misclassified confounder 1; P(X), probability of X;
, misclassified confounder 1; P(X), probability of X; 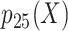 , 25th percentile of X;
, 25th percentile of X; 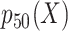 , 50th percentile of X;
, 50th percentile of X; 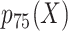 , 75th percentile of X.
, 75th percentile of X.
b Recall that the specified sensitivity of A was 0.85 and the specificity was 0.95.
The average mean difference across 10,000 simulations was unbiased at 2.000 for the correctly measured 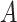 . When just
. When just 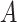 was misclassified (Figure 2A), the average mean difference of 1.058 was biased toward the null as expected, and 1.4% of the simulation estimates had a mean difference with exposure misclassification that was further from the null than the true mean difference. While 1.4% is low, these results are a demonstration of the fact that, even when the bias is toward the null as expected for this classic nondifferential misclassification scenario (i.e., binary exposure and no other misclassified variables), a given single study might not follow this rule. This is exactly the distinction between bias (which pertains to the distribution of point estimates) and error (which pertains to a single study) (5).
was misclassified (Figure 2A), the average mean difference of 1.058 was biased toward the null as expected, and 1.4% of the simulation estimates had a mean difference with exposure misclassification that was further from the null than the true mean difference. While 1.4% is low, these results are a demonstration of the fact that, even when the bias is toward the null as expected for this classic nondifferential misclassification scenario (i.e., binary exposure and no other misclassified variables), a given single study might not follow this rule. This is exactly the distinction between bias (which pertains to the distribution of point estimates) and error (which pertains to a single study) (5).
Figure 2.
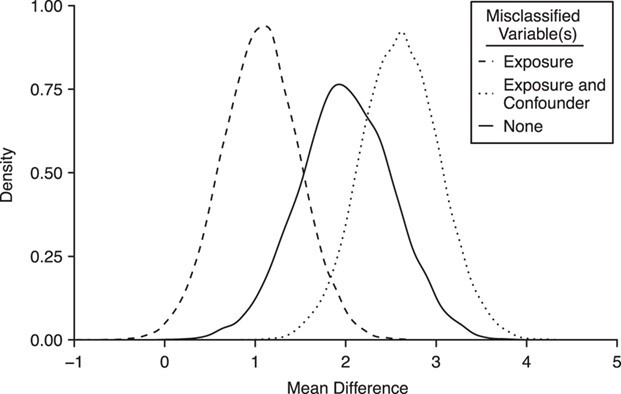
Distribution of mean difference estimates, comparing the mean difference under no misclassification with the mean difference under nondifferential misclassification of only the binary exposure 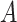 and nondifferential misclassification of
and nondifferential misclassification of 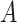 and of the confounder
and of the confounder 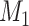 , with the misclassification errors being dependent.
, with the misclassification errors being dependent.
When we included the nondifferentially misclassified confounder and the correctly classified exposure in the model, the average mean difference of 2.312 was biased away from the null, with 72.3% of the simulations having a point estimate further from the null than the truth. This demonstrates the property that the bias is not guaranteed to be toward the null for a nonbinary variable that is nondifferentially misclassified (9, p. 139).
When the confounder and exposure were both nondifferentially misclassified and their misclassification errors were independent, the average mean difference was 1.120, with 2.2% of the simulations having a bias greater than the true mean difference. In this case, the net bias was toward the null. Finally, when the confounder and exposure were both nondifferentially misclassified and their misclassification errors were dependent (Figure 2B), the average mean difference was 2.603, and 92.1% of the 10,000 simulations had a mean difference with misclassification that was further from the null than the truth. In this case, the dependence between the misclassification errors resulted in the net bias being away from the null.
The key here is that the instructor showed students how to generate different possible nondifferential misclassification scenarios. She showed the classic scenario in which nondifferential misclassification of a single, binary variable resulted in bias toward the null. She also showed 2 cases where the net bias was away from the null: first because the single misclassified variable was nonbinary and second because there was dependence between the errors in 2 misclassified variables. This reinforces that, in real data analyses, students should pay attention not just to whether or not misclassification in a given variable is dependent on another variable (i.e., whether the misclassification is differential or nondifferential) but also to whether that variable has more than 2 levels or whether there is a chance for dependent misclassification with a second misclassified variable. The direction of the net bias becomes less certain in the latter 2 cases.
Furthermore, the simulation makes clear that “bias” does not necessarily have the same meaning for a single applied study, since it is a property of the full distribution (12). This is critical. Students may hear that one “expects” something to be the case. Not only does the above simulation demonstrate the more technical meaning of what is meant by “expects” (i.e., certain realized values may be away from the null, but on average bias is toward the null) but it also provides the opportunity to think of conditions and assumptions that must hold for a statement about bias to be true. For example, if, in addition to nondifferential exposure misclassification, there is nondifferential confounder misclassification that is crucially dependent with the exposure misclassification, bias can be away from the null.
The simple simulation here could easily be expanded. For example, students could use this as a basis for a simulation that mimics the data structure of a study they are using in a project, and they could examine how different sources of misclassification might affect their results in that data set. This simulation could also be used to demonstrate other properties of bias and error when there is misclassification, such as how the distribution of point estimates for a given scenario might differ as the sample size was increased or decreased. With smaller sample sizes, greater variation is expected, so even when bias is toward the null, more individual studies might have a point estimate further from the null than the truth (12). Students could also replicate what has been shown regarding how sensitivity and specificity, the magnitude of the true association, and exposure prevalence affect the distinction between bias and error under nondifferential misclassification of a single variable (5). Moreover, such a simulation could easily serve as the basis for diving into a more nuanced approach to bias analysis or measurement error correction methods (13).
Finally, we should reiterate that the above simulation is only 1 example of how one could induce nondifferential misclassification and dependent nondifferential misclassification. For the latter, when the exposure and confounder are binary, one could instead use the sensitivity and specificity to induce dependent misclassification. We further invite readers to explore scenarios where the exposure and the outcome are nondifferentially misclassified and scenarios where there is dependence between those misclassifications.
EXAMPLE 2: WHAT IS A P VALUE?
After obtaining a point estimate, standard practice is to quantify some measure of uncertainty in that point estimate. Typically, this is done with either P values or confidence intervals. For a number of justifiable reasons, use of the P value in the context of effect estimation has fallen out of favor (6, 7). This is partly due to the fact that P values are often misinterpreted, with common incorrect interpretations, including the belief that the P value is the probability that the null hypothesis is true or that the observed association was produced by chance alone (6, 7).
The P value definition given by the American Statistical Association is “the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between 2 compare groups) would be equal to or more extreme than its observed value” (6, p. 131). Often, in epidemiologic settings where we estimate exposure-outcome associations, the “specified statistical model” is one that states there is no actual association between the exposure and the outcome of interest (the null hypothesis). It also includes an assumption—often ignored in explanations of P values—that the model fit to the data reflects the true data-generating mechanism. Furthermore, while this is not explicitly mentioned above, P values usually require an assumption that there is no selection bias, uncontrolled confounding, or information bias (7) (although this requirement can be relaxed if the tested hypothesis is reframed as the expected value of the parameter estimate, rather than the true value of the parameter).
When lecturing on P values and confidence intervals, our instructor may provide a definition like the one above and then might ask her students to calculate the P value for some simple examples. However, given that the above definition is well-acknowledged to be nonintuitive and given the abundance of misconceptions surrounding P values, the instructor turns to simulation to concretize the concept of a P value. This also allows her to provide students with data examples and visualizations that can aid in understanding the P value. As with the misclassification demonstration, there are many ways the instructor could do this, but here we show 1 example.
She starts by setting up a simple simulation experiment. She randomizes 1,000 individuals to one of 2 levels of a binary exposure (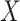 , with
, with 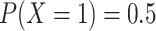 ) with a prespecified effect on a binary outcome (
) with a prespecified effect on a binary outcome (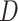 , with
, with 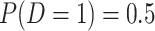 ). She sets 0.05 to be the true risk difference, comparing the risks of
). She sets 0.05 to be the true risk difference, comparing the risks of 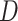 across levels of
across levels of 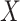 . The data are arranged such that each row corresponds to an individual, with a column for the outcome and a column for the exposure. In this initial experiment, the estimated risk difference is 4.9 per 100 observations, with a computed P value of 0.12. The logic of a P value can then be explained with a relatively simple procedure, each step of which can be translated into computer code in any given statistical software program, as follows.
. The data are arranged such that each row corresponds to an individual, with a column for the outcome and a column for the exposure. In this initial experiment, the estimated risk difference is 4.9 per 100 observations, with a computed P value of 0.12. The logic of a P value can then be explained with a relatively simple procedure, each step of which can be translated into computer code in any given statistical software program, as follows.
Step 1: Rerandomize exposure.
Create a new exposure, 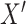 , randomly drawn from the same distribution as the original exposure (i.e., a Bernoulli distribution with
, randomly drawn from the same distribution as the original exposure (i.e., a Bernoulli distribution with 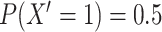 ). Because this new exposure was not used to generate
). Because this new exposure was not used to generate 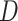 , we expect there to be no association between
, we expect there to be no association between 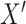 and
and 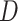 . This step reflects that we are interested in a P value which assumes that the null hypothesis of no effect is true.
. This step reflects that we are interested in a P value which assumes that the null hypothesis of no effect is true.
Step 2: Repeat.
Repeat step 1 many times (e.g., 10,000 times), and in each repetition estimate the risk difference comparing the risks of 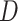 across levels of
across levels of 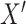 . In step 1, we said we expected that in any given repetition the association between
. In step 1, we said we expected that in any given repetition the association between 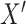 and
and 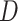 would be null. When we repeat the process, we generate the distribution of point estimates that would exist if the null hypothesis of no effect were true, given the other specifications of our experiment (e.g., prevalence of exposure, marginal risk of the outcome, and sample size).
would be null. When we repeat the process, we generate the distribution of point estimates that would exist if the null hypothesis of no effect were true, given the other specifications of our experiment (e.g., prevalence of exposure, marginal risk of the outcome, and sample size).
Step 3: Quantify the P value.
The (1- or 2-sided) P value can then be approximated by comparing the risk difference estimated in the original sample (comparing risks of 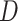 across levels of
across levels of 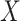 ) with this distribution of risk differences under the null hypothesis. For the 1-sided P value, quantify the proportion of the 10,000 risk differences which was greater than or equal to the original risk difference. For the 2-sided P value, take the absolute value of the 10,000 risk differences and then quantify the proportion of the distribution that was greater than or equal to the original risk difference.
) with this distribution of risk differences under the null hypothesis. For the 1-sided P value, quantify the proportion of the 10,000 risk differences which was greater than or equal to the original risk difference. For the 2-sided P value, take the absolute value of the 10,000 risk differences and then quantify the proportion of the distribution that was greater than or equal to the original risk difference.
Figure 3A shows a histogram of the 10,000 risk differences, as well as the estimate from the initial trial (the vertical dashed line). The distribution of risk differences is centered around the null value of 0, as expected. The histogram also provides some intuition on the question that the P value actually attempts to answer: Given the variability inherent in our data, if there were no actual effect of the exposure on the outcome, how likely is the result we observed? Figure 3B shows the distribution of the absolute values of the point estimates. Together, Figures 3A and 3B can be used to demonstrate the distinction between a 1-sided P value and a 2-sided P value. In our simple example, the proportion of risk differences that lie on and to the right of the dashed line in Figure 3B is 0.12, which is similar to the model-estimated 2-sided P value.
Figure 3.
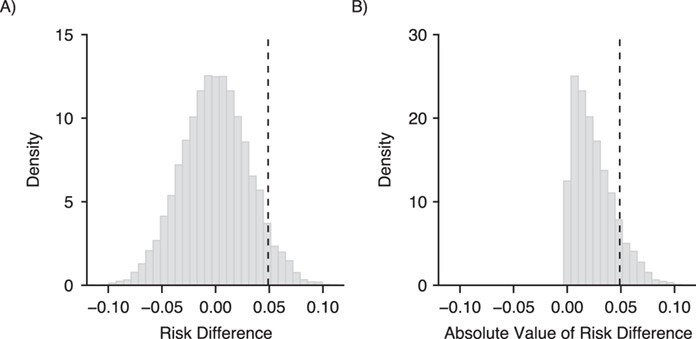
Demonstration of the definition of the P value. The dashed line represents the risk difference (RD) from the original simulated trial. The histogram in panel A illustrates the distribution of RDs under a null hypothesis of no association, generated by estimating in 10,000 simulations the association between a repeatedly rerandomized exposure and the original trial’s outcome. The proportion of RDs to the right of the dashed line can be used to estimate the 1-sided P value. Panel B illustrates the distribution of the absolute values of those RDs; now, the proportion of RDs to the right of the dashed line can be used to estimate the 2-sided P value.
By walking through this simulation step by step (or having the students do so), we are able to achieve greater clarity on what the P value obtained from a model’s output actually means. There is much nuance to the definition of a P value and the assumptions that are required, which can easily lead to misinterpretations (7). However, misunderstandings of the definition of a P value will not be resolved by simply having instructors reiterate, “The P value is the probability of observing a result as extreme as or more extreme than the current result if the null hypothesis were true.” By generating the distribution of point estimates that are used to define this probability and carefully scrutinizing the process, we believe insight can be gained. One could additionally demonstrate factors affecting the size of the P value. For example, increasing the sample size would result in a distribution that is more tightly centered around the null, yielding a smaller proportion of permuted risk differences as large as or greater than the original result (and thus a smaller P value). Similar examples can be constructed to demonstrate the impact of changing the effect size or introducing some form of bias (information, selection, or confounding).
DISCUSSION
We have provided here 2 simple examples of how simulation might be used to teach and learn epidemiologic concepts and methods. First, we showed that a student could use simulation to examine the direction of the bias under different nondifferential misclassification scenarios—for example, the classical scenario in which there is a single variable and bias toward the null versus a scenario where dependence between the errors in 2 nondifferentially misclassified variables results in net bias away from the null. Second, we demonstrated how an instructor could use simulation to parse the nonintuitive definition of the P value. It is important to highlight, though, that the simulations described above are just examples of how one could use simulation to explain misclassification and P value concepts. Other approaches could be used instead, and as stated above, we encourage readers to tweak our simulation examples to explore these concepts further.
Furthermore, these are not the only situations in which simulation can be useful for an epidemiologist. We can also use simulation to carry out sensitivity analyses, explore different data-generating mechanisms, examine the performance of an estimator for a specific data structure of interest, or conduct power calculations. Simulations are also helpful in understanding mediation structures, the scale dependence of effect-measure modification, and complex biases like collider stratification bias.
Simulation is an empowering and easily accessible tool for anyone with coding knowledge and access to statistical software. While simulation methods might seem intimidating prior to formally engaging in them, it has been our experience that we can teach the basics of this powerful problem-solving tool to students within a matter of hours and that students enjoy the experience. Furthermore, given that most graduate-level courses in epidemiologic methods already require proficiency in coding, it would be relatively simple to add lessons on basic simulation methods to existing courses with a laboratory component.
We see simulation as a particularly useful tool in our field, in part because most epidemiologists do not come from a theoretical mathematical background. Thus, seeing how software code behaves in simulated data or being able to ourselves use code to directly manipulate simulated data can greatly simplify and clarify the increasingly complex statistical methods we are using. Moreover, if our goal is to teach students how to learn rather than simply providing information, simulation puts the ability to experiment and test methods in the students’ hands. It further encourages a scientific, critical-thinking mentality that hopefully will be carried beyond the classroom into future independent self-learning and applied work.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Rollins School of Public Health, Emory University, Atlanta, Georgia, United States (Jacqueline E. Rudolph, Ashley I. Naimi); and Department of Epidemiology, School of Public Health, Boston University, Boston, Massachusetts, United States (Matthew P. Fox).
All of the authors contributed equally to this work.
This work was supported by the National Institutes of Health (grant R01 HD093602).
This work was largely inspired by Dr. Stephen R. Cole, an excellent mentor (to J.E.R. and A.I.N.). Dr. Cole routinely teaches his students the value of simulation and argues for the inclusion of simulation in epidemiology curricula.
Conflict of interest: none declared.
REFERENCES
- 1. Burton A, Altman DG, Royston P, et al. The design of simulation studies in medical statistics. Stat Med. 2006;25(24):4279–4292. [DOI] [PubMed] [Google Scholar]
- 2. Mooney C. Conveying truth with the artificial: using simulated data to teach statistics in social sciences. SocInfo Journal. 1995;1:1–5. [Google Scholar]
- 3. Hodgson T, Burke M. On simulation and the teaching of statistics. Teach Stat. 2000;22(3):91–96. [Google Scholar]
- 4. Metropolis N, Ulam S. The Monte Carlo method. J Am Stat Assoc. 1949;44(247):335–341. [DOI] [PubMed] [Google Scholar]
- 5. Jurek AM, Greenland S, Maldonado G, et al. Proper interpretation of non-differential misclassification effects: expectations vs observations. Int J Epidemiol. 2005;34(3):680–687. [DOI] [PubMed] [Google Scholar]
- 6. Wasserstein RL, Lazar NA. The ASA statement on p-values: context, process, and purpose [editorial]. Am Stat. 2016;70(2):129–133. [Google Scholar]
- 7. Greenland S, Senn SJ, Rothman KJ, et al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. Eur J Epidemiol. 2016;31(4):337–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Rudolph JE. SimTeach. https://github.com/jerudolph13/SimTeach. Published Feburary 5, 2020. Updated July 16, 2020. Accessed October 6, 2020.
- 9. Rothman KJ, Greenland S, Lash TL. Modern Epidemiology. 3rd ed. Philadelphia, PA: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 10. Brooks DR, Getz KD, Brennan AT, et al. The impact of joint misclassification of exposures and outcomes on the results of epidemiologic research. Curr Epidemiol Rep. 2018;5:166–174. [Google Scholar]
- 11. VanderWeele TJ, Hernán MA. Results on differential and dependent measurement error of the exposure and the outcome using signed directed acyclic graphs. Am J Epidemiol. 2012;175(12):1303–1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Whitcomb BW, Naimi AI. Things don’t always go as expected: the example of non-differential misclassification of exposure—bias and error. Am J Epidemiol. 2020;189(5):365–368. [DOI] [PubMed] [Google Scholar]
- 13. Lash TL, Fox MP, MacLehose RF, et al. Good practices for quantitative bias analysis. Int J Epidemiol. 2014;43(6):1969–1985. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


