Abstract
Acute graft-versus-host disease (GVHD) is a frequent complication following hematopoietic cell transplantation (HCT). Research on risk factors for acute GVHD has tended to ignore two important clinical issues. First, post-transplant mortality is high. In our motivating data, 100-day post-HCT mortality was 15.4%. Second, acute GVHD in its classic form is only diagnosed within 100 days of the transplant; beyond 100 days, a patient may be diagnosed with late onset acute or chronic GVHD. Standard modeling of time-to-event outcomes, however, generally conceive of patients being able to experience the event at any point on the time scale. In this paper, we propose a novel multi-state model that simultaneously: (i) accounts for mortality through joint modeling of acute GVHD and death, and (ii) explicitly acknowledges the finite time interval during which the event of interest can take place. The observed data likelihood is derived, with estimation and inference via maximum likelihood. Additionally, we provide methods for estimating the absolute risk of acute GVHD and death simultaneously. The proposed framework is compared via comprehensive simulations to a number of alternative approaches that each acknowledge some but not all aspects of acute GVHD, and illustrated with an analysis of HCT data that motivated this work.
Keywords: Acute graft-versus-host disease, cure models, semi-competing risks
1. Introduction
Allogenic hematopoietic stem cell transplant (HCT) is the recommended treatment for many hematologic diseases such as leukemia or bone marrow failure syndromes.1 The procedure, however, carries a high risk of graft-versus-host disease (GVHD), a debilitating syndrome in which the donor cells attack those of the recipient.2 Current consensus diagnosis and staging criteria distinguish between acute GVHD and chronic GVHD on the basis of the clinical signs and symptoms that manifest post-transplant.3 For the former, they further distinguished between two sub-categories: classic acute GVHD, for which the clinical signs manifest within 100 days of the transplant, and persistent, recurrent, or late-onset acute GVHD, for which the signs manifest after 100 days.
For the most part, clinical studies of classic acute GVHD (henceforth ‘acute GVHD’) have employed standard survival analysis techniques, such as the Kaplan–Meier estimator and/or the Cox model, or logistic regression.4–7 As applied to acute GVHD, however, these techniques fail to accommodate two important clinical issues. First, patients who undergo HCT are also at high risk for death in the short term. In our motivating data from the Center for International Blood and Bone Marrow Transplant Research (CIBMTR), for example, 100-day mortality among 9651 patients who underwent HCT between 1999 and 2011 was 15.4%. In the presence of the competing risk of death, an analyst has several approaches at her disposal to account for death. When the outcome is dichotomous, they may treat patients who die as ‘non-events’; however, this does not properly account for censoring.8 One option is to construct and model a composite endpoint of acute GVHD and death,9 although doing so changes the scientific question that is being addressed.10 A second option is to perform a competing risks analysis,11 an approach adopted by a number of clinical papers.12–15 One drawback of the competing risks framework, however, is that information on time from acute GVHD to death is discarded; this loss of information may affect estimation and inference, and also limits the scope of scientific inquiry.16 A third option is to perform the analysis within the semi-competing risks framework.17 Briefly, semi-competing risks refer to the setting where interest lies in a so-called non-terminal event (e.g. acute GVHD) the occurrence of which is subject to a terminal event (e.g. death). Broadly, methods for the analysis of semi-competing risks data can be classified into three groups: those based on copulas,17–20 those grounded in causal inference,21,22 and those based on the illness-death multi-state model.23–25
A second issue is that, in the absence of censoring and/or competing risks, standard survival methods assume that all patients will eventually experience the event of interest. This, however, is not the case for classic acute GVHD since diagnoses are, according to consensus guidelines, restricted to the first 100 days post-transplant. Survival models that ignore this defining feature therefore suffer from a form of mis-specification which may also lead to erroneous conclusions. Towards accommodating the finite support of the non-terminal event, it is first important to acknowledge that only a subset of patients are expected to be diagnosed with acute GVHD. In a sense, as in cancer prognosis studies where there are often long-term survivors, the population of patients who undergo HCT can be viewed as a mixture of patients who are susceptible to acute GVHD and those who are not susceptible. In the statistical literature, this phenomenon is often accounted for via a cure fraction model.26–30
Towards acknowledging both the competing risk of death and the finite time interval for a diagnosis of acute GVHD, we propose a novel multi-state model formulation for time-to-event outcomes defined on a finite interval. The proposed model builds on work by Conlon and colleagues31 and more recently by Beesley and colleagues32 in two important ways. First, the hazard function that dictates the rate at which patients experience the non-terminal event is specified so as to explicitly respect the finite time interval over which events can occur. Second, a subject-specific frailty term is introduced into the specification of each hazard function in the model. In doing so, the proposed model is better equipped to handle heterogeneity across and dependence within patients.33,34 While there has much research of bone marrow transplantation through the use of semi-parametric multi-state models,23,35,36 this paper adds to this literature via a novel multi-state model, acknowledging the finite interval over which acute GVHD is defined while simultaneously including a shared frailty term. An appealing benefit of adopting a fully parametric model is that the joint density can be determined on the full support of (T1, T2), where T1 and T2 denote the time to nonterminal and terminal events, respectively. Moreover, the joint density can be used to calculate patient-specific absolute risk profiles for acute GVHD and death simultaneously. Specifically, note that at any time t following transplantation, a patient could be classified as being in one of four mutually exclusive joint states: (1) alive with a diagnosis of acute GVHD; (2) dead, carrying a diagnosis of acute GVHD; (3) dead without acute GVHD; or (4) alive without acute GVHD. The probability of each of the four categories (known as transition probabilities in the multi-state model literature) can be estimated through integration of the joint density.23,35
The remainder of this paper is structured as follows. In Section 2 we provide a brief introduction to the CIBMTR data. Sections 3 and 4 present the proposed multi-state model for survival analyses on a finite time interval and the framework for estimation/inference, including derived likelihood, and joint risk prediction. Section 5 then provides a detailed simulation study aimed at evaluating small-sample operating characteristics of the proposed methods as well as investigating instances where existing methods perform either poorly or well. In Section 6 we present an illustrative analysis of the CIBMTR data that motivated this work. Finally, Section 7 concludes with a discussion and avenues for future work.
2. Acute GVHD following stem cell transplantation
The framework we propose is motivated by an on-going collaboration investigating risk factors for grade III or IV acute GVHD among patients who undergo HCT using data obtained from CIBMTR, a collaboration between the National Marrow Donor Program and the Medical College of Wisconsin representing a worldwide network of transplant centers. For the purpose of this paper, we restrict attention to n=9651 patients who underwent first HCT between 1999 and 2011. For acute GVHD, while only minimal administrative censoring was observed within the first 100 days post-transplant (0.2%), it is important to acknowledge that: (1) classic acute GVHD is defined only on the interval from (0,100) days following transplantation; and (2) only a fraction of patients who underwent HCT received a diagnosis of acute GVHD and this occurred for most patients before 100 days post-transplantation (third quartile=36 days). Specifically, at 100 days post-transplant, 1200 patients (12.4%) had been diagnosed with acute GVHD only, 502 patients (5.2%) had died without acute GVHD, 983 patients (10.2%) had experienced both and 6966 (72.2%) had not experienced either event. Table A.1 in the Supplementary Materials provides a summary of the study sample at 365 days post-transplantation.
3. The finite interval illness-death model
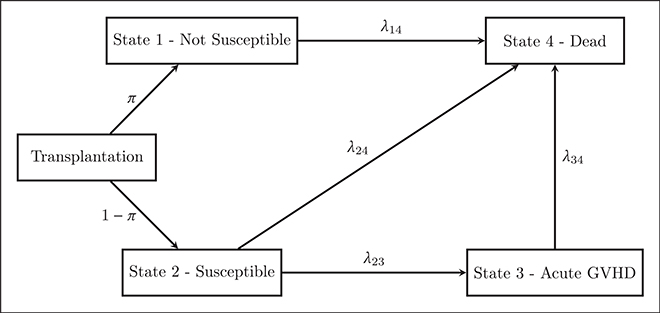
Let T1 and T2 denote the times to the non-terminal and terminal events, respectively. Following the cure model literature, we assume that patients are in one of two latent states at the time of transplantation, typically labeled ‘cured’ and ‘not cured’. For the study of acute GVHD following HCT, we prefer to use ‘non-susceptible’ to describe patients who will never receive a diagnosis of acute GVHD since HCT is performed to treat cancer (and not cure acute GVHD). Following our desire to use the term ‘non-susceptible’, it is natural to use ‘susceptible’ for the other group of patients. However, it is important to note that ‘susceptible’ patients will experience acute GVHD unless death or censoring occurs before 100 days. Based on this terminology, Figure 1 provides a schematic of the proposed finite interval illness-death model as applied to the study of acute GVHD following HCT. In the remainder of this section, we propose model specifications for the various components of the model.
Figure 1.
Schematic of the proposed finite interval illness-death model, applied to the setting of a study of acute GVHD following hematopoietic stem cell transplantation.
3.1. Latent susceptibility state
Following convention in the cure fraction literature, let L denote the latent state for a given patient with L=1 corresponding to the state of ‘non-susceptible’ and L=0 to the state of ‘susceptible’. Note that although the state is latent in the sense that it is unobserved at time of transplantation, during follow-up partial information on L may be observed; if a patient is diagnosed with acute GVHD then it must be that they were ‘susceptible’ (i.e. that L=0). Moreover, for patients who survive past τ days without a diagnosis of acute GVHD, we know that they are ‘not susceptible’. This hinges on the fact that patients who are susceptible to acute GVHD are assumed to experience the event on (0, τ). Finally, let π = P(L = 1) denote the probability of non-susceptibility to acute GVHD. We assume that π is modeled as a function of some vector of covariates, say Xs, via the generalized linear model
| (1) |
where g(·) is a user-specified link function and βs is a vector of unknown regression coefficients.
3.2. Time-to-event among the non-susceptible patients
Immediately post-transplant, a patient with L=1 is viewed as being ineligible to experience the non-terminal event but is eligible to be observed to experience the terminal event. In Figure 1 this is represented by the line that transitions between state 1 (‘non-susceptible’) and state 4 (‘death’). Following the multi-state modeling literature, the rate at which these patients with L=1 transition between these states is taken to be dictated by the 1 → 4 transition-specific intensity or hazard function
| (2) |
3.3. Semi-competing risks among the susceptible patients
Without loss of generality, we assume that if a patient is in the ‘susceptible’ state (i.e. L=0), in the absence of death or censoring, they will be observed to experience the non-terminal event at some point in the interval (0, τ) where τ < ∞. In Figure 1, this is represented by the transition from state 2 (‘susceptible’) to state 3 (‘acute GVHD’). From the figure we also see that patients who experience a non-terminal event are assumed to eventually experience the terminal event (i.e. transition from state 3 into state 4). Finally, even though a patient may be in the ‘susceptible’ state immediately post-transplantation, they may nonetheless experience the terminal event prior to experiencing the non-terminal event (i.e. transition from state 2 directly into state 4).
Let us reemphasize that a patient who makes it past time τ without experiencing the non-terminal event is necessarily ‘susceptible’ (see Section 3.1). Therefore, a patient who transitions from state 2 (‘susceptible’) to state 4 (‘death’) must have experienced the non-terminal event before the terminal event. This implies that event time T2 for the 2 → 4 transition must be defined on (0, τ). Note that for a patient who experiences the terminal event before time τ, we cannot determine from the observed data whether the patient transitions from 1 → 4 or 2 → 4, and so the likelihood contribution for such patients is marginalized with respect to the latent non-susceptibility variable, L.
Again following the multi-state modeling literature, the rates at which patients transition between these states (i.e. transitions 2 → 4, 2 → 3 and 3 → 4 in Figure 1) are defined by the hazard functions
| (3) |
| (4) |
| (5) |
The hazard functions given by expressions (4) and (5) are often referred to as defining an illness-death model. A crucial difference between this collection of hazard functions and those that have been considered for the illness-death model to-date, however, is that λ23(t1|L = 0) and λ24(t2|L = 0) are only defined on the finite interval (0, τ). For the 2 → 3 transition, this is to accommodate the clinical characteristics of the non-terminal event. For the 2 → 4 transition, we note that patients who survived past τ days without a diagnosis of acute GVHD are necessarily non-susceptible; thus, deaths without acute GVHD among susceptible patients must occur within τ days of transplantation.
3.4. Model specification
In practice, depending on the nature of the scientific question, analysts may adopt any of a broad range of model specifications for the four transition-specific hazard functions given by equations (2) to (5), including Cox-type multiplicative models,37 additive models,38 and accelerated failure time models.39 Although the framework we develop is not, in principle, restricted to any given choice, for simplicity of exposition, we consider the first of these options and model the four hazard functions as follows
| (6) |
| (7) |
| (8) |
| (9) |
where Xkj and βkj are vectors of covariates and log-hazard ratio regression parameters, respectively, for the k → j transition. In each of expressions (6) to (9), γ is a common subject-specific frailty, taken to arise from some population distribution with mean 1.0 and variance θ. Similar to a random intercept in a generalized linear mixed model,40 the frailties serve to accommodate between-subject heterogeneity that is not accounted for by the covariates included in the linear predictors and, thus, for any residual dependence between T1 and T2 not accounted for.
To complete the specification of the model, analysts will need to specify the form of the four baseline hazard functions and, if included, some population distribution for the frailties. For the latter, a common choice in the literature has been to adopt a Gamma distribution since it leads to closed-form expressions for the (induced) marginal likelihood contributions. In principle, however, any parametric distribution could be adopted, with the corresponding marginal likelihood contributions calculated via some numerical integration technique.41
Towards specification of the baseline hazard functions, an initial consideration is how to structure λ34,0(t2|T1 = t1) as a function of t1. While λ34,0(t2|T1 = t1) can, in principle, be any function of t1, two common specifications include the Markov model, for which it is taken that λ34,0(t2|T1 = t1) = λ34,0(t2), and the semi-Markov model, for which λ34,0(t2|T1 = t1) = λ34,0(t2 − t1) and focus shifts to the so-called sojourn time. Either way, analysts may choose to specify the baseline hazard functions parametrically,31 semi-parametrically,25,42 or non-parametrically.24 For the model we propose, if parametric baseline hazards are adopted, it is important to note that for a given continuous T with support on , probability density f(t) and cumulative distribution function F(t), the hazard function corresponding to the truncated distribution on (0, τ) is given by λτ(t) = f(t)/{F(τ) − F(0)}.43 For example, if T ~ Weibull(α, κ) with density f(t) = ακtα−1 exp{−κtα} for t > 0, then the truncated hazard function on (0, τ) is λτ(t) = ακtα−1/{1 – exp{−κ(τ – tα)}}.
Alternatively, suppose we model the baseline hazards more flexibly using B-splines via logλ(t) = B(t), where B(t) is a polynomial B-spline function of degree d with unique knots at t0 < t1 < … < tK < tK+1 and defined for t ∈ [t0, tK+1]. For continuous time-to-event outcomes with support on , we let t0 = 0 and tK+1 to be the largest follow-up time. For failure times defined on the finite interval (0, τ), we let t0 = 0 and tK+1 = τ Note that the B-spline function B(t) is parametrically defined as a linear combination of B-spline basis functions Bb,d(t) of degree d
where ηb are parameters, known as control points, and the B-spline basis functions are defined for t ∈ [t0, tK+1]; see De Boor (1978)44 for details.
The transition hazards (6) to (9) determine the joint distribution of T1 and T2. We denote the joint density on the observable region , by , for t1 > t2. We use the convention introduced by Xu et al.24 by assigning the remaining probability mass along the line T1 = τ, with density denoted , representing subjects who never experience the non-terminal event T1. This implies that the probability mass for non-susceptible patients (L=1) is distributed along the line T1 = τ. We derive an expression for the joint density in Section C of the Supplementary Materials.
3.5. Risk prediction
We focus on predictions of both events simultaneously at time T1 = T2 = t, where predictions are generated at the time of transplantation. The end product is a patient-specific absolute risk profile, consisting of probabilities corresponding to each of the following patient scenarios at time t: (1) experienced both events; (2) experienced the non-terminal event but not the terminal event; (3) experienced the terminal event without having experienced the non-terminal event; or (4) experienced neither event.
Whereas the current multi-state model literature calculates the components of the risk profile through the estimation of transition probabilities, our approach is to view each of the components of the risk profile as probability mass over (T1, T2) that can be quantified via integration of the joint density. We show the equivalence between the two approaches in Section D of the Supplementary Materials.
We define the four components of the absolute risk profile for both the non-terminal and terminal events at time t following the initiating event (also known as transition probabilities), conditional on γ, as follows
p(1)(t|γ) = P(experienced non-terminal event, but not the terminal event at time t|γ) =
p(2)(t|γ) = P(experienced both events by time t|γ) =
p(3)(t|γ) = P(experienced terminal event without non-terminal event by time t|γ) =
p(4)(t|γ) = P(neither events occur by time t|γ) =
A plot describing the bounds of integration is included in Figure 2. Note that the regions of integration are disjoint and exhaustive so that p(1)(t|γ) + p(2)(t|γ) + p(3)(t|γ) + p(4)(t|γ) =1. The vector, p(1)(t|γ), p(2)(t|γ), p(3)(t|γ), p(4)(t|γ), is conditional on the patient-specific frailties and covariates, whereby we refer to as patient-specific risk profiles.
Figure 2.
Diagram indicating the bounds of integration for calculating subject-specific risk profiles.
We also consider the marginal subject-specific risk profiles defined by
which averages the risk profiles, (p(1)(t|γ), p(2)(t|γ), p(3)(t|γ), p(4)(t|γ), over all values of γ.
Note that our methods complement existing methodology in the semi-parametric multi-state model literature for estimating absolute risk profiles of more than one outcome,23,42 where estimation depends heavily on observed events. If, for a given time t, the number of observed events is sparse, estimation of the transition probabilities in the semi-parametric setting fails to be robust. Moreover, the transition probabilities cannot be estimated for times t beyond the last observed event. By assuming a fully parametric baseline hazard functions, we are able to integrate the joint density at any time t following the initiating event in order to calculate the absolute risk profiles of interest.
4. Estimation and inference
4.1. The observed data likelihood
Suppose an i.i.d random sample of size n is collected from the population of interest, with T1i and T2i the times to the non-terminal and terminal events for the ith patient, respectively, and Xi a vector of patient-specific covariates that includes (at a minimum) Xs, X14, X23, X24, and X34. Letting Ci denote the (right) administrative censoring time for the ith patient, we assume that Ci is independent of (T1i, T2i) conditional on Xi. Based on this notation, the observed data for the ith patient is Di = {Yi1, δi1, Yi2, δi2, Xi}, where Yi1 = min(Ti1, Ti2, Ci, τ) with censoring indicator δi1 = I{Ti1 ≤ min(Ti2, Ci, τ)}, and Yi2 = min(Ti2, Ci) with censoring indicator δi2 = I{Ti2 ≤ Ci}. Note that if Yi1 = τ, then it is necessarily the case that δi1 = 0.
Towards developing the form of the likelihood, Table 1 shows that a patient may experience one of eight distinct post-transplant scenarios regarding their latent susceptibility status, and acute GVHD and death outcomes. Table 1 also provides the observed status indicator data that corresponds to each of the eight scenarios. From this one can see that when (δi1, δi2, yi1 < τ)=(0, 1, 1), that is that the patient was observed to die within τ days of the transplant without acute GVHD, one cannot distinguish between scenarios (iv) and (v) since there is insufficient information to indicate the patient’s susceptibility status. Similarly, when (δi1, δi2, yi1 < τ)=(0, 0, 1), the one cannot distinguish between (vii) and (viii). Hence, the likelihood contributions for patients with either of these observed status indicator combinations must be marginalized with respect to the distribution of L. Given this, adopting Weibull/truncated Weibull distributions for the baseline hazard functions for models (6) to (9) and marginalizing with respect to the distribution of the subject-specific frailties, the observed data likelihood for ϕ = (βs, α14, κ14, β14, α24, κ24, β24, α23, κ23, β23, α34, κ34, κ34, θ) is
| (10) |
where , for k = 1, … , 6, and
with , , and either if a Markov model is adopted for λ34(·) or if a semi-Markov model is adopted. Detailed derivations of the components of are given in Appendix B of the Supplementary Materials. Note: for the B-spline parameterization of the baseline hazard functions, the α and κ terms in the parameter vector (which correspond to Weibull parameters), φ, are replaced with the B-spline control points, η (see end of Section 3.4).
Table 1.
Observed status indicators and likelihood contributions corresponding to eight possible post-transplant scenarios regarding latent susceptibility, and acute GVHD and death outcomes.
| Observed data | Likelihood | ||
|---|---|---|---|
| Trajectory | (δi1, δi2, yi1 < τ) | contributiona | |
| (i) | Susceptible; observed acute GVHD & death | (1, 1, –) | f1 |
| (ii) | Susceptible; observed acute GVHD & censored before death | (1, 0, –) | f2 |
| (iii) | Not susceptible; observed death ≥ τ days | (0, 1, 0) | f3 |
| (iv) | Not susceptible; observed death < τ days w/o acute GVHD | (0, 1, 1) | f4 |
| (v) | Susceptible; observed death < τ days w/o acute GVHD | (0, 1, 1) | f4 |
| (vi) | Not susceptible; alive w/o acute GVHD & censored at ≥ τ days | (0, 0, 0) | f5 |
| (vii) | Not susceptible; alive w/o acute GVHD & censored at < τ days | (0, 0, 1) | f6 |
| (viii) | Susceptible; alive w/o acute GVHD & censored at < τ days | (0, 0, 1) | f6 |
See Section 4.1 and the Supplementary Materials for the form of the contributions.
4.2. Estimation and inference
Towards performing estimation and inference, we use maximum likelihood.45 Let denote the score function corresponding to expression (10). Using standard arguments, under certain regularity conditions and a correctly specified model, the maximum likelihood estimator of φ, obtained as the solution to and denoted , is consistent for the true ϕ0 as n → ∞. Furthermore, as n → ∞, where is the inverse of the expected information matrix
For inference, can be estimated via the inverse of the observed information matrix.
From a practical perspective, our experience in fitting the proposed model, as well as the model proposed by Conlon and colleagues,31 suggests that careful consideration of the numerical optimization algorithm used to obtain the global solution to is required together with careful choice of starting values. Our strategy was to use a quasi-Newton non-linear numerical optimization algorithm,46 as implemented in the optim() function in R.47 For both Weibull and truncated Weibull and B-spline parameterizations of the baseline hazard functions, starting values for the algorithm were generated by first assigning each subject in the sample a value for the latent non-susceptibility indicator as follows: subjects who died or were censored after 100 days without acute GVHD were considered non-susceptible (i.e. Li =1); subjects who had a diagnosis of acute GVHD (regardless of their subsequent survival experience) were considered susceptible (i.e. Li =0); the remaining subjects who died or were censored before 100 days (and for whom their susceptibility is unclear), were randomly assigned a susceptibility status. A GLM was then fit with these ‘observed’ values of L to obtain starting values for the parameters in model (1). For the proposed model with Weibull and truncated Weibull baseline hazards, to obtain starting values for the components of model (6), a univariate Weibull model was fit to the observed death times among those subjects with ‘observed’ L=1; to obtain starting values for the components of models (7) to (9) as well as the frailty variance θ, an illness-death with frailty was fit using the FreqID() function in the SemiCompRisks package for R.48 For B-spline parameterizations of the baseline hazard functions, we used the bSpline function in the splines2 package49 to generate B-spline basis functions and obtained starting values for hazard parameters as follows: fit univariate Cox models for each transition hazard model; smoothed the estimated cumulative baseline hazard functions using linear interpolation; obtained smoothed baseline hazards function via numerical differentiation followed by loess; and found the control points that minimized the distance between the smoothed log-hazard functions and B-spline functions by least squares. Finally, for the Weibull and truncate Weibull parameterized baseline hazards, the starting values obtained in this way were randomly perturbed via either an additive or multiplicative noise term, generated from a Uniform(−0.1i, 0.1i) or Uniform(1 – 0.1i, 1 + 0.1i) distribution, for i = 1, … , M where M is the number of attempts used to identify the global solution. For the simulations and analyses we present, we used M=5.
5. Simulation study
We conducted a series of simulation studies to investigate the finite-sample performance of the framework proposed in Sections 3 and 4 relative to existing methods that could be employed in the settings we consider but that fail to take into account the competing risks of death and/or the finite nature of the support for the non-terminal event. Here we present an overview of the simulation set-up and analyses conducted, together with select results.
5.1. Data generation under the baseline scenario
We used the CIBMTR data as a basis for the simulations. Specifically, the scale for T1 and T2 is taken to be ‘days’ (as in the CIBMTR data), with the values for the baseline hazard parameters taken from an initial analysis of the CIBMTR data restricting to patients 50 years or older whose initial malignancy had been diagnosed as being either intermediate or advanced stage. The distribution of simulated event times for acute GVHD and death roughly aligned with those seen in the dataset. The overarching approach taken to simulate data from the model proposed in Section 3 was to define a ‘baseline’ scenario and then perturb various aspects to investigate a range of data features. To that end, under the baseline scenario we simulated 2000 datasets of size n=5000 that consisted of a single binary covariate Xi from a Bernoulli distribution with mean 0.5 and a subject-specific frailty, γi, from a Gamma distribution with mean 1 and variance θ = exp(−1.71) = 0.18. For each patient, the (latent) susceptibility indicator was generated via model (1) using a logit link function and βs =(−0.41, 0.50); the induced marginal non-susceptibility rate was ≈46%. For patients with Li =1, T2i was generated using the inverse cumulative distribution transform method50 based on model (6) with a baseline hazard function taken to be that of a Weibull distribution with α14 = 1.4 and κ14 = 0.0002, and with β14 = 0.25. For these patients the ‘observed’ T1i was set to the minimum of τ and T2i.
For patients with Li =0, we first generated T1i via model (7) with a baseline hazard function taken to be that of a truncated Weibull distribution with τ=101, α23 = 0.5, and κ23 = 0.1, and with β23 = 0.25. Similarly, we generated T2i via model (8) with a baseline hazard function taken to be that of a truncated Weibull distribution with τ=101, α24 = 1.4, and κ23 = 0.005, and with β23 = 0.5. Given these generated T1i and T2i, if T1i ≥ T2i, we redefine T1i to be the minimum of τ and T2i. If T1i < T2i, we redefine T2i to be the sum of T1i and time from a diagnosis of acute GVHD to death generated using model (9), with a baseline hazard function taken to be that of a Weibull distribution with α34 = 1.3, k34 = 0.002, and with β34 = 0.15. Note that among the ‘susceptibles’, the hazard functions corresponding to acute GVHD and death are negatively correlated during the first month following HCT (where λ23 is a decreasing function and λ24 is increasing), which as one reviewer pointed out reflects the potential immune response that may lead to an increased risk of acute GVHD and decreased risk of death. Finally, we note that no administrative censoring was introduced under the baseline scenario.
5.2. Additional data scenarios
Building on the baseline scenario, additional scenarios examined the impact of: (i) a smaller sample size of n=1000; (ii) administrative censoring of either event via Ci simulated from an Exponential distribution with mean 100; (iii) administrative censoring solely of the terminal event at 365 days; (iv) increasing the non-susceptibility fraction from 46% to 76%; (v) modification of α23 and κ23 so that the hazard functions for the truncated and standard Weibull distributions are comparable on the interval (0, τ); and (vi) no frailty terms in the model, which is equivalent to a shared gamma frailty with zero variance.
5.3. Analyses
For each simulated dataset under each data scenario, we performed an analysis on the basis of the proposed finite interval illness-death model, defined by expressions (1) and (6) to (9) with Weibull baseline hazard functions specified in Section 3.4. In addition, we also performed a series of analyses that might (reasonably) be conducted in practice, specifically based on: (1) the proposed finite illness-death model without a shared frailty; (2) the model presented in Conlon et al.31 (i.e. a cure fraction model combined with a standard illness-death model) together with an added shared frailty; (3) the Conlon et al.31 model without a shared frailty (i.e. as they formulated it); (4) a standard illness-death model with shared frailty;25 (5) a standard cure fraction model for acute GVHD as a univariate outcome, with death treated as a censoring mechanism;27 and (6) a non-parametric multi-state illness-death model assuming separate baseline hazards for each transition. Note that the regression estimate corresponding to incident acute GVHD in model (6) aligns with estimates from a univariate Cox regression model for acute GVHD with death treated as an independent censoring mechanism. For simplicity we adopted parametric specifications for the baseline hazard functions in analyses (1) to (5) based on the Weibull distribution. Due to the fully parametric baseline hazard, a zero-tail constraint was not used to maximize the likelihood of the Conlon-type models (2) and (3). We also fit our proposed finite interval illness-death model with frailty assuming B-spline parameterized baseline hazard functions specified in Section 3.4 under data scenario (iii), administrative censoring of death at 365 days post-transplantation, which mirrors the CIBMTR data in Section 2.
5.4. Results
Following the strategy described in Section 4.2 for choosing starting values, only three of the 2000 simulated datasets resulted in a failure of convergence for the proposed analysis. Table 2 therefore presents results across 1997 simulated datasets, specifically the means of the empirical sampling distributions of parameter estimates from the various analyses described in Section 5.3 under the baseline scenario, together with the ‘true’ values used in the data generating mechanism. From the first two columns we see that the estimation procedure described in Section 4.2 yields estimates that are essentially unbiased for the true values of the parameters; that this holds for the simulations based on the scenario where n=1000, indicate good performance in smaller sample sizes (Table E.3 in the Supplementary Materials). From the third column, we see that failing to include the subject-specific frailty in the model leads to notable differences in estimation, particularly in the estimates of the log-hazard ratios for the 1 → 4 transition (compare 0.20 to 0.25 for β14,x) and the 2 → 4 transition (compare 0.41 to 0.50 for β24,x). From the fourth column, we see that failing to acknowledge the finite nature of the interval for the non-terminal event results in 20% bias in the estimate of the log-hazard ratios for the 2 → 3 transition (compare 0.25 to 0.30 for β23,x) and underestimation of the log-frailty variance (compare −2.00 to −1.71 for log(θ)). From the final three columns, each of the analyses that ignores either the latent susceptibility status and/or the illness-death formulation appears to yield estimates that are consistent for very different numerical values. For example, while the true value for β23,x is 0.25, the empirical means for the corresponding parameter from analyses (4), (5) and (6) are −0.31, 0.38, and −0.26, respectively. While one might argue that these models are not attempting to estimate the same parameter, it is clear that the conclusions that one would draw based on these analyses would be discrepant, including a negative association for analyses (4) and (6).
Table 2.
Mean point estimates, based on 2000 simulated datasets generated under the ‘baseline’ scenario with n= 5000, for the proposed finite interval illness-death model with and without frailty (FI-IDγ, FI-ID); the cure fraction illness-death model of Conlon et al.31 with and without a frailty (Conlonγ, Conlon); the illness-death model with frailty (IDγ); the cure fraction model for T1; and a multi-state illness-death model (MSM), which aligns with the results of a univariate Cox model for acute GVHD on the 2 → 3 transition.
| Truth | FI-IDγ | FI-ID | Conlonγ | Conlon | IDγ | Cure | MSM | |
|---|---|---|---|---|---|---|---|---|
| Non-susceptible fraction | ||||||||
| βs,0 | −0.41 | −0.41 | −0.31 | −0.55 | −0.40 | 0.14 | ||
| βs,x | 0.50 | 0.50 | 0.51 | 0.53 | 0.54 | 0.51 | ||
| Non-susceptible: 1 → 4 | ||||||||
| log(κ14) | −8.52 | −8.51 | −7.06 | −9.06 | −7.41 | |||
| log(α14) | 0.34 | 0.33 | 0.14 | 0.38 | 0.18 | |||
| β14,x | 0.25 | 0.25 | 0.20 | 0.33 | 0.23 | |||
| Susceptible: 2 → 4 | ||||||||
| log(κ24) | −5.30 | −5.30 | −5.17 | −5.27 | −5.09 | −5.35 | ||
| log(α24) | 0.34 | 0.34 | 0.23 | 0.30 | 0.25 | 0.08 | ||
| β24,x | 0.50 | 0.50 | 0.41 | 0.52 | 0.45 | −0.08 | 0.08 | |
| Susceptible: 2 → 3 | ||||||||
| log(κ23) | −2.16 | −2.17 | −2.31 | −1.81 | −1.77 | −1.98 | ||
| log(α23) | −0.69 | −0.69 | −0.75 | −0.63 | −0.64 | −1.10 | ||
| β23,x | 0.25 | 0.25 | 0.25 | 0.30 | 0.25 | −0.31 | 0.38 | −0.26 |
| Susceptible: 3 → 4 | ||||||||
| log(κ34) | −6.21 | −6.22 | −5.66 | −6.20 | −5.66 | −7.01 | ||
| log(α34) | 0.26 | 0.26 | 0.15 | 0.26 | 0.15 | 0.37 | ||
| β34,x | 0.15 | 0.15 | 0.14 | 0.16 | 0.14 | 0.11 | 0.14 | |
| log-frailty variance | ||||||||
| log(θ) | −1.71 | −1.73 | −2.00 | −0.49 | ||||
Note: See Section 5 for details.
Tables E.1 and E.2 in the Supplementary Materials report on standard error estimation and coverage of Wald-based 95% confidence intervals for the baseline scenario. With respect to inference, the empirical standard errors (computed as the standard deviation of the 2000 point estimates) align well with the mean of the analytic standard error estimates based on the inverse of the observed information matrix. Correspondingly, 95% confidence intervals attain nominal coverage probabilities for all parameters, including for the log-frailty variance. Furthermore, these results also hold under the data scenario where the sample size is n=1000. For the other analyses, results regarding inference were inconsistent, with some exhibiting good performance for certain parameters and others not. In most instances when coverage was less than the nominal 95%, it was due to a combination of bias in the point estimates and incorrect estimation of standard errors.
The results from the additional simulation scenarios, described in Section 5.2, are included in Appendix C of the Supplementary Materials and generally align with the findings from the baseline scenario with respect to bias and coverage. However, when administrative censoring is added, the standard errors of the parameter estimates are generally larger than those corresponding to the baseline scenario for all analyses which is to be expected (Tables E.7 and E.10 in the Supplementary Materials). Recall we fit the proposed model in Section 3 with B-spline baseline hazard functions for the case of administrative censoring of death at 365 days post-transplantation. From the third column of Table E.9, we see that there is marginal bias in the estimates corresponding to the non-susceptibility fraction, the 1 →4 and 2 →4 transitions and the log-frailty parameter ranging from 2% to 8%. Note that when we increased the sample size to 10,000, the bias became negligible (results not shown). It is possible that a better choice of number of knots, knot placement, and B-spline polynomial degree would improve results for a smaller sample size. Increasing the cure fraction from ≈46% to ≈76% redistributes the data from the 2 → 4, 2 → 3 and 3 → 4 transitions to the 1 → 4 transition, thereby decreasing the efficiency of the 2 → 4, 2 → 3 and 3 → 4 transitions parameters while increasing the precision of 1 → 4 transition estimates (Table E.13 in the Supplementary Materials). When α23 and κ23 are chosen so that the hazard functions for the truncated and standard Weibull distributions are comparable on (0, τ), we would expect Conlonγ to perform comparably to the proposed model. However, we observe bias in the log-odds ratio of non-susceptible fraction (compare −0.38 to −0.41 for βs,0) and the log-frailty variance (compare −1.90 to −1.71 for log(θ)), with corresponding coverage probabilities that are well below the nominal level (Tables E.15 and E.17 in the Supplementary Materials). In the final data scenario, we examined the model without the shared frailty. Under this scenario, the regression estimates from our proposed model and the model proposed by Conlon et al. are comparable, as our proposed model differs only in the specification of truncated Weibull baseline hazard functions for the 2 → 4 and 2 → 3 transitions. However, the models that do not take into account the susceptibility fraction, namely the illness-death and multi-state illness-death (MSM) models, provide regression estimates of the 2 → 3 transition that are in the opposite direction of the true effect (Table E. 18). In additional test simulations (not shown), decreasing the non-susceptibility fraction toward 0 gives parameter estimates from the Cox-based multi-state model that move closer to the true parameters. Focusing on Table E.18, death times are generated through separate data generating models, λ14 and λ24, with different baseline hazard functions and regression coefficients. Although non-intuitive, the resulting regression model from fitting a Cox model to such a mixture can lead to a regression coefficient for death that is not a weighted average of the true β14 and β24. Thus, the difference in conclusions drawn by competing models in the other scenarios is driven both by the specification of the shared frailty and cure fraction.
6. Analysis of the stem cell transplantation data
To illustrate the proposed model, we performed an analysis of the stem cell transplant data presented in Section 2, with τ=101 days. We analyzed assuming both Weibull or truncated Weibull baseline hazard functions, and B-spline parameterizations, separately, as specified in Section 3.4. Note that for each B-spline baseline hazard representation, knot locations as well as polynomial degree must be pre-specified. We fit five models with different combinations of knot locations and degrees across all four baseline hazard functions and selected the best model based on lowest AIC. For each of the model components (i.e. expressions (1) and (6) and (9)), we included the following covariates: disease stage (early, intermediate, advanced); HLA compatibility (identical sibling, 8/8, 7/8), and disease type (AML, ALL, CML, MDS). For the generalized linear model for the latent susceptibility state, we used a logit link so that the slope parameters are interpreted as log-odds ratios.
In addition, we fit four models that might be applied in practice: the Conlon et al.31 model, with an added shared frailty (henceforth the Conlonγ model); an illness-death model with shared gamma frailty; a standard cure model for acute GVHD; and a non-parametric multi-state illness-death model assuming separate baseline hazards for each transition, which aligns with estimates from a standard Cox proportional hazards model for acute GVHD on the 2 → 3 transition. Furthermore, death was treated as an independent censoring mechanism for the standard cure fraction model.
We then use the estimated model parameters from the main model with Weibull or truncated Weibull parameterized baseline hazard functions to generate predicted subject-specific risk profiles presented in Section 3.5 at day t = 5, 10, … , 150 post-transplantation for our proposed model and the model from Conlon et al. with an added shared frailty.31 To assess the impact of the shared frailty on joint risk prediction, we also calculated predicted subject-specific risk profiles at day 100 post-transplantation for the following values of the shared frailty, γ = 0.5,0.6, … , 1.5. We compared these estimated absolute risk profiles to the estimated marginal subjected specific risk profile that averages over the distribution of the shared frailty, defined in Section 3.5.
Select parameter estimates from the six analyses are given in Table 3 and Figures 3 to 5, with additional results provided by Table F.1 and Figure F.1 in the Supplementary Materials document.
Table 3.
Estimates and standard errors for select parameters from analyses of the CIBMTR HCT data (n= 9,651) including: the proposed finite interval illness-death model with frailty, assuming Weibull () and B-spline () baseline hazard functions described in Section 3.4; the cure fraction illness-death model of Conlon et al.31 with an additional frailty (Conlonγ); the illness-death model with frailty (IDγ); the cure fraction model for acute GVHD; and a multi-state illness-death model (MSM), which aligns with the results of a univariate Cox model for acute GVHD on the transition from HCT to acute GVHD.
|
|
|
Conlonγ |
IDγ |
Cure |
MSM |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Est | SE | Est | SE | Est | SE | Est | SE | Est | SE | Est | SE | |
| Non-susceptible fraction | ||||||||||||
| Intercept | 1.94 | 0.06 | 1.90 | 0.07 | 2.07 | 0.06 | 1.99 | 0.06 | ||||
| Intermediate stage | −0.14 | 0.07 | −0.18 | 0.07 | −0.15 | 0.07 | −0.08 | 0.07 | ||||
| Advanced stage | −0.33 | 0.08 | −0.54 | 0.08 | −0.35 | 0.08 | −0.25 | 0.07 | ||||
| HLA: 7/8 | −0.75 | 0.08 | −0.76 | 0.08 | −0.77 | 0.09 | −0.69 | 0.08 | ||||
| HLA: 8/8 | −0.42 | 0.07 | −0.43 | 0.06 | −0.47 | 0.07 | −0.40 | 0.06 | ||||
| Disease type: ALL | −0.17 | 0.08 | −0.19 | 0.07 | −0.20 | 0.08 | −0.06 | 0.07 | ||||
| Disease type: CML | −0.44 | 0.08 | −0.39 | 0.08 | −0.49 | 0.08 | −0.38 | 0.08 | ||||
| Disease type: MDS | −0.25 | 0.10 | −0.15 | 0.09 | −0.29 | 0.10 | −0.21 | 0.09 | ||||
| Non-susceptible: HCT → Death | ||||||||||||
| Intermediate stage | 0.30 | 0.06 | 0.25 | 0.06 | 0.27 | 0.06 | ||||||
| Advanced stage | 1.13 | 0.06 | 0.94 | 0.05 | 1.05 | 0.06 | ||||||
| HLA: 7/8 | 0.32 | 0.07 | 0.26 | 0.06 | 0.31 | 0.07 | ||||||
| HLA: 8/8 | 0.14 | 0.05 | 0.10 | 0.05 | 0.11 | 0.05 | ||||||
| Disease type: ALL | −0.08 | 0.06 | −0.11 | 0.06 | −0.09 | 0.06 | ||||||
| Disease type: CML | −0.53 | 0.09 | −0.51 | 0.08 | −0.52 | 0.08 | ||||||
| Disease type: MDS | −0.52 | 0.08 | −0.44 | 0.07 | −0.50 | 0.08 | ||||||
| Susceptible: HCT → Death | ||||||||||||
| Intermediate stage | −0.04 | 0.20 | 0.35 | 0.17 | 0.68 | 0.36 | 0.43 | 0.13 | 0.30 | 0.05 | ||
| Advanced stage | 0.20 | 0.22 | 0.89 | 0.16 | 1.24 | 0.37 | 1.63 | 0.13 | 1.00 | 0.05 | ||
| HLA: 7/8 | 0.68 | 0.21 | 0.46 | 0.17 | 1.29 | 0.50 | 1.55 | 0.15 | 0.34 | 0.05 | ||
| HLA: 8/8 | 0.37 | 0.19 | 0.37 | 0.15 | 1.20 | 0.47 | 1.02 | 0.12 | 0.15 | 0.04 | ||
| Disease type: ALL | 0.64 | 0.20 | 0.54 | 0.14 | 1.37 | 0.43 | 0.49 | 0.14 | 0.00 | 0.05 | ||
| Disease type: CML | 0.07 | 0.23 | 0.02 | 0.19 | 1.09 | 0.48 | 0.08 | 0.16 | −0.37 | 0.07 | ||
| Disease type: MDS | 0.11 | 0.27 | −0.09 | 0.18 | 0.75 | 0.47 | −0.04 | 0.17 | −0.40 | 0.06 | ||
| Susceptible: HCT → Acute GVHD | ||||||||||||
| Intermediate stage | −0.30 | 0.09 | −0.27 | 0.07 | −0.30 | 0.08 | 0.01 | 0.11 | −0.21 | 0.07 | 0.05 | 0.06 |
| Advanced stage | −0.24 | 0.10 | −0.31 | 0.08 | −0.22 | 0.08 | 0.51 | 0.11 | −0.10 | 0.06 | 0.21 | 0.06 |
| HLA: 7/8 | 0.44 | 0.11 | 0.32 | 0.08 | 0.42 | 0.10 | 1.24 | 0.13 | 0.47 | 0.07 | 0.66 | 0.07 |
| HLA: 8/8 | 0.44 | 0.09 | 0.27 | 0.06 | 0.37 | 0.08 | 0.87 | 0.10 | 0.37 | 0.06 | 0.40 | 0.06 |
| Disease type: ALL | 0.12 | 0.10 | 0.06 | 0.07 | 0.09 | 0.09 | 0.33 | 0.12 | 0.19 | 0.07 | 0.07 | 0.07 |
| Disease type: CML | 0.12 | 0.10 | 0.10 | 0.07 | 0.09 | 0.09 | 0.63 | 0.13 | 0.14 | 0.07 | 0.35 | 0.07 |
| Disease type: MDS | 0.04 | 0.12 | 0.08 | 0.09 | 0.02 | 0.10 | 0.33 | 0.14 | 0.12 | 0.08 | 0.19 | 0.08 |
| Susceptible: Acute GVHD → Death | ||||||||||||
| Intermediate stage | 0.15 | 0.09 | 0.13 | 0.08 | 0.15 | 0.09 | 0.33 | 0.13 | 0.13 | 0.08 | ||
| Advanced stage | 0.59 | 0.09 | 0.51 | 0.07 | 0.58 | 0.08 | 1.22 | 0.13 | 0.51 | 0.07 | ||
| HLA: 7/8 | 0.29 | 0.10 | 0.26 | 0.09 | 0.29 | 0.09 | 0.85 | 0.14 | 0.25 | 0.09 | ||
| HLA: 8/8 | 0.08 | 0.08 | 0.09 | 0.07 | 0.09 | 0.08 | 0.37 | 0.12 | 0.08 | 0.07 | ||
| Disease type: ALL | 0.01 | 0.10 | 0.01 | 0.08 | 0.01 | 0.09 | 0.12 | 0.14 | 0.01 | 0.08 | ||
| Disease type: CML | 0.15 | 0.10 | 0.12 | 0.09 | 0.15 | 0.10 | 0.42 | 0.14 | 0.13 | 0.09 | ||
| Disease type: MDS | 0.11 | 0.11 | 0.07 | 0.10 | 0.09 | 0.10 | 0.30 | 0.16 | 0.07 | 0.10 | ||
| Log-frailty variance | ||||||||||||
| log(θ) | −0.89 | 0.08 | −4.76 | 1.88 | −1.47 | 0.15 | 2.31 | 0.04 | ||||
Figure 3.
Estimated baseline survivor functions (conditional on γ= 1) from the CIBMTR HCT data for acute GVHD and death among patients who are susceptible to acute GVHD (i.e. with L= 0), based on the proposed finite-interval illness-death model with frailty (FI-IDγ) and the cure fraction illness-death model of Conlon et al.31 with an additional frailty (Conlonγ).
Figure 5.
Left panel: Estimated absolute risk profiles (conditional on frailty, γ) for Patient C at 100 days post-transplantation for varying values of the gamma frailty, γ. Right panel: Estimated marginal absolute risk profiles for Patient C at 100 days post-transplantation.
6.1. Results from fitting proposed finite interval illness-death model
After fitting the proposed model in Section 3 with Weibull or truncated Weibull and B-spline parameterized baseline hazards, we found that the conclusions drawn from both models are generally aligned, with a few exceptions (see Table 3 columns one through four). Note that for the case of B-spline parameterized baseline hazard functions, based on our proposed model selection process described in Section 6, the final model chosen placed one knot at the median of the corresponding observed event times for each of the four transitions with degree 3 polynomial B-splines. Both models supported deleterious associations between disease stage and susceptibility status, risk of death following HCT among non-susceptibles (1 → 4 transition) and death following acute GVHD (3 → 4 transition), and protective associations between disease stage and risk of acute GVHD following HCT (2 → 3 transition), with stronger effects for higher stage. We found that HLA compatibility was associated with non-susceptibility to acute GVHD and all transition hazards. Effect estimates for disease type were greatest for latent non-susceptibility, transition from HCT to death among both non-susceptibles and susceptibles (1 → 4 and 2 → 4 transitions) and were closer to the null for transitions from HCT to acute GVHD and to death after acute GVHD (2 → 3 and 3 → 4 transitions).
Regression estimates differed between the two models on the 2 → 4 transition with respect to disease stage and disease type. The estimated effect of intermediate stage for the Weibull parameterized model was close to the null with value −0.04 in contrast to the B-spline parameterized model with value 0.35. The estimated effect of advanced stage was greater for the B-spline model compared to the Weibull parameterized model (0.89 vs. 0.20), whereas the estimated log-hazard ratio for disease type MDS in the Weibull and B-spline parameterized models was in opposite directions, but close to the null. The estimated gamma frailty variance parameter for the Weibull parameterized model was exp(−0.89) ≈ 0.41 with Wald-based 95% confidence interval (0.35, 0.48), much larger than the estimate for the B-spline parameterized model, with value exp(−4.76) ≈ 0.01 and 95% confidence interval (0, 0.34). Heterogeneity not accounted for by covariates was likely accounted for by the additional flexibility of the B-spline parameterized baseline hazard functions over the Weibull-based baseline hazards.
6.2. Impact of ignoring the finite interval
Focusing on the proposed finite-interval illness-death model and the Conlonγ model, the maximized log-likelihoods are −39, 542.03 and −39, 611.93, respectively. Given that these models have the same number of parameters, this suggests that acknowledging the finite interval over which patients who are susceptible (i.e. with L=0) may be diagnosed with acute GVHD or experience a death event prior to such a diagnosis yields a much better fit of the observed data. Note that we do not report/compare the maximized log-likelihoods for the other analyses because they represent different data structures.
Interestingly, from the first, third and fifth columns of Table 3, labeled , and Conlonγ, we find that the point and standard error estimates for most of the model components are comparable between the finite-interval illness-death model and the Conlonγ model. The results for the HCT → Death transition (2 → 4 in Figure 1), however, are very different, with the estimates from the Conlonγ model being substantially larger. Thus, one would conclude much stronger associations under the Conlonγ model than under the proposed model. Some insight into these differences may be obtained through inspection of the estimated baseline survivor functions. From Figure 3, in particular, we see that the estimated baseline survivor functions for the HCT → acute GVHD transition for patients with L=0are very similar during the first 100 days under the finite-interval illness-death using Weibull parameterized baseline hazards and the Conlonγ models. The corresponding baseline survivor functions for the HCT → death transition for patients with L=0 are very different, however, with median survival among the baseline patient group estimated to be 80 days and 200 days post-transplant.
6.3. Impact of not distinguishing between susceptibles and non-susceptibles
From the seventh column of Table 3 (IDγ), we find that ignoring the latent susceptibility status and finite interval over which the diagnosis of acute GVHD is given has a dramatic impact on point estimates, with results from the standard illness-death model pointing to generally stronger associations for each of the HCT → acute GVHD, HCT → death and acute GVHD → death transitions, as compared to estimates from our proposed model with Weibull- and B-spline-based baseline hazard functions (, ). As an example, under our proposed model we find that there is insufficient evidence of an association between disease stage and the transition from HCT to acute GVHD (p-value=0.32 from a likelihood ratio test with 2 degrees of freedom), whereas under the standard illness-death model the association is signficant (p-value<0.001 from a likelihood ratio test with two degrees freedom). We also find the estimated variance of the subject-specific frailty, , under the standard illness-death model is 10.1 as compared to 0.41 under the proposed finite-interval illness-death model with Weibull and truncated Weibull parameterized baseline hazards. From the eleventh column, we also see that the conclusions from fitting a multi-state illness-death model without parametric assumptions results in discordant conclusions from our proposed model. Thus, accounting for the finite interval for a diagnosis of acute GVHD through structural changes in the model (i.e. the use of a latent non-susceptibility indicator and specification of the baseline hazards for the HCT → acute GVHD and HCT → death transitions), helps account for a substantial amount of between-subject heterogeneity in risk for the two outcomes.
6.4. Impact of treating death as an independent censoring mechanism
From the ninth column of Table 3, we find that a standard cure fraction model for acute GVHD yields estimates for the non-susceptibility fraction that are comparable to the finite-interval illness-death model. However, the conclusions drawn from the results of the HCT → acute GVHD transition differ. Under the standard cure fraction model, there is evidence of a relationship between disease type and the transition from HCT to acute GVHD (p-value=0.03), whereas this is not evident under the finite interval illness-death model (p-value=0.51).
6.5. Estimated absolute risk profiles
We plotted the estimated risk profiles at t = 1, 2, … , 150 for three patients (labeled A, B, and C) for our proposed finite interval illness-death model, assuming Weibull or truncated Weibull baseline hazard functions, in Figure 4. The plots of the estimated risk profiles over time are stacked so that at any time t the vertical distance between the: x-axis and solid line is p(1) (the probability of an acute GVHD diagnosis without death); solid and dashed line is p(2) (the probability of dying carrying a diagnosis of acute GVHD by time t); dashed and dotted line is p(3) (the probability of death without acute GVHD); and dotted line and the value 1 is p(4) (the probability of being alive without acute GVHD). At any time t, Patient A has the lowest risk of death, and Patient B has the highest risk of acute GVHD. Both Patients B and C have a large risk of death; however, the rate of increase differs between the two patients.
Figure 4.
Estimated absolute risk profiles calculated for the first 150 post-transplantation corresponding to three patients (A, B, C) based on proposed finite-interval illness-death model with frailty (FI-IDγ), assuming γ= 1.
We present a graph of the estimated risk profile (conditional on the shared frailty term, γ) for our proposed of Patient C at t=100 for γ = 0.5, 0.6, … , 1.5 in Figure 5). The marginal risk profile for Patient C at t=100 is plotted on the same axes in gray. We see a dramatic increase in the absolute risk of death for increasing values of the shared frailty term, particularly for death without acute GVHD, thereby providing evidence that the shared frailty term accounts for heterogeneity in the data set that is not accounted for by covariates. The estimated marginal absolute risk profile is plotted in gray. We see that the marginal risk profile components align with values of γ between 0.8 and 1.25.
Note that we also estimated joint risk assuming the model from Conlon et al.31 with an added shared frailty. Although the estimated regression coefficients from the Conlon et al. model differed from our proposed model for the HCT → Death transition (2 → 4 in Figure 1) as described in Section 6.2, the estimated absolute risk profiles based on the two models were comparable for this example. This is likely due to the small fraction of individuals who died without acute GVHD within 100 days (10.2%).
7. Discussion
In this paper, we have proposed a novel multi-state model that accounts for mortality through joint modeling of acute GVHD and death, and explicitly acknowledges the finite time scale in which acute GVHD occurs. Estimation was performed using maximum-likelihood estimation by directly maximizing the derived log-likelihood function. This complements the work of Conlon et al.31 and Beesley et al.32 who approached estimation in their multi-state cure models from a Bayesian perspective and using maximum-likelihood via the EM-algorithm, respectively. We conducted a simulation study based on the proposed model, where we compared the estimates from fitting our proposed model to corresponding estimates from: a finite interval multi-state cure model without frailty; the Conlon model (with and without frailty); multi-state illness-death model; and a univariate cure model. Although the interpretation of the regression coefficients of the competing models that we considered may not be comparable, they are models that an analyst might choose to implement in the setting of this problem. Our intention was to compare how the estimated regression coefficients from these other models would compare to the true estimates under our model. Our simulations show that the application of such models to this problem can lead to erroneous conclusions, which likely stem from not accounting for the underlying mixture distribution. This is further supported by our data example where wildly different parameter estimates were observed across the different models considered. Additional simulations we report also suggest that there are instances where results/conclusions will align, suggesting that the finite interval illness-death model may serve as a complement to existing methods. Furthermore, although the ideas in this paper were initially motivated by an on-going collaboration regarding acute GVHD, the central phenomenon that the event of interest is only well defined on a finite interval arises in a broad range of applications. Additional examples include acute respiratory distress syndrome which is characterized by lung injury within one week of lung trauma51; hospital quality of care metrics, including readmission and mortality rates, that focus exclusively on finite post-discharge windows, such as 30 and 90 days52; and high school attrition, only well-defined during the four years leading up to graduation.53 The methods we propose are therefore likely to be applicable in a wide range of settings.
The model presented in Section 3.4 includes a common patient-specific frailty in each of expressions (6) to (9), a specification that is consistent with prior work on illness-death models for semi-competing risks data.17,24 During the review process, one reviewer pointed out that a common patient-specific shared frailty for all transitions can be viewed as a ‘strong assumption.’ While the overall nature of the dependence between T1 and T2 (which is also driven by the interplay of the covariates and the baseline hazard functions) is unconstrained, the formulation of a shared frailty only permits the consideration of positive dependence between hazards. The inclusion of a shared frailty in our data analysis assumes that an individual with a frailty greater than one has a higher risk of both developing acute GVHD (via the hazard) and dying. To mitigate this, one could, in principle, attempt to relax the assumption by permitting different (possibly correlated) frailties in each of the hazards or through allowing a common frailty to impact the various hazard differently.34 Our experience, however, has been that these models are difficult to identify with the observed data. Moreover, our perspective is that we view the specification given by expressions (6) to (9) as a means to acknowledge residual between-subject heterogeneity that is not accounted for by the covariates that are specified in the linear predictors; in practice, depending on the goals of the analysis, it is not clear that analysts will always specify the linear predictors in such a way so that all heterogeneity is captured. With this in mind, while analysts may, of course, choose not to include the frailty, we view their inclusion as a pragmatic strategy to capturing at least some of the residual heterogeneity and, therefore, enhancing the fit of the model to the data.
The definition of the 2→3 transition on (0, τ) aligns with the clinical definition of acute GVHD. That this necessitates the 2→4 transition to be restricted to the (0, τ), however, is not immediately obvious. One approach that provides insight into this is through consideration of the corresponding data generating mechanism. Specifically, at the outcome, the latent susceptibility state is taken to be determined (in the HCT context) immediately after transplantation. If a patient is not susceptible, then they will not experience acute GVHD and time to death would be determined by λ14(·). If a patient is susceptible, then it is presumed that, in the absence of competing risks, the patient will experience the acute GVHD event within (0, τ). This is analogous to what is assumed in standard cure fraction models for patients who are ‘not cured’. To determine which of the two events occurs first, one would generate T1 and T2 from λ23(·) and λ24(·), respectively. If T1 < T2 (i.e. the patient experienced acute GVHD), then their subsequent mortality experience would be generated as a draw from λ34(·) for which there are no restrictions on the value of T2. If T2 < T1 then the patient dies before a diagnosis of acute GVHD; given that acute GVHD must be within (0, τ), it follows that T2 arising from the 2→4 transition must be within (0, τ).
For the most part, we have focused on parametric specifications for the baseline hazard functions. In the literature, a number of authors have proposed methods for non- or semi-parametric specifications.24,25,42 Note that a zero-tail constraint in the semi-parametric cure model literature is often assumed for the purpose of identifiability since information beyond the last observed failure is not observed. This forces the survivor function among the uncured population to zero beyond the last observed failure time and considers censored observations beyond the last observed failure time to be cured.29 Defining the hazard function corresponding to time-to-acute GVHD (nonterminal event) using a truncated distribution on (0, τ) is operationally similar to a zero-tail constraint. However, we are imposing this constraint in a manner that explicitly acknowledges the underlying scientific definition of acute GVHD, which is that acute GVHD can only be diagnosed within 100 days of transplantation. Note that fitting multi-state models, such as the illness-death model, that are specified without a frailty is straightforward, and typically easy to implement. However, when frailties are present, we have found from experience that nonparametric estimation is challenging. While software to implement such frailty models for the latter three references is available, our experience with these methods is that they can be unstable and care is needed to ensure that the global maximum is obtained for the frequentist penalized approach of Joly et al.42 or that the Markov chains have converged for the Bayesian approach of Lee et al.,25 especially in small-to-moderate sample sizes. In contrast, the parametric models we propose are straightforward to fit via maximum likelihood, with the caveat that starting values must be carefully chosen for the Weibull parameterization, as described in Section 4.2. When more flexibility is added to the parameterization of the baseline hazard functions via B-splines, the model fit depends on placement of the internal knots and the B-spline degrees. Beyond this, an appealing benefit of adopting a fully parametric model is that the joint density can be determined on the full support of (T1, T2). Paired with a decision rule, the set of joint absolute risks could be used to classify patients into one of the four joint outcome categories. This is an avenue of research we are currently pursuing.
Supplementary Material
Acknowledgements
The CIBMTR (grant U24-CA076518) provided the clinical data. This paper reflects the opinions of the authors and not that of the CIBMTR nor its funding sources. The authors would like to thank the reviewers and the editor of this journal for their helpful and clarifying suggestions.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: CL and SH were supported by NIH grant R01 CA181360-01. This work contributed to the doctoral dissertation of author CL during her studies at Harvard University.
Footnotes
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Supplemental material
Supplemental material for this article is available online.
References
- 1.Passweg J, Baldomero H, Bader P, et al. Hematopoietic stem cell transplantation in Europe 2014: more than 40,000 transplants annually. Bone Marrow Transplant 2016; 51: 786–792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Choi S, Levine J and Ferrara J. Pathogenesis and management of graft-versus-host disease. Immun Allergy Clin N Am 2010; 30: 75–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Filipovich A, Weisdorf D, Pavletic S, et al. National Institutes of Health consensus development project on criteria for clinical trials in chronic graft-versus-host disease: I. Diagnosis and staging working group report. Biol Blood Marrow Transplant 2005; 11: 945–956. [DOI] [PubMed] [Google Scholar]
- 4.Remberger M, Persson U, Hauzenberger D, et al. An association between human leucocyte antigen alleles and acute and chronic graft-versus-host disease after allogeneic haematopoietic stem cell transplantation. Br J Haematol 2002; 119: 751–759. [DOI] [PubMed] [Google Scholar]
- 5.Urbano-Ispizua A, Rozman C, Pimentel P, et al. Risk factors for acute graft-versus-host disease in patients undergoing transplantation with CD34+selected blood cells from HLA-identical siblings. Blood 2002; 100: 724–727. [DOI] [PubMed] [Google Scholar]
- 6.Levine J, Logan B, Wu J, et al. Acute graft-versus-host disease biomarkers measured during therapy can predict treatment outcomes: a Blood and Marrow Transplant Clinical Trials Network study. Blood 2012; 119: 3854–3860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Holtan S, Verneris M, Schultz K, et al. Circulating angiogenic factors associated with response and survival in patients with acute graft-versus-host disease: results from Blood and Marrow Transplant Clinical Trials Network 0302 and 0802. Biol Blood Marrow Transplant 2015; 21: 1029–1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kaplan E and Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc 1958; 53: 457–481. [Google Scholar]
- 9.Holtan S, DeFor T, Lazaryan A, et al. Composite endpoint of graft-versus-host disease-free, relapse-free survival after allogeneic hematopoietic cell transplantation. Blood 2015; 125: 1333–1338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jazić I, Schrag D, Sargent D, et al. Beyond composite endpoints analysis: semi-competing risks as an underutilized framework for cancer research. J Natl Cancer I 2016; 108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pintilie M Competing risks: a practical perspective. Vol. 58. New York, NY: John Wiley & Sons, 2006. [Google Scholar]
- 12.Baron F, Maris M, Sandmaier B, et al. Graft-versus-tumor effects after allogeneic hematopoietic cell transplantation with nonmyeloablative conditioning. J Support Oncol 2005; 23: 1993–2003. [DOI] [PubMed] [Google Scholar]
- 13.Kim D, Lee N, Lee MH, et al. Vascular endothelial growth factor gene polymorphisms may predict the risk of acute graft-versus-host disease following allogeneic transplantation: preventive effect of vascular endothelial growth factor gene on acute graft-versus-host disease. Biol Blood Marrow Transplant 2008; 14: 1408–1416. [DOI] [PubMed] [Google Scholar]
- 14.Levine J, Logan B, Wu J, et al. Graft-versus-host disease treatment: predictors of survival. Biol Blood Marrow Transplant 2010; 16: 1693–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sorror M, Martin P, Storb R, et al. Pretransplant comorbidities predict severity of acute graft-versus-host disease and subsequent mortality. Blood 2014; 124: 287–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Haneuse S and Lee K. Semi-competing risks data analysis. Circ Cardiovasc Qual Outcomes 2016; 9: 322–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fine J, Jiang H and Chappell R. On semi-competing risks data. Biometrika 2001; 88: 907–919. [Google Scholar]
- 18.Peng L and Fine J. Regression modeling of semicompeting risks data. Biometrics 2007; 63: 96–108. [DOI] [PubMed] [Google Scholar]
- 19.Hsieh JJ, Wang W and Ding A. Regression analysis based on semicompeting risks data. J R Stat Soc B 2008; 70: 3–20. [Google Scholar]
- 20.Lakhal L, Rivest LP and Abdous B. Estimating survival and association in a semicompeting risks model. Biometrics 2008; 64: 180–188. [DOI] [PubMed] [Google Scholar]
- 21.Egleston B, Scharfstein D, Freeman E, et al. Causal inference for non-mortality outcomes in the presence of death. Biostatistics 2007; 8: 526–545. [DOI] [PubMed] [Google Scholar]
- 22.Tchetgen Tchetgen EJ. Identification and estimation of survivor average causal effects. Stat Med 2014; 33: 3601–3628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Putter H, Fiocco M and Geskus R. Tutorial in biostatistics: competing risks and multi-state models. Stat Med 2007; 26: 2389–2430. [DOI] [PubMed] [Google Scholar]
- 24.Xu J, Kalbfleisch J and Tai B. Statistical analysis of illness–death processes and semicompeting risks data. Biometrics 2010; 66: 716–725. [DOI] [PubMed] [Google Scholar]
- 25.Lee KH, Haneuse S, Schrag D, et al. Bayesian semiparametric analysis of semicompeting risks data: investigating hospital readmission after a pancreatic cancer diagnosis. J R Stat Soc C 2015; 64: 253–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Berkson J and Gage R. Survival curve for cancer patients following treatment. J Am Stat Assoc 1952; 47: 501–515. [Google Scholar]
- 27.Farewell V. The use of mixture models for the analysis of survival data with long-term survivors. Biometrics 1982; 38: 1041–1046. [PubMed] [Google Scholar]
- 28.Kuk A and Chen CH. A mixture model combining logistic regression with proportional hazards regression. Biometrika 1992; 79: 531–541. [Google Scholar]
- 29.Sy J and Taylor J. Estimation in a Cox proportional hazards cure model. Biometrics 2000; 56: 227–236. [DOI] [PubMed] [Google Scholar]
- 30.Peng Y and Dear K. A nonparametric mixture model for cure rate estimation. Biometrics 2000; 56: 237–243. [DOI] [PubMed] [Google Scholar]
- 31.Conlon A, Taylor J and Sargent D. Multi-state models for colon cancer recurrence and death with a cured fraction. Stat Med 2014; 33: 1750–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beesley LJ and Taylor JMG. EM algorithms for fitting multistate cure models. Biostatistics 2019; 20: 416–432. DOI: 10.1093/biostatistics/kxy011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wienke A. Frailty models in survival analysis. CRC Press, 2010. [Google Scholar]
- 34.Putter H and van Houwelingen H. Frailties in multi-state models: are they identifiable? Do we need them? Stat Methods Med Res 2015; 24: 675–692. [DOI] [PubMed] [Google Scholar]
- 35.Klein J, Keiding N and Copelan E. Plotting summary predictions in multistate survival models: probabilities of relapse and death in remission for bone marrow transplantation patients. Stat Med 1993; 12: 2315–2332. [DOI] [PubMed] [Google Scholar]
- 36.De Wreede LC, Fiocco M and Putter H. The mstate package for estimation and prediction in non-and semi-parametric multi-state and competing risks models. Comput Meth Prog Bio 2010; 99: 261–274. [DOI] [PubMed] [Google Scholar]
- 37.Cox D. Regression models and life tables (with discussion). J R Stat Soc 1972; 34: 187–220. [Google Scholar]
- 38.Aalen O. A linear regression model for the analysis of life times. Stat Med 1989; 8: 907–925. [DOI] [PubMed] [Google Scholar]
- 39.Wei LJ. The accelerated failure time model: a useful alternative to the Cox regression model in survival analysis. Stat Med 1992; 11: 1871–1879. [DOI] [PubMed] [Google Scholar]
- 40.McCulloch CE and Neuhaus JM. Generalized linear mixed models. In: Armitage P and Colton T (eds) Encyclopedia of Biostatistics. 2005, p. 4. [Google Scholar]
- 41.Davis PJ and Rabinowitz P. Methods of numerical integration. 2nd ed. Courier Corporation, 1987, http://www.sciencedirect.com/science/article/pii/B9780122063602500017. [Google Scholar]
- 42.Joly P, Commenges D and Letenneur L. A penalized likelihood approach for arbitrarily censored and truncated data: application to age-specific incidence of dementia. Biometrics 1998; 54: 185–194. [PubMed] [Google Scholar]
- 43.Lai CD. Generalized Weibull distributions. Berlin, Heidelberg: Springer-Verlag, 2014. [Google Scholar]
- 44.De Boor C A practical guide to splines: Applied statistics. Vol. 27. New York, NY: Springer-Verlag, 1978. [Google Scholar]
- 45.Ferguson T A course in large sample theory. London: Chapman and Hall, 1996. [Google Scholar]
- 46.Nocedal J and Wright S. Numerical optimization. 2nd ed. New York, NY: Springer-Verlag, 2006. [Google Scholar]
- 47.R Core Team. R: A language and environment for statistical computing, 2017, https://www.R-project.org/.
- 48.Lee K, Lee C, Alvares D, et al. SemiCompRisks: Hierarchical models for parametric and semi-parametric analyses of semi-competing risks data, 2019, R package version 3.3, http://CRAN.R-project.org/package=SemiCompRisks.
- 49.Wang W and Yan J. splines2: Regression spline functions and classes too, 2017, https://CRAN.R-project.org/package=splines2.
- 50.Bender R, Augustin T and Blettner M. Generating survival times to simulate Cox proportional hazards models. Stat Med 2005; 24: 1713–1723. [DOI] [PubMed] [Google Scholar]
- 51.Ferguson N, Fan E, Camporota L, et al. The Berlin definition of ARDS: an expanded rationale, justification, and supplementary material. Intens Care Med 2012; 38: 1573–1582. [DOI] [PubMed] [Google Scholar]
- 52.Ash A, Fienberg S, Louis T, et al. Statistical issues in assessing hospital performance. Commissioned by the Committee of Presidents of Statistical Societies for the Centers for Medicare and Medicaid Services. Quantitative Health Sciences Publications and Presentations. Paper 1114. 2012, http://escholarship.umassmed.edu/qhs_pp/1114. [Google Scholar]
- 53.Stillwell R, Sable J and Plotts C. Public school graduates and dropouts from the common core of data: School year 2007–2008 (NCES 2011–312). First look, 2013. Washington DC, USA: National Center for Education Statistics. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.