Best Practices for Binary and Ordinal Data Analyses

Abstract

The measurement of many human traits, states, and disorders begins with a set of items on a questionnaire. The response format for these questions is often simply binary (e.g., yes/no) or ordered (e.g., high, medium or low). During data analysis, these items are frequently summed or used to estimate factor scores. In clinical applications, such assessments are often non-normally distributed in the general population because many respondents are unaffected, and therefore asymptomatic. As a result, in many cases these measures violate the statistical assumptions required for subsequent analyses. To reduce the influence of the non-normality and quasi-continuous assessment, variables are frequently recoded into binary (affected-unaffected) or ordinal (mild-moderate-severe) diagnoses. Ordinal data therefore present challenges at multiple levels of analysis. Categorizing continuous variables into ordered categories typically results in a loss of statistical power, which represents an incentive to the data analyst to assume that the data are normally distributed, even when they are not. Despite prior zeitgeists suggesting that, e.g., variables with more than 10 ordered categories may be regarded as continuous and analyzed as if they were, we show via simulation studies that this is not generally the case. In particular, using Pearson product-moment correlations instead of maximum likelihood estimates of polychoric correlations biases the estimated correlations towards zero. This bias is especially severe when a plurality of the observations fall into a single observed category, such as a score of zero. By contrast, estimating the ordinal correlation by maximum likelihood yields no estimation bias, although standard errors are (appropriately) larger. We also illustrate how odds ratios depend critically on the proportion or prevalence of affected individuals in the population, and therefore are sub-optimal for studies where comparisons of association metrics are needed. Finally, we extend these analyses to the classical twin model and demonstrate that treating binary data as continuous will underestimate genetic and common environmental variance components, and overestimate unique environment (residual) variance. These biases increase as prevalence declines. While modeling ordinal data appropriately may be more computationally intensive and time consuming, failing to do so will likely yield biased correlations and biased parameter estimates from modeling them.

Introduction

Measurement instruments are essential for scientific study in almost all domains. Many physical traits can be directly measured on interval-level or ratio-level scales, (such as temperature in Celsius or distance respectively), where the interval between values is constant and meaningful. For most behavioral and psychological variables, this level of precision rarely exists. Psychological and behavioral constructs are often assessed with a set of binary (e.g. yes/no) or ordinal (e.g. high, medium or low) questions. Quantifying behaviors and mental states with these relatively crude instruments has obviously yielded many insights into the etiology and epidemiology of human traits, but this does not mean that current practices cannot be improved. Ordinal-level measures require different analytical strategies from those used for continuous, normally distributed traits (Flora & Curran, 2004). Unfortunately, although there are well-established methods for analyzing such data, they seem frequently ignored because their use takes more human and computer time, which results in delays in manuscript preparation, submission, and publication. This excuse has worn thin over the last several decades, as innovations in computer hardware and software have enormously improved the efficiency and simplicity of statistical analysis. The application of suboptimal statistical approaches for the purposes of speed is now unjustified in many (but not all) cases. It is especially important to use optimal methods in the analysis of behavioral and psychological data, because the measures of interest are frequently ordinal and the effect sizes may be small. The mis-application of methods for continuous data may result in biased estimates with incorrect standard errors resulting in dubious inferences about the observed phenomena. Ideally, the methods used should yield effect size estimates that are unbiased and which have the smallest standard errors (a.k.a. minimum variance). Much has been written about the bias-variance trade-off, which we won’t reiterate here. We focus on the precision-laziness trade-off in the application of methods to assess associations.

In the following sections, we present simulation studies which show that treating ordinal variables as continuous biases correlations between them towards zero. This problem applies to correlations between different variables, repeated measures over time, and those from relatives. The direction of the bias is towards a higher Type II error rate, i.e., accepting the null hypothesis of zero correlation when the alternative hypothesis is correct. In a genome-wide association study (GWAS) loci may be thought irrelevant when they are not. In a classical twin study, estimates of additive genetic and common environment variation will be biased towards zero (Curnow, 1972; Smith, 1970). As will be shown, these problems are exacerbated when binary outcomes of interest (or particular item responses) are rare in the population. Appropriate methods, by contrast, eliminate this issue.

The Liability-Threshold Model

Statistical analyses usually begin by considering the level of measurement of the variables being analyzed: continuous (ratio and interval), ordinal, binary, or nominal. Statistical inferences are predicated on the valid and accurate estimation of the correlations between these variables. In selecting an analytical strategy, the analyst is faced with competing motivations. One motivation is to get the most accurate estimates of model parameters. The other is to get estimates as quickly as possible. Because continuous analytical methods are typically faster, there is a natural temptation to treat ordinal data as if they were continuous. Doing so, however, involves hoping that continuous analytical techniques are robust to the ordinal variables’ violations of the distributional assumptions. While it is generally understood that such violations can bias the estimates of the associations between variables, exactly how much it does is often unknown. An aim of this article is to quantify this bias for some representative situations.

Before it is possible to discuss the correlations between ordinal variables, or between ordinal and continuous variables, it is necessary to establish how the variables were collected, and what mechanisms gave rise to their distribution. As it is often impossible to directly measure a psychological trait, researchers typically ask respondents simple questions and provide a set of ordinal response options to simplify and standardize these answers across individuals. For data analysis, the observed binary or ordinal responses are assumed to be imperfect ordered classifications of an underlying (but unmeasurable) normally distributed liability. This assumption is the basis for the Liability Threshold Model (Gottesman & Shields, 1967).

The basis for assuming that the liability is normally distributed is that most human traits are very complex, arising from exposure to an almost infinite number of independent increasing and decreasing causal factors, including single nucleotide polymorphisms (SNPs), personal experiences, dietary intake, interpersonal interactions, life events and exposures to pathogens. This assumption is consistent with results from GWAS, which have consistently shown that most complex traits are highly polygenic (Boyle, Li, & Pritchard, 2017). The Central Limit Theorem states that the aggregation of an infinite number of effects of equal size will generate a normal distribution. Further developments of the theorem suggest that it holds even when the effects vary in size (Lehmann, 1998), which the results of GWAS to date suggest is the case for almost all human traits.

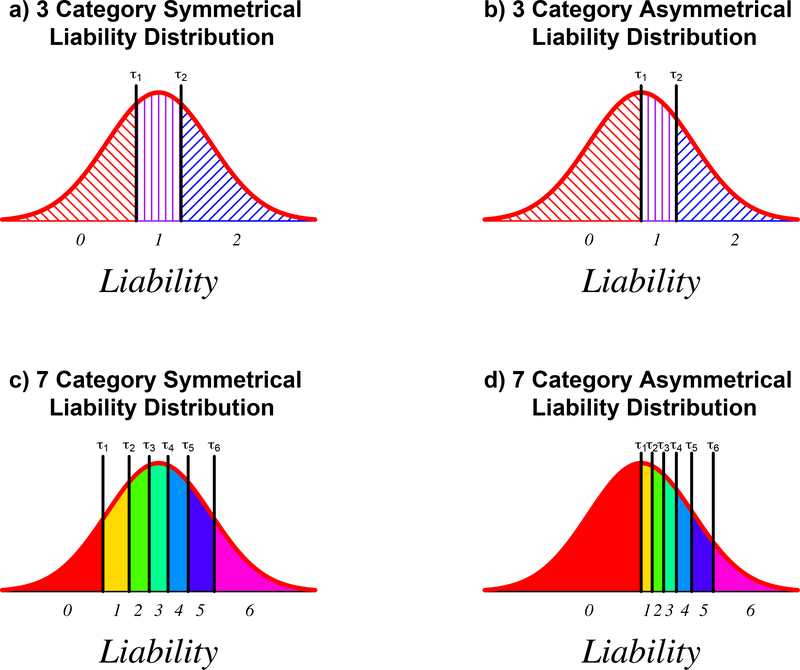
We present schematic depictions of the Liability Threshold Model in Figure 1. Figure 1a shows the density of the normal distribution of the liability with two thresholds placed at tertiles, and Figure 1b illustrates a similar but asymmetric case. Scores of 0, 1 and 2 may be assigned to the ordered categories in both cases, but they differ in several important respects. In Figure 1a phenotypic variation is spread equally across each category, whereas in Figure 1b half of the variation is in the lowest category, and the rest of the variation is equally split between the remaining two categories. As the proportion of the distribution that is captured by a specific response category increases, less is known about individuals with that value. This increase in uncertainty, decreases statistical power. While the number and distribution of ordinal categories may vary, the size of the largest subcategory is usually a good predictor of statistical power, as we show below.

Figure 1.

Threshold models illustrating (upper row) symmetric and asymmetric threshold placements which divide the distribution into equal thirds (left panel) or one-half and two fourths (right panel). The lower two figures show threshold placements for a symmetric (left panel), and asymmetric (right panel) seven-category ordinal variable (left panel). In the symmetric case, the same proportion of individuals fall into each category. For the asymmetric liability, one-half of the distribution falls below the first threshold, and the remainder are divided into six equiprobable ranges. Digits below the x-axis indicate the ordered category number or “score” for that region of the distribution. Note: τ₁ and τ₂ denote the two thresholds in the trinary case, and τ₁ - τ₆ the first and last threshold in the 7-ordered-category case.

Using the Liability Threshold Model to deal with ordinal variables has several advantages. Primarily, the univariate normal distribution directly generalizes to the multivariate case, whereas many categorical distributions do not (Teugels, 1990). Therefore, by assuming that the liabilities for all the variables in the model are normally distributed, it is possible to assume multivariate normality as is required for most analyses. By utilizing the liability threshold model, binary and ordinal variables, or other items with different levels of measurement, may be analyzed jointly (Pritikin, Brick, & Neale, 2018).

Once assumptions have been made about the univariate distributions of the constituent variables, it is possible to discuss the correlations between the variables. There are many different ways to measure correlation, so it is essential to select one that matches the variables’ levels of measurement. In practice, good matching does not always occur. Instead, the pressures for rapid analyses takes precedence over statistical accuracy. The Pearson product-moment correlation is very rapid to calculate, but is only well-suited for continuous, normally distributed data. With ordinal data, other types of correlation (such as biserial, point-biserial, polychoric, tetrachoric, and others) may be more appropriate. Specifically, when both variables are ordinal, numerical integration can be used to estimate the expected proportion of observations in each cell of the multivariate contingency table, and can be directly extended to cases involving both continuous and ordinal measures (Pritikin et al., 2018). With a limited number of ordinal variables, numerical integration is fairly rapid, but as the number of variables increases, computer time increases exponentially, making it impractical to analyze more than a dozen or so ordinal measures (e.g. 6 ordinal phenotypes per twin in a classical twin study or 3 ordinal phenotypes per family member in a nuclear family design).

In an ideal situation, Full Information Maximum likelihood (FIML) is usually the best (i.e. minimum variance of the estimates), unbiased estimation method, as it conveniently handles many patterns of missing data, and can do so very robustly. ML estimation of correlations for continuous variables is, however, much slower than using the product-moment correlation formula. Modern computers are so fast that the difference is almost imperceptible for most practical purposes except in very large scale applications, such as neuroimaging or simulation studies. For some models, short-cuts such as the Bock-Aiken marginal maximum likelihood (Bock & Aitkin, 1981) can be used – as is the practice with many item response theory applications (Chalmers, 2012), but there is no general solution, especially for non-recursive models (i.e. models with feedback loops). Weighted least squares (WLS; Browne, 1984) is a practical and high-speed alternative, available in most software packages, and one that can handle combinations of ordinal and continuous data. Unfortunately, WLS requires very large sample sizes to accurately estimate the weight matrix when the number of variables is large, and is biased when data are missing at random (as is common in data collection with skip out patterns or conditional branching; Pritikin et al., 2018). The aim here is not to provide a comprehensive review or a comparison between the types correlations, which can be found elsewhere (see Agresti, 1990 or Long, 1997), but to directly examine the impact of using the product-moment method when at least one of the variables in the analysis is not continuous.

Methods

When learning about ordinal data, students in methodology classes may ask, “how many categories are enough to treat a variable as continuous?” Instructors typically avoid answering this question directly, or use some esoteric or personal rule of thumb to provide a less-than-satisfying answer. In part, this is because the number of categories per se may have little effect on bias: more important is the placement of the thresholds along the liability distribution. We therefore compare use of the product-moment correlation to maximum likelihood estimates, when either one or both variables is ordinal. To allow the reader to explore correlations and threshold placements other than those considered in this article, we provide a general R function on GitHub (https://github.com/bradverhulst/OrdinalData).

Product-moment correlations between ordinal variables

For the first study, we simulate data with 1,000 rows of two continuous variables that correlate r = .70. Both variables are then re-coded into ordinal variables, according to whether the continuous values are above and below the specified thresholds (see Figure 1). Those below the lowest threshold score zero, and those above the highest threshold score t in there are t thresholds. Polychoric correlations are then estimated using the polycor function in R (Fox, 2019; R Core Team, 2014), and product-moment correlation are calculated using the standard formula:

$$r_{xy}=\frac{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

where $\overline{x}$ denotes the mean of x, and subscript i represents the data from observation i in the sample of i = 1 … n pairs of observations.

Two scenarios are considered: symmetric (equiprobable) and asymmetric (skewed). The symmetric scenario minimizes the proportion of the data in the most frequent category for a given number of thresholds, corresponding to Figures 1a and c. Thus, for the three-category case, $\frac{1}{3}$ of the observations are expected to fall into each category. In the asymmetric scenario, the first threshold is set to zero, and the remaining thresholds divide the upper half of the distribution into equal categories. For example, in the three-category case, the probability of falling into the first category is 0.5, whereas the second and third categories it is 0.25 (see Figure 1b). For each simulated dataset, we estimate the polychoric and the Pearson product-moment correlations. The simulations are repeated 1,000 times to approximate the distributions of the correlations.

Product-moment correlations between binary and continuous variables

A different, lesser degree of bias is expected when one variable is binary ordinal and the other is continuous. By binary ordinal we mean that the categories assess a continuum such as drug use liability (e.g. low vs high), as opposed to unordered categories, (e.g. male vs. female). We examine the Pearson product-moment correlation between continuous and binary variables as a function of the binary variable’s prevalence. To do so, we simulate data for two continuous variables with correlations ranging from .05 to .95, and recode one of the continuous variables into binary variables, using the aforementioned threshold model, with prevalences ranging from .01 to point five. To obtain accurate point estimates, we used a large sample size of 100,000 and repeated every simulation 1,000 times.

Prevalence effects on odds ratios vs. correlations

Odds ratios are favored statistics in many clinical situations. They provide physicians, genetic counselors and others a readily-communicated expression of conditional probability for a patient’s baseline risks, and alterations in their risk due to specific information, such as disease occurence in a relative. While odds ratios have great practical utility in this context, they do a poor job of measuring the degree to which variables are associated or correlated at the liability level. Absent information on base rates, odds ratios may represent widely different degrees of correlation between variables. Here we simply illustrate, using the binary-continuous simulation from the previous section to illustrate how dramatic the divergence between correlation can be as the base rate threshold of the binary variable changes. Two variables are simulated with correlations ranging from .05 to .95, and one is re-coded into an ordered binary variable via the liability threshold model. We vary the position of the threshold, and therefore the ‘base rate’ of the binary variable from .01 to .5. The simulation study was repeated 1000 times and the results averaged to increase the estimates’ precision.

Implications for Twin Models

Correlations play an integral role in twin and family models. As such, biases in the correlations can have profound effects on the estimation of variance components. To examine the effect of treating binary variables as continuous, we simulated a scenario where A, C, and E accounted for 50%, 20%, and 30% of the variance in a phenotype, respectively. This would produce an expected MZ correlation of r_MZ = 0.70, and an expected DZ correlation of r_DZ = 0.45. We used these values to simulate continuous data for each twin, and then recode the continuous variables into binary variables, for prevalences ranging from .01 to .50. In this scenario, the MZ correlations are equivalent with the the binary associations presented in the first simulation study, while the DZ correlations are analogous, albeit at a lower magnitude of association. To calculate the variance components, we use the Holzinger (Falconer) formulas (Newman, Freeman, & Holzinger, 1937), which are equivalent to the direct symmetric matrix approach (Verhulst, Prom-Wormley, Keller, Medland, & Neale, 2019) in this example. The simulation study was repeated 1000 times and the results averaged to increase the estimates’ precision.

Results

Product-moment correlations between ordinal variables

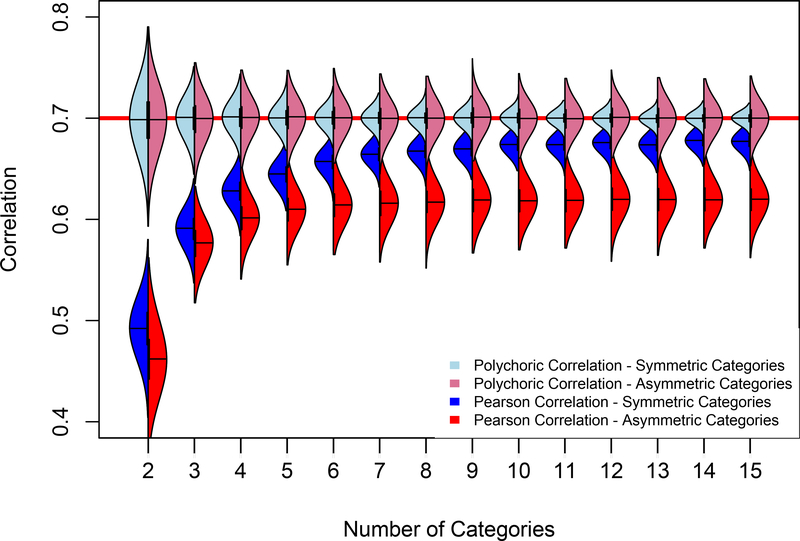
Figure 2 shows how the Pearson correlations change depending on the number of ordinal categories. The red line (at r = 0.70) plots the value of the simulated correlation. As can be seen in the light red and blue densities, the estimated polychoric correlations closely correspond to the simulated value because the model is correct for these data, regardless of the number of categories. Furthermore, when comparing the symmetric and asymmetric polychoric correlations, as shown in the light blue and red densities respectively, the variance of the polychoric correlations decreases as the number of categories increases. This change is a function of the additional categories providing more precise measures of the underlying liability of the trait. In the asymmetric data scenario, shown in the light red density plots of Figure 2, the polychoric correlations show greater variance than in the symmetric case, depicted by the light blue densities. The slower decline in the variance of polychoric correlations for the asymmetric thresholds is a function of the imprecise information about individuals in the most frequently endorsed category.

Figure 2.

Violin plots of the distributions of estimated polychoric and Pearson product-moment correlations as a function of the number and patterning of ordinal categories. Light blue and light red densities present the estimated polychoric correlations and the dark blue and dark red densities depict the Pearson product-moment correlations for the evenly-spaced and skewed ordinal categories, respectively. The red line at r = .7 represents the simulated correlation. For the skewed categories, the first threshold was set at the median, and the subsequent categories were evenly spaced along the remainder of the distribution. In the two group condition, the threshold was set at a prevalence of .25.

In contrast to the polychoric correlations, the means of the distribution of product-moment correlations increase as the number of categories increases, but the distribution of these correlations seem to asymptote at a value that is lower than the simulated association, even for as many as 15 thresholds. The effect is much more pronounced for asymmetric than symmetric threshold placement.

Product-moment correlations between continuous and binary variables.

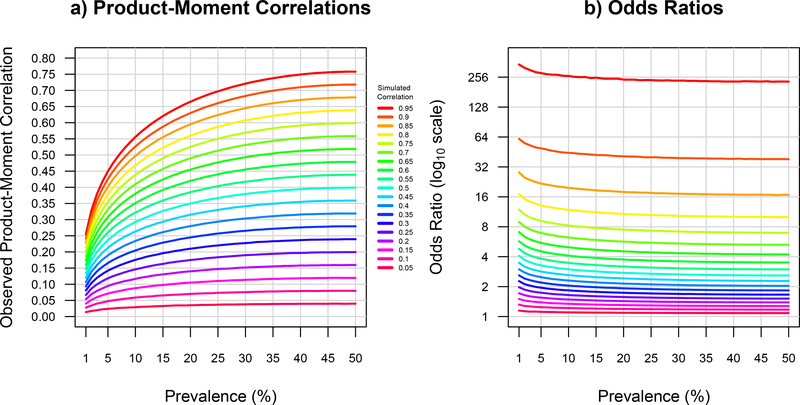
The left part of Figure 3 shows the results of the product-moment correlations for continuous-binary data simulation. Consistent with the first study, the estimated Pearson product-moment correlations are consistently lower than the simulated values and decline as the prevalence of the binary variable approaches 1%, while the point-biserial correlations stays constant at the simulated value across the range of prevalences of the binary variable. For each simulated correlation, there is approximately 20% bias towards zero of the product moment correlation, even in the best case scenario where the prevalence is $\frac{1}{2}$. This bias slowly increases as the prevalence moves from .5 to .2, and increases rapidly at lower prevalences. For example, where the correlation was simulated at .7, the Pearson product-moment correlation decreases from r ≈ .55 to r ≈ .5 as the prevalence decreases from .5 to .2, and then down to r ≈ .2 as the prevalence goes from .2 to .01. The prevalence of most psychiatric and substance use disorders is in the .2 to .01 range, where the bias in the product-moment correlation is particularly severe. Thus, if we simulate two continuous variables with correlation r = .7, and re-coded just one of the variables to have a prevalence of 1%, a threshold model maximum likelihood estimate of the correlation would accurately recover r = .7, whereas the product-moment correlation of r = .19 would be a terrible underestimate.

Figure 3.

A graphical presentation of the estimated Pearson product-moment correlations and odds ratios between continuous and binary variables as a function of the prevalence of the binary variables decreases. Panel a) depicts the downward bias of the mean estimated product-moment correlations between a continuous and binary variable for simulated correlations ranging from r = 0.05 through r = 0.95 as the prevalence of the binary trait increases from 0.01 to 0.50. Panel b) depicts the mean estimated odds ratio on a log₁₀ scale for the same data as the simulated correlations ranging from r = 0.05 through r = 0.95 as the prevalence of the binary trait increases from 0.01 to 0.50.

Prevalence effects on odds ratios vs. correlations

The right panel of Figure 3 plots, on a log scale, the odds ratio of binary data for the simulated correlations ranging from .05 to .95 in the left panel of the figure. Conversely to what was observed with the product-moment correlations, in the same data, as the prevalence decreases, the odds ratio increases. Specifically, for a simulated correlation of r = .3, when the prevalence is .5, the odds ratio is approximately 1.65, but as the prevalence decreases to .01 (holding the point-biserial correlation constant), the odds ratio increases to 2.28. The fact that the odds ratio can represent a broad range of point-biserial correlations depending on the prevalence of the ordinal trait can be directly observed in Figure 3. For example, an odds ratio of 2 describes a point-biserial correlation of r ≈ 0.20 with the prevalence is approximately 1%, a point-biserial correlation of r ≈ 0.25 with the prevalence is approximately 4%, a point-biserial correlation of r ≈ 0.30 with the prevalence is approximately 10–15%, and a point-biserial correlation of r ≈ 0.35 with the prevalence is greater than approximately 35%. These results are consistent with those of Table 2 in Smith (Smith, 1974). Accordingly, relying solely on the odds ratio without information regarding the prevalence of the outcome could lead to very different conclusions about the degree of association, even when the underlying correlation between two variables is constant.

Implications for Twin Models

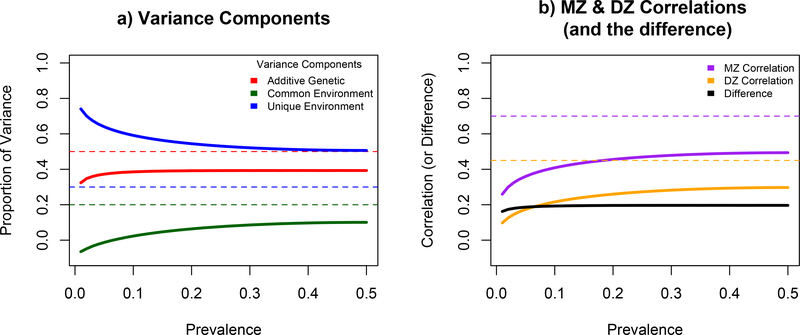
Figure 4 presents the biasing impact of treating binary variables as continuous variables on estimated variance components from a classical twin model. Consistent with the results from the previous simulation studies that focused exclusively on estimated correlations, the estimated additive genetic (A), common environmental (C), and unique environmental (E) variance components deviate from their simulated values when binary variables are erroneously treated as continuous. Collapsing across phenotypic prevalence, the E variance is overestimated while the A and C variances are underestimated. This is what would be expected if the correlations between monozygotic (MZ) twins are underestimated (as 1 − r_MZ is an estimate of E). Interestingly, as the prevalence decreases from .50 to .01 the biases in the variance components are exponentially amplified.

Figure 4.

Plots of a) the simulated and estimated variance components, and b) the simulated and estimated MZ and DZ correlations, as a function of phenotypic prevalence treating the binary phenotypes as continuous. In panel a) the dashed red, blue, and green lines represent the simulated A, C, and E variance components and the color-matched solid lines represent the estimated values of the variance components. In panel b) the dashed purple and orange lines represent the simulated MZ and DZ correlations and the color-matched solid lines represent the estimated correlations. The black line represents the difference between the MZ and DZ correlation at the specified phenotypic prevalence.

The most pronounced amplification effect occurs for the common environmental variance component, which begins to decreases exponentially as soon as the phenotypic prevalence deviates from .50. Notably, at rare prevalences, the estimate of C goes negative suggesting genetic dominance would explain a proportion of variance in the phenotype under these conditions (see Verhulst et al., 2019 for a discussion of negative variance components in twin models). Similarly, but to a much lesser extent, the proportion additive genetic variance stays generally constant between the prevalence range of .50 and .05, but at rare prevalences, the additive genetic variance component also begins to decrease exponentially. The (exponential) underestimation of the A and C variance components is mirrored and compounded by an exponential increase in the unique environmental variance component.

It is instructive to examine the observed MZ and DZ correlations to illuminate the mathematical mechanisms that result in the observed biases in the variance components. For both the MZ and DZ correlations, as the prevalence of the phenotype decreases, magnitude of the correlation declines. Notably, the difference between the correlations remains fairly constant if the phenotypic prevalence is greater than .05. Accordingly, the additive genetic variance component appears correspondingly stable for this prevalence range. Because both the MZ and DZ correlations steadily decrease with the phenotypic prevalence (even though the ratio of the MZ:DZ correlations in constant for more prevalent phenotypes), we observe decreases in the shared environmental variance component at comparatively lower levels of prevalence.

Discussion

Our primary aim was to explore and quantify some of the effects of using the quick-to-calculate Pearson product-moment correlation when data are binary/ordinal. Across the four simulation studies, we found that the product-moment correlations were consistently biased towards zero, while estimates of the correlations that accounted for the ordinal distributions of the variables conformed with the original simulated correlations. While the direction of the bias was unsurprising, the magnitude of the bias was considerable in many cases. If correlations are biased, then the parameters, such as variance components or factor loadings, that are based on those correlations are very likely to be biased as well. As such, any bias in the estimated correlations are likely to undermine the parameter estimates from all types of covariance modeling (from factor analysis to basic linear regression), inflate Type II error rates by underestimating associations, and deflating model fit statistics. Moreover, the consequences of using product-moment correlations if there is a large group of observations with the same ordinal value are even more serious (e.g., a preponderance of asymptomatic persons in the study of a disorder). While there was a notable bias in the symmetric ordinal analyses, the bias was exaggerated when thresholds were unevenly distributed as is the case when the prevalence of a trait is relatively rare. For example, if the first threshold on the liability scale captures a large proportion of observations, differentiating those who score zero from those scoring more may leave a large portion of the distribution completely undifferentiated. In this case, the downward bias of the correlation caused by treating ordinal variables as continuous is much greater, consistent with the prediction that the proportion of individuals in the largest category is the primary driver of the phenomenon.

The results of the simulation studies emphasize the necessity of appropriately analyzing ordinal data. Blindly utilizing analytical techniques designed for continuous variables will lead to severe underestimates of correlations and risk drawing dramatically different conclusions about the magnitudes of their effect sizes, resulting in an inflation of false negatives (Type II errors). The problem of underestimation is not, of course, new. It has been recognized for years, and formulas exist for calculating biserial and point-biserial correlations which temper the bias (Glass & Hopkins, 1995). While these methods are mainstream, they tend to be applied in narrow contexts, where only a few correlation methods are used. In multivariate analyses, such as structural equation or network modeling, their use seems little to none. This represents an opportunity to improve methodology.

Results of the final simulation study have direct implications for twin and family studies. The computational demands of structural equation modeling substantially increase when analyzing ordinal data. Full information maximum likelihood requires integrating over the number of variables per person (p), but in family data this number is multiplied by the number of relatives in the largest pedigree. Therefore this method rapidly becomes intractable. Unfortunately, treating ordinal variables as continuous to make the analysis practical in finite time would underestimate the MZ and DZ twin correlations. In turn, these lower correlations will reduce the estimates of the additive genetic and common environmental variance components and increase those of non-shared environmental variation. Higher correlations incur somewhat more bias than lower ones, but this increase does not approach the 2:1 expectation of additive genetic variation. As a result, the the proportion of variance attributed to the common environment is heavily biased towards zero, especially when the measures are rarely endorsed.

While we used a classical twin model to illustrate the impact of treating binary data as continuous, these results are equally applicable to more complex multivariate genetic models such as common and independent pathway models (Martin & Eaves, 1977). Greater model complexity and more variables increase computation time and as a result increases the temptation to use analytical “shortcuts”. Structural equation modeling software such as OpenMx (Boker et al., 2011; Neale et al., 2016) can estimate correlations among ordinal variables by maximum likelihood in a pairwise fashion, and compute a weight matrix across all variables suitable for WLS or WLSMV analyses, which is substantially faster than FIML. Unfortunately, family structures vary and the number of missing data patterns increases exponentially with family size, tempering the attractiveness of the faster weighted least squares methods. Further, larger pedigree sizes and more variables per individual may generate unstable weight matrices and inaccurate parameter estimates and standard errors. The problem may be exacerbated further if the study involves repeated measures over time, which vastly increases the number of observed variables. In these circumstances it may be better to use diagonally weighted least squares (DWLS), even though this approach ignores the fact that the statistics in a covariance or correlation matrix may violate the independent and identically distributed (IID) assumptions. In OpenMx, DWLS can be based on correlations estimated by maximum likelihood two variables at a time, from which the full correlation matrix is reconstructed. A disadvantage to this method is that the constructed covariance matrix, the weight matrix, or both may be non-positive definite.

The downward bias that results from treating ordinal variables as continuous also has implications for GWAS. Many GWAS software packages can handle binary data such as those from case-control studies. However, to our knowledge GW-SEM (Pritikin, Neale, Prom-Wormley, Clark, & Verhulst, Under Review; Verhulst, Maes, & Neale, 2017) is the only software package that can conduct GWAS with ordinal dependent variables under the liability threshold model. As many psychiatric traits are measured with ordinal scales, researchers are often forced to either treat the ordinal variables as continuous, which decreases the magnitude of the correlation, or recode the ordinal variables into a binary variables, which inflates the standard errors and reduces the power to detect significant associations. While treating ordinal data properly within a GWAS context may be more computational demanding, it is a relatively easy way to increase the accuracy and power of GWAS signals.

The third simulation study, comparing odds ratios to correlations illustrates that a correlation in liability can correspond to a wide range of odds ratios, depending on the population prevalence. This issue is not new (see Smith, 1974), but it bears repeating here in diagram form. That odds ratios by themselves tell us little to nothing about correlation is understood, but it is not unusual to see different odds ratios compared as if they were on a constant metric. The mere presentation of a table of odds ratios (to unfairly pick one example see Neuman et al., 2001) can invite comparisons and tempt readers to draw inferences about varying degrees of association. However, this clearly must not be done when prevalences or base rates differ. In our opinion, odds ratios should only be used to communicate risks to a patient. Absent information about base rates, odds ratios should not be used to measure association, nor be used to infer, e.g., genetic or environmental causes of variation. Correlation remains the coin of the realm for non-experimental research purposes. While correlation does not necessarily imply causation, it is important to understand mechanisms that generate correlation.

While it is commonplace to assume that the underlying liability of ordinal variables follows a multivariate normal distribution, this assumption may be violated in some situations. Faced with two binary variables, there is no information to test whether the resulting contingency table of responses is consistent with the assumption that the underlying distribution is bivariate normal. However, for measures with at least three ordered categories, it becomes possible to test for non-normality of the underlying distribution by comparing the likelihood of the threshold model to that of a saturated multinomial, where each cell’s observed proportion is its expected proportion (Jöreskog & Sörbom, 1993; Mehta, Neale, & Flay, 2004). Wherever possible, measurement instruments for behavior genetic and other studies should be designed with at least three-category response formats.

Finally, in this article we only consider the adverse effects of treating ordinal variables as continuous measures on the estimated correlations. We did not consider the effects of analyzing ordinal variables as if they were continuous on the standard errors, likelihood-ratio tests and goodness-of-fit statistics. Incorrectly treating ordinal data as continuous will typically underestimate both the correlations, as we show here, and the standard errors of these statistics. Some recovery of the standard error estimates may be achieved by using robust standard errors (Huber, 1967; White, 1980), but issues of underestimating the correlations remain. Correlations near zero have larger standard errors than those further away, so loss of statistical power may also be expected by inappropriate use of the data at hand (Fisher, 1915, 1921). Overestimating the measurement precision (and having it vary across the scale) disrupts the likelihood of the data, which in turn makes almost all goodness-of-fit statistics and inferences invalid. These reasons seem sufficient to recommend that treating ordinal as continuous data should be abandoned.

Broader Implications for the Analysis of Ordinal Variables.

Several practical issues regarding the analysis of ordinal variables beyond the incorrect use of product-moment correlations remain. First, when multiple correlated ordinal items are aggregated into a psychological scale, with each item corresponding with liability threshold distribution in Figure 1a, we observe a symmetrical distribution, though not necessarily a normal distribution. As the correlation between items increases, we begin to see an overabundance of the scores in the upper and lower tails. By contrast, if the ordinal categories are asymmetrical so that they correspond with liability threshold distribution in Figure 1b, we observe a skewed distribution of an aggregate scale. As the correlation between the asymmetrical items increases, we observe an overabundance of the scores in the upper tail of the distribution producing the reverse J-shaped distribution that is characteristic of many psychiatric disorder sum-scores. As the number of categories increase, the distinction between the symmetric and asymmetric conditions becomes more striking. Analyzing non-normally distributed sum scores, or estimated factor scores, with product moment correlations (or similar linear modeling techniques) violates the distributional assumptions and therefore is not optimal (van den Oord et al., 2000), even though it is common practice for many psychological assessments. While researchers frequently categorize sum-scores with a reverse J-shaped distribution into three-category ordinal variables, this is only a partial solution that does not address the underlying data-generating mechanism (van den Oord et al., 2000). The problems involved with the reverse J-shaped distribution arising from summing difficult (unlikely to be endorsed) items can be entirely avoided by specifying a structural equation model where the ordinal items, treated properly, are indicators of a latent factor.

Second, it is well established that continuous methods are more statistically powerful than their ordinal analoges, ceteris paribus. The distribution of the parameter estimates from ordinal analytical methods have markedly more variance (and thus larger standard errors) and require larger sample sizes to achieve the same degree of statistical precision. The problem we highlight, however, is that using continuous analytical methods with ordinal data will bias the parameter estimates towards zero. In the current context, the unbiased ordinal data estimates of correlation have larger standard errors than the biased Pearson ones. While larger sample sizes are required to obtain ordinal correlation estimates that are as precise as their continuous counterparts, the trade-off of less bias but greater variance seems essential for studying resemblance between ordinal measures.

Finally, while we strongly believe that statistical precision should be a goal of any empirical analysis, it is necessary to admit that it is impractical to use full information maximum likelihood with more than about a dozen ordinal variables in a single model, even after considering advances in modern computing. In this situation, users will often extract one or more factor scores for further analysis: two quasi-continuous measures on five occasions are much easier to analyze than a dozen ordinal items on each occasion, but the issues we highlight with the analyses remain. One hopes that the scales are tested for measurement invariance across occasions, after which analyses of the factor scores may proceed. Unfortunately, factor scores are not ‘born equal’; they may vary in their measurement precision across the scale. For example, many clinical measures do a good job of distinguishing persons at the clinically relevant end of the scale, but do very poorly at the other end of the scale. Worse yet, tests for phenomena such as gene-environment (GxE) interactions may result in false positives or false negatives, because variables correlate differently across the liability scale (L. Eaves, 2017). A potential solution to this problem is to use the corresponding test information scores as a moderator of the residual error of each individual’s score. This method can be implemented in open source software such as OpenMx (Boker et al., 2011; Neale et al., 2016), and may help to distinguish between genuine GxE interactions and methodological artifacts (L. Eaves & Verhulst, 2014).

Conclusion

Most researchers are aware that ordinal and continuous data require different statistical methods. However, due to computational difficulties involved in applying some of these alternative techniques, methods for continuous data may be used in an “off-label” fashion. Our simulation studies show that inappropriate application of continuous data methods to binary and ordinal data can seriously underestimate correlations. This bias towards zero can reduce statistical power to detect associations, and can lead to errors of inference, primarily Type II, i.e., accepting the null hypothesis when it is false. Modern methods for ordinal data – either FIML or WLS – can help avoid both biased estimates and errors of inference.

Our simulation studies support our conclusions, but they are far from comprehensive. Many other scenarios could be simulated, but the main points remain unchanged. For those interested in knowing the bias generated by treating ordinal variables as continuous for their specific application, we provide R (R Core Team, 2014) functions for this purpose on our GitHub page (https://github.com/bradverhulst/OrdinalData).