Abstract
There is a long history of fitting biometrical structural-equation models (SEMs) in the pregenomic behavioral-genetics literature of twin, family, and adoption studies. Recently, a method has emerged for estimating biometrical variance-covariance components based not upon the expected degree of genetic resemblance among relatives, but upon the observed degree of genetic resemblance among unrelated individuals for whom genome-wide genotypes are available—genomic-relatedness-matrix restricted maximum-likelihood (GREML). However, most existing GREML software is concerned with quickly and efficiently estimating heritability coefficients, genetic correlations, and so on, rather than with allowing the user to fit SEMs to multitrait samples of genotyped participants. We therefore introduce a feature in the OpenMx package, “mxGREML”, designed to fit the biometrical SEMs from the pregenomic era in present-day genomic study designs. We explain the additional functionality this new feature has brought to OpenMx, and how the new functionality works. We provide an illustrative example of its use. We discuss the feature’s current limitations, and our plans for its further development.
The intellectual tradition of pre-genomic twin, family, and adoption studies has a history of applying structural models to longitudinal and/or multitrait datasets in order to answer research questions that require more than estimation of genetic correlations and heritabilities (e.g., Neale & Cardon, 1992; Kendler, et al., 1999; Purcell, 2002; Keller et al., 2009; Posthuma, 2009; van Dongen, et al., 2012; Gillespie, et al., 2015). Classically, these structural models have ranged from direct comparison of phenotypic correlations among monozygotic and dizygotic twins, to ordinary least squares regression (e.g., DeFries-Fulker regression; DeFries & Fulker, 1985), to multitrait structural equation models. More recently, measured-genome methods have seen marked developments. Core among the measured-genome methods is a variation on mixed effects models wherein the entire sample forms a single genetically related cluster. This paper chiefly concerns the implementation of genomic-relatedness-matrix restricted maximum likelihood (GREML; Benjamin et al., 2012) in the broader context of multitrait models.
Genomic-relatedness-matrix restricted maximum likelihood refers to the statistical method that estimates the amount of variance in one or more phenotypes that is attributable to a collection of observed genetic polymorphisms. The method is so named because it models phenotypic similarity among individuals in terms of one or more genomic-relatedness matrices (GRMs, described below), and estimates such models via restricted maximum likelihood. GREML was first implemented in the software GCTA (Yang, Lee, et al., 2011; Yang, Lee, et al., 2013), and studies using it have shown that common single-nucleotide polymorphisms (SNPs) can account for a substantial proportion of variance in complex human traits such as height (e.g., Yang, Benyamin, et al., 2010; Wainschtein et al., 2019), general cognitive ability (e.g., Davies et al., 2011; Benyamin et al., 2013; Kirkpatrick et al., 2014), schizophrenia liability (e.g., Lee et al., 2012; Ripke et al., 2013), and susceptibility to type 2 diabetes (e.g., Morris et al., 2012). GREML has also demonstrated that genetic correlations among traits can be inferred from analysis of genomic data (e.g., Lee et al., 2013), and has helped elucidate the relative contributions of rare mutations vis-à-vis common markers (e.g., Gaugler et al., 2014; Wainschtein et al., 2019).
Typically, GREML is applied to a sample of classically unrelated participants who have been genotyped on a genome-wide array of SNPs. It uses at least one genomic-relatedness matrix (GRM) computed from participants’ SNP genotypes. Element i,j of such a GRM represents the pairwise degree of identity-by-state relatedness between participants i and j. In essence, the method calculates how much participants’ phenotypic resemblance corresponds to their genotypic resemblance. Thus, GREML is built upon the same biometrical-genetic foundation as twin and family studies, except that between-person genetic resemblance is derived from observed genotypes, rather than the pedigree-based expectation. The importance of GREML as a research methodology is that it allows estimation of biometrical parameters of interest—such as heritability coefficients, genetic correlations, and genetic and environmental variance components—based upon observed genetic resemblance among participants, and without relying on the assumptions of pregenomic study designs such as twin, family, and adoption studies. However, little effort has been made to enable investigators to use GREML estimation to conduct the structural-equation modeling (SEM), prevalent in the pregenomic literature, in present-day genomic study designs. Aside from our efforts described herein, we are aware of only one other project seeking to combine GRMs and SEM (St Pourcain et al., 2018), which has been applied in studies of head circumference and intracranial volume (Haworth et al., 2019), development of language and literacy skills (Verhoef et al., in press), and cognitive abilities (Shapland et al., 2020).
The present work describes a new feature in OpenMx (Boker et al., 2011; Neale et al., 2016; most recent release as of this writing is v2.18.1), a package for the R statistical computing platform (R Core Team, 2018), that integrates GREML with SEM. Essentially, OpenMx combines matrix operations with numerical optimization, for the purpose of SEM. Here, “SEM” is to be construed broadly, as the capabilities of OpenMx v2.x encompass types of modeling not conventionally regarded as part of the domain of SEM (Neale et al., 2016). OpenMx’s “frontend” is written in R, and consists of object classes and functions with which the user interacts. Typically, the user will construct an R object of class “MxModel,” which instantiates the structural model to be fitted to the data at hand. Then, at runtime, the user “runs” the MxModel, and the computational work of fitting the model takes place in OpenMx’s backend. For performance reasons, the backend is written in compiled C++, C, and Fortran code. The MxModel is then populated with the results from the backend, which are then accessible to the user in the frontend.
“mxGREML” Implementation
A model produced with OpenMx v2.x has four major components. First, there is the data component (for example, an observed covariance matrix, or a table of raw data). Second, there is the expectation, which consists of the minimal pieces of information that would be necessary to simulate data under the model; most currently implemented expectation types constitute a specification of the model-expected mean vector and covariance matrix of the endogenous variables. Third, there is the fitfunction, which is the objective function to be numerically minimized in order to estimate parameters. Fourth, there is the optimizer, which algorithmically minimizes the fitfunction when the model is run. OpenMx offers two open-source gradient-based quasi-Newton optimizers and an open-source Newton-Raphson optimizer; some builds of the package also license a proprietary third gradient-based optimizer. The new GREML feature introduces a GREML expectation, a GREML fitfunction, and a helper function for data-handling. A repository of scripts that demonstrate the capabilities of the mxGREML feature is available at https://github.com/RMKirkpatrick/mxGREMLdemos. Table I describes the scripts available in that repository as of this writing.
Table I.
Example scripts available in online repository.
| Filename | Description | |
|---|---|---|
| 1 | Analytic_vs_numeric_derivs_comparison.R | Optimizes the same “common-pathway” model twice, once with numeric derivatives and once with analytic derivatives, and obtains substantially equivalent results; compares running time and object size. |
| 2 | CommPthwy-VC-fixcomm.R | “Common-pathway” model for 5 traits; variance-components parameterization; variance of common factor is fixed for identification. |
| 3 | CommPthwy-VC-fixcomm-NodV.R | “Common-pathway” model for 5 traits; variance-components parameterization; variance of common factor is fixed for identification; does not use analytic derivatives of V. |
| 4 | Diphenotype_continuous_with_GCTA.R | Fits an unstructured model to two phenotypes; demonstrates how to fit the same model in GCTA, called from within R, and how to load in GCTA’s output file (which gives results substantially equivalent to OpenMx’s). |
| 5 | Factor_demo_with_model_comparison.R | “Common-pathway” model for 3 traits, compared to the saturated model specified with direct-variance parameterization and then with Cholesky parameterization; compares results for the two saturated-model parameterizations. |
| 6 | GREML_biometric_moderation_demo.R | Continuous-moderation model. |
| 7 | GREML_biometric_moderation_demo_nodV.R | Continuous-moderation model; does not use analytic derivatives of V. |
| 8 | GREML_diphenotype_ordinal_demo.R | Models 2 ordinal traits with 3 levels each; parameterized in terms of traits’ observed-scale variance-covariance components. |
| 9 | GREML_diphenotype_ordinal_demo_altparam.R | Models 2 ordinal traits with 3 levels each; parameterized in terms of traits’ latent-scale correlations and variance proportions. |
| 10 | GREML_diphenotype_ordinal_demo_altparam_covariates.R | Models 2 ordinal traits with 3 levels each; parameterized in terms of traits’ latent-scale correlations and variance proportions; adds covariates. |
| 11 | GREML_latent_growth_demo.R | Latent-growth model of one phenotype at 5 timepoints. |
| 12 | GREML_latent_growth_demo_NodV.R | Latent-growth model of one phenotype at 5 timepoints; does not use analytic derivatives of V. |
| 13 | IndePthwy.R | “Independent-pathway” model for 4 traits; variances of common factors are fixed for identification. |
| 14 | IndePthwy_NodV.R | “Independent-pathway” model for 4 traits; variances of common factors are fixed for identification; does not use analytic derivatives of V. |
| 15 | AGES2017/GREML_Factor_demo.R | “Common-pathway” model for 3 traits, with no residual genetic variance; demonstrates how to load data and GRM into R; includes covariates. |
| 16 | AGES2017/GREML_Factor_demo_NodV.R | “Common-pathway” model for 3 traits, with no residual genetic variance; demonstrates how to load data and GRM into R; includes covariates; does not use analytic derivatives of V. |
| 17 | AGES2017/Simple_GREML_demo.R | Single-trait analysis; demonstrates how to load data and GRM into R; includes covariates. |
| 18 | fromTestSuite/GREML_monophenotype_1GRM.R | Single-trait analysis; demonstrates 2 parameterizations; includes covariates; demonstrates how to calculate confidence intervals with a custom compute plan. |
| 19 | fromTestSuite/GREML_monophenotype_1GRM_GradDesc.R | Single-trait analysis; includes covariates; does not use analytic derivatives of V. |
Repository located at https://github.com/RMKirkpatrick/mxGREMLdemos. Table is current as of October 8, 2020; see git tag “201008” in the repository. Filenames and paths are relative to the main directory of the repository. Unless indicated otherwise, scripts use analytic derivatives of the model-expected covariance matrix, V, for optimization. Several scripts have corresponding path diagrams in the Supplementary Appendix.
GREML Expectation
As with all expectations in OpenMx, the GREML expectation consists of the minimal set of information that would be needed to generate data from a model. The GREML model for n people measured on p phenotypes with k covariates (including constants) is effectively
| (1) |
where y is the np vector of phenotypic observations, X is the np × k matrix of covariates (i.e., a design matrix for the fixed effects), b is the k vector of regression coefficients, r is the np vector of random effects (representing, at minimum, a residual term), and V is the np × np covariance matrix across observations, conditional on X. Specifically,
| (2) |
, and specification of V is left to the user. Therefore, the GREML expectation requires the user to provide information about y, X, and V. As suggested by Equation (1), the GREML expectation class is compatible only with raw phenotypic data1. Although OpenMx has support for binary and ordinal-probit (“threshold”) phenotypes, the GREML expectation necessarily treats the phenotypes as continuous2. There should be one row in the dataset per individual. In a typical OpenMx analysis of raw data, the rows of the dataset are assumed to be independent vectors of observations on one or more variables. The key distinguishing feature of an OpenMx analysis using a GREML expectation is that the observations are not assumed to be independent, and indeed, that they may all be mutually dependent of one another. The dependence across rows of data is given by the covariance matrix V. More precisely, after conditioning on X, y is assumed to be a single random draw from a multivariate-normal distribution with covariance matrix V, where V is assumed to contain few, if any, off-diagonal elements equal to zero. The user must provide the GREML expectation with an expression for the model-expected V, the names of the data columns containing the p phenotypes, and the names of the data columns containing the k covariates. S/he may also provide additional arguments related to data-handling (described further below, under “Customization: GREML Fitfunction.”). At runtime, the software will construct the y and X matrices from the specified columns of the raw dataset, subject to any optional data-handling arguments from the user.
Typically, V will be a function of one or more GRMs. OpenMx does not (and is not intended to) calculate GRMs from raw genotypic data. The GRMs must instead be calculated with an appropriate tool, such as GCTA, plink (Purcell et al., 2007), or LDAK (Speed et al., 2013). OpenMx has a function, omxReadGRMBin(), that loads binary-formatted GRMs, calculated with GCTA, into R’s workspace. However, because R’s memory management is far from optimal (Morandat et al., 2012), a newly implemented OpenMx feature can read a text-formatted matrix directly into the OpenMx backend’s memory, bypassing the slower R frontend. In any event, specifying the structure of V is left entirely up to the user, who can define it arbitrarily (within the very wide latitudes afforded by the MxMatrix and MxAlgebra object classes).
Under a GREML expectation, the model for the phenotypic mean is a generalized least-squares regression of y onto X, and thus is y conditioned on the covariates. OpenMx outputs the regression coefficients and their standard errors, and counts them when calculating the model’s degrees-of-freedom, but the coefficients are not considered explicit free parameters of the model object. This is because the optimizer does not directly adjust them in order to minimize a fit function. Instead, once is obtained, the estimates are simply computed via generalized least squares as , which is the maximum-profile-likelihood estimator of β, given (Pawitan, 2013). From a design standpoint, we assumed that users of the new feature would chiefly be interested in the random effects (the parameters in V) rather than the fixed effects3. Furthermore, the optimizer will converge more quickly than it would if the regression coefficients were explicit free parameters.
GREML Fitfunction
The GREML expectation is compatible with the new GREML fitfunction type as well as the pre-existing maximum-likelihood (ML) fitfunction type, both of which are based on the multivariate-normal log-density. In the latter case, OpenMx provides maximum-likelihood estimates of the random-effects parameters, whereas in the former case it provides less-biased restricted maximum-likelihood estimates. By default, OpenMx’s objective functions are minimized using gradient-based quasi-Newton optimizer SLSQP (Kraft, 1994; Johnson, 2020), which numerically approximates their derivatives using finite-differences. However, the user interface to the GREML fitfunction type allows the user some optimization-performance alternatives to this default, described further below, under “Customization: GREML Fitfunction.”
Data-handling
By default, the data-handling function, mxGREMLDataHandler(), is automatically called at runtime for any MxModel using GREML expectation. The data handler assumes that the dataset has one row per individual participant. It extracts the columns of the dataset containing scores on the phenotypes and covariates. It then vertically “stacks” the phenotypes into a single column vector y, and assembles the matrix of covariates, X. Then, it removes rows containing missing values in either y or X from both matrices. The indices of the removed rows are stored by the GREML expectation, so that the corresponding rows and columns of V (and any other matrix required to have the same dimensions as V) can be automatically removed in the backend. Additional details concerning the data-handler are described further below, under “Customization: Data-handling”.
Structural Equation Modeling with GREML
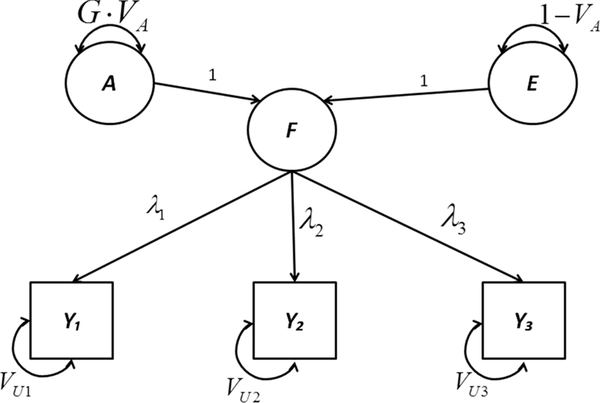
What follows in this section is an intuitive explanation of a particular structural equation model—a phenotypic common-factor model—as fit using GREML. A script that demonstrates fitting this model in OpenMx is available as demo #15 in Table I. Figure 1 depicts the “within-person” portion of this model in path-diagram format. In this model, variance in the three phenotypes y1, y2, and y3 is decomposed into (1) variance common to all three phenotypes, represented by variance in common factor F, and (2) variance unique to each phenotype, denoted by VU1, VU2, and VU3. Parameters λ1, λ2, and λ3 are the loadings of the three phenotypes onto F. The variance in F is itself broken into heritable variance, GVA, and nonshared-environmental variance, 1 − VA, where VA is the additive-genetic variance parameter and G is the individual’s diagonal element of the GRM; in a homogeneous, randomly mating population, the expectation of G is 1.0. Although it is possible to biometrically decompose the unique variance as well, we do not do so here for the sake of simplicity (readers interested in a variation of this model that does biometrically decompose the unique variance are directed to the Supplementary Appendix, and to demos #2 and #3 in Table I). The unknown parameters to be estimated from data are loadings λ1, λ2, and λ3, additive-genetic variance VA, the unique variances VU1, VU2, and VU3, and the three phenotypic means (not made explicit in the diagram).
Figure 1.
Path diagram of phenotypic common-factor model (within-person perspective).
The model portrayed in Figure 1 can also be represented by a system of structural equations. For random individual i,
| (3) |
, where y1i, y2i, and y3i are phenotype scores, λ1, λ2, and λ3 are factor loadings as before, Ai and Ei are respectively scores on biometrical factors A and E, U1i, U2i, and U3iare scores on the three unique factors corresponding to y1i, y2i, and y3i, and μy1, μy2, and μy3 are the three phenotypic means (for ease of demonstration, this model does not condition on any covariates). This system of structural equations could be represented with matrices,
| (4) |
, or more compactly,
| (5) |
. By the Fundamental Theorem of Factor Analysis (Mulaik, 2010), the variance of yi is then
| (6) |
, where:
| (7) |
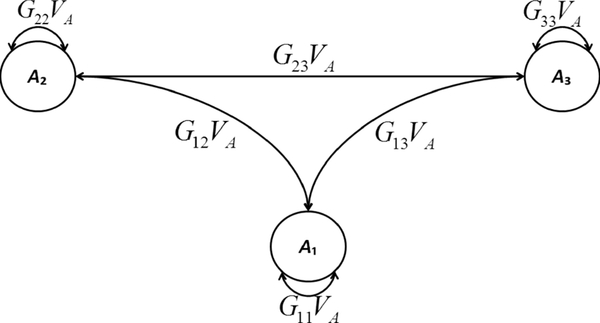
It is important to recognize that additive-genetic component VA is identified due to the between-individual genetic resemblance represented by the GRM, which dictates the covariance structure among individuals’ latent A variables. Figure 2 depicts that covariance structure, for a random sample of three individuals. As in Figure 1, the variance of an individual’s own A equals his/her diagonal GRM element times VA. Further, the covariance between two individuals’ As equals their corresponding off-diagonal GRM element times VA.
Figure 2.
Path diagram depicting the covariance structure among the A (additive-genetic) latent variables of three random participants. Ai, is the A variable of participant i, Gij is element i, j of the GRM, and VA is the additive-genetic variance component..
Although a sample of only three participants would be too small to identify all the unknown parameters of the model, the small sample size makes explication of the model’s specification more accessible to the reader. So, let us consider three random participants J, K, and L. Now, let y denote a 9-element column vector of participants’ stacked phenotype scores, “blocked by phenotype4,” let Λ denote a 9×3 matrix of factor loadings, let A and E denote 3-element column vectors of the three participants’ additive-genetic and nonshared-environmental factor scores, let F = A+E, and let U denote a 9-element column vector of unique-factor scores. That is, after adjusting for fixed effects:
| (8) |
| (9) |
| (10) |
| (11) |
Then:
| (12) |
| (13) |
| (14) |
In practice, for computational reasons, the quadratic form in Λ in (12) is replaced with
| (15) |
The example above illustrates the utility of the mxGREML feature. With the mxGREML feature, the user can (1) specify an arbitrary structure to the covariance across rows of data, and simultaneously (2) specify the covariance structure across multiple phenotypes. In Equation (15), the matrix on the left-hand side of the Kronecker-product operator specifies the covariance across multiple phenotypes according to a factor model, whereas the matrix on the right-hand side of the Kronecker-product operator specifies the covariance across multiple people according to their genetic relatedness. Importantly, the mxGREML feature is not limited to either of these structures. In the first case, the covariance structure across phenotypes could easily have been specified as a latent growth curve with the three phenotypes representing the same phenotype measured on three time points. Moreover, the user is not restricted to factor models or latent growth curves for the covariance across phenotypes. Virtually any covariance structure the user desires is possible. In the second case, the covariance structure across people is also arbitrary. Equation (12) models the covariance across people as a single GRM for additive genetic effects along with a diagonal matrix for unique environmental and residual variance. However, the user could instead easily specify multiple GRMs of arbitrary structure. Technically speaking, the GRMs need not even be computed from genetic data. Rather, any feature that accounts for covariance across people could be used as a “relatedness matrix,” as long as the structure of that matrix is known. Examples of non-genetic sources of covariance across people include but are not limited to data-collection site, geographic location of the person (e.g., postal code), common rearing environment, or even “interviewer effects” that cause individuals assessed by the same data-collector to be more similar than they would be otherwise. Such flexibility in the covariance structure across persons and phenotypes is the major strength and contribution of the mxGREML feature.
User Customization
The flexibility and generality of mxGREML are made possible by user customizations beyond the defaults described above, for the GREML fitfunction and the GREML data-handler. The customizations for the GREML fitfunction pertain to computational performance during optimization of the REML objective function. The customizations for the data-handler allow the user to tailor mxGREMLDataHandler()’s behavior as appropriate for his/her phenotypes and covariates.
Customization: GREML Fitfunction
In a GREML-type model, objective-function evaluations tend to be computationally costly because they involve inversion of a potentially large, non-sparse covariance matrix V. To reduce the number of function evaluations and speed up convergence, the GREML fitfunction backend can, at the user’s option, provide an optimizer with analytic first and second derivatives of the REML objective function with respect to the free parameters. To do so, the fitfunction object requires a user-provided expression for the first partial derivatives of V with respect to all free parameters5 (some worked examples of V’s analytic derivatives are in the Supplementary Appendix). Then, at runtime, the fitfunction’s computational backend analytically calculates the desired partial derivatives of the objective function (i.e., −2 times the restricted loglikelihood) from the user-provided “matrix derivatives” of V. It can be shown (see Supplementary Appendix) that the first and second partial derivatives of the objective at some point in the free-parameter space can be computed from these “matrix derivatives,” plus X, y, and V. That mapping from the derivatives of V to the second (but not the first) derivatives of the objective assumes that V is linear in the free parameters (Johnson & Thompson, 1995; Meyer & Smith, 1996); if the assumption is violated, the GREML fitfunction backend is only able to provide an approximation of the objective’s second derivatives. The specification of V, of course, is arbitrary and entirely up to the user, so the user bears responsibility for correctly analytically differentiating V with respect to the free parameters, so that the objective-function derivatives calculated from V’s derivatives will be correct (or at least approximately correct, for the objective’s second derivatives). However, the proprietary gradient-based optimizer NPSOL (Gill et al., 2001), which the OpenMx development team ships with their builds of the package, can optionally check the gradient it receives from the fitfunction backend against its own numeric gradient.
All three of OpenMx’s gradient-based optimizers can use analytic first derivatives of the objective, whereas OpenMx’s Newton-Raphson optimizer (Neale et al., 2016) uses and requires analytic first and second derivatives. For computational efficiency, the GREML fitfunction backend approximates the matrix of second partial derivatives (the Hessian proper) with the “average-information” matrix (Gilmour, Thompson, & Cullis, 1995), which is the observed information matrix plus the expected information matrix, divided by 2. The average information matrix can also be used in place of the Hessian proper for calculating standard errors on parameter estimates.
Additionally, if multiple CPU threads are available to OpenMx, the GREML fitfunction backend will distribute across threads the calculation of the objective-function derivatives from the matrix derivatives of V. If the average-information matrix is to be calculated, the backend uses a “greedy algorithm” to load-balance the computational work across threads, taking into consideration the number of threads available, the number of free parameters, and the size of V. Making more threads available will reduce running time, but at the cost of greater memory demand, since each thread allocates additional memory to do its job.
The user can also use multiple threads to reduce running time through a feature that does not require him/her to do any matrix calculus: if the default gradient-based optimizer SLSQP (Kraft, 1994; Johnson, 2020) is in use, it will automatically distribute its finite-differences calculation of the gradient across threads. However, numeric differentiation is slower and less accurate than analytic differentiation. As with the GREML fitfunction’s analytic differentiation, using more threads will reduce running time but at the cost of greater memory usage.
Script #1 in Table I fits the same model twice—once using numeric derivatives, and again using analytic derivatives. The script compares the two approaches’ running times (using analytic derivatives is faster), and MxModel object size, as an approximation to total runtime memory footprint (using numeric derivatives uses less memory). Specifically, the MxModel that uses numeric derivatives is about 59MB in size, whereas the one that uses analytic derivatives is about 311MB in size. On the first author’s laptop (Intel Core 2 Duo CPU at 2.4 GHz), it took about one minute to run the model using analytic derivatives, but almost 13 minutes to run it using numeric derivatives. The two approaches reach substantially equivalent solutions in the demo, but that is not guaranteed to happen in every case, as numerical optimization is not an “exact science.
As is typical in numerical optimization, choosing good start values for the free parameters is something that the user can do to make it more likely that the optimizer converges to the global minimum relatively quickly. OpenMx has a function, mxTryHard(), which makes multiple attempts to optimize a model, and randomly perturbs the start values between attempts. Several of the scripts in Table I demonstrate various strategies to find data-informed start values for the mxGREML model, for example, using Haseman-Elston regression and the residual variance from ordinary least-squares regression of phenotypes onto covariates to respectively estimate heritability and phenotypic variance (#6 and #7), or fitting a model that ignores the GRM to get start values for factor loadings (#2 and #3) or for total latent-intercept and latent-slope variance (#11 and #12). Most recently, we have implemented mxAutoStart() support for mxGREML models, which provides a general-purpose method for obtaining data-informed start values via least-squares estimation. This new feature will be included in the next stable release of OpenMx.
Customization: Data-handling
Although the default behavior is for OpenMx to call mxGREMLDataHandler() automatically at runtime, it is also possible for the user to invoke the data-handler directly. In that case, the user must provide the function with the raw dataset, the column names of the phenotypes, and the column names of the covariates. The function will then return a list with two elements. One element is an integer vector of the indices of the rows removed from y and X due to missing data. The other is a numeric matrix the first column of which is y, and the remaining columns of which are X. It is possible to use the matrix as the dataset of an MxModel, and to provide the vector of removed rows’ indices to the GREML expectation. Then, the user can instruct the GREML expectation to skip calling the data-handler at runtime, since its work has already been finished. Directly invoking mxGREMLDataHandler() in this manner is not necessary in typical use cases, but the matrix it outputs may be useful for complex cases in which the user must do some manual restructuring of the data (described below).
Exactly how the data-handler constructs y and X from the dataset’s columns depends upon the values the user provides for three logical (i.e., Boolean) arguments to mxGREMLDataHandler(); in the typical use case, the user provides these values when constructing the GREML expectation object, which then passes them to the data-handler at runtime. One of these arguments, addOnes, merely dictates whether one or more columns consisting only of 1.0 need to be included in X, for the regression intercept(s) (TRUE by default). The second such argument, blockByPheno, dictates whether the rows of y are to be “blocked” by phenotype (default) or by individual. If blocked by phenotype, then y will consist of scores on phenotype 1 for individuals 1 thru n, then phenotype 2 for individuals 1 thru n, and so forth. If blocked by individual, then y will contain individual 1’s scores on phenotypes 1 thru p, then individual 2’s scores on phenotypes 1 thru p, and so forth. Note than in either case, X will be constructed so that its rows correspond to those of the resulting y. The user must take care to define V according to how y has been blocked; the blockByPheno argument allows the user to choose the style of blocking with which s/he feels more comfortable.
The third such argument to the data-handler is staggerZeroes. The default of staggerZeroes=TRUE is meant for cases where the multiple phenotypes genuinely are different traits, likely on different scales of measurement, possibly being adjusted for different covariates, and each needing its own regression intercept. Use of staggerZeroes=FALSE is meant for cases where the multiple “phenotypes” are actually repeated observations of the same trait, and the covariates are a time variable and possibly some “time-invariant” regressors.
Some illustrative examples of the use of blockByPheno and staggerZeroes are in order. Suppose we have a sample of only 3 individuals, A, B, and C; three phenotypes y1, y2, and y3; and one covariate, x. If blockByPheno=TRUE and staggerZeroes=TRUE, then
| (16) |
. If blockByPheno=FALSE and staggerZeroes=TRUE, then
| (17) |
. If blockByPheno=TRUE and staggerZeroes=FALSE, then y is as in (16), and
| (18) |
. Finally, if blockByPheno=FALSE and staggerZeroes=FALSE, then y is as in (17), and
| (19) |
The mxGREML feature can accommodate more-complex designs as well, but such designs will require at least some manual data-structuring on the user’s part. Consider the case of three different phenotypes, where the third phenotype has repeated measures at four timepoints. In this case, the user could use direct mxGREMLDataHandler() calls to facilitate preparing the data for mxGREML, as follows. First, the user would use the data-handler with blockByPheno=TRUE to obtain the stacked vector of the first two phenotypes—say, y12—and their corresponding matrix of fixed effects—say, X12. Then, the user would again use the data-handler with blockByPheno=TRUE to obtain the stacked vector of the repeated measures on the third phenotype—say, y3—and their corresponding matrix of fixed effects—say, X3. Then, to obtain the final y vector, the user would vertically adhere y12 and y3 by stacking the former on top of the latter. To obtain the final X matrix, the user would first define a matrix of zeroes, 0, with as many rows as X12 and as many columns as X3, and define
| (20) |
. Finally, the user would horizontally adhere y to X, creating a new matrix in which the first column is y, and the remaining columns constitute X. This matrix is the dataset the user will provide to OpenMx, while making sure to set dataset.is.yX=TRUE when creating the GREML expectation object for his/her model.
Limitations and Future Directions
The motivation behind OpenMx’s GREML feature is to provide a flexible, general method for users to fit biometrical structural-equation models to samples of participants for whom genome-wide genotypic data are available. Therefore, the feature’s currently existing implementation primarily prioritizes generality and flexibility, leaving computational performance/efficiency (i.e, speed and memory usage) and ease-of-use as secondary and tertiary considerations, respectively. Thus, the limitations of the current mxGREML implementation chiefly concern its shortcomings in performance and user-accessibility, and we plan further development of the feature to address those shortcomings. We describe below our planned improvements regarding three aspects of the mxGREML implementation; for each aspect, we plan an easier and shorter-term minor improvement, as well as a longer-term major improvement that will require more effort from the OpenMx development team.
We first consider OpenMx’s numerical linear-algebra performance, that is, how quickly OpenMx carries out matrix-related computations. The OpenMx backend currently uses the Eigen library (Jacob, Guennebaud, et al., 2010) for numerical linear algebra, and profiling mxGREML analyses has shown that the most time-consuming steps in such analyses take place in the Eigen library’s code. Quite likely, the computational bottleneck is Cholesky-factoring and subsequently inverting V every time the GREML objective function must be evaluated. At compile-time, Eigen can be linked to a BLAS (Basic Linear Algebra Subsystem) implementation for it to use as a computational backend of its own (and R itself can likewise be compiled with an alternate BLAS). We have modified the OpenMx backend to allow Eigen to be linked to a BLAS when OpenMx is compiled, and thus, the minor improvement for numerical linear algebra is mostly complete. Presently, we have tested compiling OpenMx with three tuned BLAS implementations. Although we have not formally benchmarked the performance improvement6, our informal benchmarking suggests a 5.5x speedup with Intel MKL (https://software.intel.com/mkl), a 4.5x speedup with OpenBLAS (https://www.openblas.net/), and a 3x speedup with ATLAS (Whaley, Petitet, & Dongarra, 2001). We will consider this minor improvement complete once we have formally benchmarked the performance improvements and written user documentation explaining how to compile OpenMx with an alternate BLAS.
Our planned major improvement for linear-algebra performance is to modify the OpenMx backend to enable it to hand off matrix-related computations to a graphics-processing unit (GPU). Because GPUs can carry out linear-algebra computations in a massively parallel fashion, we anticipate even better performance improvements than those achieved from CPU-tuned BLAS implementations. Specifically, we will make it possible to compile OpenMx for use with NVIDIA CUDA™ (Sharma, Agarwala, & Bhattacharya, 2013). Since mxGREML is the motivating use case for an interface to CUDA, initially only backend code related to mxGREML will use it. Once OpenMx is compiled to use CUDA, the user will have to switch on an option to actually do so, since passing small-dimensional linear-algebra jobs to a GPU can be counterproductive. We will evaluate benchmark performance with CUDA and determine the practicality of extending the CUDA interface to more of OpenMx’s growing set of capabilities.
The second aspect in need of improvement is calculation of the GREML objective-function derivatives for optimization purposes. As described above, numerical differentiation (which is OpenMx’s default behavior) is slow because evaluation of the objective function is slow as well. The existing alternative is analytic differentiation, which requires the user to provide MxMatrices or MxAlgebras representing the analytic first partial derivatives of V with respect to the free parameters. Although this analytic approach does reduce the number of objective-function evaluations, it has several drawbacks. First, it increases OpenMx’s memory footprint, because the derivatives of V must be stored in memory. Secondly, and more importantly, it is a barrier to mxGREML’s ease-of-use, since many users will not know how to analytically differentiate V, and those that do are nonetheless prone to making errors in their calculus or their syntax (especially in light of how complicated the mapping from free parameters to V can be in SEM).
Therefore, our planned minor and major improvements to mxGREML’s objective-function differentiation are both intended to reduce memory demand and to automate analytic differentiation for the user’s convenience. The minor improvement might be described as “semi-analytic” differentiation—it will use OpenMx’s extant finite-difference subroutines to numerically differentiate V, and then use those derivatives of V to analytically differentiate the objective function. Each matrix derivative of V (there will be one per free parameter) would only need to be stored in memory until its corresponding objective-function derivative is calculated, at which point the matrix’s memory can be freed. Our planned major improvement relating to objective-function differentiation will be similar, but will automate analytic rather than numeric differentiation of V. That is, the major improvement will be implementation of a new OpenMx feature that automates analytic differentiation of MxAlgebra expressions, using existing automatic-differentiation libraries like Stan (Carpenter, et al., 2017) or TensorFlow (Abadi, et al., 2015). Creating an interface between OpenMx and those libraries will require more effort than implementing “semi-analytic” differentiation, but will yield more accurate derivatives.
The third aspect in need of improvement is mxGREML’s user interface. The GREML feature is part of OpenMx, and like OpenMx itself, is designed to be a powerful and versatile tool, albeit at the expense of verbose syntax and a steep learning curve. Neither “improvement” we plan for the user interface will actually alter OpenMx itself. Rather, they both will augment OpenMx with external resources to make mxGREML more accessible to the end user. The minor “improvement” is the library of demonstration scripts at https://github.com/RMKirkpatrick/mxGREMLdemos, an ongoing effort. The major “improvement” will be an R package of high-level functions that will automate fitting a set of fairly “standard” models that users are likely to fit frequently. Precedent for such packages already exists. For example, both the ‘umx’ and ‘EasyMx’ packages for R provide a suite of high-level functions that automate fitting certain kinds of model, and shield the user from the underlying complexity of OpenMx’s “nuts and bolts”.
Conclusion
In summary, we have recently developed “mxGREML”, a versatile software tool that integrates SEM and GREML. The tool is implemented as a feature in OpenMx, an R package for extended structural equation modeling. It introduces a new type of expectation (statistical model specification) and fitfunction (objective function), and new functionality for data-handling. The feature allows a great deal of user customization to accommodate complicated datasets, and to improve performance during numerical optimization. By design, the feature allows the user to structure the phenotypic covariance matrix, V, as an arbitrary matrix or function of matrices (MxAlgebra). We have provided an example of how the feature might be applied, and provide additional example scripts in an online repository. Finally, we describe the feature’s current limitations with regard to numerical linear-algebra performance, calculation of the objective-function derivatives, and ease-of-use, and we provide a clear roadmap forward for overcoming those limitations with additional development effort.
Supplementary Material
Acknowledgments
Funding: The work reported in this paper was funded by the National Institute on Drug Abuse DA026119.
Footnotes
Conflict of Interest: The authors declare they have no conflict of interest.
Compliance with Ethical Standards
Ethical Approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Here, “raw data” is meant in the OpenMx sense, i.e. “not covariance-matrix input” (which is commonly used in SEM). Although less than ideal, it is possible to run an mxGREML analysis without raw genotypic or phenotypic data. The data’s owner would need to provide the user with one or more GRMs calculated from raw genotypes, and residuals for one or more phenotypes corrected for covariates. In such a case, the residuals would be what populates y, and X would consist only of constants.
mxGREML analyses of ordinal-threshold traits is the topic of a forthcoming manuscript.
As pointed out to us by an anonymous referee, one consequence of this design assumption is that it is not straightforward to incorporate regressions among endogenous variables in an mxGREML model, since doing so would require the corresponding regression coefficients to appear in both the model-expected mean vector and covariance matrix. That is a limitation inherent to REML, and is not specific to OpenMx. The referee suggested that there might be ways to circumvent this limitation, such as mean-centering manifest endogenous variables prior to mxGREML analysis; another possibility might be to conduct the desired regressions outside of OpenMx, and analyze the resulting residuals in the mxGREML model. To date, we have not explored such workarounds. One approach to endogenous-variable regression that will certainly work is to analyze y as a dataset with 1 row and np columns, using the pre-existing mxExpectationNormal() and mxFitFunctionML(), as they allow the user to freely and explicitly specify the model-expected mean vector (e.g., Eaves et al. 2014).
See below, under “Customization: Data-handling”.
As of this writing, the GREML fitfunction requires a partial derivative for all (or none) of the model’s explicit free parameters, though that requirement will be relaxed in the future. It is true that providing a derivative of V for every free parameter can require a fair amount of input from the user—see, for example, script #13 in Table I, which has 16 free parameters.
To give the reader a sense of scale: on a computing cluster (Intel Xeon E5–2680 v4 CPU at 2.4 GHz), we recently ran script #11 (a five-timepoint latent-growth model) from Table I, except edited to have a sample size of 4000 and to use 8 processing threads. The job used about 55 GB of memory, and OpenMx’s running time was slightly under 20 hours.
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, …, Zheng X (2015). TensorFlow: Large-scale machine learning on heterogeneous systems. White paper and software available at tensorflow.org. [Google Scholar]
- Benjamin DJ, Cesarini D, van der Loos MJHM, Dawes CT, Koellinger PD, Magnusson PKE, … Visscher PM (2012). The genetic architecture of economic and political preferences. PNAS, 109(21), 8026–8031. doi: 10.1073/pnas.1120666109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benyamin B, St Pourcaine B, Davis OS, Davies G, Hansell NK, et al. (2014) Childhood intelligence is heritable, highly polygenic and associated with FNBP1L. Molecular Psychiatry, 19, 253–254. doi: 10.1038/mp.2012.184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boker S, Neale M, Maes H, Wilde M, Spiegel M, et al. (2011). OpenMx: An open source extended structural equation modeling framework. Psychometrika, 76(2), 306–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter B, Gelman A, Hoffman MD, Lee D, Goodrich B, …, Riddell A (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1). doi: 10.18637/jss.v076.i01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies G, Tenesa A, Payton A, Yang J, Harris SE, et al. (2011) Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Molecular Psychiatry 16: 996–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeFries JC, & Fulker DW (1985). Multiple regression analysis of twin data. Behavior Genetics, 15(5), 467–473. [DOI] [PubMed] [Google Scholar]
- Eaves LJ, St Pourcain B, Davey Smith G, York TP, & Evans DE (2014). Resolving the effects of maternal and offspring genotype on dyadic outcomes in genome wide complex trait analysis (M-GCTA”). Behavior Genetics, 44, 445–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaugler T, Klei L, Sanders SJ, Bodea CA, Goldberg AP, …, Buxbaum JD (2014). Most genetic risk for autism resides with common variation. Nature Genetics, 46(8), 881–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill PE, Murray W, Saunders MA, & Wright MH (2001). User’s Guide for NPSOL 5.0: A Fortran Package for Nonlinear Programming. Adapted from Stanford University Department of Operations Research Technical Report SOL; 86–1, 1986. http://www.ccom.ucsd.edu/~peg/papers/npdoc.pdf [Google Scholar]
- Gillespie NA, Eaves LJ, Maes H, & Silberg JL (2015). Testing models for the contributions of genes and environment to developmental change in adolescent depression. Behavior Genetics, 45, 382–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour AR, Thompson R, & Cullis BR (1995). Average information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics, 51(4), 1440–1450. [Google Scholar]
- Haworth S, Shapland CY, Hayward C, Prins BP, Felix JF, …, St Pourcain B (2019). Low-frequency variation in TP53 has large effects on head circumference and intracranial volume. Nature Communications, 10, 357. 10.1038/s41467-018-07863-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob B, Guennebaud G, et al. (2010). Eigen v3. http://eigen.tuxfamily.org/. [Google Scholar]
- Johnson SG (2020). The NLopt nonlinear-optimization package, http://github.com/stevengj/nlopt. [Google Scholar]
- Johnson DL, & Thompson R (1995). Restricted maximum likelihood estimation of variance components for univariate animal models using sparse techniques and average information. Journal of Dairy Science, 78, 449–456. [Google Scholar]
- Keller MC, Medland SE, Duncan LE, Hatemi PK, Neale MC, Maes HHM, & Eaves LJ (2009). Modeling extended twin family data I: Description of the cascade model. Twin Research & Human Genetics, 12(1), 8–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendler KS, Neale MC, Sullivan P, Corey LA, Gardner CO, & Prescott CA (1999). A population-based twin study in women of smoking initiation and nicotine dependence. Psychological Medicine, 29, 299–308. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick RM, McGue M, Iacono WG, Miller MB, & Basu S (2014). Results of a “GWAS Plus:” General cognitive ability is substantially heritable and massively polygenic. PLOS ONE. doi: 10.1371/journal.pone.0112390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft D (1994). Algorithm 733: TOMP—Fortran modules for optimal control calculations. ACM Transactions on Mathematical Software, 20(3), 262–281. [Google Scholar]
- Lee S, DeCandia TR, Ripke S, Yang J, The Schizophrenia Psychiatric Genome-Wide Association Study Consortium, The International Schizophrenia Consortium, … Wray NR (2012). Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nature Genetics, 44(3), 247–250. doi: 10.1038/ng.1108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SH, Cross-Disorder Group of the Psychiatric Genomics Consortium, et al. (2013). Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs. Nature Genetics, 45(9), 984–994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer K, & Smith SP (1996). Restricted maximum likelihood estimation for animal models using derivatives of the likelihood. Genetics Selection Evolution 28: 23–49. [Google Scholar]
- Morandat F, Hill B, Osvald L, & Vitek J (2012). Evaulating the design of the R language: Objects and functions for data analysis. In Noble J (ed.), ECOOP 2012—Object-Oriented Programming. New York: Springer Science+Business Media [Google Scholar]
- Morris AP, DIAGRAM Consortium, et al. (2012). Large-scale association analysis provides insights into the genetic architecture and pathophysiology of type 2 diabetes. Nature Genetics 44, 981–990. 10.1038/ng.2383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulaik SA (2010). Foundations of Factor Analysis (2nd ed.). New York: CRC Press. [Google Scholar]
- Neale MC, & Cardon L (1992). Methodology for Genetic Studies of Twins and Families. New York: Springer Science+Business Media. [Google Scholar]
- Neale MC, Hunter MD, Pritikin JN, Zahery M, Brick TR, et al. (2016). OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika, 81(2), 535–549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pawitan Y (2013). In all likelihood: Statistical modelling and inference using likelihood. Oxford: Oxford University Press. [Google Scholar]
- Posthuma D (2009). Multivariate genetic analysis. In Kim Y-K (Ed.), Handbook of Behavior Genetics (p. 47–59). New York: Springer Science+Business Media. doi: 10.1007/978-0-387-76727-7_4 [DOI] [Google Scholar]
- Purcell S (2002). Variance components models for gene-environment interaction in twin analysis. Twin Research, 5(6), 554–571. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, … Sham PC (2007). PLINK: A tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics, 81, 559–575. doi: 10.1086/519795. Software and documentation available at http://pngu.mgh.harvard.edu/~purcell/plink/. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2018). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/. [Google Scholar]
- Ripke S, O’Dushlaine C, Chambert K, Moran JL, Kähler AK, Akterin S, … Sullivan PF (2013). Genome-wide association analysis identifies 13 new risk loci for schizophrenia. Nature Genetics, 43(10), 1150–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapland CY, Verhoef E, Davey Smith G, Fisher SE, Verhulst B, Dale PS, & St Pourcain B (2020. preprint). The multivariate genome-wide architecture of interrelated literacy, language, and working memory skills reveals distinct etiologies. 10.1101/2020.08.14.251199. [DOI] [PMC free article] [PubMed]
- Sharma G, Agarwala A, & Bhattacharya B (2013). A fast parallel Gauss Jordan algorithm for matrix inversion using CUDA. Computers and Structures, 128, 31–37. [Google Scholar]
- Speed D, Hemani G, Johnson MR, & Balding DJ (2013). Improved heritability estimation from genome-wide SNPs. American Journal of Human Genetics, 91, 1011–1021. 10.1016/j.ajhg.2012.10.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- St Pourcain B, Eaves LJ, Ring SM, Fisher SE, Medland S, Evans DM, & Davey Smith G (2018). Developmental changes within the genetic architecture of social communication behavior: A multivariate study of genetic variance in unrelated individuals. Biological Psychiatry, 83(7), 598–606. 10.1016/j.biopsych.2017.09.020. Software available at https://gitlab.gwdg.de/beate.stpourcain/gsem. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dongen J, Slagboom PE, Draisma HHM, Martin NG, & Boomsma DI (2012). The continuing value of twin studies in the omics era. Nature Reviews Genetics, 13, 640–653. [DOI] [PubMed] [Google Scholar]
- Verhoef E, Shapland CY, Fisher SE, Dale PS, & St Pourcain B (in press). The amplification of genetic factors for early vocabulary during children’s language and literacy development. Accepted at Journal of Child Psychology and Psychiatry. [DOI] [PubMed] [Google Scholar]
- Wainschtein P, Jain DP, Yengo L, Zheng Z, TOPMed Anthropometry Working Group, Trans-Omics for Precision Medicine Consortium, et al. (2019. preprint). Recovery of trait heritability from whole genome sequence data. doi: 10.1101/588020 [DOI] [Google Scholar]
- Whaley RC, Petitet A, & Dongarra JJ (2001). Automated empirical optimization of software and the ATLAS project. Parallel Computing, 27, 3–35. [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, Nyholt DR, … Visscher PM (2010). Common SNPs explain a large proportion of the heritability for human height. Nature Genetics, 42(7), 565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, & Visscher PM (2011). GCTA: A tool for genome-wide complex trait analysis. The American Journal of Human Genetics, 88, 76–82. doi: 10.1016/j.ajhg.2010.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Lee SH, Goddard ME, & Visscher PM (2013). Genome-wide complex trait analysis (GCTA): Methods, data analyses, and interpretations. In Gondro C, et al. (eds.), Genome-Wide Association Studies and Genomic Prediction, Methods in Molecular Biology, vol. 1019. New York: Springer Science+Business Media; [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.