Bilayer aberration-inducing gel phantom for high intensity focused ultrasound applications

Abstract

Aberrations induced by soft tissue inhomogeneities often complicate high-intensity focused ultrasound (HIFU) therapies. In this work, a bilayer phantom made from polyvinyl alcohol hydrogel and ballistic gel was built to mimic alternating layers of water-based and lipid tissues characteristic of an abdominal body wall and to reproducibly distort HIFU fields. The density, sound speed, and attenuation coefficient of each material were measured using a homogeneous gel layer. A surface with random topographical features was designed as an interface between gel layers using a 2D Fourier spectrum approach and replicating different spatial scales of tissue inhomogeneities. Distortion of the field of a 256-element 1.5 MHz HIFU array by the phantom was characterized through hydrophone measurements for linear and nonlinear beam focusing and compared to the corresponding distortion induced by an ex vivo porcine body wall of the same thickness. Both spatial shift and widening of the focal lobe were observed, as well as dramatic reduction in focal pressures caused by aberrations. The results suggest that the phantom produced levels of aberration that are similar to a real body wall and can serve as a research tool for studying HIFU effects as well as for developing algorithms for aberration correction.

I. INTRODUCTION

High-intensity focused ultrasound (HIFU) has been identified as a promising noninvasive therapeutic modality.^1–4 HIFU therapies have been explored to treat solid tumors of the brain, breast, liver, kidney, and prostate.^5–14 Important organ targets, such as the liver and kidney, reside in the abdominal cavity. Treatment of these tumor sites requires HIFU beams to travel through inhomogeneous body wall tissues including skin, fat, and muscle. The different sound speeds of the intervening body wall tissues cause phase aberrations that degrade focusing of the HIFU beam.^15–18 In such cases, the incident energy is partially scattered away from the focus and deposited in surrounding tissues, potentially causing unwanted damage. Although organ tissues themselves are not homogeneous, they do not produce significant aberrations compared to body wall.¹⁹ Studies using diagnostic ultrasound or low-energy therapeutic focused ultrasound have also explored aberrations induced by body wall.^20–24

To characterize human body walls, Hinkelman et al.²⁰ measured wavefront distortions directly. They found that fat and muscle layers distort beams in different ways: fat layers introduce scattering from small-scale structures (in particular, the septa of fat lobules 2.5–7.5 mm across), while muscle layers exhibit anisotropic characteristics and introduce time-of-arrival variations. In a follow-up study, Mast et al.²¹ simulated linear wave propagation through representations of body walls based on scanned images. They confirmed that both fat and muscle layers introduce distortion, further noting that arrival-time fluctuations are dominated by large intra-layer inhomogeneities (e.g., fatty inclusions in muscle) while scattering from smaller inhomogeneities in fat distort wavefront shapes. These careful studies of body wall morphology and associated interactions with ultrasound beams provide a basis for designing tissue phantoms that mimic the aberrations caused by body walls.

Tissue mimicking phantoms have been used as a research tool to study HIFU fields.^25–28 Phantoms present certain advantages over ex vivo tissues such as repeatability, reproducibility, and convenience in preparation and use. Consequently, phantoms can be made with consistent and measurable acoustic properties, which is helpful for developing a mechanistic understanding of the acoustic propagation behaviors. Although various HIFU tissue-mimicking phantoms have been proposed, the majority are comprised of one homogeneous material in a rectangular shape and therefore have limited capacity to generate aberrations.

Aberration-inducing phantoms have generally been realized by introducing a material with a rippled surface and a contrasting sound speed into the ultrasound propagation path. The topography of the surface is then designed to alter the time of arrival for waves propagating at different locations, which can be modeled theoretically as a phase screen. Material surfaces have been designed to have a sinusoidal variation,²⁹ a set of cylindrical cavities,³⁰ or random patterns designed to represent phase screens characterized spatially by Gaussian autocorrelation functions.^31–33 Although these phantoms were shown to produce different levels of aberration depending on the chosen design parameters, they all utilize a single layer of rubber or plastic, which have acoustic properties quite distinct from body wall tissues.

The goal of this study was to create a bilayer phantom that mimics the body wall for HIFU applications. Unlike previous studies, the phantom was designed with one fat-like material and one muscle-like material in layers that match characteristic thicknesses of porcine body wall to approximate actual anatomical structures. Similar to phase-screen approaches, the interface between layers was defined by undulations that aberrate incident beams of ultrasound. A method of random Fourier modes was employed to generate a large range of spatial frequencies for the interface geometry. Based on this design, a bilayer phantom was fabricated, and the corresponding wave field distortions were characterized by linear measurements. Linear field simulations were also executed to evaluate the design and implementation of the phantom. Finally, nonlinear pressure measurements when focusing through the phantom and through an ex vivo porcine body wall specimen were performed and compared. Although treatment in humans is the goal, the porcine model is commonly used for HIFU pre-clinical research. Ultimately, we hope this phantom can serve as a useful tool for developing methods for correcting aberrations introduced by inhomogeneous body wall in treatments of abdominal organs.

II. MATERIALS AND METHODS

A. Theoretical phantom methods

Four phantoms were designed to study acoustic effects of a body wall: two homogeneous phantoms for measuring acoustic properties, one bilayer phantom with a flat interface for validating simulations, and one bilayer phantom with a rippled interface for inducing aberrations (Fig. 1). Two phantom materials were chosen that have different sound speeds and can consequently produce an aberration effect: polyvinyl alcohol hydrogel (PVA) and ballistics gel (BG). PVA, used to mimic muscle, is a well-characterized hydrogel used in acoustics.^34–36 It has a higher sound speed than water. BG, used to mimic fat, is an oil-based compound combined with gellants and is a solid at room temperature.^37,38 It has a lower sound speed than water and is easy to degas, melt, and mold.

FIG. 1.

(Color online) Schematic of the phantoms diagrammed in the y (vertical coordinate) and z (horizontal coordinate) plane. (a) Homogenous ballistics gel; (b) homogenous polyvinyl alcohol gel; (c) bilayer wedge phantom; (d) bilayer aberrating phantom; (e) image of the section of a porcine body wall used in nonlinear experiments. Homogeneous phantoms are of dimension 200 × 200 × 20 mm. Bilayer phantoms and porcine body wall section are of dimension 200 × 200 × 40 mm.

Homogeneous phantoms of both PVA and BG were fabricated with dimensions of 200 × 200 × 20 mm to facilitate characterization of the acoustic properties of each material [Figs. 1(a) and 1(b)]. A wedge-shaped bilayer phantom was designed to produce a refraction effect and help validate simulation and experimental results. An inclined plane surface separates BG and PVA material as diagrammed in Fig. 1(c). The outermost 10 mm on each side of the phantom is homogeneous. The middle 20-mm thickness is split between BG and PVA such that the entire phantom has a uniform thickness of 40 mm.

An aberrating phantom was designed as a bilayer phantom with a rippled nonuniform interface between the BG and PVA layers as diagrammed in Fig. 1(d). The outer 10 mm on each side of the phantom is homogeneous material. The middle 20-mm thickness is divided between the BG and PVA materials. The rippled surface between the two layers of the phantom produces variations in thickness of each material and thus variations in the time delay needed for waves to traverse the phantom. Constituent parts of an incident acoustic beam take different paths to the focus, ultimately causing aberration.

The mathematical design of the interfacial rippled surface was achieved with the method of random Fourier modes adopted from aeroacoustic studies to generate field distortions.³⁹ This method produces a smooth but nonuniform surface that contains a range of spatial harmonics relevant to features in a porcine body wall. The surface z = U(x,y) was constructed by introducing a 2D distribution of the corresponding spectral amplitudes $\eta (k_x,k_y)$, where $(k_x,k_y)$ represents all of the spatial frequencies present in the surface U(x,y).

First, for a wavenumber $k=\sqrt{k_x^2+k_y^2}$, the following power spectrum G(k) was defined:

$$G\left(k\right)=G_0\cdot \frac{\hspace{0.17em}\text{exp}\left(-k^2{l}_0^2/2\right)}{{\left(1+k^2{L}_0^2\right)}^{11/6}}.$$ (1)

Here l₀ and L₀ represent characteristic minimum and maximum scales of the surface features in the x-y plane and $G_0=G(0)$ defines the surface height in the z direction. An important aspect of the function G(k) is the possibility to choose fitting parameters in an attempt to populate the spectrum with anatomically relevant spatial scales.³⁹ Our group has previously examined numerous porcine body wall cross sections and determined important feature sizes.⁴⁰ A small inhomogeneity size constant (l₀ = 5 mm) was chosen to represent undulations at the tissue/fat interface. A large characteristic inhomogeneity size constant (L₀ = 20 mm) was chosen to represent lobes of fat tapering off into muscle tissues. Notably, these characteristic sizes roughly match previously reported observations of the sizes of distortion-inducing inhomogeneities in human body walls.^20,21 The function G(k)/G₀ for the chosen values of l₀ and L₀ is plotted in Fig. 2(a) using a logarithmic scale.

FIG. 2.

(Color online) (a) Logarithmic plot of the spatial power spectrum G(k)/G₀ and (b) surface plot of the interface between the layers of the aberrating phantom containing a large range of spatial inhomogeneities.

Next, the spectral amplitudes $\eta (k_x,k_y)$ were determined from the chosen power spectrum G(k) as

$$\eta \left(k_x,k_y\right)=\xi \left(k_x,k_y\right)\sqrt{G\left(k\right)},$$ (2)

where the randomness in the phase of each spectral component and its absolute value are introduced by a random complex function $\xi (k_x,k_y)=\xi \prime +i\xi ″$. The quantities $\hspace{0.17em}\xi \prime$ and $\xi ″$ are real random numbers taken from a sequence of numbers with a pseudorandom Gaussian distribution with zero mean and unit dispersion.

Finally, an inverse 2D discrete Fourier transform is performed on the function $\eta (k_x,k_y)$ to obtain the complex spatial distribution W(x,y) = U(x,y) + i⋅V(x,y), for which the real U and imaginary V parts represent two statistically independent realizations of the random field with the power spectrum G(k). The real part U(x,y) was selected to obtain the surface for the random interface between the layers of the aberrative phantom. In order to have the amplitude of surface variations within the anatomically relevant ± 10 mm margins, the function z = U(x,y) was stretched in the z-direction by setting an appropriate value of G₀. The resulting surface is plotted in Fig. 2(b).

For practical realization of the method, a discrete Fourier transform was used. A square region of $\left|k_x\right|,\left|k_y\right|\le K/2$, where K = 31.4 mm⁻¹ was created and filled with N × N spectral points, where N = 2000. The spatial frequency steps between the discrete harmonics were $\Delta k$= K/N= 0.0157 mm⁻¹. Corresponding grid parameters in the 2D Cartesian space for the discrete Fourier transform were $\Delta x=\Delta y$ = $2\pi /K$= 0.2 mm for the spatial grid steps and $L$ = $2\pi /\Delta k$ = 400 mm for the size of the square spatial window L × L. This window then was cropped to 200 × 200 mm dimensions of the phantom.

It is worthwhile to compare the heterogeneities present in the proposed aberrating phantom to previously reported aberration metrics of body wall sections. Hinkelman and Mast^20–24 measured and simulated numerous human body wall sections and subsequently determined a correlation length (2.6–16.6 mm) corresponding to arrival time fluctuations across a 2D aperture. We calculated a correlation function directly from the interfacial surface. The correlation length, at the half maximum of the correlation function, was 25 mm, which appeared to be a reasonable metric for a porcine body wall mimic considering the previously reported correlation lengths of human body walls and the anatomic differences between the two. Note that the inhomogeneity size constants in Eq. (6) can be adjusted to represent other anatomic structures if their approximate spatial dimensions are known.

B. Experimental implementation of phantom models

Rectangular homogeneous phantoms of PVA and BG materials were produced to characterize their acoustic properties. The PVA phantom was fabricated according to a common recipe.^34,35 Briefly, a degassed aqueous solution of 10% PVA (99+% hydrolyzed, 89–98 kDa, Sigma-Aldrich, St. Louis, MO) was poured into a rectangular acrylic mold. The container was covered and retained overnight to let the bubbles escape. The phantom was frozen for 24 h and then thawed. Ballistics gel was purchased directly from the manufacturer [Clear ballistics gelatin (10%), Clear Ballistics, Greenville, SC]. The purchased BG block was melted and degassed at 140 °C, –750 Torr inside a vacuum oven for 12 h (AccuTemp 0.9, Across International, Livingston, NJ).

The wedge phantom in Fig. 3(a) was fabricated using the tooling shown in Fig. 3(b). A steel sheet was placed at a slant within a rectangular acrylic frame; two more steel sheets were clamped onto the frame to seal the sides of the mold. Molten BG was poured to fill the mold and degassed in the vacuum oven for 12 h at 140 °C and –750 Torr. After cooling to room temperature, the BG solidified. The slanted steel sheet and extraneous BG were removed and a degassed aqueous solution of 10% PVA was poured into the complementary space within the frame. After waiting 3 h for bubbles to escape from the PVA, the entire phantom was frozen to cure the PVA. The final dimensions of the phantom after thawing were approximately 200 × 200 × 40 mm thick. After thawing, two Mylar sheets (50 um thick) were glued to the frame to keep the two layers pressed together while providing acoustic access to the phantom. B-mode ultrasound imaging of the phantom did not reveal any bubbles inside it.

FIG. 3.

(Color online) (a) Schematic of wedge phantom and (b) angled steel sheet used to cast the phantom. (c) Schematic of aberrating phantom and (d) 3D printed mold used to cast the phantom.

The aberrating phantom [Fig. 3(c)] was fabricated in a two-step procedure comparable to that used for the wedge phantom. First, heat resistant ABS-like material (ABS Tough, EnvisionTec, Dearborn, MI) was 3D printed [Fig. 3(d)] with a designed surface geometry as described in the previous subsection. The 3D printed part was placed into a rectangular acrylic frame, which was partially sealed with two steel plates. The molten BG was poured in, then degassed for 48 h at 140 °C and –750 mm torr in a vacuum oven. After cooling to room temperature, the 3D printed part was removed and a degassed solution of 10% PVA was poured in its place and frozen for curing. After thawing, two sheets of Mylar (50 um thick) were glued onto the frame. The final dimension were approximately 200 × 200× 40 mm. B-mode ultrasound imaging of the phantom did not reveal any bubbles inside the phantom. For comparing the aberration effects on nonlinear beam focusing, a real porcine body wall with approximate dimensions of 200 × 200 × 40 mm was also used.

C. Acoustic characterization of phantom materials

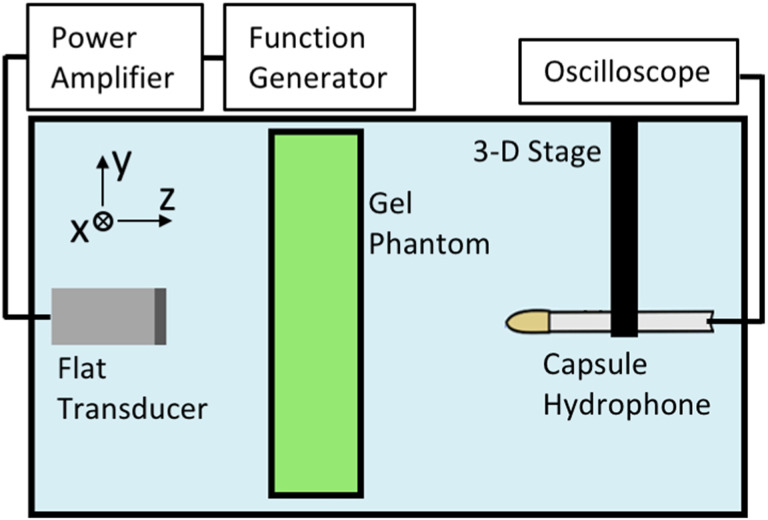
The speed of sound (c) and attenuation coefficient (α) of the homogeneous PVA and BG phantoms were measured at 1, 1.5, and 2 MHz frequency with an insertion-based technique employed in many previous studies.^35,36 In this method, the acoustic properties of a material are calculated by comparison with a chosen reference material (water). The experimental setup is diagrammed in Fig. 4. Large (200 × 200 × 20 mm) rectangular solid phase BG and PVA phantoms were specifically fabricated for measurement of their acoustic properties. Special care was taken to ensure the bulk and surface of the phantoms were free of air bubbles.

FIG. 4.

(Color online) Schematic of the experimental setup used for measuring the speed of sound (c) and attenuation coefficient (α) of the PVA and BG homogeneous phantoms.

A flat, unfocused broadband transducer (12.7 mm diameter, Olympus, Center Valley, PA) with 1 MHz central frequency was submerged in a water tank filled with degassed water of room temperature (22 °C) and dissolved oxygen levels below 30% saturation. The transducer was driven by a linear radio frequency amplifier (300 W, ENI A-300, ENI, Rochester, NY) and function generator (33500B, Keysight Technologies, Inc., Santa Rosa, CA). A PVDF capsule hydrophone (HGL-0200 with AH-2020 preamplifier, Onda Corp., Sunnyvale, CA) was mounted onto a 3D positioning stage (Velmex, Inc., Bloomfield, NY) and aligned with the major axis of the transducer.

The transducer was positioned 75 mm away from the hydrophone. It was important that the hydrophone be placed in the far field of the flat transducer source $a^2/\lambda =54$ mm at the highest 2 MHz frequency of our parameter set. Here $a$ is the transducer radius, and $\lambda$ is the ultrasonic wavelength in water.³⁵

Ten-cycle waveforms were collected in the free field in water and after propagating through the inserted phantom. Hydrophone readings were saved and averaged 512 times using an oscilloscope (DSO-X 3034A, Keysight Technologies, Inc., Santa Rosa, CA). For full accuracy, several steady state cycles of the waveform were isolated and filtered with a fast Fourier transform. The waveforms were analyzed for the sound speed (c) and attenuation coefficient (α) at 1, 1.5, and 2 MHz, as shown in Fig. 5. Three different lateral positions of the phantoms were used. A time-of-flight calculation was used to estimate the sound speed c. The time shift between the waveforms (Δt) and measured phantom thickness (h) were used to directly calculate the sound speed of the phantom material:

$$c_{\mathit{gel}}=\frac{h}{\Delta t+h/c_{\mathit{water}}}.$$ (3)

FIG. 5.

(Color online) Example waveform collected for calculation of speed of sound and attenuation at 1.5 MHz frequency. (a) 10 cycle waveform measured in water (black curve) and after passing through ballistics gel phantom (red curve). (b) Zoomed-in waveform with labels for peak pressure and time delay induced by insertion of the phantom.

The attenuation coefficient in units of Np/cm was calculated by the standard equation using the measured hydrophone voltages (V):

$${\alpha }_{\mathit{gel}}=-\frac{1}{h}\cdot \hspace{0.17em}\text{ln}\hspace{0.17em}\left(V_{\mathit{gel}}/V_{\mathit{water}}\right),$$ (4)

where V_water and V_gel are peak voltages from the hydrophone measurements in free field in water and after passing through the homogeneous phantom (Fig. 5). Each of the three measurements at different lateral phantom positions produced a value for c and α for each material and frequency. The reported values are the average of the three measurements; the reported error is the standard deviation. The calculated reflection coefficient between both the PVA–water interface and the BG–water interface was less than 1% in pressure at most and was ignored.

When measuring the attenuation α, it is necessary to take into account the refraction due to the difference in the speed of sound of the homogenous phantom and surrounding water. In the paraxial approximation, the acoustic field behind the phantom becomes shifted by an amount $h\cdot (c_{\mathit{gel}}/c_{\mathit{water}}-1)$ relative to the reference pressure distribution. Therefore, the attenuation coefficient calculated by comparing the pressure value behind the phantom to the water pressure value at the same axial position could overestimate or underestimate the attenuation coefficient. Analytical solutions for the pressure field of a circular plane transducer on the axis with and without an inserted phantom was used to introduce the correction to the measured value of the absorption at all three frequencies (+14%, +7%, and +3% for α_BG, –33%, –16%, and –16% for α_PVA at 1, 1.5, and 2 MHz, respectively). These corrected values are reported.

Two thin (0.05 mm) Mylar sheets were used in the fabrication of the wedge and aberrating bilayer phantoms to increase their structural stability. The attenuation of the Mylar sheets was determined from independent measurements in which they were installed onto a frame of the same dimensions as the bilayer phantom frame. The frame with Mylar was placed into the tank 75 mm away from the flat source in the same configuration shown in Fig. 4 at a normal beam incidence and at a 30-degree angle relative to normal beam incidence. This angle represents the characteristic maximum angular spectrum component for the focused array transducer with F# about one used in this study. The angled and normal incidence Mylar attenuation were compared to estimate an application-specific range of the attenuation values. The Mylar sheets are very thin, meaning that primary mode of their attenuation is reflection. The transmission coefficient (T_Mylar) through two Mylar sheets was defined as

$$T_{\mathit{Mylar}}=V_{\mathit{Mylar}}/V_{\mathit{water}},$$ (5)

where V_water and V_Mylar are peak voltages from the hydrophone measurements in free field in water and after passing through two Mylar sheets.

The density of the phantom materials was determined by a volume displacement measurement in a graduated cylinder (uncertainty of ±0.5 mL) and a mass measurement with an analytical balance (uncertainty of ±0.05 mg).

D. Linear and nonlinear measurements with 256-element focused array

Fields generated by a HIFU array were measured to quantify attenuation and aberration characteristics of the wedge and aberrating phantoms. A 256-element array (Imasonic, Voray sur l'Ognon, France), described in detail elsewhere,^41,42 was driven by a research ultrasound system (V1, Verasonics, LTD., Kirkland, WA). Briefly, the focused array has a 1.5-MHz frequency, a 144-mm aperture and 120-mm focal length (F# = 0.83). The array was placed in degassed water along with a hydrophone mounted to a 3D positioning stage as shown in Fig. 6 and operated at up to 2.2-kW acoustic peak power to conduct field characterization measurements with and without a phantom in the propagation path. The capsule hydrophone described above was used for low power (linear beam focusing) experiments; a fiber optic hydrophone was used for high power (nonlinear beam focusing) experiments (FOPH2000, 100 um fiber tip diameter, 100 MHz bandwidth, RP Acoustics, Leutenbach, Germany). The bilayer phantoms were inserted at a fixed 3-cm distance from the transducer apex plane.

FIG. 6.

(Color online) Photograph of the 256-element focused array, homogeneous phantom, and PVDF hydrophone used to measure the acoustic field behind the phantom in a water tank.

In the linear regime, the acoustic field was measured in the free field in the vicinity of the location of maximum pressure amplitude. Additional measurements at the same locations were recorded behind each phantom. To determine the level of aberration produced by the bilayer phantoms, the reduction in pressure due to attenuation was first estimated:

$$p/p_0=T_{\mathit{Mylar}}\cdot \hspace{0.17em}\text{exp}\left(-h\cdot \left({\alpha }_{\mathit{PVA}}+{\alpha }_{BG}\right)\right).$$ (6)

Here h is taken to be 2 cm, an average thickness of each gel layer across the phantom, and T_Mylar is determined from the Eq. (5). The maximum achievable pressure amplitude behind the phantom, focal position shift, and –6 dB beam dimensions were also measured.

In the nonlinear regime, the fiber optic hydrophone was moved to the location of the highest peak positive pressure in 3D space at the voltage that corresponded to a fully developed shock.⁴³ Waveforms were then collected across a range of output amplitudes. Again, estimating the attenuative effects of the bilayer phantoms was critical to isolate the quantitative level of aberration. Accordingly, a derating method was used to scale the system driving voltage to facilitate comparisons between waveforms measured in the free field and behind the phantoms by compensating for prefocal attenuation.⁴⁴ The corresponding scaling factor $V_{\mathit{derated}}/V_{\mathit{water}}$ was calculated:

$$\frac{V_{\mathit{derated}}}{V_{\mathit{water}}}={\left(p/p_0\right)}^{-1}=\frac{\hspace{0.17em}\text{exp}\left(h\cdot \left({\alpha }_{\mathit{PVA}}+{\alpha }_{BG}\right)\right)}{T_{\mathit{Mylar}}}$$ (7)

as the inverse value of the estimated pressure reduction given in Eq. (6) to account for the attenuation in the bilayer phantoms, assuming that nonlinearity coefficients of the phantoms are equal to water.⁴⁴

E. Acoustic simulations with 256-element array

To simulate wave propagation through the phantom, a system of coupled first-order partial differential equations of linear acoustics was used:^45,46

$$\{\begin{array}{c}\frac{\partial \mathbf{u}}{\partial t}=-\frac{1}{{\rho }_0}\nabla p,\hfill \\ \frac{\partial \rho }{\partial t}=-{\rho }_0\nabla \mathbf{u}-\mathbf{u}\nabla {\rho }_0,\hfill \\ p=c_0^2\left(\rho +\mathbf{d}\nabla {\rho }_0+\frac{\delta }{c_0^2}\frac{\partial \rho }{\partial t}\right).\hfill \end{array}$$ (8)

The first and second equations describe the momentum and mass conservation, and the third one describes the pressure-density relation for acoustic waves. Here the following notation for acoustic variables is used: p is the pressure, u is the particle velocity, d is the particle displacement, and ρ is the density. Considering an inhomogeneous propagation medium, the relevant material properties are presumed to vary in space and can be denoted as functions of the position vector r: ρ₀(r) is the ambient density, c₀(r) is the sound speed, and $\delta (\mathbf{r})$ is the diffusivity. For water, $\delta$ = 4.33⋅10⁻⁶ m²/s and, in general, $\delta (\mathbf{r})=2\alpha (\mathbf{r})c_0(\mathbf{r})/{(2\pi f_0)}^2$ are related to the absorption coefficient $\alpha$ measured at the operational frequency of the array f₀ = 1.5 MHz.

A numerical simulation model was implemented using the open-source k-Wave matlab Toolbox (http://www.k-wave.org). The algorithm is based on the k-space pseudospectral method and accounts for effects of heterogeneity and absorption.^47,48 The following parameters of the computational grid were chosen for the simulation: 640 × 640 × 512 points in the x, y, and z directions, respectively, with the z direction corresponding to the beam axis (Fig. 4). A spacing between grid points of Δx = Δy = Δz= 0.3 mm provided step sizes less than one third of the wavelength and provided sufficient accuracy for the applied numerical scheme.⁴⁹ A perfectly matched layer (PML) occupied 10 points around each edge of the spatial domain, and the time step Δt was based on the Courant–Friedrichs–Lewy (CFL) number of 0.05, where $\hspace{0.17em}\text{CFL}=c_{\text{max}}\Delta t/\Delta x$, where $c_{\text{max}}$ is the maximum sound speed used in the simulation.

For the boundary condition, the vibrational velocity u was defined at each node of the plane at z = 0, which corresponds to the apex of the transducer. Values at each node were determined based on holography measurements performed in a separate study:^41,50 ${\mathbf{u}}_{ij}^{\text{hol}}\hspace{0.17em}\text{sin}(2\pi f+{\phi }_{ij}^{\text{hol}})$. Here ${\mathbf{u}}_{ij}^{\text{hol}}$ and ${\phi }_{ij}^{\text{hol}}$ are the initial vibrational velocity amplitude and phase, and subscripts i = 1…640 and j = 1…640 represent i-th and j-th grid nodes, respectively.

III. RESULTS

A. Acoustic properties of homogeneous phantoms

Measured sound speeds (c), densities (ρ), and attenuation coefficients (α) of the two homogenous phantoms along with existing data from literature are documented in Table I.

TABLE I.

Acoustic properties of gel phantoms and porcine soft tissues.

Material	Sound Speed (m/s)	Density (kg/m3)	Attenuation (dB/cm)
Ballistics Gela	1436 ± 1.9	865 ± 15	0.40 ± 0.007 at 1.5 MHz
Polyvinyl Alcohola	1507 ±2.2	1035 ± 20	0.069 ± 0.02 at 1.5 MHz
Porcine Fat (Refs. 51 and 54)	1426–1470	870	1.6–2.7 at 1 MHz
Porcine Muscle (Refs. 52, 55, and 56)	1579–1622	1040–1110	0.8–1.2 at 1 MHz

^aMeasured values from this study.

The speed of sound of the PVA and BG materials is a key attribute as it has a direct influence on generating field distortions for the bilayer aberrating phantom. The measured BG sound speed c_BG = 1436 m/s is within the range of reported values for porcine fat (1426–1470 m/s⁵¹) and matches well with a reported literature value (1434 m/s³⁸). The measured PVA sound speed c_PVA = 1507 m/s is somewhat lower than reported values for porcine muscle (1579–1622 m/s⁵²) but matches well with reported values for PVA (1520–1560 m/s^35,53). The measured 71 m/s sound speed difference between the BG and PVA materials was expected to produce aberrations similar to real porcine tissues.

Density values of the PVA and BG materials are important to characterize the reflections at the gel interfaces. The measured densities of the tissue mimicking materials, $\rho$_BG = 865 kg/m³ and $\rho$_PVA = 1035 kg/m³, are close to the reported literature values of porcine fat (870 kg/m³) and porcine muscle (1040–1110 kg/m³). The measured PVA density also agrees well with reported literature values (1020–1030 kg/m³).^34,57 No literature density data was found for the BG material.

The results of attenuation measurements taken at 1, 1.5, and 2 MHz are plotted in Fig. 7, where error bars represent the standard deviation of three measurements taken in different lateral locations of the phantom. Measured attenuation values for BG and for PVA, such as α_BG = 0.4 dB/cm and α_PVA = 0.069 dB/cm at 1.5 MHz, are similar to reported values (0.6 dB/cm at 1.5 MHz for BG³⁸ and 0.1 dB/cm for PVA at 1.5 MHz^34,35).

FIG. 7.

(Color online) Attenuation coefficient of Polyvinyl Alcohol (PVA, red) and Ballistics Gel, (BG, green) vs frequency. The Ballistic Gel data points are fit to a power law curve.

The frequency dependence of the attenuation for values of the BG phantom were fit to a power law curve:

$${\alpha }_{BG}=A\cdot f^n.$$ (9)

Here f is measured in MHz, $\alpha$ is measured in dB/cm, and fitting parameters are A = 0.229 and n = 1.42. The measured attenuation values for PVA were quite low; perhaps due to measurement error, these data are not well described by a curve of the form in Eq. (9).

Although the measured attenuations for both PVA and BG are considerably less than the values for porcine analogs (0.8–1.2 dB/cm at 1 MHz for muscle,⁵⁶ 1.6–2.7 dB/cm at 1 MHz for fat⁵¹), absolute attenuation values are not critical for the aberrating phantom as long as it distorts the structure of the focused field like a body wall. Indeed, for both linear and nonlinear fields, the transducer output level can be scaled to account for such attenuation differences as described in Sec. II D.

The transmission coefficient of the two Mylar films attached to the sides of the bilayer phantoms, measured and calculated using Eq. (5), was Τ_Mylar = 0.96 at normal incidence and 0.94 at a 30-degree incidence beam angle. The highest value of Τ_Mylar = 0.96 was used in estimating attenuation of the bilayer phantoms in Eq. (6).

B. Distortions of the linear acoustic field by phantoms

Low-output (linear propagation regime) two-dimensional pressure fields measured by hydrophone and simulated using the k-Wave software in the focal plane are compared in Fig. 8 for propagation through water, the wedge phantom, and the aberrating phantom. Several metrics are considered for such comparisons, including the spatial peak pressure, the shift in focal position, and the –6 dB beam area.

FIG. 8.

(Color online) Measured and simulated 2D pressure amplitude distributions recorded in the transverse focal plane of the array. The distributions are collected in free field and in the same plane with phantoms inserted in the propagation path. Pressures in all plots are normalized to the maximum value in each individual plot. (a) Free field experiment; (b) free field simulation; (c) wedge phantom experiment; (d) wedge phantom simulation; (e) aberrating phantom experiment; (f) aberrating phantom simulation.

The same geometry of focusing and material parameters obtained in characterization measurements were used as inputs to simulations for direct comparison with experiments. Known uncertainties in the simulated results involve the physical properties of the phantom materials in addition to the as-tested geometry and orientation of each phantom. The Mylar layers were not simulated, but their attenuation effect was included after simulation. The axial position of the focal plane was chosen roughly at the geometric focus of the array at the distance z = 120 mm for all cases and corresponded to the maximum pressure amplitude in the free field. Simulation results showed that in the presence of the phantoms the location of the maximum pressure amplitude shifted axially less than 1 mm and changed by less than 5% as compared to the maximum pressure in the focal plane identified under free field conditions.

The wedge phantom was employed in measurements and simulations to mimic a refraction effect and estimate the average attenuation from a bilayer phantom. In the experiment, when the phantom was inserted and centered on the acoustic axis, the position of the focus shifted 0.75 mm along the y axis and 0.25 mm along the x axis [Figs. 8(a) and 8(c)]. The phantom orientation relative to the beam axis was relatively well controlled by mechanical fixturing for angular alignment around the horizontal x axis. However, alignment around the vertical y axis was only controlled visually. Hence, the unexpected shift of the focus by 0.25 mm along the x axis is likely explained by an angular phantom misalignment of approximately 15 degrees. In the simulations, the focus shifted 0.3 mm along the y axis [Figs. 8(b) and 8(d)], which is in reasonable agreement with measurements. Assuming that the beam travels through half-BG and half-PVA and two Mylar sheets as implied by Eq. (6), a reduction to 86.8% of the free field value was expected, which agrees well with the measured maximum pressure amplitude drop to 83.2%. In simulations, the pressure dropped to 85.1% of the maximum pressure simulated in the free field. This insertion loss introduced by the phantom was predicted within 2% of measured values based on independent measurements of the phantom material properties. The measured –6 dB beam area behind the wedge phantom changed from 1.0 mm² in the free field to 0.94 mm², and the simulated –6 dB beam area changed from 0.81 mm² to 0.9 mm². These measurements and simulations of the focal shift, focal pressure amplitude, and –6 dB beam area suggested that the wedge phantom introduced the expected refraction effect and did not induce significant aberrations.

The distortion of the linear field caused by the aberrating phantom is illustrated in Figs. 8(e) and 8(f). Relative to the free field case, both measurements and simulations show that the aberrating phantom shifts the focal position, yields significant reduction in the focal pressure amplitude, and smears the beam over a larger area. In the measurements, the focus is shifted by 1 mm along the y axis and 0.75 mm along the x axis. The maximum pressure amplitude is heavily reduced to 42.9% of the value in the free field. This pressure reduction is a combination of attenuation and aberration effects. To isolate the effect of aberration, the same estimate of attenuation (86.8% of the maximum in free field) for a bilayer phantom can be applied yielding almost twofold reduction (49.4%) of the maximum pressure amplitude caused by aberrations. In simulations, the focal position shifted by 0.3 mm along the y axis and 0.3 mm along the x axis. The maximum pressure was reduced to 48.1% of the free field value due to both attenuation and aberrations or to 53.2% due to a pure aberration effect, which is within 4% of the experimental values. The –6 dB beam area changed from 1.0 mm² in the free field to 4.6 mm² behind the phantom in the measurements and from 0.81 mm² to 3.5 mm² in simulations. Due to uncertainties in the as-tested geometry of the aberrating phantom, the simulation and measurement results for the shift in location of the peak pressure, focal beam shape, and beam area do not agree with very high accuracy. However, a relatively accurate peak pressure is predicted at the focus. Overall, significant reduction in peak pressure, focal shift, and the larger –6 dB beam area behind the aberrating phantom suggest that the phantom indeed produces strong aberrations.

To better understand the breadth of the possible aberration effects that the proposed phantom can produce, a series of four additional simulations was performed with the phantom shifted by 1.2 cm along each of the four lateral directions (i.e., +x, –x, +y, and –y). Again, the position of maximum pressure in 3D space was axially displaced 1 mm or less from the analyzed transverse pressure fields. Qualitatively, the pressure distributions in the focal plane are very similar to the plot in Fig. 8(f) with one large, smeared lobe and one or two smaller lobes. The –6 dB levels for the four simulated fields ranged from 1.9 mm² to 4.1 mm², indicating that the results presented in Fig. 8(f) demonstrate representative effects produced by the phantom.

C. Nonlinear acoustic field measurement results

Nonlinear measurements were recorded behind the tissue mimicking phantoms to further characterize their performance in HIFU applications. Nonlinear focal waveforms were collected with and without each phantom in the propagation path in the same way as done for the linear field measurements. After a phantom was inserted and centered relative to the acoustic axis of the transducer, the beam focus was displaced. The fiber optic hydrophone was positioned at the new focus in 3D space for all nonlinear measurements.

The wedge phantom shifted the focus 0.45 mm in the y direction and 0.2 mm axially in the z direction at a 15 V drive level. To compensate for attenuation of the phantom, a derating method was used to scale the system voltage for the waveforms measured behind the phantom in order to directly compare them with the free field waveforms⁴⁴ using Eq. (7) as described in Sec. II D. With this method developed for focused nonlinear fields, a derating factor $V_{\mathit{derated}}/V_{\mathit{water}}$ can be used to increase the source output level such that the nonlinear focal waveform under free-field conditions can be recovered if the beam propagates through an attenuative (but not aberrative) medium. Using the Eq. (7) and assuming the beam passes through half-BG and half-PVA and the Mylar sheets (h = 2 cm, T_Mylar = 0.96), the derating factor for the source's driving voltage is calculated to be 1.16. Figure 9(a) shows a free field focal waveform with a shock front as measured at a 15 V drive level. The same plot also shows the focal waveform measured behind the wedge phantom at both 15 V and 17 V drive levels, with the 17 V waveform expected to match free field conditions based on the derating strategy. Because this 17 V waveform does indeed closely match the free field waveform, it is demonstrated that the wedge phantom does not introduce significant aberration in the nonlinear regime and the reduction in peak pressures at the focus is due to attenuation losses. Considering a range of drive levels in water, Fig. 10(a) shows a trend of good agreement in peak positive and peak negative pressures between free field waveforms and corresponding derated waveforms.

FIG. 9.

(Color online) Nonlinear waveforms measured through water, phantoms, and ex vivo body wall, including derated waveforms to compensate for attenuation in the presence of a phantoms or body wall. (a) Comparison of focal waveforms for propagation through water (free field) and the wedge phantom. (b) Focal waveforms through water and aberrating phantom. (c) Focal waveforms through water and 4-cm thick body wall.

FIG. 10.

(Color online) Peak positive and negative focal pressures vs voltage including derated data to account for attenuation of the phantoms when propagating (a, b) in water only, (a) through the wedge phantom, and (b) through the aberrating phantom.

The impacts of the aberrating phantom were similarly quantified in the nonlinear regime. With the phantom, the nonlinear focus shifted 0.35 mm along the y axis, 0.2 mm along the x axis, and 2.28 mm along the z axis. To account for attenuation, we again use the derating method to scale the voltage output by a factor of 1.16. Figure 9(b) shows focal waveforms after propagation through water or through the aberrating phantom with or without derating. Insertion of the phantom suppresses formation of the shock in the focal waveform even at the derated drive level. The free field waveform with 75.4 MPa peak positive pressure is significantly different from the derated waveform (17.9 MPa) with the phantom, which suggests that the phantom induces heavy aberration in the nonlinear regime. Figure 10(b) shows this trend of significantly different peak positive pressures for water and derated phantom waveforms over a range of drive levels.

A real porcine body wall of approximately 4 cm thickness was inserted in the propagation path to compare with the aberrating phantom. Our experience with ex vivo abdomen body wall sections shows that there is a large variability between body wall samples and even variation among different positions along the same body wall. The presented measurements are not meant to be exhaustive, but serve as an example. To determine the levels of aberration, we can derate the waveforms behind the body wall. We did not measure the attenuation for this section of tissue, so we chose an attenuation value of 1.6 dB/cm.^51,52 This value is within a reasonable range and allows us to use waveforms from a collected data set. Figure 9(c) shows focal waveforms behind a body wall derated from 15 to 32 V. The derated waveform is heavily aberrated and is not shocked. Our final observation is that if we compare the derated waveform behind the aberrating phantom [Fig. 9(b)] and the derated waveform behind the real body wall [Fig. 9(c)], we see they are of similar peak positive pressures. This then suggests that the aberrating phantom produces aberrations that are similar to those of a real body wall.

IV. DISCUSSION AND CONCLUSIONS

A novel tissue-mimicking phantom of a porcine body wall was proposed as a research tool for pre-clinical HIFU applications. A successful phantom would produce similar aberrations to a real porcine abdominal body wall. Our approach was to design, fabricate, and acoustically characterize such an aberrating phantom.

The proposed approach was initiated with a mathematical design to generate inhomogeneities that are of similar sizes found in a real porcine abdominal body wall. The method of random Fourier modes yielded a random surface with ripples that corresponded to a large range of spatial harmonics. A mold for this surface was fabricated by 3D printing, which is an approach that allows for inter- and intra-laboratory replicas to be made. Another aspect of the aberrating phantom design is the presence of a bilayer structure that mimics real body walls. The phantom was fabricated with a fat-like material layer and tissue-like material layer. Careful material selection to match the sound speeds of the phantom materials to porcine fat and muscle was critical for producing the desired aberration effect.

One aspect of our approach was to measure the impact of the aberrating phantom on the linear acoustic field. Two-dimensional scans in the focal plane gave insight into how the focal region is distorted. A wedge phantom was also used to mimic refraction effect and quantify the effects of attenuation from a bilayer phantom. The principle aim for the aberrating phantom is for HIFU applications, but the phantom may be useful for other ultrasound applications through the body wall such as acoustic object manipulation.⁵⁸

Another aspect of this effort involved simulating pressure fields in the linear regime. Using the free k-Wave toolbox, we simulated the experimental configuration for propagation through both phantoms. Simulations demonstrate that quantitative comparisons can be made despite challenges in explicitly controlling the orientation of large, soft phantoms. More specifically, simulated insertion loss values were predicted within 3% of measured values for both bilayer phantoms. Although the simulated shift in the location of peak focal pressure and the change in beam area introduced by each phantom agreed less well with measurements, the predicted changes were of the same magnitude. Overall agreement between the experiment and simulation helps in validating that the experimental attenuation values were measured correctly and that the experimental geometries were controlled reasonably well. Following other efforts to rigorously compare simulated and measured fields in the presence of an inhomogeneous propagation path,⁵⁹ future work will aim to predict linear and nonlinear fields distorted by inhomogeneities relevant to abdominal HIFU treatments.

A final aspect of our approach was to measure the impact of the aberrating phantom on the nonlinear acoustic field. A clear trend was discerned: peak positive pressures in the focal waveforms in water were significantly higher than those in focal waveforms measured behind the aberrating phantom even after attenuation was accounted for. This trend means that the aberrating phantom produced high levels of aberration, which were shown to be quantitatively similar to the aberrations induced by a real porcine body wall.

The stability and ease of use of the aberrating phantom is well suited for developing phase aberration correction methods. Aberration correction methodologies calculate and input phase delays on the elements of a transducer array to mitigate the detrimental effects of phase aberrations. While it is possible to perform certain HIFU clinical treatments without correction for aberration, treatments are limited to specific applications and targets.^8,60 It is therefore imperative to develop robust aberration correction techniques to expand the breadth of HIFU applications.

This study therefore presents a model of a bilayer gel phantom than adequately mimics the aberrative properties of a porcine body wall for both linear and strongly nonlinear HIFU fields. The phantom can be used as a research tool for evaluating the effects of aberrations in various medical ultrasound applications as well as for developing and testing aberration correction algorithms.