A single-shot measurement of time-dependent diffusion over sub-millisecond timescales using static field gradient NMR

Abstract

Time-dependent diffusion behavior is probed over sub-millisecond timescales in a single shot using a nuclear magnetic resonance static gradient time-incremented echo train acquisition (SG-TIETA) framework. The method extends the Carr–Purcell–Meiboom–Gill cycle under a static field gradient by discretely incrementing the π-pulse spacings to simultaneously avoid off-resonance effects and probe a range of timescales (50–500 µs). Pulse spacings are optimized based on a derived ruleset. The remaining effects of pulse inaccuracy are examined and found to be consistent across pure liquids of different diffusivities: water, decane, and octanol-1. A pulse accuracy correction is developed. Instantaneous diffusivity, D_inst(t), curves (i.e., half of the time derivative of the mean-squared displacement in the gradient direction) are recovered from pulse accuracy-corrected SG-TIETA decays using a model-free log-linear least squares inversion method validated by Monte Carlo simulations. A signal-averaged 1-min experiment is described. A flat D_inst(t) is measured on pure dodecamethylcyclohexasiloxane, whereas decreasing D_inst(t) is measured on yeast suspensions, consistent with the expected short-time D_inst(t) behavior for confining microstructural barriers on the order of micrometers.

I. INTRODUCTION

As molecules diffuse, they interact with their surroundings and “[feel] the boundary,”¹ causing their ensemble displacement behavior to be influenced by the morphology of the microenvironment. More specifically, long-range correlations such as confining barriers impart a nonlinear time-dependence to the ensemble-averaged net mean-squared displacement, $⟨{\mathbf{r}}^2\left(t\right)⟩$ (in ${\mathbb{R}}^3$). This leads to a time-dependent diffusion coefficient,^2,3

$$D\left(t\right)=\frac{⟨{\mathbf{r}}^2\left(t\right)⟩}{6t}\equiv \frac{1}{3t}{\int }_0^t\left(t-t^{\prime }\right)\mathrm{t}\mathrm{r}\left(\mathcal{D}\left(t^{\prime }\right)\right)d{t}^{\prime },$$ (1)

where $\mathcal{D}\left(t^{\prime }\right)=H\left(t^{\prime }\right)⟨\mathbf{v}\left(t^{\prime }\right){\mathbf{v}}^{\mathrm{T}}\left(0\right)⟩\equiv {\partial }_t^2\left[H\left(t\right)⟨\mathbf{r}\left(t\right){\mathbf{r}}^{\mathrm{T}}\left(0\right)⟩\right]$ is the causal velocity autocorrelation tensor, H(t) is the unit step function, and “tr” is the trace operation.

Microstructural features can be inferred from the behavior of D(t) at limiting short and long timescales (see Refs. 4 and 5 for review). At the short-time limit, D(t) exhibits universal behavior,² which depends on the barrier surface-to-volume ratio, S/V,

$$D\left(t\right)\simeq D_0\left[1-\frac{S}{V}\left(\frac{4{\ell }_D}{9\sqrt{\pi }}\right)\right],t\to 0,$$ (2)

where ${\ell }_D=\sqrt{D_{0}t}$ is the diffusion length scale and D₀ ≡ D(t)|_t=0 is the free diffusivity. As ℓ_D increases, the barrier permeability, κ, may begin to affect D(t).^6–9 While ℓ_D remains short, barriers appear flat to the small fraction of nearby walkers that encounter them,^8,10 introducing a linear κt term in Eq. (2),

$$D\left(t\right)\simeq D_0\left[1-\frac{S}{V}\left(\frac{4{\ell }_D}{9\sqrt{\pi }}-\kappa t\right)\right],t\ll {\tau }_D,$$ (3)

where ${\tau }_D={ā}^2/\left(2D_0\right)$ is the time to diffuse across the mean pore of size $ā=6V/S$. Curvature⁸ and surface relaxivity³ may also affect D(t). Tortuosity principally affects the long-time D(t)^11,12 and can be categorized into disorder classes with the structural exponent, p.^10,13 The long-time D(t) follows a p-dependent power law,¹³

$$D\left(t\right)\simeq D_{\infty }+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\cdot t^{-𝜗},t\to \infty ,$$ (4)

where D_∞ = lim_t→∞D(t) and ϑ = (p + 3)/2.

Diffusion-weighted (DW) nuclear magnetic resonance (NMR) methods are highly sensitive to ⟨r²(t)⟩^14–20 and provide a powerful means to probe rich D(t) behaviors and infer distinct microstructural features. DW-NMR experiments have been used to study the short- and long-time D(t) in porous media ranging from sedimentary rocks to skeletal muscles.^{5,12,13,21–25}

The NMR spin echo dephasing, however, is not simply written in terms of D(t) itself. Instead, the echo dephasing is often expressed in terms of the real part, $\mathfrak{R}$, of the Fourier transform of $\mathcal{D}\left(t\right)$.^26–28 From Eq. (1),²⁸

$$\frac{\mathrm{t}\mathrm{r}\left(\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]\right)}{3}=D_0+{\int }_0^{\infty }{\partial }_t^2\left[tD\left(t\right)\right]e^{i\omega t}dt.$$ (5)

High and low frequency $\mathrm{t}\mathrm{r}\left(\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]\right)$ behaviors reveal the short- and long-time D(t), respectively. The relationship between $\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]$ and the ensemble echo dephasing follows from a cumulant expansion of the phase expectation value and a Gaussian phase distribution approximation,²⁹ yielding the normalized echo intensity,^30,31

$$\frac{I\left(T\right)}{I_0}=\exp \left(-\frac{1}{\pi }{\int }_0^{\infty }{\mathbf{F}}^{\mathrm{T}}\left(\omega \right)\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]\mathbf{F}\left(\omega \right)d\omega \right),$$ (6)

where F(ω) is the truncated Fourier transform of F(t) at the echo time, T [i.e., F(T) = 0],

$$\mathbf{F}\left(\omega \right)={\int }_0^T\mathbf{F}\left(t\right)e^{i\omega t}dt,$$ (7)

where $\mathbf{F}\left(t\right)=\gamma {\int }_0^t\mathbf{G}\left(t^{\prime }\right)d{t}^{\prime }$, G(t) is the gradient waveform, and γ is the gyromagnetic ratio. The assumed Gaussian phase approximation is valid for most relevant experimental cases (cf. Ref. 32).^33,34

Equations (6) and (7) show that spectral tuning of |F(ω)|² results in the narrow sampling of $\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]$ in the gradient direction, $\widehat{\mathbf{g}}$. G(t) can be periodically time-modulated³⁵ [e.g., by using a sinusoidal G(t)²⁴] so that the spectral density of |F(ω)|² concentrates near some frequency, ω_F. In this case, I(T)/I₀ becomes well-approximated by $\exp \left(-b\left(T\right)\times {\widehat{\mathbf{g}}}^{\mathrm{T}}\mathfrak{R}\left[\mathcal{D}\left({\omega }_F\right)\right]\widehat{\mathbf{g}}\right)$, where¹⁶

$$b\left(T\right)={\int }_0^T{\left|\mathbf{F}\left(t\right)\right|}^{2}dt\equiv \frac{1}{\pi }{\int }_0^{\infty }|\mathbf{F}\left(\omega ,T\right){|}^{2}d\omega .$$ (8)

Individual experiments become a point-wise sampling of ${\widehat{\mathbf{g}}}^{\mathrm{T}}\mathfrak{R}\left[\mathcal{D}\left({\omega }_F\right)\right]\widehat{\mathbf{g}}$. This “temporal diffusion spectroscopy”³⁶ approach is robust but has limited time resolution because it individually probes ω_F. Furthermore, the shortest probe-able timescale (i.e., largest ω_F) is limited to about 10 ms by the pulsed gradient hardware.^5,36 An alternative approach is needed for the real-time study of D(t) across timescales and to reach the information-rich short-time regime (≲1 ms) in biological systems. Static gradient (SG) hardware permits extremely fast cycling of the effective gradient direction using radiofrequency (RF) π-pulse trains and thereby provides access to these timescales.^23,35 Here, we extend the classical Carr–Purcell–Meiboom–Gill (CPMG)^37,38 experiment under an SG in the RF field to probe the time-varying sub-millisecond diffusivity in one shot.

II. THEORY

A. Time-dependent signal representation

To begin, an alternative signal representation is used. The echo attenuation is related to the stationary position autocorrelation tensor, $\mathcal{R}\left(t,t^{\prime }\right)=⟨\mathbf{r}\left(t\right){\mathbf{r}}^{\mathrm{T}}\left(t^{\prime }\right)⟩\equiv \mathcal{R}\left(|t-t^{\prime }|\right)$—again assuming a Gaussian phase distribution^30,31,39—by

$$\frac{I\left(T\right)}{I_0}=\exp \left(-\frac{{\gamma }^2}{2}{\int }_0^T{\int }_0^T{\mathbf{G}}^{\mathrm{T}}\left(t\right)\mathcal{R}\left(t,t^{\prime }\right)\mathbf{G}\left(t^{\prime }\right)dtd{t}^{\prime }\right).$$ (9)

Equation (9) can be rewritten according to Ning et al.³⁹ by integrating along the level set of t − t′. For unidirectional encoding, i.e., G(t) = $\Vert$G(t)$\Vert$ and $F\left(t\right)=\gamma {\int }_0^{t}G\left(t^{\prime }\right)d{t}^{\prime }$,

$$\frac{I\left(T\right)}{I_0}=\exp \left(-{\int }_0^T\mathcal{C}\left(t\right)D_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)dt\right),$$ (10)

where D_inst(t) is the instantaneous diffusivity along the gradient direction $\widehat{\mathbf{g}}$,

$$D_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)≔{\partial }_t\left[\frac{{\widehat{\mathbf{g}}}^{\mathrm{T}}\mathcal{R}\left(t\right)\widehat{\mathbf{g}}}{2}\right]\equiv {\partial }_t\left[\frac{⟨{\left[\mathbf{r}\left(t\right)\cdot \widehat{\mathbf{g}}\right]}^2⟩}{2}\right],t>0$$ (11)

(dropping $\widehat{\mathbf{g}}$ as implied) and $\mathcal{C}\left(t\right)$ is the cumulative integral of the γG(t) autocorrelation function,

$$\begin{array}{c}\mathcal{C}\left(t\right)={\int }_0^t\mathcal{G}\left(t^{\prime }\right)d{t}^{\prime },\\ \mathcal{G}\left(t^{\prime }\right)={\gamma }^2{\int }_0^{T}G\left(t^{\prime }\right)G\left(t^{\prime }+s\right)ds,\end{array}$$ (12)

schematized in Fig. 1. The attenuation becomes a sampling of D_inst(t) weighted by $\mathcal{C}\left(t\right)$ similar to how Eq. (6) describes a sampling of $\mathfrak{R}\left[\mathcal{D}\left(\omega \right)\right]$ by |F(ω)|².

FIG. 1.

Example $\mathcal{G}\left(t\right)$ calculation. (a) Radiofrequency (RF) pulses in a static gradient of amplitude g. (b) G(t), shifted G(t + s) (red, dashed), and F(t). (c) Corresponding $\mathcal{G}\left(t\right)$. G(t) is assumed to be zero outside of t = [0, 2τ].

B. Recasting the problem

Equation (10) is advantageous compared to Eq. (6) because $\mathcal{C}\left(t\right)$ is simple for general non-periodic G(t). The ill-posed inverse problem of finding D_inst(t) from many trivial G(t) is tractable. For a train of N echoes refocusing at times T_n, ${\mathcal{C}}_n\left(t\right)$ can be evaluated for each inter-echo attenuation I(T_n)/I(T_n−1) (T₀ = 0); that is, each pair of adjacent echoes can be treated as an independent spin echo diffusion measurement. The problem is then recast as a weighted and regularized log-linear least squares (LLS) inversion by discretizing the time domain into K bins of variable width, Δt(k),

$$\underset{\mathbf{X}}{argmin}\Vert {\mathbf{W}}^{1/2}{\left(\mathbf{A}\mathbf{X}-\mathbf{B}\right)\Vert }_2^2+\lambda \Vert \mathbf{\Gamma }{\mathbf{X}\Vert }_2^2,$$ (13)

with coefficients

$$\mathbf{A}=\left[\begin{array}{ccc}\hfill {\int }_0^{\mathrm{\Delta }t\left(1\right)}{\mathcal{C}}_1\left(t\right)dt\hfill & \hfill \dots \hfill & \hfill {\int }_{\mathrm{\Delta }t\left(K-1\right)}^{\mathrm{\Delta }t\left(K\right)}{\mathcal{C}}_1\left(t\right)dt\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill {\int }_0^{\mathrm{\Delta }t\left(1\right)}{\mathcal{C}}_N\left(t\right)dt\hfill & \hfill \dots \hfill & \hfill {\int }_{\mathrm{\Delta }t\left(K-1\right)}^{\mathrm{\Delta }t\left(K\right)}{\mathcal{C}}_N\left(t\right)dt\hfill \end{array}\right],$$

where X consists of time-interval D_inst(t) averages,

$$\mathbf{X}=\left[\begin{array}{c}\hfill \frac{1}{\mathrm{\Delta }t\left(1\right)}{\int }_0^{\mathrm{\Delta }t\left(1\right)}{D}_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)dt\hfill \\ \hfill ⋮\hfill \\ \hfill \frac{1}{\mathrm{\Delta }t\left(K\right)-\mathrm{\Delta }t\left(K-1\right)}{\int }_{\mathrm{\Delta }t\left(K-1\right)}^{\mathrm{\Delta }t\left(K\right)}{D}_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)dt\hfill \end{array}\right],$$

and ${\mathbf{B}}^{\mathrm{T}}=-\ln \left[\begin{array}{ccc}\hfill I\left(T_1\right)/I_0\hfill & \hfill \dots \hfill & \hfill I\left(T_N\right)/I\left(T_{N-1}\right)\hfill \end{array}\right]$. The regularization matrix, Γ, is chosen to consist of first and second-order finite difference matrices, reflecting an a priori assumption of the smoothness and concavity of D_inst(t). The choice of N is dictated by the echo signal decay to the noise floor. The choice of K and Δt(k) is more arbitrary. As a preliminary heuristic, K should be similar in magnitude to N, and Δt(k) should be chosen such that (1) D_inst(t) does not vary greatly over any interval and (2) the ${\mathcal{C}}_n\left(t\right)$ integrals that comprise the entries of A are appreciable. Considering the behavior of Eqs. (3) and (4), Δt(k) should start out small and may gradually lengthen. The norm is weighted by a proportionality of the signal-to-noise ratio (SNR); since B consists of log ratios, the appropriate weights matrix, W, is an N × N matrix of signal differences, i.e., I(T_n−1) − I(T_n). In this way, D_inst(t) can be estimated from a single echo train with varied ${\mathcal{C}}_n\left(t\right)$.

The motivating question of this Communication is as follows: Can a DW-NMR method probe the time-varying diffusivity in real-time? With Eq. (13) in mind, the question can be separated into two parts: (1) How can ${\mathcal{C}}_n\left(t\right)$ of various time sensitivities be produced in one echo train? (2) How can every echo be made accurate? The answer to the first part follows from a well-known DW-NMR protocol. As mentioned, the SG-CPMG experiment can produce rapid effective gradient oscillation characterized by a triangle wave F(t) with ω_F = (π/2τ) rad/s, where 2τ is the spacing between π-pulses. This SG-CPMG ω_F (up to tens of kilohertz²³) exceeds that which is attainable with oscillating or pulsed field gradient (PFG) methods (up to ∼100 Hz). As a result, the SG-CPMG method is uniquely able to probe the short-time diffusion regime in small ($ā\lesssim \mu$m) structures.^{23,35,40–44} Stimulated echoes represent another candidate DW-NMR method but are ill-suited to single-shot multi-echo acquisitions due to the signal loss inherent to π/2-pulses.

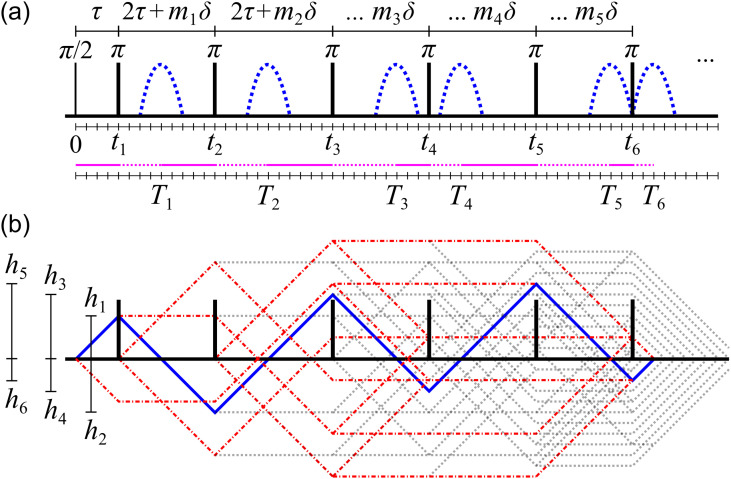
Varying the spacing of the π-pulses in an SG-CPMG styled acquisition is thus the preferred method to produce various ${\mathcal{C}}_n\left(t\right)$ in one shot. Others have explored the concept of modifying SG-CPMG pulse spacings to measure time-varying diffusion but ultimately retained a π-pulse train with repeated spacing.⁴⁴ We extend such methods by modifying every π-pulse spacing. Spacings can be incremented to retain the signal. We choose the spacing between π-pulses to take the form 2τ + m_jδ, where j indexes the π-pulse-to-pulse spacing, $m_j\in \mathbb{N}$, and δ is a unit time increment. We term this discrete spacing method the SG time-incremented echo train acquisition (SG-TIETA), e.g., see Fig. 2. For SG-TIETA,

$${\mathcal{C}}_n\left(t\right)={\gamma }^2{g}^2\left\{\begin{array}{cc}t\left(-\frac{3}{2}t+2h_n\right),\hfill & 0\le t\le h_n,\hfill \\ t\left(\frac{1}{2}t-h_n\right)+2h_n^2,\hfill & h_n\le t\le 2h_n,\hfill \end{array}\right.$$ (14)

where h_n is the nth peak of |F(t)|/γg. According to Eq. (14), the nth inter-echo interval probes D_inst(t) over the time interval [0, 2h_n], with a peak at h_n. With the core experimental method described, we turn toward the problem making each echo accurate. An initial step is to isolate the direct echo pathway.

FIG. 2.

Example SG-TIETA sequence. (a) Timings: m_j = {1, 3, 1, 2, 1}, τ = 4δ, and δ = 14 µs = 1 dash. π-pulses occur at t_n, and direct echoes (blue lines) form at T_n. Magenta line indicates timing behavior: T_n = t_n + h_n, where h_n is the normalized |F(t)|/γg “height” at t_n given by h₁ = τ and h_n = 2τ + m_nδ − h_n−1 for n > 1. (b) Direct echo F(t) and other coherence pathways that refocus (red dashed-dotted lines) or do not refocus (gray dotted lines). Relative values of h_n are indicated.

C. Isolating the direct echo pathway in the time domain

Ignoring the effects of magnetic susceptibility, surface relaxivity,³ and spin–spin (T₂) relaxation (for the meantime), the predominant source of extraneous signal behavior is off-resonance coherence transfer pathways (CTPs). When the bandwidth of Larmor precession frequencies spanned by an SG exceeds the bandwidth of π-pulses, every pulse is slice-selective and excites all CTPs.²⁰ For SG-CPMG measurements, the number of refocused off-resonance CTPs grows exponentially with N (∼3^N),⁴⁵ resulting in significant deviations from the expected echo attenuation.^45–48 Phase cycling remediation schemes require ∼2^N steps⁴⁹ and are thus infeasible. Unconventional approaches such as time-based avoidance of CTPs^50,51 become necessary. An SG aids these time-based approaches by acting as an always-on crusher gradient. The minimum time separation to avoid the undesired signal, τ_sep, is shortened. Specifically, τ_sep is constrained by τ_sep ≥ τ_p, where τ_p = 2π/(γgΔz) is the length of the π-pulse and Δz is the resulting slice thickness. The echo width under an SG is of the order of τ_p⁵² such that this constraint can be understood as avoiding undesired echo overlap. For hard π-pulses, τ_p is on the order of ∼μs.

In the interest of acquiring an accurate direct echo CTP, we should ask the following question: What choice of m_j, τ, and δ separates off-resonance CTPs from the direct echo CTP by ≥τ_p? Consider that CTPs are piecewise linear functions in F(t). The three magnetization states for a spin-1/2 nuclei (in shorthand: M ∈ {+, −, 0}⁴⁸) correspond to +γg, −γg, and 0 slopes, respectively [see Fig. 2(b)]. Refocusing of the undesired signal occurs when the summed difference between an off-resonance F(t) and the direct echo F(t), ∑ΔF(t), equals 0. Rules for m_j, τ, and δ are developed. Singly stimulated echoes (e.g., +0−) arise due to two h_n matching. Thus,

• (i)absolute F(t) heights, or h_n, may not be repeated.

Next, consider CTPs that see the initial π/2-pulse. These CTPs can alter ∑ΔF(t)/γg by one of $\left\{\mathrm{0,1,2}\right\}\times {\left(-1\right)}^{j-1}\left(2\tau +m_j\delta \right)$. Accounting for ∑ΔF(t) = 0 with up to four non-zero terms:

• (ii)m_j and m_j±Δj with odd Δj may not be the same.
• (iii)Twice any m_j may not equal the sum of m_j+Δj and m_j−Δj for even Δj.
• (iv)Any two m_j with even j may not equal the sum of any two m_j with odd j.
• (v)Twice any m_j with even j may not equal the sum of any two m_j with odd j and vice versa.

Another class of off-resonance CTPs is associated with the introduction of transverse magnetization from spins that incorrectly see π-pulses as initial π/2-pulses. These CTPs emerge at the time of π-pulses and thus invariably start with ∑ΔF(t) containing an odd multiple of τ (i.e., τ + 2jτ). Choosing τ and δ such that (τ mod δ) = δ/2 ensures that ∑ΔF(t) ≥ δ/2. Incorporating τ_p,

• (vi)δ and τ satisfy (τ mod δ) = δ/2 and δ > 2τ_p.

Note that (τ mod δ) = 0 results in the refocused CTPs in Fig. 2(b). The sequence in Fig. 2 does, in fact, satisfy rules (i)–(v). This limited ruleset [(i)–(vi)] may be sufficient to ostensibly avoid off-resonance effects, considering that singly stimulated echoes are known to be the most significant contributor to SG-CPMG off-resonance effects.^45,48

The generation of m_j that satisfies rules (i)–(v) is discussed in Sec. I of the supplementary material. The Python code is provided. A solution for τ, δ, and m_j, used throughout, is

$$\begin{array}{c}\tau =49\mu \mathrm{s},\delta =14\mu \mathrm{s},\\ m_j=\left\{\begin{array}{cccccccccc}\hfill 1\hfill & \hfill 3\hfill & \hfill 6\hfill & \hfill 7\hfill & \hfill 10\hfill & \hfill 12\hfill & \hfill 11\hfill & \hfill 15\hfill & \hfill 20\hfill & \hfill 21\hfill \\ \hfill 24\hfill & \hfill 26\hfill & \hfill 20\hfill & \hfill 21\hfill & \hfill 33\hfill & \hfill 35\hfill & \hfill 33\hfill & \hfill 34\hfill & \hfill 33\hfill & \hfill \dots \hfill \end{array}\right\},\end{array}$$ (15)

which gives time sensitivity over t ∼ 50–500 µs,

$$h_n=\left\{\begin{array}{cccccccc}\hfill 49\hfill & \hfill 63\hfill & \hfill 77\hfill & \hfill 105\hfill & \hfill 91\hfill & \hfill 147\hfill & \hfill 119\hfill & \hfill 133\hfill \\ \hfill 175\hfill & \hfill 203\hfill & \hfill 189\hfill & \hfill 245\hfill & \hfill 217\hfill & \hfill 161\hfill & \hfill 231\hfill & \hfill 329\hfill \\ \hfill 259\hfill & \hfill 301\hfill & \hfill 273\hfill & \hfill 287\hfill & \hfill \dots \hfill \end{array}\right\}\mu \mathrm{s}.$$

III. EXPERIMENTAL SETUP

NMR measurements were performed at B₀ = 0.3239 T (proton ω₀ = 13.79 MHz) using a PM-10 NMR MOUSE single-sided permanent magnet⁵³ (Magritek, Aachen, Germany) and a Kea 2 spectrometer (Magritek, Wellington, New Zealand). The decay of the magnetic field with a distance from the magnet produces a strong SG of g = 15.3 T/m (650 kHz/mm). Measurements used a home-built test chamber and a 13 × 2 mm² solenoid RF coil and RF circuit. Additional information concerning the experimental setup can be found in the work of Williamson et al.⁵⁴ The SG-TIETA pulse program was written in Prospa V3.22 by modifying the standard CPMG sequence. See Sec. IV of the supplementary material for details.

For measurements on twice-distilled water, decane (Sigma-Aldrich, St. Louis, MO), 1-octanol (Sigma-Aldrich), and dodecamethylcyclohexasiloxane (D6) with kinematic viscosity = 6.6 cSt @ 25 °C (Gelest, Inc., Morrisville, PA), the liquids were transferred to 2 cm glass capillary sections (1.1 mm OD, Kwik-Fil^TM, World Precision Instruments, Inc., Sarasota, FL), and the capillaries were sealed with a hot glue gun.

For measurements on yeast (S. cerevisiae), 1.72 g of dry yeast was mixed in 10 ml of tap water and stored in a 50 ml tube with the lid screwed on loosely to allow the gas to escape. After three days (72 h), the yeast was re-suspended and samples were taken for NMR experiments and for cell density measurement. The density of the first sample (yeast 1) was measured to be 2.84 × 10⁹ cells/ml using a hemocytometer. The remaining yeast was centrifuged, the pellet was rediluted to 2X the initial concentration, and a second sample (yeast 2) was taken for NMR experiments. Immediately prior to experiments, yeast was transferred to 2 cm KrosFlow^® Implant Membrane sections (500 000 Da molecular weight cutoff, 1 mm outer diameter, SpectrumLabs, Waltham, MA, USA) and the membranes were sealed by pinching the membrane with heated forceps. Yeast was kept from drying out by performing measurements immediately upon filling and sealing the capillary and by lining the inside with wet tissue paper to increase humidity.

Experiments were performed at ambient temperature. The sample temperature was monitored with a fiber optic sensor (PicoM Opsens Solutions, Inc., Québec, Canada). The average temperatures of the samples during the course of the experiments were 25 °C, 22 °C, 22 °C, 23 °C, and 24 °C for the water, decane, octanol-1, D6, and yeast, respectively.

IV. RESULTS AND DISCUSSION

As an initial proof-of-principle, the LLS inversion described in Eq. (13) was performed on noisy SG-TIETA decays generated using the timings in Eq. (15) and $⟨{\left[\mathbf{r}\left(t\right)\cdot \widehat{\mathbf{g}}\right]}^2⟩$ curves from Monte Carlo simulations,⁵⁵ as shown in Fig. 3. Further details and the MATLAB code are provided in Sec. II of the supplementary material. Inverted X values are shown to be accurate and robust to noise. No systematic errors other than potential over-regularization are observed.

FIG. 3.

LLS inversion on Monte Carlo simulated data. (a) Simulated $⟨{\left[\mathbf{r}\left(t\right)\cdot \widehat{\mathbf{g}}\right]}^2⟩$ (D₀ = 2.15 μm²/ms) for free diffusion (black) and restricted geometries (see Fig. S1). $\sum {\mathcal{C}}_n\left(t\right)$ (a.u.) for Eq. (15) is overlaid, omitting the first two echoes. (b) Echo decays simulated from same color curves in (a) for γg = 4.093 μm⁻¹ ms⁻¹. Insets show B with 2W^1/2 for the black curve and A for Δt(k) = {50, 50, 50, 50, 75, 75, 125, 139} μs. (c) D_inst(t) from the gradient of $⟨{\left[\mathbf{r}\left(t\right)\cdot \widehat{\mathbf{g}}\right]}^2⟩$ curves in (a) (solid lines) compared to X inverted from decays in (b) with added Gaussian noise (SNR = 25). Error bars = ±1 SD from 100 replications. Initial X guesses were D₀ for the first point and D_∞ (dashed lines, {0.9, 1.45, 1.48} μm²/ms) for the remaining points. λ = 2 × 10⁻⁶ is selected manually. See Eq. (S1) for Γ.

Echo-to-echo accuracy remains experimentally difficult to achieve, however. Consider the signal decay due to T₂ and pulse inaccuracy effects.⁴⁸ Relaxation may be ignored if (2τ + m_jδ) ≪ T₂ ∀ j. Diffusion-weighted T₂ values for each sample, as shown in Table I, indicate that this condition holds for all pure liquids studied here. However, the yeast is described by a distribution of T₂ with a 5% water population with T₂ similar to $\mathrm{m}\mathrm{a}\mathrm{x}\left\{2\tau +m_j\delta \right\}=539\mu \mathrm{s}$. The instantaneous diffusion measurements of yeast may be slightly weighted by T₂ relaxation. See Sec. IV D of the supplementary material for relaxation measurement methods and a T₂ distribution analysis for yeast 2. Unlike T₂, pulse inaccuracy cannot be ignored. Inaccuracy effects may be described using an n-dependent pulse accuracy factor, A_p(n).⁴⁸ The signal is then corrected as $I\left(T_n\right)/I_0\times \left[1/{\prod }_{l=1}^n{A}_p\left(l\right)\right]$, assuming total avoidance of off-resonance CTPs via rules (i)–(vi).

TABLE I.

Relaxation times.

Sample	T1 (ms)	T2 (ms)
Water	3250	133
Decane	1340	166
Octanol-1	440	217
D6	788	292
Yeast 1 (2.84B cells/ml)	625	59
Yeast 2 (5.68B cells/ml)	319	41

Calibration A_p(n) values were approximated from decays of pure liquids, as shown in Fig. 4. Echo amplitudes were calculated as the sum of all real signal points within the echo window, which was set to 16 µs. All decays were normalized to the first echo, and each repetition consisted of 32 summed (i.e., signal-averaged) scans. To elucidate the expected A_p(n) behavior, we consider the spatial, i.e., slice effects. The bandwidth/slice excited by refocusing π-pulses has inconsistent frequency content^56,57 such that A_p(n) < 1. With each pulse, spins that rotate by angles other than π do not refocus until only a stable central slice remains. In the time domain, this slice-thinning and loss of frequency content are expected to broaden the echo width, which we experimentally verify in Fig. 5. Based on the evolution of the echo shape, A_p(n) should sharply increase and then taper. This behavior is observed in Fig. 4(c) and is consistent across liquids of vastly different D₀. Similar A_p(n) values were also obtained for τ = 77 µs (see Sec. III and Fig. S5 of the supplementary material), further supporting that A_p(n) is independent of the diffusion weighting.

FIG. 4.

SG-TIETA A_p(n) calibration using pure liquids. (a) Observed SG-TIETA decays compared to exp(−bD₀). D₀ is measured (see Sec. IV of the supplementary material) in the legend order as 2.22 ± 0.01, 1.27 ± 0.01, 0.121 ± 0.002 μm²/ms. Error bars = ±1 SD for 25, 38, and 70 repetitions, respectively. (b) Decay vs exp(−bD₀) ratio truncated at n = 12, 15, 25. Inset shows cubic spline fits. (c) A_p(n) approximated using adjacent fitted ratios.

FIG. 5.

Comparison of the direct echo SG-TIETA (blue) and CPMG (orange) attenuation and echo shape for 1-octanol with 2τ = TE = 98 ms. Echo shapes show the real (solid lines) and imaginary (dotted lines) signals normalized by the area under the real signal curve in a 16 µs window. The CPMG echo width decreases with n and stabilizes around n = 3, consistent with the approach to the asymptotic behavior described by Hürlimann and Griffin.⁵⁷ In contrast, the SG-TIETA echo width increases and stabilizes around n = 3, consistent with the direct echo CTP being preferential to the on-resonance signal (see Figs. S7 and S8 for all echo shapes and an exemplar echo decay, respectively)

Another pre-processing step is designed to mitigate the effects of early A_p(n) variability and to ensure the non-negativity of B and W entries. A piecewise linear fit of adjacent ln (I(T_n)/I₀) points vs b is performed, specifying (1) an intercept with [b, ln (I(T_n)/I₀)] = [0, 0], (2) that no slope exceeds D₀, and (3) that the piecewise slopes decrease monotonically [i.e., D_inst(t) has non-negative concavity]. Altogether, SG-TIETA decays are analyzed in five steps: (1) summing 32×, (2) normalization to the first echo, (3) $I\left(T_n\right)/I_0\times \left[1/{\prod }_{l=1}^n{A}_p\left(l\right)\right]$ correction, (4) a constrained log b domain fit to the repetition(s), and, finally, (5) the LLS inversion. This pipeline was applied to SG-TIETA decays of D6 and yeast using the 1-octanol and water A_p(n) values obtained in Fig. 4(c), respectively.

Results are summarized in Fig. 6. The D_inst(t) for D6—with D₀ = 0.114 ± 0.008 μm²/ms—is expectedly flat, thus validating the A_p(n) correction. The D_inst(t) for yeast are the key results of this Communication. For comparison, the short-time D_inst(t) predicted by Eq. (3) (i.e., $d\left[tD\left(t\right)\right]/dt$) is plotted for several S/V and κ values. Figure 6(b) indicates that $ā\simeq 2\mu$m and that a doubling of the cell density approximately halves $ā$. For yeast’s ≈4 μm spherical diameter,⁵⁸ $ā$ is calculated as 42 and 21 μm at these cell densities, suggesting contributions from sub-cellular length scales. This ensemble $ā$ estimate of ≃2 μm (≡V/S ≃ 3 μm) is within the range of estimates ($ā\sim 1-5\mu$m) reported in previous PFG and SG DW-NMR studies of similar yeast densities.^58–62

FIG. 6.

SG-TIETA decays and inverted X for D6, yeast, and water. (a) Decays analyzed as described in the text. See Sec. II of the supplementary material for fitting procedures. Error bars = ±1 SD in the legend order for 38, 3, 4, and 25 repetitions truncated at N = 34, 17, 17, and 15, respectively. Note the erratic early A_p(n) behavior. (b) X solutions. Inversion parameters are identical to Fig. 3 other than Δt(k) for D6. Initial guesses of D₀ = 2.22, D_∞ = {0.9, 1.1} μm²/ms for yeast, and D₀ = D_∞ = 0.114 μm²/ms for D6 are provided. Zoomed-in plot compares short-time D_inst(t) plotted up to t < 0.08 × τ_D.

Several factors may contribute to the discrepancy between the experimental and the predicted short-time D_inst(t). On the numerical side, over-regularization may artificially flatten D_inst(t) at short times, as shown in Fig. 3. Values of X are also plotted inexactly at the midpoints of ∑_kΔt(k). On the theoretical side, Eq. (3) does not include a term for the curvature, which may be significant at these timescales for sub-cellular water. Consider, also, the confounding effects of T₂, surface relaxation, the Gaussian phase approximation, and the assumption of echo number translation invariance [i.e., that each C_n(t) is presumed to start from t = 0]. Echo number translation invariance does not hold for spatially heterogeneous microenvironments. If different water pools exhibit varying decay rates, the relative signal contributions will depend on the echo number, n. Indeed, spatial heterogeneity and the resulting weighting toward slowly decaying water pools at larger n may explain the convergence of the yeast X values. These yeast results are thus non-quantitative. Nonetheless, the sensitivity of SG-TIETA to apparent microstructural features is clear.

V. CONCLUSIONS

We have developed a real-time protocol to measure time-varying diffusion. Inversion for D_inst(t) from experimental SG-TIETA decays is demonstrated. An ∼1-min (32× repetition time of 2 s) experiment is described. In contrast to conventional temporal diffusion spectroscopy methods, the single-shot nature of SG-TIETA permits true signal averaging in order to improve the SNR. A post hoc A_p(n) correction is proposed to improve the quantitative accuracy of the method. To support the validity of this correction, we present preliminary evidence in the observed echo shape behavior and in the consistency of A_p(n) values across different diffusion weightings. Regarding potential applications, SG-TIETA at this g can probe the porous media microstructure on micrometer length scales, i.e., over sub-millisecond timescales. SG-TIETA can also be used to study the phenomena associated with other long-range correlations, e.g., polymer dynamics,⁶³ the glass transition,⁶⁴ and high Pèclet fluxes driven by flagella,⁶⁵ which likewise exhibit time-dependence in this sub-millisecond range. The methods contained in this Communication may open new avenues of research within DW-NMR.

SUPPLEMENTARY MATERIAL

See the supplementary material for (I) the Python code to generate m_j, (II) the representative MATLAB code for the Monte Carlo simulations, fitting procedures, and LLS inversion, (III) replication of the analysis in Figs. 4 and 6 using SG-TIETA decays for τ = 77 µs, and (IV) the additional NMR experimental methodology, which includes all echo shapes and a stitched echo decay for 1-octanol.

AUTHORS’ CONTRIBUTIONS

P.J.B., T.X.C., N.H.W., and V.J.W. conceptualized the work, T.X.C. developed the theory and performed computations, N.H.W., V.J.W., and R.R. designed and performed experiments, N.H.W. and T.X.C. analyzed the data, T.X.C. prepared this manuscript, and P.J.B. supervised the project. All authors edited this manuscript.

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding author upon reasonable request. The SG-TIETA pulse program and macro can be downloaded from the GitHub repository: https://github.com/nathanwilliamson/SG-TIETA.