Abstract
It is challenging to parameterize the force field for calcium ions (Ca2+) in calcium-binding proteins because of their unique coordination chemistry that involves the surrounding atoms required for stability. In this work, we observed a wide variation in Ca2+ binding loop conformations of the Ca2+-binding protein calmodulin, which adopts the most populated ternary structures determined from the molecular dynamics simulations, followed by ab initio quantum mechanical (QM) calculations on all 12 amino acids in the loop that coordinate Ca2+ in aqueous solution. Ca2+ charges were derived by fitting to the electrostatic potential in the context of a classical or polarizable force field (PFF). We discovered that the atomic radius of Ca2+ in conventional force fields is too large for the QM calculation to capture the variation in the coordination geometry of Ca2+ in its ionic form, leading to unphysical charges. Specifically, we found that the fitted atomic charges of Ca2+ in the context of PFF depend on the coordinating geometry of electronegative atoms from the amino acids in the loop. Although nearby water molecules do not influence the atomic charge of Ca2+, they are crucial for compensating for the coordination of Ca2+ due to the conformational flexibility in the EF-hand loop. Our method advances the development of force fields for metal ions and protein binding sites in dynamic environments.
I. INTRODUCTION
Calcium ions (Ca2+) are a key second messenger controlling many biological processes, such as enzyme activation, muscle contraction, and neural signal transduction. A broad spectrum of Ca2+ signals are encoded by the protein calmodulin (CaM) through specific binding with various targets that regulate CaM-dependent Ca2+ signaling pathways in neurons.1–3 CaM can bind up to four Ca2+ ions through its four helix–coil–helix (called EF-hand) structures.4 In the coil connecting the two helices, termed the EF-hand loop, there are usually six residues that cooperatively coordinate Ca2+ to form a pentagonal bipyramidal geometry [Figs. 1(a) and 1(b)]. Binding of Ca2+ in the EF-hand structure widens the angle between the two helices, as seen in the right inter-helical angle in Fig. 1(a). Although the four Ca2+ binding loops present similar helix–coil–helix structures, they show dissimilar capacities of retaining Ca2+. The two loops in the N-lobe of CaM (nCaM) bind Ca2+ faster than those in the C-lobe of CaM (cCaM), and Ca2+ dissociates faster from nCaM than from cCaM.5 The reasons are elusive and lie in the subtle difference in the amino acid sequences of the four EF-hand loops and the mobility of the water molecules packed in the loops (Table I).
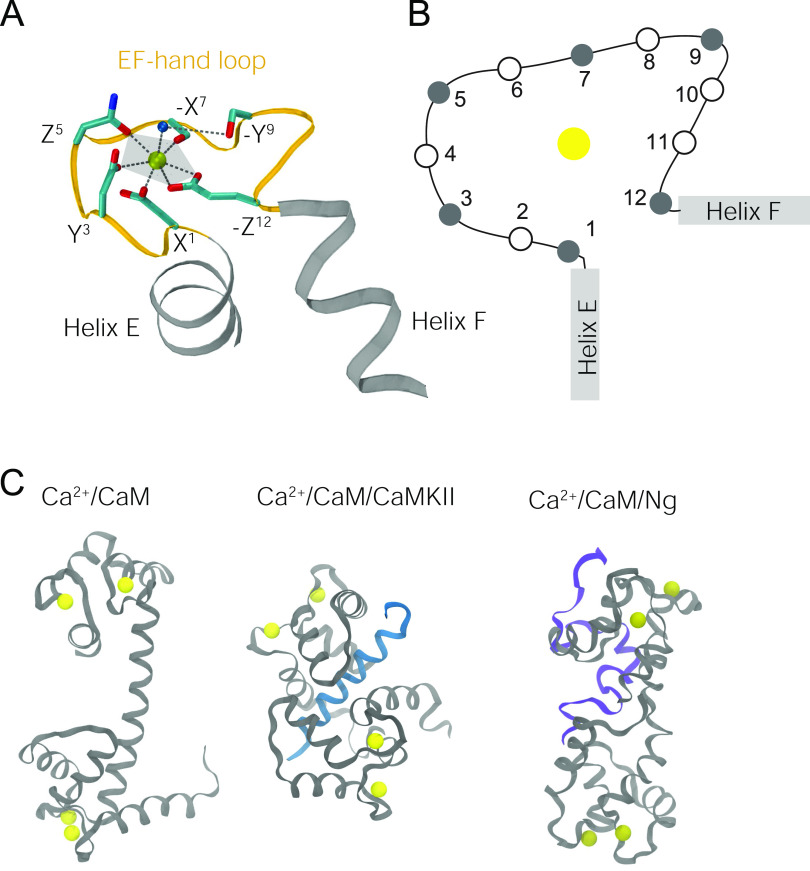
FIG. 1.
Coordination of Ca2+ in the EF-hand loops: (a) The coordination geometry in EF-hand 3 from the crystal structure of Ca2+/CaM (PDB ID: 1CLL). An EF-hand is made up of helix E (gray), EF-hand loop (orange), and helix F (gray). The Ca2+ ion is represented by a yellow bead. Side chains of the Ca2+-coordinating residues in the EF-hand loop are represented by sticks (coloring: red → oxygen; cyan → carbon; blue → nitrogen). The oxygen atom of the bridging water molecule is represented as a blue bead. The coordination positions of the Ca2+ ion are denoted (±X, ±Y, and ±Z). (b) Schematic illustration of the positions of the residues in an EF-hand loop. The filled circles are the ones that coordinate Ca2+ (Table I). (c) Illustration of the structures of Ca2+/CaM (PDB ID: 1CLL), the Ca2+/CaM/CaMKII peptide (PDB ID: 1CDM), and the Ca2+/CaM/Ng peptide (reconstructed from previous coarse-grained simulations, as described in Sec. II A). Ca2+ is in yellow, CaM is in gray, the CaMKII peptide is in blue, and the Ng peptide is in purple. Abbreviations: CaMKII (Ca2+/CaM-dependent protein kinase II); Ng (neurogranin).
TABLE I.
Amino acid sequences of the four Ca2+ binding loops (EF-1, EF-2, EF-3, and EF-4) in calmodulin. Their coordination positions for Ca2+ ions are also provided. # denotes the residue that coordinates Ca2+ ions through backbone oxygen. * denotes the residue that indirectly coordinates Ca2+ through a water molecule.
| Residue index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coordination position | X | Y | Z | −Y# | −X* | −Z | |||||||
| nCaM | EF-1 | D | K | D | G | D | G | T | I | T | T | K | E |
| EF-2 | D | A | D | G | N | G | T | I | D | F | P | E | |
| cCaM | EF-3 | D | K | D | G | N | G | Y | I | S | A | A | E |
| EF-4 | D | I | D | G | D | G | Q | V | N | Y | E | E | |
The conformation of the calcium binding loop in CaM is finely tuned by CaM-binding proteins,6 which underscores the reciprocal relationship of transmitting calcium signals to target selection regulating downstream proteins, and vice versa, in a CaM-depending calcium signaling pathway. Such an aspect has been underappreciated in the community of molecular dynamics (MD) simulations with di-valent ions, where the charges of divalent ions are typically fixed in a mean-field approach.
MD simulations are an excellent tool to investigate the subtle difference in the calcium binding affinities in the four EF-hand loops of CaM. However, there is a lack of adequate force fields including adequate polarization effects for Ca2+ in Ca2+-binding proteins due to several major limitations. First, developing more accurate MD force fields (MDFFs) for Ca2+ and its binding component usually requires a series of computationally demanding quantum mechanical (QM) calculations to provide electronic structures whose computational cost increases quartically with the system size.7 Second, when mapping the electronic structures to a point charge in MDFFs in exchange for speed in MD simulations, the interaction between a divalent ion and its receptor protein is simplified and devoid of strong polarization as well as charge-transfer effects.8–12 Third, the Ca2+-binding component in the protein, due to structural flexibility in both the backbone and side chains, usually generates a myriad of ensemble conformations, further increasing the computational cost associated with collecting more configurations in an attempt to attain statistical significance by minimizing sampling errors.13 Even when the many-body polarization effect has been included in Ren’s ab initio calculations,11 the heavy calculation was based on single structure for a protein without the consideration of the thermodynamic effect.
In a crystal structure of the EF-hand loop, Ca2+ is coordinated in a pentagonal bipyramidal coordination geometry (Fig. 1), where Ca2+ is coordinated not only by carboxylate oxygen atoms from the side chains but also by one carbonyl oxygen atom from the backbone and the oxygen atoms from water molecules (one typical example is in the crystal structure of Ca2+/CaM, as shown in Table I). The coordination geometry is vital in stabilizing the ion.14–16 To address the many-body polarization effect11 and taking the loop flexibility into account, we derived the charges of Ca2+ using ab initio quantum calculations of the Ca2+ embedded in EF-hand loops (including coordinating water molecules) in several hundred distinct conformations. These loop conformations were based on CaM in Ca2+-retaining/Ca2+-releasing environments from the existing solved structures or all-atomistic models reconstructed from our prior work.8 The structural flexibility in the Ca2+-binding protein can cause the change in the Ca2+-coordinating atoms and charge transfer between Ca2+ and protein. We show that the derived Ca2+ charges and the charges on the protein change with the varying loop conformations. We have concluded that because of the variation in the Ca2+ charge, one set of parameters are not suitable to study the dynamics of Ca2+-protein interaction. Our method/workflow can be easily applied to other Ca2+ binding environments and other di-valent ions17,18 such as Mg2+ in cases when the coordination geometry of the cation dynamically adapts to the environment.
II. MATERIALS AND METHODOLOGY
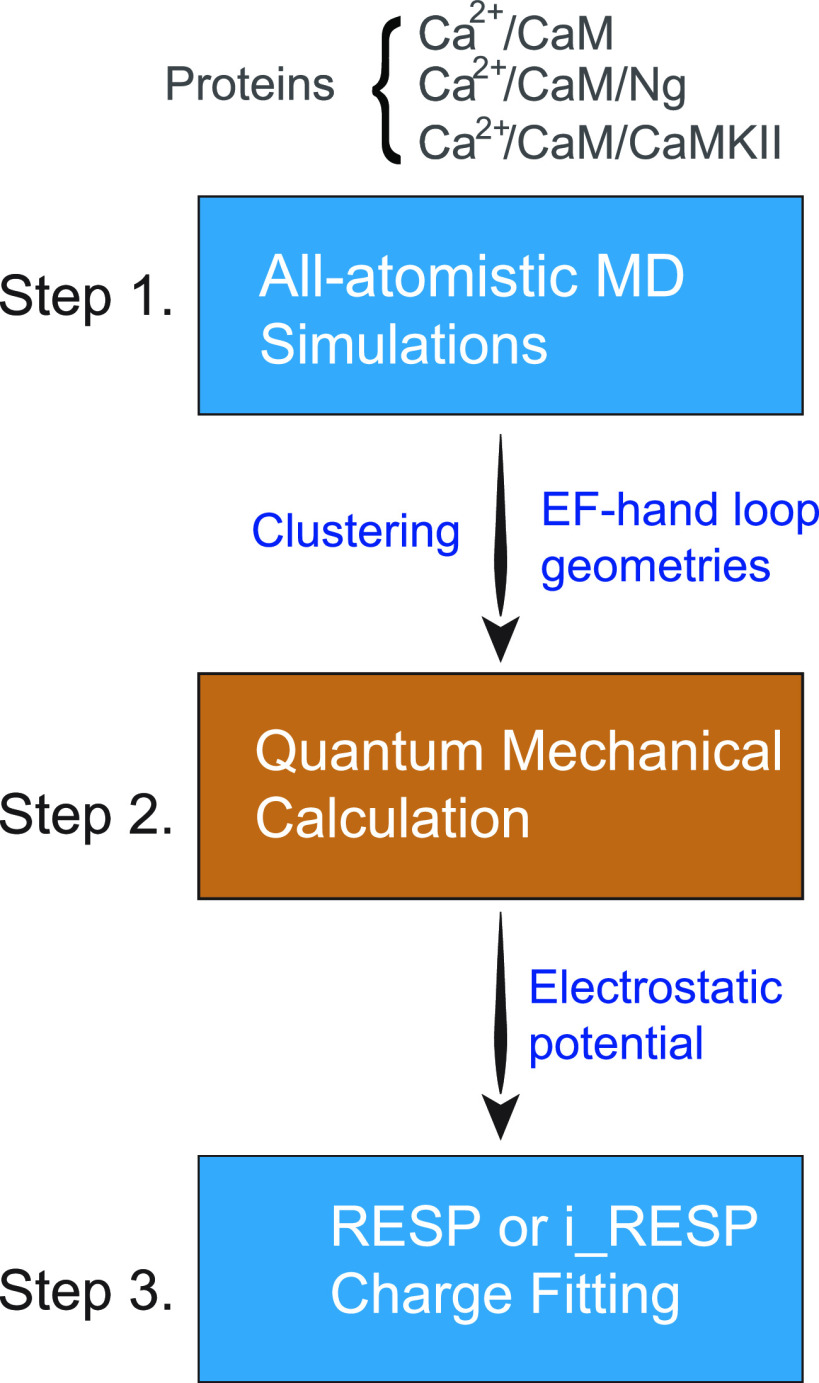
The atomic partial charge is built on the existing nonpolarizable force field (NFF)19,20 or polarizable force field (PFF) methodology21–26 taking polarization interactions into consideration. The steps to determine the atomic charges are shown in Fig. 2. The parameters of NFF and PFF have been derived using a broad collection of Ca2+-binding loops from all-atomistic MD simulations in an explicit solvent for an isolated CaM (Ca2+/CaM) or its bound complexes from an available database. This approach warrants a broad coverage of the configuration space of Ca2+ and the dynamics of its binding EF-hand loops involving the steps shown below in Fig. 2.
FIG. 2.
Flowchart of the determination of atomic charges from MD-generated geometries using the RESP/i_RESP charge fitting method.
A. Sample selections for the initial conditions
Samples of Ca2+/CaM from all-atom models in the following three conditions were examined. (1) Neat Ca2+/CaM: the crystal structure (PDB ID: 1CLL) was used as the initial structure; (2) Ca2+-retaining environment consisting of the Ca2+/CaM/CaM-dependent protein kinase II (CaMKII) peptide: the crystal structure (PDB ID: 1CDM, respectively) was used as the initial structure; (3) Ca2+-releasing environment consisting of the Ca2+/CaM/neurogranin (Ng) peptide: three representative complex structures were used as the initial structures. We reconstructed those structures into all-atomistic models from coarse-grained models with constraints inferred from the changes in the chemical shifts obtained from nuclear magnetic resonance (NMR) experiments.6,8 The coordinates of the reconstructed all-atomistic models of Ca2+/CaM/Ng are provided in the PDB format in the supplementary material.
B. Generation of the ensemble structures by molecular dynamics simulations
To generate a broad ensemble of Ca2+-binding EF-hand loop geometries, all-atom MD simulations of the three systems were performed with GROMACS version 201827 in a periodic box of ∼10 × 10 × 10 nm3 with an explicit solvent. CaM or CaM in complex with a CaM-binding target (CaMBT; CaMBT can be CaMKII or Ng peptide) was placed at least 1 nm away from the edges of the cubic box. The system was solvated by explicit water molecules using the rigid three-site TIP3P model.28 The lengths of bonds involving H atoms in the proteins were constrained using the LINCS algorithm.29 The system was neutralized by K+ and Cl− ions, maintaining a physiological ionic strength of 150 mM. The AMBER force field FF-99SB-ILDN30 was adopted. Electrostatic interactions between periodic images were treated using the particle mesh Ewald (PME) approach,31 with a grid size of 0.16 nm, fourth-order cubic interpolation, and a tolerance of 10−5. Neighbor lists were updated dynamically. A cutoff of 10 Å was used for van der Waals (vdW) interactions, for real space Coulombic interactions, and for updating the neighbor lists.
For each simulated system, energy minimization was carried out with the steepest descent method to remove unfavorable clashes between atoms. Next, the system was gradually heated to 300 K in a canonical ensemble (NVT) in 1 ns, followed by 1 ns of equilibration of the solvents and ions (the proteins were constrained in their current positions) in an isothermal–isobaric ensemble (NPT) to fix the density. The constraints on the proteins were then released, and the system was further equilibrated for 5 ns. Finally, a 100 ns NPT simulation was carried out for the production run. All NPT simulations maintained a constant pressure of 1 bar using a Parrinello–Rahman barostat.32 The equation of motion was integrated using a time step of 2 fs. Snapshots were saved for analysis every 1 ps.
In total, we generated 500 000 snapshots of Ca2+/CaM from the MD simulations. With four EF-hand loops in each CaM, we generated 2 × 106 loop structures and further applied clustering analyses to extract the most dominant configurations for the QM calculations.
C. Importance sampling of Ca2+/binding EF-hand geometries: Application of neural-net clustering to molecular dynamics snapshots
We applied a nonhierarchical clustering algorithm33 to 2M snapshots of Ca2+-binding loop geometries. We used normalized radial and angular distribution functions as the molecular feature34,35 in the neural-net clustering analysis. We focus on the chemical environment surrounding Ca2+ by using distribution functions to remove the translational and rotational degrees of freedom. The equations and description of the distribution functions are provided in the supplementary material. A common cutoff of 0.6 was used for EF-hand loops 1–4 to generate 155, 242, 215, and 164 clusters, respectively, for further ab initio calculations. In addition to the selected EF-hand loops, the corresponding Ca2+ ions and the water molecules in the first solvation shell were extracted for the QM ab initio calculations.
D. Ab initio quantum mechanical calculations
To determine the magnitude of charge transfer between Ca2+ ions and the amino acids in the calcium-binding loop, we performed a large-scale ab initio quantum mechanical calculation in terms of both the number of atoms and the number of snapshots. Ab initio calculations were conducted for loop fragments including Ca2+ ions and water molecules in the first solvation shell of Ca2+. The loop structures were capped with acetyl and methyl groups at the C- and N-termini, respectively, before performing the ab initio calculations. We explicitly included water molecules in the polarizable environment in the QM calculations instead of treating the solvent as a polarizable continuum. All ab initio calculations were performed with the Gaussian1636 program. The molecular electrostatic potential (ESP) derived from the electronic structures by the ab initio calculations was further used for fitting excess atomic charges in the context of either a nonpolarizable force field (NFF) or a polarizable force field (PFF).
E. The development of atomic charges in the nonpolarizable force field and polarizable force field
We employed the restrained electrostatic potential (RESP) and i_RESP charge fitting parameterization protocol to fit the partial atomic charges for the NFF and PFF, respectively. For PFF, the atomic charges conforming to the Thole-linear polarization model were fitted to the molecular electrostatic potentials with the i_RESP program.37 The 1–2 and 1–3 short-range interactions were excluded from the fitting, while the 1–4 long-range interactions were included. In the fitting involving water molecules, we used atomic charges and polarizabilities from the POL3 water model.38 For Ca2+ ions, we used an experimental ionic polarizability of 3.26 a.u. (0.483 Å3).39
III. RESULTS
A. The B3LYP/SVP basis set balances accuracy and computational cost in ab initio quantum mechanical calculations
As the first attempt to run QM calculations at the MP2/aug-cc-pVTZ theory level, which was used for deriving the original AMBER Thole-linear polarization force field,40 we set up small systems involving only three amino acid side chains (2 Asp and 1 Glu in EF-3) and Ca2+ ions. However, this basis set is not available for Ca2+ ions. We next mixed the aug-cc-pVTZ basis set for the side chain atoms with the cc-pVTZ basis set that is available for Ca2+ ions, but it often led to an unstable self-consistent field (SCF) process for many configurations and required a prohibitively long computation time. To stabilize the configuration by satisfying the coordination chemistry of Ca2+ ions, it is necessary to include all loop residues and water molecules from the first solvation shell.
However, once we increased the number of residues to include the entire calcium-binding loop in the QM calculations, the computational cost immediately became prohibitive. To make our large-scale QM calculations feasible, we applied the B3LYP-type exchange and correlation functional41 and the split-valence polarization (SVP) basis set.42 We validated our choice of B3LYP/SVP instead of the MP2/aug-cc-pVTZ level of theory for charge derivation by performing a series of QM calculations at both the B3LYP/SVP and MP2/aug-cc-pVTZ levels of theory for various tetrapeptides, ACE-Ala-X-Ala-NME, where X is one of the eight amino acids observed in CaM calcium binding loops, as summarized in Table I.
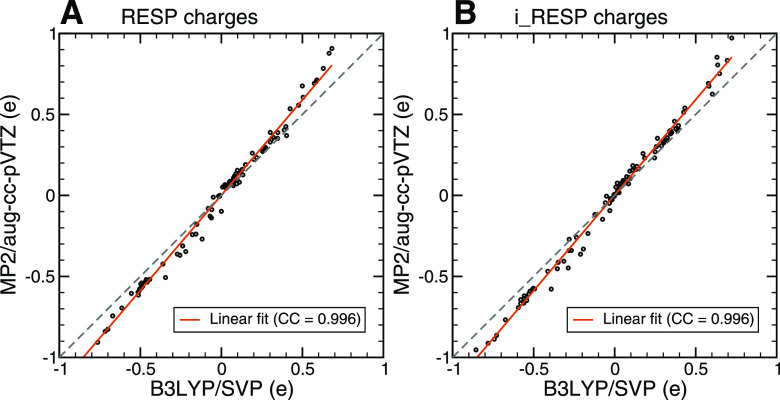
In the calculations, we considered five standard conformations for each tetrapeptide, namely, parallel β-sheet, antiparallel β-sheet, right-handed α-helix, left-handed α-helix, and PPII (left-handed polyproline II helical structure). The final atomic charges were fitted with the RESP and i_RESP programs (Fig. 2) for each tetrapeptide, treating either each conformation separately or jointly (joint fit across five conformations). As summarized in Table SI, the mean absolute difference (MAD) between the i_RESP atomic charges derived at the B3LYP/SVP and MP2/aug-cc-pVTZ levels of theory is small, smaller than 0.11e on average. The root mean square difference (RMSD) between the i_RESP charges at these two QM levels of theory has a similar magnitude and does not exceed 0.13e. Interestingly, both MAD and RMSD parameters are smaller (by 15%–40%) for charges obtained from the joint fit of five conformations compared to the separate fit (Table SI).
We found that regardless of which fitting method (RESP or i_RESP) was used, the atomic charges obtained from the ESPs with the two levels of theory were in strong agreement and were highly correlated (Fig. 3). Thus, the B3LYP/SVP level of theory for derivation of charges has reasonable accuracy compared to that of MP2/aug-cc-pVTZ for the systems we studied.
FIG. 3.
Correlation between the fitted charges using electrostatic potentials (ESPs) at the B3LYP/SVP and MP2/aug-cc-pVTZ levels of theory: (a) Atomic charges were fitted using RESP. (b) Atomic charges were fitted using i_RESP. The ESPs were calculated using QM for the tetrapeptides ACE-Ala-X-Ala-NME, where X is one of the eight different amino acids observed in CaM Ca2+ binding loops.
B. Setting up an appropriate radius for the Ca2+ ion is crucial to fit the accurate atomic charge
The results for the tetrapeptides showed that not only B3LYP/SVP is comparable to MP2/aug-cc-pVTZ, but it also enables us to expand the number of atoms in the QM calculations and will enable us to determine the many-body effect with only a minor loss of precision. Furthermore, it permits the efficient computation of the electronic structures from a large ensemble of loop conformations, which improves the accuracy of the overall distribution of the atomic charges. Altogether, the calculations were performed for 776 different loop conformations and involved 173–194 atoms and 1693–1861 basis set functions.
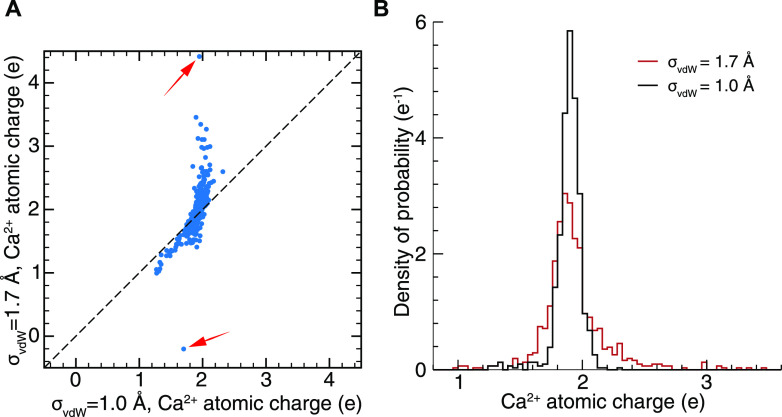
In the calculation of the ESPs from the electronic structures of the Ca2+-binding loops, we needed to manually define the vdW radius for the Ca2+ ions (σvdW) to build the surface grids. Initially, we set σvdW = 1.7 Å, the same as the vdW radius used in the AMBER force fields adapted from Aqvist.43 By fitting to the obtained ESPs using the RESP or i_RESP method, we acquired the atomic charges of the Ca2+ ion and of the atoms in the protein. We found that unphysical values for the Ca2+ i_RESP charges were generated, e.g., Q > 4e or Q < 0 [Fig. 4(a)]. More unphysical values were obtained for the protein atomic charges. Specifically, for the i_RESP charges, there was a long tail of unphysical charges >3e in the Gaussian-like distribution of the Ca2+ atomic charges [Fig. 4(b)].
FIG. 4.
Comparison between the i_RESP charges of the Ca2+ ion from the electrostatic potential using the vdW radii of Ca2+ = 1.0 Å and 1.7 Å. (a) Direct comparison between the two sets of i_RESP charges. The red arrows indicate excessively unphysical charges generated using σvdW = 1.7 Å. (b) Distribution of the i_RESP charges. The distribution was obtained using 776 representative EF-hand loop structures.
We noted that such irregularities were due to the radius of Ca2+. The default radius of 1.7 Å for Ca2+ in the AMBER force field is the vdW radius for the atomic Lennard-Jones potential of calcium, while the ionic radius of Ca2+ should be smaller. The ionic radius of Ca2+ depends on the coordination number (CN); for CN = 6, 7, and 8, σvdW was determined to be 1.00, 1.06, and 1.12 Å, respectively.44 Therefore, we explored the dependency of the Ca2+ atomic charges on the ionic radii over a range of values. We compared the Ca2+ atomic charges derived from ESPs using σvdW = 1.00, 1.06, 1.12, and 1.70 Å using the specific structure for which the Ca2+ i_RESP charge was +4.4e. We show in Fig. S4 that, unlike at σvdW = 1.70 Å, the i_RESP charges of Ca2+ at σvdW = 1.00–1.12 Å were ∼1.95e. On the other hand, the RESP charges of Ca2+ at σvdW = 1.00–1.12 Å were ∼1.7e, which is slightly larger than that derived at σvdW = 1.70 Å (1.6e). Moreover, the calcium ion charges were insensitive to σvdW values from 1.00 to 1.12 Å. Therefore, we set the ionic radius σvdW = 1.0 Å in the calculations for all conformers of the EF-hand loops, where the CN may vary.
For the i_RESP atomic charges of Ca2+ for all conformers, the Gaussian-like distribution was narrower at σvdW = 1.0 Å than at σvdW = 1.7 Å. Most importantly, unphysical charges greater than +3e or less than 0 have never been observed [Fig. 4(b)]. For the RESP charges, the width of the distribution became narrower at σvdW = 1.0 Å, and the mean shifted from 1.5e to ∼1.8e (Fig. S3). We showed that the use of the ionic radius (σvdW = 1.0 Å) was more appropriate than using the covalent radius for addressing Ca2+ molecular ESPs in Ca2+-binding proteins with explicit water molecules. By using σvdW = 1.0 Å, we found that compared with the Mulliken charges or the RESP charges, the i_RESP charges present the largest mean and standard deviation values. This is because the i_RESP charges are more susceptible to the variation in the neighboring atoms by including the polarization effect. Details can be found in Fig. S1 and Text S1 of the supplementary material.
C. Nearby water molecules have no substantial effect on tuning the atomic charge of Ca2+
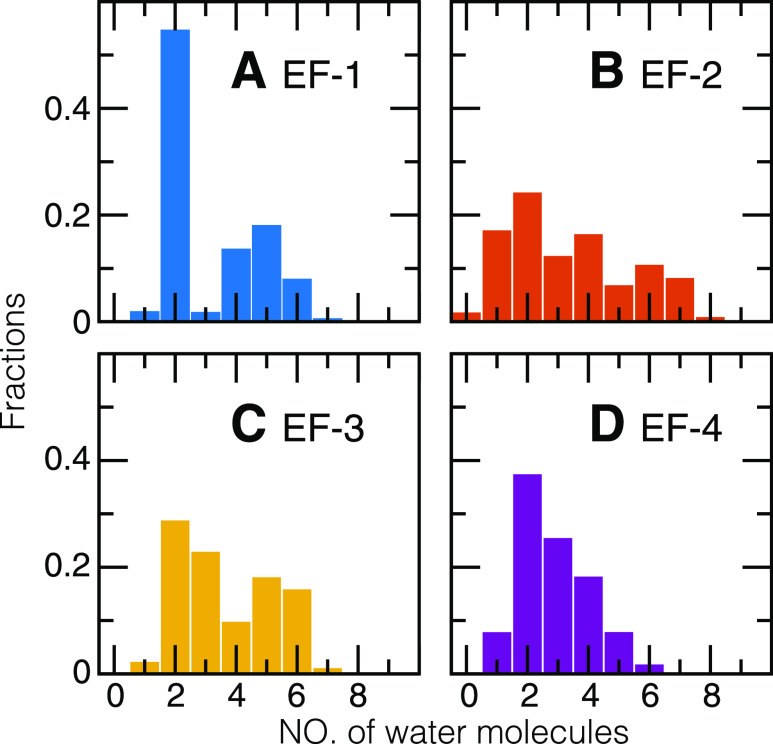
We found that the number of water molecules that chelates Ca2+, Nwater, varies in the EF-hand loops. In the crystal structure of the EF-hand loops in CaM (PDB ID: 1CLL), there can be one crystal water molecule that chelates Ca2+. In the MD simulations, the first solvation shell extended up to 3.3 Å away from the Ca2+ ion [see the radial distribution function gCa–O(r) for Ca2+ and the oxygen atoms in the water molecules in Text S2 and Fig. S5 of the supplementary material]. The probability distribution of Nwater (Fig. 5) shows that most EF-hand loops retain two water molecules. Specifically, for EF-1, in more than half of the snapshots, there are two water molecules, whereas Nwater ranges from 4 to 6 for the others; for EF-2, Nwater varies from 1 to 7 with similar probabilities; for EF-3 and EF-4, the probability of observing Nwater decreases almost monotonically from 2 to 6.
FIG. 5.
Fraction of the number of water molecules in individual Ca2+-binding EF-hand loops. The distributions were calculated by considering all the trajectories from all-atomistic molecular dynamics simulations of Ca2+/CaM, Ca2+/CaM/CaMKII, and Ca2+/CaM/Ng in explicit solvents. The water molecules were counted within the first solvation shell of Ca2+ ions.
Nwater is further tuned by target-binding. In the CaM/Ng complex, Nwater varies from 2 to 7 (Fig. S6), as the Ca2+ ion is not favorably retained because of the shape of the loops, which are more flexible and less spherical (Fig. 8). This effect is mainly due to the disruptive interaction between the Ng peptide and the Ca2+-binding loops in CaM.
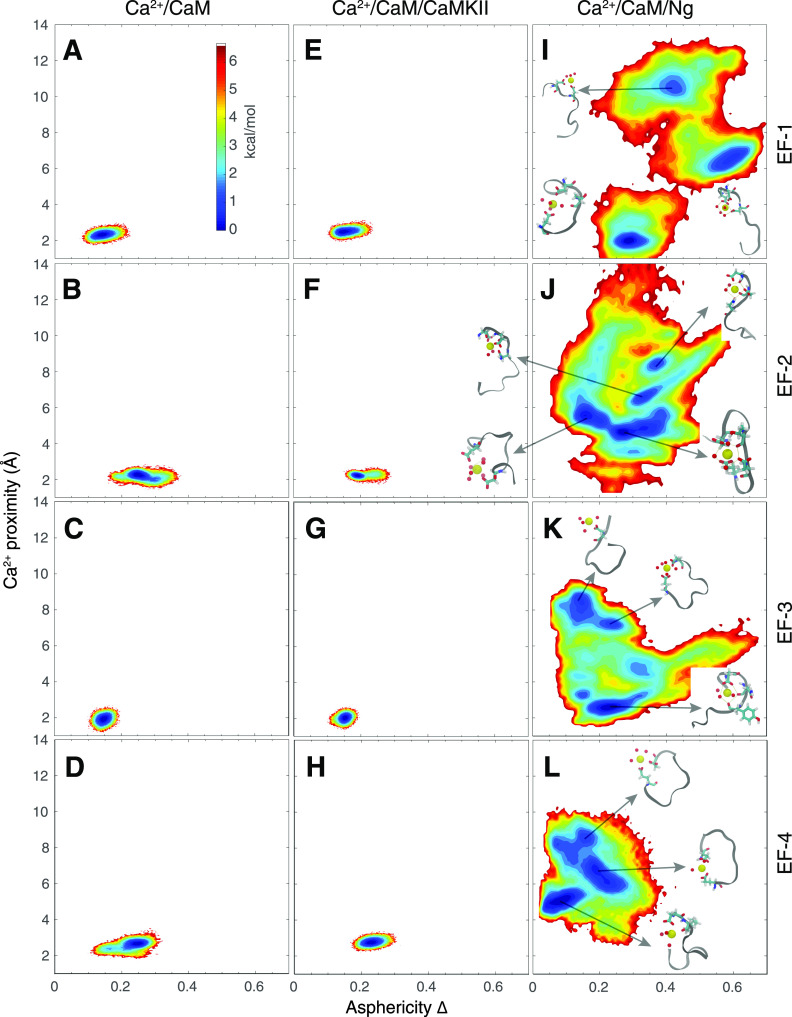
FIG. 8.
The potential of the mean force (PMF) as a function of the asphericity (Δ) of the loop and the distance between Ca2+ and the center of mass of the loop. The PMFs are plotted for four individual EF-hand loops from three types of sample systems: (a)–(d) Ca2+/CaM, (e)–(h) Ca2+/CaM/CaMKII, and (i)–(l) Ca2+/CaM/Ng. The color bar is scaled by kcal/mol, and the lowest PMF value is set to 0 kcal/mol.
Next, we investigated the effect of water molecules on the atomic charge of Ca2+ ions and proteins. To determine how many water molecules are needed to derive reliable atomic charges of Ca2+ ions, we systematically varied the number of water molecules in the calculation from 0 to 4. As we learned that i_RESP charges are more susceptible to the environment (see Text 1 of the supplementary material), we focused on i_RESP charges here. In the fitting, we kept the original parameters of the POL3 water model, including atomic partial charges, atomic polarizabilities of O and H, and the screening factor. We selected 163 representative EF-hand loop structures from the simulation of Ca2+/CaM and Ca2+/CaM/CaMKII. In 152 structures, the number of water molecules in the first solvation shell varied from 1 to 4; in the remaining 11 structures, water was absent.
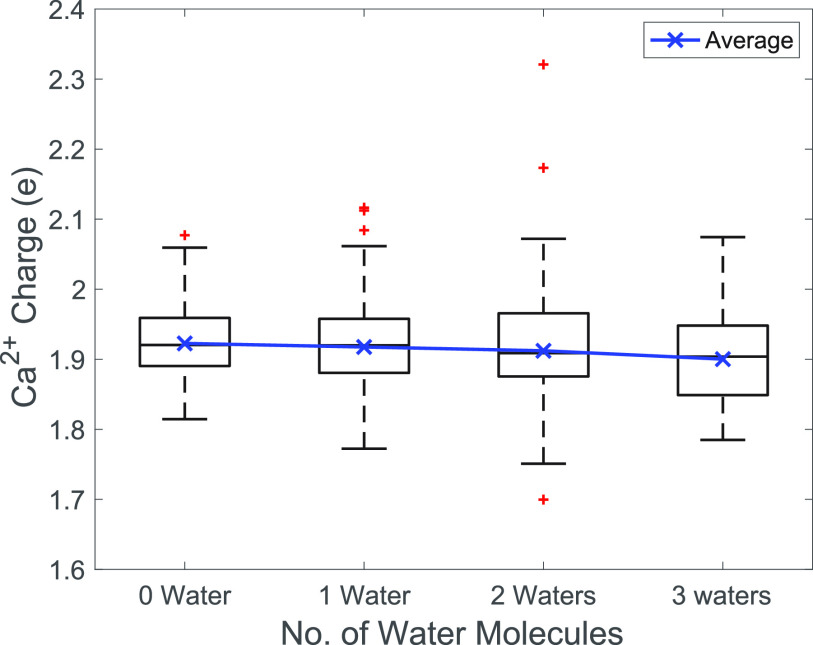
The average generated i_RESP charges of Ca2+ as a function of the number of water molecules around the ion are shown in Fig. 6. In general, the Ca2+ atomic charge gradually decreased with an increasing number of water molecules; however, the change in the Ca2+ charge was almost negligible (<1%). This indicates that although the number of water molecules surrounding Ca2+ in the calcium binding loop varies, water is noninfluential in determining the charge of Ca2+. Therefore, we suggest including one water molecule to maintain the correct coordination chemistry of the pentagonal bipyramidal geometry in the quantum chemical calculations to determine the Ca2+ charge.
FIG. 6.
Boxplot of the atomic charges of Ca2+ with different numbers of water molecules included in the calculation. The mean value of the Ca2+ charges is shown by the blue solid line. The boxplot is shown in black, and the outliers are shown in red.
D. Charges are distributed unevenly in each EF-hand loop
Since water does not have a substantial role in determining the atomic charge of Ca2+, we further investigated the charge distribution on the amino acids from the four EF-hand loops. In Fig. 7, we plotted the averaged i_RESP charges on each residue in the EF-hand loop and the atomic charges on Ca2+. The charge of the Glu residue at position 12 was less than −1e by ∼20% commonly in all four EF-hand loops because in solution, the side chain of the residue at the 12th position is usually in the bidentate coordination mode,45 and it is expected that more charge transfer occurs between this residue and the Ca2+ ion. For other coordinating residues, i.e., residues at positions 1, 3, 5, 7, and 9, on average, there could be an increase in the magnitude of the negative charges or barely any charge redistribution (close to −1e or 0). Surprisingly, for the residues that are not actively involved in Ca2+ coordination, the average amino acid charges also deviate from the default/nominal values, especially for Lys at the second position in EF-1, where charge transfer seems to occur between neighboring Ca2+-coordinating residues, such as the three Asp residues at the first, third, and fifth positions. Furthermore, large standard deviations were observed for all of the amino acid charges on the protein (Fig. S7), which suggests that these charges are systematically dependent on the loop configurations; hence, methodical charge assignment on the protein is required in the MD force field development of Ca2+ and amino acids in the protein ion binding site.
FIG. 7.
Average net charges per residue in the EF-hand loops. The i_RESP fitted charges are summed for each residue in each loop. The mean and the standard deviation of the residual charges are shown for the four EF-hand loops (a)–(d). Residues chelating Ca2+ in the crystal form of the EF-hand loop in Ca2+/CaM are colored blue, other residues are colored gray, and Ca2+ is colored orange.
E. The conformation of the Ca2+ binding loops dictates the number of water molecules coordinating Ca2+
We show that the conformation of the Ca2+ binding loops that vary with CaM-binding targets (CaMBTs) dictates the number of water molecules that coordinates Ca2+. To explore the conformational variation of the EF-hand loops in our MD simulations, we plotted (Fig. 8) the potential of mean force (PMF) as a function of the asphericity of the EF-hand (Δ; see the definition in the supplementary material) and the distance from the Ca2+ ion to the center of mass (COM) of the corresponding loop (dCOM). There are substantial differences in the PMFs between the Ca2+-retaining (Ca2+/CaM or Ca2+/CaM/CaMKII) and Ca2+-releasing (Ca2+/CaM/Ng) environments. In the former, the position of Ca2+ is restricted and close to the center of the loop (dCOM = 2–3 Å), as shown in Figs. 8(a)–8(h), and the EF-hand loops are generally spherical with Δ = 0.2–0.3 to promote the holospherical coordination of Ca2+ by the EF-hand loop. In the latter, there are several basins along a wide range of both Δ and dCOM, as shown in Figs. 8(i)–8(l). dCOM varies from 2 Å to as large as 10 Å, which means that Ca2+ in the CaM/Ng complex can be bound, loosely bound, or unbound. Δ varies from 0 to 0.6, corresponding to the spherical and largely linear EF-hand loops. The spherical shape of the EF-hand loops mostly corresponds to close proximity of Ca2+, which leads to the bound state of Ca2+ in a holospherical coordination geometry. A more linear shape of the EF-hand loops leads to hemispherical or planar geometries of coordination of Ca2+ by the EF-hand loops, where nearby water molecules take the place of the protein oxygen atoms and Nwater increases.
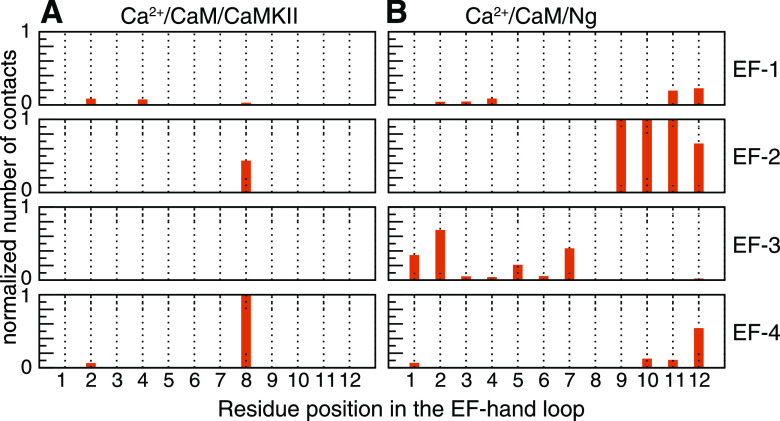
To gain a deeper understanding of the role of the amino acids in the EF-hand loops in determining the Ca2+ stability in the EF-hand loops, we investigated the intermolecular interaction between the loop and the CaMBT. The following describes tiers of residues that were found to be involved in these interactions. (i) The residues at positions 1 and 12 coordinate Ca2+ most consistently, while other residues are more often substituted by water molecules when Ca2+ is loosely bound (Fig. 8). These two residues are rarely involved in the interaction with CaMBT (Fig. 9). (ii) In the crystal structure of CaM, to coordinate Ca2+, the residue at position 7 extends its backbone oxygen toward Ca2+, and the subsequent residue at position 9 moves far away from Ca2+, requiring a water molecule to chelate Ca2+. These “frustrated” residues are dedicated to forming an EF-hand β-scaffold with their counterparts in the neighboring EF-hand loop to stabilize the shape of the two EF-hands in the same lobe of CaM.8 (iii) Residue 8 is usually hydrophobic and not actively involved in Ca2+ coordination. Its backbone is part of the EF-hand β-scaffold, and the direction of the side chain is tuned by CaMBT. When the side chain points toward CaMKII (contacts are found between residue 8 and CaMKII in Fig. 9), Ca2+ binding is enhanced; when the side chain points away from Ng (no contact between residue 8 and Ng is observed in Fig. 9), Ca2+ binding is weakened.
FIG. 9.
Contact formation between loops and the target. Snapshots from all-atomistic molecular dynamics simulations of Ca2+/CaM/CaMKII and Ca2+/CaM/Ng. A contact is formed if the distance between any atom from a residue in the loop and any atom from the residues in the CaMBT is within 4 Å. The number of contacts is then normalized by the number of snapshots and corresponding maximum number of contacts in each system.
IV. DISCUSSION
A. Water molecules contribute to the coordination of divalent Ca2+ in EF-hand loops
We have established a feasible functional for the quantum mechanical calculation of Ca2+ in the EF-hand loops of the CaM protein. With the electronic structures involving all the amino acids in a calcium binding loop and Ca2+, we showed that the geometry of the calcium binding loop is essential in stabilizing the pentagonal bipyramidal coordination of divalent Ca2+. Ca2+ is a metal ion that exhibits variability in coordination number and geometry because of its relatively large size, allowing close packing of its ligands.18,46 Ca2+ ions are most commonly coordinated by seven or eight ligands in the crystal form.47 For the EF-hand loops in a Ca2+-binding protein, the coordination of Ca2+ usually presents a pentagonal bipyramidal geometry (Fig. 1). In the crystal structure of CaM, to form the pentagonal geometry, the crucial feature is the conserved 12th residue, which contributes two carboxylate oxygen groups (bidentate) due to its long side chain. Mutating the 12th residue to a shorter side chain, such as Asp, leads to an octagonal geometry and a decrease in Ca2+ affinity by 100fold.47 The bidentate feature has been thought to be the main reason that EF-hands can bind Ca2+ with higher affinity over other divalent ions such as Mg2+ or Zn2+.47
For the two apexes in the bipyramidal geometry, a water molecule is necessary as a bridge between the Ca2+ and a side chain that remains too far away either because of the limited length of the side chain or to fulfill its active role in other functions. Regarding the latter reason, one example is the ninth residue belonging to the β-sheet structure between two EF-hand loops in a lobe of CaM, which is termed the EF-hand β-scaffold.48 Interactions between this residue and the other loop, with or without interactions with CaMBT, can affect the stability and conformation of the EF-hand loop, which further influences the Ca2+ coordination geometry.8 Due to the mobility of the water molecules, the pentagonal bipyramidal geometry can be easily converted to six-coordinate (octagonal geometry) or eight-coordinate, where two water molecules are observed as in the crystal structures.47
In our MD simulations, we show that packing two water molecules around the Ca2+ ion is of the highest probability (Fig. 5). This agrees with the classical MD simulations of Ca2+ in an EF-hand loop without polarization effects.49 For the Ca2+-retaining environment, the water molecules surrounding the Ca2+ ion allow for flexibility in the protein dynamics while retaining Ca2+ in the pentagonal bipyramidal geometry. For the Ca2+-releasing environment Ca2+/CaM/Ng, there are three to six water molecules in the first solvation shell. Ca2+ ions are likely to be partially or completely exposed to the solvent and partially coordinated by EF-hand loops [Figs. 8(i)–8(l)]. This also suggests that the coordination geometry of Ca2+ involving at least one water molecule dynamically responds to changes in the local environment, which could be the result of binding or dissociation of a CaM binding target.
B. Determining the atomic charge of Ca2+ requires information on the loop geometry
For divalent ions such as Ca2+, force field development has been limited to bare ions in aqueous solution.10 To address the force field of Ca2+ in protein environments, Jungwirth’s group accounted for the effective polarization9 by scaling the ionic charges by a factor of 0.75 in a classical force field. In this case, the computed value of the affinity of Ca2+ in the four individual EF-hands of CaM is approximately twice the experimentally measured values.50 This mean-field approach does not determine charge distribution on the protein directly, which impacts the shape of the EF-hand loop and the affinity and dynamics of Ca2+ binding. An ensemble average approach was adopted by Cheung et al.8,51 that averages an ensemble of semi-empirically determined atomic charges obtained from an ensemble of protein configurations involving the loops, where the Ca2+ atomic charge ranges from +1.2 to +1.8e. However, the polarization effect was not explicitly included.
To fix the correct coordination geometry, multi-site models for divalent ions have been developed by including multiple fixed or constrained dummy cations around the divalent ion center.52–54 However, since different coordination geometries for Ca2+ are observed in experimental solved structures of Ca2+ binding proteins,55 it is expected that the coordination geometry changes when the binding site is conformationally flexible, especially during association/dissociation of Ca2+. Those multi-site models are incapable of capturing the change in the coordination geometry.
According to the work performed by Jing et al.,11 many-body effects play an essential role in correctly determining the Ca2+ affinity. In this work, we show that there is nonuniform charge redistribution across all residues in the EF-hand loop in Fig. 7, meaning that their interactions with Ca2+ cannot be simplified by considering only a few amino acids from the entire loop. Therefore, we allow all possible coordination geometries around the ion by including all the residues in the loop and the coordinating water with Ca2+ in the ESP calculation.
According to our collected EF-hand loop geometries, we showed that RESP charges vary from 1.5 to 1.9e, and this is consistent with the charge values by the aforementioned studies by Jungwirth, where polarization effects were effectively included by scaling down the Ca2+ charge (2e) as used in popular MD force fields. In contrast, for the i_RESP charges, which are applicable to AMBER polarizable force fields where the polarization effect is explicitly included, the values vary in the range of 1.2 to 2.4e.
C. Ionic radius of Ca2+ in the electrostatic potential calculation
In this work, we compared the atomic charges fitted to ESPs generated using several ionic radii of Ca2+. In order to determine the grid for ESP calculation at the quantum level, we first explored vdW radii of Ca2+ ions from MD force fields. We noticed that there were discrepancies between the vdW radii of Ca2+ ions in the Lennard-Jones potential in popular nonpolarizable force fields. In the AMBER, CHARMM/27, and OPLS-AA force fields, 1.7 Å is used; in GROMOS, ∼2.0 Å is used; in CHARMM/36, 1.37 Å is used. Controversial results were found for all those values in the calculation of the hydration free energy or binding affinity.8,49,56–58 The discrepancies do not necessarily imply that the current vdW parameters of Ca2+ in those nonpolarizable force fields are unreasonable since those ion parameters were developed to reproduce molecular properties such as hydration free energy and coordination numbers in aqueous solution. Moreover, we cannot separate the radius and well-depth when determining the VDW parameters. However, these vdW radii for Ca2+ are found inappropriate for the calculation of ESPs of the Ca2+ binding proteins at the quantum mechanical level. We showed that a value of 1.7 Å failed to generate physical atomic charges for Ca2+ for some geometries, and the result did not improve by performing energy minimization before the QM calculation. In more detail, as shown in Fig. S8 of the supplementary material, the distribution of the Ca2+ i_RESP partial charges from QM energy minimized structures is wide and similar to the distribution of charges obtained directly using the MD structures. Those geometries extracted from the MD trajectories are stabilized by using the vdW parameters from the MD force field; however, in the QM calculation, the Ca2+ radius is improperly large to cause artifacts, especially when the coordinating water molecules are explicitly included. Nevertheless, a large radius of 2.28 Å was adopted to account for the solvation effects when the COnductor-like Screening MOdel (COSMO) implicit water model was used.59 We suggest that small ionic radii for Ca2+ and other divalent ions should be used in the RESP/i_RESP charge fitting when the solvent molecules are explicitly included.
V. CONCLUSIONS
CaM senses a broad spectrum of oscillatory Ca2+ signals for eukaryotic cells and acts as a hub for many downstream pathways.2,60 From incoming calcium signals to a particular pathway, an additional peptide (i.e., CaMBT) is required for tuning CaM’s response.61 Specific regions in CaMBT can tune the Ca2+ binding affinity for the EF-hand loop by stabilizing or disrupting interactions with the EF-hand loop.8 Because of such conformational flexibility in the EF-hand loop and dynamically adapting coordination geometries of the Ca2+ ions, we developed an approach of deriving conformational dependent atomic charges that is based on QM calculations including all the residues in the EF-hand loop.
Applying the approach to snapshots of Ca2+ in an EF-hand loop from MD simulations of CaM and a couple of CaMBTs, we show that in response to the dynamic coordination geometry of Ca2+, the atomic charge of Ca2+ alters and follows a Gaussian-like distribution. However, the underlying connection between the Ca2+ charge and the structure of the Ca2+ binding site as well as the coordination geometry is elusive. We will use machine learning methods to address this connection and implement a model into a MD package in our future study.
Our approach can be applied to Ca2+ in other protein environments and other divalent ions for advancing the development of both nonpolarizable and polarizable force fields for divalent ions in dynamic environments.
SUPPLEMENTARY MATERIAL
See the supplementary material for the initial structures of the complex of the Ca2+/CaM and Ng peptide, representative EF-hand loop structures including the derived Ca2+ charges, and additional details about the settings, parameters, and discussion about the charge derivation.
DATA AVAILABILITY
The data that support the findings of this study are available within the article and its supplementary material. The EF-hand loop structures and derived charge data are available from the corresponding author upon reasonable request.
ACKNOWLEDGMENTS
We thank Dr. Neal M. Waxham for stimulating discussions. We wish to thank Mr. Nate Jennings and Jules Nde for reading and comments on this manuscript. This work was supported by a grant from the National Institutes of Health (Grant No. 2R01GM097553). The authors acknowledge the computing resources from the Extreme Science and Engineering Discovery Environment (Grant No. TG-MCB190109) and computing clusters uHPC and Sabine at University of Houston.
Note: This paper is part of the JCP Special Collection in Honor of Women in Chemical Physics and Physical Chemistry.
REFERENCES
- 1.Waxham M. N. and Cheung M. S., in Encyclopedia of Computational Neuroscience, edited by Jaeger D. and Jung R. (Springer, 2013). [Google Scholar]
- 2.Yamniuk A. P. and Vogel H. J., Mol. Biotechnol. 27, 33 (2004). 10.1385/mb:27:1:33 [DOI] [PubMed] [Google Scholar]
- 3.Xia Z. and Storm D. R., Nat. Rev. Neurosci. 6, 267 (2005). 10.1038/nrn1647 [DOI] [PubMed] [Google Scholar]
- 4.Tidow H. and Nissen P., FEBS J. 280, 5551 (2013). 10.1111/febs.12296 [DOI] [PubMed] [Google Scholar]
- 5.Faas G. C., Raghavachari S., Lisman J. E., and Mody I., Nat. Neurosci. 14, 301 (2011). 10.1038/nn.2746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hoffman L., Chandrasekar A., Wang X., Putkey J. A., and Waxham M. N., J. Biol. Chem. 289, 14644 (2014). 10.1074/jbc.m114.560656 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Foresman J. B. and Frisch Æ., Exploring Chemistry with Electronic Structure Methods, 2nd ed. (Gaussian Inc., Wallingford, CT, 1995), p. 122. [Google Scholar]
- 8.Zhang P., Tripathi S., Trinh H., and Cheung M. S., Biophys. J. 112, 1105 (2017). 10.1016/j.bpj.2017.01.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Leontyev I. and Stuchebrukhov A., Phys. Chem. Chem. Phys. 13, 2613 (2011). 10.1039/c0cp01971b [DOI] [PubMed] [Google Scholar]
- 10.Jiao D., King C., Grossfield A., Darden T. A., and Ren P., J. Phys. Chem. B 110, 18553 (2006). 10.1021/jp062230r [DOI] [PubMed] [Google Scholar]
- 11.Jing Z., Liu C., Qi R., and Ren P., Proc. Natl. Acad. Sci. U. S. A. 115, E7495 (2018). 10.1073/pnas.1805049115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Melcr J. and Piquemal J. P., Front. Mol. Biosci. 6, 143 (2019). 10.3389/fmolb.2019.00143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kobayashi C. and Takada S., Biophys. J. 90, 3043 (2006). 10.1529/biophysj.105.078071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ikeda T., Boero M., and Terakura K., J. Chem. Phys. 127, 074503 (2007). 10.1063/1.2768063 [DOI] [PubMed] [Google Scholar]
- 15.Ikura M., Trends Biochem. Sci. 21, 14 (1996). 10.1016/s0968-0004(06)80021-6 [DOI] [PubMed] [Google Scholar]
- 16.Nelson M. R. and Chazin W. J., Protein Sci. 7, 270 (1998). 10.1002/pro.5560070206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Harding M. M., Acta Crystallogr., Sect. D: Biol. Crystallogr. 55, 1432 (1999). 10.1107/s0907444999007374 [DOI] [PubMed] [Google Scholar]
- 18.Dudev T. and Lim C., Chem. Rev. 103, 773 (2003). 10.1021/cr020467n [DOI] [PubMed] [Google Scholar]
- 19.Bayly C. I., Cieplak P., Cornell W., and Kollman P. A., J. Phys. Chem. 97, 10269 (1993). 10.1021/j100142a004 [DOI] [Google Scholar]
- 20.Cieplak P., Cornell W. D., Bayly C., and Kollman P. A., J. Comput. Chem. 16, 1357 (1995). 10.1002/jcc.540161106 [DOI] [Google Scholar]
- 21.Borodin O., J. Phys. Chem. B 113, 11463 (2009). 10.1021/jp905220k [DOI] [PubMed] [Google Scholar]
- 22.Schulten K. and Tesch M., Chem. Phys. 158, 421 (1991). 10.1016/0301-0104(91)87081-6 [DOI] [Google Scholar]
- 23.Hooper J. B., Starovoytov O. N., Borodin O., Bedrov D., and Smith G. D., J. Chem. Phys. 136, 194506 (2012). 10.1063/1.4718800 [DOI] [PubMed] [Google Scholar]
- 24.Starovoytov O. N., Torabifard H., and Cisneros G. A., J. Phys. Chem. B 118, 7156 (2014). 10.1021/jp503347f [DOI] [PubMed] [Google Scholar]
- 25.Duke R. E., Starovoytov O. N., Piquemal J.-P., and Cisneros G. A., J. Chem. Theory Comput. 10, 1361 (2014). 10.1021/ct500050p [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Torabifard H., Starovoytov O. N., Ren P., and Cisneros G. A., Theor. Chem. Acc. 134, 101 (2015). 10.1007/s00214-015-1702-y [DOI] [Google Scholar]
- 27.Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., and Lindahl E., SoftwareX 1-2, 19 (2015). 10.1016/j.softx.2015.06.001 [DOI] [Google Scholar]
- 28.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 29.Hess B., Bekker H., Berendsen H. J. C., and Fraaije J. G. E. M., J. Comput. Chem. 18, 1463 (1997). [DOI] [Google Scholar]
- 30.Lindorff-Larsen K., Piana S., Palmo K., Maragakis P., Klepeis J. L., Dror R. O., and Shaw D. E., Proteins 78, 1950 (2010). 10.1002/prot.22711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Darden T., York D., and Pedersen L., J. Chem. Phys. 98, 10089 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 32.Parrinello M. and Rahman A., J. Appl. Phys. 52, 7182 (1981). 10.1063/1.328693 [DOI] [Google Scholar]
- 33.Guo Z. and Thirumalai D., Folding Des. 2, 377 (1997). 10.1016/s1359-0278(97)00052-7 [DOI] [PubMed] [Google Scholar]
- 34.Rai B. K. and Bakken G. A., J. Comput. Chem. 34, 1661 (2013). 10.1002/jcc.23308 [DOI] [PubMed] [Google Scholar]
- 35.Behler J., J. Chem. Phys. 145, 170901 (2016). 10.1063/1.4966192 [DOI] [PubMed] [Google Scholar]
- 36.Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A. V., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Williams D., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., J. A. Montgomery, Jr., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J. J., Brothers E. N., Kudin K. N., Staroverov V. N., Keith T. A., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B., and Fox D. J., Gaussian 16, Rev. C.01, Gaussian Inc., Wallingford, CT, 2016. [Google Scholar]
- 37.Cieplak P., Caldwell J., and Kollman P., J. Comput. Chem. 22, 1048 (2001). 10.1002/jcc.1065 [DOI] [Google Scholar]
- 38.Caldwell J. W. and Kollman P. A., J. Phys. Chem. 99, 6208 (1995). 10.1021/j100016a067 [DOI] [Google Scholar]
- 39.Öpik U., Proc. Phys. Soc 92, 566 (1967). 10.1088/0370-1328/92/3/308 [DOI] [Google Scholar]
- 40.Wang J., Cieplak P., Li J., Wang J., Cai Q., Hsieh M., Lei H., Luo R., and Duan Y., J. Phys. Chem. B 115, 3100 (2011). 10.1021/jp1121382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Becke A. D., J. Chem. Phys. 98, 5648 (1993). 10.1063/1.464913 [DOI] [Google Scholar]
- 42.Schäfer A., Horn H., and Ahlrichs R., J. Chem. Phys. 97, 2571 (1992). 10.1063/1.463096 [DOI] [Google Scholar]
- 43.Ȧqvist J., J. Phys. Chem. 94, 8021 (1990). 10.1021/j100384a009 [DOI] [Google Scholar]
- 44.Shannon R. D., Acta Crystallogr., Sect. A 32, 751 (1976). 10.1107/s0567739476001551 [DOI] [Google Scholar]
- 45.Nara M., Morii H., and Tanokura M., Biochim. Biophys. Acta 1828, 2319 (2013). 10.1016/j.bbamem.2012.11.025 [DOI] [PubMed] [Google Scholar]
- 46.Falke J. J., Drake S. K., Hazard A. L., and Peersen O. B., Q. Rev. Biophys. 27, 219 (1994). 10.1017/s0033583500003012 [DOI] [PubMed] [Google Scholar]
- 47.Katz A. K., Glusker J. P., Beebe S. A., and Bock C. W., J. Am. Chem. Soc. 118, 5752 (1996). 10.1021/ja953943i [DOI] [Google Scholar]
- 48.Grabarek Z., J. Mol. Biol. 359, 509 (2006). 10.1016/j.jmb.2006.03.066 [DOI] [PubMed] [Google Scholar]
- 49.Marchand S. and Roux B., Proteins 33, 265 (1998). [DOI] [PubMed] [Google Scholar]
- 50.Kohagen M., Lepšík M., and Jungwirth P., J. Phys. Chem. Lett. 5, 3964 (2014). 10.1021/jz502099g [DOI] [PubMed] [Google Scholar]
- 51.Wang Q., Zhang P., Hoffman L., Tripathi S., Homouz D., Liu Y., Waxham M. N., and Cheung M. S., Proc. Natl. Acad. Sci. U. S. A. 110, 20545 (2013). 10.1073/pnas.1312788110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Oelschlaeger P., Klahn M., Beard W. A., Wilson S. H., and Warshel A., J. Mol. Biol. 366, 687 (2007). 10.1016/j.jmb.2006.10.095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Aaqvist J. and Warshel A., J. Am. Chem. Soc. 112, 2860 (1990). 10.1021/ja00164a003 [DOI] [Google Scholar]
- 54.Saxena A. and Sept D., J. Chem. Theory Comput. 9, 3538 (2013). 10.1021/ct400177g [DOI] [PubMed] [Google Scholar]
- 55.Pidcock E. and Moore G. R., J. Biol. Inorg. Chem. 6, 479 (2001). 10.1007/s007750100214 [DOI] [PubMed] [Google Scholar]
- 56.Chen C., Huang Y., Jiang X., and Xiao Y., Phys. Rev. E 87, 062705 (2013). 10.1103/physreve.87.062705 [DOI] [PubMed] [Google Scholar]
- 57.Basit A., Mishra R. K., and Bandyopadhyay P., “Calcium ion binding to calmodulin: binding free energy calculation using the molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) method by incorporating implicit polarization,” J. Biomol. Struct. Dyn. (published online). 10.1080/07391102.2020.1810125 [DOI] [PubMed] [Google Scholar]
- 58.Lawrenz M., Wereszczynski J., Amaro R., Walker R., Roitberg A., and McCammon J. A., Proteins 78, 2523 (2010). 10.1002/prot.22761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lepsik M. and Field M. J., J. Phys. Chem. B 111, 10012 (2007). 10.1021/jp0716583 [DOI] [PubMed] [Google Scholar]
- 60.Hoeflich K. P. and Ikura M., Cell 108, 739 (2002). 10.1016/s0092-8674(02)00682-7 [DOI] [PubMed] [Google Scholar]
- 61.Kubota Y., Putkey J. A., and Waxham M. N., Biophys. J. 93, 3848 (2007). 10.1529/biophysj.107.106849 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for the initial structures of the complex of the Ca2+/CaM and Ng peptide, representative EF-hand loop structures including the derived Ca2+ charges, and additional details about the settings, parameters, and discussion about the charge derivation.
Data Availability Statement
The data that support the findings of this study are available within the article and its supplementary material. The EF-hand loop structures and derived charge data are available from the corresponding author upon reasonable request.