Elementary Motion Detection in Drosophila: Algorithms and Mechanisms

Abstract

Motion in the visual world provides critical information to guide the behavior of sighted animals. Furthermore, as visual motion estimation requires comparisons of signals across inputs and over time, it represents a paradigmatic and generalizable neural computation. Focusing on the Drosophila visual system, where an explosion of technological advances has recently accelerated experimental progress, we review our understanding of how, algorithmically and mechanistically, motion signals are first computed.

INTRODUCTION

Visual motion cues guide a range of critical behaviors for sighted animals across many taxa. Global patterns of motion generated when the visual world moves relative to the animal provide key information for navigation, course control, and gaze stabilization (Cohen et al. 1977, Götz 1968, Srinivasan et al. 1996). Furthermore, predators, prey, and conspecifics each produce different patterns of local motion signals that can elicit appropriate behavioral responses (Butler 1973, Fotowat & Gabbiani 2011, Land & Collett 1974). In addition to its profound ethological significance, motion detection has provided a well-constrained computational framework for dissecting the circuit mechanisms of feature selectivity (Barlow & Levick 1965, Hassenstein & Reichardt 1956, Movshon et al. 1978). In this review, we focus on the peripheral visual circuits that initially extract motion signals.

To utilize motion signals, an animal’s brain must first compute them. Input to the retina is light that varies in intensity over space, time, and wavelength. Motion represents a particular pattern of change in this input, one in which the intensity of individual points in space at one time correlates closely with that of adjacent points in space at a later time (Figure 1a). These correlations can be spatially limited, such as those caused by the movement of a small object, or can span much of the visual field, corresponding to global patterns that emerge through the movement of the animal itself. In its most minimal form, motion detection requires a local comparison between two points in space across two points in time; these local motion signals can then be combined into neural representations of global patterns, providing information to guide behavior.

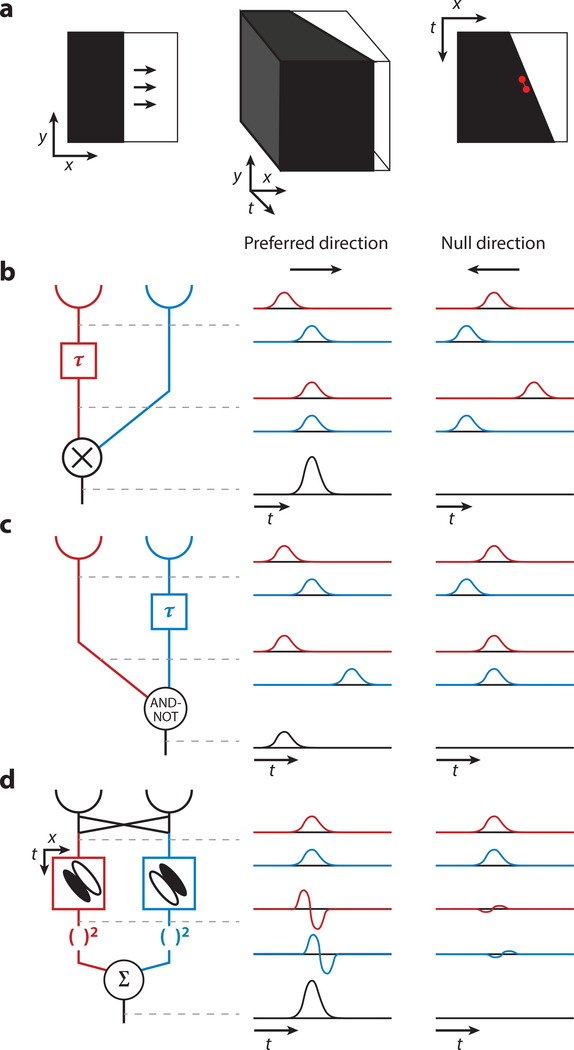
Figure 1.

Classical algorithms of elementary motion detection. (a) Motion produces correlated changes in light intensity over space and time. (Left) An illustration of a vertical, dark edge moving to the right. (Middle) A three-dimensional spatiotemporal representation of the same stimulus. (Right) A spatiotemporal representation of the moving edge that excludes the y spatial dimension, which is unchanging over time. This is equivalent to a horizontal slice through the three-dimensional diagram (middle). As depicted in red, the intensity at one point in space-time is correlated with that of an adjacent point. (b–d, left) A schematic of the motion detection algorithm; (middle) idealized responses at each stage of the algorithm to an edge moving in the detector’s preferred direction; (right) responses to a stimulus moving in the null direction. (b) The Hassenstein-Reichardt correlator. An edge moving in the preferred direction first encounters the red photoreceptor and then the blue photoreceptor. The red signal is delayed (represented by the τ), such that it arrives at the multiplication stage at the same time as the blue signal. Multiplication of these two coincident signals produces a large output. An edge moving in the null direction first encounters the blue photoreceptor and then the red photoreceptor. Delaying the red signal further separates it in time from the blue signal, such that multiplication produces little response. (c) The Barlow-Levick model. An edge moving in the preferred direction produces a signal in the red arm of the detector followed by a delayed, inhibitory signal in the blue arm. These two are not coincident, so the blue signal does not suppress the red signal and an output is produced. An edge moving in the null direction encounters the blue photoreceptor and then the red photoreceptor. The blue signal is delayed (represented by the τ), such that it arrives at the AND-NOT stage at the same time as the red signal and suppresses it. (d) The motion energy model. From non-direction-selective inputs (top traces), spatiotemporally oriented linear filters produce stronger responses in the preferred direction than in the null direction (middle traces). Squaring and summing quadrature pairs then produces positive output to preferred-direction motion and little to no response to null-direction motion (bottom traces).

The processing of visual motion has been characterized in a number of different species across the animal kingdom (Gibson 1950, Nakayama 1985). There has been a rich history studying insects, and with the recent explosion of genetic, physiological, behavioral, and anatomical techniques in the fruit fly Drosophila melanogaster, our understanding of motion detection in this system has advanced rapidly, providing critical insight into this fundamental computation. Here, by examining different abstractions ranging from algorithmic models to neural circuit implementations, we comprehensively summarize the current understanding of local motion detection in the fruit fly. We also discuss the open questions that remain and comment on how we believe they can be most fruitfully addressed. We end by comparing motion detection in flies to the equivalent computation in vertebrates.

CLASSICAL ALGORITHMS OF ELEMENTARY MOTION DETECTION

In both vertebrates and invertebrates, neural circuits first compute motion by generating signals selective for the direction of motion in a local region of the visual field (Barlow & Hill 1963, Hubel & Wiesel 1959, Reichardt 1961). However, there are multiple ways that this computational problem, often referred to as elementary motion detection, can be solved. Three dominant algorithms have been proposed: the Hassenstein-Reichardt correlator (Hassenstein & Reichardt 1956), the Barlow-Levick model (Barlow & Levick 1965), and the motion energy model (Adelson & Bergen 1985). Historically, studies of insects have viewed motion detection through the lens of the Hassenstein-Reichardt correlator; those of vertebrate retina have favored the Barlow-Levick model; and studies of vertebrate visual cortex have favored the motion energy model. Formally, however, any of these three could underlie motion detection in Drosophila. In this section, we describe these models as they were originally articulated to establish a theoretical framework for understanding elementary motion detection. However, as we detail later, in fact none of these models exactly account for motion detection in flies, leading the field toward a number of alternative variants.

Hassenstein-Reichardt Correlator

From quantitative characterization of the behavior of the beetle Chlorophanus, Hassenstein & Reichardt (1956) developed the first mathematical model of elementary motion detection. The Hassenstein-Reichardt correlator postulates a motion detector with two input channels representing photoreceptors that respond to changes in light intensity (Figure 1b). The signal from one photoreceptor is delayed (modeled as a low-pass filter) and then multiplied with a non-delayed signal from the spatially adjacent photoreceptor. This circuit responds preferentially to a stimulus moving in the direction whereby it encounters the delayed arm before the non-delayed arm: The time delay in the circuit matches the time it takes the stimulus to move to the second receptor, and the arithmetic multiplication of these coincident signals thereby produces a strong output. A stimulus moving in the opposite direction first encounters the non-delayed arm before the delayed arm; as a result, the delay in the circuit produces signals that are even more separated in time and cannot be productively multiplied. This circuit responds with positive signals to stimuli moving in the preferred direction and no signal to stimuli moving in the non-preferred or null direction. To produce a signal for stimuli moving in the opposite direction, Hassenstein and Reichardt envisioned an additional mirror-symmetric circuit from the same two photoreceptors that reverses the delayed and non-delayed arms. The outputs of the two circuits are then subtracted, producing a signal where the sign indicates the direction of motion and the magnitude indicates how well the speed of the moving stimulus matches the circuit’s time delay. Importantly, the Hassenstein-Reichardt correlator responds identically to moving light and dark stimuli. A light stimulus is a contrast increment and has a positive contrast value, while a dark stimulus is a contrast decrement and has a negative value; arithmetic multiplication of pairs of either contrast yields positive signals.

To observe a readout of Chlorophanus’s motion detector, Hassenstein and Reichardt examined the direction and strength of optomotor responses, the behavior in which a visual stimulus rotating around the animal elicits turning in the same direction as the motion (Hassenstein 1951, Hassenstein & Reichardt 1956, Reichardt 1961). Their model quantitatively predicted behavioral responses to many motion stimuli across a wide range of conditions (Reichardt 1961). For example, the relationship between the magnitude of the stimulus contrast and the strength of the behavioral response was quadratic, consistent with a multiplicative step. Furthermore, a reverse-phi stimulus, a so-called apparent motion stimulus where the contrast of the moving object inverts as it moves, produced turning behavior in the opposite direction, as expected from the multiplication of one positive and one negative signal.

Although the Hassenstein-Reichardt correlator predicts behavior well, sign-correct multiplication is biologically implausible, so an elaborated model that separates positive and negative contrast inputs, the four-quadrant model, was also proposed (Hassenstein & Reichardt 1956). Specifically, each photoreceptor signal is split and half-wave rectified to produce a channel that responds positively to light contrasts and not at all to dark and another that responds positively to dark and not at all to light. All four pairwise combinations of positive and negative signals feed into separate correlators that are then summed with equal weights to produce an output identical to that of the original model.

Barlow-Levick Model

Based on electrophysiological recordings of direction-selective ganglion cells in the rabbit retina, Barlow & Levick (1965) developed an alternative model for elementary motion detection (Figure 1c). Like the Hassenstein-Reichardt correlator, the signal from one photoreceptor is delayed while the other is not. However, the signals from the two arms are combined through an inhibitory mechanism, a logical AND-NOT gate. A moving stimulus that first encounters the delayed arm and then the non-delayed arm generates little to no signal because the coincidence of the two signals results in suppression by the AND-NOT operation. This is defined as the null direction. A stimulus moving in the preferred direction produces a positive response because the signal through the non-delayed arm precedes the delayed signal and therefore is not inhibited. This algorithm described the responses of ganglion cells to moving bars. In addition, it explained ganglion cells’ responses to the presentation of apparent motion stimuli. Two thin bars were flashed sequentially in the preferred or null direction, producing direction-selective responses. Critically, the null-direction response was always smaller than the sum of the responses to the independent presentations of the two bars, indicating inhibition of the null-direction response.

Motion Energy Model

To provide a theoretical mechanism for human motion detection using biologically plausible processing elements, Adelson & Bergen (1985) proposed an additional algorithm for elementary motion detection (Figure 1c). This model relies on the fact that motion is an oriented pattern in space-time (Figure 1a) and therefore can be initially extracted by a linear filter selectively tuned for this pattern, much like how receptive fields oriented purely in space are sensitive to the spatial orientation of bars (Hubel & Wiesel 1959). Summation of at least two filters that are biphasic in time and have center-surround organization in space can produce such a spatiotemporally oriented linear filter (Adelson & Bergen 1985). While this filter responds more strongly to motion in the preferred direction than in the null direction, the response oscillates depending on how the moving pattern aligns with the receptive field at each moment, and the sign of the response depends on the contrast polarity of the pattern. Therefore, Adelson and Bergen further proposed a quadrature pair of these oriented filters—that is, two filters that are phase offset by 90°—whose responses are then squared and summed, resulting in a direction-selective signal of motion energy that is positive for the preferred direction and small or zero for the null direction. Subtraction of two of these detectors preferring opposite directions produces opponent responses, where the sign indicates the direction of motion. Interestingly, an algebraic identity shows that the output of this motion energy model is mathematically equivalent to the output of the Hassenstein-Reichardt correlator despite the fact that the intermediate steps of the two algorithms are quite different.

THE BIOLOGICAL IMPLEMENTATION OF ELEMENTARY MOTION DETECTION

The Hassenstein-Reichardt correlator, the Barlow-Levick model, and the motion energy model each provide a solution to the problem of local motion detection. However, in addition to being computationally distinct, they also require different biological implementations. How, then, do visual circuits in the fly detect motion?

Following the pioneering framework established by Hassenstein and Reichardt, much of the immediately subsequent work examined optomotor behavioral responses to motion stimuli. These studies demonstrated that motion detection in flies—blowflies, houseflies, and fruit flies—like in beetles, quantitatively matches predictions from the Hassenstein-Reichardt correlator across a range of stimulus parameters. Importantly, the strength of the behavior is dependent on the ratio between the speed and spatial wavelength of the pattern—the temporal frequency—and not on the speed alone (Buchner 1984, Götz 1964, Heisenberg & Buchner 1977, McCann & MacGinitie 1965, Reichardt 1987). The optimal temporal frequency is approximately 1 Hz, a measurement that allowed the temporal filters of the hypothesized Hassenstein-Reichardt correlator to be estimated (Borst & Bahde 1986, Guo & Reichardt 1987, Reichardt 1961). Additionally, the spatial sampling of the motion detector matches the optical resolution of the flies’ eyes, indicating the detector compares neighboring points in visual space (Buchner 1976, Eckert 1973, Götz 1964, Marmarelis & McCann 1973). Lastly, as predicted by the Hassenstein-Reichardt correlator, fruit flies experience the reverse-phi illusion and turn against the direction of motion when presented such stimuli (Clark et al. 2011, 2014; Leonhardt et al. 2017; Tuthill et al. 2011, 2013).

The first point of access to the circuit implementation of motion detection was provided by the discovery of direction-selective neurons sensitive to wide-field motion, lobula plate tangential cells (LPTCs) (Bishop et al. 1968, Dvorak et al. 1975, Hausen 1976). LPTCs respond with depolarization or increased spike rate to motion in their preferred direction and hyperpolarization or suppressed spiking to null-direction motion. Overall, their responses are consistent with fly behavior as well as the predicted outputs of a Hassenstein-Reichardt correlator (Egelhaaf & Reichardt 1987, Egelhaaf et al. 1989, Haag et al. 2004, Hausen 1982, Joesch et al. 2008). However, as they are wide-field neurons with opponent responses, LPTCs are not the site of origin of direction-selective signals; they instead sum inputs from many local motion detectors (Krapp & Hengstenberg 1996, Riehle & Franceschini 1984, Single & Borst 1998). Identifying and characterizing these local motion detectors in detail would then await work in Drosophila utilizing genetic tools.

Anatomy—Circuit Components

Visual processing in Drosophila begins in the retina. Each compound eye is composed of approximately 800 ommatidia, or facets, each of which contains eight photoreceptors. These photoreceptors can be grouped into two classes, the outer photoreceptors R1–6, which all express the opsin Rh1 (O’Tousa et al. 1985), and the inner photoreceptors R7 and R8, each of which selectively expresses one of two different opsins and is involved in color vision (Chou et al. 1996, Huber et al. 1997, Papatsenko et al. 1997). Motion vision draws its major input from R1–6 (Heisenberg & Buchner 1977, Yamaguchi et al. 2008). However, there is also crosstalk from gap junctions between the inner and outer photoreceptors, and these connections improve motion discrimination (Figure 2) (Wardill et al. 2012).

Figure 2.

A diagram of the functionally and anatomically validated neural circuitry that implements elementary motion detection in Drosophila. Photoreceptors in the retina (Re) synapse onto first-order interneurons in the lamina (La). These lamina monopolar cells synapse onto second-order interneurons in the medulla (Me), which synapse onto the direction-selective cells T4 and T5 in the medulla and lobula (Lo), respectively. T4 and T5 then synapse in the lobula plate (LP) in layers by their preferred direction. The feedforward pathway for detecting moving light edges is depicted in green, and the pathway for detecting moving dark edges is in magenta. L1 is both green and magenta, as it contributes to both light- and dark-edge motion detection. Because the role of L4 remains controversial, it is colored a lighter magenta. Medulla feedback neurons are depicted in blue and show the neuropils they connect instead of the specific neurons they synapse onto. The connection between R1–6 and R7/8 indicates a gap junction. Cells that are anatomically connected to the depicted neurons but have not been shown to have a functional (behavioral or physiological) role are excluded from this schematic.

From the retina, R1–6 project their axons to the lamina, the first optic neuropil (Figure 2). The lamina is retinotopically organized into columns, each corresponding to a point in visual space. In Drosophila, the anatomy and synaptic connections of lamina neurons were characterized in detail at the light and electron microscopic levels nearly three decades ago (Fischbach & Dittrich 1989, Meinertzhagen & O’Neil 1991, Rivera-Alba et al. 2011). The lamina provides feedforward input to the next optic neuropil, the medulla, through the five columnar lamina monopolar cells (LMCs), called L1–5 (Fischbach & Dittrich 1989, Takemura et al. 2008). L1–3 are directly postsynaptic to R1–6, while L4 and L5 receive only indirect input (Meinertzhagen & O’Neil 1991, Rivera-Alba et al. 2011). Genetic access to individual cell types, combined with genetically encoded effectors that block neuronal output, has enabled the functional importance of these neurons to be established. Rister and colleagues (2007) combined cell-type-specific silencing of L1 and L2 with optomotor behavior and demonstrated that these neurons are redundantly required for optomotor responses. Two subsequent studies, using electrophysiological recordings from LPTCs and behavioral assays, demonstrated that this redundancy was because the processing of moving light edges and moving dark edges diverges in the lamina: L1 is essential for the detection of moving light edges while L2 is required for the detection of moving dark edges (Clark et al. 2011, Joesch et al. 2010). As a result, for a grating stimulus, which contains both light and dark edges, either L1 or L2 is dispensable for normal behavioral responses. Combinatorial silencing experiments revealed that L1 and L3 also make critical contributions to dark-edge motion detection, demonstrating that while L2 provides necessary inputs to this pathway, these inputs are not sufficient (Silies et al. 2013). The role of L4 in motion detection remains controversial, as its morphology and connectivity suggest that it is important (Strausfeld & Braitenberg 1970, Takemura et al. 2011), but the behavioral and electrophysiological studies in which it has been synaptically silenced are contradictory, with some work showing that it is required while other work has indicated that it is important only for non-motion stimuli (Bahl et al. 2015, Meier et al. 2014, Silies et al. 2013, Tuthill et al. 2013, Zhu et al. 2009). A study examining the contribution of all 12 lamina neurons to a large panel of visual stimuli demonstrated that feedback neurons from the medulla, including C2, C3, Lawf1, and Lawf2, also shape behavioral responses to motion under some regimes (Figure 2) (Tuthill et al. 2013). Given the dense connectivity among lamina neurons, it is likely that a substantial fraction of them shape motion detection across the broad range of visual stimuli and behavioral states Drosophila experience.

The medulla is also retinotopically organized, and there are approximately 60 columnar cell types that provide a large set of elements that could contribute to motion detection (Fischbach & Dittrich 1989). However, limiting this list of candidates, the cells and synaptic connections in several medulla columns have been mapped through electron microscopic reconstruction (Takemura et al. 2008, 2013, 2017). Before we describe the specific cells involved, we first introduce their downstream partners, the earliest direction-selective neurons in the visual system, as the medulla input neurons were identified through their connections to these cells.

T4 and T5 are direction-selective columnar neurons sensitive to motion in a small region of visual space (Figure 2). T4 has its dendrites in the proximal medulla and its axon terminal in the lobula plate neuropil (Fischbach & Dittrich 1989). T5’s dendrites are in the first layer of the lobula, a neuropil that receives direct projections from the medulla, and has its axon terminal in the lobula plate. For each column, there are four subtypes of T4 and four of T5. The dendrites of these four subtypes overlap, but each subtype projects to one of the four layers of the lobula plate, where the T4 and T5 axon terminals of the two neurons with the same spatial receptive field project to the same location. This striking anatomy suggested that T4 and T5 may function in motion detection. Activity labeling using 2-deoxygluose demonstrated that the four layers of the lobula plate are tuned for motion in the four cardinal directions—front-to-back, back-to-front, up, and down—and that the proximal medulla and the first layer of the lobula where T4 and T5 dendrites reside are active during motion stimuli (Bausenwein & Fischbach 1992, Buchner et al. 1984). An electrophysiological recording from a blowfly further suggested that T5 is direction-selective (Douglass & Strausfeld 1995). In vivo calcium imaging conclusively demonstrated that each subtype of T4 and T5 is selective for the cardinal direction that matches the direction preference of the lobula plate layer it projects to (Maisak et al. 2013). T4 and T5 are also orientation selective: They respond to static bars oriented with their long axis perpendicular to the preferred-direction-null-direction axis but do not respond to static bars oriented parallel to this axis (Fisher et al. 2015b). This response property sharpens their directional tuning for the cardinal axes. T4 and T5 are distinguished by their contrast polarity: T4 is selective for moving light edges, and T5 is selective for moving dark edges (Fisher et al. 2015b, Maisak et al. 2013). Critically, T4 and T5 are required for optomotor behavior (Bahl et al. 2013, Leonhardt et al. 2017, Maisak et al. 2013, Mauss et al. 2017, Schnell et al. 2012, Strother et al. 2017). They also synapse directly onto LPTCs and are required for their responses to motion (Bahl et al. 2015; Maisak et al. 2013; Mauss et al. 2014, 2017).

Through the use of a combination of electron microscopic reconstruction techniques, all of the synaptic inputs to T4 have been identified (Takemura et al. 2013, 2017). T4 receives the largest number of synapses from the columnar neurons Mi1 and Tm3, which in turn receive a large fraction of their input from L1 (Figure 2). In addition, T4 receives input from the columnar neurons Mi4, Mi9, and C3; the large tangential cell CT1; TmY15; and T4s of the same subtype from neighboring columns (Takemura et al. 2017). Along with Mi1 and Tm3, Mi4 and Mi9 are T4’s columnar, feedforward input. All models of motion detection require spatially asymmetric inputs, and consistent with this, Mi9 and Mi4 inputs onto individual T4 cells are drawn from spatially offset columns. Furthermore, the neurotransmitter phenotypes of these inputs are known (Takemura et al. 2017): Mi1, Tm3, and T4 itself release acetylcholine, the major excitatory neurotransmitter in Drosophila (Buchner & Rodrigues 1983); Mi4, TmY15, CT1, and C3 are GABAergic and hence inhibitory; and Mi9 releases glutamate, which is either excitatory or inhibitory in Drosophila (Jan & Jan 1976, Liu & Wilson 2013) but is likely inhibitory in this context (Strother et al. 2017, Takemura et al. 2017).

Functionally, silencing experiments demonstrated that Mi1 is required for T4 responses as well as LPTC and behavioral responses to moving light edges across a range of stimuli (Ammer et al. 2015, Strother et al. 2017). While Tm3 is also a critical input, the effect of silencing it appears to depend more on the stimulus parameters. One study reported that it is required only for fast stimuli, while another showed that it is essential regardless of velocity (Ammer et al. 2015, Strother et al. 2017). In contrast, silencing Mi4 or Mi9 only subtly changes T4 responses and behavior (Strother et al. 2017). The functional contributions of the other T4 input neurons remain to be characterized, and combinatorial silencing of multiple input neurons or the use of different stimuli should provide additional insight.

T5, like T4, has four columnar, feedforward inputs: Tm1, Tm2, Tm4, and Tm9 (Figure 2) (Shinomiya et al. 2014). Tm1, Tm2, and Tm4 are postsynaptic to L2 and together receive a large fraction of L2’s output, while Tm9 is postsynaptic to L3 (Takemura et al. 2013). As the electron microscopic reconstruction of T5 circuitry is incomplete, it is likely that there are other cells that synapse onto T5 that remain to be identified. All four of T5’s known inputs are cholinergic (Shinomiya et al. 2014). Functionally, Tm1, Tm2, Tm4, and Tm9 all contribute to dark-edge motion detection, as assayed through LPTC recordings, optomotor behavior, and in the case of Tm9, T5 calcium imaging; however, silencing any of the neurons individually has only partial effects (Fisher et al. 2015a, Serbe et al. 2016).

Response Properties of Inputs to T4 and T5

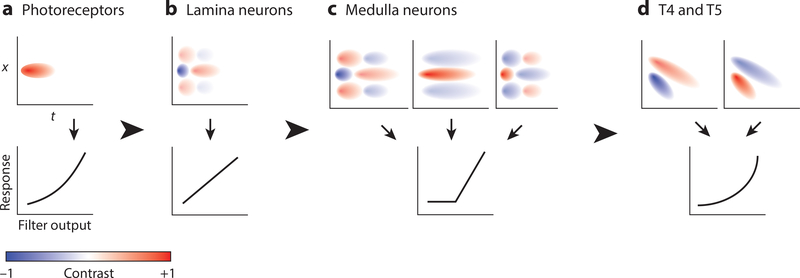
Many studies have examined how these circuit elements process visual information. Electrophysiological recordings in blowflies demonstrated that LMCs respond with graded changes in membrane potential, hyperpolarizing to light and depolarizing to dark; these studies also showed that, unlike the photoreceptors from which they receive synaptic input, LMCs have center-surround spatial receptive fields and biphasic impulse responses (temporal filters) (Figures 3a,b) (Dubs 1982, Hardie & Weckström 1990, Laughlin 1987, Srinivasan et al. 1982, Zettler & Järvilehto 1971, 1972). More recently, optical recordings of calcium and voltage responses through imaging of genetically encoded indicators have extended these observations in Drosophila (Clark et al. 2011, Freifeld et al. 2013, Reiff et al. 2010, Silies et al. 2013, Yang et al. 2016). By expressing the indicator in an individual LMC type, these experiments defined the similarities and differences in the response properties of L1–3. L1 and L2 respond rapidly and transiently with indistinguishable kinetics, but L3 has slower, sustained responses (Clark et al. 2011, Freifeld et al. 2013, Reiff et al. 2010, Silies et al. 2013, Yang et al. 2016). Furthermore, L1 and L2 are approximately linear with respect to contrast, responding with equal magnitude to light and dark, while L3 modestly favors dark (Clark et al. 2011, Freifeld et al. 2013, Silies et al. 2013, Yang et al. 2016). Therefore, though L1 and L2 feed preferentially into light- and dark-edge motion detection, contrast selectivity arises downstream of these cells, but selectivity for dark begins in L3 itself.

Figure 3.

An idealized representation of neuronal response properties at each stage of the motion detection circuitry. Responses are schematized as spatiotemporal linear filters followed by a static nonlinearity. (a) Photoreceptors have monophasic temporal impulse responses, lack a spatial surround, and have modestly larger responses to light than to dark. (b) The lamina neurons L1 and L2 have biphasic impulse responses and center-surround organization and are linear with respect to contrast. L3 (not shown) has a slow, monophasic impulse response and is modestly contrast selective. (c) At the next stage, there is a diversification in the response properties. There are both ON and OFF medulla neurons. Temporally, they span a range from slow to fast kinetics and can have either biphasic or monophasic impulse responses. This is also the stage in which half-wave rectification emerges. (d) Direction selectivity originates in T4 and T5, and nonlinear preferred-direction amplification and null-direction suppression have both been observed.

The columnar medulla neurons that synapse onto T4 and T5 have also been characterized through electrophysiology and imaging (Arenz et al. 2017; Behnia et al. 2014; Fisher et al. 2015a; Meier et al. 2014; Serbe et al. 2016; Strother et al. 2014, 2017; Yang et al. 2016). The presynaptic partners of T4 and T5 are all graded-potential neurons but unlike the LMCs, generally differ in the sign of their responses (Figure 3c). The neurons in the dark-edge pathway, Tm1, Tm2, Tm4, Tm9, all depolarize to dark; of the neurons in the light-edge pathway, Mi1, Tm3, and Mi4 depolarize to light, but interestingly, Mi9 depolarizes to dark (Arenz et al. 2017, Behnia et al. 2014, Fisher et al. 2015a, Meier et al. 2014, Serbe et al. 2016, Strother et al. 2014, 2017, Yang et al. 2016). Furthermore, they are all strongly selective for their preferred contrast, which possibly contributes to the selectivity for light and dark edges observed in T4 and T5. These neurons have a range of temporal response properties, providing a potential means for extracting the timing differences necessary to compute motion. Of the T4 inputs, Mi1 and Tm3 have faster kinetics than Mi4 and Mi9, and their impulse responses are biphasic, while Mi4’s and Mi9’s are monophasic (Arenz et al. 2017, Behnia et al. 2014, Strother et al. 2017, Yang et al. 2016). For the neurons presynaptic to T5, Tm2 has the fastest kinetics and Tm9 has the slowest; Tm4 and Tm1 fall between the two (Arenz et al. 2017, Behnia et al. 2014, Fisher et al. 2015a, Meier et al. 2014, Serbe et al. 2016, Yang et al. 2016). All of their impulse responses are biphasic, though the extent depends on the neuron and visual stimulus presented (Arenz et al. 2017, Behnia et al. 2014, Fisher et al. 2015a, Meier et al. 2014, Serbe et al. 2016, Yang et al. 2016). Finally, most of these T4 and T5 input neurons have center-surround receptive fields in which the center corresponds to a single point in visual space (Arenz et al. 2017, Fisher et al. 2015a, Meier et al. 2014, Serbe et al. 2016, Strother et al. 2017). Surprisingly, Tm3 has a larger receptive field center than the other T4 input neurons (Arenz et al. 2017, Behnia et al. 2014). Tm9 may have a larger receptive field than the other T5 input neurons, but there are conflicting results that are not yet reconciled (Arenz et al. 2017, Fisher et al. 2015a, Serbe et al. 2016).

Physiology of T4 and T5

To generate direction-selective outputs, motion detection algorithms utilize nonlinear amplification of preferred-direction signals, nonlinear suppression of null-direction signals, or a combination of both. Several studies have therefore asked which of these occurs in T4 and T5 (Fisher et al. 2015b; Gruntman et al. 2018; Haag et al. 2016, 2017; Leong et al. 2016; Salazar-Gatzimas et al. 2016). Across these studies, both nonlinear amplification of preferred-direction signals and suppression of null-direction signals have been described in T4 and T5 (Figure 3d). However, as we describe below, the two processes have not always been observed in each experiment, possibly because of differences among the visual stimuli used or because of differences between the voltage and calcium signals of these cells.

Four research groups used different apparent motion stimuli in which neighboring points in space were sequentially stimulated by light flashes to mimic motion (Fisher et al. 2015b; Gruntman et al. 2018; Haag et al. 2016, 2017; Salazar-Gatzimas et al. 2016). By comparing these apparent motion responses with linear predictions based on the responses to the component flashes, nonlinear amplification or suppression can be demonstrated. Two studies using calcium imaging found that on short timescales, preferred-direction signals were amplified in T4 and T5, but null-direction signals were not suppressed (Fisher et al. 2015b, Salazar-Gatzimas et al. 2016). In contrast, Gruntman and colleagues (2018) used whole-cell electrophysiological recordings and found that null-direction signals were suppressed in T4 but preferred-direction signals were not amplified. Lastly, measuring calcium responses in T4 and T5, Haag and colleagues (2016, 2017) observed both preferred-direction amplification and null-direction suppression; interestingly, the two processes were spatially segregated within the neurons’ receptive fields such that preferred-direction amplification occurred on the preferred-direction side and null-direction suppression occurred on the null-direction side. Taking a different approach, Leong and colleagues (2016) presented noise stimuli and broadly characterized the spatiotemporal receptive fields of T4 and T5. These receptive fields contained two adjacent spatiotemporally oriented subfields, one preferring light and one preferring dark. They then extracted a linear-nonlinear description of T5 in which the nonlinearity was half-wave rectified and expansive; when combined with the receptive field, these results indicated that T5 nonlinearly amplifies preferred-direction signals and suppresses null-direction signals.

Work has begun to examine the mechanisms by which amplification and suppression emerge. Simultaneous optogenetic activation of the T4 input neurons Tm3 and Mi1 (but no other pairwise combination of the columnar inputs) produces a supralinear calcium signal in T4. This suggests that a specific amplifying mechanism does exist for T4, though it is unclear whether the Tm3-Mi1 interaction is direction selective (Strother et al. 2017). Suggesting a mechanism for suppression, electrophysiological recordings of T4 revealed that it receives inhibitory inputs on the null-direction side of its receptive field; such inputs could generate direction selectivity in a biophysical model (Gruntman et al. 2018). Additionally, application of the GABA_A antagonist picrotoxin eliminates direction selectivity in T4 and T5 by enhancing null-direction responses, suggesting that GABAergic inhibition somewhere in the circuit—possibly directly onto T4 and T5—suppresses null-direction signals (Fisher et al. 2015b). Cell-type-specific disruption of inhibitory glutamatergic input onto T4 and T5 shifted temporal tuning of optomotor behavior, demonstrating that multiple inhibitory mechanisms are critical for motion detection (Strother et al. 2017).

Insights from Theory—Scene Statistics and Higher-Order Correlations

Parallel theoretical work considering the statistics of visual stimuli has provided additional insight into the computations performed by the Drosophila elementary motion detector. The classical algorithms of elementary motion detection consider only pairwise or two-point correlations (two points in space-time). Such pairwise estimators produce relatively unreliable estimations of local motion signals when presented with naturalistic stimuli (Clark et al. 2014, Dror et al. 2001, Fitzgerald & Clark 2015). Naturalistic moving stimuli contain higher-order correlations (three or more points in space-time) that also signal motion (Anderson & Giannakis 1995, Clark et al. 2014, Fitzgerald et al. 2011), and flies respond appropriately to motion stimuli that lack informative two-point correlations (Clark et al. 2014, Leonhardt et al. 2016, Quenzer & Zanker 1991, Theobald et al. 2008). Critically, when considered along with two-point correlations, three-point (and higher odd-ordered) correlations improve motion estimation; however, this is true only when the visual stimulus has an asymmetric distribution of light and dark contrasts (Clark et al. 2014, Fitzgerald et al. 2011). As natural visual scenes are highly contrast asymmetric (Ratliff et al. 2010), these correlations are informative under real-world conditions. However, many experimental stimuli are symmetric (e.g., gratings) and therefore led to the development of algorithms that do not consider light-dark asymmetries. Nevertheless, modifying existing models with biologically plausible processing steps allows this additional information to be extracted to improve motion estimation (Fitzgerald & Clark 2015), and it has been shown that the Drosophila light and dark motion processing pathways are temporally asymmetric in a way that could take advantage of stimulus contrast asymmetries (Leonhardt et al. 2016). Furthermore, T4 and T5, as well as their inputs L1–3, are required for behavioral responses to three-point correlations (Clark et al. 2014, Leonhardt et al. 2016), suggesting that as the neuronal circuits of the Drosophila visual system compute motion, they either explicitly or implicitly incorporate higher-order correlations in addition to two-point correlations.

MODELING DROSOPHILA ELEMENTARY MOTION DETECTION

Dissection of the biological implementation of elementary motion detection in Drosophila has revealed unexpected complexities in both circuitry and responses that have provided new constraints that classical algorithms do not account for. As such, researchers have proposed a diverse array of alternative models to capture and explain these findings. Here we focus on three key features that have reshaped our understanding of the biological algorithm.

Light and Dark Pathways

One striking observation is that flies possess two different motion detectors, one specialized for moving light edges, and one specialized for moving dark edges (Clark et al. 2011, Joesch et al. 2010). Two conceptually distinct models can produce this kind of selectivity. In one view, a moving edge produces changes in both light and dark contrasts, creating three-point correlations that are specific for the contrast polarity of the edge (Clark et al. 2014, Fitzgerald & Clark 2015, Fitzgerald et al. 2011). A motion detector selective for one edge-contrast polarity then responds to a particular combination of light and dark inputs (Clark et al. 2011, 2014; Fitzgerald & Clark 2015; Fitzgerald et al. 2011; Leong et al. 2016; Strother et al. 2017). As a result, information about both contrast increments and contrast decrements is represented in both the light-edge and dark-edge motion detectors. An alternate view is that contrast selectivity in a motion detector arises strictly through half-wave rectification of the initial inputs, creating ON and OFF signals that are then compared in separate pathways (Eichner et al. 2011; Joesch et al. 2013; Leonhardt et al. 2016, 2017). Responses to specific light-dark correlations (such as reverse-phi or three-point correlations) are then achieved by precise tuning of asymmetries in the rectification threshold and temporal filtering in each pathway. The success of this approach demonstrates that correlations need not be computed explicitly to significantly influence output (Eichner et al. 2011, Joesch et al. 2013, Leonhardt et al. 2017).

Temporal Processing

Many instantiations of the Hassenstein-Reichardt correlator use first-order high-pass and low-pass filters with relatively large temporal offsets between input channels to represent neuronal temporal processing (Borst & Bahde 1986, Borst & Egelhaaf 1987, Egelhaaf & Reichardt 1987, Guo & Reichardt 1987, Reichardt 1961). However, physiological measurements of the neurons that provide input to the Drosophila motion detector revealed biphasic impulse responses that are very different in form from such mathematically simple filters and that have quite small temporal offsets (Arenz et al. 2017, Behnia et al. 2014, Fisher et al. 2015a, Strother et al. 2017, Yang et al. 2016). Strikingly, using these biologically derived filters in a Hassenstein-Reichardt correlator can reproduce the temporal frequency optimum seen with behavioral and physiological measurements (Behnia et al. 2014). Such a model also captures the timescale over which T4 and T5 are sensitive to correlations, though it does not predict the direction selectivity of that sensitivity (Salazar-Gatzimas et al. 2016). Other models based on experimentally measured neuronal filtering have further examined temporal differences that can support the extraction of motion (Arenz et al. 2017, Serbe et al. 2016). Finally, some studies have argued that temporal filtering by neurons upstream of T4 and T5 is not required for direction selectivity and that temporal filtering can emerge within the dendrites of T4 and T5 themselves through signal transduction delays involving specific neurotransmitter receptors (Shinomiya et al. 2014, Strother et al. 2017).

Algorithmic Variants

As the classical algorithms of elementary motion detection do not simultaneously incorporate preferred-direction amplification and null-direction suppression, the observation that T4 and T5 likely perform both has motivated alternative models (Haag et al. 2016, Leong et al. 2016, Strother et al. 2017). To account for these observations, Leong and colleagues (2016) proposed a modified motion energy model in which the nonlinearity is half-wave rectified and expansive, meaning that it has both suppressive and amplifying character. Furthermore, this nonlinearity contains odd-ordered components; when combined with the excitatory and inhibitory lobes of the spatiotemporal filter, this model becomes sensitive to three-point correlations while the original motion energy model, with its quadratic nonlinearity, is not.

In a different approach, models that explicitly combine the Hassenstein-Reichardt correlator and the Barlow-Levick model have been developed to capture preferred-direction amplification and null-direction suppression (Arenz et al. 2017; Haag et al. 2016, 2017; Strother et al. 2017). One of these models has three arms: the central arm is non-delayed and shared between the Hassenstein-Reichardt-like enhancing half on the preferred-direction side and the Barlow-Levick-like suppressing half on the null-direction side, each of which contributes a delayed arm. The signals from the three arms are nonlinearly combined by multiplying the enhancing signal and dividing by the suppressing signal. Alternatively, utilizing a biologically motivated architecture, a conceptually similar model incorporating Hassenstein-Reichardt-like and Barlow-Levick-like nonlinearities has been developed for T4 (Strother et al. 2017).

SYNTHESIS AND FUTURE DIRECTIONS

Elementary motion detection is a well-constrained, paradigmatic neural computation, and as we have described, our field has exploited most of the techniques of modern circuits neuroscience toward understanding it. We now know an essentially complete set of circuit elements, as well as their connections, response properties, and necessity for behavior across a range of visual stimuli. Furthermore, computational theories have provided a rich set of conceptual frameworks for understanding the experimental data and generating predictions for future work. As a result, elementary motion detection in Drosophila is one of the best understood neural circuit computations. Nevertheless, as a field, we cannot claim to have “solved” elementary motion detection. We cannot satisfactorily answer the question, How do flies compute motion? There exists no model that describes the elementary motion detection algorithm and its mechanistic implementation by specific neurons, synapses, molecules, and circuits. However, we believe that the field is poised to answer this question, and we outline some of the ways forward, both experimentally and conceptually.

Relating Models and Experiments

Our field benefits from considerable consensus regarding the experimental data, yet there is significant variation in the interpretation and modeling of these results. To pick just one example, there are no less than three different models that incorporate preferred-direction amplification and null-direction suppression, and it would not be difficult to write down several more structurally distinct models that capture these same two essential features. However, it is unclear whether all of these models can equally account for the key observations of previous experiments (and there is even debate about whether both preferred-direction amplification and null-direction suppression are necessary). When the goal is to provide an accurate description of the entire circuit, such an accounting is essential. However, when the goal of modeling is to generate a simple intuition for some specific aspect of the computation, the value of the model lies in its ability to inspire future experiments, not in its realism. The field would benefit from being clear about which of these two goals any model fulfills. In addition, since multiple algorithms can produce the same output, it is important to perform experiments that distinguish between particular algorithms. For example, one feature that distinguishes between motion-energy-like models and Hassenstein-Reichardt- or Barlow-Levick-like models is whether the direction-selective signal first originates through a linear mechanism, as in the former, or first originates through a nonlinear mechanism, as in the latter. As the field moves toward a model of the biological implementation of elementary motion detection that explains all of the data, it would be most informative if future experiments provided new constraints on the space of possible models.

Challenging Assumptions

As a field, we have implicitly assumed that there exists one motion detector using one algorithm. The identification of distinct light and dark pathways, and of T4 and T5, has shifted this view to two motion detectors, but other than considering some quantitative differences between them (Leonhardt et al. 2016), the field has continued to search for a unitary solution to motion detection, spanning all stimulus conditions and both T4 and T5. We instead propose that the Drosophila motion detection circuitry uses structurally distinct algorithms under different contexts. There are many hints that this may be occurring. For example, apparent motion stimuli revealed that preferred-direction amplification is observed only when the motion is fast (Fisher et al. 2015b; Haag et al. 2016, 2017; Salazar-Gatzimas et al. 2016). Flies can respond to much slower motion, but this mechanism does not appear to capture it, suggesting that T4 and T5 use a different means to estimate slower motion signals. Another clue comes from the observation that light-edge and dark-edge motion play different roles in shaping rotational and translational behavioral responses and that the input channels to the dark-edge pathway are differentially required depending on the behavioral output (Katsov & Clandinin 2008, Silies et al. 2013). To explore the possibility that different algorithms are at play under different stimulus conditions, we propose that the tuning of T4 and T5 be examined systematically across spatial, temporal, and contrast parameters for each type of stimulus. Furthermore, we suggest that the circuits that provide input to T4 and T5 are qualitatively different in how they compute motion. The columnar inputs to T4 and T5 are not simply contrast-inverted copies of each other: The two pathways differ in neurotransmitter phenotypes, the signs of their responses to light and dark, and their mixtures of temporal tuning properties (Arenz et al. 2017, Serbe et al. 2016, Shinomiya et al. 2014, Strother et al. 2017, Takemura et al. 2017). Since the internal elements are distinct, we speculate that T4 and T5 compute motion differently and that what we observe to be true for one cell type may not hold for the other.

Another assumption is that a model’s mathematical operations map cleanly onto specific cellular components. For example, there exists no experimental evidence that each input neuron should be assigned uniquely to one input channel of any computational model. We should use cell-type-specific silencing experiments to explicitly test the mapping of cells to computational processes, while exploring a range of visual stimuli from structured stimuli to noise. On the basis of these results, the field can develop algorithms and models that capture the key transformations each cell type performs.

Understanding Motion Processing at the Molecular Level

The experimental dissection of motion detection has used a wide range of techniques, but targeted molecular manipulations have rarely been utilized. We believe that such experiments can provide fundamental new insight and are now eminently tractable, especially in light of recent technical developments (Caussinus et al. 2012, Dietzl et al. 2007, Fisher et al. 2017, Nagarkar-Jaiswal et al. 2017, Xue et al. 2014). More precisely, we propose cell-type-specific gene disruption of key molecular components involved in synaptic signaling or neuronal biophysics combined with a range of visual stimuli and physiological measurements of the appropriate cell type. For example, voltage-gated ion channels in T4 and T5 could implement amplification of preferred-direction signals. These types of experiments will not only provide more mechanistic insight into the biological implementation of motion detection, but they will also be highly informative about the algorithms the system uses. That is, the existence of a molecular mechanism for a particular transformation necessitates that models incorporate that operation, thereby establishing particular frameworks and eliminating others.

COMPARISONS TO ELEMENTARY MOTION DETECTION IN OTHER SYSTEMS

Elementary motion detection is an important computation across sighted animals. In the vertebrate retina, direction selectivity first arises in the starburst amacrine cells (reviewed by Mauss et al. 2017, Taylor & Smith 2012). These are radially symmetric neurons in which individual dendrites prefer stimuli that move outward from the soma to the tips (Euler et al. 2002). Recent results suggest that in these cells, dendritic filtering enables a constructive summation of spatially offset excitatory inputs that is specific to motion in the preferred direction (Ding et al. 2016, Hausselt et al. 2007, Tukker et al. 2004, Vlasits et al. 2016). That is, like in T4 and T5, the algorithm underlying direction selectivity likely utilizes preferred-direction amplification. Inhibition enhances direction selectivity in the starburst amacrine cells but does not appear to be required to compute it (Ding et al. 2016, Hausselt et al. 2007, Poleg-Polsky et al. 2018, Tukker et al. 2004). This direction selectivity is then relayed to the next level of the circuit, the retinal ganglion cells, via null-direction inhibition (Briggman et al. 2011, O’Malley et al. 1992, Yoshida et al. 2001), consistent with the observations of Barlow & Levick (1965). Thus, at high level, there are algorithmic similarities between flies and the vertebrate retina, but the cellular and molecular implementations are likely to be quite different. For example, starburst amacrine cell dendrites are approximately an order of magnitude longer than the dendrites of T4 and T5, fundamentally altering biophysical mechanisms (Shinomiya et al. 2014, Takemura et al. 2017, Tukker et al. 2004). Direction selectivity in vertebrates is also computed de novo in simple cells of primary visual cortex (Hubel & Wiesel 1959, 1968). In this system, the dendrites of cortical neurons use linear summation of thalamic inputs at different spatiotemporal offsets to produce receptive fields that are oriented in space-time (Hamilton et al. 1989, Jagadeesh et al. 1993, Lien & Scanziani 2018, Livingstone 1998, McLean & Palmer 1989, Movshon et al. 1978, Reid et al. 1991). These signals are then passed through an expansive, thresholding nonlinearity, thought to be mediated by voltage-gated sodium channels, to produce a direction-selective spiking output. As such, the motion energy model appears to provide a strong description of the system. Notably, like T4 and T5, many simple cells are selective for either light or dark and are orientation tuned. As our understanding of the algorithms and mechanisms of elementary motion detection across systems advances, ever more detailed comparisons will be possible. Such comparisons will reveal the space of biological solutions to this evolutionarily conserved problem and the ways these solutions have adapted to shared and divergent constraints.

CONCLUDING REMARKS

We believe that the field is tantalizingly close to “solving” elementary motion detection in Drosophila. However, getting there will require a combination of new experiments and new approaches to thinking about the problem. More broadly, we believe that understanding the elementary motion detector in flies provides insights into how biological systems compute and that the successes and challenges the field has experienced provide conceptual and experimental lessons that can be applied to a wide range of problems in circuits neuroscience.