Sustainable production and waste management policies for COVID-19 medical equipment under uncertainty: A case study analysis

Abstract

Unfortunately, an abrupt corona-virus disease (COVID-19) outbreak brought a drastic change in human lives. Almost every sector of human-beings and their related activities are severely infected and affected by this COVID-19 pandemic. As days are passing, the impact of the COVID-19 epidemic is going to be more severe. The fundamental needs for personal protective equipment (PPEs) are rising drastically all over the world. In India, many non-pharmaceutical companies or organizations such as automobile companies are engaged in producing the PPEs at a very marginal rate. Thus this paper proposes a modeling and optimization framework for sustainable production and waste management (SPWM) decision-making model for COVID-19 medical equipment under uncertainty. To quantify the uncertainties among parameter values, we have taken advantage of the intuitionistic fuzzy set theory. A robust ranking function is presented to obtain a crisp version of it. Furthermore, a novel interactive intuitionistic fuzzy programming approach is developed to solve the proposed SPWM model. An ample opportunity to generate the desired solution sets are also depicted. The performance analysis based on multiple criteria such as savings from baseline, co-efficient of variations, and desirability degrees is also introduced. Practical managerial implications are also discussed based on the significant findings after applying to the real case study data-set. Finally, conclusive remarks and the future research direction are also addressed on behalf of the current contributing study.

1. Introduction

The whole world is currently in the trap of the “global war against the corona-virus disease (COVID-19) pandemic.” It comes from a family of vital viruses. Starting from China as an epicenter, it has widely been spread all over the world expediently. In China, the first case was detected in Wuhan, and after that, the chain of transmission began to date. Fighting against COVID-19, many precautionary and preventive measures have been initiated since the starting of October 2019. The ruling government of all the country have strictly imposed the complete Lockdown for the protection and welfare of peoples and citizens. The anticipated demand for medical equipment has been immensely raised due to low production and consumption in the regular days. Thus need for the Personal Protective Equipment (PPE) is among one the most demanded and consumed medical equipment. According to the World Health Organization (WHO), the PPE comprises garments used by healthcare workers or any other person from getting infected. It generally consists of standard precautions such as gloves, masks, and medicated gowns. It includes face protection, goggles, face shield, gloves, shoe cover, head cover, rubber boots in blood, or high airborne infections. PPEs kits are used by medical personnel working in isolation areas and intensive care units to protect them from acquiring infections. With the prospect of a massive requirement of PPEs arising shortly, many countries made proactive efforts to promote its manufacturing in its own country.

To meet the expected demand for highly demanded medical equipment, we have developed a multiobjective mixed-integer linear programming problem as a sustainable production and waste management (SPWM) model for COVID-19 medical equipment under uncertainty. The presented modeling approach comprises multiple objectives such as total cost, revenue, and total delivery time, exclusively related to medical equipment. The proposed SPWM model also reflects the very critical aspects of real-life such as budget allocation, safety measures, environmental protection, and various restrictions over production processes simultaneously. Most of the practical situations are consist of unavoidable uncertainty in the modeling processes of the proposed SPWM model. Due to the complexity of real-life problems, the decision-makers or managers most often face risks in determining parameter values. For instance, production processes vary with the availability of raw materials, human resources, working efficiency of machines, transportation of newly launched products for the first time from sources to consumer points may yield in an uncertain cost and time. Additionally, abrupt changes in environmental conditions, natural calamities, different modes of transportation, variations in the load capacity of various conveyances, unexpected changes in the price of fuel, total expected demand for new products, safety measures of the items due to road conditions are some influential factors for the existence of uncertainties among the parameters.

Impreciseness and vagueness among the input data are inevitable, and hence the data are not precise always and simultaneously are treated with the estimated values. Uncertainty among input data may take different forms, such as fuzzy, stochastic, and other uncertain types. The existence of uncertainty due to vagueness or ambiguity is dealt with fuzzy techniques, whereas uncertainty arises due to randomness treated with stochastic approaches. Both kinds of uncertainties have their limitations. For instance, if the decision-maker intends to quantify the value of different medical equipment requirements with some estimated value, such as each hospital requires approximately 14,000 items/day. The most likely estimated interval would be 12,000–16,000 items/day, along with some hesitation degree that may be given as 10,000–18,000 items/day, which ensures less violation of risks with acceptance and non-acceptance. Thus, this kind of quantification of parameters’ values reflects the more realistic approach to estimate the uncertain parameter compared to fuzzy and stochastic parameters.

Therefore, a well-organized multidimensional inter-connected setup for sustainable production and waste management model for COVID-19 medical equipment is much needed in the current scenario. An optimal production policy for newly manufactured medical equipment and adequate waste management strategies of the used medical equipment creates an eco-friendly production waste management planning network and contributes to the development of social prosperity and environmental protections.

1.1. Shortcomings of some solution methods and research gaps

Literature reveals several studies have taken the uncertain parameters, either fuzzy numbers or random variables followed by some distribution function. The fuzzy data only deals with the acceptance degree into the feasible solution set and does not consider the element’s rejection degree into the same feasible solution set. The random parameters need historical data for estimation purposes. It may not always be possible to have factual information for which the estimated values of parameters are suggested with the help of a suitable probability distribution function. In both cases (fuzzy and stochastic), the representation of parameters is not worth the effectiveness of yield incomparable outcomes and lacks the critical aspects of uncertainties. To overcome these issues, we have presented the intuitionistic fuzzy parameters, consisting of the element’s acceptance and rejection degrees, into the same feasible solution set. There is no scope for the historical data for the representation of intuitionistic fuzzy parameters.

The solution method proposed by Lai and Hwang, 1993, Lai and Hwang, 1994 discuss the overall achievement function by considering only the membership functions of each objective and do not consider the non-membership function simultaneously. Likewise, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988 suggested the overall satisfaction level using the membership function with their respective weight parameters and do not consider the non-membership functions at a time. Furthermore, Torabi and Hassini (2008) presented the overall achievement level by depicting the convex combination of the lower bound for satisfaction degree of each objective and the weighted sum of these achievement degrees and do not consider the non-membership function and upper bound of the dis-satisfaction degrees. Thus, the proposed IIFPA is exempted from the various shortcomings, drawbacks, and research gaps of the existing methods such as Lai and Hwang, 1993, Lai and Hwang, 1994, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988, Zimmermann, 1978, Torabi and Hassini, 2008. The detailed explanations are provided in Section 4.2. Therefore, the proposed IIFPA considers two aspects of the decision-making scenario by simultaneously dealing with membership and non-membership functions. This study fills the research gap by incorporating the intuitionistic fuzzy set theory in the parameters and solution techniques.

1.2. Motivation and research contributions

• •The proposed sustainable production policies and waste management strategies for COVID-19 medical equipment through a robust SPWM modeling framework need the present time. During the COVID-19 pandemic, the demand for personal protective equipment (PPEs) is very high, and the current production rate is unable to meet them efficiently. PPEs comprise medicated gown, N-95 masks, face shield, hand gloves, shoe-cover, sanitizers. In India, most of the PPEs were imported from outside of European countries. Nevertheless, the uncontrollable demand and an essential or indispensable requirement for PPEs worldwide made it crucial to export the PPEs to every leading exporting country. As a result, many automobiles and small-scale companies have taken initiatives to produce this medical equipment to meet the domestic demand. Thus, it is a very tough challenge before these companies to manufacture or produce PPEs due to the incomplete, inconsistent, inappropriate, and irrational knowledge and experiences to deal with this medical equipment explicitly starting from the acquirement of raw-materials, initiating the production and transportation processes and finally, the disposal operations to them. Preliminary safety measures and precautionary protection factors must be undertaken while handling this medical equipment starting from its production to its end-of-life phases. Thus an innovative, robust, and most prominent modeling approach for sustainable production and waste management policies for this COVID-19 medical equipment under a high level of uncertainty among different parameters is the essence of current time in decision-making scenarios.
• •In India, many companies from non-pharmaceuticals sectors are coming forward to contribute the society and humanity at this crucial time to build a one-nation spirit. As the managers or decision-makers are entering first time to manufacture and produce this medical equipment at high-level, it is obvious the lack or absence of historical data related to raw materials and this medical equipment such as purchasing, production, processing, transportation, service operating, inventory costs, quantity, time, budgets, safety factors. Thus to identify, assess, and quantify these data profitably and scientifically, the proposed SPWM model inevitably considered it an uncertain parameter. For example, in India, the expected demand for N-95 masks is around 31.6 million per day, while the COVID-19 cases are increasing rapidly day by day. In this situation, the uncertainty quantification based on the intuitionistic fuzzy concept would be more reliable and provide better estimates to those N-95 masks. Using fuzzy set theory, the most optimistic, the most likely, and the most pessimistic estimate maybe 25.2, 31.6, and 38.6 million per day, which violates the degree of hesitation regarding the rejection of these estimates. While using the intuitionistic fuzzy set theory, the projected estimation of these N-95 would be 27.2 to 35.6 million per day, along with the hesitation degrees of 22.5 to 42.67 million per day, which ensures less violation of shortages-risks with degrees of acceptance and rejection.
• •Of particular interest, the most crucial contribution is a novel Interactive Intuitionistic Fuzzy Programming Approach (IIFPA) to solve the crisp SPWM model under uncertainty.
• •The exclusive rationality and robustness of intuitionistic fuzzy parameters and the proposed IIFPA are also presented by proofing various theorems while solving the crisp SPWM model.
• •A marginal evaluation of each objective function means that degree of satisfaction level while obtaining the compromise solution by considering the multiple commensurable and conflicting objectives at a time. The marginal evaluations can be elicited by various sorts of membership functions such as linear, exponential, hyperbolic, modified S-curve that exist in the literature. A wide choice for selecting the desired form of marginal evaluations are suggested to the decision-makers or managers by incorporating the discussed membership and non-membership functions under the intuitionistic fuzzy environment. The robustness, rationality, and distinguishability of these marginal evaluations are reflected by proofing the appropriate theorems.
• •Performance analysis of the proposed SPWM model under different membership functions is measured based on multiple criteria. For this purpose, savings compared to baseline solution, co-efficient of variations and degrees of desirability (discussed in Section 4.3) are considered multiple criteria and used to examine the performances of applied solution approaches.
• •The whole solution schemes comprise various pre-determined parameters such as $d_m,\gamma ,\lambda$ and ${\eta }_m$ (these parameters are defined at their usual place in Section 4) which are solely assigned by the decision-makers or practitioners. Thus there is an ample opportunity to generate as many solution sets as decision-makers or managers want and select the most desired ones.
• •A real case-study description is implemented and modeled as a crisp SPWM model under intuitionistic fuzzy environment. The proposed IIFPA with different membership functions approaches are applied, and outcomes are analyzed with the significant findings efficiently. The performance analysis is also depicted based on the obtained solution results. Managerial implication is also highlighted, which is worth the essential backbone of the current study. At last, conclusions and future research are also suggested.

The rest part of the manuscript is presented as follows: In Section 2, the related literature review is discussed while Section 3 represents the descriptions of proposed SPWM model. The solution methodology and proposed interactive intuitionistic fuzzy programming approach is investigated in Section 4, whereas Section 5 reveals a case study description to show the applicability and validity of the proposed modeling and solution approach. Finally, conclusions and future research scope are discussed in Section 6.

2. Literature review

Available literature work reveals a tremendous amount of research work that has been carried out in the production and waste management of healthcare products. Here, we present a few relevant research work on this current study. The production planning problem is one of the most suitable and well-known applications of multiobjective linear programming problems (MOLPPs). Different objectives such as minimization of production cost and time, maximization of total profit, quality of the products, and workers’ satisfaction are the most commonly occurring objectives under a set of resources, budget, machines capacity, etc. restrictions in production planning problems. Pandian, Nagarajan, and Yaacob (2003) suggested a decision-making approach using modified S-curve membership function and applied to production planning problems. Bhattacharya and Vasant (2007) also discussed soft-sensing satisfaction level for product mix-problem and solved using robust heuristic fuzzy programming approach. Wang and Lee (2015) proposed an algorithm for location-allocation problem with risky demand in supply chaiin planning network. Zabihzadeh and Rezaeian (2016) presented two meta-heurstic algorithm for flexible flow shop scheduling and transportation problem under release time. Chien, Dou, and Fu (2018) have also developed a smart production planning under uncertain demand ratios. Darvishi, Yaghin, and Sadeghi (2020) have also integrated the fabric procurement and production planning problem and solved using a hybrid fuzzy-robust stochastic programmig approach. Sooncharoen, Pongcharoen, and Hicks (2020) discussed the Grey wolf method for production scheduling problem for the capital goods industry. Zhou and Liao (2020) have developed a multiobjective hybridized particle swarm optimization approach for solving a job shop green sceduling with production and crane transportation problems. Ahmad, Adhami, and Smarandache (2020) also discussed closed-loop supply chain plannig problem under uncertainty and solved using modified neutrosophic optimization technique.

Furthermore, Wang, Deschamps, and Dupas (2016) presented production-transportation problem via co-operative game theoretic approaches. Postan and Filina-Dawidowicz (2016) discussed a dynamic optimization model for supply, production and trnsportation of the perishable products. Ekşioğlu, Karimi, and Ekşioğlu (2016) developed an effective integrated production-transportation optimization model and algorithm for coal-fire power plants. Maity, Roy, and Verdegay (2019) discussed the time-variant interval-valued transportation problem in the sustainable environment. Das and Roy (2019) pointed out the effect of variable carbon emission in a multi-objective transportation-p-facility location problem under neutrosophic environment. Roy and Midya (2019) attempted to solve the multiobjective fixed-charge solid transportation problem with product blending under an intuitionistic fuzzy environment. Roy and Midya, 2019, Roy et al., 2018, Midya and Roy, 2020 also solved multiobjective multi-item fixed-charge solid transportation problem under twofold uncertainty, rough random variables, and using rough programming. Midya and Roy, 2017, Roy and Midya, 2019 presented an analytical study on interval programming in different environments and its application to the fixed-charge transportation problem. Ahmad, Ahmad, and Sharaf (2021) solved the supplier selection problem using a neutrosophic algorithm under Type-2 fuzzy parameters. Ahmad, Ahmad, Zaindin, and Adhami (2021) discussed the energy-food-water security nexus management using neutrosophic optimization approach. Adhami and Ahmad (2020) also proposed the interactive Pythagorean-hesitant fuzzy method to solve the transportation problem. Ahmad and Adhami, 2019a, Ahmad and Adhami, 2019b solved the multiobjective transportation problem under neutrosophic environment. Ahmad, Adhami, and Smarandache (2018) proposed a novel computational algorithm to solve the multiobjective nonlinear programming problem.

Díaz-Madroñero, Mula, and Peidro (2017) have also investigated a mathematical model for an integrated production and procurement transportation problems. Li, Su, and Ma (2017) have also addressed the production outsourcing decisions in supply chain network under single and multiple carbon policies. Fakhrzad, Talebzadeh, and Goodarzian (2018) have studied a green closd-loop suply chain planning problem by considering the production, transportation and distribution under uncertain supply and demand. Fathollahi-Fard, Hajiaghaei-Keshteli, and Mirjalili (2018) have presented a multiobjective supply chain problem by considering social aspects. Feng, Liu, Wu, and Chu (2018) also addressed two heuristic approaches for integrated production-transportation problem under uncertainty. Gharaei and Jolai (2018) proposed a multiagent approach for integrated production scheduling and distribution problem in multi-factory supply chain network. Jia, Zhuo, Leung, and Li (2019) also discussed production for parallel batch machine and minimize the total weighted delivery time. He and Li (2019) also addressed two-echelon multi-trip vehicle routing problem for crop harvesting and transportation planning problems. Chen (2020) suggested an production multi-dimensional manufacturing system analysis. Kilic and Yalcin (2020) discussed two phase fuzzy goal programming method for integrated green supplier selection problem in supply chain network. Liu, Li, Li, and Zou (2020) also investigated co-ordinated production-transportation sceduling problems with minimum sum of total delivery time. Díaz-Madroñero, Peidro, and Vasant (2010) studied a vendor selection using modified S-curve membership function and used Torabi and Hassini (2008) method to solve it. Zheng, Yi, Wang, and Liao (2017) presented an efficient solution concept under multiobjective programming problems and applied it to different real-life applications.

Regarding the healthcare waste management, many researchers have presented emperical, theoritical and modeling studies under different scenarios. Recently, Accenture (2020) provided an empirical study on the consumption of healthcare products during the COVID-19 outbreak. Aung, Luan, and Xu (2019) performed analytical multi-criteria decision-making study for the healthcare waste management system in Mayanmar. Azzurra, Massimiliano, and Angela (2019) presented the sustainable food consumption policies and examined on a case study. Bradley, Parry, and O’Regan (2020) addressed a functional and sustainable business model for production and consumption purposes. Fernando and Wah (2017) also discussed the impact of eco-innovation drivers on the environment and performed an empirical study on the Malaysian context. Joshi and Rahman (2017) investigated a study reflecting the consumers’ sustainable buying behavior. Joshi and Bhargava (2019) integrated the waste management quality with Green Quality Function Deployment strategies for healthcare wastes. Lüdeke-Freund, Carroux, Joyce, Massa, and Breuer (2018) performed a study on sustainable business model pattern taxonomy to support the business models. Chien et al. (2018) also carried out a study for the strategic smart production planning and presented a model under the demand uncertainty. de Sousa Jabbour et al. (2020) performed a theoretical study on the sustainable supply chain in the wake of the COVID-19 outbreak. Deress, Jemal, Girma, and Adane (2019) presented a green practice for dental healthcare wastes. Moreover, Dewi, Sukendi, Ikhwan, and Nazrianti (2019) highlighted the essential and factors associated with dental healthcare wastes thorough an empirical study. Eren and Tuzkaya (2019) discussed health and safety-oriented waste management policies and implemented them in a case study in Istanbul. Khan, Cheng, Khan, and Ahmed (2019) also presented a mini-review for healthcare waste management strategies in Asian developing countries. Khobragade (2019) addressed healthcare waste management by avoiding hazards due to living and non-living environment. Kleber and Cohen (2020) performed a study for waste reduction and increased the sustainability of healthcare wastes management. Padmanabhan and Barik (2019) also efficiently studied hazard waste disposal management. Rehman and Yu (2020) discussed the assessment procedure of eco-environmental performances. Ahmad, Adhami, and Smarandache (2019) also presented an overall water management system during shale gas extraction processes in intuitionistic fuzzy environment. Tabrizi, Saadati, Heydari, Rezapour, and Zamanpour (2019) also suggested practice to improve healthcare waste management and applied on a case study in Iran. World Health Organization (2020) discussed the management of water, sanitation, and healthcare wastes amid COVID-19 pandemic situations. The interested reader may find the relevant information describing the effective waste management policies in the articles Win et al., 2019, Zamparas et al., 2019. Thus production and waste management planning are integral components of the industrial supply chain network.

All the above mentioned studies have their own importance depending upon criteria and domain of research. This current study solely highlights the modeling and formulation of the proposed SPWM model which deals with production and waste management of medical equipment in the time of financial and social crisis.

3. Problem description and modeling under uncertainty

A systematic production configuration and waste management strategies for the flow of newly manufactured medical equipment and generated wastes after its use are the most significant constituent of the proposed sustainable production and waste management model. The highly consumed medical equipment durnig COVID-19 outbreak is shown in Fig. 1 . The optimal production, consumption, and waste management plan of action signify the smooth running of the companies’ production processes. Thus a wholesome and robust optimization model may formulate the operating services under the different echelons and produce effective production, consumption, and waste management policies. Therefore the proposed SPWM model exhibits similar characteristics features, which is much required to such a non-pharmaceuticals company that indulges in producing the medical equipment at the time of need. It consists of various raw material supplier points, advanced manufacturing, plants, demand markets or consumption points, collection centers, distribution centers, and finally, various disposal facilities. The suppliers are responsible for the procurement of raw materials such as cotton, plastics, foam, silks, etc. to the advanced manufacturing plants. At the advanced manufacturing units, the medical equipment is produced under the optimum utilization of various resources such as the ratio of raw materials, available machine hour, budget availability, safety measures while handling (see, Baidya et al., 2013, Baidya et al., 2014), production capacity, mode of conveyance, different echelons’ capacities and warehouse storage space for the newly manufactured medical equipment to meet the anticipated demand. These medical equipment are transported from advanced manufacturing plants to expected demand markets such as hospitals and COVID-19 treatment facility centers. After their end-of-life phase, the accumulation or collection is done by collection centers. The used medical equipment is sent to the distribution center for disassembling and distribution purposes to other functional facility units. After inspecting the recoverable or recyclable medical equipment, they are directly sent back to the advanced manufacturing plants for further processing. The rest of the used medical equipment is shipped to the disposal facility center either for under-ground disposal or incineration purposes. The cycle of manufacturing is continuous to meet them on time expected demand. The Central Government of India highly recommends the production of medicated gown, N-95 masks, face shield, hand-gloves, sanitizers, and shoe-cover at massive scale due to their shortages and ever unmet demand.

Fig. 1.

Highly consumed COVID-19 medical equipments.

It is quite apparent to face the uncertainty factor in the relevant parameters’ values. The existence of uncertainty is a more realistic phenomenon in this real-world. Hence the proposed SPWM model also enviably exhibits the uncertainty among different parameters’ values or input data-set. It is incorporating the logic behind uncertainty quantification scientifically based on the intuitionistic fuzzy theory. Unlike fuzzy and random parameters, uncertain parameters are depicted as triangular intuitionistic fuzzy numbers. A fuzzy parameter only deals with the degree of belongingness (acceptance) of the element into a feasible solution set. It does not consider the degree of non-belongingness (rejections) of the component into the same feasible solution set, an integrated part of the decision-making processes. Furthermore, uncertainty due to randomness is indicated with random parameters. Sometimes, it may not be possible to have historical data for which the random parameters are estimated. According to some specified probability distribution function, the forecasting pattern and parameters estimation of random variables is much dependent on the behavior and nature of the historical data. An intuitionistic fuzzy parameter deals with the degree of belongingness (acceptance) and degree of non-belongingness (rejections) of the element into the same feasible solution set, simultaneously. Alsw, there is no scope for the historical data while dealing with intuitionistic fuzzy parameters. Thus, the main aim and motive behind the selection of intuitionistic fuzzy parameters are to avoid the above shortcomings of fuzzy and random parameters. By keeping these issues in mind, the SPWM model is developed under the intuitionistic fuzzy uncertainty. The useful notions and descriptions are summarized in Table 1, Table 2 . The diagrammatic representation of the proposed SPWM model is depicted in Fig. 2 .

Table 1.

Notions and descriptions.

Indices	Descriptions
i	Denotes the number of raw material suppliers $(i=1,2,\cdots ,I)$
j	Denotes the number of advanced manufacturing plants $(j=1,2,\cdots ,J)$
k	Denotes the number of demand markets/consumption points $(k=1,2,\cdots ,K)$
l	Denotes the number of collection centers $(l=1,2,\cdots ,L)$
n	Denotes the types of conveyance (mode of transportatation) $(n=1,2,\cdots ,N)$
w	Denotes the number of distribution centers $(w=1,2,\cdots ,W)$
p	Denotes the number of disposal facility $(p=1,2,\cdots ,P)$
q	Denotes the types of medical equipment $(q=1,2,\cdots ,Q)$
Decision variable
$x_{i,j,n}^q$	Units of raw material for medical equipment q shipped from supplier i to manufacturing plants j using conveyance n
$x_{j,k,n}^q$	Units of medical equipment type q transported from manufacturing plants j to demand markets/consumption points k using conveyance n
$x_{k,l,n}^q$	Units of used medical equipment q collected from consumption points k to collection centers k using conveyance n
$x_{l,w,n}^q$	Units of medical equipment q transported from collection centers k to distribution centers w using conveyance n
$x_{w,j,n}^q$	Units of recoverable medical equipment q shipped from distribution centers w to manufacturing plants j using conveyance n
$x_{w,p,n}^q$	Units of scrap medical equipment q shipped from distribution centers w to disposal facility p using conveyance n
$y_{(·,·,·)}^q$	Represents the binary variable such that $y_{(·,·,·)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(·,·,·)}^q>0\hfill \\ 0,\hfill & x_{(·,·,·)}^q=0\hfill \end{array}\right)$
$z_{(j,k,n)}^q$	Tells us whether the route $(j,k)$ using conveyance n is active or not i.e., $z_{(j,k,n)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(j,k,n)}^q>0\hfill \\ 0,\hfill & x_{(j,k,n)}^q=0\hfill \end{array}\right)$
Parameters
${\tilde{R}}_j^q$	Rejection rates of medical equipment q at manufacturing plants j (unit)
${\tilde{T}}_{j,k,n}^q$	Total delivery time required to ship medical equipment q from manufacturing plants j to demand markets/consumption points k using conveyance n (hr)
${\widetilde{\mathit{REV}}}^q$	Total revenue generated by treating of unit medical equipment q ($/unit)
${\widetilde{\mathit{RC}}}_i^q$	Unit raw material cost required to produce medical equipment q at supplier i ($/unit)
${\widetilde{\mathit{PC}}}_j^q$	Unit production cost of medical equipment q at manufacturing plants j ($/unit)
${\tilde{H}}_j^q$	Time for machine usage to manufacture unit medical equipment q at manufacturing plants j (hr/unit)
${\widetilde{\mathit{TCC}}}_n^q$	Maximum capacity allowed for medical equipment q by using conveyance n
$\tilde{B}$	Total available budget for production and transportation purpose ($)
$\tilde{S}$	Desired safety value
${\widetilde{\mathit{SF}}}_{(·,·,·)}^q$	Protection factor related to medical equipment q during handeling
${\mathit{MC}}_j$	Maximum available machine capacity at manufacturing plants j (hr/unit)
${\mathit{WS}}_j$	Warehouse space per unit delivered at manufacturing plants j (ft2/unit)
${\mathit{MWS}}_k$	Maximum available warehouse space for demand markets/consumption points k (ft2)

Table 2.

Notions and descriptions.

Parameters	Descriptions
${\widetilde{\mathit{TC}}}_{i,j,n}^q$	Unit transportation cost of raw materials for medical equipment q from supplier i to manufacturing plants j by conveyance n ($/unit)
${\widetilde{\mathit{TC}}}_{j,k,n}^q$	Unit transportation cost of medical equipment q from manufacturing plants j to demand/consumption points k by conveyance n ($/unit)
${\widetilde{\mathit{TC}}}_{k,l,n}^q$	Unit transportation cost of medical equipment q from demand/consumption points k to collection center l by conveyance n ($/unit)
${\widetilde{\mathit{TC}}}_{l,w,n}^q$	Unit transportation cost of medical equipment q from collection center l to distribution center w by conveyance n ($/unit)
${\widetilde{\mathit{TC}}}_{w,j,n}^q$	Unit transportation cost of medical equipment q from distribution center w to manufacturing plants j by conveyance n ($/unit)
${\widetilde{\mathit{TC}}}_{w,p,n}^q$	Unit transportation cost of medical equipment q from distribution center w to disposal facilities p by conveyance n ($/unit)
${\widetilde{\mathit{IC}}}_l^q$	Unit inspection and accumulation cost for used medical equipment q at collection center l ($/unit)
${\widetilde{\mathit{DSC}}}_o^q$	Unit distribution cost of used medical equipment q at distribution center w ($/unit)
${\widetilde{\mathit{DRC}}}_j^q$	Unit disassembly and recovery cost of recoverable medical equipment q at manufacturing plants j ($/unit)
${\widetilde{\mathit{DC}}}_p^q$	Unit disposing cost of scrap medical equipment q at disposal facility p ($/unit)
${\widetilde{\mathit{INC}}}_o^q$	Unit inventory holding cost of medical equipment q at distribution center w ($/unit)
${\widetilde{\mathit{IHC}}}_o^q$	Total inventory holding capacity of scrap medical equipment q at distribution center w ($/unit)
${\widetilde{\mathit{MCS}}}_i^q$	Maximum supply capacity of raw material for medical equipment q at supplier i
${\widetilde{\mathit{TS}}}_j^q$	Total availability of medical equipment q at manufacturing plants j
${\widetilde{\mathit{TD}}}_k^q$	Total expected demand of medical equipment q at demand/consumption point k
${\widetilde{\mathit{MCC}}}_l^q$	Maximum capacity of accumulation for used medical equipment q at collection center l
${\widetilde{\mathit{MCD}}}_p^q$	Maximum capacity for disposing purpose of medical equipment q at disposal facilities p

Fig. 2.

Diagrammatic representation of proposed SPWM model.

3.1. Objective functions

Objective 1: Minimization of total economic cost

The total economic cost involved in the proposed SPWM model has a significant impact while extracting the overall profits for the organizations or firms. It consists of purchasing, production, transportation, and service operating costs associated with different service providing sectors to COVID-19 medical equipment. Thus the first objective function is linear and represented by (1) encompasses minimization of the total economic cost. The different prices associated with COVID-19 medical equipment are as follows: cost of purchasing raw material and transportation cost from supplier point to advanced manufacturing/ plant, production cost and transportation cost from advanced manufacturing plant to demand market, collection cost and transportation cost from demand market to collection center, distribution and inventory holding costs at the distribution center, transportation cost from collection center to the distribution center, disassembly, manufacturing, and transportation cost from distribution center to manufacturing plant, and disposal and transportation cost from distribution center to disposal facility by using various modes of transportation (conveyances).

$$\begin{array}{cc}\mathit{Minimize}{F}_1=\hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\displaystyle \sum _i}{\widetilde{\mathit{RC}}}_i^q\times x_{i,j,n}^q\right)+\left({\widetilde{\mathit{PC}}}_j^q\times x_{j,k,n}^q\right)+\left({\displaystyle \sum _o}\left({\widetilde{\mathit{DSC}}}_o^q+{\widetilde{\mathit{INC}}}_o^q\right)\times x_{l,w,n}^q\right)+\hfill \\ \hfill & {\displaystyle \sum _i}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\times x_{i,j,n}^q\right)+{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\times x_{j,k,n}^q\right)+{\displaystyle \sum _k}{\displaystyle \sum _l}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\times x_{k,l,n}^q\right)+\hfill \\ \hfill & {\displaystyle \sum _l}{\displaystyle \sum _o}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\times x_{l,w,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\times x_{w,j,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _p}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\times x_{w,p,n}^q\right)+\hfill \\ \hfill & \left({\displaystyle \sum _l}{\widetilde{\mathit{IC}}}_l^q\times x_{k,l,n}^q\right)+\left({\displaystyle \sum _j}{\widetilde{\mathit{DRC}}}_j^q\times x_{w,j,n}^q\right)+\left({\displaystyle \sum _p}{\widetilde{\mathit{DC}}}_p^q\times x_{w,p,n}^q\right)+\left({\displaystyle \sum _o}{\tilde{R}}_j^q\times x_{w,j,n}^q\right)\hfill \\ \hfill & \forall i,j,k,l,w,n,q\text{.}\hfill \end{array}$$ (1)

Objective 2: Maximization of total revenue gained

Sustainable or green practices for the management of generated waste are quite indispensable for both economic and environmental points of view. The end-of-life phase of COVID-19 medical equipment has a severe impact on the ecosystem, as most raw materials are plastics and foams. After their useful life, there is an option before the managers or decision-makers re-manufacture into some other trivial products. Therefore the collected COVID-19 medical equipment wastes are distributed from distribution centers to either advanced manufacturing plants or directly disposal facilities for land-fills and incineration purposes. Thus the second objective function represented by (2) ensures the maximization of the total revenue gained on the unit recoverable or re-manufactured product transported from distribution centers to advanced manufacturing plants.

$$\mathit{Maximize}{F}_2={\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _q}{\displaystyle \sum _n}{\widetilde{\mathit{REV}}}^q\times x_{w,j,n}^q\forall w,j,q,n\text{.}$$ (2)

Objective 3: Minimization of total delivery time

In the current COVID-19 situations, on-time deliveries of sufficient medical equipment are of prime concern for the firms or companies. Instant delivery policy enhances the company’s market values and goodwill, which is an utmost competitive advantage. Hence, the third objective function depicted by (3) assures the significant reduction in total delivery time for medical equipment transported from advanced manufacturing plant to demand market or consumption points.

$$\mathit{Minimize}{F}_3={\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _q}{\displaystyle \sum _n}{\tilde{T}}_{j,k,n}^q\times z_{j,k,n}^q\forall j,k,q,n\text{.}$$ (3)

3.2. Constraints

The entire modeling configuration of the proposed SPWM model exhibits the integration of well-known planning and strategic policies such as purchasing, production, transportation, collection, distribution, storage, supply, demand, safety, disposal, and budgets, respectively. Thus, restrictions imposed over different parameters inevitably signify the more effective and realistic modeling framework.

Production and consumption constraints:

In COVID-19 crucial situations, availability and acquirement of raw materials are not easily possible for every production company at a commercial level. In India, some NGOs and non-profit organizations are also producing this medical equipment for distribution among medical personnel and hospitals. Thus suppliers have a limited amount of raw materials for commercial purposes. Hence the constraint (4) ensures the unit of raw materials supplied to advanced manufacturing plants must be less than or equals to its maximum capacities at different supplier points. The total machine capacity to produce each of these medical equipment at advanced manufacturing plants must be less than and equals to its respective maximum positions in the production processes. Thus, the constraint (5) ensures the total machine capacity available at each advanced manufacturing plant to produce the optimal number of this medical equipment. Alsw, this medical equipment’s total quantity must be less than and equal to the respective supply capacity at each advanced manufacturing plant and represented by constraint (6). The storage capacity due to space limitations is also an important issue associated with this medical equipment. To ensure the maximum warehouse space utilization at each demand market or consumption points, the constraint (7) is incorporated. Most importantly, this medical equipment requirement is essential for medical personnel or practitioners to treat COVID-19 infected patients. Thus constraint (8) ensures the maximum shipment of this medical equipment must be higher than or equals to the total expected demand that is to be met at different consumption zones or hospitals.

$${\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{i,j,n}^q⩽{\widetilde{\mathit{MCS}}}_i^q$$ (4)

$${\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{H}_j^q\times x_{i,j,n}^q⩽{\mathit{MC}}_i$$ (5)

$${\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩽{\widetilde{\mathit{TS}}}_j^q$$ (6)

$${\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}{\mathit{WS}}_j\times x_{j,k,n}^q⩽{\mathit{MWS}}_k$$ (7)

$${\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩾{\widetilde{\mathit{TD}}}_k^q$$ (8)

Budget availability constraint:

The total availability of budget for the purchasing, production, and transportation purpose of this medical equipment must be in the prescribed limit. To ensure the budget restrictions, constraint (9) is constrained in the proposed SPWM model.

$$\begin{array}{cc}\hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{RC}}}_i^q\times x_{i,j,n}^q\right)+\left({\widetilde{\mathit{PC}}}_j^q\times x_{j,k,n}^q\right)+{\displaystyle \sum _i}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\times x_{i,j,n}^q\right)+{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\times x_{j,k,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _k}{\displaystyle \sum _l}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\times x_{k,l,n}^q\right)+{\displaystyle \sum _l}{\displaystyle \sum _o}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\times x_{l,w,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\times x_{w,j,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _o}{\displaystyle \sum _p}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\times x_{w,p,n}^q\right)⩽\tilde{B}\hfill \end{array}$$ (9)

Safety factor constraint:

Moreover, the most important characteristic feature of the proposed SPWM model is to enhance the safety factors associated with this medical equipment while handling it at different points as the contamination and transfusion rates of COVID-19 is very high and drastically communicable. The safety factors are measured using the concept of Baidya et al., 2013, Baidya et al., 2014. To achieve the desired safety protection related to each of this medical equipment, the constraint (10) is depicted.

$$\begin{array}{cc}\hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _i}{\displaystyle \sum _j}{\widetilde{\mathit{SF}}}_{i,j,n}^q\times y_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}{\widetilde{\mathit{SF}}}_{j,k,n}^q\times y_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}{\widetilde{\mathit{SF}}}_{k,l,n}^q\times y_{k,l,n}^q\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _o}{\widetilde{\mathit{SF}}}_{l,w,n}^q\times y_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}{\widetilde{\mathit{SF}}}_{w,j,n}^q\times y_{w,j,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _p}{\widetilde{\mathit{SF}}}_{w,p,n}^q\times y_{w,p,n}^q>\tilde{S}\hfill \end{array}$$ (10)

Transportation capacity constraint:

Related to the transportation problem, the usage of appropriate conveyance is somehow economic in some places. The maximum quantity of this medical equipment from various sources to different destination points must be less than or equals to its respective maximum conveyance capacities. Thus constraint (11) ensures the restrictions over conveyances capacity.

$${\displaystyle \sum _n}{\displaystyle \sum _q}\left({\displaystyle \sum _i}{\displaystyle \sum _j}{x}_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}{x}_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}{x}_{k,l,n}^q+{\displaystyle \sum _l}{\displaystyle \sum _o}{x}_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}{x}_{w,j,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _p}{x}_{w,p,n}^q\right)⩽{\widetilde{\mathit{TCC}}}_n^q$$ (11)

Capacity constraints:

After a one-time-use of this medical equipment, the end-of-life phase initiates, and they are treated as generated wastes. The proper management of this used medical equipment needs careful precaution while handling them. The various collection, distribution, and disposal facilities are build-up for the treatment of these wastes efficiently. There is a maximum capacity associated with each of these facilities centers for the allocation of quantity or units of these wastes to different facilities. Thus the maximum units of these waste medical equipment that are shipped from consumption points to a collection center, from collection center to distribution center and from distribution center to disposal facilities must be less than or equals to their respective maximum allowed capacities and represented in constraints (12), (13), (14), respectively. The constraint (15) ensures the flow of medical equipment associated with different sources to various destinations in the proposed SPWM model. Constraint (16) tells us whether the given route are active or not. The non-negativity restriction (17) is also presented.

$${\displaystyle \sum _k}{\displaystyle \sum _l}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{k,l,n}^q⩽{\widetilde{\mathit{MCC}}}_l^q$$ (12)

$${\displaystyle \sum _l}{\displaystyle \sum _o}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{l,w,n}^q⩽{\widetilde{\mathit{IHC}}}_o^q$$ (13)

$${\displaystyle \sum _o}{\displaystyle \sum _p}{\displaystyle \sum _q}{\displaystyle \sum _n}{x}_{w,p,n}^q⩽{\widetilde{\mathit{MCD}}}_p^q$$ (14)

$$y_{(·,·,·)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(·,·,·)}^q>0\text{;}{\widetilde{\mathit{SF}}}_{(·,·,·)}^q>0\hfill \\ 0,\hfill & x_{(·,·,·)}^q=0\text{;}{\widetilde{\mathit{SF}}}_{(·,·,·)}^q=0\hfill \end{array}\right\}\forall i,j,k,l,w,p,q$$ (15)

$$z_{(j,k,n)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(j,k,n)}^q>0\hfill \\ 0,\hfill & x_{(j,k,n)}^q=0\hfill \end{array}\right)$$ (16)

$$x_{i,j,n}^q,x_{j,k,n}^q,x_{k,l,n}^q,x_{l,w,n}^q,x_{w,j,n}^q,x_{w,p,n}^q⩾0\forall i,j,k,l,w,p,q\text{.}$$ (17)

Thus the formulation of intuitionistic fuzzy sustainable production and waste management model (IFSPWM) (18) can be summarized as follows:

$$\begin{array}{cc}\mathit{Minimize}{F}_1=\hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\displaystyle \sum _i}{\widetilde{\mathit{RC}}}_i^q\times x_{i,j,n}^q\right)+\left({\widetilde{\mathit{PC}}}_j^q\times x_{j,k,n}^q\right)+\left({\displaystyle \sum _o}\left({\widetilde{\mathit{DSC}}}_o^q+{\widetilde{\mathit{INC}}}_o^q\right)\times x_{l,w,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _i}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\times x_{i,j,n}^q\right)+{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\times x_{j,k,n}^q\right)+{\displaystyle \sum _k}{\displaystyle \sum _l}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\times x_{k,l,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _o}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\times x_{l,w,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\times x_{w,j,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _p}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\times x_{w,p,n}^q\right)\hfill \\ \hfill & +\left({\displaystyle \sum _l}{\widetilde{\mathit{IC}}}_l^q\times x_{k,l,n}^q\right)+\left({\displaystyle \sum _j}{\widetilde{\mathit{DRC}}}_j^q\times x_{w,j,n}^q\right)+\left({\displaystyle \sum _p}{\widetilde{\mathit{DC}}}_p^q\times x_{w,p,n}^q\right)+\left({\displaystyle \sum _o}{\tilde{R}}_j^q\times x_{w,j,n}^q\right)\hfill \\ {\mathit{MaximizeF}}_2=\hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _q}{\displaystyle \sum _n}{\widetilde{\mathit{REV}}}^q\times x_{w,j,n}^q\hfill \\ {\mathit{MinimizeF}}_3=\hfill & {\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _q}{\displaystyle \sum _n}{\tilde{T}}_{j,k,n}^q\times z_{j,k,n}^q\hfill \\ \mathrm{subject}\mathrm{to}\hfill & \hfill \\ \hfill & {\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{i,j,n}^q⩽{\widetilde{\mathit{MCS}}}_i^q\hfill \\ \hfill & {\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{H}_j^q\times x_{i,j,n}^q⩽{\mathit{MC}}_i\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩽{\widetilde{\mathit{TS}}}_j^q\hfill \\ \hfill & {\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}{\mathit{WS}}_j\times x_{j,k,n}^q⩽{\mathit{MWS}}_k\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩾{\widetilde{\mathit{TD}}}_k^q\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{RC}}}_i^q\times x_{i,j,n}^q\right)+\left({\widetilde{\mathit{PC}}}_j^q\times x_{j,k,n}^q\right)+{\displaystyle \sum _i}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\times x_{i,j,n}^q\right)+{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\times x_{j,k,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _k}{\displaystyle \sum _l}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\times x_{k,l,n}^q\right)+{\displaystyle \sum _l}{\displaystyle \sum _o}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\times x_{l,w,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _j}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\times x_{w,j,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _o}{\displaystyle \sum _p}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\times x_{w,p,n}^q\right)⩽\tilde{B}\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _i}{\displaystyle \sum _j}{\widetilde{\mathit{SF}}}_{i,j,n}^q\times y_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}{\widetilde{\mathit{SF}}}_{j,k,n}^q\times y_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}{\widetilde{\mathit{SF}}}_{k,l,n}^q\times y_{k,l,n}^q\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _o}{\widetilde{\mathit{SF}}}_{l,w,n}^q\times y_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}{\widetilde{\mathit{SF}}}_{w,j,n}^q\times y_{w,j,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _p}{\widetilde{\mathit{SF}}}_{w,p,n}^q\times y_{w,p,n}^q>\tilde{S}\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}\left({\displaystyle \sum _i}{\displaystyle \sum _j}{x}_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}{x}_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}{x}_{k,l,n}^q+{\displaystyle \sum _l}{\displaystyle \sum _o}{x}_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}{x}_{w,j,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _n}{\displaystyle \sum _q}\left({\displaystyle \sum _o}{\displaystyle \sum _p}{x}_{w,p,n}^q\right)⩽{\widetilde{\mathit{TCC}}}_n^q\hfill \\ \hfill & {\displaystyle \sum _k}{\displaystyle \sum _l}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{k,l,n}^q⩽{\widetilde{\mathit{MCC}}}_l^q\hfill \\ \hfill & {\displaystyle \sum _l}{\displaystyle \sum _o}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{l,w,n}^q⩽{\widetilde{\mathit{IHC}}}_o^q\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _p}{\displaystyle \sum _q}{\displaystyle \sum _n}{x}_{w,p,n}^q⩽{\widetilde{\mathit{MCD}}}_p^q\hfill \\ \hfill & y_{(·,·,·)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(·,·,·)}^q>0\text{;}{\widetilde{\mathit{SF}}}_{(·,·,·)}^q>0\hfill \\ 0,\hfill & x_{(·,·,·)}^q=0\text{;}{\widetilde{\mathit{SF}}}_{(·,·,·)}^q=0\hfill \end{array}\right\}\forall i,j,k,l,w,p,q\hfill \\ \hfill & z_{(j,k,n)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(j,k,n)}^q>0\hfill \\ 0,\hfill & x_{(j,k,n)}^q=0\hfill \end{array}\right)\hfill \\ \hfill & x_{i,j,n}^q,x_{j,k,n}^q,x_{k,l,n}^q,x_{l,w,n}^q,x_{w,j,n}^q,x_{w,p,n}^q⩾0\hfill \end{array}$$ (18)

where $\widetilde{(·)}$ represents the triangular intuitionistic fuzzy parameters involved in the objective functions and constraints, respectively.

3.3. Treating intuitionistic fuzzy parameters

For treating intuitionistic fuzzy parameters, we have discussed some basic concepts related to intuitionistic fuzzy set (IFS).

Definition 1 Atanassov (1986) Intuitionistic Fuzzy Set —

Assume that there be a univeral set X. Then, an intuitionistic fuzzy set $\tilde{Y}$ in X is difined by the ordered triplets as follows:

$$\tilde{Y}=\{x,{\mu }_{\tilde{Y}}(x),{\nu }_{\tilde{Y}}(x\left)\right|x\in X\}$$

where ${\mu }_{\tilde{Y}}\left(x\right):X\to [0,1]$ denotes the membership function and ${\nu }_{\tilde{Y}}\left(x\right):X\to [0,1]$ denotes the non-membership function of the element $x\in X$ into the set $\tilde{Y}$, respectively, with the conditions $0⩽{\mu }_{\tilde{Y}}\left(x\right)+{\nu }_{\tilde{Y}}\left(x\right)⩽1$. The value of ${\varphi }_{\tilde{Y}}\left(x\right)=1-{\mu }_{\tilde{Y}}\left(x\right)-{\nu }_{\tilde{Y}}\left(x\right)$, is called the degree of uncertainty of the element $x\in X$ to the IFS $\tilde{Y}$. If ${\varphi }_{\tilde{Y}}\left(x\right)=0$, an IFS becomes fuzzy set and takes the form $\tilde{Y}=\{x,{\mu }_{\tilde{Y}}(x),1-{\mu }_{\tilde{Y}}(x\left)\right|x\in X\}$.

Definition 2 Ahmad et al. (2019) Intuitionistic fuzzy number —

An intuitionistic fuzzy set $\tilde{Y}=\{x,{\mu }_{\tilde{Y}}(x),{\nu }_{\tilde{Y}}(x\left)\right|x\in X\}$is said to be an intuitionistic fuzzy number if and only iff

• 1.There exist a real number $x_0\in \mathrm{IR}$ for which ${\mu }_{\tilde{Y}}\left(x\right)=1$ and ${\nu }_{\tilde{Y}}\left(x\right)=0$.
• 2.The membership function ${\mu }_{\tilde{Y}}\left(x\right)$ of $\tilde{Y}$ is fuzzy convex and non-membership function ${\nu }_{\tilde{Y}}\left(x\right)$ of $\tilde{Y}$ is fuzzy concave.
• 3.Alsw, ${\mu }_{\tilde{Y}}\left(x\right)$ is upper semi-continuous and ${\nu }_{\tilde{Y}}\left(x\right)$ is lower semi-continuous.
• 4.The support of $\tilde{Y}$ is given by $\left(x\in \mathrm{IR}:{\nu }_{\tilde{\mathrm{Y}}}\left(\mathrm{x}\right)⩽1\right)$.

Definition 3 Ahmad et al. (2019) Triangular intuitionistic fuzzy number —

A triangular intuitionistic fuzzy number (TrIFN) is represented by $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ where $z_1,y_1,y_2,y_3,z_3\in \mathrm{IR}$ such that $z_1⩽y_1⩽y_2⩽y_3⩽z_3$; and its membership function ${\mu }_{\tilde{Y}}\left(x\right)$ and non-membership function ${\nu }_{\tilde{Y}}\left(x\right)$ is of the form

$${\mu }_{\tilde{Y}}\left(x\right)=\left\{\begin{array}{cc}\frac{x-y_1}{y_2-y_1},\hfill & \mathrm{if}{y}_1<x<y_2,\hfill \\ 1,\hfill & \mathrm{if}x=y_2,\hfill \\ \frac{y_3-x}{y_3-y_2},\hfill & \mathrm{if}{y}_2<x<y_3,\hfill \\ 0,\hfill & \mathrm{if}\mathrm{otherwise}\text{.}\hfill \end{array}\right)\mathrm{and}{\nu }_{\tilde{Y}}\left(x\right)=\left\{\begin{array}{cc}\frac{y_2-x}{y_2-z_1},\hfill & \mathrm{if}{z}_1<x<y_2,\hfill \\ 0,\hfill & \mathrm{if}x=y_2,\hfill \\ \frac{x-y_2}{z_3-y_2},\hfill & \mathrm{if}{y}_2<x<z_3,\hfill \\ 1,\hfill & \mathrm{if}\mathrm{otherwise}\text{.}\hfill \end{array}\right)$$

Definition 4 Ahmad et al. (2019) —

Consider that a TrIFN is given by $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ where $z_1,y_1,y_2,y_3,z_3\in \mathrm{IR}$ such that $z_1⩽y_1⩽y_2⩽y_3⩽z_3$. Then the parametric form of $\tilde{Y}$ are $u\left(\tau \right)=\left(\overline{u\left(\tau \right)},\underset{\_}{u\left(\tau \right)}\right)$ and $v\left(\tau \right)=\left(\overline{v\left(\tau \right)},\underset{\_}{v\left(\tau \right)}\right)$. Further, $u\left(\tau \right)$ and $v\left(\tau \right)$ are the parametric form of TrIFN corresponding to membership and non-membership functions such that $\overline{u\left(\tau \right)}=y_3-\tau (y_3-y_1),\underset{\_}{u\left(\tau \right)}=y_1-\tau (y_2-y_1)$ and $\overline{v\left(\tau \right)}=y_2-(1-\tau )(y_2-z_1),\underset{\_}{v\left(\tau \right)}=y_2+(1-\tau )(z_3-y_2)$ respectively. A TrIFN $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ is said to be positive TrIFN if $z_1>0$ and hence $y_1,y_2,y_3,z_3$ are all positive numbers.

Some important properties of TrIFN are as follows:

Property 1

Assume that$\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$and$\tilde{W}=\left((w_1,w_2,w_3)\text{;}(v_1,w_2,v_3)\right)$are two TrIFNs. Then addition of$\tilde{Y}$and$\tilde{W}$is again a TrIFN.

$$\tilde{Y}+\tilde{W}=\left[\left(y_1+w_1,y_2+w_2,y_3+w_3\right)\text{;}\left(z_1+v_1,y_2+w_2,z_3+v_3\right)\right]$$

Property 2

Consider that$\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$be a TrIFN and$k\in \mathrm{IR}$. Then scaler multiplication of$\tilde{Y}$is again a TrIFN.

$$k\left(\tilde{Y}\right)=\left\{\begin{array}{cc}({\mathit{ky}}_1,{\mathit{ky}}_2,{\mathit{ky}}_3\text{;}{\mathit{kz}}_1,{\mathit{ky}}_2,{\mathit{kz}}_3)\hfill & k>0\hfill \\ ({\mathit{ky}}_3,{\mathit{ky}}_2,{\mathit{ky}}_1\text{;}{\mathit{kz}}_3,{\mathit{ky}}_2,{\mathit{kz}}_1)\hfill & k<0\hfill \\ (0,0,0\text{;}0,0,0),\hfill & k=0\hfill \end{array}\right)$$

Property 3

The two TrIFNs$\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$and$\tilde{W}=\left((w_1,w_2,w_3)\text{;}(v_1,w_2,v_3)\right)$are said to be equal iff$y_1=w_1,y_2=w_2,y_3=w_3\text{;}{z}_1=v_1,y_{2=w_2},z_3=v_3$.

Definition 5 Ahmad et al. (2019) Expected interval and expected value of TrIFNs —

The concept of expected interval and expected value was defined by Heilpern (1992). Thus, we re-defined it for TrIFNs. Suppose that $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ be a TrIFN and ${\mathit{EI}}^{\mu }$ and ${\mathit{EI}}^{\nu }$ depict the expected intervals for membership and non-membership functions respectively. Thus, these can be defined as follows:

$$\begin{array}{cc}\hfill {\mathit{EI}}^{\mu }\left(\tilde{Y}\right)=& \left[{\int }_0^1\underset{\_}{u\left(\tau \right)}d\tau ,{\int }_0^1\overline{u\left(\tau \right)}d\tau \right]\hfill \\ \hfill =& \left[{\int }_0^1{y}_3-\tau (y_3-y_1)d\tau ,{\int }_0^1{y}_1-\tau (y_2-y_1)d\tau \right]\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathit{EI}}^{\nu }\left(\tilde{Y}\right)=& \left[{\int }_0^1\underset{\_}{v\left(\tau \right)}d\tau ,{\int }_0^1\overline{v\left(\tau \right)}d\tau \right]\hfill \\ \hfill =& \left[{\int }_0^1{y}_2-(1-\tau )(y_2-z_1)d\tau ,{\int }_0^1{y}_2+(1-\tau )(z_3-y_2)d\tau \right]\hfill \end{array}$$

Moreover, consider that ${\mathit{EV}}^{\mu }\left(\tilde{Y}\right)$ and ${\mathit{EV}}^{\nu }\left(\tilde{Y}\right)$ represent the expected values corresponding to membership and non-membership functions respectively. These can be depicted as follows:

$${\mathit{EV}}^{\mu }\left(\tilde{Y}\right)=\frac{{\int }_0^1\underset{\_}{u\left(\tau \right)}d\tau +{\int }_0^1\overline{u\left(\tau \right)}d\tau }{2}=\frac{y_1+2y_2+y_3}{4}$$ (19)

$${\mathit{EV}}^{\nu }\left(\tilde{Y}\right)=\frac{{\int }_0^1\underset{\_}{v\left(\tau \right)}d\tau +{\int }_0^1\overline{v\left(\tau \right)}d\tau }{2}=\frac{z_1+2y_2+z_3}{4}$$ (20)

The expected value EV of a TrIFN $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ is given as follows:

$$\mathit{EV}\left(\tilde{Y}\right)=\psi {\mathit{EV}}^{\mu }\left(\tilde{Y}\right)+(1-\psi ){\mathit{EV}}^{\nu }\left(\tilde{Y}\right),\mathrm{where}\psi \in [0,1]$$

Definition 6 Accuracy function —

The expected value $\left(\mathit{EV}\right)$ for TrIFN $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ with the help of Eqs. (19), (20) and for $\psi =0.5$ can be represented as follows:

$$\mathit{EV}\left(\tilde{Y}\right)=\frac{y_1+y_3+4y_2+z_1+z_3}{8}$$

Thus $\mathit{EV}\left(\tilde{Y}\right)$ is also known as accuracy function of $\tilde{Y}$.

Theorem 1

Suppose that$\tilde{Y}$be a TrIFN. Then for any$\mathit{EV}:\mathit{IF}\left(\mathrm{IR}\right)\to \mathrm{IR}$; the expected value$\mathit{EV}\left(k\tilde{A}\right)=\mathit{kEV}\left(\tilde{A}\right)$for all$k\in \mathrm{IR}$.

Proof

Let us consider that $\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$ be a TrIFN. Then, based on the nature of k, three different cases will arise:

Case I: when $k=0$, there is nothing to prove.

Case II: when $k>0$, then we have $k\tilde{Y}=k\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)=({\mathit{ky}}_1,{\mathit{ky}}_2,{\mathit{ky}}_3\text{;}{\mathit{kz}}_1,{\mathit{ky}}_2,{\mathit{kz}}_3)$ by using Property 2. Now taking expected value of $k\tilde{Y}$, we get

$$\begin{array}{cc}\hfill \mathit{EV}\left(k\tilde{A}\right)=& \mathit{EV}({\mathit{ky}}_1,{\mathit{ky}}_2,{\mathit{ky}}_3\text{;}{\mathit{kz}}_1,{\mathit{ky}}_2,{\mathit{kz}}_3)\hfill \\ \hfill =& \frac{\left({\mathit{ky}}_1+2{\mathit{ky}}_2+{\mathit{ky}}_3+{\mathit{kz}}_1+2{\mathit{ky}}_2+{\mathit{kz}}_3\right)}{8}\hfill \\ \hfill =& k\frac{\left(y_1+4y_2+y_3+z_1+z_3\right)}{8}\hfill \\ \hfill =& \mathit{kEV}\left(\tilde{A}\right)\hfill \end{array}$$

Case III: when $k<0$, then we have $k\tilde{Y}=k\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)=({\mathit{ky}}_3,{\mathit{ky}}_2,{\mathit{ky}}_1\text{;}{\mathit{kz}}_3,{\mathit{ky}}_2,{\mathit{kz}}_1)$ by using Property 2. Now taking expected value of $k\tilde{Y}$, we get

$$\begin{array}{cc}\hfill \mathit{EV}\left(k\tilde{A}\right)=& \mathit{EV}({\mathit{ky}}_3,{\mathit{ky}}_2,{\mathit{ky}}_1\text{;}{\mathit{kz}}_3,{\mathit{ky}}_2,{\mathit{kz}}_1)\hfill \\ \hfill =& \frac{\left({\mathit{ky}}_1+2{\mathit{ky}}_2+{\mathit{ky}}_3+{\mathit{kz}}_1+2{\mathit{ky}}_2+{\mathit{kz}}_3\right)}{8}\hfill \\ \hfill =& k\frac{\left(y_1+4y_2+y_3+z_1+z_3\right)}{8}\hfill \\ \hfill =& \mathit{kEV}\left(\tilde{A}\right)\hfill \end{array}$$

In each case, we have proven that $\mathit{EV}\left(k\tilde{A}\right)=\mathit{kEV}\left(\tilde{A}\right)$. □

Theorem 2

Suppose that$\tilde{Y}$and$\tilde{W}$be two TrIFNs. Then the accuracy function$\mathit{EV}:\mathit{IF}\left(\mathrm{IR}\right)\to \mathrm{IR}$is a linear function i.e.,$\mathit{EV}(\tilde{Y}+k\tilde{W})=\mathit{EV}\left(\tilde{Y}\right)+\mathit{kEV}\left(\tilde{W}\right)$for all$k\in \mathrm{IR}$.

Proof

Please visit Singh and Yadav (2018). □

Theorem 3

Suppose that$\tilde{Y}=\left((y_1,y_2,y_3)\text{;}(z_1,y_2,z_3)\right)$be a TrIFN. If$z_1=y_1,z_3=y_3$, then$\mathit{EV}\left(\tilde{Y}\right)=\frac{y_1+2y_2+y_3}{4}$, which is ranking of triangular fuzzy number based on expected values.

Proof

Please visit Singh and Yadav (2018). □

Theorem 4

The expected value$\mathit{EV}\left(k\right)=k$, where$k\in \mathrm{IR}$.

Proof

Please visit Singh and Yadav (2018).  □

With the aid of accuracy function $\left(\mathit{EV}\right)$, the IFSPWM model (18) can be transformed into the crisp SPWM model (21) and can be stated as follows:

$$\begin{array}{cc}{\mathit{MinimizeF}}_1=\hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left({\displaystyle \sum _i}\mathit{EV}\left({\widetilde{\mathit{RC}}}_i^q\right)\times x_{i,j,n}^q\right)+\left(\mathit{EV}\left({\widetilde{\mathit{PC}}}_j^q\right)\times x_{j,k,n}^q\right)+\left({\displaystyle \sum _o}\left(\mathit{EV}\left({\widetilde{\mathit{DSC}}}_o^q\right)+\mathit{EV}\left({\widetilde{\mathit{INC}}}_o^q\right)\right)\times x_{l,w,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _i}{\displaystyle \sum _j}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\right)\times x_{i,j,n}^q\right)+{\displaystyle \sum _j}{\displaystyle \sum _k}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\right)\times x_{j,k,n}^q\right)+{\displaystyle \sum _k}{\displaystyle \sum _l}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\right)\times x_{k,l,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _o}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\right)\times x_{l,w,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _j}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\right)\times x_{w,j,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _p}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\right)\times x_{w,p,n}^q\right)\hfill \\ \hfill & +\left({\displaystyle \sum _l}\mathit{EV}\left({\widetilde{\mathit{IC}}}_l^q\right)\times x_{k,l,n}^q\right)+\left({\displaystyle \sum _j}\mathit{EV}\left({\widetilde{\mathit{DRC}}}_j^q\right)\times x_{w,j,n}^q\right)+\left({\displaystyle \sum _p}\mathit{EV}\left({\widetilde{\mathit{DC}}}_p^q\right)\times x_{w,p,n}^q\right)+\left({\displaystyle \sum _o}\mathit{EV}\left({\tilde{R}}_j^q\right)\times x_{w,j,n}^q\right)\hfill \\ {\mathit{MaximizeF}}_2=\hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _q}{\displaystyle \sum _n}\mathit{EV}\left({\widetilde{\mathit{REV}}}^q\right)\times x_{w,j,n}^q\hfill \\ {\mathit{MinimizeF}}_3=\hfill & {\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _q}{\displaystyle \sum _n}\mathit{EV}\left({\tilde{T}}_{j,k,n}^q\right)\times z_{j,k,n}^q\hfill \\ \mathrm{subject}\mathrm{to}\hfill & \hfill \\ \hfill & {\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{i,j,n}^q⩽\mathit{EV}\left({\widetilde{\mathit{MCS}}}_i^q\right)\hfill \\ \hfill & {\displaystyle \sum _i}{\displaystyle \sum _j}{\displaystyle \sum _n}{\displaystyle \sum _q}{H}_j^q\times x_{i,j,n}^q⩽{\mathit{MC}}_i\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩽\mathit{EV}\left({\widetilde{\mathit{TS}}}_j^q\right)\hfill \\ \hfill & {\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}{\mathit{WS}}_j\times x_{j,k,n}^q⩽{\mathit{MWS}}_k\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _j}{\displaystyle \sum _k}{\displaystyle \sum _n}{\displaystyle \sum _q}\left(x_{w,j,n}^q+x_{j,k,n}^q\right)⩾\mathit{EV}\left({\widetilde{\mathit{TD}}}_k^q\right)\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _j}{\displaystyle \sum _k}\left(\mathit{EV}\left({\widetilde{\mathit{RC}}}_i^q\right)\times x_{i,j,n}^q\right)+\left(\mathit{EV}\left({\widetilde{\mathit{PC}}}_j^q\right)\times x_{j,k,n}^q\right)+{\displaystyle \sum _i}{\displaystyle \sum _j}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{i,j,n}^q\right)\times x_{i,j,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _j}{\displaystyle \sum _k}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{j,k,n}^q\right)\times x_{j,k,n}^q\right)+{\displaystyle \sum _k}{\displaystyle \sum _l}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{k,l,n}^q\right)\times x_{k,l,n}^q\right)+{\displaystyle \sum _l}{\displaystyle \sum _o}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{l,w,n}^q\right)\times x_{l,w,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _o}{\displaystyle \sum _j}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{w,j,n}^q\right)\times x_{w,j,n}^q\right)+{\displaystyle \sum _o}{\displaystyle \sum _p}\left(\mathit{EV}\left({\widetilde{\mathit{TC}}}_{w,p,n}^q\right)\times x_{w,p,n}^q\right)⩽\mathit{EV}\left(\tilde{B}\right)\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}{\displaystyle \sum _i}{\displaystyle \sum _j}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{i,j,n}^q\right)\times y_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{j,k,n}^q\right)\times y_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{k,l,n}^q\right)\times y_{k,l,n}^q\hfill \\ \hfill & +{\displaystyle \sum _l}{\displaystyle \sum _o}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{l,w,n}^q\right)\times y_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{w,j,n}^q\right)\times y_{w,j,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _p}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{w,p,n}^q\right)\times y_{w,p,n}^q>\mathit{EV}\left(\tilde{S}\right)\hfill \\ \hfill & {\displaystyle \sum _n}{\displaystyle \sum _q}\left({\displaystyle \sum _i}{\displaystyle \sum _j}{x}_{i,j,n}^q+{\displaystyle \sum _j}{\displaystyle \sum _k}{x}_{j,k,n}^q+{\displaystyle \sum _k}{\displaystyle \sum _l}{x}_{k,l,n}^q+{\displaystyle \sum _l}{\displaystyle \sum _o}{x}_{l,w,n}^q+{\displaystyle \sum _o}{\displaystyle \sum _j}{x}_{w,j,n}^q\right)\hfill \\ \hfill & +{\displaystyle \sum _n}{\displaystyle \sum _q}\left({\displaystyle \sum _o}{\displaystyle \sum _p}{x}_{w,p,n}^q\right)⩽\mathit{EV}\left({\widetilde{\mathit{TCC}}}_n^q\right)\hfill \\ \hfill & {\displaystyle \sum _k}{\displaystyle \sum _l}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{k,l,n}^q⩽\mathit{EV}\left({\widetilde{\mathit{MCC}}}_l^q\right)\hfill \\ \hfill & {\displaystyle \sum _l}{\displaystyle \sum _o}{\displaystyle \sum _n}{\displaystyle \sum _q}{x}_{l,w,n}^q⩽\mathit{EV}\left({\widetilde{\mathit{IHC}}}_o^q\right)\hfill \\ \hfill & {\displaystyle \sum _o}{\displaystyle \sum _p}{\displaystyle \sum _q}{\displaystyle \sum _n}{x}_{w,p,n}^q⩽\mathit{EV}\left({\widetilde{\mathit{MCD}}}_p^q\right)\hfill \\ \hfill & y_{(·,·,·)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(·,·,·)}^q>0\text{;}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{(·,·,·)}^q\right)>0\hfill \\ 0,\hfill & x_{(·,·,·)}^q=0\text{;}\mathit{EV}\left({\widetilde{\mathit{SF}}}_{(·,·,·)}^q\right)=0\hfill \end{array}\right\}\forall i,j,k,l,w,p,q\hfill \\ \hfill & z_{(j,k,n)}^q=\left\{\begin{array}{cc}1,\hfill & x_{(j,k,n)}^q>0\hfill \\ 0,\hfill & x_{(j,k,n)}^q=0\hfill \end{array}\right)\hfill \\ \hfill & x_{i,j,n}^q,x_{j,k,n}^q,x_{k,l,n}^q,x_{l,w,n}^q,x_{w,j,n}^q,x_{w,p,n}^q⩾0\hfill \end{array}$$ (21)

Of particular interest, we have proven the existence of an efficient solution of the IFSPWM model (18) and the convexity property of the crisp SPWM model (21) in the Theorem 5, Theorem 6, respectively. Hence the obtained crisp SPWM model (21) can be solved using the proposed interactive intuitionistic fuzzy programming approach (see Section 4.2) to get the optimal global solutions.

Definition 7

Assume that X be the set of feasible solution for the crisp SPWM model (21). Then a point $x^{\ast }$ is said to be an efficient or Pareto optimal solution of the crisp SPWM model (21) if and only iff there does not exist any $x\in X$ such that, $F_m\left(x^{\ast }\right)⩾F_m\left(x\right),\forall m=1,2,3$ and $F_m\left(x^{\ast }\right)>F_m\left(x\right)$ for all at least one $\forall m=1,2,3$. Here, m is the number of objective function present in the proposed sustainable production and waste management model.

Definition 8

A point $x^{\ast }\in X$ is said to be weak Pareto optimal solution for the crisp SPWM model (21) if and only iff there does not exist any $x\in X$ such that, $F_m\left(x^{\ast }\right)⩾F_m\left(x\right),\forall m=1,2,3$.

Theorem 5

An efficient solution of the crisp SPWM model(21)is also an efficient solution for the IFSPWM model(18).

Proof

The proof is similar to Singh and Yadav (2018).  □

Definition 9

Let $F_1$ and $F_2$ be comonotonic functions, then for any intuitionistic fuzzy parameter $\tilde{Y}$, we have

$$\mathit{EV}\left[F_1\left(\tilde{Y}\right)+F_2\left(\tilde{Y}\right)\right]=\mathit{EV}\left[F_1\left(\tilde{Y}\right)\right]+\mathit{EV}\left[F_2\left(\tilde{Y}\right)\right]$$

For the sake of simplicity, let us consider an auxiliary model (22) which is an equivalent to the crisp SPWM model (21) and can be given as follows:

$$\begin{array}{cc}\mathrm{Optimize}(\mathrm{Max}/\mathrm{Min})\hfill & \mathit{EV}\left[F(X,\tilde{Y})\right]=\left(\mathit{EV}\left[F_1(X,\tilde{Y})\right],\dots ,\mathit{EV}\left[F_m(X,\tilde{Y})\right]\right)\forall m=1,2,3\text{.}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & \hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (22)

where $\mathit{EV}[·]$ in auxiliary model (22) represents the expected values (accuracy function) of the intuitionistic fuzzy parameters.

In the Theorem 5, we have already proven the expected value EV efficient solution for the IFSPWM model (18). This concept is obtained by presenting the crisp SPWM model (21) in which the objective functions are the expected value of the intuitionistic fuzzy uncertain objectives of the IFSPWM model (18). Intuitionally, if the intuitionistic fuzzy uncertain vectors in the auxiliary model (22) are degenerated into intutionistic fuzzy parameters, then the following convexity Theorem 6 of the auxiliary model (22) can be proved.

Theorem 6

Suppose that the function$F(X,\tilde{Y})$is differentiable and a convex vector function with respect to X and$\tilde{Y}$. Thus, for any given$X_1,X_2\in X$, if$F_m(X_1,\tilde{Y})$and$F_m(X_2,\tilde{Y})$are comonotonic on intuitionistic fuzzy parameters$\tilde{Y}$, then the auxiliary model(22)is a convex programming problem.

Proof

Since, the feasible solution set X is a convex set, intuitionally, it is sufficient to obtain that the auxiliary model (22) is a convex vector function.

Note that the $F(X,\tilde{Y})$ is a convex vector function on X for any given $\tilde{Y}$, the inequality

$$F\left(\delta X_1+(1-\delta )X_2,\tilde{Y}\right)\leqq \delta F(X_1,\tilde{Y})+(1-\delta )F(X_2,\tilde{Y})$$

holds for any $\delta \in \left[0.1\right]$ and $X_1,X_2\in X$, i.e.;

$$F_m\left(\delta X_1+(1-\delta )X_2,\tilde{Y}\right)\leqq \delta F_m(X_1,\tilde{Y})+(1-\delta )F_m(X_2,\tilde{Y})$$

holds for each $m,1⩽m⩽3$.

By using the assumed condition that $F_m(X_1,\tilde{Y})$ and $F_m(X_2,\tilde{Y})$ are comonotonic on $\tilde{Y}$, it follows from Definition 9 that

$$\mathit{EV}\left[F_m\left(\delta X_1+(1-\delta )X_2,\tilde{Y}\right)\right]\leqq \delta \mathit{EV}\left[F_m(X_1,\tilde{Y})\right]+(1-\delta )\mathit{EV}\left[F_m(X_2,\tilde{Y})\right],\forall m\text{;}$$

which implies that

$$\mathit{EV}\left[F\left(\delta X_1+(1-\delta )X_2,\tilde{Y}\right)\right]\leqq \delta \mathit{EV}\left[F(X_1,\tilde{Y})\right]+(1-\delta )\mathit{EV}\left[F(X_2,\tilde{Y})\right]$$

The above inequality shows that $\mathit{EV}\left[F(X,\tilde{Y})\right]$ is a convex vector function. Hence the auxiliary model (22) is a convex programming problem. Consequently, the crisp SPWM model (21) is also a convex programming problem. Thus Theorem 6 is proved. □

The convexity property (Theorem 6) of the crisp SPWM model (21) typically ensures or strongly guarantees the existence of convex decision set under which the optimal solution exists. Moreover, it also supports the robust modeling approach of the crisp SPWM model (21) which also validate the scope for obtaining the optimal solution sets under intuitionistic fuzzy uncertainty.

4. Solution methodology

Most often, real-life problems exhibits optimization of more than one objectives at a time. The most promising solution set that satisfies each objectives efficiently is termed as the best compormise solution. In the past few decades, it is observed that the situation may arise where the degree of hesitation may exists in real life decision-making problems. Since fuzzy set (FS) deals with the membership function (degree of belongingness) only, it is not capable to capture the hesitation degrees simultaneously. Therefore, the further generalization of FS is presented by introducing a new member into the feasible decision set. First, Atanassov (1986) investigated intuitionistic fuzzy set which comprise membership (degree of belongingness) and non-membership (degree of non-belongingness) functions of the element into feasible solution set. The IFS is based on more intuition as compared to FS and generalizes the decision-making processes more conveniently. Based on IFS, Angelov (1997) developed the intuitionistic fuzzy optimization techniques for the multiobjective programming problem under intuitionistic fuzzy uncertainty. Recent literature on IFS reveals that many researchers have shown the research interest in the intuitionistic fuzzy domain and would be a prominent emerging research area in future. The current study is also taken advantage of the versatile and effective texture of a intuitionistic fuzzy decision set to develop the proposed interactive intuitionistic fuzzy programming approach. The proposed IIFPA quantify the marginal evaluation of each objective function by depicting membership and non-membership functions, respectively. In the proposed IIFPA, an achievement function is represented by the convex combination of the overall satisfactory degrees and weighted intuitionistic score functions of multiple objective programming problem under a set of well-defined constraints. Moreover the proposed IIFPA is elaborately discussed in Section 4.2. Thus the intuitionistic fuzzy optimization techniques for multiobjective programming problem has a significant role in the implementation and execution of the hesitation degrees in decision-making processes.

To construct the membership and non-membership functions for each objectives of the crisp SPWM model (21), the minimum and maximum values of each objective functions can be calculated and are represented by $L_m$ and $U_m$ as follows:

$$U_m=\max \left[F_m\right(x\left)\right]\mathrm{and}{L}_m=\min \left[F_m\right(x\left)\right]\forall m=1,2,3,\dots ,M\text{.}$$ (23)

Now, we will proceed towards the characterization of marginal evaluations (membership functions) for each objectives under intuitionistic fuzzy uncertainty. For this purpose, we present different kinds of membership functions along with their robustness properties in decision-making scenario.

4.1. Characterization of various membership functions

In MOLPP, the marginal evaluation of each objective function is depicted by its respective membership and non-membership functions under intuitionistic fuzzy uncertainty. Most commonly, the marginal evaluations are evaluated by using linear type membership function to obtain the individual satisfactory degree. However, it may be possible to represent the achievement level of each objectives with the aid of nonlinear membership and non-membership functions. The flexible behavior of non-linear membership and non-membership functions are also well enough to quantify the marginal evaluations of each objectives and, consequently determine the satisfaction degrees more efficiently. It also depends on some additional parameters’ value that are assigned by the decision-makers only. By tuning the additional parameters such as shape, scale, measures of vaguness, etc., the decision-maker(s) are well enough capable to execute his/her(their) strategy effectively. There are different types of membership functions that exist in the literature such as linear, exponential, hyperbolic, modified S-curve etc. Therefore, to deal with the crisp SPWM model (21) under intuitionistic fuzzy uncertainty, one can apply linear, exponential, hyperbolic or modified S-curve membership functions depending upon the choice of decision-makers. Thus the linear, exponential, hyperbolic or modified S-curve membership functions are constructed under intuitionistic fuzzy environment. Each of them are defined as the acceptance (degree of belongingness) and rejection (degree of non-belongingness) degrees of each objective functions which seems to be more realistic in nature.

• •Linear membership and non-membership functions
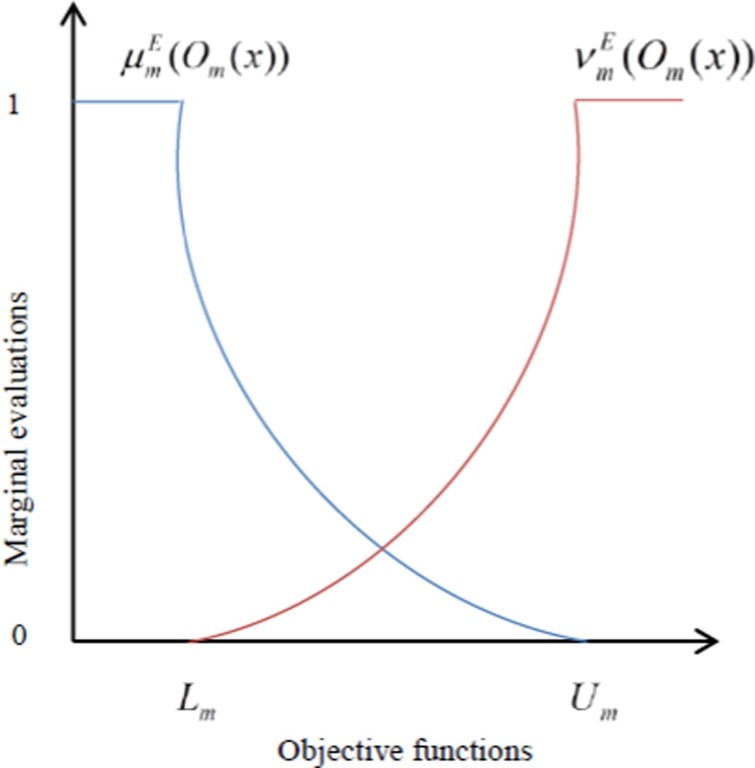
  In general, the most extensive and widely used membership function is linear one due to its simple structure and easier implications. The linear membership function contemplates over constant marginal rate of satisfaction or dissatisfaction degrees towards an objective. The graphical depiction of linear membership and non-membership functions is done in Fig. 3 . Thus the linear membership ${\mu }_m^L\left(F_m\right(x\left)\right)$ and non-membership ${\nu }_m^L\left(F_m\right(x\left)\right)$ functions under intuitionistic fuzzy uncertainty can be furnished as follows:

  $${\mu }_m^L\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{U_m-F_m\left(x\right)}{U_m-L_m}\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 0\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)$$

  $${\nu }_m^L\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{F_m\left(x\right)-L_m}{U_m-L_m}\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 1\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)$$

  In the above case, $L_m^{(.)}\ne U_m^{(.)}$ for all m objective function. If for any membership $L_m^{(.)}=U_m^{(.)}$, then the value of these membership will be equal to 1.
• •Exponential membership and non-membership functions
  An exponential membership reflects the situation when decision-maker is worse off with respect to an objective and choose for a higher marginal rate of satisfaction. Thus by prefering an exponential membership function, the decision-maker can also able to reduce duality gaps by selecting appropriate shape parameters involved in the development of membership function. The pictorial depiction of exponential membership and non-membership functions is presented Fig. 4 . The exponential membership ${\mu }_m^E\left(F_m\right(x\left)\right)$ and non-membership ${\nu }_m^E\left(F_m\right(x\left)\right)$ functions under intuitionistic fuzzy uncertainty can be stated as follows:

  $${\mu }_m^E\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{e^{-d_m\left(\frac{F_m\left(x\right)-L_m}{U_m-L_m}\right)}-e^{-d_m}}{1-e^{-d_m}}\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 0\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)$$

  $$\begin{array}{c}{\nu }_m^E\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{e^{-d_m\left(\frac{U_m-F_m\left(x\right)}{U_m-L_m}\right)}-e^{-d_m}}{1-e^{-d_m}}\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 1\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)\hfill \end{array}$$

  where $d_m,m=1,2,\cdots ,M$ are the measures of vagueness degree (shape parameter) and assigned by the decision-makers.
• •Hyperbolic membership and non-membership functions
  A hyperbolic membership function shows the flexible characteristic behavior with respect to objective function. It is convex over a part of the objective function values and is concave over the remaining part. When the decision maker is worse off with respect to a goal, the decision-maker tends to have a higher marginal rate of satisfaction with respect to that goal. A convex shape part of the membership function captures that behavior. On the other hand, when decision-maker is better off with respect to a goal, the decision maker tends to have a smaller marginal rate of satisfaction. Such behavior is modeled using the concave portion of the membership functions. The graphical representation of hyperbolic membership and non-membership functions is shown in Fig. 5 . Hence the hyperbolic membership ${\mu }_m^H\left(F_m\right(x\left)\right)$ and non-membership ${\nu }_m^H\left(F_m\right(x\left)\right)$ functions under intuitionistic fuzzy uncertainty can be depicted as follows:

  $${\mu }_m^H\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{1}{2}\left[1+\tanh \left({\theta }_m\left(\frac{U_m+L_m}{2}-F_m\left(x\right)\right)\right)\right]\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 0\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)$$

  $$\begin{array}{c}{\nu }_m^H\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}{F}_m\left(x\right)⩽L_m\hfill \\ \frac{1}{2}\left[1+\tanh \left({\theta }_m\left(F_m\left(x\right)-\frac{U_m+L_m}{2}\right)\right)\right]\hfill & \mathit{if}{L}_m⩽F_m\left(x\right)⩽U_m\hfill \\ 1\hfill & \mathit{if}{F}_m\left(x\right)⩾U_m\hfill \end{array}\right)\hfill \end{array}$$

  where ${\theta }_m=\frac{6}{U_m-L_m},\forall m=1,2,\dots ,M$.
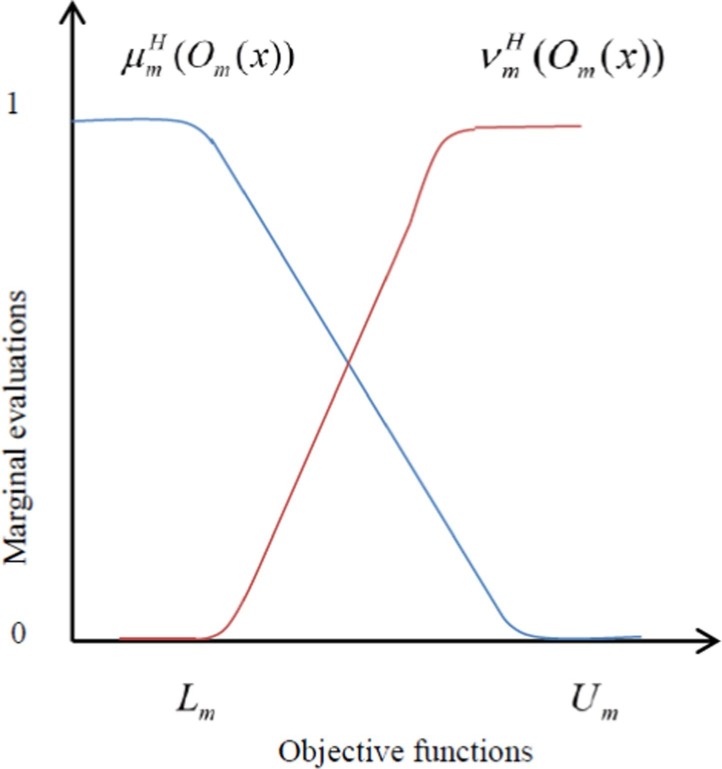
• •Modified S-curve membership and non-membership functions
  A special case of logistic function at different values of parameters are known as modified S-curve membership function. The structure of modified S-curve membership function allows the decision-maker to incorporatte the degree of vaguness hesitations under intuitionistic fuzzy uncertainty. Unlike other linear and nonlinear membership functions, the modified S-curve membership function is more flexible and much dependent on the various parameters involved for marginal evaluations of each objective functions. The diffrent parameters such as $B^{\prime },C^{\prime }$ and $\gamma$ are responsible for the abrupt change or fluctuation in the shape of modified S-curve membership function and assist in the quantification of acceptance and rejection degrees of each objectives efficiently. The parameter $\gamma$ depicts degree of vagueness, meaning the larger value of $\gamma$ signify the higher degree of vagueness. Therefore the greater concern to fuzziness or ambigousness can be measured at $\gamma \to \infty$ whereas $\gamma =0$ implies crisp. It is quite indespensable that the value of $\gamma$ should be determined by experts based on the heuristical and experimental studies. The values of $B^{\prime },C^{\prime }$ and $\gamma$ are to be determined. An analytical study performed by Peidro and Vasant (2011) calculated these values as $B^{\prime }=1,C^{\prime }=0.001001001$ and $\gamma =13.813$ respectively. The continuous flexible nature of modified S-curve membership function provides an opportunity to the decision-maker(s) to execute the desired strategies at different parameters’ values. The graphical representation of modified S-curve membership and non-membership functions is depicted in Fig. 6 . Thus the modified S-curve membership ${\mu }_m^S\left(F_m\right(x\left)\right)$ and non-membership ${\nu }_m^S\left(F_m\right(x\left)\right)$ functions under intuitionistic fuzzy uncertainty can be furnished as follows:

  $${\mu }_m^S\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}1\hfill & \mathit{if}{F}_m\left(x\right)<L_m\hfill \\ 0.999\hfill & \mathit{if}{F}_m\left(x\right)=L_m\hfill \\ \frac{B^{\prime }}{1+C^{\prime }{e}^{\gamma \left(\frac{F_m\left(x\right)-L_m}{U_m-L_m}\right)}}\hfill & \mathit{if}{L}_m<F_m\left(x\right)<U_m\hfill \\ 0.001\hfill & \mathit{if}{F}_m\left(x\right)=L_m\hfill \\ 0\hfill & \mathit{if}{F}_m\left(x\right)>U_m\hfill \end{array}\right)$$

  $${\nu }_m^S\left(F_m\right(x\left)\right)=\left\{\begin{array}{cc}0\hfill & \mathit{if}{F}_m\left(x\right)<L_m\hfill \\ 0.001\hfill & \mathit{if}{F}_m\left(x\right)=L_m\hfill \\ \frac{B^{\prime }}{1+C^{\prime }{e}^{\gamma \left(\frac{U_m-F_m\left(x\right)}{U_m-L_m}\right)}}\hfill & \mathit{if}{L}_m<F_m\left(x\right)<U_m\hfill \\ 0.999\hfill & \mathit{if}{F}_m\left(x\right)=L_m\hfill \\ 1\hfill & \mathit{if}{F}_m\left(x\right)>U_m\hfill \end{array}\right)$$

  where $\gamma >0$ is the measure of fuzziness degree.

Fig. 3.

Linear membership and non-membership functions.

Fig. 4.

Exponential membership and non-membership functions.

Fig. 5.

Hyperbolic membership and non-membership functions.

Fig. 6.

Modified S-curve membership and non-membership functions.

4.2. Proposed interactive intuitionistic fuzzy programming approach

The concept of fuzzy decision (FD), fuzzy goal (FG) and fuzzy constraints (FC) was first discussed by Bellman and Zadeh (1970) and extensively used in many real life decision-making problems under fuzziness. Therefore, fuzzy decision set can be defined as follows:

$$\mathit{FD}=\mathit{FG}\cap \mathit{FC}$$

Consequently, intuitionistic fuzzy decision set $D_I$, with the set of intuitionistic fuzzy objectives and constraints, can be defined as follows:

$$D_I=\left({\cap }_{m=1}^M{F}_m\right)\left({\cap }_{m\prime =1}^{M\prime }{C}_{m\prime }\right)=(x,{\mu }_D(x),{\nu }_D(x\left)\right)$$

where

$${\mu }_D\left(x\right)=\mathit{min}\left\{\begin{array}{c}{\mu }_{F_1}\left(x\right),{\mu }_{F_2}\left(x\right),\dots ,{\mu }_{F_m}\left(x\right)\hfill \\ {\mu }_{C_1}\left(x\right),{\mu }_{C_2}\left(x\right),\dots ,{\mu }_{C_{m\prime }}\left(x\right)\hfill \\ \hfill \end{array}\right\}\forall x\in X$$

$${\nu }_D\left(x\right)=\mathit{max}\left\{\begin{array}{c}{\nu }_{F_1}\left(x\right),{\nu }_{F_2}\left(x\right),\dots ,{\nu }_{F_m}\left(x\right)\hfill \\ {\nu }_{C_1}\left(x\right),{\nu }_{C_2}\left(x\right),\dots ,{\nu }_{C_{m\prime }}\left(x\right)\hfill \\ \hfill \end{array}\right\}\forall x\in X$$

where ${\mu }_D\left(x\right)$ and ${\nu }_D\left(x\right)$ are the membership and non-membership functions of intuitionistic fuzzy decision set $D_I$ respectively.

By utilizing the concept of Bellman and Zadeh (1970), our intention is to maximize the minimum of membership (degree of belongingness) and minimize the maximum of non-membership (degree of non-belongingness) functions at a time. Therefore an acheivement function can be defined as the differences of satisfaction and dissatisfaction degrees to reach the optimal solution of each objectives under intuitionistic fuzzy uncertainty. Thus the mathematical expression for achievement function is defined as follows (24):

$$\begin{array}{cc}\hfill & \mathit{Max}{\mathit{min}}_{m=1,2,3,\dots ,M}{\mu }_m^{(·)}\left(F_m\right(x\left)\right)\hfill \\ \hfill & \mathit{Min}{\mathit{max}}_{m=1,2,3,\dots ,M}{\nu }_m^{(·)}\left(F_m\right(x\left)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (24)

where the superscript $(·)$ in the membership ${\mu }_m^{(·)}\left(F_m\right(x\left)\right)$ and non-membership ${\nu }_m^{(·)}\left(F_m\right(x\left)\right)$ functions represent the different types of membership functions such as linear $\left(L\right)$, exponential $\left(E\right)$, hyperbolic $\left(H\right)$ and modified S-curve $\left(S\right)$ respectively.

Using the auxiliary variables $\alpha$ and $\beta$, the problem (24) can be transformed into the following problem (25):

$$\begin{array}{cc}\hfill & \mathit{Max}\left(\alpha -\beta \right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & {\mu }_m^{(·)}\left(F_m\right(x\left)\right)⩾\alpha ,\hfill \\ \hfill & {\nu }_m^{(·)}\left(F_m\right(x\left)\right)⩽\beta ,\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (25)

To solve a MOLPPs, Torabi and Hassini (2008) presented a single-phase solution method and named as TH-method by overcoming the drawbacks of existing approaches suggested by Lai and Hwang, 1993, Lai and Hwang, 1994, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988, Zimmermann, 1978, Ahmadini and Ahmad, in press. In Torabi and Hassini (2008) approach, the achievement function is defined as a convex combination of the lower bound for satisfaction degree of objectives $\left(\alpha \right)$, and the weighted sum of these achievement degrees $\left({\mu }_m^{(·)}\left(F_m\right(x\left)\right)\right)$ to confirm the yielding an adjustably balanced compromise solution. The shortcomings of existing methods Lai and Hwang, 1993, Lai and Hwang, 1994, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988 is pointed out by Torabi and Hassini (2008) and presented TH method (Torabi & Hassini, 2008) to overcome these issues. Of particular interest, the TH method (Torabi & Hassini, 2008) deals only the satisfaction degree of each objective function and do not considers the dissatisfaction degree which is also an important integrated part of the decision-making processes. All the above discussed methods Lai and Hwang, 1993, Lai and Hwang, 1994, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988, Zimmermann, 1978, Torabi and Hassini, 2008 do not takes into consideration the degree of dissatisfation (rejection) that exists in real-life decision-making scenarios. To integrate the dissatisfaction degree in TH method (Torabi & Hassini, 2008), we have re-defined a new achievement function and consequently proposed a novel interactive intuitionistic fuzzy programming approach (hereafter the FA method) to obtain the optimal compromise solution. More specifically, the proposed IIFPA can be considered as the extended version of TH method (Torabi & Hassini, 2008). Therefore proposed IIFPA (26) can be an equivalent modeling and optimizing approach for solving the crisp SPWM model (21). Thus the problem (25) can be transformed into an equivalent proposed IIFPA (26) and can be summarized as follows:

$$\begin{array}{cc}\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^{(·)}\left(F_m\right(x\left)\right)-{\nu }_m^{(·)}\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & {\mu }_m^{(·)}\left(F_m\right(x\left)\right)⩾\alpha ,\hfill \\ \hfill & {\nu }_m^{(·)}\left(F_m\right(x\left)\right)⩽\beta ,\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (26)

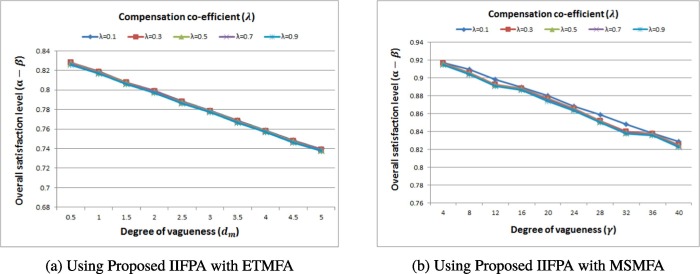
where ${\mu }_m^{(·)}\left(F_m\right(x\left)\right)$ and ${\nu }_m^{(·)}\left(F_m\right(x\left)\right)$ represent the satisfaction and dissatisfaction degrees of m-th objective function under intuitionistic fuzzy environment. Also $\alpha =\min \left[{\mu }_m^{(·)}\left(F_m\right(x\left)\right)\right]$ and $\beta =\max \left[{\nu }_m^{(·)}\left(F_m\right(x\left)\right)\right]$ denote the minimum satisfaction and maximum dissatisfaction degrees of each objectives, respectively. Thus the formulation of proposed IIFPA (26) has a new achievement function which is elicited as a convex combination of the difference between lower and upper bounds for satisfaction and dissatisfaction degrees of objectives $(\alpha -\beta )$, and the weighted sum of the difference between these achievement degrees $\left({\mu }_m^{(·)}\left(F_m\right(x\left)\right)-{\nu }_m^{(·)}\left(F_m\right(x\left)\right)\right)$ to make sure generating an established balanced compromise solution. Furthermore, ${\eta }_m$ and $\lambda$ depict the relative preference of the m-th objective function and the co-efficient of compensation, respectively. The ${\eta }_m$ parameters are identified by the decision-maker based on her/his importances such that ${\sum }_m{\eta }_m=1,{\eta }_m>0$. Further, $\lambda$ monitors the overall satisfaction level of objectives as well as the compromise achievement degrees among the objective functions implicitly. It means that the proposed IIFPA (26) is most promising and reliable of generating both unbalanced and balanced compromised solutions for a given MOLPPs situation based on the decision maker’s importances through tuning the value of parameter $\lambda$.

Remark 1

In current context, a greater value for $\lambda$ means more concern is offered to determine a higher overall bounds for satisfaction and dissatisfaction degrees of objectives $(\alpha -\beta )$ and consequently more balanced compromise solutions.On the other hand, the smaller value for $\lambda$ means more concern is shown to get a solution with high satisfaction and low dissatisfaction degrees for some objectives with higher relative preference without any attention paid to the overall satisfaction degree of other objective functions. It should be worth important to note that there exists a correlation between $\lambda$ and the range of ${\eta }_m$ values (i.e. ${\max }_m\left[{\eta }_m\right]-{\min }_m\left[{\eta }_m\right]$) so that there will be specific pre-determined interval of $\lambda$ in which it could be chosen for a given $\eta$ vector. Furthermore, Singh and Goh (2019) also investigated that Torabi and Hassini (2008) method outperform with respect to their proposed algorithm. For instance, for the probably high values of this range, consequent $\lambda$ should be chosen as a small value (e.g. less than 0.2) because of explicit importance of the decision-maker for obtaining an unbalanced compromise solution in this case.

Definition 10

A vector $x^{\ast }\in X$ is said to be an optimal solution to proposed IIFPA (26) or an efficient solution to the crisp SPWM model (21) if and only iff there does not exist any $x\in X$ such that, ${\mu }_m\left(x\right)⩾{\mu }_m\left(x^{\ast }\right)$ and ${\nu }_m\left(x\right)⩽{\nu }_m\left(x^{\ast }\right),\forall m=1,2,3$. Alsw, ${\mu }_t\left(x\right)>{\mu }_t\left(x^{\ast }\right)$ and ${\nu }_t\left(x\right)<{\nu }_t\left(x^{\ast }\right)$ for at least one $t\in (1,2,3)$.

Theorem 7: A unique optimal solution of proposed IIFPA (26) is also an efficient solution to the crisp SPWM model (21).

Proof

Consider that $x^{\ast }$ be a unique optimal solution of proposed IIFPA (26) which is not an efficient solution to crisp SPWM model (21). It means that there must be an efficient solution, say $x^{**}$, for the crisp SPWM model (21) so that we can have: ${\mu }_m\left(x^{**}\right)⩾{\mu }_m\left(x^{\ast }\right)$ and ${\nu }_m\left(x^{**}\right)⩽{\nu }_m\left(x^{\ast }\right)\text{;}\forall m=1,2,\cdots ,M$. Alsw, there exists $t\left|{\mu }_t\right(x^{**})>{\mu }_t(x^{\ast })$ and ${\nu }_m\left(x^{**}\right)<{\nu }_m\left(x^{\ast }\right)$ for at least one t. Thus for the minimum satisfaction and maximum dissatisfaction levels of each objective functions in $x^{\ast }$ and $x^{**}$ solutions, we would have $\left(\alpha -\beta \right)\left(x^{**}\right)⩾\left(\alpha -\beta \right)\left(x^{\ast }\right)$, and concerning the related objective values we would have the following inequalities:

$$\begin{array}{cc}\hfill \psi \left(x^{\ast }\right)=& \lambda \left(\alpha -\beta \right)\left(x^{\ast }\right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^{(·)}\left(F_m\right(x^{\ast }\left)\right)-{\nu }_m^{(·)}\left(F_m\right(x^{\ast }\left)\right)\right)\hfill \\ \hfill =& \lambda \left(\alpha -\beta \right)\left(x^{\ast }\right)+\left(1-\lambda \right)\left[{\displaystyle \sum _{m\ne t}}{\eta }_m\left({\mu }_m^{(·)}\left(F_m\right(x^{\ast }\left)\right)-{\nu }_m^{(·)}\left(F_m\right(x^{\ast }\left)\right)\right)+{\eta }_t\left({\mu }_t^{(·)}\left(F_t\right(x^{\ast }\left)\right)-{\nu }_t^{(·)}\left(F_t\right(x^{\ast }\left)\right)\right)\right]\hfill \\ \hfill <& \lambda \left(\alpha -\beta \right)\left(x^{**}\right)+\left(1-\lambda \right)\left[{\displaystyle \sum _{m\ne t}}{\eta }_m\left({\mu }_m^{(·)}\left(F_m\right(x^{**}\left)\right)-{\nu }_m^{(·)}\left(F_m\right(x^{**}\left)\right)\right)+{\eta }_t\left({\mu }_t^{(·)}\left(F_t\right(x^{**}\left)\right)-{\nu }_t^{(·)}\left(F_t\right(x^{**}\left)\right)\right)\right]\hfill \\ \hfill =& \psi \left(x^{**}\right)\text{.}\hfill \end{array}$$

Hence, we have arrived at a contradiction that $x^{\ast }$ is not a unique optimal solution of proposed IIFPA (26). This completes the proof of Theorem 7. □

4.2.1. Linear-type membership functions approach (LTMFA)

Assuming that ${\mu }_m^L\left(F_m\right(x\left)\right)⩾\alpha$ and ${\nu }_m^L\left(F_m\right(x\left)\right)⩽\beta$, for all m. Using the linear-type membership and non-membership functions, the proposed IIFPA (26) can be transformed into problem (27):

$$\begin{array}{cc}\left(\mathit{LTMFA}\right)\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^L\left(F_m\right(x\left)\right)-{\nu }_m^L\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & F_m\left(x\right)+(U_m-L_m)\alpha ⩽U_m,\hfill \\ \hfill & F_m\left(x\right)-(U_m-L_m)\beta ⩽L_m,\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (27)

Remark 2

The ultimate aim of problem (27) (LTMFA) manifests the maximization of minimum possibility level (degree of belongingness) to accept the best possible solution and minimization of maximum possibility level (degree of non-belongingness) to reject the worst possible solution by considering all the objective functions at a time. It means that we try to determine a solution in such a way that it maximizes the minimum membership (acceptance) and minimizes the maximum non-membership (rejection) degrees by taking all objectives simultaneously, to attain the optimal compromise solution.

Theorem 7

A unique optimal solution of problem(27)(LTMFA) is also an efficient solution for the crisp SPWM model(21).

Proof

The proof is similar to Singh and Yadav (2018).  □

4.2.2. Exponential-type membership functions approach (LTMFA)

We assume that ${\mu }_m^E\left(F_m\right(x\left)\right)⩾\alpha$ and ${\nu }_m^E\left(F_m\right(x\left)\right)⩽\beta$, for all m. With the help of exponential-type membership and non-membership functions, the proposed IIFPA (26) can be transformed into problem (28):

$$\begin{array}{cc}\left(\mathit{ETMFA}\right)\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^E\left(F_m\right(x\left)\right)-{\nu }_m^E\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \frac{e^{-d_m\left(\frac{F_m\left(x\right)-L_m}{U_m-L_m}\right)}-e^{-d_m}}{1-e^{-d_m}}⩾\alpha ,\hfill \\ \hfill & \frac{e^{-d_m\left(\frac{U_m-F_m\left(x\right)}{U_m-L_m}\right)}-e^{-d_m}}{1-e^{-d_m}}⩽\beta ,\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (28)

Remark 3

If $d_m\to 0$, then the exponential-type membership functions will be reduced into linear-type membership functions.

Theorem 8

A unique optimal solution of problem(28)(ETMFA) is also an efficient solution for the crisp SPWM model(21).

Proof

The proof is similar to Singh and Yadav (2018).  □

4.2.3. Hyperbolic-type membership functions approach (HTMFA)

Consider that ${\mu }_m^H\left(F_m\right(x\left)\right)⩾\alpha$ and ${\nu }_m^H\left(F_m\right(x\left)\right)⩽\beta$, for all m. With the aid of hyperbolic-type membership and non-membership functions, the proposed IIFPA (26) can be converted into problem (29):

$$\begin{array}{cc}\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^H\left(F_m\right(x\left)\right)-{\nu }_m^H\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \frac{1}{2}\left[1+\tanh \left({\theta }_m\left(\frac{U_m+L_m}{2}-F_m\left(x\right)\right)\right)\right]⩾\alpha ,\hfill \\ \hfill & \frac{1}{2}\left[1+\tanh \left({\theta }_m\left(F_m\left(x\right)-\frac{U_m+L_m}{2}\right)\right)\right]⩽\beta ,\hfill \\ \hfill & \alpha ⩾\beta ,{\theta }_m=\frac{6}{U_m-L_m},\forall m=1,2,\dots ,M\hfill \\ \hfill & 0⩽\alpha +\beta ⩽1,\alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (29)

Equivalently, we have problem (30) as follows:

$$\begin{array}{cc}\left(\mathit{HTMFA}\right)\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^H\left(F_m\right(x\left)\right)-{\nu }_m^H\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & {\theta }_m{F}_m\left(x\right)+{\tanh }^{-1}\left(2\alpha -1\right)⩽\frac{{\theta }_m}{2}\left(U_m+L_m\right),\hfill \\ \hfill & {\theta }_m{F}_m\left(x\right)-{\tanh }^{-1}\left(2\beta -1\right)⩽\frac{{\theta }_m}{2}\left(U_m+L_m\right),\hfill \\ \hfill & \alpha ⩾\beta ,{\theta }_m=\frac{6}{U_m-L_m},\forall m=1,2,\dots ,M\hfill \\ \hfill & 0⩽\alpha +\beta ⩽1,\alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (30)

Theorem 9

A unique optimal solution of problem(30)(HTMFA) is also an efficient solution for the crisp SPWM model(21).

Proof

The proof is similar to Singh and Yadav (2018).  □

4.2.4. Modified S-curve membership functions approach (MSMFA)

Alsw, assume that ${\mu }_m^S\left(F_m\right(x\left)\right)⩾\alpha$ and ${\nu }_m^S\left(F_m\right(x\left)\right)⩽\beta$, for all m. Using the modified S-curve membership and non-membership functions, the proposed IIFPA (26) can be converted into problem (31):

$$\begin{array}{cc}\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^S\left(F_m\right(x\left)\right)-{\nu }_m^S\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & \frac{B^{\prime }}{1+C^{\prime }{e}^{\gamma \left(\frac{F_m\left(x\right)-L_m}{U_m-L_m}\right)}}⩾\alpha ,\hfill \\ \hfill & \frac{B^{\prime }}{1+C^{\prime }{e}^{\gamma \left(\frac{U_m-F_m\left(x\right)}{U_m-L_m}\right)}}\beta ⩽\beta ,\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (31)

Consequently, we have problem (32) as follows:

$$\begin{array}{cc}\left(\mathit{MSMFA}\right)\hfill & \mathit{Max}\psi \left(x\right)=\lambda \left(\alpha -\beta \right)+\left(1-\lambda \right){\displaystyle \sum _{m=1}^M}{\eta }_m\left({\mu }_m^S\left(F_m\right(x\left)\right)-{\nu }_m^S\left(F_m\right(x\left)\right)\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & C^{\prime }{e}^{\gamma \left(\frac{F_m\left(x\right)-L_m}{U_m-L_m}\right)}⩾\left(\frac{B^{\prime }}{\alpha }-1\right),\hfill \\ \hfill & C^{\prime }{e}^{\gamma \left(\frac{U_m-F_m\left(x\right)}{U_m-L_m}\right)}⩽\left(\frac{B^{\prime }}{\beta }-1\right),\hfill \\ \hfill & \alpha ⩾\beta ,0⩽\alpha +\beta ⩽1,\hfill \\ \hfill & \alpha ,\beta ,\lambda \in \left[0,1\right]\hfill \\ \hfill & \mathrm{all}\mathrm{the}\mathrm{constraints}\mathrm{of}\left(21\right)\hfill \end{array}$$ (32)

Theorem 10

A unique optimal solution of problem(32)(MSMFA) is also an efficient solution for the crisp SPWM model(21).

Proof

Suppose that $\left(\overline{x},\overline{\alpha },\overline{\beta }\right)$ be a unique optimal solution of problem (32) (MSMFA). Then, $\left(\overline{\alpha }-\overline{\beta }\right)>\left(\alpha -\beta \right)$ for any $\left(x,\alpha ,\beta \right)$ feasible to the problem (32) (MSMFA). On the contrary, assume that $\left(\overline{x},\overline{\alpha },\overline{\beta }\right)$ is not an efficient solution of the crisp SPWM model (21). For that, there exists $x^{\ast }\left(x^{\ast }\ne \overline{x}\right)$ feasible to the crisp SPWM model (21), such that $F_m\left(x^{\ast }\right)⩽F_m\left(\overline{x}\right)$ for all $m=1,2,\cdots ,M$ and $F_m\left(x^{\ast }\right)<F_m\left(\overline{x}\right)$ for at least one m.

Hence, we have

$e^{\gamma \left(\frac{F_m\left(x^{\ast }\right)-L_m}{U_m-L_m}\right)}⩾e^{\gamma \left(\frac{F_m\left(\overline{x}\right)-L_m}{U_m-L_m}\right)}$for all $m=1,2,\cdots ,M$ and

$e^{\gamma \left(\frac{F_m\left(x^{\ast }\right)-L_m}{U_m-L_m}\right)}>e^{\gamma \left(\frac{F_m\left(\overline{x}\right)-L_m}{U_m-L_m}\right)}$for all $m=1,2,\cdots ,M$ for at least one m.

Thus, ${\min }_m\left(e^{\gamma \left(\frac{F_m\left(x^{\ast }\right)-L_m}{U_m-L_m}\right)}\right)⩾(>){\min }_m\left(e^{\gamma \left(\frac{F_m\left(\overline{x}\right)-L_m}{U_m-L_m}\right)}\right)$.

If ${\alpha }^{\ast }={\min }_m\left(e^{\gamma \left(\frac{F_m\left(x^{\ast }\right)-L_m}{U_m-L_m}\right)}\right)$, then ${\alpha }^{\ast }⩾(>)\overline{\alpha }$.

Similarly, we have $\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}⩾\frac{U_m-F_m\left(\overline{x}\right)}{U_m-L_m}$ for all $m=1,2,\cdots ,M$ and $\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}>\frac{U_m-F_m\left(\overline{x}\right)}{U_m-L_m}$ for at least one m.

Consequently, it gives

$e^{\gamma \left(\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}\right)}⩽e^{\gamma \left(\frac{U_m-F_m\left(\overline{x}\right)}{U_m-L_m}\right)}$for all $m=1,2,\cdots ,M$ and

$e^{\gamma \left(\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}\right)}<e^{\gamma \left(\frac{U_m-F_m\left(\overline{x}\right)}{U_m-L_m}\right)}$for at least one m.

Hence, ${\max }_m\left(e^{\gamma \left(\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}\right)}\right)⩽(<){\max }_m\left(e^{\gamma \left(\frac{U_m-F_m\left(\overline{x}\right)}{U_m-L_m}\right)}\right)$.

Assuming ${\beta }^{\ast }={\max }_m\left(e^{\gamma \left(\frac{U_m-F_m\left(x^{\ast }\right)}{U_m-L_m}\right)}\right)$, we have ${\beta }^{\ast }⩽(<)\overline{\beta }$.

This gives $\left(\overline{\alpha }-\overline{\beta }\right)<\left({\alpha }^{\ast }-{\beta }^{\ast }\right)$. Thus, we have arrived at a contradiction with the fact that $\left(\overline{x},\overline{\alpha },\overline{\beta }\right)$ is the unique optimal solution of (MSMFA). Therefore, it is also an efficient solution of the crisp SPWM model (21). This completes the proof of Theorem 11. □

4.3. Performance analysis based on multiple criteria

• •Savings compared to baseline solution: The most reasonable compromise solution is assumed to be a baseline solution for each objective function. The comparison is made with a different optimal solution which is then selected in terms of more savings.
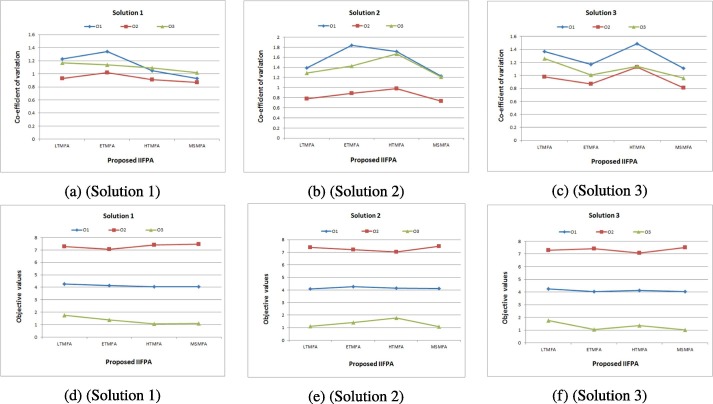
• •Co-efficient of variation (CV): It is a relative measure and most suitable method to compare two series. The size of the measure of dispersion also depends on the size of the measurement. Thus, it is an appropriate measure of dispersion to compare two series which differs largely in respect of their means. Moreover, a series or a set of values having a lesser co-efficient of variation as compared to others is more consistent. It also indicates how much fluctuation is happening in the existing mean response. The lower value of co-efficient of variation indicates the more homogeneous and robustness of the data.
• •Degrees of desirability: The concept of degrees of desirability has been first proposed by Baril et al., 2007, Baril et al., 2011, Baril et al., 2013. Linear physical programming Abdel Haleem (1991) is a method that is used to depict the degrees of desirability (priority) for each objective function of MOLPP. The degree of desirability is a beneficial and handy tool for assigning the target values ($T_m$) for the objective function and for categorizing the solutions. By obtaining the individual best and worst solution of each objective function, the upper and lower bound for target values ($T_m$) can be determined directly. By using the pay-off matrix (individual best and worst solutions of each objective function), bound ($T_{\mathit{mmax}}$) and ($T_{\mathit{mmin}}$) can be obtained. These bounds provide the reduction in solvability set which can be denoted as ${\chi }^{\prime }$ and mathematically it can be shown expressed as ${\chi }^{\prime }=\left\{\chi \right|T_{\mathit{mmin}}⩽T_m⩽T_{\mathit{mmax}}\text{;}\forall m=1,2,\dots ,M\}$ where $\chi$ is a set of parameter values for which the problem is solvable. Thus, the reduced solvability set can be used for defining the degree of desirability in the form of linguistic preferences. For more information and a stepwise procedure, one can visit the research paper by Baril et al. (2011). The details can be found in Baril et al., 2007, Baril et al., 2011, Baril et al., 2013.

4.4. Proposed solution algorithm

The step-wise procedures for modeling and optimization of integrated production-transportation planning problem is summarized as follows:

• Step-1. Formulate the IFSPWM (18) under intuitionistic fuzzy uncertainty.

• Step-2. Using accuracy function, obtain the crisp SPWM model (21).

• Step-3. Solve each objective function individually and determine the upper $U_m$ and lower $L_m$ bounds using Eq. (23).

• Step-4. With the help of $U_m$ and $L_m$, define the membership and non-membership functions under intuitionistic fuzzy envirnment.

• Step-5. Elicit the various types of marginal evaluations such as linear, exponential, hyperbolic or modified S-curve membership functions (see Section 4.1) according to decision-makers’ preferences.

• Step-6. Follow up with proposed IIFPA (26), construct the various approaches with diffrent membership functions such as LTMFA (27) or ETMFA (28) or HTMFA (30) or MSMFA (32) under the well-defined constraints of the crisp SPWM model (21).

• Step-7. Solve the obtained intuitionistic fuzzy programming model to determine the balanced optimal compromise solution using appropriate techniques or some optimizing software packages.

• Step-8. To generate the desired number of solution sets, tune the compensation co-efficient $\lambda$ parameter. Moreover, one can tune some additional parameters such as $d_m,\gamma$ and ${\eta }_m$ to get the ample number of solution sets.

• Step-9. Execute performance analyses by using different criteria such as savings compared to baseline solution, CV and degree of desirability (discussed in subSection 4.3) to analyze the better performance of different solution schemes and choose the desired balanced compromise solutions.

5. A case study

The central government has ramped up domestic manufacturing of personal protective and medical equipment, including ventilators, to meet the increasing demand, amid serious concerns over shortage of PPE for health workers. The prevention, containment, and management of COVID-19 in the country are monitored at the highest level governing body. Various actions have been initiated in collaboration with the States. Talking about the criterion used, besides the number of cases, ”density of population, testing ratio and the likelihood of an area posing a challenge have also been considered while classifying States into red and orange zones.” The biggest challenge is not whether a State is in the red or orange zone, but if the containment measures are being adequately followed to curb the spread of the COVID-19. Containment zones should be delineated duly, considering mapping cases and contacts, geographical dispersion of cases and contacts, areas with a well-demarcated perimeter, and enforceability. States and UTs are also advised that containment zones can be residential colony/mohallas/municipal wards or police station area/municipal zones/towns in urban areas as appropriate. In containment zones, stringent perimeter control, active search for cases through house-to-house surveillance by special teams formed for the purpose, testing all cases as per sampling guidelines, contact tracing, and clinical management of all confirmed cases need to be done. In buffer zones, extensive surveillance through monitoring of ILI/SARI cases in health facilities need to be expedited.

The Central Government of India has scaled up medical equipment production in response to the coronavirus disease (Covid-19) outbreak and ordered its preparedness to tackle the infectious disease. Some government institutes like Defense Research and Development Organization (DRDO), South India Textile Research Association (SITRA), and Ordnance Factory Board are the front runners in developing new technologies, materials, and testing facilities. DRDO has also developed new PU coated nylon/polyester for supply to domestic manufacturers. Arvind, The Trident Group, Welspun JCT Mills, and Shahi Exports are domestic companies involved in the production.

The strategy devised is to see an opportunity to create supply chains and manufacturing in India by helping existing producers expand and identify new manufacturers. To meet the requirement of PPEs, especially medicated gown, face masks, face shields, hand gloves, sanitizers, and shoe covers, factories producing essential items are working around the clock, and ordinance factories are trying to produce personal protection equipment for medical personnel. Thus in containment zones, a leading Indian based automobile company gear up its production towards the above furnished COVID-19 medical equipment for the first time. For the raw material acquirement, the company has an agreement with six raw materials suppliers in Chennai, Coimbatore, Bengaluru, Kochi, Delhi, and Patna, respectively. The automobile company has established twelve advanced manufacturing plants in a different part of the nation. The medical equipment is transported to highly demanded zones at thirty-two markets of Maharashtra, Delhi, Chandigarh, Punjab, Karnataka, and Chennai from these production units. The six medical equipment is identified as an essential requirement for health personnel and sanitation workers to fight with COVID-19 battle, namely; medicated gown, face masks, face shield, hand gloves, sanitizers, and shoe covers are successfully produced to meet the anticipated demand. The end-of-life phase is initiated after its use, where the well-functional collection centers are responsible for collecting used medical equipment for further processing. For this purpose, eight different collection centers are established near the medical equipment’s high demand zones. After accumulating used medical equipment, four distribution centers receive the generated wastes for assembling and recovery purposes by inspecting them one-by-one with proper safety measures. Those wastes that can be recovered are shipped to the advanced manufacturing plants for further processing. Finally, non-recoverable or end-of-use wastes are transported to six different disposal facilities such as under-ground dumping and incineration purpose to reduce the social and ecological impacts. Thus the SPWM model under intuitionistic fuzzy uncertainty is easily implemented on the presented case study data. To examine the applicability and validity of the proposed modeling and optimizing approach, the manager has will-fully provided the relevant data in uncertain form except for the maximum machine capacity, available warehouse space limitation, and maximum available warehouses space. All the relevant data-set are summarized in Table 3 . The managers intend to minimize the total economic costs and delivery time and maximize the revenue gained by enhancing it as an objective function under the well-defined constraints.

Table 3.

Triangular intuitionistic fuzzy parameters.

Parameters	Highly consumed COVID-19 medical equipments
	Medical gown	Face mask	Face shield	Hand gloves	Hand sanitizer	Shoe cover
${\tilde{R}}_j^q\left(\mathrm{unit}\right)$	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)	(35,37,39; 34,37,40)
${\tilde{T}}_{j,k,n}^q\left(\mathrm{inhr}\right)$	(60,65,70; 55,65,75)	(66,69,72; 65,69,73)	(71,74,77; 70,74,78)	(25,27,29; 24,29,34)	(35,39,43; 33,39,45)	(50,53,56; 49,53,57)
${\widetilde{\mathit{REV}}}^q(''\$''/\mathrm{unit})$	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)	(35,37,39; 34,37,40)
${\widetilde{\mathit{RC}}}_i^q(''\$''/\mathrm{unit})$	(28,29,30; 27,29,31)	(35,37,39; 34,37,40)	(42,44,46; 40,44,48)	(33,36,39; 32,36,40)	(25,27,29; 24,27,30)	(45,48,51; 44,48,52)
${\widetilde{\mathit{PC}}}_j^q(''\$''/\mathrm{unit})$	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)	(35,37,39; 34,37,40)
${\tilde{H}}_j^q(\mathrm{hr}/\mathrm{unit})$	(40,42,44; 38,42,46)	(45,48,51; 44,48,52)	(50,55,60; 45,55,65)	(60,65,70; 58,65,77)	(66,69,72; 65,69,73)	(25,27,29; 24,29,34)
${\widetilde{\mathit{TCC}}}_n^q\left(\mathrm{units}\right)$	(44,48,52; 42,48,54)	(50,53,56; 49,53,57)	(55,59,63; 54,59,64)	(52,56,60; 50,56,62)	(60,63,66; 58,62,66)	(35,39,43; 33,39,45)
${\widetilde{\mathit{TC}}}_{i,j,n}^q(''\$''/\mathrm{unit})$	(34,36,38; 32,36,40)	(66,69,72; 65,69,73)	(52,56,60; 50,56,62)	(60,63,66; 59,63,67)	(66,67,68; 65,67,69)	(50,53,56; 49,53,57)
${\widetilde{\mathit{TC}}}_{j,k,n}^q(''\$''/\mathrm{unit})$	(52,56,60; 50,56,62)	(60,63,66; 59,63,67)	(66,69,72; 65,69,73)	(66,67,68; 65,67,69)	(50,53,56; 49,53,57)	(34,36,38; 32,36,40)
${\widetilde{\mathit{TC}}}_{k,l,n}^q(''\$''/\mathrm{unit})$	(50,53,56; 49,53,57)	(34,36,38; 32,36,40)	(66,69,72; 65,69,73)	(52,56,60; 50,56,62)	(66,67,68; 65,67,69)	(60,63,66; 59,63,67)
${\widetilde{\mathit{TC}}}_{l,w,n}^q(''\$''/\mathrm{unit})$	(34,36,38; 32,36,40)	(66,69,72; 65,69,73)	(66,67,68; 65,67,69)	(50,53,56; 49,53,57)	(66,69,72; 65,69,73)	(34,36,38; 32,36,40)
${\widetilde{\mathit{TC}}}_{w,j,n}^q(''\$''/\mathrm{unit})$	(28,29,30; 27,29,31)	(35,37,39; 34,37,40)	(42,44,46; 40,44,48)	(50,53,56; 49,53,57)	(34,36,38; 32,36,40)	(66,69,72; 65,69,73)
${\widetilde{\mathit{TC}}}_{w,p,n}^q(''\$''/\mathrm{unit})$	(66,69,72; 65,69,73)	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)
${\widetilde{\mathit{IC}}}_l^q(''\$''/\mathrm{unit})$	(28,29,30; 27,29,31)	(35,37,39; 34,37,40)	(42,44,46; 40,44,48)	(33,36,39; 32,36,40)	(25,27,29; 24,27,30)	(45,48,51; 44,48,52)
${\widetilde{\mathit{DSC}}}_o^q(''\$''/\mathrm{unit})$	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)	(35,37,39; 34,37,40)
${\widetilde{\mathit{DRC}}}_j^q(''\$''/\mathrm{unit})$	(40,42,44; 38,42,46)	(45,48,51; 44,48,52)	(50,55,60; 45,55,65)	(60,65,70; 58,65,77)	(66,69,72; 65,69,73)	(25,27,29; 24,29,34)
${\widetilde{\mathit{DC}}}_p^q(''\$''/\mathrm{unit})$	(44,48,52; 42,48,54)	(50,53,56; 49,53,57)	(55,59,63; 54,59,64)	(52,56,60; 50,56,62)	(60,63,66; 58,62,66)	(35,39,43; 33,39,45)
${\widetilde{\mathit{INC}}}_o^q(''\$''/\mathrm{unit})$	(60,65,70; 55,65,75)	(66,69,72; 65,69,73)	(71,74,77; 70,74,78)	(25,27,29; 24,29,34)	(35,39,43; 33,39,45)	(50,53,56; 49,53,57)
${\widetilde{\mathit{IHC}}}_o^q(''\$''/\mathrm{unit})$	(30,32,34; 28,32,36)	(34,36,38; 32,36,40)	(38,40,42; 36,40,44)	(35,39,43; 33,39,45)	(38,40,42; 36,40,44)	(35,37,39; 34,37,40)
${\widetilde{\mathit{TS}}}_j^q\left(\mathrm{units}\right)$	(28.2,29.4,30.5; 27.6,29.5,31.9)	(35.2,37.5,39.5; 34.2,37.8,40.7)	(42.8,44.2,46.4; 40.5,44.6,48.6)	(33.7,36.2,39.9; 32.5,36.1,40.5)	(25.8,27.4,29.3; 24.4,27.6,30.3)	(45.4,48.9,51.8; 44.9,48.5,52.6)
${\widetilde{\mathit{TD}}}_k^q\left(\mathrm{units}\right)$	(32.6,34.8,36.5; 30.4,34.2,38.3)	(35.6,39.4,43.2; 34.5,39.2,44.3)	(41.7,42.9,43.4; 40.8,42.6,44.2)	(50.8,51.6,52.7; 48.2,51.9,54.6)	(71.4,73.8,75.6; 70.1,73.3,76.8)	(30.7,32.6,34.4; 28.2,32.6,36.9)
${\widetilde{\mathit{SF}}}_{·,·,·}^q$	(0.55,0.60,0.65; 0.54,0.60,0.66)	(0.65,0.67,0.69;0.64,0.67,0.70)	(0.71,0.73,0.75;0.70,0.73,0.76)	(0.28,0.29,0.30; 0.26,0.29,0.31)	(0.35,0.37, 0.39; 0.34,0.37,0.40)	(0.35,0.37,0.39; 0.34,0.37,0.40)
$\tilde{B}\left(''\$''\right)$	(350000, 450000, 490000, 550000; 300000, 400000, 500000, 600000)
$\tilde{S}$	(0.98, 0.85, 0.88, 0.94; 0.92, 0.83, 0.89, 0.96)
${\mathit{MC}}_j(\mathrm{hr}/\mathrm{unit})$	(4200, 4600, 5250, 5820, 3800, 4400, 5160, 5980)
${\mathit{WS}}_j$(ft2/unit)	(0.34, 0.48, 0.54, 0.64, 0.28, 0.44, 0.56, 0.36, 0.37, 0.15, 0.24, 0.35, 0.48, 0.21)
${\mathit{MWS}}_k$(ft2)	(5500, 5720, 6180, 6690, 5200, 5650, 6430, 7120, 8420, 8460, 7950, 6940, 7460, 9280)
${\widetilde{\mathit{MCS}}}_i^q\left(\mathrm{units}\right)$	(6180, 6690, 5200, 5650; 7950, 6940, 7460, 9280)
${\widetilde{\mathit{MCC}}}_l^q\left(\mathrm{units}\right)$	(3600, 4200, 4600, 4400; 3800, 5160, 5980, 6600)
${\widetilde{\mathit{MCD}}}_p^q\left(\mathrm{units}\right)$	(5500, 5720, 5650, 6430; 7120, 8420, 8460, 7950)

5.1. Analysis of the solution results

The case study consisting of multiple objectives under the set of constraints, is implemented to show the crisp SPWM model modeling and optimization algorithms’ validity and applicability. The crisp SPWM model is coded in AMPL language and solved using solver Knitro 10.3.0 through NEOS server version 5.0 on-line facility provided by Wisconsin Institutes for Discovery at the University of Wisconsin in Madison for solving optimization problems, see Dolan, 2001, Server, 2016.

The individual best and worst solution sets are calculated and presented in Table 4 . Based on some vague experience and by using pay-off matrix (summarized in Table 4), the baseline solution for each objectives is assumed to be $ 7.2154E+06 (total economic cost), $ 15.9218E+05 (revenue gained) and 452184 h (medical equipment delivery time) resectively. The reduced solvability set for the proposed IIFPA with LTMFA is $ 7.1687E+06 $⩽T_1⩽$$ 9.9238E+09, 12.3846E+05 $⩽T_2⩽$16.2815E+05 and 436521 h $⩽T_3⩽$562841 h; the reduced solvability set for ETMFA is $ 8.2356E+06 $⩽T_1⩽$$ 11.4132E+06, $ 12.7311E+05 $⩽T_2⩽$$ 15.8343E+05 and 452672 h $⩽T_3⩽$552864 h; the reduced solvability set for HTMFA is $ 8.4842E+06 $⩽T_1⩽$$ 11.2133E+06, 11.3861E+05 $⩽T_2⩽$13.3974E+05 and 442987 h $⩽T_3⩽$536428 h and; finally, the reduced solvability set for MSMFA is $ 8.6824E+06 $⩽T_1⩽$$ 11.8642E+06, 10.4251E+05 $⩽T_2⩽$13.6821E+05 and 452196 h $⩽T_3⩽$502874 h, respectively. Thus these reuduced sets are used to define the degree of desirability in three different linguistic scale such as most desirable (MD), desirable (D) and most undesirable (MU) and, can be represented in Table 7. The problem isn solved three times to obtain the three compromise solution sets. The scope for generating many number of solutions can be carried out by tuning the compensation co-effcient $\lambda$ untill satisfaction. At first, the degree of desirability for each objectives are fixed at $F_1⩽$$ 7.1687E+06, $F_2⩾$16.6312E+05 and $F_3⩽$425122 h (best among all solutions using different approaches). Secondly, the degree of desirability for each objectives are fixed at $F_1⩽$$ 11.6459E+06, $F_2⩾$13.2823E+05 and $F_3⩽$556842 h (most desirable). At third time, the degree of desirability for each objectives are fixed at $F_1⩽$$ 14.2876E+06, $F_2⩾$10.3821E+05 and $F_3⩽$598142 h (most undesirable). The proposed IIFPA with four types of membership and non-membership functions namely; LTMFA (Section 4.2.1), ETMFA (Section 4.2.2), HTMFA (Section 4.2.3), and HTMFA (Section 4.2.4) methods have been applied to solve the crisp SPWM model optimization model and results have been summarized in Table 5 , respectively.

Table 4.

Individual best and worst solution for each objectives.

Objective functions	Individual solutions
	Minimum $\left(F_1\right)$	Maximum $\left(F_2\right)$	Minimum $\left(F_3\right)$
Total economic cost $F_1\left(X\right)$	6.2418E+06	12.5438E+05	562327
Maximum revenue gained $F_2\left(X\right)$	9.4877E+06	17.0237E+05	512481
Minimum medical equipment delivery time $F_3\left(X\right)$	11.3018E+06	13.6489E+05	439471

Table 7.

Degrees of desirability for each objective functions.

Objective functions	Most Desirable (MD)	Desirable (D)	Most Undesirable (MU)
Minimum $F_1\left(X\right)$ (Total economic cost)	7.1687E+06	11.6459E+06	14.2876E+06
Maximum $F_2\left(X\right)$ (Maximum revenue gained)	16.6312E+05	13.2823E+05	10.3821E+05
Minimum $F_3\left(X\right)$ (Minimum medical equipment delivery time)	425122	556842	598142

Table 5.

Solution results obtained by using proposed IIFPA.

Objective values	Proposed IIFPA with LTMFA
	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
Minimum $\left(F_1\right)$	9.0021E+06	9.0154E+06	9.0351E+06	9.0498E+06	9.0743E+06
Maximum $\left(F_2\right)$	13.2014E+05	13.1984E+05	13.1821E+05	13.1564E+05	13.1258E+05
Minimum $\left(F_3\right)$	502412	512288	522102	531919	539774
Marginal evaluations
$\left({\mu }_1^L\left(F_1\right),{\nu }_1^L\left(F_1\right)\right)$	(0.8823, 0.5587)	(0.8803, 0.5602)	(0.8788, 0.5614)	(0.8753, 0.5621)	(0.8736, 0.5643)
$\left({\mu }_2^L\left(F_2\right),{\nu }_2^L\left(F_2\right)\right)$	(0.9129, 0.6395)	(0.9109, 0.6431)	(0.9077, 0.6451)	(0.9053, 0.6468)	(0.9011, 0.6467)
$\left({\mu }_3^L\left(F_3\right),{\nu }_3^L\left(F_3\right)\right)$	(0.8725, 0.5421)	(0.8709, 0.5436)	(0.8684, 0.5455)	(0.8671, 0.5468)	(0.8669, 0.5477)
Overall satisfaction
$\left(\alpha -\beta \right)$	0.8634	0.8623	0.8611	0.8591	0.8516
CPU Time (sec.)	0.2541	2.1562	1.6214	2.6514	1.6842
Objective values	Proposed IIFPA with ETMFA
	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
Minimum $\left(F_1\right)$	10.2314E+06	10.2454E+06	10.2549E+06	10.2652E+06	10.2798E+06
Maximum $\left(F_2\right)$	11.2654E+05	11.2532E+05	11.2475E+05	11.2367E+05	11.2251E+05
Minimum $\left(F_3\right)$	522398	523214	534148	541845	542712
Marginal evaluations
$\left({\mu }_1^E\left(F_1\right),{\nu }_1^E\left(F_1\right)\right)$	(0.8751, 0.5621)	(0.8743, 0.5642)	(0.8719, 0.5664)	(0.8705, 0.5672)	(0.8683, 0.5689)
$\left({\mu }_2^E\left(F_2\right),{\nu }_2^E\left(F_2\right)\right)$	(0.8839, 0.6401)	(0.8821, 0.6418)	(0.8806, 0.6429)	(0.8789, 0.6441)	(0.8773, 0.6454)
$\left({\mu }_3^E\left(F_3\right),{\nu }_3^E\left(F_3\right)\right)$	(0.8624, 0.6532)	(0.8611, 0.6543)	(0.8587, 0.6557)	(0.8567, 0.6566)	(0.8551, 0.6573)
Overall satisfaction
$\left(\alpha -\beta \right)$	0.8498	0.8474	0.8467	0.8446	0.8422
CPU Time (sec.)	1.2564	0.2154	0.2198	0.6214	2.6315
Objective values	Proposed IIFPA with HTMFA
	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
Minimum $\left(F_1\right)$	11.6215E+06	11.6398E+06	11.6481E+06	11.6532E+06	11.6647E+06
Maximum $\left(F_2\right)$	10.8451E+05	10.8325E+05	10.8265E+05	10.8162E+05	10.8021E+05
Minimum $\left(F_3\right)$	531398	532254	536191	546847	547981
Marginal evaluations
$\left({\mu }_1^H\left(F_1\right),{\nu }_1^H\left(F_1\right)\right)$	(0.8545, 0.5782)	(0.8523, 0.5796)	(0.8512, 0.5811)	(0.8491, 0.5826)	(0.8478, 0.5844)
$\left({\mu }_2^H\left(F_2\right),{\nu }_2^H\left(F_2\right)\right)$	(0.8635, 0.6512)	(0.8619, 0.6523)	(0.8604, 0.65419)	(0.8393, 0.65531)	(0.8367, 0.6571)
$\left({\mu }_3^H\left(F_3\right),{\nu }_3^H\left(F_3\right)\right)$	(0.8496, 0.6621)	(0.8481, 0.6634)	(0.8468, 0.6651)	(0.8451, 0.6668)	(0.8443, 0.6678)
Overall satisfaction
$\left(\alpha -\beta \right)$	0.8251	0.8227	0.8219	0.8202	0.8183
CPU Time (sec.)	2.0146	0.6487	0.6874	1.3264	1.0548
Objective values	Proposed IIFPA with MSMFA
	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
Minimum $\left(F_1\right)$	8.6421E+06	8.6547E+06	8.6687E+06	8.6712E+06	8.6851E+06
Maximum $\left(F_2\right)$	14.6521E+05	14.6482E+05	14.6416E+05	14.6374E+05	14.6325E+05
Minimum $\left(F_3\right)$	483603	483784	483889	484197	484324
Marginal evaluations
$\left({\mu }_1^S\left(F_1\right),{\nu }_1^S\left(F_1\right)\right)$	(0.9412, 0.5378)	(0.9393, 0.5389)	(0.9379, 0.5404)	(0.9365, 0.5427)	(0.9351, 0.5462)
$\left({\mu }_2^S\left(F_2\right),{\nu }_2^S\left(F_2\right)\right)$	(0.9616, 0.6204)	(0.9592, 0.62026)	(0.9576, 0.6239)	(0.9565, 0.6256)	(0.9552, 0.6271)
$\left({\mu }_3^S\left(F_3\right),{\nu }_3^S\left(F_3\right)\right)$	(0.9135, 0.5169)	(0.9119, 0.5188)	(0.9096, 0.5211)	(0.9074, 0.5233)	(0.9061, 0.5247)
Overall satisfaction
$\left(\alpha -\beta \right)$	0.9254	0.9243	0.9219	0.9211	0.9202
CPU Time (sec.)	1.6452	0.2451	0.6871	0.6524	0.9532
Objective values	(Ahmad, Ahmad, & Sharaf, 2021) approach
	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
Minimum $\left(F_1\right)$	8.6529E+06	8.6651E+06	8.6698E+06	8.6772E+06	8.6897E+06
Maximum $\left(F_2\right)$	14.6481E+05	14.6429E+05	14.6408E+05	14.6351E+05	14.6317E+05
Minimum $\left(F_3\right)$	483723	483863	483993	484287	484472
Marginal evaluations
$\left({\mu }_1^S\left(F_1\right),{\nu }_1^S\left(F_1\right)\right)$	(0.9412, 0.5378)	(0.9393, 0.5389)	(0.9379, 0.5404)	(0.9365, 0.5427)	(0.9351, 0.5462)
$\left({\mu }_2^S\left(F_2\right),{\nu }_2^S\left(F_2\right)\right)$	(0.9616, 0.6204)	(0.9592, 0.62026)	(0.9576, 0.6239)	(0.9565, 0.6256)	(0.9552, 0.6271)
$\left({\mu }_3^S\left(F_3\right),{\nu }_3^S\left(F_3\right)\right)$	(0.9135, 0.5169)	(0.9119, 0.5188)	(0.9096, 0.5211)	(0.9074, 0.5233)	(0.9061, 0.5247)
Overall satisfaction
$\left(\alpha -\beta \right)$	0.9254	0.9243	0.9219	0.9211	0.9202
CPU Time (sec.)	1.6452	0.2451	0.6871	0.6524	0.9532

Due to space limitations, the optimal allocation of COVID-19 medical equipment among different echelons is not presented. The compromise solution for all three conflicting objectives is obtained at $({\eta }_3={\eta }_2={\eta }_3=0.33)$ and different compensation co-efficient ($\lambda$). From Table 5, it can be observed that by using proposed IIFPA with LTMFA; the value of first objective (Minimization of total economic cost), second objective (Maximization of revenue) and the third objective (Minimization of medical equipment delivery time) are found to be $ 9.0021E+06, $ 13.2014E+05, and 502461 h at compensation co-efficient $\lambda =0.1$ respectively. As for compensation co-efficient $\lambda$ increases, each objective’s values also reach towards its worst solution, and at $\lambda =0.9$, the worst values of each objective are $ 9.0743E+06, $ 13.1258E+05, and 539794 h which shows the more consciousness of decision-makers towards the vagueness or uncertainty. The overall satisfaction level $\left(\alpha -\beta \right)$ is also maximum at $\lambda =0.1$ which is 0.8634 and approaching towards its worst values 0.8516 at $\lambda =0.9$ which shows the inverse effects of compensation co-efficient $\lambda$ with the satisfactory degrees.

Similarly, proposed IIFPA with ETMFA also yield in different compromise solution sets. The obtained compromise solution outcomes are depicted in Table 5. At $\lambda =0.1$, the values of each objectives by using ETMFA have been found to be $ 10.2314E+06, $ 11.2654E+05, and 522461 h, respectively. As for compensation co-efficient $\lambda$ increases, all the objectives reach towards their worst solution, and at $\lambda =0.9$, it approaches to $ 10.2798E+06, $ 11.2251E+05, and 542794 h due to supreme importance has been given to risk violation by decision-makers. The overall satisfaction level $\left(\alpha -\beta \right)$ is found to be maximum at $\lambda =0.1$, which is 0.8498 and approaching towards its worst values 0.8422 at $\lambda =0.9$ which shows the inverse relationships between compensation co-efficient and the overall satisfactory degrees. Furthermore, the proposed IIFPA with HTMFA results in different objective values at various compensation co-efficient $\lambda$. The corresponding compromise solution results are presented in Table 5. At $\lambda =0.1$, the magnitude of each objectives have been obtained as $ 11.6215E+06, $ 10.8451E+05, and 531461 h, respectively. With the increase in compensation co-efficient $\lambda$, it is observed that each objective reaches towards their worst outcomes, which reveals that the manager has given more importance to the risk violation under vagueness or uncertainty. The overall satisfaction level $\left(\alpha -\beta \right)$ is found to be maximum at $\lambda =0.1$, which is 0.8251 and approaching its worst values 0.8183 at $\lambda =0.9$ which shows the inverse relationships between compensation co-efficient and the overall satisfactory degrees. Finally, from Table 5, it can be observed that by using proposed IIFPA with MSMFA, the total economic cost, maximum safety factors for the products, and minimum multi-products delivery time are found to be $ 8.6421E+06, $ 14.6521E+05, and 483652 h at compensation co-efficient $\lambda =0.1$ respectively. As for compensation co-efficient $\lambda$ increases, the values of each objective also reach towards its worst solution, and at $\lambda =0.9$, the worst values of each objective are $ 8.6851E+06, $ 14.6325E+05, and 484381 h which shows the more consciousness of decision-makers towards the vagueness or uncertainty. The overall satisfaction level $\left(\alpha -\beta \right)$ is also maximum at $\lambda =0.1$ which is 0.9254 and reaching towards its worst values 0.9202 at $\lambda =0.9$ which shows the inverse effects of compensation co-efficient $\lambda$ with the satisfactory degrees.

Moreover, if we perform the comparison among all four approaches concerning objective functions, then it can be observed that MSMFA results in better outcomes for all the objectives over the other three approaches for each compensation co-efficient $\lambda$. Consequently, the performances can be evaluated based on the marginal evaluations as $\mathit{ModifiedS}-\mathit{curve}\left(\mathit{MSMFA}\right)>\mathit{Linear}$   $\left(\mathit{LTMFA}\right)>\mathit{Exponential}\left(\mathit{ETMFA}\right)>\mathit{Hyperbolic}\left(\mathit{HTMFA}\right)$, respectively. Hence all four approaches are well capable in generating a better solution for different objectives. The proposed SWPM model explicitly captures the production company’s actual problem regarding the transportation and safety factors of the multi-products and delivery time.

The main aim of this study is to establish a wholesome and reliable trade-off among multiple conflicting objectives under intuitionistic fuzzy uncertainty. The obtained results unanimously reflect the unifying characteristic features of each goal according to the decision-maker’s preferences. The two essential aspects have indicated that inherently involved in decision-making processes: (1) violation of risk under vague uncertainty and (2) balancing the global optimality of each objective. The proposed research work solely highlights the modeling and optimization framework for the SWPM model under an intuitionistic fuzzy environment. Uncertainty is discussed in the parameters’ values, which is resolved by robust ranking function techniques. Various multiobjective optimization methods are suggested to solve MOLPPs. The optimal production, consumption, and waste management policies are derived after obtaining the outcomes. A concise overview of sustainable production and waste management strategies related to various important aspects is depicted in Fig. 7 . It includes consumption of raw materials, budget shares holding for production, different service operation and transportation purpose, pre-determined safety factors while handling, utilization of various waste management options, total shares in revenue generation, and finally the contribution to fulfill the total expected demand of the various COVID-19 medical equipment.

Fig. 7.

Production and waste management policies for COVID-19 medical equipments.

Regarding the consumption of raw materials required to manufacture the medicated gown, face mask, face shield, hand gloves, hand sanitizer, and shoe cover, the total shares are shown by obtaining the ratio of total availability and consumed amount of raw materials. Fig. 7a, consumption of raw material is found to be 29% for the medicated gown, 19% for the face mask, 13% for a face shield, 17% for hand gloves, 06% for hand sanitizer and 16% for shoe cover, respectively. The maximum proportion of raw material is consumed to produce the medicated gown for the doctors or medical personals, which ensures the gown’s foremost need to treat the COVID, infected patients. From Fig. 7b, it can be observed that the total budget that is exhausted over various medical equipment are 24% for the medicated gown, 21% for the face mask, 10% for a face shield, 16% for hand gloves, 18% for hand sanitizer and 11% for shoe cover, respectively. In this case, the maximum allocation of budget is utilized to produce the medicated gown to fulfill total expected demands. Pre-cautionary safety measures are also calculated based on the ratio of required safety factors for each medical equipment and availability of useful practicing protective measures at different sources point to various destinations. In Fig. 7c, safety factors associated with the COVID-19 medical equipment are found to be 22% for the medicated gown, 17% for the face mask, 15% for a face shield, 19% for hand gloves, 11% for hand sanitizer and 16% for shoe cover. The high safety measures are associated with medicated gown production due to its more significant contamination during the treatment of COVID-19 infected patients.

Moreover, the management of generated waste after using medical equipment is of prime concern as its impact is severe both socially and environmentally. The contamination or transfusion rate of used medical equipment is very high and may severely impact if the concrete waste management initiatives have not been taken. Thus the opportunity of disposing of is depicted. From Fig. 7d, it can be observed that the used medical equipment wastes are efficiently managed by under-ground disposal facility, incineration, and advanced manufacturing plants and are found to be 652354, 236548 and 712564 units of the medicated gown are transported for under-ground disposal, incineration and advanced manufacturing plants respectively. Similarly, 269541, 352145, and 865239 units of face mask are shipped for under-ground disposal, incineration, and advanced manufacturing purposes, about 241365, 248931 and 569245 units of face shield are sent for under-ground disposal, incineration, and advanced manufacturing processes, respectively. Further, 265874, 352947, and 784325 units of hand gloves are transported for under-ground disposal, incineration, and advanced manufacturing purposes. Similarly, the respective units of hand sanitizer and shoe cover are 265842, 397842 and 698741 units, and 312896, 386721, and 583194 units, respectively. The outcomes emphasize manufacturing each medical equipment, and the maximum units are shipped for manufacturing purposes to meet the anticipated demand.

In Fig. 7e, the contribution of each medical equipment in generating the revenue is found to be 27% from the medicated gown, 20% from a face mask, 18% from face shield, 26% from hand gloves, 08% from hand sanitizer and 06% from shoe cover respectively. The medicated gown also contributes the larger shares to revenue generation. The total expected demand is met by either newly produced or re-manufactured medical equipment. Fig. 7f, the expected demand for the medicated gown is met by 782473 newly produced and 287391 re-manufactured units, respectively. Similarly, 872943 newly produced and 398456 re-manufactured face mask units are shipped to the market for the fulfillment of anticipated demand. About 572913 newly produced and 286179 re-manufactured units of face shield are sent to the market. Further, 786245 newly produced and 358746 re-manufactured units of hand gloves are transported to meet the expected demand. Similarly, the respective units of hand sanitizer and shoe cover are 684265 and 584921 newly produced units, and 492875 and 386172 re-manufactured units, respectively.

The proposed research work solely highlights the modeling and optimization framework for the crisp SPWM model under an intuitionistic fuzzy environment. Uncertainty is discussed in the parameters’ values, which is resolved by robust ranking function techniques. Various multiobjective optimization methods are suggested to solve MOLPPs. The proposed IIFPA solution approaches may solve many other problems in different fields, such as engineering, management sciences, economics, agriculture. Different criteria for selecting a better solution amongst best are also among the remarkable strengths of the proposed study. Apart from these contributions, a few more aspects have been left untouched, reflecting the presented work’s weakness. Uncertainty due to randomness and opportunity for choices of parameters’ values have not been addressed in this research since the proposed solution methods are conventional optimization techniques that may not be appropriate for the large dimensions of the crisp SPWM model.

5.1.1. Overall satisfaction degrees for managers at various $d_m$ and $\gamma$

After getting the fruitful solution results by using the proposed IIFPA with different sorts of membership and non-membership functions as presented in Tables 5, there is still an ample opportunity to obtain more specific and comprehensive outcomes by tuning additional parameters $d_m$ and $\gamma$ (vagueness degrees) present in the exponential and modified S-curve membership functions, respectively. The Table 5 illustrate an overall satisfaction level solution for single value of vagueness degree at $d_m=0.1$ and $\gamma =13.813$. Hence it would be worth useful for managers to observe or record the influence of these parameters ($d_m$ and $\gamma$) with the overall satisfaction level $\left(\alpha -\beta \right)$ which is graphically represented in Fig. 8 . For exponential-type membership and non-membership functions, the parameter $d_m$ is tuned for different values and the results are shown in Table 6 . The graphical representation are depicted in Fig. 8a. As Table 6 and Fig. 8a reveal that when parameter $d_m$ (vagueness degree) increases, the overall satisfaction degree of managers decreases. It may be concluded that the nearer the $d_m$ values reaches to 0, the more likely the problem be to a crisp SPWM model and the overall degree of satisfaction will always 1. This same behavior is noticed for different compensation co-efficient $\lambda$ values, the only difference being the initial point for the minimum vagueness degrees. For $d_m=0.5,\lambda =0.1$, the satisfaction level is found to be 0.8229 and reaches towards its worst at $d_m=5,\lambda =0.9$ which is 0.7518. As discussed before, a higher overall satisfaction level $\left(\alpha -\beta \right)$ can be attained with higher compensation co-efficient $\lambda$ values. In Fig. 8a, the downward trend is shown for the parameter $d_m$ means that an increment in these values will lead to the reduction in overall satisfaction level $\left(\alpha -\beta \right)$ and vice versa.

Fig. 8.

Overall satisfaction level $\left(\alpha -\beta \right)$.

Table 6.

Overall satisfaction level $\left(\alpha -\beta \right)$ achieved by using ETMFA and MSMFA.

Degree of vagueness	Compensation co-efficient
$\left(d_m\right)$	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
0.5	0.8289	0.8277	0.8268	0.8261	0.8156
1	0.8187	0.8179	0.8171	0.8167	0.8156
1.5	0.8121	0.8113	0.8198	0.8187	0.8173
2	0.8076	0.8064	0.8059	0.8056	0.8049
2.5	0.8027	0.8022	0.8013	0.8005	0.7986
3	0.7931	0.7919	0.7902	0.7989	0.7971
3.5	0.7822	0.7809	0.7896	0.7881	0.7873
4	0.7788	0.7781	0.7776	0.7771	0.7767
4.5	0.7667	0.7653	0.7641	0.7635	0.7622
5	0.7543	0.7534	0.7531	0.7524	0.7518
Degree of vagueness	Compensation co-efficient
$\left(\gamma \right)$	$\lambda =0.1$	$\lambda =0.3$	$\lambda =0.5$	$\lambda =0.7$	$\lambda =0.9$
4	0.9125	0.9166	0.9157	0.9151	0.9144
8	0.9063	0.9059	0.9051	0.9046	0.9037
12	0.8943	0.8927	0.8921	0.8916	0.8907
16	0.8898	0.8881	0.8876	0.8869	0.8861
20	0.8779	0.8772	0.8766	0.8758	0.8742
24	0.8661	0.8657	0.8651	0.8646	0.8635
28	0.8528	0.8522	0.8515	0.8509	0.8501
32	0.8412	0.8403	0.8491	0.8486	0.8477
36	0.8384	0.8376	0.8371	0.8366	0.8358
40	0.8251	0.8248	0.8243	0.8236	0.8229

In a similar manner, for modified S-curve membership and non-membership functions, the parameter $\gamma$ is changed for different values and the results are depicted in Table 6. The graphical representation is shown in Fig. 8b. As Table 6 and Fig. 8b reflect that when parameter $\gamma$ (vagueness degree) increases, the overall satisfaction degrees of managers decreases. For a value $\gamma =4,\lambda =0.1$, the oveall satisfaction level is depicted to be 0.9125 and moves towards its worst at $\gamma =40,\lambda =0.9$ which is 0.8229. It may be deduced that the closer the $\gamma$ values comes to 0, the more surely the problem be to a crisp SPWM model and the overall degree of satisfaction will always 1. The exact behavior is observed for different compensation co-efficient $\lambda$ values, the only difference being the starting point for the minimum vagueness degrees. As discussed earlier, a higher overall satisfaction level $\left(\alpha -\beta \right)$ can be achieved with higher compensation co-efficient $\lambda$ values. In Fig. 8b, the downward trend is revealed for the parameter $\gamma$ means that an increase in this value will results in the reduction of overall satisfaction level $\left(\alpha -\beta \right)$ and vice versa.

In order to determine the best possible outcomes in the proposed IIFPA, the managers has to identify the most appropriate parameters ($d_m$ and $\gamma$) when exponential and modified S-curve is implemented for marginal evaluation purpose. Thus, the presented ETMFA and MSMFA is more flexible, versatile and convenient than the LTMFA and HTMFA. Consequently, the proposed IIFPA is most promising and reliable while dealing with MOLPPs. Moreover the proposed IIFPA can generate both unbalanced and balanced efficient solutions based on the managers choices, and can offer the suitable flexibility to provide different solutions helping in the selection of most preferred compromise solution.

5.2. Performances analysis

The three different solution sets based on the degree of desirability scenario have been generated, and the corresponding performances of each solution method (e.g. Proposed IIFPA with LTMFA, ETMFA, HTMFA and MSMFA) under the different solution sets are also recorded. From Table 8 (solution 1), the LTMFA reveals that total economic cost can be reduced by 24.82%, total revenue can be enhanced by 11.83%, and product delivery time can be mitigated by 38.68% as compared to the savings from baseline solution. Furthermore, ETMFA yield in the reduction of economic cost by 13.24%, a significant increment in the revenue gained by 18.84% and notably decrement in the product delivery time by 73.83% as compared to the baseline solution. Similarly, on applying HTMFA, it is observed that the economic cost can be reduced by 12.84%, revenue generation can be enhanced by 17.61%, and product delivery time can be mitigated by 22.49% as compared to the baseline solution. At last, it is found that the MSMFA results in the significant reduction in the total economic cost by 17.21%, enhancement in revenue generation by 23.73%, and product delivery time can be mitigated by 21.63% as compared to the baseline solution. Likewise, from Table 9 (solution 2), the LTMFA shows that total economic cost can be diminished by 15.81%, revenue gained from re-manufactured products can be increased by 22.77%, and product delivery time can be reduced by 17.15% as compared to the baseline solution. Furthermore, The ETMFA results in the reduction of economic cost by 13.63%, a significant increment in the revenue generation by 19.56%, and notably decrement in the product delivery time by 13.55% as compared to the baseline solution. Similarly, on applying HTMFA, it is observed that the economic cost can be mitigated by 15.01%, revenue gained from the re-manyfactured products can be enhanced by 16.63%, and product delivery time can be reduced by 19.26% as compared to the baseline solution. Finally, it is found that the MSMFA results in the significant reduction in the total economic cost by 18.61%, enhancement in revenue gained by 22.94%, and product delivery time can be mitigated by 12.97% as compared to the baseline solution. From Table 10 (solution 3), the LTMFA ensures that total economic cost can be reduced by 13.64%, revenue generation can be achieved by 21.62%, and products delivery time can be mitigated by 18.36% as compared to the baseline solution. Furthermore, the ETMFA results in the reduction of economic cost by 15.54%, a significant increment in the revenue gained by 20.65%, and remarkable decrement in the products delivery time by 17.66% as compared to the baseline solution. Similarly, on applying the HTMFA, it is observed that the total economic cost can be reduced by 14.31%, revenue generation from the products can be enhanced by 17.27%, and products delivery time can be mitigated by 18.61% as compared to the baseline solution. Lastly, it is observed that the MSMFA results in the significant reduction in the total economic cost by 19.61%, enhancement in revenue gained by 23.61%, and product delivery time can be mitigated by 13.54% as compared to the baseline solution.

Table 8.

Solution 1: ($F_1⩽$7.1687E+06, $F_2⩾$16.6312E+05 and $F_3⩽$425122).

Objective functions		Proposed IIFPA
		LTMFA		ETMFA		HTMFA		MSMFA
	Baseline solution	Solution	CV	Solution	CV	Solution	CV	Solution	CV
$F_1\left(X\right)$ (Total economic cost)	7.2154E+06	6.6218E+06	1.23	6.9248E+06	1.34	6.26584E+06	1.05	6.2451E+06	0.93
$F_2\left(X\right)$ (Revenue gained)	15.9218E+05	15.9624E+05	0.93	15.9236E+05	1.02	15.9318E+05	0.91	15.9818E+05	0.87
$F_3\left(X\right)$ (Medical equipment delivery time)	452184	452136	1.17	452062	1.14	451981	1.09	451824	1.02

Table 9.

Solution 2: ($F_1⩽$11.6459E+06, $F_2⩾$13.2823E+05 and $F_3⩽$556842).

Objective functions		Proposed IIFPA
		LTMFA		ETMFA		HTMFA		MSMFA
	Baseline solution	Solution	CV	Solution	CV	Solution	CV	Solution	CV
$F_1\left(X\right)$ (Total economic cost)	7.2154E+06	6.8293E+06	1.39	6.3912E+06	1.84	6.7218E+06	1.71	6.1925E+06	1.23
$F_2\left(X\right)$ (Revenue gained)	15.9218E+05	16.3029E+05	0.78	16.2698E+05	0.89	16.1364E+05	0.98	16.7291E+05	0.73
$F_3\left(X\right)$ (Medical equipment delivery time)	452184	452118	1.29	452089	1.43	451912	1.67	451866	1.21

Table 10.

Solution 3: ($F_1⩽$14.2876E+06, $F_2⩾$10.3821E+06 and $F_3⩽$598142).

Objective functions		Proposed IIFPA
		LTMFA		ETMFA		HTMFA		MSMFA
	Baseline solution	Solution	CV	Solution	CV	Solution	CV	Solution	CV
$F_1\left(X\right)$ (Total economic cost)	7.2154E+06	6.7521E+06	1.37	6.8164E+06	1.17	6.9384E+06	1.49	6.2910E+06	1.11
$F_2\left(X\right)$ (Revenue gained)	15.9218E+05	16.6145E+05	0.98	16.7822E+05	0.87	16.4254E+05	1.13	16.9061E+05	0.81
$F_3\left(X\right)$ (Medical equipment delivery time)	452184	452041	1.26	451995	1.01	451901	1.14	451851	0.96

For solution 1, a comparative study with the co-efficient of variation shows that all the objective functions are more homogeneous under variation while using the LTMFA over others. Similarly, more robust (homogeneous) results of each objective function have been achieved for solution 2 while using ETMFA. Furthermore, it is also observed that all the objective functions are more homogeneous under variation while using the MSMFA for solution 3. The trending behavior of co-efficient of variations has also been shown in Fig. 9 . The representation of fluctuating behavior for solution 1 (Fig. 9a), solution 2 (Fig. 9a), and solution 3 (Fig. 9c) by using different techniques reflects homogeneity or robustness under the variation. In addition to the co-efficient of variations, the behavior of the different techniques has been depicted in Fig. 9 for each solution set. The graphical representation of solution 1 (Fig. 9a), solution 2 (Fig. 9a), and solution 3 (Fig. 9c) by using different techniques reveals the performances of proposed IIFPA with each types of marginal evaluations. Finally, the optimal solution results for three different solution sets have been summarized in Table 11 . From Table 11, all the solution sets are under the most desirable zone, which provides an opportunity to select a better one amongst the best solution sets. Thus these criteria (savings compared to baseline solution, CV, and degrees of desirability) for selection of optimal solution results are proven to be quite helpful tools while dealing with multiple objective optimization problems.

Fig. 9.

Co-efficient of variation and objective functions v/s Proposed IIFPA.

Table 11.

Comparision of optimal solutions with multiple criteria.

Multiple criteria	Prpopsed IIFPA
	LTMFA	ETMFA	HTMFA	MSMFA
	$F_1$: 55.01% $\downarrow$	55.81% $\downarrow$	56.13% $\downarrow$	57.22% $\downarrow$
Baseline solution	$F_2$: 23.12% $\uparrow$	16.63% $\uparrow$	23.24% $\uparrow$	25.91% $\uparrow$
	$F_3$: 87.45% $\downarrow$	87.15% $\downarrow$	87.66% $\downarrow$	88.11% $\downarrow$
	$F_1$: 1.05	1.39	1.17	0.99
CV	$F_2$: 0.91	0.78	0.87	0.76
	$F_3$: 1.09	1.29	1.01	0.97
	$F_1$: 9.0553E+09 (MD)	10.0714E+09 (MD)	10.9421E+09 (MD)	8.0391E+09 (MD)
Degree of desirability	$F_2$: 13.4162E+05 (MD)	11.3954E+05 (MD)	10.4235E+05 (MD)	14.3751E+05 (MD)
	$F_3$: 445897 (MD)	458139 (MD)	475291 (MD)	436521 (MD)

5.3. Managerial insight

The presented study inherently includes managerial level implications by exploring promising SPWM model practices in an automobile company in the Indian context, which also contemplates over a scientific approach that recognizes and eradicates the internal hurdles among the SPWM model. A significant output of the study provides in-depth aid and supports to the managers or practitioners of automobile companies to identify, classify, and analyze the current policies’ hidden shortcomings for a continuous period. It also indicates the more suitable and appropriate practices that can be adopted for attaining sustainability in the SPWM model.

The current research contribution towards managerial insight is classified into four leading categories depending on the nature of the issues addressed. The first managerial implication can be identified to develop a robust model for sustainable production and waste management policies for the COVID-19 medical equipment. The optimal production, consumption, and waste management policies for new or first-time medical equipment producing for the automobile company leads to systematic and well-organized decision-making scenarios. The SPWM model formulation unanimously adheres and exhibits realistic decision-making processes while producing COVID-19 medical equipment. The depiction of different objective functions and associated constraints are a much reliable optimization framework in the current COVID-19 situation. The proposed SPWM model act as an aid and support to the managers or practitioners to adopt the prominent strategy and get the optimal results. On implementing the proposed SPWM model, the outcomes have shown the dynamic and promising characteristic features about the production policies and waste management strategies. The second managerial implication is identifying the most critical aspects of uncertainty among parameters and selecting appropriate techniques to capture uncertain behavior parameters. A more practical approach to overcome the issue of uncertainty in a more practical way, triangular intuitionistic fuzzy numbers are suggested that provide both aspects of parameters’ acceptance and rejection under hesitations.

Most importantly, the third managerial implication can be considered to develop a novel IIFPA approach, a scientific solution method, to solve the proposed SPWM model. The propounded IIFPA is easily applicable and very co-operative with different membership and non-membership functions such as linear, exponential, hyperbolic, and modified S-curve, respectively. The opportunity to obtain the optimal solution’s desired number is also a remarkable aid to the managers or policy-makers. Based on different comparing criteria, the selection of better optimal solution sets among the bests is a benchmarking contribution to the fourth managerial implication. Performances analyses are also performed on the obtained solutions and can be implemented according to the resources, demand, budget, and time. The current SPWM model outcomes ensure maximum emphasis on the medicated gown production and its management to meet the anticipated demand and extract the revenues regularly. It can be further analyzed that sanitizer production is comparatively lower than other medical equipment that reveals the less demand and waste management policies are required. An increase in the production of unit medicated gown can contribute to fulfilling the current demand and results in a significant revenue generation too.

The strategy advised is to provide an opportunity to create supply chains and manufacturing within India by helping existing manufacturers to expand, identifying new manufacturers, hand-holding and facilitating, teams of officers, engineers, and scientists deployed and import only if necessary to meet timelines. Thus during COVID-19 pandemic, any non-pharmaceutical company or organization can start production and waste management initiatives to strengthening and enabling the nation while fighting with the virus. Finally, managers or policy-makers can take advantage of the current study and extract the fruitful pieces of information and knowledge regarding the optimal policies and strategies while making decisions.

The advantages and disadvantages of the proposed IIFPA method can be highlighted. The propounded IIFPA considers both the membership and non-membership functions consisting of the element’s acceptance and rejection degrees into the same feasible solution set and ensures less violation of risks due to hesitation degree. The proposed IIFPA is exempted from the various shortcomings and drawbacks of the existing methods such as Lai and Hwang, 1993, Lai and Hwang, 1994, Li et al., 2006, Selim and Ozkarahan, 2008, Werners, 1988, Zimmermann, 1978, Torabi and Hassini, 2008. It also provides an ample opportunity to generate as many solution sets as decision-makers or managers want and select the most desired ones. The proposed IIFPA deals with the degree of acceptance and the rejection in the solution set. Sometimes, a situation may arise where the degree of indeterminacy exists. In such a case, the proposed IIFPA cannot be used to solve the multiobjective optimization problem. The proposed IIFPA may not generate the optimal solution for large-dimensional problems due to the model’s complex configuration.

There are some limitations of this research work. The study is designed and developed according to the current situation of the COVID-19 pandemic; however, situations will be changed with time, and the modeling approach would be outdated and are not eternal. The SPWM model is not considered sustainable, as it is indispensable to address sustainability in current scenarios. Environmental impact assessment is not performed in this research study, which can be regarded as a limitation of the study. Health personnel safety, such as their service hour, a routine checkup of health workers, and 24$\times$7 availability of PPEs, is not considered in the proposed SPWM model, which is the essential aspects in the current situations.

In the future, proposed IIFPA can be applied to a vast range of real-world applications such as humanitarian relief logistics management, inventory control, supply chain management, supplier selection, transportation problem, assignment problems, etc. The proposed SPWM model is implemented on small data-set and dimensions, but it can be further applied to large-scale or state and country level.

6. Conclusions

The mixed-integer multiobjective modeling and optimization framework for sustainable production and waste management policies for COVID-19 medical equipment is presented under uncertainty. Triangular intuitionistic fuzzy numbers have depicted impreciseness among different parameters. A robust ranking function based on expected values $\left(\mathit{EV}\right)$ is introduced to quantify the triangular intuitionistic fuzzy parameters scientifically into its crisp form. The working efficiency of the proposed SPWM model is also discussed through the existence of its convexity property. Furthermore, a new solution method IIFPA with different membership and non-membership functions is developed and successfully employed to solve the proposed SPWM model. A tremendous amount of solution results are generated by tuning the various parameters that allow managers or decision-makers to select the most favorable or desirable solution sets. Moreover, the multiple criteria such as savings from baseline solution, CV, and degrees of desirability are introduced to measure the performance analysis of the proposed IIFPA with LTMFA, ETMFA, HTMFA, and MSMFA approach. The outcomes and findings are elaborately discussed in the context of the compelling managerial implications. Thus modeling and optimization texture of the proposed SPWM model reveals a similar scenario for newly engaged manufacturing companies to produce the COVID-19 medical equipment the first time. The achieved objectives are highly favorable and satisfactory, which encourages automobile companies to manufacture such medical equipment.

Some crucial aspects have been untouched due to manuscript writing constraints and can be studied as future research scope. The crisp SPWM model has not considered the distribution of products integrated into the supply chain design. Implementation of other uncertain forms of parameters such as multi-choice and stochastic random variables can also be regarded as future research scope. The various conventional techniques such as TOPSIS, fuzzy TOPSIS, and intuitionistic fuzzy TOPSIS can be further applied to compare the performances of the proposed IIFPA. Additionally, some metaheuristic optimization techniques such as Artificial Neural Network, Genetic Algorithm, and Particle Swarm Optimization can also be implemented to solve the crisp SPWM model.

Funding

The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding this work through research group No. (RG- 1438-089).

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.