The use of consensus sequence information to engineer stability and activity in proteins

Abstract

The goal of protein design is to create proteins that are stable, soluble, and active. Here we focus on one approach to protein design in which sequence information is used to create a “consensus” sequence. Such consensus sequences comprise the most common residue at each position in a multiple sequence alignment (MSA). After describing some general ideas that relate MSA and consensus sequences and presenting a statistical thermodynamic framework that relates consensus and non-consensus sequences to stability, we detail the process of designing a consensus sequence and survey reports of consensus design and characterization from the literature. Many of these consensus proteins retain native biological activities including ligand binding and enzyme activity. Remarkably, in most cases the consensus sequence shows significantly higher stability, as measured by thermal or chemical denaturation, consistent with the statistical thermodynamic model. To understand this stability increase, we compare various features of consensus sequences with the extant MSA sequences from which they were derived. Consensus sequences show enrichment in charged residues (most notably glutamate and lysine) and depletion of uncharged polar residues (glutamine, serine, and asparagine). Surprisingly, a survey of stability changes resulting from point substitutions show little correlation with residue frequencies at the corresponding positions within the MSA, suggesting that the high stability of consensus proteins may result from interactions among residue pairs or higher-order clusters. Whatever the source, the large number of reported successes demonstrates that consensus design is a viable route to generating active and in many cases highly stabilized proteins.

1. Introduction

A major goal of protein design is to generate proteins that have high activity and are well-behaved. Typically, well-behaved proteins have high thermodynamic stability. High stability not only ensures that a protein adopts its target fold, it promotes long “shelf-life” (that is, it remains active over a long period of time) by keeping the protein folded, because unfolded proteins are often inactivated through aggregation, chemical modification, or surface adsorption.

There are several distinct but complementary approaches to protein design, including de novo methods (Huang et al., 2016), directed evolution (Arnold, 2015, 2019), and sequence-based phylogenetic approaches (Magliery, 2015; Poole & Ranganathan, 2006; Porebski & Buckle, 2016). De novo design typically seeks to generate novel folds, and often uses physics-based energy terms, although local structural preferences from data bases can be included. One successful approach to de novo design uses the Rosetta energy function (Alford et al., 2017; Kuhlman, 2019). Rosetta has been highly successful in generating very stable proteins that adopt all sorts of target structures (e.g., Brunette et al., 2015; Lu et al., 2018; Marcos et al., 2018), although these proteins typically lack biological activity. Designing in biological activity into novel folds can be a major challenge.

In contrast, directed evolution and bioinformatic approaches to protein design are restricted to proteins that are found in nature and adopt stable folds. These two methods are more likely to generate active proteins. This is especially true for directed evolution, where activity is often a selected property. Bioinformatic approaches include consensus design and ancestral reconstruction. Although activity is not a selected property in bioinformatic approaches, activity often leaves a strong imprint on protein sequence. Thus, activity is likely to be imparted on proteins that are designed using sequence information from naturally occurring proteins.

In this chapter, we will discuss the consensus approach to protein design, in which a consensus sequence is created from an alignment of many proteins from the same family. The consensus sequence is simply the most frequently occurring residue at each position within the multiple sequence alignment (MSA, Figure 1). Since residues that are important for activity are highly conserved, active sites and binding interfaces are likely to be retained in consensus sequences.

Figure 1. Extracting a consensus sequence from a multiple sequence alignment.

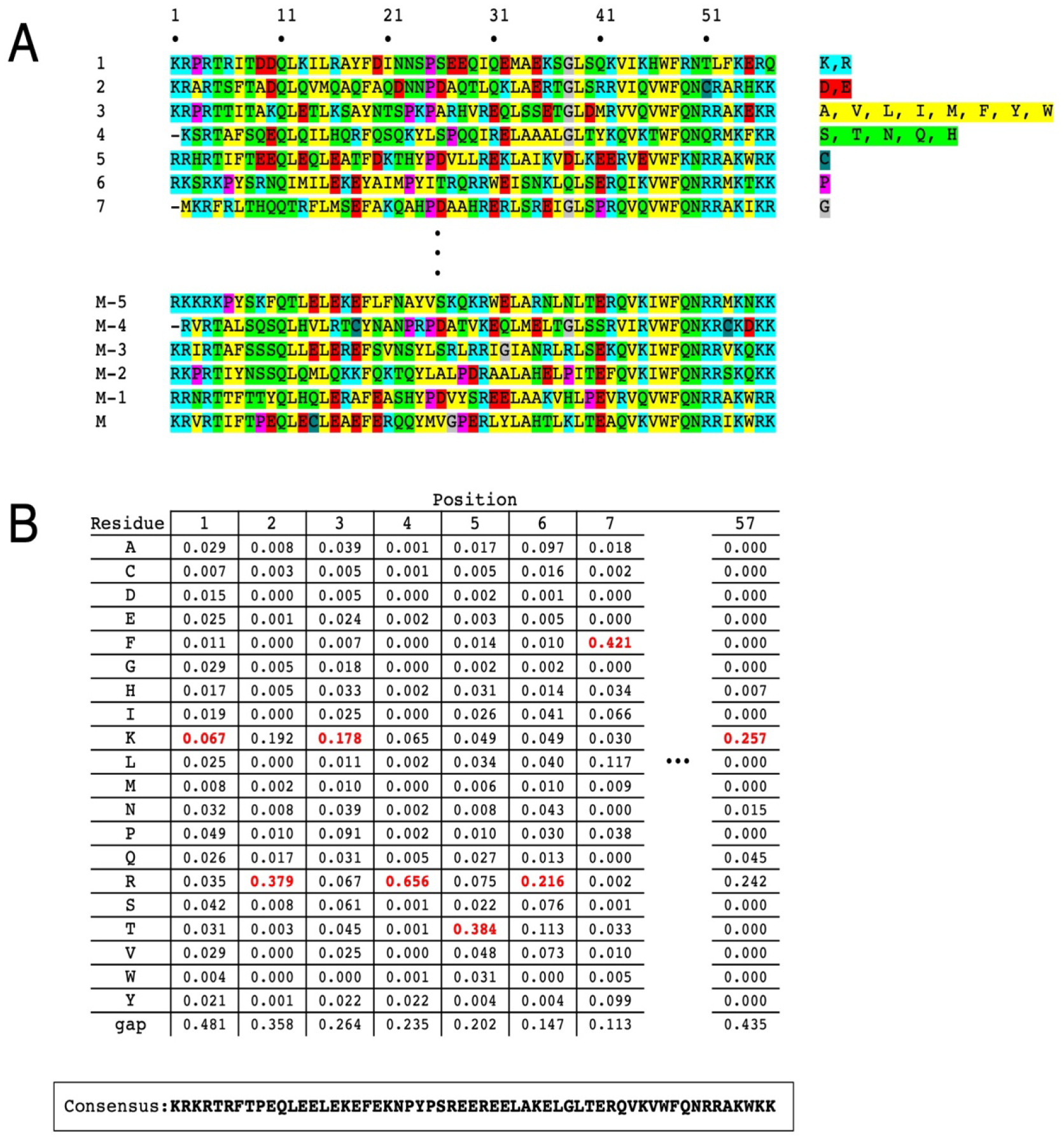
(A) An alignment of M=4,571 homeodomain sequences, each of length L=57 residues. Residues with similar (or unique) chemical features are highlighted to illustrate conservation. Positions with a gap in more than half the sequences are eliminated from the alignment. From such an alignment, the frequency of each type of residue (including remaining “gap residues”) is determined. (B) The consensus sequence (bottom) is obtained by taking the residue with the highest frequency (excluding gaps, see Section 3) at each position (red).

By definition, consensus sequences bear strong resemblance to naturally occurring sequences they are designed from, which we will refer as “extant MSA sequences” in this chapter. Yet, as will be discussed below, consensus sequences are quite different from naturally occurring sequences in terms of overall residue composition. Moreover, consensus design is agnostic to sequence correlations involving two or more residues, since positional frequencies are evaluated independently of residue identities at other positions.¹ It might be expected that these sequence differences would result in decreased stabilities for consensus proteins, compared to the extant MSA sequences. However, as described below, many studies have found consensus proteins to be more stable than their naturally occurring counterparts.

In this chapter, we focus on consensus proteins, their design, and their properties, with emphasis on thermodynamic stabilities. We first consider multiple sequence alignments and the resulting consensus sequences using a statistical thermodynamic framework. Next, we describe some methods we use to generate consensus sequences. We then review findings from a number of laboratories on the results of consensus design, which demonstrate consensus proteins adopt their target folds, often maintain biological activities, and usually possess very high thermodynamic stabilities, and compare these findings to those from ancestral reconstruction. Finally, we explore some of the sequence features of consensus proteins, in part to look for clues for the origins of increased stability, and highlight some open questions and future directions.

2. Protein stability and sequence conservation

2.1. A thermodynamic view of the multiple sequence alignment

In this section, we will use a statistical thermodynamic model to interpret multiple sequence alignments, relating the folding free energy to frequencies in an MSA (e.g., Figure 1B). By assuming that each position in the protein is independent of the others, the model provides relationships between the energy and the frequency of each residue at each position in the native state². In this model, each sequence in the alignment is treated as a replica in a thermodynamic ensemble, in the same way that the ensemble method is applied to equilibrium systems in statistical thermodynamics (Hill, 1987; McQuarrie, 1984). This view of multiple sequence alignments and resulting consensus sequences has previously been described by Steipe (Steipe, 2004). The goal of this model is the derivation of a “residue partition function”, which directly relates to the probabilities of each residue at a given position.

Consider sequence variation at position i of a protein L residues in length. The residue at position i can be of any of twenty residue types along with a gap, denoted as the set r = {Ala, Cys, …, Tyr, gap}. We will consider each of the 20 residues (and the gap) to have an energy that depends on residue identity and the environment in the solvated native protein (Figure 2). Following the standard approach in statistical thermodynamics (Hill, 1987; McQuarrie, 1984), we will build an ensemble of a large number of replicas, each containing a single solvated protein molecule in its native state. We will allow each replica to equilibrate over 21 energy levels corresponding to different residues at position i. This equilibration is equivalent to an alchemical reaction among the different side chains. To connect with the Gibbs free energy, we will also allow the system to equilibrate with a large bath at constant temperature T and pressure p, via heat-flow and volume change for each replica (Barrick, 2017).

Figure 2. An ensemble model for sequence variation at a specific site in a native protein.

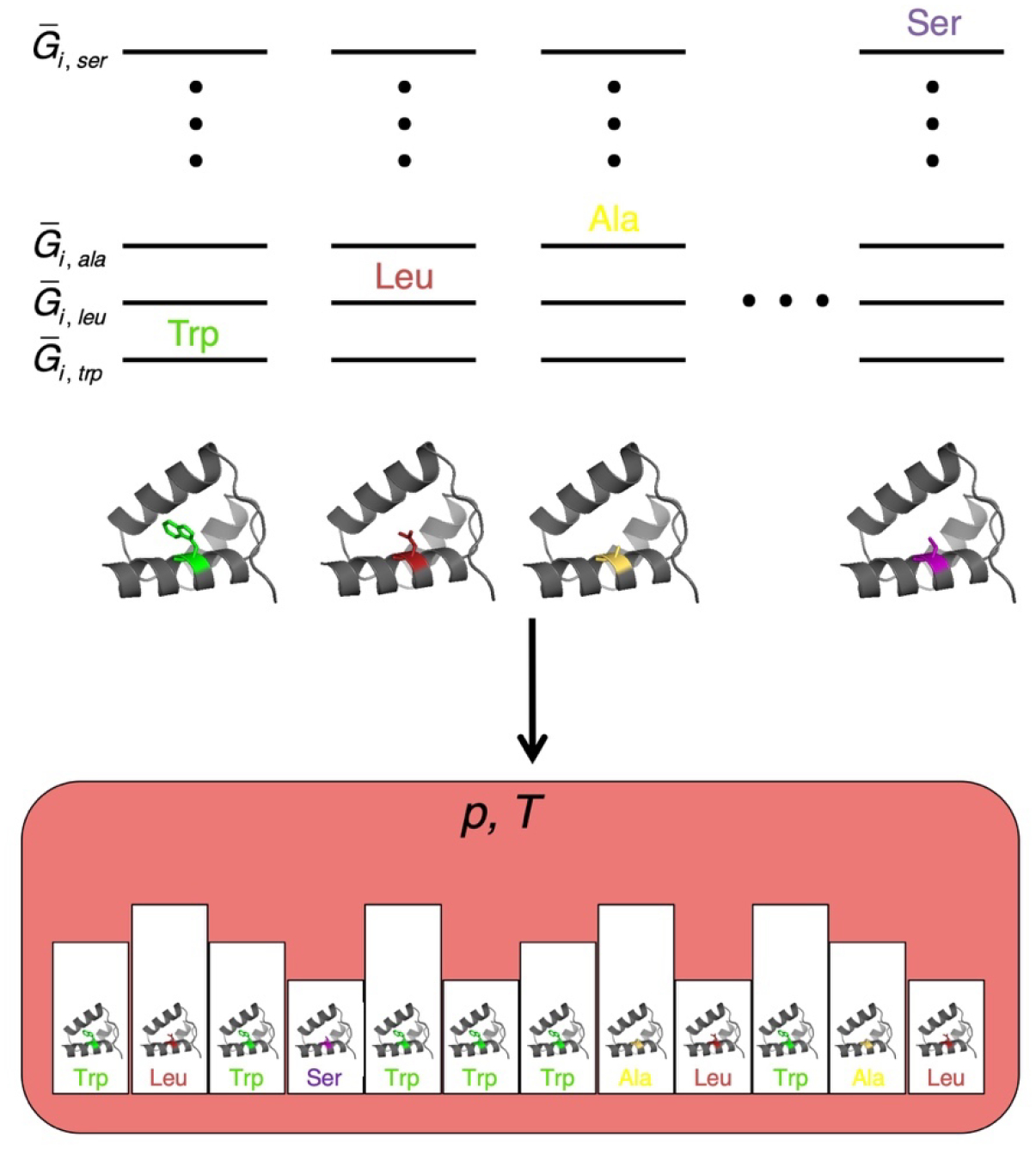
(Top) Gibbs free energy values (where the overbar indicates molar energies) for each of the 20 residues (plus a gap) at position i in the native state. Each side-chain free energy is determined by specific interactions between the side chain and the protein and solvent in all conformations available to the side chain. (Bottom) an isothermal isobaric ensemble (defined by the temperature and pressure of a large reservoir, pink) containing single-chain replicas that can exchange heat and volume with the reservoir. Side chains are allowed to equilibrate over the set r through alchemical transformation, producing equilibrium populations that reproduce residue frequencies at site i in an MSA, and are related to side-chain free energies through Boltzmann-like terms. For simplicity, only the four residues from panel A are shown.

After equilibration, the number of replicas containing each of the 21 residues will match equilibrium populations. We will assume that these populations match the frequencies for each residue at position i in a suitably large multiple sequence alignment. Using Lagrange multipliers, we can relate these populations to the free energies of each side chain in the native state through a reaction partition function for position i:

$${\rho }_i=\sum _{xaa\in r}{\theta }_{i,xaa}=\sum _{xaa\in r}{e}^{-{\overline{G}}_{i,xaa}/RT}$$ (1)

The quantity θ_{i, xaa} is a partition function for residue xaa at position i.³ The overall reaction partition function ρ_i is obtained by summing the set of 21 θ_{i, xaa} terms, since each residue is mutually exclusive—a protein chain cannot have two residues at a single position. Note that the statistical weight for each residue is Boltzmann-like, where the energy is the Gibbs free energy.

With this residue partition function, we can calculate the probability of a given residue at position i from the ratio of the statistical weight for that residue divided by the partition function:

$$p_{i,xaa}=\frac{{\theta }_{i,xaa}}{{\rho }_i}=\frac{e^{-{\overline{G}}_{i,xaa}/RT}}{{\rho }_i}$$ (2)

As long as a multiple sequence alignment is large enough to give good statistical averaging, the frequency of residue xaa at position i (f_{i, xaa}) should be approximately equal to this probability⁴. In principle, Equation 2 provides a way to connect the population to the free energy. However, Equation 2 depends on all 21 residue free energies at position i, not just that of residue xaa. Fortunately, there are 20 such equations⁵, so we can combine equations to determine free energies. One particularly useful way of getting free energies in a way that relates to experimentally measured free stabilities is to compute the ratios of p_i values for different pairs of residues:

$$\frac{p_{i,xaa}}{p_{i,yaa}}=\frac{{\theta }_{i,xaa}/{\rho }_i}{{\theta }_{i,yaa}/{\rho }_i}=\frac{e^{-{\overline{G}}_{i,xaa}/RT}}{e^{-{\overline{G}}_{i,\text{ y}aa}/RT}}=e^{-\left({\overline{G}}_{i,xaa}-{\overline{G}}_{i,\text{ y}aa}\right)/RT}=e^{-\Delta {\overline{G}}_{i,yaa\to xaa}/RT}$$ (3)

Taking the logarithm of Equation 3 gives

$$\Delta {\overline{G}}_{i,yaa\to xaa}=-RT\text{ln}\left(\frac{p_{i,xaa}}{p_{i,yaa}}\right)\approx -RT\text{ln}\left(\frac{f_{i,xaa}}{f_{i,yaa}}\right)$$ (4)

where the approximation on the right-hand side holds as long as frequencies are taken from a large MSA. Ignoring effects of sequence substitution in the denatured state, the free energy in Equation 4 is equal to the $\Delta \Delta \overline{G}$ value for a substitution (that is, the difference in the folding free energy between xaa and yaa at position i).

Finally, we note that an overall “sequence partition function” can be generated by multiplying the corresponding residue partition functions at each position:

$$\sigma =\prod _{i=1}^L{\rho }_i=\prod _{i=1}^L\sum _{xaa\in r}{\theta }_{i,xaa}$$ (5)

Such multiplication is appropriate, since all positions are assumed to be independent. The resulting product of L single residue partition functions contains a term for every possible sequence (a total of 20^L), and each of these is a product of the statistical weight of each residue at each position in that sequence. The largest term among these 20^L sequence weights will be the one that combines the largest θ_{i, xaa} term at each position. Each of these maximum terms corresponds to the most probable residue at each position, i.e., the consensus sequence. Thus, in an ensemble in which all L positions equilibrated simultaneously, the consensus sequence would be the most probable sequence. Moreover, since each θ_{i, xaa} term is related to the free energy through Equation 1, the maximum probability consensus sequence is the sequence with the lowest free energy residue at each position, and thus the lowest free energy overall.

2.2. A non-thermodynamic view of the multiple sequence alignment

The statistical thermodynamic treatment above makes a number of unrealistic assumptions about protein sequences. One of the most glaring assumptions is that residues are “equilibrated” across an MSA. This is clearly not the case; rather, these sequences all derive from a common ancestor⁶ and sequence differences result from mutation under selective pressure along with genetic drift, and many sequence features may be conserved due to a common origin rather than a favorable effect on stability (or fitness, more generally). Another assumption is that the variations in residue frequencies are determined by energetic terms within the native state. Although there is no doubt a strong evolutionary pressure for folding, there are additional pressures for activity, for solubility, and for turn-over. Some of these conserved features are likely to be destabilizing. For example, active site residues have been shown to decrease stability (Shoichet et al., 1995). Likewise, low stability may be beneficial for proteins that require short half-lives. And while proteins that require long half-lives (such as extracellular enzymes that function in harsh environments) may benefit from high thermodynamic stability, examples have been found where long half-life arises from kinetic (rather than thermodynamic) control (Baker et al., 1992; Jaswal et al., 2005).

3. Obtaining an MSA and determining a consensus sequence

One important but easily overlooked feature of consensus sequence design is that any consensus sequence is dependent on the MSA used to generate it, which is at best a random sample of the full biome⁷. Consensus sequences determined from MSAs that contain a small number of sequences will be highly dependent on the sequences included in the MSA, and will likely provide a poor representation of the sequence family as a whole. Consensus sequences created from large MSAs should provide better representation of the sequence family.

However, even with unlimited sequence data, several steps must be taken to edit an MSA prior to consensus sequence determination. In this section we outline strategies for collecting a set of sequences for consensus design and for editing those sequences to generate an optimal MSA. An outline of the steps in this consensus design strategy is shown in Figure 3A. Several of these steps require subjective decisions, including cutoff values for length variation, sequence identity, inserts, and gaps. Here we provide recommendations based on our own experiences, but these can be easily modified as desired.

Figure 3. Generating a consensus sequence.

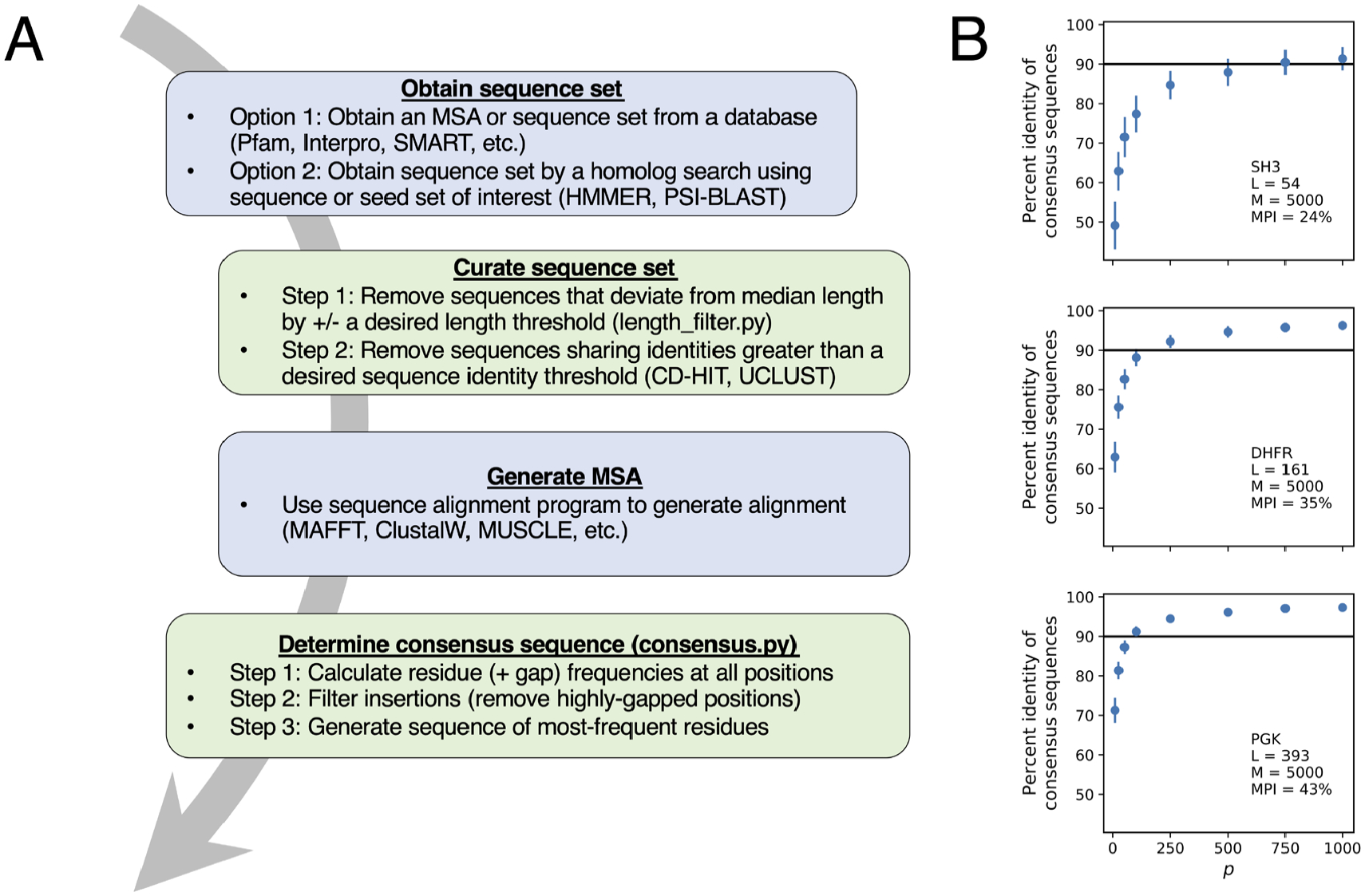
(A) Workflow for consensus sequence design. Major steps involve obtaining sequences, eliminating sequences with atypical length and high sequence identity, (re)aligning sequences, filtering gaps and insertions, and calculating residue frequencies. Examples of available databases and programs are highlighted where applicable. Green boxes contain steps that can be done using Python scripts noted in Section 3.3. (B) Identities among consensus sequences generated from random draws (sampling without replacement) of p sequences from a 5000 sequence MSA for SH3 domain (top), dihydrofolate reductase (middle), and phosphoglycerate kinase (bottom). Points represent the mean pairwise identity of 100 consensus sequences each obtained from random subsets of p sequences, and bars represent one standard deviation. Inset text indicates the length of each protein family (L), the number of sequences in each MSA (M), and the mean pairwise identity (MPI) of sequences in each 5,000 sequence MSA.

3.1. Collecting a sequence set for consensus design

Collecting a high-quality starting MSA is the most important step in obtaining a consensus sequence. There are two strategies for gathering sequences. The easiest strategy is to obtain a sequence set that already exists as an MSA from a database such as Pfam (El-Gebali et al., 2019). As of March of 2020, Pfam contained MSAs for nearly 18,000 protein families and domains. For each family, Pfam offers a small manually-curated “seed” alignment (typically on the order of 10’s or 100’s of sequences) in addition to larger but less well-curated “full” alignments (typically on the order of 1,000’s [and sometimes 10,000’s] of sequences). Other database options that often offer large sequence sets include Interpro (Mitchell et al., 2019) for protein and domain families and SMART (Letunic & Bork, 2018) for domain families only. However, the large sequence sets in these databases are unaligned; thus, an alignment must be generated by the user.

A second strategy for gathering sequences is to build an MSA from a particular query sequence or a small set of sequences using search and alignment tools such as HMMER (Finn et al., 2011) and PSI-BLAST (Altschul et al., 1997). HMMER offers customizable options to identify sequence homologs through iterative searches of various protein sequence databases, using a profile-HMM built on a user-supplied seed sequence or small sequence set. This strategy provides control over the parameters used for homolog identification that is not available when starting with a pre-aligned MSA.

Although a taxonomically broad MSA may be expected to give the best “equilibration” in sequence space, such breadth may not be ideal for all design targets. For example, if distant lineages have evolved specialized subfunctions, including all lineages may compromise activity. Indeed, Magliery and coworkers have shown that although a consensus SOD1 protein constructed from an MSA restricted to eukaryotic sequences showed near-native enzyme activity, a consensus SOD1 from an MSA with both eukaryotic and bacterial sequences had low catalytic activity (Goyal & Magliery, 2018). However, successful consensus protein designs have been created from MSAs that include all domains of life (Sternke et al., 2019; Sullivan et al., 2011) as well as MSAs restricted to a single phylogenetic clade (Goyal & Magliery, 2018; Tripp et al., 2017). The optimal taxonomic distribution of sequences for consensus design likely depends on the target and the goals of the design. Pfam, Interpro, and SMART each allow filtering sequences by specific taxa if a limited phylogenetic distribution is desired.

Relatedly, computed consensus sequences are dependent on the number of sequences in the starting alignment. For MSAs composed of a small number of sequences, the calculated residue frequency distributions are likely to be rather poor approximations of the true residue frequencies, especially at weakly conserved positions, and the resulting consensus sequence may be a poor representation of the sequence family. Large MSAs should provide a better approximation of frequencies, allowing weak conservation signals to be accurately captured in the consensus sequence. Consistent with this idea, we found that a consensus homeodomain designed from an MSA of 4,571 sequences (cHD2, see Table S1) shows an increased stability (with a decreased folding free energy of −2.7 kcal/mol) over a consensus homeodomain designed from 182 sequences (Sternke et al., 2019; Tripp et al., 2017).⁸

The number of sequences necessary to achieve a good approximation of true residue frequencies is dependent on the extent of conservation among sequences in the MSA. To illustrate this dependence, we randomly sampled subsets of sequences from 5,000 sequence MSAs that have different levels of conservation, and compared the identities of consensus sequences determined from different random samples. We find that subsets of a few hundred sequences generate consensus sequences with about 90% identity to one another, and as expected, the number of sequences necessary to achieve an average of 90% identity decreases as the average conservation among sequences within the MSA increases (Figure 3B). We see similar results if we compare consensus sequences from “synthetic” alignments where MSA sequences are generated by randomly selecting residues at each position using probabilities determined from the residue frequencies of the 5,000 sequence alignment (not shown).

Although consensus sequences are sensitive to the number of sequences used to generate residue frequencies, there are examples where stable consensus sequences have been generated from a small number of sequences. One notable example is a consensus version of a phytase enzyme, where only 13 sequences were used to generate residue frequencies. Surprisingly, the consensus phytase had an increased T_m of 16 °C (Lehmann et al., 2000). Thus, limited sequence availability for a particular protein family need not be a deterrent to attempt consensus protein design, although more sequences is probably better.

3.2. Curating a sequence set

Once a suitable set of sequences is obtained, additional curation steps are often needed to create an alignment of diverse yet non-redundant sequences. Although MSAs obtained from sequence databases can in principle be used directly for consensus sequence design without manipulation, we and others have found that even the curated alignments contain sequence truncations and highly-similar sequences that may bias the resulting consensus sequence (Sullivan et al., 2011). In our studies of consensus proteins, we apply the following steps to curate sequence sets. First, we remove sequence fragments (which often result from terminal truncations) and anomalously long sequences (often from large internal insertions). In our studies, we eliminate sequences that deviate by more than 30% from the median sequence length of the alignment. Second, we remove sequences that share high identity to avoid sequencing biases. We have used a clustering program such as CD-HIT (Li & Godzik, 2006) or UCLUST (Edgar, 2010) to cluster sequences at a 90% sequence identity threshold and choose one representative sequence per cluster for inclusion in the final MSA. An alternative strategy is to include all sequences but decrease the weight of sequences that share high identity to many other sequences in the MSA (Morcos et al., 2011; Socolich et al., 2005).

After modifications for length and identity, we generate a new alignment using a sequence alignment program such as MAFFT (Katoh et al., 2002), ClustalW (Larkin et al., 2007), or MUSCLE (Edgar, 2004). In many cases the default parameters in these alignment programs produce quality MSAs. Nonetheless, results should be visually inspected before determining consensus sequences.

3.3. Generating a consensus sequence

The first step in creating a consensus sequence from an MSA is calculating the residue (and gap) frequencies at each position. These frequencies are then used to edit the MSA one last time to eliminate rare insertions (that is, extra residues in a small number of sequences). Rare insertions in an MSA appear as a region where most sequences have a gap, leading to a gap frequency near one. For large MSAs, this occurs at a majority of positions in the alignment. To avoid including rare insertions in a consensus sequence, we eliminate all positions with gap frequencies greater than one-half, and select the most-frequent non-gap residue⁹ at all remaining positions in the MSA for the consensus sequence. Another strategy for removing insertions is to eliminate all positions where the gap frequency exceeds the frequency of the most common residue (Porebski & Buckle, 2016), which can fall below 0.5 at some positions. We find that consensus sequences generated using a gap threshold of 0.5 match more closely to the average lengths of sequences in the alignment. As a third strategy for eliminating insertions, if there is a particular extant sequence of interest in an alignment, all MSA sequences can be trimmed to include only positions occupied by residues in that particular sequence.

An attractive feature of consensus sequence design is its ease of implementation. In contrast, de novo design and directed evolution are considerably more labor intensive. For example, designing proteins using Rosetta requires considerable expertise, and can be computationally intensive. Directed evolution requires expertise in recombinant DNA and biochemistry, and depends on a biological activity that can be selected for through multiple rounds of selection and amplification. Determining a consensus sequences only requires a curated MSA and basic computer fluency. To assist interested users with the process of designing consensus sequences, we have made available basic Python scripts for cleaning and curating MSAs, calculating residue frequencies from these MSAs, and determining the consensus sequences. These scripts, including examples for how to use them, can be found on Github at: github.com/msternke/protein-consensus-sequence. As a last step in consensus design, the final MSA should be saved in a permanent record, so that sequence features that generated the consensus sequence can be evaluated at a later date. In addition, we recommend publishing the final MSA and the consensus sequence as supplementary material.

4. Survey of consensus proteins

4.1. Thermodynamic stabilities of consensus proteins

In a survey of consensus proteins in the literature, we have found 20 examples in which unique globular protein families have been targets for successful consensus protein designs using the wholesale consensus approach (Table S1), adding to the examples identified in a previous review (Porebski & Buckle, 2016). This large and growing number suggests a high success rate for wholesale consensus design, although it is hard to assess the actual success rate (success / (success + failure)) because failures are not likely to be published. The earliest example we have found is the design of a consensus zinc finger by Berg and coworkers (Desjarlais & Berg, 1993). Another early success includes a consensus phytase that has a T_m 27 °C higher than the average T_m of the extant MSA sequences (and 20 °C higher than the T_m of the most stable extant phytase measured; Lehmann et al., 2000). One surprising aspect of these studies is that they used fairly small MSAs. The consensus zinc finger sequence was determined from 131 sequences, and the consensus phytase sequence was determined from only 13 sequences. These small sequence sets, which are likely the result of the small sequence databases available at the time, are likely to provide a poor representation of true residue frequencies at positions with weak conservation.

In an attempt to see how widely applicable the consensus approach is, we designed a set of seven consensus proteins using MSAs curated as described in Section 3. In these designs, the number of sequences in each MSA ranged from 3500 to 14000. Five out of the seven resulting consensus proteins are more stable than the extant sequences that had been reported in the literature (Sternke et al., 2019), with decreased folding free energies ranging from −1.4 to −8.3 kcal/mol compared to average stabilities of extant sequences. The exceptions to this stability trend are consensus SH3 and PGK. Consensus SH3 is modestly less stable compared to typical extant SH3 domains (increased folding free energy of 0.3 kcal/mol compared to the extant mean free energy). Consensus PGK has a folding free energy nearly as low as those of the most stable extant PGK sequences, though since unfolding transitions are likely to be multistate, these free energies should be interpreted cautiously. This high level of success shows consensus design to be an effective way to stabilize a folded protein, and is significantly less labor intensive than an iterative approach using point substitutions.

Successful consensus design does not appear to be limited by size. Although some stabilized consensus designs are small proteins, such as NTL9 (L=46), albumin binding domain (L=46) and homeodomain (L=57; Jacobs et al. 2015; Tripp et al. 2017; Sternke, Tripp, and Barrick 2019) some consensus designs are quite large, such as PGK (L=392), EF-Tu (L=394), serine protease (L=396), and fungal phytase (L=476; (Cole & Gaucher, 2011; Lehmann et al., 2000; Porebski et al., 2016; Sternke et al., 2019). Thus, it does not appear that the large networks of interactions present in larger protein domains limits the consensus design approach.

In addition to globular protein targets, several repeat protein families have been the targets of consensus protein design (Table S2). Repeat proteins are particularly amenable to consensus design, given the abundance of sequence information resulting from repeating sequence elements (Aksel et al., 2011; Binz et al., 2003; Main et al., 2003; Mosavi et al., 2002; Parker et al., 2014; Parmeggiani et al., 2008). A number of consensus ankyrin and tetratricopeptide repeat proteins have been designed using MSAs of different origins and sizes; many of these (especially ankyrin repeat proteins) are considerably more stable than corresponding extant MSA proteins, with thermal unfolding midpoints ranging from 50–85 °C (Aksel et al., 2011; Binz et al., 2003; Main et al., 2003; Mosavi et al., 2002). Four-ankyrin-repeat consensus arrays have folding free energies ranging from ranging from −9.5 to −11.4 kcal/mol (Aksel et al., 2011), whereas four-repeat arrays from the Notch ankyrin domain have free energies of 0.3 and −1.8 kcal/mol (Mello & Barrick, 2004). In contrast, leucine-rich repeat and armadillo repeat arrays have proved to be more difficult targets for consensus design, exhibiting poor expression, limited solubility, molten globule characteristics, and noncooperative folding transitions

4.2. Structural features of consensus proteins

Although structural data is not available for many of the consensus proteins in Table S1, the data that is available shows that consensus proteins adopt the same folds as the extant proteins they were designed from. High-resolution crystal structures have been solved for 4 of the 20 globular consensus protein families in Table S1. For the FN3 family, structures of three different consensus sequences have been solved. These structures are all quite similar to structures of extant proteins in the same family. Interestingly, consensus proteins for which crystal structures are available tend to be on the large side, and tend to have charge densities that are closer to densities seen for extant proteins. It is possible that the high charge density of some consensus sequences (see Section 5) interferes with crystallization. In contrast, there are more crystal structures available for consensus repeat proteins; again, these proteins adopt the same structures as extant counterparts (Madhurantakam et al., 2012; Marold et al., 2015).

Though there are few crystal structures of short globular consensus proteins, these proteins tend to give high-quality NMR spectra (as do some of the larger proteins; (Sternke et al., 2019)). These include consensus HD, SH2, SH3, NTL9 (and DHFR, AK, and PGK). Analysis of backbone chemical shifts from these four proteins show that α-helices and β-strands closely match secondary structures of extant MSA sequences for which structural information is available. For consensus HD, a CS-Rosetta structure restrained with backbone chemical shifts and long-range NOEs matches the homeodomain tertiary structure, with an RMSD of 2.14 Å to the D. melanogaster engrailed homeodomain (Tripp et al., 2017).

Given that average sequence identities between consensus sequences and extant sequences in the MSA range from 40–60% (Sternke et al., 2019), the observation that consensus proteins adopt folds that are characteristic of their protein families is not a surprise. Nonetheless, the structural data confirm that consensus design faithfully generates proteins that have the intended fold.

4.3. Activities of consensus proteins

Consensus proteins have been successfully designed from protein families that display a variety of functions, including binding of proteins, peptides, and DNA, and catalysis. Several groups have used consensus proteins as scaffolds to engineer either DNA binding or protein affinity (Binz et al., 2003; Parmeggiani et al., 2008). An early study used consensus zinc fingers, varying the residues in each finger that are known to contact DNA. The consensus zinc fingers have K_D’s ranging from 11μM – 2 nM (Desjarlais & Berg, 1993). Similarly, consensus repeat proteins have been used to generate novel binding partners. These studies randomize weakly conserved surface positions to create libraries that can be selected for binding the specific targets. Plückthun and coworkers have used this approach and generated consensus ankyrin repeats that have high binding affinities, with K_D’s as low as 4.4 nM (Binz et al., 2004). This strategy makes use of the high stability of consensus repeats and the ability to change the size of the binding surface by varying the number of repeats.

In addition, several consensus proteins designed from families that bind specific ligands have been characterized, and in many cases, retain binding affinity. A consensus homeodomain was shown to bind its cognate DNA sequence with 100-fold higher affinity than a well-studied extant homeodomain (Tripp et al., 2017). A consensus albumin binding domain has been shown to bind albumin from several species with dissociation constants as high as 75 pM (Jacobs et al., 2015). These examples highlight that consensus design may be an effective route to generate tight binders to both native and novel binding partners.

In addition to binding, consensus proteins derived from enzymes have been shown to retain catalytic activity. A set of consensus chorismate mutases showed activities ranging from 2-fold higher to 30-fold lower than the extant sequence used for comparison (Jäckel et al., 2010). Interestingly, consensus β-lactamase has lower activity with penicillin but is more active with third generation antibiotics, demonstrating that the specificity of consensus proteins may differ from extant counterparts (Risso et al., 2014). Consensus DHFR, AK, and PGK all show substantial catalytic activity with K_m values similar to those of extant enzymes (Sternke et al., 2019). However, the k_cat values are lower than their mesophilic counterparts, although they are comparable or slightly lower than the thermophilic homologues. A consensus DnaE intein was shown to undergo faster splicing than the extant proteins, and was active in both high denaturant and high temperatures, unlike an extant intein (Stevens et al., 2016). Together these studies present an intriguing idea that may have industrial implications: that the consensus proteins may be a good route for obtaining proteins that are active under harsh conditions.

5. Sequence and structural features of consensus proteins

The general increased stability of consensus proteins compared to extant MSA sequences may reflect a general mechanism underlying consensus stabilization. Extant protein sequences are under selective pressure to be able to find and maintain their native-state structures in order to perform their respective functions. Finding and maintaining native-state structures requires proteins to be thermodynamically stable. Based on the statistical thermodynamic interpretation of the MSA in Section 2, such a stability requirement for evolved sequences would be expected to be imprinted in the consensus sequence. Thus, we might expect that by comparing consensus and extant protein sequences, we might be able to identify the sequence features that contribute to increased stability. Here we explore the sequence features of consensus sequences, focusing on differences between extant MSA sequences and stabilized consensus sequences derived from these MSA sequences.

5.1. Comparisons of consensus sequences to extant sequences

By definition, a consensus sequence represents the sequence that shares the highest average identity to all sequences in an MSA. The average sequence identity that a consensus sequence shares with its MSA sequences depends on sequence variation within the MSA, but for large well-sampled MSAs (composed of >1,000 extant sequences), average identities between consensus and MSA sequences typically range from 40–60% (Sternke et al., 2019). This is greater than the ~25–45% average identity that is typical of extant sequence pairs within the MSA. However, there are significant sequence differences between the consensus and the most-similar sequence in the founding MSA, with identities ranging from 65–85% (Sternke et al., 2019).

Given the high average identities of consensus sequences to their MSA sequences, it might be expected that consensus sequences have residue compositions similar to these extant sequences. Although some residues in a set of seven consensus sequences that we previously designed (Sternke et al., 2019) have similar average residue frequencies as their respective MSA sequences (e.g., arginine, tryptophan, and tyrosine), other residues have different frequencies (glutamate, lysine and glycine are enriched in the seven consensus sequences; glutamine, serine, and isoleucine are depleted).

This analysis can be extended to consensus sequences reported from other labs by comparing the residue frequencies of the consensus sequences¹⁰ to average residue frequencies from a nonredundant sampling of sequences from the PDB. To obtain this nonredundant sequence, we selected one sequence from each cluster in the weekly BLASTclust clustering of all protein chains in the PDB (accessed on 2/4/2020) at a 30% sequence identity threshold (Altschul et al., 1990). Residue frequencies in consensus sequences compared to this PDB reference set shows similar residue biases as described above (Sternke et al., 2019): consensus sequences are enriched in glutamate residues (the larger set also shows some enrichment in lysine and glycine, although these biases are quite variable), and depleted in isoleucine, methionine, asparagine, glutamine, cysteine, and serine residues (Figure 4A; again, the biases can be quite variable).

Figure 4. Features of consensus sequences.

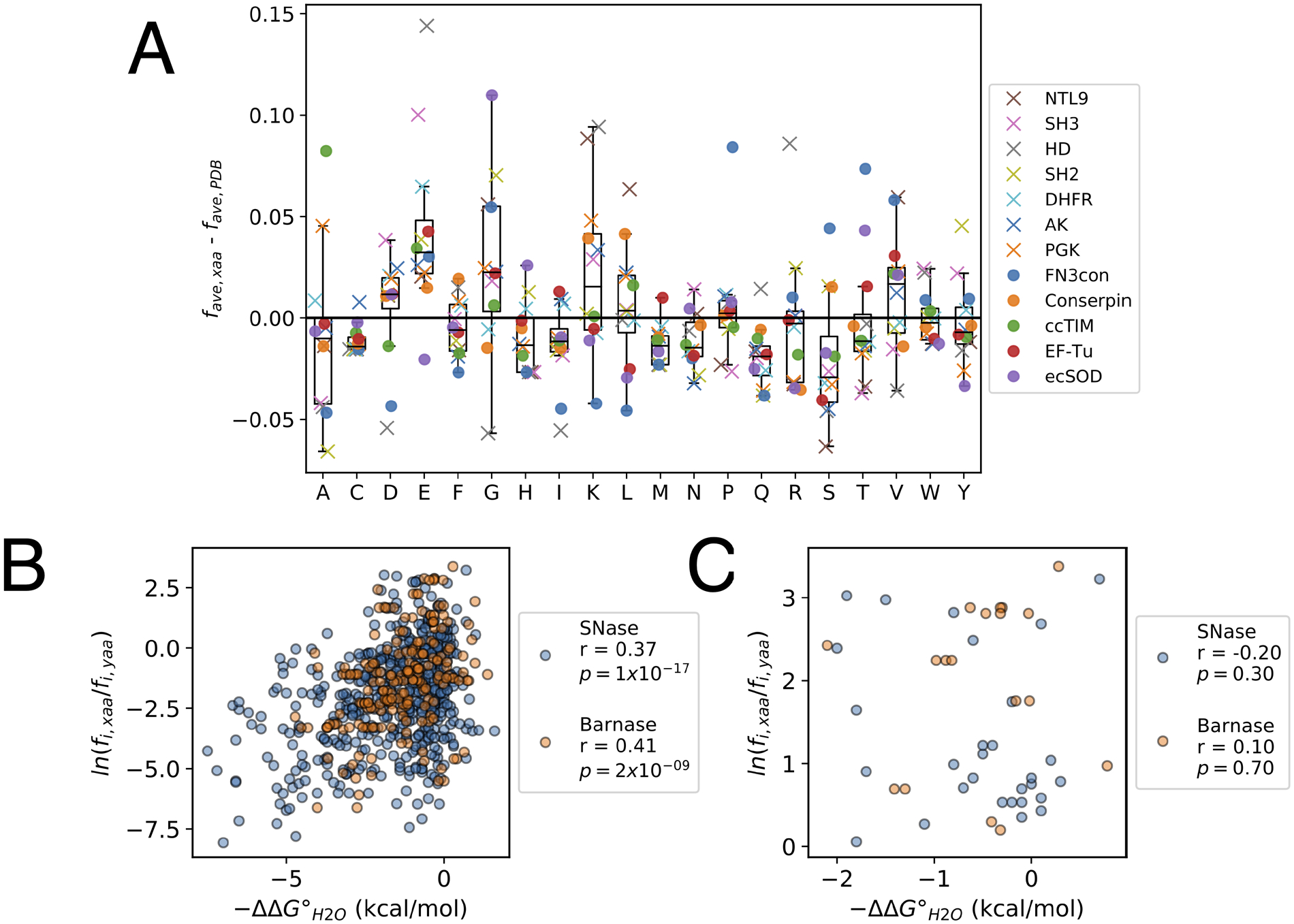
(A) Average residue frequencies in consensus compared to extant sequences. Each marker represents the difference in the average frequency of a residue in a consensus sequence from the literature (f_{avg, xaa}; obtained by dividing the number of residues of a given type by the consensus sequence length L) and the average residue frequency of the same residue among sequences obtained from a nonredundant set from the PDB (f_{avg, PDB}). X’s indicate sequences designed by our lab, circles indicate sequences designed in other labs (Table S1). The analysis above is limited to consensus sequences designed from MSAs with more than 100 sequences. The box indicates the interquartile range (IQR), the line within the box indicates the median, and the whiskers extend to the last data point within +/− 1.5*IQR. (B) and (C) Correlations between folding free energy changes (ΔΔG°_H2O) from the Protherm database and the Boltzmann-like energies for point substitutions determined from the residue frequencies in MSAs in SNase (blue, n = 514 substitutions) and Barnase (orange, n = 200 substitutions). Pearson correlation coefficients (r) and p values (p) for the correlation coefficients are shown for each distribution. Panel (B) shows all substitutions; panel (C) shows only the subset of the substitutions to consensus residues from panel B.

The individual residue enrichments and depletions are also apparent when residues with similar chemical properties are grouped. The seven consensus proteins we designed using the approach described in Section 3 (Sternke et al., 2019) are an average of two standard deviations above the mean of their MSA sequences in the total proportion of charged residues, and lie two or more standard deviations below the mean of their MSA sequences in the total proportion of polar uncharged residues. The substitutions that result in this enrichment in charged residues and depletion of polar uncharged residues occur most commonly at nonconserved positions on the protein surface (Sternke et al., 2019). We note that charge enrichment is less pronounced for consensus proteins designed by other groups. It should also be noted that some of the largest sequence biases occur in the shortest consensus proteins (e.g. HD and SH3), which is not unexpected since a single substitution generates a larger compositional change in a small protein. It remains unclear which (if any) of these composition differences contribute to the enhanced stability of consensus proteins.

As with sequence features, consensus proteins may show shared structural features that contribute to enhanced thermodynamic stability. Lehmann and coworkers report that a crystal structure of a stabilized consensus phytase shows improved hydrophobic packing in the protein core as well as stabilization of a surface loop relative to structures of less-stable natural phytases (Lehmann et al., 2000). Using ¹⁵N spin relaxation measurements by NMR spectroscopy, we found that a stabilized consensus homeodomain shows decreased dynamic motions in loop regions relative to the naturally-occurring D. melanogaster Engrailed homeodomain (Tripp et al., 2017), suggestive of a similar loop stabilization. Buckle and coworkers report that a crystal structure of a highly-stabilized consensus FN3 domain shows more hydrogen bonds and salt bridges, a smaller solvent accessible surface area, and a smaller total solvent inaccessible cavity volume than is seen in a set of less-stable natural and designed FN3 domain structures (Porebski et al., 2015). However, the crystal structure of a similarly highly-stabilized consensus serpin determined by Buckle and coworkers shows the consensus serpin shows fewer hydrogen bonds and salt bridges and a larger solvent accessible surface area than a set of less-stable natural serpins (Porebski et al., 2016). A complete understanding of how these structural features may contribute to the enhanced thermodynamic stabilities of consensus proteins will require further structural and thermodynamic studies of a broader set of consensus proteins.

5.2. Comparisons to thermophilic proteins

Like consensus proteins, proteins from thermophilic organisms have high thermodynamic stability (Hollien & Marqusee, 1999; Razvi & Scholtz, 2006). It is possible that both groups of proteins owe their high stabilities to the same compositional or structural features. Thermophilic protein sequences share some of the same residue composition biases (albeit weak ones) as consensus sequences: glutamate and lysine residues are enriched in both sets, whereas cysteine, histidine, glutamine, and serine residues are depleted (Kumar et al., 2000; Y. Li et al., 2010; Sternke et al., 2019). However, thermophilic sequences are enriched in isoleucine, arginine, and tyrosine residues, whereas consensus sequences are either depleted or show no bias for these residues.

It is possible that the partial similarities between consensus and thermophilic sequences may just result from a large number of thermophilic sequences in the starting MSAs. It is often difficult to determine whether sequences in MSAs have thermophilic versus mesophilic origins, since sequence records do not always specify the organism from which the sequence derives, and even when they do, the environmental preferences of the organism often cannot be determined. However, several highly stable consensus proteins have been derived exclusively from eukaryotic sequences (see Section 3). With just a few exceptions, eukaryotes are mesophiles (and sometimes psychrophiles). For designs from MSAs that contain sequences from thermophilic bacteria and archaea (NTL9, DHFR, AK, and PGK; Table S1), nearly identical consensus sequences (>98%) are obtained when thermophilic sequences are removed from the MSAs (Sternke et al., 2019). Thus, if similar sequence features contribute to thermodynamic stability in consensus and thermophilic proteins, these same biases must also be present (albeit to a lesser extent) in the sequence biases of mesophilic proteins.

5.3. Comparison to ancestral proteins.

Another bioinformatic approach that is similar in some ways to consensus sequence design is ancestral reconstruction, where a set of aligned extant protein sequences is analyzed to deduce a likely phylogenetic tree and the sequences of extinct ancestral proteins within the tree (Hochberg & Thornton, 2017; Merkl & Sterner, 2016; Risso et al., 2018; Wheeler et al., 2016a). It has often (but not always) been observed that ancestral proteins have higher stabilities than extant proteins. For example, a comparison of ancestral β-lactamases with consensus proteins from the same sequence alignments showed higher stabilities for the ancestors than for the consensus proteins, though all were more stable than the extant TEM-1 β-lactamase (Risso et al., 2014). Although all enzymes showed reduced activities towards benzylpenicillin, the ancestors showed increased activities for third-generation antibiotics; one of the consensus proteins showed modest activity increases towards these antibiotics, whereas another did not. Likewise, ancestral DNA gyrases were shown to be more stable than a consensus gyrase and to have higher activity (Satoshi Akanuma et al., 2011). In contrast, a consensus L-threonine 3-dehydrogenase was found to be more stable than the corresponding ancestral version, with both enzymes showing high levels of activity (Nakano et al., 2018). An ancestral nucleotide diphosphate kinase was shown to be more stable than a consensus enzyme from the same set of sequences (S. Akanuma et al., 2013), and two out of three ancestral Ef-TU proteins were shown to be more stable than a consensus Ef-TU (Okafor et al., 2018). A study of ancestral RNaseH proteins showed a deep ancestor that is more stable than mesophilic sequences in the starting alignment, but less stable than thermophilic sequences (Wheeler et al., 2016b).

Though these studies show that ancestral proteins are more often more stable than consensus versions, it is clear that both methods usually lead to increased stability. One simple explanation for the success of both methods is that ancestral and consensus sequences look alike. This similarity is not surprising since both methods extract sequences from a multiple sequence alignment. Tawfik and coworkers have argued that consensus information may be overrepresented in ancestral reconstruction, although this only partly explains the stability enhancement of ancestral sequences (Trudeau et al., 2016). One possible explanation for the increased stability of a majority of ancestral proteins compared to consensus proteins is that ancestral reconstruction is more likely to capture stabilizing coupling between nearby residues (S. Akanuma et al., 2013).

5.4. Correlations of residue frequencies with effects on stability

In the statistical thermodynamic framework presented in Section 2, residue frequencies at each position of an MSA represent equilibrium populations within an ensemble and thus are related to the energies of the residues in the protein native state. As such, substitutions to residues of higher frequency should be stabilizing, whereas substitutions to residues of lower frequency should be destabilizing (Equation 4). Indeed, some studies have found that stability changes resulting from point-substitution are partially correlated with residue conservation (Amin et al., 2004; Di Nardo et al., 2003; Loening et al., 2006; Nikolova et al., 1998; Polizzi et al., 2006; Steipe et al., 1994; Wang et al., 1999), although some of these correlations involve a rather small data set.

To examine the extent of this correlation on a broader scale, we surveyed the ProTherm database (Gromiha et al., 1999) to find proteins where a large number of stability changes resulting from point substitutions have been reported, and where large MSAs could be obtained. The two proteins that best satisfy these criteria are Staphylococcal nuclease (SNase; 514 point substitutions) and Barnase (200 point substitutions). We compared the effects of point substitutions on folding free energies (ΔΔG°_H2O) to the log ratio of the residue frequencies that define the point substitution, ln(f_i,xaa/f_i,yaa). Within the framework of the statistical thermodynamic model, this log ratio should be proportional to the free energy difference between the two residues xaa and yaa at position i (see Section 2).

Contrary to expectation, neither protein shows a strong correlation between the stability changes resulting from point substitution and residue frequencies (Figure 4B). Although for SNase substitutions to residues of higher frequencies are stabilizing more often than substitutions to residues of lower frequencies (18% of substitutions compared to 8%), for Barnase substitutions to residues of higher frequencies and substitutions to residues of lower frequencies show similar effects on stability (12% of substitutions compared to 11%). In short, the majority of substitutions towards residues of higher frequencies are destabilizing for both proteins. Furthermore, restricting this analysis to substitutions to consensus residues (substitutions to the residue of greatest frequency at a given position) gives an even weaker correlations (Figure 4C); as with the larger data set, only a minority of these substitutions are stabilizing (21% and 11% for SNase and Barnase). This analysis indicates that at a given position, substitution toward consensus should be destabilizing more frequently than it is stabilizing.

The lack of correlation between residue conservation and effects of point-substitution on stability for SNase and Barnase is inconsistent with the high thermodynamic stability of consensus proteins (Table S1). Although the publication process may impart some bias toward consensus sequence stabilization in the literature (unstable consensus proteins will be likely to be unfolded and unpublishable), an unbiased test of consensus design on seven targets resulted in stability increases in five cases (Sternke et al., 2019), and all seven proteins well-folded. This observation suggests that the success of consensus design in generating proteins with high stability is not primarily a result of publication filter.

The discrepancy between the stability changes associated with point substitutions and wholesale consensus substitution is striking and is worthy of further study. One possible (though speculative) explanation is that the consensus stability increment is a collective feature of all (or at least a subset of) consensus substitutions, and cannot be attributed to individual substitutions in an extant sequence background. Consistent with this explanation, Magliery and coworkers showed that stability changes resulting from single substitutions toward consensus differ qualitatively from stability changes when those substitutions are combined (Sullivan et al., 2012b). Specifically, TIM constructs that combine 6 and 13 substitutions toward consensus (plus an additional compensatory substitution) were both destabilized compared to the expected summed effect from the individual substitutions. Although this difference goes the opposite direction to the proposed explanation for the ΔΔG values in Figure 4 (where DDG values are mostly destabilizing, and the consensus is assumed to be stabilized¹¹), it does demonstrate non-additivity. In some of these cases, evaluation of pairwise sequence correlations showed that destabilizing substitutions toward consensus often show strong coupling with neighboring residues (Sullivan et al., 2012a). An additional testing for this type of synergistic effect could involve large-scale studies of substitutions that traverse sequence space between extant MSA sequences and stabilized consensus sequences via different paths. In addition to resolving the above discrepancy, it is expected that such studies will provide insight into which types of substitutions result in consensus stabilization. These insights might be used to increase protein stability using a relatively small number of substitutions.

6. Summary and open questions

As numerous studies now show, consensus design provides a simple strategy to make proteins that are folded and active, and in many cases show significantly increased stability compared to the extant protein sequences from which they are derived. The increase in stability is consistent with a statistical thermodynamic framework for protein sequence families, although that framework seems at odds with data from point substitutions which show little correlation between residue conservation and stability.

The origins of increased stability in consensus proteins remains an open question; answering this question may provide a route to selectively stabilizing proteins with fewer sequence substitutions than are typically made in a wholesale consensus substitution. The possibility that the consensus stability increment results from nonadditive interactions involving groups of residues is consistent with the discrepancy with the point substitution results, and is worth testing by comparing different paths through sequence space from extant to consensus proteins. If synergy among groups of residues is in fact responsible for consensus stabilization, patterns deduced from covariance analysis within the MSA may provide a route to further stabilization.