Molecular radiative energy shifts under strong oscillating fields

Abstract

Coherent manipulation of light-matter interactions is pivotal to the advancement of nanophotonics. Conventionally, the non-resonant optical Stark effect is harnessed for band engineering by intense laser pumping. However, this method is hindered by the transient Stark shifts and the high-energy laser pumping which, by itself, is precluded as a nanoscale optical source due to light diffraction. As an analog of photons in a laser, surface plasmons are uniquely positioned to coherently interact with matter through near-field coupling, thereby, providing a potential source of electric fields. Herein, we report the first demonstration of plasmonic Stark effect and attribute it to a newly uncovered energy-bending mechanism. As a complementary approach to the optical Stark effect, we envision the plasmonic Stark effect will advance fundamental understanding of coherent light-matter interactions and will also provide new opportunities for advanced optoelectronic tools, such as ultrafast all-optical switches and biological nanoprobes at lower light power levels.

Graphical Abstract

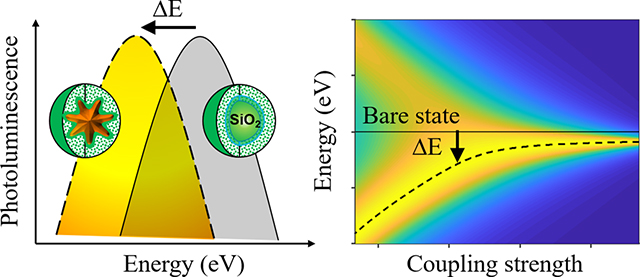
This study presents discovery and mechanistic elucidation of the plasmonic Stark effect. As opposed to the transient optical Stark effect achieved under intense laser pumping, the plasmonic Stark effect renders permanent energy-level modification with the in-built plasmonic field. This discovery paves the way for advanced optoelectronic tools such as ultrafast all-optical switches and biological nanoprobes using lower excitation energies.

1. Introduction

Light-matter interactions are central to nanophotonic phenomena. In a cavity quantum electrodynamic (QED) system, the interplay between Rabi oscillation and energy decay defines two fundamental coupling mechanisms, that is weak and strong coupling.^1–3 While the maximum coupling strength is achieved in the resonant limit, the non-resonant excitation results in the distinct optical Stark effect (OSE) that is fundamental to coherent light-matter interactions.^4–10 As a nonlinear effect, OSE is manifested as the transient perturbation to energy levels under non-resonant laser pumping. Harnessing the unique properties of OSE enables coherent manipulation of hybrid states by ultrafast all-optical tuning, as has been demonstrated in monolayer transition metal dichalcogenides,^{7, 9–10} perovskite thin films,⁸ and quantum dots^4–5 among others. However, the occurrence of OSE is strongly dependent on the laser pumping. The induced transient energy-level shifts disappear shortly after relaxation of the excited states. Degradation of materials occurs under prolonged laser illumination due to heating and excessive band filling. The intrinsic light diffraction also precludes the use of laser as a source of optical energy concentrated in the nanoscale. Therefore, it is desirable to explore coherent, intense, and ultrafast optically induced sources that offer alternatives to a laser for producing confined electric fields to study light-matter interactions.

Surface plasmons (SPs) present a potentially promising solution. With their remarkable capabilities to confine electromagnetic radiations into the nanoscale far below the diffraction limit of light in the form of collective charge oscillations, SPs exhibit extraordinary coherence, ultrafast dynamics, a large dipole moment, and an ultrasmall mode volume that is particularly suited for near-field coupling to quantum emitters (QEs), such as semiconductor quantum dots and organic dyes.^11–15 Notably, SPs display bosonic behaviors just as photons do.¹¹ Such salient features have been recently leveraged for developing a nanoscale optical source named SPASER, which is the plasmonic counterpart of laser.^16–19 Successful demonstration of SPASER highlights the promise of SPs to work in an analogous manner to photons in a laser. Indeed, analogous to light-matter interactions, coherent plasmon-QEs interactions in a plasmonic cavity lead to the formation of entangled plasmon-exciton states, often referred to as plexcitons.²⁰ In the strong-coupling regime, the plexcitonic states display similar energy-splitting and anti-crossing behaviors that have become the driving force for studying single-molecule strong coupling at room temperature^{12, 21–22}, vibro-polariton coupling^23–24, and quantum plasmonic biosensing²⁵, supported by the broad availability and wide spectral tunability of SPs on a plethora of gold and silver nanostructures.^26–28 Yet, employing SPs as an alternative to optical sources to engineer plexcitonic energy levels in a manner analogous to OSE has not been reported before.

In this study, we create a pair of contrived systems, and demonstrate, for the first time, the plasmonic counterpart of optical Stark effect, by measuring the photoluminescence (PL) spectra of organic dyes under laser pumping and the plasmonic field, respectively. We first invoke the Jaynes-Cummings model^2–3 to lay out the theoretical framework for the optical Stark effect. To investigate coherent interactions between surface plasmon and QEs, we phenomenologically incorporated the energy dissipation rates into the Hamiltonian matrix for the coupled plasmon-QEs system. Our analysis implies that, in addition to the extensively studied strong-coupling regime where the energy-splitting occurs, there is a region where the plexcitonic energy levels repulse and bend outward from the bare states for both surface plasmons and QEs. This newly uncovered energy-bending mechanism is responsible for the observed molecular energy shifts under the plasmonic field. Given the rapid advancement in materials fabrication, we envision that our successful demonstration of the plasmonic analog of optical Stark effect will create new opportunities to engineer nanoscale optoelectronic devices by leveraging the unique features of surface plasmons.

2. Results and Discussion

2.1. Observation of molecular radiative energy shifts

In the first place, we unambiguously demonstrate OSE by studying the PL spectral profiles of free dyes. In Fig. 1(a), we observed that the PL spectra of Cy7 in dimethylformamide (DMF) under pulsed laser pumping (with an excitation wavelength of 680 nm, a pulse repetition rate of 20 Hz, a pulse duration of ~6 ns, and an energy density of about 30 mJ/cm²) underwent a radiative energy shift of ΔE = 7 meV when compared to that under continuous illumination of a monochromatic light at 680 nm with a power density of ~0.5 mW/cm². We attribute this effect to laser-induced perturbation to molecular energy levels as the laser pumping generates a strong oscillating electric field and thereby enables coherent atom-field interaction. In equilibrium, dye molecules can be approximated as a two-level atomic system with the ground |g⟩ and excited |e⟩ states separated by a transition energy of ω₀. The pulsed laser is modeled as a strong oscillating bosonic field with a frequency of ω_b, as shown in Fig. 1(b). Periodic in time, the Floquet Hamiltonian for the coupled atom-field system exhibits a periodic structure that permits quasi-static eigenstates evenly spaced in energy units of the bosonic field.²⁹ The atom can either absorb from the ground state or emit from the excited state an integer number n of bosons, forming quasi-static Floquet states |g + nω_b⟩ and |e − nω_b⟩, as shown schematically for the first-order Floquet states in Fig. 1 (c). As a result, the interaction between the Floquet and equilibrium states repulses the energy levels and contributes to the observed molecular radiative energy shifts.

Figure 1. Observation of molecular radiative energy shifts.

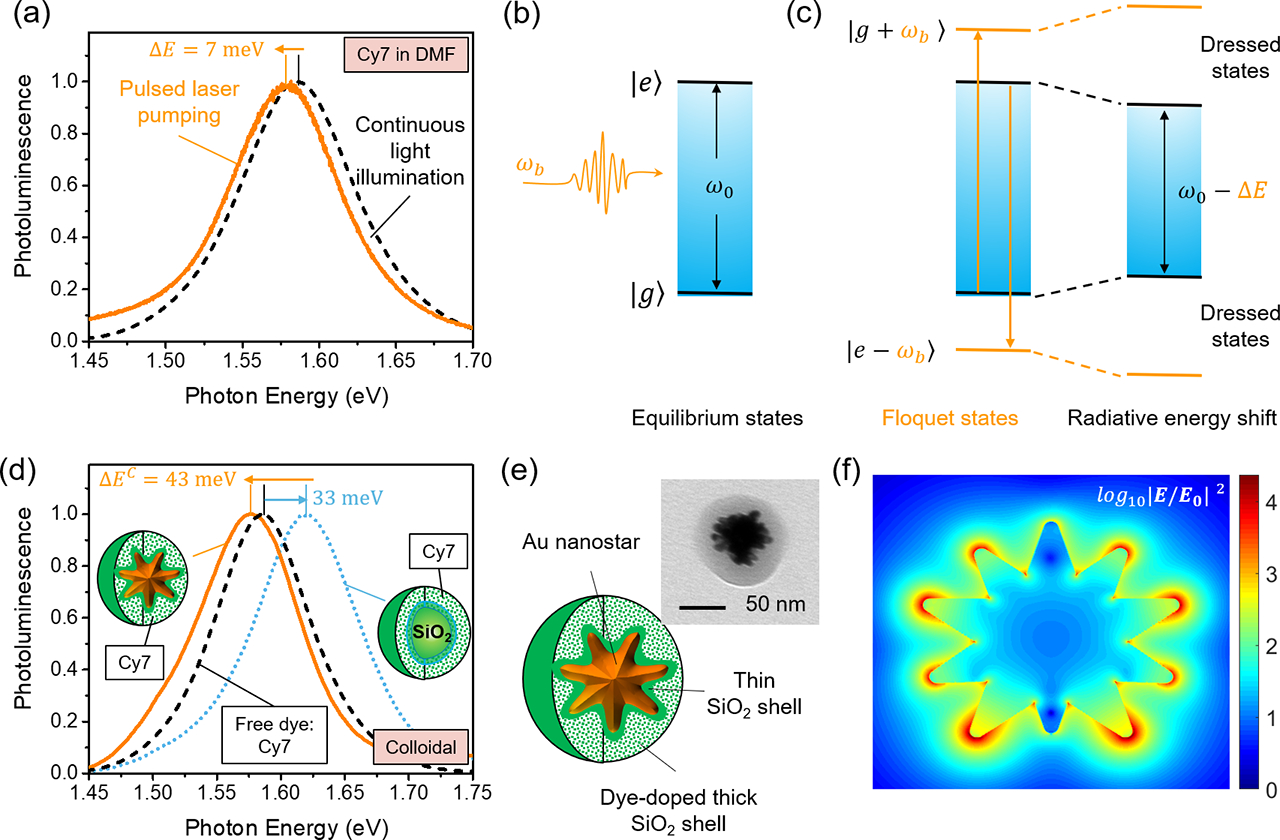
(a) Observation of radiative energy shift (ΔE = 7 meV) of Cy7 dye spectral profiles in dimethylformamide (DMF) under pulsed laser pumping (with an excitation wavelength of 680 nm, a pulse repetition rate of 20 Hz, a pulse duration of ~6 ns, and an energy density of about 30 mJ/cm2) when compared to that under continuous illumination of a monochromatic light at 680 nm with a power density of ~0.5 mW/cm2. (b) Schematic of an oscillating bosonic field with an oscillating frequency of ω_b and a two-level |g⟩ and |e⟩ atomic system in the equilibrium states with a transition frequency of ω₀. (c) Coherent coupling between the equilibrium atomic states |g⟩ and |e⟩ with the Floquet states |e − ω_b⟩ and |g + ω_b⟩ that contributes to energy shift. (d) Observation of radiative energy shift (ΔE^C = 43 meV) for the spectral profiles of an optical nanoprobe made of colloidal Au nanostar@thin-SiO2@Cy7-SiO2 as compared to the control sample made of colloidal SiO2@thin-SiO2@Cy7-SiO2. The SiO2 core nanoparticle has a similar mean diameter of 60 nm as the Au nanostar. It is noted that there is a radiative energy blue shift of 33 meV for the spectral profiles of the Cy7 molecule after it was made into the colloidal SiO2@thin-SiO2@Cy7-SiO2 nanoparticles. (e) Schematic of the optical nanoprobe: Au nanostar@thin-SiO2@dye-SiO2 core-shell (the inset shows a representative TEM image); (f) The electric field distribution averaged from two orthogonal polarizations perpendicular to the shown cross section for a single gold nanostar calculated by finite-difference time-domain (FDTD) simulations at the peak plasmon resonance wavelength.

Intriguingly, we observed similar molecular radiative energy shifts when the laser field was replaced with a plasmonic field. Under the continuous illumination of a monochromatic light at 680 nm with a power density of ~0.5 mW/cm², we observed a radiative energy shift of ΔE^C = 43 meV for the PL spectral profiles of colloidal Au nanostar@thin-SiO₂@Cy7-SiO₂ nanoparticles in water when compared to the control sample SiO₂@Cy7-SiO₂ which are also dissolved in water, as shown in Fig. 1(d). The structure and representative TEM image for Au nanostar@thin-SiO₂@dye-SiO₂ are shown in Fig. 1(e); the absorption spectrum for colloidal Au nanostars is shown in Fig. S1(a). To highlight the similarity of the strong oscillating electric fields produced by the laser field and the plasmonic field, we simulated the local electric field enhancement at the peak plasmon wavelength (Fig. S1(b)) and presented it in Fig. 1(f).

While local thermal effect may be generated as a result of the plasmon dephasing, it only opens additional non-radiative energy decay channels by either dynamic quenching (increased collisions among molecules) or intersystem crossing (singlet to triplet transition for the excited states), thereby solely affecting the PL intensity rather than shifting the radiative energy.^30–31 Any possible role hot carriers may have played is also eliminated by the presence of the thin SiO₂ insulating layer (ca. 2–3 nm).

We also observe that the control sample SiO₂@dye-SiO₂ exhibits an energy blueshift when compared to the free dyes in DMF. Such a blueshift arises from the inhibition of the solvation dynamics. For free dyes in DMF, after excitation, the dye molecules and the solvent dipole are not in equilibrium. The solvent dipole would rotate to align with the dye molecules, reducing their interaction energy and lowering the energy of the excited dye molecules.³² However, after the dyes are embedded into the SiO₂ shell that is encapsulated onto the SiO₂ core nanoparticles, the solvation process is significantly hindered, thereby, contributing to the observed blueshift.

2.2. Ubiquitous molecular radiative energy shifts in diverse colloidal plasmon-QEs systems

In order to validate the ubiquity of the above experimental observations in Fig. 1, we measured the PL spectral profiles for various other dyes in DMF, including Cy7.5, DyLight800, and IR-140, using the pulsed laser pumping and continuous illumination under the same conditions as in Fig. 1. Similar molecular radiative energy shifts were seen in Fig. 2(a)–(b) and Fig. S2. Likewise, we also observed molecular radiative energy shifts in other colloidal plasmon-QEs systems in water for the PL spectral profiles of Au nanostar@thin-SiO2@Cy7.5-SiO2 nanoparticles and Au nanorod@thin-SiO2@Cy7.5-SiO2 nanoparticles when compared to the control sample made of colloidal SiO2@Cy7.5-SiO2 nanoparticle in water, seen in Fig. 2(c)–(d). Despite being of varying magnitudes, the observed molecular radiative energy shifts present themselves as a general phenomenon independent of the type of organic dyes or the shape of plasmonic metallic nanoparticles, further underscoring the analog of the strong oscillating fields generated by the pulsed laser pumping and SPs.

Figure 2. Ubiquitous molecular radiative energy shifts in diverse colloidal plasmon-QEs systems.

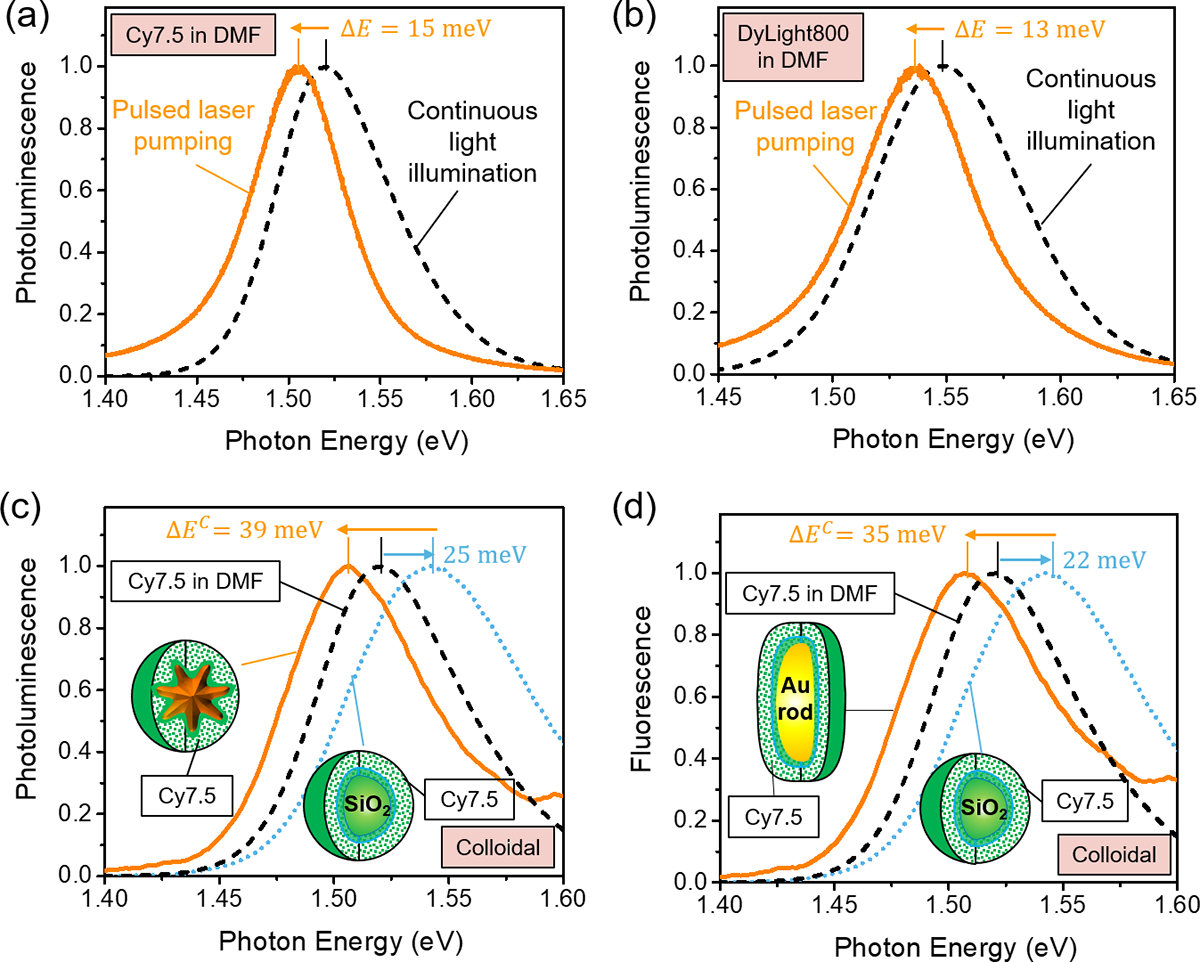
Similar molecular radiative energy shifts for free dyes were demonstrated under pulsed laser pumping in (a) Cy7.5 dyes in DMF ((ΔE = 15 meV) and (b) DyLight 800 dyes in DMF ((ΔE = 13 meV) when compared to under continuous illumination, which were measured under the same condition as in Fig. 1(a). Also demonstrated were the molecule radiative energy shifts in the colloidal plasmon-QEs systems in water (c) for an optical nanoprobe made of colloidal Au nanostar@thin-SiO2@Cy7.5-SiO2 and (d) for an optical nanoprobe made of colloidal Au nanorod@thin-SiO2@Cy7.5-SiO2 as compared to the control sample made of colloidal SiO2@thin-SiO2@Cy7.5-SiO2 under the same experimental condition as in Fig. 1(d).

2.3. Molecular radiative energy shifts in the plasmon-QEs systems under dried condition

In order to eliminate any possible influence of the polarity-dependent solvation processes on the PL spectral profiles, we further conducted PL measurements under dried condition for Au nanostar@thin-SiO₂@Cy7-SiO₂ and Au nanostar@thin-SiO2@Cy7.5-SiO2 using an XploRA PLUS Raman microscope (HORIBA Instruments Inc., Edison, NJ, USA) under a 638 nm diode laser with a power of ~ 1 mW. Compared to the respective control sample made of SiO₂@thin-SiO₂@Cy7-SiO₂ and SiO₂@thin-SiO2@Cy7.5-SiO2, unequivocal molecular radiative energy shifts were also observed that bear a resemblance to observations made in Fig. 1(d) and Fig. 2(c)–(d). The above demonstrations in diverse plasmon-QEs systems and dielectric environments further underscore the ubiquity of perturbation to the molecular radiative energy levels under strong oscillation fields.

It is worth noting that colloidal nanoparticles with similar core-shell nanostructures have been widely explored as optical nanoprobes^33–34 and nanoscale lasers^{16–19, 35}. Similar phenomena of molecular radiative energy shifts of various magnitudes can be found in relevant literature reports but have not been thoroughly investigated, as the focus was primarily on the radiative emission intensity modification.^36–38 Hence, the possibility of plasmon-induced changes in the radiative energy have been surprisingly underappreciated. Given the striking similarity between the laser-induced and plasmon-induced radiative energy shifts, the perturbation to the energy levels observed in optical nanoprobes could be similarly understood in the framework of the coherent atom-field interaction. The calculated intense local electric fields seen in Fig. 1(f) highlight the analogous role of laser and SPs, even though the strong energy dissipation in metallic plasmonic systems complicates plasmon-QEs interactions.

2.4. Analysis of the coupled atom-field system by the Jaynes-Cummings model

In order to understand the mechanism that governs the shifts in the PL spectral profiles for free dyes under pulsed laser pumping, we invoke the Jaynes-Cummings model to study the coupled atom-field system. In this case, we start by considering that no energy dissipation is involved. Under the rotating wave approximation, the total Hamiltonian for the coupled atom-field system can be written as¹

$$\widehat{H}={\omega }_b{\widehat{b}}^{†}\widehat{b}+{\omega }_0{\widehat{\sigma }}_z+\lambda ({\widehat{\sigma }}_{+}\widehat{b}+{\widehat{\sigma }}_{-}{\widehat{b}}^{†})$$ (1)

where ${\omega }_b{\widehat{b}}^{†}\widehat{b}$ is the Hamiltonian for the quantized bosonic field with an oscillating frequency of ω_b. ${\widehat{b}}^{†}$ and $\widehat{b}$ are the bosonic creation and annihilation operators. ${\omega }_0{\widehat{\sigma }}_z$ is the Hamiltonian for the two-level system with a transition energy of ω₀. $\lambda ({\widehat{\sigma }}_{+}\widehat{b}+{\widehat{\sigma }}_{-}{\widehat{b}}^{†})$ is the atom-field interaction Hamiltonian with a coupling strength of λ, twice of which is the Rabi frequency (ω_R = 2λ). The energy detuning is defined as Δ = ω₀ − ω_b. The operator ${\widehat{\sigma }}_{+}\widehat{b}$ corresponds to the atomic transition from the ground state |g⟩ to the excited state |e⟩ by annihilating (absorbing) a boson; ${\widehat{\sigma }}_{-}{\widehat{b}}^{†}$ is the opposite process accounting for the atomic relaxation from the excited |e⟩ to the ground state |g⟩, which ends up creating (emitting) a boson.

In the non-interacting limit (λ → 0), only bare states |e,n⟩ and |g,n + 1⟩ exist, as shown in Fig. 4. The energy eigenvalues are simply the sum of the atom-field energy levels: ${\widehat{H}}_0|e,n⟩=(\frac{1}{2}{\omega }_0+{\omega }_{b}n)|e,n⟩$ and ${\widehat{H}}_0|g,n+1⟩=(-\frac{1}{2}{\omega }_0+{\omega }_b(n+1))|g,n+1⟩$. Their energy difference is exactly the energy detuning Δ. After incorporating the atom-field interaction Hamiltonian ${\widehat{H}}_I=\lambda ({\widehat{\sigma }}_{+}\widehat{b}+{\widehat{\sigma }}_{-}{\widehat{b}}^{†})$, new dynamics are enabled which, however, is also constrained by the selection rule imposed by the interaction Hamiltonian. The only allowed transitions occur between the states |ψ_1n = |e,n⟩ and |ψ_2n = |g,n + 1⟩, where either the excited-state atom relaxes to the ground state by emitting a boson or the ground-state atom becomes excited by absorbing a boson. The Hamiltonian matrix can thus be constructed as

$$H=\left[\begin{array}{cc}{\omega }_0/2+{\omega }_{b}n& \lambda \sqrt{n+1}\\ \lambda \sqrt{n+1}& -{\omega }_0/2+{\omega }_b(n+1)\end{array}\right]$$ (2)

Figure 4. Energy splitting and bending behaviors for the coupled atom-field system.

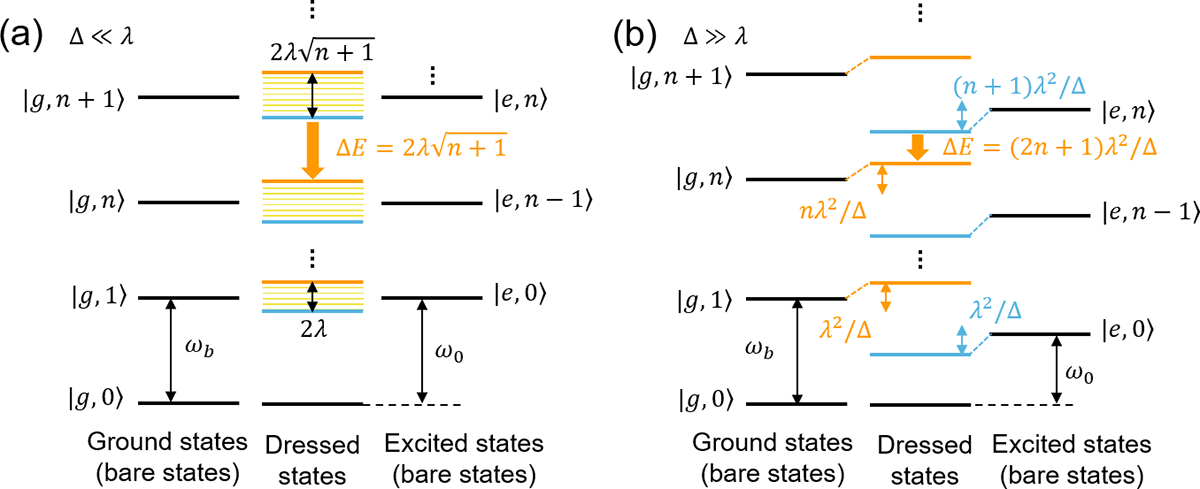
(a) Energy diagram of the bare (left: ground atomic state; right: excited atomic state) and dressed (center) states in the resonant limit (Δ ≪ λ). The dressed states undergo a Rabi splitting of $2\lambda \sqrt{n+1}$ of with n bosons in the excited atomic states, resulting in an energy shift of $\mathrm{\Delta }E=2g\sqrt{n+1}$. When the coupling strength is not very strong, the dressed energy levels could become broadened and even obscure the splitting (marked as fine yellow lines in the interior of the dressed states) given the finite lifetime of the atom-field system owing to the Heisenberg uncertainty relationship between energy and time. (b) In the dispersive limit (Δ ≫ λ), the ground |0,n⟩ and excited |1,n⟩ bare states with n bosons undergo an energy shift of nλ²/Δ and (n + 1)λ²/Δ, resulting in an energy shift of ΔE = (2n + 1)λ²/Δ.

By diagonalizing the Hamiltonian matrix in eq. (2), the energy eigenvalues for the two dressed states are obtained as $E_{n,\pm }={\omega }_b(n+1/2)\pm \sqrt{4{\lambda }^2(n+1)+{\mathrm{\Delta }}^2}/2$, which are separated by the generalized Rabi frequency ${\mathrm{\Omega }}_R=\sqrt{4(n+1){\lambda }^2+{\mathrm{\Delta }}^2}$. By comparing the dressed to the bare states, the energy shift can be obtained as

$$\mathrm{\Delta }E=\sqrt{4(n+1){\lambda }^2+{\mathrm{\Delta }}^2}-\mathrm{\Delta }.$$ (3)

In the resonant limit (Δ ≪ λ), the energy shift is approximated as the Rabi splitting of the dressed states: $\mathrm{\Delta }E\approx 2\lambda \sqrt{n+1}={\omega }_R$, as shown in Fig. 4(a). In the dispersive limit (Δ ≫ λ), the energy shift can be approximated by expanding ΔE to the second order in $\lambda /\mathrm{\Delta }:{\mathrm{\Delta }E}_{\mathrm{\Delta }\gg \lambda }=2(n+1){\lambda }^2/\mathrm{\Delta }=2{\lambda }_{eff}^2/\mathrm{\Delta }$, where λ_eff is the effective coupling strength. Such a non-resonant energy shift is attributable to the energy-level bending of the bare states seen in Fig. 4(b) and is the origin of the OSE seen in Fig. 1(a) for free dyes under laser pumping.

On the other hand, following the Hamiltonian treatment in circuit QED,^39–40 we conducted unitary transformation of the form $U=\mathrm{e}\mathrm{x}\mathrm{p}[\lambda ({\widehat{\sigma }}_{+}\widehat{b}-{\widehat{\sigma }}_{-}{\widehat{b}}^{†})/\mathrm{\Delta }]$ for the total Hamiltonian $\widehat{H}$ and expanded it to the second order in λ/Δ. The transformed Hamiltonian was obtained as: $UH{U}^{†}={\omega }_b{\widehat{b}}^{†}\widehat{b}+{[\omega }_0{+(2{\lambda }^2/\mathrm{\Delta }{)\widehat{b}}^{†}\widehat{b}+{\lambda }^2/\mathrm{\Delta }]\widehat{\sigma }}_z$. This suggests that the atomic transition undergoes an energy-level shift that consists of two parts: the first part $2n{\lambda }^2/\mathrm{\Delta }$ is the bosonic number-dependent OSE, which is the same as the result obtained in the dispersive limit by expanding ΔE to the second order in λ/Δ; the second part λ²/Δ is the Lamb shift, which is induced by vacuum energy fluctuations owing to virtual photons being created and annihilated in the atom-field interacting system regardless of the bosonic number states. The Lamb shift, however, is challenging to be discerned, as the required precision for measuring such tiny energy level shift is orders of magnitude smaller than that for the spectral linewidth broadening, and thereby, it is often negligible outside the field of atomic physics. In the limit of n ≫ 1 which is the case for the laser pumping, the Lamb shift is absorbed into the optical Stark shift, and thus recovering the OSE ${\mathrm{\Delta }E}_{\mathrm{\Delta }\gg \lambda }=2{\lambda }_{eff}^2/\mathrm{\Delta }$, further validating the origin of energy shifts attributable to the energy-bending effect. Based on eq. (3), we also calculated the effective coupling strength λ_eff using the fitting parameters from the measured PL spectra as summarized in Table 1.

Table 1.

Radiative transitions (ω₀, ${\omega }_0^{\mathrm{\prime }}$) for different dyes in DMF under the continuous light illumination and the pulsed laser pumping. The effective coupling strength was calculated based on eq. (3).

Free dyes in DMF	Continuous illumination	Pulsed laser pumping	Observed energy shift (meV)	Calculated λeff,meV
	ω0, eV	${\omega }_0^{\mathrm{\prime }},\mathrm{e}\mathrm{V}$	${{\Delta \omega }_0=\omega }_0^{\mathrm{\prime }}-{\omega }_0$
Cy7	1.586	1.579	−7	29
Cy7.5	1.521	1.506	−15	48
Dylight800	1.549	1.536	−13	43
IR-140	1.485	1.432	−53	98

2.5. Analysis of the coupled plasmon-QEs systems with energy dissipations

To further unveil the mechanism responsible for the observed radiative energy shifts under the plasmonic field, we turn to QED and phenomenologically incorporate the dissipation rates γ₀ for the two-level atomic system representing QEs (i.e. dyes) and γ_b for the plasmonic cavity into the system, as shown in Fig. 5(a). The Hamiltonian matrix for the coupled plasmon-QEs system is created as

$$H=\left[\begin{array}{cc}{\omega }_0-i{\gamma }_0& \lambda \\ \lambda & {\omega }_b-i{\gamma }_b\end{array}\right]$$ (4)

Figure 5. Energy splitting and bending behaviors for the coupled plasmon-QEs system with dissipation.

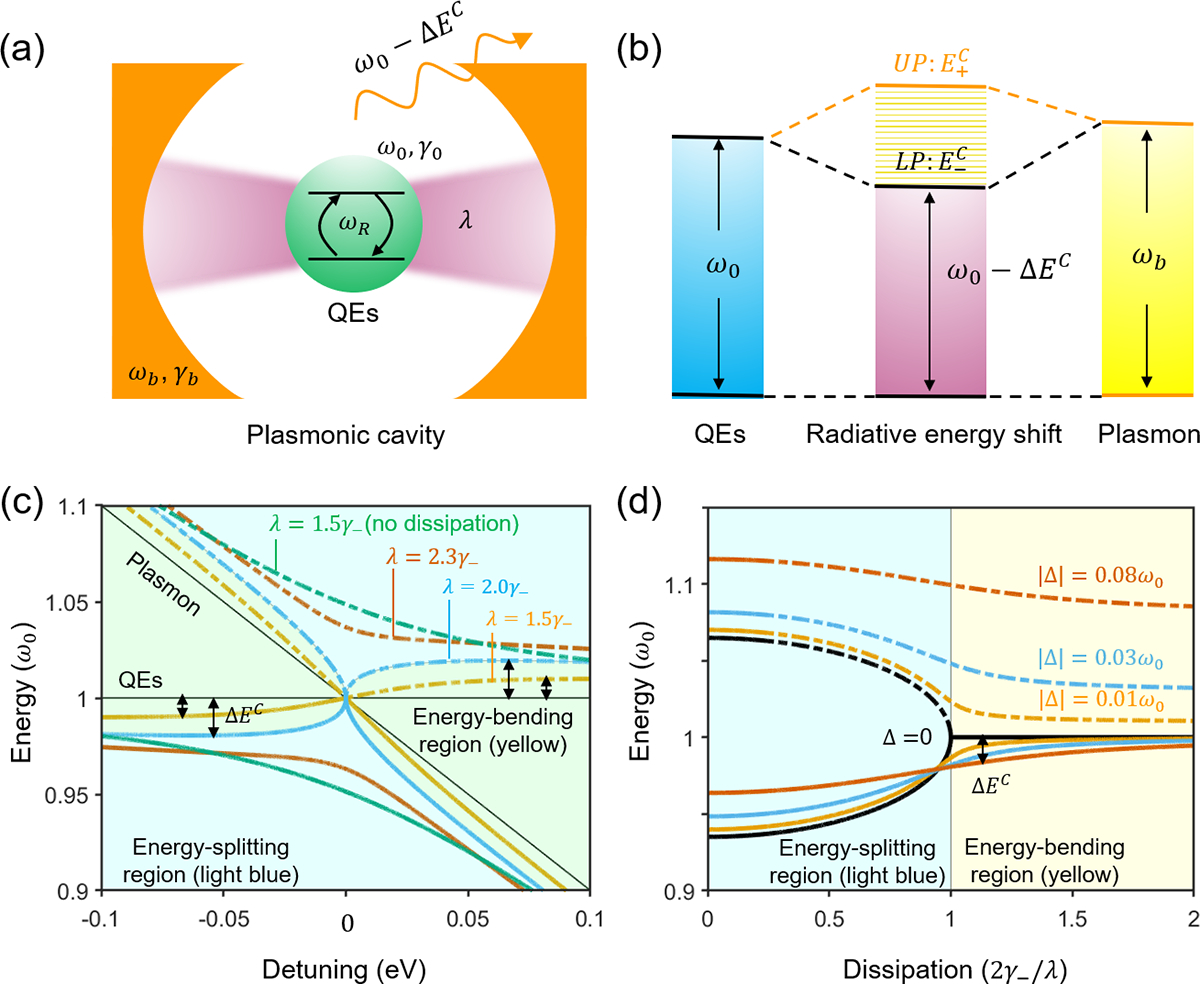
(a) Schematic representation of the QED system comprising of a two-level atomic system representing QEs with a transition frequency ω₀ and decay rate γ₀ coherently interacting with a single mode of the oscillating bosonic field in a plasmonic cavity with a resonant frequency ω_b and dissipation rate γ_b. The effective coupling strength is λ. (b) Energy diagram of the system featuring two plexcitonic states (UP and LP) with the energy eigenvalues of $E_{\pm }^C$. (c) Energy levels of the system as a function of the energy detuning Δ = ω₀ − ω_b for different coupling strengths as marked. The two thin black lines are the bare atomic and plasmonic states. (d) Energy levels of the system as a function of the energy dissipation γ₋ for different energy detuning. At zero detuning Δ = 0, the threshold for Rabi splitting occurs at γ₋/(2λ)=1. In (c) and (d), the dash-dot lines represent upper plexcitonic states while the solid represent lower plexcitonic states. Yellow-shaded area: an energy-bending region where no energy splitting is allowed; instead, the energy level of QEs undergoes an energy shift of ΔE^C owing to the perturbation of the plasmonic field. Light blue-shaded area: an energy-splitting region where distinct anti-crossing plexcitonic states are γ₋ is defined as γ₋ = |γ₀ − γ_b|/4.

By diagonalizing the Hamiltonian matrix in eq. (4), the complex energy eigenvalues are obtained $E_{\pm }^C=({\omega }_0+{\omega }_b)/2-i({{\gamma }_0+\gamma }_b)/2\pm \sqrt{4{\lambda }^2-{({4\gamma }_{-}+i\mathrm{\Delta })}^2}/2$. They are the plexcitonic states schematically shown in Fig. 5(b). Twice the last term is defined as the generalized Rabi frequency ${\mathrm{\Omega }}_R^C=\sqrt{4{\lambda }^2-{({4\gamma }_{-}+i\mathrm{\Delta })}^2}$ in its complex form with the reduced energy dissipation rate defined as ${\gamma }_{-}=({\gamma }_0-{\gamma }_b)/4$. At zero detuning, the threshold for energy splitting occurs at $\lambda =2{\gamma }_{-}$, which divides the energy space into two regions that we term as the energy-bending region and the energy-splitting region, as shown in Fig. 5(c)–(d).

In the energy-splitting region, the coupling strength is more than two times greater than the reduced energy dissipation rate ($\lambda >2{\gamma }_{-}$), and therefore, a full Rabi cycle can be completed. Such coherent plasmon-QEs interactions are characterized by the rapid and reversible energy exchange, resulting in the formation of a pair of plexcitonic states called upper plexciton (UP) and lower plexciton (LP). In the energy-splitting threshold with zero detuning where the coupling strength is exactly offset by twice the reduced energy dissipation rate, the generalized Rabi frequency becomes zero. Such a singular state is protected against perturbation from the plasmon-QEs interaction and is manifested as the point of intersection for the energy-bending and energy-splitting regions seen in Fig. 5(c).

Of particular interest to the study of the radiative energy shifts is the energy-bending region, where the coupling strength is less than twice the reduced energy dissipation rate ($\lambda <2{\gamma }_{-}$). The generalized Rabi frequency becomes purely imaginary and thereby merely opens an additional energy dissipation channel instead of splitting the plexcitonic states. Consequently, the plasmon-QEs interaction bends the energy levels for both QEs and SPs. This finding, echoing the one we made on the perturbation of the molecular energy levels through OSE by laser pumping, highlights the analogous roles of SPs and laser in fine-tuning the hybrid states of a coupled system. To the best of our knowledge, this is the first report of the energy-level perturbation by the plasmonic effect that is analogous to OSE, and we term it the “plasmonic Stark effect”.

We noted that the optical Stark effect could be manifested as Mollow triplet^41–42 but expect it not to occur in our current study. As Mollow triplet is characteristic of resonance fluorescence in the strong field achieved under resonant pumping, its two sidebands are essentially the two photon-dressed states and result from Rabi splitting of the two bare transition states, which are responsible for the optical Stark effect. However, the occurrence of the optical Stark effect, as demonstrated in our work, does not necessarily depend on the emergence of Mollow triplet. That is because at vanishing to low pumping for the strongly coupled atom-cavity system, it is the Rabi doublet rather than the Mollow triplet that would occur. Only by increasing the pumping to a certain level will the transition from Rabi doublet to Mollow triplet occur.^{3, 43} Moreover, the plasmonic Stark effect relies on the strong fields generated by plasmons, which are the plasmonic counterpart of laser pumping, as the driving fields to achieve coherent plasmon-QEs coupling. As surface plasmons can be excited under white light continuous illumination in the limit of vanishing pumping, no actual laser pumping is needed. Instead of Mollow triplet, only Rabi doublet would have been formed if the coupling strength is more than two times greater than the reduced energy dissipation rate. But as the coupling strength falls short of overcoming the strong dissipation of metallic nanoparticles, the Rabi frequency becomes purely imaginary and displays energy-level bending instead of splitting, which underscores the distinct feature of the plasmonic Stark effect.

One can also observe that the reduced energy dissipation-to-coupling strength ratio $2{\gamma }_{-}/\lambda$ serves as an important tuning parameter that dictates whether a coupled system falls into the energy-splitting or energy-bending region seen in Fig. 5(c)–(d). While the anti-crossing plexcitonic states are distinctly observed in the energy-splitting region, strong energy dissipation obscures energy splitting, and inversely, suppressed energy dissipation helps promote energy splitting. This effect can be clearly seen in a coupled system with a coupling strength of $\lambda =1.5{\gamma }_{-}$ in the energy-bending region (Fig. 5(c)), where the plexcitoninc states are upgraded to the energy-splitting region if the energy dissipation is completely suppressed.

The energy bending is also found to be a bidirectional effect. By modifying the relative energies of SPs and QEs, the energy-bending effect can be modulated to be either blue- or red-shifted (Fig. 5(c)). We note that the prevailing method to induce OSE is based on a red-shifted laser pumping. The discovery of the bidirectional tunability of the plasmonic Stark effect lends great flexibility to conduct coherent manipulation of the plexcitonic energy levels. In addition, the energy-bending effect can completely disappear at zero detuning seen in Fig. 5(c)–(d), which underscores the non-resonant nature of the plasmonic Stark effect.

Based on the above analysis, the energy shifts of QEs under the perturbation of a plasmonic field can be calculated by taking the difference between the bare and plexcitonic energy levels, the complex form of which is given by

$${\mathrm{\Delta }E}^C=\mathrm{\Delta }/2-i2{\gamma }_{-}+\sqrt{4{\lambda }^2-{({4\gamma }_{-}+i\mathrm{\Delta })}^2}/2$$ (5)

To confirm that the studied optical nanoprobes indeed fall into the energy-bending region, the coupling strength and ratios $2{\gamma }_{-}/\lambda$ were calculated based on eq. (5) using the fitting parameters from the measured absorption and PL spectra, as summarized in Table 2. The ratios $2{\gamma }_{-}/\lambda$ are found to be 1.975 for Au nanostar@thin-SiO₂@Cy7-SiO₂ and 1.823 for Au nanostar@thin-SiO2@Cy7.5-SiO2, which are well into the energy-bending region as shown in Fig. 5(d). This corroborates the origin of the observed radiative energy shifts being attributable to the plasmonic Stark effect.

Table 2.

Radiative transitions (ω₀, ${\omega }_0^{\mathrm{\prime }}$) for dye-doped silica shell in the absence (SiO2 nanoparticles with a mean diameter of 60 nm as the core) and presence (gold nanostars with a size of about 60 nm as the core) of the plasmon field. The plasmon resonance frequency (ω_b) and linewidth (γ_b) is 1.648 eV and 498 meV for gold nanostars. The parameters (ω_b, ω₀, ${\omega }_0^{\mathrm{\prime }}$, γ₀) are obtained by fitting the experimentally measured absorption and PL spectra. The coupling strength λ is calculated based on eq. (5).

No plasmon field			Under the plasmon field		Observed energy shift (meV)	Calculated λ, meV	|γ−|	Ratio: 2γ−|/λ
dyes-SiO2	ω0, eV	γ0, meV	Au@dyes-SiO2	${\omega }_0^{\mathrm{\prime }},\mathrm{e}\mathrm{V}$	Δω0
Cy7	1.619	97	Au star-Cy7	1.576	−43	94	102	1.975
Cy7.5	1.546	123	Au star-Cy7.5	1.507	−39	96	103	1.823

2.6. Validation of the energy-bending mechanism by the generalized Wiener-Khintchine spectrum

To further validate the energy-bending mechanism, we invoke the generalized Wiener-Khintchine spectrum to calculate the PL spectra using the fitting parameters from the optical nanoprobe (Au nanostar@thin-SiO₂@Cy7-SiO₂). The formula for the PL spectrum was derived previously⁴⁴ and is written as

$$PL(\omega )=\frac{{\gamma }_b}{\pi }{\left|\frac{-i\lambda }{{({\gamma }_{+}+i\mathrm{\Delta }/2-i\omega )}^2+{({\mathrm{\Omega }}_R^C/2)}^2}\right|}^2$$ (6)

where ${\gamma }_{+}=|{\gamma }_0+{\gamma }_b|/4$ with other parameters defined previously. The calculated PL spectra based on eq. (6) are plotted for various coupling strengths $2{\gamma }_{-}/\lambda$ seen in Fig. 6(a). The PL spectra display both energy bending and energy splitting that are strongly dependent on the ratio $2{\gamma }_{-}/\lambda$, consistent with the energy-bending mechanism. The energy-bending effect from the bare-state emission line seen in Fig. 6(a) recapitulates our experimental observations of the radiative energy shifts seen in Fig. 1(d) and S1(d). The energy bending can be suppressed at zero detuning based on the radiative energy from the calculated PL spectra seen in Fig. 6(b), which is consistent with the behavior of the plexcitonic energy levels predicted by Rabi splitting. The generalized Wiener-Khintchine spectrum suggests that the PL spectral splitting occurs at a more stringent condition than the energy-splitting threshold ($2{\gamma }_{-}/\lambda =1)$ that is predicted by the generalized Rabi frequency. In other words, the occurrence of Rabi splitting does not necessarily guarantee the observation of PL spectral splitting, as it can be obscured by various mechanisms such as internal relaxation, radiative and nonradiative decay, among other energy dissipation channels. This finding underscores the challenge to achieve PL spectral splitting for coupled plasmon-QEs systems. Nevertheless, the energy-bending region is found to be greatly expanded under the PL spectral splitting condition, and thereby is predicted to dominate a wide range of ratios $2{\gamma }_{-}/\lambda$, which provides a vast parameter space for fine-tuning the energy levels based on this newly discovered plasmonic Stark effect.

Figure 6. Shift and splitting of the PL emission under different coupling strengths.

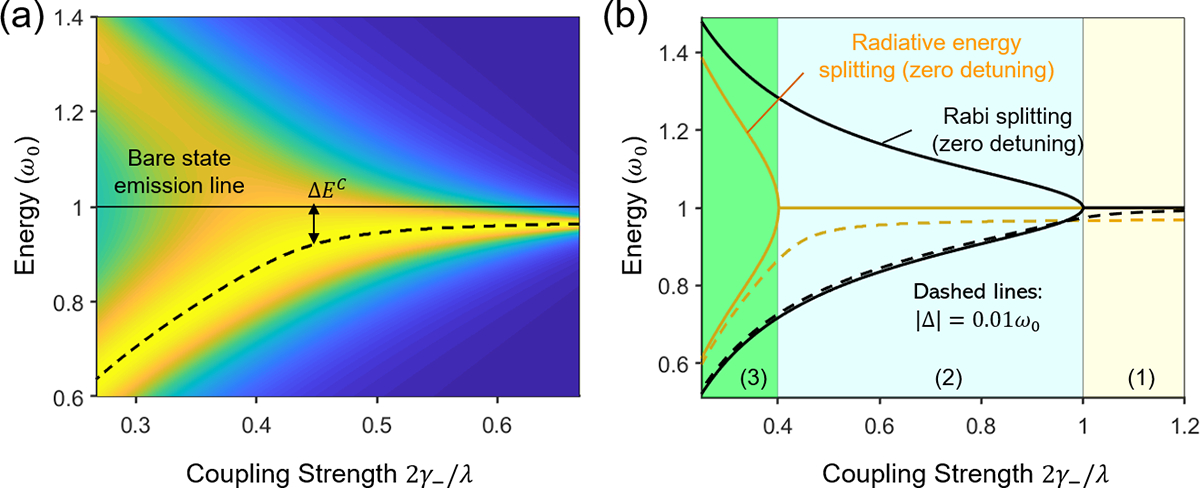
(a) The radiative energy shift occurs at lower coupling strengths and transits to splitting at higher ones from the calculated PL spectra for the coupled plasmon-QEs system. (b) Radiative energy splits at a higher coupling strength than the Rabi splitting; below the threshold for splitting, radiative energy shifts occur at nonzero detuning. The yellow- and light blue-shaded areas (1) and (2) are the energy-bending and energy-splitting regions judging by the Rabi splitting. However, based on the radiative study, area (2) still falls into the energy-bending region while area (3) is the energy-splitting region. This observation underscores the difference between the Rabi splitting and the observed PL peak splitting.

As light-driven collective oscillation waves of free charges, SPs have long been conceptualized to share important features with photons in a laser such as the bosonic character, electrical neutrality, and coherence.^{11, 45} Our success in the demonstration and mechanistic elucidation of the plasmonic Stark effect further highlights such a similarity. Importantly, SPs exhibit distinct advantages: SPs can be excited under white light illumination, which essentially eliminates the need for high-energy laser pumping; SPs offer nanoscale coherent manipulation of light-matter interactions, which is unachievable by lasers owing to light diffraction; as opposed to the transient Stark shifts under laser pumping, the plasmonic Stark effect renders permanent energy-level modification with the in-built plasmonic field for optical nanoprobes.

3. Conclusion

In conclusion, we observe analogous molecular radiative energy shifts by measuring the PL spectra for free dyes under non-resonant laser pumping and optical nanoprobes embedded with dyes under the plasmonic field as compared to their respective bare states. Using the Jaynes–Cummings model, we lay out a theoretical framework for the coherently coupled atom-field system and pinpoint the origin of the laser pumping-induced energy shifts being the optical Stark effect in the dispersive limit. Based on the cavity electrodynamic study of the coupled plasmon-QEs system with strong energy dissipation, we uncover an energy-bending mechanism under the non-resonant condition that is responsible for the radiative energy shifts observed in optical nanoprobes. Given the striking similarity in the experimental observations, theoretical models, and behaviors for both surface plasmons and photons in a laser, we term the newly discovered mechanism plasmonic Stark effect. We envision that successful demonstration of the plasmonic Stark effect paves the way for exploiting the unique features of surface plasmons to generate nanoscale optical sources, and to develop advanced optoelectronic tools for applications in ultrafast all-optical switching and biological nanosensing.

Figure 3. Molecular radiative energy shifts in the plasmon-QEs systems under dried condition.

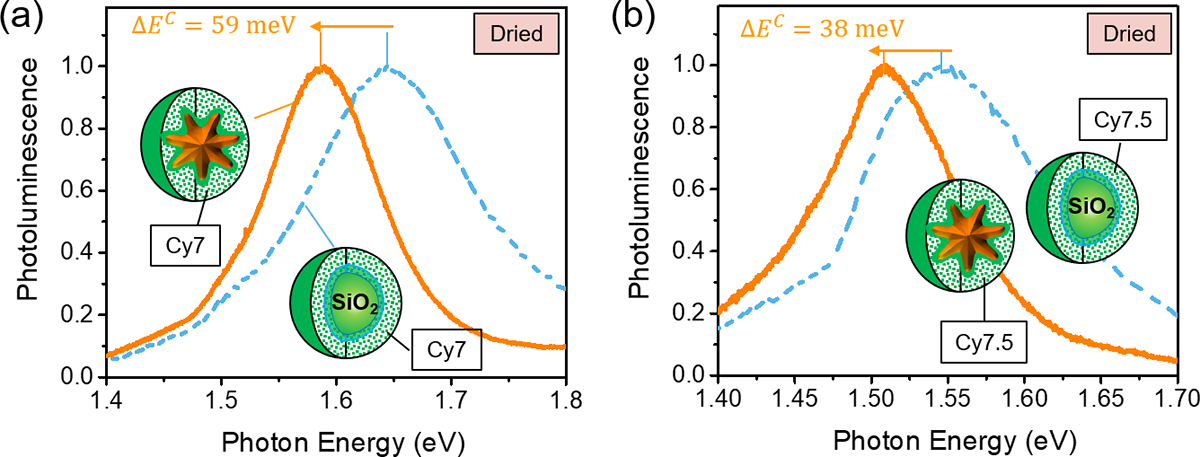
Under dried conditions, molecular radiative energy shifts were also observed in the plasmon-QEs systems made of (a) Au nanostar@thin-SiO₂@Cy7-SiO₂ and (b) Au nanostar@thin-SiO2@Cy7.5-SiO2 using an XploRA PLUS Raman microscope (HORIBA Instruments Inc., Edison, NJ, USA) under a 638 nm diode laser with a power of ~ 1 mW as compared to the control sample made of SiO₂@thin-SiO₂@Cy7-SiO₂ and SiO₂@thin-SiO2@Cy7.5-SiO2, respectively.