Machine learning-accelerated prediction of overpotential of oxygen evolution reaction of single-atom catalysts

Summary

The oxygen evolution reaction (OER) is a critical reaction for energy-related applications, yet suffers from its slow kinetics and large overpotential. It is desirable to develop effective OER electrocatalysts, such as single-atom catalysts (SACs). Here, we demonstrate machine learning (ML)-accelerated prediction of OER overpotential of all transition metals. Based on density functional theory (DFT) calculations of 15 species of SACs, we design a topological information-based ML model to map the OER overpotentials with atomic properties of the corresponding SACs. The trained ML model not only yields remarkable prediction precision (relative error of 6.49%) but also enables a 130,000-fold reduction of prediction time in comparison with pure DFT calculation. Furthermore, an intrinsic descriptor that correlates the overpotential of an SAC with its atomic properties is revealed. The approach and results from this study can be readily applicable to screen other SACs and significantly accelerate the design of high-performance catalysts for many other reactions.

Graphical abstract

Highlights

• •We present a topology-based machine learning (ML) approach to predict OER activity
• •The prediction by the ML model is of high precision (relative error of 6.49%).
• •The ML model is 130,000 times faster than pure density function theory calculation

Artificial Intelligence; Catalysis; Electrochemistry; Energy Materials

Introduction

The economical, highly efficient, eco-friendly energy storage and conversion systems such as water electrolyzers and metal-air batteries (Luo et al., 2014) have attracted extensive interests due to their merits of clean and sustainable ways in consuming molecular hydrogen (H₂). In these electrochemical reaction-governed systems, the half-reaction known as the oxygen evolution reaction (OER) plays a substantial role (Amiinu et al., 2018; Li and Lu, 2017). The commonly used electrocatalysts for OER are platinum and noble metal oxides (Chen et al., 2014; Wang et al., 2015). These precious-metal-group materials are of high cost and scarcity and thus not suitable for large-scale (Bai et al., 2016) and sustainable applications (Greeley et al., 2009). Hence, there exist significant efforts to develop cheaper catalysts including metal-free catalysts and alloys with cheaper elements. In addition, downsizing the precious-metal-group materials to provide the highest number of active sites in the catalyst and achieve the maximum utilization efficiency is also widely studied (Qiao et al., 2011).

Recently, transition metal single-atom catalysts (SACs) dispersed on a carbon substrate have attracted extensive research attention as a new frontier in catalysis science (Li et al., 2021; Liu et al., 2018; Liu and Corma, 2018; Sun et al., 2019; Yan et al., 2018). Transition metals have an incomplete d-orbital that allows the metal to facilitate exchange of electrons, thus can both give and accept electrons easily. By taking advantage of the metal d orbitals, the transition metal atoms bonded to the defective sites of a graphene can accelerate reactions by means of coordination, ligand exchange, insertion, and elimination, leading to the cleavage or formation of OH, O, and OOH bonds (Jiang et al., 2017; Xu et al., 2018). Transition metal SACs possess unique physical and chemical properties that are distinct from conventional nanoparticles (NPs) and metal catalysts, including high selectivity (Kwon et al., 2017; Lee et al., 2020; Li et al., 2019), tunable high activity (Wang et al., 2019), and maximum atomic efficiency (Zhang et al., 2019). Graphene has received enormous interest in the field of electrochemistry as a promising catalytic support due to its lightweight, low cost, adjustable porosity, high chemical and thermal stability, and controllable chemical properties by heteroatom doping (Wang et al., 2012, 2013, 2014a, 2014b). Furthermore, the surface of carbon nanomaterials (e.g., NPs and nanowires) shows high capacity for stabilizing metal SACs, resulting from the existence of defects in the surface (Wei et al., 2018; Wu et al., 2020a, 2020b).

Promise of transition metal SACs on a carbon surface aside, it remains a grand challenge to search for highly efficient transition metal SACs using trial and error approaches in a reasonable timescale from hundreds of possible combinations of transition metal species and various defect structures on the carbon surface.

Machine learning (ML) algorithms with multiple processing layers to enable data learning via multiple levels of abstraction have begun to be utilized in materials science research, e.g., identifying structural flow defects in disordered solids (Cubuk et al., 2015), modeling and designing composite materials (Chen and Gu, 2019; Gu et al., 2018a, 2018b), discovering inorganic-organic hybrid materials (Raccuglia et al., 2016), and predicting the new stable structure of quaternary Heusler compounds (Kim et al., 2018). In searching for high performance catalysts, ML has been used to establish the correlations of physical properties and adsorption strength of the reaction intermediates (O'Connor et al., 2018) and to identify the relationships between the intermediate adsorption strengths and the performance of the catalyst (Ma et al., 2015) (Lin et al., 2020). Recently, the ML algorithm is also used to depict the underlying pattern of the physical properties of 104 graphene-supported SACs and their limiting potentials toward the oxygen reduction reaction/OER/hydrogen evolution reaction and predict the catalytic performance of 260 other graphene-supported metal-nitrogen/carbon systems (Lin et al., 2020). However, the amount of training data of the ML model in Ref. 40 is large and thus requires significant computation cost.

Aiming to address the above challenges, here we report a simulation-based, ML-accelerated prediction of the OER overpotential of SACs of all non-radioactive transition metals on a graphene. We first perform density functional theory (DFT) calculations to evaluate the overpotential of OER of 15 common transition metals (i.e., Ti, V, Cr Mn, Fe, Co, Ni, Cu, Mo, Ru, Pd, Ag, Pt, Au, and Zn) stabilized at two types of vacancy defects on graphene. Then, we use the DFT results from the 15 transition metal species as the training and testing data sets for a topological information-based ML algorithm, which in turn can predict the OER catalytic performance of SACs of all non-radioactive transition metals. We define an intrinsic descriptor to characterize the OER catalytic activities of various SACs on graphene. The ML-accelerated design is shown to drastically reduce the computation time to predict and evaluate the OER catalytic performance of SACs of all non-radioactive transition metals, 130,000 times faster than the approach based on pure DFT calculation, yet with an encouraging prediction precision (<6.49% error). The simulation-based, ML-accelerated prediction strategy offers quantitative guidance for rational selection of transition metals to fabricate SACs with desirable electrocatalyst activity and at a significantly reduced cost.

Results

OER performance of transition metal SACs

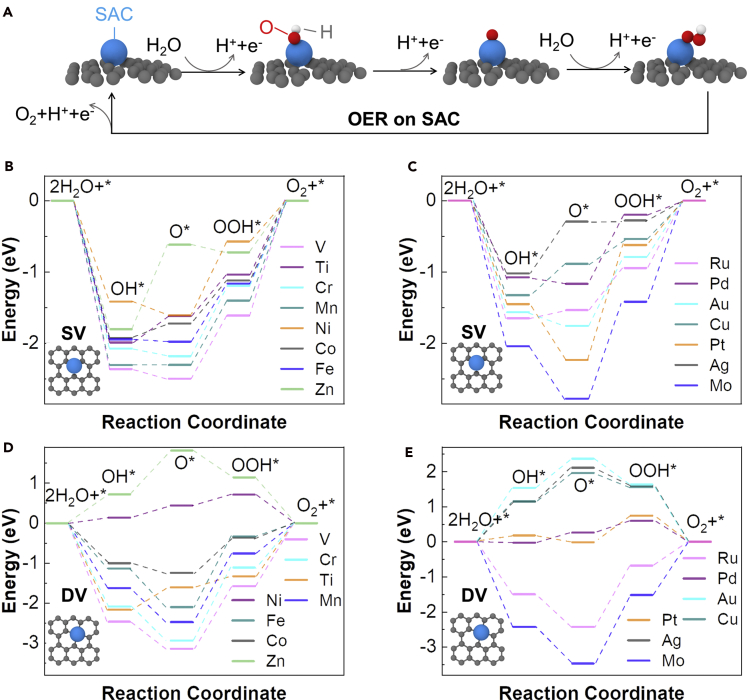
Previous experimental studies have shown that the realistic active sites of SACs supported on graphene are actually isolated metal atoms coordinated by carbon atoms (Yao et al., 2019). Based on our previous study (Wu et al., 2020a), we construct two models, in which a metal SAC is doped on a graphene with different coordination environments: the SAC at a single vacancy site (SV site) with three carbon neighbors and the SAC at a double vacancy site (DV site) with four carbon neighbors, respectively. The detailed geometric and electronic structures of the metal atoms on graphene are shown in Figures S1–S16. According to the typical experimental electrocatalytic conditions for SACs supported on a graphene, we evaluate the OER performance of the SACs in an acidic electrolyte (Calle-Vallejo et al., 2015) (see transparent methods for details). Consistent with other studies (Liao et al., 2012), we assume a four-step OER mechanism that proceeds through OOH∗, O∗, and OH∗ (the asterisk denotes the adsorption site). The reaction scheme with the intermediates in the OER process on SACs at the SV site and DV site is shown in Figure 1A.

Figure 1.

Evaluation of catalytic activity of transition metal SACs

(A) The reaction scheme with the intermediates in the OER process of an SAC on an SV site.

(B–E) Free energy diagram at 1.23 V for OER over the SV site (B, C) and the DV site (D, E).

The calculated OER energy diagrams at 1.23 V for the SACs of 14 transition metals at the SV site and the DV site following the suggested reaction pathways are presented in Figures 1B–1E. We choose to show the OER energy diagrams at 1.23 V because the reaction free energies of all four proton transfer steps should be the same at zero potential (4.92 V/4 = 1.23 V) for an ideal catalyst. From the OER energy diagram, we can directly evaluate the overpotential η^OER using the limiting reaction barrier determined from the free energy of the rate-determining step (RDS). For nine species of SACs (Co, Cr, Cu, Fe, Mn, Mo, Ti, V, and Ru) on the SV site, the RDS is the last step to form the O₂ with a limiting reaction barrier ranging from 0.52 to 1.43 eV. For Ag and Zn SACs on the SV site, the RDS is the oxidation of OH∗ to O∗ with a limiting reaction barrier of 0.72 eV and 1.18eV, respectively. For other species of SACs (Au, Ni, Pd, and Pt) on the SV site, the RDS is the oxidation of O∗ to OOH∗ with limiting barrier ranging from 0.99 to 1.06 eV. For the species of SAs on the DV site, the RDS is the oxidation of O∗ to OOH∗ (Co, Cr, Fe, Mn, Mo, Pd, Pt, Ru, and V), or is the oxidation of OH∗ to O∗ (Ni and Zn), or is the first step to form OH∗ (Ag and Au), or is the last step to form O₂ (Ti). The limiting reaction barrier for the SAs on DV sites range from 0.29 (Ni) to 1.94 eV (Mo).

The DFT calculated overpotential η^OER of transition metal SACs as shown in Figure 1 offers quantitative guidance on the catalytic performance of SACs of various species in the OER process. However, such a calculation requires tremendous computation cost. For example, on average, it takes ~1,445 CPU-hour (~36.125 CPU-hour in parallel on a 40-core supercomputer [Intel E5-2680, 2.80GHz]) to calculate one overpotential η^OER value using the Vienna Ab Initio Simulation Package (VASP). The high computation cost poses a significant challenge to a comprehensive study of the OER activity of all transition metals, a highly desirable parameter to close the loop of the rational selection and design of high-performance SACs.

Topological information-based ML algorithm

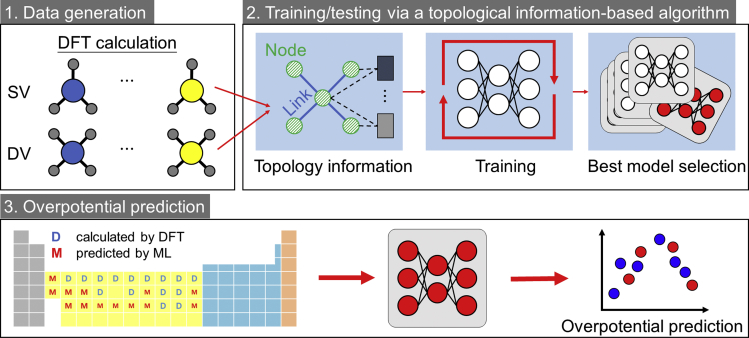
To address the challenge of prohibitive computing expense to screen all transition metal SACs and evaluate their OER performance using pure DFT calculations, we introduce a topological information-based ML algorithm to predict the OER overpotential of all transition metal SACs. Figure 2 illustrates the implementation of the ML-based prediction, which contains three steps:

Step 1

Data generation. First, the OER overpotential of 15 transition metal SACs obtained by DFT calculations is collected to serve as the target data. Since the electronic characteristics of catalytic centers influence the electron transfer and reaction energy in OER (Nayak et al., 2019; Qiu et al., 2015; Wang et al., 2017), five parameters of transition metals in two categories (Table S1), including atomic dimension and structure (atomic mass M, atomic radius r_M, and d-electron count θ_d), and reactivities (electronegativity E_M, electron affinity E_A, and first ionization energy E_i), are identified as the input data. The input data (x_i = [M,r_M,θ_d,E_M,E_A]) and target data (η^OER) of the 15 studied transition metals form a data set for the ML model.

Step 2

Training/testing via a topological information-based algorithm. The ML model is composed of multiple processing layers to extract the features of input data with multiple levels of abstraction (Lillicrap et al., 2016). The data set containing 15 input-target pairs obtained in step 1 is split into two sub-data sets: a testing sub-data set containing four input-target pairs corresponding to Mn/Mo and Mn/Cr in SV and DV sites, respectively, and1 a training sub-data set containing the remaining 26 input-target pairs. The partition method of the data set into two sub-data sets is completely random.

In consideration of a single transition metal atom supported on graphene with different coordination environment, we use the topological information to represent the geometric spatial structure between the transition metal atom and carbon atoms. Specifically, we set the atomic parameters identified in step 1 as the node information and build the links according to the bonding states. The established topological information is identified as the inputs of the ML model, which contains six convolutional layers and three full connection layers. The convolutional layers are used to extract multiple-level features between the transition metal atom and carbon atoms. The outputs of the last convolutional layer serve as the inputs of the full connection layers, which make a regression to predict the overpotential of the transition metal atom.

We implement the ML model in PyTorch (Paszke et al., 2019) and then feed the two sub-data sets into the ML model to optimize the model parameters. The training process is performed using the Adam algorithm (Kingma and Ba, 2014) with a fixed learning rate of 0.001 for 180 epochs. In each training process, we use mean squared error as the loss function (Adamson and Smith, 2018). We run 50 training processes and select the ML model with the lowest relative deviation, $e=\sum _i^n\frac{\left|x_i-\overline{x}\right|}{\overline{x}}$, for the testing sub-data set as the best performing ML model, as shown in Figure S17. To demonstrate the ML model is not overfit, we record the relative deviation during the training process, as shown in Figure S18. The ML training and testing step is carried out for the case of an SAC on an SV site and the case of an SAC on a DV site independently. At the end of the ML training and testing step, the OER overpotentials predicted by the best performing ML model agree with those obtained from the DFT calculations within an error of 6.70% and 6.49% in training and testing data sets, respectively (detailed in Section 2.3, Figure 3).

Step 3

Model prediction. The best performing ML models obtained in step 2 is then used to predict the OER catalytic activities η^OER of an SAC of the remaining 14 transition metal species (that is, Sc, Y, Zr, Tc [Tc is radioactive but included here. The most stable isotopes of Tc have a half-life ranging from 211,000 years to 4.21 million years.], Nb, Rh, Cd, Hf, Ta, W, Re, Os, Ir, and Hg) on an SV site and a DV site on a carbon surface, respectively.

Figure 2.

Diagram describing the training strategy for ML models involving (1) data generation, (2) training/test via a topological information-based algorithm, and (3) overpotential prediction workflow.

Figure 3.

Machine learning drastically accelerates the prediction of OER catalytic activity

(A) Comparison between DFT and ML predicted overpotential values of η^OER;

(B) PCC of the five atomic properties of an SAC on an SV site and a DV site.

(C) Comparison of the average computation costs for predicting the OER catalytic activity of a transition metal SAC via pure DFT calculations and ML prediction.

ML-enabled predictions of OER catalytic activity

Figure 3A compares the ML predictions and DFT data on OER overpotential of the 12 transition metal SACs in the training set and 2 in the testing set. The values of OER overpotential of different SACs by DFT and ML are listed in Table S2. The mean relative error is 6.70% for the training data and 6.49% for the testing data, which clearly demonstrate the impressive precision of the ML predictions based on topological information-based algorithm. Further, we calculate 6 models (Rh-SV, Rh-DV, W-DV, W-SV, Hf-SV, and Hf-DV) using DFT to compare with the ML predicted value for validation. Our ML predicted errors are only 2.07%, 0.54%, 9.83%, 8.98%, 9.43%, and 12.84% for Rh-SV, Rh-DV, W-DV, W-SV, Hf-SV, and Hf-DV, respectively. To evaluate the correlation between each atomic parameter of a transition metal SAC and its OER overpotential, we calculate the Pearson correlation coefficient (PCC) to compare the importance of these five atomic parameters (Figure 3B). We find that the dominating parameters are d-electron count (θ_d), the atomic radius (r_M), and electron affinity (E_A), with the PCC value of 0.478, −0.334, and 0.308, respectively, followed by electronegativity (E_M) and atomic mass (M), with the PCC value of 0.188 and 0.095, respectively.

It is worth noting that the ML model can drastically accelerate the prediction of η^OER with a high efficiency and a high accuracy. For comparison, we time the central processing unit hours (CPU-h) to evaluate the computation cost of DFT-based calculations and ML-based predictions of η^OER. For DFT-based calculations, the calculation of η^OER for a given transition metal SAC is performed using the VASP on a 40-core supercomputer (Intel E5-2680, 2.80GHz), which on average takes ~36.125 CPU-h to calculate one η^OER value, equivalent to ~1,445 CPU-h on a single core CPU. By contrast, for ML-based predictions, it takes only ~40 s, starting from ML model training, to model testing, and to model predicting, on a single core CPU. In other words, ML-based predictions of the catalytic activity of transition metal SACs are more than 130,000 times faster than the DFT-based calculation (Figure 3C). Such a remarkable reduction of computation cost by ML-accelerated material discovery approach effectively overcomes the challenge of low efficiency of DFT calculations in identifying high performance transition metal SACs.

To help identify the optimal SAC, we identify an intrinsic catalytic activity descriptor to establish a “volcano” relationship between η^OER and the descriptor (Nørskov et al., 2009). According to the importance in predicting OER activity using the DFT calculation and ML models, we introduce an intrinsic catalytic activity descriptor as follows:

$$\varphi =E_i{\theta }_{d}M\left(\frac{E_M}{r_M}+\frac{n_C{E}_C}{r_C}\right),$$ (Equation 1)

where E_C and r_Crepresent the electronegativity and atomic radius of carbon, respectively. n_C represents the nearest neighbor carbon atoms.

Figures 4A and 4B plot the overpotential η^OER of the SACs of all transition metals (from both DFT calculations and ML predictions) on an SV site and a DV site on a carbon surface, respectively, as a function of ϕ, both of which show a volcano relationship. For example, for SACs on an SV site, Cu appears at the peak of the volcano (Figure 4A, i.e., with the best OER catalytic activity), while for SACs on a DV site, Rh appears at the peak of the volcano (Figure 4B). The volcano relationships between η^OER and ϕ shown in Figures 4A and 4B are instrumental in selecting SACs of transition metals with desirable OER catalytic activity. We further compare our calculation results with experimental measurements (Fei et al., 2018). Experiments in (Fei et al., 2018) show that the OER activity at a current density of 10 mA cm-2 (η10) of the single metal atom on doped holey graphene frameworks (NHGFs) is Ni > Co > Fe. Specifically, the Ni-NHGF catalyst shows that its potential of η10 is 331 mV, lower than that of Co-NHGF (402 mV) and Fe-NHGF (488 mV). Our DFT calculations performed on the SV site and DV site show the same trend of their OER activities (i.e., Ni > Co > Fe).

Figure 4.

The volcano relationships between η^OER and descriptor ϕ

OER catalytic activities as a function of an intrinsic catalytic activity descriptor ϕ of SACs on an SV site (A) and a DV site (B).

Conclusions

In summary, using a topological information-based algorithm, we built two ML models to reveal the underlying correlation of physical properties and overpotentials toward the OER of graphene-supported SACs. An intrinsic descriptor is identified to be able to well correlate with OER catalytic activity of transition metal SACs in a volcano relationship, which enables a facile selection of optimal SACs with desirable catalytic performance. The ML model featuring a topological information-based algorithm enables a 130,000-fold acceleration of the computational efficiency in calculating the OER catalytic activity of transition metal SACs. The approach and results from this study can be readily applicable to screen other SACs and significantly accelerate the design of high-performance catalysts for many other reactions.

Limitations of the study

Our work demonstrates an ML-accelerated approach for the prediction of the overpotential of OER and shows the OER overpotential of all the transition SACs on the SV site and DV site of a carbon surface. However, the influence of the substrate on the OER activity needs to be further investigated.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Teng Li (lit@umd.edu).

Materials availability

This study did not generate new reagents.

Data and code availability

This article includes all data sets/code generated or analyzed during this study.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: May 21, 2021