Deep Learning–Based Fluence Map Prediction for Pancreas Stereotactic Body Radiation Therapy With Simultaneous Integrated Boost

Abstract

Purpose

Treatment planning for pancreas stereotactic body radiation therapy (SBRT) is a challenging task, especially with simultaneous integrated boost treatment approaches. We propose a deep learning (DL) framework to accurately predict fluence maps from patient anatomy and directly generate intensity modulated radiation therapy plans.

Methods and Materials

The framework employs 2 convolutional neural networks (CNNs) to sequentially generate beam dose prediction and fluence map prediction, creating a deliverable 9-beam intensity modulated radiation therapy plan. Within the beam dose prediction CNN, axial slices of combined structure contour masks are used to predict 3-dimensional (3D) beam doses for each beam. Each 3D beam dose is projected along its beam’s-eye-view to form a 2D beam dose map, which is subsequently used by the fluence map prediction CNN to predict its fluence map. Finally, the 9 predicted fluence maps are imported into the treatment planning system to finalize the plan by leaf sequencing and dose calculation. One hundred patients receiving pancreas SBRT were retrospectively collected for this study. Benchmark plans with unified simultaneous integrated boost prescription (25/33 Gy) were manually optimized for each case. The data set was split into 80/20 cases for training and testing. We evaluated the proposed DL framework by assessing both the fluence maps and the final predicted plans. Further, clinical acceptability of the plans was evaluated by a physician specializing in gastrointestinal cancer.

Results

The DL-based planning was, on average, completed in under 2 minutes. In testing, the predicted plans achieved similar dose distribution compared with the benchmark plans (-1.5% deviation for planning target volume 33 V_33Gy), with slightly higher planning target volume maximum (+1.03 Gy) and organ at risk maximum (+0.95 Gy) doses. After renormalization, the physician rated 19 cases clinically acceptable and 1 case requiring minor improvement.

Conclusions

The DL framework can effectively plan pancreas SBRT cases within 2 minutes. The predicted plans are clinically deliverable, with plan quality approaching that of manual planning.

Introduction

Pancreatic cancer is associated with high rates of local recurrence with its attendant morbidity and mortality, although often overshadowed by high rates of distant metastases development. In recent years, stereotactic body radiation therapy (SBRT) has shown encouraging results in the neoadjuvant and definitive setting.1, 2, 3, 4, 5 However, the complex anatomy of pancreas planning target volumes (PTVs) and organs-at-risk (OARs), including the stomach and the duodenum/bowel, poses a significant challenge. Gastrointestinal (GI) dose constraints often have to be prioritized over delivering uniform high dose to target structures. With intensity modulated radiation therapy (IMRT), a higher prescription dose can be concurrently delivered to the gross tumor volume within the PTV, that is, simultaneous integrated boost (SIB).6, 7, 8 The reporting of promising local control and moderate toxicity rates has encouraged further dose escalation approaches to improve treatment outcomes.^9,10 However, dose escalation further adds to the complexity of the treatment planning tasks given GI luminal OARs are sensitive to higher radiation doses. When using SIB techniques, the boost target (gross tumor volume) dose usually exceeds the dose limit of GI luminal OARs. Although achieving this high dose gradient is a major objective in planning, a trade-off is usually required to deliver as much high dose to the target as possible while respecting normal organ dose constraints. This challenging task generally requires extensive and superior treatment planning skills to achieve the desired goals and adds significant time and cost to the planning process. Therefore, plan quality can be highly dependent on the planner’s experience and time resources available.¹¹

Over the past decade, machine learning has been used to assist at several key steps during IMRT treatment planning, where clinical knowledge from previous high-quality plans is extracted and used to create optimized plans for new patients. Dose prediction has been the key focus of most knowledge-based and automated planning approaches, including the prediction of dose-volume histogram (DVH)12, 13, 14, 15, 16, 17, 18, 19 and 3-dimensional (3D) dose distribution.20, 21, 22, 23, 24, 25, 26, 27 This prediction paradigm requires an additional inverse optimization step to translate the predicted DVH/dose to deliverable fluence maps, which correspond to machine parameters such as multileaf collimator (MLC) leaf control points. The predicted DVH and 3D dose distributions are used as constraints to guide the inverse optimization toward the desired plans.^{16,19,21,26,28} This 2-step approach is suboptimal, given that, even though the best achievable DVH/dose distributions have been predicted, translating them into actual optimal plans still requires the human planner skillfully operating the inverse optimization process, often requiring multiple iterations.

A more direct approach to automated treatment planning is to predict the fluence map itself, without inverse planning. A fluence map is a 2-dimensional (2D) photon intensity image of 1 beam, which determines this beam’s dose distribution in the patient. We have previously proposed a deep learning framework to predict fluence maps for pancreas SBRT with a single PTV.²⁹ A few studies have also addressed the direct generation of fluence maps in automated treatment planning. Lee et al³⁰ used a convolutional neural network (CNN) to generate fluence maps from clinical plan dose distributions for prostate IMRT. However, the study did not provide a solution on how to obtain the clinical plan’s beam dose distribution as the input when the clinical plan is unknown (not planned yet) for new patients. Furthermore, the prediction of dose per beam has not been widely investigated. Existing studies in the literature all focus on total dose prediction. A more complete system was developed by Sheng et al³¹ to generate fluence maps for 1 or 2 pairs of tangential beams for whole breast radiation therapy based on a random forest model. In their model, the fluence maps are predicted from patient anatomy, which are directly converted to optimal clinical plans and dose distributions via leaf sequencing.

In this study, we propose using a novel deep learning (DL) framework to predict fluence maps for plans with multiple PTV prescriptions. We hypothesize that, given standardized beam orientation and prescription doses, deep neural networks can be trained to predict the optimal fluence maps directly from patient anatomy and thus lead to high quality plans without inverse optimization. We have applied this DL framework in automated treatment planning approaches for pancreas SBRT to evaluate its feasibility in challenging SIB scenarios.

Methods and Materials

Materials

One hundred patients with pancreatic cancer previously treated with SBRT at Duke University Medical Center were randomly selected for this retrospective study after institutional review board approval. Eighty cases were randomly selected for training, with the remaining 20 cases for testing. Because SBRT is a rapidly evolving treatment modality for pancreatic cancer, the prescriptions to the boost target volume, the dose limits to the GI structures, as well as the treatment beam setting, have varied over time. Therefore, in this study, a set of benchmark plans was designed by clinical physicists who specialized in GI treatment using the unified prescription template shown in Table 1, partially based on a prior phase II study using 5 fractions.³² All benchmark plans were IMRT plans generated in the Eclipse treatment planning system (TPS) (version 15.6; Varian Medical Systems, Palo Alto, CA) using 9 equally spaced beams and created for Varian TrueBeam Linear Accelerator with Millennium 120 MLC. All plans were reviewed and deemed clinically acceptable before they were used for training and validation in this study.

Table 1.

Clinical protocol used for generating the benchmark plans

Planning structure	Structure name	Prescription
Elective target volume	PTV25	25 Gy to >95% volume
Boost target volume	PTV33	33 Gy ideally to >95% volume Yield to GI max dose limit
Duodenum	OAR	Maximum dose (0.1 cc) <29 Gy
Stomach
Bowels
Bilateral kidney	Lt kidney & Rt kidney	V15Gy <15%
Liver	Liver	V15Gy <10%

Abbreviations: GI = gastrointestinal; OAR = organ at risk; PTV = planning target volume.

The networks were trained on a server with an Intel Xeon W-2195 processor and 256 GB of RAM, using 1 Nvidia Quadro RTX 8000 graphics card. Model testing was performed on a workstation with an Intel Xeon E5 v4 processor, 64 GB of RAM, and a Nvidia Quadro M4000 graphics card.

DL framework

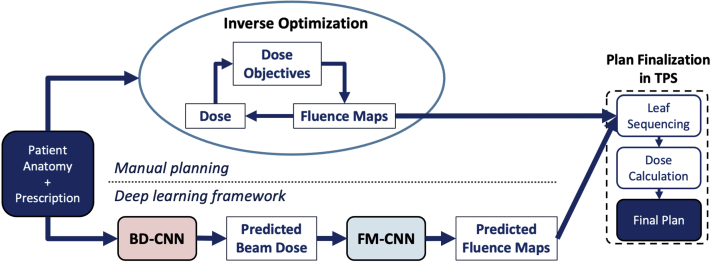
The proposed DL framework aims to eliminate the inverse optimization process, as illustrated in Figure 1. In manual planning, the optimization engine produces optimal fluence maps with many iterations to minimize the objective function. In contrast, the DL framework directly predicts fluence maps with 2 CNNs, fully replacing the inverse optimization process (Fig 1). The predicted fluence maps are then sent to the TPS to finalize the plan.

Figure 1.

The proposed deep learning (DL) framework for fluence map prediction compared with manual planning. The 9-beam intensity modulated radiation therapy (IMRT) benchmark plans are generated manually with the traditional inverse planning workflow. In the DL framework, the BD-CNN predicts beam dose from the anatomy and prescription. The predicted beam dose is used as the input for FM-CNN to predict the fluence map. Both benchmark plans (manual) and predicted plans (DL) are finalized in the TPS using 9 fluence maps. Abbreviations: BD-CNN = beam dose convolutional neural network; FM-CNN = fluence map convolutional neural network; TPS = treatment planning system.

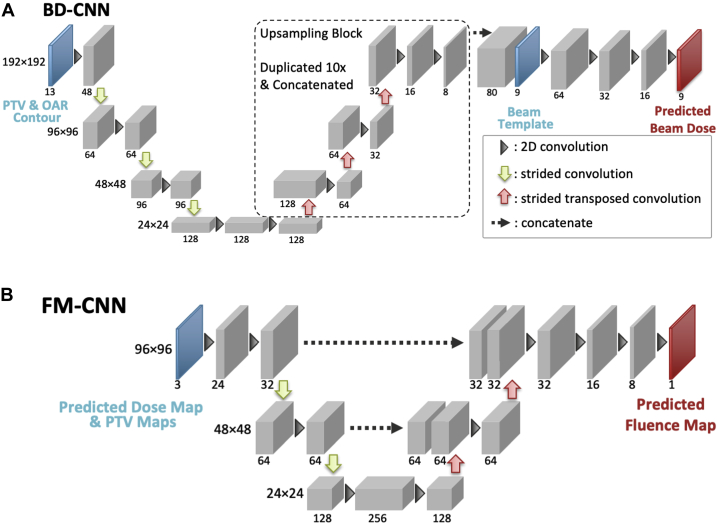
Figure 2 illustrates the architectures of the 2 consecutive CNNs in the DL framework. The beam dose CNN (BD-CNN) predicts the 3D dose contribution of each beam. This component of the DL framework takes the patient anatomy as input and predicts as output the dose contribution of each beam, which we refer to as “predicted beam dose.” All 9 beam doses are predicted simultaneously. In the next step, these 3D predicted beam doses are projected along the beam’s eye view (BEV) and converted to 2D beam dose maps. Additionally, 2 3D PTV volumes (primary and boost) are similarly converted to 2D PTV maps as the other input. In the final step, the 2D beam dose map and the 2 2D PTV maps associated with each beam are then taken together as the input to the fluence map CNN (FM-CNN) to predict this beam’s FM. A single FM-CNN is used to separately predict FMs for different beam angles.

Figure 2.

The network architectures of the BD-CNN (A) and the FM-CNN (B). The BD-CNN uses an encoder-decoder structure with 4 resolution levels. The FM-CNN uses a customized U-Net structure with 3 resolution levels. The predicted beam dose slices from the same beam are stacked to create the 3-dimensional (3D) beam dose, which is subsequently projected to create a 2-dimensional (2D) beam dose map. Abbreviations: BD-CNN = beam dose convolutional neural network; FM-CNN = fluence map convolutional neural network; OAR = organ at risk; PTV = planning target volume; TPS = treatment planning system.

Once all 9 FMs are predicted, they are sent to the TPS for plan finalization, which performs MLC leaf sequencing and dose calculation. Although the 2 CNNs were trained and validated independently, they were integrated as a whole framework to replace the manual iterative inverse planning process, as shown in Figure 1.

Individual BD prediction

The BD-CNN is a CNN with an encoder-decoder structure. The PTV and OAR contours are converted to masks and partitioned to their corresponding dose prescriptions. The combined contour mask is fed to the CNN network in 13 consecutive axial slices. Nine beam dose distributions for the central slice are generated, 1 in each output channel. This CNN design allows the independent prediction of each axial slice while incorporating contour variation in the superior-inferior direction. This process was repeated for all PTV slices iteratively; then, the predicted beam dose slices from the same angle were stacked to create a 3D beam dose for FM prediction.

The loss function of the BD-CNN is defined as a weighted sum of BD error and total dose (TD) error, with the hyperparameter $\alpha$ tuned during validation. The prediction errors are calculated in a region-of-interest (ROI), which is the PTV25 expanded by 1 cm. The loss function is expressed as

$$L_{BD}=\frac{1}{N\left(ROI\right)}\sum _{ROI}\left[{\left(B{D}_{true}-B{D}_{pred}\right)}^2+\alpha {\left(T{D}_{true}-T{D}_{pred}\right)}^2\right].$$ (1)

Of all the training data, 10% were held out as a validation set to fine-tune the model architecture and hyperparameters, including the loss function weight $\alpha .$ The model was trained with early stopping based on validation loss and a maximum of 150 epochs.

FM prediction

The FM-CNN adopts a U-net³³ shape with 3 resolution levels and predicts the FM for each beam individually. The input includes a BD map and the projected contour maps of PTV25 and PTV33. The BD map is each beam’s predicted dose contribution (output of BD-CNN) projected along the BEV. The output is the FM of the corresponding beam. The loss function of the FM-CNN ($L_{FM}$) is a modified mean absolute error, which is formulated as

$$L_{FM}=\left(1+\lambda \right)\frac{\sum \left|y_{true}-y_{pred}\right|}{N\left(y_{true}>0\right)},$$ (2)

where $y_{true}$ and $y_{pred}$ are the ground truth (benchmark) and predicted values of the FM, and $N(y_{true}>0)$ is the count of ground truth pixels with nonzero values. $\lambda$ is a coefficient that prevents FM-CNN from over- or underestimating the FMs. It is expressed as

$$\lambda =\frac{\left|N\left(y_{true}-y_{pred}>y_{th}\right)-N\left(y_{true}-y_{pred}<-y_{th}\right)\right|}{N\left(y_{true}>0\right)},$$ (3)

where the fluence error threshold $y_{th}$ was selected during the validation stage.

Similar to BD-CNN training, 10% of the training data were used for validation to fine tune the model architecture and hyperparameters. The model was trained with early stopping based on validation loss and a maximum of 150 epochs.

DL framework evaluation

The framework is evaluated using the 20 test cases in 3 aspects: (1) planning time, (2) FM prediction, and (3) dosimetric quality of the final plans generated from the predicted FMs.

Each step of the DL framework was timed and averaged among all test cases. The prediction error of each FM was calculated as

$$Err\left(F_{true},F_{pred}\right)=\frac{\sum \left|F_{true}-F_{pred}\right|}{\sum F_{true}}.$$ (4)

In addition to the fluence prediction error, we also compared the similarity between the predicted FM and that of the benchmark plan, and normalized cross correlation was calculated for each beam. A cutoff threshold of 20% of the maximum fluence value was used to define the area of interest, that is, values below the threshold were set to 0.

Although the direct output of the DL framework is FMs, the quality of the final plans ultimately determines the usefulness of the model in the clinic. Thus, the predicted FMs were imported into the Eclipse TPS to generate the predicted plan for each test case. The predicted plans were compared with the benchmark plans based on clinically relevant dosimetric endpoints, including PTV33 D_max, PTV33 D_95%, PTV33 V_33Gy, PTV33 D_mean, PTV25 V_25Gy, PTV25-33 D_mean, OAR D_max, OAR D_1cc, and OAR D_2cc. The dice coefficients between prescription (25 or 33 Gy) isodose and PTV contours were calculated to represent the dose conformity of the benchmark and predicted plans.

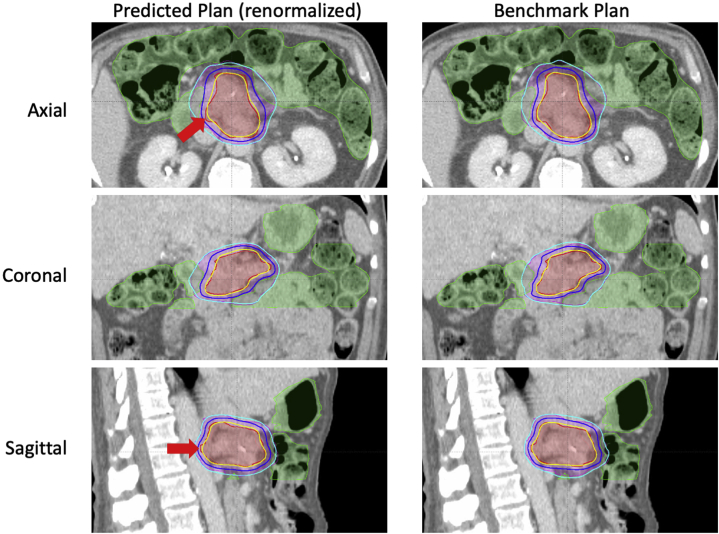
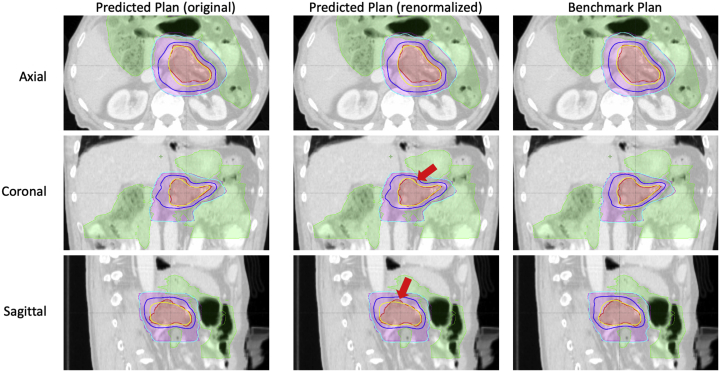
Finally, the predicted plans were evaluated and compared with the corresponding benchmark plans by an attending physician specializing in GI cancers. All plans were directly generated from DL prediction and no renormalization was performed. The predicted plans were assigned 1 of 4 grades (A, B, C, D) by the physician.³⁴ The detailed evaluation criteria are described in the Supplementary Materials. Plans with grade A or B were considered clinically acceptable, while plans with grade C or D were renormalized and re-evaluated. The grades served as a quantitative measure of clinical acceptability of the predicted plans. The pooled grade point averages of all test cases were used to measure the overall performance of the proposed framework.

Results

Model training and prediction time

For the BD-CNN, 7718 slices from 80 cases were used for training. The BD-CNN has the capacity of 4.4 million trainable parameters, and the training process took approximately 6 hours to finish 100 epochs with early stopping to avoid overtraining. The loss function weight α was 0.1. Compared with the BD-CNN, the FM-CNN had fewer trainable parameters (0.8 million). There were 720 FMs (9 each from 80 cases) for the FM-CNN training. The training process took 5 minutes to finish 75 epochs with early stopping as well. The fluence error threshold $y_{th}$ was 0.005.

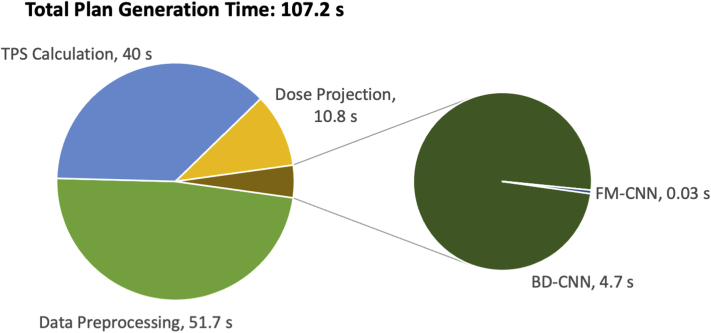
After model training, the DL framework takes little time to generate plans for new cases. Figure 3 illustrates the average time taken by the major steps of the proposed method. For the 20 test cases, the PTV25 volume was an excellent indicator of the input size (average, 234.4 cm³; range, 37.1-550.0 cm³; standard deviation, 162.7 cm³). The total planning time was 107.2 seconds on average (range, 78.2-142.6 seconds; standard deviation, 18.3 seconds). Because all 3D planning elements were upsampled to 1 × 1 × 1 mm³ voxel size, data preprocessing took the longest time (average, 51.7 seconds; range, 29.6-94.5 seconds; standard deviation, 16.1 seconds) in the workflow. On average, individual beam’s dose projection to the BEV plane took 10.8 seconds per patient (range, 3.5-19.5 seconds; standard deviation, 5.6 seconds), and the combined prediction time of the 2 CNNs was only 4.73 seconds (range, 3.2-7.2; standard deviation, 1.3 seconds). The plan finalization step in the TPS took 40 seconds per patient, which includes leaf sequencing and final dose calculation. This step also takes place in the manual planning workflow (after inverse optimization) and consumes the same amount of time. In total, a deliverable plan could be generated within 2 minutes, which is significantly faster than manual planning.

Figure 3.

The breakdown of plan generation time per patient for the proposed method. Abbreviations: BD-CNN = beam dose convolutional neural network; DL = deep learning; FM-CNN = fluence map convolutional neural network; TPS = treatment planning system.

Evaluation of predicted FMs

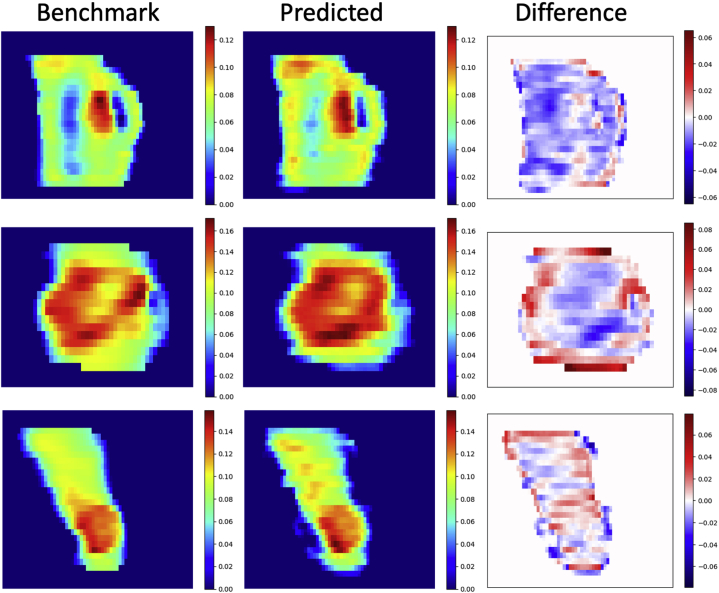
The predicted fluence maps had an error (Eq. 4) of 4.0% ± 1.0% (mean ± standard deviation) relative to the mean values of benchmark FMs. The normalized cross correlation between the benchmark plan’s FM and predicted plan’s FM was 0.949 ± 0.022 (mean ± standard deviation), with the range (0.878-0.992). Figure 4 shows the predicted FMs side-by-side with the benchmark FMs from 3 randomly selected test cases. The results highlight the high similarity of the FM pattern between the predicted and benchmark FMs.

Figure 4.

Fluence map comparisons (left column, benchmark; center column, predicted; right column, difference [benchmark – predicted]). The fluence map pairs were randomly selected from 3 of the 20 test cases. Each pair used the same color map. The predicted fluence maps exhibited similar patterns as the benchmark fluence maps, especially in high fluence regions. (A color version of this figure is available at https://doi.org/10.1016/j.adro.2021.100672.)

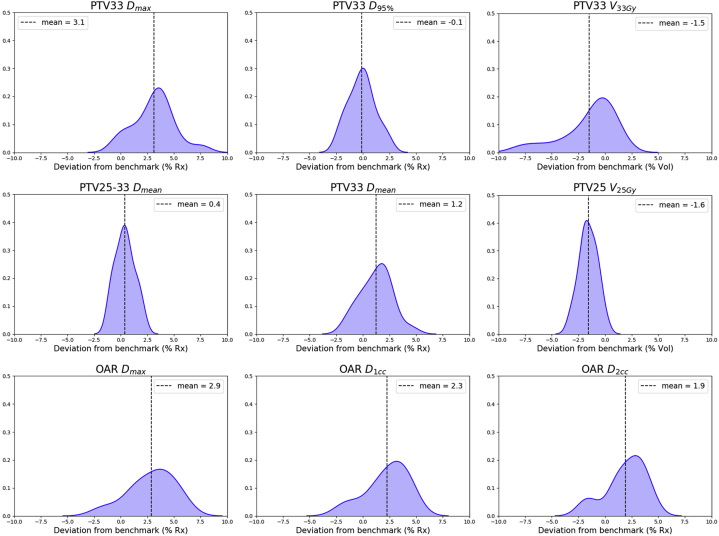
Evaluation of predicted plan quality

To illustrate the predicted plans’ dosimetric deviations from the benchmark plans and the general trend of DL predicted plan quality, we show in Figure 5 probability density plots of the deviations measured in the 20 test plans for each dosimetric endpoint. A plot with a narrower peak, such as PTV25-33 D_mean and PTV25 V_25Gy, corresponds to smaller variation between the predicted and benchmark plans. The predicted plans’ PTV33 and OAR maximum doses are 1.03 Gy and 0.95 Gy higher than those in the benchmark plans on average, while the other dose metrics have relatively smaller deviations. The mean deviation values are denoted on the plots as vertical dashed lines. Bilateral kidneys and liver dose were all well below protocol constraint for both plan groups.

Figure 5.

The probability density plots for dose metric deviations of predicted plans from benchmark plans. As all dose metrics are relative values of dose or volume, the deviation values (X axis) are in percentage differences with the benchmark plans. The probability density plots display the deviation distributions for all 20 test cases. All plots have the same scale in Y axis, which denotes the relative likelihood of the deviation. For each dose metric, the mean deviation value is denoted by the dashed line. Abbreviations: OAR = organ at risk; PTV = planning target volume.

The total monitor units (mean ± standard deviation) of the predicted plans (1480.3 ± 182.0) and benchmark plans (1529.4 ± 235.6) are comparable, suggesting similar FM complexity. The dice coefficients between the 25 Gy isodose line and PTV25 contour are 0.924 ± 0.061 (benchmark) and 0.918 ± 0.058 (predicted) (paired t test P = .08). The dice coefficients between the 33 Gy isodose line and PTV33 contour are 0.902 ± 0.051 (benchmark) and 0.876 ± 0.050 (predicted) (paired t test P < .01).

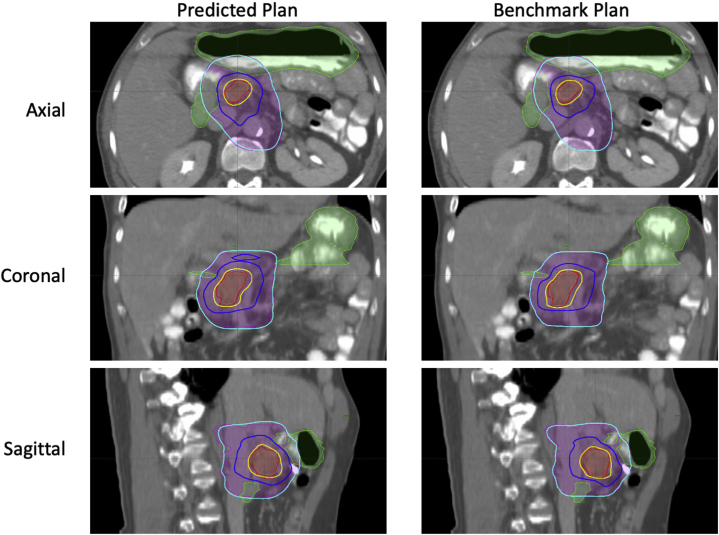
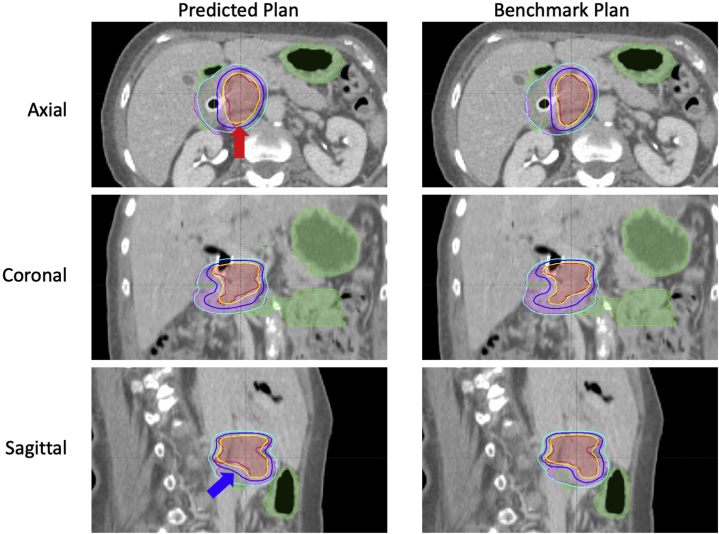
In the initial evaluation of predicted plans, the physician assigned 8 plans the grade of A; 5 grade B; 6 grade C; and 1 grade D. An example case is shown in the Supplementary Materials for each grade. After renormalization, 19 out of 20 predicted plans were deemed acceptable by the physician for clinical treatment, with the overall grade point averages improved from 3.0 to 3.35.

Discussion

In this feasibility study, we investigated a DL framework designed for pancreas IMRT planning with simultaneous boost targets. This framework transforms 3D anatomic images to 2D FM, a process traditionally performed by the time-consuming inverse optimization. We split the problem into 2 independent tasks, each solved by a deep neural network. The BD-CNN operates in the 3D anatomy/dose space, whereas the FM-CNN operates in the 2D beam’s eye view/fluence space. Combining the 2 networks, our framework can produce a deliverable plan in 2 minutes, allowing fast plan generation without inverse optimization. This plan generation process is also free from human intervention, which avoids inconsistency in plan quality due to planner experience. With more optimized code and higher computation power, the time for data preprocessing and dose projection could be reduced even more, offering the potential of real time automated planning for clinical practice.

The dice coefficients suggest that both planning methods can generate prescription isodose lines highly conformal to PTV targets, with benchmark plans having slightly better PTV33 conformity than predicted plans. Although the overall PTV coverage and OAR sparing have achieved clinical quality, dose in certain local areas may be overlooked by the DL framework when attempting to reduce the total error during model training. This could have a significant effect on certain dose metrics such as the maximum point dose.

In this study, we focused on high-dose conformity (ie, dose gradient) around the PTV, especially in the PTV-OAR overlapping regions, with an L2-norm penalty function designed in the BD-CNN. Hence, large dose gradient variations are heavily penalized in model training whereas maximum point dose variation in the PTV is not. Such balance helps us achieve overall dosimetry quality in the predicted plans. In addition, in the context of SBRT planning, higher maximum dose within the PTV (compared with standard IMRT/volumetric-modulated arc therapy planning) is often acceptable, with high-precision imaging guidance radiation therapy implemented for those treatments. We acknowledge that there is room for improvement to reduce hotspots, and it will be investigated in future studies.

The structure of the BD-CNN model also restricts the beam setting to a certain number of fixed beam angles (eg, 9 in this study). The predicted plans should have the same beam settings as the training plans. Although this limitation has a relatively smaller effect on pancreas SBRT planning with its naturally central disease locations, the BD-CNN’s model architecture will require modification for sites such as the lung, where variable beam angles are essential.

This study is an important step toward automating FM prediction and plan generation for pancreas SBRT treatment planning. Translating this technique to clinical deployment may require additional methods in place in the future to further enhance the versatility of the tool in tailoring the dose for a specific patient. Such areas may include customizable hotspot volume, adjustable dose gradient level to enhance or relax OAR dose, tradeoff toggle between PTV coverage and OAR sparing, and so forth. These additional steps would further enhance the user experience when the tool is deployed clinically.

Conclusions

A novel DL framework was developed to directly predict FMs, and it has demonstrated feasibility for pancreas SIB-SBRT. The framework uses 2 CNNs to perform BD prediction and FM prediction, which bypasses the time-consuming inverse optimization process. This approach enables rapid IMRT plan generation, which provides a valuable tool for a high throughput clinic.

Supplementary Materials

Fig. E1.

Fig. E2.

Fig. E3.

Fig. E4.