Abstract
Ultrasound-enhanced recombinant tissue plasminogen activator (rt-PA) mediated thrombolysis is under development as an adjuvant to ischemic stroke therapy. The goal of this study was to design a pulsed ultrasound (US) scheme that reduced intracranial constructive interference and tissue heating, and maintained thrombolytic efficacy relative to continuous wave (CW) insonation. Three 220-kHz US schemes were evaluated, two pulsed insonation schemes (15 cycles, 68 μs pulse duration, 33% or 62.5% duty cycle) and an intermittent CW insonation scheme (50 s active, 30 s quiescent) over a 30-min treatment period. An in silico study using a finite-difference model of transcranial US propagation was performed to estimate the intracranial acoustic field and temperature rise in the skull for each insonation scheme. In vitro measurements with flow were performed to assess thrombolysis using time-lapse microscopy. Intracranial constructive interference was not reduced with pulsed US using a pulse length of 15 cycles compared to intermittent CW US. The 33.3% duty cycle pulsed US scheme reduced heating in the temporal bone as much as 60% relative to the intermittent CW scheme. All insonation schemes promoted sustained stable cavitation in vitro and augmented thrombolysis compared to rt-PA alone (p<0.05). Ultraharmonic and harmonic cumulative energy over a 30-min treatment period was significantly higher (p<0.05) for the intermittent CW US scheme compared to either pulsed US scheme. Despite the difference in cavitation emissions, no difference was observed in the clot lysis between the three US schemes. These findings demonstrate that a 33.3% duty cycle pulsed US scheme with a 15-cycle burst can reduce bone heating and achieve equivalent thrombolytic efficacy as an intermittent CW scheme.
Keywords: Stroke, thrombolysis, therapeutic ultrasound, rt-PA, duty cycle, stable cavitation
1. Introduction: 1
Stroke is the fifth leading cause of mortality and a leading cause of morbidity with ischemic stroke accounting for 87% of all strokes in the United States (Benjamin et al 2018). Although intravenous (IV) recombinant tissue plasminogen activator (rt-PA), a common stroke treatment, is the only FDA approved thrombolytic, only 1.7-4.8% of stroke patients receive this lytic (Benjamin et al 2018). Unfortunately, the median time to recanalization in patients treated with IV rt-PA exceeds 2 hours, which results in significant morbidity and mortality (Broderick and Hacke 2002, Emberson et al 2014). Ultrasound (US) enhanced thrombolysis (UET) has been studied extensively in vitro and in vivo as an adjuvant to rt-PA therapy (Leeman et al 2012, Prokop et al 2007, Xu et al 2008, Acconcia et al 2013, Pfaffenberger et al 2003, Petit et al 2015, Holland et al 2008). Microbubbles produced in the ultrasound field or supplied exogenously expedite thrombolysis (Tachibana and Tachibana 1995). Fluid mixing caused by acoustic cavitation of microbubbles and radiation force is as an important mechanism responsible for this lytic enhancement (Nyborg 1953, Pfaffenberger et al 2003, Frenkel et al 2006, Bader et al 2015). Cavitation dynamics can be subdivided into two types, inertial and stable. Inertial cavitation corresponds to volumetric growth and rapid collapse of a bubble exposed to an acoustic wave (Holland and Apfel 1989). The growth and collapse of the bubble is dominated by the inertia of the fluid, generating a shockwave (Holzfuss et al 1998) and mechanical disruption during bubble collapse (Weiss and Selvaraj 2013). Stable cavitation describes gentler, sustained bubble activity, which promotes fluid mixing, lytic penetration into the clot, and debris removal (Elder 1959, Collis et al 2010). Increased lytic efficacy has been correlated with the presence of inertial cavitation (Chuang et al 2010, Weiss and Selvaraj 2013, Chen et al 2014) and with stable cavitation (Prokop et al 2007, Datta et al 2006, Hitchcock et al 2011, Bader et al 2015). Datta et al (2006) observed that thrombolytic efficacy was greater with stable cavitation alone compared to stable cavitation and inertial cavitation, due to sustained bubble activity instead of bubble destruction.
Insonation parameters can be chosen to promote stable cavitation and avoid inertial cavitation to improve therapeutic efficacy (Leeman et al 2012, Gruber et al 2014, Lin et al 2017, Xie et al 2011, Shi et al 2010). Hitchcock et al (2011) and Bader et al (2015) demonstrated enhanced thrombolytic efficacy using 120 kHz intermittent continuous wave (CW) ultrasound schemes. An intermittent insonation scheme takes advantage of a quiescent period to allow a fresh bolus of an ultrasound contrast agent (UCA) or other cavitation nucleation agent to infuse the therapeutic region of interest. This intermittent CW ultrasound scheme was chosen to maximize stable cavitation emissions (Hitchcock et al 2011). However bubbles as large as 53 μm in diameter, which may have been caused by coalescence of liberated microbubbles from Definity® that were contaminated with air, were observed in vitro by Bader et al (2015) under similar insonation conditions. Bader et al (2015) noted that these large bubbles were loci for thrombolysis, but that bubbles of this size could potentially cause embolization in vivo (Muth and Shank 2000). The growth and coalescence of liberated microbubbles in an ultrasound field are determined by several factors including acoustic pressure (Fan et al 2014, Shekhar et al 2017), pulse duration (Chen et al 2016), and resonant size (Crum 1984). (Postema et al 2004) have shown that liberated microbubbles coalesce and grow up to the resonant size. The resonant diameter of liberated microbubbles insonified at 220 kHz is 26 μm (Minnaert 1933), approximately half the size of the bubbles observed by Bader et al (2015). By limiting the pulse duration, bubble coalescence would be mitigated. No adverse effects have been reported from clinical use of this size contrast agent (Parker et al 2013).
In addition to bubble size, the intracranial pressure and temperature need to be controlled to prevent off-target bioeffects. Significant concern has been raised following the TRUMBI trial, in which 13 out of 14 patients treated with IV rt-PA and transcranial 300 kHz pulsed ultrasound suffered intracerebral hemorrhage (Daffertshofer et al 2005). The TRUMBI trial used a pulsed insonation scheme with a 500 μs pulse duration, which was six times greater than the transit time across an average human skull (Bouchoux et al 2014, Ammi et al 2008). Baron et al (2009) showed that for the TRUMBI trial, the interaction between the transmitted field and subsequent reflections from the contralateral bone resulted in regions of constructive interference. Contralateral local maxima up to 1.1 times the pressure amplitude in the intracranial location of a thrombus were predicted for a single element 120-kHz transducer (Bouchoux et al 2014).
O’Reilly et al (2010) have shown that standing waves can be minimized by controlling the pulse duration and duty cycle. Though constructive interference cannot be avoided completely, limiting the pulse duration to less than the transit time across the skull (~75 μs) confines the region of interaction to the contralateral side of the brain deep to the skull. Additionally, allowing each transmitted pulse to reflect three times before it interacts with the next pulse reduces the amplitude between 71-99% at 120 kHz (Bouchoux et al 2012), and this effect would be more pronounced at 220 kHz.
A shorter exposure time would also reduce another bioeffect, tissue heating. Bouchoux et al (2014) predicted that tissue heating in excess of 3.8-13.4 °C would occur in the near field in the temporal bone exposed to 120 kHz – 500 kHz CW ultrasound. Thermal damage to the brain cortex adjacent to skull has been observed for 230 kHz CW therapeutic ultrasound (McDannold et al 2016). A short pulse duration (~75 μs) and low duty cycle (33%) would reduce constructive interference and tissue heating, sources of potential adverse bioeffects. A 15-cycle pulse with a 33.3% duty cycle was chosen to limit thermal and mechanical bioeffects in transcranial therapy. The 33.3% duty cycle pulsed ultrasound scheme was compared to the intermittent CW scheme (50 s active, 30 s quiescent) and a 15-cycle pulsed ultrasound scheme with a 62.5% duty cycle which matches the total on time of the intermittent CW scheme. However, cavitation amplitude could be reduced using pulsed schemes which may inhibit cavitation mediated thrombolysis (Lin et al 2017, Pouliopoulos et al 2016).
The goal of this study was to evaluate the thrombolytic efficacy of these three ultrasound schemes in vitro. First, a finite-difference model of transcranial ultrasound propagation was used to simulate the acoustic field, degree of constructive interference, temperature rise, and thermal dose in 20 stroke patients due to the three 220 kHz insonation schemes. Subsequently, the thrombolytic efficacy was evaluated for the two 220-kHz pulsed schemes, one with a duty cycle of 33.3%, the other 62.5%) and an intermittent CW (50 s active, 30 s quiescent) scheme. Cavitation emissions were quantified to assess the contributions of stable cavitation on clot lysis for all three ultrasound schemes.
2. Materials and Methods:
2.1. Pulse design
The three insonation schemes are shown in figure 1. The intermittent CW ultrasound scheme is based on Bader et al (2015), who determined that ultraharmonic (UH) cavitation emissions were maximized and broadband cavitation emissions were minimized with a 50 s CW insonation period and 30 s quiescent period. In the present study, a calculation of the spatial pulse length for the pulsed simulations was determined by measuring the minimum distance between the ipsilateral temporal bone and the distal skull on cranial CT (Computed Tomography) images of 20 stroke patients (Bouchoux et al 2014). This minimum distance was computed by aligning the natural focus (53 mm) of a 38-mm diameter 220-kHz unfocused single-element ultrasound transducer with the middle cerebral artery (MCA) in each patient using the CT-based positioning algorithm developed by Bouchoux et al (2014). The distance measured corresponds to approximately 15 cycles at 220 kHz. A 33.3% duty cycle (4.9-kHz pulse repetition frequency, PRF) was selected to reduce the possibility of constructive interference between consecutive pulses. A 62.5% duty cycle (9.2-kHz PRF) was tested to achieve equivalent insonation time over a 30-min treatment duration as the intermittent CW scheme when the same transmit pressure amplitude was employed.
Figure 1.
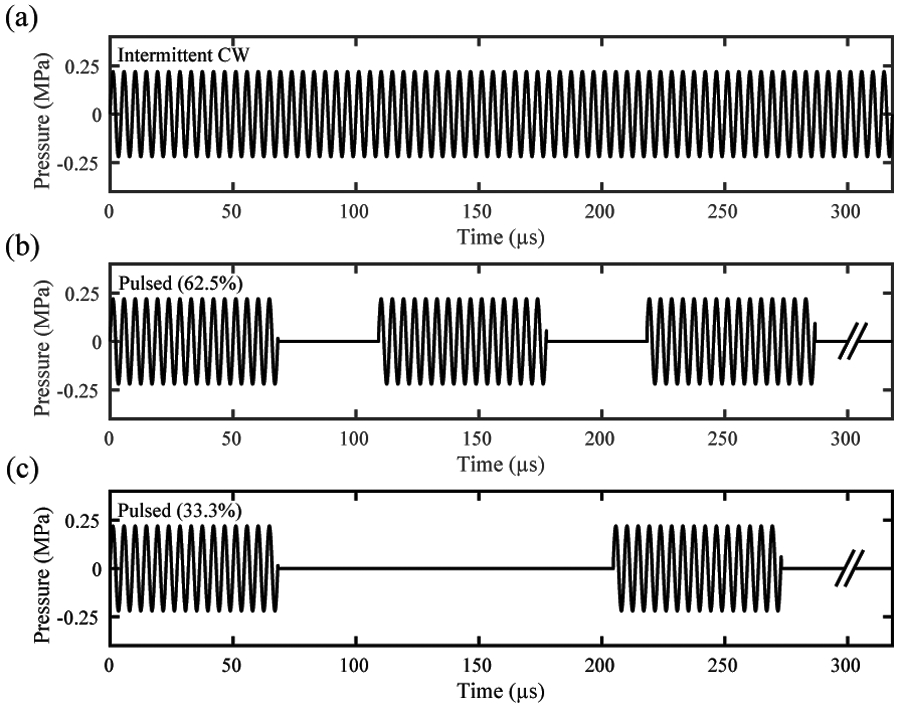
Insonation schemes for (a) the intermittent continuous wave (CW) ultrasound with 50 seconds active and 30 quiescent, (b) the 62.5% and (c) the 33.3% duty cycle pulsed ultrasound with 15-cycle pulses. A limited time period is shown for all three insonation schemes for clarity. The hash marks indicate that the pulse continues on with the same pulse duration and quiescent time as seen before the hash marks.
2.2. Computational modeling of 220-kHz ultrasound propagation through the skull
The acoustic fields for all three schemes were calculated using a finite-difference time-domain (FDTD) method developed and validated by Bouchoux et al (2012) and extended for pulsed ultrasound. This computational method was used to predict the pressure and temperature in the M1 region of the MCA, the brain, the bone, and the extracranial soft tissue. This model assumes linear propagation and neglects shear-waves (which is appropriate for an 11.7 ± 5.6° angle between the transducer axis and the normal to the bone). The acoustic and thermal simulations were implemented in MATLAB (R2016b, The Mathworks, Natick, MA, USA) and C. The computations were run on a PC with 16 GB RAM and a 3.5 GHz processor with six cores (i7-7800X, Intel, Santa Clara, CA, USA). The transducer was modeled as a single element, cylindrical velocity source with a 38 mm diameter and 220 kHz center frequency. Three source excitation patterns were implemented: 1) a 70-cycle pulse to approximate CW excitation, and four pulses of 15 cycles with either 2) 62.5% duty cycle, or 3) 33.3% duty cycle. These source excitation patterns allowed a sampling of the steady state acoustic pressure field for 40 cycles in the intermittent CW scheme, and a complete period of the 15 cycle pulsed ultrasound schemes. The instantaneous acoustic pressure field in the steady state was used to determine the instantaneous acoustic intensity as input to the bioheat transfer equation to predict tissue heating (Pennes 1948).
We extended the FDTD model of Bouchoux et al (2012) to include the computation of the instantaneous intensity for each temporal step as (Pierce 1989). An analysis of the error in the intensity calculation using the plane wave approximation instead of this computational approach is discussed in the appendix. The temporal average intensity magnitude at each point in space, ITA(x, y, z), is now estimated from Ii as
| (1) |
where pi is the instantaneous acoustic pressure, is the instantaneous particle velocity, and τ is the time interval over which the intensity is calculated. For the CW case, τ was chosen to be 181.8 μs (40 cycles), after an initial 30 cycles to ensure steady state intensity within the skull. For the pulsed schemes, τ was chosen to be 204.6 μs and 109.1 μs for the 33.3% and 62.5% duty cycle, respectively, to capture the intensity of one full pulse with 15 cycles and the subsequent quiescent period. The temporal averaged intensity was calculated after the second pulse. By implementing this algorithm, the change in intensity from pulse to pulse was less than 0.5%, thus ensuring a steady state intensity throughout the skull.
2.3. Acoustic and thermal parameters
Maximum peak-to-peak pressure, acoustic intensity, and temperature elevation were characterized for all three insonation schemes. Four regions of interest (ROI) were defined for each CT scan based on the tissue type: the extracranial soft tissue (ST), the bone, the brain, and the clot. The acoustic output of the 220 kHz transducer was adjusted to keep the maximum acoustic pressure in the clot consistent across all three schemes (0.44 MPa). The maximum spatial-peak temporal-peak pressure and the maximum temperature in each ROI was recorded for each insonation scheme. Temperature elevation in the external soft tissue, bone, brain, and clot was estimated using the bioheat transfer equation as implemented in Bouchoux et al's (2014) algorithm, adapted for pulsed and intermittent CW ultrasound. Tissue perfusion was modeled in the external soft tissue and the brain, but was neglected in the bone (Bouchoux et al 2014). This assumption is valid as (Duck 1990) reports perfusion in the bone is an order of magnitude lower than in the soft tissue Additionally, Conner and Hynynen (2004) found that inclusion of bone perfusion resulted in a 2.5% lower maximum temperature than if bone perfusion were neglected. Perfusion in the MCA was also neglected to model a full occlusion of the MCA, which is a worst-case scenario for heating of the clot and nearby tissue. The time-averaged intensity was used to compute the thermal source over every point in space, Q = 2αITA, where α is the acoustic absorption coefficient. The thermal relaxation time for human tissue, 0.464 – 6.825 s based on the tissue parameters (Zhang 2009), exceeds the time between pulses, 136 μs and 109 μs, corresponding to the 33.3% and 62.5% duty cycle schemes, respectively. For intermittent CW ultrasound, the time-averaged intensity over the last 40 cycles was used as the thermal source for each 50 s active period. The thermal source was assumed to be zero during each 30 s quiescent period. The resultant temperature was predicted to oscillate in a steady state pattern after 400 s that varied less than 5% for the intermittent CW US scheme. This time period was determined empirically and applied to the pulsed US schemes. Using the spatial maximum temperature in each skull, the thermal dose was calculated. The thermal dose (TD) was calculated as the cumulative equivalent minutes at 43 °C,
| (2) |
where Δt is the time step (1 s), and T(t) is the instantaneous temperature (Sapareto and Dewey 1984). For the pulsed ultrasound schemes, the thermal dose for each 30-minute treatment was calculated using the time-temperature curve from the bioheat transfer equation over the first 400 s, and then a steady-state temperature was assumed for the remaining 1400 s. For CW excitation, the thermal dose was calculated in a similar manner until steady state (400 s), and contributions for 17.5 subsequent 80 s thermally oscillating periods were simply added.
2.4. 220-kHz transducer
A single-element piezoelectric composite ultrasound transducer was fabricated in Dr. Xiasheng Guo’s laboratory (Nanjing University, Nanjing, China) and used for in vitro thrombolysis efficacy experiments. The center frequency and aperture of the transducer were 220 kHz and 38 mm, respectively. The −3 dB beamwidth was 1.06 cm and the −3 dB depth of field was 7.38 cm. The natural focus of the transducer was 5.4 cm, consistent with the average propagation depth to the MCA occlusions in 20 ischemic stroke patients (Bouchoux et al 2014). A custom matching network was built to ensure efficient transmission of energy. The transducer was calibrated using a hydrophone, TC4038 (Reson, Goleta, CA, USA) in a vibration isolated degassed water tank.
2.5. Clot lysis
Human whole blood was drawn from four donors following an approved Institutional Review Board protocol (IRB #2012-2527). Donors provided written informed consent prior to each blood draw. The donors had not taken any medications known to affect blood clotting or lysis. Clots were prepared following the protocol reported by Bader et al (2015). In brief, blood clots were formed around 7-0 silk sutures within borosilicate glass capillary tubes (1.12 mm inner diameter). Clots were incubated at 37 °C for 3 hours, followed by 72 hours incubation at 4 °C to allow for clot retraction. Each clot was suspended inside a 2.15 mm diameter glass micropipette by the suture and placed in flow (0.65 mL/min) using a syringe pump. The flow rate (0.65 mL/min) in this study is in the range of flow rates observed clinically in the MCA during stroke (Alexandrov et al 2010). An inverted microscope was used to examine the proximal end of the clot to monitor average clot width over 30 minutes (figure 2). Images were captured at a frame rate of 2.33 Hz and with a shutter speed of 16 ms. The experimental arms included plasma alone (negative control), plasma with rt-PA, or plasma with rt-PA and Definity® (2 μL/mL) exposed to one of three different ultrasound insonation schemes. The concentration of Definity® microbubbles in this study (2.4 x 107 particles/mL) was several orders of magnitude higher than the dose approved for diagnostic purposes (1.7 x 106 particles/mL). However concentrations greater than this have been used safely in animal studies for therapeutic applications (Auboire et al 2018). Additionally the Definity® concentration was the same as the concentration used by Bader et al (2015) to generate robust cavitation for ultrasound exposure at 120 kHz. Definity® was activated according to Lantheus’ instructions and added to the reservoir of 37 °C human plasma. The treatment reservoir containing the plasma, rt-PA, and Definity® was mixed using a 10 mL pipet before each experiment. Experimental arms with rt-PA had a concentration of 3.15 μL/mL, which is the steady state concentration of rt-PA achieved in human ischemic stroke treatment (Seifried et al 1989, Tanswell et al 1991). A total of 80 clots were employed in this study (4 clots per donor per experimental arm, with five experimental arms).
Figure 2.
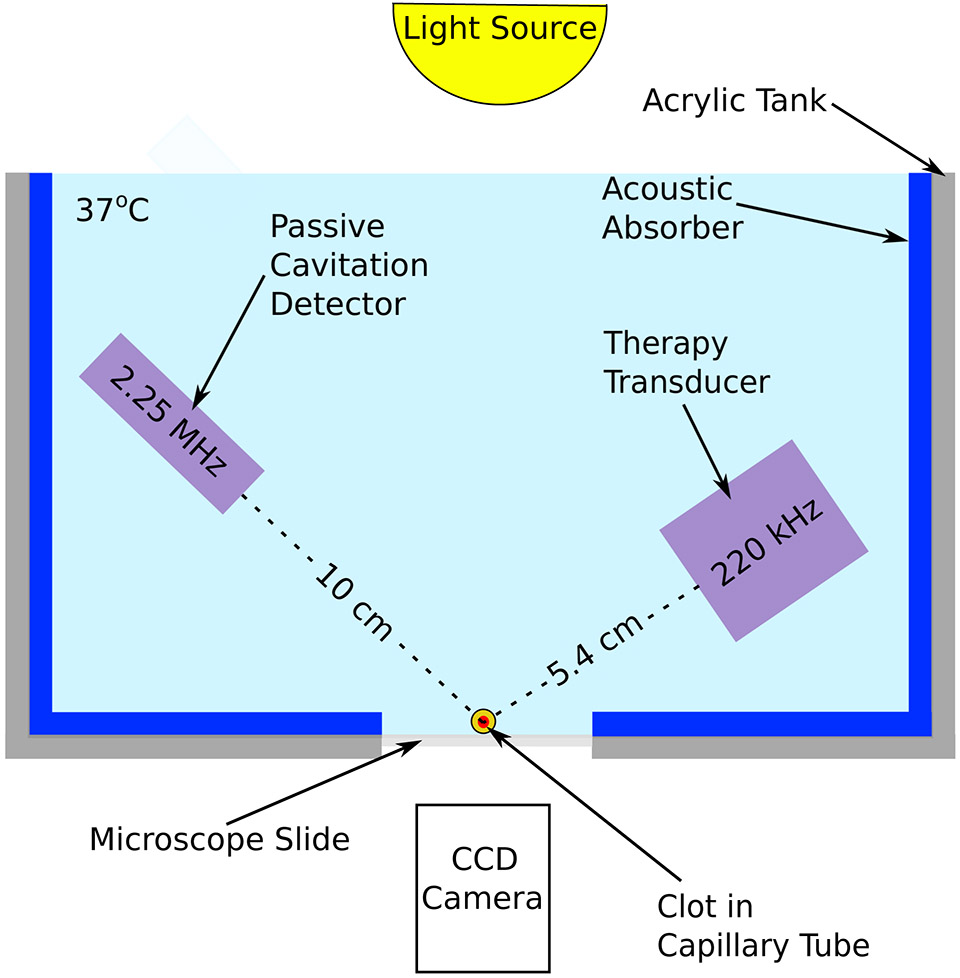
Time-lapse microscopy system used to monitor clot lysis during treatment. An acrylic tank was lined with an acoustic absorber to attenuate tank reflections. Clots were loaded in a glass micropipette confocal with both the therapy transducer (220 kHz single-element transducer) and the passive cavitation detector (2.25 MHz single-element transducer). The clot width was monitored using a CCD camera. The clot was exposed to a flow rate of 0.65 mL/min with the human plasma, recombinant tissue plasminogen activator, and Definity® included as appropriate.
The instantaneous clot width and the clot position were evaluated from images acquired by time-lapse microscopy using MATLAB (The Mathworks®, Natick, MA, USA), as described previously (Cheng et al 2005). An edge detection algorithm developed by Meunier et al (2007) and employed by Bader et al (2015), was applied to each gray scale image to determine clot width (shown in green in supplementary video 2 online). The mean clot diameter, , was calculated from the average distance from one edge of the clot to the other. The width of the suture was determined on an image of the suture upstream of the clot and was subtracted from the mean clot diameter. The fractional clot loss (FCL) and average lytic rate (ALR) were calculated using equation (3) and (4) respectively,
| (3) |
| (4) |
where d(t) is the clot diameter and t is time. If the clot completely separated from the suture during lysis, FCL and ALR were calculated until the time of separation.
2.6. Cavitation detection and quantification
The 220-kHz therapy transducer was aligned with the clot using a pulser-receiver (Panametrics 5077 PR, Olympus NDT, Waltham, MA, USA) to maximize the signal reflected from the micropipette filled with air. The acoustic field was mapped using a Reson TC4038 hydrophone (Reson, Goleta, CA, USA) so that the micropipette was within the −3 dB beamwidth of the transducer. Cavitation emissions were monitored using a single-element passive cavitation detector (595516C, Picker International, Ohio, USA) with a 19 mm aperture diameter and a center frequency of 2.25 MHz. The passive cavitation detector (PCD) was aligned orthogonally to the clot, and confocally with the 220-kHz transducer using the same pulser-receiver and micropipette target. The cavitation signal was filtered using an analog 10-MHz low pass filter (J73E, TTE Inc, Los Angeles, CA, USA) to reduce electrical noise and passed into a pre-amplifier (CLC100, Cadeka Microcircuits LLC, Colorado, USA). Cavitation emissions were quantified from a 10 ms signal acquired by the PCD and digitized at a sampling frequency of 31.25 MHz. Signals were acquired every 43 ms following each video frame acquisition. Each pulse within the 10 ms signal window was isolated using an envelope detection scheme and converted to the frequency domain. For the intermittent CW insonation scheme, the entire 10 ms window was converted to the frequency domain. In this way cavitation was not evaluated during the quiescent periods for either the CW or pulsed insonation schemes. The energy was calculated using equation (5) (Haworth et al 2017)
| (5) |
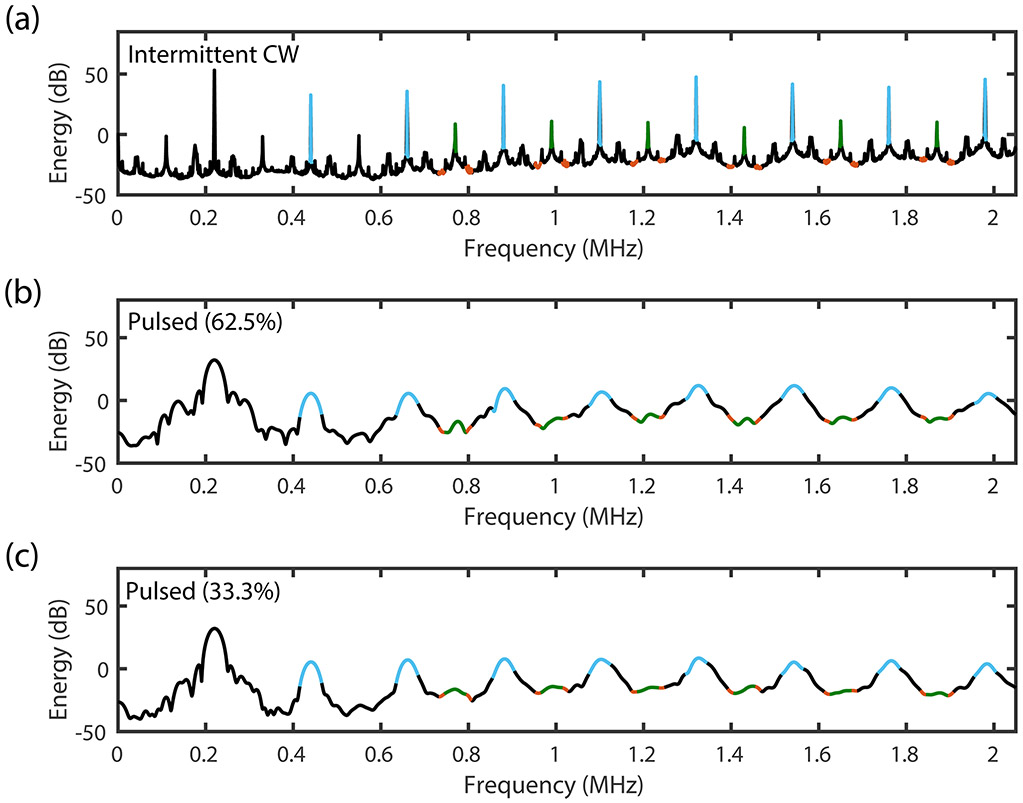
where E is proportional to energy (in units of mV2), x(t) is the digitized signal, w(t) is the Hanning window, T is the duration of the acoustic signal that is converted to the frequency domain, and fs is the sampling frequency. The total harmonic and UH energies were computed by summing the energy in each relevant frequency band over the 30-min treatment period. UH energy was calculated using frequency bands between 550 kHz and 1870 kHz. Harmonic energy was calculated using the harmonics between 440 kHz and 1980 kHz (figure 3). These UH and harmonic frequency bands were selected based on criteria used by Santin et al (2008), as they had at least 10 dB greater amplitude in the presence of ultrasound and Definity® compared to ultrasound and degassed water without Definity®. The intermittent CW cavitation data was processed following the method of Gruber et al (2014). To minimize the effect of spectral broadening in analyzing the emissions from the pulsed insonation schemes, different frequency bandwidths were tested. Received passive cavitation signals from the first two clots exposed to rt-PA, plasma, Definity®, and intermittent CW 220-kHz ultrasound (section 2.5) were subdivided into 15-cycle segments and converted to the frequency domain. The harmonic and ultraharmonic cavitation energies were calculated according to equation 5 using bandwidths ranging from 0 kHz to 60 kHz. The energies calculated from the segmented signals were compared to the energies computed from the unsegmented signals. A frequency band of 50 kHz was the smallest bandwidth that yielded a mean harmonic energy difference between the segmented and unsegmented signals of less than 1%. The mean calculated ultraharmonic energy using the two methods was within 10%. Thus a 50 kHz band was used to compute the harmonic and ultraharmonic energies for the pulsed ultrasound schemes. For all three insonation schemes, the inharmonic energy was quantified in 25-kHz wide bands centered 37.5 kHz on either side of each UH band.
Figure 3.
Energy Spectra for (a) continuous wave (CW), (b) 62.5% duty cycle pulsed ultrasound (US), and (c) 33.3% duty cycle pulsed ultrasound. The frequency bandwidth for the harmonic (blue) and ultraharmonic (green) in the CW US scheme is 4 kHz, and the inharmonic band (red) is two frequency bands of 25-kHz bandwidths surrounding each ultraharmonic. The frequency bandwidth for harmonic and ultraharmonic frequency bands in the pulsed US schemes are 50-kHz.
To improve the fidelity of cavitation signal analysis, energy associated with acoustic clutter caused by the tank reflections acquired in the absence of cavitation was subtracted from the signal. The harmonic peaks had a high signal-to-noise ratio (SNR) (>30 dB over the noise floor obtained when insonifying degassed water in the flow phantom) for each peak, but spectral broadening from the harmonic peaks leaked into the UH bands, confounding the quantification of UH energy for the pulsed ultrasound schemes. A custom algorithm was implemented in MATLAB to determine which UH bands had an SNR of at least 3 dB above neighboring inharmonic bands. Only the UH frequency bands which met this criterion were included in the quantification of UH energy.
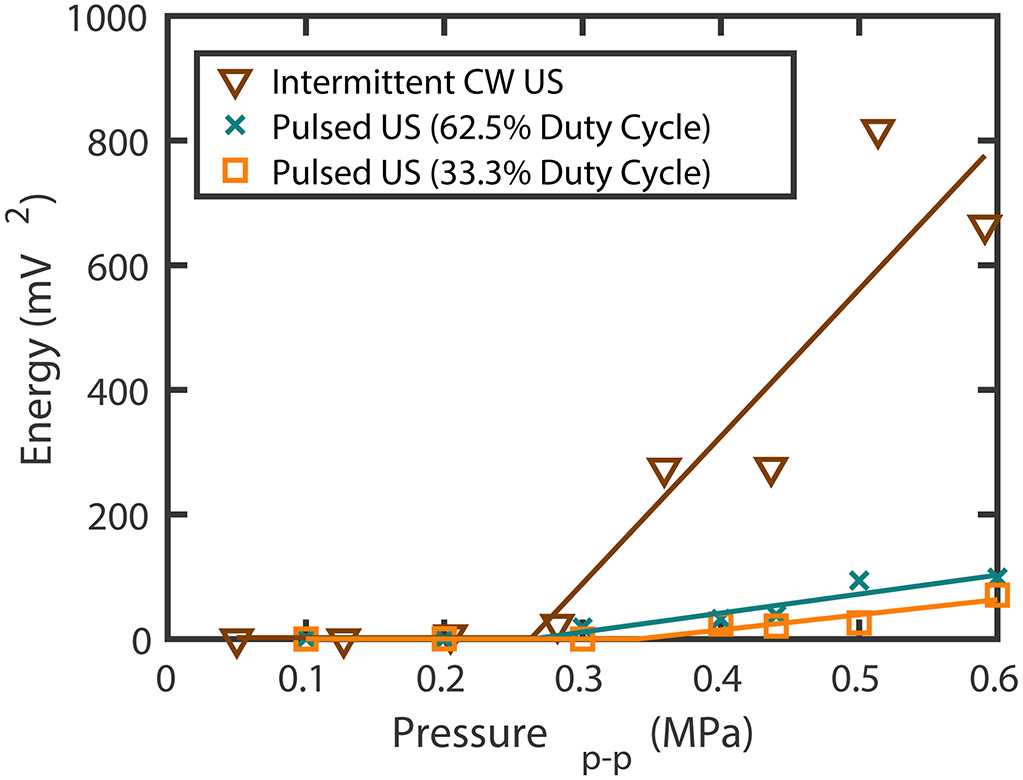
In order to guide the choice of the acoustic pressure amplitude employed for sonothrombolysis experiments, the stable cavitation threshold for each scheme was determined by varying the peak-to-peak pressure and recording the cavitation signal at each pressure for all three ultrasound schemes. Each point was the summation of UH cavitation emissions acquired over 80 seconds at each pressure. The received UH energy was plotted as a function of the peak-to-peak pressure amplitude and fit with a two-segment piece-wise linear equation (Radhakrishnan et al 2013). The point of change in the slope defined by the two segments was the stable cavitation threshold. The peak-to-peak stable cavitation thresholds were found to be 0.34 MPa, 0.26 MPa, and 0.25 MPa for 15-cycle pulsed ultrasound at 33% duty cycle, 62.5% duty cycle, or intermittent CW US respectively (figure 4). Thus, a peak-to-peak pressure amplitude of 0.44 MPa was employed in order to exceed the stable cavitation threshold at 220 kHz for all ultrasound schemes. This pressure amplitude corresponded to a spatial-peak temporal-average intensity (Ispta) of 1860 ± 980 , 1040 ± 510 and 570 ± 360 mW/cm2 for the intermittent CW scheme, 62.5% and 33.3% duty cycle pulsed ultrasound schemes respectively, calculated using the method outlined in section 2.2. This pressure amplitude promoted UH emissions and minimized inharmonic emissions for intermittent CW ultrasound insonation at 120 kHz (Bader et al 2015).
Figure 4.
Ultraharmonic energy measurements as a function of the peak-to-peak pressure for 33.3% duty cycle 15 cycle pulsed ultrasound (US), 62.5% duty cycle 15 cycle pulsed US, and intermittent continuous wave (CW) US at 220 kHz. Each point is the summation of the cavitation signal over 80 seconds. The point of change in the slope defined by the piecewise linear fit is defined as the cavitation threshold.
2.7. Statistical analysis
The D’Agostino & Pearson normality test was used to evaluate the computationally simulated pressure and temperature data in stroke patients, as well as the FCL, ALR, UH and harmonic cavitation energy. Though the FCL and ALR were found to be Gaussian, neither the simulated pressure and temperature nor the UH and harmonic cavitation signals were normal. Monte Carlo simulations (n = 100 for each maximum pressure and temperature in each of 4 tissues) for each subject were performed to account for the uncertainty of the finite difference method based on the errors reported by Bouchoux et al (2012, 2014) at 120 kHz. The resulting means of the Monte Carlo simulations were compared using a Friedman’s test to account for the repeated simulations on the same CT scans and a Nemenyi pairwise comparison was performed to determine which comparisons were significant. This analysis was performed in R Studio version 3.5.2 (RStudio Team, Boston, MA).
FCL and ALR were compared between each treatment protocol using a one-way unbalanced ANOVA with a post hoc analysis using a Tukey’s honest significance difference test. The UH and harmonic energies, were analyzed using a Kruskal-Wallis test with post hoc analysis using a Dunn test. These analyses were performed using GraphPad Prism 8 (GraphPad Software Inc., La Jolla, CA, USA). A significance level of 0.05 was used to reject the null hypothesis that there was no difference between the means for each ultrasound insonation scheme.
3. Results:
3.1. Transcranial pressure reduction, constructive interference and heating
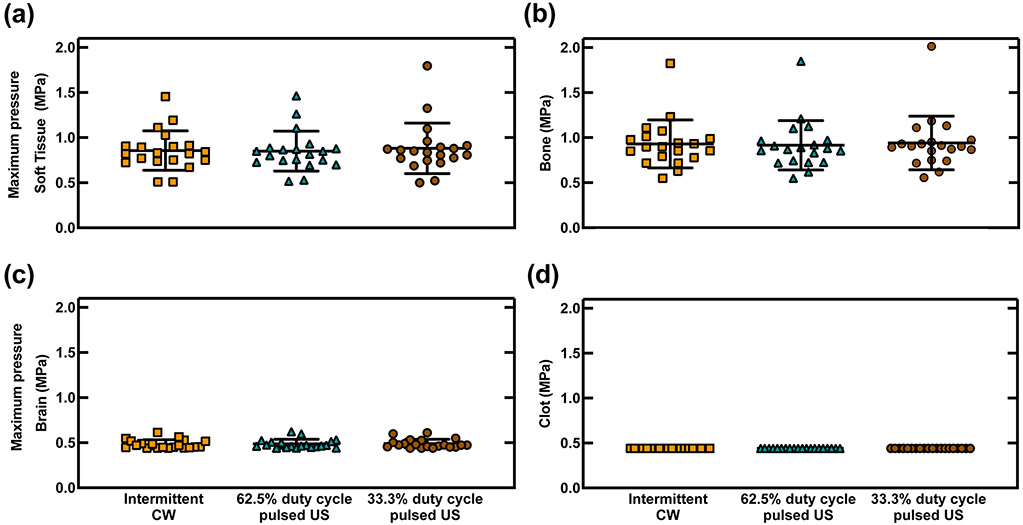
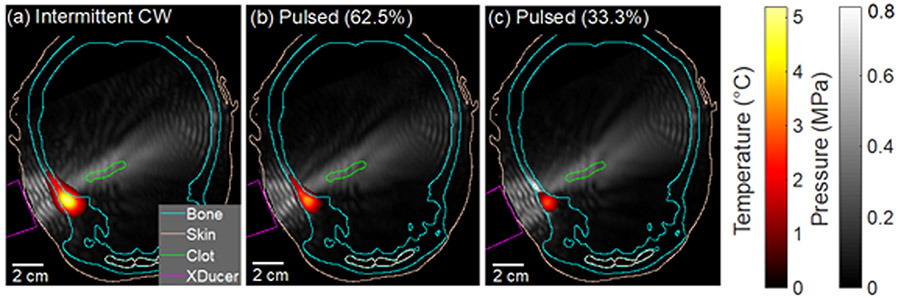
The maximum peak-to-peak pressure in all tissues was not significantly different for the three ultrasound schemes in any of the regions (p≥0.14) (figure 5). A representative video of the simulated acoustic field for 33% duty cycle pulsed ultrasound scheme is shown in supplemental video 1 online. Constructive interference patterns, characterized by nodes that were half a wavelength (3.5 mm) apart, were noted in several locations of the head including the contralateral brain and the extracranial soft tissue adjacent to the transducer. The acoustic field in the extracranial soft tissue on the ipsilateral side of the head had prominent constructive interference because of the primary reflection from the temporal bone (figure 6). The peak-to-peak pressure in the extracranial soft tissue and in the bone was as high as 1.80 MPa and 2.01 MPa, respectively, which was four to five times the pressure in the clot (0.44 MPa) for all three ultrasound schemes (figure 5). In the same patient with the maximum pressure in the skull, the peak-to-peak acoustic pressure at the transducer face was of 0.48 MPa. The acoustic pressure maximum in the brain parenchyma ranged from 0.44-0.62 MPa for all three schemes, which occurred either close to the clot, in the contralateral brain near the bone, or in the brain adjacent to the orbital shelf where some constructive interference was observed.
Figure 5.
Simulated peak-to-peak pressure maximums in four tissues in 20 CT scans for 220 kHz continuous wave (CW) ultrasound (US), and 220 kHz pulsed US with 15-cycle pulses at 62.5% duty cycle and 33.3% duty cycle. The pressure was reported in four regions: (a) extracranial soft tissue (ST) ,(b) bone, (c) brain, and (d) clot. The pressure maximum in the clot was fixed at 0.44 MPa for all 20 patients. No statistically significant difference in the pressure was found within each region examined
Figure 6.
Simulated temperature and acoustic pressure fields in a representative subject for (a) continuous wave (CW) ultrasound, (b) pulsed ultrasound with 62.5% duty cycle, and (c) pulsed ultrasound with 33.3% duty cycle. The absolute peak-to-peak pressure maximum for the simulations is displayed in gray scale. Temperature is displayed using a heat map with a minimum color priority threshold of 1 °C. CT features such as the bone (cyan) and the skin and internal epithelium (beige), and the clot (green), are plotted using contour lines. The transducer is outlined in magenta. Constructive interference is prominent in the soft tissue between the temporal bone and the transducer. Some constructive interference is also present in the brain tissue close to the contralateral temporal bone, however, the pressure in this region did not exceed the pressure in the M1 section of the middle cerebral artery. Temperature rise was prominent in the ipsilateral bone along the transducer axis.
The maximum temperature in the bone was significantly lower (p<0.0001) for the 33.3% duty cycle pulsed ultrasound scheme (0.5 - 6.7 °C) than for the intermittent CW scheme (1.1 - 16.7 °C, figure 7). Similarly, the temperatures in the brain, extracranial soft tissue, and clot were also significantly different between the 33.3% duty cycle pulsed ultrasound and the intermittent CW ultrasound schemes (p<0.0001). Additionally, a significant difference in temperature was observed between 62.5% duty cycle pulsed US and the intermittent CW US schemes for all regions except for the temperature in the bone (p>0.25). The thermal dose varied over the 20 patient skulls for the intermittent CW scheme, 62.5% duty cycle pulsed ultrasound scheme, and 33.3% duty cycle pulsed ultrasound scheme from 9 x 10−2 to 1 x 107 min, 3 x 10−2 to 3 x 103 min, and 1 x 10−2 to 5 x 102 min, respectively.
Figure 7.
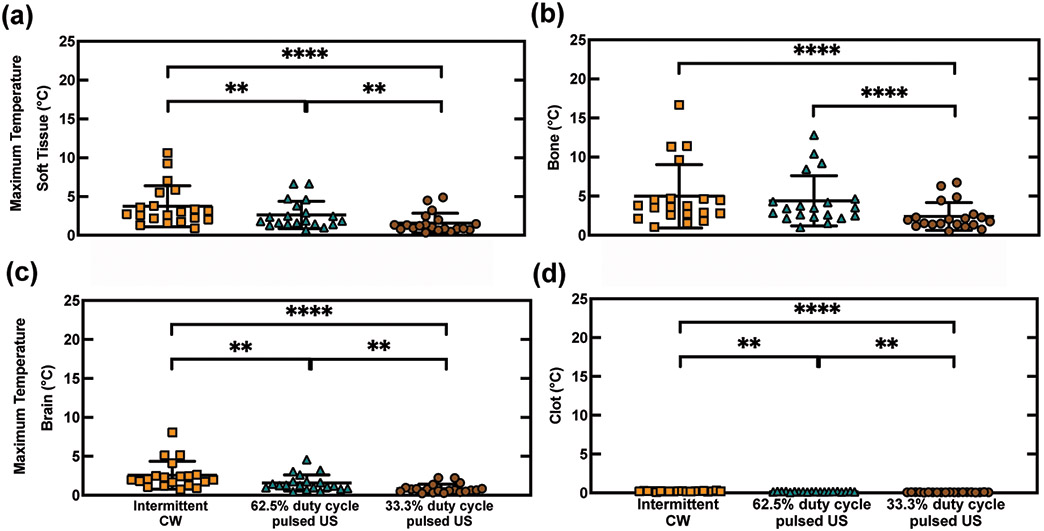
Simulated temperatures in 20 patients for 220 kHz continuous wave (CW) or pulsed ultrasound (US) with 15-cycle pulses at either 62.5% duty cycle or 33.3% duty cycle. Temperature was calculated using the bioheat transfer equation. A heating source was determined from the time-averaged intensity derived from the acoustic pressure (eq.4). The maximum temperature after 400 s was reported in four regions: (a) extracranial soft tissue (ST), (b) bone, (c) brain, and (d) clot. Statistically significant differences between insonification schemes are denoted by asterisks ** : p < 0.01, **** : p < 0.0001).
3.2. Clot lysis
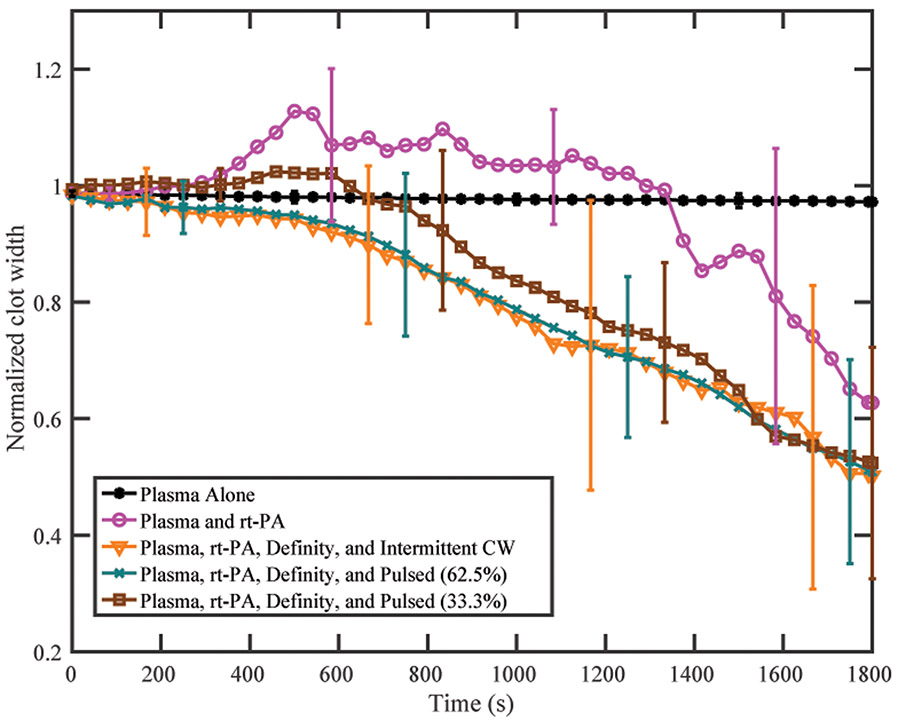
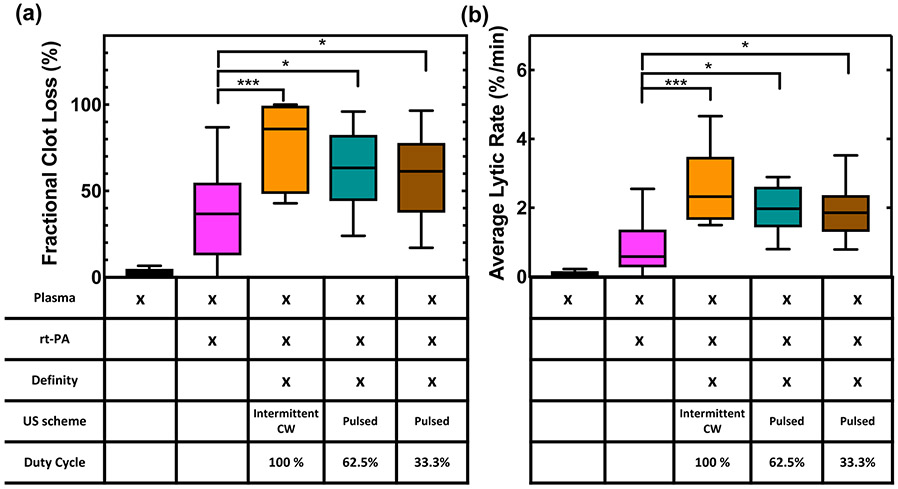
FCL was plotted as a function of time over 30 min for plasma alone, plasma with rt-PA, and plasma with rt-PA and US for all three insonation schemes (figure 8). A representative video of sonothrombolysis for the intermittent CW exposure is shown in supplementary video 2 online. No change in clot width was observed in the first five minutes. Clots treated with plasma and rt-PA alone increased in width between five and fifteen minutes followed by a gradual reduction over the last fifteen to twenty minutes (figure 8). This effect was also present in the clots treated with plasma, rt-PA, Definity®, and 33.3% duty cycle pulsed US scheme although clot expansion was less prominent and clot lysis occurred more rapidly than for clots treated with plasma and rt-PA alone. Clots treated with plasma, rt-PA, Definity®, and either the 62.5% duty cycle pulsed US scheme or the intermittent CW US scheme did not expand initially. Despite the different patterns of lysis, all clots treated with plasma, rt-PA, Definity®, and ultrasound had equivalent lysis after 30 minutes (figures 8, 9). The FCL and ALR of US-treated clots were significantly higher than clots treated with plasma and rt-PA alone (p<0.05) (figure 9). No significant difference was observed between clots treated with plasma, rt-PA, Definity®, and any of the three insonation schemes.
Figure 8.
Normalized clot width as a function of time for each treatment. All clots were treated in human fresh frozen plasma. A clot fraction over 100% indicates clot swelling and consequent increase in diameter. Clot swelling was observed early during treatment for clots treated with recombinant tissue plasminogen activator (rt-PA) alone. Clots treated with rt-PA, Definity®, and the 33.3% pulsed scheme showed minor clot swelling in the first few minutes. Each line is the mean of 16 measurements with the standard deviation given by the error bars.
Figure 9.
(a) Fractional clot loss (FCL) and (b) average lytic rate (ALR) achieved with each treatment group. The recombinant tissue plasminogen activator (rt-PA) concentration was 3.15 μg/mL. All ultrasound (US) groups included plasma and rt-PA (3.15 μg/mL) and Definity® (2 μL/mL) in the presence of flow (0.65 mL/min). Statistical significance using a one-way ANOVA is shown with brackets, where p < 0.05 is denoted by *, and p < 0.001 is denoted by ***. N=16 for each group. The median value is given by the center line in each box. A Tukey boxplot is used where the boxes span the interquartile range and the bars span the data from maximum to minimum excluding any outliers.
3.3. Cavitation detection
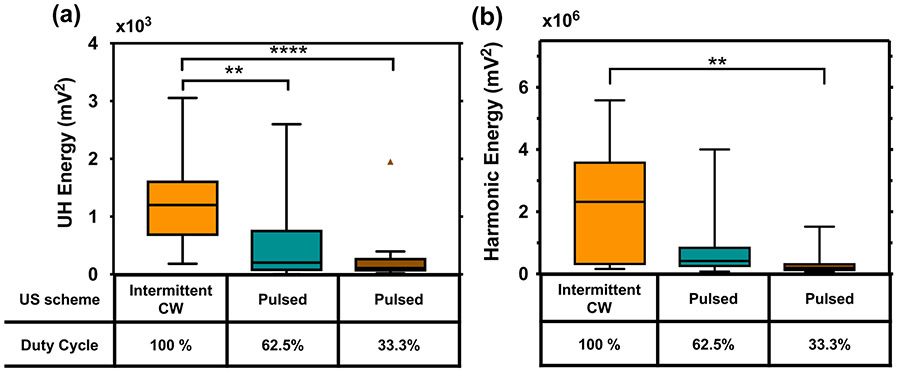
The harmonic and UH energy for each US treatment scheme was plotted in figure 10. Harmonic energy during the intermittent CW US scheme was significantly higher than the 33.3% duty cycle (p<0.001). Similarly, the UH energy was significantly different between the intermittent CW scheme and either the 33.3% duty cycle (p<0.001) or the 62.5% duty cycle pulsed ultrasound schemes (p < 0.01). The total mean and standard deviation of the harmonic and UH energy (3.01×105 ± 3.65×105 mV2 and 254.6 ± 467.4 mV2, respectively) for the 33.3% duty cycle pulsed ultrasound scheme was also approximately half of that for the 62.5% duty cycle pulsed ultrasound scheme (7.16×105 ± 9.67×105 mV2 and 516.1 ± 689.7 mV2, respectively). The variance of the cavitation energy within each insonation scheme was large, leading to a lack of statistically significant differences.
Figure 10.
(a) Ultraharmonic (UH) energy and (b) harmonic energy for the ultrasound (US) insonation schemes used in this study. Energy was summed over a frequency bandwidth of 4-kHz around the center frequency for the continuous wave (CW) US scheme and 50-kHz for the pulsed US. Ultraharmonics and harmonics were chosen based on frequencies below 2-MHz with a signal-to-noise ratio greater than 10 dB. Note the higher magnitude of energy in the harmonic frequencies. Statistical significance using a Kruskal-Wallis test is shown with brackets, where p < 0.05 is denoted by *, p < 0.01 is denoted by **, and p < 0.001 is denoted by ***. A Tukey boxplot is used where the boxes span the interquartile range and the bars span the data from maximum to minimum excluding any outliers. One outlier is present in the UH energy for 33.3% duty cycle pulsed US.
4. Discussion
4.1. Transcranial pressure reduction, constructive interference and heating
The results of simulations with 220-kHz intermittent CW ultrasound follow similar trends as reported by Bouchoux et al (2014) for 120-kHz and 500-kHz CW insonations in the same 20 ischemic stroke subjects. Using the CT-based alignment protocol, Bouchoux et al (2014) reported a simulated maximum acoustic pressure in the clot of 53.9 ± 10.5% and 50.1 ± 11.2% relative to the free field maximum at 120 kHz and 500 kHz, respectively. The average simulated maximum acoustic pressure in the clot for the 220-kHz transducer with CW insonation was 77.7 ± 14.7% relative to the free field maximum (figure 6). The 220-kHz ultrasound transducer was designed to have a natural focus of 5.4 cm, the average distance to the M1 section of the MCA in humans (Bouchoux et al 2014). Note that the 120 kHz and 500 kHz transducers used in Bouchoux et al's (2014) simulations had natural foci of 1.8 cm and 8.0 cm, respectively. Thus, the clots were in the farfield of the 120 kHz transducer. Despite higher attenuation in the skull at 220 kHz compared to 120 kHz, the pressure amplitudes achieved in the clots at 220 kHz were higher because of the alignment of the clot with the natural focus of this transducer. The maximum pressure predicted in the ipsilateral temporal bone for Bouchoux et al's (2014) study was 2.0 to 2.6 times higher than the maximum pressure in the clot.
No significant differences in the intracranial acoustic pressure field characteristics were observed amongst the intermittent CW and pulsed ultrasound schemes (p > 0.14) at 220 kHz (figure 5). An adequate pressure amplitude was predicted which could sustain cavitation within the clots for all three insonation schemes in all 20 patients. Although the acoustic field varied between patients based on the skull morphology, the choice of insonation schemes did not impact the pressure maxima for each patient. The parallel reflections between the ipsilateral skull and the transducer face created prominent constructive interference with pressures reaching up to 4.1 times the pressure amplitude in the clot (figure 6). Safety concerns at these acoustic pressures need to be assessed further to avoid off-target deleterious bioeffect. Another region of constructive interference was noted when the acoustic beam impinged on the ipsilateral orbital shelf, though this scenario occurred for a small number of patients and was dependent on transducer orientation. A third region of constructive interference was observed near the contralateral skull, but the acoustic pressure did not exceed the pressure in the clot. This result was surprising as one of our goals with the pulsed ultrasound scheme was to reduce the constructive interference. However, the pulse duration was still too long to remove the interference pattern between the transducer and the ipsilateral skull, as well as within the contralateral brain. Pulse durations shorter than 15 cycles may help to prevent some constructive interference.
For the intermittent CW US scheme, the maximum temperature in bone was 5.13 ± 4.11 °C (figure 7) and was in the range of temperatures predicted by Bouchoux et al (2014) for 120 kHz (3.8 ± 2.2 °C) and 500 kHz (13.4 ± 3.3 °C). These predicted temperature increases in the temporal bone agree with measurements made by McDannold et al (2016) in four macaques insonified with a 230-kHz source. In our simulations, the temperature rise in the temporal bone was reduced 1.9-fold by lowering the duty cycle from 62.5% to 33.3% (figure 7). The thermal dose in the temporal bone for the 62.5% duty cycle pulsed US scheme was lower than the intermittent CW scheme, and approached the conservative thresholds for neuronal damage and ablation at a thermal dose of 4 hours in all but two patients (McDannold et al 2016). Additionally, the thermal dose for the 33.3% duty cycle pulsed US scheme was below 5.4 min for all but two patients (32.4 min and 45.0 min), which has not been associated with tissue damage in vivo (McDannold et al 2016). The decreased tissue heating predicted for the 33.3% duty cycle pulsed scheme is thus attractive in transcranial applications for thrombolysis.
4.2. Clot lysis
Clot width loss did not change significantly in the first five minutes of treatment. Both Bajd et al (2010) and Bader et al (2015) have observed an initial delay in lysis and consequently used a sigmoidal curve to model the rate of thrombolysis. The initial penetration of rt-PA and plasminogen across the clot surface is likely responsible for this delay. No appreciable clot lysis was observed for clots treated with human plasma alone. Clots treated with rt-PA and human plasma initially expanded, followed by a gradual loss in clot width (figure 8). Clot width loss occurred sporadically, with some sections breaking down very quickly, and others resisting lysis for several minutes. This pattern of expansion followed by lysis was uncommon in clots exposed to rt-PA and ultrasound, except for the 33.3% duty cycle pulsed ultrasound treated clots. This expansion could be simply due to a lower rate of lysis (figure 9), or perhaps to the presence of less bubble activity in the 33.3% duty cycle pulsed ultrasound scheme compared to the 62.5% duty cycle pulsed ultrasound or intermittent CW schemes. Such bubble activity has been shown to enhance fluid motion and aid in diffusion of both rt-PA and plasminogen into the clot (Datta et al 2008, Sutton et al 2013, Bader et al 2015). All clots exposed to rt-PA demonstrated highly variable lytic rate. Some clots exhibited gradual and continuous lysis, and others experienced sporadic lysis and some even sudden detachment from the silk suture holding the whole blood clot within the flow of plasma and rt-PA. No displacement of the clots due to radiation force was observed for either pulsed ultrasound insonation scheme, though the 2.33 Hz image acquisition rate was not sufficient to visualize potential displacement from a single pulse.
4.3. Cavitation energy and clot lysis
Despite no statistical difference in the FCL or ALR amongst the three ultrasound insonation schemes (figure 9), the UH and harmonic energy differed significantly between the intermittent CW and pulsed ultrasound schemes (figure 10). This was unexpected as Xu et al (2008) have observed increased thrombolysis with subharmonic emissions in the absence of nucleating agents or therapeutics and Bader et al (2015) have reported a weak relationship between UH energy and average lytic rate. The cavitation activity exhibited stochastic temporal variation similar to that observed by Pouliopoulos et al (2016). For the two pulsed ultrasound schemes, cavitation was present over the entire 30 minutes with random fluctuations in the ultraharmonic energy as a function of time. For the intermittent CW scheme, cavitation activity only occurred when the transducer was active and there were also random fluctuations in the ultraharmonic energy over time. The lack of a relationship between cavitation emissions and thrombolytic efficacy in our data might be due to a saturation effect of the bubble activity.
In order to enhance thrombolysis, acoustically activated bubbles must be in proximity of the fibrin mesh and thereby enhance penetration of rt-PA and plasminogen via fluid mixing, pore formation, and fibrin network damage (Caskey et al 2009, Acconcia et al 2013). Given the size of the fibrin mesh in the human whole blood clots used in this study, it is likely that Definity® penetrated the clot surface. Acoustically driven advection of rt-PA, plasminogen, and Definity® across the clot surface area likely contributed to the observed thrombolysis. The clot surface area will limit the number of bubbles that can enhance thrombolysis. The passive cavitation detector is sensitive to bubble activity within a volume larger than the clot surface where lysis would occur, thus measuring cavitation from bubbles farther from the clot surface as well. In addition, the SNR for the cavitation detection system for the three insonation schemes differed by as much as 25 dB (figure 4). The contribution of inertial cavitation to clot lysis could not be assessed for the pulsed insonation schemes because the quantification of inharmonic energy was confounded by spectral broadening from both the harmonic and ultraharmonic peaks (figure 3).
The overall UH and harmonic energy was lower for the two pulsed schemes compared to the intermittent CW scheme (figure 10). One possible explanation is the poor fidelity in quantifying the pulsed ultrasound cavitation emissions due to the lower SNR compared to the intermittent CW. Spectral broadening also necessitated using a frequency bandwidth of 50 kHz to capture the UH signal. However, the 50 kHz bandwidth used was constrained in its width because of spectral broadening of the neighboring harmonics. As a result, the ultraharmonic energy may be underestimated in the pulsed case. Another potential contributing factor to the difference in energy could be that cavitation emissions depend both on bubble growth and the bubble dissolution which are effected by the active and quiescent times during insonation (Chen et al 2003, Ciaravino et al 1981, Brayman et al 1996). Bader and Holland (2013) noted that the number of cycles required for bubble exposed to 220 kHz ultrasound to achieve steady state oscillation was approximately 6 cycles. Though the pulsed ultrasound scheme with 62.5% duty cycle in our study had the same ultrasound on time as the intermittent CW scheme, the pulse duration of 15 cycles likely limited steady state oscillations and contributed to the lower UH emissions observed. Additionally, the aggregation and coalescence of bubbles in an ultrasound field increases with pulse duration, which could affect bubble activity (Chen et al 2016).
4.4. Clot lysis, duty cycle, and pulse duration
No enhancement in lytic efficacy was observed with increasing duty cycle (figure 9), which is consistent with the results reported by (Holland et al 2008, Xu et al 2008). Meunier et al (2007) observed a linear relationship between duty cycle and thrombolysis in a similar clot width model. However, Meunier et al's (2007) experiment did not use an ultrasound contrast agent, did not have flow, and did not quantify the cavitation activity during their experiment. Additionally, their peak-to-peak pressure amplitude was only 0.35 MPa, thus it is likely cavitation was not sustained. It is of interest to note that Xu et al (2008) observed an increase in thrombolysis at a duty cycle of 10% as pulse duration increased and a concurrent increase in the stable and inertial cavitation dose. However, for our two pulsed ultrasound schemes, the pulse duration of 68 μs was below the minimum pulse duration (400 μs) for which this effect was observed (Xu et al 2008). This effect might have contributed to the increased lysis observed for the intermittent CW scheme, which had a pulse duration of 50 seconds despite the lack of statistical significance. The relationship between pulse duration and thrombolytic efficacy has also been explored by others. Blinc et al (1993) and Suchkova et al (2002) observed that fractional clot lysis was weakly dependent on pulse duration. Meunier et al (2007) observed a linear correlation between pulse duration and thrombolysis in the presence of rt-PA.
4.5. Absence of large bubbles
In a previous study, Bader et al (2015) observed large bubbles (53±19 μm) in the field of view when human whole blood clots were exposed to rt-PA, Definity® and 120 kHz intermittent CW ultrasound. Such bubbles would be large enough to occlude the arterioles and small feeding arteries critical to tissue perfusion (Parker et al 2013). At 220 kHz, no bubbles larger than 8 μm (the resolution of the imaging system) were observed for any of the insonation schemes. Given the limited frame acquisition rate (2.33 Hz) and shutter speed (16 ms), it is possible that some bubbles may not have been detected due to the lack of persistence or rapid translation across the field of view. Note that this study was performed using the same image acquisition parameters and instrumentation as Bader et al (2015). Nonetheless, we obtained thrombolytic enhancement despite the absence of 53 μm diameter bubbles, which is encouraging for the future translation of this approach.
4.6. Study Limitations
Several limitations of our study must be acknowledged. The simulations were based on patient-derived CT scans using a model which underestimated intracranial acoustic pressure by less than 4% at 120 kHz (Bouchoux et al 2012). This underestimation in the acoustic pressure was attributed to the use of skull acoustic properties at 270 kHz (Pichardo et al 2011). Note that the center frequency used in our study was 220 kHz. One of the limitations of the Friedman’s test is that variability between subjects is ignored. The lack of significant difference among the maximum pressures simulated in different regions of the skull and brain could simply reflect high variability in skull properties, particularly with respect to temporal bone window insufficiency (Kollár et al 2004). Transducer self-heating was also neglected in this model and should be addressed before translation.
The flow rate used was fixed (0.65 mL/min), which did not consider the increase in flow rate with the progression of lysis expected in vivo. Furthermore, the presence of flow does not model the environment of a fully occlusive thrombus. The highly retracted clots used in this study fall within the range of clot properties seen clinically, but do not model the softer, fresh clots which can occur in vivo, which are more responsive to rt-PA (Mercado-Shekhar et al 2018). The PRF of the pulsed ultrasound was higher than the frame rate of our camera, limiting our ability to resolve radiation force-induced motion for pulsed insonation.
A living vessel would add complexities of the autocrine and paracrine functions of the vessel on the lytic process. Endothelium produces pro- and anti-thrombotic factors which vary in response to occlusion or recanalization (Faille et al 2014). A vessel is also dynamic and responds to the presence of a clot with vasospasm or vasodilation, which is not present in our flow model. The data from our model are consistent with other thrombolysis studies which include flow in living vessels (Hitchcock et al 2011, Sutton et al 2013).
Frequency domain analysis of cavitation activity from pulsed ultrasound exposure is limited by inherent spectral broadening. Additionally, cavitation detection using a single element transducer provides limited localization of the cavitation activity. Transcranial passive cavitation imaging has been demonstrated in silico, in vitro, and in vivo (O’Reilly et al 2014, Arvanitis et al 2015) and could be used to regulate and direct sonothrombolysis in the future.
5. Conclusions
Simulations reported in this study predict 220-kHz pulsed ultrasound with a duty cycle of 62.5% or 33.3% to cause a maximum temperature rise in the temporal bone of 6.7 °C or 12.8 °C, respectively. The maximum temperature rise in the temporal bone exposed to intermittent CW ultrasound was 16.7 °C. The simulated ultrasound pressure fields in the skull were similar for both the pulsed insonation schemes and the intermittent CW insonation scheme. Both harmonic and UH energy, indicative of stable cavitation, were lower for clots exposed to either pulsed ultrasound schemes than the intermittent CW scheme. Nonetheless, all three ultrasound exposure schemes enhanced clot lysis relative to rt-PA alone in an in vitro flow model. The pulsed ultrasound schemes achieved similar lytic efficacy as the intermittent CW US (58.7 ± 24.7%, 62.2 ± 21.5%, compared to 75.78 ± 24.26% fractional clot loss respectively). The findings of this study will inform the choice of insonation scheme for future pre-clinical studies to develop ultrasound-enhanced thrombolysis.
Supplementary Material
6. Acknowledgements:
The authors would like to thank Guillaume Bouchoux, PhD, who developed the finite difference model that was used in this work. This work was supported by the National Institutes of Health (grant number NIH R01NS047603, K25HL133452, R01CA158439) and the University of Cincinnati MSTP training grant (grant number NIGMS T32GM062483). The authors thank Professor Xiasheng Guo (Nanjing University), for providing the transducer used in the in vitro studies.
7. Appendix
Error of Planar Wave Assumption on Intensity Calculation
The acoustic intensity for the field of an ultrasound transducer is often assumed to be proportional to the squared pressure amplitude (Baron et al 2009, McDannold et al 2016). This assumption is accurate when the transducer aperture is much greater than the wavelength, but is not accurate for a 220-kHz center frequency transducer with an aperture diameter of 38 mm. The error in this approximation can be demonstrated using the exact solution for the on-axis pressure field of a baffled circular piston (Pierce 1989, Mast and Yu 2005). The exact and approximate on-axis instantaneous intensity magnitudes, Ii(z) and Ii,approx(z) respectively, can be written
| (A1) |
| (A2) |
where z is distance along the piston’s axis, p is the amplitude of the acoustic pressure, u is the axial particle velocity, ρ and c are the medium density and sound speed, is the distance from the piston’s radius, a, to the axial field point, z, k is the wavenumber, and is the maximum on-axis intensity for a nominal pressure, p0, at the piston surface.
When evaluated at the piston’s natural focus, z0 = ka2/(2π), the intensity approximation error, ϵ, can be written as
| (A3) |
where . The normalized error, ϵ(ka)/I0 (see figure A1), falls below 1% for ka < 0.3 or ka > 30.9, but reaches a maximum of 18.9% at ka ≈ 3.3. For comparison, ka ≈ 17.1 for the 38 mm diameter, 220 kHz source used in these simulations, with a corresponding intensity approximation error ϵ/I0 of 3.1%.
Figure A1.
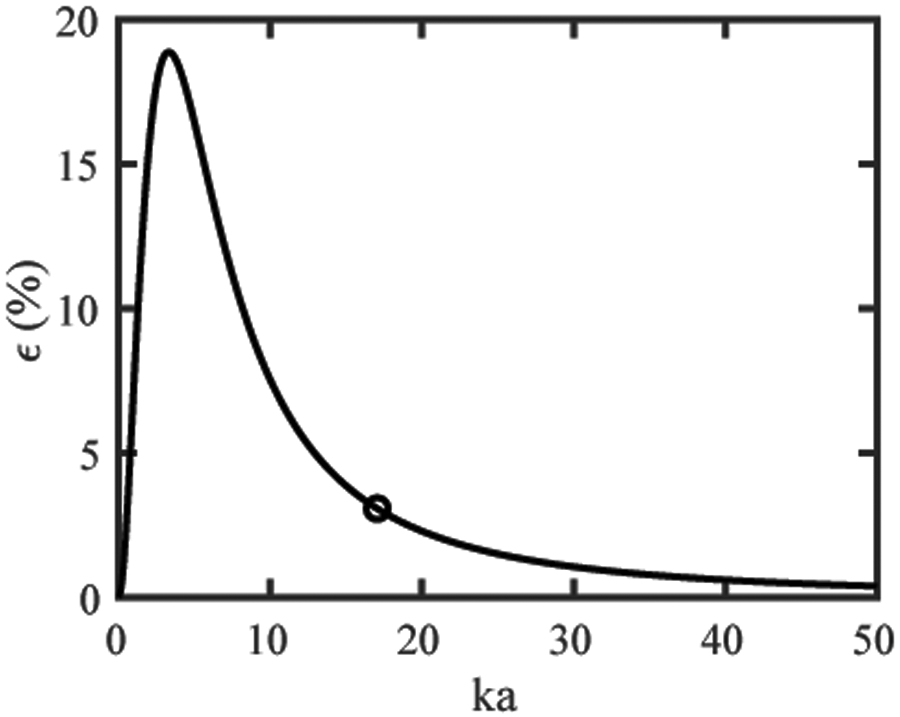
Normalized error between exact and approximate solutions for intensity as a function of the aperture radius normalized by the wavelength (ka). For 0.3 < ka < 30.9, the assumption that the acoustic propagation resembles a plane wave at the natural focus is invalid. Outside of this ka range, the intensity is proportional to the square of the pressure.
Footnotes
Publisher's Disclaimer: This is the Accepted Manuscript version of an article accepted for publication in Physics in Medicine and Biology. IOP Publishing Ltd is not responsible for any errors or omissions in this version of the manuscript or any version derived from it. The Version of Record is available online at https://iopscience.iop.org/article/10.1088/1361-6560/ab293b.
Declarations of interest: none
Abbreviations: IV: intravenous, rt-PA: recombinant tissue plasminogen activator, US: ultrasound, UET: ultrasound enhanced thrombolysis, CW: continuous wave, UCA: ultrasound contrast agent, UH: ultraharmonic, MCA: middle cerebral artery, PRF: pulse repetition frequency, FDTD: finite-difference time-domain, ROI: region of interest, ST: soft tissue, TD: thermal dose FCL: fractional clot loss, ALR: average lytic rate, PCD: passive cavitation detector, SNR: signal to noise ratio, , HSD: honest significant difference.
References:
- Acconcia C, Leung BYC, Hynynen K and Goertz DE 2013. Interactions between ultrasound stimulated microbubbles and fibrin clots Appl. Phys. Lett 103 053701 (1-4) [Google Scholar]
- Alexandrov AV, Tsivgoulis G, Rubiera M, Vadikolias K, Stamboulis E, Molina CA and Alexandrov AW 2010. End-Diastolic Velocity Increase Predicts Recanalization and Neurological Improvement in Patients With Ischemic Stroke With Proximal Arterial Occlusions Receiving Reperfusion Therapies Stroke 41 948–52 [DOI] [PubMed] [Google Scholar]
- Ammi AY, Mast TD, Huang IH, Abruzzo TA, Coussios CC, Shaw GJ and Holland CK 2008. Characterization of Ultrasound Propagation Through Ex-vivo Human Temporal Bone Ultrasound Med. Biol 34 1578–89 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arvanitis CD, Clement GT and McDannold N 2015. Transcranial assessment and visualization of acoustic cavitation: Modeling and experimental validation IEEE Trans. Med. Imaging 34 1270–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auboire L, Sennoga CA, Hyvelin JM, Ossant F, Escoffre JM, Tranquart F and Bouakaz A 2018. Microbubbles combined with ultrasound therapy in ischemic stroke: A systematic review of in-vivo preclinical studies PLoS One 13 1–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Gruber MJ and Holland CK 2015. Shaken and Stirred: Mechanisms of Ultrasound-Enhanced Thrombolysis Ultrasound Med. Biol 41 187–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB and Holland CK 2013. Gauging the likelihood of stable cavitation from ultrasound contrast agents Phys. Med. Biol 58 127–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajd F, Vidmar J, Blinc A and Serša I 2010. Microscopic clot fragment evidence of biochemo-mechanical degradation effects in thrombolysis Thromb. Res 126 137–43 [DOI] [PubMed] [Google Scholar]
- Baron C, Aubry JF, Tanter M, Meairs S and Fink M 2009. Simulation of Intracranial Acoustic Fields in Clinical Trials of Sonothrombolysis Ultrasound Med. Biol 35 1148–58 [DOI] [PubMed] [Google Scholar]
- Benjamin EJ, Virani SS, Callaway CW, Chamberlain AM, Chang AR, Cheng S, Chiuve SE, Cushman M, Delling FN, Deo R, De Ferranti SD, Ferguson JF, Fornage M, Gillespie C, Isasi CR, Jiménez MC, Jordan LC, Judd SE, Lackland D, Lichtman JH, Lisabeth L, Liu S, Longenecker CT, Lutsey PL, MacKey JS, Matchar DB, Matsushita K, Mussolino ME, Nasir K, O’Flaherty M, Palaniappan LP, Pandey A, Pandey DK, Reeves MJ, Ritchey MD, Rodriguez CJ, Roth GA, Rosamond WD, Sampson UKA, Satou GM, Shah SH, Spartano NL, Tirschwell DL, Tsao CW, Voeks JH, Willey JZ, Wilkins JT, Wu JHY, Alger HM, Wong SS and Muntner P 2018. Heart disease and stroke statistics - 2018 update: A report from the American Heart Association Circulation 137(12) E67–492 [DOI] [PubMed] [Google Scholar]
- Blinc BA, Francis CW, Trudnowski JL and Carstensen EL 1993. Characterization of Ultrasound-Potentiated Fibrinolysis In Vitro Blood 81 2636–43 [PubMed] [Google Scholar]
- Bouchoux G, Bader K B, Korfhagen JJ, Raymond JL, Shivashankar R, Abruzzo T a and Holland CK 2012. Experimental validation of a finite-difference model for the prediction of transcranial ultrasound fields based on CT images Phys. Med. Biol 57 8005–22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouchoux G, Shivashankar R, Abruzzo TA and Holland CK 2014. In silico study of low-frequency transcranial ultrasound fields in acute ischemic stroke patients Ultrasound Med. Biol 40 1154–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brayman AA, Azadniv M, Cox C and Miller MW 1996. Hemolysis of Albunex-supplemented, 40% Hematocrit Human Erythrocytes in Vitro By 1-MHz Pulsed Ultrasound: Acoustic Pressure and Pulse Length Dependence Ultrasound Med. Biol 22 927–38 [DOI] [PubMed] [Google Scholar]
- Broderick JP and Hacke W 2002. Treatment of acute ischemic stroke part I: Recanalization strategies Circulation 106 1563–9 [DOI] [PubMed] [Google Scholar]
- Caskey CF, Qin S, Dayton PA and Ferrara KW 2009. Microbubble tunneling in gel phantoms J. Acoust. Soc. Am 125 EL183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen WS, Brayman AA, Matula TJ and Crum LA 2003. Inertial cavitation dose and hemolysis produced in vitro with or without Optison Ultrasound Med. Biol 29 725–37 [DOI] [PubMed] [Google Scholar]
- Chen X, Leeman JE, Wang J, Pacella JJ and Villanueva FS 2014. New insights into mechanisms of sonothrombolysis using ultra-high-speed imaging Ultrasound Med. Biol 40 258–62 [DOI] [PubMed] [Google Scholar]
- Chen X, Wang J, Pacella J and Villanueva FS 2016. The dynamic behavior of microbubbles during long ultrasound tone-burst excitation: mechanistic insights into ultrasound-microbubble mediated therapeutics using high-speed imaging and cavitation detection Ultrasound Med. Biol 150 137–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng JY, Shaw G J and Holland C K 2005. In vitro microscopic imaging of enhanced thrombolysis with 120-kHz ultrasound in a human clot model Acoust. Res. Lett. Online 6 25–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chuang YH, Cheng POW, Chen SC, Ruan JL and Li PC 2010. Effects of ultrasound-induced inertial cavitation on enzymatic thrombolysis Ultrason. Imaging 32 81–90 [DOI] [PubMed] [Google Scholar]
- Ciaravino V, Flynn H and Miller M 1981. Pulsed Enhancement of acoustic cavitation: a postulated model. Ultrasound Med. Biol 7 159–66 [DOI] [PubMed] [Google Scholar]
- Collis J, Manasseh R, Liovic P, Tho P, Ooi A, Petkovic-Duran K and Zhu Y 2010. Cavitation microstreaming and stress fields created by microbubbles Ultrasonics 50 273–9 [DOI] [PubMed] [Google Scholar]
- Connor CW and Hynynen K 2004. Patterns of thermal deposition in the skull during transcranial focused ultrasound surgery IEEE Trans. Biomed. Eng 51 1693–706 [DOI] [PubMed] [Google Scholar]
- Crum L A 1984. Rectified diffusion Ultrasonics 22 215–23 [Google Scholar]
- Daffertshofer M, Gass A, Ringleb P, Sitzer M, Sliwka U, Els T, Sedlaczek O, Koroshetz WJ and Hennerici MG 2005. Transcranial low-frequency ultrasound-mediated thrombolysis in brain ischemia: Increased risk of hemorrhage with combined ultrasound and tissue plasminogen activator - Results of a phase II clinical trial Stroke 36 1441–6 [DOI] [PubMed] [Google Scholar]
- Datta S, Coussios CC, Ammi AY, Mast TD, de Courten-Myers GM and Holland CK 2008. Ultrasound-Enhanced Thrombolysis Using Definity as a Cavitation Nucleation Agent Ultrasound Med. Biol 34 1421–33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta S, Coussios CC, McAdory LE, Tan J, Porter T, De Courten-Myers G and Holland CK 2006. Correlation of cavitation with ultrasound enhancement of thrombolysis Ultrasound Med. Biol 32 1257–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duck FA 1990. Physical Properties of Tissue. A Comprehensive Reference Book (San Diego: Academic Press; ) [Google Scholar]
- Elder SA 1959. Cavitation microstreaming J. Acoust. Soc. Am 31 54–64 [Google Scholar]
- Emberson J, Lees KR, Lyden P, Blackwell L, Albers G, Bluhmki E, Brott T, Cohen G, Davis S, Donnan G, Grotta J, Howard G, Kaste M, Koga M, Von Kummer R, Lansberg M, Lindley RI, Murray G, Olivot JM, Parsons M, Tilley B, Toni D, Toyoda K, Wahlgren N, Wardlaw J, Whiteley W, Del Zoppo GJ, Baigent C, Sandercock P and Hacke W 2014. Effect of treatment delay, age, and stroke severity on the effects of intravenous thrombolysis with alteplase for acute ischaemic stroke: A meta-analysis of individual patient data from randomised trials Lancet 384 1929–35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faille D, Labreuche J, Meseguer E, Huisse MG, Ajzenberg N and Mazighi M 2014. Endothelial markers are associated with thrombolysis resistance in acute stroke patients Eur. J. Neurol 21 643–7 [DOI] [PubMed] [Google Scholar]
- Fan Z, Chen D and Deng CX 2014. Characterization of the dynamic activities of a population of microbubbles driven by pulsed ultrasound exposures in sonoporation Ultrasound Med. Biol 40 1260–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frenkel V, Oberoi J, Stone MJ, Park M, Deng C, Wood BJ, Neeman Z, Horne M and Li KCP 2006. Pulsed High-Intensity Focused Ultrasound Enhances Thrombolysis in an in Vitro Model Radiology 239 86–93 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber MJ, Bader KB and Holland CK 2014. Cavitation thresholds of contrast agents in an in vitro human clot model exposed to 120-kHz ultrasound J. Acoust. Soc. Am 135 646–53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haworth KJ, Bader KB, Rich KT, Holland CK and Mast TD 2017. Quantitative frequency-domain passive cavitation imaging IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64 177–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hitchcock KE, Ivancevich NM, Haworth KJ, Caudell DN, Vela DC, Sutton JT, Pyne-Geithman GJ and Holland CK 2011. Ultrasound-enhanced rt-PA thrombolysis in an ex vivo porcine carotid artery model Ultrasound Med. Biol 37 1240–51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holland CK and Apfel RE 1989. An Improved Theory for the Prediction of Microcavitation Thresholds IEEE Trans. Ultrason. Ferroelectr. Freq. Control 36 204–8 [DOI] [PubMed] [Google Scholar]
- Holland CK, Vaidya SS, Datta S, Coussios C-C and Shaw GJ 2008. Ultrasound-enhanced tissue plasminogen activator thrombolysis in an in vitro porcine clot model Thromb. Res 121 663–73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzfuss J, Rüggeberg M and Billo A 1998. Shock wave emissions of a sonoluminescing bubble Phys. Rev. Lett 81 5434–7 [Google Scholar]
- Kollár J, Schulte-Altedorneburg G, Sikula J, Fülesdi B, Ringelstein EB, Mehta V, Csiba L and Droste DW 2004. Image quality of the temporal bone window examined by transcranial doppler sonography and correlation with postmortem computed tomography measurements Cerebrovasc. Dis 17 61–5 [DOI] [PubMed] [Google Scholar]
- Leeman JE, Kim JS, Yu FTH, Chen X, Kim K, Wang J, Chen X, Villanueva FS and Pacella JJ 2012. Effect of Acoustic Conditions on Microbubble-Mediated Microvascular Sonothrombolysis Ultrasound Med. Biol 38 1589–98 [DOI] [PubMed] [Google Scholar]
- Lin Y, Lin L, Cheng M, Jin L, Du L, Han T, Xu L, Yu ACH and Qin P 2017. Effect of acoustic parameters on the cavitation behavior of SonoVue microbubbles induced by pulsed ultrasound Ultrason. Sonochem 35 176–84 [DOI] [PubMed] [Google Scholar]
- Mast TD . and Yu F 2005. Simplified expansions for radiation from a baffled circular piston J. Acoust. Soc. Am 118 3457–64 [Google Scholar]
- McDannold N, Livingstone MS, Top CB, Sutton JT, Todd N and Vykhodtseva N 2016. Preclinical evaluation of a low-frequency transcranial MRIguided focused ultrasound system in a primate model Phys. Med. Biol 61 7664–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mercado-Shekhar KP, Kleven RT, Aponte Rivera H, Lewis R, Karani K, Vos HJ, Abruzzo TA, Haworth KJ and Holland CK 2018. Effect of clot stiffness on recombinant tissue plasminogen activator lytic susceptibility in vitro Ultrasound Med. Biol 44 2710–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier JM, Holland CK, Lindsell CJ and Shaw GJ 2007. Duty Cycle Dependence of Ultrasound Enhanced Ulrasound Med. Biol 33 576–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Minnaert M 1933. On musical air-bubbles and the sounds of running water London, Edinburgh, Dublin Philos. Mag. J. Sci 16 235–48 [Google Scholar]
- Muth CM and Shank ES 2000. Gas embolism N. Engl. J. Med 342 476–82 [DOI] [PubMed] [Google Scholar]
- Nyborg WLM 1953. Acoustic Streaming due to Attenuated Plane Waves J. Acoust. Soc. Am 25 68–75 [Google Scholar]
- O’Reilly MA (University of T, Huang Y and Kullervo H (University of T 2010. The impact of standing wave effects on transcranial focused ultrasound disruption of the blood-brain barrier in a rat model Phys. Med. Biol 55 5251–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Reilly MA, Jones RM and Hynynen K 2014. Three-dimensional transcranial ultrasound imaging of microbubble clouds using a sparse hemispherical array IEEE Trans. Biomed. Eng 61 1285–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker JM, Weller MW, Feinstein LM, Adams RJ, Main ML, Grayburn PA, Cosgrove DO, Goldberg BA, Darge K, Nihoyannopoulos P, Wilson S, Monaghan M, Piscaglia F, Fowlkes B, Mathias W, Moriyasu F, Chammas MC, Greenbaum L and Feinstein SB 2013. Safety of ultrasound contrast agents in patients with known or suspected cardiac shunts Am. J. Cardiol 112 1039–45 [DOI] [PubMed] [Google Scholar]
- Pennes HH 1948. Analysis of tissue and arterial blood temperatures in the resting human forearm J. Appl. Physiol 1 93–122 [DOI] [PubMed] [Google Scholar]
- Petit B, Bohren Y, Gaud E, Bussat P, Arditi M, Yan F, Tranquart F and Allémann E 2015. Sonothrombolysis: The Contribution of Stable and Inertial Cavitation to Clot Lysis Ultrasound Med. Biol 41 1402–10 [DOI] [PubMed] [Google Scholar]
- Pfaffenberger S, Devcic-Kuhar B, El-Rabadi K, Groschl M, Speidl W, Weiss T, Benes E, Wojta G and Gottsauner-Wolf M 2003. 2 MHz ultrasound enhances t-PA-mediated thrombolysis: comparison of continuous versus pulsed ultrasound and standing versus travelling acoustic waves Thromb. Haemost 89 583–9 [PubMed] [Google Scholar]
- Pichardo S, Sin VW and Hynynen K 2011. Multi-frequency characterization of the speed of sound and attenuation coefficient for longitudinal transmission of freshly excised human skulls Phys. Med. Biol 56 219–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce AD 1989. Acoustics: An Introduction to Its Physical Principles and Applications, 2nd ed. (New York:NY: Acoustical Society of America; ) [Google Scholar]
- Postema M, Marmottant P, Lancée CT, Hilgenfeldt S and De Jong N 2004. Ultrasound-induced microbubble coalescence Ultrasound Med. Biol 30 1337–44 [DOI] [PubMed] [Google Scholar]
- Pouliopoulos AN, Li C, Tinguely M and Garbin V 2016. Rapid short-pulse sequences enhance the spatiotemporal uniformity of acoustically driven microbubble activity during flow conditions J. Acoust. Soc. Am 140 2469–80 [DOI] [PubMed] [Google Scholar]
- Prokop AF, Soltani A and Roy RA 2007. Cavitational Mechanisms in Ultrasound-Accelerated Fibrinolysis Ultrasound Med. Biol 33 924–33 [DOI] [PubMed] [Google Scholar]
- Radhakrishnan K, Bader KB, Haworth KJ, Kopechek JA, Raymond JL, Huang S-L, McPherson DD and Holland CK 2013. Relationship between cavitation and loss of echogenicity from ultrasound contrast agents Phys. Med. Biol 58 6541–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santin M, Bridal SL, Haak A and O’Brien WD 2008. Spectral and temporal signal modifications occuring between stable and transient inertial cavitation Proceedings - IEEE Ultrasonics Symposium (Bejing, China) pp 989–92 [Google Scholar]
- Sapareto SA and Dewey WC 1984. Thermal dose determination in cancer therapy Int. J. Radiat. Oncol. Biol. Phys 10 787–800 [DOI] [PubMed] [Google Scholar]
- Seifried E, Tanswell P, Ellbruck D, Haerer W and Schmidt A 1989. Pharmacokinetics and haemostatic status during consecutive infusions of recombinant tissue-type plasminogen activator in patients with acute myocardial infarction Thromb. Haemost 61 497–501 [PubMed] [Google Scholar]
- Shekhar H, Bader K B, Huang S, Peng T, Huang S, Mcpherson D D and Holland C K 2017. In vitro thrombolytic efficacy of echogenic liposomes loaded with tissue plasminogen activator and octafluoropropane gas Phys. Med. Biol 62 517–38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi W T, Gao S, Powers J E, Drvol L, Jung K W, Xie F, Lof J, Everbach E C and Porter T R 2010 Investigation of Effectiveness of Microbubble Stable Cavitation in Thrombolysis 2010 IEEE International Ultrasonics Symposium (San Diego: IEEE; ) pp 330–3 [Google Scholar]
- Suchkova V, Carstensen EL and Francis CW 2002. Ultrasound enhancement of fibrinolysis at frequencies of 27 to 100 kHz Ultrasound Med. Biol 28 377–82 [DOI] [PubMed] [Google Scholar]
- Sutton JT, Haworth KJ, Pyne-Geithman G and Holland CK 2013. Ultrasound-mediated drug delivery for cardiovascular disease. Expert Opin. Drug Deliv 10 573–92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tachibana K and Tachibana S 1995. Albumin microbubble echo-contrast material as an enhancer for ultrasound accelerated thrombolysis Circulation 92 1148–50 [DOI] [PubMed] [Google Scholar]
- Tanswell P, Seifried E, Stang E and Krause J 1991. Pharmacokinetics and hepatic catabolism of tissue-type plasminogen activator. Arzneimittelforschung. 41 1310–9 [PubMed] [Google Scholar]
- Weiss HL and Selvaraj P 2013. Mechanical clot damage from cavitation during sonothrombolysis J. Acoust. Soc. Am 133 3159–75 [DOI] [PubMed] [Google Scholar]
- Xie F, Everbach EC, Gao S, Drvoll LK, Shi WT, Vignon F, Powers JE, Lof J and Porter TR 2011. Effects of Attenuation and Thrombus Age on the Success of Ultrasound and Microbubble-mediated Thrombus Dissolution Ultrasound Med. Biol 37 280–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu S, Li X, Liu Y, Xu C and Wan M 2008. Cavitation enhanced ultrasound thrombolysis IEEE Ultrasonics Symposium (Bejing, China: IEEE) pp 2052–5 [Google Scholar]
- Zhang Y 2009. Generalized dual-phase lag bioheat equations based on nonequilibrium heat transfer in living biological tissues Int. J. Heat Mass Transf 52 4829–34 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.