Experimental approaches for investigating ion atmospheres around nucleic acids and proteins

Graphical abstract

Abstract

Ionic interactions are crucial to biological functions of DNA, RNA, and proteins. Experimental research on how ions behave around biological macromolecules has lagged behind corresponding theoretical and computational research. In the 21st century, quantitative experimental approaches for investigating ionic interactions of biomolecules have become available and greatly facilitated examinations of theoretical electrostatic models. These approaches utilize anomalous small-angle X-ray scattering, atomic emission spectroscopy, mass spectrometry, or nuclear magnetic resonance (NMR) spectroscopy. We provide an overview on the experimental methodologies that can quantify and characterize ions within the ion atmospheres around nucleic acids, proteins, and their complexes.

1. Introduction

Ions are essential for life. Cellular fluids contain various inorganic and organic ions. These ions strongly influence thermodynamics and kinetics of macromolecular interactions [1], [2], [3], [4]. Such influences on DNA, RNA, and proteins depend not only on ionic strength, but also on ionic species, as well-known for Hofmeister series of ions that affect solubility and stability of proteins [3], [5]. While ions are important as essential constituents of biological systems, it is not well understood how these ions interact with biological macromolecules and impact their functions.

Largely due to their mobile nature, ions around nucleic acids and proteins are difficult to directly observe. Protein Data Bank (PDB) has collected > 170,000 structures of biological macromolecules and their complexes over the past five decades [6]. Multivalent ions tightly bound to particular sites are seen in many PDB structures. However, the vast majority of monovalent cations and anions undergo territorial binding (as opposed to site binding) and are unresolved even in high-resolution crystal structures of biological macromolecules. The spatial distribution of mobile ions and their interactions with macromolecules remains elusive in structural biology.

On the other hand, the ion atmosphere where counterions are condensed around nucleic acids was proposed even prior to the inception of PDB. In 1950–60 s, studies using electrophoresis, volumetry, and dialysis equilibrium approaches had suggested that nucleic acids are surrounded by counterions [7], [8], [9], [10]. As three-dimensional structures of DNA and RNA were revealed, researchers developed theoretical models of ionic distribution around nucleic acids and its relevance to the thermodynamics of nucleic acid-protein interactions [11], [12], [13]. In 1970–90 s, the theoretical models for the ion atmosphere were used to explain thermodynamic and ²³Na nuclear magnetic resonance (NMR) data [14], [15], [16]. However, the validity range of the theoretical models remained to be addressed. The ion atmosphere can be convoluted with solvation or conformational dynamics, which may limit the validity of simple models. It could be even more challenging to theoretically describe the ion atmosphere around proteins because their overall charges are smaller and the charge distribution on the molecular surfaces is more uneven. Validations through experiments are essential for any theoretical models. However, in the 20th century, experimental research on the ion atmosphere lagged far behind theoretical and computational research.

In the first two decades of the 21st century, there has been remarkable progress in experimental research on the ion atmosphere around DNA, RNA, and proteins. Some newly developed approaches have greatly facilitated examination and validation of theoretical models and yielded deeper insight into how ions behave around biological macromolecules. In this mini-review, we provide an overview on the recent progress in the experimental approaches for investigating the ion atmosphere around nucleic acids and proteins. Introducing some relevant fundamental concepts, we explain the basic principles of these experimental approaches and their applications.

2. Theoretical aspects of ion accumulation around biological macromolecules

2.1. The concept of ion atmosphere

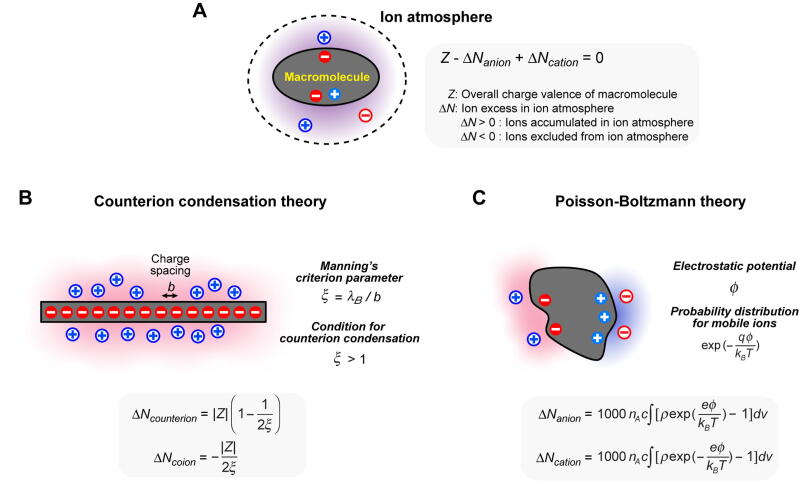
The ion atmosphere of a macromolecule is a zone near the macromolecular surface where the probability distribution of mobile ions differs from the background due to their electrostatic interactions with the macromolecule. For nucleic acids, cations acting as counterions are accumulated in the ion atmosphere and anions acting as coions are excluded from the ion atmosphere. It is important to note that the charge neutralization of a macromolecule occurs not only via accumulation of counterions in the ion atmosphere but also via exclusion of coions from the ion atmosphere (Fig. 1A). The space comprising of the macromolecule and its ion atmosphere should satisfy Z – ΔN_anion + ΔN_cation = 0, where Z is the overall charge valence of the macromolecule; ΔN is a parameter referred to as ‘ion excess’ and represents the number of ions accumulated in (ΔN > 0) or excluded from (ΔN < 0) the ion atmosphere per macromolecule. An ion excess ΔN represents the difference between the number of ions in the ion atmosphere and the number of ions in the same volume outside the ion atmosphere (i.e., the background).

Fig. 1.

Concepts of the ion atmosphere and relevant theories. (A) Charge neutralization for the space comprising of a macromolecule and its ion atmosphere. (B) View of the counterion condensation theory. λ_B is the Bjerrum length. For nucleic acids, ΔN_counterion = ΔN_cation and ΔN_coion = ΔN_anion. (C) View of the Poisson-Boltzmann theory. Symbols used in the ion-excess numbers ΔN_cation and ΔN_anion are as follows: n_A is Avogadro’s number; c is the bulk ion concentration in mol/L units; ρ defines ion accessibility in the box with ρ = 1 for accessible regions and ρ = 0 for regions that are inaccessible due to macromolecular atoms; q, the ionic charge; e, the elementary charge; k_B, the Boltzmann constant; T, the temperature; and v, the volume in m³. A factor of 1000 is for the conversion of the volume unit from L to m³. Subtraction of 1 in the integral corresponds to subtraction of the Boltzmann factor for the background with an electrostatic potential of zero. The shown equations for ion excess are for monovalent ions.

2.2. Counterion condensation theory

The counterion condensation theory is a relatively simple theory about condensation around linear polyelectrolytes such as nucleic acids. It was developed by Manning in 1969 [12], [17], [18], and applied to the thermodynamics of nucleic acid-protein interactions by Record in late 1970 s [13], [19], [20]. According to this theory, counterion condensation around a linear polyelectrolyte occurs when its effective mean charge spacing b is smaller than the Bjerrum length λ_B (=7.14 Å for water at 25 °C). The so-called Manning parameter ξ = λ_B / b is of key importance in this theory. ξ > 1 is the criterion for the counterion condensation. B-form DNA is predicted to condense counterions because b = 1.7 Å (i.e., two phosphates per 3.4 Å along the double-helical axis) and ξ = 4.2. The ion-excess numbers ΔN_cation and ΔN_anion can be estimated from ξ and the overall macromolecular charge valance Z. The total number of counterions in the condensation region is |Z|[1 − ξ^-1], whereas the total number of excluded coions is |Z|(2ξ)^-1 [12]. Manning’s theory separately considers ‘condensed counterions’ and ‘uncondensed counterions’ for the charge neutralization, but this distinction has been criticized as a nonphysical treatment [11], [21]. When screening over the entire atmosphere is considered for monovalent ions, the ion-excess numbers are ΔN_counterion = |Z|[1 − (2ξ)^-1] and ΔN_coion = −|Z|(2ξ)^-1 (Fig. 1B) [13]. For example, this theory predicts that a chemically synthesized 24-bp B-form DNA (Z = -46) accumulates 40.5 cations in the ion atmosphere and excludes 5.5 anions (i.e., ΔN_cation = 40.5 and ΔN_anion = -5.5).

The counterion condensation theory has been successful in explaining various experimental data. In particular, for DNA, this theory explained the salt concentration dependence of thermodynamics for many DNA-protein association processes [22], [23]. However, due to the assumption of linear charge distribution, the counterion condensation theory is not applicable for globular proteins and folded RNAs. Another limitation is that this theory does not predict the dependence of ΔN on ionic strength. Recent studies by ion-counting methods clearly showed that ΔN_cation and ΔN_anion significantly depend on ionic strength, especially when ionic strength is >100 mM [24], [25].

2.3. Poisson-Boltzmann theory

If the three-dimensional structure is known for a macromolecule, the spatial probability distribution of mobile ions around the macromolecular surface at a particular ionic strength can be predicted by the Poisson-Boltzmann theory [26], [27]. In this theory, the Poisson equation for electrostatics is combined with the assumption that the probability distribution of mobile ions is given by a Boltzmann factor with respect to the electrostatic potential. The Poisson-Boltzmann equation is a second-order differential equation and can be numerically solved using atomic coordinates of biomolecules. Software for this purpose such as APBS [28] and DelPhi [29], [30] has gained popularity in a wide variety of research areas. Using the calculated electrostatic potentials, the spatial distribution of mobile ions can be predicted from the Boltzmann factors. Based on the probability distribution of mobile ions, the ion-excess numbers ΔN_cation and ΔN_anion can also be predicted using the equations shown in Fig. 1C.

The Poisson-Boltzmann theory is approximate under assumptions that simplifies calculations [31]. The lack of consideration of correlations between ions can diminish accuracy in calculations of electrostatic potentials for systems at high ionic strength [32]. Solvation of ions and macromolecules is neglected and ions are treated as point charges. Due to the assumption of a dielectric continuum, the electrostatic potentials predicted with the Poisson-Boltzmann theory may be inaccurate for zones near the first hydration layer. Many Poisson-Boltzmann models assume a uniform dielectric constant for the interior or exterior of the macromolecule, creating a sharp dielectric jump at the boundary that could cause problems. Modified Poisson-Boltzmann models have been proposed for improvement, for example, by including corrections for finite ion sizes or solvent dielectric saturation effects [33], [34], [35], [36]. There are needs of examinations for the theoretical models through experiments.

3. Experimental methods for investigating ion atmosphere around biological macromolecules

Since Hofmeister discovered a series of ions that affect the solubility and stability of proteins in the late 19th century, there have been numerous investigations into ionic interactions of proteins and nucleic acids [2], [3], [4]. Here, we focus on recently developed methods that are truly quantitative in determining the ion-excess numbers or/and are incisive in characterizing ions in the ion atmosphere. These methods are summarized in Table 1.

Table 1.

Quantitative experimental methods suited for investigations of the ion atmosphere.

	Methods
Investigations	AES	ICP-MS	ASAXS	NMR
Quantification of ions in the ion atmosphere	Yes [24], [37]	Yes [25], [38], [39]	Yes [40]	Yes [41]
Competition between ions for macromolecules	Yes [24]	Yes [42]	Yes [43], [44]	Yes [41], [45], [46]
Spatial distribution of ions around macromolecules	n.a.	n.a.	Yes [43], [47]	Yes [41], [48], [66]
Diffusional properties of ions interacting with macromolecules	n.a.	n.a.	n.a.	Yes [41], [46]
Ion release upon macromolecular association	p.a.	p.a.	p.a.	Yes [41], [46]

Yes: The feasibility demonstrated in the cited references.

n.a.: Not applicable.

p.a.: Potentially applicable.

3.1. ASAXS methods

Small-angle X-ray scattering (SAXS) is a powerful technique that can provide global structural information of biological macromolecules in solution. Anomalous SAXS (ASAXS) occurs at wavelengths near the X-ray absorption edge of an element [50]. When SAXS data are recorded using a wavelength close to the absorption edge of an element (resonant) and another wavelength slightly far from the absorption edge, only the resonant element exhibits differences between the two datasets. Subtraction of resonant from non-resonant scattering profile yields ASAXS data, which provide information about the resonant element (e.g., ions) correlated with a non-resonant structure (e.g., DNA). Although ASAXS for Na⁺, K⁺, and Mg²⁺ ions are difficult to detect due to interference by water [51], ASAXS can readily be measured for heavier ions such as Rb⁺, Sr²⁺ and Co³⁺.

In 2003, using ASAXS, Pollack and coworkers achieved the first direct confirmation of the physical presence of the ion atmosphere around DNA [47]. They measured ASAXS for Rb⁺ and Sr²⁺ ions in solutions of a 25-bp DNA duplex. Ionic competition between Co³⁺ and Rb⁺ ions for DNA phosphates was also studied by ASAXS [44]. In the charge neutralization of DNA, multivalent ions were found to occupy the ion atmosphere more favorably than monovalent ions. It was also demonstrated that the ASAXS-based methodology can quantify the number of ions around DNA [40]. ASAXS was used to study ion atmosphere around RNA as well. The anomalous profiles of Rb⁺ and Sr²⁺ ions around 25-bp DNA and RNA duplexes of the same sequence were compared [52]. The data show that the RNA duplex attracts both monovalent and divalent ions closer to its surface and hence have more effective charge screening as compared to the corresponding DNA duplex. The discrepancy was attributed to the topological difference between the A-form RNA and the B-form DNA.

ASAXS data agreed well with the predictions from the Poisson-Boltzmann theory with finite ion sizes taken into account [53], [54], [55]. Excellent agreement was also found between ASAXS profile of short double-stranded RNA and the results from explicit solvent molecular dynamics (MD) simulations [56]. However, for a RNA pseudoknot, both experimental ASAXS and atomistic MD results were significantly different from the Poisson-Boltzmann-based predictions from the crystal structure. These findings encourage further improvement of theoretical models for dynamic structures. Thus, ASAXS greatly facilitated the examination of theoretical models on spatial distribution of mobile ions around DNA and RNA.

3.2. BE-AES and BE-ICP-MS methods

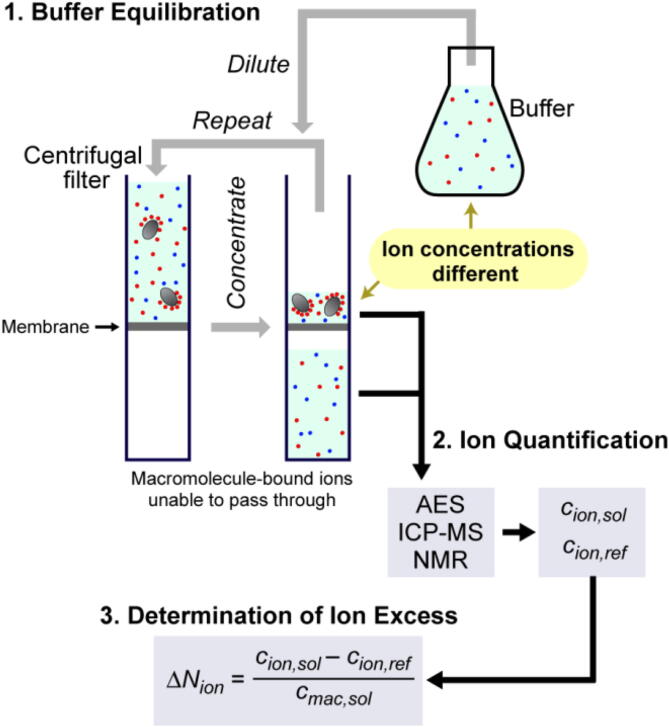
The buffer equilibration-atomic emission spectroscopy (BE-AES) method is an ion-counting method that allows for quantifying ions within the ion atmosphere [24], [37], [57]. The first step in ion-counting methods is buffer equilibration using centrifugal filters (Fig. 2) or dialysis membrane [58]. Ions in the final macromolecular solution and in the flow-through liquid are quantified using atomic emission spectroscopy (AES). The quantification of ions can also be performed by inductively coupled plasma mass spectroscopy (ICP-MS) [25], [38], [42] or NMR [41], [46]. The BE-AES and BE-ICP-MS methods can quantify various elements and analyze biologically relevant ions such as Na⁺, K⁺, and Mg²⁺ ions [57], [58].

Fig. 2.

Ion-counting methods for quantifying ions in the ion atmosphere. The ion excess per macromolecule (ΔN_ion) is determined from the ion concentrations in the final solution (c_ion,sol) and in the reference buffer used for the equilibration (c_ion,ref) as well as the macromolecular concentration in the final solution (c_mac,sol).

The BE-AES ion-counting method also allows for investigations of competition between ions for nucleic acids [24]. Competition experiments using this method showed that Mg²⁺ and Ca²⁺ ions associate with DNA ~ 40-fold more strongly than Na⁺ and K⁺ ions. The BE-AES method was also used to investigate anion exclusion. The ion-excess numbers at high salt concentrations were found to depend strongly on the mean activity coefficients of the salts. The BE-AES or BE-ICP-MS methods have been used to study ion atmosphere around RNA as well [38]. As anticipated from the structural difference, the cation-excess number determined for a 24-bp RNA duplex was larger than that for the corresponding DNA duplex of the same sequence [38]. The BE-ICP-MS method has been applied to study the ion atmosphere around a nucleosome core particle [39]. Intriguingly, although the nucleosome formation reduces the overall charge by half, the ion-counting data suggested that a strong negative electrostatic field remains.

The BE-AES and BE-ICP-MS ion-counting data illuminated the strengths and limitations of the theoretical models on the ion atmosphere. The discrepancies between Poisson-Boltzmann predictions and experimental data were more significant for ions with higher valence or larger size. Based on the experimental data, new theoretical models that can better reproduce the experimental ion-counting data were developed [59], [60], [61]. The ion-counting methods helped advance knowledge about the ion atmosphere surrounding nucleic acids.

3.3. NMR methods for quantifying and characterizing ions in the ion atmosphere

NMR spectroscopy is a powerful technique for probing the structural and dynamic properties of biomolecules [62]. In 1970–80 s, ²³Na NMR was used to study interactions between Na⁺ ions and DNA [45], [63], [64]. Later on, magnetic field-dependence of ²³Na NMR relaxation was used to invetigate more details about the behavior of Na⁺ ions interacting with DNA [49]. In 1990s, NMR paramagnetic relaxation enhancement (PRE) arising from Mn²⁺ ions as well as nuclear Overhauser effects (NOEs) for NH₄⁺ ions were also used to investigate ion-DNA interactions [48], [65], [66]. More recently, NMR-based ion-counting methods have been developed for more quantitative investigations of ions around nucleic acids and proteins [41], [46].

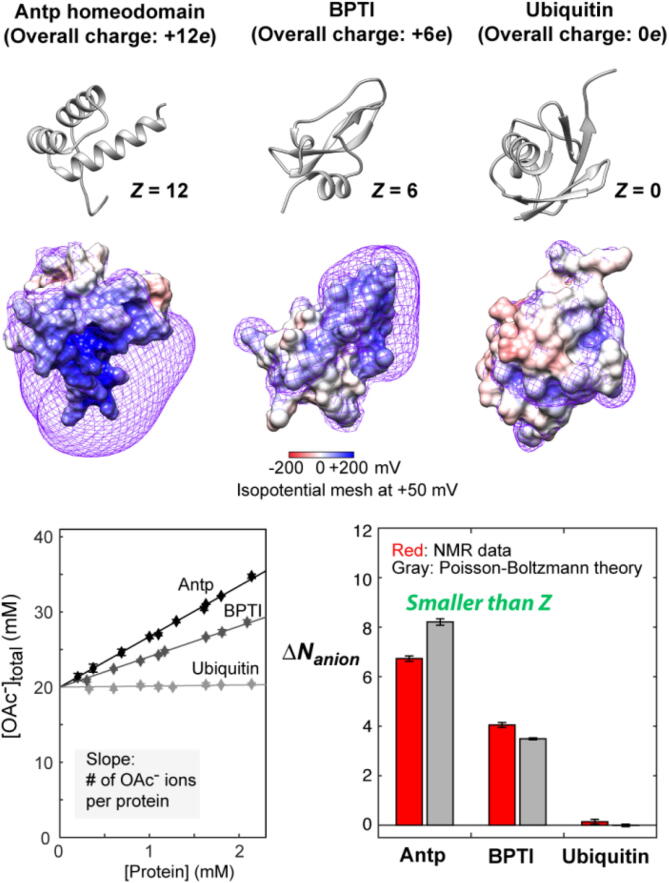
The NMR-based ion-counting method were applied to both DNA and proteins. The ion-excess number ΔN_anion was measured for the Antp homeodomain, bovine pancreatic trypsin inhibitor (BPTI) and ubiquitin (Fig. 3) [41]. The NMR experiments clearly showed accumulation of anions around the positively charged proteins. The measured ΔN_anion was significantly smaller than the overall charge valence (Z) of each protein, which suggest that the charge neutralization occurs via both the accumulation of counterions and the exclusion of coions [41]. The experimental results were consistent with the predication from the Poisson-Boltzmann theory (Fig. 3).

Fig. 3.

NMR-based quantification of anions accumulated around the Antp homeodomain, BPTI, and ubiquitin. Note that the measured ΔN_anion was smaller than the overall charge valence Z. This means that the charge neutralization occurs not only via accumulation of anions, but also via exclusion of cations from the ion atmosphere. Adopted from Yu et al. [41]

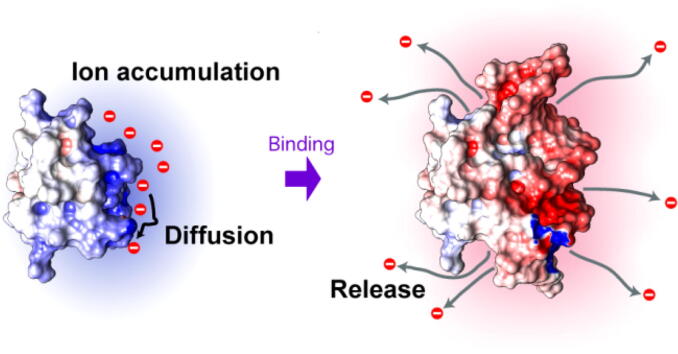
Unlike other ion-counting methods, the NMR-based method can also provide information about the diffusional properties of ions within and outside the ion atmosphere [41], [46]. NMR-based diffusion experiments showed that the acetate ions in the ion atmosphere are only loosely constrained by the proteins. By comparing the apparent diffusion coefficients of ions in solutions of free proteins, free nucleic acids, and the complex as well as those in the sample buffer alone, the number of ions released upon the formation of the protein-nucleic acid complex can also be determined. NMR-based diffusion data showed the release of 7 anions from the ion atmosphere around Antp homeodomain and 11 cations from the ion atmosphere around a 15-bp DNA duplex upon the formation of the protein-DNA complex [41], [46].

3.4. NMR methods for investigating spatial distribution of ions in the ion atmosphere

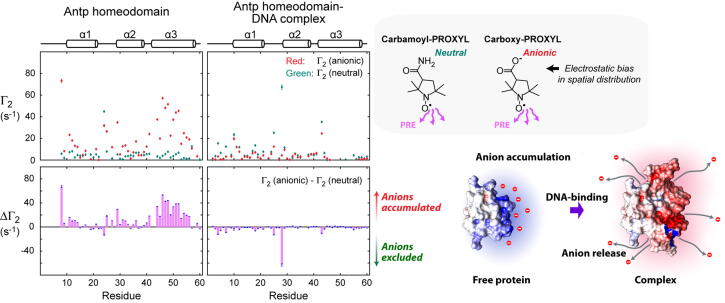
NMR PRE arising from paramagnetic cosolutes, carboxy-PROXYL (anionic) and carbamoyl-PROXYL (neutral), can be used to investigate anion distribution around a protein. The PRE rate for the transverse nuclear magnetizations, Г₂, is sensitive to spatial distribution of paramagnetic cosolutes [67]. The difference (ΔГ₂) between the PRE Г₂rates for the anionic and neutral PROXYL derivatives at the same concentration reflect a bias in spatial distribution of anions due to electrostatic interactions with the protein. Fig. 4 shows examples of ΔГ₂ data for the Antp homeodomain in the free state and those for the Antp homeodomain-DNA complex. Many residues of the Antp homeodomain in the free state exhibited large positive ΔГ₂ values, suggesting that anions are accumulated around the positively charged surface of this protein. In contrast, most residues in the complex with DNA exhibited negative ΔГ₂, suggesting that anions are excluded from the complex surface. This is reasonable since the overall charge for the Antp homeodomain-DNA complex is −16e. Moreover, the negative ΔГ₂ is consistent with the NMR diffusion data indicating anion release from the Antp homeodomain upon binding to DNA. The NMR-based approaches for investigating the ion atmosphere can readily be applied to many other systems of proteins, nucleic acids, and their complexes.

Fig. 4.

NMR paramagnetic relaxation enhancement (PRE)-based approach for investigating the spatial distribution of anions around the Antp homeodomain and its complex with 15-bp DNA. The data were adopted from Yu et al. [41] Comparison of PRE arising from analogous anionic and neutral paramagnetic cosolutes provides site-specific information about ion accumulation or exclusion. The data shown on the left-hand side suggest that anions are accumulated around the Antp homeodomain in the free state but excluded upon formation of the protein-DNA complex.

4. Future perspectives

Many experimental data show that thermodynamics and kinetics of protein-nucleic acid or protein–protein association are strongly influenced by ions [16], [22], [68], [69]. Such influences may arise not only from the screening effect [70], but also from the entropic effects of the ion release upon the macromolecular complex formation [4], [16], [22]. Further research on the ion atmospheres around macromolecules may explain why activities of some proteins strongly depend on types of ions present in the same solutions. For instance, when glutamate (Glu^-) ions are used instead of Cl^- ions in biochemical experiments, some DNA-binding proteins exhibit substantially stronger (>100-fold for some cases) affinity for DNA [71], [72]. This effect may be related to differences in the behavior of Glu^-and Cl^- ions around positively charged proteins. Future applications of the aforementioned methodologies will likely provide mechanistic insight into how ions affect functions of proteins and nucleic acids. Since NMR methods for charged moieties of proteins are available [74], [75], more detailed investigations of interactions between ions and individual charged side chains of proteins will be feasible.

Further methodological progress can be made through an advancement in hardware. For instance, advances in synchrotron radiation sources and corresponding detectors would improve the precision of the ASAXS method and may extend its capability toward more proximal ionic interactions [73]. Advances in NMR instrumentation will facilitate diffusion coefficient measurements for various ions. Typical NMR probes can generate magnetic field gradients of up to ~55 gauss/cm. This magnitude of gradients is sufficient for diffusion experiments on ¹H, ¹³C, ¹⁵N, ¹⁹F and ³¹P nuclei, but insufficient for diffusion experiments on ²³Na and ³⁵Cl nuclei. Because quadrupole nuclei exhibit rapid longitudinal relaxation and relatively small gyromagnetic ratios, diffusion NMR experiments for these nuclei require special broadband probe hardware that can generate far stronger field gradients (e.g., >200 gauss/cm). Such hardware will enable investigations of the diffusional properties of physiologically important Na⁺ and Cl^- ions in the vicinity of nucleic acids and proteins.

5. Concluding remarks

In the past two decades, there have been great advances in experimental research on the ion atmospheres around biomolecules. ASAXS, BE-AE and BE-ICP-MS methods have provided significant insights into the ion atmosphere around DNA and RNA. More recently, NMR-based methods that are capable of quantifying, characterizing, and visualizing ions in the ion atmosphere have provided unprecedented information about the ion atmosphere around nucleic acids and proteins. These experimental approaches can readily generate mutually beneficial feedback loops between theoretical/computational and experimental studies. Further research on weak interactions between ions and macromolecules will likely advance our knowledge about how ions impact biological macromolecules and their functions in living systems.

CRediT authorship contribution statement

Binhan Yu: Writing - original draft. Junji Iwahara: Funding acquisition, Conceptualization, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.