Abstract
Understanding adaptation mechanisms is important in evolutionary biology. Parallel adaptation provides good opportunities to investigate adaptive evolution. To confirm parallel adaptation, it is effective to examine whether the phenotypic similarity has one or multiple origins and to use demographic modeling to consider the gene flow between ecotypes. Solidago yokusaiana is a rheophyte endemic to the Japanese Archipelago that diverged from Solidago virgaurea. This study examined the parallel origins of S. yokusaiana by distinguishing between multiple and single origins and subsequent gene flow. The haplotypes of noncoding chloroplast DNA and genotypes at 14 nuclear simple sequence repeat (nSSR) loci and single-nucleotide polymorphisms (SNPs) revealed by double-digest restriction-associated DNA sequencing (ddRADseq) were used for phylogeographic analysis; the SNPs were also used to model population demographics. Some chloroplast haplotypes were common to S. yokusaiana and its ancestor S. virgaurea. Also, the population genetic structures revealed by nSSR and SNPs did not correspond to the taxonomic species. The demographic modeling supported the multiple origins of S. yokusaiana in at least four districts and rejected a single origin with ongoing gene flow between the two species, implying that S. yokusaiana independently and repeatedly adapted to frequently flooding riversides.
Subject terms: Structural variation, Plant evolution
Introduction
Natural selection causes various mechanisms and magnitudes of adaptive evolution and results in speciation. Understanding adaption mechanisms is an important topic in evolutionary biology (Rougemont et al. 2017). Parallel adaptive changes provide strong evidence for the consequences of natural selection (Jones et al. 2012; Butlin et al. 2014) and phenotypic or genotypic parallelism often results from adaptation to similar environments (Cooper et al. 2003; Meier et al. 2017). Parallel adaptations, which we may recognize as phenotypic similarity of polyphyletic or paraphyletic populations, may generate ecotype pairs structured by geographic proximity (Trucchi et al. 2017). For example, in the case of a marine snail (Littorina saxatilis), “wave” and “crab” ecotypes indicated parallel adaptations and geography-dependent genetic structures were found irrespective of ecotypes (Butlin et al. 2014). These ecotype pairs are often considered the repeat consequences of natural selection and adaptive evolution to similar environments, which is considered natural replication of adaptive evolution (Butlin et al. 2014; Welch and Jiggins 2014; Rougemont et al. 2017). Although comparisons of a single ecotype pair may be affected by random processes (Nosil and Feder 2013), multiple natural replicates provide a good opportunity to investigate adaptive evolution (Johannesson et al. 2010; Roesti et al. 2014; Welch and Jiggins 2014).
Ecotype pairs are possible natural replicates of adaptive evolution. Several genetic studies of ecotype pairs have indicated multiple origins by revealing closer genetic distances between populations of different ecotypes in geographic proximity than between populations of derived ecotypes in remote places (Arroyo-García et al. 2006; Foster et al. 2007) or a single origin by revealing closer genetic distances between each ecotype than between populations of different ecotypes in geographic proximity (Crandal et al. 2000; Sakaguchi et al. 2018a). However, these genetic structures may also have resulted from distinct demographic divergence scenarios (Johannesson et al. 2010; Bierne et al. 2013; Welch and Jiggins 2014). Considering methods of demographic history, recent studies of ecotype pairs imply that a derived ecotype can result from multiple complicated origins (Butlin et al. 2014; Yuan et al. 2014; Meier et al. 2017; Trucchi et al. 2017), secondary contact (Rougemont et al. 2017), or a single origin (Molina et al. 2011). These studies indicate the need to consider the demographic divergence history to elucidate the origin of ecotype pairs. For example, Meier et al. (2017) found parallel speciation of the two cichlid species, Pundamilia pundamilia and P. nyererei. Based on demographic modeling, they indicated that Pundamilia ancestor first speciated into P. pundamilia and P. nyererei at open lake, and then two species colonized the Mwanza Gulf and admixed there, and last, this hybrid population speciated again into P. pundamilia and P. nyererei.
Inadequate analysis of gene flow in a species or ecotype may lead to incorrect inference of evolutionary scenarios (Li et al. 2012; Welch and Jiggins 2014; Rougemont et al. 2017). Secondary contact can erase the signals of a phylogenetic relationship between populations of each ecotype at neutral loci (Bierne et al. 2013; Welch and Jiggins 2014; Leaché et al. 2014) and gene flow between paraphyletic populations may increase support for a monophyletic gene tree (Leaché et al. 2014).
Rheophytes are riparian plants that are adapted and confined to frequently flooded riversides. The rheophytic phenotype has evolved in different phylogenetic groups and has parallel phenotypic traits, such as narrow leaves, thicker roots, and tough, flexible stems (van Steenis 1981; Kato 2003). These traits are likely adaptive; therefore, ecotype pairs of a rheophyte and its ancestor occurring in proximity but away from the riverside are natural replicates and provide a model system for studying adaptive evolution. Parallel rheophytic adaptations have been often suggested to have multiple origins based on population genetic structure or historical demographic modeling without gene flow between the rheophyte and terrestrial populations (e.g., Nomura et al. 2010; Sakaguchi et al. 2018b; Yoichi et al. 2018), although there is a small probability that strong gene flow has caused misleading paraphyletic results. To confirm whether the adapted traits have single or multiple origins, we need to consider gene flow between ecotypes in geographic proximity. Here, we examined whether rheophyte traits have multiple origins or a single origin with secondary contact between rheophyte and terrestrial populations in the goldenrod genus Solidago.
Solidago virgaurea (Asteraceae) is a perennial herb that is widely distributed in Eurasia (Kawano 1988; Semple 2016). In the Japanese Archipelago, the S. virgaurea complex is extremely divergent ecologically and morphologically (Kawano 1988; Sakaguchi et al. 2018a). Solidago yokusaiana, a rheophytic congener of S. virgaurea, is endemic to Japan from Tohoku to Okinawa Districts (Sakaguchi et al. 2018b; Semple and Ohi-Toma 2017) (Fig. 1). Although Sakaguchi et al. (2018b) suggested that S. yokusaiana has multiple origins based on the population genetic structures of ecotype pairs, it remains necessary to evaluate the effects of gene flow among populations and reassess the phylogeny. To distinguish several evolutionary scenarios for parallelism (Li et al. 2012; Welch and Jiggins 2014; Rougemont et al. 2017), we performed coalescent simulation analyses incorporating gene flow between ecotypes in geographic proximity.
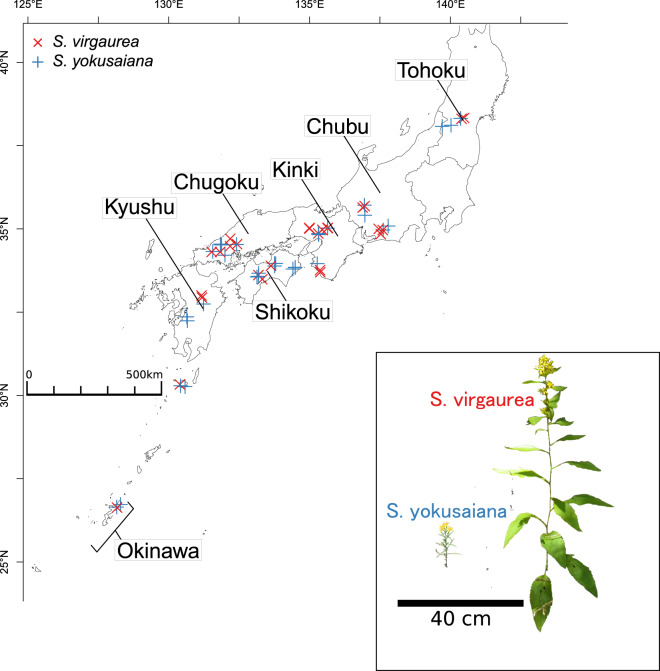
Fig. 1. Sampling locations for Solidago virgaurea (red) and S. yokusaiana (blue).
The morphology of the two Solidago species is shown at the bottom right.
In this study, we examined whether the rheophyte S. yokusaiana has single or multiple origins based on demographic modeling with gene flow using double-digest restriction-associated DNA sequencing (ddRADseq), noncoding chloroplast DNA sequences, and nuclear simple sequence repeat (nSSR) genotypes. Reconstructing the demographic divergence history of S. virgaurea and S. yokusaiana, we explore demographic scenarios in the evolution of rheophytism in S. yokusaiana, including multiple origins, a single origin, or secondary contact after a single origin.
Materials and methods
Population sampling
To evaluate the genetic diversity of Solidago yokusaiana (Makino 1898) and its putative ancestor S. virgaurea subsp. asiatica in the Japanese Archipelago, S. yokusaiana populations were sampled throughout its distribution (35 populations) and S. virgaurea populations were sampled from the areas adjacent to the S. yokusaiana populations (26 populations) (Fig. 1 and Table S1). Mature leaves were sampled haphazardly at intervals of at least a few meters to avoid repeated collection of the same genet. The collected leaf samples were frozen at −20 °C or kept at room temperature after drying with silica gel.
Molecular experiments
Total DNA was extracted from 50 to 150 mg of leaf tissue using the cetyltrimethylammonium bromide method (Doyle and Doyle 1990). Four chloroplast noncoding regions from 2 to 10 individuals from each population were sequenced: ndhF-rpl32 (Shaw et al. 2007), psbB-psbF (Hamilton 1999), trnG (GCC)-trnfM (CAU), and rpl32-trnL (UAG) (Shaw et al. 2007) (Table S1). Polymerase chain reaction (PCR) was performed in 10-µL volumes, each containing 15–30 ng of genomic DNA, 0.15 µM of each primer, 0.2 mM of each dNTP (Promega, Madison, WI), 0.5 mM of MgCl2, 1 µL of ×10 PCR buffer, and 0.5 U of Taq polymerase (Promega). Thermal cycling was initiated at 95 °C for 4 min, followed by 30 cycles of 95 °C for 30 s, 52.5 °C for 1 min, and 72 °C for 1 min for ndhF-rpl32, 30 cycles of 95 °C for 30 s, 53 °C for 1 min, and 72 °C for 1 min for psbB-psbF, 30 cycles of 95 °C for 30 s, 55 °C for 1 min, and 72 °C for 30 s for trnG (GCC)-trnfM (CAU), or 35 cycles of 95 °C for 30 s, 53 °C for 1 min, and 72 °C for 1 min for rpl32-trnL (UAG), with a final 5 min at 72 °C. The PCR products were purified using a GENECLEAN II kit (MP Biomedicals, Santa Ana, CA) or ExoSAP-IT Express (Thermo Fisher Scientific, Waltham, MA) and diluted to 30 µL with deionized water. Cycle sequencing was performed in 10-µL volumes, containing 7.7 µL of the purified PCR products, 0.2 µM of each primer, 1.9 µL of 5× sequencing buffer, and 0.2 µL of BigDye Terminator v3.1 Cycle Sequencing Kit (Thermo Fisher Scientific). Thermal cycling was initiated at 96 °C for 1 min, followed by 30 cycles of 96 °C for 10 s, 50 °C for 5 s, and 60 °C for 4 min, with a final 1 min at 60 °C. Sanger sequencing was performed on an ABI Prism 3100 or 3130 Genetic Analyzer (Thermo Fisher Scientific).
Fourteen nSSR loci (Sakata et al. 2013; Sakaguchi and Ito 2014; Table S2) were genotyped for 2–35 individuals from each population (Tables S1 and S2). PCR was performed in 2-µL volumes, containing 20–50 ng of DNA, 1 µL of 2× Type-it Multiplex PCR Master Mix (QIAGEN, Hilden, Germany), and 0.025 µM each of six primers [Sol_2003053, Sol_2005991, Sol_2007258, Sol_2007556, Sol_2012220, and Sol_2013075 (Sakaguchi and Ito 2014)], 0.05 µM each of six primers [Sol_2001876, Sol_2003631, Sol_2006931, Sol_2071098 (Sakaguchi and Ito 2014), Salt1, and Salt3 (Sakata et al. 2013)], or 0.1 µM each of two primers [Sol_2013411 (Sakaguchi and Ito 2014) and Salt17 (Sakata et al. 2013)]. The lengths of the PCR products were measured using an ABI Prism 3130 Genetic Analyzer and genotyped using Gene Mapper (Thermo Fisher Scientific).
Double-digest restriction-associated DNA sequencing (ddRADseq)
A ddRADseq library (Peterson et al. 2012) was prepared for S. yokusaiana (87 individuals, 12 populations) and S. virgaurea (63 individuals, 14 populations) (Table S1) using a modification of Peterson’s protocol (Sakaguchi et al. 2018b), as follows. First, 10 ng of genomic DNA was digested with EcoRI and BglII (New England Biolabs, Ipswich, MA). Then, adapter ligation was performed at 37 °C overnight in a 10-µL volume containing 1 µL of ×10 New England Biolabs (NEB) buffer 2, 0.1 µL of ×100 bovine serum albumin (NEB), 0.4 µL of 5 µM EcoRI adapter and BglII adapter, 0.1 µL of 100 mM ATP, and 0.5 µL of T4 DNA ligase (QIAGEN). The reaction solution was purified using AMPure XP (Beckman Coulter, Brea, CA). The PCR was performed with 3 µL of the purified DNA in a 10-µL volume containing 1 µL each of 10 µM index and TruSeq universal primer, 0.3 µL of KOD-Plus-Neo enzyme, 1 µL of ×10 PCR buffer (Toyobo, Osaka, Japan), 0.6 µL of 25 mM MgSO4, and 1 µL of 10 mM dNTP. Thermal cycling was initiated at 94 °C for 2 min followed by 20 cycles of 98 °C for 10 s, 65 °C for 30 s, and 68 °C for 30 s. The pooled PCR products were purified again using AMPure XP to give fragments of around 320 base pairs using E-Gel SizeSelect (Thermo Fisher Scientific) with 2.0% agarose gels. After assessing quality using an Agilent 2100 Bioanalyzer (Agilent Technologies, Santa Clara, CA), the library was sequenced with 51-bp single-end reads in one lane of an Illumina HiSeq2000 (Illumina, San Diego, CA). The primer sequences used in this study are described in Sakaguchi et al. (2015).
Trimming adapters, other Illumina-specific sequences, and low-quality regions (Phred quality scores <20) were decided using Trimmomatic (Bolger et al. 2014). De novo assembly was performed using Stacks (Catchen et al. 2011, 2013) with a minimum rate of individuals (r) of 0.3 and a minimum stack depth (m) of 8. The SNPs with minor allele counts <2, which excludes singletons, a missing genotype rate of SNPs (geno) >0.3, a missing genotype rate of individual (mind) >0.4, and significant deviation from Hardy–Weinberg equilibrium (P < 0.00001) were filtered out and leave other options default using plink 1.90b6.21 (Purcell et al. 2007; https://www.cog-genomics.org/plink/1.9/) and selected one SNP per read.
Data analysis
The chloroplast sequences were edited and aligned using BioEdit v7.1.9 (Hall 1999). We recovered haplotypes without insertions or deletions because of the uncertain effects of indels on sequencing and alignment, inferred relationships between the haplotypes using TCS 1.21 (Clement et al. 2000), conducted hierarchy analysis of molecular variance (AMOVA) (Excoffier et al. 1992) to partition the genetic variation into species and populations using Arlequin 3.5.1.3 (Excoffier and Lischer 2010) with 10,000 permutations, and analyzed the mismatch distribution to test for sudden demographic expansion using Arlequin 3.5.1.3 with 1000 replications.
To infer the population genetic structure, we performed Bayesian clustering on the nSSR data using STRUCTURE 2.3.4 (Pritchard et al. 2000) with ten replicates each assuming clusters (K = 1–20), 100,000 burn-in, 10,000 sampling steps, fixing the allele frequency prior hyperparameter lambda = 0.3, and using the LOCPRIOR model with population IDs as sampling locations, and then identified the most likely number of clusters based on the ΔK method (Evanno et al. 2005) using Structure Harvester (Earl and vonHoldt 2012). The ten replicates for the most likely number of clusters were averaged using CLUMPP ver. 1.1.2 (Jakobsson and Rosenberg 2007) with a greedy algorithm. We performed partial Mantel tests (Smouse et al. 1986) between the Euclidean distances of the rates of the clusters in each population and geographic distance, with a difference in species as a dummy variable using the R-package “phytools” (Revell 2012) with 10,000 permutations.
To infer phylogenetic relationships among populations from the SNP data, we constructed unrooted phylogenetic trees using the neighbor-joining method (Saitou and Nei 1987) with DA distance between populations (Nei 1972) and the node support values were evaluated by 1000 bootstrap replicates using the R-package “poppr” (Kamvar et al. 2014). We conducted hierarchy AMOVA to partition the genetic variation into species and populations using the R-package “pegas” (Paradis 2010) with 10,000 permutations. To infer population genetic structure in the SNP data, we performed Bayesian clustering using STRUCTURE 2.3.4 with ten replicates each assuming clusters (K = 1–10), 20,000 burn-in, 10,000 sampling steps, fixing the allele frequency prior hyperparameter lambda = 0.3, and using the LOCPRIOR model with the population IDs as the sampling locations, and then identified the most likely number of clusters based on the ΔK method using Structure Harvester as above. We also performed principal component analysis (PCA) of the SNP data to infer genetic structure using the R-package “adegenet” (Jombart 2008). We performed partial Mantel tests between the Euclidean distance of the rates of the clusters in each population and geographic distance, with a difference in species as a dummy variable using the R-package “phytools” with 10,000 permutations. Correlations between DA distance for SNP data and geographic distance, isolation-by-distance (IBD) patterns, for each species, were evaluated for populations with more than one individual with 9999 bootstrap replicates based on the Mantel test (Mantel 1967) using the R-package “ade4” (Dray and Dufour 2007). The demographic history of the effective population size for each Solidago species was estimated using a generalized skyline plot (Strimmer and Pybus 2001) using the R-package “ape” (Paradis and Schliep 2019) followed by construction of a UPGMA phylogenetic tree (Sokal and Michener 1958) for individuals based on the number of nucleotide differences. Admixture tests for all possible combinations of four S. yokusaiana populations were performed by minimum Patterson’s D statistics (Patterson et al. 2012) using Dsuite (Malinsky et al. 2020).
Demographic modeling
To elucidate the genetic background of the parallel rheophytic changes of S. yokusaiana, we selected four districts: Tohoku, Chubu, Chugoku, and Okinawa (Fig. 1 and Table S1). For each district, S. virgaurea population and S. yokusaiana population were selected for demographic modeling. To include the entire distribution of S. yokusaiana, the northern- and southern-most districts in the distribution of S. yokusaiana were selected and two remote districts filled the gap between the most distant districts. To estimate the order of speciation and range expansion of the two Solidago species, we compared 12 alternative demographic models in all possible six combinations by choosing two districts from the four districts, each having four populations (Fig. 1 and Table S1). These combinations were composed of two populations (each of S. virgaurea and S. yokusaiana) in one district and also two populations (each of S. virgaurea and S. yokusaiana) in another district. To make the observed minor allele site frequency spectrum (SFS), apart from the population genetic analyses, we removed individuals with a relatively high missing genotype rate and filtered out SNPs with a minor allele count <1, which excludes monomorphic sites, missing genotype rates of SNPs (geno) >0.0, missing genotype rates of individuals (mind) >1.0, and significant deviation from Hardy–Weinberg equilibrium (P < 0.01) and leave other options default using plink 1.90b6.21 and selected one SNP per read toward raw data processed by Stacks.
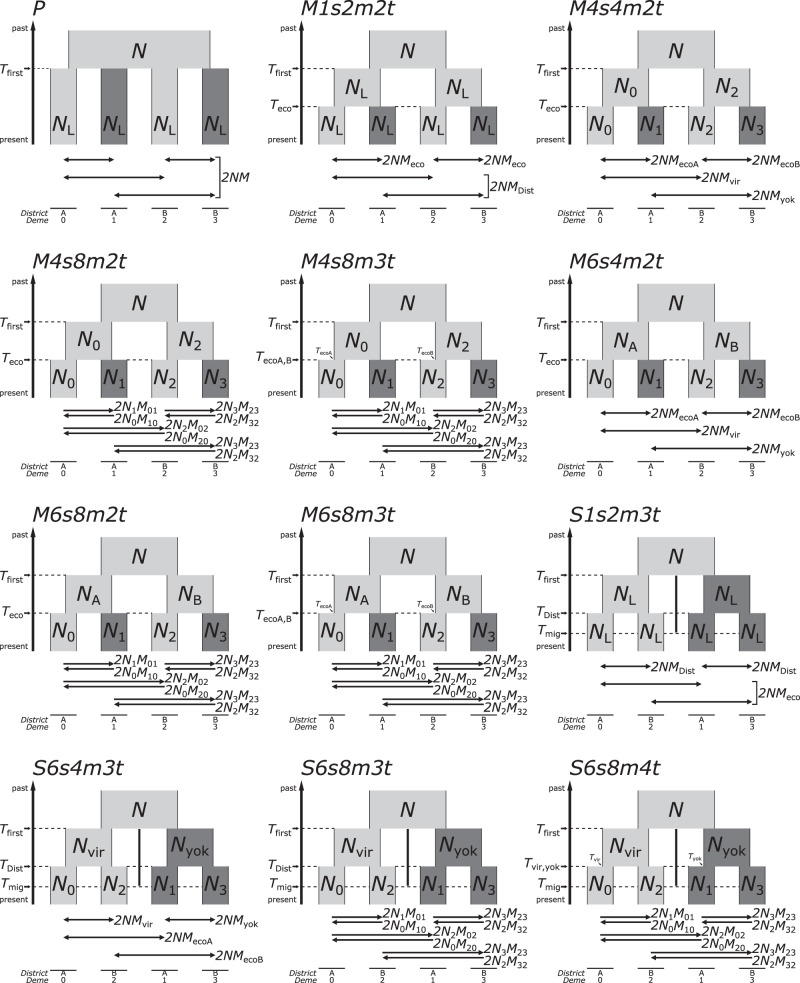
To distinguish between multiple origins and a single origin with gene flow between S. yokusaiana and S. virgaurea in geographic proximity, we performed demographic modeling using fastsimcoal2 (Excoffier et al. 2013) based on the minor allele SFS, and fitted the simulated multidimensional minor allele SFS to the observed multidimensional minor allele SFS of the ddRADseq data without missing genotypes by maximizing the composite likelihood. For demographic modeling, we constructed and compared three origin scenarios with 12 alternative demographic models, including one polytomous divergence scenario, seven different complex models of multiple-origin scenarios, and four different complex models of secondary contact after single-origin scenarios (Fig. 2 and Table S3).
Fig. 2. Illustrations of the demographic models used for model selection.
The polytomy model for the null hypothesis (P), multiple origins with different complexities (M1s2m2t, M4s4m2t, M4s8m2t, M4s8m3t, M6s4m2t, and M6s8m2t), and single origin with different complexities (S1s2m3t, S6s4m3t, S6s8m3t, and S6s8m4t) are shown. The first alphabet of the model codes indicates polytomy (P), multiple origins (M), or single origin (S), and the following combination of a digit and an alphabet of the model codes correspond to the number of parameters and a class of the parameters; each class of the parameters corresponds to the population size (s), the number of migrants (m), and the divergence time (t). For example, a model code M6s4m2t indicates that the model supposes multiple origins and includes six parameters for population size, four parameters for the number of migrants, and two parameters for divergence time. The colors of the rectangles indicate Solidago virgaurea (light gray) and S. yokusaiana (dark gray) populations. The horizontal arrows below each model denote the direction of migration. Bidirectional arrows indicate that the number of migrants in each direction is equal for each population. The arrows to the left of the models indicate generations when events occurred backward in time. The vertical bars in the single-origin models denote the period of S. virgaurea and S. yokusaiana allopatry. District and deme correspond to the combinations of populations in Table 1. N, ancestral effective population size fixed to 10,000. NL and N0–3, ratio of contemporary effective population size to N. NA, NB, Nvir, and Nyok, ratio of district or species effective population size to N. Tfirst, the divergence time of a district or species. Teco and TecoA, B, the divergence time of species, and species in district A or B corresponding to TecoA and TecoB, respectively. TDist and Tvir, yok, the divergence time of districts, and districts for S. virgaurea and S. yokusaiana corresponding to Tvir and Tyok, respectively. Tmig–present, period of sympatry. 2NMDist, eco, and ecoA, B, vir and yok, the numbers of migrants between districts, ecotypes, and ecotypes in district A or B, for S. virgaurea and S. yokusaiana, respectively. 2NjMij, the number of migrants to Deme j from Deme i. The parameter codes (N, 2NM, and T) with different subscripts mean the same class of parameters but different parameters in demographic modeling (e.g., N1 and N2 are parameters of population sizes for deme 1 and 2, respectively, and these population sizes differ each other).
The models of multiple origins represented scenarios for independent speciation (differentiation) in each district after range expansion of an ancestor, and included different population sizes between the ancestral and descendant populations for district divergence or speciation events (one, four, or six sizes), different numbers of migration events (two, four, or eight times), or different numbers of divergence events (two or three times) (Fig. 2 and Table S3). As we considered S. virgaurea to be the ancestor of S. yokusaiana, the local ancestral population could be considered an identical current population of S. virgaurea. Therefore, we also reconstructed the models of multiple origins in which the size of each local ancestral population equaled that of current S. virgaurea.
The models of a single origin represented scenarios for secondary contact between the species in each district after the speciation and range expansion of each species, and included periods of allopatry between the species, different population sizes between the ancestral and descendant populations with district divergences or speciation (one or six sizes), different numbers of migration events (two, four, or eight times), or different numbers of divergent events (two or three times) (Fig. 2 and Table S3). As we considered secondary contact between the species, we included periods of allopatry between the species after range expansion (Tfirst–Tmig) in the models of single origin (Fig. 2).
For the demographic parameters of the coalescent simulations, we fixed the population size of the common ancestral population to 10,000 for all demographic models because we could not use a precise estimate for the mutation rate in Solidago. For the other demographic parameters, we used wide initial search ranges with log-uniform distributions (Table S3). For each demographic model, we estimated the multidimensional minor allele SFS (-u -m) using a composite likelihood method (-M) with 100,000 coalescent simulations (-n 100,000) and 20 expectation–maximization cycles (-L 20), performed ten independent runs to check convergence, and kept the run with the lowest Akaike’s information criterion (AIC; Akaike 1974). The AIC values were calculated from the composite likelihood and the number of parameters (Excoffier et al. 2013).
To reconstruct the demographic divergence history of the species, the best-fitting models for each district combination were identified from among the 12 alternative demographic models using AIC and used to estimate the demographic parameters. To obtain the highest-density intervals (HDIs) for the parameter estimates of the best models, we generated 100 bootstrap pseudo-observed data for each district combination and estimated the parameters from those pseudo-observed data by specifying the initial parameter values, which were point estimates of the best models. Then, we computed the 95% HDIs using the R-package “HDInterval” (Meredith and Kruschke 2018). To estimate the detailed demographic history, we performed Wilcoxon signed-rank tests between the population size of current S. virgaurea and that of S. yokusaiana in the same district, and the population sizes of the current and ancestral S. virgaurea. We also performed pairwise comparisons of the models of multiple origins using the Wilcoxon rank-sum test on wait time to speciation, the proportions of the number of generations between range expansion events, and district speciation event(s) to the number of generations after the range expansion event (1 − Teco/Tfirst).
Results
Chloroplast haplotypes
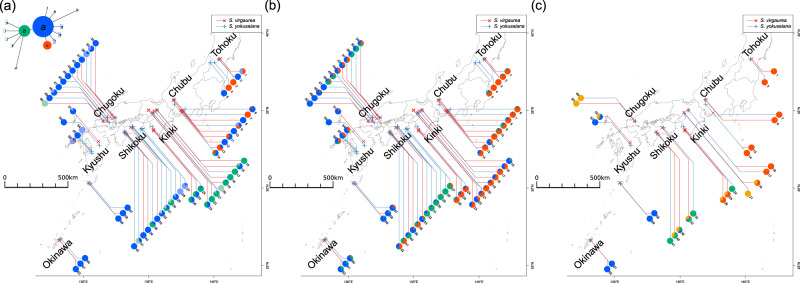
We identified 14 chloroplast haplotypes over four noncoding regions from 408 samples (Fig. 3a). Genetic differentiation did not correspond to the species (AMOVA P = 0.7000), but to populations within species (P < 0.0001). The two major haplotypes (a, b) were common to both species, seven minor haplotypes (e–k) were S. yokusaiana-specific, three minor haplotypes (l–n) were S. virgaurea-specific, and two minor haplotypes (c, d) were common to both species. The two most common haplotypes (a, b) were broadly distributed and centered in the haplotype network (Figs. 3a and S1). The most common haplotype (a) was distributed throughout the Japanese Archipelago, while the second most common haplotype (b) was distributed mainly in Kinki District. The third most common haplotype (c) was distributed north of Chubu. The species-specific haplotypes were population- or district-specific, and were not clustered by taxonomy (Figs. 3a and S1). The distribution of haplotype a and its derivatives overlapped the distribution of haplotype b and its derivatives in Kinki and Shikoku Districts. The boundary of the distribution of haplotype a and its derivatives and b and its derivatives corresponded to the boundary between Chubu and Kinki Districts.
Fig. 3. Phylogeographic structure of Solidago species.
The colors of the symbols and leader lines indicate S. virgaurea (red) and S. yokusaiana (blue). The pie charts denote the proportions of haplotypes or genetic clusters in the populations. a Geographic distribution of chloroplast haplotypes (nearly 1500 bp, 14 haplotypes). The colors correspond to the haplotype network (top left). The three major haplotypes are shown in different colors (red, green, and blue), derivatives of haplotype a are light blue, and derivatives of haplotype b are light green. b Geographic distribution of three genetic clusters of 164 alleles over 14 nSSR loci. c Geographic distribution of three genetic clusters of 2321 unlinked ddRADseq SNPs.
Although the mismatch distribution of the chloroplast haplotypes was unimodal, the distribution did not fit the model of sudden population-size expansion (P = 0.039, Fig. S2).
Nuclear single-sequence repeat loci
For population genetic structure analysis, we found 153 alleles across 14 nSSR loci (genotyping rate >99%). Bayesian clustering analysis of nSSR genotype data implied that three genetic clusters (K = 3) were optimal by the ΔK method (Fig. S3a). The Euclidean distance of the ratio of the three clusters correlated with the geographic distance (partial Mantel P = 0.0001), but not with a difference in species (P = 0.8785). The three clusters of nSSR loci were distributed in Kinki District northward (red), in eastern Chugoku and Shikoku Districts (green), and western Chugoku, Kyushu, and Okinawa Districts (blue) (Figs. 3b and S3b). The proportion of the southern cluster (blue) in each population gradually decreased from south to north, while the proportion of the northern cluster (red) in each population gradually increased from south to north. The proportion of the intermediate cluster (green) in each population gradually increased from west to east, although there was a boundary in the cluster distribution between Shikoku and Kinki Districts (Figs. 3b and S3b).
ddRADseq
To analyze population genetic structure, we used 2321 SNPs from 98 samples (genotyping rate 68%) and 52 samples were filtered out because of high missing genotyping rate. The phylogenetic analysis indicated that the genetic relationship did not correspond to taxonomic groups, but to geographic areas (Fig. 4). Genetic differentiation did not correspond to species (AMOVA, P = 0.2532), but to populations within species (P < 0.0001). The generalized skyline plot indicated that the population size of both Solidago species had increased exponentially (Fig. S4). The correlations of genetic and geographic distances showed IBD patterns for S. virgaurea and S. yokusaiana (P = 0.0904 and P = 0.0001, respectively), and the coefficient of determination was larger for S. yokusaiana (r2 = 0.71) than for S. virgaurea (r2 = 0.12). Bayesian clustering analysis of the SNP data implied that four genetic clusters were optimal by the ΔK method (Fig. S5a). The Euclidean distance of the ratio of the four clusters correlated to the geographic distance (partial Mantel P = 0.0001), but not to a difference in species (P = 0.6864). The four clusters were distributed mainly from Kinki District northward (red), and in Shikoku District (green), Kyushu and Okinawa Districts (blue), and Chugoku District (yellow) (Figs. 3c and S5b). The proportion of the southern cluster (blue) in each population decreased gradually from south to north, while the proportion of the northern cluster (red) increased gradually from south to north. The intermediate clusters were located on Shikoku and around (green), and Chugoku and around (yellow), but were relatively infrequent in other populations. The PCA showed that individuals were clustered by populations, and populations were also clustered by districts (Fig. S6). The minimum Patterson’s D statistics for all 495 combinations of four S. yokusaiana were not significant (Benjamini and Hochberg q values > 0.1).
Fig. 4. Unrooted population tree made by the neighbor-joining method.
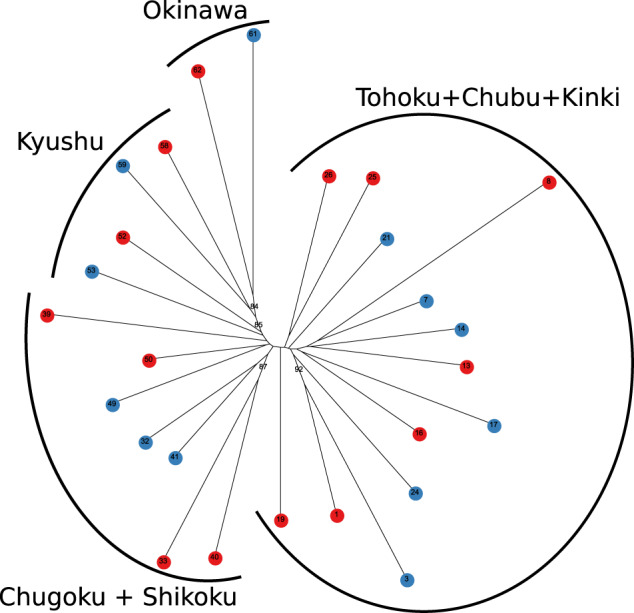
The numbers on the branches are the percentage bootstrap values (>70%). The colors of the circles indicate S. virgaurea (red) and S. yokusaiana (blue). The outer arcs indicate districts of the Solidago populations.
Demographic modeling
For demographic modeling, we used 347–577 SNPs for six district pairs (Table 1) after excluding loci with missing data in any individual from the analysis. Model selection based on the AIC values supported the models representing the scenarios for multiple origins for all district pairs (Fig. 2 and Table 2). The M6s4m2t model was supported in four combinations of districts (Tohoku–Chugoku, Tohoku–Okinawa, Chubu–Okinawa, and Chugoku–Okinawa), the M4s4m2t model was supported for the Tohoku–Chubu combination, and the M6s8m3t model was supported for the Chubu–Chugoku combination (Table 2). The models representing the scenarios for multiple origins were also supported as the second and third best models for all district pairs (Table 2).
Table 1.
District combinations and species assignments of the population pairs used for demographic modeling.
| Combinations | Districts A | Districts B | Number of SNPs | ||
|---|---|---|---|---|---|
| Tohoku–Chubu | Tohoku | Chubu | 425 | ||
| Tohoku–Chugoku | Tohoku | Chugoku | 577 | ||
| Tohoku–Okinawa | Tohoku | Okinawa | 476 | ||
| Chubu–Chugoku | Chubu | Chugoku | 387 | ||
| Chubu–Okinawa | Chubu | Okinawa | 347 | ||
| Chugoku–Okinawa | Chugoku | Okinawa | 511 | ||
| Svir | Syok | Svir | Syok | ||
| Deme 0 | Deme 1 | Deme 2 | Deme 3 | ||
Table 2.
Comparison of the alternative demographic models for each district combination using the ΔAIC values.
| Model | Pa | M1s2m2tb | M4s4m2tb | M4s8m2tb | M4s8m3tb | M6s4m2tb | M6s8m2tb | M6s8m3tb | S1s2m3tc | S6s4m3tc | S6s8m3tc | S6s8m4tc |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tohoku–Chubu | 36.6 | 25.9 | 0 | 3.8 | 5.8 | 0.3 | 8 | 9.7 | 27.2 | 9.4 | 12.6 | 15.4 |
| Tohoku–Chugoku | 61 | 53.5 | 5.3 | 7.5 | 11 | 0 | 7.1 | 4.8 | 59.1 | 14.8 | 16.8 | 21 |
| Tohoku–Okinawa | 171 | 134.1 | 4.2 | 3.7 | 7.2 | 0 | 8.1 | 9.9 | 138.1 | 24.8 | 11.5 | 15.6 |
| Chubu–Chugoku | 27.9 | 15.9 | 4.3 | 13.3 | 17.5 | 3.3 | 10.7 | 0 | 10.4 | 9.3 | 15.5 | 21.5 |
| Chubu–Okinawa | 87 | 56.6 | 2.7 | 4 | 2.9 | 0 | 2.8 | 4 | 59.8 | 15.6 | 8.5 | 10.4 |
| Chugoku–Okinawa | 89 | 77.8 | 16.9 | 20.1 | 20.1 | 0 | 4.5 | 3.8 | 83.5 | 27.4 | 19.4 | 13.5 |
The minimum AIC values in each district combination are in bold.
aPolytomous scenario.
bMultiple-origin scenarios.
cSecondary contact scenarios after a single origin.
As the population size of the common ancestral population was fixed to 10,000 for the demographic modeling, all demographic parameters, except for the number of migrants, will deviate due to deviation of the fixed ancestral population size from the true value, and therefore the relative value may be more robust than absolute values (Butlin et al. 2014). To interpret the demographic parameters as relative values, we divided the population size and time parameters by 10,000 or 20,000, respectively. Except for the Chubu–Chugoku combination, the supported models did not include the order of speciation between the districts and different numbers of migrants by the direction of gene flow (Fig. 2). The size of the local ancestral S. virgaurea population differed from those of the current S. virgaurea populations in each district, except for the Tohoku–Chubu combination, for which the local ancestral and current S. virgaurea populations were equal based on the best models (Fig. 2).
The point estimates of the parameters of the best models were included within the 95% HDIs based on the bootstrap pseudo-observed data, although the ranges of the 95% HDIs were wide for some parameters (Table 3). For the bootstrap data estimate, the current population sizes of S. virgaurea were larger than those of S. yokusaiana in Tohoku District in all three combinations with other districts, and in Chugoku and Okinawa Districts in two of three combinations (Chubu–Chugoku, Chubu–Okinawa, and Chugoku–Okinawa) (Wilcoxon signed-rank test, Holm-adjusted P values < 0.05), and the current populations of S. virgaurea were smaller than those of ancestral S. virgaurea in Chubu, Chugoku, and Okinawa Districts in all combinations (Wilcoxon signed-rank test, Holm-adjusted P values < 0.05). For the wait times to speciation (1 − Teco/Tfirst) for the bootstrap samples, the Tohoku–Chubu combination was smaller than the other combinations, and Chugoku District in the Chubu–Chugoku combination was smaller than Chubu District in the Chubu–Chugoku combination (Wilcoxon rank-sum test, Holm-adjusted P values < 0.05).
Table 3.
Estimates of demographic parameters and the 95% highest-density intervals of the six district combinations.
| Tohoku–Chubu | Tohoku–Chugoku | Tohoku–Okinawa | Chubu–Chugoku | Chubu–Okinawa | Chugoku–Okinawa | |
|---|---|---|---|---|---|---|
| M4s4m2t | M6s4m2t | M6s4m2t | M6s8m3t | M6s4m2t | M6s4m2t | |
| N0 | 56.12 (1.84–95.11) | 33.83 (0.15–84.31) | 23.20 (0.26–84.87) | 1.17 (0.11–26.31) | 3.80 (0.23–30.20) | 3.02 (0.42–16.06) |
| N1 | 0.53 (0.13–8.22) | 0.53 (0.12–16.40) | 0.31 (0.12–16.38) | 1.19 (0.13–20.33) | 5.15 (0.20–37.14) | 1.72 (0.16–7.26) |
| N2 | 2.82 (0.18–18.41) | 2.08 (0.12–11.29) | 0.53 (0.11–6.69) | 5.03 (0.12–19.72) | 1.72 (0.16–14.01) | 1.21 (0.14–10.09) |
| N3 | 4.99 (0.35–29.86) | 1.48 (0.11–12.93) | 0.57 (0.13–6.18) | 1.39 (0.11–7.68) | 0.97 (0.12–5.29) | 0.72 (0.11–3.18) |
| NA | 52.09 (0.12–105.02) | 32.05 (0.19–95.51) | 19.31 (0.11–79.80) | 13.98 (0.13–78.97) | 16.22 (0.14–81.94) | |
| NB | 9.29 (0.11–78.25) | 2.41 (0.11–77.22) | 8.69 (0.12–86.18) | 26.09 (0.29–94.89) | 14.64 (0.24–83.33) | |
| 2NMecoA | 1.28 (0.00–9.90) | 1.53 (0.00–4.10) | 1.68 (0.00–11.49) | 0.02 (0.00–4.39) | 0.01 (0.00–2.66) | |
| 2NMecoB | 1.01 (0.00–6.58) | 0.00 (0.00–2.03) | 0.03 (0.00–0.95) | 0.15 (0.00–1.09) | 0.01 (0.00–1.00) | |
| 2NMvir | 0.42 (0.00–7.10) | 0.29 (0.00–3.59) | 0.46 (0.00–1.81) | 0.16 (0.00–0.83) | 0.14 (0.00–1.06) | |
| 2NMyok | 0.19 (0.00–3.56) | 0.18 (0.00–1.24) | 0.00 (0.00–0.48) | 0.04 (0.00–0.56) | 0.14 (0.00–1.06) | |
| 2N1M01 | 0.06 (0.00–9.73) | |||||
| 2N0M10 | 0.00 (0.00–13.05) | |||||
| 2N3M23 | 0.61 (0.00–2.33) | |||||
| 2N2M32 | 0.18 (0.00–2.22) | |||||
| 2N2M02 | 0.08 (0.00–2.33) | |||||
| 2N0M20 | 0.01 (0.00–1.79) | |||||
| 2N3M13 | 1.92 (0.00–7.34) | |||||
| 2N1M31 | 0.05 (0.00–3.26) | |||||
| Teco | 0.55 (0.02–3.47) | 0.15 (0.01–3.21) | 0.14 (0.02–3.10) | 0.31 (0.02–3.32) | 0.19 (0.03–2.38) | |
| TecoA | 0.06 (0.01–2.14) | |||||
| TecoB | 0.67 (0.01–2.83) | |||||
| Tfirst | 0.69 (0.14–3.93) | 0.71 (0.18–4.19) | 0.66 (0.14–4.12) | 0.77 (0.34–3.94) | 1.44 (0.23–4.68) | 1.00 (0.28–4.05) |
N1, N2, N3, N4, NancA and NancB are ratios of contemporary population size to ancient population size. Tfirst is the first divergence time in units of twofold ancient population size (number of genes). Teco, TecoA, and TecoB are local divergence times in units of twofold ancient population size (number of genes). 2NMecoA, 2NMecoB, 2NMvir, 2NMyok, 2N1M01, 2N0M10, 2N3M32, 2N2M32, 2N2M02, 2N0M20, 2N3M13, and 2N1M31 are the numbers of migrants in a generation. 95% highest intervals are in parenthesis.
Discussion
Multiple origins of Solidago yokusaiana
The geographic trends for the chloroplast haplotype diversity and genetic clusters estimated by Bayesian clustering based on nSSR and SNPs, and PCA based on SNPs, did not correspond to taxonomic species, but to population differences or localities, implying that S. yokusaiana had multiple origins in several districts. The reconstructed phylogenetic tree and IBD patterns with SNPs also indicated that Solidago did not cluster by taxonomic species, but by population localities. There were no significantly positive values in Patterson’s D statistics, suggesting that all combinations of four S. yokusaiana populations are consistent with one of the three simple tree topologies. Because violation of the topologies indicates sharing of alleles between genetically distant populations, there seem to be no admixture and homogenization of S. yokusaiana and local S. virgaurea. However, possibility of admixture with genetically very close S. virgaurea cannot be fully excluded. The model selection based on SNP data supported the multiple-origin scenarios in all district combinations examined. Schmid and Bazzaz (1990) pointed out limited contribution of plasticity in morphology of the genus Solidago (Schmid and Bazzaz 1990). Actually, in S. virgaurea in Japan, genetic differentiation was reported between populations with large phenotypic diversity along an elevational gradient (Hirano et al. 2017). In addition, morphological differences between S. virgaurea and S. yokusaiana were maintained in common garden experiments (personal observations). These facts suggest that phenotypic plasticity is not mainly responsible for rheophytic characters in S. yokusaiana. These results imply that S. yokusaiana is a paraphyletic taxon resulting from multiple origins and the single-origin scenarios were rejected, even after considering secondary contact. The model selection results indicate that S. yokusaiana originated at least four times from adjacent S. virgaurea populations in four districts (Tohoku, Chubu, Chugoku, and Okinawa). Moreover, it is possible that S. yokusaiana originated independently in other districts because we considered only these four districts for model selection. Because the recurrent origin of S. yokusaiana also implies that the species is not cladistic species, taxonomic treatment of S. yokusaiana should be reconsidered in future studies.
The best-supported models, except for the combination Chubu–Chugoku, considered the single-model parameter for time of speciation in each district (Teco). Therefore, parameter estimation for the best-supported models could not detect differences in the divergence times among the districts, because the models indicated that S. yokusaiana populations have differentiated on each district almost at the same time. These results imply that some S. yokusaiana populations might have diverged at nearly the same time. More detailed analyses of the divergence times are necessary in further study.
Speciation of Solidago yokusaiana
The wait time to speciation was smaller for the Tohoku–Chubu combination than for the others, implying that the populations in these districts experienced a different scenario, with rapid speciation or unique ancestor colonization. Sakaguchi et al. (2018b) suggested that the northern and southern lineages of the Japanese S. virgaurea complex admix in the middle of the Tohoku and Chubu Districts. Therefore, a smaller wait time to speciation might be reflected in an underestimated divergence time due to ancestral gene flow (Leaché et al. 2014) or recent redivergence after admixture, implying that gene flow or admixing preceded the speciation of S. yokusaiana. We should examine secondary contact of the northern and southern lineages in the Japanese Archipelago carefully because other local endemic Solidago taxa have been described, including S. horieana, S. minutissima, and S. virgaurea subsp. gigantea and var. praeflorens.
The point estimates and upper ranges of the 95% HDIs of the numbers of migrants per generation for the two species tended to be higher in the northern districts than in the southern districts (Table 3). In the Chubu–Chugoku combination, S. yokusaiana might have evolved more recently in Chubu District than in Chugoku District. These results were consistent with each other. However, the model selection might suggest that speciation occurred at a shortened timescale in both the northern and southern areas because the only different speciation times for all district combinations were for the Tohoku–Chubu combination, which showed more recent evolution than the others, and the populations in Chubu District, which showed more recent evolution than in Chugoku District or the Chubu–Chugoku combination.
Demography of the two Solidago species
The estimated current population sizes of S. yokusaiana tended to be smaller than those of S. virgaurea, except in Chubu District, where the S. yokusaiana population is larger than the S. virgaurea population. These results are consistent with confinement of the rheophyte habitat to frequently flooded riversides, which is obviously more restricted than the habitat of the ancestor (Mitsui and Setoguchi 2012). In Chubu District, the presence of many relatively large riversides likely caused the opposite result, as the Japanese Alps (the three highest mountain ranges in Japan, the Hida, Kiso, and Akaishi Mountains) are located in Chubu District. The abundance of steep valleys and large riversides may harbor larger S. yokusaiana populations or the concentrated riversides may raise the possibility of gene flow between sampled and unsampled S. yokusaiana populations, which may cause overestimation of the population size (Beerli 2004). This might explain why the Chubu populations experienced a unique scenario that differed from those in other districts. To test the hypothesis, we need to estimate size of riverside area in each habitat.
The upper ranges of the 95% HDIs of the numbers of migrants between districts were high in geographically close combinations (e.g., 7.10 and 3.56 between Tohoku and Chubu (450 km) and 1.81 and 0.485 between Tohoku and Okinawa (1800 km), Table 3), which is consistent with the IBD patterns for each Solidago species. Nei’s standard genetic distance and geographic distance were also significantly correlated. The coefficient of determination of S. yokusaiana (r2 = 0.71) was larger than that of S. virgaurea (r2 = 0.12), implying that S. yokusaiana better fits an IBD pattern than S. virgaurea. Therefore, direct or indirect migration among S. yokusaiana populations might be relatively restricted in comparison with current S. virgaurea populations. The restriction of direct migration is also consistent with the narrow S. yokusaiana habitats, and restriction of indirect migration, i.e., migration between S. virgaurea and S. yokusaiana populations, might be consistent with the lower fitness of rheophytic traits away from riversides (Mitsui et al. 2011).
The parameter estimations and 95% HDIs based on bootstrap data indicated that the current population size of S. virgaurea in Tohoku District in the Tohoku–Chugoku and Tohoku–Okinawa combinations was not smaller than the ancestral population size. These results are partially consistent with the supported model for the Tohoku–Chubu combination, M4s4m2t, in which the considered population sizes are equal to the current and ancestral S. virgaurea populations. In the other districts, the current S. virgaurea populations may be smaller than the ancestral population. However, the results of the mismatch distribution of chloroplast haplotypes and Bayesian clustering with nSSR and SNPs and generalized skyline plot based on SNPs did not imply shrinking populations over the entire distribution range. Since unsampled populations were not involved in our coalescent simulations, subdivision or derivation of a population from the ancestral population might have caused the seeming shrinking of populations in the Chubu, Chugoku, and Okinawa Districts.
Mechanism of multiple origins
The multiple-origin scenarios were supported by the chloroplast haplotypes, nSSR, SNPs, and demographic modeling. So while the single-origin scenarios can be excluded, the alternative mechanisms for multiple origins described by Johannesson et al. (2010) cannot be excluded easily. According to Sakaguchi et al. (2018b), the Japanese S. virgaurea complex may have expanded its range to the Japanese Archipelago via a northern route through Sakhalin and a southern route through the Korean Peninsula during the last glacial period. The northern route crosses the Mamiya and Soya Straits, where land bridges formed in the last glacial period (Yashima and Miyauchi 1990) and the Tsugaru Strait, where a land bridge formed during the last glacial maximum (Yashima and Miyauchi 1990); the southern route crosses the Tsushima Strait, where a land bridge may also have formed (Matsui et al. 1998). The timing of differentiation between the northern and southern lineages (Sakaguchi et al. 2018b) may correspond to the last glacial maximum (26.5–19.0 kya, Clark et al. 2009), implying that S. yokusaiana diverged from its ancestor after the last glacial maximum. Before 14 kya, the paleoclimate in the central Japanese Archipelago was cold and dry (Kigoshi et al. 2017); therefore, there might have been insufficient suitable environments for rheophytes. When the climate became warm and wet 14 kya (Kigoshi et al. 2017), S. yokusaiana might have subsequently been formed in parallel. Therefore, the wait times to speciation in the four district combinations, which comprised 80% of the time after divergence of the district populations, could be partially interpreted as the time lag between range expansion and the formation of rheophytic environments.
Since the results of the demographic analyses indicated multiple origins in four districts, and S. yokusaiana has multiple, common rheophytic traits as a taxonomic species, it is unlikely that the S. yokusaiana in each district evolved via independent de novo mutations after the last glacial maximum, because this would have required adaptive mutations to arise in multiple districts and at loci related to rheophytic traits in a relatively short period. Therefore, independent selection from the standing genetic variation, which leads to faster adaptation than de novo mutation (Hermisson and Pennings 2005; Barrett and Schluter 2008; Clark et al. 2009; Anderson 2012; Ralph and Coop 2015) and may be a major source of adaptive alleles (Barrett and Schluter 2008; Anderson 2012; Roda et al. 2013) might be the mechanism of the multiple origins of S. yokusaiana. Although adaptation by independent de novo mutation is unlikely, the spread of adaptive alleles, regardless of their origin, could have been a limited mechanism for the multiple origins of S. yokusaiana. The spread of adaptive alleles with high selection coefficients requires only very low gene flow (Morjan and Rieseberg 2004) and is enhanced by long-distance dispersal (Rieseberg and Burke 2001), which could be facilitated by the plumed seeds of Asteraceae (Sheldon and Burrows 1973). Although rheophytic adaptive alleles may be deleterious to S. virgaurea, such alleles might be able to spread only in short distances before their elimination by selection (Schluter and Conte 2009). Or, although they might be recessive and maintained at very low frequencies in normal habitats (Haenel et al. 2019), the frequency will increase in the habitat where rheophytic phenotypes are selected for.
The mechanisms of the multiple origins of de novo mutations, selection from standing genetic variation, and spread of adaptive alleles are not mutually exclusive (Johannesson et al. 2010). It is possible that some rheophytic traits or adaptive alleles came from selection on standing genetic variation and others came from other mechanisms. The mechanisms of multiple origins may also differ on scales of time or space. Therefore, further studies of loci under divergent selection between species are needed to elucidate the mechanism for the origins of the rheophytic traits of S. yokusaiana, such as small linear lanceolate leaves with an almost entire margin, crowded leaves, condensed capitula on stems, and hairy achenes.
Data archiving
The haplotype sequences are now being registered in GenBank (NCBI/DDBJ/EMBL) database and the SNP datasets will be uploaded to the Dryad Digital Repository until publication.
Supplementary information
Acknowledgements
We thank Y. Waki for help collecting the samples and S. Horie for technical help. This study was supported by JSPS KAKENHI Grants (No. 15K07186, 16H04827, 26271054, and 24657059).
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Associate Editor: Thomas Meagher
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41437-021-00408-x.
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Autom Control. 1974;19:716–723. doi: 10.1109/TAC.1974.1100705. [DOI] [Google Scholar]
- Anderson CJR (2012) The role of standing genetic variation in adaptation of digital organisms to a new environment. Proceedings of the 2019 Artificial Life Conference. 24. p 3–10
- Arroyo-García R, Ruiz-Garcia L, Bolling L, Ocete R, Lopez MA, Arnold C, et al. Multiple origins of cultivated grapevine (Vitis vinifera L. ssp. sativa) based on chloroplast DNA polymorphisms. Mol Ecol. 2006;15:3707–3714. doi: 10.1111/j.1365-294X.2006.03049.x. [DOI] [PubMed] [Google Scholar]
- Barrett RDH, Schluter D. Adaptation from standing genetic variation. Trends Ecol Evol. 2008;23:38–44. doi: 10.1016/j.tree.2007.09.008. [DOI] [PubMed] [Google Scholar]
- Beerli P. Effect of unsampled populations on the estimation of population sizes and migration rates between sampled populations. Mol Ecol. 2004;13:827–836. doi: 10.1111/j.1365-294X.2004.02101.x. [DOI] [PubMed] [Google Scholar]
- Bierne N, Gagnaire P-A, David P. The geography of introgression in a patchy environment and the thorn in the side of ecological speciation. Curr Zool. 2013;59:72–86. doi: 10.1093/czoolo/59.1.72. [DOI] [Google Scholar]
- Bolger AM, Lohse M, Usadel B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics. 2014;30:2114–2120. doi: 10.1093/bioinformatics/btu170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butlin RK, Saura M, Charrier G, Jackson B, André C, Caballero A, et al. Parallel evolution of local adaptation and reproductive isolation in the face of gene flow. Evolution. 2014;68:935–949. doi: 10.1111/evo.12329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catchen J, Hohenlohe PA, Bassham S, Amores A, Cresko WA. Stacks: an analysis tool set for population genomics. Mol Ecol. 2013;22:3124–3140. doi: 10.1111/mec.12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catchen JM, Amores A, Hohenlohe P, Cresko W, Postlethwait JH. Stacks: building and genotyping loci de novo from short-read sequences. G3 Genes Genomes Genet. 2011;1:171–182. doi: 10.1534/g3.111.000240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark PU, Dyke AS, Shakun JD, Carlson AE, Clark J, Wohlfarth B, et al. The last glacial maximum. Science. 2009;325:710–714. doi: 10.1126/science.1172873. [DOI] [PubMed] [Google Scholar]
- Clement M, Posada D, Crandall KA. TCS: a computer program to estimate gene genealogies. Mol Ecol. 2000;9:1657–1659. doi: 10.1046/j.1365-294x.2000.01020.x. [DOI] [PubMed] [Google Scholar]
- Cooper TF, Rozen DE, Lenski RE. Parallel changes in gene expression after 20,000 generations of evolution in Escherichia coli. Proc Natl Acad Sci. 2003;100:1072–1077. doi: 10.1073/pnas.0334340100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crandal KA, Harris DJ, Fetzner JW. The monophyletic origin of freshwater crayfish estimated from nuclear and mitochondrial DNA sequences. Proc R Soc Lond B Biol Sci. 2000;267:1679–1686. doi: 10.1098/rspb.2000.1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle JJ, Doyle JL. Isolation of plant DNA from fresh tissue. Focus. 1990;12:13–15. [Google Scholar]
- Dray S, Dufour A-B. The ade4 package: Implementing the duality diagram for ecologists. J Stat Softw. 2007;22:1–20. doi: 10.18637/jss.v022.i04. [DOI] [Google Scholar]
- Earl DA, vonHoldt BM. STRUCTURE HARVESTER: a website and program for visualizing STRUCTURE output and implementing the Evanno method. Conserv Genet Resour. 2012;4:359–361. doi: 10.1007/s12686-011-9548-7. [DOI] [Google Scholar]
- Evanno G, Regnaut S, Goudet J. Detecting the number of clusters of individuals using the software structure: a simulation study. Mol Ecol. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Dupanloup I, Huerta-Sánchez E, Sousa VC, Foll M. Robust demographic inference from genomic and SNP data. PLOS Genet. 2013;9:e1003905. doi: 10.1371/journal.pgen.1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L, Lischer HEL. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour. 2010;10:564–567. doi: 10.1111/j.1755-0998.2010.02847.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Smouse PE, Quattro JM. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics. 1992;131:479–491. doi: 10.1093/genetics/131.2.479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster SA, McKinnon GE, Steane DA, Potts BM, Vaillancourt RE. Parallel evolution of dwarf ecotypes in the forest tree Eucalyptus globulus. N Phytol. 2007;175:370–380. doi: 10.1111/j.1469-8137.2007.02077.x. [DOI] [PubMed] [Google Scholar]
- Haenel Q, Roesti M, Moser D, MacColl ADC, Berner D. Predictable genome-wide sorting of standing genetic variation during parallel adaptation to basic versus acidic environments in stickleback fish. Evol Lett. 2019;3:28–42. doi: 10.1002/evl3.99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall TA (1999) BioEdit: a user-friendly biological sequence alignment editor and analysis program for Windows 95/98/NT, Nucleic acids symposium series, vol 41. London, Information Retrieval Ltd., p 95–98. c1979-c2000
- Hamilton MB. Four primer pairs for the amplification of chloroplast intergenic regions with intraspecific variation. Mol Ecol. 1999;8:521–523. [PubMed] [Google Scholar]
- Hermisson J, Pennings PS. Soft sweeps: molecular population genetics of adaptation from standing genetic variation. Genetics. 2005;169:2335–2352. doi: 10.1534/genetics.104.036947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirano M, Sakaguchi S, Takahashi K. Phenotypic differentiation of the Solidago virgaurea complex along an elevational gradient: insights from a common garden experiment and population genetics. Ecol Evol. 2017;7:6949–6962. doi: 10.1002/ece3.3252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsson M, Rosenberg NA. CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics. 2007;23:1801–1806. doi: 10.1093/bioinformatics/btm233. [DOI] [PubMed] [Google Scholar]
- Johannesson K, Panova M, Kemppainen P, André C, Rolán-Alvarez E, Butlin RK. Repeated evolution of reproductive isolation in a marine snail: unveiling mechanisms of speciation. Philos Trans R Soc B Biol Sci. 2010;365:1735–1747. doi: 10.1098/rstb.2009.0256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jombart T. adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics. 2008;24:1403–1405. doi: 10.1093/bioinformatics/btn129. [DOI] [PubMed] [Google Scholar]
- Jones FC, Grabherr MG, Chan YF, Russell P, Mauceli E, Johnson J, et al. The genomic basis of adaptive evolution in threespine sticklebacks. Nature. 2012;484:55–61. doi: 10.1038/nature10944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamvar ZN, Tabima JF, Grünwald NJ. Poppr: an R package for genetic analysis of populations with clonal, partially clonal, and/or sexual reproduction. PeerJ. 2014;2:e281. doi: 10.7717/peerj.281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato M. Evolution and adaptation in the rheophytes. Bunrui. 2003;3:107–122. [Google Scholar]
- Kawano S. Life history of Solidago virgaurea. Shokubutsu No Sekai. 1988;3:52–79. [Google Scholar]
- Kigoshi T, Kumon F, Kawai S, Kanauchi A. Quantitative reconstruction of paleoclimate in central Japan for the past 158,000 years based on a modern analogue technique of pollen composition. Quat Int. 2017;455:126–140. doi: 10.1016/j.quaint.2017.05.015. [DOI] [Google Scholar]
- Leaché AD, Harris RB, Rannala B, Yang Z. The influence of gene flow on species tree estimation: a simulation study. Syst Biol. 2014;63:17–30. doi: 10.1093/sysbio/syt049. [DOI] [PubMed] [Google Scholar]
- Li J, Li H, Jakobsson M, Li S, Sjödin P, Lascoux M. Joint analysis of demography and selection in population genetics: where do we stand and where could we go? Mol Ecol. 2012;21:28–44. doi: 10.1111/j.1365-294X.2011.05308.x. [DOI] [PubMed] [Google Scholar]
- Makino T. Plantae Japonenses novae vel minus cognitae. Bot Mag Tokyo. 1898;12:45–52. doi: 10.15281/jplantres1887.12.136_en45. [DOI] [Google Scholar]
- Malinsky M, Matschiner M, Svardal H (2020) Dsuite—fast D‐statistics and related admixture evidence from VCF files Mol Ecol Resour 21:584–595 [DOI] [PMC free article] [PubMed]
- Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967;27:209–220. [PubMed] [Google Scholar]
- Matsui H, Tada R, Oba T. Low-salinity isolation event in the Japan Sea in resoponse to Eustatic sea-level drop during LGM: Reconstruction based on salinity-balance model. Quat Res Daiyonki-Kenkyu. 1998;37:221–233. doi: 10.4116/jaqua.37.221. [DOI] [Google Scholar]
- Meier JI, Sousa VC, Marques DA, Selz OM, Wagner CE, Excoffier L, et al. Demographic modelling with whole-genome data reveals parallel origin of similar Pundamilia cichlid species after hybridization. Mol Ecol. 2017;26:123–141. doi: 10.1111/mec.13838. [DOI] [PubMed] [Google Scholar]
- Meredith M, Kruschke J (2018) HDInterval: highest (posterior) density intervals
- Mitsui Y, Nomura N, Isagi Y, Tobe H, Setoguchi H. Ecological barriers to gene flow between riparian and forest species of Ainsliaea (asteraceae) Evolution. 2011;65:335–349. doi: 10.1111/j.1558-5646.2010.01129.x. [DOI] [PubMed] [Google Scholar]
- Mitsui Y, Setoguchi H. Recent origin and adaptive diversification of Ainsliaea (Asteraceae) in the Ryukyu Islands: molecular phylogenetic inference using nuclear microsatellite markers. Plant Syst Evol. 2012;298:985–996. doi: 10.1007/s00606-012-0608-6. [DOI] [Google Scholar]
- Molina J, Sikora M, Garud N, Flowers JM, Rubinstein S, Reynolds A, et al. Molecular evidence for a single evolutionary origin of domesticated rice. Proc Natl Acad Sci. 2011;108:8351–8356. doi: 10.1073/pnas.1104686108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morjan CL, Rieseberg LH. How species evolve collectively: implications of gene flow and selection for the spread of advantageous alleles. Mol Ecol. 2004;13:1341–1356. doi: 10.1111/j.1365-294X.2004.02164.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nei M. Genetic distance between populations. Am Nat. 1972;106:283–292. doi: 10.1086/282771. [DOI] [Google Scholar]
- Nomura N, Takaso T, Peng C-I, Kono Y, Oginuma K, Mitsui Y, et al. Molecular phylogeny and habitat diversification of the genus Farfugium (Asteraceae) based on nuclear rDNA and plastid DNA. Ann Bot. 2010;106:467–482. doi: 10.1093/aob/mcq139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosil P, Feder JL. Genome evolution and speciation: toward quantitative descriptions of pattern and process. Evolution. 2013;67:2461–2467. doi: 10.1111/evo.12191. [DOI] [PubMed] [Google Scholar]
- Paradis E. pegas: an R package for population genetics with an integrated–modular approach. Bioinformatics. 2010;26:419–420. doi: 10.1093/bioinformatics/btp696. [DOI] [PubMed] [Google Scholar]
- Paradis E, Schliep K. ape 5.0: an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics. 2019;35:526–528. doi: 10.1093/bioinformatics/bty633. [DOI] [PubMed] [Google Scholar]
- Peterson BK, Weber JN, Kay EH, Fisher HS, Hoekstra HE. Double digest RADseq: an inexpensive method for de novo SNP discovery and genotyping in model and non-model species. PLoS ONE. 2012;7:e37135. doi: 10.1371/journal.pone.0037135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Moorjani P, Luo Y, Mallick S, Rohland N, Zhan Y, et al. Ancient admixture in human history. Genetics. 2012;192:1065–1093. doi: 10.1534/genetics.112.145037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ralph PL, Coop G. The role of standing variation in geographic convergent adaptation. Am Nat. 2015;186:S5–S23. doi: 10.1086/682948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revell LJ. phytools: an R package for phylogenetic comparative biology (and other things) Methods Ecol Evol. 2012;3:217–223. doi: 10.1111/j.2041-210X.2011.00169.x. [DOI] [Google Scholar]
- Rieseberg LH, Burke JM. The biological reality of species: gene flow, selection, and collective evolution. TAXON. 2001;50:47–67. doi: 10.2307/1224511. [DOI] [Google Scholar]
- Roda F, Liu H, Wilkinson MJ, Walter GM, James ME, Bernal DM, et al. Convergence and divergence during the adaptation to similar environments by an Australian groundsel. Evolution. 2013;67:2515–2529. doi: 10.1111/evo.12136. [DOI] [PubMed] [Google Scholar]
- Roesti M, Gavrilets S, Hendry AP, Salzburger W, Berner D. The genomic signature of parallel adaptation from shared genetic variation. Mol Ecol. 2014;23:3944–3956. doi: 10.1111/mec.12720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rougemont Q, Gagnaire P-A, Perrier C, Genthon C, Besnard A-L, Launey S, et al. Inferring the demographic history underlying parallel genomic divergence among pairs of parasitic and nonparasitic lamprey ecotypes. Mol Ecol. 2017;26:142–162. doi: 10.1111/mec.13664. [DOI] [PubMed] [Google Scholar]
- Saitou N, Nei M. The neighbor-joining method: a new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- Sakaguchi S, Horie K, Kimura T, Nagano AJ, Isagi Y, Ito M. Phylogeographic testing of alternative histories of single-origin versus parallel evolution of early flowering serpentine populations of Picris hieracioides L. (Asteraceae) in Japan. Ecol Res. 2018;33:537–547. doi: 10.1007/s11284-017-1536-2. [DOI] [Google Scholar]
- Sakaguchi S, Ito M. Development and characterization of EST-SSR markers for the Solidago virgaurea complex (Asteraceae) in the Japanese archipelago. Appl Plant Sci. 2014;2:1400035. doi: 10.3732/apps.1400035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakaguchi S, Kimura T, Kyan R, Maki M, Nishino T, Ishikawa N, et al. Phylogeographic analysis of the East Asian goldenrod (Solidago virgaurea complex, Asteraceae) reveals hidden ecological diversification with recurrent formation of ecotypes. Ann Bot. 2018;121:489–500. doi: 10.1093/aob/mcx182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakaguchi S, Sugino T, Tsumura Y, Ito M, Crisp MD, Bowman DMJS, et al. High-throughput linkage mapping of Australian white cypress pine (Callitris glaucophylla) and map transferability to related species. Tree Genet Genomes. 2015;11:121. doi: 10.1007/s11295-015-0944-0. [DOI] [Google Scholar]
- Sakata Y, Kaneko S, Hayano A, Inoue-Murayama M, Ohgushi T, Isagi Y. Isolation and characterization of microsatellite loci in the invasive herb Solidago altissima (Asteraceae) Appl Plant Sci. 2013;1:1200313. doi: 10.3732/apps.1200313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schluter D, Conte GL. Genetics and ecological speciation. Proc Natl Acad Sci. 2009;106:9955–9962. doi: 10.1073/pnas.0901264106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid B, Bazzaz FA. Plasticity in plant size and architecture in rhizome‐derived vs. seed‐derived Solidago and Aster. Ecology. 1990;71:523–535. doi: 10.2307/1940306. [DOI] [Google Scholar]
- Semple JC. An intuitive phylogeny and summary of chromosome number variation in the goldenrod genus Solidago (Asteraceae: Astereae) Phytoneuron. 2016;32:1–9. [Google Scholar]
- Semple JC, Ohi-Toma T. Typification of Solidago yokusaiana (Asteraceae: Astereae), a distinctive Japanese species. Phytoneuron. 2017;16:1–6. [Google Scholar]
- Shaw J, Lickey EB, Schilling EE, Small RL. Comparison of whole chloroplast genome sequences to choose noncoding regions for phylogenetic studies in angiosperms: the tortoise and the hare III. Am J Bot. 2007;94:275–288. doi: 10.3732/ajb.94.3.275. [DOI] [PubMed] [Google Scholar]
- Sheldon JC, Burrows FM. The dispersal effectiveness of the achene–pappus units of selected Compositae in steady winds with convection. N Phytol. 1973;72:665–675. doi: 10.1111/j.1469-8137.1973.tb04415.x. [DOI] [Google Scholar]
- Smouse PE, Long JC, Sokal RR. Multiple regression and correlation extensions of the Mantel test of matrix correspondence. Syst Zool. 1986;35:627–632. doi: 10.2307/2413122. [DOI] [Google Scholar]
- Sokal RR, Michener CD. A statistical method for evaluating systematic relationships. Univ Kans Sci Bull. 1958;38:1409–1438. [Google Scholar]
- Strimmer K, Pybus OG. Exploring the demographic history of DNA sequences using the generalized skyline plot. Mol Biol Evol. 2001;18:2298–2305. doi: 10.1093/oxfordjournals.molbev.a003776. [DOI] [PubMed] [Google Scholar]
- Trucchi E, Frajman B, Haverkamp THA, Schönswetter P, Paun O. Genomic analyses suggest parallel ecological divergence in Heliosperma pusillum (Caryophyllaceae) N Phytol. 2017;216:267–278. doi: 10.1111/nph.14722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Steenis C (1981) Rheophytes of the world. Alpen aan den Rijn, Sijthoff and Noordhoff
- Welch JJ, Jiggins CD. Standing and flowing: the complex origins of adaptive variation. Mol Ecol. 2014;23:3935–3937. doi: 10.1111/mec.12859. [DOI] [PubMed] [Google Scholar]
- Yashima K, Miyauchi T. The Tsugaru land bridge problem related to Quaternary coastal tectonics, northeast Japan. Quat Res Daiyonki-Kenkyu. 1990;29:267–275. doi: 10.4116/jaqua.29.267. [DOI] [Google Scholar]
- Yoichi W, Kawamata I, Matsuki Y, Suyama Y, Uehara K, Ito M. Phylogeographic analysis suggests two origins for the riparian azalea Rhododendron indicum (L.) Sweet. Heredity. 2018;121:594–604. doi: 10.1038/s41437-018-0064-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J-H, Cornille A, Giraud T, Cheng F-Y, Hu Y-H. Independent domestications of cultivated tree peonies from different wild peony species. Mol Ecol. 2014;23:82–95. doi: 10.1111/mec.12567. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The haplotype sequences are now being registered in GenBank (NCBI/DDBJ/EMBL) database and the SNP datasets will be uploaded to the Dryad Digital Repository until publication.