Abstract
Currently, the coronavirus disease 2019 (COVID19) pandemic has killed more than one million people worldwide. In the present outbreak, radiological imaging modalities such as computed tomography (CT) and X-rays are being used to diagnose this disease, particularly in the early stage. However, the assessment of radiographic images includes a subjective evaluation that is time-consuming and requires substantial clinical skills. Nevertheless, the recent evolution in artificial intelligence (AI) has further strengthened the ability of computer-aided diagnosis tools and supported medical professionals in making effective diagnostic decisions. Therefore, in this study, the strength of various AI algorithms was analyzed to diagnose COVID19 infection from large-scale radiographic datasets. Based on this analysis, a light-weighted deep network is proposed, which is the first ensemble design (based on MobileNet, ShuffleNet, and FCNet) in medical domain (particularly for COVID19 diagnosis) that encompasses the reduced number of trainable parameters (a total of 3.16 million parameters) and outperforms the various existing models. Moreover, the addition of a multilevel activation visualization layer in the proposed network further visualizes the lesion patterns as multilevel class activation maps (ML-CAMs) along with the diagnostic result (either COVID19 positive or negative). Such additional output as ML-CAMs provides a visual insight of the computer decision and may assist radiologists in validating it, particularly in uncertain situations Additionally, a novel hierarchical training procedure was adopted to perform the training of the proposed network. It proceeds the network training by the adaptive number of epochs based on the validation dataset rather than using the fixed number of epochs. The quantitative results show the better performance of the proposed training method over the conventional end-to-end training procedure.
A large collection of CT-scan and X-ray datasets (based on six publicly available datasets) was used to evaluate the performance of the proposed model and other baseline methods. The experimental results of the proposed network exhibit a promising performance in terms of diagnostic decision. An average F1 score (F1) of 94.60% and 95.94% and area under the curve (AUC) of 97.50% and 97.99% are achieved for the CT-scan and X-ray datasets, respectively. Finally, the detailed comparative analysis reveals that the proposed model outperforms the various state-of-the-art methods in terms of both quantitative and computational performance.
Keywords: COVID19, ML-CAMs, Computer-aided diagnosis, Deep learning, Medical image classification
1. Introduction
Recently, the outbreak of coronavirus disease 2019 (COVID19) has led the entire world toward the verge of devastation. The World Health Organization (WHO) announced COVID19 as a global pandemic on March 11, 2020 [1]. As per given statistics until April 12, 2021, approximately 135,646,617 cases of COVID19 infection have been reported, including 2,930,732 deaths (with a fatal rate of 2.16%) in more than 200 countries [2]. Until now, various experimental vaccines have been developed and undergone rigorous clinical trials to ensure their effectiveness and safety before obtaining official approval. Recently, a few vaccines have obtained the Food and Drug Administration (FDA) or European Medicines Agency (EMA) approval after completing the clinical trials effectively. As of 11 April 2021, a total of 727,751,744 vaccine doses have been administered [2]. However, the massive production and distribution of these vaccines are still a challenging and time-taking task. Therefore, early diagnosis and appropriate safety measures should be accomplished to control the transmissibility of COVID19 infection. For COVID19 diagnosis, the reverse transcription-polymerase chain reaction (RT-PCR) test has been adopted as the gold standard. However, the subjective dependencies and strict requirements for testing environments restrict the quick and precise testing of suspected subjects. In addition to RT-PCR testing, radiological imaging modalities, such as computed tomography (CT) and X-ray, have shown effectiveness in diagnosis as well as evaluation of disease evolution as a complementary assessment [3], [4]. A recent clinical study with 1014 patients in Wuhan, China, showed that chest CT scan analysis can achieve a sensitivity of 0.97 for the detection of COVID19 with RT-PCR results for reference [3]. Similar results have also been stated in recent studies [4], [5], suggesting that radiological imaging modalities may be advantageous in the initial diagnosis of COVID19 in epidemic areas. However, the diagnostic assessment of radiographic scans (i.e., CT scans and X-ray images) can only be performed by a specialized radiologist, who must utilize substantial effort and time to make an effective decision. Therefore, such subjective assessment may not be appropriate for real-time screening in epidemic regions.
Recent advancements in artificial intelligence (AI) have shown a remarkable breakthrough in the development of computer-aided diagnosis (CAD) tools [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], [26], [27]. In particular, with the advent of deep learning algorithms, such automated tools have shown significant decision-making performance in different medical domains, including radiology. These tools can mimic the human brain in making a diagnostic decision with extraordinary performance, particularly in real-time population screening applications. In the present era of deep learning-based algorithms, convolutional neural networks (CNNs) have achieved significant renown in general as well as medical image-based applications. In the case of COVID19 screening, these networks can also be trained to identify normal and diseased patterns in given radiographic scans (i.e., CT scans and X-ray images) within a second. However, a sufficient amount of training data is required to train a CNN model, which can be considered as a major restraint in the deep learning methods. The layout of a CNN model mainly comprises convolutional layers that include a number of learnable filters with different sizes. In the first stage, training is performed to learn the trainable filters using the available training dataset. After the training process, the trained model can explore the given testing samples and ultimately predict the accurate output.
In this study, a comprehensive analysis of various machine learning and deep learning algorithms were performed in response to COVID19. Finally, a light-weighted deep CNN model was proposed with significant gains in terms of accuracies and computational cost. The overall performance of the proposed network is greater than those of various state-of-the-art methods. To highlight the key findings and significance of the proposed work, the main contributions are summarized as follows:
-
1.
In this study, an efficient ensemble network was proposed to diagnose COVID19 pneumonia from a large-scale radiographic database including both CT scans and X-ray images. This is the first ensemble design (based on MobileNet, ShuffleNet, and FCNet) in medical domain (particularly for COVID19 diagnosis) that encompasses reduced number of trainable parameters and outperforms various existing models. In the comparative analysis, the performances of various baseline methods (based on deep learning and handcrafted features) were evaluated using the same experimental setup and datasets. Finally, the proposed network exhibits promising results and outperforms various state-of-the-art methods.
-
2.
Additionally, a multilevel activation visualization (MLAV) layer was introduced to visualize the progression of multilevel discriminative patterns inside the network. The MLAV layer visualizes the lesion patterns along with the final diagnostic decision (either COVID19 positive or negative) as multilevel class activation maps (ML-CAMs). Such additional output presents a visual insight into the CAD decision and may assist in correct validation by medical professionals.
-
3.
To perform the appropriate training of the proposed network, a novel hierarchical training procedure was defined, which executed the training up to the optimal number of epochs based on the validation dataset. The optimal number of epochs was determined based on convergence criteria of Algorithm 1 in Section 3.2. The quantitative results show the better performance of the defined method over the end-to-end training procedure.
-
4.
Finally, the proposed network and data splitting information (including the indices of training, validation, and testing dataset) was made publicly accessible through [28] for further research and development.
The subsequent sections of this paper are organized in the following order: Section 2 presents a short summary of state-of-the-art studies related to the proposed work. A comprehensive explanation of the proposed network and the complete experimental setup (including dataset and performance evaluation metrics) are provided in Sections 3, 4, respectively. Subsequently, Section 5 presents the experimental results of the proposed network along with a detailed comparative analysis with existing methods. Finally, a brief decision of the overall proposed work and conclusion is presented in Sections 6, 7, respectively.
2. Related works
In this pandemic era, AI-empowered CAD tools are being evolved to significantly contribute to a reliable, cost-effective, and automated diagnostic method for COVID19 pneumonia with the help of radiological imaging modalities. Recently, several CAD tools have been presented in the literature with the ultimate objective of discerning COVID19 positive and negative patients after processing their radiographic scans, such as CT or X-ray images [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. Most of these studies utilized the strength of deep-learning-driven detection, segmentation, or classification methods to make the decision. For example, Ghoshal et al. [6] proposed a Bayesian CNN to classify a given X-ray image into one of the following four classes: COVID19 positive, viral pneumonia, bacterial pneumonia, and normal case. An existing deep residual network (ResNet) [29] was modified to enhance the overall classification results. In the context of the limited COVID19 X-ray dataset, Oh et al. [7] presented a patch-based deep features extraction approach that included a small number of trainable parameters. The overall pipeline included a fully connected-dense network (FC-DenseNet) followed by ResNet18 to perform lung segmentation and then patched-based deep feature extraction. A similar data limitation problem was further explored by Singh et al. [9] using the CT scan dataset. A multi-objective differential evolution (MODE) method was proposed to obtain a high performance pre-trained CNN model. However, an existing deep network was used with the ultimate objective of classifying the COVID19 positive and negative cases.
Moreover, a computationally-efficient version of a standard Inception network (InceptionNet) [30], namely truncated InceptionNet, was proposed by Das et al. [8] to categorize a given X-ray image into one of the four classes of COVID19 positive, pneumonia, tuberculosis, and normal cases. Owing to the reduced number of inception modules, their proposed model was computationally efficient compared with the original version. In another study, Pereira et al. [10] investigated the significance of conventional handcrafted feature descriptors in conjunction with a deep network. They proposed an ensemble of multiple texture descriptors and a pre-trained InceptionNet model to exploit both visual and hidden patterns in X-ray scans. Additionally, a resampling method was proposed to resolve the class imbalance problem caused by the different number of data samples in each class. Finally, feature-level fusion was performed before and after application of the resampling algorithm to exploit the overall network performance as an ablation study. Later, Khan at al. [11] proposed a deep network, namely CoroNet, to classify X-ray data samples into four different categories, as in [6]. The proposed model was based on Xception [31], an existing pretrained deep network, followed by additional dense blocks to exploit further high-level features.
In a comparative analysis study, Asnaouia et al. [12] investigated the collective response of existing pre-trained CNN models toward COVID19. The comparative results of seven CNN models were evaluated to classify X-ray images into three classes: bacterial pneumonia, COVID19, and normal class. Further experimental results have proved the higher performance of the inception residual network (InceptionResNet) [32] compared with other networks. Later, Brunese et al. [13] performed a hierarchical diagnostic of COVID19 pneumonia using cascade connectivity of two existing VGG16 [33] networks. In the first step, the given X-ray image was categorized as either normal or diseased, and the second network further distinguished between COVID19 and other pneumonia. Furthermore, Mahmud et al. [15] presented a deep CNN model, namely CovXNet, which utilized the strength of depth-wise convolution (DW-conv) [34] with varying dilation rates for extracting the more diversified features from a chest X-ray dataset. In a recent study, Han et al. [14] considered a complete 3D volume of CT-scan slices to make the diagnostic decision. An attention-based deep 3D multiple instance learning (AD3D-MIL) model was proposed to analyze all the CT-scan slices of a patient to detect COVID19 pneumonia rather than using a single CT-scan image.
These existing methods consider the limited COVID19 data samples and make the end-to-end decision (i.e., either a patient has COVID19 or not) without offering additional information that may assist radiologists in performing further subjective validation. Therefore, in this work, a large-scale COVID19 dataset was considered (includes both CT scans and X-ray images) and a light-weighted ensemble network was proposed to achieve its improved performance. Moreover, the proposed network provides additional information about the CAD decision in terms of ML-CAMs, which are being used to make the ultimate decision. Finally, Table 1 briefly highlights the key differences among the existing state-of-the-art methods along with the proposed diagnostic network.
Table 1.
Comparative summary of the proposed and the existing state-of-the-art methods for automatic diagnosis of COVID19 pneumonia. (V.C: Varicella, S.T: Streptococcus, P.M: Pneumocystis, T.B: Tuberculosis, M.R: MERS, S.R: SARS, P.N: Pneumonia, B.P: Bacterial pneumonia, V.P: Viral pneumonia, ACC: Accuracy, F1: F1 score, AP: Average precision, AR: Average recall, Spec: Specificity, Kap: Kappa statistics, Others: Combination of different diseased and normal classes beside COVID19).
| Literature | Method | Class name (No. of classes) | Dataset (No. of images) |
Imaging modality | Result (%) | Strength | Limitation | |
|---|---|---|---|---|---|---|---|---|
| COVID19+ | COVID19 | |||||||
| Ghoshal et al. [6] | Bayesian CNN | COVID19/B.P/V.P/ Normal (4) |
68 | 5873 | X-ray | ACC: 89.82 | Enhanced detection performance compared to Standard ResNet | Limited COVID19 data samples |
| Oh et al. [7] |
FC-DenseNet+ResNet18 | COVID19/B.P/V.P/T.B/ Normal (5) |
180 | 322 | X-ray | ACC: 88.9, F1: 84.4, AP: 83.4, AR: 85.9, Spec: 96.4 | Provides clinically interpretable saliency maps | - Limited COVID19 data samples - Patch processing required high computational cost |
| Das et al. [8] |
Truncated InceptionNet | COVID19/P.N/T.B/ Normal (4) |
162 | 6683 | X-ray | ACC: 98.7, F1: 97, AP: 99, AR: 95, Spec: 99, AUC: 99 | Enhanced computational performance compared to Standard InceptionNet | Limited COVID19 data samples |
| Singh et al. [9] | MODE-based CNN | COVID19/Others (2) |
69 | 63 | CT | ACC: 93.5, F1: 89.9, AR: 90.75, Spec: 90.8, Kap: 90.5 | Applicable in real-time screening | - Limited dataset - Lack of ablation study |
| Pereira et al. [10] | Texture Descriptors and InceptionNet | COVID19/M.R/S.R/ V.C/S.T/P.M/Normal (7) |
180 | 2108 | X-ray | F1: 89 | High COVID19 recognition rate | - Limited COVID19 data samples - Required high computational power |
| Khan et al. [11] |
CoroNet | COVID19/B.P/V.P/ Normal (4) |
284 | 967 | X-ray | ACC: 89.6, F1: 89.8, AP: 90, AR: 89.92, Spec: 96.4 | High COVID19 detection rate compared to other classes | - Limited COVID19 data samples - Lack of ablation study |
| Asnaoui et al. [12] | InceptionResNet | COVID19/B.P/Normal (3) |
231 | 5856 | X-ray | F1: 92.08, AP: 92.38, AR: 92.11, Spec: 96.06 | Detailed performance analysis under the same experimental protocol | - Low COVID19 detection rate compared to other classes - Limited COVID19 data samples |
| Brunese et al. [13] |
VGG16 | COVID19/P.N/Normal (3) |
250 | 6273 | X-ray | ACC: 97 | High COVID19 detection rate compared to other classes | - Lack of ablation study - Limited COVID19 data samples |
| Han et al. [14] | AD3D-MIL | COVID19/P.N/Normal (3) |
230 | 230 | CT | ACC: 94.3, F1: 92.3, AP: 95.9, AR: 90.5, AUC: 98.8, Kap: 91.1 | Provides clinically interpretable saliency maps | - Required high computational power |
| Mahmud et al. [15] | CovXNet | COVID19/B.P/V.P/ Normal (4) |
305 | 915 | X-ray | ACC: 90.2, F1: 90.4, AP: 90.8, AR: 89.9, Spec: 89.1, AUC: 91 | Generate clinically interpretable activation maps | - Limited dataset - Low COVID19 detection rate |
| Proposed | Ensemble-Net | COVID19/Others (2) | 3296 | 4143 | X-ray | ACC: 95.83, F1: 95.94, AP: 95.68, AR: 96.20, AUC: 97.99 | - Reduced number of trainable parameters - Visualize clinically interpretable ML-CAMs | - Training time is longer than the conventional end-to-end training method |
| 3254 | 2217 | CT | ACC: 94.72, F1: 94.60, AP: 95.22, AR: 94.00, AUC: 97.5 | |||||
3. Proposed method
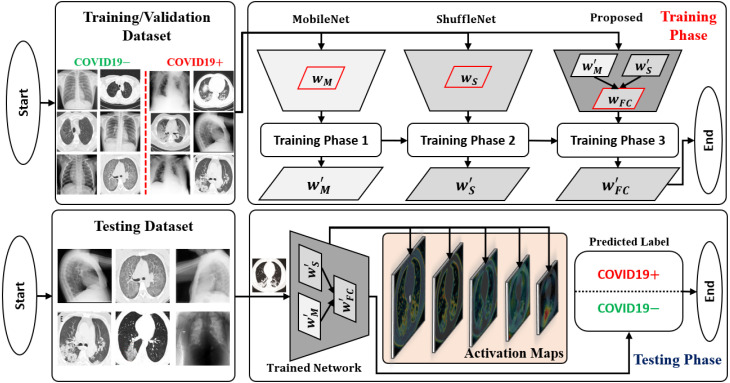
An abstract workflow of the proposed framework is shown in Fig. 1. The development cycle of the proposed framework mainly includes the following three steps: (1) implementing a deep network architecture with the ultimate goal of achieving higher performance regarding the accuracy and computational cost; (2) performing a hierarchical training procedure to obtain the well-trained parameters of the proposed network based on the training and validation datasets; (3) testing the network performance and visualizing the output in terms of the predicted label (either COVID19 positive or negative) and ML-CAMs corresponding to each radiographic image. The subsequent subsections provide detailed explanations of these three steps.
Fig. 1.
Overall workflow of the proposed framework visualizing the progression of both training and testing phases distinctly.
3.1. Deep network architecture
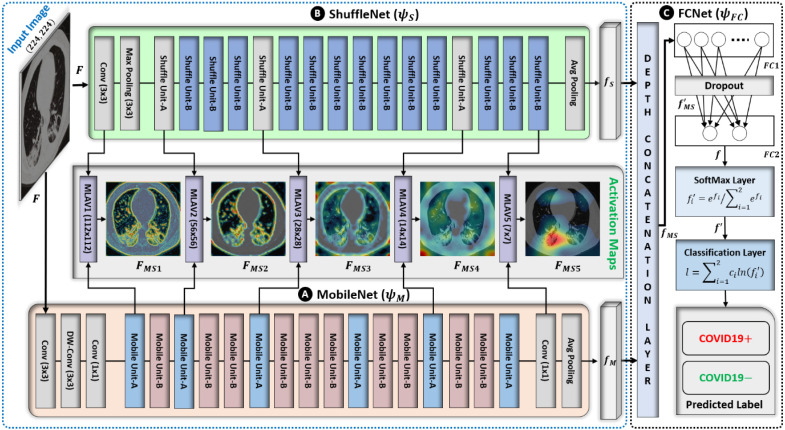
The proposed network is based on the parallel connectivity of mobile network (MobileNet) [34] and shuffle network (ShuffleNet) [35], followed by a fully connected network (FCNet), as shown in Fig. 2. This is the first ensemble design (based on MobileNet, ShuffleNet, and FCNet) in medical domain (particularly for COVID19 diagnosis) that encompasses the reduced number of trainable parameters and outperforms the various existing models. The experimental results prove that the proposed network outperforms the individual performances of both MobileNet and ShuffleNet. Moreover, the addition of a third subnetwork (FCNet) gives an additional performance gain over the simple ensemble of MobileNet and ShuffleNet. In this way, the newly included FCNet also makes the intended design different from the simple ensemble of MobileNet and ShuffleNet. The main reason for selecting MobileNet and ShuffleNet is their optimized architectures regarding memory utilization and computing speed at a minimum cost in terms of error [34]. Cost-effective memory consumption is a desirable quality in the context of an ensemble of networks, and the fast execution speed sufficiently reduces the training as well as testing time. These characteristics are driven by the use of DW-conv, which distinguishes them from other conventional convolution-based deep networks [29], [30], [31], [32], [33]. Generally, a standard convolutional layer [36] processes an input tensor (activation maps) of size and performs a convolutional kernel to generate an output tensor of size . A total computation cost of is required for performing this standard convolution operation. However, the DW-conv layer requires a total computation cost of (sum of the depthwise and 1 × 1 pointwise convolutions) to perform a similar operation. In this way, DW-conv decreases the average computation cost by a factor of compared to the standard convolution operation. In the proposed network, both subnetworks use the convolutional kernel of size 3 × 3 , so the total computation cost is 8–9 times lower than that of the standard convolutional layer.
Fig. 2.
Architecture of the proposed ensemble network based on MobileNet, ShuffleNet, and FCNet. Both MobileNet and ShuffleNet are connected in parallel and their outputs are simultaneously cascade-connected to FCNet.
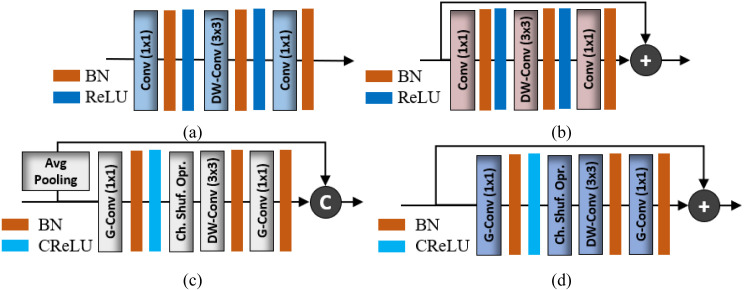
The general architecture of MobileNet mainly comprises the serial connectivity of two basic structural units labeled as mobile unit-A and mobile unit-B in Fig. 3a–b, respectively. These building blocks mainly include a DW-conv layer and two additional 1 × 1 conventional layers to control the depth size. The main difference between mobile units A and B is the addition of shortcut connectivity (Fig. 3a–b) and the use of different stride values in the DW-conv layer (as given in Table 2). Primarily, mobile unit-A is responsible for reducing the spatial dimension (from to ) of the input tensor using a stride of 2 in the DW-conv layers. Meanwhile, mobile unit-B performs feature extraction without reducing the spatial dimension of the input tensor. There are a total of 16 mobile units (including 6 mobile unit-A and 10 mobile unit-B) and a few extra layers (labeled as DW-conv, conv, and avg. pooling layers in Fig. 2) that also contribute to the development of the complete network architecture.
Fig. 3.
MobileNet and ShuffleNet basic building blocks: (a) Mobile Unit-A, (b) Mobile Unit-B, (c) Shuffle Unit-A, and (d) Shuffle Unit-B. (BN: Batch normalization, ReLU: Rectified linear unit, CReLU: Clipped ReLU, Ch. Shuf. Opr: Channel shuffle operation).
Table 2.
Layer-wise configuration details of the proposed network. (Itr.: Iterations, #Filt.: Number of filters, Str. Stride value, #Par.: Number of trainable parameters).
| Subnetwork | Layer name | Itr. | Input size | Output size | Filter size | #Filt. | Str. | #Par. |
|---|---|---|---|---|---|---|---|---|
| (A) Mobile Net | Input | – | 224 × 224 3 | n/a | n/a | n/a | n/a | n/a |
| Conv | 1 | 224 × 224 3 | 112 × 112 32 | () | 32 | 2 | 960 | |
| DW-conv | 1 | 112 × 112 32 | 112 × 112 32 | () | 32 | 1 | 384 | |
| Conv | 1 | 112 × 112 32 | 112 × 112 16 | () | 16 | 1 | 560 | |
| Mobile Unit-A | 1 | 112 × 112 16 | 56 × 56 24 | (1 1) | 96, 96, 24 | 1, 2, 1 | 5352 | |
| Mobile Unit-B | 1 | 56 × 56 24 | 56 × 56 24 | (1 1) | 144, 144, 24 | 1, 1, 1 | 9144 | |
| Mobile Unit-A | 1 | 56 × 56 24 | 28 × 28 32 | (1 1) | 144, 144, 32 | 1, 2, 1 | 10,320 | |
| Mobile Unit-B | 2 | 28 × 28 32 | 28 × 28 32 | (1 1) | 192, 192, 32 | 1, 1, 1 | 30,528 | |
| Mobile Unit-A | 1 | 28 × 28 32 | 14 × 14 64 | (1 1) | 192, 192, 64 | 1, 2, 1 | 21,504 | |
| Mobile Unit-B | 3 | 14 × 14 64 | 14 × 14 64 | (1 1) | 384, 384, 64 | 1, 1, 1 | 165,312 | |
| Mobile Unit-A | 1 | 14 × 14 64 | 14 × 14 96 | (1 1) | 384, 384, 96 | 1, 1, 1 | 67,488 | |
| Mobile Unit-B | 2 | 14 × 14 96 | 14 × 14 96 | (1 1) | 576, 576, 96 | 1, 1, 1 | 239,040 | |
| Mobile Unit-A | 1 | 14 × 14 96 | 7 × 7 160 | (1 1) | 576, 576, 160 | 1, 2, 1 | 156,576 | |
| Mobile Unit-B | 2 | 7 × 7 160 | 7 × 7 160 | (1 1) | 960, 960, 160 | 1, 1, 1 | 644,160 | |
| Mobile Unit-A | 1 | 7 × 7 160 | 7 × 7 320 | (1 1) | 960, 960, 320 | 1, 1, 1 | 476,160 | |
| Conv | 1 | 7 × 7 320 | 7 × 7 1280 | () | 1280 | 1 | 413,440 | |
| Avg Pooling | 1 | 7 × 7 1280 | 1 × 1 1280 | () | 1 | 1 | – | |
| (B) Shuffle Net | Conv | 1 | 224 × 224 3 | 112 × 112 24 | () | 24 | 2 | 720 |
| Max Pooling | 1 | 112 × 112 24 | 56 × 56 24 | () | 1 | 2 | – | |
| Shuffle Unit-A | 1 | 56 × 56 24 | 28 × 28 136 | (1 1) (3 × 3)* |
112, 112, 112 1 |
1, 2, 1 2 |
5824 | |
| Shuffle Unit-B | 3 | 28 × 28 136 | 28 × 28 136 | (1 1) | 136, 136, 136 | 1, 1, 1 | 35,088 | |
| Shuffle Unit-A | 1 | 28 × 28 136 | 14 × 14 272 | (1 1) (3 × 3)* |
136, 136, 136 1 |
1, 2, 1 2 |
11,696 | |
| Shuffle Unit-B | 7 | 14 × 14 272 | 14 × 14 272 | (1 1) | 272, 272, 272 | 1, 1, 1 | 293,216 | |
| Shuffle Unit-A | 1 | 14 × 14 272 | 7 × 7 544 | (1 1) (3 × 3)* |
272, 272, 272 1 |
1, 2, 1 2 |
41,888 | |
| Shuffle Unit-B | 3 | 7 × 7 544 | 7 × 7 544 | (1 1) | 544, 544, 544 | 1, 1, 1 | 473,280 | |
| Avg Pooling | 1 | 7 × 7 544 | 1 × 1 544 | () | 1 | 1 | – | |
| (C) FCNet | Depth Concatenation | 1 | 1 × 1 1280 1 × 1 544 |
1 × 1 1824 | – | 1 | ||
| FC1 | 1 | 1 × 1 1824 | 1 × 1 32 | – | – | – | 58,400 | |
| FC2 | 1 | 1 × 1 32 | 1 × 1 2 | – | – | – | 66 | |
| SoftMax | 1 | 1 × 1 2 | 1 × 1 2 | – | 1 | |||
| Classification | 1 | – | 1 | |||||
| Total learnable parameters: 3,161,106 | ||||||||
Similarly, ShuffleNet comprises the serialized connectivity of two basic structural units, labeled as shuffle unit-A and shuffle unit-B in Fig. 3c–d, respectively. The basic structural units of both MobileNet and ShuffleNet (Fig. 3) utilize the same DW-conv operation to exploit the key features. However, two additional layers (a group convolutional (G-conv) layer [35] followed by a channel shuffle operation [35]) are included in both shuffle units (Fig. 3c–d). The purpose of the G-conv layer is to reduce the computational complexity of conventional 1 × 1 convolution operations [36]. However, in the case of multiple G-conv layers, the outputs from a specific channel are only obtained from a small percentage of input channels. This characteristic halts the data flow between channel groups and impairs the feature extraction procedure. To overcome this problem, a channel shuffle operation was included to allow cross-group data flow for multiple G-conv layers. This additional operation allows the development of more robust structures with multiple G-conv layers. Both shuffle units comprise the same layer-wise configuration (G-conv, channel shuffle operation, and DW-conv layers) with a few modifications. Shuffle unit-A was devised from shuffle unit-B with the following two modifications: (1) including a 3 × 3 average pooling layer on the residual path; (2) replacing the point-wise addition with a depth concatenation layer, which easily expands the channel dimension with minimal computation cost. In shuffle unit-A, the average pooling layer incorporates residual information while reducing the spatial dimension (from to ) of the input tensor . By contrast, shuffle unit-B performs feature extraction without reducing the spatial dimension of the input tensor. The complete ShuffleNet architecture includes a total of 16 shuffle units (including 3 shuffle unit-A and 13 shuffle unit-B) with some additional layers (labeled as max pooling, avg. pooling, and conv layers in Fig. 2).
Comprehensive layer-wise configuration details of the proposed network are given in Table 2. Initially, both subnetworks (MobileNet and ShuffleNet) processed the input image in parallel and transformed it from high-level semantics into low-level features, as shown in Fig. 2. In the case of MobileNet, the first convolutional layer (comprising 32 filters of size 3 × 3) processed the input image and generated the output tensor (activation maps) of size 112 × 112 × 32. Subsequently, a DW-conv layer (comprising 32 filters of size 3 × 3) further explored the deep features in the previous output and transformed into a new tensor of the same size 112 × 112 × 32. Subsequently, a pointwise-conv layer (with a total of 16 filters of size 1 × 1) reduced its depth size and transformed into a tensor of size 112 × 112 × 16. After these initial layers, a stack of 16 mobile units (including 6 mobile unit-A and 10 mobile unit-B) continued to explore more deep features sequentially, as shown in Fig. 2 and Table 2. The output of the third convolutional layer was processed through the stack of these structural units and ultimately converted into a tensor of size 7 × 7 × 320. Each mobile unit processed the preceding output tensor and transformed it into a new one after exploring deeper features. Finally, a low-dimension feature vector (labeled as in Fig. 2) of size was generated after processing the output of the last mobile unit through a pointwise convolutional layer (with 1280 filters of size 1 × 1) and an average pooling layer of size 7 × 7. Similarly, in the case of ShuffleNet, the input image also passed through the first convolutional layer (having 24 filters of size 3 × 3) and converted into a tensor of size 112 × 112 × 24. Subsequently, a max pooling layer of size 3 × 3 further reduced its (output of first convolutional layer) spatial dimension and generated a new tensor of size 56 × 56 × 24. Subsequently, a stack of 16 shuffle units (including 3 shuffle unit-A and 13 shuffle unit-B, as shown in Fig. 2) explored the additional features and converted the intermediate tensor (obtained after the max pooling layer) into a new output tensor of size 7 × 7 × 544. Ultimately, a low-dimension feature vector (labeled as in Fig. 2) of size 1 × 1 × 544 was generated after processing this output tensor (obtained after the last shuffle unit) through an average pooling layer of size 7 × 7. The dimensional details of all the intermediate tensors (generated after each mobile unit, shuffle unit, and other layers) are given in Table 2.
It can be observed that the depths of all the intermediate tensors (in the case of both subnetworks) increased and the spatial size decreased progressively after passing through different layers, as described in Table 2. Finally, low-level features ( and after MobileNet and ShuffleNet, respectively) were obtained that incorporate the distinctive information to differentiate COVID19 positive and negative cases. In the proposed network, both low-level features jointly contributed to making the diagnostic decision. Additionally, a FCNet was included after MobileNet and ShuffleNet to further improve the discriminative capability of these two features ( and ) and perform the final classification. Initially, FCNet included a depth concatenation layer that concatenates both and and generates a jointly connected feature vector (labeled as in Fig. 2) of size . Subsequently, the FC1 layer further explored the significant features in and converted into a low-dimensional feature vector, , of size 1 × 1 × 32. This newly included layer showed a significant performance gain in the proposed network and differentiated it from the conventional ensemble networks. Finally, a stack of the FC2, softmax, and the classification layers worked as a classifier and further processed to calculate the final class label for the input image. In this stack, the FC2 layer recognized the larger patterns in by fusing all the feature values and transformed into a binary feature vector, , of size 1 × 1 × 2. Subsequently, the next softmax layer transformed (output of FC2 layer) in terms of a probability vector, , after using the softmax function [37]. Eventually, the classification layer assigned each input in (output of softmax layer) to one of the two jointly exclusive classes (i.e., COVID19+ and COVID19) using a cross-entropy loss function [37].
3.2. Hierarchical training procedure
To perform sufficient training of the proposed network, a hierarchical training procedure was adopted. Initially, independent training of both pretrained MobileNet and ShuffleNet was performed using training data samples and validation data samples denoted as and in algorithm 1, respectively. The main objective was to perform the transfer learning of both MobileNet and ShuffleNet for the target domain and obtain the initial fine-tuned weights and , respectively. These learned parameters were further utilized to initialize the initial weights of MobileNet and ShuffleNet in the proposed network rather than performing their training from scratch. Fine-tuning a deep network through transfer learning is much easier and faster than training it from scratch. Afterward, the training of FCNet was only performed from scratch by freezing all the weights in previous layers (i.e., keeping and unchanged by initializing the learning rates in those layers to zero). Finally, the learned parameters of FCNet were obtained. Thus, the freezing mechanism solves the overfitting problem, particularly in the case of a small dataset and significantly fast network training.
The main reason behind this training procedure was to perform appropriate training of the proposed network with a limited dataset. In conventional transfer learning approach, a simple fine-tuning of the complete ensemble network is performed in a single step. In particular, different pretrained backbone networks are combined in first step and then training is performed. Whereas, in the selected training method, the independent training of each backbone network was performed in first step, then these learned weights were transferred to the intended ensemble network and finally FCNet was trained in second step. In this aspect, the adopted training procedure is different from the conventional single-step end-to-end training method. The end-to-end training of the proposed model was also performed, but the overall performance was significantly lower than that of the defined training procedure in this study. Additionally, convergence criteria were defined based on the validation dataset to stop the training procedure of each subnetwork (i.e., MobileNet, ShuffleNet, and FCNet) rather than completing the training until the maximum number of epochs, which may cause an overfitting problem. In this criterion, the validation accuracy of each subnetwork is calculated after completing the training for one epoch. Subsequently, the validation accuracy for the current and previous epochs is compared to evaluate the training convergence. In the case of minimum difference (i.e., less than a certain threshold), the network training is stopped for the subsequent epochs.
In this way, sufficient training of each subnetwork is performed using an independent validation dataset, which ultimately results in a significant performance gain of the proposed network. Additionally, Algorithm 1 presents a simple workflow of the defined hierarchical training procedure as pseudo-code. Finally, the total loss function of the proposed network can be interpreted as:
| (1) |
where , , and represent MobileNet, ShuffleNet, and FCNet in terms of a transfer function, respectively; and represent the set of training data samples and their corresponding class labels, respectively. To find their respective trained weights, , , and, , the MobileNet, ShuffleNet, and FCNet loss functions were sequentially minimized for available training data . In Eq. (1), the cross-entropy loss is computed as where and represent the predicted and actual class labels, respectively. A well-known backpropagation algorithm, stochastic gradient descent [38], was used to perform the training of the proposed and other baseline networks. The initial hyperparameters were as follows: learning rate equal to 0.001, learning rate drop factor as 0.1, min-batch size equal to 10 (i.e., passing 10 images per gradient update in each iteration), L2-regularization equal to 0.0001, and a momentum factor of 0.9. Additionally, an independent validation dataset was also used in the training procedure to check the convergence of each subnetwork, as mentioned in Algorithm 1.
3.3. ML-CAMs visualization
After completing the training procedure, the trained network was employed to efficiently predict the class label (either COVID19+ or COVID19) based on the associated class prediction probability for each testing data sample. In the new task of COVID19 screening, it is advantageous to provide additional information to the radiologists regarding the computer decision together with the final predicted result. In most of the existing studies [39], [40], [41], the conventional CAM visualization is based on a single network and presents the intermediate features of each subnetwork separately in case of an ensemble design.
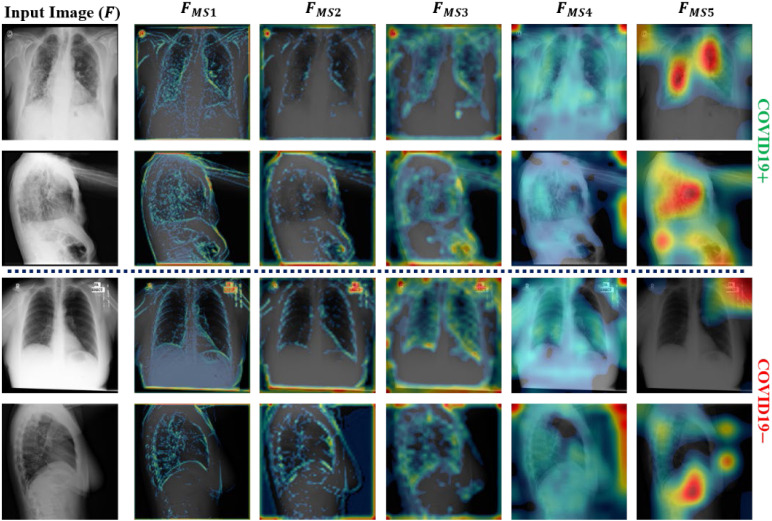
Different from the existing studies [39], [40], [41], an additional MLAV layer was introduced that visualizes the collective activation maps of both subnetworks (MobileNet and ShuffleNet) as a single CAM image from the corresponding layers (Fig. 2). The MLAV layer can provide a common and collective visualization of multiple backbone networks in case of an ensemble design. In the proposed ensemble architecture, a total of five MLAV layers (Fig. 2) were included that present the collective response of both MobileNet and ShuffleNet as a stack of CAM images namely ML-CAMs. These newly proposed ML-CAMs visualize the progression of multilevel discriminative patterns (beginning from low-level to high-level features) inside the network and give a visual clue of the network prediction. Furthermore, such additional information can assist radiologists in performing subjective analyses of infectious areas in case of several medical conditions. Therefore, the proposed diagnostic network, along with the mechanism of ML-CAMs, has significant potential in clinical applications.
To generate these ML-CAMs, the defined MLAV layer performs the following operations: (1) apply depth-wise averaging to transform the input tensor (activation maps) of size into a single channel activation map of size as ; (2) resize according to the input image size and present the resized activation map as a CAM image (with a pseudo color scheme) to visualize the key features more appropriately; (3) finally, overlay the original image with the final CAM image to highlight the activated patterns inside the image. In the defined network architecture, the given input image is gradually down-sampled into five spatial sizes (such as 112 × 112, 56 × 56, 28 × 28, 14 × 14, 7 × 7) after passing through the multiple layers. Therefore, a total of five different locations were selected inside the network to obtain multilevel tensors of five spatial sizes. Following this, these tensors were transformed into ML-CAMs with five MLAV layers in specified locations of the proposed network, as shown in Fig. 2.
4. Datasets and experimental setup
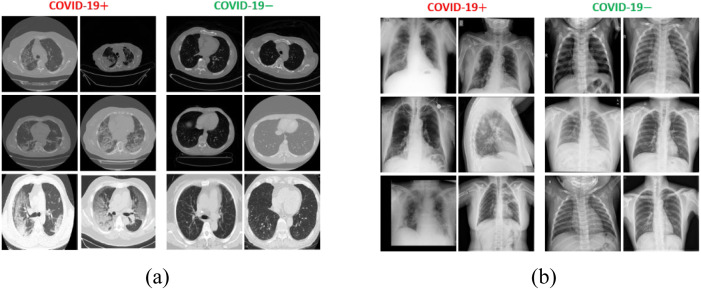
A collection of six publicly available datasets was used to validate the diagnostic capability of the proposed network. These datasets included both COVID19 positive and negative data samples, captured using CT and X-ray imaging modalities. Table 3 provides a summary of the total number of positive and negative cases (in terms of the number of images and number of patients) included in each dataset. Additionally, Fig. 4 shows a few sample images of both imaging modalities to highlight the visual difference between COVID19 positive and negative data samples. Generally, the COVID19 positive scans encompass a few distinctive radiographic patterns, namely ground-glass opacity, consolidation, bilateral, peripheral, pleural effusion, and crazy-paving pattern [42], [43], in medical terminology.
Table 3.
Brief description of datasets selected in this study.
| Modality | Dataset | COVID19+ |
COVID19 |
||
|---|---|---|---|---|---|
| #Images | #Patients | #Images | #Patients | ||
| CT | BIMCV COVID19 [44] | 2905 | 1311 | – | – |
| COVID-CT [45] | 349 | 349 | 397 | 397 | |
| Cancer Archive [46] | – | – | 1820 | 732 | |
| Total | 3254 | 1660 | 2217 | 1129 | |
| X-ray | BIMCV COVID19 [44] | 3296 | 1311 | – | – |
| Shenzhen [47] | – | – | 662 | 662 | |
| Montgomery [47] | – | – | 138 | 138 | |
| CoronaHack [48] | – | – | 3343 | 3343 | |
| Total | 3296 | 1311 | 4143 | 4143 | |
Fig. 4.
Example images from the selected datasets to show the visual difference between COVID19 positive and negative cases: (a) CT scan images; (b) X-ray images.
Such radiographic patterns can provide key evidence to a deep learning model to perform classification and severity assessment of COVID19 pneumonia. As the main goal is to classify a given radiographic image either as COVID19 positive or negative, all data samples of each individual modality were divided into two main classes according to their ground truth labels. All COVID19 positive images were considered as one class and the remaining data samples (including normal as well as bacterial and viral pneumonia cases in some datasets) as another class of each modality. In this way, two main datasets were obtained based on the modality types. Each dataset included a sufficient number of COVID19 positive and negative radiographic images. Finally, all the data samples were resized to 224 224 according to the fix size of the input layer in the proposed model.
A deep learning toolbox [49] accessible in MATLAB R2019a (MathWorks, Inc., Natick, MA, USA) was used to implement and simulate the proposed network. All the experiments were completed on a desktop computer with the following specifications: intel Corei7-3770K CPU with 3.50 GHz clock speed, 16 GB RAM, Windows 10 operating system, and NVIDIA GeForce GTX 1070 GPU. Additionally, five-fold cross-validation was completed in all the experiments using 70% of patient data in training, 10% in validation, and finally 20% in testing. For a fair evaluation of the proposed method in a real-world setting, different patient data were included in the training, validation, and testing datasets, as described in Table 4. Finally, the testing results of the proposed and various baseline methods (including both deep learning and conventional machine learning methods) were assessed based on the following quantitative metrics: accuracy (ACC), F1 score (F1), average precision (AP), average recall (AR), and the area under the curve (AUC) using receiver operating characteristic (ROC) curves [50]. All these metrics calculate the overall performance of a classification method from various perspectives.
Table 4.
Summary of the total number of data samples included in the training, validation, and testing datasets.
| Dataset | Data splitting | COVID19+ |
COVID19 |
||
|---|---|---|---|---|---|
| #Images | #Patients | #Images | #Patients | ||
| CT | Training | 2278 | 1162 | 1552 | 790 |
| Validation | 325 | 166 | 222 | 113 | |
| Testing | 651 | 332 | 443 | 226 | |
| Total | 3254 | 1660 | 2217 | 1129 | |
| X-ray | Training | 2307 | 918 | 2900 | 2900 |
| Validation | 330 | 131 | 414 | 414 | |
| Testing | 659 | 262 | 829 | 829 | |
| Total | 3296 | 1311 | 4143 | 4143 | |
5. Results and analysis
This section describes the quantitative results of the proposed network along with the individual performance of each subnetwork as an ablation study. Subsequently, a detailed comparative analysis was performed with various state-of-the-art deep learning as well as conventional machine learning methods to highlight the significance of the proposed solution.
5.1. Results with an ablation study
In the first experiment, the diagnostic performance of the proposed network was measured for both datasets. Table 5 presents the quantitative results of the proposed network along with the individual performance of each subnetwork as an ablation study that highlights the significance of each subnetwork in developing the overall network architecture. In Table 5, it can be observed that the ensemble of three subnetworks resulted in significant performance gain (particularly in the case of the CT scan dataset) compared with the individual results of each subnetwork. In addition, an ensemble of MobileNet and ShuffleNet (named MobShufNet in Table 5) outperforms each subnetwork and is ranked the second-best network. However, its performance gain is not significantly high compared with the individual performances of both MobileNet and ShuffleNet. Therefore, a third subnetwork, namely FCNet, was assembled with MobShufNet to further enhance its performance. In this way, the proposed network outperforms MobShufNet (a second-best network) with average gains of 1.19%, 1.18%, 0.87%, 1.45%, and 0.62% for the ACC, F1, AP, AR, and AUC, respectively (in cases of both datasets). However, the performance difference between the proposed method and MobileNet is higher with average gains of 1.48%, 1.5%, 1.29%, 1.7%, and 0.74% for the ACC, F1, AP, AR, and AUC, respectively. Similarly, the performance gains for the proposed network vs. ShuffleNet were 1.97%, 1.99%, 1.7%, 2.25%, and 1.18% in ACC, F1, AP, AR, and AUC, respectively. All these results present the average performance gains of both datasets.
Table 5.
Quantitative results of the proposed network including the ablated performance of each subnetwork.
| Dataset | Network | ACC std | F1 std | AP std | AR std | AUC std |
|---|---|---|---|---|---|---|
| CT | ShuffleNet | 91.65 ± 6.14 | 91.52 ± 6.10 | 92.69 ± 4.41 | 90.40 ± 7.68 | 95.61 ± 5.61 |
| MobileNet | 92.95 ± 5.25 | 92.85 ± 5.27 | 93.81 ± 3.93 | 91.90 ± 6.57 | 96.51 ± 3.68 | |
| MobShufNet | 93.11 ± 7.64 | 93.07 ± 7.46 | 94.25 ± 5.25 | 92.00 ± 9.43 | 96.57 ± 5.82 | |
| Proposed | 94.724.76 | 94.604.75 | 95.223.63 | 94.005.82 | 97.504.17 | |
| X-ray | ShuffleNet | 94.97 ± 0.40 | 95.03 ± 0.46 | 94.81 ± 0.41 | 95.30 ± 0.51 | 97.53 ± 0.38 |
| MobileNet | 94.65 ± 1.49 | 94.68 ± 1.58 | 94.51 ± 1.42 | 94.90 ± 1.74 | 97.51 ± 0.46 | |
| MobShufNet | 95.07 ± 1.39 | 95.10 ± 1.46 | 94.91 ± 1.35 | 95.30 ± 1.58 | 97.69 ± 0.42 | |
| Proposed | 95.830.25 | 95.940.28 | 95.680.26 | 96.200.29 | 97.990.14 | |
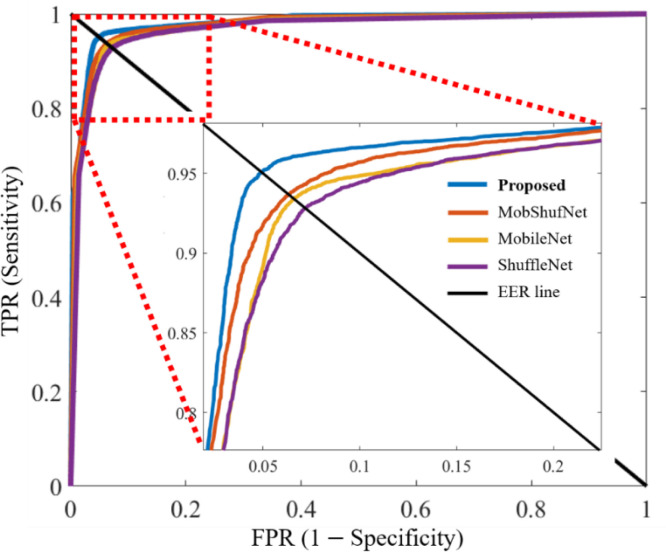
Fig. 5 represents the ROC curves of the proposed network and each subnetwork. Each curve shows a tradeoff between the different values of the true positive rate (TPR) and corresponding false positive rate (FPR) results for a particular network. For each network, different values of TPR and FPR were calculated by varying the classification threshold from 0 to 1 with increments of 0.001. An equal error rate (EER) line is also included in the ROC plot to present the high values of TPR and FPR corresponding to each network. In Fig. 5, all the curves present the average ROC performance of both datasets to envisage the collective performance gain of both datasets for a particular network. Additionally, the average AUCs of 96.57%, 97.01%, 97.13%, and 97.74% were obtained in the cases of ShuffleNet, MobileNet, MobShufNet, and the proposed network from these ROC plots, respectively. The ROC plots further highlight the significance of each subnetwork in developing the final architecture.
Fig. 5.
Receiver operating characteristic curves of ShuffleNet, MobileNet, MobShufNet, and proposed network. The true positive rate (TPR) is plotted against the false positive rate (FPR) of each network at distinct thresholds from 0 to 1 in 0.001 increments.
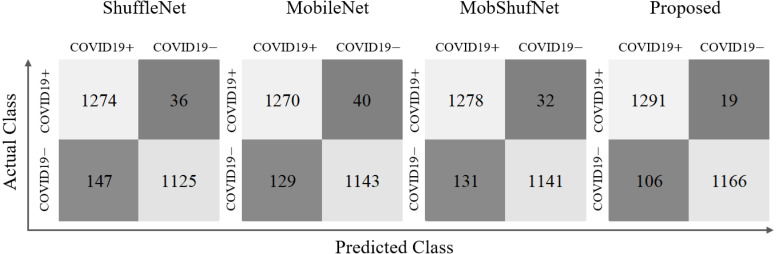
In addition, the predicted numbers of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) data samples are also presented corresponding to each network. Fig. 6 summarizes these results as confusion matrices for ShuffleNet, MobileNet, MobShufNet, and finally the proposed network. These confusion matrices present the collective number of TP, FP, TN, and FN of both datasets after combining their individual results. It can be observed that the total number of TP and TN of the proposed network increased significantly from 1278 to 1,291 and 1141 to 1166 compared with the MobShufNet (second best network), respectively. Meanwhile, FN and FP reduced from 32 to 19 and 131 to 106, respectively. These results highlight the significance of FCNet (with an additional fully connected layer labeled as FC1 in Fig. 2) included after the feature concatenation of MobileNet and ShuffleNet. Moreover, Table 6 provides the comparative results of the adopted hierarchical training procedure (explained in Algorithm 1) compared to the end-to-end training method. In the case of the CT scan dataset, the performance gains (hierarchical training vs. end-to-end) were 3.49%, 3.54%, 2.74%, 4.3%, and 1.77% in ACC, F1, AP, AR, and AUC, respectively. Meanwhile, for the X-ray dataset, the performance gains were lower than those of the CT scan dataset (i.e., 0.08%, 0.11%, 0.09%, 0.1%, and 0.11% in ACC, F1, AP, AR, and AUC, respectively). The average performance gains (hierarchical training vs. end-to-end) of both datasets were 1.79%, 1.83%, 1.42%, 2.2%, and 0.94% in ACC, F1, AP, AR, and AUC, respectively. In conclusion, the defined training procedure performs appropriate training of the proposed network and outperforms the end-to-end training method with significant performance gain.
Fig. 6.
Confusion matrices of the proposed network and each subnetwork. These results present the individual performance of each network in terms of the actual number of true positive (TP), true negative (TN), false positive (FP), and false negative (FN) data samples. (Note: In each confusion matrix, Top-left-box: TP, Top-right-box: FN, Bottom-left-box: FP, Bottom-right-box: TN).
Table 6.
Comparative results of the adopted hierarchical training procedure vs. end-to-end training method.
| Dataset | Training procedure | ACC std | F1 std | AP std | AR std | AUC std |
|---|---|---|---|---|---|---|
| CT | end-to-end | 91.23 ± 5.84 | 91.06 ± 5.88 | 92.48 ± 4.66 | 89.70 ± 7.02 | 95.73 ± 4.57 |
| Hierarchical | 94.724.76 | 94.604.75 | 95.223.63 | 94.005.82 | 97.504.17 | |
| X-ray | end-to-end | 95.75 ± 0.37 | 95.83 ± 0.41 | 95.59 ± 0.38 | 96.10 ± 0.43 | 97.88 ± 0.17 |
| Hierarchical | 95.830.25 | 95.940.28 | 95.680.26 | 96.200.29 | 97.990.14 | |
5.2. Comparative study
In this section, a comprehensive comparison of the proposed method is made with existing state-of-the-art deep feature-based CAD methods related to COVID19 diagnostics [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25]. Most of these methods used the existing pretrained networks and applied the end-to-end transfer learning approach for the automated diagnosis of COVID19 infection. Primarily, these studies aimed to perform the comparative analysis of existing pretrained models and attained the best model based on its high performance. However, these comparative studies used limited radiographic datasets and different experimental protocols. For a fair comparison, the quantitative results of these baseline methods [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25] were assessed based on the selected datasets and experimental protocol. In details, the pretrained backbones of the baseline methods [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25] were selected and fine-tuned with the selected datasets. The training parameters were chosen with the experimental data during the fine-tuning of backbones of the baseline methods [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25], and same method was adopted for the proposed model. Additionally, the same experimental protocol (including five-fold cross-validation) was adopted for the performance comparisons of the baseline methods [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25] and the proposed model. Consequently, this comparative study is more precise and detailed than those in [13], [16], [17], [18], [19], [20], [21], [22], [23], [24], [25]. Table 7 presents the comparative results of all related studies, along with the proposed method.
Table 7.
Quantitative performance comparison of proposed network with the state-of-the-art deep learning methods. (#Par: Total number of parameters).
| Study | Method | #Par (Million) | Dataset 1: CT |
Dataset 2: X-ray |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | F1 | AP | AR | AUC | ACC | F1 | AP | AR | AUC | |||
| Minaee et al. [16] | SqueezeNet | 1.24 | 89.84 | 89.48 | 89.91 | 89.06 | 93.86 | 93.51 | 93.56 | 93.43 | 93.70 | 97.03 |
| Brunese et al. [13] | VGG16 | 134.27 | 89.66 | 89.54 | 91.43 | 87.81 | 92.35 | 95.79 | 95.91 | 95.65 | 96.18 | 97.79 |
| Khan et al. [17] | VGG19 | 139.58 | 91.54 | 91.33 | 92.26 | 90.47 | 94.54 | 95.30 | 95.39 | 95.14 | 95.65 | 97.84 |
| Martínez et al. [25] | NASNet | 4.27 | 93.68 | 93.49 | 94.19 | 92.82 | 96.67 | 94.06 | 94.06 | 93.89 | 94.23 | 97.07 |
| Misra et al. [24] | ResNet18 | 11.18 | 92.96 | 92.76 | 93.41 | 92.14 | 95.06 | 95.59 | 95.69 | 95.44 | 95.95 | 97.79 |
| Farooq et al. [23] | ResNet50 | 23.54 | 90.30 | 90.22 | 92.17 | 88.53 | 92.79 | 94.73 | 94.77 | 94.62 | 94.92 | 97.66 |
| Ardakani et al. [20] | ResNet101 | 42.56 | 90.30 | 90.26 | 92.17 | 88.64 | 95.71 | 94.53 | 94.58 | 94.44 | 94.72 | 97.19 |
| Jaiswal et al. [19] | DenseNet201 | 18.11 | 94.17 | 94.03 | 94.63 | 93.46 | 97.36 | 93.41 | 93.39 | 93.38 | 93.39 | 97.31 |
| Hu et al. [22] | ShuffleNet | 0.86 | 91.65 | 91.52 | 92.69 | 90.44 | 95.61 | 94.97 | 95.03 | 94.81 | 95.25 | 97.53 |
| Apostolopoulos et al. [18] | MobileNetV2 | 2.24 | 92.95 | 92.85 | 93.81 | 91.94 | 96.51 | 94.65 | 94.68 | 94.51 | 94.85 | 97.51 |
| Tsiknakis et al. [21] | InceptionV3 | 21.81 | 94.57 | 94.41 | 94.89 | 93.94 | 97.93 | 95.44 | 95.53 | 95.29 | 95.78 | 97.52 |
| Proposed | Ensemble-Net | 3.16 | 94.72 | 94.60 | 95.22 | 94.00 | 97.50 | 95.83 | 95.94 | 95.68 | 96.20 | 97.99 |
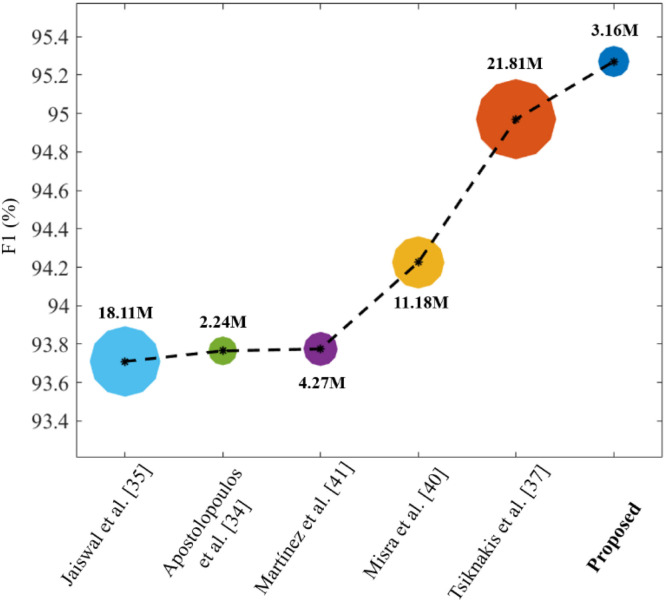
The following interpretations can be inferred from these comparative results: (1) The methods of Tsiknakis et al. [21] and Brunese et al. [13] show comparable results in the cases of the CT scan and X-ray datasets, respectively. Although their quantitative results are comparable, the number of learnable parameters of the proposed network are significantly lower than in [13], [21], as mentioned in Table 7; (2) The networks proposed by Minaee et al. [16], Apostolopoulos et al. [18], and Hu et al. [22] incorporate a lower number of parameters than the proposed network. However, the quantitative results (Table 7) of the proposed network outperform these methods [16], [18], [49] with significant performance gain in terms of all the performance metrics. Additionally, Fig. 7 visualizes the tradeoff between the number of learnable parameters and accuracies (as an average F1 result of both datasets) of the top five baseline models along with the proposed network. It can be observed that the proposed network outperforms these state-of-the-art methods in terms of both accuracy and computational complexity.
Fig. 7.
Tradeoff between the number of parameters and accuracies of the proposed and top five baseline networks.
Before the advent of deep learning algorithms, handcrafted feature-based methods were developed to perform different medical image analysis tasks. Such conventional algorithms mainly include a feature descriptor followed by a classification algorithm. In this image classification pipeline, a feature descriptor exploits the key features (such as points, edges, or texture information) in the given data, and then a classifier performs the class prediction using these features. In the literature, various well-known feature descriptors and classification algorithms have been proposed in general as well as the medical image analysis domain. In this section, the performance of three known feature descriptors, specifically: local binary pattern (LBP) [51], multilevel LBP (MLBP) [52], and histogram of oriented gradients (HoG) [53] were evaluated in combination with four classifiers: AdaBoostM2 [54], support vector machine (SVM) [55], random forest (RF) [56], and k-nearest neighbor (KNN) [57]. The main objective of this analysis was to evaluate the response of conventional machine learning methods toward the current COVID19 pneumonia. Therefore, the quantitative performance of these three descriptors were evaluated along with each classifier (as mentioned earlier) using the same datasets and experimental protocol. In this way, the performance of twelve handcrafted feature-based methods were obtained, as presented in Table 8. Among these conventional methods, the HoG feature extractor followed by the SVM classifier exhibited the best performances, with AUCs of 94.24% and 96.94% for the CT scan and X-ray datasets, respectively. In the case of the CT-scan dataset, the performance of the MLBP feature descriptor with the AB classifier (in terms of ACC, F1, AP, and AR) is higher than that of HoG + SVM. It can be concluded that both the HoG + SVM and MLBP+ AB methods show promising performances toward COVID19 diagnosis in contrast to other methods. However, the overall performance differences between these (i.e., HoG + SVM and MLBP+ AB) and the proposed method are significantly high, particularly in the case of the CT scan dataset. In conclusion, the proposed network shows promising results compared with conventional machine learning (Table 8) as well as state-of-the-art deep learning (Table 7) methods.
Table 8.
Quantitative performance comparison of proposed network with the conventional handcrafted feature-based methods.
| Method | Dataset 1: CT scan |
Dataset 2: X-ray |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ACC | F1 | AP | AR | AUC | ACC | F1 | AP | AR | AUC | |
| LBP & SVM, | 80.18 | 79.64 | 79.52 | 79.77 | 83.06 | 79.89 | 79.63 | 80.41 | 78.87 | 86.80 |
| LBP & KNN, | 82.71 | 81.97 | 82.60 | 81.37 | 81.37 | 88.76 | 88.62 | 88.62 | 88.63 | 88.63 |
| LBP & RF, | 83.40 | 82.75 | 83.78 | 81.81 | 90.35 | 88.95 | 88.91 | 88.80 | 89.03 | 94.82 |
| LBP & AB, | 85.73 | 85.20 | 86.00 | 84.46 | 89.73 | 88.88 | 88.79 | 88.73 | 88.84 | 94.15 |
| MLBP & SVM, | 83.49 | 83.16 | 82.93 | 83.39 | 88.30 | 86.82 | 86.71 | 87.13 | 86.30 | 92.61 |
| MLBP & KNN, | 84.15 | 83.51 | 83.98 | 83.06 | 83.06 | 90.15 | 90.04 | 90.02 | 90.06 | 90.06 |
| MLBP & RF, | 87.22 | 86.72 | 87.36 | 86.10 | 93.23 | 90.39 | 90.39 | 90.24 | 90.53 | 95.31 |
| MLBP & AB, | 89.05 | 88.65 | 89.23 | 88.09 | 92.01 | 92.26 | 92.25 | 92.09 | 92.42 | 95.60 |
| HoG & SVM, | 88.10 | 87.82 | 88.98 | 86.73 | 94.24 | 94.19 | 94.24 | 94.02 | 94.46 | 96.94 |
| HoG & KNN, | 84.63 | 83.99 | 85.24 | 82.88 | 82.88 | 93.17 | 93.12 | 93.00 | 93.25 | 93.25 |
| HoG & RF, | 87.81 | 87.53 | 89.27 | 85.94 | 92.65 | 92.23 | 92.34 | 92.10 | 92.58 | 96.79 |
| HoG & AB, | 86.82 | 86.68 | 88.88 | 84.73 | 87.57 | 93.92 | 93.99 | 93.75 | 94.22 | 96.25 |
| Proposed | 94.72 | 94.60 | 95.22 | 94.00 | 97.50 | 95.83 | 95.94 | 95.68 | 96.20 | 97.99 |
6. Discussion
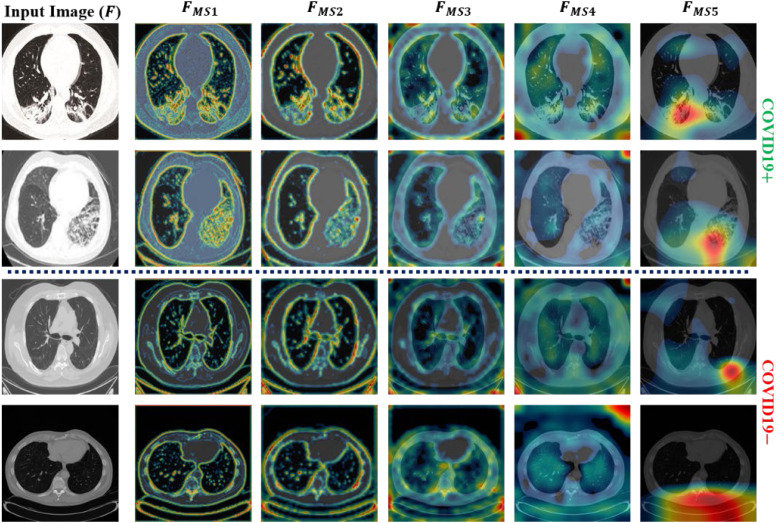
This section highlights the key aspects and the limitations of the proposed method by considering state-of-the-art models. In this study, an efficient deep architecture was initially proposed to identify COVID19 infection from a large-scale radiographic database including both CT-scan and X-ray images. In addition, a hierarchical training procedure was implemented to perform the appropriate training of the proposed network. The experimental results (Table 6) demonstrate the improved performance of the adopted training procedure compared with the end-to-end training method. On average, performance gains (hierarchical training vs. end-to-end) of 1.79%, 1.83%, 1.42%, 2.2%, and 0.94% were obtained in terms of ACC, F1, AP, AR, and AUC, respectively. Additionally, an MLAV layer was introduced to visualize the progression of multilevel features (starting from low-level to high-level features) inside the network as ML-CAMs. These ML-CAMS provide a visual insight into the network decision and may assist radiologists in further validating its subjectivity in case of ambiguous prediction. To visualize such ML-CAMs, a total of five MLAV layers were introduced in different parts of the network (Fig. 2). Ultimately, for each input image, these layers generated a total of five CAM images labeled , , , , and (Fig. 2) with spatial sizes of 112 × 112, 56 × 56, 28 × 28, 14 × 14, and 7 × 7, respectively. Fig. 8, Fig. 9 show the outputs of these MLAV layers as ML-CAMs for the given data samples (including both COVID19 positive and negative cases from each dataset). These additional results (Fig. 8, Fig. 9) can address the following questions that remained unanswerable in most of the previous methods: (1) how does a deep network converge toward a final diagnostic decision (either COVID19+ or COVID19) based on key features (including diseased and normal patterns) in the given data sample? (2) Which areas can be suspected of having COVID19 pneumonia in case of positive prediction? (3) Does the CAD decision comply with that of medical experts? The answers to these questions are essential and lead to the best possible diagnostic decision that can be based on the mutual consent of both computers and medical experts.
Fig. 8.
Additional output of MLAV layers as ML-CAMs for the given CT scan images (including both COVID19 positive and negative data samples).
Fig. 9.
Additional output of MLAV layers as ML-CAMs for the given X-ray images (including both COVID19 positive and negative data samples).
The proposed network is based on an ensemble of three subnetworks, namely MobileNet, ShuffleNet, and FCNet, as shown in Fig. 2. Therefore, a detailed ablation study (Table 5) was also conducted to highlight the impact of each subnetwork in building the overall network architecture. Table 5 shows that the proposed model achieved higher performance than all the subnetworks individually. On average, the performance gains (proposed vs. MobShufNet) were 1.19%, 1.18%, 0.87%, 1.45%, and 0.61% in ACC, F1, AP, AR, and AUC, respectively. Additionally, a comprehensive analysis of various machine learning (Table 8) and deep learning algorithms (Table 7) was also performed to highlight the better performance of the proposed network compared with the existing state-of-the-art methods. For a fair one-to-one comparison, the performance of these existing methods were assessed using same datasets. The number of trainable parameters of the proposed network is about 86% lower than that of the second-best method [21] (i.e., proposed: 3.16M and Tsiknakis et al. [21]: 21.81M). Moreover, the average inference time of the proposed network was about 10.95 ms on a single image, whereas the second-best method [21] takes approximately 23.41 ms. The average inference time was calculated using a stand-alone desktop computer including Intel Core i7 CPU, 16 GB RAM, NVIDIA GeForce graphics processing unit (GPU) (GTX 1070), and Windows 10 operating system. Finally, the proposed model and data splitting information were made publicly available as part of this study, which can be used as a benchmark for future trials.
Although the proposed network shows promising performance, there are a few limitations that may affect the overall performance of the proposed network in a real-world clinical setting. Due to the recent pandemic of COVID19 pneumonia, publicly available datasets are limited and encompass a narrow range of radiological imaging modalities. Therefore, the diversity of these radiological imaging modalities may raise the issues of the generalizability of this network. However, it is a data-driven problem that can be resolved with the availability of more diversified radiographic datasets related to COVID19 pneumonia. Additionally, the ML-CAM output cannot perfectly segment out the infectious regions but only highlight the likelihood of infected areas in each data sample. Nevertheless, these semi-localized activation maps provide initial clues regarding infectious regions and further assist field specialists in making effective diagnostic decisions.
7. Conclusion
This study aimed to provide an AI-based diagnostic solution to distinguish COVID19 pneumonia from other types of community-acquired pneumonia. Therefore, an efficient ensemble network was developed to distinguish COVID19 positive and negative cases from chest radiographic scans, including X-rays and CT scans. In addition, the performances of various existing methods (including a total of 12 handcrafted feature-based and 11 deep-learning-based methods) were analyzed using the same dataset and experimental protocol. The best diagnostic ACCs of 94.72% and 95.83% with AUCs of 97.50% and 97.99% were obtained for the CT scan and X-ray datasets, respectively. The detailed comparative results demonstrate the higher performance of the proposed network over the various state-of-the-art methods. Moreover, the reduced size of the proposed network allows its implementation in smart devices and provides a cost-effective solution, particularly in real-time screening applications. Finally, the source code of the proposed network and other data splitting information (such as training and testing data indices) are publicly available for other researchers.
Future work of this study includes the development of another deep learning solution to localize and quantify infected regions (caused by COVID19) in radiographic scans. Moreover, the number of infected cases will also be increased by exploring more radiographic datasets to further enhance the generality of the proposed network.
CRediT authorship contribution statement
Muhammad Owais: Design methodology, Implementation, Writing of the manuscript. Hyo Sik Yoon: Comparative analysis. Tahir Mahmood: Literature analysis. Adnan Haider: Data preprocessing. Haseeb Sultan: Data collection. Kang Ryoung Park: Reviewing and editing, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
This work was supported in part by the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (MSIT) through the Basic Science Research Program (NRF-2020R1A2C1006179), in part by the MSIT, Korea, under the ITRC (Information Technology Research Center) support program (IITP-2021-2020-0-01789) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation), and in part by the NRF funded by the MSIT through the Basic Science Research Program (NRF-2019R1A2C1083813).
References
- 1.World Health Organization . 2020. WHO director-general’s opening remarks at the media briefing on COVID-19-11 2020. https://www.who.int/dg/speeches/detail. (Accessed 18 October 2020) [Google Scholar]
- 2.World Health Organization . 2020. WHO coronavirus disease (COVID-19) dashboard. https://covid19.who.int/. (Accessed 13 April 2021) [Google Scholar]
- 3.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., et al. Correlation of chest CT and RT-PCR testing for coronavirus disease 2019 (COVID-19) in China: a report of 1014 cases. Radiology. 2020;296 doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of chest CT for COVID-19: comparison to RT-PCR. Radiology. 2020;296 doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ng M.-Y., Lee E.Y., Yang J., Yang F., Li X., Wang H., et al. Imaging profile of the COVID19 infection: radiologic findings and literature review. Radiol. Cardiothorac. Imaging. 2020;2 doi: 10.1148/ryct.2020200034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ghoshal. A. Tucker B. 2020. Estimating uncertainty and interpretability in deep learning for coronavirus (COVID-19) detection. arXiv:2003.10769. https://arxiv.org/abs/2003.10769. [Google Scholar]
- 7.Oh Y., Park S., Ye J.C. Deep learning COVID-19 features on CXR using limited training data sets. IEEE Trans. Med. Imaging. 2020;39:2688–2700. doi: 10.1109/TMI.2020.2993291. [DOI] [PubMed] [Google Scholar]
- 8.Das D., Santosh K.C., Pal U. Truncated inception net: COVID-19 outbreak screening using chest X-rays. Australas. Phys. Eng. Sci. Med. 2020;43:915–925. doi: 10.1007/s13246-020-00888-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Singh D., Kumar V., Kaur M. Classification of COVID-19 patients from chest CT images using multi-objective differential evolution–based convolutional neural networks. Eur. J. Clin. Microbiol. Infect. Dis. 2020;39:1379–1389. doi: 10.1007/s10096-020-03901-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pereira R.M., Bertolini D., Teixeira L.O., Jr C.N.S., Costa Y.M.G. COVID-19 identification in chest X-ray images on flat and hierarchical classification scenarios. Comput. Meth. Programs Biomed. 2020;194 doi: 10.1016/j.cmpb.2020.105532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Khan A.I., Shah J.L., Bhat M.M. CoroNet: a deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Meth. Programs Biomed. 2020;196 doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Asnaoui K.E., Chawki Y. Using X-ray images and deep learning for automated detection of coronavirus disease. J. Biomol. Struct. Dyn. 2020;1:1–22. doi: 10.1080/07391102.2020.1767212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brunese L., Mercaldo F., Reginelli A., Santone A. Explainable deep learning for pulmonary disease and coronavirus COVID-19 detection from X-rays. Comput. Meth. Programs Biomed. 2020;196 doi: 10.1016/j.cmpb.2020.105608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Han Z., Wei B., Hong Y., Li T., Cong J., Zhu X., et al. Accurate screening of COVID-19 using attention based deep 3D multiple instance learning. IEEE Trans. Med. Imaging. 2020;39:2584–2594. doi: 10.1109/TMI.2020.2996256. [DOI] [PubMed] [Google Scholar]
- 15.Mahmud T., Rahman M.A., Fattah S.A. CovXNet: A multi-dilation convolutional neural network for automatic COVID-19 and other pneumonia detection from chest X-ray images with transferable multi-receptive feature optimization. Comput. Biol. Med. 2020;122 doi: 10.1016/j.compbiomed.2020.103869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Minaee S., Kafieh R., Sonka M., Yazdani S., Soufi G.J. Deep-COVID: predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020;65 doi: 10.1016/j.media.2020.101794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khan I.U., Aslam N. A deep-learning-based framework for automated diagnosis of COVID-19 using X-ray images. Information. 2020;11(419) doi: 10.3390/info11090419. [DOI] [Google Scholar]
- 18.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Australas. Phys. Eng. Sci. Med. 2020;43:635–640. doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jaiswal A., Gianchandani N., Singh D., Kumar V., Kaur M. Classification of the COVID-19 infected patients using DenseNet201 based deep transfer learning. J. Biomol. Struct. Dyn. 2020;1:1–8. doi: 10.1080/07391102.2020.1788642. [DOI] [PubMed] [Google Scholar]
- 20.Ardakani A.A., Kanafi A.R., Acharya U.R., Khadem N., Mohammadi A. Application of deep learning technique to manage COVID-19 in routine clinical practice using CT images: Results of 10 convolutional neural networks. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tsiknakis N., Trivizakis E., Vassalou E.E., Papadakis G.Z., Spandidos D.A., Tsatsakis A., et al. Interpretable artificial intelligence framework for COVID-19 screening on chest X-rays. Exp. Ther. Med. 2020;20:727–735. doi: 10.3892/etm.2020.8797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hu R., Ruan G., Xiang S., Huang M., Liang Q., Li J. 2020. Automated diagnosis of COVID-19 using deep learning and data augmentation on chest CT; pp. 1–11. medRxiv. [DOI] [Google Scholar]
- 23.Farooq M., Hafeez A. 2020. COVID-ResNet: a deep learning framework for screening of COVID19 from radiographs. arXiv:2003.14395. https://arxiv.org/abs/2003.14395v1. [Google Scholar]
- 24.Misra S., Jeon S., Lee S., Managuli R., Jang I.-S., Kim C. Multi-channel transfer learning of chest X-ray images for screening of COVID-19. Electronics. 2020;9(1388) doi: 10.3390/electronics9091388. [DOI] [Google Scholar]
- 25.Martínez F., Martínez F., Jacinto E. Performance evaluation of the NASNet convolutional network in the automatic identification of COVID-19. Int. J. Adv. Sci. Eng. Inf. Technol. 2020;10:662–667. https://core.ac.uk/download/pdf/325990317.pdf. [Google Scholar]
- 26.Nour M., Cömert Z., Polat K. A Novel medical diagnosis model for COVID-19 infection detection based on deep features and bayesian optimization. Appl. Soft. Comput. 2020 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hernandez-Matamoros A., Fujita H., Hayashi T., Perez-Meana H. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl. Soft. Comput. 2020;96 doi: 10.1016/j.asoc.2020.106610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.2020. Dongguk CAD model for effective diagnosis of COVID19 pneumonia. Available online: http://dm.dgu.edu/link.html. (Accessed 18 October 2020) [Google Scholar]
- 29.He K., Zhang X., Ren S., Sun J. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016. Deep residual learning for image recognition; pp. 770–778. [DOI] [Google Scholar]
- 30.Szegedy C., Vanhoucke V., Ioffe S., Shlens J., Wojna Z. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016. Rethinking the inception architecture for computer vision; pp. 2818–2826. [DOI] [Google Scholar]
- 31.Chollet F. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017. Xception: deep learning with depthwise separable convolutions; pp. 1251–1258. [DOI] [Google Scholar]
- 32.Szegedy C., Ioffe S., Vanhoucke V., Alemi A. 2016. Inception-v4, inception-resnet and the impact of residual connections on learning. arXiv:1602.07261. https://arxiv.org/abs/1602.07261. [Google Scholar]
- 33.Simonyan K., Zisserman A. 2014. Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556. https://arxiv.org/abs/1409.1556. [Google Scholar]
- 34.Sandler M., Howard A., Zhu M., Zhmoginov A., Chen L.-C. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2018. Mobilenetv2: inverted residuals and linear bottlenecks; pp. 4510–4520. [DOI] [Google Scholar]
- 35.Zhang X., Zhou X., Lin M., Sun J. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2018. ShuffleNet: an extremely efficient convolutional neural network for mobile devices; pp. 6848–6856. [DOI] [Google Scholar]
- 36.Howard A.G., Zhu M., Chen B., Kalenichenko D., Wang W., Weyand T., et al. 2017. MobileNets: efficient convolutional neural networks for mobile vision applications. arXiv:1704.04861. https://arxiv.org/abs/1704.04861. [Google Scholar]
- 37.Heaton J. 2015. Artificial Intelligence for Humans, Vol 3: Neural Networks and Deep Learning. [Google Scholar]
- 38.Li X.-L. Preconditioned stochastic gradient descent. IEEE Trans. Neural Netw. Learn. Syst. 2018;29:1454–1466. doi: 10.1109/TNNLS.2017.2672978. [DOI] [PubMed] [Google Scholar]
- 39.Gupta A., Gupta S., Katarya R. InstaCovNet-19: A deep learning classification model for the detection of COVID-19 patients using chest X-ray. Appl. Soft. Comput. 2020;90 doi: 10.1016/j.asoc.2020.106859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Owais M., Arsalan M., Mahmood T., Kim Y.H., Park K.R. Comprehensive computer-aided decision support framework to diagnose tuberculosis from chest X-ray images: data mining study. JMIR Med. Inf. 2020;8 doi: 10.2196/21790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Ezzat D., Hassanien A.E., Ella H.A. An optimized deep learning architecture for the diagnosis of COVID-19 disease based on gravitational search optimization. Appl. Soft. Comput. 2020;98 doi: 10.1016/j.asoc.2020.106742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pan F., Ye T., Sun P., Gui S., Liang B., Li L., et al. Time course of lung changes on chest CT during recovery from 2019 novel coronavirus (COVID-19) pneumonia. Radiology. 2020;295 doi: 10.1148/radiol.2020200370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wong H.Y.F., Lam H.Y.S., Fong A.H.-T., Leung S.T., Chin T.W.-Y., Lo C.S.Y., et al. Frequency and distribution of chest radiographic findings in COVID-19 positive patients. Radiology. 2020;296 doi: 10.1148/radiol.2020201160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.de la I. Vayá M., Saborit J.M., Montell J.A., Pertusa A., Bustos A., Cazorla M., et al. 2020. BIMCV COVID-19+: a large annotated dataset of RX and CT images from COVID-19 patients. arXiv:2006.01174, v3. https://arxiv.org/abs/2006.01174v3. [Google Scholar]
- 45.Yang X., He X., Zhao J., Zhang Y., Zhang S., Xie P. 2020. COVID-CT-dataset: a CT-scan dataset about COVID-19. arXiv:2003.13865, v3. https://arxiv.org/abs/2003.13865. [Google Scholar]
- 46.Clark K., Vendt B., Smith K., Freymann J., Kirby J., Koppel P., et al. The cancer imaging archive (TCIA): maintaining and operating a public information repository. J. Digit. Imaging. 2013;26:1045–1057. doi: 10.1007/s10278-013-9622-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Candemir S., Jaeger S., Palaniappan K., Musco J.P., Singh R.K., et al. Lung segmentation in chest radiographs using anatomical atlases with nonrigid registration. IEEE Trans. Med. Imaging. 2014;33:577–590. doi: 10.1109/TMI.2013.2290491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cohen J.P., Morrison P., Dao L., Roth K., Duong T.Q., Ghassemi M. 2020. arXiv:2006.11988, v1. https://arxiv.org/abs/2006.11988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.2019. Deep learning toolbox. https://in.mathworks.com/products/deeplearning.html. (Accessed 15 May 2020) [Google Scholar]
- 50.Hossin M., Sulaiman M.N. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process. 2015;5:1–11. doi: 10.5121/ijdkp.2015.5201. [DOI] [Google Scholar]
- 51.Subrahmanyam M., Maheshwari R.P., Balasubramanian R. Local maximum edge binary patterns: A new descriptor for image retrieval and object tracking. Signal Process. 2012;92:1467–1479. doi: 10.1016/j.sigpro.2011.12.005. [DOI] [Google Scholar]
- 52.Nguyen D.T., Pham T.D., Baek N.R., Park K.R. Combining deep and handcrafted image features for presentation attack detection in face recognition systems using visible-light camera sensors. Sensors. 2018;18(699) doi: 10.3390/s18030699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Velmurugan K., Baboo S.S. Image retrieval using Harris corners and histogram of oriented gradients. Int. J. Comput. Appl. 2011;24:6–10. doi: 10.5120/2968-3968. [DOI] [Google Scholar]
- 54.Freund Y., Schapire R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. System Sci. 1997;55:119–139. doi: 10.1006/jcss.1997.1504. [DOI] [Google Scholar]
- 55.Hsu C.-W., Lin C.-J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural. Netw. 2002;13:415–425. doi: 10.1109/72.991427. [DOI] [PubMed] [Google Scholar]
- 56.Breiman L. Random forests. Mach. Learn. 2001;45:5–32. https://link.springer.com/content/pdf/10.1023/A:1010933404324.pdf. [Google Scholar]
- 57.Cover T.M., Hart P.E. Nearest neighbor pattern classification. IEEE Trans. Inform. Theory. 1967;13:21–27. doi: 10.1109/TIT.1967.1053964. [DOI] [Google Scholar]