Abstract
X-ray-induced acoustic computed tomography (XACT) is a promising imaging modality to monitor the position of the radiation beam and the deposited dose during external beam radiotherapy delivery. The purpose of this study was to investigate the feasibility of using a transperineal ultrasound transducer array for XACT imaging to guide the prostate radiotherapy. A customized two-dimensional (2D) matrix ultrasound transducer array with 10000 (100×100 elements) ultrasonic sensors with a central frequency of 1 MHz was designed on a 5 cm×5 cm plane to optimize three-dimensional (3D) volumetric imaging. The CT scan and dose treatment plan for a prostate patient undergoing intensity modulated radiation therapy (IMRT) were obtained. In-house simulation was developed to model the time varying X-ray induced acoustic (XA) signals detected by the transperineal ultrasound array. A 3D filtered back projection (FBP) algorithm has been used for 3D XACT image reconstruction. Results of this study will greatly enhance the potential of XACT imaging for real time in vivo dosimetry during radiotherapy.
Index Terms: X-ray-induced Acoustic Computed Tomography (XACT), 2D matrix ultrasound array, 3D volumetric imaging, transperineal ultrasound, in vivo dosimetry, prostate radiotherapy
I. Introduction
External beam radiotherapy (EBRT) is one of the standard options in treating prostate cancer [1, 2]. EBRT for the prostate must be carefully planned and delivered to provide the required dose to the target organ while sparing the radio-sensitive bladder and rectal structures. During EBRT treatment, dosimetric differences between planned and delivered doses can cause treatment failure [3, 4]. However, in such a widely used intervention in the clinic, the delivered radiation dose can only be planned and/or verified via simulation with phantoms, and an in vivo and in-line verification of delivered dose is still unavailable in the clinic setting.
Modern EBRT for prostate cancer involves the delivery of high doses using highly conformal delivery techniques [4]. Delivering an increased prostate dose has been shown to improve treatment outcomes [3, 5]. Additionally, hypofractionation has been shown to be an attractive delivery method due to a low alpha/beta ratio for the prostate [6, 7]. Increasing the total treatment dose or the dose per fraction requires ever more accurate delivery verification in vivo during EBRT. However, both interfractional and intrafractional motion of prostate caused by the accumulation of colorectal gas, a full bladder, or patient movement can result in dose deviations from the treatment plan. in vivo verification of the delivered dose is important to reduce the failure of dose delivery, thus preventing potentially negative consequences.
Relatively few technologies have been previously employed for in vivo dosimetry [8–11]. Thermoluminescent dosimeters (TLDs) have been used because of their small size and tissue equivalence [12]. However, TLDs can provide only a cumulative dose and require a complicated readout process with expensive specialized equipment [13]. As a result, the delivered dose is not known instantaneously, but rather with some delay after the treatment. Metal oxide semiconductor field effect transistors (MOSFETs) have also been used for internal in vivo dosimetry [14]. They are capable of real-time measurement and are very small, providing excellent spatial resolution and perturbing the beam minimally. Unfortunately, MOSFETS have short lifespans and must be replaced relatively often. Furthermore, they require a number of corrections, are expensive, and possess poorer intrinsic precision than other detectors. The plastic scintillation detector (PSD) is a good candidate for in vivo measurements. PSDs are capable of providing real-time data because they have a response time on the order of nanoseconds [13]. However, the PSDs detectors may still have minimal dose perturbation because the catchers are typically placed within the radiation beam path. Recently, Cherenkov emission was found to be useful for in vivo radiation dose mapping, but only suitable for surface dosimetry [15, 16]. Therefore, there is a great need for the development of high-resolution 3D in vivo dosimetry techniques for real time monitoring of the in-patient radiation dose during prostate external radiotherapy.
X-ray acoustic computed tomography (XACT) is an emerging imaging modality that forms images by detecting the X-ray radiation induced ultrasound. XACT has been proposed as an in vivo dosimetry tool for radiation therapy since 2013, and has been investigated by several different groups [17–20]. Comprehensive computer simulation work Monte Carlo (MC) dose calculations and acoustic wave transport techniques have been developed to guide experimental investigations and have been validated experimentally using simple geometries with metal block measurements [21]. Later studies investigated using XACT to image dose distributions of various shapes and sizes in a homogeneous water tank [22]. Experimental XACT images have been obtained by keeping an immersion transducer stationary while a linear accelerator (LINAC) collimator was rotated. These studies experiments demonstrated the ability of XACT to image a puzzle piece shaped field and the agreement between profiles extracted from experimental and simulated XACT images and ion chamber measurements. A subsequent XACT characterization study demonstrated that XACT images of acceptable SNR can be formed at a dose level as low as 11.6 mGy, and that changes in field size of 4 mm, field location of 2 mm, and field magnitude of 3% are detectable with the above implementation of XACT. Recently, XACT with biological tissue phantoms as a sample has been demonstrated by Lei et al. on veal liver [23]. In their study, the authors employed conventional ultrasound imaging combined with XACT imaging to overlay the two images and image tissue and radiation beam simultaneously. The beam intensity inside fat tissue was clearly visible, and beam alignment could be monitored in addition to dose distribution, representing the first XACT deployment in a biological sample. These latest studies demonstrated the feasibility of using XACT as a viable dosimetry technique in a clinical radiotherapy environment. However, it currently takes more than 30 minutes to get a 2D image with the current XACT imaging system, and configuration of the current imaging system makes real time mapping of the dose in 3D during radiation therapy impossible.
In this paper, we developed a simulation workflow to assess the ability of XACT to act as an in vivo dosimetry tool for prostate radiotherapy. First, the radiation dose distribution in a 3D digital prosate phantom was converted to an initial pressure distribution. The 3D propagation of the acoustic waves was then modelled using a pseudospectral method. Finally, the time-varying pressure signals detected at each transducer location are then used to reconstruct an image of the initial pressure distribution with 3D filtered back projection (FBP) image reconstruction algorithm, which is related back to dose. Finally, the reconstructed XACT images of the radiation beams were overlaid onto a prostate CT. We expect XACT imaging can used to 1) localize the radiation beam and 2) estimate the in-line verify radiation dose in real time during prostate radiotherapy.
II. Principles
A. X-ray induced acoustic signal generation and detection
In XACT, the rising of the temperature due to an arbitrary excitation source exciting an absorbing target leads to the generation and propagation of the X-ray induced acoustic (XA) signal. The following wave equation will model this process [24]:
| (1) |
where vs is the speed of sound, p(r, t) is the acoustic pressure rise at location r and time t, β denotes the thermal coefficient of volume expansion, T(r, t) denotes the change in temperature, and κ denotes the isothermal compressibility.
The relationship between the temperature rise T(r, t) and the heating function H(r, t) as follows [25]:
| (2) |
where ρ is the mass density of the material, Cv is the specific heat capacity at constant volume, λ is the thermal conductivity. H(r, t) is defined as the heat absorbed per unit volume and per unit time. In thermal confinement, the term λ∇2T(r, t) can be neglected, thus, the wave equation can be rewritten as:
| (3) |
where, is the specific heat capacity at a constant pressure. The left-hand side of Eq. (3) represents the wave propagation term in tissue, whereas the right-hand side shows the source. H(r, t) is related to the specific power deposition Ap [26]:
| (4) |
where ηth is the percentage of absorbed electrical energy converted into thermal energy. Substituting Eq. (4) into Eq. (3), we can obtain the following wave equation:
| (5) |
The XA pressure at the transducer position r and time t can be calculated using the Green’s function approach by the following equation:
| (6) |
where Г is the Grüneisen parameter defined as:
| (7) |
where KT=1/k is the isothermal bulk modulus. In order to satisfy stress confinement, we select a transducer with frequency acoustic detection range. Hence, of a single X-ray pulse can be considered as a Dirac delta function and XA signal can be obtained as follows:
| (8) |
which can be also described as:
| (9) |
where p0(r′) is the initial X-ray induced acoustic pressure rise.
The Eq. (9) shows that the process of the generation and propagation of XA pressure p at location r∈R3 and time t. The acoustic waves induced by the X-ray beams will be detected by a customized transperineal 2D ultrasound transducer array. Once the XA pressure was obtained by each element of the 2D transducer array, a 3D filtered back-projection (FBP) algorithm was used to reconstruct the XA image.
B. Relationship between initial pressure and radiation dose
In XACT, the amplitude of acoustic emission generated by a single X-ray pulse is proportional to the specific X-ray power deposition in tissue when both thermal confinement and stress confinement are satisfied [24]. In this situation, the relationship between initial pressure p0(r) induced by X-ray excitation in the target and the X-ray energy deposition Ap(r) can be obtained from Eq. (8) and Eq. (9):
| (10) |
Note that we use the standard SI-units Pa for initial acoustic pressure, J/m3 for the X-ray energy deposition.
In the process of the target absorbing X-ray energy, the generation of initial XA pressure is an inevitable result of the transformation from dose deposition. Dose and pressure are quantified in Grays and Pascals according to the standard SI-units. Meanwhile, 1Gy and 1Pa can be described as 1Gy =1J/kg and 1Pa=1N/m2 =1 J/m3, respectively [27]. If we assume the X-ray pulse is applied for a short time, the initial acoustic pressure in the target is related to the delivered dose by:
| (11) |
Where D(r) is the dose deposited. The standard SI-units kg/m3 is used for the mass density. The thermal diffusion can be neglected due to the dose deposited instantaneously, thus, the Eq. (11) can be rewritten as [24, 28]:
| (12) |
Therefore, generated the initial acoustic pressure p0(r) inside the target, which can be derived from Eq. (12), is proportional to the dose delivered D(r). The correlation between the initial pressure p0(r) and the local dose absorbed D(r) will reveal 1) the beam location in real time, and 2) the relative dose distribution during the radiation therapy.
III. Methods
The proposed technique can be used for in vivo dosimetry for prostate radiotherapy with XACT using a LINAC system and a transperineal 2D matrix ultrasound transducer array which has been widely used in monitoring prostate motion during radiotherapy. Fig. 1 shows the patient set-up and transperineal ultrasound array configuration. Fig. 1A illustrates a 3D model of XACT technology used for a patient with prostate cancer who is treated with radiation therapy. The machine on top of the patient is the Varian VitalBeam® LINAC. The red cylinder with the white cylinder inside represents the X-ray beam. The light blue arc lines represent the pressure waves induced. The pink irregular shape represents prostate while blue ellipse confined to the prostate signify tumor. A customized 2D matrix ultrasound transducer array, placed just below the prostate and closed to the skin, was used to detect the generated XA signal. Fig. 1B–D shows the dose distribution for a prostate cancer patient overlaid with a planning CT in the coronal, axial, and sagittal planes, respectively. Where the yellow line represents the prostate. The colors correlate with dose magnitude, red representing the highest dose to blue representing the lowest dose.
Fig.1.
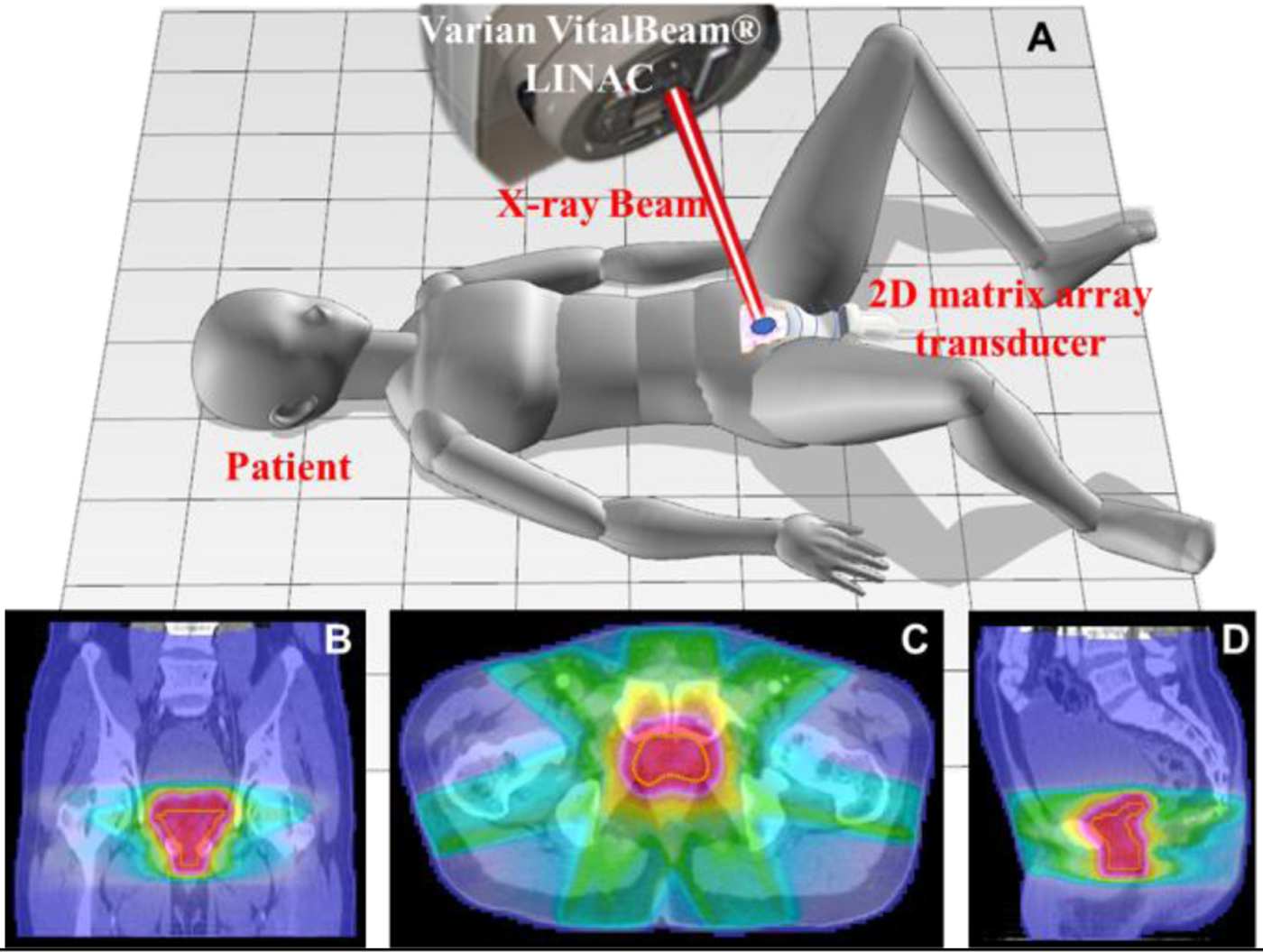
Schematic diagrams of a prostate cancer patient set-up and transperineal ultrasound array configuration. Fig. 1A shows a three-dimensional (3D) model of X-ray acoustic computed tomography (XACT) technology used for a patient with prostate cancer who is treated with radiation therapy. The light blue arc lines represent the pressure waves induced. The pink irregular shape represents prostate while blue ellipse confined to the prostate signify tumor. Fig. 1B-D show dose distribution for the patient covering a planning CT in coronal plane, axial plane and sagittal plane, respectively. Where yellow line represent prostate. The colors represent the magnitude of the dose, from red being the highest dose to blue being the lowest dose.
In this study, both theoretical calculation and numerical simulation have been performed to assess the ability of XACT to act as an in vivo dosimetry tool for prostate radiotherapy. The entire process of XACT imaging was simulated by the commercial software MATLAB R2018a (Mathworks, Natick, Massachusetts) and the K-wave simulation Toolbox for MATLAB [29–31]. Fig. 2 shows the workflow of the XACT imaging for real time radiation therapy guidance for prostate cancer. Fig. 2A shows the process of the radiation dose distribution acquisition.
Fig. 2.
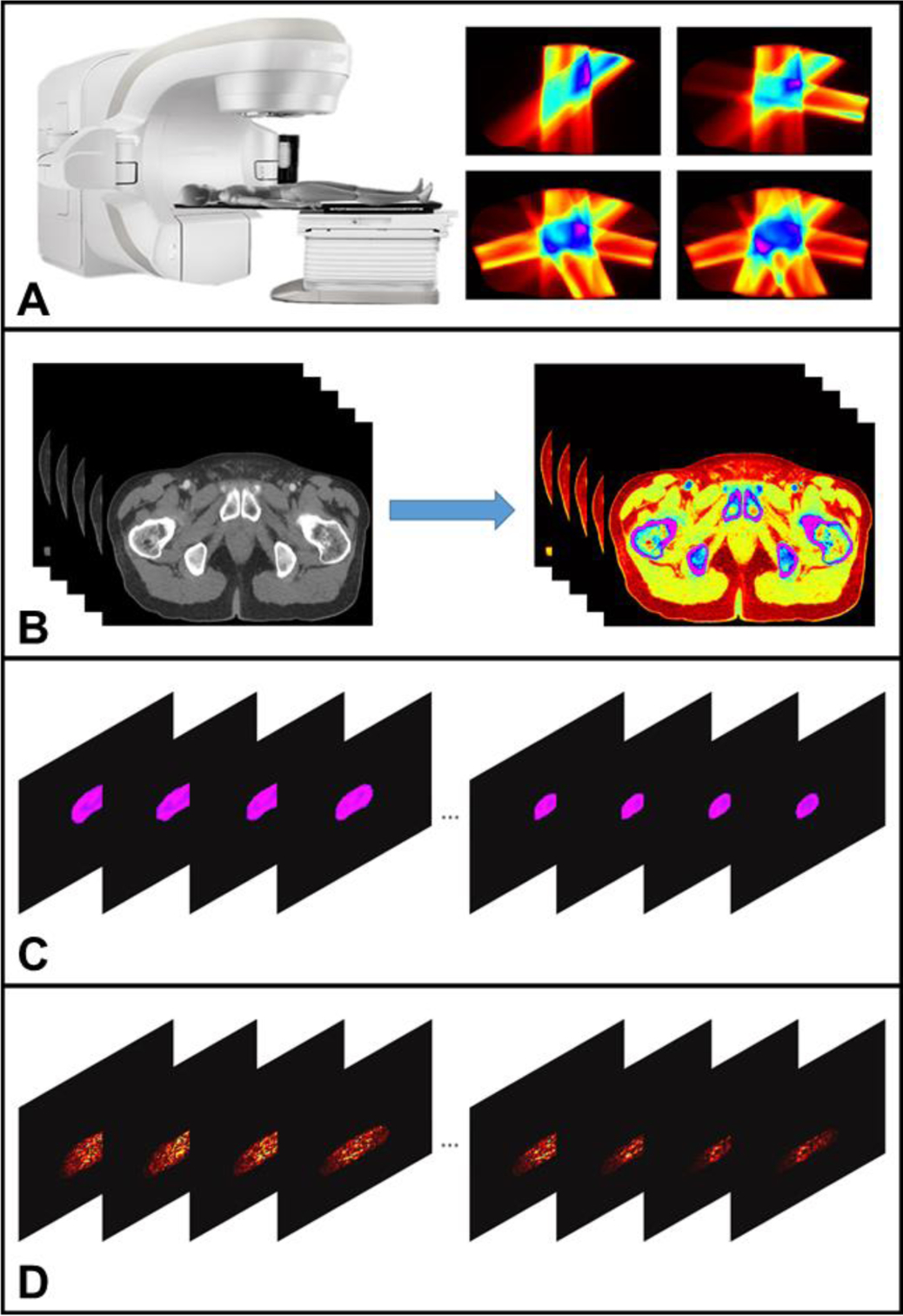
The workflow of the XACT imaging for real time radiation therapy guidance for prostate cancer. Fig. 2A shows the process of the radiation dose distribution acquisition. Fig. 2B represents different tissues segmentation according to their tissue properties. Fig. 2C illustrates initial acoustic signal generation which can be obtained by combining Fig. 2A and Fig. 2B. The process from Fig. 2C to Fig. 2D represents 3D XACT reconstruction.
Fig. 2B shows example slices during segmentation of the planning CT based on tissue properties. Fig. 2C illustrates example slices showing the initial acoustic signal generation in the prostate, which can be obtained by combining Fig. 2A and Fig. 2B. The sample slices showing 3D XACT reconstruction can be shown from Fig. 2C to Fig. 2D. The detailed process of XACT imaging simulations for guiding prostate radiotherapy will be discussed below.
A. Treatment planning for prostate radiotherapy
The treatment planning CT scans with the associated dose maps from a patient were imported. This patient was treated with intensity-modulated radiotherapy (IMRT) with therapeutic radiation doses for prostate cancer in October 2017. Dose distribution were generated by making treatment planning using heterogeneity correction algorithms with Eclipse (Varian Medical System, Palo Alto, CA, USA) software for photon radiation therapy (RT). For the patient, the IMRT planning was created with seven non-uniformly distributed coplanar fields to deliver all prescribed doses to the prostate. The dose maps that were obtained from the treatment planning are shown in Fig. 1B–D. The detailed parameter values were listed for all beams in prostate treatment plan as shown in Table I. The angles of the beams are 0 degree, 51 degrees, 102 degrees, 153 degrees, 204 degrees, 255 degrees and 306 degrees from beam1 to beam7. The photon energy for every beam is 6 MV. The distance between the source and the isocenter is 1m. The prescribed dose per faction is 2Gy. The monitor units per faction for beam1 to beam7 are 167MU, 156MU, 138MU, 135MU, 187MU, 149MU and 127MU, respectively. The absorbed dose to the prostate was 64Gy in 32 factions. The treatment planning was optimized in that at least 99% of the clinical target volumes, the prescribed dose was delivered. Also, less than 1% of volumes had 110% of the prescribed dose.
TABLE I.
Parameters for Seven Beams in Prostate Treatment Planning
| Quantity | Parameter values | ||||||
|---|---|---|---|---|---|---|---|
| Beam | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Angle (degrees) | 0 | 51 | 102 | 153 | 204 | 255 | 306 |
| Beam Energy (MV) Source | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| Distance (mm) Prescribed | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 |
| Dose Per Tx (Gy) Monitor Units | Rx | Rx | Rx | Rx | Rx | Rx | Rx |
| Per Tx (MU) | 167 | 156 | 138 | 135 | 187 | 149 | 127 |
Prescribed Dose Per Tx (Gy) represents the prescribed dose per faction (Gy); Monitor Units Per Tx (MU) represents the monitor units per faction (MU); Rx represents the values of prescribed dose per faction (Gy) which is 0.28571.
B. Different tissues segmentation
1). Segmenting different tissues
The different tissues are segmented after conversion into HU values. The planning CT is a 512×512×87 rank 3 tensor in the left-right (LR), anterior-posterior (AP) and cranio-caudal (CC) orientations. We crop the volume of the CT into a 236×355×87 space in the AP, LR and CC directions to minimize air around the CT volume in order to optimize simulation time. The planning CT was divided into four tissue types with air, fat, muscle or organ, and bone according to their different HU values based on a threshold segmentation algorithm [27]. The representative parameter values for different tissue are listed in Table II. Fig. 3A shows an RGB image of the planning CT slice in axial plane with HU values. Fig. 3B–3D display the speed of sound, the mass density and the Grüneisen parameter for different tissue type calculated by Fig. 3A and detailed in Table II. Different tissue types are indicated in Fig. 3B. We limit the range of Fig. 3A and Fig. 3B in order to make the maps look clear. The colors in Fig. 3A–3D represent the magnitude of different parameters with magenta being the strongest and black being the weakest. And the all CT images in the Fig. 3 are based on the same slice.
TABLE II.
CT Values and Corresponding Parameters for Different Tissues
| Tissue | CT values (HU) | υ (m/s) | ρ (kg/m3) | Γ | ρΓ (kg/m3) |
|---|---|---|---|---|---|
| Air | (−∞, −200 | 343 | 1.2 | 0.376 | 0.45 |
| Fat | (−200, −50) | 1480 | 920 | 0.877 | 806.84 |
| Muscle, | (−50, 100) | 1540 | 1040 | 0.208 | 216.32 |
| Bone | (100, +∞) | 3200 | 2000 | 0.788 | 1576 |
υ represents the speed of sound; Γ represents the Grüneisen parameter;
ρ represents the tissue density; ρΓ represents the dose coefficient.
Fig. 3.
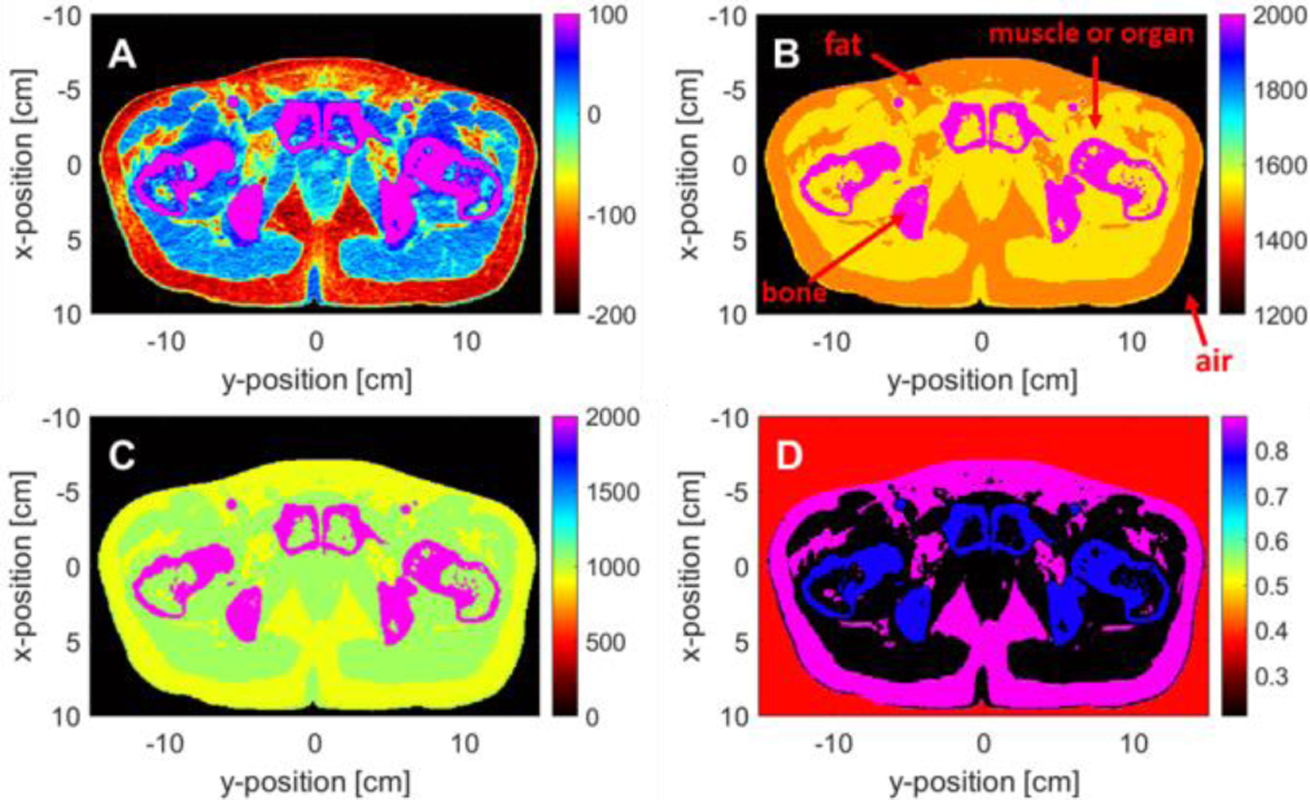
Simulation parameters of the planning CT of a prostate cancer patient. Fig. 3A shows an RGB image of the planning CT slice in axial plane with HU values. Fig. 3B-3D display the speed of sound, the mass density and the Grüneisen parameter for different tissue type. Different tissue types are indicated in the Fig. 3B. The colors in Fig. 3A-3D represent the magnitude of different parameters with magenta being the strongest and black being the weakest.
C. Initial X-ray acoustic pressure generation
Based on the relationship between radiation dose distribution and initial XA pressure derived in section II, the dose distribution was converted into the initial XA pressure as p0(r) = ρГ D(r) according to equation (12). The dose coefficient ρГ of different tissue was calculated by representative values for the thermal coefficient of volume expansion, the isothermal compressibility and the specific heat capacity based on different tissue property. The detailed parameter values for ρГ are shown in Table II. The matrix size and relative position between dose coefficient and dose distribution are set to be the same as the matrix size and relative position between the planning CT slice and the dose distribution in order to have a precise initial XA pressure. Fig. 4 display the simulation process of converting the radiation dose distribution into the initial XA pressure. Fig. 4A shows the dose distribution in axial plane, where the part of magenta represents dose distribution delivered to prostate. The dose coefficient map for different tissue is shown in Fig. 4B. Fig. 4C illustrates the initial XA pressure distribution relative to Fig. 4A and 4B. The colors represent the magnitude of dose distribution, dose coefficient and corresponding to the initial pressure, from magenta being the largest intensity to black being the lowest intensity.
Fig. 4.

The process of converting the radiation dose distribution into the initial XA pressure. Fig. 4A shows the dose distribution in axial plane, where the magenta represents dose distribution delivered to prostate. The dose coefficient map for different tissue is shown in Fig. 4B. Fig. 4C illustrates the initial XA pressure distribution relative to Fig. 4A and 4B. The colors represent the magnitude of dose distribution, dose coefficient and corresponding to the initial pressure, from magenta being the largest intensity to black being the lowest intensity.
D. K-wave acoustic signal simulation
The initial XA pressure distribution used as the input was imported into the K-wave acoustic toolbox for MATLAB which was used to model XA propagation signal in 3D. The matrix size of initial pressure for prostate is 40×80×60 with a pixel spacing of 0.5×0.5×0.5mm3 in the AP, LR and CC directions, respectively. A planar ultrasound transducer array with 10000 (100×100 elements) ultrasonic sensors with a central frequency of 1 MHz with 100% bandwidth, and a sampling rate of 10 MHz was designed to be distributed on a 5 cm×5 cm plane. The distance between the prostate and the ultrasound transducer was set to be 4 cm in the vertical direction. A 10 voxel perfectly matched layer (PML) was used in the simulation. The size of the grid points was set to be 120×140×180 including the PML in the x, y and z direction. This size was chosen in order to both include the initial pressure distribution and the ultrasound transducer and minimize computational requirements. Thermal noise was also added to the detected XA signal. The design of the 3D digital model for initial pressure generated on the prostate and the 2D matrix array transducer is shown in Fig. 5C. The 2D matrix plane represents the ultrasound transducer while the 3D irregular shape below the transducer is the initial pressure distribution.
Fig. 5.
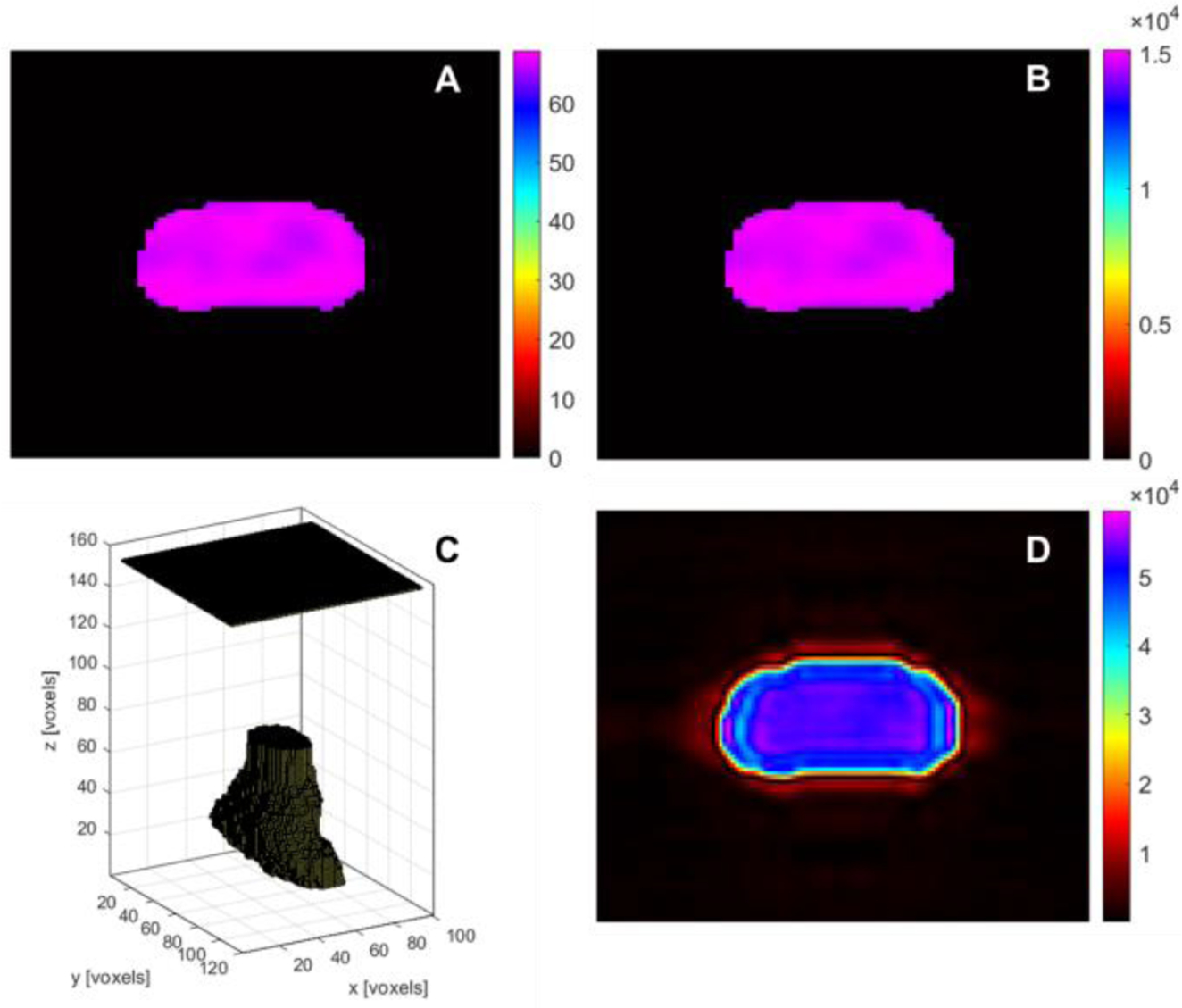
A simulated example of XACT reconstruction as a tool for imaging in-plane profiles. Fig. 5A shows prostate dose distribution acquired from seven beams using thresholding segmentation method according to the prescription doses delivered to prostate. Fig. 5B is the initial XA pressure distribution of the prostate. Fig. 5C displays the 3D digital model for initial pressure generated on the prostate and the 2D matrix array transducer. The 2D matrix plane represents the ultrasound transducer while the 3D irregular shape below the transducer is initial pressure distribution Fig. 5D shows the reconstructed XA. The fuzzy edges of reconstructed pressure distribution were observed in the XACT image due to the limitation of ultrasonic detection bandwidth.
In XACT, the thermal noise from ultrasound detector is one of the main noise contributors [32]. Thermal noise can be expressed by the noise equivalent pressure (NEP) as follows [33]:
| (14) |
where kB is the Boltzmann constant (1.38 × 10−23J/K), and T is the room temperature of the medium with 300K. Fn represents the noise factor of the amplifier and has a typical value of 2 over its bandwidth. η(f) denotes the on-resonant efficiency related to the center frequency fc and the detection bandwidth Δf of the acoustic transducer, which has a typical value of 0.5(−3dB). Za is the characteristic acoustic impedance of the medium with 1.5 × 106 Rays. A is the surface area of the detector (0.25mm2), BW =fc × 100% (Hz). The customized ultrasonic detector has [34]. Thus, the NEP used in the simulation was estimated as ~352mPa, which is theoretically the minimum detectable pressure signal amplitude.
E. 3D XACT image reconstruction
A 3D FBP image reconstruction algorithm was performed to reconstruct an XACT image for the model in our study [35,36]. And the reconstruction scripts were written in MATLAB environment. For different absorber points in the prostate, generated XA pressure signals on the same sphere can be simultaneously detected by the corresponding acoustic transducer element. After that the absorber points on the sphere of different depths can be resolved by calculating of the time of arrival of XA signals gathered by each element of the acoustic transducer. The reconstructed XA pixel intensity can be calculated by the following equation [37]:
| (15) |
| (16) |
where represents the specific location of different XA source. K is the total number of detectors used to gather the XA signal, while k is No. k detector in the 2D ultrasound transducer array. is the sensor data representing signal intensity stored in the kth detector at source position . represents the XA signal travel time from to . is the distance between the X-ray absorption source point at position and the kth detector. υ denotes the average speed at which sound travels in the different biological tissues. Since the ultrasound transducer has limited reception bandwidth, its impulse response h(t) is included in the Eq. (15). The ang represents the angle between and axis z, while θ denotes the direction angle of each detector of the 2D ultrasound transducer array. The direction angle of each transducer element is set to be 60° in our simulation. The transducer element is considered to be active when the angle of and axis z is not more than the half direction angle of the detector as shown in Eq. (16).
IV. Results
A. XACT as a tool for imaging in-plane profiles
In order to investigate the capability of XACT as a tool for imaging in-plane profiles, the simulation was performed to reconstruct one slice of axial plane for prostate dose. Fig. 5 shows a simulated example of reconstruction for imaging in axial plane. First, acquired prostate dose distribution from seven beams using a thresholding segmentation method according to the doses shown in Fig. 5A. Then, the initial XA pressure was imported into the K-wave acoustic toolbox for simulation. Fig. 5B shows the initial XA pressure distribution. The amplitude of initial XA pressure rise generated from prostate is ρГ times of that dose distribution from prostate on the same slice. The generated initial XA pressure waves then transmit in all directions. The time-dependent XA signals can be collected in the range of direction angle of the acoustic transducer element as shown in Fig. 5C and then used to reconstruct the pressure for prostate using a 3D XACT reconstruction technology based on 3D FBP algorithm. As a sample for XACT imaging, the reconstructed XA pressure is illustrated in Fig. 5D. As expected, the pressure distribution of the prostate is distinguishable in the reconstructed XACT image. In addition, to quantitatively evaluate the agreement of the reconstructed and initial pressure distributions, we used a unitless and intuitive measurement called the normalized root mean square error (NRMSE) [37]. The NRMSE is defined as:
| (17) |
where N is the number of pixels within the prostate for the pressure distribution, Xf,n is the nth pixel within the prostate for the reconstructed pressure distribution, and Xi,n is the nth pixel within the prostate for the initial pressure distribution. Xf,max and Xf,min are the maximum and minimum pixel values within the prostate for the reconstructed pressure distribution. We calculated the NRMSE within the prostate for the different number of radiation beams during treatment. The NRMSE values between the initial and XACT reconstructed pressure distributions for one beam, four beams and seven beams structures are 3.21%, 3.10% and 4%, respectively. Compared to the previous XACT reconstruction simulated by Hickling in 2014, our pressure distributions are even less different [39]. The NRMSE value for the same pixels calculated in her simulation was 4.1%, while none of our calculation values were higher than 4%. Therefore, we believe XACT imaging could allow for the verification of radiation dose is being delivered to the prostate in the patient with the simulated results. However, fuzzy edges of reconstructed pressure distribution were observed in the XACT image due to bandwidth limitations.
B. XACT for visualizing the 3D dose distribution in prostate
Fig. 6 shows the 3D initial pressure and reconstructed dose. Fig. 6A shows sample slices (left) of the initial pressure and the reconstruction (roght). Fig. 6B is the 3D visualization of the initial pressure (left) and the reconstructed dose (right) shown using the V3D (version v2.031) software package. The z axis is the axial direction to the transducer array, and the prostate is contained from points 41 to 70. As can be noted in Fig. 6, the 3D XACT reconstruction for dose distribution in prostate is discernible. However, some “invisible” parts of the object boundaries which are outside the “detection region” with sufficient detection views were blurred away due to the limited-view problem [38], which lead to a poor reconstruction of the dose distribution in the middle of the prostate as shown in the right column in Fig. 6B.
Fig. 6.
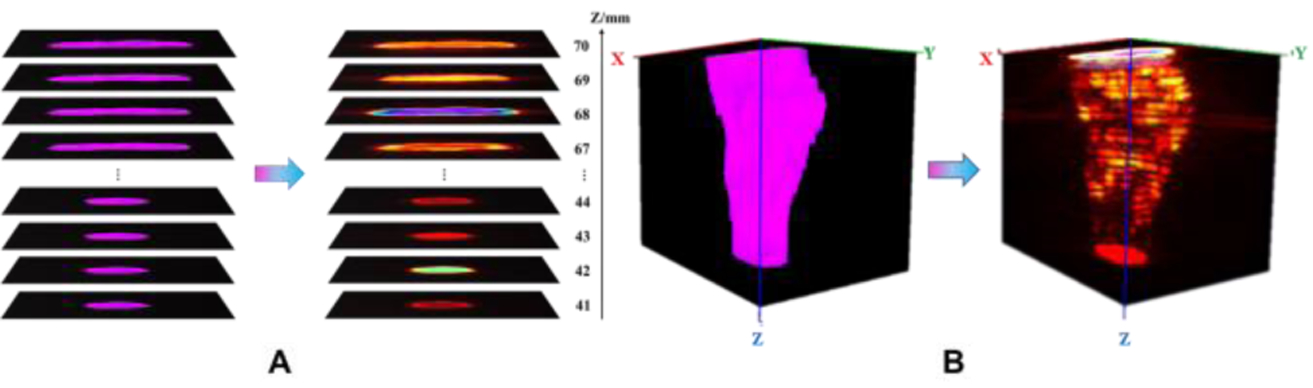
The numerical simulation of the 3D XACT imaging reconstruction process of dose distribution in the whole prostate. Fig. 6A shows samples slices from the initial pressure mapped to the reconstruction. The left column in A represents the initial dose distribution selected several 2D projection sections at different depths in the prostate, while the slices in right column is the corresponding reconstructed prostate dose distribution. B is the 3D image from initial dose distribution (left), with a reconstructed dose distribution (right), which was generated with the V3D (version v2.031) software package. The z axis represents the distance between the prostate dose distribution slices at different depths and the 2D matrix ultrasound transducer array, where the positions from 41 to 70 correspond to the position of the prostate.
C. XACT imaging for real time monitoring of radiation beams during treatment
In order to demonstrate the feasibility of XACT for real time monitoring of the radiation beams during the treatment, we investigated the differences in the dose distribution of the prostate when different numbers of radiation beams were delivered to the prostate. Fig. 7 shows the simulation of XACT imaging for different dose distributions in vivo, by delivering a different number of radiation beams during the treatment. The simulations were successfully performed using the XACT method, while the initial XA pressure was reconstructed by a 3D FBP image reconstruction algorithm. Fig. 7A, 7D and 7G represent the dose distribution with one beam, four beams and seven beams, and the computed initial XA pressure for one eam, four beams and seven beams structures are shown in Fig. 7B, 7E and 7H. As a sample for XACT imaging, the reconstructed pressure distribution for one beam, four beams and seven beams structures are illustrated in Fig. 7C, 7F and 7I. The colors display the magnitude of dose distribution and pressure distribution, from magenta being the strongest intensity to black being the weakest intensity. The magnitude of dose distribution is highest in the prostate, while that in the surrounding organs at risk was significantly reduced. As can be noted in the maps of dose distribution, the radiation beams are created with non-uniformly distributed coplanar fields to deliver full prescribed doses to the prostate. We can observe significant differences in the dose distributions in the prostate based on one beam, four beams and seven beams from XACT images shown in Fig. 7C, 7F and 7I. Therefore, XACT imaging can be demonstrated to be a promising imaging modality to monitor the position of the radiation beam based on the dose distribution in prostate during EBRT delivery according to our simulation results.
Fig. 7.
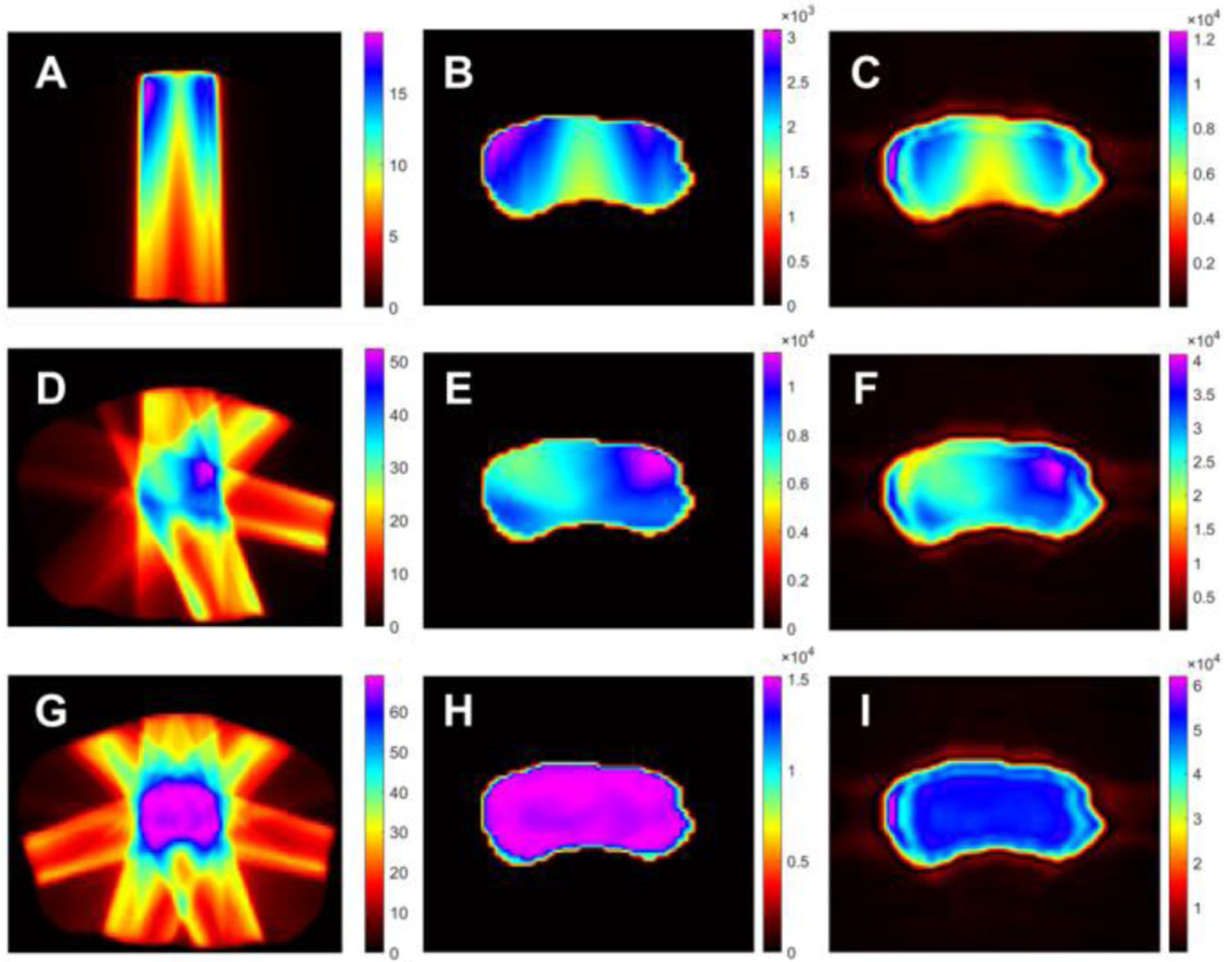
The simulation of XACT imaging for different dose distributions in vivo, by delivering a different number of radiation beams during the treatment. A, D and G display the dose distribution with one beam, four beams and seven beams. B, 7 and H. show the computed initial XA pressure for one beam, four beams and seven beam structures. Fig. C, F and I illustrate the reconstructed pressure distribution for one beam, four beams and seven beams structures as a sample for XACT imaging. The colors represent the magnitude of dose and pressure distributions, from magenta being the strongest intensity to black being the weakest intensity.
D. Image registration with XACT and prostate CT images
In order to demonstrate the feasibility of using a transperineal ultrasound transducer array for XACT imaging to guide prostate radiotherapy, image registration with XACT and planning CT images of prostate cancer was performed in this section. Fig. 8 shows XACT images over a planning CT images of prostate cancer with seven radiation beams. Fig. 8A displays a one frame composite image of reconstructed dose distribution and a planning CT image in 3D, the 3D irregular shape in the middle is the reconstructed dose distribution using a 3D FBP image reconstruction algorithm. The seven cylinders represent different beams delivered to prostate, the blue parallelogram border called B represents a slice of the 3D composite image. Fig. 8B is a 2D composite image of the reconstructed dose distribution in prostate overlaid atop a planning CT slice image with seven beams, corresponding to the plane from Fig. 8A. It can be seen that the total prescribed doses delivered to prostate are generated by delivering all seven beams. Sufficient dose build-up and distribution in the prostate from beam overlap is key to EBRT outcomes. Therefore, XACT dose mapping in could enable radiation therapy guidance in real-time.
Fig. 8.
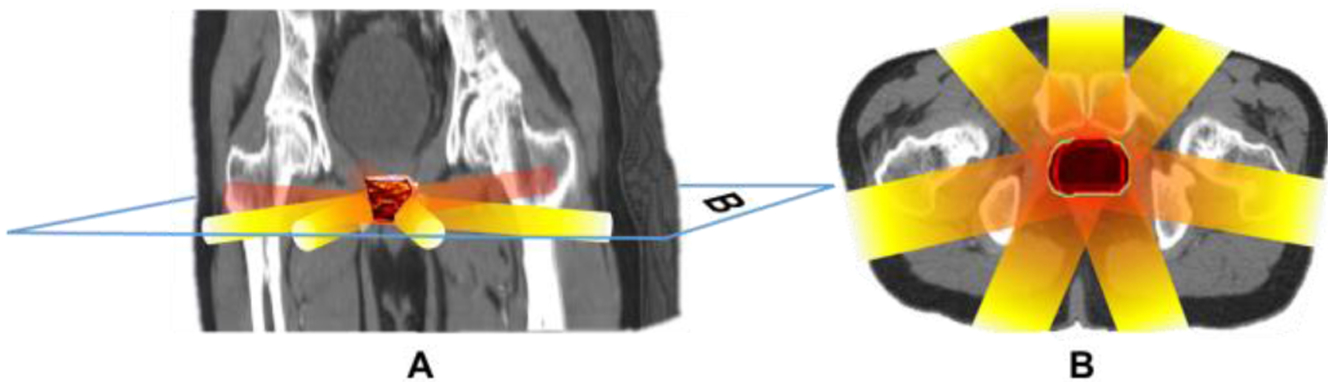
XACT images over a planning CT images of prostate cancer with seven radiation beams. Fig. 8A displays one frame composite image of reconstructed dose distribution in prostate and a planning CT image in 3D, where the 3D planning CT image is generated by the V3D, the 3D irregular shape in the middle is reconstructed dose distribution in prostate by a 3D FBP image reconstruction algorithm, the seven cylinders represent different beams delivered to prostate, the blue parallelogram border called B represents a slice of the 3D composite image. Fig. 8B is a 2D composite image of reconstructed dose distribution in prostate and a planning CT slice image with seven beams in axial plane, which is correspond to the B plane in the Fig. 8A.
V. Discussions
A. Transperineal ultrasound for monitoring prostate radiotherapy
Here we chose Transperineal ultrasound (TPUS) probe for the detection of X-ray induced acoustic waves. In TPUS imaging, the ultrasound probe is positioned on the perineum of the patient (Fig. 1A). TPUS imaging does not exploit the acoustic window of the bladder to obtain images of the prostate and therefore it requires a less strict bladder filling protocol. A semi-filled bladder is still beneficial since it yields good imaging contrast distal to the prostate. In addition, as the distance between the prostate and the perineum is small (<5 cm), relatively good image quality can be achieved [39]. More importantly, since the probe setup dose not interfere with the radiation beam (Fig. 2A), TPUS imaging can potentially be used also for intrafraction monitoring of the prostate radiotherapy. Currently there are commercial systems available that enables the inter- and intrafraction prostate motion monitoring during the radiation treatment workflow using TPUS imaging which show the potential of combining XACT imaging and ultrasound imaging within a single imaging system in the future.
B. Imaging resolution and speed
Recent studies demonstrate the feasibility of using XACT as a viable dosimetry technique in a clinical radiotherapy environment [18, 20, 22, 23, 40]. However, it currently takes tens of minutes to get a 2D image with the current XACT imaging system, which renders real time mapping of the dose during radiation therapy impossible [18, 20, 22, 32, 41]. For the first time, we propose to build a clinically translatable XACT dosimetric scanner with a high-resolution (<1 mm) 3D dose map imaging capability in real time during prostate external radiotherapy, unlike any existing XACT imaging systems [18, 20, 23, 32, 42]. The real time imaging capability will be enabled with a 2D matrix ultrasound transducer array (100 × 100 elements). The XACT imaging speed will be improved by three orders of magnitude if a multiple-channel field programmable gate array (FPGA)-based parallel data acquisition system is used in lieu of a single transducer-based system [18, 20, 23, 32, 41, 42]. The proposed XACT imaging system can provide 4D imaging capability in the future clinical applications.
C. Quantify in vivo radiation dose
In radiation therapy, which is widely used for clinical intervention, the delivered radiation dose can only be planned and/or verified via simulation with phantoms, and an in vivo and in-line verification of delivered dose is absent. XACT imaging therefore has many advantageous characteristics that make its implementation as a radiotherapy dosimeter attractive: 1) XACT is a real-time technique, meaning in vivo images can be obtained during treatment to ensure the delivered dose is as expected. 2) XACT does not perturb the beam because the transducers are placed outside of the beam path, eliminating the need for perturbation correction factors required by many other dosimetry techniques. 3) XACT is an absolute dosimetry technique if the thermal expansion coefficient, physical density, and Grüneisen coefficient are accurately determined, and the transducer and amplification system is well defined and calibrated [43]. However, our current study has not been yet achieved absolute dose measurement because the simplified model with only the initial pressure distribution in the prostate itself is used in k-Wave simulations. Recently, it has been suggested that the deployment of iterative reconstruction algorithms could enable absolute dosimetry in XACT [44], but research is ongoing.
VI. Conclusions
A simulation study was conducted in this paper to evaluate the feasibility of using a transperineal ultrasound transducer array for XACT imaging to guide the prostate radiotherapy. In-house simulations were developed to model the time varying X-ray induced acoustic (XA) signals detected by a transperineal ultrasound array. A 3D filtered back projection (FBP) algorithm has been used for 3D XACT image reconstruction. These results suggested a potential application of XA imaging method, specifically XACT, as a novel in vivo dosimetric tool in external beam radiotherapy (EBRT). After validating the feasibility of XACT in computer simulation, we will further develop an XA and US dual-modality imaging system utilizing a commercial ultrasound unit, aiming to obtain XA image and US image simultaneously, both in real time. As demonstrated by the simulation results, the XA image showing the deposited radiation dose and the US image capturing the motion of target tissue can be naturally co-registered, offering a potential approach for image-guided radiotherapy (IGRT) [45–52].
Acknowledgments
The work was supported by the National Natural Science Foundation of China (NO.61471226), Natural Science Foundation of Shandong Province (NO. JQ201516, 2018GGX101018), and the Taishan scholar project of Shandong Province (NO. tsqn20161023) to Dr. Dengwang Li for supporting Mengxiao Wang’s visit to Dr. Liangzhong Xiang’s lab at OU. This work was partially supported by National Institute of Health (R37CA240806), American Cancer Society (133697-RSG-19-110-01-CCE), and the Oklahoma Center for the Advancement of Science and Technology (HR19-131) to Dr. Liangzhong Xiang. The authors would like to acknowledge the support from Stephenson Cancer Center bridge fund, IBEST-OUHSC fund, and a grant from the Research Council of the University of Oklahoma Norman Campus as well. Asterisk indicates corresponding author.
Contributor Information
Mengxiao Wang, Shandong Province Key Laboratory of Medical Physics and Image Processing Technology, School of Physics and Electronics, Shandong Normal University, Jinan, Shandong, 250358, China..
Pratik Samant, Stephenson School of Biomedical Engineering, University of Oklahoma, Norman, OK, 73019, USA..
Siqi Wang, School of Electrical and Computer Engineering, University of Oklahoma, Norman, OK, 73019, USA..
Jack Merill, Stephenson School of Biomedical Engineering, University of Oklahoma, Norman, OK, 73019, USA..
Dengwang Li, Shandong Province Key Laboratory of Medical Physics and Image Processing Technology, School of Physics and Electronics, Shandong Normal University, Jinan, Shandong, 250358, China..
Liangzhong Xiang, School of Electrical and Computer Engineering, University of Oklahoma, Norman, OK, 73019, USA..
References
- [1].Pisansky TM, “External-beam radiotherapy for localized prostate cancer,” N. Engl. J. Med, vol. 355, no. 15, pp. 1583–91, Oct. 2006. [DOI] [PubMed] [Google Scholar]
- [2].Tsubokura T et al. , “Comparison of image-guided intensity-modulated radiotherapy and low-dose rate brachytherapy with or without external beam radiotherapy in patients with localized prostate cancer,” Int. J. Radiat. Sci Rep, vol. 8, no. 1, p. 10538, Jul. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hanks GE, Hanlon AL, Schultheiss TE, Pinover WH, Movsas B, Epstein BE, and Hunt MA, “Dose escalation with 3D conformal treatment: five year outcomes, treatment optimization, and future directions,” Int. J. Radiat. Oncol. Biol. Phys, vol. 41, no. 3, pp. 501–10, Jun. 1998. [DOI] [PubMed] [Google Scholar]
- [4].Hardcastle N, Cutajar DL, Metcalfe PE, Lerch ML, Perevertaylo VL, Tomé WA, and Rosenfeld AB, “In vivo real-time rectal wall dosimetry for prostate radiotherapy,” Phys. Med. Biol, vol. 55, no. 13, pp.3859–71, Jul. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Zelefsky MJ, Leibel SA, Gaudin PB, Kutcher GJ, Fleshner NE, Venkatramen ES, Reuter VE, Fair WR, Ling CC, and Fuks Z, “Dose escalation with three-dimensional conformal radiation therapy affects the outcome in prostate cancer,” Int. J. Radiat. Oncol. Biol. Phys, vol. 41, no. 3, pp. 491–500, Jun. 1998. [DOI] [PubMed] [Google Scholar]
- [6].Brenner DJ, and Hall EJ, “Fractionation and protraction for radiotherapy of prostate carcinoma,” Int. J. Radiat. Oncol. Biol. Phys, vol. 43, no. 5, pp. 1095–101, Mar. 1999. [DOI] [PubMed] [Google Scholar]
- [7].Brenner DJ, Martinez AA, Edmundson GK, Mitchell C, Thames HD, and Armour EP, “Direct evidence that prostate tumors show high sensitivity to fractionation (low alpha/beta ratio), similar to late-responding normal tissue,” Int. J. Radiat. Oncol. Biol. Phys, vol. 52, no. 1, pp. 6–13, Jan. 2002. [DOI] [PubMed] [Google Scholar]
- [8].Meijer GJ, Minken AW, van Ingen KM, Smulders B, Uiterwaal H, and Mijnheer BJ, “Accurate in vivo dosimetry of a randomized trial of prostate cancer irradiation,” Int. J. Radiat. Oncol. Biol. Phys, vol. 49, no. 5, pp. 1409–18, Apr. 2001. [DOI] [PubMed] [Google Scholar]
- [9].Kroonwijk M, Pasma KL, Quint S, Koper PCM, Visser AG, and Heijmen BJM, “In vivo dosimetry for prostate cancer patients using an electronic portal imaging device (EPID); demonstration of internal organ motion,” Radiother. Oncol, vol. 49, no. 2, pp. 125–132, Nov. 1998. [DOI] [PubMed] [Google Scholar]
- [10].Cantley JL, Cheng CW, Jesseph FB, Podder TK, Colussi VC, Traughber BJ, Ponsky LE, and Ellis RJ, “Real-time in vivo dosimetry for SBRT prostate treatment using plastic scintillating dosimetry embedded in a rectal balloon: a case study,” J. Appl. Clin. Med. Phys, vol. 17, no. 6, pp. 305–311, Nov. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Legge K, Cutajar D, Wilfert A, Martin J, Rozenfelf A, O’Connor DJ, and Greer P, “Real-Time in vivo dosimetry of prostate SBRT boost treatments using MOSkin detectors,” (in English), Medical Physics, vol. 43, no. 6, pp. 3538–3538, Jun. 2016. [Google Scholar]
- [12].Hsi WC, Fagundes M, Zeidan O, Hug E, and Schreuder N, “Image-guided method for TLD-based in vivo rectal dose verification with endorectal balloon in proton therapy for prostate cancer,” Med. Phys, vol. 40, no. 5, p. 051715, May 2013. [DOI] [PubMed] [Google Scholar]
- [13].Wootton L, Kudchadker R, Lee A, and Beddar S, “Real-time in vivo rectal wall dosimetry using plastic scintillation detectors for patients with prostate cancer,” Phys. Med. Biol, vol. 59, no. 3, pp. 647–660, Feb. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Den RB, Nowak K, Buzurovic I, Cao J, Harrison AS, Lawrence YR, Dicker AP, and Showalter TN, “Implanted dosimeters identify radiation overdoses during IMRT for prostate cancer,” Int. J. Radiat. Oncol, vol. 83, no. 3, pp. e371–e376, Jul. 2012. [DOI] [PubMed] [Google Scholar]
- [15].Bruza P, Andreozzi JM, Gladstone DJ, Jarvis LA, Rottmann J, and Pogue BW, “Online combination of EPID & Cherenkov imaging for 3-D dosimetry in a liquid phantom,” IEEE T. Med. Imaging, vol. 36, no. 10, pp. 2099–2103, Oct. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Glaser AK, Zhang R, Davis SC, Gladstone DJ, and Pogue BW, “Time-gated Cherenkov emission spectroscopy from linear accelerator irradiation of tissue phantoms,” Opt. Lett, vol. 37, no. 7, pp. 1193–5, Apr. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Sampaio DRT, Uliana JH, Carneiro AAO, Pavoni JF, Pavan TZ, and Borges LF, (2015, Oct.). X-ray acoustic imaging for external beam radiation therapy dosimetry using a commercial ultrasound scanner. Presented at 2015 IEEE International Ultrasonics Symposium (IUS). [online]. Available: 10.1109/ULTSYM.2015.0400 [DOI] [Google Scholar]
- [18].Hickling S, Hobson M, and El Naqa I, “Feasibility of X-Ray Acoustic Computed Tomography as a Tool for Noninvasive Volumetric In Vivo Dosimetry,” (in English), International Journal of Radiation Oncology Biology Physics, vol. 90, no. 1S, pp. S843–S843, Sep. 2014. [Google Scholar]
- [19].Diao X, Zhu J, Li W, Deng N, Chin CT, Zheng X, Zhang X, Chen X, Li X, and Kuang Y, (2015, Oct.). Broadband detection of dynamic acoustic emission process induced by 6 MV therapeutic X-ray beam from a clinical linear accelerator. Presented at 2015 IEEE International Ultrasonics Symposium (IUS). [online]. Available: 10.1109/ULTSYM.2015.0241 [DOI] [Google Scholar]
- [20].Hickling S, Lei H, Hobson M, Léger P, Wang X, and El Naqa I, “Experimental evaluation of x-ray acoustic computed tomography for radiotherapy dosimetry applications,” Med. Phys, vol. 44, no. 2, pp. 608–617, Feb. 2017. [DOI] [PubMed] [Google Scholar]
- [21].Hickling S, Leger P, and El Naqa I, “On the Detectability of Acoustic Waves Induced Following Irradiation by a Radiotherapy Linear Accelerator,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 63, no. 5, pp. 683–690, May 2016. [DOI] [PubMed] [Google Scholar]
- [22].Hickling S, Hobson M, and El Naqa I, “Characterization of x-ray acoustic computed tomography for applications in radiotherapy dosimetry,” IEEE Transactions on Radiation and Plasma Medical Sciences, vol. 2, no. 4, pp. 337–344, Feb. 2018. [Google Scholar]
- [23].Lei H, Zhang W, Oraiqat I, Liu Z, Ni J, Wang X, and El Naqa I, “Towards in vivo dosimetry in external beam radiotherapy using X-ray acoustic computed tomography: A soft-tissue phantom study validation,” Med. Phys, vol. 45, no. 9, pp. 4191–4200, Sep. 2018. [DOI] [PubMed] [Google Scholar]
- [24].Zhou Y, Yao J, and Wang LV, “Tutorial on photoacoustic tomography,” J. Biomed. Opt, vol. 21, no. 6, Jun. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kruger RA, Liu P, Fang YR, and Appledorm CR, “Photoacoustic ultrasound (PAUS)--reconstruction tomography,” Med. Phys, vol. 22, no. 10, pp. 1605–9, Oct. 1995. [DOI] [PubMed] [Google Scholar]
- [26].Wang LV, and Wu H, Biomedical optics: Principles and imaging. Hoboken, USA: John Wiley & Sons, Inc., 2007, pp. 283–321. [Google Scholar]
- [27].Patch SK, Hoff DEM, Webb TB, Sobotka LG, and Zhao T, “Two-stage ionoacoustic range verification leveraging Monte Carlo and acoustic simulations to stably account for tissue inhomogeneity and accelerator-specific time structure - A simulation study,” Med. Phys, vol. 45, no. 2, pp. 783–793, Feb. 2018. [DOI] [PubMed] [Google Scholar]
- [28].Gebauer B, and Scherzer O, “Impedance- acoustic tomography,” SIAM J. APPL. MATH, vol. 69, no. 2, pp. 565–576, Dec. 2008. [Google Scholar]
- [29].Treeby BE, and Cox BT, “k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields,” J. Biomed. Opt, vol. 15, no. 2, Apr. 2010. [DOI] [PubMed] [Google Scholar]
- [30].Treeby BE, Jaros J, Rendell AP, and Cox BT, “Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using a k-space pseudospectral method,” J. Acoust. Soc. Am, vol. 131, no. 6, pp. 4324–4336, Jun. 2012. [DOI] [PubMed] [Google Scholar]
- [31].Treeby BE and Cox BT, “Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian,” J. Acoust. Soc. Am, vol. 127, no. 5, pp. 2741–2748, May 2010. [DOI] [PubMed] [Google Scholar]
- [32].Xiang L, Tang S, Ahmad M, and Xing L, “High resolution X-ray-induced acoustic tomography,” Sci. Rep, vol. 6, no. 26118, May 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Winkler AM, Maslov K, and Wang LV, “Noise-equivalent sensitivity of photoacoustics,” J. Biomed. Opt, vol. 18, no. 9, Sep. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Tang S, Chen J, Samant P, Stratton K, and Xiang L, “Transurethral photoacoustic endoscopy for prostate cancer: A simulation study,” IEEE Trans. Med. Imaging, vol. 35, no. 7, pp. 1780–7, Jul. 2016. [DOI] [PubMed] [Google Scholar]
- [35].Kruger RA, Reinecke DR, and Kruger GA, “Thermoacoustic computed tomography–technical considerations,” Med. phys, vol. 26, no. 9, pp. 1832–1837, Sep. 1999. [DOI] [PubMed] [Google Scholar]
- [36].Xu M, and Wang LV, “Universal back-projection algorithm for photoacoustic computed tomography,” Phys. Rev. E, vol. 71, pp. 016706, Jan. 2005. [DOI] [PubMed] [Google Scholar]
- [37].Tang S, Yang K, Chen Y, and Xaing L, “X-ray-induced acoustic computed tomography for 3D breast imaging: A simulation study,” Med. phys, vol. 45, no. 4, pp. 1662–1672, Apr. 2018. [DOI] [PubMed] [Google Scholar]
- [38].Xu Y, and Wang LV, “Reconstructions in limited-view thermoacoustic tomography,” Med. phys, vol. 31, no. 4, pp. 724–33, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [39].Camps SM, Fontanarosa D, de With PHN, Verhaegen F, and Vanneste BGL, “The use of ultrasound imaging in the external beam radiotherapy workflow of prostate cancer patients,” Biomed. Res. Int, vol. 2018, no. 7569590, pp. 1–16, Jan. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Sanli C, Kipergil EA, and Unlu MB. (2018, Jan.). Simple analytic model for radiotherapeutic X-ray induced acoustic signal as a function of absorption parameters. Med. Phys [Online]. Available: arXiv:1801.05956 [Google Scholar]
- [41].Xiang L, Han B, Carpenter C, Pratx G, Kuang Y, and Xing L, “X-ray acoustic computed tomography with pulsed x-ray beam from a medical linear accelerator,” Med. Phys, vol. 40, no. 1, p. 010701, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Xiang L, Ahmad M, Carpenter C, Pratx G, Nikoozadeh X, Yakub BK, and Xing L, “X-Ray Acoustic Computed Tomography: Concept and Design,” (in English), Medical Physics, vol. 40, no. 6, Jun. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Hickling S, Xiang L, Jones KC, Parodi K, Assmann W, Avery S, Hobson M, and El Naqa I, “Ionizing radiation-induced acoustics for radiotherapy and diagnostic radiology applications,” Med. Phys, vol. 45, no. 7, pp. e707–721, Jul. 2018. [DOI] [PubMed] [Google Scholar]
- [44].Forghani F, Mahl A, Patton TJ, Jones BL, Borden MA, Westerly DC, Altunbas C, Miften M, Thomas DH, Simulation of x-ray-induced acoustic imaging for absolute dosimetry: Accuracy of image reconstruction methods, Medical Physics. n/a (n.d.) 10.1002/mp.13961. [DOI] [PubMed] [Google Scholar]
- [45].Agarwal A, Shao X, Rajian JR, Zhang H, Chamberland DL, Kotov NA, and Wang X, “Dual-mode imaging with radiolabeled gold nanorods,” J. Biomed. Opt, vol. 16, no. 5, p.051307, May 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Xu G, Rajian JR, Girish G, Kaplan MJ, Fowlkes JB, Carson PL, Wang X, “Photoacoustic and ultrasound dual-modality imaging of human peripheral joints,” J. Biomed. Opt, vol. 18, no. 1, p. 10502, Jan. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Chen SL, Xie Z, Guo LJ, and Wang X, “A fiber-optic system for dual-modality photoacoustic microscopy and confocal fluorescence microscopy using miniature components,” Photoacoustics, vol. 1, no. 2, pp. 30–35, May 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Xie Z, Hooi FM, Fowlkes JB, Pinsky RW, Wang X, and Carson PL, “Combined photoacoustic and acoustic imaging of human breast specimens in the mammographic geometry,” Ultrasound Med. Biol, vol. 39, no. 11, pp. 2176–84, Nov. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Yuan J, Xu G, Yu Y, Zhou Y, Carson PL, Wang X, and Liu X, “Real-time photoacoustic and ultrasound dual-modality imaging system facilitated with graphics processing unit and code parallel optimization,” J. Biomed. Opt, vol. 18, no. 8, p. 086001, Aug. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Hu Z, Zhang H, Mordovanakis A, Paulus YM, Liu Q, Wang X, and Yang X, “High-precision, non-invasive anti-microvascular approach via concurrent ultrasound and laser irradiation,” Sci. Rep, vol. 7, no. 40243, Jan. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Tian C, Zhang W, Mordovanakis A, Wang X, and Paulus YM, “Noninvasive chorioretinal imaging in living rabbits using integrated photoacoustic microscopy and optical coherence tomography,” Opt. Express, vol. 25, no. 14, pp. 15947–15955, Jul. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Tian C, Zhang W, Nguyen VP, Wang X, and Paulus YM, “Novel Photoacoustic Microscopy and Optical Coherence Tomography Dual-modality Chorioretinal Imaging in Living Rabbit Eyes,” J. Vis. Exp, no. 132, p. e57135, Feb. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]


