Assessment of basic reproductive number for COVID-19 at global level

Abstract

Background:

There are large knowledge gaps regarding how transmission of 2019 novel coronavirus disease (COVID-19) occurred in different settings across the world. This study aims to summarize basic reproduction number (R₀) data and provide clues for designing prevention and control measures.

Methods:

Several databases and preprint platforms were retrieved for literature reporting R₀ values of COVID-19. The analysis was stratified by the prespecified modeling method to make the R₀ values comparable, and by country/region to explore whether R₀ estimates differed across the world. The average R₀ values were pooled using a random-effects model.

Results:

We identified 185 unique articles, yielding 43 articles for analysis. The selected studies covered 5 countries from Asia, 5 countries from Europe, 12 countries from Africa, and 1 from North America, South America, and Australia each. Exponential growth rate model was most favored by researchers. The pooled global R₀ was 4.08 (95% CI, 3.09–5.39). The R₀ estimates for new and shifting epicenters were comparable or even higher than that for the original epicenter Wuhan, China.

Conclusions:

The high R₀ values suggest that an extraordinary combination of control measures is needed for halting COVID-19.

1. Introduction

In January 2020, the general public became aware of an outbreak of a novel coronavirus strain, now termed severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) which had been affecting Wuhan city, China. The disease has been spreading rapidly worldwide, leading the World Health Organization (WHO) to declare a pandemic on March 11, 2020. While majority of cases have been relatively mild outside of Wuhan,^[1] a lot of uncertainties remain about the severity of the 2019 novel coronavirus disease (COVID-19) on a per-case basis. Furthermore, higher-than-normal spread rates expected from this virus may result in population-level severe morbidity and mortality even if the case-fatality ratio remains low.

There exist large knowledge gaps regarding how transmission of SARS-CoV-2 occurred in different settings across the world. The basic reproduction number (R₀) is one of the fundamental and most often used metrics that describes the contagiousness or transmissibility of the infectious agent at the beginning of an epidemic. The proportion of the population needed to be vaccinated for the elimination of an infection can be based on R₀ values.^[2] Estimating R₀ is a requisite for designing prevention and control measures for infectious diseases such as COVID-19.

Although many researchers estimated the reproductive number of COVID-19, their results, as well as stages of infection, measurement methods, and applied preventive interventions differ substantially across the studies. Considering the variability of the reproductive numbers among the countries, we attempt to summarize available R₀ estimates of COVID-19 at the global level. The pooled statistical findings might help to characterize the spread of the disease and inform public health policy.

2. Methods

2.1. Search strategy

Our study conforms to the Preferred Reporting Items for Systematic Reviews and Meta-analysis guidelines.^[3] We retrieved literature from the PubMed, EmBase, China National Knowledge Infrastructure (Chinese), WanFang (Chinese) database, and BioRxiv, MedRxiv, arXiv preprint platforms in August, 2020. The search terms included: (“novel coronavirus” or “SARS-CoV-2” or “2019 novel coronavirus disease” or “COVID-19”) and (“basic reproduction number” or “R₀” or “transmission” or “epidemic dynamics”). To identify additional studies, we reviewed and hand searched the references of important articles.

2.2. Study selection

Two independent authors screened the titles and abstracts for relevance. Articles were evaluated for inclusion according to the following criteria: described the early epidemic dynamics of COVID-19 in the country or region; reported basic reproduction number based on daily data of COVID-19 case counts; and presented in English or Chinese language.

Nonhuman and laboratory studies were excluded, as well as studies merely reporting time-dependent reproductive number. No exclusions were made for modeling methods used for R₀ estimation.

2.3. Data extraction

The name of the first author, country or region, estimation period, measurement method, the estimated R₀ value (with certain confidence interval [CI]) and digital object identifier were extracted from the articles. All studies that estimated R₀ for COVID-19 were used for systemic review, while only those with 95% CI were entered into the meta-analysis.

2.4. Statistical analysis

We stratified the analysis by prespecified modeling method to make the R₀ values comparable, and by country/region to examine if R₀ estimates differed across the world. The average R₀ values were pooled using a random-effects model. The I² values were used for heterogeneity evaluation. A threshold of I² ≥ 50% indicated high heterogeneity. Publication bias was assessed with Begg and Egger tests, as well as the funnel plots visually. Moreover, sensitivity analysis was performed using a 1-study-removed analysis.

All statistical analyses were conducted using Stata software (version 15.0, StataCorp, TX, USA). Statistical significance was defined as a P value < .05. The map was performed using ArcGIS software (version 10.6, Esri, USA).

3. Result

3.1. Study selection and characteristics

Our database search led to 413 studies, 228 of which were duplicates, and 72 of which were deemed irrelevant based on review of their titles and abstracts. Of the remaining 113 studies, 32 did not report the reproduction number, 21 reported effective reproduction number (Re) or real-time reproduction number (Rt) rather than R₀, 9 lacked data source and 8 lacked methodology for estimation. Finally, a total of 43 studies were included for the analysis (Fig. 1).^[4–46]

Figure 1.

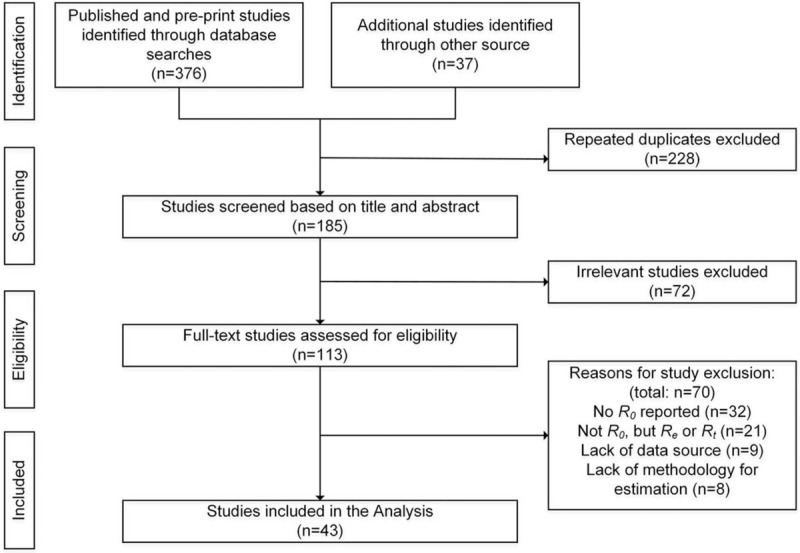
Flow diagram for study selection.

From the 43 studies (Tables 1 and 2), 61 estimates of R₀ values were exacted, majority (39) of which were for China (including for Wuhan city specifically). The remaining estimates were presented for Korea (6), United States (3), Italy (2), Iran (2), followed by Japan (1), India (1), The United Kingdom (1), France (1), Germany (1), Spain (1), Brazil (1), Australia (1), and top 12 countries in Africa (1).

Table 1.

R₀ estimates for cities and provinces within China.

Author	Location	Estimation period	Methods	R0	95% CI
Li JH[7]	Wuhan	January 10–23, 2020	EGR	5.54	5.07–6.06
Liu T[8]	Wuhan	By February 7, 2020	EGR	4.40	4.30–4.60
Liu T[8]	China	By February 7, 2020	EGR	4.50	4.40–4.60
Sanche S[9]	Wuhan	January 15–30, 2020	EGR	5.70	3.80–8.90
Song QQ[10]	China	January 15–31, 2020	EGR	3.74	3.63–3.87
Wang Y[5]	China	Jan 17 to February 8, 2020	EGR	3.49	3.42–3.58
Zhao QY[11]	Wuhan	By January 23, 2020	EGR	5.70	3.40–9.20
Zhao S[12]	China	January 10–24, 2020	EGR	2.24	1.96–2.55
Zhao S[12]	China	January 10–24, 2020	EGR	3.58	2.89–4.39
Zhao S[13]	Wuhan	January 1–15, 2020	EGR	2.56	2.49–2.63
Li JH 7	Wuhan	January 10–23, 2020	SEIR	3.55	2.97–4.21
Read J[14]	China	January 1–22, 2020	SEIR	3.11	2.39–4.13
Shen MW[15]	China	December 12, 2019 to January 22, 2020	SEIR	4.71	4.50–4.92
Song QQ[10]	China	January 15–31, 2020	SEIR	3.91	3.71–4.11
Tang B[16]	China	By January 22, 2020	SEIR	6.47	5.71–7.23
Zhou T[17]	China	By 25 January, 2020	SEIR	2.80–3.30 (3.05)	/
Zhou WK[18]	China	By January 10, 2020	SEIR	5.32	/
Cao ZD[19]	China	By January 23, 2020	SEIRDC	4.08
Chen TM[20]	Wuhan	December 7, 2019 to January 1, 2020	SEIAR	3.58	/
LI Y[21]	China	By January 23, 2020	SEIQR	5.60	/
Li JH[7]	Wuhan	January 10–23, 2020	MLE	2.65	2.64–2.67
Song QQ[10]	China	January 15–31, 2020	MLE	3.16	2.90–3.43
Tang B[22]	China	January 1–23, 2020	MLE	3.80	3.50–4.20
Tang B[22]	Guangdong	January 19–31, 2020	MLE	3.00	2.60–3.30
Wang Y[5]	China	January 17 to February 8, 2020	MLE	2.99	2.93–3.06
Jung SM[23]	China	By January 24, 2020	Epidemic growth model	2.10	2.00–2.20
Jung SM[23]	China	By January 24, 2020	Epidemic growth model	3.20	2.70–3.70
Li JH[7]	Wuhan	January 10–23, 2020	Sequential Bayesian method	1.68	1.09–2.33
Wang Y[5]	China	January 17 to February 8, 2020	Sequential Bayesian method	2.80	2.42–3.15
Li JH[7]	Wuhan	January 10–23, 2020	Time dependent reproduction number	5.95	4.96–7.03
Wang Y[5]	China	January 17 to February 8, 2020	Time dependent reproduction number	4.48	4.26–4.71
Cao ZD[24]	Wuhan	By January 23, 2020	Geo-stratified debiasing estimation framework	3.24	/
Chinazzi M[25]	China	By January 23, 2020	GLEAM and SLIR	2.57	2.37–2.78 (90% CI)
Li Q[26]	China	By January 22, 2020	Fitted transmission model with zoonotic infection	2.20	1.40–3.90
Du ZW[27]	Wuhan	By January 22, 2020	Hierarchical model	1.90	1.47–2.59
Imai N[28]	China	By January 18, 2020	Mathematical model	1.50–3.50	/
Majumder M[29]	Wuhan	December 8, 2019 to January 26, 2020	Incidence Decay and Exponential Adjustment (IDEA) model	2.00–3.10 (2.50)	/
Wu J[30]	Wuhan	December 31, 2019 to January 28, 2020	Markov Chain Monte Carlo methods	2.68	2.47–2.86
Riou J[31]	China	By January 18, 2020	Stochastic simulations of early outbreak trajectories	2.20	1.40–3.80 (90% HDI)

CI = confidence interval, EGR = exponential growth rate, GLEAM = global epidemic and mobility model, HDI = high-density interval, MLE = maximum likelihood estimation, SEIAR = susceptible, exposed symptomatic, infectious asymptomatic, infectious removed, SEIQR = susceptible, exposed, infected but not hospitalized, infectious and isolated recovered, SEIR = susceptible-exposed-infected-removed, SEIRDC = SEIR with death cumulative, SLIR = susceptible latent infectious recovered.

Table 2.

Country-level R₀ estimates across the world except China.

Author	Location	Estimation period	Methods	R0	95% CI
de Souza W[32]	Brazil	February 25 to March 19, 2020	EGR	3.10	2.40–5.50
Dwivedi L[33]	India	March 14 to April 3, 2020	EGR	2.56	/
Ki M[34]	Korea	January 20 to February 10, 2020	EGR	0.48	0.25–0.84
Musa SS[4]	Africa	March 1–19, 2020	EGR	2.37	2.22–2.51
Yuan J[35]	France	February 23 to March 9, 2020	EGR	6.32	5.72–6.99
Yuan J[35]	Germany	February 21 to March 9, 2020	EGR	6.07	5.51–6.69
Yuan J[35]	Italy	February 23 to March 9, 2020	EGR	3.27	3.17–3.38
Yuan J[35]	Spain	February 19 to March 9, 2020	EGR	5.08	4.51–5.74
Choi S[36]	Korea	January 20 to February 17, 2020	SEIR	0.56	0.51–0.60
Dropkin G[37]	United Kingdom	January 30 to March 31, 2020	SEIR	6.94	6.52–7.39
Kuniya T[38]	Japan	January 15 to February 29, 2020	SEIR	2.60	2.40–2.80
D’Arienzo M[39]	Italy	January 25 to March 12, 2020	SIR	2.43–3.10	/
Khosravi A[40]	Iran	February 20 to March 5, 2020	MLE	2.74	2.10–3.40
Tang B[22]	Korea	January 23 to March 2, 2020	MLE	2.60	2.50–2.70
Muniz-Rodriguez K[41]	Iran	February 19 to March 1, 2020	Generalized growth model	4.40	3.90–4.90
Shim E[6]	Korea	January 20 to February 26, 2020	Generalized growth model	1.50	1.40–1.60
Fellows IE[42]	United States	January 22 to March 14, 2020	Sequential Bayesian method	2.37	2.22–2.52
Gunzler D[43]	USA	By March 17, 2020	Sequential Bayesian method	4.02	3.69–5.15
Zhuang Z[44]	Korea	January 31 to March 1, 2020	Stochastic model	2.60	2.30–2.90
Zhuang Z[44]	Korea	February 5 to March 1, 2020	Stochastic model	3.20	2.90–3.50
Rockett R[45]	Australia	January 21 to March 28, 2020	Agent-based model	2.27	/
Ives AR[46]	New York state, USA	February 26 to April 20, 2020	Time-varying autoregressive state-space model	6.40	4.30–9.00

CI = confidence interval, EGR = exponential growth rate, MLE = maximum likelihood estimation, SEIR = susceptible-exposed-infected-removed, SIR = susceptible- infected-removed.

3.2. Methodological approaches used by the selected studies

As shown in Table 1, the evaluation techniques or models for R₀ estimation were diverse. Exponential growth rate (EGR) model, susceptible-exposed-infected-removed (SEIR) model or other susceptible-infected-removed-based models, maximum likelihood estimation (MLE) model were the top 3 methods favored by researchers. Other methods include generalized growth model, sequential Bayesian method, stochastic model, etc. (Tables 1 and 2).

3.3. Overview of R₀ estimates across the world

As shown in Figure 2, the R₀ estimates were conducted for 6 continents, Asia (5 countries), Europe (5 countries), Africa (12 countries), Australia (1 country), North America (1 country), and South America (1 country). The map represented individual R₀ estimate for 12 countries, and a single R₀ for Africa covering 12 countries, which was a study at a regional scale.^[4] The highest country-level R₀ estimates are for France (R₀, 6.32; 95% CI, 5.72–6.99), following Germany (R₀, 6.07; 95% CI, 5.51–6.69) and Spain (R₀, 5.08; 95% CI, 4.51–5.74). The R₀ for Wuhan city, China and New York state, USA were 4.47 (95% CI 3.10–6.44) and 6.40 (95% CI, 4.30–9.00) respectively.

Figure 2.

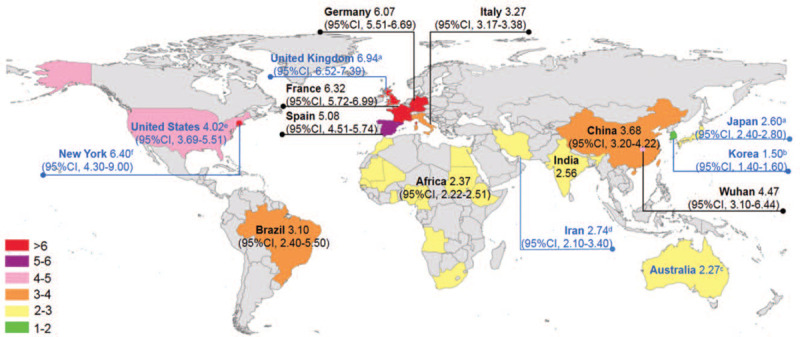
Distribution map of R₀ estimates (EGR model-based if not specified) ^aSEIR model; ^bGeneralized growth model; ^cAgent-based model; ^dMLE model; ^eSequential Bayesian method; ^fTime-varying autoregressive state-space model. EGR = exponential growth rate, MLE = maximum likelihood estimation, SEIR = susceptible-exposed-infected-removed.

After pooling the 5 R₀ estimates based on EGR models, we got the average R₀ as 4.47 (95% CI, 3.10–6.44, I² = 99.5%) for Wuhan. The pooled R₀ for China was estimated as 3.83 (95% CI, 3.30–4.44; I² = 98.8%). Moreover, combining the pooled result for China and EGR model-based estimates for other 7 countries or regions, we obtained the pooled global R₀ for COVID-19 was 3.42 (95% CI, 2.59–4.51; I² = 98.6%). If the R₀ estimate for Korea based on data collected before its exponential growth is excluded, the pooled global R₀ may be 4.08 (95% CI 3.09–5.39) (Fig. 3).

Figure 3.

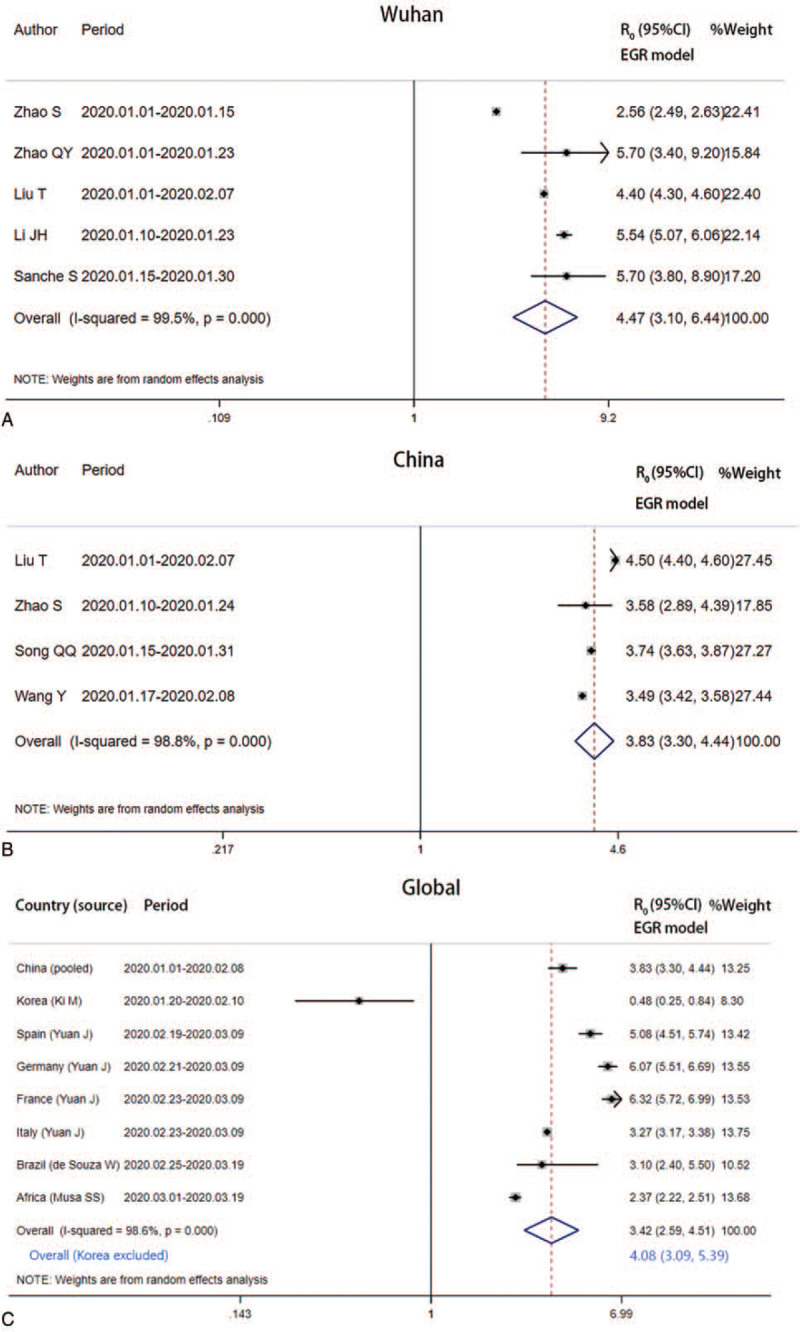
Forest plot of the pooled EGR model-based R₀ estimates. EGR = exponential growth rate.

SEIR models have been used for R₀ estimates for China, Japan, and Korea. The pooled R₀ for China was estimated as 4.50 (95% CI, 3.71–5.46; I² = 96.1%). The pooled Asian R₀ was 3.50 (95% CI, 1.64–5.36; I² = 99.8%) from the meta-analysis (see Figure s1, Supplemental Content, which illustrates the forest plot of the pooled SEIR model-based R0 estimates). Meanwhile, MLE models have also been applied to estimate R₀ for China, Korea, and Iran. The pooled R₀ for China was estimated as 3.28 (95% CI, 2.87–3.76, I² = 92.3%). The pooled Asian R₀ estimate was 2.85 (95% CI, 2.41–3.37; I² = 81.1%) (see Figure s2, Supplemental Content, which illustrates the forest plot of the pooled MLE model-based R₀ estimates).

3.4. Sensitivity analysis and publication bias

The sensitivity analysis showed that no individual study significantly affected the summarized results of R₀ (see Figures 3, which illustrates the sensitivity analysis plot of meta-analysis for EGR model-based R₀ estimates). The publication bias was P > .05 in both Begg and Egger tests (data not shown). Figures 4 (Supplemental Content, which illustrates the funnel plot of meta-analysis for EGR model-based R₀ estimates) showed the Begg funnel plots.

4. Discussion

Knowledge of the basic reproductive number is critical for understanding the dynamics of the novel coronavirus disease. As the pandemic progresses in space and time, this needs to be re-evaluated. To the best of our knowledge, this study for the first time summarized the R₀ values at the global level. This study might help to characterize the spread scale of the disease, and convey a clear message to public health decision makers.

R₀ is affected by lots of biosocial factors and is estimated by various complex mathematical models. Therefore, the R₀ values are usually dependent on model structures and assumptions. It is recommended not to compare values based on different models.^[2] Based on this review, the EGR model was the most common method addressed by the available studies. It has been more than 3 decades since the development of EGR model which embraces both the infection cycle and the change in number of new case counts within the Lotka–Euler framework.^[47] By comparing 4 methods, Wang et al^[5] found that EGR model fitted the Chinese COVID-19 data best. Our study calculated pooled R₀ values with the same method respectively, avoiding the limitation of different modeling. Through this approach we got more comparable estimates than previous meta-analyses.^[48]

Using the assumption of exponential growth (EGR models), we found R0 values of 4.54 (95% CI 3.18–5.90) and 3.69 (95% CI 3.17–4.21) for Wuhan and China respectively. Compared with severe acute respiratory syndrome (SARS, R₀ = 3, range 2.2–3.6) and Middle East respiratory syndrome (R₀ range 0.8–1.3),^[49,50] COVID-19 has a higher R₀, suggesting the novel coronavirus be more contagious and stringent public health strategies be necessary. One modeling study indicated that if R₀ were above 3.5, even near perfect case isolation and contact tracing would not be sufficient to control COVID-19 outbreaks.^[51] Lessons from influenza pandemics also tell us that timely implementation of nonpharmaceutical interventions (NPIs), including infection control, social distancing, small area lockdown, and travel restrictions, is warranted.^[52]

It is on January 30, 2020 that the WHO declared the COVID-19 a public health emergency of international concern, 1 week after Chinese government launched the unprecedented lockdown in Wuhan epicenter and other 12 cities in Hubei province. Significant decrease in the growth rate of COVID-19 cases within China was reported by us and other researchers.^[53,54] In contrast, new epicenters were developing and shifting across the world during the same period. Some epidemiological parameters in countries except China could be different based on control strategies. However, it is clear that the R₀ values for United States, France, Germany, Italy, and Spain from February to March were comparable or even higher than that of Wuhan. Africa, the last continent to be hit by the COVID-19 pandemic, is expected to be the most vulnerable continent. Interestingly, most of the identified COVID-19 cases in Africa had been imported from Europe and the United States, rather than from the original COVID-19 epicenter China.^[55] Maybe, this situation would have been different if the alert call from WHO and the NPI example from China were taken into consideration on time by these authorities.^[56]

It is worth noting that some estimates of R₀ were significantly lower for Korea than those for most other countries. The previous 2 studies reporting subexponential growth dynamic in Korea used data collected before February 17, 2020. However, it was on February 19, 2020 when the number of confirmed COVID-19 cases started to increase rapidly. The increased spread of COVID-19 in Korea may be attributed to one superspreading event that had resulted in more than 3900 secondary cases stemming from church services in the city of Daegu.^[6]

Admittedly, there are several limitations in this study. First, the study covered a small number of world countries and was not enough to cover the geographical dimensions of the continents. Second, the study did not assess meteorological characteristics of a location and demographic characteristics of that location's population which might influence the disease transmission pattern. Last, some articles included for analysis are preprints that might affect the overall quality of the review to some extent.

In conclusion, the relatively high value for R₀ suggests that an extraordinary combination of control measures is needed for halting COVID-19. Indeed, at the expected transmissibility of the pandemic pathogen, timely NPIs should be implemented before a highly efficacious vaccine could become available. Such efforts will be the key to quell local outbreaks and reduce the risk of further global dissemination.

Acknowledgments

The authors thank Prof Lei Zhang from Xi’an Jiaotong University Health Science Center for his valuable scientific comments and advices.

Author contributions

GQ designed the study protocol. CJY, ZXW, and YX did the literature search. The titles, abstracts, and full texts were screened and selected by CJY and MXH. The data were extracted and analysed by CJY, MXH and KC. CJY, ZXW, and YX drafted the manuscript. GQ edited the draft. All authors read and approved the final manuscript.