Abstract
Objective:
To obtain definitive cancer diagnosis for suspicious lesions, accurate needle deployment and adequate tissue sampling in needle biopsy are essential. However, the single-bevel needles in current biopsy devices often induce deflection during insertion, potentially causing lesion missampling/undersampling and cancer misdiagnosis. This study aims to reveal the biopsy needle design criteria enabling both low deflection and adequate tissue sampling.
Methods:
A novel model capable of predicting needle deflection and tissue deformation was first established to understand needle-tissue interaction with different needle tip geometries. Experiments of needle deflection and ex-vivo tissue biopsy were conducted for model validation.
Results:
The developed model showed a reasonably good prediction on the correlation of needle tip type vs. the resultant needle deflection and tissue sampling length. A new multi-bevel needle with the tissue separation point below the needle groove face has demonstrated to be an effective design with an 87% reduction in deflection magnitude and equivalently long tissue sampling length compared to the current single-bevel needle.
Conclusion:
This study has revealed two critical design criteria for biopsy needles: 1) multiple bevel faces at the needle tip can generate forces to balance bending moments during insertion to enable a low needle deflection and 2) the tissue separation point should be below the needle groove face to ensure long tissue sampling length.
Significance:
The developed methodologies and findings in this study serve as proof-of-concept and can be utilized to investigate various biopsy procedures to improve cancer diagnostic accuracy as well as other procedures requiring accurate needle insertion.
Index Terms—: Needle deflection, tissue deformation, tissue sampling, needle insertion modeling, Lagrangian analysis, smoothed particle Galerkin method
I. Introduction
Needle biopsy is widely performed as a minimally invasive tissue sampling method for cancer diagnosis of prostate, lymph node, lung, and liver [1]–[3]. Accurate needle deployment and adequate tissue sampling in biopsy are essential for accurate cancer diagnosis and individualized treatment decisions [4]–[7]. Advances in medical imaging, particularly magnetic resonance imagining (MRI), have enabled early identification of suspicious cancerous lesions [8]–[ll]. This is followed by a targeted needle biopsy to sample the identified lesion site for subsequent confirmatory pathological diagnosis. In a targeted biopsy procedure, the pre-biopsy MRI and ultrasound images can be fused to display the lesion site, allowing real-time needle guidance to the targeted sampling location [12]–[16]. An example of this is the co-registered MRI-ultrasound fusion targeted biopsies (MRF-TB) forprostate cancer diagnosis [11], [17]–[19].
The MRF-TB procedure is illustrated in Fig. 1. This procedure is commonly performed using a trucut needle biopsy device which is also commonly utilized in lymph node [20], breast [21], liver [22] and other biopsy procedures. As shown in Fig. 1(a), the trucut biopsy device has an inner solid needle and an outer hollow cannula for tissue sampling. The needle has a sharp tip with a single-bevel face and a groove (on the same side). To perform a biopsy, the needle and cannula are first positioned in proximity to the targeted lesion site as Step 1 shown in Fig. 1(a). Next, the biopsy device sequentially actuates the needle and cannula in Steps 2 and 3, respectively, advancing them through the targeted lesion site at high speed (about 4 m/s) to cut and store the tissue sample inside the needle groove. During MRF-TB, shown in Fig. 1(b), the MRI-ultrasound fusion software generates features on the real-time ultrasound image to guide clinicians to deploy the needle to the pre-biopsy MRI-identified lesion, including a blue dashed line representing the estimated needle trajectory and the lesion outline and center (marked as the green contour and red point, respectively) forbiopsy. [23].
Fig. 1.
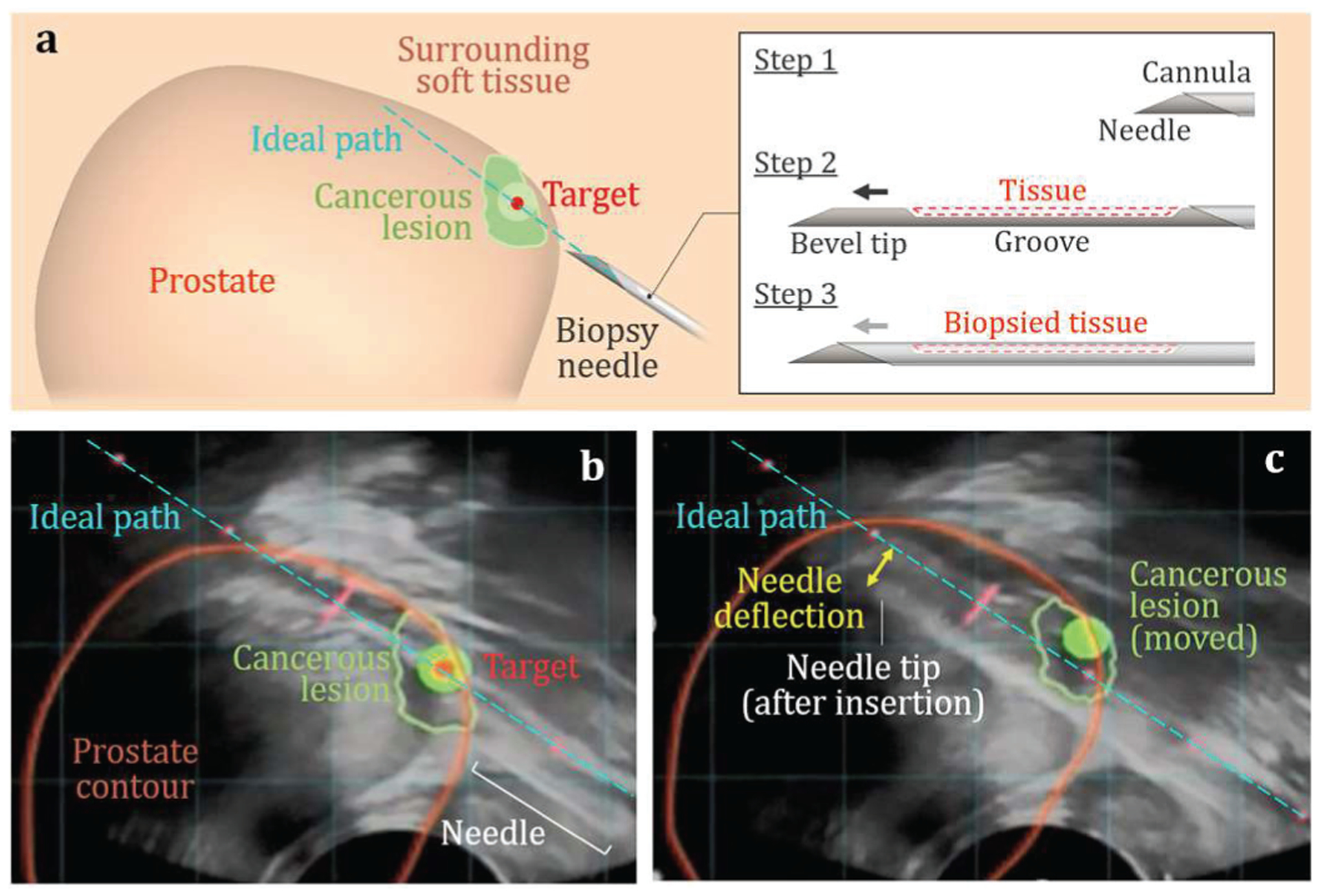
Needle deflection in MRF-TB for prostate cancer diagnosis: (a) Overall three-dimensional model of the cancerous prostate, needle, and cannula. The MRI-ultrasound fused images (b) before and (c) after the needle insertion in biopsy.
Despite the advanced imagining guidance, the current single-bevel trucut biopsy needles often induce significant deflection, with the median deflection of 1.77 mm for an 18 gauge needle (1-mm diameter) found in prostate biopsy [24]. This causes variance between the targeted and actual locations of the sampled tissue core. As shown in Fig. 1(c), the needle deflects after insertion, forming an arc rather than an ideal straight line through the targeted lesion center. Such needle deflection could lead to lesion missampling or undersampling [25] as well as false-negative cancer misdiagnosis [26], [27]. Moreover, biopsy sites may be in proximity to critical vessels and nerves in the biopsy of lymph node [28], [29], pulmonary alveolus in lung [30], [31], and gall bladder in liver [6], The deflected needle could be off target and cause unintended damage, putting patients at a higher risk of complications[6], [32].
Robotic needle steering has been developed for accurate needle guidance and insertion [7], [33], [34]. Multiple degrees-of-freedom robots were coupled with an imaging system to navigate the needle, compensate for the deflection, and achieve sub-mm targeting accuracy [35]–[37]. However, high cost and low availability prohibit the robotic technique from most clinical procedures [38]. Most biopsy procedures are performed using the hand-held needle biopsy devices where needle deflection remains an issue (Fig. 1(c)). A hand-held biopsy needle with a predictable straight insertion trajectory allows the clinician to directly aim to the target and can improve needle sampling and cancer diagnostic accuracy.
Our preliminary study has shown that a biopsy needle with multiple bevels at the tip can balance the bending moments to reduce needle deflection during insertion compared to existing single-bevel needles [25]. However, the proposed multi-bevel needles altered the tissue separation point and thus reduced tissue sampling length, potentially compromising the cancer diagnostic accuracy in biopsy [25]. The goal of this study is to extend the previous findings to reveal the criteria for trucut biopsy needle design enabling low deflection and without sacrificing tissue sampling length. In this paper, the needle deflection and tissue sampling length of the current single-bevel and new multi-bevel needle tip geometries are quantified and compared. To understand needle-tissue interaction under different needle tip geometries, a novel modeling approach using the Lagrangian analysis coupled with the smoothed particle Galerkin method is established to simultaneously predict the needle deflection and tissue deformation during insertion. The predicted needle deflections are experimentally verified using optically transparent tissue-mimicking phantoms. The model-predicted tissue contact with the needle groove is compared with the length of sampled ex-vivo chicken breast tissue samples.
II. Materials and Methods
A. Mechanics of Needle Deflection in Biopsy
Figure 2(a) shows the needle deflection mechanics in biopsy for a single-bevel needle (commonly used in current commercial biopsy devices). Assuming the bevel facet at the tip faces toward the negative y axis and the needle is inserted along the x axis, the tissue is cut and separated at tip point A, generating the cutting force Fc, top bevel face force Ft, top tissue load Pt, and friction force Ff. The location of point A causes the forces to concentrate on the top of the needle and create a downward bending moment Mt, bending this single-bevel needle downward by a deflection δs (along positive y axis). Since most biopsy needles have a high aspect ratio (commonly over 200, length >> diameter), the axial bending moments created by Fc and Ff are negligibly small compared to the longitudinal bending moments created by Ft and Pt. Using the Euler-Bemoulli beam bending equation, the δs can be modeled as:
| (1) |
| (2) |
where E is the Young’s modulus, I is the second moment of area of the single-bevel needle cross-section at x, Mt(x) is the Mt at x, C1 and C2 are constants, θt is the tip bevel angle, L is the needle length, and Pt(x) is the top tissue force per unit length. Although the needle tip and groove have varying cross-sections, the length from the tip point A to the end of the groove is negligibly small compared to the total needle length; therefore, I of a biopsv needle can be regarded as a constant.
Fig. 2.
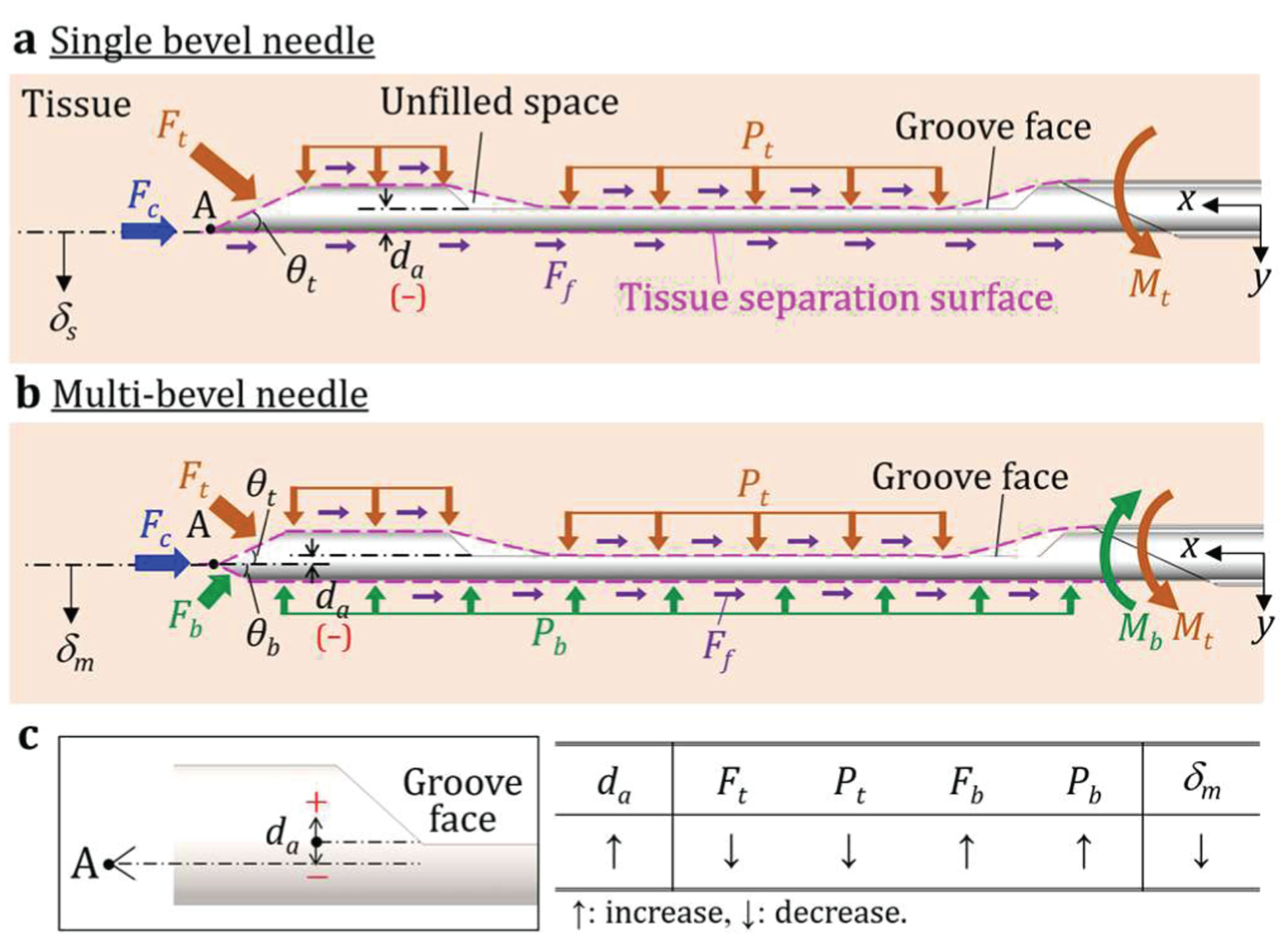
Needle deflection mechanics in biopsy for (a) a single-bevel needle (in current commercial biopsy devices) and (b) a multi-bevel needle with two bevel facets (as an example), and (c) the definition of da and its relationship with each variable.
To reduce δs, the multi-bevel needles have demonstrated the ability to alter the bending moments and reduce the resultant deflection [25]. Figure 2(b) shows the insertion of a multi-bevel needle with two bevel facets (as an example) converging to the tip point A. Due to the location of point A, the separated tissue at the bottom of the needle is slightly under compression during insertion, generating the bottom bevel face force Fb and the bottom tissue force load Pb. The combination of Fb and Pb creates an upward bending moment Mb against Mt to reduce downward deflection. Therefore, the deflection of a multi-bevel needle, defined as δm, can be modeled as:
| (3) |
| (4) |
| (5) |
where Mb(x) is the Mb at x, θt is the top bevel angle, θb is the bottom bevel angle, and Pb(x) is the bottom tissue force per unit length. Comparing (1) and (3), since the only difference between the single- and multi-bevel needles is the tip geometry, C1 and C2 are the same due to the same boundary conditions, and Mb opposes Mt, it can be concluded that δn < δs (i.e. the downward deflection is reduced).
Given the fact that most commercial trucut biopsy needles have the similar needle groove geometries (similar I), needle tip geometry becomes a dominant factor altering the forces acting on the needle. For a multi-bevel needle tip, the location of tip point A, which dictates the magnitudes of Ft, Pt, Fb, and Pb, can be defined by the distance from the needle tip point A to the needle groove face da, as shown in Fig. 2. Therefore, Mt(x) – Mb(x) in (3) and the resultant δm can be regarded as a function of da(i.e. δm=F(da)).
Fig. 2(c) shows the geometrical definition of da and its relationship with each variable. Positive and negative da mean the tip point A (tissue separation point) is above and below the groove face, respectively. When da increases, the area of bottom bevel increases, which increases Fb and Pb against the downward bending moments, and thus the resultant δm can be reduced. However, increasing da may cause the deflection to become significantly upward instead. Furthermore, increasing da may alter the tissue separation point to be above the needle groove face, which reduces the tissue contact inside the groove and compromises the subsequent tissue acquisition by the cannula [25]. It has been hypothesized that the tissue separation point may need to be below the needle groove face (negative da as shown in Fig. 2) to enable sufficient tissue sampling. This study aims to evaluate this hypothesis and confirm the effect of da on needle deflection and tissue sampling length.
B. Needle Tip Geometry
In this study, the existing single-bevel (SB) needle, as shown in Fig. 3(a), and three new multi-bevel needles, as shown in Figs. 3(b)–(d), are investigated. To maintain a low tissue separation point (decreasing da) while ensure the forces at the bottom of the needle can still reduce δm, this study invents a new multi-bevel needle geometry with four facets, top bevel (on the same side of the groove face), bottom bevel, and two side bevels. The side bevels are designed to not only partially generate the upward face forces, denoted as Fs in Fig. 3, to further reduce the downward bending, but also converge the facets to form a sharp needle tip point A, allowing effective tissue cutting during insertion [40].
Fig. 3.
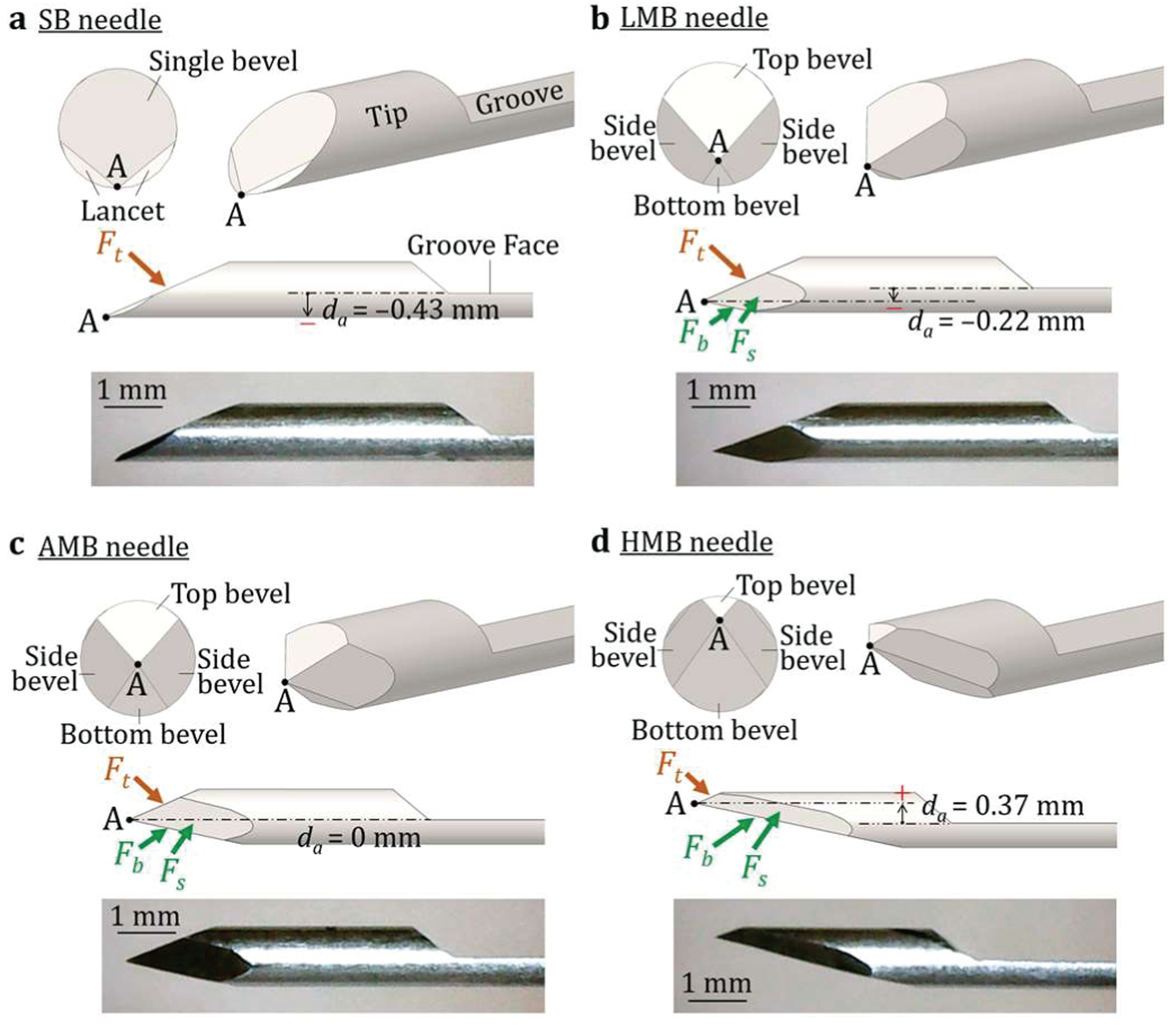
The needle tip geometry, tip face forces, and optical microscopy image of the (a) SB, (b) LMB, (c) AMB, and (d) HMB needles.
To investigate the effect of da, the three multi-bevel needles, shown in Figs. 3(b)–(d), with the negative, zero, and positive da, are investigated and denoted as the low multi-bevel (LMB), aligned multi-bevel (AMB), and high multi-bevel (HMB), respectively. In this study, four needle tip geometries and the groove were fabricated using the 18-gauge (1 mm diameter) AISI 304 stainless steel rod. In the fabrication, the steel rod was first tilted by a θt of 23.5° (Fig. 2) to grind a baseline bevel facet (for the SB needle). The lancets for the SB needle was added onto this bevel face to create a single cutting point [40], as shown in Fig. 3(b). For LMB, AMB, and HMB needles, the rod was then tilted to a θb of 12° and rotated around the needle centerline axis by 180° and ±110° from the baseline bevel facet to create the bottom and two side bevel facets, respectively. The ground amount for each bevel facet was determined by the da value listed in Fig. 3. Finally, the rod was tilted back to 0° to grind a needle groove with the length and thickness of 22 and 0.43 mm, respectively. All four needles had the same groove geometry for comparisons among the four needle tip geometries.
C. Needle-Tissue Interaction Model Formulation
This study develops a needle-tissue interaction modeling using the Lagrangian analysis coupled with the smoothed particle Galerkin (SPG) method, denoted as L-SPG, to investigate the needle deflection and tissue deformation in biopsy. Prior research on needle-tissue interaction utilized finite element analysis (FEA) to visualize the tissue deformation and contact with the needle during insertion. The cohesive zone (CZ) method in Lagrangian FEA was applied to model the tissue rupture by assigning the FEA element separation threshold level when contacting with the needle [41]–[43]. However, the CZ method requires a pre-defined element separation path during needle insertion and has limited accuracy due to large tissue deformation and mesh distortion at the needle tip. A coupled Eulerian-Lagrangian FEA has demonstrated the capability to effectively simulate tissue rupture and large tissue deformation by modeling the tissue and needle using the Eulerian and Lagrangian analysis, respectively [25]. However, the aforementioned studies assumed a rigid needle (no bending/deflection), and therefore have limited implication for improved needle design to achieve higher cancer diagnostic accuracy. A model to investigate the simultaneous needle deflection and tissue deformation, i.e., the coupled needle-tissue interaction phenomenon, remained unexplored prior to this study.
This study establishes a novel modeling approach using L-SPG to simultaneously predict the needle deflection and tissue deformation during insertion. SPG is a mesh-free method which discretizes the simulated object into particles [44] and has demonstrated the capability of modeling soft blood clot deformation in mechanical thrombectomy without mesh distortion [45]. However, the capability of modeling the interaction between two deformable objects (needle and tissue in this case) with a significant difference in hardness has not been investigated using SPG. In this study, the SPG method was coupled with the Lagrangian FEA to formulate the L-SPG, enabling the modeling of both tissue deformation and needle deflection during insertion. The Lagrangian mesh defines the needle boundary with fine spatial resolution to precisely represent the needle geometry (particularly the sharp needle tip) and bending deformation during interaction. The needle was modeled by the Lagrangian meshed elements which ensured continuity between neighboring elements (no interaction bonds as SPG particles), allowing the representation of needle deflection while maintaining the contact boundary when interacting with highly deformable tissue.
The three-dimensional (3D) L-SPG model was developed in LS-DYNA (v971 R11 by LSTC, Livermore, California, USA). An example of the SB needle insertion into the soft tissue is shown in Fig. 4. The L-SPG model comprises three regions: tissue, needle, and cannula. Due to the symmetry of geometry, only half of tissue, needle, and cannula were modeled. Fig. 4(a) shows an isometric view from the symmetric plane CDEF before the needle insertion. The tissue was modeled as a cuboid CDEFGHIJ (40 mm × 8 mm × 2 mm) and discretized into the SPG particles with the particle center equally spaced by 0.4 mm in all three (xyz) directions, as shown in Figs. 4(b)–(d). The SPG kernel function was cubic B-spline function with normalized dilation parameter of 1.8 in LS-DYNA [46]. The symmetric plane CDEF was constrained in z-axis, allowing the deformation on the xy plane as shown in Fig. 4(c). Three outer boundary surfaces CFJG, GHIJ, and HDEI were fixed in all three (xyz) directions. Surfaces FEIJ (the entry surface of the needle insertion) and CDHG (the back surface of the tissue model) were set as the free surfaces allowing the deformation in all three (xyz) directions as shown in Fig. 4(d).
Fig. 4.
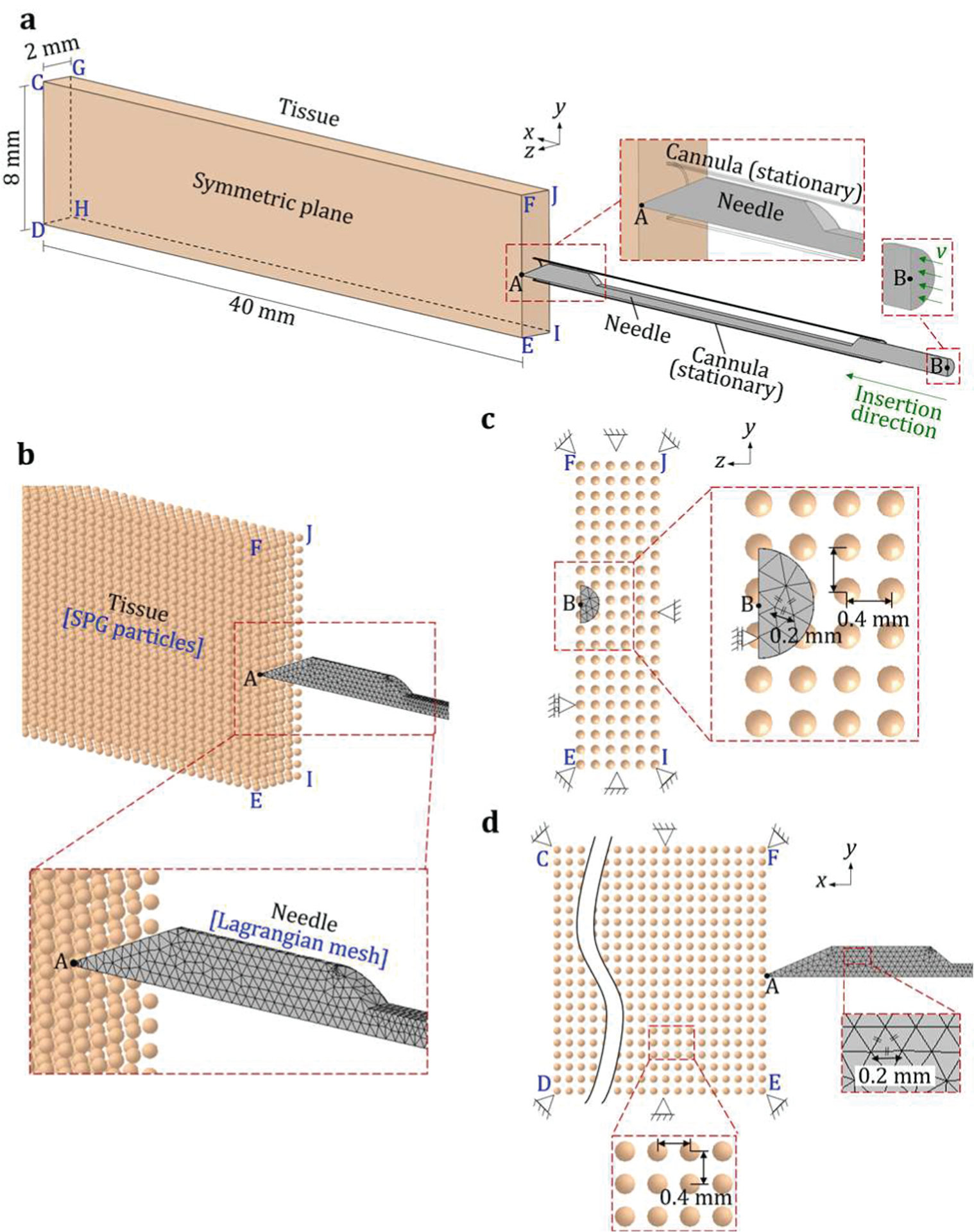
An overview of a 3D L-SPG model of needle-tissue interaction: (a) an isometric view of the SB needle insertion into the soft tissue and the (b) isometric, (c) front (yz plane), and (d) side (xy plane) views of the SPG tissue particles and Lagrangian needle meshes.
Four needles (SB, LMB, AMB, and HMB needles) were modeled using the Lagrangian mesh in the L-SPG model with geometries defined in Fig. 3. The needle was meshed by the 10-node quadratic tetrahedron elements with the initial size of 0.2 mm element edge length using Abaqus (v6.11 by Dassault Systèmes, Vélizy-Villacoublay, France). The meshes in regions around the sharp needle tip and groove edges were automatically refined to precisely represent the geometrical features as the close-up view shown in Fig. 4(b). The refined meshes of four needles were imported to the L-SPG model in LS-DYNA. The needle symmetric plane (coincident with plane CDEF) was constrained in z-axis while allowing the needle deflection on the xy plane, as shown in Fig. 4(c). The needle base plane, the plane through the base point B and perpendicular to the axis, as shown in Fig. 4(a), defined the given needle motion. This base plane was accelerated from 0 to 8 m/s along the x-axis in 0.75 ms for a 30-mm travel in x-axis, which were measured experimentally using the high-speed camera images of a needle biopsy device used in this study.
The stationary cannula, as shown in Fig. 4(a), supported the needle during the insertion to stabilize the needle tip for the initial contact with the tissue and avoid needle buckling. This cannula was modeled as a rigid shell with an outer diameter of 1.27 mm and a thickness of 0.05 mm (18 gauge), as shown in Fig. 4(a), and fixed in all three (xyz) directions.
D. Material and Contact Properties
In the L-SPG model, the AISI 304 stainless steel needle was modeled as a linear elastic material with the elastic modulus E, Poisson’s ratio v, and density ρ of 193 GPa, 0.29, and 8 g/cm3, respectively. The tissue-mimicking polyvinyl chloride (PVC) material was used as a soft tissue surrogate in the model and the needle deflection experiments for model validation. The transparent PVC materials, with the hardness and needle insertion properties similar to in-vivo prostate tissues [47], [48], are commonly used as the tissue surrogates in the needle insertion studies to act as an accessible, controllable, and consistent experimental platform to observe and quantify needle-tissue interaction prior to ex-vivo tissue or human studies [25], [39], [47]–[50]. In this study, the softener, PVC polymer (both by M-F Manufacturing, Ft. Worth, Texas, USA), and mineral oil (by W.S. Dodge Oil, Maywood, California, USA) were blended together to create the tissue surrogate material with Shore OOO-S hardness of 34, v of 0.45, and ρ of 0.98 g/cm3 to mimic the healthy prostate tissue based on clinician’s haptic estimation for the hardness of prostate [25], [48].
For the SPG-modeled object, any two neighboring particles have an interaction bond [46]. This interaction bond is disconnected once the average effective strain and stretch ratio reach a specific threshold level and then the material separation occurs. To simulate the rupture/separation of the SPG-modeled tissue in this study, the PVC tensile and rupture properties were obtained based on the ASTM D412 uniaxial tensile test of 16.5 mm gauge length. Five specimens were tested to obtain the average true stress vs. true strain curve up to the rupture point. The resultant average true stress vs. true strain curve was then fitted using a power law plasticity equation: σ = kɛn, where σ is the true stress, k is the strength coefficient, ɛ is the true strain, and n is the hardening coefficient. For the PVC in this study, k = 0.35 MPa, n = 2.75, and the root mean square error for this fitting was equal to 0.002. For the tissue separation in the L-SPG model, two adjacent SPG particles would separate when the average effective tensile strain exceeds 1.84 based on the derived stress-strain curve. To account for the strain rate dependency of the PVC during the high-speed needle insertion in biopsy, the Cowper and Symonds model [51] was used to scale the true stress with a factor of where C and p are two material constants and is the strain rate. In this study, the C and p were set as 0.1 ms−1 and 0.1, respectively. The friction coefficient μ of 0.18 was used at the contact between the needle and tissue [25].
E. Needle Deflection Experimental Setup
The setup for the needle deflection experiment is shown in Fig. 5. The PVC tissue-mimicking material applied in the L-SPG model was used to fabricate the transparent PVC phantom with 100 mm in length, 80 mm in width, and 30 mm in height, as shown in Fig. 5(a). A commercial spring-loaded needle biopsy device (SelectCore Variable Throw Biopsy Device by Inrad, Kentwood, Michigan, USA) was used to perform the needle insertion with a 25 mm firing length for both needle and cannula (Fig. 5(b)). Both needle and cannula were installed on the biopsy device and supported by a prostate biopsy guide (Endfire Biopsy Guide by BK Medical, Peabody, Massachusetts, USA). The biopsy guide had a plastic semi-cylindrical body for the ultrasound probe guide and a metal tube for the needle guide (Fig. 5(a)). The needle guide was fixed to position the needle and support it to avoid buckling during needle insertion. In the experiment, the needle guide was used to place the needle at the surface of the phantom for insertion. The biopsy device fired only the needle at a high speed (about 4 m/s) to have a clear view of the needle deflection.
Fig. 5.
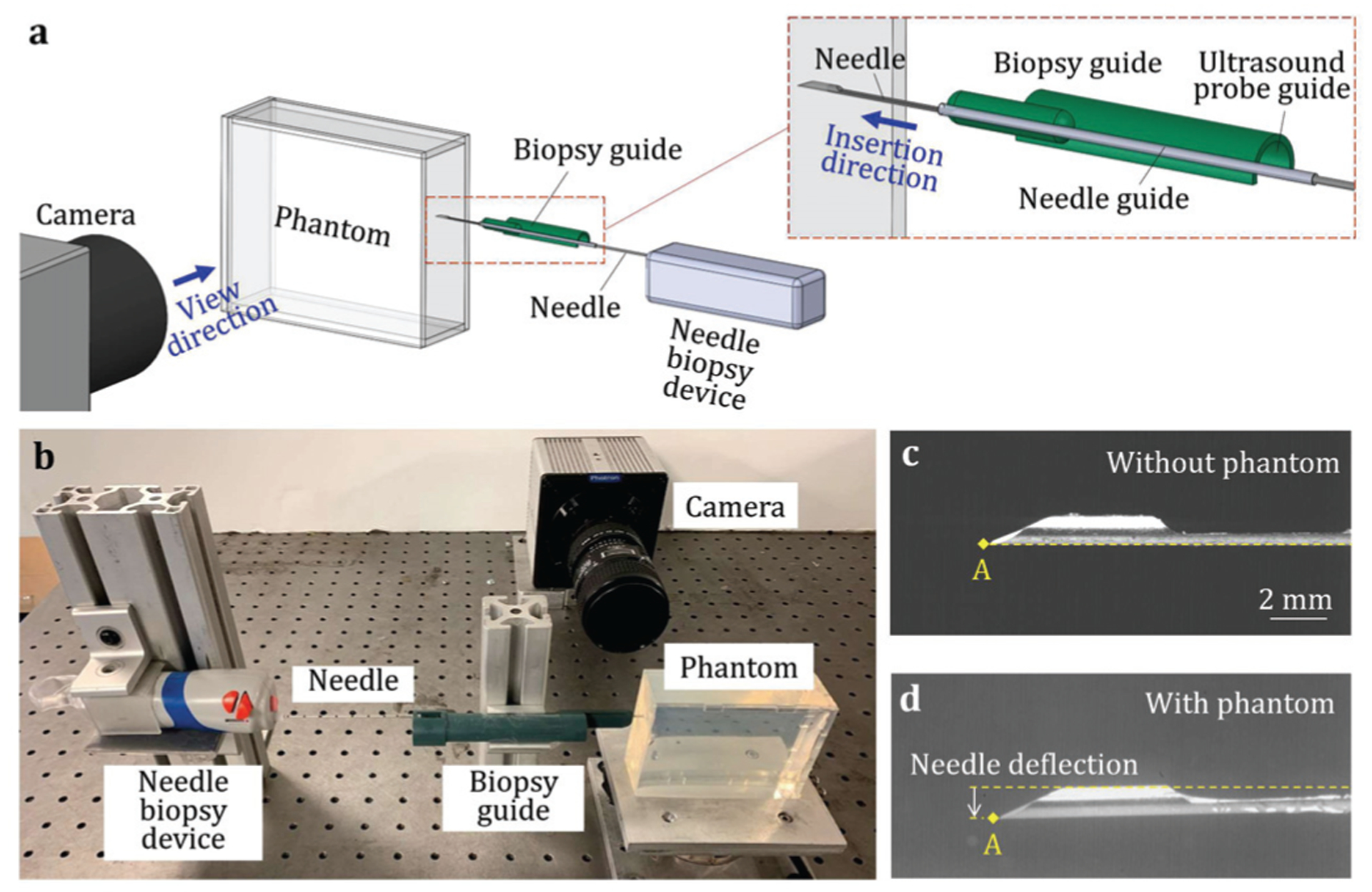
(a) An overview of the needle deflection experiment, (b) the experimental setup, and the images with the locations of SB needle tip point A at the end of the insertion (c) without and (d) with the PVC phantom.
To quantify the needle deflection, this study adopted a method used in the clinical biopsy procedures [24] by measuring the differences between the needle tip positions before and after the insertion. In this study, a high-speed camera (Model 100K by Photron, San Diego, California, USA) with 1024×1024 pixel resolution and a 5.6× magnification was used to capture the images of needle tip before and after the insertion into the transparent tissue-mimicking phantom. To acquire the baseline tip position without deflection, the needle was first inserted without the phantom as the image of SB needle shown in Fig. 5(c). The needle was then advanced by the biopsy device into the transparent phantom as shown in Fig. 5(d). The needle deflection δ was calculated as the vertical distance between the final tip locations with and without the phantom [24], [25]. Ten insertions of each needle tip type (SB, LMB, AMB, and HMB) were performed at different locations in the phantom. A total of 40 needle insertion tests were performed. The images were analyzed using Matlab (R2019a by MathWorks, Natick, Massachusetts, USA) to identify the needle tip locations and quantify the deflections.
F. Ex-Vivo Tissue Sampling Test
The tissue sampling length, which is a parameter used clinically to quantify the sampling amount in biopsy [25], were quantified for four needle tip types (SB, LMB, AMB, and HMB) in the trucut needle biopsy test using the ex-vivo chicken breast tissue. The needle and outer cannula were sequentially fired by the biopsy device via the biopsy guide (Fig. 5(b)) into the ex-vivo tissue fixed on a platform for tissue sampling. For each type of needle tip, ten insertions were performed at different locations of the ex-vivo tissue. A total of 40 needle insertion tests were conducted. The length of each tissue sample was measured using a digital caliper with the sample stayed on the needle groove after biopsy. The needle and cannula were rinsed for cleaning before the next insertion.
G. Statistical Analysis
The one-way analysis of variance (ANOVA) tests were performed using SPSS (by SPSS, Chicago, Illinois, USA) to calculate the statistical significance among the experimental data of needle deflection and the lengths of tissue samples for SB, LMB, AMB, and HMB needles. Each needle has ten data points for each measured variable. A total of 40 data points were used in each ANOVA test. The mean values in each experiment of any two of the four needles were compared (pairwise comparisons) to calculate the p values with Bonferroni correction at 95% confidence level.
III. Results
A. Needle-Tissue Interaction Modeling Results
The needle-tissue interactions for SB, LMB, AMB, and HMB needles in the L-SPG model are illustrated in Figs. 6 and 7. Results of the full insertion for each needle are shown in Supplementary Video SI. Fig. 6 presents the model-predicted displacement of the needle and tissue in the y-axis (the direction of needle deflection) during insertion. The model-predicted needle deflection δp was defined as the y-displacement at the needle tip point A. The SPG particles highlighted by the pink circles delineate the shape of the separated tissue within the needle groove. Fig. 7 shows the distribution of the minimal principle strain computed in the L-SPG model, denoted as strain hereafter, to qualitatively study the resultant tissue deformation. Fig. 6(a) shows the side view of symmetric plane CDEF with the undeformed SB needle (as an example) and tissue at the start of needle insertion (L = 0 mm). The undeformed tissue has zero strain as shown in Fig. 7(a).
Fig. 6.
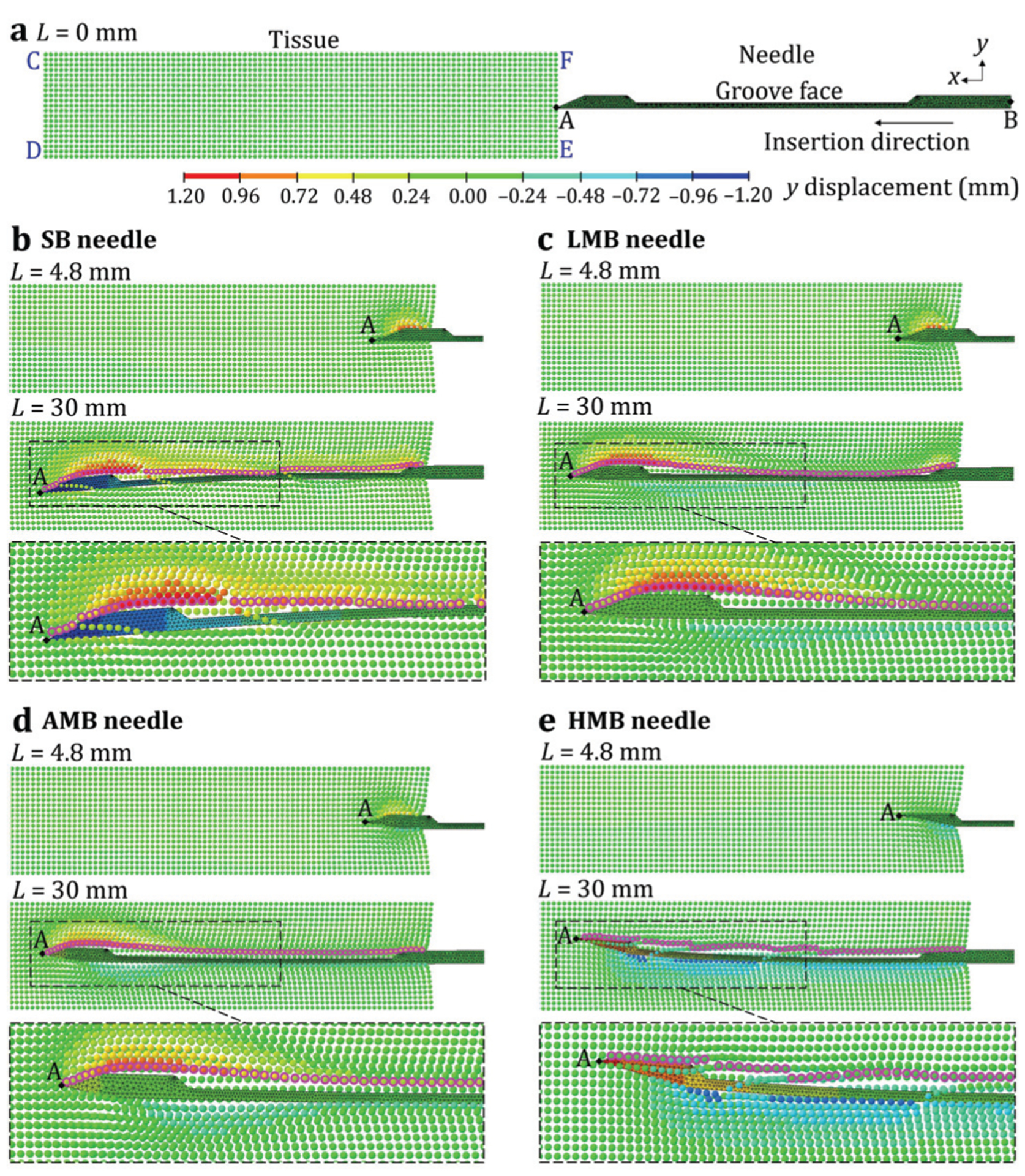
The L-SPG displacement results of the needle and tissue: (a) the undisplaced SB needle and the tissue before the insertion and the (b) SB, (c) LMB, (d) AMB, and (e) HMB needles during the insertion.
Fig. 7.
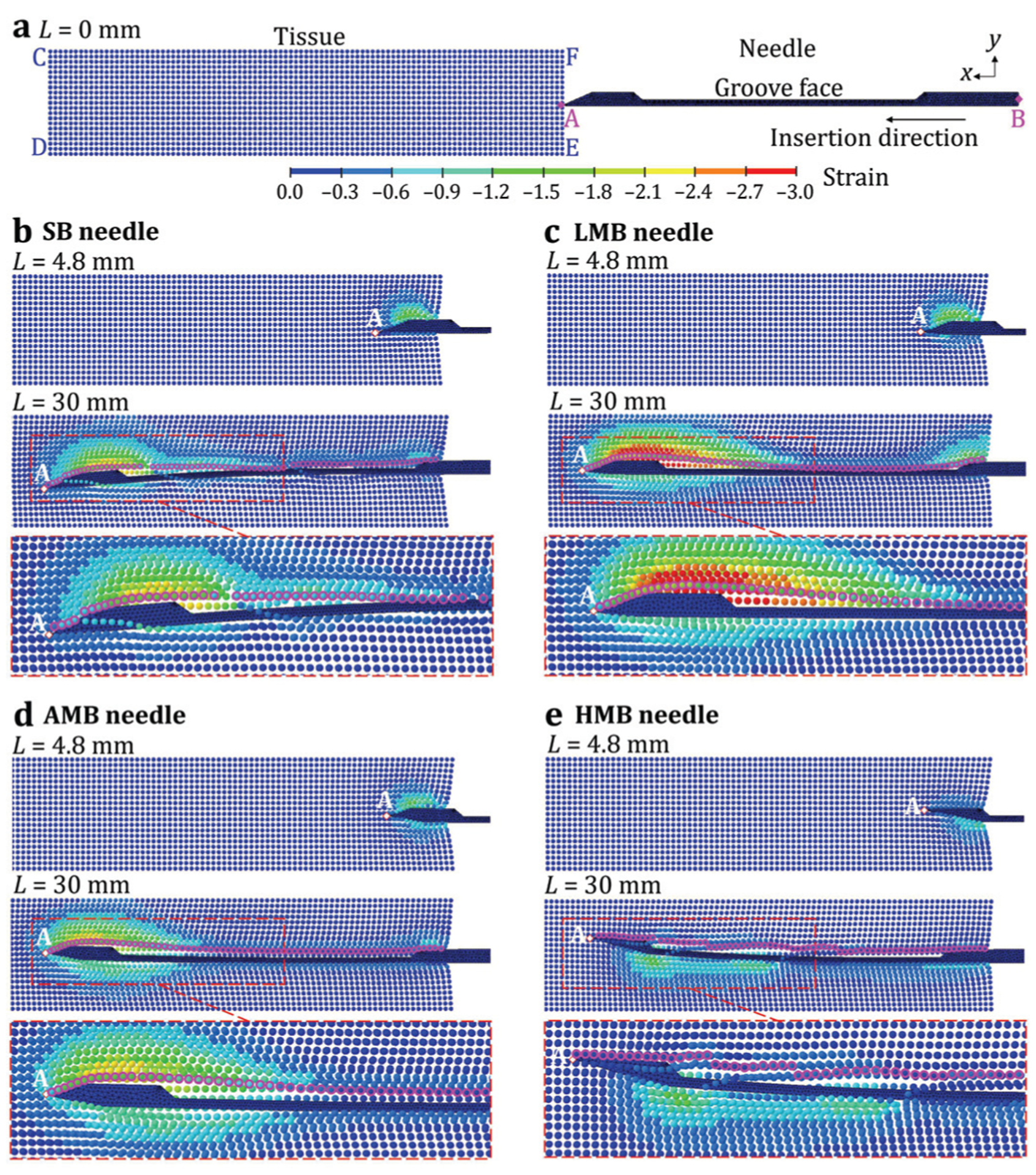
The L-SPG stain results of the needle and tissue: (a) the undisplaced SB needle and the tissue before the insertion and the (b) SB, (c) LMB, (d) AMB, and (e) HMB needles during the insertion.
Fig. 6(b) shows the distribution of displacement during the insertion of SB needle (da = −0.43 mm) at insertion length L = 4.8 and 30 mm. At L = 4.8 mm, the δp was almost 0 mm and the needle was mostly supported by the cannula without deflection. The tissue was cut and separated at the needle tip point A. The separated tissue on the top of the needle was pushed upward, resulting in a high compressive strain of about −1.2 around the needle tip, as shown in Fig. 7(b). The bottom separated tissue was almost undeformed with zero strain because point A was at the bottom of the needle tip surface. At L = 30 mm, as shown in Fig. 6(b), the needle deflected significantly downward with the δp of −1.15 mm. This δp is similar to the clinically measured 1.77 mm needle defection (using ultrasound images) in prostate biopsy [24]. The tissue in front of the needle was greatly deformed with a highly concentrated compressive strain of about −1.8 at the top of the needle tip as shown in Fig. 7(b). Such tissue deformation exerted a high reaction force on the bevel face of the needle tip, inducing over 1 mm downward deflection of the needle tip. Once the separated tissue reached the groove opening, it rebounded from its compression state and filled in the groove. The SB needle has the tissue separation point below the groove face (da < 0) which allowed the rebounded tissue to contact the groove face as illustrated by the highlighted tissue shape within the groove in Figs. 6(b) and 7(b). Such contact could enable the needle and outer cannula to acquire a long tissue sample length in needle biopsy. However, the filled tissue remained at the slight compression state with the compressive stain of about −0.6, generating a compressive load on the groove face and further aggravating the downward needle deflection.
Fig. 6(c) shows the distribution of displacement during the insertion of LMB needle (da = −0.23 mm). At L = 4.8 mm, similar to the SB needle, the δp was 0 mm. The multi-bevel LMB needle, compared to the SB needle, had the bottom and side bevel faces deforming and pushing the tissue downward (negative y-displacement) during the insertion. This led a compressive strain of about −0.45 at the bottom of the needle tip, generating the upward face forces to help prevent the needle tip from downward deflection, as shown in Fig. 7(c). At L = 30 mm, the needle deflection magnitude was much reduced compared to that of SB needle with the upward δp of 0.12 mm (Fig. 6(c)), as a result of the multi-bevel faces at the needle tip. Since the LMB needle also has the da < 0, the tissue also rebounded to contact the groove face as illustrated by the highlighted tissue shape in Figs. 6(c) and 7(c), similar to the tissue contact observed in the SB needle insertion. The filled tissue in the needle groove was also in a compressive state with compressive strain of about −0.6, generating tissue pressure on the groove face as shown in Fig. 7(c). However, the upward face forces on the bottom and side bevel faces provided the opposing bending moments to reduce the downward deflection caused by the top bevel face force and the tissue pressure on the groove face. This enabled the LMB needle to have low needle deflection and high tissue sampling in biopsy.
Fig. 6(d) shows the insertion of AMB needle (da = 0 mm) with the resultant displacement. At L = 4.8 mm, compared to the LMB needle, the AMB needle further deformed the tissue downward during the insertion due to the larger bottom and side bevel faces, causing a compressive strain of about −0.6 at the bottom of the needle tip. At L = 30 mm, the upward needle deflection was increased compared to that of the LMB needle with a δp of 0.28 mm. Compared to the LMB needle, as shown in Fig. 7(d), the compressive strain at the bottom of the needle tip was increased to about −0.9 which caused larger upward face forces, deflecting the needle upward. The AMB needle has a higher tissue separation point relative to the groove face (da = 0) compared to the SB and LMB needles, leading to almost no tissue contact inside the groove as the highlighted tissue shape shown in Figs. 6(d) and 7(d). At this state, tissue around the groove mostly rebounded back to the undeformed state with the strain close to 0. This phenomenon can lead to reduced tissue sampling length compared to the SB and LMB needles.
Fig. 6(e) show the insertion of HMB needle (da = 0.37 mm). At L = 4.8 mm, the HMB needle mostly deformed and pushed the separated tissue downward as a result of the bottom bevel face which was much larger than the other three faces. This led to a concentrated compressive strain of about −0.75 at the bottom of the needle tip as shown in Fig. 7(e). At L = 30 mm, the needle was significantly deflected upward with a δp of 1.03 mm (Fig. 6(e)). At this state, the tissue at the bottom of the needle was greatly deformed with the compressive strain of about −1.20, as shown in Fig. 7(e). This generated a large force on the bottom bevel face of the HMB needle, significantly deflecting the needle upward. The HMB needle had the highest tissue separation point (da > 0) amongst the four needles. This resulted in no tissue contact with the groove face and further increased the gap between the tissue and the groove compared to that of AMB needle, as the tissue shape delineated by the highlighted SPG particles shown in Figs. 6(e) and 7(e).
B. Needle Deflection Measurement Results
To verify the modeling results, the L-SPG predicted δp was compared with the experimentally measured needle deflection δ in the experiments using the optically transparent PVC tissue-mimicking phantoms (with the same material properties used in the L-SPG model). Fig. 8(a) shows the images of needle tip point A in the experiment. The top images show the baseline needle tip location before the insertion with the yellow dashed line marked as the insertion path without deflection. The bottom images show the needle with δ after inserting into the transparent phantom. Results of the full insertion into the phantom for each needle are shown in the Supplementary Video SI.
Fig. 8.
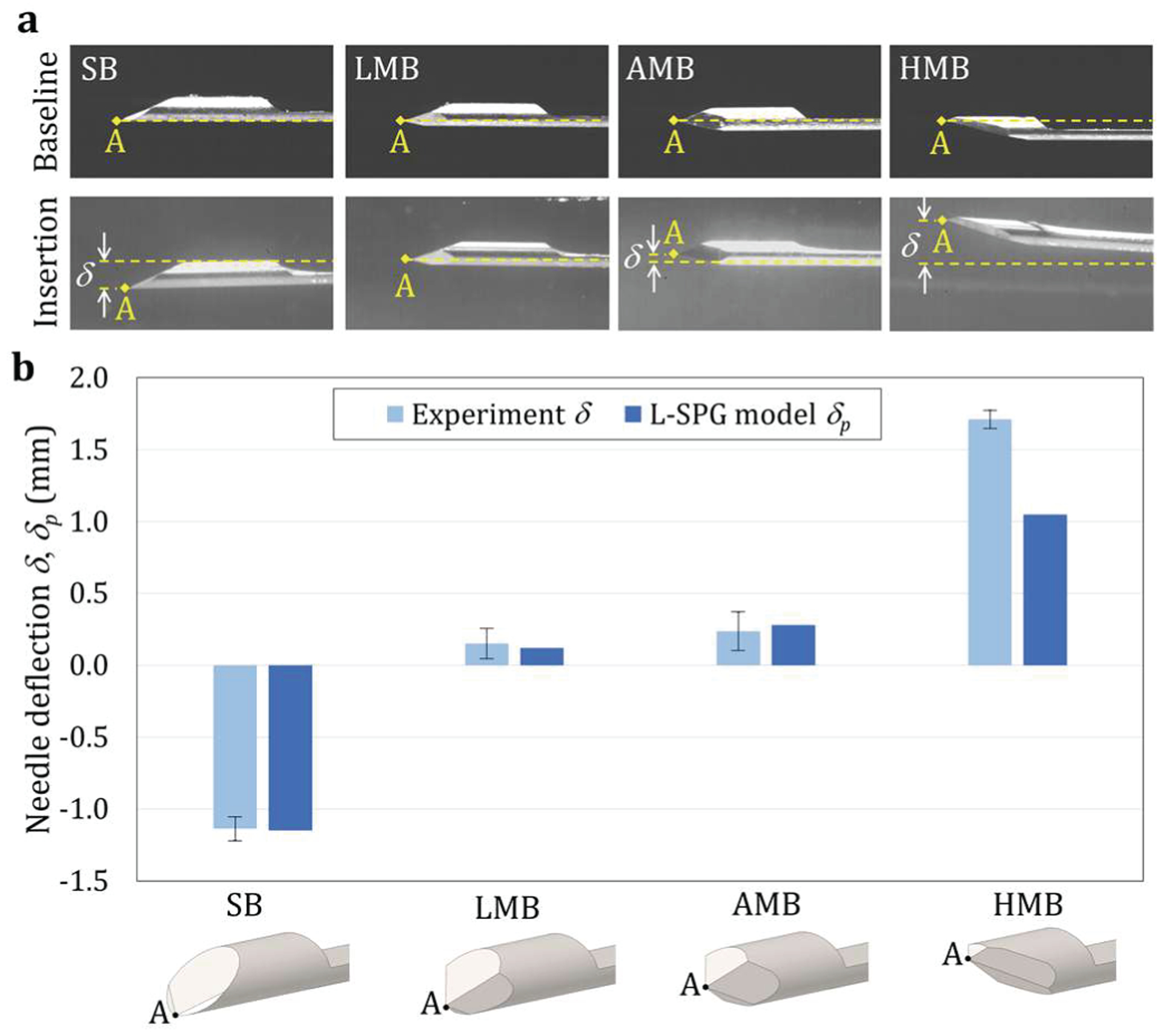
Needle deflection measurement results: (a) the experimental images of needle tip point A at the baseline locations (top) and after the insertion into the transparent PVC phantom in the experiment (bottom) and (b) the L-SPG predicted needle deflection δp vs. the experimental measured needle deflection δ (error bars representing one standard deviation from 10 insertions) for the SB, LMB, AMB, and HMB needles.
Fig. 8(b) shows the average δ vs. δp for SB, LMB, AMB, and HMB needles. The error bars of δ represents one standard deviation from 10 insertion tests. Results show that the L-SPG model yielded the same needle deflection trend as observed in the experiments. The ANOVA analysis for δ also indicates that the effect of needle tip geometry on δ was statistically significant at 0.05 significance level with a yielded F ratio of 1220.4 and three degrees of freedom. The SB needle had the average δ and δp of −1.14 and −1.15 mm (downward), respectively. The magnitude of δ was comparable to the clinically measured needle deflection with a median value of 1.77 mm in prostate biopsy [24]. The downward forces on the single bevel tip and thin groove significantly deflected the needle (Figs. 6(b) and 7(b)). This resulted in the largest downward δ amongst the four needles (all with pairwise p < 0.001), as shown in Fig. 8(a).
The LMB needle had a low average δ and δp of 0.15 and 0.12 mm (upward), respectively. Compared to the SB needle, the magnitude of δ for the LMB needle was much lower (p < 0.001) with an 87% reduction in deflection magnitude. This indicated that the LMB needle could potentially have better needle deployment accuracy in clinical biopsy procedures. The bottom and side bevel faces generated upward face forces which helped balance the downward bending moments caused by the top face force and tissue pressure on the groove face (Figs. 6(c) and 7(c)). This resulted in a slightly upward δ as shown in Fig. 8(a).
The AMB needle had the upward average δ and δP of 0.24 and 0.28 mm, respectively. Compared to the LMB needle, the AMB needle had larger bottom and side bevel faces and generated upward forces deflecting the needle upward (Figs. 6(d) and 7(d)). This led to a slightly larger upward but similar δ compared to that of LMB needle (p = 0.457, non-significant), as shown in Fig. 8(a). The HMB needle had the largest upward average δ and δp of 1.71 and 1.03 mm, respectively. Since the bottom bevel face was much larger than the other three faces, the combined bottom and side face forces significantly deflected the needle upward (Figs. 6(e) and 7(e)). This caused the largest upward δ among four needles (all with pairwise p < 0.001).
The L-SPG model demonstrated a reasonably good prediction, with the δ and δp discrepancy of 0.01, 0.03, and 0.04 mm for the SB, LMB, and AMB needles, respectively. The error for L-SPG model prediction of HMB needle was the largest amongst the four needles. The model underpredicted the upward deflection of HMB needle by 0.68 mm. This was possibly due to computational errors at the needle-tissue contact under large needle deflection which caused particle penetration issues as observed in the SB (Figs. 6(b) and 7(b)) and HMB (Fig. 6(e) and 7(e)) needle insertions. In the HMB needle, it was observed that the particle penetration at the tip led to reduced tissue contact with the bottom and side bevel faces at the HMB needle tip. This was reflected in the tissue at the bottom of the needle tip which was almost undeformed (almost no contact at the region close to the needle tip point A). Therefore, the upward face forces and the resultant needle deflection for the HMB needle in the L-SPG model were underpredicted.
C. Tissue Sampling Length Measurement Results
To evaluate the effect of needle tip geometry on tissue sampling, the L-SPG model predicted shape of the separated tissue within the groove was qualitatively compared to the sampling length of ex-vivo tissue in trucut biopsy. Fig. 9 shows the experimentally measured tissue sampling length ls for SB, LMB, AMB, and HMB needles. The error bars represent one standard deviation of 10 insertion tests. Results show that the da, which affects the shape of tissue within the needle groove (as shown in the L-SPG modeling results), correlates with ls for all four needles. The ANOVA analysis for ls also indicates that the effect of needle tip geometry on ls was statistically significant at 0.05 significance level with a yielded F ratio of 17 and three degrees of freedom.
Fig. 9.
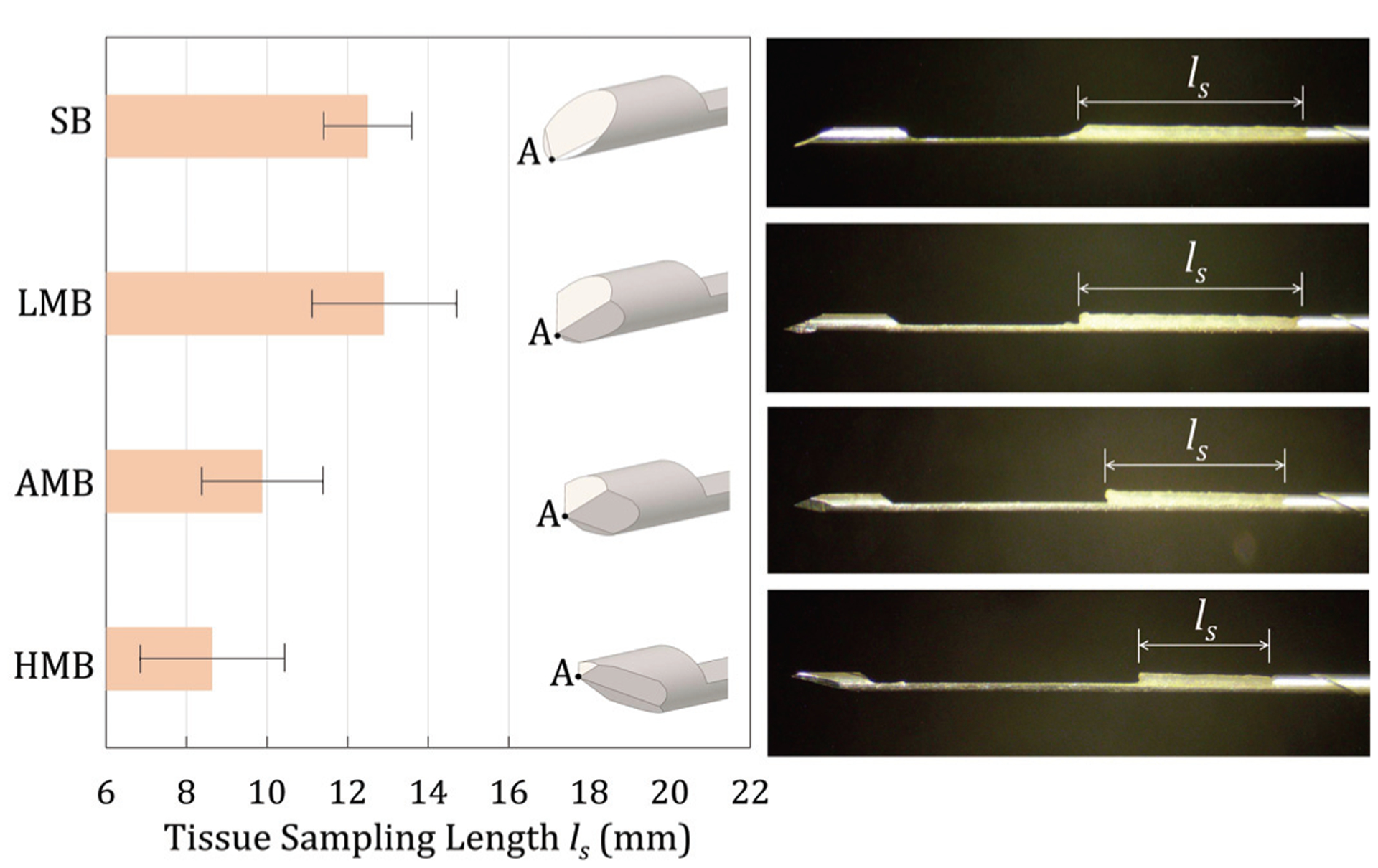
The experimental results of ex-vivo tissue sampling length ls (left) and the microscopy images (right) of tissue samples for the SB, LMB, AMB, and HMB needles (the error bar representing one standard deviation from 10 biopsies)
The SB (da = −0.43 mm) and LMB (da = −0.22 mm) needles yielded longer sampling lengths with an average ls of 12.5 and 12.9 mm, respectively. The LMB needle demonstrated similar sampling performance with ls equivalent to that of SB needle (p = 1.000, non-significant). For both SB and LMB needles, as shown in Figs. 7(b) and (c), respectively, the tissue was cut and separated below the groove face (da < 0) which allowed the rebounded tissue to fill and contact the groove. Such tissue contact enabled the long (over 12 mm) tissue samples in biopsy. The AMB needle (da = 0 mm) had the ls of 9.9 mm. The AMB needle, compared to the SB and LMB needles, had a higher da, leading to almost no tissue contact inside the groove as shown in Fig. 7(d). This was reflected as a shorter ls compared to the SB and LMB needles (p < 0.005 with both SB and LMB needles). The HMB needle had the highest da (= 0.37 mm) among four needles and the shortest ls of 8.6 mm. This high da also increased the gap between the tissue and the needle groove face (as shown in Fig. 7(e)) and resulted in a short ls compared to the other three needles (p < 0.001 with both SB and LMB needles, p = 0.510 with the AMB needle).
IV. Discussion
There are two major contributions from this study to potentially enable accurate needle deployment and adequate tissue sampling to improve cancer diagnostic accuracy in needle biopsy. First, a novel modeling approach using L-SPG has been established and demonstrated the capability of simultaneously modeling the needle deflection and tissue deformation during needle insertion. Unlike existing FEA models which are limited to rigid needle insertion [25], [41]–[43], this new L-SPG methodology allows a more realistic investigation of needle-tissue interaction with coupled needle deflection and tissue deformation. The L-SPG modeling results in this study showed a reasonably good prediction on the correlation of the needle tip type (SB, LMB, AMB, and HMB needles) vs. the resultant needle deflection and tissue sampling length. However, some SPG particle penetrations (a few separated SPG particle lines crossed through the needle) were found under large needle deflection, as observed in the SB (Figs. 6(b) and 7(b)) and HMB (Fig. 6(e) and 7(e)) needle insertions. These were potentially due to the relatively coarse SPG particle density compared to the needle meshes, which caused some computational errors under large tissue deformation when interacting with the deflected needle. Such errors led to the non-physical phenomenon of several SPG particles still connected to and not fully separated from the tissue during needle insertion. Future work will focus on evaluating the numerical stability and sensitivity of the proposed L-SPG method. The L-SPG mesh density including the needle Lagrangian elements and tissue SPG particles will be adjusted to more accurately represent the tissue deformation at the contact with the needle and assess the convergence in numerical analysis to avoid the particle penetration issues observed in this study. A more accurate tissue material model will also be explored to account for the hyperelastic behavior and inhomogeneity of real tissue, and the deformation and rupture under high strain rate in biopsy. The L-SPG modeling developed here is aimed to provide the insights of needle-tissue interaction, revealing the effect of needle tip geometry on needle deflection and tissue sampling length in biopsy.
Second contribution is the criteria of trucut biopsy needle design enabling low deflection and high tissue sampling length. The SB needle (da < 0) in current trucut biopsy devices caused large deflection but long tissue sample as a result of the single-bevel face at the tip. This SB tip separated the tissue at the bottom of the needle and deformed the tissue upward, generating large downward force to significantly deflect the needle [7], [24], [25]. Since the tissue separation point is below the groove face with da < 0, the SB needle allowed the tissue to fill the groove and enabled a long (over 12 mm) tissue sample [25]. However, such tissue contact generated the tissue pressure on the groove face which further aggravated the needle deflection.
The LMB needle (da < 0) was found to enable both low deflection and long tissue sampling. Compared to the SB needle, the LMB needle maintained a low tissue separation point while the bottom and side bevel faces generated upward face forces to balance the downward bending moments caused by the top face force and tissue pressure on the groove face. This resulted in a much lower deflection with an 87% reduction in deflection magnitude compared to that of SB needle. Since da < 0, the LMB needle also allowed the tissue to rebound and generate a good tissue contact with the needle groove face, similar to the SB needle insertion, ensuring the adequate tissue sampling for a long sampling length in biopsy.
The AMB needle (da = 0), compared to the LMB needle, also had a low deflection but with a shorter tissue sample length. The multiple faces at the AMB needle tip generated upward forces against the downward needle bending. However, since da = 0, the location of the tissue separation point was higher than that of SB and LMB needles, resulting in the shorter tissue sampling length. The HMB needle had the highest da among four needles, leading to a large upward deflection and the shortest tissue sampling length.
While the findings of needle deflection are limited to the homogeneous PVC tissue-mimicking phantoms, this study is the first step to evaluate the effectiveness of the multi-bevel biopsy needles in improving needle deployment accuracy as a proof-of-concept. Further assessments via ex-vivo tissue and in-vivo human prostate studies will be needed to confirm the clinical feasibility and safety of the developed LMB needle biopsy technology.
V. Conclusions
This study investigated the needle-tissue interaction to establish the scientific and technological foundations for accurate needle insertion with adequate tissue sampling in biopsy for cancer diagnosis. The L-SPG modeling methodology developed here can have broad applications for various clinical procedures to provide the insights of the interaction between the surgical tool and soft tissues. This L-SPG model can also serve as an evaluation platform to guide the development of needle technology enabling minimal needle deflection and tissue deformation.
This study has revealed two critical design criteria for an ideal needle in trucut biopsy: 1) the tissue separation point should be below the needle groove face (da < 0) to ensure long tissue sampling length and 2) the multi-bevel needle tip geometry, which can have bevel faces generating upward forces while maintaining a low tissue separation point, can be utilized to balance bending moments during insertion enabling a low needle deflection. In this study, the LMB needle has demonstrated to be an effective needle design with the lowest needle deflection and the highest average tissue sampling length amongst all four needles. This indicates that the LMB needle could potentially improve the needle deployment accuracy while maintaining adequate tissue sampling in clinical biopsy procedures. This LMB needle technology can be applied to various biopsy procedures as well as other procedures requiring accurate needle insertion.
Supplementary Material
Acknowledgments
This work was supported in part by NSF INTERN program #17-091, in part by NSF CMMI grant #1266063, and in part by NIH NCI STTR Phase I grant #1R41CA183315-01 through ProDevice Medical Supplies and Equipment LLC.
Contributor Information
Annie D.R. Li, Department of Mechanical Engineering, University of Michigan, Ann Arbor, Michigan, USA
Yang Liu, Department of Mechanical Engineering, University of Michigan, Ann Arbor, Michigan, USA..
Jeffrey Plott, Department of Mechanical Engineering, Department of Surgery, and Department of Biomedical Engineering, University of Michigan, Ann Arbor, Michigan, USA..
Lei Chen, Department of Mechanical Engineering, University of Massachusetts Lowell, Lowell, Massachusetts, USA and the Department of Psychiatry, University of Michigan, Ann Arbor, Michigan, USA..
Jeffrey S. Montgomery, Department of Urology, Michigan Medicine, University of Michigan, Ann Arbor, Michigan, USA.
Albert Shih, Department of Mechanical Engineering and Department of Biomedical Engineering, University of Michigan, Ann Arbor, Michigan, USA..
References
- [1].Kasraeian S, Allison DC, Ahlmann ER, Fedenko AN, and Menendez LR, “A Comparison of Fine-needle Aspiration, Core Biopsy, and Surgical Biopsy in the Diagnosis of Extremity Soft Tissue Masses,” Clin. Orthop. Relat. Res, vol. 468, no. 11, pp. 2992–3002, November. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Yang YJ and Damron TA, “Comparison of Needle Core Biopsy and Fine-Needle Aspiration for Diagnostic Accuracy in Musculoskeletal Leisons,” Arch. Pathol. Lab. Med, vol. 128, no. July, pp. 759–764, 2004. [DOI] [PubMed] [Google Scholar]
- [3].Kar A, Satapathy B, Pattnaik K, and Dash P, “Trucut biopsy vs FNAC of pelvic tumors-who wins the match?,” J. Cytol, vol. 35, no. 3, p. 179, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Schoots IG, Roobol MJ, Nieboer D, Bangma CH, Steyerberg EW, and Hunink MGM, “Magnetic Resonance Imaging-targeted Biopsy May Enhance the Diagnostic Accuracy of Significant Prostate Cancer Detection Compared to Standard Transrectal Ultrasound-guided Biopsy: A Systematic Review and Meta-analysis,” Eur. Urol, vol. 68, no. 3, pp. 438–450, September. 2015. [DOI] [PubMed] [Google Scholar]
- [5].Wu JS, Goldsmith JD, Horwich PJ, Shetty SK, and Hochman MG, “Bone and Soft-Tissue Lesions: What Factors Affect Diagnostic Yield of Image-guided Core-Needle Biopsy?,” Radiology, vol. 248, no. 3, pp. 962–970, September. 2008. [DOI] [PubMed] [Google Scholar]
- [6].Maier-Hein L et al. , “In vivo accuracy assessment of a needle-based navigation system for CT-guided radiofrequency ablation of the liver,” Med. Phys, vol. 35, no. 12, pp. 5385–5396, November. 2008. [DOI] [PubMed] [Google Scholar]
- [7].Abolhassani N, Patel RV, and Ayazi F, “Minimization of needle deflection in robot-assisted percutaneous therapy,” Int. J. Med. Robot. Comput. Assist. Surg, vol. 3, no. 2, pp. 140–148, June. 2007. [DOI] [PubMed] [Google Scholar]
- [8].Saslow D et al. , “American Cancer Society Guidelines for Breast Screening with MRI as an Adjunct to Mammography,” vol. 57, no. 2, pp. 75–89, 2007. [DOI] [PubMed] [Google Scholar]
- [9].Fütterer JJ et al. , “Can Clinically Significant Prostate Cancer Be Detected with Multiparametric Magnetic Resonance Imaging? A Systematic Review of the Literature,” Eur. Urol, vol. 68, no. 6, pp. 1045–1053, December. 2015. [DOI] [PubMed] [Google Scholar]
- [10].M. J. Berg WA, Zhang Z, Lehrer D, Jong RA, Pisano ED, Barr RG, Bohm-Velez M, Mahoney MC, Evans WP, Larsen LH and Morton, “Detection of breast cancer with addition of annual screening ultrasound or a single screening MRI to mammography in women with elevated breast cancer risk,” JAMA - J. Am. Med. Assoc, vol. 307, no. 13, pp. 1394–1404, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Valerio M et al. , “Detection of Clinically Significant Prostate Cancer Using Magnetic Resonance Imaging–Ultrasound Fusion Targeted Biopsy: A Systematic Review,” Eur. Urol, vol. 68, no. 1, pp. 8–19, July. 2015. [DOI] [PubMed] [Google Scholar]
- [12].Abi-Jaoudeh N et al. , “Multimodality Image Fusion-Guided Procedures: Technique, Accuracy, and Applications,” Cardiovasc. Intervent. Radiol, vol. 35, no. 5, pp. 986–998, October. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ewertsen C, Henriksen B, Torp-Pedersen S, and Bachmann Nielsen M, “Characterization by Biopsy or CEUS of Liver Lesions Guided by Image Fusion between Ultrasonography and CT, PET/CT or MRI,” Ultraschall der Medizin - Eur. J. Ultrasound, vol. 32, no. 02, pp. 191–197, January. 2011. [DOI] [PubMed] [Google Scholar]
- [14].Nakano S et al. , “Fusion of MRI and Sonography Image for Breast Cancer Evaluation Using Real-time Virtual Sonography with Magnetic Navigation: First Experience,” Jpn. J. Clin. Oncol, vol. 39, no. 9, pp. 552–559, September. 2009. [DOI] [PubMed] [Google Scholar]
- [15].Park HJ et al. , “Fusion Imaging-Guided Percutaneous Biopsy of Focal Hepatic Lesions With Poor Conspicuity on Conventional Sonography,” J. Ultrasound Med, vol. 32, no. 9, pp. 1557–1564, September. 2013. [DOI] [PubMed] [Google Scholar]
- [16].Sonn GA, Margolis DJ, and Marks LS, “Target detection: Magnetic resonance imaging-ultrasound fusion-guided prostate biopsy,” Urol. Oncol. Semin. Orig. Investig, vol. 32, no. 6, pp. 903–911, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Le JD et al. , “Magnetic Resonance Imaging-Ultrasound Fusion Biopsy for Prediction of Final Prostate Pathology,” J. Urol, vol. 192, no. 5, pp. 1367–1373, November. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mendhiratta N et al. , “Magnetic Resonance Imaging-Ultrasound Fusion Targeted Prostate Biopsy in a Consecutive Cohort of Men with No Previous Biopsy: Reduction of Over Detection through Improved Risk Stratification,” J. Urol, vol. 194, no. 6, pp. 1601–1606, December. 2015. [DOI] [PubMed] [Google Scholar]
- [19].Filson CP et al. , “Prostate cancer detection with magnetic resonance-ultrasound fusion biopsy: The role of systematic and targeted biopsies,” Cancer, vol. 122, no. 6, pp. 884–892, March. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Levy MJ, Lou Jondal M, Clain J, and Wiersema MJ, “Preliminary experience with an EUS-guided trucut biopsy needle compared with EUS-guided FNA,” Gastrointest. Endosc, vol. 57, no. 1, pp. 101–106, January. 2003. [DOI] [PubMed] [Google Scholar]
- [21].Lam WW, Chu WC, Tse GM, Ma TK, and Tang AP, “Role of fine needle aspiration and tru cut biopsy in diagnosis of mucinous carcinoma of breast—from a radiologist’s perspective,” Clin. Imaging, vol. 30, no. 1, pp. 6–10, January. 2006. [DOI] [PubMed] [Google Scholar]
- [22].Kalambokis G et al. , “Transjugular liver biopsy – Indications, adequacy, quality of specimens, and complications – A systematic review,” J. Hepatol, vol. 47, no. 2, pp. 284–294, August. 2007. [DOI] [PubMed] [Google Scholar]
- [23].Kim T-M et al. , “Regional biases in mutation screening due to intratumoural heterogeneity of prostate cancer,” J. Pathol, vol. 233, no. 4, pp. 425–435, August. 2014. [DOI] [PubMed] [Google Scholar]
- [24].Halstuch D, Baniel J, Lifshitz D, Sela S, Ber Y, and Margel D, “Assessment of Needle Tip Deflection During Transrectal Guided Prostate Biopsy: Implications for Targeted Biopsies,” J. Endourol, vol. 32, no. 3, pp. 252–256, March. 2018. [DOI] [PubMed] [Google Scholar]
- [25].Li ADR, Plott J, Chen L, Montgomeiy JS, and Shih A, “Needle deflection and tissue sampling length in needle biopsy,” J. Mech. Behav. Biomed. Mater, vol. 104, p. 103632, April. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Mozer PC, Partin AW, and Stoianovici D, “Robotic image-guided needle interventions of the prostate.,” Rev. Urol, vol. 11, no. 1, p. 7,2009. [PMC free article] [PubMed] [Google Scholar]
- [27].DiMaio SP et al. , “A System for MRI-guided Prostate Interventions,” in The First IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics, 2006. BioRob 2006, 2006, vol. 2006, pp. 68–73. [Google Scholar]
- [28].Ferrucci JT and Wittenberg J, “CT Biopsy of Abdominal Tumors: Aids for Lesion Localization,” Radiology, vol. 129, no. 3, pp. 739–744, December. 1978. [DOI] [PubMed] [Google Scholar]
- [29].Ridder GJ, Technau-Ihling K, and Boedeker CC, “Ultrasound-Guided Cutting Needle Biopsy in the Diagnosis of Head and Neck Masses,” Laryngoscope, vol. 115, no. 2, pp. 376–377, February. 2005. [DOI] [PubMed] [Google Scholar]
- [30].Atashzar SF, Khalaji I, Shahbazi M, Talasaz A, Patel RV, and Naish MD, “Robot-assisted lung motion compensation during needle insertion,” in 2013 IEEE International Conference on Robotics and Automation, 2013, pp. 1682–1687. [Google Scholar]
- [31].Zhou Y, Thiruvalluvan K, Krzeminski L, Moore WH, Xu Z, and Liang Z, “CT-guided robotic needle biopsy of lung nodules with respiratory motion - experimental system and preliminary test,” Int. J. Med. Robot. Comput. Assist. Surg, vol. 9, no. 3, pp. 317–330, September. 2013. [DOI] [PubMed] [Google Scholar]
- [32].Loeb S, Carter HB, Bemdt SI, Ricker W, and Schaeffer EM, “Complications After Prostate Biopsy: Data From SEER-Medicare,” J. Urol, vol. 186, no. 5, pp. 1830–1834, November. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Cowan NJ et al. , Surgical Robotics. Boston, MA: Springer US, 2011. [Google Scholar]
- [34].Lee H and Kim J, Intelligent Autonomous Systems 13, vol. 302. Cham: Springer International Publishing, 2016. [Google Scholar]
- [35].Fichtinger G et al. , “Robotic assistance for ultrasound-guided prostate brachytherapy,” Med. Image Anal, vol. 12, no. 5, pp. 535–545, October. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Krieger A et al. , “Development and Evaluation of an Actuated MRI-Compatible Robotic System for MRI-Guided Prostate Intervention,” IEEE/ASME Trans. Mechatronics, vol. 18, no. 1, pp. 273–284, February. 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Stoianovici D et al. , “Multi-Imager Compatible, MR Safe, Remote Center of Motion Needle-Guide Robot,” IEEE Trans. Biomed. Eng, vol. 65, no. 1, pp. 165–177, January. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Barbash GI and Glied SA, “New technology and health care costs—the case of robot-assisted surgery,” N. Engl. J. Med, vol. 363, no. 8, pp. 701–704, 2010. [DOI] [PubMed] [Google Scholar]
- [39].Abolhassani N, Patel R, and Moallem M, “Needle insertion into soft tissue: A survey,” Med. Eng. Phys, vol. 29, no. 4, pp. 413–431, May 2007. [DOI] [PubMed] [Google Scholar]
- [40].Wang Y, Tai BL, Chen RK, and Shih AJ, “The Needle With Lancet Point: Geometry for Needle Tip Grinding and Tissue Insertion Force,” J. Manuf Sci. Eng, vol. 135, no. 4, p. 041010, May 2013. [Google Scholar]
- [41].Misra S, Reed KB, Douglas AS, Ramesh KT, and Okamura AM, “Needle-tissue interaction forces for bevel-tip steerable needles,” in 2008 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, 2008, vol. 29, no. 4, pp. 224–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Oldfield M, Dini D, Giordano G, and Rodriguez y Baena F, “Detailed finite element modelling of deep needle insertions into a soft tissue phantom using a cohesive approach,” Comput. Methods Biomech. Biomed. Engin, vol. 16, no. 5, pp. 530–543, 2013. [DOI] [PubMed] [Google Scholar]
- [43].Tai BL, Wang Y, and Shih AJ, “Cutting Force of Hollow Needle Insertion in Soft Tissue,” in Volume 1: Processing, 2013, p. V001T01A007. [Google Scholar]
- [44].Wu Y, Wu CT, and Hu W, “Parametric and Convergence Studies of the Smoothed Particle Galerkin (SPG) Method in Semi-brittle and Ductile Material Failure Analyses,” 15th Int. LS-DYNA Users Conf, pp. 1–12, 2018. [Google Scholar]
- [45].Liu Y, Zheng Y, Li AD-R, Liu Y, Savastano LE, and Shih AJ, “Cutting of blood clots – Experiment and smooth particle Galerkin modelling,” CIRPAnn., vol. 68, no. 1, pp. 97–100, 2019. [Google Scholar]
- [46].Wu CT, Guo Y, and Hu W, “An Introduction to the LS-DYNA ® Smoothed Particle Galerkin Method for Severe Deformation and Failure Analyses in Solids,” 13th Int. LS-DYNA Users Conf., pp. 1–20, 2014. [Google Scholar]
- [47].Li W et al. , “Polyvinyl chloride as a multimodal tissue-mimicking material with tuned mechanical and medical imaging properties,” Med. Phys, vol. 43, no. 10, pp. 5577–5592, September. 2016. [DOI] [PubMed] [Google Scholar]
- [48].Li D, Yeh J-K, Lin W, Montgomeiy JS, and Shih A, “An Experimental Method of Needle Deflection and Prostate Movement Using the Anatomically Accurate Prostate Simulator and the Electromagnetic Tracking System,” in Volume 4: Bio and Sustainable Manufacturing, 2017, p. V004T05A010. [Google Scholar]
- [49].Li D-R, Yeh J-K, Putra K, and Shih A, “Optical Measurement of Tissue Deformation in Needle Insertion,” Procedia CIRP, vol. 65, pp. 175–179, 2017. [Google Scholar]
- [50].van Gerwen DJ, Dankelman J, and van den Dobbelsteen JJ, “Needle–tissue interaction forces – A survey of experimental data,” Med. Eng. Phys, vol. 34, no. 6, pp. 665–680, July. 2012. [DOI] [PubMed] [Google Scholar]
- [51].Snedeker JG et al. , “Strain-rate dependent material properties of the porcine and human kidney capsule,” J. Biomech, vol. 38, no. 5, pp. 1011–1021, May 2005. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


