Programmable Bloch polaritons in graphene

When light-matter polaritons travel in periodic media, they acquire properties akin to Bloch quasi-particles in crystals.

Abstract

Efficient control of photons is enabled by hybridizing light with matter. The resulting light-matter quasi-particles can be readily programmed by manipulating either their photonic or matter constituents. Here, we hybridized infrared photons with graphene Dirac electrons to form surface plasmon polaritons (SPPs) and uncovered a previously unexplored means to control SPPs in structures with periodically modulated carrier density. In these periodic structures, common SPPs with continuous dispersion are transformed into Bloch polaritons with attendant discrete bands separated by bandgaps. We explored directional Bloch polaritons and steered their propagation by dialing the proper gate voltage. Fourier analysis of the near-field images corroborates that this on-demand nano-optics functionality is rooted in the polaritonic band structure. Our programmable polaritonic platform paves the way for the much-sought benefits of on-the-chip photonic circuits.

INTRODUCTION

Photons provide an unparalleled resource for quantum technology (1–3), including quantum communications (4, 5), sensing (6), and computation (7, 8). However, free-space photons do not directly interact with electric or magnetic fields, making it difficult to efficiently program their properties. Hybridizing photons with matter gives rise to composite light-matter quasi-particles known as polaritons and creates new pathways for programmable optical phenomena (9–11). For example, the hybridization of photons and excitons in semiconductors results in exciton-polaritons that are amenable to both electronic and optical means of manipulation (12–20). Another prominent example of coupled light-matter quasi-particles are surface plasmon polaritons (SPPs), which are hybrids of photons and free electrons in conducting surfaces (21). Sophisticated designs of plasmonic structures have uncovered numerous ways to program SPPs (22–24). In complete analogy to Bloch electrons in solids or photons in photonic crystals, the dispersion of SPPs in periodic media reveals discrete bands separated by bandgaps (25–28). Thus, polaritonic crystals enable new means for programming the directional motion of SPPs by electrostatic control in planar gated structures.

Graphene SPPs are deeply subdiffractional optical modes (29, 30) with high quality factor. Systematic efforts uncovered the inherent tunability of graphene SPP wavelengths by gate voltage (31–38)—a feat that is difficult to achieve using alternative plasmonic media. We devised and demonstrated an as-yet-unexplored method for steering the direction of SPP travel in a pristine graphene layer. Specifically, we created a graphene polaritonic crystal (28) by introducing a periodic spatial modulation of the Fermi energy (39). In these designer crystals, graphene SPPs with continuous dispersion are transformed into Bloch polaritons residing in discrete bands (26, 28, 40–42). The propagation direction of Bloch polaritons is governed by the polaritonic bands in which they reside and can be readily controlled by gate voltage. Prior demonstrations of directional SPPs all relied on manipulating the photonic constituents of the polaritonic quasi-particles by selecting the handedness of the exciting laser beam (22, 43–50). We programmed Bloch polaritons by controlling their matter constituents using gate voltages.

RESULTS AND DISCUSSION

A schematic of our graphene polaritonic crystal is shown in Fig. 1A. A graphene device fully encapsulated between thin layers of hexagonal boron nitride (hBN) resides on top of a Si substrate with a thermally grown SiO₂ layer. The SiO₂ layer is patterned into a hexagonal array of pillars with lattice periodicity a = 85 nm (28, 39). An infrared laser beam at energy ω = 890 cm⁻¹ illuminates the entire device. Patterned gold launchers on top of the device excite Bloch polaritons propagating along the polaritonic crystal (Fig. 1A) (51). Our patterning techniques largely preserve the quality of the graphene devices (39), and we achieved a polariton damping rate of γ = 12 cm⁻¹ at low temperature.

Fig. 1. A platform for programmable Bloch polaritons.

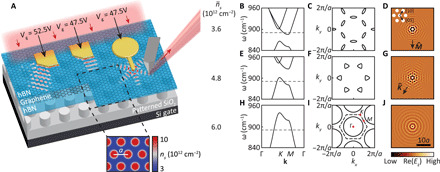
(A) Schematic of a back-gated graphene polaritonic crystal. Gold launchers excite Bloch polaritons propagating along designated directions controlled by the gate voltage V_g. Inset shows the carrier density distribution in the graphene layer with average carrier density ${\overline{n}}_s=4.5\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$. (B) Simulated polaritonic band structure at ${\overline{n}}_s=3.6\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$. Dashed line corresponds to ω = 890 cm⁻¹. (C) Simulated equi-energy contours at ${\overline{n}}_s=3.6\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$ and ω = 890 cm⁻¹, showing the polaritonic pockets around M points. (D) Simulated electric field Re(E_z) of polaritons excited by a point source at ${\overline{\mathit{n}}}_{\mathit{s}}=3.6\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$ and ω = 890 cm⁻¹. Bloch polaritons propagate predominantly along $\hat{M}=\mathrm{\langle }-11\mathrm{\rangle }$directions. Inset shows an enlarged real-space lattice pattern. (E) to (G), (H) to (J), same as (B) to (D) at ${\overline{n}}_s=4.8\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$ and ${\overline{n}}_s=6.0\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$, respectively. At ${\overline{n}}_s=4.8\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$, Bloch polaritons reside in the lower band (E), emerge in the K pockets (F), and propagate along $\widehat{\mathit{K}}=\langle 10\rangle$ directions (G). At ${\overline{\mathit{n}}}_{\mathit{s}}=6.0\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$, Bloch polaritons reside entirely in the lower band (H), exhibit circular equi-energy contours (I) and propagate isotropically in all directions (J). Inset of (I) shows the first BZ marked with symmetry points.

Optical phenomena in our patterned polaritonic platform can be categorized under the notion of a polaritonic crystal (25). Specifically, the patterned substrate introduces a nanoscale periodic variation of the dielectric constants in the immediate proximity of the graphene layer. Under the application of a back gate, the variations in the capacitive coupling is imprinted as carrier density modulation in graphene (Fig. 1A, inset). Propagating polaritons scatter and interfere in regions with varying carrier densities, leading to the formation of the polaritonic band structure and Brillouin zones (BZ) (Fig. 1, B, E, and H) (26). At crystal momentum away from the BZ boundary, polariton dispersion is minimally affected by the periodic modulation and largely follows the dispersion in unpatterned devices as ${\mathrm{\omega }}_{\text{SPP}}\propto \sqrt{{\mathit{E}}_{\mathrm{F}}\mathit{k}}$, where E_F is the graphene Fermi energy and k is the SPP momentum. Near the boundary of the BZ, polariton dispersion is strongly modified, which leads to the formation of a complete bandgap for laser energies between 870 and 890 cm⁻¹ (Fig. 1B). At a probe laser energy of ω = 890 cm⁻¹, we excite polaritons residing in the upper polaritonic band. By tuning the graphene carrier density from ${\overline{\mathit{n}}}_{\mathit{s}}=3.6\times {10}^{12} \mathrm{c}{\mathrm{m}}^{-2}$ to ${\overline{\mathit{n}}}_{\mathit{s}}=6.0\times {10}^{12} \mathrm{c}{\mathrm{m}}^{-2}$, the polaritonic band structure shifts upward in energy and the polaritonic bandgap emerges at 950 cm⁻¹ (Fig. 1H and movie S1). In the latter setting, the incident laser beam excites polaritons in the lower polaritonic band. By tuning the gate voltage, we gain access to both the upper and the lower polaritonic bands (Fig. 1, B, E, and H) at a given laser energy ω.

To gain insight into the properties of Bloch polaritons, we explored the equi-energy contours (Fig. 1, C, F, and I) composed of all modes supported by the polaritonic band structure at a given laser energy ω. When ω intersects with the upper polaritonic band (${\overline{\mathit{n}}}_{\mathit{s}}=3.6\times {10}^{12} \mathrm{c}{\mathrm{m}}^{-2}$, Fig. 1B) just above the bandgap, equi-energy contours emerge around M points in the BZ (Fig. 1C). The propagation direction of Bloch polaritons is governed by their group velocity, which is largely aligned with the crystal momentum in BZ. This latter conjecture is supported by real-space polariton propagation simulations where we plotted the electric field Re(E_z) of Bloch polaritons launched by a point source in the polaritonic crystal (Fig. 1D). Simulations confirm that Bloch polaritons only propagate along $\widehat{\mathit{M}}=\langle -11\rangle$directions. Provided that the laser energy falls in the polaritonic bandgap, polariton propagation is completely inhibited (not shown). Next, when the lower polaritonic band is raised further toward ω (${\overline{\mathit{n}}}_{\mathit{s}}=4.8\times {10}^{12} \mathrm{c}{\mathrm{m}}^{-2}$, Fig. 1E), equi-energy contours reemerge in the K/K′ valleys (Fig. 1F). Bloch polaritons switch their propagation direction from $\widehat{\mathit{M}}=\langle -11\rangle$to $\widehat{\mathit{K}}=\langle 10\rangle$ (Fig. 1G). Last, when the carrier density is increased to ${\overline{\mathit{n}}}_{\mathit{s}}=6.0\times {10}^{12} \mathrm{c}{\mathrm{m}}^{-2}$, the equi-energy contours evolve to near-perfect circles around the center of the BZ (Fig. 1I), and Bloch polaritons propagate isotropically in all directions (Fig. 1J), similar to their counterparts in unpatterned graphene devices. The above modeling uncovers the utility of graphene polaritonic crystals for programmable steering of Bloch polaritons.

We used low-temperature near-field optical microscopy to image Bloch polariton propagation in real space and to extract the equi-energy contours in momentum space. In these experiments, the entire device is illuminated by an infrared light from a CO₂ laser. The metallic tip of an atomic force microscope (AFM) acts as an optical antenna that outcouples Bloch polaritons into free-space photons, enabling real-space polaritonic imaging deeply below the diffraction limit (31, 32). The tip-scattered light is registered by a detector, and the amplitude s(r) and phase ϕ(r) of the corresponding near-field signal are extracted by a proper demodulation scheme (Materials and Methods). We mainly analyzed the near-field amplitude images s(r). All the near-field measurements were performed at T = 60 K to reduce SPP losses due to phonon scattering (34) and to minimize broadening of the polaritonic band structure.

Near-field images close to a gold launcher show directional propagation of Bloch polaritons (Fig. 2). The leading edges of the launcher form a 30° angle, thus exciting Bloch polaritons propagating along $\widehat{\mathit{K}}$ and $\widehat{\mathit{M}}$ directions (arrows in Fig. 2A). In the course of our measurements, we kept the laser energy at ω = 890 cm⁻¹ while tuning the gate voltage. It is instructive to plot the gate-voltage dependence of the band structure at ω = 890 cm⁻¹ (Fig. 2B and fig. S1). This new representation contains the same physics as Fig. 1 (B, E, and H) but facilitates a more direct connection to our imaging data. Specifically, Fig. 2B reveals that polaritons reside near M points at lower carrier densities, whereas their K point counterparts are activated at higher carrier densities. At gate voltage V_g = 47.5 V (Fig. 2C), Bloch polaritons only propagate along the $\widehat{\mathit{M}}$ direction. This phenomenon is particularly apparent when comparing the line profiles along $\widehat{\mathit{M}}$ (black) and $\widehat{\mathit{K}}$ (cyan) directions (Fig. 2F). A combination of V_g = 47.5 V and ω = 890 cm⁻¹ produces polaritonic fringes only in the $\widehat{\mathit{M}}$ direction, which also indicates that polaritons reside in the upper polaritonic band (Fig. 2B, top dashed line). At a slightly higher gate voltage V_g = 52.5 V, Bloch polariton propagation is inhibited in the $\widehat{\mathit{M}}$ direction, and the launcher only excites SPPs traveling diagonally along the $\widehat{\mathit{K}}$ direction (Fig. 2D). Line profiles in Fig. 2F confirm that Bloch polaritons propagate predominantly in the $\widehat{\mathit{K}}$ direction and that they can only be excited in the lower polaritonic band (Fig. 2B, middle dashed line). At even higher gate voltage V_g = 72.5 V, the laser energy is away from the polaritonic bandgap (Fig. 2B, bottom dashed line) and Bloch polaritons propagate isotropically in all directions (Fig. 2, E and F). Near-field images also reveal periodic dark spots, which are attributed to variation in the local polaritonic density of states (28) that is peripheral to our focus on directional Bloch polaritons. We have investigated multiple devices at a variety of gate voltages across the bandgap (fig. S2). All devices show consistent control of polariton propagation by gate voltage. The agreement between our experimental observations and band structure calculations demonstrates the ability to steer Bloch polaritons along the specified trajectories in our planar structure using the electric field effect.

Fig. 2. Directional launching of Bloch polaritons.

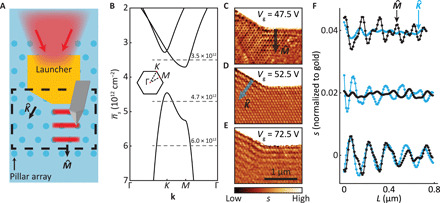
(A) Schematic of the device with the scanned region marked in the dashed box. The shades of blue colors represent different carrier densities in graphene. (B) Dependence of the polariton momentum k on average carrier density ${\overline{\mathit{n}}}_{\mathit{s}}$ at ω = 890 cm⁻¹. Dashed lines correspond to the experimental conditions in (C) to (E). Inset: BZ of the polaritonic crystal marked with symmetry points. (C) Near-field image acquired at T = 60 K and V_g = 47.5 V. Bloch polaritons propagate in $\hat{M}=\mathrm{\langle }-11\mathrm{\rangle }$direction, as marked by the black arrow. (D) and (E) same as (C) at V_g = 52.5 V and V_g = 72.5 V, respectively. (D) shows that Bloch polaritons propagate predominantly in $\widehat{\mathit{K}}=\langle 10\rangle$ direction, as marked by the cyan arrow. (E) reveals isotropic polariton propagation in all directions. (F) Averaged line profiles along $\widehat{\mathit{K}}$ and $\widehat{\mathit{M}}$ directions acquired from (C) to (E). Line profiles are normalized to gold and shifted vertically by multiples of 0.02 units for clarity.

Fourier analysis of the polaritonic patterns confirms that the directional launching is governed by the polaritonic band structure. Experimental inputs for this analysis are acquired by imaging Bloch polaritons emanating from the gold launcher in Fig. 3A, which resembles a point source for polaritonic waves (fig. S3). A gate voltage of V_g = −45 V implies that Bloch polaritons reside above the polaritonic bandgap and propagate along the $\widehat{\mathit{M}}$ direction (Fig. 3B). The symmetrized Fourier transform (Materials and Methods) of the near-field image (Fig. 3C) yields prominent features around M points in the BZ, forming a hexagonal motif. A similar pattern is also observed in modeling results in Fig. 3D. The agreement between gross features in the data and the modeling corroborates that the directional Bloch polariton propagation is governed by the band structure. Propagating Bloch polaritons vanish for gate voltages within the bandgap at V_g = −50 V (fig. S4). At even lower gate voltages such as V_g = −52.5 V, polariton propagation direction is switched to $\widehat{\mathit{K}}$ (Fig. 3E). The Fourier transform of the near-field image reveals the formation of polaritonic pockets near K points (Fig. 3, F and G, the complete field of view of the Fourier image is shown in fig. S5). Last, at V_g = −60 V, equi-energy contours appear as near-perfect circles within the first BZ (Fig. 3, I and J). The three selected panels of Fig. 3 (C, F, and I) are displayed again in Fig. 3K and are seen to be in close agreement with the simulated polaritonic band structure.

Fig. 3. Fourier analysis of polaritonic images.

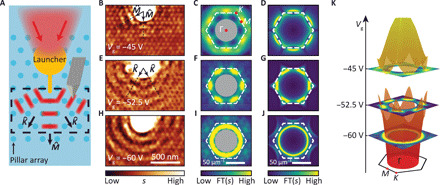
(A) Schematic of the device with the scanned region marked in the dashed box. (B) Near-field image obtained at V_g = −45 V, showing Bloch polaritons traveling predominantly in $\widehat{\mathit{M}}$ directions. (C) Symmetrized Fourier transform (FT) of the image in (B). The six bright features represent Bloch polaritonic modes around M points. Polaritonic features close to the Γ point are extraneous to our study and thus are shaded in the gray circle. Inset: First BZ marked with symmetry points. (D) Simulated Fourier transform at ${\overline{n}}_s=3.5\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$. (E) to (G) same as (B) to (D) at V_g = −52.5 V and ${\overline{n}}_s=4.8\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$. Bloch polaritons propagate predominantly along $\widehat{\mathit{K}}$ directions (E). The Fourier transform (F) shows six polaritonic pockets near K points in accord with the simulation (G). (H) to (J) same as (B) to (D) at V_g = −60 V and ${\overline{n}}_s=6.0\times {10}^{12}\mathrm{c}{\mathrm{m}}^{-2}$. The near-field image shows that Bloch polaritons propagate isotropically in all directions (H) and the Fourier transform (I) shows circular equi-energy contours, which agrees with the simulation (J). (K) Stacked equi-energy contours for selected gate voltages and overlaid with the theoretical polaritonic band structure.

Outlook

We demonstrated programmable Bloch polaritons in a graphene polaritonic crystal platform. Bloch polaritons propagate along designated directions set by the applied gate voltage. The same general approach is well suited to the manipulation of other polaritonic systems, such as exciton polaritons and magnon polaritons. Relatively straightforward improvements of our platform aimed at reducing plasmonic damping and working gate voltages will enable operation at ambient conditions. Furthermore, our back-gated platform is compatible with ubiquitous metal oxide semiconductor field effect transistor technology and sets the stage for integrated photonic circuits (52, 53).

MATERIALS AND METHODS

Cryogenic near-field imaging techniques

Cryogenic near-field imaging measurements were performed using a home-built scattering-type scanning near-field optical microscope (s-SNOM) (54). The s-SNOM apparatus is based on a taping mode AFM, coupled to a continuous-wave CO₂ laser (Access Laser), operating in ultrahigh vacuum (UHV) and cryogenic temperatures. The incoming laser beam is focused on the sample using a high-NA off-axis parabolic mirror inside the UHV chamber. The metallic AFM tip is tapped above the sample surface at a frequency of ~250 kHz. The tip-scattered light is demodulated using a pseudo-heterodyne detection scheme to extract both the near-field amplitude s(r, ω) and the phase ϕ(r, ω). The images shown in the main text are the near-field amplitude s(r, ω) normalized to the gold launcher. Gold deposited using thermal evaporation serves as a good reference for the demodulated signal. To properly suppress background contributions to the near-field signal, we demodulate at the third harmonic of the tip tapping frequency (28).

Sample fabrication

The patterned dielectric superlattices (PDSLs) (28, 39) consisting of a hexagonal array of pillars were fabricated by plasma etching the SiO₂ using a thin polymethyl methacrylate (PMMA) mask. Si substrates with thermally grown SiO₂ of thickness 285 nm were spin-coated with a layer of 495 A2 PMMA of thickness 50 nm. The hexagonal pattern was written by e-beam lithography in a Nanobeam nB4 system at a current of 300 to 400 pA. SiO₂ pillars were etched in an Oxford Plasmalab 80 Plus system using a mixture of CHF₃ gas (40 sccm) and Ar gas (5 sccm) to a depth of ~50 nm. The PMMA mask was removed through an O₂ plasma etching, and the PDSL was cleaned by piranha chemical etching. The resulting superlattice is an array of pillars with 46- to 48-nm diameter and 58-nm height that form a hexagonal lattice, with lattice periodicity 85 nm in the device shown in Fig. 2 and 80 nm in the device shown in Fig. 3.

A mechanically exfoliated graphene and hBN heterostructure was placed onto the PDSL by mechanical transfer (55). The heterostructure consists of a top h¹¹BN layer of ~4 nm, a layer of graphene, and a bottom h¹¹BN layer of ~4 nm and was assembled using a polypropylene carbonate (PPC) transfer slide. Given the challenges involved in picking up an hBN layer as thin as 4 nm, such as the topmost layer, using PPC, we dug a circular hole (diameter 7 to 11 μm) out of a thick (30 to 60 nm) hBN flake using e-beam lithography. This thick hBN flake could be easily picked up by the PPC, and the thin h¹¹BN and graphene flakes were positioned so that they covered the circular hole from below and could be picked up by the van der Waals interaction between them and the thick top hBN flake. Therefore, inside the circular hole (not shown in experimental images) we had a thin h¹¹BN-graphene-h¹¹BN heterostructure. Metal contacts and launchers were deposited using standard e-beam lithography processes. The graphene device is a single crystal within our field of view, as confirmed by near-field imaging results. All the reported back gate voltages are measured from the charge neutrality point of the devices. The residual charge density in the absence of gate voltage is estimated to be n_s = 1.75 × 10¹¹ cm⁻².

The monoisotopic h¹¹BN single crystals were synthesized by the metal flux method (56). High-purity elemental ¹¹B (99.41%) was first mixed with Ni and Cr powders in a weight ratio of 1:12:12. These materials were then loaded into an alumina crucible and heated to a molten state with a flowing mixture of nitrogen (95%) and hydrogen (5%) at 1550°C. The h¹¹BN crystals were precipitated on the flux surface by slowly cooling (1°C/hour) to 1500°C. After the growth process, the mixture temperature was quickly quenched to room temperature. The crystal flakes were obtained from the solidified flux with tape.

Symmetrization of Fourier space images

Near-field images acquired near the apex of the gold launcher were cropped to remove the gold launcher. The cropped near-field images were subsequently Fourier-transformed, using a Hann window, to get the raw image in reciprocal space. To enhance the signal-to-noise ratio and better reveal the excited polaritonic modes, we applied all the symmetry operations of the hexagonal lattice to the raw Fourier image and averaged the resulting images. More specifically, we consecutively rotated the raw Fourier image in 60° intervals, leading to six transformed images. We then applied the mirror operation to these six transformed images, resulting in six additional images. The average of all 12 transformed images results in the Fourier images shown in Fig. 3. The Fourier transform method is commonly used to analyze polaritonic equi-energy contours (57–60).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/19/eabe8087/DC1