A new SEIAR model on small-world networks to assess the intervention measures in the COVID-19 pandemics

Abstract

A new susceptible-exposed-infected-asymptomatically infected-removed (SEIAR) model is developed to depict the COVID-19 transmission process, considering the latent period and asymptomatically infected. We verify the suppression effect of typical measures, cultivating human awareness, and reducing social contacts. As for cutting off social connections, the feasible measures encompass social distancing policy, isolating infected communities, and isolating hub nodes. Furthermore, it is found that implementing corresponding anti-epidemic measures at different pandemic stages can achieve significant results at a low cost. In the beginning, global lockdown policy is necessary, but isolating infected wards and hub nodes could be more beneficial as the situation eases. The proposed SEIAR model emphasizes the latent period and asymptomatically infected, thus providing theoretical support for subsequent research.

Introduction

Emerging infectious disease events have significantly increased over time and are caused mainly by mutual infection between humans and animals, especially wildlife [1]. Since 2007, large-scale pandemics claimed as Public Health Emergency of International Concern (PHEIC) by the World Health Organization (WHO) have occurred six times, the first five of which were H1N1, polio, the Ebola in West Africa [2], the Zika [3], and the Ebola in Congo (DRC). At the end of 2019, a pandemic caused by a new kind of coronavirus (SARS-CoV-2), called COVID-19, broke out and spread rapidly worldwide, challenges the world’s medical and health systems. Statistics show that the disease is highly infectious and has serious consequences [4], [5], [6], causing over 100 million infections and over 3 million deaths worldwide until now. The COVID-19 is the most widespread global infectious disease encountered by humans in the past 100 years, posing a continuous threat to human life and health, economic and social development.

Vaccination is one of the most effective protective measures for combating infectious diseases [7], [8] but requires a long time to develop. In the absence of vaccines, grasping the spread of infectious diseases is of great significance for epidemic prevention and control in the early stages of an outbreak, providing theoretical support for rationally arranging medical resources and implementing effective epidemic prevention measures.

The dynamic model can effectively simulate the spread of viruses and has become a hot technology in infectious disease research [9]. The compartment model proposed by Kermack and Mckendrick [10], [11] in 1927 pioneered the study of infectious disease models, among which SIR (susceptible-infected-removed) is the most classic infectious disease model, dividing individuals into three categories: susceptible, infected, and removed. Later studies focused on the improvement of the SIR model, including SIS (susceptible-infected-susceptible), SEIR (susceptible-exposed-infected-removed), SEIRS (susceptible-exposed-infected-removed-susceptible), and other models.

With the outbreak of COVID-19, numerous studies have emerged to characterize the propagation process of the SARS-CoV-2. As susceptible people will be vigilant in the presence of infectious diseases, thus reducing the probability of contact with suspected infected people, Zhang and Li [12] introduce human awareness into a SEIR model and prove that disease will eventually decrease as human awareness increases. Liu et al. [13] developed a SAIR model with asymptomatic infections, finding that the spread of the epidemic can be contained by increasing the recovery rate and removal rate or cutting off the connection between heterogeneous nodes and neighboring nodes. As quarantine strategies are frequently used to reduce the transmission risks of epidemic diseases, Zhu Yi-min et al. [14] add quarantined patients in the SEIR model and simulate the changing trend of the number of latent and infected persons with different levels of prevention and control measures. This paper improves the SEIR model by considering isolation measures and transmission characteristics of COVID-19 and proves that the isolation plays a significant role in preventing the spread of the epidemic on a larger scale. Chen et al. [15] established an SEIR model that considers asymptomatic infections and population migration, then compared the number of infections and the basic reproductive number before and after the prevention and control measures were taken, verifying the importance of restricting population movement. These researches incorporate disease transmission characteristics into the models and investigate the effect of various types of intervention measures on propagation while assuming that the population distribution is uniformly mixed.

However, the contact relationship between real social groups is mixed heterogeneously and shows some complex network characteristics [16], [17]. Thus, mathematical models with the homogeneousness assumption do not apply to reality. Besides, disease propagation in real society is closely related to the number of infected individuals, the size of the infection rate, and contact between individuals, which can be described by the complex network as it abstracts individuals as network nodes and the contact relationship between individuals as connections between nodes. Although the above researches have effectively promoted transmission models, few existing studies have simulated innovative, dynamic propagation models on complex networks [18].

A growing number of investigations have focused on simulations in heterogeneous populations since Watts and Strogatz proposed small-world networks (SWN) to mimic real social networks [17], [19]. To explore the relative effects of random vaccinations and random avoidance of infected individuals, Thomas E. Stone et al. [20] construct an SIR epidemic model on dynamic small-world contact networks. This paper derives an expression that gives the disease’s infectivity, recovery rate, avoidance rate, vaccination rate necessary to prevent a disease-free to epidemic transition from occurring for any mobility level. It also confirms the significance of avoidance and concludes that it can enhance the effects of vaccination if using a dual strategy. To estimate the COVID-19′s transmission potential in Wuhan, Toronto, and Italy, Xue et al. [21] add asymptomatically infected, hospitalized and dead state into SEIR model and propose a SEAIHRD model on SWN. This paper reflects the differences in the underlying transmission mechanisms and potential spread in the regions by analyzing the differences in these fitted parameters and starting times. Braun et al. [22] construct a theoretical SIR model that exhibits presymptomatic, asymptomatic, and symptomatic stages in two possible pathways. Then investigate the impact of three control measures by using agent-based simulations on SWN and find self-isolation must be prompted if a social contact is known to be infected to halt the spread of COVID-19.

Moreover, in the spread of COVID-19, an official report [23] points out that the SARS-CoV-2 is infectious during the incubation period, and part infected do not show any symptoms, called asymptomatically infected. However, there are two forms of “not showing any symptoms” [24], (1) after infected with the novel coronavirus, the patient will not show any self-perceived or clinically recognizable symptoms during the 14-day isolation medical observation even throughout the process; (2) state in the incubation period. Thus, inspired by the abovementioned studies, we propose a new SEIAR model where the asymptomatic infection referred to the first situation.

In addition, people living in big cities tend to have proportionally more social interactions than those living in small towns [25] and the closer connections between people greatly increase the risk of infectious transmission [26]. Large metropolises may become infection hubs with potentially higher and earlier peaks of infected people [27]. Therefore, we investigate how those prevention and control measures affect the development of the epidemic in cities of different sizes, thus providing insights for a better understanding of the spreading of COVID-19 in urban areas.

Taking the latent period and asymptomatically infected into account, we propose a new SEIAR model on SWN to assess and confirm the effectiveness of the prevention and control measures taken by the government. This paper considers human subjective awareness through the simulation on the SWN and evaluates three intervention measures about social contacts, global lockdown, isolating infected communities, and inhibiting large gatherings.

This paper is organized as follows. In Sect. 2, a SEIAR model is established, and the basic reproduction number is obtained. Next, numerical simulations including human awareness and social contact are conducted on the SWN models in Sect. 3. Then, discussions about the measurements during the outbreak of COVID-19 are given in the Sect. 4. Finally, conclusions are drawn in Sect. 5.

SEIAR model based on SWN

The classic SI, SIS, SIR, and SEIR models cannot fit the spread of the COVID-19 properly. In addition, real social networks usually conform to the characteristics of SWN [28]. Accordingly, this paper proposes a new SEIAR infectious disease propagation model on SWN.

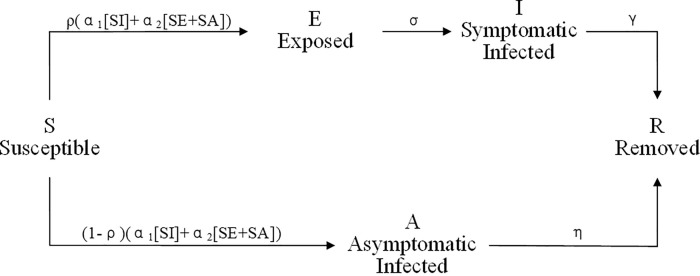
As depicted in Fig. 1 , the SEIAR model divides the population into five types: susceptible (S), exposed (E), symptomatic infected (I), asymptomatic infected (A), and removed (R) individuals.

Fig. 1.

State transition diagram

For susceptible people, they have not been infected, and it is possible for them to become asymptomatically or symptomatically infected after contact with infected individuals. Particularly, exposed groups include part infected people who still in the incubation period without showing symptoms, and will become symptomatic later. For symptomatic infected, they are diagnosed after the incubation period and could get immunized against the virus. For asymptomatic infected, they have been infected after carrying the virus, but will not show any symptoms during the whole process. For removed people, they will recover from disease or die after medical care, and the recovered will produce antibodies and will not get infected by the virus again.

Compared with the entire life cycle of an individual, the duration of the epidemic is considerably shorter. Thus, this paper does not consider the natural birth rate and death rate of the population.

The degree distribution in the SWN obeys the Poisson distribution, and the degree value of most nodes is equal to the whole network’s average degree $〈K〉$. Therefore, the average field theory is generally used to construct an infectious disease dynamic model in the SWN [29], which assumes that the degrees of each node in the SWN are the same and equal to the average of the network degree $〈K〉$.

Define the $S\left(t\right)$, $E\left(t\right)$, $I\left(t\right)$, $A\left(t\right)$, $R\left(t\right)$ as the proportion of susceptible, exposed, symptomatic infected, asymptomatic infected, and removed individuals in the total population at time t. Apparently, formula $S\left(t\right),E\left(t\right),I\left(t\right),A\left(t\right),R\left(t\right)⩾1$ as well as $S\left(t\right)+E\left(t\right)+I\left(t\right)+A\left(t\right)+R\left(t\right)=1$ holds. Therefore, the propagation process of the SEIAR model can be described by formula (1), where the parameter is defined as Table 1 .

Table 1.

Definition of parameters.

Parameters	Definition	Value	Reference
α1	Transmission rate of symptomatically infected individuals (I)	0.271	[11]
α2	Transmission rate of exposed individuals (E) and asymptomatically infected individuals (A)	0.1897	[30]
ρ	Rate of being exposed (E) after infected	0.6	[31]
1-ρ	Rate of being asymptomatically infected (A) after infected	0.4	[31]
1/σ	Average incubation time of exposed individuals(E)	7	[23]
1/γ	Average recovery time of symptomatically individuals (I)	10	[30]
1/η	Average recovery time of asymptomatically individuals (A)	19	[30]

At time t, susceptible nodes  (S) have $〈K〉$ adjacent nodes in the network on average and the numbers of exposed nodes (E), infected nodes (I), and asymptomatic infected nodes (A) are, $〈K〉E\left(t\right)$, $〈K〉I\left(t\right)$ and $〈K〉A\left(t\right)$. The parameters ${\alpha }_1$ and ${\alpha }_2$respectively represent the probability of the susceptible group being infected after contact with the infected group (I) and groups of the exposed (E) and the asymptomatic infected (A). Therefore, the differential equation of susceptible person (S) can be expressed by formula (1) as:

$$\frac{dS\left(t\right)}{\mathit{dt}}=-S\left(t\right)\left(1-{\left(1-{\alpha }_1\right)}^{〈K〉I(t)}\right)-S\left(t\right)\left(1-{\left(1-{\alpha }_2\right)}^{〈K〉\left(E\left(t\right)+A\left(t\right)\right)}\right)$$ (1)

Formula (2) can be obtained by expanding the first term on the right side of equation (1) according to Taylor’s formula, in the form of $a^x$:

$$-S\left(t\right)\left(1-\left(1+〈K〉I\left(t\right)ln\left(1-{\alpha }_1\right)\right)\right)$$ (2)

Expand $ln\left(1-{\alpha }_1\right)$in formula (2) according to Taylor's formula, we can get formula (3):

$$-S\left(t\right)\left(1-\left(1-{\alpha }_1〈K〉I\left(t\right)\right)\right)$$ (3)

Expand the second term on the right side of the equation (1) in the same way, and equation (4) can be obtained:

$$-S\left(t\right)\left(1-\left(1-{\alpha }_2〈K〉\left(E\left(t\right)+A\left(t\right)\right)\right)\right)$$ (4)

After simplification, formula (2) can get formula (5):

$$\frac{dS\left(t\right)}{\mathit{dt}}=-{\alpha }_1〈K〉S\left(t\right)I\left(t\right)-{\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)$$ (5)

After calculate $\frac{dE\left(t\right)}{\mathit{dt}}$, $\frac{dI\left(t\right)}{\mathit{dt}}$, $\frac{dA\left(t\right)}{\mathit{dt}}$ and $\frac{dR\left(t\right)}{\mathit{dt}}$ in the same way, the differential equation of the SEIAR model in the WS-SWN can be expressed as formula (6):

(6)

The basic reproduction number $R_0$ is the number of secondary cases caused by incomplete immunity of infected individuals [32], which is an important indicator of the infectious disease’s incidence.

If $R_0<1$, it represents the average number of people infected by an infected person is less than one during the infection period. Thus, the virus cannot spread among the crowd and will gradually disappear; if $R_0>1$, it indicates the virus will continue to spread.

According to formula (6), the stability of the removed people (R) is determined by the stability of groups of S, E, I, A. Therefore, we only consider the stability of the first four equations of the model, then the formula (6) can be written as the formula (7):

(7)

Define $X={\left(E,I,A,S\right)}^T$, then equation (7) can be written as the following equation (8):

(8)

It is obvious that equation (8) has a disease-free equilibrium $X_0={\left(0,0,0,1\right)}^T$ if $E=I=A=0$. Then write formula (8) as the following formula (9):

$$\frac{\mathit{dX}}{\mathit{dt}}=F\left(X\right)-V\left(X\right)$$ (9)

According to the next-generation matrix method [33], the quadratic growth rate matrix $F$ and removal rate matrix $V$ are obtained. The expressions of matrix $F$ and matrix $V$ are as follows:

$$F\left(X\right)=\left[\begin{array}{c}\rho \left({\alpha }_1〈K〉S\left(t\right)I\left(t\right)+{\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\right)\hfill \\ 0\hfill \\ \left(1-\rho \right)\left({\alpha }_1〈K〉S\left(t\right)I\left(t\right)+{\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\right)\hfill \\ 0\hfill \end{array}\right]$$ (10)

$$V\left(X\right)=\left[\begin{array}{c}\sigma E\left(t\right)\hfill \\ -\sigma E\left(t\right)+\gamma I\left(t\right)\hfill \\ \eta A\left(t\right)\hfill \\ {\alpha }_1〈K〉S\left(t\right)I\left(t\right)+{\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\hfill \end{array}\right]$$ (11)

Then the basic reproduction number is $R_0=\rho \left(F_1{V}_1^{-1}\right)$ , where $\rho \left(·\right)$ is the spectral radius of the matrix, and we get:

(12)

Thus, we get the basic reproduction number:

(13)

From formula (13), we find that the first term $\rho {\alpha }_2〈K〉/\sigma$ represents the average number of individuals who are infected by an exposed during latent period; the second term $\rho {\alpha }_1〈K〉/\gamma$ is the average number of individuals who could be infected by symptomatically infected during the infectious period, whereas the third term $(1-\rho ){\alpha }_2〈K〉/\eta$ indicates the average number of individuals who might be infected by an asymptomatically infected individual during the infectious period.

The practical significance of $R_0$ is ensuring the measures are taken appropriately, as too strict measures could negatively affect the society, and loose measures may malfunction in controlling the spread of the epidemic. By calculating the $R_0$, the measures can be controlled within a reasonable strictness range, and performs both economical and effective.

Numerical simulation and intervention effects analysis

This paper uses the Watts-Strogatz algorithm [19] to generate WS networks of $N=10000$. Specifically, sets the initial number of links $m$ for each node as 4, then reconnect each edge with probability $p=0.4$ and replace each edge with a new one with probability $p_0=0.4$. Furthermore, consider the impact of population density on virus transmission, this paper conducts simulations in SWN with average degree 4,6,8 to simulate the spread of epidemics in cities of different sizes. As cutting off links between nodes at each step is a random dynamical process, we conduct the random numerical simulation for 300 times at each experiment and average the values obtained to get the values $S_k\left(t\right)$, $E_k\left(t\right)$, $I_k\left(t\right)$, $A_k\left(t\right)$, $R_k\left(t\right)$.

In this section, we mainly consider the impact of human consciousness and hub nodes isolation, cutting off connections, and community isolation on the transmission of the epidemic, providing a theoretical basis for reality. Furthermore, we set different network average degree to imitate different size of city. According to Six Degrees of Separation theory, there will be no more than five people between any two people in the world. Therefore, we set network of average degree = 6 as normal size city, while set the network of average degree = 4 as small city and the network of average degree = 8 as big metropolis in SWN.

Human awareness

The fear of viruses will prompt people to enhance the awareness of self-protection, which will affect the spread of viruses. Therefore, this section considers the human subjective consciousness into the model. At the beginning of the outbreak, people’s awareness continues to increase as the number of confirmed cases rises. However, after the awareness reaches the limit, people tend to slack once the epidemic eases, with the awareness beginning to weaken.

Therefore, we assume the awareness could be described by (14), the gradient of the logistic function, where x represents the reported number of infected cases and $a,b,r=1,1,1$:

$$\lambda ={\left(\frac{a}{b+e^{-rx}}\right)}^{\text{'}}=\left(\frac{\mathit{ar}}{b^2{e}^{\mathit{rx}}+e^{-rx}+2b}\right)$$ (14)

Thus, the basic SEIAR model on SWN considering human awareness is as follows:

$$\left\{\begin{array}{c}\frac{dS\left(t\right)}{\mathit{dt}}=-\lambda {\alpha }_1〈K〉S\left(t\right)I\left(t\right)-\lambda {\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\hfill \\ \frac{dE\left(t\right)}{\mathit{dt}}=\rho \left(\lambda {\alpha }_1〈K〉S\left(t\right)I\left(t\right)+\lambda {\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\right)-\sigma E\left(t\right)\hfill \\ \frac{dI\left(t\right)}{\mathit{dt}}=\sigma E\left(t\right)-\gamma I\left(t\right)\hfill \\ \frac{dA\left(t\right)}{\mathit{dt}}=\left(1-\rho \right)\left(\lambda {\alpha }_1〈K〉S\left(t\right)I\left(t\right)+\lambda {\alpha }_2〈K〉S\left(t\right)\left(E\left(t\right)+A\left(t\right)\right)\right)-\eta A\left(t\right)\hfill \\ \frac{dR\left(t\right)}{\mathit{dt}}=\gamma I\left(t\right)+\eta A\left(t\right)\hfill \end{array}\right)$$ (15)

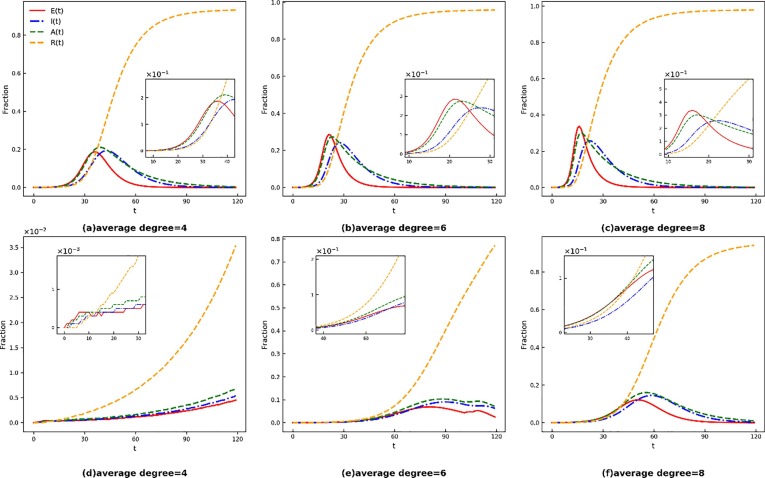
To explore the role of human consciousness in the spread of the epidemic, we simulated the SEIAR model’s spread under conscious and unconscious scenarios. Specifically, it shows in the bottom Panel, when considering human consciousness, the growth rate of R(t) is still accelerating at t = 120 (see Fig. 2 d). In contrast, R(t) almost reaches its peak at t = 120 in the unconscious state (see Fig. 2 a). The same applies to Panels (b) and (c) as well as Panels (e) and (f). These findings indicate that human consciousness can restrain and delay the spread of the epidemic.

Fig. 2.

Time evolution of E(t), I(t), A(t) and R(t). The red solid line, blue dotted-dashed line, green dashed line, and orange dashed line represent the fraction of the exposed, symptomatically infected, asymptomatically infected, and removed individuals, respectively. Take human awareness into account in the bottom Panel and not in the top Panel. In Panels (a), (d), the network average degree = 4, which represents sparsely populated city; In Panels (b), (c), the network average degree = 6, which represents normal size city; In Panels (c), (f), the network average degree = 8, which represents densely populated city. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Comparing Panels (a) and (d), the exposed group represented by the red line grows fastest and reaches its peak (E(37) = 0.186) earliest before human consciousness is taken into consideration (see Fig. 2 a), but its propagation speed is significantly reduced after considering human consciousness (see Fig. 2 d). As also can be observed in the bottom Panels, the exposed group is increasing slower than symptomatic infected and asymptomatic infected. Thus, human consciousness has the most significant impact on the exposed. It must also be mentioned that in Panel (e), the curve of E(t) shows a small rebound and peaks again at 0.0476 in t = 105. With human consciousness gradually wearing off, many individuals have recovered at that moment and will be immune to the disease due to carrying antibodies. Besides, the situation will not be as severe as before when the second epidemic breaks out because people are experienced in responding to emergencies. Overall, people’s protection awareness lags behind the development of the epidemic but will be raised if the pandemic becomes prevalent again.

Furthermore, to investigate how human awareness facilitate curbing the pandemic’s spread in cities of different size, we simulate the model under networks of different average degree. In Panels (a), (b) and (c), E(t) reaches the highest value 0.187, 0.285 and 0.338 in t = 37, 22 and 17, and returns to 0 from peak in t = 95, 77, and 72, respectively. Through horizontal comparison, it can be drawn that the higher the average degree of the network, the sooner E(t) reaches its peak and the shorter the duration of the epidemic. However, E(t) does not reach its peak within 120 days in Panels (d) but peaks at 0.069 and 0.121 in t = 82 and 52 in Panels (e) and (f) respectively. It shows that human awareness plays a limited role in big cities though enhancing human awareness is conducive to reducing the risk of infection by prompting people to take self-protection measures like wearing masks.

In conclusion, human consciousness can significantly curb the spread of the epidemic, especially the proportion of exposed group, which group is the least likely to be detected in reality and thus hinders epidemic prevention and control. Therefore, measures to cultivate human awareness are crucial for controlling the epidemic, such as popularizing the knowledge of epidemic prevention among citizens. Besides, since the positive impact is more significant in cities with low population density, other intervention measures should be employed in concert with enhancing human awareness and should be implemented strictly in densely populated cities.

As human prevention awareness plays a limited role in densely populated cities, the government should also reduce the density of the social networks by decreasing people’s contact in large cities.

Social contacts

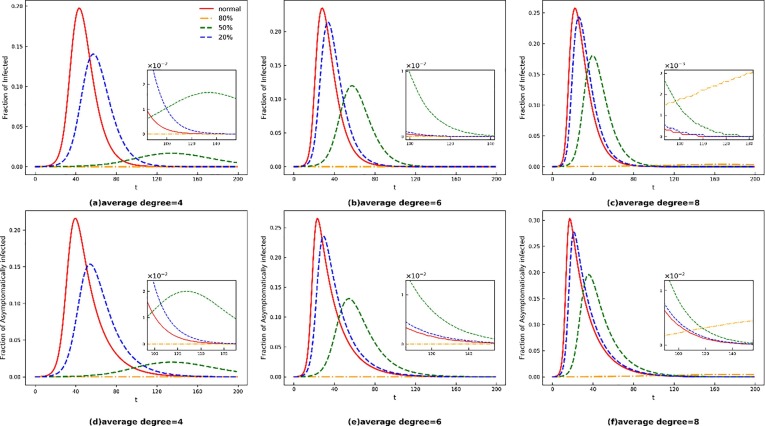
In order to explore the impact of reducing social contacts on the inhibition of COVID-19, we simulate three measures: cutting off social connections randomly, isolating infected communities, and isolating hub nodes.

First, we investigate how the strictness of social distancing policy affects the effectiveness of epidemic prevention by randomly cutting off connections between nodes in the networks with 20%, 50%, and 80%, representing varying degrees of strictness. As shown in Panels (a) of Fig. 3 , I(t) represented by red lines peaks at 0.198(t = 44), 0.140(t = 58) and 0.0168(t = 136) under normal state, 20% and 50% situations, respectively. Specifically, the spread of the virus will be completely blocked when cutting off 80% connections between nodes and the higher the ratio of disconnected connections, the more pronounced the curbing effect. It can be inferred that as most nodes are homogeneous in the WS-SWN, cutting off most connections basically destroys the network's structure, thus making it difficult for viruses to form a long spread chain in the network. Therefore, strict social distancing policy will effectively curb the spread of the epidemic, and the strictness of the implementation measures should depend on the circumstances. Besides, comparing Panels (a), (b), and (c), it shows that I(t) peaks at 0.198, 0.235 and 0.258 in t = 44, 29, and 23 respectively under normal state, and reaches the highest value 0.140, 0.214 and 0.243 in t = 58, 35 and 27 respectively under 20% situation. It can be concluded that as the average degree of network structure increases, the suppression effect is less obvious. The same applies to A(t) in Panels (d) (e) and (f). Therefore, consistent with the previous conclusion, the stricter measure should be taken for cities with greater population density.

Fig. 3.

Time evolution of I(t), A(t) under different measures. The top Panel and bottom Panel indicate the fraction of symptomatically infected and asymptomatically infected, respectively. The red solid line shows the normal development of the epidemic, while the orange dotted-dashed line, green dashed line and blue dashed line represent development under the measures of cutting off 80%,50%,20% nodes in the network respectively. Different proportions represents the strictness of the social distancing policy. In Panels (a), (d), the network average degree = 4, which represents sparsely populated city; In Panels (b), (e), the network average degree = 6, which represents normal size city; In Panels (c), (f), the network average degree = 8, which represents densely populated city. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

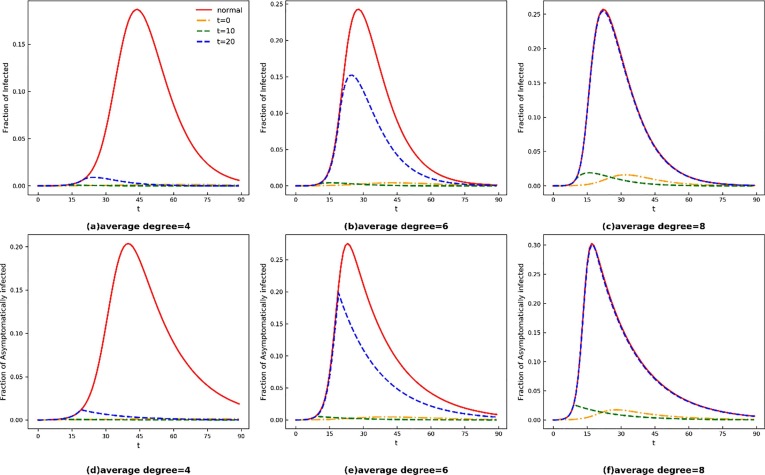
Next, we explore how the timing of the isolating measures affects the epidemic’s spread and the effect of isolating infected communities by designing a method to simulate the Lockdowns of the infected wards at different periods. As strict measures need to pay substantial economic costs, Bhattacharyya and Vinay [34] explore more cost-efficient measures to encountering pandemics and find that isolating infected wards can outperform global Lockdowns. The reason is that isolating infected community can fundamentally reduce the spread of the virus quickly with low controlling cost. So We use community detecting algorithms, greedy modularity [35], [36] to partition communities, and then cut off the external connections of infected wards in the SWN models at t = 0, 10 and 20, respectively. In Panel (a) of Fig. 4 , it shows that isolating infected communities stops the development of the epidemic when implemented at t = 0, which performs equally with cutting off 80% connections in the network. Furthermore, it carries out strikingly efficient when implemented at t = 10 and 20, as the curve of I(t) reaches the peaks at 0.0043 and 0.152 in t = 16 and t = 26, respectively. Thus, it can be concluded that the earlier the measures are taken, the better the effect of suppressing the epidemic. Besides, comparing the Panels (a), (b), and (c) of Fig. 4, it can be observed that the measures barely work in the network with a degree of 8 while suppressing the disease more effectively in other networks when implemented at t = 20. The same applies to A(t) in Panels (d) (e) and (f). It is consistent with the previous conclusion that the measures are less effective in cities with high population density. Therefore, when clusters of infected cases emerge, isolating the infected communities is the most suitable and economical choice, and measures should be taken early, especially in big cities with high population density. However, it is merely theoretically possible to detect the infected person in time and immediately block the community where they are located, which requires response time in reality, thus causing a discrepancy.

Fig. 4.

Time evolution of I(t), A(t) under different measures. The top Panel and bottom Panel indicate the fraction of symptomatically infected and asymptomatically infected, respectively. The red solid line shows the normal development of the epidemic, while blue dotted-dashed line, green dashed line and orange dashed line represent development under the measures of isolating communities when t = 0,10,20 respectively. In Panels (a), (d), the network average degree = 4, which represents sparsely populated city; In Panels (b), (e), the network average degree = 6, which represents normal size city; In Panels (c), (f), the network average degree = 8, which represents densely populated city. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

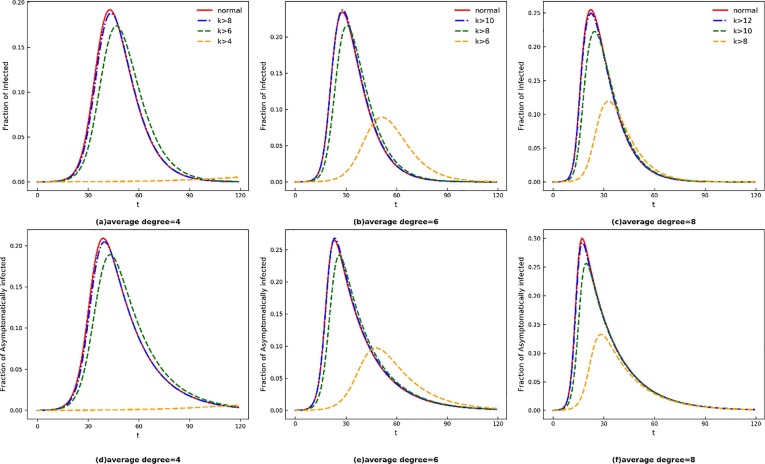
Last, this part investigates the effect of prohibiting large gatherings in restraining the COVID-19 by isolating hub nodes with plenty of connections in the network and have a bigger degree than the average degree of the network. In reality, to maintain the regular operation of society, it is impossible to implement strict isolation measures during the whole transmission period. Therefore, to secure guarantees for the basic life of impoverished people affected by the novel coronavirus epidemic, prohibiting large gatherings is a common choice. Given the definition of hub nodes, we cut off the connections of hub nodes with degrees of 4, 6, and 8 to simulate the different strictness of the measures in a network with an average degree of 4. Similar in other networks. As shown in Fig. 5 , isolating hub nodes have a remarkable suppression effect on the epidemic. Specifically, in Panel (a), isolating nodes with degree above 4 greatly delays the transmission in networks with an average degree of 4, yet isolating hub nodes with a degree above 8 have a poor performance in curbing the pandemic’s spread. The main reason is in the SWN, most nodes’ degree values are close to the average degree of the network, and there are few hub nodes with a large degree. Therefore, only isolating this part of the nodes has no noticeable effect. Comparing Panels (a), (b), and (c), the fraction of I(t) represented by the orange dashed line does not reach the highest value in Panel(a) but peaks at 0.089 and 0.119 in t = 52 and 34, respectively. The same applies to A(t) in Panels (d) (e) and (f). It can be concluded that after isolating hub nodes in the SWN, the duration time is shorter, and the peak value is higher as the average degree of the network structure increases. Therefore, more attention should be paid to controlling the large-scale gatherings such as cinemas and tourist attractions in small cities and even take the most stringent measures.

Fig. 5.

Time evolution of I(t), A(t) under different measures. The top Panel and bottom Panel indicate the fraction of symptomatically infected and asymptomatically infected, respectively. The red solid line shows the normal development of the epidemic, while blue dotted-dashed line, green dashed line and orange dashed line represent development under the measures of isolating nodes which degree > 8,6,4 respectively. In Panels (a), (d), the network average degree = 4, which represents sparsely populated city, and nodes which degree > 4, 6, and 8 represents hub nodes of different levels; In Panels (b), (e), the network average degree = 6, which represents normal size city, and nodes which degree > 6 ,8, and 10 represents hub nodes of different levels; In Panels (c), (f), the network average degree = 8, which represents densely populated city, and nodes which degree > 8, 10, and 12 represents hub nodes of different levels. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Discussion

Since the COVID-19 is still causing damages to global health and disturbing the social order, the success of China’s national defense epidemic is worthy of deep thinking. In June 2020, the Chinese government issued a report on China’s fight against the epidemic, dividing China’s fight against the epidemic into five stages [37]. Combined with the report, this section covers the spread of the epidemic using the national confirmed case data published by the Chinese government from January 16 to May 31, 2020. Specifically, define the net increment of confirmed cases as the severity of the epidemic.

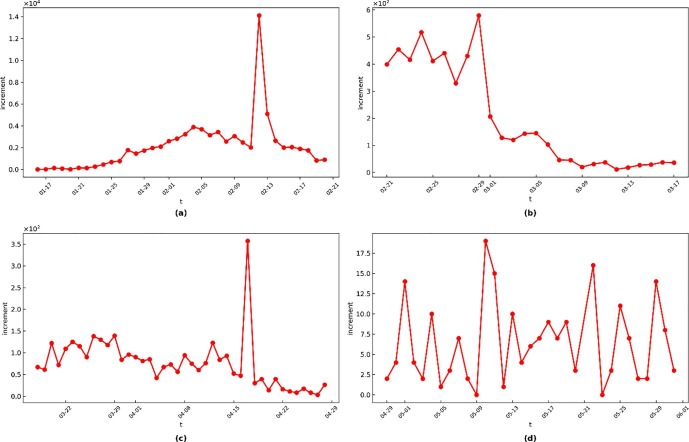
Before January 20, 2020, the prevention and control process were in the first stage, according to the report. As manifested in Panel (a) of Fig. 6 , the epidemic broke out on a small scale. The main measures adopted were to analyze the virus’s source and prevent large-scale gatherings.

Fig. 6.

(a) the net increment of the infected from January 16 to February 20, 2020. (b) the net increment of the infected from February 21 to March 17. (c) the net increment of the infected from March 18 to April 28. (d) the net increment of the infected from April 29 to May 31.

After January 20, 2020, the data did not reveal the actual situation until then due to the incubation period and the asymptomatically infected. In the second phase, the epidemic broke out rapidly, reaching a peak on February 4. Then, the controlling measures have achieved initial results, initially curbing the epidemic’s spread. In the Panels (b), the increment is gradually shrinking, mainly because the government sent additional medical teams, imposed strict traffic control and Lockdown policy on the hard-hit areas (such as Wuhan, Hubei Province). It confirms that cutting off social contacts on a large scale can significantly halt the development of the epidemic.

In the third stage, the main anti-epidemic measures are to strengthen entry health and quarantine work as well as strictly implement health checks and temperature checks on entry personnel to prevent the cross-border spread of the epidemic. The government gradually lowered its response levels to major public health emergencies and lifted restrictions on transportation. With the deepening of the understanding of the virus, the precaution awareness of human beings has continued to increase. Generally speaking, the Chinese government adopted more focused epidemic prevention measures and no longer strictly cut off social connections at this stage. As shown in Panel (b), the number of new local cases gradually dropped to single digits, consistent with the previous observation. Therefore, partially lifting the ban on social contacts and cultivating self-protection awareness can also control the epidemic’s development at this stage.

In the fourth stage, Wuhan and Hubei’s anti-epidemic defense war achieved decisive results as the number of confirmed cases was cleared. In terms of resumption of work and production, the government lifted the Lockdown measure, and the personnel from Hubei Province used the health green code for movement. Simultaneously, the government ensured that industries with a low flow of people would resume work first and delayed resumption works in labor-intensive industries, such as tourist attractions, sports, and entertainment. As presented in Fig. 6 c, the increment fluctuates for imported cases from abroad but shows a decreasing trend, verifying the effect of isolating hub nodes.

In the fifth stage, epidemic prevention and control measures have become normalized, and the anti-epidemic process has been fully standardized. The government mainly takes preventive strategy to cultivate people’s awareness of autonomous protection and urge people to develop the habit of wearing masks and washing hands frequently. At this stage, the number of new cases nationwide remained within 20 (see Fig. 6 d), reflecting the importance of self-protection consciousness in regular epidemic prevention and control.

Overall, the effects of the Chinese government’s measures are consistent with the conclusions of the previous article’s simulation measures. When the epidemic situation begins to worsen, most social connections should be cut off immediately, with social distancing strategy and traffic control. Considering the cost issue, quarantining the communities where infectious cases are detected can also play a role in suppressing transmission, and the earlier measures are taken, the better the effect. Furthermore, it is necessary to isolate hub nodes in the entire process, which means to inhibit aggregations. The most important thing is that we should focus on cultivating people’s awareness of self-protection against epidemics while taking measures. In reality, the smooth progress of work and production resumption is inseparable from people’s awareness of self-protection and preventive behavior.

Conclusion

In this paper, we propose a new SEIAR model on SWN regarding the novel coronavirus’s intrinsic characteristics to depict the spread of COVID-19. Furthermore, we evaluate measurements that the government has taken during the outbreak. By calculating the basic reproduction number and carrying out the simulations, we obtain that the measures suggested by us are in fair agreement with the measures the government had taken to control the pandemic’s spread.

The results indicate that human subjective consciousness’s plays a decisive role in suppressing the virus’s spread. Furthermore, we simulate three measures to reduce social contacts. Along with the simulation results, data from China proves that government should choose appropriate measures at different epidemic stages. Specifically, in the early stage of the epidemic, strict social distancing measures should be taken to cut off most social connections. Also, considering the expenditure of fighting the epidemic, isolating communities is more appropriate than undifferentiated cutting off connections. Throughout the entire process of fighting the epidemic, on the one hand, we should restrict gathering activities; on the other hand, we should prompt segregation as soon as possible when an infected is detected. Finally, taking into account cities’ population density, measures should be more stringent for densely populated cities.

CRediT authorship contribution statement

Jie Li: Conceptualization, Methodology, Supervision. Jiu Zhong: Visualization, Writing - original draft, Investigation. Yong-Mao Ji: Data curation, Software, Validation. Fang Yang: Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.