Directed Evolution of Microbial Communities

Abstract

Directed evolution is a form of artificial selection that has been used for decades to find biomolecules and organisms with new or enhanced functional traits. Directed evolution can be conceptualized as a guided exploration of the genotype–phenotype map, where genetic variants with desirable phenotypes are first selected and then mutagenized to search the genotype space for an even better mutant. In recent years, the idea of applying artificial selection to microbial communities has gained momentum. In this article, we review the main limitations of artificial selection when applied to large and diverse collectives of asexually dividing microbes and discuss how the tools of directed evolution may be deployed to engineer communities from the top down. We conceptualize directed evolution of microbial communities as a guided exploration of an ecological structure–function landscape and propose practical guidelines for navigating these ecological landscapes.

DIRECTED EVOLUTION OF ORGANISMS AND BIOMOLECULES

Evolution has given shape to all forms of life, and humans have harnessed its power for millennia. Our ancestors learned to domesticate animals, plants, and a wide range of microorganisms by artificial selection long before they were aware of evolution itself (27, 92). The revolution in our understanding of evolutionary biology, genetics, and molecular biology in the nineteenth and twentieth centuries, together with the development of novel genomic and molecular technologies (1, 31, 100, 102, 115), has allowed us to extend artificial selection beyond animal and plant domestication and learn how to direct the evolution of biomolecules (12, 48), genetic circuits (126), microorganisms (80), and viruses (16) to improve their phenotypes and even to invent new ones (48, 81). A major advantage of using directed evolution to engineer biological systems from the top down, as opposed to engineering them from the bottom up, is that the latter works with already known parts and traits, whereas the former does not require any a priori knowledge of the mechanisms responsible for the desired function; thus, directed evolution may allow us to find entirely new pathways and mechanisms encoded in hitherto unexplored regions of the genotype space.

Beyond its practical utility, directed evolution can also lead to profound insights into fundamental biological principles. For instance, directed evolution in vitro and in silico has revealed principles of organization of genetic and metabolic networks (11, 34, 125, 126), and it has been instrumental to our growing understanding of the mapping between genotype and phenotype in biomolecules (14, 89, 108), metabolic pathways (79), and other cellular traits (115). In turn, as our understanding of the genetic basis of adaptation has improved, it has enabled us to design more efficient strategies and methods for directed evolution (1, 6, 7, 64, 89, 102, 128).

The genotype–phenotype map (often referred to as the fitness landscape in the context of directed evolution) is defined as the relationship between the DNA sequence of a gene (or a higher-level functional unit, such as a pathway or genetic network) and the magnitude of the quantitative trait(s) it codes for in a given environment. Directed evolution can be conceptualized as a guided exploration of this genotype–phenotype map in search of genotypes with improved or novel functions (89, 108). Traditionally, directed evolution starts by first generating a library of genetic variants (74). All variants are then scored for the phenotype under selection, and those that are closer to the desired value (referred to below as the fittest) are chosen for reproduction. From this selected group, a new generation of genotypic variants is created through random mutagenesis or recombination (74). This two-step process is generally applied iteratively for as many rounds as needed. In recent years, several techniques have been developed that increase the throughput of the process and reduce human intervention (31, 115), but the fundamental evolutionary process remains the same (64, 90).

ARTIFICIAL SELECTION ABOVE THE ORGANISM

Given the growing appreciation of the many important roles that groups of individuals (populations, communities, and ecosystems) play in natural and technological processes (13, 49, 57, 63, 69, 72, 84, 97, 110, 120), it has been proposed that artificial selection may also be applied above the level of the organism to engineer community-level functions from the top down (25, 72, 104).

Conditions for Artificial Selection: Heritability and Variation

Artificial selection can, in principle, be applied to any level of biological organization, provided that the evolving units exhibit phenotypic variation along the axis of selection, and that a substantial fraction of this variation can be reliably passed from parents to offspring (66) (Figure 1a). Selection can be very efficient at the organismal level, as organisms fulfill both criteria: The phenotypes of an organism are (at least in part) determined by its genotype, which is either partially or entirely passed from parent to offspring. This ensures that many phenotypes have a heritable component upon which selection can act. Whether the conditions that are required for natural selection [which, in addition to the two mentioned above, include that phenotypic differences must be associated with fitness differences between the replication units (66)] are met by any supra-organismal entities in nature has remained controversial. However, there is solid empirical and theoretical evidence that those conditions can be met under artificial selection conditions (15, 26, 40, 43, 65, 111, 113, 114, 118, 119, 123).

Figure 1.

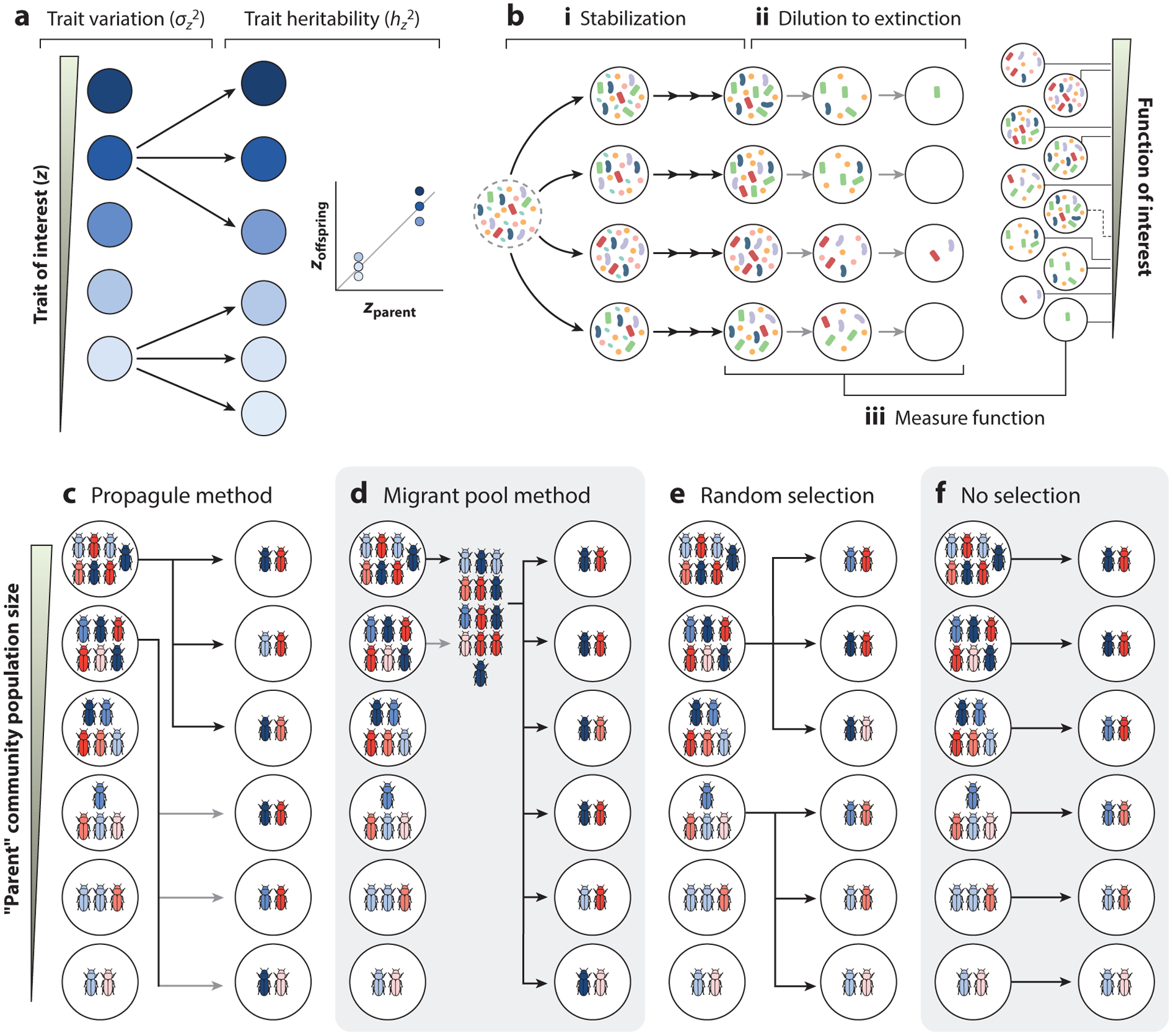
Methods of top-down engineering above the individual organism. (a) Any biological system can be subject to artificial selection as long as it exhibits variation along a trait of interest (z), and that trait is heritable, i.e., can be reliably passed into descendants derived from it in a subsequent generation. (b) Typical workflow for an enrichment approach to engineering communities from the top down. Multiple enrichment communities are set up by inoculating habitats from a species pool. Typically, the environment is selective for the desired function. The enrichment communities can be stabilized by serial passaging. Then, a severe bottleneck (dilution-to-extinction) is applied to subsample from the stable communities and find simpler communities that maintain the function, and the best among those is selected. (c–d) A depiction of the two main methods of artificial population-level selection, representing their original application in animal populations (40, 43, 111, 112). The methods shown are (c) the propagule method and (d) the migrant pool method, together with (e) a random selection control and (f) the no-selection control.

Artificial Selection of Populations and Small Synthetic Communities

The idea that groups of organisms could respond to group-level selection was originally tested in small animal populations (111, 112) and two-species communities (40, 43). In these experiments, the selection units were populations containing N ∼ 10 genetically diverse, sexually reproducing animals (belonging to the flour beetle Tribolium genus), which interacted exclusively with one another but not with individuals from other populations. These populations were scored for an emergent trait that was a property of the entire group, such as the total number of adult animals in the population after approximately 40 days of incubation. The best-performing communities (i.e., the parental groups) were then selected and used as the genetic stock to breed a new generation of groups (i.e., the offspring groups) (Figure 1b,c). As controls, some of these studies established random selection lines (where the populations selected for reproduction were chosen randomly, without regard for their phenotype), as well as no-selection lines (where all parent populations were selected for reproduction, and each seeded exactly one offspring population) (Figure 1d,e).

To generate an offspring group, these studies employed two different strategies. One reproduction strategy was called the propagule method (43). In this method, a small (N ~ 10) random subset of individuals from the selected parental population was introduced into the new habitat, acting as the inoculum for the offspring population (Figure 1b). The second reproduction method is referred to as the migrant pool method (43). It consists of pooling together all of the animals from the selected parental populations and then selecting a small random subset (also N ~ 10) from that pool to seed an offspring population in a new habitat (Figure 1c).

All of these experiments found a robust directional change in the mean phenotype of the population of populations (referred to below as the metapopulation) in response to selection at the population level. Indeed, the metapopulations in these experiments fulfilled the two conditions that are required for artificial selection to work. First, the authors found a significant between-population variation in the phenotype under selection due to the combination of small, genetically diverse populations and sexual recombination. Second, follow-up studies also demonstrated that this variation had a heritable component, stemming from interactions between specific combinations of genotypes, which were directly responsible for the population-level trait under selection (e.g., the number of adult individuals) (41, 43).

Artificial Selection of Microbial Communities and Ecosystems

In the early 2000s, artificial selection above the organismal level was extended from populations and small pairwise communities to entire microbial ecosystems. In a landmark set of studies (103, 104), Swenson and coworkers adapted the propagule and migrant pool strategies to select for microbial ecosystems with high scores in three emergent community-level traits: (a) the pH of the aquatic medium on which the ecosystems were growing; (b) the collective degradation of 3-chloroaniline, a water contaminant; and (c) an indirect microbiome phenotype, such as the above-earth biomass of the plants on which those communities had been inoculated. Although these experiments were promising, the effect of selection was modest compared to the robust and large responses observed in animal populations (40, 43, 111, 112).

These studies were followed by a handful of additional artificial microbiome selection experiments, all of which adopted similar protocols and selection strategies. Using a migrant pool method, Panke-Buisse et al. (75, 76) artificially selected for soil microbiomes that induced either early or late flowering in various genotypes of Arabidopsis thaliana and Brassica rapa. This experiment found a strong and statistically significant relative difference between the mean flowering times of microbiomes that were selected for early versus late flowering. However, both lines drifted over time and flowered later than the starting (nonselected) microbiomes. In a later study, Blouin et al. (15) used an experimental design with multiple artificial selection (as well as random selection) lines and selected for low CO₂ emission in aquatic ecosystems. The amount of respiration was lower in the artificially selected lines than in the random controls. In both, however, the amount of CO₂ produced declined over time. More recent studies have attempted to select microbiomes that degrade extracellular polymers (18, 121), protect plants against drought (55, 71), alter the development of animal embryos (8), and facilitate the growth of a species that could not grow on its own (18). We believe that it is fair to say that success has been mixed (some experiments succeeded while others failed or were inconclusive) and generally modest.

What Limits the Success of Artificial Selection at the Community Level?

As we discuss above, artificial selection at the community level requires that communities exhibit variation on the selected trait, and that this trait is reliably passed from parent to offspring communities. With regard to the heritability of community-level traits, the method used to generate offspring communities from their parents is therefore critical (83). Due to the success of the propagule and migrant pool strategies in animal populations, both methods have been universally adopted in all microbial community-level selection studies of which we are aware. There are, however, important quantitative differences between animal populations and microbial communities. First, microbial communities are generally several orders of magnitude larger. A conservative estimate of the number of bacterial cells that were used to inoculate each generation in previous experiments is N ~ 10⁶, and the actual number is likely to have been several orders of magnitude higher (19). This large inoculum size could limit the power of stochastic sampling to generate large between-population variation, which is a critical factor on which selection acts (19). In animal populations, sexual reproduction and a genetically diverse starting pool of animals also ensured a high between-population variation (Figure 1b). By contrast, most microbes reproduce asexually (despite the potential for horizontal gene transfer), and recombination is generally rare, diminishing the potential to generate novel genotypes using standing genetic variation alone. Stochasticity and selection are both needed for an efficient exploration of the adaptive landscape (122).

With regard to between-ecosystem variation, Blouin et al. (15) discussed the conflict that exists between this variation and selection. As discussed above, selection runs on phenotypic variance. Yet, as selection proceeds, it will exhaust this variance, as it will inevitably eliminate alleles and species from the metapopulation (Figure 2a). In the absence of mechanisms that regenerate between-community variation (discussed in more detail below), we should expect diminishing returns in artificial selection: The amount of heritable variation should decrease with every selection round, leading to an ever-weakening response to selection. Regenerating this variation is thus critical if we want artificial selection to be successful beyond the first few rounds. Below, we address how this variation may be replenished (Figure 2a).

Figure 2.

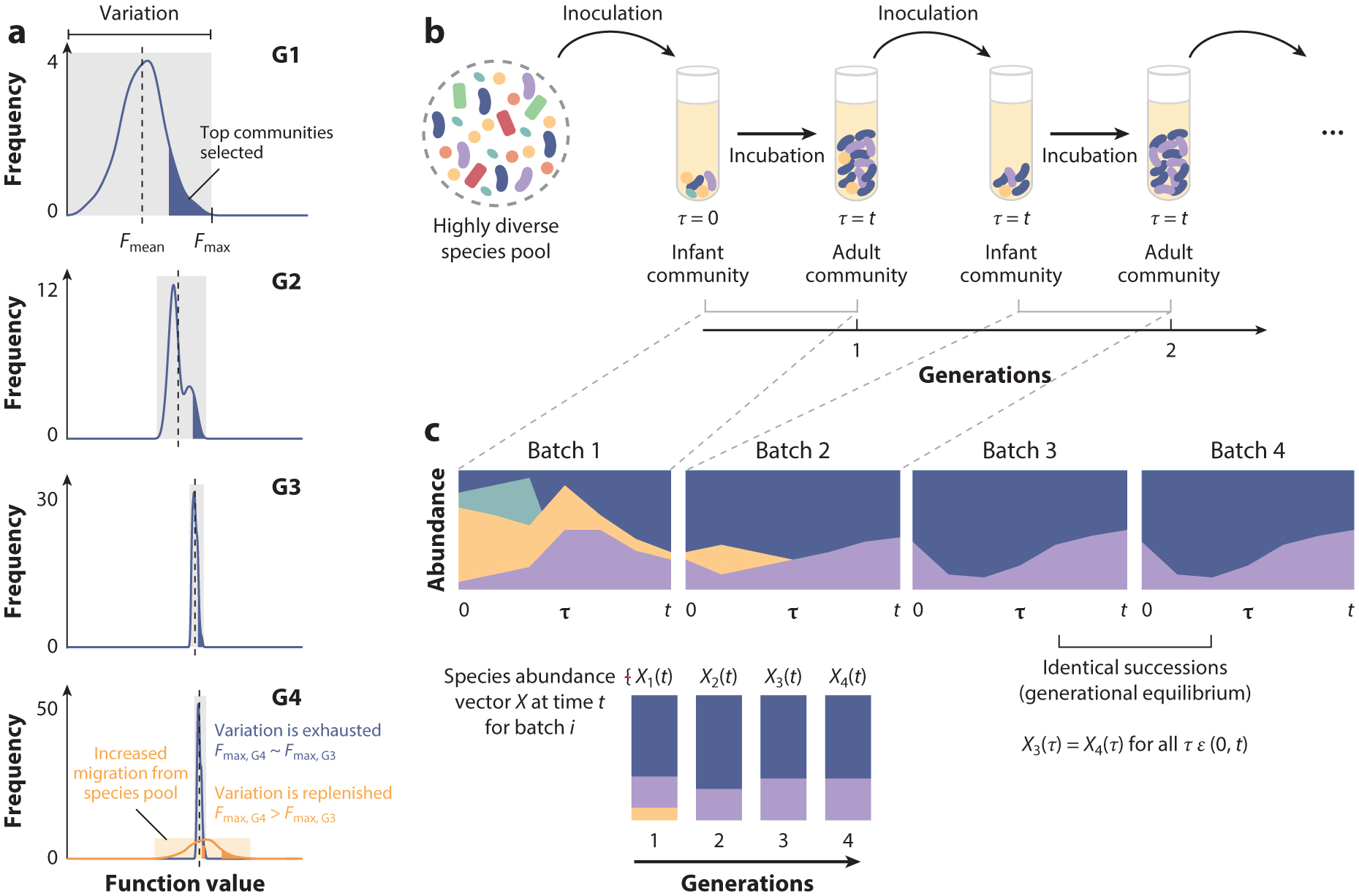
Limitations of artificial selection at the level of communities. (a) Schematic illustrating the conflict between heritable variation and selection. As the top-performing communities get selected, the worst-performing communities get purged from the metacommunity, and as a result, F_mean increases, and the amount of heritable variation decreases over generations (G). After multiple rounds of selection, and without any novel variants being introduced, the heritable variation is exhausted, and selection has nothing upon which to act. Variation can be replenished by, for instance, introducing migrants from a species pool, which may allow communities to reach new function peaks (F_max). (b) Microbial community growth in serial batch culture (without selection). Communities are initially seeded from a highly diverse species pool into a new habitat (infant community) and then allowed to grow for an incubation time t (at which point they are an adult community). Without selection, a small and random fraction of the cells from the adult community are inoculated into a new habitat, forming a new infant. This growth and dilution process is repeated multiple times. (c) Within each batch incubation, the species undergo an ecological succession as they grow and interact with each other. After multiple rounds of serial passage, communities reach a generationally stable equilibrium, which is seen when the species abundance vectors X during (and at the end of) the ith and all subsequent incubation periods are identical, i.e., when X_i(τ) = X_i+j(τ) for all τ ε (0,t) and j ≥ 1. Without such generational stability, community heritability is very low, and the success of ecosystem-level selection at the level of communities is strongly reduced.

A second important limitation of artificial selection at the level of communities or ecosystems is the inherently dynamic nature of these systems. In most artificial selection experiments, selection is applied to communities that are grown in serial batch mode (Figure 2b). In the absence of selection, serial batch culture starts by seeding a habitat with individuals coming from a previous batch (the parental batch) and continues by letting this new batch grow in an environment that is, in principle, identical or at least as similar as possible to the one in the previous generation. At the end of the batch-incubation time t, cells are again randomly drawn from the offspring batch to inoculate yet another habitat and continue the process (Figure 2b). Within each batch incubation, all species grow and undergo an ecological succession (24, 29, 33) (Figure 2c). These successions are not necessarily identical between parent and offspring batches, and neither are their compositions at the end of their respective batch incubations (Figure 2c). As we discuss below, and as has been demonstrated elsewhere (19), this generational instability can have detrimental effects on heritability and severely limit the success of ecosystem-level selection in multispecies consortia (see the section titled Appendix: The Structure–Function Landscape).

Artificial Selection as Top-Down Engineering

In the first paper on artificial ecosystem selection, Swenson et al. (104) advanced the idea that artificial selection could be used to engineer microbiomes from the top down. However, the main goal of this and other previous studies was not so much to engineer ecosystems but to demonstrate the feasibility of ecosystem-level selection and to study its fundamental limits. Perhaps for this reason, most studies have focused on the directional response of the mean function to selection, generally by comparing it to a random selection control, and none of the microbiome selection experiments of which we are aware has included a no-selection control. A no-selection control is, in essence, an exercise in ecological prospecting (18): One sets up a diverse set of enrichment communities; lets them stabilize without mixing; and, in the end, chooses whichever has the most desirable trait. In the absence of sexual recombination, the advantages of selection over ecological prospecting are not obvious, and therefore, ecological prospecting represents a benchmark against the success of a selection strategy. Importantly, the ultimate goal of artificial selection as a means of top-down microbiome engineering is not to improve the mean function in the metacommunity, but instead to find a microbiome that is fitter than the best of those with which we started (19). As we discuss above, directed evolution at or below the organismal level seeks to find optima in the genotype–phenotype space. In what follows, we argue that the directed evolution of microbial communities can similarly be conceptualized as a guided exploration of an ecological structure–function landscape: the map between community composition and community function (see the section titled Appendix: The Structure–Function Landscape).

DIRECTED EVOLUTION AS A GUIDED EXPLORATION OF THE ECOLOGICAL STRUCTURE–FUNCTION LANDSCAPE

Before we describe how directed evolution may help us explore the ecological structure–function landscape in search of communities with optimal traits, it is important to clarify what we mean by the ecological structure–function landscape and in what ways it differs from the genotype–phenotype map. This will help us better appreciate the differences that exist between directed evolution above and below the organismal level.

The Dynamical Ecological Structure–Function Landscape of Microbial Communities

Much like a fitness landscape is a map of genotypes to phenotypes, the ecological structure–function landscape is a map between community composition (i.e., the vector of abundances of all taxa in the community) and the traits (or functions) of the community (see the section titled Appendix: The Structure–Function Landscape). The idea that community composition impacts emergent or collective community functions is an old one in ecology (67, 85, 106, 107, 117). In recent years, the structure–function landscape of microbial communities has been explicitly formalized (45–47, 94, 95) and combinatorially explored (10, 28, 32, 45–47, 52, 54, 58, 94, 101) by mapping numerous different combinations of bacteria with one or more of their quantitative collective-level properties.

Perhaps the biggest practical difference between fitness landscapes and ecological structure–function landscapes is that, as described above, community composition changes within a batch, from the moment of inoculation to the point of harvesting. Moreover, the successional dynamics within a batch are not necessarily the same in the parent as in the offspring community, even in the absence of group-level selection (19). This means that the state of the community, which is defined by the vector of species abundances at the end of the batch incubation X, will change over generations, even when no artificial selection is applied (Figure 2c). Eventually, the communities may converge to a state of generational stability, which can be represented as a fixed point in their dynamical landscape (Figure 3a).

Figure 3.

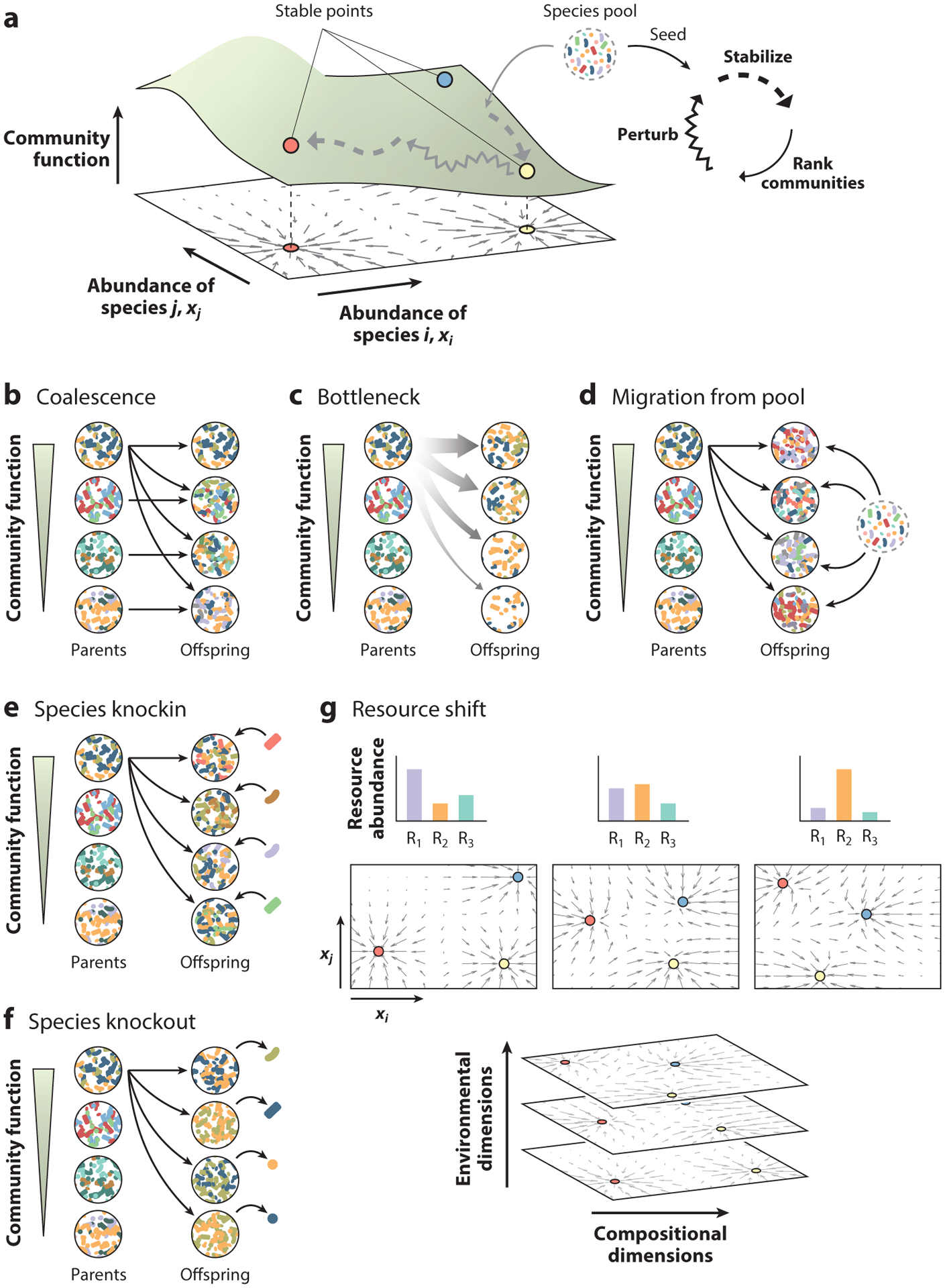
Directed evolution as navigation of an ecological structure–function landscape. (a) In this schematic, for simplicity, we project the community function over an ecological space defined by the abundance of just two species (i and j). The depicted ecological dynamics are multistable, and communities converge to one of three different attractors (stable points), colored by red, yellow, and blue circles. This ecological landscape can be navigated through an iterative process of perturbation, stabilization, ranking, and selection. (b–f) Six different methods to create a library of compositional variants of the selected community. The methods shown are (b) coalescence, (c) bottleneck, (d) migration from a pool, (e) species knockin, and (f) species knockout. (g) Altering resource concentration may also be a way to change the fitness of different species within the community and, therefore, to change the composition of generationally stable communities (60).

It is pertinent to ask at this point whether a generationally stable state of reproducible successions is ever to be expected. Early work proposed that community assembly might be chaotic, so that communities that are seeded with slightly different initial compositions (due to unavoidable random sampling) would diverge in both composition and function over time (104). Enrichment experiments with multiple replicates [which are the equivalent of a no-selection control in artificial selection experiments (19, 111)] have found, however, that community assembly is not chaotic (30): Replicate habitats that were seeded from the same inoculum generally adopted a discrete set of alternative (generationally) stable states (30, 39). These experiments have mapped the basin of attraction of stable states in self-assembled communities and even found stochastic transitions among them (30, 109). Other studies with synthetic or bottom-up communities have similarly found evidence of dynamical multistability in microbial communities (4, 20, 23, 36). Because different stable community states contain different species, they may also differ in a range of community-level properties and functions (37). These studies, along with related theoretical work (26), support the idea that the structure–function landscape is more than a convenient metaphor and that, despite its limitations (see the section titled Appendix: The Structure–Function Landscape and above), it is a practical and useful tool to help us think through the process of directed evolution of biological systems above the organism.

Directed Evolution of Microbial Communities: Methods to Explore the Ecological Structure–Function Landscape

At the community level, directed evolution would start by creating a library of generationally stable communities that differ from each other in the collective, community-level trait under selection. The fittest community is then selected and used to generate a new library of proximal compositional variants. Those variants are propagated by serial batch culture until they are generationally stable, and the fittest among these is again selected so that the process can be iterated as many times as needed (Figure 3a). A key step in the development of directed evolution for protein and network engineering has been the invention of methods for gene diversification, which enable the exploration of the fitness landscape of the system under selection (74). If we wish to apply directed evolution to microbial communities, we should similarly ask how exactly we can generate a library of compositional variants of a selected community. Many ideas and methods have been already tested empirically in enrichment-based approaches for the top-down engineering of microbial communities (22, 38, 56, 60, 62, 77, 127). Below, we discuss these and a few other possibilities (19).

Horizontal gene transfer and mobile elements.

Mobile elements can create new strains whose contribution to community-level functions may differ from those of their ancestor (Figure 3a). This suggests that adding mobile elements (e.g., bacteriophages and plasmids) to different communities in a metacommunity may stochastically lead to the appearance of new strains in the community and, therefore, to between-community variation in function. In a recent study, Quistad et al. (78) transplanted mobile elements from one community to another, and this process led to genetic changes (e.g., amplification of genes involved in nitrogen metabolism) in the recipient species. These genetic changes were associated with functional changes at the community level (e.g., biochemical rates of ammonification), demonstrating that stimulated species-level evolution can be a means to create compositional and functional variants of a successful community. More targeted tools to deliver plasmids to a stable microbiome by horizontal gene transfer have been developed in recent years (91).

Coalescence.

A library of variants of the selected community may also be created by coalescing the selected, stable community with each of the nonselected ones (68, 86, 87, 99) (Figure 3b). Multiple theoretical and empirical lines of evidence show that mixing two communities together produces a new offspring community that resembles both of its parents both in composition and function (99, 105).

Horizontal migration.

Randomly sampled species from one or more natural species pools could be dded to the community to generate proximal variants (Figure 3c). These invasive species may displace some of the resident taxa or augment the community by fixing without driving others extinct (61). Even those species that do not fix may, in principle, push a community to an alternative state (4).

Selective knockins.

Species that are deemed to have a beneficial effect on the selected function can be selectively added one at a time to the community, thus generating a library of compositional variants (Figure 3d). To ensure that this added species will not be outcompeted by the resident species, an exclusive metabolic niche (i.e., a nutrient that the added species may utilize but that most members in the invaded community do not) could be supplied together with the added species (96).

Bottlenecking.

Variants of a selected community can be generated by subjecting it to multiple harsh bottlenecks, an approach known as dilution-to-extinction (22, 35, 53, 56, 62) (Figure 3e). If a sufficiently low number of cells is sampled from the community during each bottleneck, then the inherent sampling stochasticity will ensure that each of the variants will have a different community composition (56). The specific bottleneck size that will maximize functional variation between compositional variants can be determined empirically, as it is a function of the population size (19, 53).

Selective knockouts or knockdowns.

Individual species from the resident community may also be selectively targeted for elimination or growth suppression, for instance, by narrow-spectrum antibiotics or bacteriophages (17, 70, 73, 124) (Figure 3f). This will create community variants with different compositions. In addition, bacteriophages and antibiotics also represent selective pressures that can alter the genotypic composition of communities (3, 116), presenting an additional mechanism to generate compositional variants.

Environmental pulse perturbations.

In addition to adding and removing species, one may push communities into random directions of the ecological landscape by transiently changing the environment, for instance, by altering nutrient composition; by increasing the temperature, salinity, or pH; or through other means (Figure 3g). This will alter the fitness of all members of the community, allowing some of the rarer members to increase in abundance and some of the more abundant members to decline. When the environment is returned to its normal state, the perturbed communities may converge to a different fixed point due to either species loss or multistability. Environmental pulse perturbations can also result in phenotypic switching in microbial populations (9). We speculate that cellular memory may allow us to push microbial communities to new functional states even in the absence of changes in their genotypic composition.

Environmental press perturbations.

Finally, whereas all of the above strategies to create compositional variants involve the communities jumping to a new stable state, another possibility is to change the environment in a small but permanent way, thereby creating new stable states that did not exist before (60) (Figure 3h). We speculate that this may allow finer control over the community composition, as the press perturbations may be made, in principle, as small as desired, thus potentially allowing for very small changes in species abundances (60).

Summary.

The above methods are not exhaustive. The reader will have noticed that the two methods used in artificial selection, the propagule and the mixed pool, are also means to explore the ecological structure–function landscape. The bottleneck method is essentially an extreme form of the propagule method, where a very small number of cells is chosen to seed the offspring generation. As for the migrant pool method, it is also an example of coalescence, where more than two communities are mixed in equal ratios. Both of these methods can successfully create a new library of variants if the number of cells that is sampled is small enough (18).

Directed Evolution of Microbial Communities: Selection and Heritability at the Community Level

After a sufficiently heterogeneous library of variants has been generated, we must reckon with the fact that not all of the variation will be heritable. For instance, some variation may come from measurement error in determining the function of each community. How does this nonheritable component affect selection? The community-level heritability quantifies the degree to which community functions are passed from a parent community to its offspring. If heritability is very low, then this means that there exists a low correlation between the parent and offspring community function. Therefore, high community-level heritability is critical for directed evolution to work. To understand how this heritability is affected by different experimental and ecological processes, let us first consider a metacommunity that is being passaged in the absence of artificial community-level selection (Figure 2b) until all communities are successionally stable (see the section titled Appendix: The Structure–Function Landscape).

Let us denote by f_x and f_y the experimentally measured functions of a parent community and its offspring. By assumption, both communities are in the same generational equilibrium state X*. The functions of both communities can be written as

$$f_x=F\left(X^{*}\right)+{\xi }_x,$$

$$f_y=F\left(X^{*}\right)+{\xi }_y,$$

where F(X*) denotes the function associated with the equilibrium state X* in the structure–function landscape, and ξ_x and ξ_y are uncorrelated random variables of zero mean and equal variance (σ_ξ²). These two variables capture the effect of small stochastic deviations in community composition from the true equilibrium due to drift (e.g., due to the stochastic sampling introduced by pipetting), as well as measurement error, environmental fluctuations, and other stochastic factors. If we regress the function of the offspring on the parent function across the entire metacommunity, then the regression slope will be given by b = Cov(f_x,f_y)/σ_x², where σ_x² is the experimentally measured variance in the parent metacommunity. The experimentally measured variance will, in turn, be given by σ_x² = σ_F² + σ_ξ², where σ_F² represents the component of the variance that is due to different communities in the parent metacommunity being in different equilibria, i.e., the variance in F(X*) over the metacommunity.

By assumption, each offspring community is fluctuating around the same dynamical equilibrium state as its parent. Therefore, the component of the variance that derives from different communities being in different steady states (σ_F²) will be passed intact from the parent to the offspring metacommunity. By contrast, σ_ξ² is nonheritable, as it includes all of the sources of variation that are stochastic and are uncorrelated between parent and offspring communities, from drift in population dynamics to environmental fluctuations or measurement error. Because, by assumption, ξ_x and ξ_y are uncorrelated, Cov(f_x, f_y) = σ_F² The slope of the regression between parent and offspring function will thus be equal to b = σ_F²/σ_x². It is straightforward to see that the slope b is equal to the fraction of the total variation in function across the parent metacommunity that is heritable, i.e., the community heritability h² (15, 42):

$$h^2={{\sigma }_F}^2/{{\sigma }_x}^2={{\sigma }_F}^2/\left({{\sigma }_F}^2+{{\sigma }_{\xi }}^2\right)={\left(1+{{\sigma }_{\xi }}^2/{{\sigma }_F}^2\right)}^{-1}.$$

The larger σ_ξ²is relative to σ_F ², the weaker will be the response to selection. This highlights the detrimental role of all nonheritable components for community-level selection. The effect of pipetting errors has been recently examined (123), and other factors such as the importance of precise and accurate measurements of community-level functions and of working with genetically diverse communities in equilibrium have also been highlighted. Uneven spatial and temporal environmental conditions among the populations should be avoided.

SUMMARY AND OUTLOOK

Our motivation for writing this review was to synthesize the differences and similarities that exist between directed evolution of biological systems above and below the organismal level. Just as directed evolution has been used to engineer proteins and microbial strains, it may be used to engineer communities and organisms as well. The underlying idea is similar, but important differences exist. Unlike the genotype of an organism (which is stable throughout its lifespan) or of a molecule, the composition of a community changes not only during the successions within each batch, but also across successive batches. Only after the communities stabilize can their composition and collective properties be reliably passed from parent to offspring communities. At that point, communities become a valid unit of selection and can be subject to directed evolution. In this review, we discuss how one may carry out such an experiment and provide ideas that we hope will be useful for other researchers as they design their own approaches.

Artificial selection: the process of intervening in the natural reproduction cycle of organisms to favor those individuals that exhibit desirable traits

Directed evolution: an iterative process of randomization and selection that is used to engineer biological systems from the top down

Fitness landscape: the map between the genotype of a gene or organism and its phenotype or fitness

Ecological structure–function landscape: the map between community composition and the function or functions associated with it

Generational stability: a state reached by serially passaged batch cultures where the ecological successions in successive batches converge to be identical

APPENDIX: THE STRUCTURE–FUNCTION LANDSCAPE

We argue that the functions of a community are determined by their structure. Can we be more precise? For the structure–function landscape to be meaningful, we must specify what exactly are the function and the structure. To address this question, it is helpful to think of a concrete example, which is inspired by recent experiments in our laboratory (94). Let us consider a community of species that is seeded into a habitat at time τ = 0 and allowed to grow in it. Species abundances [listed by the vector X(τ)] will change over time according to X’(τ) = dX/dτ = g[X(τ);Θ (τ)], where Θ(τ) represents the set of all environmental parameters. As the species grow in this habitat, some of these environmental parameters change as well. For instance, species may be secreting an enzyme into the environment. The concentration of this enzyme in the habitat [C(τ)] will increase as a result of secretion, but it may also decline as the enzymes become degraded by proteases or inactivated through other means. The concentration of enzyme C(τ) will thus be governed by a differential equation, just as the species abundance is, where

$$C\prime \left(\tau \right)=h\left(X,X\prime ,\Theta \right)-C\left(\tau \right)m\left(X,X\prime ,\Theta \right).$$

In this case, we introduce a function h(.), which captures the instantaneous rate of enzyme production in the community, and a second function m(.), which reflects the instantaneous rate of degradation or dilution per enzyme. The total secretion rate will be a function of the abundances of all secreting species X(τ) (94) and potentially also of the growth rates of all species X′(τ), as the expression of most genes is regulated by growth rate (59). Finally, it may also be a function of the total concentration of the enzyme in the environment, as the byproducts of an enzyme are often inhibitors of its expression (44, 94). This rate may also depend on additional factors, such as the previous growth history of all cells, as gene expression can exhibit hysteresis (9, 88).

In this example, the enzyme concentration at the end of the batch incubation (i.e., the harvesting time) t is a community trait for which one may want to select, and therefore, it is a potential function (F) of the community: F = C(t). The abundance of all species at the time of harvest, X(t), could be thought of as the structure of the community. Yet the function F is in this case a cumulative property of the community over the incubation time t. In principle, F will causally depend not only on the species abundances at time t, but also on their entire ecological (i.e., succession) dynamics over the incubation time t, i.e., on {X(τ),X′(τ),Θ(τ)}, where τ ∈ (0, t) (Figure 2b,c). Therefore, it is unclear that a structure–function landscape F[X(t)] that uniquely maps every structure [i.e., the abundance vector X(t)] with a function F even exists in this case.

This situation is resolved if we think of a population in equilibrium. It may sound strange to speak of communities being in equilibrium, given that they are being serially passaged and therefore engaging in a dynamical ecological succession during each incubation. A community is generationally stable when the ecological successions within subsequent incubations are identical (26), and as a result, the abundance vectors at the end of the ith and all subsequent incubation periods are also identical, i.e., if X_i(t) = X_i+j(t) (j > 1). If two consecutive successions are identical, then X_i(τ) = X_i+1(τ) for all τ ∈ (0,t), and we should expect that the same equality will hold for X′(τ) and Θ(τ) and, therefore, for C(τ). We thus argue that the structure–function landscape F[X(t)] is well defined for communities that are generationally stable. It is important to note, however, that F is not causally determined by X(t), but rather, that X(t) and F(t) are both linked together through the same underlying dynamical process. Although there exists an association between both, this association does not immediately imply causation.

Finally, we should also note that the function F can (and often does) feed back to population dynamics. For instance, the concentration of extracellular enzymes will affect the fitness of different microbial strains (20, 93), and the per-capita contribution of each strain to this function may also be costly at the individual level (98). This can lead high-function states to be vulnerable to invasion by cheater strains that have high fitness when the function is high but that do not contribute to its production, thus avoiding the cost. Understanding how multilevel selection can contribute to avoiding cheater invasion is an area of intense theoretical and experimental interest (2, 21, 50, 51, 82) that can help us design efficient methods of artificial community-level selection (5, 123).