EGGTART: A tool to visualize the dynamics of biophysical transport under the inhomogeneous l-TASEP

Abstract

The totally asymmetric simple exclusion process (TASEP), which describes the stochastic dynamics of interacting particles on a lattice, has been actively studied over the past several decades and applied to model important biological transport processes. Here, we present a software package, called EGGTART (Extensive GUI gives TASEP-realization in Real Time), which quantifies and visualizes the dynamics associated with a generalized version of the TASEP with an extended particle size and heterogeneous jump rates. This computational tool is based on analytic formulas obtained from deriving and solving the hydrodynamic limit of the process. It allows an immediate quantification of the particle density, flux, and phase diagram, as a function of a few key parameters associated with the system, which would be difficult to achieve via conventional stochastic simulations. Our software should therefore be of interest to biophysicists studying general transport processes and can in particular be used in the context of gene expression to model and quantify mRNA translation of different coding sequences.

Significance

Stochastic transport phenomena on inhomogeneous lattices are complex and typically accessible only through simulations or approximations, as closed-form formulas are often intractable. Recently, we obtained the stationary solution to the so-called inhomogeneous $\ell$-TASEP, a central model of biophysical transport, in the limit of large lattice length. We found that ultimately, there are only six parameters contributing substantially to particle currents and densities—the key quantities associated with transport efficiency. Based on this theoretical advance, we present here a computational tool to visualize and interactively explore the relationship between the key system parameters we have identified and steady-state densities and currents, thus enabling one to explore the robustness and optimality of transport systems.

Introduction

The totally asymmetric exclusion process (TASEP) is a stochastic process used to model a large variety of transport phenomena involving interacting particles (1). Although it has been studied extensively over the past several decades, it is still the subject of active research and is replete with many open problems motivated by biophysical applications. In particular, the recent emergence of experimental data through advances in microscopy and sequencing techniques has revealed a wealth of molecular processes that are well described by TASEP models, including the motion of ribosomes (2, 3, 4), RNA polymerase (5), and motor proteins (6). Such processes require extending the classical TASEP by several layers of complexity, and as a result, their analysis has remained elusive and restricted to particular cases that do not adequately reflect biology. This shortcoming recently led us to study the so-called inhomogeneous $\ell$-TASEP, in which particles of size $\ell$ traverse a lattice of inhomogeneous jump rates. By considering the hydrodynamic limit of the process, we obtained exact formulas for particle currents and locally averaged occupation probabilities (7), offering immediate quantification of the particle density, flux, and phase diagram, which would be difficult to achieve via conventional stochastic simulations.

To help to visualize these theoretical results, we present here a software package called EGGTART (extensive GUI gives TASEP realization in real time). For an arbitrary specification of the key system parameters (particle size, entrance rate, exit rate, and site-specific jump rates), EGGTART provides a graphical user interface that allows us to extract the main quantities of interest (e.g., the current and local densities, i.e., smoothed occupation probabilities, of particles), in addition to providing a phase diagram that fully describes different types of traffic behavior. We demonstrate how it can recover various versions of the TASEP studied in the past literature as special cases. By facilitating the exploration and visualization of both theoretical and practical aspects of the inhomogeneous $\ell$-TASEP, we anticipate our computational tool to be broadly helpful to mathematicians, physicists, and biologists in studying various biophysical transport phenomena.

Methods

The inhomogeneous $\ell$-TASEP

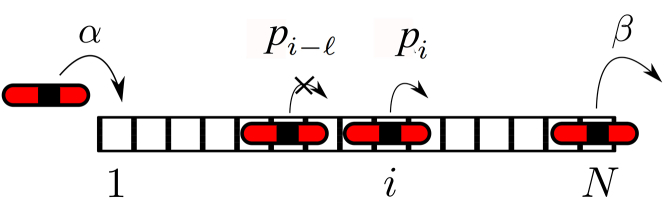
The inhomogeneous $\ell$-TASEP is a Markov process, illustrated in Fig. 1, in which particles of size $\ell$ jump unidirectionally along a lattice of N sites under mutual exclusion: a particle at site i ∈ {1, …, N − 1} remains at its position if the site i + $\ell$ is occupied and jumps at exponential rate p_i to position i + 1 otherwise. Particles can enter the lattice at the first site at rate α while respecting the mutual exclusion constraint and leave the lattice at the last site at rate β.

Figure 1.

Illustration of the inhomogeneous $\ell$-TASEP with open boundaries. Particles (of size $\ell$ = 3 here) enter the first site of the lattice at rate α, and a particle at position i (here denoted by the position of the midpoint of the particle) moves one site to the right at rate p_i, provided that site i + $\ell$ is empty. A particle at the end of the lattice exits at rate β. To see this figure in color, go online.

The hydrodynamic limit

Although solving the inhomogeneous $\ell$-TASEP is in general intractable, we can do so in the continuum limit of N → ∞. More precisely, denoting by τ(t) ∈ {0, 1}^N a configuration at time t and assuming that λ(x) = $\underset{N\to \infty }{lim}\frac{1}{\ell }\sum _{i=0}^{\ell -1}{p}_{⌊Nx⌋+i}$ exists and is differentiable, we have shown in (7) that the $\ell$-smoothed density of particles ρ(x, t)dx = $\underset{N\to \infty }{lim}\frac{1}{N}\sum _{n=1}^{N-\ell +1}\frac{1}{\ell }\sum _{i=0}^{\ell -1}{\tau }_{n+i}\left(Nt\right){\delta }_{\frac{n+i}{N}}\left(\text{d}x\right)$ satisfies the inhomogeneous conservation law

$${\partial }_t\rho =-{\partial }_x\left[\lambda \left(x\right)\rho G\left(\rho \right)\right],$$ (1)

where G(ρ) = $\left(1-\ell \rho \right)/\left(1-\left(\ell -1\right)\rho \right)$. Constant jump rates and $\ell$ = 1 yield the one-dimensional Burgers’ equation, known as the hydrodynamic limit of the classical TASEP (8). As shown next, increasing $\ell$ and introducing spatial inhomogeneity lead to more complex solutions.

Analytical solutions and phase diagram

Equation 1 can be solved using the method of characteristics (7), wherein the two boundary points 0 and 1 each emit a characteristic curve whose evolution determines the long-term behavior of the system. These curves are controlled by boundary conditions, which yield a phase diagram in α and β. Surprisingly, this phase diagram is completely characterized by four parameters: the particle size $\ell$ and the minimal, initial, and terminal jump rates λ_min := min_xλ(x), λ₀ := λ(0), and λ₁ := λ(1), respectively. These parameters determine the critical rates α^∗ = α^∗($\ell$, λ₀, λ_min) and β^∗ = β^∗($\ell$, λ₁, λ_min) at which phase transitions occur (precise expressions are provided in (7)). The different regions of the phase diagram are characterized as follows (note that Eq. 1 cannot describe critical behavior, in which residual stochasticity persists; see (7) and references therein):

• 1)α < α^∗ and β > β^∗: In this low-density regime (LD), the low entrance rate coupled with large exit rate establish an overall small density ρ_L(x) = ${\rho }_L\left(\lambda \left(x\right),\ell ,J_L\right)<{\rho }^{\text{∗}}:={\left(\ell +\sqrt{\ell }\right)}^{-1}$, where J_L = $\alpha \left({\lambda }_0-\alpha \right)/\left({\lambda }_0+\left(\ell -1\right)\alpha \right)$ is the particle current.
• 2)α > α^∗ and β < β^∗: Particles are injected frequently and drained slowly, shaping the high-density phase (HD). The associated density ρ_R(x) = ρ_R(λ(x), $\ell$, J_R) > ρ^∗ is strictly larger than ρ_L, with a current now given by J_R = $\beta \left({\lambda }_1-\beta \right)/\left({\lambda }_1+\left(\ell -1\right)\beta \right)$.
• 3)α < α^∗ and β < β^∗: A phase transition occurs along the nonlinear curve J_L = J_R, with J_L < J_R resulting in LD densities and currents and J_L > J_R in HD ones.
• 4)α > α^∗ and β > β^∗: This phase characterizes the maximal current regime (MC). The maximal current J_max = λ_min × ${\left(1+\sqrt{\ell }\right)}^{-2}$ results from of superposition of high and low densities $\rho \left(x\right)={\rho }_R\left(x\right)\times {\mathbb{1}}_{x\le x_{\text{min}}}+{\rho }_L\left(x\right)\times {\mathbb{1}}_{x\ge x_{\text{min}}}$, where x_min = argmin_xλ(x).

General description of the software and availability

For any parameterization of the inhomogeneous $\ell$-TASEP (e.g., particle size, entrance, exit, and site-specific rates), our computational tool EGGTART integrates the analytical formulas given above into a graphical user interface that provides a quantification and visualization of key properties, such as the particle current, densities, and phase diagram associated with different types of particle traffic behavior. It has been developed in Python 3.6 and uses the numpy and pyqtgraph packages. Versions for Mac OS X, Linux (Ubuntu), and Windows (10) are available at https://github.com/songlab-cal/eggtart, together with a user manual describing general features and a tutorial to be used with the demo .csv input files.

Results

We demonstrate the utility of EGGTART for a wide range of applications and examples, ranging in order of increasing complexity from the original TASEP model to the general inhomogeneous $\ell$-TASEP. Illustrations of EGGTART’s accuracy through Monte Carlo simulations are provided in the Supporting materials and methods.

The homogeneous $\ell$-TASEP

The classical TASEP model, for homogeneous rates (p_i $\equiv$ 1) and $\ell$ = 1, has been analytically solved through the matrix ansatz method (9). In the top left panel of Fig. 2, we show that EGGTART recovers the classical results obtained therein as special cases of the general model; because of the symmetry of particles and holes, the resulting phase diagram is symmetric in α and β, with three regions (LD, HD, and MC; see Methods) separated by simple lines intersecting at the critical point (α^∗, β^∗) = (1/2, 1/2). Particle currents J in LD, HD and MC are α(1 − α), β(1 − β), and 1/4, respectively, with bulk densities ρ given by α, 1 − β, and 1/2.

Figure 2.

The effect of inhomogeneous jump rates and extended particles. The various impacts of increasing particle sizes and introducing inhomogeneity on the phase diagram, density profile, and current are displayed using EGGTART. Particle size and rates can be adjusted independently to investigate individual (top right and bottom left) and joint effects (bottom right). To see this figure in color, go online.

General transport phenomena typically require particle size $\ell$ > 1; e.g., ribosomes translating mRNA sequences occupy roughly 10 codons. The $\ell$-TASEP for arbitrary $\ell$ ≥ 1 models this effect. As in the case for ℓ = 1, mean-field approaches can provide approximations to the phase diagram, currents, and densities (10, 11, 12), which are made precise in the hydrodynamic limit (13). EGGTART also recovers these results, as seen in the top right panel of Fig. 2. The critical values α^∗ and β^∗ shrink to $1/\left(1+\sqrt{\ell }\right)$, whereas J decreases to $\alpha \left(1-\alpha \right)/\left(1+\left(\ell -1\right)\alpha \right)$, $\beta \left(1-\beta \right)/\left(1+\left(\ell -1\right)\beta \right)$, and $1/{\left(1+\sqrt{\ell }\right)}^2$ in LD, HD, and MC, respectively (with similar adjustment for ρ), showing that increasing the size of particles leads to a global decrease of densities, currents, and transport capacity.

Intermediate cases: bottlenecks and linear rate function

Simple lattice inhomogeneities have been studied extensively, as they promise closer modeling of actual transport phenomena while maintaining theoretical tractability. The most fundamental examples include single defects or defect clusters, i.e., sites with lower rates, that can model “slow” codons in translation or structural imperfections of the structure in microtubular transport (14,15). Processes with monotonically varying jump rates, which are most simply modeled by linear functions, constitute another class of examples of inhomogeneity and have notably been observed in translation as the so-called “5′ translational ramp” (16). EGGTART readily visualizes and quantifies such configurations, reproducing previously reported results. We provide more details on these intermediate examples and their corresponding biophysical applications in the Supporting materials and methods.

The inhomogeneous $\ell$-TASEP

The most general case treated by our model combines extended particles and heterogeneous rates. Such a generalization is, for example, necessary to properly model mRNA translation because the local elongation rate of ribosomes (which occupy 10 codons) depends on multiple factors (17). Therefore, most realistic modeling of translation dynamics has been based on the inhomogeneous $\ell$-TASEP (2), with estimates of rates obtained using measurements of transfer RNA usage (2,18) or, more recently, by analyzing ribosome profiling data (17). Until recently (7,19), detailed analyses under such heterogeneous lattices have been restricted to numerical simulations (2) or mean-field approximations suffering from numerical instabilities and imprecisions (20). With EGGTART, we are able to quantify and discern from each other effects due to particle size and inhomogeneity; we observe 1) the reduction in transport capacity and critical rates (α^∗ and β^∗) associated with a decrease of the limiting jump rate λ_min (bottom left panel in Fig. 2) and extended particles (bottom right panel), 2) deformation of the LD-HD phase separation (bottom panels), 3) the branch switching of ρ in MC (bottom panels), and 4) the impact of λ₀ on the sensitivity of particle current to the initiation rate (see the Supporting materials and methods). Each of these principles has important consequences for optimizing ribosome usage and translation efficiency (7). Therefore, using the software can help practitioners understand a gene’s evolutionary constraints or devise sequences most suitable for specific needs.

Discussion

Although the TASEP has been widely used and studied for several decades (1,2,8), we provide here, to the best of our knowledge, the first computational tool for visualizing phase transitions, densities, and fluxes of the TASEP in full generality, with an arbitrary particle size and inhomogeneous jump rates. Our tool has several advantages compared to numerical simulations. By tuning the parameters of the model through a graphical interface, the user can quickly visualize their impact, particularly that of the six key parameters that govern transport efficiency (7). In the context of translation, exploring these parameters allows to address various biological questions, like quantifying how far individual genes are from their transport capacity, and to which parameters protein production is most sensitive (7). As a computational tool that allows immediate quantification and fine-tuning of the TASEP, EGGTART can thus aid in studying the properties of biophysical transport systems while serving as a basis for future improvements and extensions (e.g., the inclusion of Langmuir kinetics (21)).

Author contributions

Y.S.S., K.D.D., and D.D.E.-P. designed the research. W.S. wrote the software. Y.S.S., K.D.D., and D.D.E.-P. wrote the article.

Editor: Alan Grossfield.