Abstract
In this study, we develop a computational model of the interaction between ryanodine receptor type 2 (RyR2) and calmodulin (CaM) to explore the mechanistic link between CaM-RyR2 interactions and cardiac arrhythmia. Our starting point is a biophysically based computational model of CaM binding to a single RyR2 subunit, which reproduces single-channel RyR2 measurements in lipid bilayers. We then integrate this CaM-RyR2 model into a spatially distributed whole-cell model of Ca cycling, which is used to investigate the relationship between CaM and Ca cycling homeostasis. We show that a reduction in CaM concentration leads to a substantial increase in the rate of spontaneous Ca sparks, and this induces a marked reduction in sarcoplasmic reticulum Ca load during steady-state pacing. Also, we show that a reduction in CaM modifies the RyR2 open probability, which makes the cell more prone to Ca wave propagation. These results indicate that aberrant Ca cycling activity during pacing is determined by the interplay between sarcoplasmic reticulum load reduction and the threshold for Ca wave propagation. Based on these results, we show that when CaM is reduced, Ca waves can occur in a cell and induce action potential perturbations that are arrhythmogenic. Thus, this study outlines a novel, to our knowledge, mechanistic link between CaM-RyR2 binding kinetics and the induction of arrhythmias in the heart.
Significance
In this article, we develop a computational model of the interaction between calmodulin and the ryanodine receptor. Using this model, we show how the binding reactions between these proteins can induce aberrant calcium cycling activity at the whole-cell level. Based on these results, we describe a mechanistic link between calmodulin regulation of RyR2 and cardiac arrhythmias.
Introduction
Calmodulin (CaM) is an important calcium (Ca) binding protein that regulates a wide range of cellular functions. CaM is composed of four EF-hand Ca binding motifs that are connected by a flexible linker (1). As the Ca concentration is raised, Ca ions bind to the EF-hand, and this induces a conformational change of CaM that allows it to selectively bind to various proteins. This architecture allows CaM to regulate an array of cellular components in a Ca-concentration-dependent manner (2,3). In the cardiac cell, CaM plays an important role as a key regulator of the ryanodine receptor type 2 (RyR2), which controls the flow of Ca between intracellular stores (4, 5, 6). However, the precise mechanism by which CaM modulates the RyR2 open probability and the subsequent downstream effect in the cell are still not fully understood.
Many studies have demonstrated that the interaction between CaM and the RyR2 plays an important role in various heart rhythm disorders (7). In particular, mutations in CaM have been implicated as a potential underlying mechanism for catecholaminergic polymorphic ventricular tachycardia (CPVT) (8, 9, 10, 11). Also, various heart failure models have shown that CaM binding to the RyR2 is compromised (12, 13, 14). In both of these cases, it was demonstrated that defective CaM-RyR2 interactions disrupted the Ca cycling homeostasis of the cell, which led to adverse downstream consequences. In heart failure, it is believed that the main effect is a depletion of the sarcoplasmic reticulum (SR) load caused by an increase in spontaneous Ca sparks (10). Also, studies have demonstrated that abnormal CaM regulation can lead to an increase in the number of subcellular Ca waves (10,11). It is believed that these Ca waves then perturb Ca-sensitive membrane currents, which can induce membrane excitations such as delayed afterdepolarizations (DADs), which can proceed to initiate an arrhythmia (15,16). These studies indicate that the CaM-RyR2 interaction may be a focal point to understand the underlying mechanism for a wide variety of cardiac abnormalities.
A fundamental difficulty in establishing the link between CaM-RyR2 interactions and the initiation of arrhythmia is that the underlying phenomena span a vast range of length and timescales. In particular, it is not well understood how a molecular interaction between CaM and the RyR2 can translate to a whole-heart arrhythmia. The RyR2 is composed of four identical subunits that form a tightly bound tetramer. Detailed cryo-electron microscopy (cryo-EM) images show that the pore is formed at the center of the tetramer and is lined by four S6 segments from each subunit (17, 18, 19). When Ca binds to the Ca binding activation site at each subunit, a conformational change is induced that switches the S6 segment from a closed to an open position. If a sufficient number of subunits switch to the open state, the pore diameter will increase and allow Ca ions to flow through. Each subunit of the RyR2 is regulated by CaM at a specific region, which corresponds to residues 3614–3643 in the type 1 ryanodine receptor (RyR1), and this is referred to as the CaM binding domain (CaMBD) (20). Subsequent high-resolution cryo-EM studies have identified this domain as residues 3581–3610 within the full-size RyR2 and also imaged the bound CaM-RyR2 complex at different levels of Ca concentration (21). However, despite these advances in imaging, it is still not understood how CaM regulates the conformational state of the RyR2 subunit.
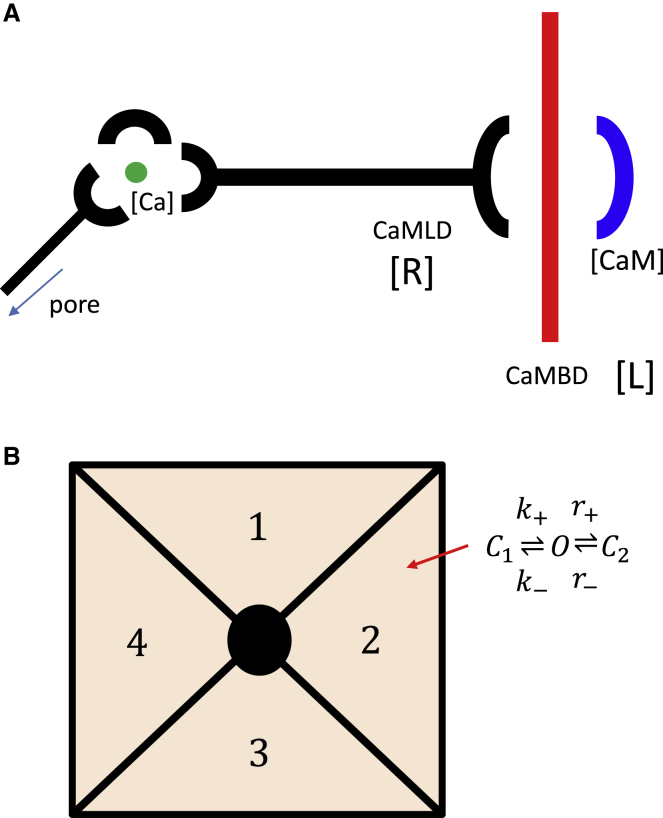
For RyR1, a plausible mechanism has been proposed by Xiong et al. (22) and later corroborated by Gangopadhyay and Ikemoto (23). These studies suggest that RyR1 itself contains a CaM-like domain (CaMLD) which interacts directly with the CaMBD and competes with CaM for this binding site. They hypothesized that when the CaMLD binds to the CaMBD, this interaction induces a conformational change that leads to an increase in the RyR2 open probability. Thus, CaM controls the RyR1 open probability by regulating the availability of the CaMBD. This hypothesis is consistent with more recent cryo-EM studies that indicate, in both RyR1 and RyR2, that the CaMLD is positioned directly adjacent to the Ca binding activation site and therefore can be coupled to the S6 segment lining the pore (21). Thus, these structural studies support the hypothesis that the CaMLD is a key component linking the CaMBD and the pore. In Fig. 1 A, we illustrate the spatial relationship between CaM, the CaMBD, the CaMLD, and the Ca binding activation site, which links the CaMLD to the pore. Based on this assumption that the CaMLD is directly linked to the Ca binding activation site, we hypothesize that the transition to the open state of an RyR2 subunit is dependent on the amount of Ca bound to the CaMLD-CaMBD complex. Thus, by regulating the availability of the CaMBD, CaM will modulate the open probability of the RyR2 channel.
Figure 1.
(A) Illustration of the proposed mechanism underlying CaM regulation of the RyR2 open probability. Here, CaM competes with the CaMLD for binding to the CaMBD. Once the CaMLD binds to the CaMBD, Ca can bind to the CaMLD-CaMBD complex at a different site to induce a conformational change at the pore. (B) Tetrameric structure of the RyR2 channel is shown. Each subunit is described by the minimal Markovian model shown. To see this figure in color, go online.
In this study, we develop a computational model of the CaM-RyR2 interaction that is based on the aforementioned experimental work showing that CaM and a CaM-like domain on the RyR2 compete for a specific binding region on the RyR2 (22,23). We have integrated this model with a whole-cell spatially distributed model of an atrial myocyte to show that a reduction in CaM leads to an increased Ca leak because of a higher frequency of spontaneous Ca sparks. Also, a reduction in CaM reduces the threshold SR Ca concentration necessary for Ca waves to propagate in the cell. Thus, the effect of CaM on Ca wave propagation is dependent on the interplay between SR load reduction and the threshold for Ca waves. We show that these two effects compete, and we outline the conditions that lead to the formation of subcellular Ca waves during steady-state pacing. Using these results, we show that a reduction in CaM can promote Ca waves that disrupt the rhythmic release of Ca in cardiac cells. This process is highly nonlinear and leads to dangerous action potential (AP) perturbations, which can drive localized conduction block in cardiac tissue. Thus, this work outlines a novel, to our knowledge, mechanistic relationship between the disruption of CaM-RyR2 interactions and the formation of an arrhythmogenic substrate in the heart.
Methods
Model of CaM regulation of a RyR2 subunit
To describe the effect of CaM on RyR2, we will follow the hypothesis of Xiong et al. (22) and develop a simplified mathematical model of the competitive binding reactions of CaM and CaMLD to the CaMBD. Although this mechanism has been proposed only in the context of RyR1, the close structural similarity between RyR1 and RyR2 makes this mechanism a reasonable starting point for model building of the cardiac system. Using this approach, we will develop a Markovian model of a RyR2 subunit in which the transition rates are regulated by the binding reactions at the CaMBD. To proceed, let us denote the concentration of free CaMBD as [L] and the total concentration as LT. Similarly, we will denote the free concentration of CaMLD as [R] and the total concentration as RT. Finally, we will denote [CaM] as the concentration of free CaM. The binding reactions at the CaMBD are described by
| (1) |
and
| (2) |
where [LCaM] is the concentration of the bound CaM-CaMBD complex; [LR] is the concentration of the bound CaMLD-CaMBD complex; and α, β, α′, and β′ are the transition rates. The reaction kinetics are governed by
| (3) |
and
| (4) |
and the total concentrations are given by
| (5) |
and
| (6) |
Because the CaMBD and CaMLD are both part of the RyR2, they have the same total concentration, which we will denote as Q = LT = RT. In this study, we will consider the case in which [CaM] is constant so that all the reactions at the CaMBD have reached equilibrium. In this limit, we find that the equilibrium concentration of the CaMLD-CaMBD complex is given by
| (7) |
where
| (8) |
and where KCaM = β/α and KCaMLD = β′/α′ are the dissociation constants for the CaM and the CaMLD reactions to the CaMBD, respectively. Note here that a crucial role is played by the ratio of KCaM/KCaMLD, which gives a measure of the relative strength of the reaction of the CaMBD to CaM and the CaMLD. Because this ratio has not been measured experimentally, we will make the simplifying assumption that KCaM/KCaMLD ≪ 1, which corresponds to the case in which binding to CaM is favored over binding to the CaMLD. This is a reasonable assumption because for CaM to be an effective regulator, it is likely to bind preferentially to the CaMBD. In this limit, we have
| (9) |
which gives a more simplified relationship between the amount of bound complex as a function of [CaM].
Once the CaMLD-CaMBD complex is formed, it can then bind to Ca at a different binding site to form a Ca-CaMLD-CaMBD complex that regulates the RyR2 open probability. This reaction is
| (10) |
where [CaLR] is the concentration of the Ca-CaMLD-CaMBD complex and [LR′] is the concentration of the CaMLD-CaMBD complex that is not bound to Ca, so that the total concentration is [LR′] + [CaLR] = [LR]eq. Also, note here that [Ca] denotes the Ca concentration on the cytosolic side of the RyR2 subunit. In the cardiac cell, this concentration will correspond to the Ca concentration in the immediate vicinity of RyR2 subunits. To proceed, we note that the rates α″ and β″ have not been measured experimentally. However, because it is known that RyR2s can be activated by rapid submillisecond spikes of local Ca (24), it is safe to assume that the reaction is fast compared with the reactions given by Eqs. 1 and 2, and we can apply the rapid equilibrium approximation. This gives
| (11) |
where KCa = β″/α″ is the dissociation constant for Ca binding. The final concentration is given by
| (12) |
Thus, in this approach, Ca serves as an agonist for the reaction that forms the Ca-CaMLD-CaMBD complex, and CaM serves as the antagonist.
A Markovian model of the RyR2 tetramer
To describe the RyR2 open probability, we will model each subunit using a reaction scheme given by
| (13) |
where C1 is the closed conformation, O is the open state, and C2 is an additional closed state. Here, we follow Mukherjee et al. (25) and introduce a second closed state C2 to account for experimental observations of flicker closings that are more evident at high Ca concentration >10 μM. To model the Ca dependence of the subunit open probability, we will require that the open rate be proportional to the concentration of the Ca-CaMLD-CaMBD concentration given by Eq. 12. Thus, we will take the open rate of a single subunit to have the form
| (14) |
where is a proportionality constant that absorbs the constants that originate from the binding reactions. Given the paucity of information on the binding kinetics, we will rely on RyR2 transition rate measurements to constrain this proportionality constant. Also, because the RyR2 open probability is known to be dependent on the SR load (26,27), we will include a function Φ([Ca]jsr), which represents the dependence of the forward rate on the Ca concentration [Ca]jsr on the luminal side of the RyR2 subunit.
The full RyR2, as illustrated in Fig. 1 B, is composed of four bound subunits. To model cooperativity, we introduce an energy penalty ɛ for two neighboring subunits to be in different states. This approach is inspired by previous work that applied cooperativity to explain the sensitivity of a channel complex to changes in the concentration of a ligand (28). To implement the subunit interactions, we will label each subunit in the clockwise direction using the index i = 1, 2, 3, 4 (Fig. 1 B). Each subunit will be assigned a state si that can be one of the three subunit states C1, O, or C2. To model nearest-neighbor interactions, we let subunit in the tetramer transition to the open state with rate
| (15) |
where Q(si, sj) denotes the interaction energy between subunit i and j in states si and sj, respectively. Because there is an energetic cost for neighboring subunits to be in different conformational states, we will assign
| (16) |
| (17) |
| (18) |
and
| (19) |
Here, we will not assign an energy penalty between two neighboring subunits in different closed states so that C can be either C1 or C2. Similarly, the reverse rate for subunit i will be
| (20) |
Using this approach, we can adjust the cooperativity between RyR2 subunits by changing the subunit interaction energy ɛ. To complete the RyR2 tetrameric model, it is necessary to assign how many subunits need to transition to the open state for the pore to open. However, this number is not known, so we will leave it as a control parameter that will be adjusted later to model experimentally measured features of Ca spark statistics. For now, we will take the state of the tetramer to be
| (21) |
where ni = 0 if si = C1 or C2 and ni = 1 if si = O. The RyR2 will then be in the open state if m ≥ mo, where mo can have the value 1, 2, 3, or . We will then vary the necessary number of open channels mo to fit single RyR2 or Ca spark data.
Fitting the model to RyR2 open probability measurements
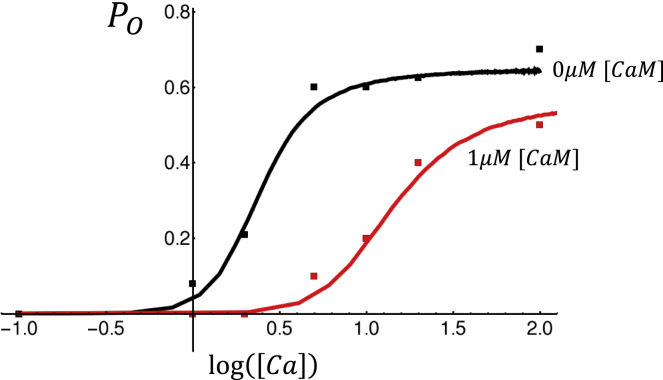
To determine parameters for our RyR2 model, we will rely mainly on a study by Xu and Meissner (29), who measured the functional effects of CaM on RyR2 in lipid bilayers. In this study, the authors varied the cytosolic Ca concentration from 0.1 to 100 μM and measured RyR2 open probability in the absence and presence of a maximally inhibiting 1 μM CaM. To model their data, we will first determine RyR2 parameters in the case in which [CaM] = 0 μM. To fit their open probability data at fixed cytosolic Ca, we vary the subunit interaction strength ɛ, the number of subunits in the open state mo required to open the channel, and the threshold for Ca activation KCa. Also, because the Ca concentration on the luminal side of the lipid bilayer is held fixed, we will set Φ([Ca]jsr) = 1. In a later section, we will include the SR load dependence to model Ca release at a RyR2 cluster.
Xu and Meissner (29) also measured the mean RyR2 closed time at [Ca] = 2 μM to be τc = 13.6 ms and the mean open time to be τo = 1.6 ms, which can be used to constrain the values of the rate constants and . To proceed and fit the transition rates to the second closed state, we rely on recent work by Mukherjee et al. (25), who noted that at high Ca ([Ca] > 10 μM), the RyR2 channel makes frequent transitions to a closed state in a Ca-independent manner. This result is consistent with the experimental measurements of Xu and Meissner, who showed that for large Ca levels ([Ca] > 100 μM), the open probability of RyR2 is saturated near Po ∼0.7. This indicates that even when the C1 to O transition is large (k+ ≫ k−), the RyR2 subunit does not reside in the open state but makes frequent transitions to a new closed state, which reduces the open probability. Mukherjee et al. (25) measured the mean time of the closed state and found τc ∼0.36 ms, which fixes the backward rate r−. The forward rate r+ is then adjusted to match the open probability of RyR2 measured at high Ca. Finally, we determine the dissociation constant KCaM by searching for a good fit to the data acquired at [CaM] = 1 μM. In Fig. 2, we plot the experimental data extracted from the Xu and Meissner study (29) along with our best-fit curves. The parameters used are given in Table 1. Here, we find excellent quantitative fits, indicating that the effect of CaM can be effectively modeled as an antagonist that competes with the CaMLD for the Ca binding site on RyR2. This approach predicts that the binding kinetics of CaM to RyR2 can be described using a binding dissociation constant KCaM = 0.364 μM.
Figure 2.
RyR2 open probability in the absence and presence of 1 μM CaM. Open probability measured by Xu and Meissner (29) is denoted by square symbols with black and red denoting 0 and 1 μM [CaM], respectively. Solid lines correspond to the fitted Markovian model. To see this figure in color, go online.
Table 1.
RyR2 Markovian model parameters
| Parameter | Value | Units |
|---|---|---|
| 2.79 | (ms)−1 | |
| 0.33 | (ms)−1 | |
| r+ | 0.25 | (ms)−1 |
| r− | 0.6 | (ms)−1 |
| ɛ | 0.8 | dimensionless |
| KCa | 15 | micromolar |
| KCaM | 0.364 | micromolar |
| mo | 3 | channels |
| cth | 700 | micromolar |
| γ | 5 | dimensionless |
A novel, to our knowledge, aspect of our RyR2 subunit model is that we have explicitly modeled the dynamics of individual subunits. In this formulation, Ca-dependent activation of a single subunit is determined by the Ca dissociation constant KCa. However, the sigmoid nature of the Ca dependence is dicated by cooperativity, which is determined by the interaction energy ɛ, and the number of subunits mo required to be in the open state for the full RyR2 to be open. We found that KCa = 15 μM gave an excellent fit to the experimental data and was also substantially larger than the typical resting Ca levels in a myocyte, for which [Ca] ∼0.1 μM. This choice is consistent with the observation that RyR2 clusters, in the absence of stimulus from the L-type calcium current (LCCs), have a low open probability, so that LCC fluxes have to raise local Ca substantially above resting levels to induce channel openings. To fit the sigmoid response measured by Xu and Meisner (29), we have set the interaction energy to be ɛ = 0.8. However, we note that the experimental data were not sufficient to constrain this parameter precisely, and good fits can be found in the range 0.4 < ɛ < 1.4. Finally, we have set the number of open subunits required for channel opening to be mo = 3. In our simulations, we found that setting mo < 3 led to substantial RyR2 openings even at resting Ca concentration levels. Interestingly, these background fluctuations led to persistent RyR2 cluster openings, which made Ca sparks highly unstable even at resting Ca levels. We also found that setting single-channel and cluster dynamics was insensitive to mo for mo ≥ 3. Thus, we picked mo = 3 as a reasonable compromise given the lack of data to constrain this parameter.
The effect of CaM on the dynamics of a Ca spark
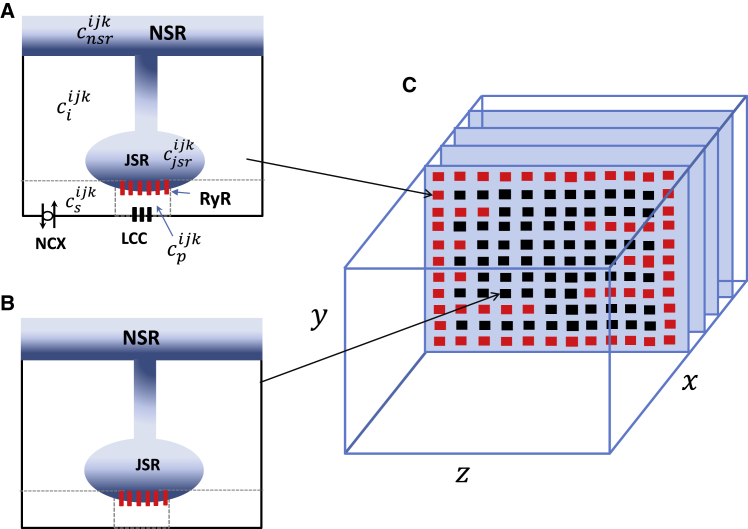
In a cardiac cell, RyR2s are arranged in clusters so that Ca release from one or a few RyR2s will induce regenerative release from the cluster. These release events are localized in the vicinity of the cluster and are referred to as Ca sparks. In this section, we determine the relationship between the concentration of CaM and the properties of Ca sparks. To accomplish this, we will integrate our CaM-RyR2 model with a spatially distributed cell model originally from Restrepo and Karma (30), which has been extended to describe atrial myocytes (31,32). In this approach, the cell interior is divided into compartments that contain the key Ca cycling ion channels (see Fig. 3 captions for details). The basic unit of the model is referred to as a Ca release unit (CRU), which is composed of the main compartments that surround a RyR2 cluster in the cell (Fig. 3 A) along with an array of membrane-bound ion channels, such as the LCC and the sodium-calcium exchanger (NCX). Here, all ion channels are described using experimentally based Markovian models that evolve in time in a fully stochastic manner. The Ca concentration regulating RyR2 is referred to as the dyadic junction Ca concentration, denoted as in Fig. 3 A. To describe an atrial myocyte, we note that the cell membrane forms invagination into the cell referred to as t-tubules (TTs) as shown in Fig. 3 C. In atrial myocytes, these t-tubules are sparse and do not penetrate fully into the cell, in sharp contrast to ventricular myocytes where TTs extend deep into the cell interior. To account for this feature, we allow membrane-bound channels to penetrate into the cell a distance that is taken from an exponential distribution. In this manner, we allow some degree of invagination that is representative of an atrial myocyte. Details of our computational model and the statistical modeling of the t-tubule system are given in a recent study (31).
Figure 3.
Schematic illustration of the spatial architecture of Ca signaling in an atrial myocyte. The basic unit of Ca signaling is the CRU, which is composed of six compartments distributed in the cell. Concentrations at each CRU are designated with a superscript ijk at position i, j, k in a three-dimensional grid representation of the cell. The compartments are the dyadic junction with concentration , the submembrane space with concentration , the local cytosol concentration , the junctional SR (JSR) concentration , and finally the local concentration in the network SR (NSR) . To model an atrial myocyte, we distinguish junctional CRUs close to the cell membrane that (A) possess LCC and NCX channels, whereas nonjunctional CRUs (B) do not have these membrane channels. (C) Spatial architecture of the cell interior showing TT invaginations along z planes is given. All compartments in the outer boundary and along transverse TT invaginations are treated as junctional CRUs (red squares). To see this figure in color, go online.
Results
Model of an isolated RyR2 cluster
In this section, we will apply a stripped-down version of our atrial cell model to first evaluate the properties of an RyR2 cluster in isolation. Thus, we will place a single RyR2 cluster with NRyR = 25 channels within an array of 5 × 5 × 5 CRUs. All other CRUs will be devoid of ion channels and transporters. To achieve robust closing of the RyR2 cluster, it is necessary to include a dependence on the junctional SR (JSR) Ca concentration. Thus, we will include a term
| (22) |
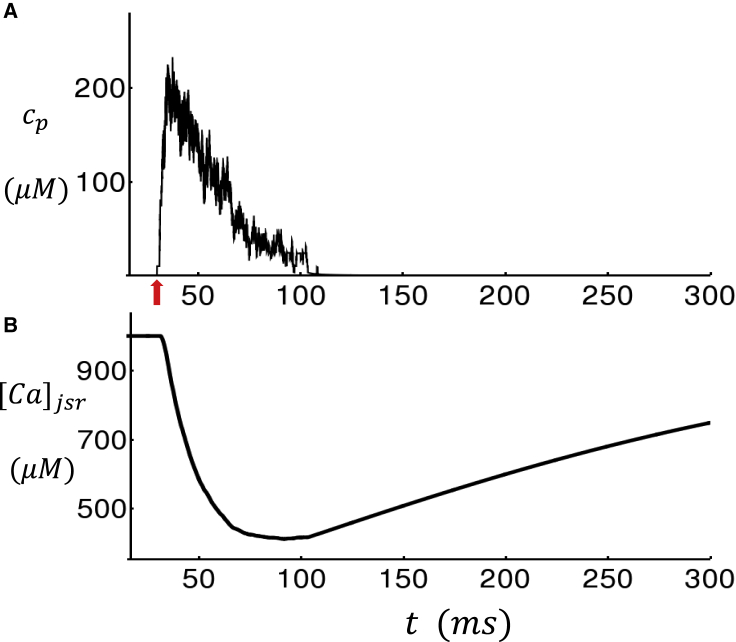
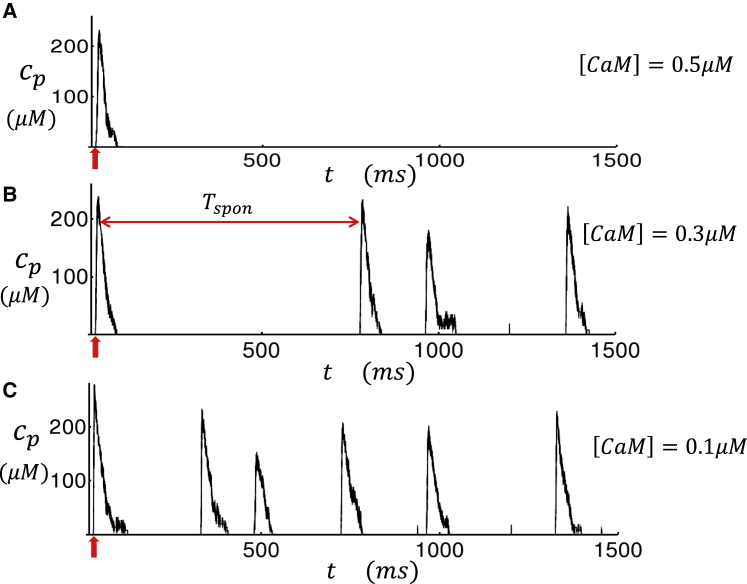
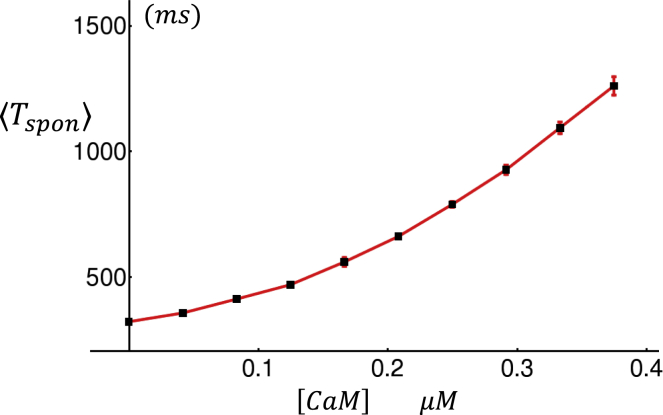
where cth is the threshold for the luminal [Ca] concentration dependence, and γ is the Hill coefficient. This term is included in our formulation of the RyR2 subunit opening rate given in Eq. 14. In our simulations, we find that including this term ensures robust Ca spark termination that is driven by the negative feedback due to the depletion of the local JSR. To gain further insight on the effect of this JSR load dependence, in Fig. S2 we show the RyR2 open probability as a function of [Ca]jsr for a range of fixed cytosolic Ca concentration levels. Here, we note that although the mechanism for RyR2 closing is still not fully understood, our model serves as a possible mechanism that is based on previous experimental data and modeling work (33,34). In Fig. 4 A, we show the local dyadic junction concentration cp during a Ca spark that is initiated by a small current stimulus at t = 30 ms (red arrow). Here, we observe that during the Ca spark, cp rises to ∼200 μM and then decays to ∼50 μM in ∼30 ms, followed by a slower decay consistent with Ca spark flux measurements (35). At the same time, the JSR load [Ca]jsr decreases from the initial 1000 μM to roughly 400 μM. To ensure robust Ca spark termination, we have used cth = 700 μM. In Fig. 5, A–C, we show cp for a longer timescale of 1500 ms and also vary the CaM concentration. Here, we find that the stimulated Ca spark is followed by spontaneous sparks, which fire solely because of RyR2 fluctuations in the absence of a current stimulus. To quantify the timing of spontaneous sparks more precisely, we measured the average waiting time from a stimulated spark to the first spontaneous spark. We measure this quantity because spontaneous Ca sparks typically occur during the AP after stimulation from LCC openings. The average waiting time , computed from 5000 independent simulation runs, is plotted versus [CaM] in Fig. 6, which shows the strong sensitivity of the spontaneous spark rate on the CaM concentration. Here, we mention that we have also explored the changes in the time course of Ca release during a spark. Indeed, we also find that as [CaM] is reduced, the local flux is increased because of an increase in the RyR2 open probability. However, this effect is small, and our simulations indicate that the main effects of [CaM] on Ca release is due primarily to the modulation of the spontaneous spark rate rather than the current flux.
Figure 4.
Simulation of a Ca spark due to an isolated RyR2 cluster in a small system of 5 × 5 × 5 CRUs. (A) The dyadic junction Ca concentration cp in the vicinity of the central RyR2 cluster after a 3 ms current stimulus is injected at t = 30 ms is shown (red arrow). (B) The JSR Ca concentration ([Ca]jsr) during the spark is shown. To see this figure in color, go online.
Figure 5.
Long-time simulation of an RyR2 cluster in a small system of 5 × 5 × 5 CRUs. (A–C) The dyadic junction Ca concentration cp is shown in the vicinity of the central RyR2 cluster for different levels of [CaM]. Current stimulus is delivered at t = 30 ms (red arrow) to induce a Ca spark. Subsequent Ca release events are spontaneous Ca sparks, which are due to regenerative release that are triggered by RyR2 fluctuations. The mean waiting time from the first excitation to the next spontaneous excitation is denoted as Tspon. To see this figure in color, go online.
Figure 6.
The average time between a triggered Ca spark and a spontaneous spark, denoted as , as a function of [CaM]. Points are computed by averaging over 5000 independent simulation runs. Error bars are computed as the standard deviation of five averages of 1000 simulation runs. To see this figure in color, go online.
Dependence of Ca cycling homeostasis on [CaM]
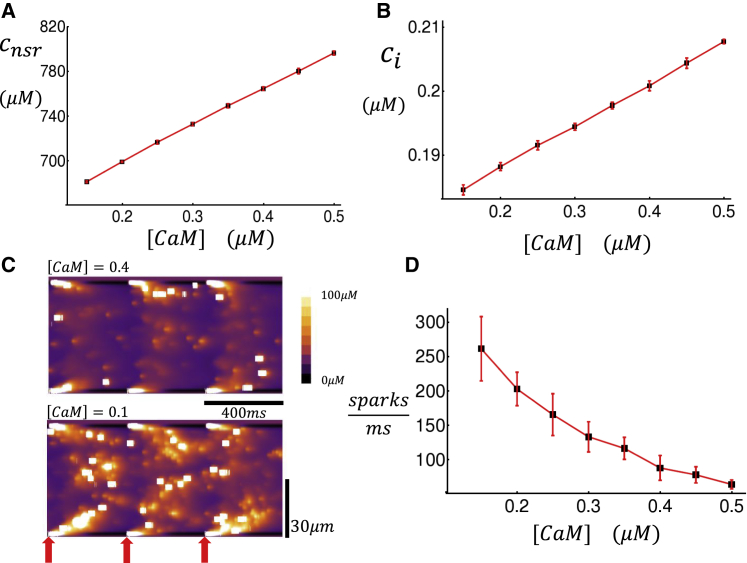
In this section, we apply our spatially distributed model to simulate a full cardiac cell of 40 × 20 × 20 CRUs that is paced by a freely running AP. To model the AP, we have integrated our Ca cycling equations with the major ion currents from the Grandi et al. (36) human atrial cell model. All Ca cycling components used in the Grandi model have been replaced by the spatially distributed model described above. Details of this coupled voltage and Ca system have been described in our previous publications (31,32). Using this model, we will evaluate the effect of CaM on Ca cycling homeostasis. To study homeostasis, we pace our cell model until a steady state is reached in which the SR load and diastolic Ca levels remain effectively constant from beat to beat. In our simulations, reaching the steady state typically requires 20–30 beats of pacing until all concentration variables fluctuate near their equilibrium values. In Fig. 7 A, we plot the steady-state network SR (NSR) load, which is defined as the average concentration in all NSR compartments in the cell, as a function of [CaM]. Here, we pace the cell at a cycle length of CL = 400 ms for 30 beats and then measure the NSR concentration at the beginning of the last paced beat. Our results show that the steady-state NSR load decreases substantially as the CaM concentration is reduced. In Fig. 7 B, we have also computed the diastolic Ca concentration ci, which is defined as the average concentration of all cytosols in the cell interior, as a function of [CaM]. Here, we observe that the steady-state ci also decreases with decreasing CaM, although the observed change is small. To assess the underlying mechanism for the reduced SR load in Fig. 7 C, we plot a linescan image of subcellular Ca at two concentrations of [CaM]. These simulations show that as [CaM] is reduced, the number of Ca sparks in the cell interior is increased substantially. Now, because the TT system is sparse, this implies that the bulk of these Ca sparks are spontaneous and are not initiated by LCC openings. Thus, it is clear that the rate of spontaneous Ca sparks is markedly increased with a reduction in [CaM]. To quantify this effect, we have computed the number of Ca sparks that occur during one CL at steady state. In Fig. 7 D, we plot the number of sparks in the cell per unit time on the last beat of pacing, after pacing for 30 beats. Indeed, we find that the number of Ca sparks recruited increases substantially as the CaM concentration is reduced. These results demonstrate that the dominant homeostatic change, due to a reduction in CaM, is an increase in the rate of spontaneous Ca sparks, which in turn leads to a substantial reduction in SR load.
Figure 7.
The dependence of Ca cycling homeostasis on CaM. (A) Plot of the average NSR load (cnsr) as a function of CaM is given. (B) Plot of the average diastolic Ca concentration as a function of CaM is given. Both the average diastolic Ca and NSR load are computed just before the 31st AP is triggered. The cell is paced at CL = 400 ms. (C) Longitudinal linescan of subcellular Ca at the indicated levels of [CaM] is shown. (D) The total number of sparks divided by CL for the last beat is given, taken at steady state after pacing for 30 beats. Error bars are computed as the standard deviation of 10 independent simulation runs. To see this figure in color, go online.
The dependence of Ca wave propagation on CaM
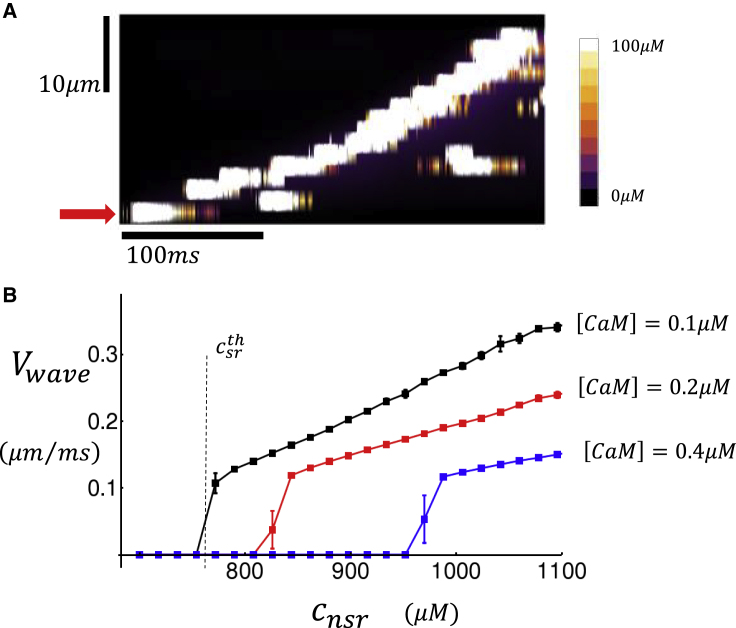
In this section, we will evaluate the relationship between Ca wave propagation in the cell interior and CaM. Our approach will be to induce a Ca wave within our three-dimensional cell model and compute the velocity of propagation for different levels of [CaM]. To accomplish this, we simulate wave propagation in our spatially distributed cell model. To induce a Ca wave, we first remove all LCC channels except those within a 20 × 20 transverse plane at one end of the cell. We then apply an AP to the cell and trigger Ca release only within this planar region where the LCCs reside. The SR load of the cell is then gradually increased so that at a critical load, a Ca wave will form that will propagate in the longitudinal direction. In Fig. 8 A, we show a longitudinal linescan of a Ca wave that is nucleated at one end of the cell (red arrow) and then propagates to the other end. To compute the wave velocity, we measure the time it takes for the planar excitation to reach the distal end of the cell. To get a more complete picture, in Fig. 8 B we plot the wave velocity as a function of the initial SR load for three concentrations of [CaM]. Here, we have computed the wave velocity, denoted as Vwave, by repeating each run 50 times and computing the average speed. A plot of Vwave as a function of the initial NSR load (cnsr) shows that the average Ca wave speed increases rapidly near a threshold denoted as (vertical dashed line for the case [CaM] = 0.1 μM). Here, we point out that the threshold for wave propagation is sharp in the sense that the interface between propagation and no propagation is much smaller than the dynamic range of the SR load during pacing. In particular, we find that the wave velocity increases from 0 to ∼0.1 μM/ms over a range of ∼20 μM, whereas the dynamic range of SR load during pacing is ∼500 μM. It is in this sense that the Vwave dependence on SR load exhibits a sharp threshold behavior. Note that in these simulations, we have also computed the standard error of Vwave using our 50 simulation runs, showing that error bars are small above and below threshold (Fig. 8 B) but can be large near threshold. This is because near-threshold wave propagation will be highly sensitive to stochasticity, so that fluctuations of wave speed will be substantial. Thus, the main finding is that a reduction in [CaM] decreases the critical threshold for wave propagation and also increases the velocity of longitudinal wave propagation.
Figure 8.
Dependence of Ca wave propagation on CaM. (A) An example of Ca wave propagation in a cell of dimension 18 × 20 × 20 is given. A line scan along the longitudinal direction is shown. To initiate the wave, the first sarcomere (red arrow) is ignited by applying an AP, and LCCs are removed in all other sarcomeres. In this simulation, we set [CaM] = 0.3 μM, and the initial SR load is cnsr = 900 μM. (B) Ca wave velocity is shown as a function of the initial SR load at the time the stimulation is applied. The vertical dashed line denotes the critical threshold load necessary for waves to propagate in the cell. The wave velocity shown corresponds to an average over 50 independent simulations. Error bars are computed as the standard deviation of five averages of 10 independent simulations. To see this figure in color, go online.
AP perturbations during rapid pacing
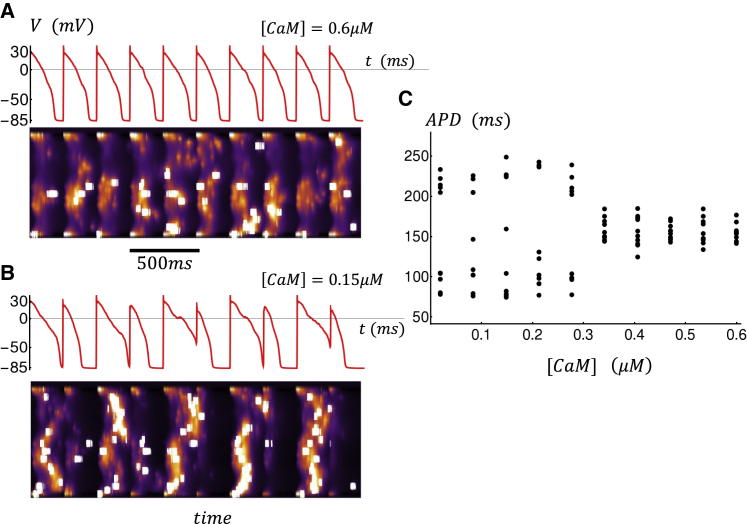
In this section, we will explore the role of CaM on the dynamics of subcellular Ca during rapid pacing. Our model analysis reveals that the system can exhibit complex beat-to-beat dynamics in response to changing levels of CaM. In particular, we find that a reduction in CaM can induce nonlinear instabilities in the system in the case when the excitability of the Ca cycling system is increased. To probe this parameter regime, we found it necessary to increase the strength of the whole-cell LCC by 15%, which leads to an increase in the steady-state SR load. However, at high SR loads we found that RyR2 clusters did not close reliably, which prevented Ca waves from propagating in the cell. Thus, it was necessary to stabilize RyR2 clusters in the closed state by increasing the coupling parameter to ɛ = 1.2. In this way, we effectively increased the excitability of the Ca cycling system while keeping local Ca release stable. To study the V-Ca dynamics under these conditions, we paced our cell model for 50 beats at CL = 250 ms. We then analyzed the voltage and Ca for the last 10 beats after the cell had reached steady state. In Fig. 9 A, we plot the membrane voltage of the cell as a function of time for the last several beats, along with a simulated longitudinal linescan. In this simulation, we have fixed [CaM] = 0.6 μM. In this case, we find that during pacing, Ca sparks in the cell interior are rare, and that most of the Ca release occurs at the cell boundaries. This is due to the fact that Ca sparks are induced by LCCs, which are distributed mostly at the cell boundaries because TTs are sparse in atrial myocytes. In Fig. 9 B, we repeat the simulation with [CaM] = 0.15 μM. In this case, we find that the voltage response displays aperiodic behavior with substantial beat-to-beat variations in the action potential duration (APD). In particular, we note that the subcellular Ca waves that propagate into the interior are induced during rapid pacing. In the example shown, wave propagation into the cell interior tends to occur on alternate beats, which induces a corresponding beat-to-beat alternation in the APD. To capture the beat-to-beat variations of the AP at steady state, we have plotted the APD for the last 10 beats. This simulation is then run at different levels of [CaM], and the steady-state APD (last 10 beats) is plotted as a function of CaM (Fig. 9 C). Indeed, we find that for this set of parameters, a reduction in [CaM] can induce a substantial beat-to-beat variation of the APD at steady state.
Figure 9.
Role of CaM during rapid pacing. (A and B) Membrane voltage and longitudinal line scan for the last 10 beats after pacing for 50 beats at CL = 250 ms are shown. (C) APD for the last 10 beats, after pacing for 50 beats, is given as a function of [CaM]. Here, APD is computed as the time for the AP to cross Vc = −30 mV. In some beats, the voltage V(t) does not cross this threshold, and we do not compute APD for those beats. In this simulation model, parameters have been modified to induce dynamical instability at rapid pacing rates. To do this, we have adjusted the following parameters in the model: the whole-cell LCC strength has been increased by 15%. The uptake strength, denoted as vup, has been reduced by 33%. Subunit coupling strength is increased to ɛ = 1.2, and threshold SR concentration is increased to cth = 800 μM. To see this figure in color, go online.
Discussion
In this study, we have developed a computational model of the interaction between CaM and a RyR2 subunit. Our model is based on the work of Xiong et al. (22), who identified a CaM-like region of RyR1 that binds to the CaMBD and is believed to regulate the RyR2 open probability. This mechanism is consistent with high-resolution cryo-EM imaging, which reveals that the main Ca binding activation site, which regulates the pore open probability, is in close proximity to a CaM-like region (CAMLD) of RyR1, which in turn, resides in the vicinity of the CaMBD (37). Given the strong structural similarity between RyR1 and RyR2, we have applied this mechanism to develop a computational model of RyR2 that accounts for CaM. Our approach is to model the key interactions at the CaMBD to extract the CaM dependence of the RyR2 open probability. Our computational model is sufficient to fit existing experimental data from RyR2 open probability measurements in lipid bilayers (29). At the single-channel level, we find that a decrease in the CaM concentration leads to a marked increase in the RyR2 open probability. This increase occurs via a leftward shift of the open probability, along with an increase in the plateau open probability measured at high Ca concentrations. Interestingly, both of these effects can be explained by our model, in which the open rate of an RyR2 subunit is proportional to the concentration of the Ca-CaMLD-CaMBD complex. Thus, our results suggest that RyR2 properties observed in lipid bilayers can be reproduced by assuming that individual RyR2 subunits are regulated by Ca and CaM binding reactions. An application of our model is that it can be used to investigate downstream consequences of a disruption in the binding of CaM to the CaMBD. It is well known that various arrhythmias, such as CPVT, can be traced to specific mutations that are known to disrupt the interaction of CaM and RyR2 (8,10). Within our model framework, the key parameters governing the RyR2 transition rates are the dissociation constants KCaM and KCaMLD, which determine the relative strength of the respective reactions at the CaMBD. Thus, our computational model can be used to evaluate how changes in the local binding kinetics can control the RyR2 open probability. We expect that this computational framework can be applied to investigate how specific mutations in RyR2 can induce cardiac arrhythmias at the whole-heart level.
We have integrated our CaM-RyR2 model with a spatially distributed Ca cycling model to investigate the relationship between homeostasis and CaM. The main result is that a reduction in CaM leads to a higher frequency of spontaneous Ca sparks, which induces a marked reduction in the steady-state SR Ca load. These spontaneous Ca sparks are due to RyR2 fluctuations, which induce regenerative openings of clusters of RyR2, independently of Ca entry due to membrane-bound channels. These regenerative openings occur when local Ca concentration fluctuations induce RyR2 transitions to the open state. A reduction in CaM makes these transitions more frequent because it suggests that the CaMLD more readily binds to the CaMBD in the absence of CaM. Thus, a reduction in CaM will increase the probability of a spontaneous Ca spark. In our computational simulations, this was the dominant effect of CaM on the dynamics of Ca sparks. The consequence of this change at the whole-cell level is that the steady-state SR load decreases substantially with decreasing CaM. This reduction in SR load is due to an autoregulation response caused by a rebalancing of the fluxes across the SR membrane (38,39). To describe these changes, we define the total number of Ca ions that flow out of the SR due to RyR in one beat as
| (23) |
where JRyR(t) is the total RyR2 flux flowing out of the SR at time t, n is the beat number, and T is the pacing period. Similarly, we define
| (24) |
where Jup(t) is the total flux flowing into the SR from the sarco/endoplasmic reticulum calcium ATPase pump. Now, when the cell reaches equilibrium, we have Qup(n) ≈ QRyR(n), where n > neq and where neq is the number of paced beats for equilibrium to be reached (in our simulations, neq ∼30 beats). For convenience, we will refer to Qup and QRyR as the total Ca influx and efflux, respectively, over one beat at steady state, i.e., for n > neq. In our simulations, we find that a reduction in CaM has the effect of increasing QRyR(n) for n < neq because of the increased frequency of spontaneous Ca sparks. However, the corresponding changes in Qup(n) are not enough to compensate for this change so that QRyR(n) > Qup(n), and there is a net outward flux that depletes the SR as long as n < neq. However, when n > neq, then steady state is reached, and the SR will be depleted to a level such that QRyR ≈ Qup. This new equilibrium is reached because the driving force across the SR membrane decreases with SR load. Thus, to compensate for the increased number of Ca sparks, the SR load is simply adjusted so that the overall Ca efflux is decreased to match the uptake. Therefore, the dominant homeostatic response to a reduction in [CaM] is depletion of the SR, which compensates for the increased frequency of spontaneous Ca sparks.
In this study, we have also explored the dependence of Ca waves on CaM. Our key finding is shown in Fig. 8 B, which demonstrates that the velocity of subcellular Ca waves exhibits a sharp threshold dependence on the SR load.
Effectively, below a critical SR load , waves do not propagate, whereas above that threshold, waves propagate in the longitudinal direction over many sarcomeres. Here, we note that this transition is sharp in the sense that Vwave changes substantially over a range of SR loads (∼20 μM), which is much smaller than the full dynamic range (∼500 μM) of the SR load during pacing. This behavior is due to the highly nonlinear nature of Ca wave nucleation, which is highly sensitive to the SR load near the onset of wave propagation. Note that above the onset of Ca wave propagation, the Ca wave velocity increases linearly as a function of SR load. Using our computational model, we show that decreases and the velocity of wave propagation Vwave increases as the CaM concentration is decreased. The underlying mechanism for this effect is the Ca dependence of the RyR2 open probability Po and its dependence on CaM. Specifically, we find that a decrease in CaM concentration has two distinct effects on the RyR2 open probability. The first is a leftward shift of the Ca concentration at the half maximum of Po, and the second is an increase in the maximal Po measured at high Ca. The combined effect of these two changes is that the excitability of a RyR2 cluster is directly modulated by the concentration of CaM. As a consequence, the onset and propagation velocity of Ca waves is highly sensitive to the CaM concentration in the cell.
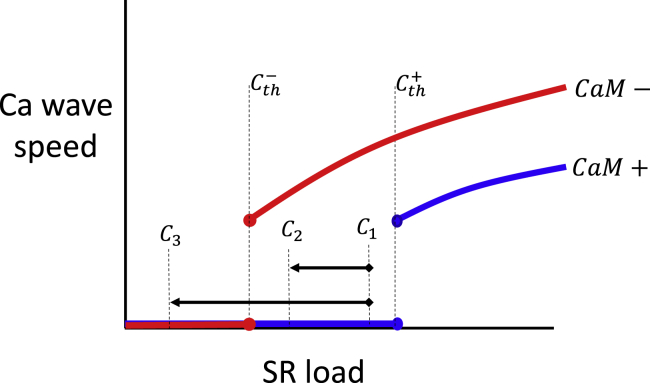
In this study, we have identified the two main effects of CaM on Ca cycling. The first is a marked reduction in the steady-state SR load, which is driven by the increased spontaneous spark rate. The second is a shift in the critical SR load for the onset of Ca wave propagation. A natural question to address is how these two effects combine to determine the dynamics of a paced cardiac cell. In Fig. 10, we illustrate the basic relationship between Vwave and the SR load for the case of a high [CaM] concentration (blue line, CaM+), and also for the case of a lower concentration (red line, CaM−). Here, the main effect of this change is that the threshold for wave propagation is reduced from to . Now, let us say that the steady-state SR load at high [CaM] is given by C1. Here, we assume that the cell is stable and does not exhibit Ca wave propagation. Upon a reduction in [CaM], there are now two distinct scenarios; the first is an SR load reduction from C1 → C3. In this case, the reduction in CaM is largely protective because no Ca waves are induced at the new steady-state SR load because C3 < . However, if the steady-state SR load reduction is C1 → C2, then the cell becomes susceptible to Ca waves because the system is above the wave propagation threshold, i.e., C2 > . In this case, the reduction in CaM is arrhythmogenic because the steady-state SR load of the cell is above the wave propagation transition. Thus, the effect of CaM on the beat-to-beat dynamics of the cell is dependent on the interplay between the homeostatic balance setting the SR load and the threshold for Ca wave propagation. These findings suggest that pharmacologic interventions that reduce the SR load below the wave propagation threshold may be protective to arrhythmias. One possibility to achieve this is to modulate the strength of the sarcoplasmic reticulum Ca2+-ATPase transporter, which is known to regulate the steady-state SR load (40). However, a systematic approach to control Ca cycling homeostasis is lacking and deserves further study.
Figure 10.
Illustration of the interplay between Ca wave propagation velocity and Ca cycling homeostasis. The blue (red) line represents the relationship between Vwave and SR load in the case of high (CaM+) and low (CaM−) CaM. C1, C2, and C3 each represent a possible SR load at steady state. Here, we distinguish the two cases. The first is when a reduction in [CaM] reduces the steady-state SR load from C1 to C3 < . In this case, the change is protective because Ca waves do not propagate at C3. The second case is when the steady-state SR load changes from C1 to C2 > . In this case, the reduction in [CaM] is arrhythmogenic because Ca waves can propagate at the reduced SR load. To see this figure in color, go online.
We have applied our computational model to explore the beat-to-beat dynamics of an atrial cell that is rapidly paced. Our main result is that a reduction in CaM can induce the propagation of Ca waves that occur during pacing and can disrupt the one-to-one relationship between the AP and Ca release. The emergence of these waves at rapid pacing is dependent on the structure of the TT system (31,41). In cells where the TT system is sparse, then there is a large population of RyR2 clusters that have not been excited and can provide an excitable substrate for Ca waves to propagate. This subcellular architecture is found in atrial and Purkinje myocytes, which both have an underdeveloped TT system (42,43) that is concentrated at the cell boundary. This is in sharp contrast to ventricular myocytes, which have a well-developed TT system that penetrates deep into the cell, so that the bulk of the interior RyR2 clusters are ignited by the AP. Thus, in ventricular cells we expect that the frequency of Ca waves during the AP will be substantially reduced and that waves will occur later in the AP, after RyR2 clusters have recovered from excitation. However, in heart failure the TT system is substantially disrupted (44), so Ca waves should occur with shorter latency in these cells. Thus, it is possible that the phenomenology described in this study may be applicable to heart failure ventricular myocytes. However, we note here that heart failure is a complex diseased state and that many properties of Ca cycling itself will be altered. Now, when the concentration of CaM is reduced, the threshold for wave propagation is lowered, and the Ca sparks ignited at the cell boundary can coalesce and nucleate wave propagation into the cell interior. Effectively, the lowering of CaM makes the cell more excitable, and the presence of unrecruited RyR2 clusters in the interior favors the formation of wave propagation. In our simulations, we found that lowering CaM can induce intermittent Ca waves with a timing that was random and highly dependent on the pacing rate. Because these waves are nucleated at RyR2 clusters, their timing and degree of propagation depend on the intrinsic fluctuations of RyR2s. In the specific example shown in Fig. 9 B, we find that the cell tended to settle in a roughly alternating pattern in which Ca waves are nucleated at multiple sites, followed by a beat during which few waves occur. This alternating pattern is reminiscent of cardiac alternans and is due to the highly nonlinear relationship between Ca release and SR load (41). Effectively, because the wave propagation transition is sharp, this endows the cell with a highly nonlinear release load relationship that can drive alternans. However, because the underling dynamics is stochastic, this alternating response varies substantially from beat to beat. Now, once Ca waves occur in the cell, the NCX channel will be activated by the increased Ca release into the cell. This increase of NCX can then perturb the AP. In our simulations, we find that the dominant effect on the AP is a prolongation of the APD. Thus, under rapid pacing we observed substantial beat-to-beat variations of the APD, which were driven by the underlying Ca waves. Thus, changes in CaM can have a profound effect on the voltage time course of the cell.
The computational framework developed in this study can be applied to explore how the Markovian scheme describing an RyR2 subunit can influence cell wide arrhythmogenic activity. In particular, it is useful to evaluate the role of the second closed state, denoted as C2 in Eq. 13, on the system behavior. Thus, we have applied our computational model to determine the model predictions in the scenario where the RyR2 is governed only by the transitions from C1 to O (see Supporting materials and methods). In particular, eliminating C2 induces a leftward shift of the RyR2 open probability Po, along with an increase in the plateau open probability at high [Ca] (see Fig. S1 A). Interestingly, this change in Po only has a modest effect on the time course of a Ca spark (Fig. S1 B). However, we find that the mean time to a spontaneous Ca spark (Fig. S1 C) and the propagation velocity of a Ca wave (Document S1. Supporting materials and methods and Figs. S1 and S2, Document S2. Article plus supporting material D) are sensitive to the presence of the C2 state. This is because eliminating C2 makes the RyR2 more sensitive to changes in [Ca] and therefore makes the system more excitable. Thus, although the time course of the local Ca dynamics is insensitive to C2, features related to the excitability of an RyR2 cluster are highly sensitive to the presence of this state. However, it should be noted here that the shape of the nonlinear dependence of system properties on [CaM] is due primarily to the sigmoid dependence of PO on [Ca], which is due to the cooperative interactions between RyR2 subunits. Thus, although specific Markov states can modulate the quantitative features of the system, the nonlinear properties are fundamentally due to the effect of cooperativity.
Several studies have shown that mutations in CaM are associated with cardiac arrhythmias such as CPVT. In particular, Nishimura et al. (45) showed that a mutation at the CaMLD that led to excessively tight binding with the CaM binding site was associated with lethal arrhythmias in mice. These authors also showed that this mutation led to a higher frequency of Ca sparks and waves. In other studies, calcium dysregulation in Purkinje myocytes has been implicated as the source of arrhythmogenic activity in CPVT mouse models (46). However, the mechanism translating the cellular physiology to a whole-heart arrhythmia remains unclear. Our computational model suggests that the increased frequency of Ca waves induces slowed repolarization of the AP because of NCX, which raises the diastolic potential before the next action potential stimulus. This increase in diastolic potential, if large enough, can then induce conduction block of the next action potential stimulus. Indeed, we found in our previous study that during rapid pacing of 2D cardiac tissue, a planar wave can fractionate and form reentry via localized conduction block (31). The regions at which block occurred corresponded to those regions in tissue with a higher frequency of Ca waves and therefore a more pronounced increase of diastolic potential. Because Ca cycling in different regions of tissue evolves in a beat-to-beat manner and is unlikely to be synchronized, then conduction block will be spatially localized. When this occurs, wave break and reentry can ensue under the appropriate conditions. Here, we point out that this mechanism is distinct from DADs, which occur because of spontaneous Ca waves. Although these excitations occur and are potentially dangerous, the conditions for their relevance in cardiac arrhythmias are more stringent (47,48). This is because spontaneous Ca waves occur during the diastolic interval and require a long pause. Also, because these waves occur in a stochastic manner, the formation of a DAD in tissue requires a large population of cells to be synchronized (16,49). These conditions are restrictive, so DADs are unlikely to play a role during rapid pacing. Our work suggests an alternative viewpoint, in which defective CaM binding promotes localized conduction block, leading to wave break and reentry.
Author contributions
D.G. and Y.S. designed research, performed research, contributed analytic tools, analyzed data, and wrote the manuscript.
Footnotes
Editor: Eric Sobie.
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2021.02.016.
Supporting material
References
- 1.Gifford J.L., Walsh M.P., Vogel H.J. Structures and metal-ion-binding properties of the Ca2+-binding helix-loop-helix EF-hand motifs. Biochem. J. 2007;405:199–221. doi: 10.1042/BJ20070255. [DOI] [PubMed] [Google Scholar]
- 2.Wehrens X.H., Lehnart S.E., Marks A.R. Ca2+/calmodulin-dependent protein kinase II phosphorylation regulates the cardiac ryanodine receptor. Circ. Res. 2004;94:e61–e70. doi: 10.1161/01.RES.0000125626.33738.E2. [DOI] [PubMed] [Google Scholar]
- 3.Means A.R., VanBerkum M.F., Rasmussen C.D. Regulatory functions of calmodulin. Pharmacol. Ther. 1991;50:255–270. doi: 10.1016/0163-7258(91)90017-g. [DOI] [PubMed] [Google Scholar]
- 4.Meissner G., Henderson J.S. Rapid calcium release from cardiac sarcoplasmic reticulum vesicles is dependent on Ca2+ and is modulated by Mg2+, adenine nucleotide, and calmodulin. J. Biol. Chem. 1987;262:3065–3073. [PubMed] [Google Scholar]
- 5.Yamaguchi N., Xu L., Meissner G. Molecular basis of calmodulin binding to cardiac muscle Ca(2+) release channel (ryanodine receptor) J. Biol. Chem. 2003;278:23480–23486. doi: 10.1074/jbc.M301125200. [DOI] [PubMed] [Google Scholar]
- 6.Hamilton S.L., Serysheva I., Strasburg G.M. Calmodulin and excitation-contraction coupling. News Physiol. Sci. 2000;15:281–284. doi: 10.1152/physiologyonline.2000.15.6.281. [DOI] [PubMed] [Google Scholar]
- 7.Nyegaard M., Overgaard M.T., Børglum A.D. Mutations in calmodulin cause ventricular tachycardia and sudden cardiac death. Am. J. Hum. Genet. 2012;91:703–712. doi: 10.1016/j.ajhg.2012.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu X., Yano M., Matsuzaki M. Defective calmodulin binding to the cardiac ryanodine receptor plays a key role in CPVT-associated channel dysfunction. Biochem. Biophys. Res. Commun. 2010;394:660–666. doi: 10.1016/j.bbrc.2010.03.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Søndergaard M.T., Tian X., Overgaard M.T. Arrhythmogenic calmodulin mutations affect the activation and termination of cardiac ryanodine receptor-mediated Ca2+ release. J. Biol. Chem. 2015;290:26151–26162. doi: 10.1074/jbc.M115.676627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gomez-Hurtado N., Boczek N.J., Knollmann B.C. Novel CPVT-associated calmodulin mutation in CALM3 (CALM3–A103V) activates arrhythmogenic Ca waves and sparks. Circ. Arrhythm. Electrophysiol. 2016;9:e004161. doi: 10.1161/CIRCEP.116.004161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hwang H.S., Nitu F.R., Knollmann B.C. Divergent regulation of ryanodine receptor 2 calcium release channels by arrhythmogenic human calmodulin missense mutants. Circ. Res. 2014;114:1114–1124. doi: 10.1161/CIRCRESAHA.114.303391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang Y., Guo T., Bers D.M. Cardiac myocyte Z-line calmodulin is mainly RyR2-bound, and reduction is arrhythmogenic and occurs in heart failure. Circ. Res. 2014;114:295–306. doi: 10.1161/CIRCRESAHA.114.302857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Walweel K., Oo Y.W., Laver D.R. The emerging role of calmodulin regulation of RyR2 in controlling heart rhythm, the progression of heart failure and the antiarrhythmic action of dantrolene. Clin. Exp. Pharmacol. Physiol. 2017;44:135–142. doi: 10.1111/1440-1681.12669. [DOI] [PubMed] [Google Scholar]
- 14.Gangopadhyay J.P., Ikemoto N. Aberrant interaction of calmodulin with the ryanodine receptor develops hypertrophy in the neonatal cardiomyocyte. Biochem. J. 2011;438:379–387. doi: 10.1042/BJ20110203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vermeulen J.T., McGuire M.A., Janse M.J. Triggered activity and automaticity in ventricular trabeculae of failing human and rabbit hearts. Cardiovasc. Res. 1994;28:1547–1554. doi: 10.1093/cvr/28.10.1547. [DOI] [PubMed] [Google Scholar]
- 16.Colman M.A. Arrhythmia mechanisms and spontaneous calcium release: Bi-directional coupling between re-entrant and focal excitation. PLoS Comput. Biol. 2019;15:e1007260. doi: 10.1371/journal.pcbi.1007260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Peng W., Shen H., Yan N. Structural basis for the gating mechanism of the type 2 ryanodine receptor RyR2. Science. 2016;354:aah5324. doi: 10.1126/science.aah5324. [DOI] [PubMed] [Google Scholar]
- 18.Santulli G., Lewis D., Frank J. Ryanodine receptor structure and function in health and disease. In: Boekema E.J., Harris J.R., editors. Membrane Protein Complexes: Structure and Function. Springer; 2018. pp. 329–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zalk R., Clarke O.B., Marks A.R. Structure of a mammalian ryanodine receptor. Nature. 2015;517:44–49. doi: 10.1038/nature13950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maximciuc A.A., Putkey J.A., Mackenzie K.R. Complex of calmodulin with a ryanodine receptor target reveals a novel, flexible binding mode. Structure. 2006;14:1547–1556. doi: 10.1016/j.str.2006.08.011. [DOI] [PubMed] [Google Scholar]
- 21.Gong D., Chi X., Yan N. Modulation of cardiac ryanodine receptor 2 by calmodulin. Nature. 2019;572:347–351. doi: 10.1038/s41586-019-1377-y. [DOI] [PubMed] [Google Scholar]
- 22.Xiong L., Zhang J.-Z., Hamilton S.L. A Ca2+-binding domain in RyR1 that interacts with the calmodulin binding site and modulates channel activity. Biophys. J. 2006;90:173–182. doi: 10.1529/biophysj.105.066092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gangopadhyay J.P., Ikemoto N. Interaction of the Lys(3614)-Asn(3643) calmodulin-binding domain with the Cys(4114)-Asn(4142) region of the type 1 ryanodine receptor is involved in the mechanism of Ca2+/agonist-induced channel activation. Biochem. J. 2008;411:415–423. doi: 10.1042/BJ20071375. [DOI] [PubMed] [Google Scholar]
- 24.Zahradníková A., Zahradník I., Györke S. Rapid activation of the cardiac ryanodine receptor by submillisecond calcium stimuli. J. Gen. Physiol. 1999;114:787–798. doi: 10.1085/jgp.114.6.787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mukherjee S., Thomas N.L., Williams A.J. A mechanistic description of gating of the human cardiac ryanodine receptor in a regulated minimal environment. J. Gen. Physiol. 2012;140:139–158. doi: 10.1085/jgp.201110706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Terentyev D., Viatchenko-Karpinski S., Györke S. Luminal Ca2+ controls termination and refractory behavior of Ca2+-induced Ca2+ release in cardiac myocytes. Circ. Res. 2002;91:414–420. doi: 10.1161/01.res.0000032490.04207.bd. [DOI] [PubMed] [Google Scholar]
- 27.Gyorke S., Gyorke I., Wiesner T.F. Regulation of sarcoplasmic reticulum calcium release by luminal calcium in cardiac muscle. Front Biosci. 2002;7:d1454–d1463. doi: 10.2741/A852. [DOI] [PubMed] [Google Scholar]
- 28.Duke T.A., Le Novère N., Bray D. Conformational spread in a ring of proteins: a stochastic approach to allostery. J. Mol. Biol. 2001;308:541–553. doi: 10.1006/jmbi.2001.4610. [DOI] [PubMed] [Google Scholar]
- 29.Xu L., Meissner G. Mechanism of calmodulin inhibition of cardiac sarcoplasmic reticulum Ca2+ release channel (ryanodine receptor) Biophys. J. 2004;86:797–804. doi: 10.1016/S0006-3495(04)74155-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Restrepo J.G., Weiss J.N., Karma A. Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys. J. 2008;95:3767–3789. doi: 10.1529/biophysj.108.130419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shiferaw Y., Aistrup G.L., Wasserstrom J.A. Remodeling promotes proarrhythmic disruption of calcium homeostasis in failing atrial myocytes. Biophys. J. 2020;118:476–491. doi: 10.1016/j.bpj.2019.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Shiferaw Y., Aistrup G.L., Wasserstrom J.A. Synchronization of triggered waves in atrial tissue. Biophys. J. 2018;115:1130–1141. doi: 10.1016/j.bpj.2018.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Györke I., Györke S. Regulation of the cardiac ryanodine receptor channel by luminal Ca2+ involves luminal Ca2+ sensing sites. Biophys. J. 1998;75:2801–2810. doi: 10.1016/S0006-3495(98)77723-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sobie E.A., Dilly K.W., Jafri M.S. Termination of cardiac Ca(2+) sparks: an investigative mathematical model of calcium-induced calcium release. Biophys. J. 2002;83:59–78. doi: 10.1016/s0006-3495(02)75149-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cheng H., Lederer W.J. Calcium sparks. Physiol. Rev. 2008;88:1491–1545. doi: 10.1152/physrev.00030.2007. [DOI] [PubMed] [Google Scholar]
- 36.Grandi E., Pandit S.V., Bers D.M. Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 2011;109:1055–1066. doi: 10.1161/CIRCRESAHA.111.253955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.des Georges A., Clarke O.B., Frank J. Structural basis for gating and activation of RyR1. Cell. 2016;167:145–157.e17. doi: 10.1016/j.cell.2016.08.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Eisner D., Bode E., Trafford A. Calcium flux balance in the heart. J. Mol. Cell. Cardiol. 2013;58:110–117. doi: 10.1016/j.yjmcc.2012.11.017. [DOI] [PubMed] [Google Scholar]
- 39.Eisner D.A., Choi H.S., Trafford A.W. Integrative analysis of calcium cycling in cardiac muscle. Circ. Res. 2000;87:1087–1094. doi: 10.1161/01.res.87.12.1087. [DOI] [PubMed] [Google Scholar]
- 40.Lyon A.R., Bannister M.L., Harding S.E. SERCA2a gene transfer decreases sarcoplasmic reticulum calcium leak and reduces ventricular arrhythmias in a model of chronic heart failure. Circ. Arrhythm. Electrophysiol. 2011;4:362–372. doi: 10.1161/CIRCEP.110.961615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Song Z., Liu M.B., Qu Z. Transverse tubular network structures in the genesis of intracellular calcium alternans and triggered activity in cardiac cells. J. Mol. Cell. Cardiol. 2018;114:288–299. doi: 10.1016/j.yjmcc.2017.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Trafford A.W., Clarke J.D., Dibb K.M. Calcium signalling microdomains and the t-tubular system in atrial mycoytes: potential roles in cardiac disease and arrhythmias. Cardiovasc. Res. 2013;98:192–203. doi: 10.1093/cvr/cvt018. [DOI] [PubMed] [Google Scholar]
- 43.Di Maio A., Ter Keurs H.E., Franzini-Armstrong C. T-tubule profiles in Purkinje fibres of mammalian myocardium. J. Muscle Res. Cell Motil. 2007;28:115–121. doi: 10.1007/s10974-007-9109-6. [DOI] [PubMed] [Google Scholar]
- 44.Wei S., Guo A., Song L.-S. T-tubule remodeling during transition from hypertrophy to heart failure. Circ. Res. 2010;107:520–531. doi: 10.1161/CIRCRESAHA.109.212324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nishimura S., Yamamoto T., Kato T. Mutation-linked, excessively tight interaction between the calmodulin binding domain and the C-terminal domain of the cardiac ryanodine receptor as a novel cause of catecholaminergic polymorphic ventricular tachycardia. Heart Rhythm. 2018;15:905–914. doi: 10.1016/j.hrthm.2018.02.006. [DOI] [PubMed] [Google Scholar]
- 46.Herron T.J., Milstein M.L., Jalife J. Purkinje cell calcium dysregulation is the cellular mechanism that underlies catecholaminergic polymorphic ventricular tachycardia. Heart Rhythm. 2010;7:1122–1128. doi: 10.1016/j.hrthm.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen W., Asfaw M., Shiferaw Y. The statistics of calcium-mediated focal excitations on a one-dimensional cable. Biophys. J. 2012;102:461–471. doi: 10.1016/j.bpj.2011.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Xie Y., Sato D., Weiss J.N. So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophys. J. 2010;99:1408–1415. doi: 10.1016/j.bpj.2010.06.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wasserstrom J.A., Shiferaw Y., Aistrup G.L. Variability in timing of spontaneous calcium release in the intact rat heart is determined by the time course of sarcoplasmic reticulum calcium load. Circ. Res. 2010;107:1117–1126. doi: 10.1161/CIRCRESAHA.110.229294. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.